Carbonate system distribution, anthropogenic carbon and acidification in the western tropical South Pacific (OUTPACE 2015 transect)

The western tropical South Pacific was sampled along a longitudinal 4000 km transect (OUTPACE cruise, 18 February, 3 April 2015) for the measurement of carbonate parameters (total alkalinity and total inorganic carbon) between the Melanesian Archipelago (MA) and the western part of the South Pacific gyre (WGY). This paper reports this new dataset and derived properties: pH on the total scale (pH_T) and the CaCO₃ saturation state with respect to aragonite (Ω_ara). We also estimate anthropogenic carbon (C_ANT) distribution in the water column using the TrOCA method (Tracer combining Oxygen, inorganic Carbon and total Alkalinity). Along the OUTPACE transect a deeper penetration of C_ANT in the intermediate waters was observed in the MA, whereas highest C_ANT concentrations were detected in the subsurface waters of the WGY. By combining our OUTPACE dataset with data available in GLODAPv2 (1974–2009), temporal changes in oceanic inorganic carbon were evaluated. An increase of 1.3 to 1.6 µmol kg⁻¹ a⁻¹ for total inorganic carbon in the upper thermocline waters is estimated, whereas C_ANT increases by 1.1 to 1.2 µmol kg⁻¹ a⁻¹. In the MA intermediate waters (27 kg m⁻³ $<{\mathit{\sigma }}_{\mathit{\theta }}<\mathrm{27.2}$ kg m⁻³) an increase of 0.4 µmol kg⁻¹ a⁻¹ C_ANT is detected. Our results suggest a clear progression of ocean acidification in the western tropical South Pacific with a decrease in the oceanic pH_T of up to −0.0027 a⁻¹ and a shoaling of the saturation depth for aragonite of up to 200 m since the pre-industrial period.

1 Introduction

Human activities inject about 10 petagrams of carbon per year into the atmosphere, which might have major consequences on climate. It is recognized that the ocean plays a key role in the control of atmospheric CO₂ through uptake by the so-called “oceanic carbon pump”. Through this “pump”, the ocean sequesters ca. 25 % of the CO₂ injected annually into the atmosphere by human activities (Le Quéré et al., 2018). A consequence of the ocean carbon uptake is a decrease in the oceanic pH (Feely et al., 2004), which is described as ocean acidification (the so-called “other” CO₂ problem). Effects of ocean acidification have been observed in marine organisms and could affect the marine ecosystems (Riebesell et al., 2000). Improving our understanding of the oceanic CO₂ uptake relies primarily on observations of the marine carbonate cycle. Studies on the oceanic carbonate cycle have been mostly conducted in the framework of international programs. The World Ocean Circulation Experiment (WOCE) and the Joint Global Flux Study (JGOFS) in the 1990s coordinated oceanographic cruises along large sections in the ocean to collect samples through the water column and to perform accurate measurements of carbonate parameters and ancillary parameters (temperature, salinity, dissolved oxygen, nutrients, etc.). Since 2000, efforts have been made to revisit oceanic sections according to the WOCE strategy in order to assess oceanic changes at the scale of a decade. These programs have generated important databases for oceanic carbonate chemistry (e.g., GLODAPv2, Olsen et al., 2016; Key et al., 2015).

In order to better assess the role of the ocean for the global carbon cycle, the concept of oceanic anthropogenic carbon (C_ANT) has been introduced and refers to the fraction of dissolved inorganic carbon (C_T) in the ocean that originates from carbon injected into the atmosphere by human activities since the industrial revolution. As C_ANT is not a directly measurable quantity, it can only be estimated through assumptions that are subject to intense scientific debate (Sabine and Tanhua, 2010). In particular, it has been recently recognized that ocean circulation changes drive significant variability in carbon uptake (DeVries et al., 2017). Detecting, separating and attributing decadal changes in the carbonate system (C_T and total alkalinity, A_T), C_ANT and pH in the ocean at global or regional scales remains challenging.

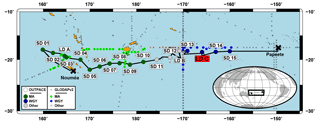
Figure 1 Map of the OUTPACE cruise transect. Melanesian Archipelago (MA) stations are indicated by large dark green large dots and the western gyre (WGY) stations by large dark blue dots. Stations outside of these two areas are in gray. The station in red corresponds to the station where the deep cast and intercomparison cast were made. Stations from the GLODAPv2 database are indicated with small crosses: small green dots correspond to GLODAPv2 stations considered for comparison in the MA area; small blue dots correspond to GLODAPv2 stations considered for comparison in the WGY area and small gray dots are the other GLODAPv2 stations considered for comparison.

Within this context, the Pacific Ocean is a particularly challenging area to study due to its size (ca. one-third of the Earth's and one half of the oceanic surface). Even if, due to its remoteness from land, it remains largely underexplored by oceanographic vessels compared to other oceanic areas, the Pacific Ocean has been covered by cruises along long sections (the “P sections” from the WOCE program). Most of these sections have been revisited during the last years (e.g., Sabine et al., 2008; Kouketsu et al., 2013). In a recent study based on repeated sections in the Pacific (P16 at 150^∘ W), Carter et al. (2017) observed a significant increase in C_ANT in the top 500 m around 10–30^∘ S and a local carbon storage maximum around 20^∘ S in recent years (between 2005 and 2014). In this context, the OUTPACE data presented in this study, associated with historical observations (since the pioneer 1974 GEOSECS, Geochemical Ocean Sections Program) offer a new view to evaluate variability and decadal changes in C_T, C_ANT and pH_T in the tropical Pacific, here focusing on the western tropical South Pacific (WTSP).

The aim of this paper is to report a new dataset of oceanic inorganic carbon (based on measurements of C_T and A_T) acquired in the WTSP during the OUTPACE (Oligotrophic to UltTra oligotrophic PACific Experiment) cruise performed in 2015 (Moutin et al., 2017). The main focus of the OUTPACE cruise was to study the complex interactions between planktonic organisms and the cycle of biogenic elements on different scales, motivated by the fact that the WTSP has been identified as a hot spot of N₂ fixation (Bonnet et al., 2017). The data presented here have been partially used in another paper of this special issue (Moutin et al., 2018) in order to study the biological carbon pump in the upper (surface to 200 m) water column. In this paper we will explore the carbonate data between the surface and 2000 m depth. The OUTPACE transect (Fig. 1) is close to existing WOCE and GO-SHIP (Global Ocean Ship-based Hydrographic Investigations Program) lines in the South Pacific: it is parallel to the zonal P21 line (18^∘ S visited in 1994 and 2009) and the P06 line (32^∘ S visited in 1992, 2003 and 2010), it is crossed by the meridional P14 line (180^∘ E visited in 1994 and 2007) and P15 line (170^∘ W visited in 2001, 2009 and 2016), and it is situated at the eastern side of the P16 line (150^∘ W visited in 1992, 2005 and 2014). However, the OUTPACE transect does not correspond to any earlier occupation of the “WOCE lines” in the South Pacific and no tracers of water mass age were measured during the cruise, which limits the possibilities of a robust analysis of C_ANT accumulation in the area. Moreover, the horizontal and vertical resolution of the OUTPACE dataset is low. In consequence, the OUTPACE dataset cannot be used to look at decadal changes in C_ANT content in the South Pacific (e.g., Carter et al., 2017; Kouketsu et al., 2013). Here, C_ANT estimates based on the TrOCA (Tracer combining Oxygen, inorganic Carbon and total Alkalinity) method will be used as as a tool to investigate changes in C_T. Moreover, comparing our data with the high-quality data (internally consistent through a secondary quality control; Olsen et al., 2016) available in the Global Ocean Data analysis Project version 2 (GLODAPv2 database) will allow us to evaluate C_T, A_T, C_ANT (from TrOCA) and pH_T trends in subsurface waters and at depth.

Table 1 General description of the casts sampled for carbonate chemistry parameters during the OUTPACE cruise.

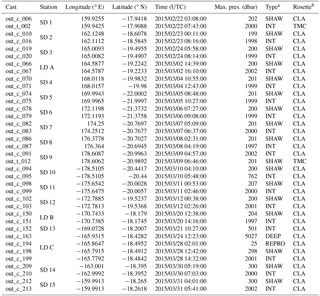
^a SHAW stands for casts up to 200 dbar, INT stands for casts up to 2000 dbar, DEEP stands for the deep cast and REPRO stands for the cast with reproducibility measurements. ^b A CTD was rosette used for the cast. CLA is the normal CTD rosette, and TMC is the trace metal clean rosette (see Sect. 2.1).

The paper is organized as follows: after describing the methods used to acquire the dataset and the way the auxiliary data have been used in Sect. 2, we briefly present the hydrographic context of the cruise in Sect. 3. We then present in Sect. 4, the carbonate dataset acquired during the cruise. In Sect. 5, estimated C_ANT values in the water column are presented, the validity of these estimates based on the TrOCA method is discussed and geographical patterns are evoked. In Sect. 6, the temporal changes in oceanic inorganic carbon in the WTSP combining data available in GLODAPv2 and our OUTPACE dataset are presented and discussed. Finally, in Sect. 7, some features in relation to ocean acidification are inferred from our dataset.

2 Material and methods

2.1 Cruise and sampling strategy

The OUTPACE cruise took place between 18 February and 3 April 2015 from Nouméa (New Caledonia) to Papeete (French Polynesia), in the WTSP on board the French research vessel L'Atalante (Fig. 1). A total of 18 stations were sampled, mostly in the top 2000 m of the water column along a ∼4000 km transect from Melanesia to the South Pacific gyre (Moutin et al., 2017). A conductivity–temperature–depth (CTD) rosette was deployed to acquire data with CTD and associated sensors along vertical profiles and to collect discrete seawater samples from twenty-four 12 L Niskin bottles for chemical analysis. Due to technical failures on the main CTD rosette, for two of the casts considered in this study, a trace metal clean CTD rosette (TM-R) equipped with 24 teflon-lined GO-FLO bottles devoted to trace metal analyses was used. The configurations of both CTD rosettes are detailed elsewhere (Moutin et al., 2017).

For carbonate parameters, seawater was sampled from 37 casts over the 18 stations. At each station, on a regular basis, samples were collected at 12 depths between the surface and 2000 m on two distinct casts: six samples on a 0–200 m cast and six samples on a 0–2000 m cast. At station SD 13, only one cast was sampled down to 500 m depth. In addition, at station LD C, samples were collected at 24 depths on a deep cast (down to 5000 m) and 12 samples were collected at the same depth (25 m) on a “repeatability” cast. Details on the casts performed for this study are summarized in Table 1.

2.2 Chemical measurements on discrete samples

All samples were collected within less than 1 h after arrival of the CTD rosette on deck.

2.2.1 Total alkalinity and dissolved inorganic carbon

Samples for A_T and C_T were collected in one 500 mL borosilicate glass flask (Schott Duran^®) and poisoned with HgCl₂ immediately after collection (final concentration 20 mg L⁻¹). Samples were stored at 4 ^∘C during transport and were analyzed (within 10 days of each other) 5 months after the end of the cruise at the SNAPO-CO₂ (Service National d'Analyse des paramètres Océaniques du CO₂ – LOCEAN – Paris). A_T and C_T were measured on the same sample based on a potentiometric titration in a closed cell (Edmond, 1970). A nonlinear curve fitting approach was used to estimate A_T and C_T from the recorded titration data (Dickson, 1981; Dickson and Goyet, 1994). Measurements were calibrated with certified reference material (CRM) provided by Andrew Dickson, University of Southern California (batch 139 – C_T: 2023.23±0.70 µmol kg⁻¹ and A_T: 2250.82±0.60 µmol kg⁻¹; see Dickson, 2010). The reproducibility, expressed as the standard deviation of the CRM analysis (n=15), was 4.6 µmol kg⁻¹ for A_T and 4.7 µmol kg⁻¹ for C_T. Based on replicate measurements at station LD C (cast out_c_194; see Table 1), the reproducibility, expressed as the standard deviation of the analysis of the replicates collected at the same depth (ca. 25 m, n=12) from different Niskin bottles, was 3.6 µmol kg⁻¹ for A_T (average value:2324.7 µmol kg⁻¹) and 3.7 µmol kg⁻¹ for C_T (average value:1969.7 µmol kg⁻¹).

2.2.2 Oxygen concentration

Dissolved oxygen concentration [O₂] was measured following the Winkler method (Winkler, 1888) with potentiometric endpoint detection (Oudot et al., 1988). For sampling, reagent preparation and analysis, the recommendations from Langdon (2010) were carefully followed. The thiosulfate solution was calibrated by titrating it against a potassium iodate certified standard solution of 0.0100 N (CSK standard solution – WAKO^™). The reproducibility, expressed as the standard deviation of replicates samples was 0.8 µmol kg⁻¹ (n=15; average value:195.4 µmol kg⁻¹).

2.3 Vertical profiles of hydrological and biogeochemical parameters

2.3.1 CTD measurements

CTD measurements were ensured by a Seabird^™ 911+ underwater unit, which interfaced an internal pressure sensor, two redundant external temperature probes (SBE3plus) and two redundant external conductivity cells (SBE4C). The sensors were calibrated pre- and post-cruise by the manufacturer. No significant drift between the redundant sensors was observed. For vertical profiles, full-resolution data (24 Hz) were reduced to 1 dbar binned vertical profiles on the downcast with a suite of processing modules using the Seabird^™ dedicated software (SbeDataProcessing). For values at the closure of the Niskin bottles, values collected at 24 Hz were averaged 3 s before and 5 s after closure of the bottle. In this study, for temperature and conductivity the signal of the first sensors has been used systematically. For the two TM-R casts, no significant difference with the main CTD rosette on temperature and conductivity was observed.

2.3.2 Oxygen measurements

[O₂] was also measured with a SBE43 electrochemical sensor interfaced with the CTD unit. The raw voltage was converted to oxygen concentration with 13 calibration coefficients based on the Seabird^™ methodology derived from Owens and Millard (1985). Three of these coefficients (the oxygen signal slope, the voltage at zero oxygen signal, the pressure correction factor) were adjusted with the concentrations estimated with the Winkler method on samples collected at the closure of the bottles. One unique set of calibration coefficients has been applied to all oxygen profiles from the cruise because no significant drift of the sensor was observed during the time of the cruise. For the two TM-R casts, values have been corrected with a drift and offset based on the comparison of 15 pairs of casts (main CTD rosette/TM-R) collected close in time (less than 2 h) and space (less than 1 nautical mile) over the entire OUTPACE transect.

2.4 Derived parameters

Practical salinity (S_P) was derived from conductivity, temperature and pressure with the EPS-78 algorithm. Absolute salinity (S_A), potential temperature (θ), conservative temperature (Θ) and potential density (σ_θ) were derived from S_P, temperature, pressure and the geographic position with the TEOS-10 algorithms (Valladares et al., 2011). These five derived parameters were calculated within the processing with Seabird^™  dedicated software.

Seawater pH on the total scale (pH_T) and the CaCO₃ saturation state with respect to aragonite (Ω_ara) were derived from A_T and C_T with the “Seacarb” R package (Gattuso and Lavigne, 2009). CaCO₃ saturation state with respect to calcite was not considered because seawater up to 2000 dbar was supersaturated with respect to calcite (Ω_cal>1). Following the recommendations from Dickson et al. (2007), the constants for carbonic acid K₁ and K₂ from Lueker et al. (2000), the constant for hydrogen fluoride K_F from Pérez and Fraga (1987), and the constant for hydrogen sulfate K_S from Dickson (1990) were used. Orthophosphate and silicate concentration were considered in the calculation. Methods for nutrient measurement are presented in detail in Fumenia et al. (2018). When nutrient data were not available (station SD 8), silicate and orthophosphate were estimated from the nutrient profile measured on cast out_c_163 (interpolated values). Apparent oxygen utilization (AOU) was computed from the difference between oxygen solubility (at p=0 dbar, and S_P) estimated with the “Benson and Krause coefficients” in Garcia and Gordon (1992) and in situ [O₂].

For the estimation of C_ANT, the TrOCA method was used. The TrOCA approach was first proposed in Touratier and Goyet (2004a, b) with improvements in Touratier et al. (2007). In brief, the TrOCA parameter is defined as a combination of A_T, C_T and [O₂] that accounts for biologically induced relative changes among these parameters (with constant stoichiometric ratios). TrOCA is thus a quasi-conservative tracer derived from C_T in the ocean. Within a defined water mass, changes in TrOCA over time are independent of biology and can be attributed to the penetration of C_ANT. In consequence C_ANT can be calculated in a parcel of water from the difference between current and pre-industrial TrOCA (TrOCA^∘) divided by a stoichiometric coefficient. The simplicity of the TrOCA method relies on the fact that a simple formulation for TROCA^∘ has been proposed based on potential temperature and alkalinity and thus an estimation of C_ANT can be done by a simple calculation using C_T, A_T, [O₂] and θ. In this study, the formulation proposed in Eq. (11) in Touratier et al. (2007) is used to calculate C_ANT and is recalled here in Eq. (1).

$$\begin{array}{ll}{\displaystyle }{C}_{\mathrm{ANT}}& {\displaystyle }=\left(\right[{\mathrm{O}}_{\mathrm{2}}]+\mathrm{1.279}\left(C_{\mathrm{T}}-{\displaystyle \frac{A_{\mathrm{T}}}{\mathrm{2}}}\right)-\exp (\mathrm{7.511}\\ \text{(1)}& {\displaystyle }& {\displaystyle }-\mathrm{1.087}\times {\mathrm{10}}^{-\mathrm{2}}\mathit{\theta }-{\displaystyle \frac{\mathrm{7.81}\times {\mathrm{10}}^{-\mathrm{5}}}{A_{\mathrm{T}}^{\mathrm{2}}}}\left)\right)/\mathrm{1.279}\end{array}$$

This formulation is based on an adjustment of the TrOCA coefficients using Δ¹⁴C and CFC-11 from the GLODAPv1 database (Key et al., 2004). Touratier et al. (2007) estimated the overall uncertainty of the C_ANT with TrOCA method to be ca. 6 µmol kg⁻¹ based on the random propagation of the uncertainties in the variables (C_T, A_T, [O₂] and θ) and coefficients used in Eq. (1). The limitations and validity of the TrOCA method will be discussed in detail in Sect. 5.

2.5 Data from available databases

For comparison with existing values of carbonate chemistry in the area of the OUTPACE cruise, relevant data were extracted from GLODAPv2 database (NDP-93 – Olsen et al., 2016; Key et al., 2015). The specific data file for the Pacific Ocean was used (downloaded from https://www.nodc.noaa.gov/ocads/oceans/GLODAPv2/, last access: 14 December 2017). For comparison with OUTPACE data, GLODAPv2 data were selected between 22 and 17^∘ S and between 159^∘ E and 159^∘ W (going westwards). For specific comparisons in the MA and the South Pacific western gyre waters (WGY) a zonal subset of the extracted data was used: 159^∘ E and 178^∘ W for MA and 170 to 159^∘ W for WGY (see Fig. 1).

3 Hydrological context along the OUTPACE transect

The hydrological context encountered during the OUTPACE transect is presented with a Θ−S_A diagram between 0 and 2000 dbar in Fig. 2. A detailed description of the water masses encountered during the OUTPACE cruise can be found in Fumenia et al. (2018). Briefly, from the surface to 2000 dbar, the following features are distinguished: the surface waters (σ_θ<23.5 kg m⁻³) were characterized by temperatures over 25 ^∘C with increasing temperature and salinity towards the east and AOU close to zero. Under the surface water, the upper thermocline waters (UTW) presented a maximum in salinity, reaching values higher than 36 g kg⁻¹ in the eastern part of the cruise. In the lower thermocline waters, S_A decreased with depth with a more pronounced decrease in the eastern part than in the western part, whereas AOU is higher in the eastern part than in the western part of the studied area. These differences in lower thermocline waters have been described for South Pacific Central Waters (SPCW) with more saline western (WSPCW) and less saline eastern (ESPCW) waters (Tomczak and Godfrey, 2003). Below the thermocline, intermediate waters are made up of Subantarctic Mode Waters (SAMW) and Antarctic Intermediate Waters (AAIWs). AAIWs have a salinity minimum close to the σ_θ=27 kg m⁻³ isopycnal. Hartin et al. (2011) defines SAMW as having σ_θ values between 26.80 and 27.06 kg m⁻³, corresponding to a minimum in potential vorticity, and AAIW as having σ_θ values between 27.06 and 27.40 kg m⁻³. The separation of both waters is not trivial in the subtropical area. SAMW is generally associated with lower AOU than AAIW. Finally, deep waters made up of Upper Circumpolar Deep Waters (UCDW) correspond to an increase in salinity and AOU for depth corresponding to σ_θ>27.4 kg m⁻³.

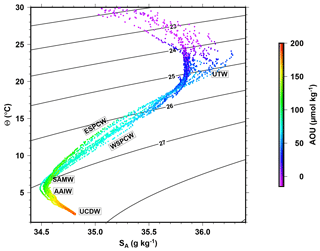
Figure 2 Θ−S_A diagram with colors indicating the AOU. Black contour lines represent the isopycnal horizons based on potential density referenced to a pressure of 0 dbar (σ_θ).

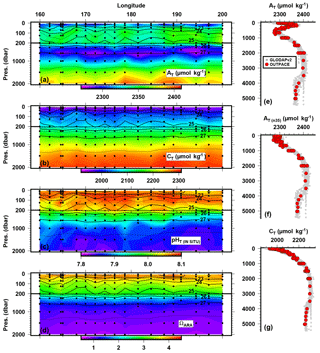
Figure 3 Longitudinal variations in (a) A_T, (b) C_T, (c) pH_T and (d) Ω_ara along the OUTPACE transect between the surface and 2000 dbar depth. Black contour lines represent the isopycnal horizons based on potential density referenced to a pressure of 0 dbar. Vertical profiles of (e) A_T, (f) A_T n35 and (g) C_T of the entire OUTPACE dataset (red dots) superimposed on the GLODAPv2 data corresponding to the OUTPACE area (gray dots).

In this study, discussion will sometimes make a distinction between two subregions along the OUTPACE transect: MA and WGY (see Sect. 2.5 for definition). This distinction is mainly based on geographic and oceanographic arguments. Indeed, these two subregions are geographically separated by the Tonga volcanic arc. WGY is characterized by higher surface temperature and a higher salinity in the upper thermocline waters than MA. The difference between these subregions is evidenced by the difference in oligotrophy (Moutin et al., 2018). Due to specific conditions in the transition area between the MA and WGY (de Verneil et al., 2017), SD 11, SD 12 and LD B were discarded from both groups in this study following the arguments in Moutin et al. (2018).

4 Carbonate chemistry along the OUTPACE transect

A_T and C_T measured along the OUTPACE transect are presented in Fig. 3a and b. All vertical profiles for A_T, A_T normalized to S_A=35 g kg⁻¹ (A_T n35) and C_T are presented in Fig. 3e, f and g. A_T ranged between 2300 and 2400 µmol kg⁻¹. Below the surface, a pronounced maximum in A_T was observed associated with the saltier upper thermocline waters. When normalized to S_A=35 g kg⁻¹, A_T n35 values are remarkably constant in the upper 500 dbar with values between 2270 and 2310 µmol kg⁻¹. Below 500 dbar, A_T increases with depth up to ca. 2400 µmol kg⁻¹ indicating that alkalinity changes are mostly due to salinity changes in the upper water column, whereas the increase in the deep waters is mainly due to carbonate biomineral remineralization. C_T values are close to 1950 µmol kg⁻¹ in the surface and increase with depth up to 2300 µmol kg⁻¹ at 2000 dbar. The C_T gradient in the upper water column has been described in Moutin et al. (2018). Below 2000 dbar, C_T is relatively invariant with slightly lower values in the bottom waters (below 4000 dbar) due to the presence of very old deep waters originating from the North Pacific relative to the northward moving bottom waters that have not accumulated as much carbon (Murata et al., 2007). A_T and C_T values in deep waters measured during OUTPACE are in good agreement with the data of the GLODAPv2 database (Fig. 3e, f and g). No systematic adjustment of the OUTPACE dataset with the GLODAPv2 dataset was performed because only very few data are available in the deep ocean where crossover comparison can be performed for cruises carried out in different decades. Nevertheless, for the only “deep” cast performed during OUTPACE (out_c_163 at station LD C), we performed a simple crossover analysis with the station 189 (located at 107 km kilometers from OUTPACE station LD C) of the Japanese “P21 revisited” cruise in 2009. We compared interpolated profiles on density surfaces values (27.75 kg m⁻³ $<{\mathit{\sigma }}_{\mathit{\theta }}<\mathrm{27.83}$ kg m⁻¹ corresponding to pressure levels of ca. 3000 to 5500 dbar). The estimated offsets are $-\mathrm{2.0}\pm \mathrm{4.2}$ µmol kg⁻¹ for A_T and $-\mathrm{2.0}\pm \mathrm{4.4}$ µmol kg⁻¹ for C_T suggesting measurement biases are likely no larger. This simple quality control procedure seems to indicate that no systematic adjustment is needed.

Derived parameters from the A_T and C_T measurements are presented in Fig. 3c for pH_T values (estimated at in situ temperature and pressure). pH_T decreases from values close to 8.06 in surface to values close to 7.84 at 2000 m. Surface values of pH_T are typical of subtropical warm waters and are in a similar range as the austral summer values estimated by Takahashi et al. (2014) in this area (8.06–8.08). Figure 3d represents the vertical distribution of computed values of Ω_ara along the OUTPACE transect. Seawater is supersaturated with respect to aragonite (Ω_ara>1) at the surface with Ω_ara values of ca. 4.0 again in good agreement with the austral summer values of 4–4.4 estimated by Takahashi et al. (2014) in this area. Values of Ω_ara decrease with depth, and seawater becomes undersaturated with respect to aragonite (Ω_ara<1) at an horizon situated below 1000 dbar in the west and above 1000 dbar in the eastern part of the cruise, with a general shoaling of the Ω_ara values from west to east, in good agreement with a previous study by Murata et al. (2015) in this area.

5 Anthropogenic carbon estimation along the OUTPACE transect

The TrOCA method is a way to quantify C_ANT in the ocean based on C_T, A_T, [O₂] and θ. This method has been used and compared to other methods in different oceanic areas (e.g., Lo Monaco et al., 2005; Álvarez et al., 2009; Vázquez-Rodríguez et al., 2009). Based on specific C_ANT inventories in the water column, the TrOCA method reasonably agreed with the other methods (including the transient tracer-based method). However, Yool et al. (2010) “tested” the TrOCA method within an ocean general circulation model and argued that the use of globally uniform parameterization for the estimation of the pre-industrial TrOCA is a source of significant overestimation but also that even with regionally “tuned” parameters a global positive bias in the method exists. As no tracers of water mass age were measured during the OUTPACE cruise, the main motivation for using the TrOCA method was to make C_ANT estimations based on a simple calculation from parameters acquired within the cruise as done in other cruises conducted in tropical South Pacific waters (e.g., Azouzi et al., 2009; Ganachaud et al., 2017). Even if C_ANT estimates from TrOCA are biased, the application of a simple back-calculation method that accounts for biologically induced relative changes in C_T is used here to identify some spatial features in the distribution of the carbonate system along the OUTPACE transect. Here, an error in the TrOCA C_ANT estimates of 67 % will be considered based on the standard deviation for the TrOCA variant optimized with world ocean data and normalized such that standard deviation in the simulated C_ANT in the ocean general circulation model is exactly 1 (see Table 2 in Yool et al., 2010).

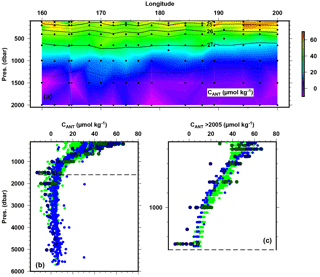
Figure 4 Longitudinal variations in C_ANT (estimated with the TrOCA method) along the OUTPACE transect between 100 and 2000 dbar depth (a). Black contour lines represents the isopycnal horizons based on potential density referenced to a pressure of 0 dbar. Vertical profiles of C_ANT for the entire OUTPACE dataset superimposed on the values estimated from the GLODAPv2 data (b) and vertical profiles of C_ANT between 100 and 1500 dbar superimposed on the values estimated from the recent (after 2005) GLODAPv2 data (c). The color code for the dots is the same as for Fig. 1.

As mentioned by Touratier et al. (2007), C_ANT estimates cannot be considered within the mixed layer because the underlying hypotheses used in the formulation of TrOCA may not be verified due to biological activity and gas transfers across the air–sea interface. To avoid this issue, C_ANT estimates are generally used below the “permanent” mixed layer depth (e.g., Álvarez et al., 2009; Carter et al., 2017). For the OUTPACE area, Moutin et al. (2018) show that the mixed layer depth does not exceed 70 m in the area. Even if the depths of the deep chlorophyll maximum were encountered below 100 dbar along the transect, we will consider C_ANT values up to 100 dbar. It can be mentioned that the C_ANT values of 50–60 µmol kg⁻¹ in the top of the water column (100 dbar) are in reasonable agreement with a rough estimate of thermodynamically consistent C_T changes: by assuming that CO₂ in surface seawater is in equilibrium with the atmosphere, we estimated that with a partial pressure of CO₂ (pCO₂) of 280 µatm in the pre-industrial period, a pCO₂ of 380 µatm during OUTPACE (Moutin et al., 2018) and a constant A_T over time of 2300 µmol kg⁻¹, C_T change in surface waters between the pre-industrial period and 2015 is ca. 65 µmol kg⁻¹ for a temperature of surface waters between 25 and 28 ^∘C. For OUTPACE, C_ANT estimates below 1000 dbar were not significantly different from 0 µmol kg⁻¹, with a standard deviation of 6.3 µmol kg⁻¹.

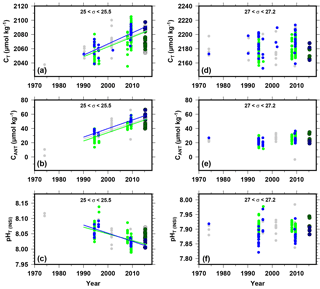
Figure 5 Temporal evolution in the OUTPACE area of C_T (a, d), C_ANT (b, e) and pH_Tinsi (c, f) based on GLODAPv2 and OUTPACE data along two isopycnal layers: 25–25.5 kg m⁻³ (a, b, c) and 27–27.2 kg m⁻³ (d, e, f). The color code for the dots is the same as for Fig. 1.

C_ANT distribution along the OUTPACE transect is presented in Fig. 4a, and all vertical profiles for C_ANT are presented in Fig. 4b with a more detailed view of the first 1500 dbar of the water column in Fig. 4c. Figure 4b and c distinguish values from the MA and the WGY area. The C_ANT vertical profiles suggest a penetration of anthropogenic carbon up to 1000 dbar. As mentioned before, estimated values of C_ANT reach values of 60±40 µmol kg⁻¹ at a depth of 100 dbar; C_ANT then regularly decreases to values close to 10–20±13 µmol kg⁻¹ at a depth of 1000 dbar and reaches values close to 0 µmol kg⁻¹ below 1500 dbar. The zonal C_ANT section along the OUTPACE transect (Fig. 4a) presents two features: (1) a deeper penetration of C_ANT in the western part of the transect with values of C_ANT reaching 40±25 µmol kg⁻¹ around the isopycnal layer of 27 kg m⁻³ (ca. 700 dbar) with a coherent behavior with the distribution of AOU and (2) a larger accumulation of C_ANT in the eastern part of the transect centered around the isopycnal layer of 25 kg m⁻³ (ca. 200 dbar).

Several studies have identified deeper C_ANT penetration in the western South Pacific than in the eastern South Pacific at tropical and subtropical latitudes. The primary reason for this longitudinal difference might be associated with deeper convection in the western part and upwelling in the eastern part. AAIW has been described as the lower limit of the penetration of C_ANT in the ocean interior of the South Pacific (Sabine et al., 2004). Moreover, a recent study by DeVries et al. (2017) shows that ocean circulation variability is the primary driver for changes in oceanic CO₂ uptake at decadal scales. Based on C_T changes between the two repeated visits of the longitudinal P21 line (18^∘ S close to the OUTPACE transect) in 1994 and 2009, Kouketsu et al. (2013) show a faster increase in C_ANT in the western part than in the eastern part of the section. They also postulate that C_ANT may have been transported by deep circulation associated with the AAIW. In the subtropical Pacific along the P06 line (longitudinal section at ca. 32^∘ S), Murata et al. (2007) also identified an increase in C_ANT in the SAMW and AAIW. Waters et al. (2011) attribute the deeper penetration of C_ANT in the western part of the section to the local formation of subtropical mode water in the area based on the extended multiple linear regression (eMLR) method along the P06 line (and taking into account a third visit).

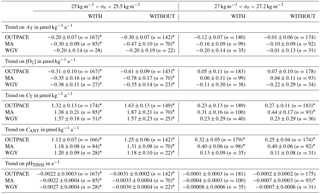
Table 2 Estimated trends on A_T, [O₂], C_T , C_ANT and pH_T changes in two different layers of the water column defined by isopycnal layers between 1980 and 2015 based on GLODAPv2 with (column WITH) and without (column WITHOUT) OUTPACE data added. Estimated trends are obtained from slope values of a linear regression between the studied parameters and time.

^∗ Trend significant (p level<0.05).

In the eastern part of the OUTPACE cruise, the detected accumulation of C_ANT in the upper thermocline waters may be related to recent observations of a significant accumulation of C_ANT at latitudes around 20^∘ S on the P16 meridional transect along 150^∘ W by Carter et al. (2017). This change in C_ANT accumulation is attributed to changes in the degree of the water mass ventilation due to variability in a southern Pacific subtropical cell. Along the P16 line, Carter et al. (2017) observed high values of C_ANT (up to 60 µmol kg⁻¹) for the upper water column at the latitude of the OUTPACE area in good agreement with our estimates in WGY in the upper water column. Finally, it should also be mentioned that, due to the presence of one of the main oxygen minimum zone (OMZ) area, denitrification occurs in the eastern South Pacific and can be traced by the N^* parameter (Gruber and Sarmiento, 1997). Denitrification, by transforming organic carbon to inorganic carbon without the consumption of oxygen, could induce an overestimation of C_ANT by the TrOCA method (and other back-calculation methods) due to a biological release of C_T that is not taken into account in the formulation of the quasi-conservative TrOCA tracer. Horizontal advection by the south equatorial current of the strong negative N^* signal originating from the eastern Pacific towards the western Pacific has been described previously (Yoshikawa et al., 2015). Fumenia et al. (2018) have estimated N^* along the OUTPACE transect and show slightly negative N^* values in the upper thermocline waters at the eastern side of the OUTPACE transect where the highest C_ANT values are estimated. However, Murata et al. (2015) showed that, based on a direct relation between C_T and N^*, the influence of denitrification should be negligible on C_ANT estimations in this area. Therefore, the N^* correction has not been introduced in the C_ANT estimates and the effect of denitrification was not quantified here.

6 Temporal changes in carbonate chemistry in the OUTPACE area

Based on the available GLODAPv2 data, temporal changes in the OUTPACE area have been assessed (Fig. 5 and Table 2). The variation in oceanic parameters with time is estimated on two isopycnal layers: a layer with 25 kg m${}^{-\mathrm{3}}<{\mathit{\sigma }}_{\mathit{\theta }}<\mathrm{25.5}$ kg m⁻³ (hereafter named σ_θ 25) and a layer with 27 kg m${}^{-\mathrm{3}}<{\mathit{\sigma }}_{\mathit{\theta }}<\mathrm{27.2}$ kg m⁻³ (hereafter named σ_θ27). These two layers correspond to the features in C_ANT discussed in the previous section. σ_θ25 can be considered characteristic of the upper thermocline waters (core of the salinity maximum, Fig. 2), whereas σ_θ27 can be considered characteristic of intermediate waters of southern origin (core of the salinity minimum). All the values associated with these two layers are spread between 145 and 301 dbar for σ_θ25 and between 571 and 896 dbar for σ_θ27. It must be mentioned that the study of temporal changes is based on a large sampling grid, which covers the entire OUTPACE transect (see Sect. 2.5 and Fig. 1). This could add a spatial variability that may interfere in the estimation of temporal changes.

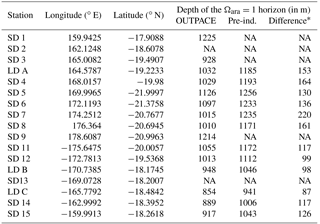
Table 3 Estimated depth of the Ω_ara=1 horizon along the OUTPACE cruise (see text for details). No values are available for stations where data up to 2000 dbar were not available (SD2 and SD13). No values were estimated for stations with $C_{\mathrm{ANT}}<-\mathrm{6}$ µmol kg⁻¹.

^∗ Difference (in m) between the depth of the Ω_ara=1 horizon at the pre-industrial period and the OUTPACE cruise. NA – not available.

Temporal variations in C_T and C_ANT between 1970 and 2015 are presented in Fig. 5. As mentioned earlier, even if C_ANT estimates from TrOCA are biased, a previous study by Pérez et al. (2010) suggests that the TrOCA method gives similar values to other methods for estimating C_ANT accumulation rates. A linear fit was applied to the observed temporal variations for A_T, [O₂], C_T and C_ANT to check for significant trends on data collected between 1980 and 2015. The results of the performed regression analyses are presented in Table 2. Trends are evaluated with and without the data of the OUTPACE cruise in order to estimate the influence of this new dataset on the observed trends. Trends are evaluated for the entire OUTPACE area and for the MA and the WGY area. Even if presented in Fig. 5, data collected before 1980 from the GLODAPv2 database are disregarded in the estimation of the temporal trends. Indeed, for the OUTPACE area, data prior to 1980 originate from one single GEOSEC cruise in 1974, with only one measured point for σ_θ27 at WGY and no points at σ_θ25 for WGY and MA.

At σ_θ25, a significant decrease in A_T of $-\mathrm{0.20}\pm \mathrm{0.07}$ µmol kg⁻¹ a⁻¹ is observed over the entire OUTPACE area. A decrease of $-\mathrm{0.30}\pm \mathrm{0.09}$ µmol kg⁻¹ a⁻¹ is also observed in the MA area, whereas no significant trend is observed for the WGY area. However, when A_T is normalized to salinity, no significant trends are observed in A_T n35 suggesting that the observed trend in A_T can be attributed to salinity changes rather than changes in calcification. Significant negative trends are observed for [O₂] over the entire area ($-\mathrm{0.31}\pm \mathrm{0.10}$ µmol kg⁻¹ a⁻¹), in MA ($-\mathrm{0.35}\pm \mathrm{0.16}$ µmol kg⁻¹ a⁻¹) and in WGY ($-\mathrm{0.38}\pm \mathrm{0.11}$ µmol kg⁻¹ a⁻¹). The decrease in [O₂] which corresponds to a positive trend in AOU suggested an increase in the remineralization of organic matter at σ_θ25. Significant increasing trends were observed for C_T over the entire area ($+\mathrm{1.32}\pm \mathrm{0.13}$ µmol kg⁻¹ a⁻¹), in MA ($+\mathrm{1.38}\pm \mathrm{0.21}$ µmol kg⁻¹ a⁻¹) and in WGY ($+\mathrm{1.57}\pm \mathrm{0.13}$ µmol kg⁻¹ a⁻¹). For C_ANT, the trends were slightly slower ($+\mathrm{1.12}\pm \mathrm{0.07}$ to $+\mathrm{1.2}\pm \mathrm{0.09}$ µmol kg⁻¹ a⁻¹) and not significantly different between MA and WGY. Taking into account the OUTPACE dataset does not change the overall significance of the observed trends and only minor changes (mostly within the error of the estimates) are observed. If we assume a C_T increase of 0.5 to 1 µmol kg⁻¹ a⁻¹ (depending on the buffer factors considered) associated with the recent rise in atmospheric CO₂ (see for example Murata et al., 2007), the C_T increase in the OUTPACE area is faster than thermodynamics would govern, whereas the C_ANT is closer to this thermodynamic value. The higher increase in C_T could be related to an increase in remineralization processes as deduced from [O₂] trends, with an overall consistency between the rate of C_T increase and the rate of decrease in [O₂]. However, the important increase in C_ANT observed between 2005 and 2015 between 10 and 30^∘ S on the P16 line (at the eastern side of the OUTPACE transect) by Carter et al. (2017) is not supported by significant differences in the trends of C_ANT observed between MA and WGY in this study.

At σ_θ27, the only significant trend observed is an increase in C_ANT of ca. 0.40±0.06 µmol kg⁻¹ a⁻¹ in the MA area. When the OUTPACE dataset is not considered, a similar trend is observed for C_T in the MA area. This trend is compatible with the observed increase in C_ANT by Kouketsu et al. (2013) along the P21 line close to the isopycnal layer 27 kg m⁻³. As this increase is not observed in WGY and if we assume that the σ_θ27 is filed with AAIWs, this suggest that the accumulation of C_ANT in AAIW is faster west of the 170^∘ W line than to the east, but no clear explanation for this trend can be given.

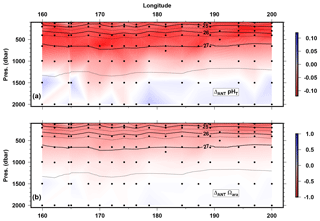
Figure 6 Longitudinal variations in (a) pH_T changes and (b) Ω_ara changes between the pre-industrial period and the present time along the OUTPACE transect between 100 and 2000 dbar depth (see text for details). Black contour lines represent the isopycnal horizons based on potential density referenced to a pressure of 0 dbar.

7 Towards an enhanced “ocean acidification” in the WTSP?

Temporal variations in pH_T between 1970 and 2015 are presented in Fig. 5c and f with rates of pH_T decrease of $-\mathrm{0.0022}\pm \mathrm{0.0004}$ a⁻¹ for MA and $-\mathrm{0.0027}\pm \mathrm{0.0004}$ a⁻¹ for WGY at σ_θ25 (Table 2) between 1980 and 2015. Based on the C_ANT rates estimated in the previous section (1.1 to 1.2 µmol kg⁻¹ a⁻¹) and based on a constant value of A_T of 2285 µmol kg⁻¹ (mean value of A_T n35 on σ_θ25) and a constant temperature of 20 ^∘C (mean value of temperature on σ_θ25), we can estimate a pH_T decrease rate of −0.0023 to −0.0025 a⁻¹. This indicates that rates of oceanic pH_T decrease (ocean acidification) can mostly be explained by the increase in C_ANT. These rates of acidification are higher than the values reported by Waters et al. (2011) in the western South Pacific along the P06 Line (south of OUTPACE area at 32^∘ S) between two visits in 1992 and 2008. They are also higher than the surface rates of pH_T decrease of $-\mathrm{0.0016}\pm \mathrm{0.0001}$ a⁻¹ recorded at the HOT station in the tropical North Pacific and of $-\mathrm{0.0017}\pm \mathrm{0.0001}$ and $-\mathrm{0.0018}\pm \mathrm{0.0001}$ a⁻¹ in the tropical North Atlantic at BATS and ESTOC stations, respectively (Bates et al., 2014). However, differences in buffer factors between the surface and subsurface can partially explain these differences. Nevertheless, our results in the subsurface (σ_θ25) based on GLODAPv2 and OUTPACE data (C_T and A_T) are similar to pH_T trends derived from fCO₂ surface observations (e.g., Lauvset et al., 2015). In the southern subtropical and equatorial Pacific regions, using SOCAT version2, Lauvset et al. (2015) evaluate contrasting fCO₂ and pH_T trends, ranging between +1.1 and +3.5 µatm a⁻¹ for fCO₂ and between −0.001 and −0.0023 a⁻¹ for pH_T. If we revisit these estimates, using surface fCO₂ observations available in the OUTPACE region (18–22^∘ S/170–200^∘ E) in SOCAT version 6 (Bakker et al., 2016; http://www.socat.info, last access: 10 August 2018) and assuming a constant alkalinity (2300 µmol kg⁻¹, average of surface data), we can calculate pH_T and C_T from fCO₂ and temperature data. The resulting long-term trends for the period 1980–2016 for fCO₂, C_T and pH_T are, respectively, $+\mathrm{1.27}\pm \mathrm{0.01}$ µatm a⁻¹, $+\mathrm{1.03}\pm \mathrm{0.01}$ µmol kg⁻¹ a⁻¹ and $-\mathrm{0.0013}\pm \mathrm{0.0001}$ a⁻¹. Interestingly, for the period 2000–2016 the trends are $+\mathrm{2.53}\pm \mathrm{0.02}$ µatm a⁻¹, $+\mathrm{2.02}\pm \mathrm{0.02}$ µmol kg⁻¹ a⁻¹ and $-\mathrm{0.0025}\pm \mathrm{0.0003}$ a⁻¹, suggesting an acceleration of the signals in recent years. These results, based on fCO₂ observations in surface waters, confirm the trends we detected for C_T and pH_T in subsurface layers (σ_θ25).

In Fig. 6, estimates of the so-called “anthropogenic pH_T change” (Δ_ANTpH_T) and “anthropogenic Ω_ara change” (Δ_ANTΩ_ara), which correspond to the difference in pH_T and Ω_ara between the time of the OUTPACE cruise (modern time) and the pre-industrial period, are presented. The pH_T and Ω_ara correspond to the values presented in Fig. 3, whereas the pre-industrial values corresponds to pH_T and Ω_ara estimated with C_T minus C_ANT. All other parameters (temperature, salinity, alkalinity and nutrients) are assumed to remain constant over time. The main features for the distribution of Δ_ANTpH_T and Δ_ANTΩ_ara logically reflect the distribution of the estimated C_ANT in this study because C_ANT is the only driving force in these estimations. The estimated pH_T decrease reaches values slightly higher than 0.1 and the estimated Ω_ara decrease reaches values of 0.75 since the pre-industrial period for areas with the highest C_ANT accumulation. When considering an error in C_ANT of 6 µmol kg⁻¹, we can assume that we are able to distinguish changes of 0.0012 for pH_T and 0.06 for Ω_ara. Decreases in pH_T and Ω_ara are thus detectable below 1000 dbar in the MA waters and above 1000 dbar in WGY waters.

A decrease in pH_T of 0.1 units since the pre-industrial period is a generally accepted value for oceanic waters affected by C_ANT penetration (e.g., Royal Society (Great Britain), 2005). Several studies have assessed the rate of ocean acidification based on successive visits to different oceanic areas. For the South Pacific Ocean, Carter et al. (2017) reports decreases in oceanic pH_T since the pre-industrial period of −0.09 and −0.11 pH_T units for the latitude band from 10 to 20^∘ S and from 20 to 30^∘ S, respectively, along the P16 line (150^∘ W) situated on the eastern side of the OUTPACE area. These are in good agreement with our estimates in this area.

Based on an interpolation of the estimated Ω_ara during OUTPACE and the pre-industrial Ω_ara, we calculated the depth of the horizon where Ω_ara=1 for the different stations of the OUTPACE transect (Table 3) in 2015 and the pre-industrial period based on the Δ_ANTΩ_ara estimates. We observed an upward migration of the aragonite saturation horizon of up to 220 m in the MA area along the OUTPACE transect (Table 3). This upward migration of the Ω_ara=1 horizon is higher than the migration of 30 to 100 m observed between the 1990s and the pre-industrial period in early studies (Feely et al., 2004) in the Pacific based on the WOCE dataset illustrating the continuous acidification of the WTSP.

8 Conclusions

Based on A_T and C_T data and related properties collected during the OUTPACE cruise, we estimated different parameters of the carbonate system along a longitudinal section of nearly 4000 km and up to 2000 dbar in WTSP. Even if the vertical and horizontal resolution is low compared to the WOCE lines and precludes a rigorous comparison with this high-quality dataset, we estimated that the measured carbonate chemistry parameters are in good agreement with previous data collected in this area. Based on the estimation of C_ANT from the TrOCA method, we find C_ANT penetration in the WTSP and impacts on pH_T and saturation state of calcium carbonate since the pre-industrial period that are in good agreement with previous observations in this area. As mentioned above, C_ANT values from TrOCA estimates are not reliable in surface layer. However, based on GLODAPv2 and the SOCAT database, our estimation of C_ANT in the subsurface seems to be in good agreement with expected changes in surface waters. The enhanced impact of ocean acidification in the subtropical South Pacific suggested by our study highlights the necessity of sustained research efforts in this largely underexplored part of the world ocean. The presented dataset collected along the OUTPACE transect could complement existing sections visited nearly every decade in the South Pacific Ocean and in particular the P21 line, which was last visited in 2009.