How long does carbon stay in a near-pristine central Amazon forest? An empirical estimate with radiocarbon

Amazon forests play a significant role in the global C cycle by assimilating large amounts of CO₂ through photosynthesis and by storing C largely as biomass and soil organic matter. To evaluate the net budget of C in the Amazon, we must also consider the amplitude and timing of losses of C back to the atmosphere through respiration and biomass burning. One useful timescale metric that integrates such information in terrestrial ecosystems is the transit time of C, defined as the time elapsed between C entering and leaving the ecosystem; the transit time is equivalent to the age of C exiting the ecosystem, which occurs mostly through respiration. We estimated the mean transit time of C for a central Amazon forest based on the C age during ecosystem respiration (ER), taking advantage of the large variations in CO₂ in the atmosphere below the forest canopy to estimate the radiocarbon signature of mean ER ($\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$) using Keeling and Miller–Tans mixing models. We collected air samples to evaluate changes in the isotopic signature of the main ER sources by estimating the $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$. We collected air samples in vertical profiles in October 2019 and December 2021 at the Amazon Tall Tower Observatory (ATTO) in the central Amazon. Air samples were collected in a diel cycle from two heights below the canopy (4 and 24 m above ground level (a.g.l.)). Afternoon above-canopy samples (79 and 321 m a.g.l.) were collected as the background. For the campaign of October 2019, the mean $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ ranged from 24 ‰ to 41 ‰ with both Keeling and Miller–Tans methods. In December 2021, mean $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ ranged from 53 ‰ to 102 ‰. The $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ showed a smaller variation, being −27.8 ‰ ± 0.3 ‰ in October 2019 and −29.0 ‰ ± 0.5 ‰ in December 2021. The $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ estimates were compared with the record of atmospheric radiocarbon from the bomb period, providing estimates of mean transit time of 6 ± 2 years for 2019 and 18 ± 4 years for 2021. In contrast to steady-state carbon balance models that predict constant mean transit times, these results suggest an important level of variation in mean transit times. We discuss these results in the context of previous model-based estimates of mean transit time for tropical forests and the Amazon region. In addition, we discuss previous studies that indicate that approximately 70 % of assimilated carbon is respired as autotrophic respiration in the central Amazon. Our results suggest that newly fixed carbon in this terra firme tropical forest is respired within 1 to 2 decades, implying that only a fraction of assimilated C can act as a sink for decades or longer.

1 Introduction

Tropical forests play a relevant role in the global carbon (C) cycle for two main reasons: (i) due to their high assimilation rate of carbon dioxide (CO₂) through photosynthesis (gross primary production, GPP, at ecosystem level; Beer et al., 2010; Jung et al., 2020) and (ii) due to their high storage of C in vegetation and soils, representing up to a quarter of the total C mass in terrestrial ecosystems (Carvalhais et al., 2014; Malhi et al., 2011).

In particular, the Amazon rainforest, as the largest continuous rainforest in the world, plays an important role in the global C cycle, taking up significant amounts of CO₂ from the atmosphere (Stephens et al., 2007; Malhi et al., 2015; Phillips and Brienen, 2017; Baker and Spracklen, 2019; Botía et al., 2022) and storing this carbon in terrestrial ecosystems for times that can range from hours to centuries (Sedjo and Sohngen, 2012; Sierra et al., 2021a).

Although the rates of C uptake in Amazon forests are among the largest in terrestrial ecosystems (Malhi et al., 1999), C losses through respiration are also very high, and autotrophic respiration is estimated in around two-thirds of assimilated C in the central Amazon, compensating for most of the C uptake (Chambers et al., 2004, 2013; Sierra et al., 2007; Malhi et al., 2011). Additionally, several studies have found high variability in the magnitude and direction of C fluxes in the Amazon region because of anthropogenic disturbances (e.g., fires and deforestation) and extreme drought events (e.g., associated with El Niño) (Brienen et al., 2015; Phillips and Brienen, 2017; Hubau et al., 2020; Gatti et al., 2021). Therefore, to better understand the overall carbon balance of the Amazon forests, it is important to know not only the amount of carbon uptake but also for how long C is retained within these ecosystems (Muñoz et al., 2023).

A key diagnostic metric for characterizing timescales of C cycling in ecosystems is the transit time of C, which can be defined as the age of C during ecosystem respiration (Rasmussen et al., 2016; Sierra et al., 2017; Lu et al., 2018). The total respiration flux of an ecosystem is composed of C that spends different amounts of time stored in different ecosystem compartments (Trumbore, 2006), and it captures the metabolic activity of both autotrophic and heterotrophic organisms. Therefore, the age of C in ecosystem respiration, i.e., the transit time of C through the ecosystem, serves as a key diagnostic metric to characterize how long, on average, a C atom is stored in ecosystems before it is respired back to the atmosphere as CO₂.

Radiocarbon (¹⁴C) can be used as a tracer of C dynamics in ecosystems and to track how C moves across different ecosystem C pools. Measurements of radiocarbon in respiration can also be used to quantify the transit time of C through ecosystems (Trumbore and De Camargo, 2009). Radiocarbon is produced naturally in the upper atmosphere by the interaction of thermal neutrons from cosmic rays with ¹⁴N in the atmosphere. Additionally, nuclear weapon tests in the atmosphere during the late 1950s and early 1960s produced a large number of thermal neutrons that led to the production of excess ¹⁴C. After natural and anthropogenic production, ¹⁴C is oxidized to CO₂ and is incorporated into the global carbon cycle. After the Limited Test Ban Treaty in 1963, the concentration of ¹⁴CO₂ in the atmosphere started to decline due to its incorporation into the biosphere and surface ocean (Levin et al., 2022). Atmospheric CO₂ containing ¹⁴C that has changed over time since the 1960s is assimilated by terrestrial ecosystems in the same manner as natural isotopes of C. For instance, C in freshly fixed plant metabolites (e.g., leaf sugars) will have the same ratio of ¹⁴C content as the atmosphere at the time they are assimilated. Yet, ¹⁴C respired from organic matter decomposition would reflect the age of C used to grow plant tissue, as well as the time it takes for decomposition to occur, leading to C ages of respiration from organic matter that are generally higher than 1 year. CO₂ respired by fast-cycling pools (e.g., canopy leaves) should have a ¹⁴C isotopic signature close to the contemporaneous atmospheric ¹⁴C signal. Thus, the age of C in ecosystem respiration is a mix of ages of C respired from different compartments with distinct isotopic signatures and integrates the timescales of different processes such as production, allocation, and decomposition (Trumbore and De Camargo, 2009; Chanca et al., 2022).

An estimate of the whole ecosystem's respiration ¹⁴C isotopic ratio can be obtained from the covariation of ¹⁴C with CO₂ concentration in the air using end-member mixing analysis methods such as the Keeling plot (Keeling, 1958, 1961) or the Miller–Tans plot (Miller and Tans, 2003) methods. Traditionally, Keeling plots have been applied to terrestrial ecosystems to characterize the stable C isotopic signatures of the main sources of ecosystem respiration that have different δ¹³C values, i.e., the deviation in parts per thousand of sample ${}^{\mathrm{13}}\mathrm{C}/{}^{\mathrm{12}}\mathrm{C}$ in comparison to a standard material (Pataki et al., 2003), but the method can also be used to obtain the radiocarbon signature of ecosystem respiration (Phillips et al., 2015). A comparison between the mean ¹⁴C isotopic signature of the whole ecosystem's respiration and the time history of the ¹⁴C isotopic signature in atmospheric CO₂ provides an estimate of the mean transit time for C, i.e., the time C takes to move through the whole ecosystem, from photosynthesis to respiration.

We used isotopic mixing models of radiocarbon in atmospheric CO₂ below and above the canopy level to address two questions:

• i.

  What is the mean transit time of C for an Amazon terra firme forest as estimated with Keeling and Miller–Tans methods using ¹⁴CO₂?

• ii.

  How does this empirical estimate compare with other model-based estimates of mean transit time for tropical forests?

To address these questions, we first provide a brief introduction to end-member mixing analysis as applied for radiocarbon measurements in CO₂, describing the sampling sites and statistical methods. We then report our estimates of mean transit times and discuss the results in the context of previous model-based estimates of mean transit time for tropical forests and the Amazon region.

2 Materials and methods

2.1 Study site

Atmospheric air samples below and above the canopy level were collected at an 80 m tall walk-up tower (coordinates (WGS 84): 02°08.6470^′ S, 58°59.9920^′ W) located at the Amazon Tall Tower Observatory (ATTO) site in the Uatumã Sustainable Development Reserve in the central Amazon. The ATTO site is located ca. 150 km NE of the city of Manaus. In addition, the site includes two other towers: the ATTO tall tower (02°08.7520^′ S, 59°00.3350^′ W; 325 m tall) and a triangular mast (02°08.6020^′ S, 59°00.0330^′ W; 81 m tall) (Andreae et al., 2015). Meteorological conditions are measured continuously at the 80 m walk-up tower.

The three towers are located on a plateau area, with vegetation characterized as old-growth closed-canopy terra firme (non-flooded) forest. Around the towers, the canopy rises to approximately 35 m, with emergent trees reaching 45 m above ground level (a.g.l.). Areas surrounding the tower include a network of plateaus and valleys connected by relatively steep slopes with a maximum relief height of ca. 100 m, with the base of the tall tower being located at an elevation of 120 m above sea level (a.s.l.) (Andreae et al., 2015).

The mean annual precipitation measured locally between the years 2012 and 2019 was 1934.1 mm yr⁻¹ (Botía et al., 2022). Mean air temperatures do not vary strongly in the central Amazon, including at the ATTO site. However, temperature maxima at the canopy level may vary between seasons. During the dry season (August–November), the daytime temperature maxima at the canopy top are slightly above 30 °C. During the wet season (February–May), the daytime temperature maxima are around 28 °C. In both seasons, the temperature minima are around 22 °C (Andreae et al., 2015).

2.2 Sampling

Forest air samples were collected from two heights within the canopy, at 4 and 24 m a.g.l., during two campaigns conducted during the dry season and during the transition from the dry to the wet season. The first campaign took place in October 2019, and the second campaign took place in December 2021. A few samples were collected from the top level of the 80 m walk-up tower (79 m a.g.l.) to be used as a reference of the above-canopy air for the Miller–Tans plots, which consist of an approach where the values (Δ¹⁴C–CO₂, CO₂ concentrations) observed within the canopy are plotted after subtraction of the values observed in the tropospheric background (Miller and Tans, 2003). The canopy level at the study plot is around 35 m high, making the 79 m level reasonably appropriate as a background (Pataki et al., 2003). At the ATTO tall tower, since September 2021, air samples have been collected into flasks from 321 m a.g.l. Additionally, since February 2019, 1-month-integrated samples have been collected by means of the absorption of CO₂ in NaOH solution for radiocarbon analysis at 321 m through the method detailed by Levin et al. (1980).

Air from the different heights was collected through Synflex^® metal–plastic composite tubings of $\mathrm{1}/{\mathrm{4}}^{\prime \prime }$ o.d. connected at heights of 4, 24, and 79 m a.g.l. at the 80 m walk-up tower and 321 m a.g.l. at the ATTO tall tower. The air flowing from the tubing inlets was transferred to glass flasks of 3 L volume. The flasks contain valves of PCTFE (polychlorotrifluoroethylene) seals and are the standard flasks of ICOS class-1 stations (Levin et al., 2020). Before shipment and sampling, flasks were conditioned (i.e., evacuated, baked, and filled with dry air) at the ICOS Central Analytical Laboratory.

At the 80 m walk-up tower, air samples were collected with a portable flask sampler, which is a compressor module that comprises a membrane pump and compressor, and gauges for monitoring the flow of air and the pressure inside the flasks (Heimann et al., 2022). The aim is to pump air from the desired height into the flask while simultaneously compressing the air to keep a final absolute pressure of about 1.6 bar inside the flask. Additionally, a drying agent can be attached to the system; the drying agent is particularly relevant when one is interested in the δ¹⁸O–CO₂ (Steur et al., 2023), which was not the case here. Nevertheless, for the campaign of 2021, when the air relative humidity was high (dry-to-wet season), we decided to use anhydrous magnesium perchlorate inside a cartridge before the flask to trap the water vapor from the air and to avoid interferences in the airflow and eventual damage to the sampler due to water condensation on pieces of the equipment. Each sample was flushed for 15 min at a flow rate of ca. 2 L min⁻¹. Additional details on the standard flask sampling protocol at the Max Planck Institute for Biogeochemistry (MPI-BGC), as well as the flask sampling instructions for the portable sampler, can be found in Heimann et al. (2022).

At the ATTO tall tower, air samples were collected with an automated sampler from the ICOS network (Levin et al., 2020) from an inlet at 321 m a.g.l. once per week between 13:00 and 14:00 local time (LT, UTC-0400) at a flow of $\mathrm{1}/t$, which guarantees that the sample represents a real 1 h mean air collection. During collection, the 3 L flasks are filled with samples of local air at about 1.6 bar absolute pressure.

Our reference background for CO₂ concentrations in 2019 consisted of flask samples taken at 79 m a.g.l. during the afternoon (13:29 and 17:09 LT). The CO₂ concentration of a sample collected on 16 December 2021 was used as the CO₂ background reference for the sub-canopy samples collected in December 2021. Background Δ¹⁴C–CO₂ in October 2019 was based on a 1-month-integrated sample collected between 9 September 2019 and 15 October 2019. For the background Δ¹⁴C–CO₂ in December 2021, two samples, collected during 24 November–19 December 2021 and 19 December 2021–26 January 2022, were averaged.

In 2019, samples of air below the canopy were collected following a 24 h cycle with sampling times of roughly every 2 h between 5 and 6 October, totaling 20 sub-canopy samples. Including the samples collected at 79 m, a total of 24 samples were collected in October 2019. On 19 and 20 December 2021, samples were collected in intervals of 3–4 h during the day and intervals of up to 8 h during the night, adding up to 12 samples. Flasks sampled between local sunrise (05:45 LT) and local sunset (18:00 LT) are considered to constitute the daytime; otherwise, they are considered to constitute the nighttime. During laboratory analyses, some samples were disregarded for being inconsistent with ambient air samples (e.g., SF₆ mole fraction equal to the one of the dry air used to fill the flasks for transport); additionally, some other flasks got broken, and so the final data comprise 18 samples for October 2019 and 10 samples for December 2021.

2.3 Analytical methods and data analyses

CO₂ concentrations and C isotope ratios (δ¹³C–CO₂ and Δ¹⁴C–CO₂) from flask samples were measured in the laboratories (GasLab, IsoLab, and ¹⁴C-Analytik) of MPI-BGC in Jena, Germany, except for the Δ¹⁴C–CO₂ of samples collected in October 2019, whose values were determined by the Integrated Carbon Observation System–Central Radiocarbon Laboratory (ICOS-CRL) facility in Heidelberg University, Germany, in collaboration with the Curt-Engelhorn-Zentrum Archäometrie (CEZA) AMS facility in Mannheim, Germany.

The CO₂ concentrations inside the flasks were measured in the GasLab at MPI-BGC with an Agilent 6890 gas chromatograph equipped with an electron capture detector (ECD) and a flame ionization detector (Ni_cat-FID). Additionally, in the MPI-BGC, the δ¹³C–CO₂ of the air in the flasks was measured in the BGC IsoLab using a fully automated cryogenic extraction line (BGC-AirTrap) coupled to the dual-inlet system of a Finnigan MAT 252 stable isotope ratio mass spectrometer (IRMS, Thermo Fisher Scientific, Bremen, Germany) (Heimann et al., 2022). Calibration was performed against the international Jena Reference Air Set (JRAS-06) scale (Wendeberg et al., 2013). The δ¹³C (of CO₂) corresponds to

$$\begin{array}{}\text{(1)}& \mathit{\delta }{}^{\mathrm{13}}\mathrm{C}=\left({\displaystyle \frac{{\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\text{sample}}}{{\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\text{standard}}}}-\mathrm{1}\right)\times \mathrm{1000}\left[\mathrm{‰}\right].\end{array}$$

The Δ¹⁴C notation is used to express the isotopic ratio ${}^{\mathrm{14}}\mathrm{C}/\mathrm{C}$, with a correction for mass-dependent fractionation and radioactive decay. Specifically,

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{}^{\mathrm{14}}\mathrm{C}=\left(F{}^{\mathrm{14}}\mathrm{C}{e}^{\mathit{\lambda }(\mathrm{1950}-y_{\text{meas}})}-\mathrm{1}\right)\times \mathrm{1000}\left[\mathrm{‰}\right],\end{array}$$

where F¹⁴C ($=\frac{A_{\text{SN}}}{A_{\text{ON}}}$) is the fraction modern, with A_SN being the specific activity of the sample and A_ON being the specific activity of oxalic acid standard material (OxII), both normalized to $\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}=-\mathrm{25}\mathrm{‰}$ with respect to the V-PDB standard; λ is the updated ¹⁴C decay constant ($\frac{\mathrm{1}}{\mathrm{8267}}$ yr⁻¹); and y_meas is the year of measurement. Δ¹⁴C is corrected for mass-dependent fractionation through AMS online δ¹³C, assuming ¹⁴C fractionates approximately twice as much as ¹³C (Stuiver and Polach, 1977; Reimer et al., 2004).

Δ¹⁴C from CO₂ in the air samples collected in flasks was determined after cryogenic extraction of CO₂ in a vacuum line and its conversion to graphite, which is the target of the Cs sputtering in the AMS at both CEZA and MPI-BGC. At the ICOS-CRL facility, CO₂ extraction is performed using a dedicated automated extraction and graphitization line (EGL) (Lux, 2018). At MPI-BGC, the extraction of CO₂ for radiocarbon analysis follows the same principles as EGL. ¹⁴C-to-C ratios at both CEZA and MPI-BGC are corrected for mass-dependent fractionation by δ¹³C measurements in the AMS and are calibrated against oxalic acid standard material (OxII).

The Δ¹⁴C values of the reference background (321 m a.g.l.) are based on radiometric analysis of radiocarbon from samples of CO₂ absorbed in a NaOH solution (Levin et al., 1980). Δ¹⁴C values from the integrated air in NaOH samples were determined through low-level gas proportional counting at the Institute of Environmental Physics in Heidelberg, Germany (Kromer and Münnich, 1992). For samples collected in 2019, the year of measurement (y_meas, Eq. 2) for radiocarbon analysis was 2020, and for samples collected in 2021, y_meas was 2023.

2.4 End-member mixing analysis

The Keeling plot and Miller–Tans plot methods are based on two conservation equations. First, it is assumed that the concentration of CO₂ below a forest canopy ([CO₂]_can) is the mix of CO₂ from a tropospheric background ([CO₂]_trop) and the CO₂ released from ecosystem respiration ([CO₂]_ER) (Eq. 3) (Keeling, 1958, 1961; Miller and Tans, 2003). Second, isotopic mixing in CO₂ below the canopy is proportional to the concentration of CO₂ in the tropospheric background and ecosystem respiration (Eq. 4) (Tans, 1980). These assumptions lead to the following equations:

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}=[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}+[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{ER}},\text{(4)}& {\displaystyle }& {\displaystyle }{R}_{\text{can}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}=R_{\text{trop}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}+R_{\text{ER}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{ER}},\end{array}$$

where R is the isotopic ratio of C in CO₂, expressed as δ¹³C for the stable C isotopes and as Δ¹⁴C or F¹⁴C for the ¹⁴C isotope over total C.

Using the mass conservation of Eq. (3), Eq. (4) can be reduced to

$$\begin{array}{}\text{(5)}& R_{\text{can}}={\displaystyle \frac{[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}}{[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}}}\times (R_{\text{trop}}-R_{\text{ER}})+R_{\text{ER}}.\end{array}$$

Equation (5) is, in essence, a linear equation of the form $y=ax+b$, where the independent variable x is $\frac{\mathrm{1}}{[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}}$; y is the isotopic signature observed in the canopy R_can; $a=(R_{\text{trop}}-R_{\text{ER}})[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}$; and b, or, hereafter, the y intercept, is R_ER, i.e., the isotopic signature of CO₂ respired by the whole ecosystem. Using linear regression, the values of a and b can be obtained if the values of x and y are known. This approach for obtaining the isotopic signature of a source in a two-end-member mixing model is commonly known as the Keeling plot method (Keeling, 1958). In this study, we are particularly interested in the radiocarbon signature of ecosystem respiration, which we express as $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ (and F¹⁴C_ER in the Appendix).

Notice that Eq. (4) leads to the requirement that the background signal does not change over time (Eq. 5) (Keeling, 1958, 1961). Miller and Tans (2003) rearranged Eq. (4), obtaining the following equation:

$$\begin{array}{}\text{(6)}& {\displaystyle }\begin{array}{rl}{\displaystyle }{R}_{\text{can}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}& {\displaystyle }-R_{\text{trop}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}=\\ {\displaystyle }& {\displaystyle }{R}_{\text{ER}}\left(\right[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}-\left[{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}\right).\end{array}\end{array}$$

This can also be expressed as a linear function where the intercept b equals zero. Here, x is ([CO₂]_can−[CO₂]_trop), i.e., the difference between CO₂ concentrations below and above canopy; y is $R_{\text{can}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{can}}-R_{\text{trop}}\times [{\mathrm{CO}}_{\mathrm{2}}{]}_{\text{trop}}$; and the slope a is R_ER, i.e., the isotopic signature of ecosystem respiration.

Such rearrangement removes the requirement of a constant background over time in the Keeling plot approach. However, it becomes necessary to explicitly account for the background concentration and C isotope ratio values in Eq. (6).

The isotopic carbon signatures of ecosystem respiration ($\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ and $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$) were estimated with both the Keeling and Miller–Tans approaches. Both end-member mixing models considered all the heights below and above the canopy, i.e., 4, 24, 79, and 321 m, and were not separated according to the time of day. The results of the analyses were estimated by linear regression fits with ordinary least squares (model-I regression) (Zobitz et al., 2006). We report the mean values, with 1 standard error (σ), of the intercept obtained by the regressions in the Keeling approach and of the slope of the regression in the Miller–Tans approach. In both cases, we also report the 95 % confidence interval (CI, ranging between percentiles 2.5 and 97.5).

Because of the correction for mass-dependent fractionation, both Δ¹⁴C and F¹⁴C do not reflect the effects of isotope fractionation. The variations in the radiocarbon signature will be related to the age of the carbon.

2.5 Conversion to mean transit time and reference atmospheric radiocarbon

To obtain a mean transit time from the estimated ¹⁴C signature of ecosystem respiration, it is necessary to use atmospheric radiocarbon data as a reference. We used a compilation of recently reported data from the CORSO project as a reference for the atmospheric radiocarbon data in our study region, which include time series of atmospheric radiocarbon measured at research stations in the tropical region and surroundings. The data used for the conversion of $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ into mean transit time included the stations BHD (Baring Head, Aotearoa / New Zealand ), CGO (Cape Grim, Australia), MER (Mérida Observatory, Venezuela) and SMO (Cape Matatula, Samoa) (Graven et al., 2012; Turnbull et al., 2017; Levin et al., 2010, 2022). The data were smoothed using curve fitting methods applied to time series in NOAA/ESRL/GMD (https://gml.noaa.gov/ccgg/mbl/crvfit/crvfit.html, last access: 15 December 2023) (Thoning et al., 1989), accounting for interannual variability, and this is reported in decimal years. The atmospheric Δ¹⁴C–CO₂ was averaged by year to have one value of Δ¹⁴C–CO₂ per year for the comparison with the year of collection of samples. The CORSO data are available in the Heidelberg University repository (https://heibox.uni-heidelberg.de/d/1f481155f63c46a8aaf0/, last access: 21 November 2023), and the CORSO report, with details of the collection and filtering of data, is available on the ICOS Carbon Portal (https://meta.icos-cp.eu/objects/HnpnYFcQljQ-SJer66F-hr-b, last access: 21 November 2023).

To estimate the time between C assimilation and release from the ecosystem (mean transit time), the $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ obtained from the intercept of the Keeling plot and the slope of the Miller–Tans plot was compared to the subset of the CORSO data described above. The difference between the year of collection of the samples and the equivalent calendar years where $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ = atmospheric Δ¹⁴C–CO₂ translates into an estimate of mean transit time in units of years (yr). When $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ is not equal to the atmospheric Δ¹⁴C–CO₂ of a given year, the calendar year with the closest atmospheric Δ¹⁴C–CO₂ to $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ is taken. Estimates of mean transit time are based on the variability of the mean $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ ± σ (standard error of the linear regression), with the 95 % confidence interval of the mean reported within parentheses.

2.6 Comparison with other approaches

The values of $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ obtained from end-member mixing analysis were converted to mean transit time and compared with predictions of two carbon balance models that can estimate the mean transit time of C in tropical ecosystems and with an estimate of the mean transit time produced from a synthesis of carbon and radiocarbon studies in the central Amazon region (Trumbore and De Camargo, 2009).

The first model is a simple one-pool model obtained as the total ecosystem C stock divided by the input GPP flux. This ratio provides an estimate of turnover time, as reported by Carvalhais et al. (2014) for tropical forests at the global scale. The assumption of a one-pool model with this turnover time results in a probability distribution of turnover times that follows an exponential distribution with a mean equal to the turnover time (Metzler and Sierra, 2018). Because, for a one-pool model, the age, turnover, and transit time of C are equal (Bolin and Rodhe, 1973; Sierra et al., 2017), we assume that this distribution of turnover times is equivalent to the distribution of transit times.

The second model is a multi-compartmental model developed for the Porce region of Colombia (Sierra et al., 2021b). This model tracks the movement of C across seven ecosystem compartments, namely foliage, fine litter, wood, coarse woody debris, fine roots, coarse roots, and soil carbon (0–30 cm). It produces estimates of the transit time distribution of carbon assuming a constant GPP input flux of 24 ± 2 $\mathrm{Mg}\mathrm{C}{\mathrm{ha}}^{-\mathrm{1}}{\mathrm{yr}}^{-\mathrm{1}}$.

A third estimate of a transit time distribution of C for tropical forests was obtained from the synthesis of the carbon and radiocarbon studies of Trumbore and De Camargo (2009). These authors reported a mean age of ecosystem respired CO₂ of 3–7 years. Their estimate was based on respiration fluxes and the mean ages of C in CO₂ derived from the decomposition of wood and roots in addition to radiocarbon-based turnover times of soil carbon (Chambers et al., 2004; Vieira et al., 2005; Telles et al., 2003; Trumbore et al., 2006).

All computations were performed in the R environment (R v.4.2.2) using RStudio (version 2023.03.0+386).

3 Results

3.1 Keeling plots

We produced Keeling plots for both isotopes, δ¹³C–CO₂ and Δ¹⁴C–CO₂, and for the two separate sampling campaigns in 2019 and 2021. For δ¹³C–CO₂, the intercept of the Keeling plot yielded a value of −27.8 ‰ ± 0.3 ‰ for October 2019 and a value of −29.0 ‰ ± 0.5 ‰ for December 2021 (Fig. 1). The statistical fit of the data to the linear model was remarkably good, with the values of the R² coefficient being equal to 1.0.

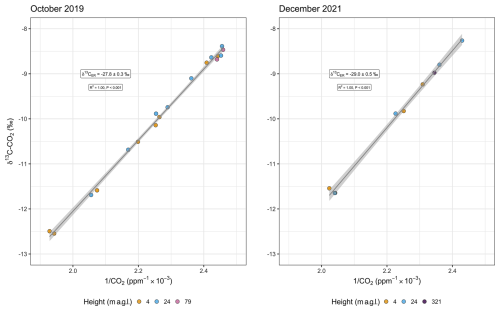
Figure 1 Keeling plot of δ¹³C–CO₂ from below-canopy (4 and 24 m a.g.l.) and above-canopy (79 m a.g.l.) air for 5–6 October 2019 and 19–20 December 2021. The y intercept ($\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$) changes from −27.8 ‰ ± 0.3 ‰ to −29.0 ‰ ± 0.5 ‰. Analytical errors of δ¹³C–CO₂ ranged from 0.005 ‰ to 0.04 ‰. Similarly, analytical errors of CO₂ vary between 0.01 and 0.3 ppm. Therefore, error bars are not easily visible in this scale.

The $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ (i.e., y intercept) values obtained from the Keeling plots for October 2019 and December 2021 were significantly different (year predictor p value<0.001). The daytime CO₂ range (i.e., the difference between minimum and maximum concentrations over all heights) was approximately 111 ppm in October 2019, and in December 2021, it was slightly lower at 92 ppm. During the nighttime, the CO₂ range was about 50 ppm in 2019 and 66 ppm in 2021 (Fig. S1 in the Supplement). The δ¹³C–CO₂ mean value during the nighttime was −10.5 ‰, which agrees well with the mean observed in 2019. The daytime mean δ¹³C–CO₂ was more enriched in the heavier isotope (−9.3 ‰) based on 13 daytime samples in 2019 and 4 daytime samples in 2021. Minimum values of δ¹³C–CO₂ during the daytime and nighttime are, nevertheless, very similar (−11.5 ‰ and −11.6 ‰, respectively).

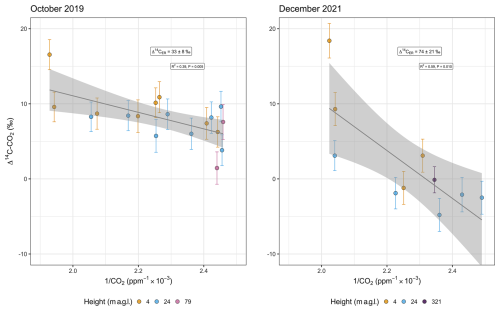
Variability during the daytime and nighttime and between sampling campaigns was much more pronounced for radiocarbon (Fig. 2) than for δ¹³C–CO₂. The statistical fit of the linear regression of the Keeling plot was relatively low for radiocarbon (R²=0.39 in 2019 and 0.59 in 2021), although the obtained values of the intercepts were statistically significant (p values=0.005 and 0.010 for 2019 and 2021, respectively).

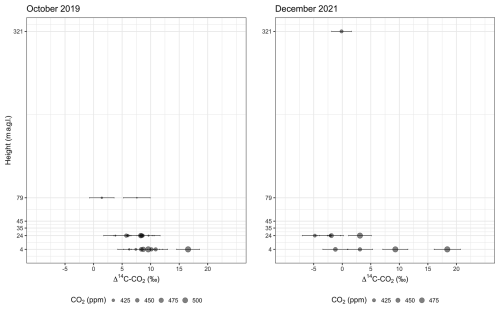
Figure 2 Distribution of values of Δ¹⁴C–CO₂ and CO₂ concentrations according to the sampling heights below (4 and 24 m a.g.l.) and above (79 and 321 m a.g.l.) the canopy. The canopy level in the study plot is around 35 m, and some emergent trees occur at 45 m height. The CO₂ concentration at 321 m is based on measurements from a flask, and the Δ¹⁴C value is the average between two integrated samples (see main text). Analytical errors of Δ¹⁴C–CO₂ measurements vary between 1.7 ‰ and 2.3 ‰.

Δ¹⁴C–CO₂ comprised a larger range of values in the second campaign, including more negative values at 24 m and a higher maximum (18.4 ‰ ± 2.3 ‰) occurring during the daytime (Fig. 2). The minimum Δ¹⁴C–CO₂ during the daytime was −2.5 ‰ ± 2.2 ‰, while, during the nighttime, it was −4.8 ‰ ± 2.2 ‰, both measured at 24 m. However, the ΔCO₂ was smaller in the second campaign, which implied a larger error in the Keeling plot, as a consequence of the extended extrapolation to obtain the y intercept. The $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ mean values and standard error were 33 ‰ ± 8 ‰ and 74 ‰ ± 21 ‰ in October 2019 and December 2021, respectively (Fig. 3).

Figure 3 Keeling plot of Δ¹⁴C–CO₂ for sampling campaigns in October 2019 and December 2021. $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ values change from 33 ‰ ± 8 ‰ to 74 ‰ ± 21 ‰. The light-gray ribbon represents the 95 % confidence interval of the predictions.

3.2 Miller–Tans model

The background CO₂ concentration for October 2019 was 408.2 ppm (σ=2.2 ppm) based on two flasks collected at 79 m in the afternoon because flask sampling at 321 m started only in 2021. The background CO₂ concentration for December 2021 was 426.4 ppm (σ=0.002 ppm) based on one flask collected at 321 m. Based on continuous measurements in 2022, a daily variation of CO₂ is estimated to be approximately 34 ppm at 81 m and approximately 14 ppm at 321 m (Fig. S2).

Alongside the small variation in the CO₂ concentrations at 79 m in 2019, δ¹³C–CO₂ varied from −8.5 ‰ to −8.7 ‰. Nevertheless, the estimates of $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ are not significantly different between Keeling and Miller–Tans approaches despite the explicit incorporation of background variations in the latter method, remaining at around −27.8 ‰ ± 0.3 ‰ for October 2019 and −29.0 ‰ ± 0.5 ‰ for December 2021 (Miller–Tans plot not shown for δ¹³C–CO₂).

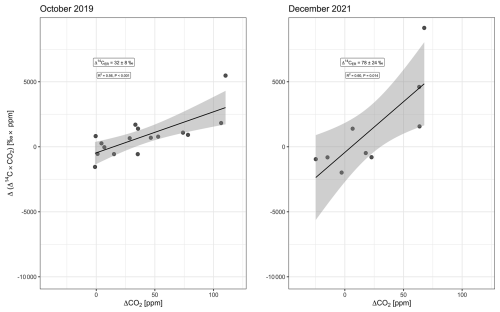
Background Δ¹⁴C–CO₂ is based on 1-month-integrated samples. For the campaign of October 2019, we used a sample collected between 9 September 2019 and 15 October 2019, with a Δ¹⁴C–CO₂ of 8 ‰ ± 2 ‰. For the December 2021 campaign, two samples collected between 24 November 2021 and 26 January 2022, were averaged, providing a Δ¹⁴C–CO₂ equal to 0 ‰ ± 2 ‰ (unpublished data). The Miller–Tans-based mean $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}\pm \mathrm{1}\mathit{\sigma }$ was 32 ‰ ± 8 ‰ (15 ‰–48 ‰, 95 % CI) in October 2019 and 78 ‰ ± 24 ‰ (21 ‰–135 ‰, 95 % CI) in December 2021 (Fig. 4). Estimates in F¹⁴C are given in the Appendix (Fig. A1).

Figure 4 Miller–Tans model (with ordinary least squares regression) for October 2019 and December 2021. The light-gray ribbon represents the 95 % confidence interval.

3.3 Estimates of mean transit time and comparison to other values from the literature

Our values of $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ obtained through end-member mixing analysis were compared with radiocarbon atmospheric records to estimate the mean age of the respired CO₂ – in other words, the mean transit time of carbon.

The Keeling plot for the campaign in October 2019 results in a mean $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ of 33 ‰, with a standard error of 8 ‰ (17 ‰–50 ‰, 95 % CI), which corresponds to the atmospheric Δ¹⁴C–CO₂ of the years 2015 to 2011 CE (common era) (2017 to 2008 CE, 95 % CI) based on the CORSO data. Thus, the corresponding mean age of respired CO₂ for the samples collected in October 2019, i.e., 2019 minus 2015 and 2019 minus 2011, is 4–8 years (2–11 years, 95 % CI). The $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ based on the samples collected in December 2021 corresponds to the atmospheric Δ¹⁴C–CO₂ of the years 2007 to 1999 CE (2015 to 1994 CE, 95 % CI), which corresponds to a mean age of ecosystem respiration of 14–22 years (6–27 years, 95 % CI).

The Miller–Tans approach for the campaign in October 2019 results in a $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ range that corresponds to the atmospheric Δ¹⁴C–CO₂ of the years 2015 to 2011 CE (2017 to 2009 CE, 95 % CI) based on the CORSO data, i.e., a similar range as the Keeling plots. Thus, the corresponding mean age of respired CO₂ for the samples collected in October 2019 by the Miller–Tans approach is 4–8 years (2–10 years, 95 % CI). The $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ based on the samples collected in December 2021 corresponds to the atmospheric Δ¹⁴C–CO₂ of the years 2007 to 1998 CE (2016 to 1993 CE, 95 % CI), which corresponds to a mean age of ecosystem respiration of 14–23 years (5–28 years, 95 % CI).

Estimates of the mean transit time of tropical ecosystems are available from three other approaches (Table 1). In the first approach (where turnover time equates to stock over flux), Carvalhais et al. (2014) reported a mean turnover time of 14 years (12–18 years, 95 % CI), obtained as the ratio of the total C stock to GPP for tropical forests. It represents the mean of an exponentially distributed transit time distribution (Metzler and Sierra, 2018).

Table 1 Estimates of mean transit time of C for ATTO for the years 2019 and 2021 based on the conversion of $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ (mean values ±σ) into mean transit time of carbon. The mean transit time based on the 95 % CI range is presented within parentheses. Comparison between different approaches, namely the end-member mixing analyses of this study at the ATTO site (Keeling plot and Miller–Tans plot), and estimates for other sites and tropical regions. For steady-state systems, the estimate of the mean transit time of C does not change with the year. The turnover time is as estimated by Carvalhais et al. (2014). The seven-pool model was computed by Sierra et al. (2021b). The data synthesis was done by Trumbore and De Camargo (2009).

In a multi-compartmental approach, the transit time distribution reported from a seven-pool model for the Porce region of Colombia has a mean value of 11 ± 1 years (Sierra et al., 2021b).

Based on a synthesis of carbon and radiocarbon data, Trumbore and De Camargo (2009) reported an average age of respired CO₂ weighted by the fluxes of different compartments (e.g., litter, wood) that ranged from 3 to 7 years for central Amazon forests near Manaus.

4 Discussion

4.1 What is the mean transit time of C for an Amazon terra firme forest estimated with Keeling and Miller–Tans plots of ¹⁴CO₂?

We estimated the mean transit time of C for a tropical forest ecosystem using Keeling and Miller–Tans plots from field measurements of ¹⁴C–CO₂. Although Keeling plots have been successfully used over decades to characterize the δ¹³C signature of ecosystem respiration (e.g., Ehleringer and Cook, 1998; Knohl et al., 2005; de Araújo et al., 2008; Mauritz et al., 2019), the method has rarely been used with ¹⁴CO₂. The Miller–Tans approach with radiocarbon was used previously to understand biogenic and fossil sources contributing to the atmospheric air in urban environments (Miller et al., 2020). To our knowledge, the study of Phillips et al. (2015) was the first that combined isotope mixing analysis with ¹⁴CO₂ measurements to estimate the age of respired carbon in a temperate forest ecosystem.

Our approach provided estimates of mean transit time in a range from 2 to 28 years (95 % CI), differing depending on the sampling campaign. These estimates of mean transit time suggest that the carbon fixed during photosynthesis in these tropical forests is respired, on average, within 1 to 3 decades. The $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ estimated through the Keeling plot is equal to the estimate obtained through the Miller–Tans plot (where the background is explicitly incorporated). The similarity of $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ estimates in both methods suggests that the small variations in CO₂ concentrations and δ¹³C–CO₂ at 79 m were small enough not to violate the implicit assumption of a stable background in the Keeling plot method. The results of $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ suggest that the source of ecosystem respiration has shifted between the two sampling campaigns from a value of −27.8 ‰ ± 0.3 ‰ in 2019 to a more depleted value of −29.0 ‰ ± 0.5 ‰ in 2021 (p<0.001 with the year as a predictor). These changes in δ¹³C–CO₂ are known to occur in the Amazon region due to changes in precipitation (Ometto et al., 2002; Pataki et al., 2003). Assuming that the environmental factors altering δ¹³C–CO₂ are also responsible for the changes in the Δ¹⁴C–CO₂, the observed difference in $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ may help to explain the differences in mean transit time that we observed among the two field campaigns. Changes in other environmental factors such as soil moisture may have also contributed to this difference in mean transit times. Chambers et al. (2004) have demonstrated that, for example, high soil respiration fluxes correlate with low soil moisture levels in the central Amazon. Furthermore, changes in the composition of pools contributing to respired C can alter its C transit time (Lu et al., 2018). Meteorological data from the 80 m walk-up tower show that precipitation and soil water content were higher during the campaign of December 2021 than in the campaign of October 2019 (Figs. S4 and S6).

Allowing the background to vary (Miller–Tans approach) requires knowing the values of the Δ¹⁴C–CO₂ and CO₂ concentrations during the sampling period. In this study, we used a few afternoon samples from the height of 79 m a.g.l., which, despite being reasonable, may still not be the best option for our fits, especially because it does not cover the whole sampling period. The measurements from 321 m a.g.l. are closer to an actual background; however, the resolution of 1 month in those samples could impair our ability to distinguish small variations that we may have captured in our 2 d campaigns.

Moreover, the estimate of mean transit time is done by comparison with long-term records of Δ¹⁴C–CO₂ in the background atmosphere. This implies the need for a time series of Δ¹⁴C–CO₂ that is representative of the study region. Even though the division of regions in the bomb curve (Hua et al., 2022) is a useful guide, direct measurements of Δ¹⁴C–CO₂ are still largely lacking in the Amazon region. Moreover, the atmospheric dynamics over the Amazon Basin are not trivial (Ancapichún et al., 2021), and the location of ATTO is influenced by mixed sources throughout the year (Botía et al., 2022).

Based on back-trajectory footprint analysis, the air circulation over ATTO between 80 and 1000 m a.s.l. is highly influenced by the oscillation of the Intertropical Convergence Zone (ITCZ). During the wet season (February–May), the air masses predominantly follow a northeastern path, while, during the dry season (August–November), the dominant wind directions come from the southeast, where the arc of deforestation is located in Brazil (Pöhlker et al., 2019; Saturno et al., 2018). The ITCZ also influences the air movement over ATTO during the dry-to-wet (December–January) and wet-to-dry (June–July) seasons, making the ATTO site meteorologically located in the Northern Hemisphere (NH) during the former and meteorologically located in the Southern Hemisphere (SH) during the latter (Andreae et al., 2015). According to the division of zones proposed by Hua et al. (2022), which also takes into account the ITCZ patterns, the ATTO site would be located in SH Zone 3. However, the patterns of air movement above the central Amazon suggest that a mixed curve (Marsh et al., 2018) must be more appropriate when estimating mean transit times based on Δ¹⁴C–CO₂ in the central Amazon.

Keeling plots of Δ¹⁴C–CO₂ (where no background subtraction is applied) differ from the Miller–Tans approach by a few per mille, which corresponds to 1 to 2 years in mean transit time considering a steady annual decline of 3 ‰ to 5 ‰ in atmospheric Δ¹⁴C–CO₂. This indicates that choosing between Keeling and Miller–Tans approaches for estimating the $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ is not the main factor impacting the precision and accuracy of the mean transit time estimate based on observations of ¹⁴C–CO₂ in a vertical subcanopy profile. The sample size and uncertainty of C isotopic ratio measurements may have a larger influence on the standard errors of the y intercept and slope of the regression lines in the Keeling plot and Miller–Tans plot, respectively. The method of employing end-member mixing analysis to ¹⁴CO₂ measurements thus also seems promising for the tropical regions alongside the temperate regions, as demonstrated before by Phillips et al. (2015). Nevertheless, more work is needed to repeat the measurements with seasonal frequency in the Amazonian region and to obtain similar estimates in other tropical regions worldwide. Additional estimates of empirical mean transit time would better quantify spatial and temporal variations in the C mean transit time. Furthermore, they would help to understand whether variations in the mean transit time are due to interannual variability or a trend in shifting mean transit times in tropical terrestrial ecosystems (Sierra et al., 2023).

4.2 How does this empirical mean transit time compare to model estimates of transit time in the Amazon region?

We compared our observation-based results with three previous estimates of mean transit time for tropical forests: the apparent turnover time estimated by Carvalhais et al. (2014) from GPP and total carbon stocks, the estimate of the age of respired carbon from a synthesis of observations reported by Trumbore and De Camargo (2009) for the central Amazon region, and the mean value of a transit time distribution computed with a seven-pool model for the Porce region of Colombia (Sierra et al., 2021b; Chanca et al., 2022).

In two short campaigns such as ours, the observed increase in the radiocarbon signature may be related to a short-term increase in the flux of one of the older respiration sources. Potential sources of radiocarbon that could be relevant due to being large enough and having high enough radiocarbon contents are dead wood (either as standing dead trees or as coarse woody debris) or old soil organic matter that gets destabilized with high water contents during the rainy season. For the ATTO site, there is good evidence that shows strong differences in temperature, precipitation, solar radiation, and soil water content between the two sampling campaigns (Figs. S3–S6), which may help to explain differences in transit times.

To evaluate changes in the isotopic signature of the main ER sources, the $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ was estimated through Keeling plots using the same samples. The $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ showed a smaller variation than $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$, being −27.8 ‰ ± 0.3 ‰ in October 2019 and −29.0 ‰ ± 0.5 ‰ in December 2021. A similar variability in $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ has been observed in a topographical gradient at the Reserva Cueiras, a site in the central Amazon approximately 80 km away from ATTO (de Araújo et al., 2008). In that case, the valleys presented more negative $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ values than the plateau areas during the dry season. The variability observed by de Araújo et al. (2008) indicated a correlation between $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ and the water vapor saturation deficit in the air (D), which was more evident on the plateaus than on the valleys. In their study, a $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ about 1 ‰–1.5 ‰ lighter was linked to a high D with low soil water contents, which resembles our campaign of October 2019 in comparison to December 2021.

Our data are spatially and temporally limited. Although the observed difference in $\mathit{\delta }{{}^{\mathrm{13}}\mathrm{C}}_{\text{ER}}$ is statistically significant, it is not possible to set apart the effects of seasonal variability or changes on the fluxes of the respiration sources on the C isotopic signatures. Hence, the observed differences in $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ and, thus, mean transit time might be related to seasonal variabilities that cannot be fully assessed with sporadic campaigns. To effectively elucidate the underlying drivers of the variability in the mean transit time, more ecosystem respiration sampling for radiocarbon measurements (and δ¹³C as the ancillary) is needed.

The mean transit time for the campaign in 2021 agrees with the turnover time estimated by Carvalhais et al. (2014); however, the same does not hold for the campaign in 2019, when the mean transit time based on end-member mixing analysis is shorter. The approach of Carvalhais et al. (2014) to obtain a turnover time integrates over large temporal and spatial scales by incorporating gross primary production values and C stocks over several years and with a resolution of 0.5°. However, it does not discern between pools of different ages that contribute in varied proportions to the total respiration flux. Therefore, it cannot account for pools with different Δ¹⁴C but can only approximate the radiocarbon signature within a well-mixed total ecosystem respiration. Moreover, some of the potential reasons for the mismatch in 2019 include a seasonal variability of Δ¹⁴C–CO₂ in the central Amazon, different contributions of respiration sources from year to year due to climate variations, or even a poor representation of local measurements in a short-term campaign in comparison to the dynamics of the whole Amazon rainforest. More studies conducted in different seasons, targeting individual respiration sources, and covering larger temporal and spatial scales are needed to overcome these different possibilities. The comparison with other estimates of mean transit time, however, suggests that this metric might not be constant over time, even for old-growth forests in the central Amazon.

In contrast, in sites close to Manaus, Trumbore and De Camargo (2009) estimated a mean transit time of 3 to 7 years, which is similar to the value obtained in this study if we consider only the campaign of October 2019. The $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ of the second campaign (December 2021) generates a mean transit time of about 14 to 23 years, which is about 3 times higher than the estimate by Trumbore and De Camargo (2009) for the central Amazon; however, this is similar to the age estimate of 24 years by Fung et al. (1997) for heterotrophically respired C in broad-leaved evergreen tropical forests, also cited by Trumbore and De Camargo (2009). However, the model used by Fung et al. (1997) assumed that 50 % of C was respired autotrophically, with one-third of the remaining 50 % being allocated to leaves, one-third being allocated to stems, and one-third being allocated to roots. In contrast, the study of respiration fluxes (Chambers et al., 2004) demonstrated that autotrophic respiration returned 70 % of the C assimilated by a central Amazon rainforest to the atmosphere; thus, we expect the transit time estimate of Fung et al. (1997) to be systematically too long. The estimates of Trumbore and De Camargo (2009) were based on respiration fluxes, mean ages of C in decomposing wood and roots, and turnover times of soils based on radiocarbon data (Chambers et al., 2004; Vieira et al., 2005; Telles et al., 2003; Trumbore et al., 2006). Such information was summarized into an estimate of the mean time lag between photosynthetic assimilation and ecosystem C release through respiration. This time lag can be compared to our estimate of mean transit time based on $\mathrm{\Delta }{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}$ as both are defined similarly and either intrinsically or explicitly incorporate the path of C through multiple interconnected pools with different turnover times.

A seven-pool model developed for a tropical forest in Colombia (Porce model) has a mean transit time of 10 to 12 years (Sierra et al., 2021b), which falls in between the mean transit time we estimated for October 2019 and December 2021. Therefore, it suggests that a multi-compartmental model estimates an average of the differences or trends of the ecosystem's mean transit time. The Porce model accounts for the C composition and C age structure of different compartments. A similar model for the central Amazon could be parameterized to account for the potential respiration sources that could drive the radiocarbon isotopic signature of ecosystem respiration by being large enough and by having high radiocarbon contents, such as dead wood (Chambers et al., 2004). This way, the empirical estimate of mean transit time can help to constrain a multi-compartmental model that is more representative of the central Amazon forest.

Our analysis shows that an empirical mean transit time based on forest air Δ¹⁴C–CO₂ coupled to isotope mixing analysis compares well with model estimates and other experimental approaches, at least for tropical forests. The differences from one year to the other or even between seasons imply a potential natural variability in the weights of fluxes from different C pools, with large differences in their turnover times. This variability could influence the C balance calculation in Amazon forests more than previously thought. In this sense, a practical method to calculate an ecosystem time metric such as transit time might improve our understanding of the C balance in Amazon forests and their role as C sources and sinks of atmospheric CO₂. This method also has the resolution to tackle temporal and spatial variabilities of the mean transit time of ecosystem respiration.

5 Conclusions

We obtained, for the first time in a tropical forest, an empirical estimate of a mean transit time of the carbon of ecosystem respiration based on end-member mixing analysis of radiocarbon measurements of ambient and atmospheric CO₂. We estimate the mean transit time of carbon for a plateau area of a near-pristine central Amazon forest, ranging from 1 to almost 3 decades. Our results suggest that a potentially large proportion of carbon assimilated through photosynthesis is released back to the atmosphere relatively quickly. This could affect interpretations of the role of Amazon forests as a C sink or source.

Our results also showed that the age of respired carbon may be highly dynamic, with important changes among seasons or years. This is in contrast to model-based estimates of transit time that often make the assumption of equilibrium and therefore cannot predict a time-dependent mean transit time. Potential reasons for the variability of transit times include (i) natural variation of ecosystem processes due to the seasonality and inter-annual variability of environmental factors (e.g., changes in precipitation), (ii) human activities such as fire that release old carbon and affect atmospheric Δ¹⁴C–CO₂, and (iii) high spatial and temporal heterogeneity in the sources of respired C at the ecosystem level. Hence, it is essential to monitor the mean transit time of tropical ecosystems because it can change over time. Additionally, studies exploring the ¹⁴CO₂ respired by different components can help to define the underlying distribution of the transit time of C that can have its mean value compared to the empirical estimate obtained through end-member mixing analysis.

The method presented here was scarcely employed in the past and was non-existent as applied to an Amazon forest. However, this method has large potential for understanding not only the source of respired carbon but also its age and the speed at which carbon is assimilated and respired by forest organisms. The method is particularly useful in tropical forests because of the large gradients and diurnal variations in the CO₂ concentration and its Δ¹⁴C in the dense forest canopy. We showed that our sampling design was effective in obtaining a meaningful mean transit time of C with observations and isotope mixing analysis. Our mean transit time also compares well to other previous estimates based on model or data syntheses.

Appendix A: End-member mixing models with F¹⁴C notation

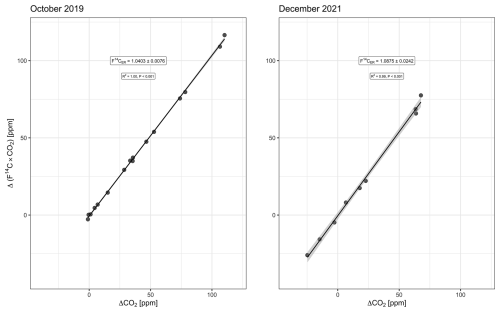
Figure A1 Miller–Tans model (with ordinary least squares regression) for October 2019 and December 2021. Slope of the regression line is the radiocarbon isotopic signature of the ecosystem respiration in F¹⁴C notation, i.e., F¹⁴C_ER. $F{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}=\mathrm{1.0403}$ ± 0.0076 in October 2019 and $F{{}^{\mathrm{14}}\mathrm{C}}_{\text{ER}}=\mathrm{1.0875}$ ± 0.0242 in December 2021. The light-gray ribbon represents the 95 % confidence interval.

In other studies using Miller–Tans plots of Δ¹⁴C–CO₂, the context of interest has been to determine the fossil fraction in CO₂ emissions in urban areas (e.g., Miller et al., 2020). In such contexts, Δ¹⁴C–CO₂ has values that are always below zero (down to −1000 ‰ if 100 % fossil). On the other hand, ecosystem respiration can have a variety of Δ¹⁴C–CO₂ values, linked to the varied radiocarbon signatures of its sources. Therefore, in the context of this study, Δ¹⁴C–CO₂ can be positive (e.g., decomposition of old carbon with bomb signature), negative (pre-bomb or contemporaneous atmosphere), and zero (when the atmospheric value crosses from the bomb ¹⁴C signature to natural levels). In the Miller–Tans plots, the y axis is the product of the C isotopic ratio by the CO₂ concentration (of the subcanopy values minus the background value) (Eq. 6). Thus, in Δ¹⁴C notation, a data point with a y value equal to zero can be a consequence of (i) a subcanopy combination (Δ¹⁴C×CO₂) equal to the current atmosphere or (ii) simply a Δ¹⁴C equal to zero. Such ambiguity does not occur when F¹⁴C is used instead because F¹⁴C can only assume positive values. Calculating the Miller–Tans plot with F¹⁴C or Δ¹⁴C does not change the value of the slope of the regression line; therefore, it does not change the estimate of the mean transit time.