The effect of carbonate mineral additions on biogeochemical conditions in surface sediments and benthic–pelagic exchange fluxes

Coastal sediments are hotspots of biogeochemical processes that are impacting subsurface and overlying water conditions. Fluid composition in sediments is altered through the mineralization of organic matter which, under oxic conditions, further lowers both pH and the carbonate saturation state. As a potential mitigation strategy for this sediment acidification, we explored the effects of mineral additions to coastal sediments. We experimentally quantified carbonate mineral dissolution kinetics of carbonate shells suitable for field application and then integrated these data into a reactive transport model that represents early diagenetic cycling of C, O, N, S, and Fe and traces total alkalinity, pH, and saturation state of CaCO₃. Model simulations were carried out to delineate the impact of mineral type and amount added, porewater mixing, and organic matter mineralization rates on sediment alkalinity and its flux to the overlying water. Model results showed that the added minerals undergo initial rapid dissolution and generate saturated conditions demonstrating the potential of alkalinity enhancement in mitigating surface sediment acidification. Aragonite dissolution led to higher total alkalinity concentrations than calcite. Simulations of carbonate mineral additions to sediment environments with low rates of organic matter mineralization exhibited a substantial increase in mineral saturation state compared to sediments with high CO₂ production rates, highlighting the environment-specific extent of the effect of mineral addition. Our work indicates that carbonate additions have the potential to effectively buffer surficial sediments over multiple years, yielding biogeochemical conditions that counteract the detrimental effect of low-pH sediment conditions on larval recruitment and potentially increase benthic alkalinity fluxes to support marine carbon dioxide removal (mCDR) in the overlying water.

1 Introduction

In coastal systems, ocean–freshwater mixing, terrestrial inputs, and active biogeochemical transformations (Cai et al., 2017; Soetaert et al., 2007) lead to natural fluctuations in pH that are large and decoupled from the decrease in pH observed in the open ocean due to ocean acidification (Hofmann et al., 2011). Especially in shallow-water environments, sediments play a significant role as benthic fluxes can constitute a substantial alkalinity source to the overlying water, increasing its buffering capacity (Rassmann et al., 2016; Krumins et al., 2013; Cyronak et al., 2013b). Sediments receive organic matter (OM) from the overlying water, which fuels the dissolution of carbonate minerals and early diagenetic processes. Aerobic respiration and other processes consuming dissolved O₂ can lead to steep pH decreases within the oxygenated sediment and the interaction of OM mineralization, and mineral dissolution determines the balance of the porewater carbonate system (Burdige et al., 2010; Jourabchi et al., 2005). Mineral dissolution and early diagenesis are connected through the changes in carbonate system, which impacts mineral saturation states and hence the rate of dissolution (e.g., Morse et al., 2007). Apart from its impact on mineral dissolution, OM mineralization is also a significant contributor to alkalinity generation under suboxic and anoxic conditions (Hu and Cai, 2011a). These early diagenetic processes determine the composition of the porewaters, which affect benthic calcifying organisms; furthermore, they can affect the biogeochemical conditions in the overlying water through benthic fluxes releasing nutrients and alkalinity.

In surface sediments, porewater pH is generally lower than in the overlying water, in particular when sediment O₂ uptake is elevated due to burrowing and irrigation activities by benthic macrofauna (e.g., Aller, 1982). This exposes benthic organisms that live in the upper layers of the sediment to more corrosive conditions (Green et al., 2013; Waldbusser and Salisbury, 2014). Combined with abundant OM, enhanced supply of O₂ into the sediment also leads to elevated fluxes of alkalinity and dissolved inorganic carbon (DIC) to the water column (Mucci et al., 2000; Burdige, 2007).

In this study, we investigate the effects of the addition of carbonate minerals in the coastal sediments focusing on benthic alkalinity generation and release in a shallow-water environment. Such ocean alkalinity enhancement (OAE) aims to buffer increased dissolved CO₂ in the ocean by dissolving carbonate or silicate minerals, producing alkalinity. OAE is mainly studied for its effect on ocean–atmosphere CO₂ exchange, the impact on organisms (Renforth and Henderson, 2017), and its potential to mitigate ocean acidification and lower atmospheric CO₂ concentrations (marine carbon dioxide removal; mCDR). Previous studies have shown that increasing ocean alkalinity through enhanced weathering has the potential to reverse global ocean acidification in an intermediate CO₂ emission scenario (RCP 4.5) and reduce its impacts if emissions were to continue to rise throughout the 21st century (RCP 8.5) (Taylor et al., 2016). To date, OAE implementations mainly have targeted the open ocean and have been aimed at identifying the potential of scaling up the mCDR efforts to a global scale (Fennel et al., 2023). Recent studies also focused on the impact of OAE on marine ecosystems such as fish and plankton communities (Goldenberg et al., 2024; Paul et al., 2024; Ferderer et al., 2022). Only a few studies have focused on coastal OAE and even fewer on sedimentary applications (Green et al., 2009, 2013; Hangx and Spiers, 2009; Fuhr et al., 2024), where the effectiveness of OAE mainly depends on the dissolution rate of the mineral which is controlled by the mineral and the chemistry of the water and physical properties of the environment (Hartmann et al., 2013; Montserrat et al., 2017). One benefit of implementing OAE in coastal sediments is the generally higher rate of organic matter remineralization. This elevated CO₂ generation aids mineral dissolution, given most overlying marine waters are typically super-saturated with respect to carbonate minerals. Here, we simulate this effect of adding carbonate minerals to the sediment using a reactive transport model. We use measurements of carbonate mineral dissolution rates to assess the extent and duration of buffering in surficial sediments and the impact on benthic alkalinity fluxes. Building on the previous work by Krumins et al. (2013) that explored the interaction of carbonate chemistry with early diagenesis in coastal sediments, our work identifies factors that determine the impact of sediment alkalinization on the spatial and temporal distribution of buffering by exploring the effect of mineral type, amount, organic matter remineralization rate, and bioturbation.

2 Methods

2.1 Dissolution experiments

Dissolution rates for the minerals used in this model were derived from lab-based experiments detailed in Myers (2022). We provide pertinent details below. Two biomineral calcium carbonates – calcitic oyster shells of Crassostrea gigas (below referred to as “biocalcite”) and aragonitic soft-shell clam shells of Mya arenaria (“bioaragonite”) – were collected from Oregon Oyster Farm in Newport, Oregon, USA, and from Broad Cove in Yarmouth, Maine, USA, respectively. The biomineral samples were briefly cleaned, dried, crushed, and sieved through a 2000 µm sieve and retained on 710 µm, for an approximately median grain size of 1 mm. We measured the mineral dissolution rate across four saturation states experimentally; Ω_calcite=0.25 (low), 0.45 (middle), 0.85 (high), and 1.03 (saturated); carbonate chemistry conditions are detailed in Table S1 in the Supplement. A flow-through, feedback-controlled with pH monitoring and a CO₂ injection seawater system similar to Waldbusser et al. (2011), was used for manipulations at the Hatfield Marine Science Center (HMSC), Newport, OR, USA (additional details in Myers, 2022). pH measurements from each manipulation tank were compared against a benchtop meter daily during the experiment. pH was additionally compared against a reference sample in which pCO₂ and TCO₂, in situ temperature, and salinity were measured to calculate pH on the NBS scale. pH (all tanks) and temperature (low and pretreatment tanks) data were recorded every 10 min. The coefficient of determination (R²) between measured benchtop pH data and the pH data calculated from pCO₂ and TCO₂ measurements for header tanks in all experiments was consistently greater than 0.9 across all experiments (Fig. S2 in the Supplement). Plug-flow style dissolution chambers were 2.5 cm i.d., 12.7 cm long, schedule 40 PVC pipe, with 150 µm Nitex mesh on either end of the upright chambers. Approximately 50 (±0.1) g of biomineral was used in each chamber; water was initially added slowly and agitated to remove air bubbles prior to initiating flow. Flow rates were controlled to 17 (±1.2) mL min⁻¹ and experiments were run for 3–4 d to verify consistent alkalinity concentrations, as observed in trials conducted to optimize the experiment (Myers, 2022). Using the inlet and outlet measured alkalinity concentrations from an individual chamber (mol alkalinity L⁻¹), the measured flow rate (L d⁻¹), and the known amount of sample added (g_mineral), the change in alkalinity in mol alkalinity $g_{\mathrm{mineral}}^{-\mathrm{1}}$ d⁻¹ was recorded as Eq. (1):

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }={\displaystyle \frac{\left({\left[\mathrm{alkalinity}\right]}_{\mathrm{outlet}}-{\left[\mathrm{alkalinity}\right]}_{\mathrm{inlet}}\right)}{\left(\mathrm{mineral}\mathrm{amount}\right)}}\times \text{flow\hspace{0.17em} rate}.\end{array}$$

The early diagenetic model (see below) uses a rate law in which the volumetric dissolution rate R_d (in mol_mineral m${}_{\mathrm{sediment}}^{-\mathrm{3}}$ d⁻¹) depends on the concentration of the mineral (mol_mineral m${}_{\mathrm{sediment}}^{-\mathrm{3}}$), the saturation state Ω (= ion concentration product/solubility K_sp), and the dissolution rate constant k_d (d⁻¹) (Jourabchi et al., 2008):

$$\begin{array}{}\text{(2)}& R_{\mathrm{d}}=k_{\mathrm{d}}\left[\mathrm{mineral}\right]{\left(\mathrm{1}-\mathrm{\Omega }\right)}^n.\end{array}$$

In the experiment, the dissolving mineral is the entire solid phase so that g_mineral=g_{solid phase}. Hence, the mineral concentration in mol${}_{\mathrm{mineral}}/g_{\mathrm{solid}\mathrm{phase}}$ is the molecular weight of the mineral (MW_mineral), and k_d can be calculated from the measured Δ as

$$\begin{array}{}\text{(3)}& k_{\mathrm{d}}={\displaystyle \frac{\mathrm{\Delta }\times {\mathrm{MW}}_{\mathrm{mineral}}}{\frac{\mathrm{dTA}}{\mathrm{d}R}\times {\left(\mathrm{1}-\mathrm{\Omega }\right)}^n}},\end{array}$$

where dTA/dR is the mineral to alkalinity stoichiometric ratio in the dissolution reaction (+2 mol_alkalinity / mol_mineral; Table 3) and n is the rate order.

2.2 Carbonate chemistry measurements

2.2.1 Alkalinity

Open-cell alkalinity titrations were conducted over the course of the experiment, utilizing a two-point titration after Edmond and Gieskes (1970), as modified by Waldbusser et al. (2011). A micrometer burette was used with a micro pH probe with precisions of 0.002 mL and ±0.02, respectively. The probe was calibrated with NBS calibration standards (pH =4, 7, and 10) daily before being used to take measurements. As outlined in Waldbusser et al. (2011), Baker Analyzed Reagent grade 0.0995–0.1005 normal HCl acid was used as the titrant with reagent grade NaCl to a final molar concentration of 0.7 to minimize gap junction potentials during titrations. Analytical precision and accuracy were compared against triplicate titrations and Dickson CRM batch 142, respectively, and found to have an average coefficient of variance of 0.07 % and typically ±16 µmol or less, for precision and accuracy.

2.2.2 Dissolved inorganic carbon, pCO₂, and carbonate calculations

pCO₂ and TCO₂ samples were collected in clean amber glass ∼350 mL bottles preserved with 30 µL of saturated HgCl₂ and sealed with polyurethane-lined crimp-sealed metal caps. Analysis via the Burkalator was carried out to measure pCO₂ and TCO₂ via near-infrared detection following the procedure of Bandstra et al. (2006), modified for discrete samples as in Hales et al. (2005), Barton et al. (2012), and Hales et al. (2017). Liquid and gas standards were employed to ensure the accuracy of pCO₂ and TCO₂ measurements. The system can resolve the accuracy and precision of TCO₂ concentrations within ±0.02 % and 2 % for pCO₂ (Hales et al., 2017). Carbonate chemistry parameters were calculated using dissociation constants from Millero (2010). Salinity was measured on the sample bottles following pCO₂ and TCO₂ measurements via a salinometer (8400B Autosal Laboratory Salinometer; Guildline Instruments, Sorrento, FL, USA). Calculated carbonate chemistry variables presented in association with the mineral dissolution experiments were computed using CO2calc and the K₁ and K₂ carbonic acid dissociation constants from Lueker et al. (2000), $K_{{\mathrm{HSO}}_{\mathrm{4}}}$ constants from Dickson (1990), sulfate constants from Morris and Riley (1966), fluorine constants from Riley (1965), and boron constants from Uppström (1974).

Table 1 State variables and their upper boundary conditions. Seawater compositions are computed with AquaEnv (Hofmann et al., 2010) for the pressure, temperature, and salinity given in Table 2.

Table 2 Environmental parameters.

2.3 Reactive transport modeling

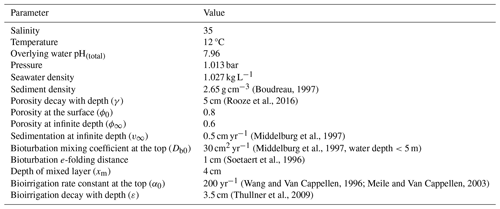
A one-dimensional diagenetic model was developed to simulate the distribution of chemical species with depth in the sediment over time. The model domain extended 20 cm deep into the sediment discretized into 50 intervals with a linearly increasing grid size of 1 mm at the top and 1 cm at the bottom. The model included 13 state variables, representing chemicals involved in the main early diagenetic reactions and mineral dissolution/precipitation (Table 1). At the upper boundary, the concentrations of solutes and fluxes of solids were imposed, while at the bottom boundary, no gradient conditions were imposed for all chemicals.

The spatiotemporal evolution of the concentrations was described by an advection–diffusion equation with the addition of bioturbation and bioirrigation and the effect of reactions. Bioturbation was treated as a diffusive process (Boudreau, 1997), and bioirrigation was described as a non-local exchange between porewater at depth and the overlying water (Boudreau, 1984). The governing equations were

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}\mathit{\varphi }{\displaystyle \frac{\partial C_i}{\partial t}}& =-{\displaystyle \frac{\partial \mathit{\varphi }u{C}_i}{\partial x}}+{\displaystyle \frac{\partial }{\partial x}}\left(\mathit{\varphi }\left(D_i+D_{\mathrm{b}}\right){\displaystyle \frac{\partial C_i}{\partial x}}\right)\\ & +\sum _r{s}_{ir}{R}_r+B_i\end{array}\text{(5)}& {\displaystyle }\begin{array}{rl}\left(\mathrm{1}-\mathit{\varphi }\right){\displaystyle \frac{\partial C_j}{\partial t}}& =-{\displaystyle \frac{\partial \left(\mathrm{1}-\mathit{\varphi }\right)v{C}_j}{\partial x}}\\ & +{\displaystyle \frac{\partial }{\partial x}}\left(\left(\mathrm{1}-\mathit{\varphi }\right)D_{\mathrm{b}}{\displaystyle \frac{\partial C_j}{\partial x}}\right)+\sum _r{s}_{jr}{R}_r\end{array},\end{array}$$

where t is time, x is depth in sediment, ϕ is porosity, C_i (C_j) is the concentration of the solute i (in mol per volume pore fluid; solid j in mol per volume solid phase), u is the burial velocity for solutes (v for solids), D_i is the diffusion coefficient of the solute i, D_b is the depth bioturbation coefficient, R_r is the rate of production/consumption through reaction r (in mass per total volume and time), s is the stoichiometric coefficient for solute i or solid j in reaction r, and B_i represents bioirrigation for solute i.

Porosity is constant with time but depth-dependent and exponentially decreases with depth, reflecting steady-state sediment compaction (Eq. 6):

$$\begin{array}{}\text{(6)}& {\mathit{\varphi }}_x={\mathit{\varphi }}_{\mathrm{\infty }}+\left({\mathit{\varphi }}_{\mathrm{0}}-{\mathit{\varphi }}_{\mathrm{\infty }}\right)e^{-\frac{x}{\mathit{\gamma }}},\end{array}$$

where ϕ_∞ and ϕ₀ are the porosities at infinite depth and at the top of the sediment, respectively, and γ is the e-folding distance for the porosity. Burial velocities were corrected for compaction (Berner, 1980):

$$\begin{array}{}\text{(7)}& {\displaystyle }{u}_x=v_{\mathrm{\infty }}{\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{\infty }}}{\mathit{\varphi }}}\text{(8)}& {\displaystyle }{v}_x=v_{\mathrm{\infty }}{\displaystyle \frac{(\mathrm{1}-{\mathit{\varphi }}_{\mathrm{\infty }})}{\left(\mathrm{1}-\mathit{\varphi }\right)}}.\end{array}$$

Diffusion coefficients were calculated using the R package marelac after Boudreau (1997) at a given salinity, temperature, and pressure (Soetaert et al., 2010) and corrected for tortuosity (Boudreau, 1996) so that

$$\begin{array}{}\text{(9)}& D_i={\displaystyle \frac{D_{\mathrm{aq},i}}{\mathrm{1}-\mathrm{2}\ln \left({\mathit{\varphi }}_x\right)}},\end{array}$$

where D_aq is the molecular diffusion coefficient of solute i in solution. The bioturbation coefficient decreases exponentially with depth below the mixed layer:

$$\begin{array}{}\text{(10)}& D_{\mathrm{b}}=D_{\mathrm{b}\mathrm{0}}{e}^{-\max (\mathrm{0},x-x_m)},\end{array}$$

where x_m is the depth of the mixed layer and D_b0 is the bioturbation coefficient at the sediment–water interface (SWI), calculated as a function of water depth (Middelburg et al., 1997).

Bioirrigation is defined as an exchange between the surface layer and deeper layers of the sediment, which was constrained by a bioirrigation coefficient exponentially decreasing with depth:

$$\begin{array}{}\text{(11)}& B_x={\mathit{\alpha }}_{\mathrm{0}}{e}^{(-\frac{x}{\mathit{\epsilon }})}{\mathit{\varphi }}_x\left(C_{i,\mathrm{0}}-C_{i,x}\right),\end{array}$$

where α₀ is the bioirrigation coefficient at the SWI, ε is the e-folding distance for bioirrigation, and C_i,x is the concentration of solute i at depth x.

Table 3 Reactions included in the model. Benthic primary production is assumed to be negligible, and organic matter has Redfield stoichiometry (a=1, $b=\mathrm{16}/\mathrm{106}$, $c=\mathrm{1}/\mathrm{106}$). Alkalinity production or consumption in each reaction is determined following Wolf-Gladrow et al. (2007). The total mineralization rate is defined as $R_C=R_C^{\mathrm{0}}\times \exp (-x/{\mathit{\gamma }}_{\mathrm{om}})$ after Wang and Van Cappellen (1996), where γ_om is e-folding distance for OM mineralization.

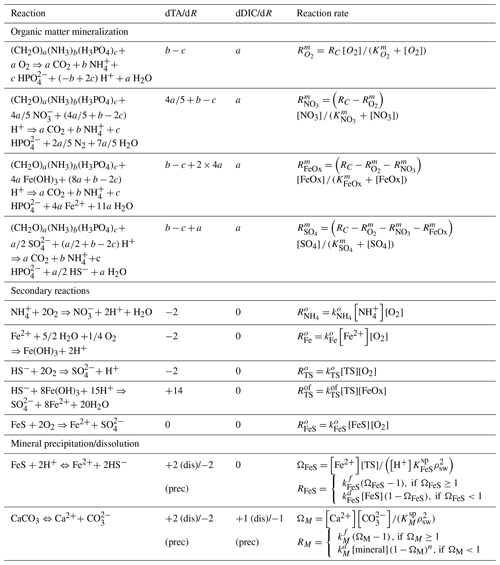
Reactions considered in the model include organic matter mineralization with aerobic and anaerobic pathways, reoxidation of reduced species, and mineral formation/dissolution reactions (Table 3). Each reaction has an impact on the total alkalinity (TA), which was taken from previous studies (Wolf-Gladrow et al., 2007; Dickson, 1981).

Organic matter is mineralized using O₂, NO${}_{\mathrm{3}}^{-}$, iron (oxyhydr)oxides (FeOx), and SO${}_{\mathrm{4}}^{\mathrm{2}-}$ as terminal electron acceptors and modeled with Monod kinetics. The OM mineralization rate ($R_C^{\mathrm{0}}$) was adjusted to yield a TA flux of ∼1200 µmol cm⁻² yr⁻¹. This value was chosen to match open-core top incubations measured in Yaquina Bay (Myers, 2022), with the resulting $R_C^{\mathrm{0}}$ value being comparable to earlier measurements by D'Andrea and DeWitt (2009) (∼200–460 µmol C cm⁻³ yr⁻¹) and higher than values reported for deeper coastal environments (Wang and Van Cappellen, 1996; Krumins et al., 2013). Reactions considered further include nitrification, iron oxidation, sulfide oxidation with O₂ and FeOx, and iron sulfide oxidation, as well as the formation/dissolution of CaCO₃ minerals and FeS (Table 3). Following Rooze et al. (2020), at each time step, DIC is speciated to calculate CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentration and pH from DIC and alkalinity, assuming seawater concentrations of borate and negligible contributions of phosphate, silicic acid, nitrite and hydrogen fluoride, and other acids or bases.

Table 4 Reaction constants. Carbonate dissolution rate constants determined experimentally in this study are described in the results.

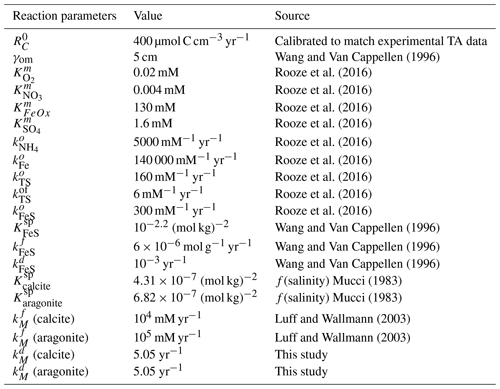
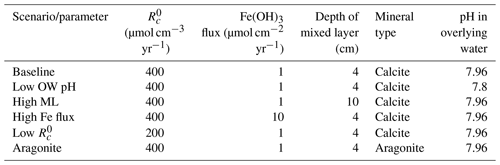
Table 5 Sensitivity analyses. Rows represent the scenario tested. Columns show the parameters changed. OW – overlying water; ML – mixed-layer depth.

2.3.1 Application

To establish initial conditions, each simulation was first run to steady state with a zero-deposition flux of calcium carbonate. After that, 8 wt % or 16 wt % (weight of mineral/total weight of the sediment) CaCO₃ was added to the top 2 cm of sediment, representing the sudden, one-time addition of the buffering carbonate minerals. To assess the magnitude and temporal evolution of the impact of the alkalinization experiment on sediment biogeochemistry and benthic fluxes, transient simulations using these new initial conditions were then carried out, covering periods of up to 50 years.

We tested the impact of several environmental factors on the buffering effect of carbonate mineral additions to surficial sediments in comparison to the baseline addition scenario (Table 5). Specifically, we lowered the overlying water pH from 7.96 to 7.8, representing the impact of ocean acidification. The depth of the bioturbated layer affects the distribution of minerals added, which may impact the effectiveness of the extent of buffering; it was varied from the relatively shallow mixing depth of 4 cm in the baseline implementation to the global average depth of bioturbation of 10 cm (Boudreau, 1997). We also varied the deposition flux of iron (oxy)hydroxides from 1 to 10 µmol cm² yr⁻¹ to assess differences between sites that vary in the extent of coupling between Fe, S, and C cycles. And as the rate of organic matter mineralization has a major impact on sediment redox conditions and porewater composition, $R_C^{\mathrm{0}}$ was varied from the baseline value of 400 to 200 µmol cm⁻³ yr⁻¹ to represent environments with different O₂ penetration depths. Finally, simulations were carried out to assess the impact of the type of mineral in the system (calcite vs. aragonite). The spinup simulations were specific to each model run and as such represent the environmental conditions (e.g., high vs. low rate of mineralization or a setting in which either aragonite or calcite are the only carbonate mineral considered). Simulations were performed in R using the ReacTran package (Soetaert and Meysman, 2012).

2.3.2 CO₂ drawdown

We estimated the potential impact of enhanced sediment TA fluxes on atmospheric CO₂ uptake in an enclosed bay using a simple box model. Water exchange is due to the tides, and riverine impact was assumed negligible, reflecting for example the strong coupling of Yaquina Bay with the coastal ocean (Brown and Ozretich, 2009).

To estimate the order of magnitude of the impact of mineral additions on CO₂ uptake, we used a simple mass balance approach similar to Brenner et al. (2016), which focuses on the ratio of DIC over TA as the controlling factor of CO₂ uptake (Egleston et al., 2010). We calculated the mass balance for TA and DIC prior to and 2 years after the mineral addition and attributed the difference in atmospheric CO₂ exchange to the mineral addition. As described in detail in the Supplement, we first estimated tidal water exchange from water level measurements. The characteristics of the inflowing marine (alkalinity =2.2 mmol L⁻¹, pH =8.0) and outflowing bay water (alkalinity =1.9 mmol L⁻¹, pH =7.96) were chosen to be representative of a coastal setting such as Yaquina Bay and were informed by unpublished temperature, salinity, and pH data (George Waldbusser, personal communication, 2024). Combined with our modeled benthic exchange fluxes, this allowed us to estimate the alkalinity production in the water column (R_TA; Eq. 12). At steady state, the alkalinity balance is given by

$$\begin{array}{}\text{(12)}& F_i^{\mathrm{TA}}-F_{\mathrm{o}}^{\mathrm{TA}}+F_{\mathrm{b}}^{\mathrm{TA}}+R^{\mathrm{TA}}=\mathrm{0},\end{array}$$

where $F_i^{\mathrm{TA}}$ is the tidal influx of TA as a function of water exchange rate and oceanic TA ($F_i^{\mathrm{TA}}=v\left[{\mathrm{TA}}_{\mathrm{ocean}}\right]$), $F_{\mathrm{o}}^{\mathrm{TA}}$ is the tidal outflux of TA from the bay to the ocean as a function of tidal velocity and TA of the study site ($F_{\mathrm{o}}^{\mathrm{TA}}=v\left[{\mathrm{TA}}_{\mathrm{site}}\right]$), $F_{\mathrm{b}}^{\mathrm{TA}}$ is the benthic flux computed by the reactive transport model, and R^TA is the areal net rate of water column TA production/consumption resulting from primary productivity and respiration.

Next, we used the alkalinity and pH to calculate the DIC and converted the net alkalinity production rate into net DIC production in the water column, assuming Redfield stoichiometry. This finally allowed us to estimate the CO₂ exchange flux ($F_{\mathrm{a}}^{\mathrm{DIC}}$) necessary to close the DIC mass balance for benthic fluxes with and without mineral additions to quantify its effect on ocean CO₂ uptake.

The mass balance for DIC is given by

$$\begin{array}{}\text{(13)}& F_i^{\mathrm{DIC}}-F_{\mathrm{o}}^{\mathrm{DIC}}+F_{\mathrm{b}}^{\mathrm{DIC}}+F_{\mathrm{a}}^{\mathrm{DIC}}+R^{\mathrm{DIC}}=\mathrm{0},\end{array}$$

where $F_i^{\mathrm{DIC}}$ is the tide-driven influx of DIC ($F_i^{\mathrm{DIC}}=v\left[{\mathrm{DIC}}_{\mathrm{ocean}}\right]$), $F_{\mathrm{o}}^{\mathrm{DIC}}$ is the outflux of DIC ($F_{\mathrm{o}}^{\mathrm{DIC}}=v\left[{\mathrm{DIC}}_{\mathrm{bay}}\right]$), $F_{\mathrm{b}}^{\mathrm{DIC}}$ is the benthic flux of DIC, $F_{\mathrm{a}}^{\mathrm{DIC}}$ is the atmospheric CO₂ uptake (negative values indicate outgassing), and R^DIC is the net areal reaction rate producing/consuming DIC.

3 Results and discussion

3.1 Mineral dissolution rates

Dissolution rates of minerals were highest under highly undersaturated conditions (Fig. 1). Dissolution rates are approximately proportional to the degree of saturation. Thus, the dissolution rate constant k_d for each mineral was estimated using Eqs. (1) and (2) with a dissolution order (n) of 1. However, we acknowledge the large variability in mineral dissolution dynamics (especially n) in previous studies (see, e.g., Adkins et al., 2021; Subhas et al., 2018), which is a critical factor for the evolution of the dissolution rate over time. Our results are in line with previous data synthesis studies focused on mineral dissolution (e.g., Morse et al., 2007; Jourabchi et al., 2005, 2008). The kinetic constant for aragonite dissolution was previously reported as 5 yr⁻¹ (Luff and Wallmann, 2003), which was comparable to the 5.2 yr⁻¹ derived from our measurements. For n=1, Jourabchi et al. (2005) reported a dissolution rate constant of 3.65 yr⁻¹, while our estimation for biocalcite was 5 yr⁻¹. Measured dissolution rates did not show significant differences between two mineral types (t test with p value >0.05). Therefore, a kinetic constant for both minerals was calculated as 5.05 yr⁻¹.

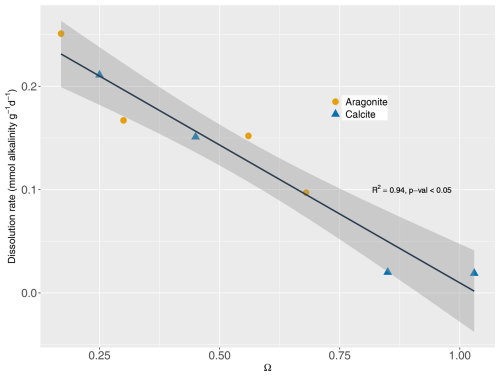
Figure 1 Saturation state for aragonite and calcite vs. their respective dissolution rates (mmol alkalinity g${}_{\mathrm{solid}}^{-\mathrm{1}}$ d⁻¹). Line shows the fit with n=1. R²: coefficient of determination. p value: statistical significance of the fit. Shaded area represents the 95 % confidence interval.

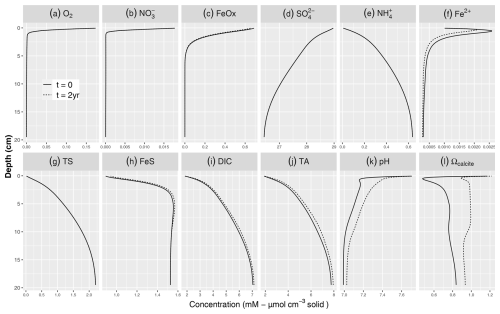
Figure 2 Simulated baseline porewater profiles of (a) O₂, (b) NO${}_{\mathrm{3}}^{-}$, (c) FeOx, (d) SO${}_{\mathrm{4}}^{\mathrm{2}-}$, (e) NH${}_{\mathrm{4}}^{+}$, (f) Fe²⁺, (g) TS, (h) FeS, (i) DIC, (j) TA, (k) pH, and (l) Ω_calcite with 8 % calcite addition. The solid lines denote the steady-state profiles prior to the addition of calcite to the top 2 cm, while the dashed lines indicate the simulated profiles 2 years after the mineral addition (some coincide with the solid lines and hence not visible). Dissolved constituents are in mmol L⁻¹ porewater, while solids are given in µmol cm⁻³ solid phase.

3.2 Early diagenetic modeling

To assess the impact of sediment alkalinization through the addition of carbonate minerals to the sediment, early diagenetic model simulations were carried out that describe the spatiotemporal distribution of porewater and solid phase constituents.

Prior to the addition of minerals, the simulated porewater profiles show sequential depletion of electron acceptors with depth, with O₂, NO${}_{\mathrm{3}}^{-}$, and reactive FeOx only present in the top 5 cm (solid lines in Fig. 2). SO${}_{\mathrm{4}}^{\mathrm{2}-}$ is present throughout the depth range and only decreases by about 2.5 mM. As a result of mineralization reactions, the concentrations of reduced porewater constituents (TS (total sulfide), NH${}_{\mathrm{4}}^{+}$, Fe²⁺) increase with depth (Fig. 2). Reduced dissolved iron (Fe²⁺) peaked around 1 cm and then decreased with depth due to the precipitation of FeS, which in our baseline simulation limited the buildup of hydrogen sulfide (TS) and dissolved reduced iron (Fe²⁺). These porewater profiles reflect the sequential use of electron acceptors in the mineralization of organic matter, through aerobic respiration and anaerobic pathways such as denitrification, dissimilatory iron, and sulfate reduction. The dominant OM mineralization pathway was SO${}_{\mathrm{4}}^{\mathrm{2}-}$ reduction, (78.9 %) followed by aerobic mineralization (17.2 %), denitrification, (3.9 %) and iron reduction (0.06 %).

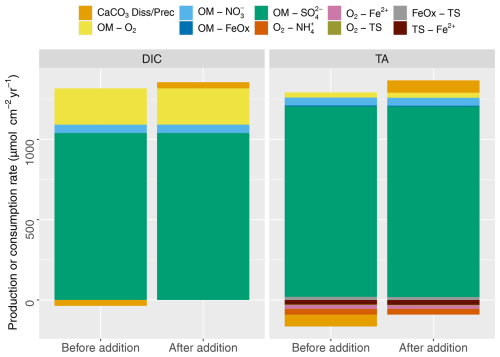
Figure 3 DIC and TA production (positive) and consumption (negative) by different early diagenetic processes integrated over the entire model domain for steady state (t=0; before addition) and 2 years after the addition.

DIC and TA show pronounced concentration increases with depth, reflecting OM mineralization (Fig. 2i, j). The pH profile exhibits a rapid decrease in the top centimeter to about 7, showing the impact of CO₂ production without the concurrent consumption of protons through aerobic mineralization (Table 3; Jahnke et al., 1994; Green et al., 2013). Below the oxic layer, active anaerobic OM mineralization pathways such as iron and sulfate reduction can generate considerable amounts of TA if the reaction products are not oxidized (Thomas et al., 2009). This was observed in the buildup of reduced species such as TS (discussed below), which limited the drop in pH and increased saturation state (from 0.5 to >0.8) in the deeper layers of the sediment (Fig. 2k, l). pH values were in the lower part of the range reported in Krumins et al. (2013), reflecting the lack of carbonates buffering the pH prior to the mineral additions. Sulfate reduction produced the majority of the TA and DIC (Fig. 3), consistent with the findings of Krumins et al. (2013), Brenner et al. (2016), and Gimenez (2018). Aerobic mineralization produced considerable amounts of DIC, in line with previous work (Thamdrup and Canfield, 2000), while generating less TA than anaerobic processes and mineral dissolution (Fig. 3), leading to a low porewater pH (Soetaert et al., 2007; Hofmann et al., 2011). DIC and TA production by denitrification and in particular dissimilatory iron reduction was substantially less. With a high dTA/dR value (Table 3), TS oxidation with FeOx also contributed to alkalinity production. Consumption of TA was dominated by secondary redox reactions that oxidize reduced species with O₂. Due to fast kinetics, Fe²⁺ oxidation with O₂ and nitrification and precipitation of FeS were the major TA-consuming reactions. Brenner et al. (2016) identified sulfide oxidation and nitrification as the dominant alkalinity-consuming processes in the shallow-water sediments in southern North Sea. This discrepancy may be due to the potentially substantial impact of sulfide oxidation on alkalinity dynamics in organically rich nearshore sediments (Krumins et al., 2013). The oxidation of reduced products of organic matter mineralization such as ammonium, hydrogen sulfide, and dissolved Fe²⁺ with O₂ all lower alkalinity, albeit using different amounts of molecular oxygen. However, the oxidation of hydrogen sulfide with iron oxide as an electron donor produces a large amount of alkalinity that either accumulates if the reduced iron produced is captured in the sediment or is removed if the Fe²⁺ subsequently reacts with O₂ in the oxic zone (see Table 3). Coupling of SO${}_{\mathrm{4}}^{\mathrm{2}-}$ reduction with FeS precipitation has been shown to be an important mechanism for TA burial on continental shelves (Gustafsson et al., 2019). However, in our simulations, FeS formation was limited by Fe availability, which led to the buildup of hydrogen sulfide in the porewater.

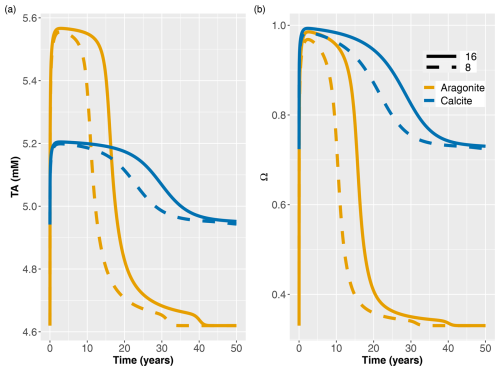
Figure 4 Temporal evolution of depth-averaged TA after addition of bioaragonite and biocalcite (a) and saturation states (b) in the baseline simulation. Concentrations and saturation states are averaged over the top 10 cm of sediment. Colors show the type of mineral added. Solid and dashed lines show the addition of 16 % and 8 %, respectively.

3.2.1 Effect of carbonate mineral additions

After adding carbonate minerals, the concentration profiles of primary redox species remained largely unchanged (Fig. 2). This is because the organic matter mineralization rate expressions (Table 3) do not contain dependencies on the carbonate system or pH, as is common in early diagenetic models (e.g., Jourabchi et al., 2008; Morse and Mackenzie, 1990). Mineral addition slightly decreased Fe²⁺ while increasing FeS concentrations. This is due to TA production due to carbonate dissolution, which elevates the pH and increases the saturation state of FeS (Table 3), promoting FeS formation, which eventually can lead to the long-term removal of reduced sulfur through pyrite burial (Hu and Cai, 2011a)

The added carbonate minerals started to dissolve in our model, producing one DIC and two TA per carbon (Burdige et al., 2010; Zeebe and Wolf-Gladrow, 2001) so that both the pH (Fig. 2k) and porewater saturation state (Figs. 2l and 4b) initially increased (Cai et al., 2011). After 2 years, CO₂ production still lowered pH in the oxic layer and prevented full saturation. However, Ω was always above 0.9 and reached 1 at and below a depth of approximately 2.5 cm, and subsequent decrease was observed below 12 cm. Following the addition of carbonates, the extent of the undersaturated conditions was constrained to the top 2 cm only, while in the natural buffering scenario reported in Krumins et al. (2013) porewater remained undersaturated in the top 10 cm. This demonstrates the potential of OAE in mitigating surface sediment acidification and providing potential benefits for calcifiers living in the upper sediment layers. As mineral addition counteracts porewater acidification, it generates biogeochemical conditions conducive to the survival of juvenile bivalves.

Our results are in line with the literature showing that the main alkalinity-producing processes were calcite mineral dissolution, sulfate reduction, denitrification, and sulfide oxidation with iron oxides (Krumins et al., 2013; Berelson et al., 2007). Although organic matter mineralization reactions generate alkalinity, they have lower dTA / dDIC ratios than mineral dissolution on a per carbon basis (Table 3), and the TA-producing mineralization reactions are mostly coupled to TA-consuming reoxidation reactions. Therefore, the net effect of (some) mineralization pathways on TA production can be limited (Krumins et al., 2013). For example, the amount of TA generated by benthic denitrification was almost balanced out by NH${}_{\mathrm{4}}^{+}$ oxidation (Fig. 3), which results in the small effect of N cycling on alkalinity. This is in line with previous studies showing strong coupling between oxidation/reduction of N in the marine environment (Middelburg et al., 1996) and its weak impact on buffering capacity of the overlying water (Hu and Cai, 2011b). Since reoxidation reactions are dependent on the availability of O₂, enhanced biological mixing can also increase TA consumption, as previously demonstrated by Rao et al. (2014) for Fe²⁺ oxidation by O₂. Although total production of TA was around 1300 µmol cm⁻² yr⁻¹ (Fig. 3, baseline with biocalcite), total TA fluxes from biocalcite were slightly lower, which points to the importance of consumption of TA in the oxic layer as previously reported in Krumins et al. (2013). Finally, before mineral addition, we observed a small production of calcite at the top of the sediment due to oversaturated conditions in overlying water. After the addition, however, the added mineral dissolved in deeper layers, which led to net dissolution and generation of alkalinity in the sediment column.

3.2.2 Temporal evolution of buffering with different minerals and amounts

Longer-term simulations (50 years) were performed to investigate the evolution of the buffering with time, considering different amounts and types of minerals added. We focused on the biogeochemical conditions in the top 10 cm of sediment, because the surficial sediment is most relevant for juvenile bivalves impacted by acidification. Figure 4 shows the temporal evolution of TA and saturation state following the addition of minerals to the steady-state conditions at t=0. Depth-averaged TA concentrations in the top 10 cm peaked around the second year after addition, with a significant drop starting around year 10 for the 8% mineral addition and around year 15 for the 16 % addition and then a return to steady-state levels after more than 30 years (Fig. 4a). Doubling the amount of mineral added generated slightly higher TA and extended the length of the peak buffering period. The simulation of aragonite addition produced higher alkalinity concentrations than that of calcite by approximately 0.3 mM at the peak time, reflecting its higher solubility. However, TA levels in aragonite application dropped faster after approximately 10 and 15 years and approached the initial premineral application levels after about 30 and 40 years, for 8 % and 16 % additions, respectively. In contrast, following the addition of calcite, TA concentrations remained elevated over longer time periods. Averaging over 4 cm (not shown) yielded the same patterns (with slightly lower TA concentrations) as shown in Fig. 4.

Being less stable than calcite, aragonite had a slightly faster dissolution rate constant and a larger solubility product (Burdige et al., 2010). Therefore, it generated higher TA concentrations and benthic fluxes early on. Because of its higher solubility, it initially took aragonite slightly longer to reach saturation than calcite (i.e., orange curve reaches maximum slightly after the blue one). As the rate of dissolution is set to be proportional not only to the degree of undersaturation but also the carbonate mineral concentration (Eq. 2), doubling the mineral addition had a more pronounced effect on aragonite, which approached saturation more slowly than calcite (Fig. 4b). Burial of carbonate minerals below 10 cm led to a faster decrease in TA in aragonite due to its higher dissolution. Initial conditions in 50-year simulations with calcite had a higher saturation state than aragonite implementation. Therefore, after the impact of addition was buried, calcite leveled at a higher saturation state and TA than aragonite.

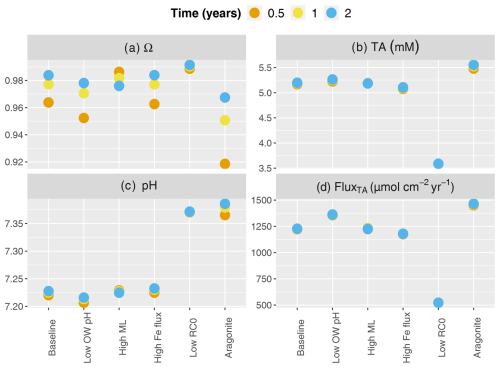
Figure 5 Buffering response after carbonate mineral additions for a range of environmental conditions. Concentrations are averaged over the top 10 cm. Scenarios listed on the x axis (from left to right) represent the baseline simulation the baseline with lower overlying water pH representing the ocean acidification scenario (7.8), the baseline with the deeper mixed layer (10 cm), the baseline with a higher Fe flux (10 µmol cm⁻² yr⁻¹), the baseline with lower $R_C^{\mathrm{0}}$ (200 µmol cm⁻³ yr⁻¹), and the baseline with aragonite instead of calcite.

3.2.3 Sensitivity analyses

The impact of mineral additions on the generation of alkalinity depends not only on the type of mineral added, but also on which early diagenetic processes dominate (Fig. 3). The relative magnitude of these processes depends on a number of factors, including the rate of organic matter mineralization, the extent of bioturbation, the deposition fluxes of potential electron acceptors such as iron oxyhydroxides, and the composition of the overlying water. Varying these factors in our model, we explore their impact on both the environmental conditions in the surficial sediment and the impact on benthic alkalinity fluxes.

In our simulations, under all scenarios, mineral saturation states reached similar values at the end of the 2 years with a low $R_C^{\mathrm{0}}$ scenario generating the highest values (blue dots in Fig. 5a). However, saturation was reached fastest in the deeper mixed-layer scenario, which then decreased by years 1 and 2. Baseline, high FeOx flux and low $R_C^{\mathrm{0}}$ scenarios showed a similar time course, while the addition of aragonite instead of calcite exhibited the slowest increase in saturation state (Fig. 5a). Depth-averaged TA concentrations were highest following the addition of aragonite (Fig. 5b). Deepening the bioturbation layer did not have much of an impact. The high FeOx flux scenario produced slightly lower TA than the baseline, and the lowest amounts of alkalinity were produced by the low $R_C^{\mathrm{0}}$ scenario. pH increased the most and fastest in the aragonite implementation, followed by low $R_C^{\mathrm{0}}$ conditions (Fig. 5c). Although the deep mixed-layer scenario increased pH faster than the baseline and high-FeOx-flux scenarios, these three scenarios converged to a similar pH to the impact of mineral dissolution developed. The highest benthic TA fluxes were generated during the dissolution of aragonite, while the lowest values were produced in the low $R_C^{\mathrm{0}}$ scenario (Fig. 5d). Baseline and deeper bioturbation layer scenarios produced very similar results, while the high-FeOx-flux scenario produced slightly lower TA fluxes. Lowering overlying water pH led to decreases in saturation state and pH while increasing concentration and flux of alkalinity.

A lower pH in the overlying water that represents ocean acidification led to a lower pH in the porewater and less saturated conditions in surface sediments (Fig. 5). This promoted mineral dissolution and therefore led to increased TA production and flux to the overlying water. This demonstrates the sensitivity of buffering to the overlying water conditions. Deeper bioturbation led to faster downward mixing and subsequent dissolution of the added mineral, which then led to a rapid increase in TA, pH, and saturation state (also seen in dpH/dTA; Fig. 4). Higher mixing led to faster transport of minerals inducing enhanced dissolution in year 0.5 (i.e., Fig. 5; higher buffering after 0.5 than 2  years after mineral addition). However, faster transport extended the depth of buffering and diluted dissolution products, which caused a slight decrease in pH and saturation state after 2 years at the top 10 cm (Fig. 5). Increased FeOx input to the sediment led to enhanced FeOx reduction, which produced TA. However, increased reoxidation of Fe²⁺ led to decreased availability of O₂ and consumption of TA. This balanced out the additional TA produced through FeOx reduction and led to the additional net consumption of ∼46 µmol cm⁻² yr⁻¹ of TA. Overall, increased iron oxide supply led to slight decreases in TA concentrations and fluxes and small increases in pH, showing an effect similar to decreasing the OM mineralization rate (Fig. 5). TA production and flux were significantly lower in the scenario with a low OM reaction rate (Fig. 5d), which showed the critical impact of OM mineralization on TA dynamics. The lower rate of OM mineralization decreases TA production, both through the reduction of overall mineralization rates and the reduction of the relative contribution of anaerobic mineralization pathways like dissimilatory sulfate reduction. The low rate of aerobic mineralization also led to reduced H⁺ production, which in turn slows carbonate dissolution (Morse and Mackenzie, 1990). However, even with lower dissolution, this situation led to higher pH than the baseline, suggesting that the artificial buffering might not be needed to maintain saturated conditions in environments where OM reactivity is low. In deeper layers where the surficial mineral addition is not as effective, TA and mineral saturation states will be lower due to lower anaerobic TA production. Notably, the effect of changing the OM mineralization rate is not linear, and halving the rate reduced the benthic alkalinity flux by a factor of about 2.5. In our simulations, the lower OM mineralization rate led to depth-integrated reduction by 29 % for aerobic mineralization, 19 % for denitrification, 55 % for sulfate reduction, and 380 % for mineral dissolution. Aside from the impact on the partitioning of OM mineralization between metabolic pathways, this mainly reflects that changes in mineralization rates lead to differences in the porewater conditions, which in turn alter the rate of mineral dissolution/precipitation. Due to the higher solubility and hence larger degree of undersaturation, initial aragonite dissolution was faster than calcite. Hence, aragonite produced the largest TA in 2 years, generated the highest benthic TA fluxes, and increased the pH the most. The addition of aragonite produced more buffering than the scenario with lower OM mineralization, which shows the potential of artificial buffering overcoming the acidification impact due to OM mineralization.

3.3 Limitations and challenges

Our model demonstrates the potential for coastal sediment alkalinization to improve the biogeochemical conditions for juvenile calcifying organisms living in surficial sediments. However, alkalinity fluxes are sensitive to overlying water conditions; temporal changes in overlying water should be considered. These changes include the impact of short-term diel patterns and small-scale spatial heterogeneity on benthic fluxes (Gadeken et al., 2023), seasonal changes such as temperature (Rao et al., 2014), and long-term changes such as anthropogenic impacts (Pacella et al., 2018; e.g., eutrophication, Cai et al., 2011). In addition, in particular in nearshore shallow-water environments, one may have to take into consideration the input of groundwater (Cyronak et al., 2013a), advective flow through sand ripples (Huettel et al., 1998), and other factors driving advective flow in marine sediments (Santos et al., 2012), which can impact sediment biogeochemistry and alkalinity fluxes. Furthermore, the prediction of the time course of buffering by mineral dissolution may need to consider dissolution rate expressions that account for changes in mineral surface areas, rather than bulk concentrations (Morse et al., 2007), and the potential for washing away or enhancing dissolution (Meysman and Montserrat, 2017) of minerals deposited to the sediment in high-energy environments.

Our results indicate a lasting buffering effect of mineral additions. This finding depends on the kinetics of the mineral dissolution rate, in particular the reaction order. Given the range of observations (Adkins et al., 2021; Subhas et al., 2018), the temporal evolution of the dissolution rates in the field needs to be explored further. In addition, our model assumes that the minerals are mixed into the upper 2 cm of sediment, matching recent field manipulation experiments in Yaquina Bay. However, an important consideration is how the minerals are applied to the surface sediment. For example, a simple “top-dressing” approach would involve less disturbance to the sediment and less labor than surface raking, but it may be washed away more easily and react less readily with the metabolic acids produced in the underlying sediment. Thus, optimal mineral application and subsequent effects clearly require field trials across a range of hydrodynamic settings.

3.4 Potential impact of benthic fluxes on marine CO₂ uptake

Benthic alkalinity fluxes are critical for water column C dynamics, especially in shallow-water environments where water column and atmospheric interactions are more sensitive to processes occurring in the sediment (Brenner et al., 2016). The significant decrease in shells due to overharvesting has likely altered alkalinity cycling in estuarine waters, such as the Chesapeake Bay (Waldbusser et al., 2013). One outcome of this benthic–pelagic connection is the impact of benthic fluxes on oceanic CO₂ uptake, which was estimated to have a significant influence in the North Sea (Thomas et al., 2009), and the potential for shallow-water sediment alkalinization to alter overlying water.

We estimated the potential impact of enhanced sediment TA fluxes on atmospheric CO₂ uptake in Yaquina Bay, OR (USA), using the diagenetic model output (baseline scenario) in a simple box model during the peak buffering period (∼2 years after addition). The bay was found to be net heterotrophic, with tidal exchange and net respiration in the water column impacting air–sea CO₂ flux the most. The impact of sediment buffering on the air–sea CO₂ was estimated as the difference in atmospheric CO₂ fluxes between before and after the mineral addition. Mineral addition resulted in a TA flux enhancement of ∼126 µmol cm⁻² yr⁻¹ and a decrease in CO₂ flux by approximately 58 µmol cm⁻² yr⁻¹, which was comparable to previous studies (Brenner et al., 2016). Scaling to a 10 m water depth (or per liter of water), this stoichiometrically estimated marine carbon dioxide removal (mCDR) due to the application and subsequent dissolution of carbonate minerals by the sediments results in a similar amount of mCDR to the current estimates of the anthropogenic C (C_anth) concentration in the US Pacific coast waters, 30–60 µmol L⁻¹ (Feely et al., 2016; Pacella et al., 2024). It is important to note three key points in this estimate: first, the uptake of C_anth by marine waters from anthropogenic activities results in an increase in DIC without any concurrent change in alkalinity and thus acidification. Second, alkalinity enhancement shifts the carbonate speciation and allows increased uptake of atmospheric CO₂ by marine waters. Thus, ocean alkalinity enhancement increases the total amount of C_anth in seawater. Third, however, C_anth and DIC both increase with OAE; the mineral dissolution due to sediment respiration results in an increase in the TA : DIC ratio, thus providing the mCDR benefit of atmospheric removal as well as mitigating existing acidification impacts. The annual mCDR effect modeled here, while notable compared to the total anthropogenic impact, is minuscule compared to the total air–sea exchange flux, which is driven by tidal exchange of DIC and alkalinity between the bay and the coastal ocean and biogeochemical processes in the water column. The signal-to-noise ratio of this potentially significant effect also highlights the existing measurement challenges in accurately discerning OAE effects within coastal systems.

4 Conclusions

Our study successfully combines lab experiments and modeling to investigate the impact of coastal alkalinity enhancement, points to critical aspects to be considered, and presents the potential of carbonate additions as a mitigation strategy for the effects of climate change in coastal settings. We demonstrated that addition of minerals increased pH and saturation state of the sediment over the time span of a few months and had the potential to persist over 30–40 years, after which subsequent additions might be needed to sustain buffering. During the peak buffering period, porewater in the top 10 cm of the sediment was almost fully saturated with respect to the mineral added, which implies favorable conditions for benthic calcifying organisms. We showed that two main pathways of producing TA in the sediment were sulfate reduction and mineral dissolution, with sulfate reduction having a larger impact. We also demonstrated that the type of mineral was an important factor affecting benthic fluxes and that the application of an increased amount of minerals was effective in extending the duration rather than the strength of the buffering.

Our analysis suggests that buffering through mineral additions to coastal sediments can establish biogeochemical conditions that are conducive to the growth and development of calcifying benthic organisms. However, the effect of mineral additions can vary substantially between environments. Sensitivity analyses demonstrated that the OM mineralization had a significant impact on mineral dissolution, pH, and mineral saturation. The type of mineral added also showed a significant effect, with aragonite producing more TA and higher pH. Increased mixing depth led to a faster increase in saturation state, while increased iron flux caused reduction in TA concentration and benthic fluxes. Overall, the addition of minerals with higher dissolution rates would be most effective especially in environments with high OM degradation and undersaturated water conditions. Similarly, the type of mineral and the environmental conditions affect mCDR potential through benthic fluxes. Importantly, the implementation of OAE can lead to unforeseen effects, including ecological feedback such as changes in species composition (Bach et al., 2019; Köhler et al., 2013), and the effectiveness of carbonate additions may depend strongly on site characteristics. Thus, studies should combine field, lab, and modeling components (Meysman and Montserrat, 2017) to improve predictive capabilities and decrease uncertainty.