Landscape analysis of soil methane flux across complex terrain

Relationships between methane (CH₄) fluxes and environmental conditions have been extensively explored in saturated soils, while research has been less prevalent in aerated soils because of the relatively small magnitudes of CH₄ fluxes that occur in dry soils. Our study builds on previous carbon cycle research at Tenderfoot Creek Experimental Forest, Montana, to identify how environmental conditions reflected by topographic metrics can be leveraged to estimate watershed scale CH₄ fluxes from point scale measurements. Here, we measured soil CH₄ concentrations and fluxes across a range of landscape positions (7 riparian, 25 upland), utilizing topographic and seasonal (29 May–12 September) gradients to examine the relationships between environmental variables, hydrologic dynamics, and CH₄ emission and uptake. Riparian areas emitted small fluxes of CH₄ throughout the study (median: 0.186 µg CH₄–C m⁻² h⁻¹) and uplands increased in sink strength with dry-down of the watershed (median: −22.9 µg CH₄–C m⁻² h⁻¹). Locations with volumetric water content (VWC) below 38 % were methane sinks, and uptake increased with decreasing VWC. Above 43 % VWC, net CH₄ efflux occurred, and at intermediate VWC net fluxes were near zero. Riparian sites had near-neutral cumulative seasonal flux, and cumulative uptake of CH₄ in the uplands was significantly related to topographic indices. These relationships were used to model the net seasonal CH₄ flux of the upper Stringer Creek watershed (−1.75 kg CH₄–C ha⁻¹). This spatially distributed estimate was 111 % larger than that obtained by simply extrapolating the mean CH₄ flux to the entire watershed area. Our results highlight the importance of quantifying the space–time variability of net CH₄ fluxes as predicted by the frequency distribution of landscape positions when assessing watershed scale greenhouse gas balances.

1 Introduction

Considerable effort has been directed to the study of carbon dioxide (CO₂) fluxes in a variety of diverse terrestrial ecosystems using both spatially distributed chamber measurements and eddy covariance methods (e.g., Lavigne et al., 1997; Sotta et al., 2004; Webster et al., 2008; Riveros-Iregui and McGlynn, 2009; Allaire et al., 2012). However, challenges associated with measuring upland methane (CH₄) fluxes (Denmead, 2008; Wolf et al., 2011) have made similar studies less prevalent, despite CH₄ being a more potent greenhouse gas (GHG) than CO₂. Global CH₄ emissions have increased by 47 % since 1970 (IPCC, 2014), and though the soil CH₄ sink is significantly smaller than its chemical oxidation in the atmosphere, the uncertainty in the size of the soil CH₄ sink is on par with the annual atmospheric CH₄ growth rate (Kirschke et al., 2013). Despite progress in our understanding of CH₄ dynamics in saturated soils, assessing the variability of CH₄ fluxes in aerated soils and exploring how landscape structure influences CH₄ fluxes and watershed CH₄ budgets have been limited. Topography can create predictable physical redistribution of resources across a landscape, suggesting that these patterns (e.g., soil moisture: Western et al., 1999; temperature: Urban et al., 2000; Emanuel et al., 2010; soil organic matter and nutrients: Creed et al., 2002; Mengistu et al., 2014) could produce observable landscape patterns in soil C fluxes (Webster et al., 2008; Riveros-Iregui and McGlynn, 2009; Pacific et al., 2011).

Net soil CH₄ flux can be highly variable in space and time, particularly because microbial production and consumption of CH₄ can occur simultaneously in the soil profile. Methane is predominantly consumed in aerated upland soils and produced in saturated or nearly saturated riparian soils. Methanogenesis occurs under anoxic conditions and at low redox potential through two major microbial pathways (CO₂ reduction and acetate fermentation) (Hanson and Hanson, 1996; Le Mer et al., 2001). Under aerobic conditions, methanotrophic bacteria oxidize CH₄ to CO₂, but anaerobic oxidation of methane (AOM) can also occur in a variety of environments, including forest soils (e.g., Blazewicz et al., 2012; Gauthier et al., 2015). The interactions of local thermodynamics and environmental conditions – including soil moisture, temperature, substrate availability, pH, and oxygen status – have made it difficult to determine the most influential parameters across ecosystems (e.g., temperate forest, desert: Luo et al., 2013). In addition, the environmental factors that create the observed heterogeneity of CH₄ fluxes can be influenced by the spatial scale of analysis. For example, the microbial dynamics that drive CH₄ cycling are influenced by small-scale (centimeter) environmental conditions (e.g., substrate availability and redox state) (Born et al., 1990; Conrad, 1996). However, at larger scales these environmental conditions can be heavily influenced by physical processes such as landscape scale (kilometer) hydrology (Burt and Pinay, 2005; Lohse et al., 2009), and at still larger scales (hundreds of kilometers, which we will refer to as “ecosystem scale”) parent material and climate create the setting in which these processes occur (Potter et al., 1996; Tang et al., 2006; Tian et al., 2010).

A spatially explicit understanding of heterogeneity in CH₄ fluxes is necessary for appropriate watershed scale budgets (Ullah and Moore, 2011; Bernhardt et al., 2017), particularly in mountainous regions, where the spatial distribution of resources could have a significant influence on the direction and magnitude of CH₄ fluxes due to the lateral redistribution of water and substrates caused by convergent and divergent areas of the landscape (Davidson and Swank, 1986; Meixner and Eugster, 1999; Wachinger et al., 2000; von Fischer and Hedin, 2002). Although many studies have quantified the magnitude and variability of CH₄ fluxes, they often covered large spatial extents (from transects that are tens of meters to hundreds of kilometers long) which captured significant environmental gradients at those scales, but sampling locations were generally sparse (Del Grosso et al., 2000; Dalal and Allen, 2008; Yu et al., 2008; Teh et al., 2014; Tian et al., 2014). The smaller-scale patterns of CH₄ fluxes within these landscapes has not been investigated as thoroughly as ecosystem scale gradients, which could be problematic if those patterns are important for estimating CH₄ fluxes (Fiedler and Sommer, 2000; Ullah and Moore, 2011; Nicolini et al., 2013).

Functional landscape elements have proven useful for assessing spatial heterogeneity and influences of scale in hydrology (Wood et al., 1988), ecology (Forman and Godron, 1981), and biogeochemistry (Corre et al., 1996; Reynolds and Wu, 1999). Functional landscape elements and terrain metrics that represent topographically driven hydrologic gradients have been used to analyze and scale biogeochemical cycles (e.g., carbon: Creed et al., 2002; Riveros-Iregui and McGlynn, 2009; Pacific et al., 2011; nitrogen: Hedin et al., 1998b; Creed and Beall, 2009; Duncan et al., 2013; Anderson et al., 2015; phosphorus: Devito et al., 2000; sulfate: Welsch et al., 2004), but limited analogous work has been done for CH₄ consumption. The importance of soil moisture in mediating CH₄ fluxes has been shown across ecosystems (Smith et al., 2000; von Fischer and Hedin, 2007), but studies of how this influence is related to, or predictable from, landscape characteristics have been limited (Boeckx et al., 1997; Creed et al., 2013). Continuous topographic metrics such as the topographic wetness index (TWI, a surrogate for water accumulation) could represent hydrologic influences on variables relevant for CH₄ fluxes (e.g., redox state, diffusivity of CH₄ and O₂, and substrate availability). Here, we build on previous research from Tenderfoot Creek Experimental Forest (TCEF) that has demonstrated how topographic metrics can represent landscape structure and its influence on hydrologic processes (Jencso et al., 2009; Jencso and McGlynn, 2011) and carbon cycling (Riveros-Iregui and McGlynn, 2009; Pacific et al., 2010, 2011). Our objectives were to determine how locally and distally mediated environmental conditions influence CH₄ fluxes, and to estimate the net seasonal CH₄ balance of the upper Stringer Creek watershed. Spatially distributed measures of soil moisture, groundwater elevation, and landscape position provide the opportunity to investigate spatial patterns of CH₄ fluxes, linking the point scale conditions to watershed scale hydrologic patterns. We suggest these approaches are beneficial for interpolating, scaling, and predicting CH₄ dynamics, particularly in complex terrain. We address the following questions to assess spatial and temporal dynamics of CH₄ fluxes across this semi-arid, subalpine landscape; examine environmental relationships; and estimate net watershed balances:

• How do environmental variables relate to CH₄ flux across a subalpine watershed through the growing season?

• How does landscape structure relate to relative magnitude and direction of CH₄ fluxes across the landscape?

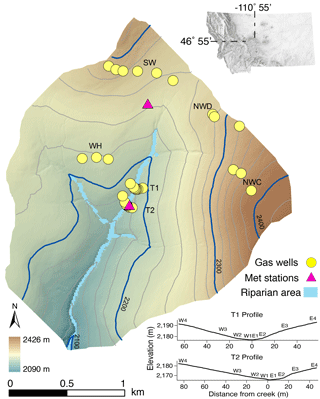
Figure 1 Map of upper Stringer Creek watershed (394 ha), located in central Montana, showing sampling locations and meteorological towers. Inset shows profiles of transects T1 and T2, where site number increases away from the creek on the west and east sides.

Figure 2 Streamflow and precipitation inputs to upper Stringer Creek over the 2013 growing season. Gas sampling began on 29 May, shortly after the first hydrograph peak.

2 Methods

2.1 Site description

Tenderfoot Creek Experimental Forest (46.55^∘ N, 110.52^∘ W) is located in the Little Belt Mountains of central Montana (Fig. 1). This study was conducted in the upper Stringer Creek watershed (394 ha; elevation 2090–2425 m), a sub-watershed of TCEF. The gentle to steep gradient slopes (average: 15 %) and the range of aspect and topographic convergence/divergence in upper Stringer Creek are characteristic of the greater Tenderfoot Creek watershed (Jencso et al., 2009).

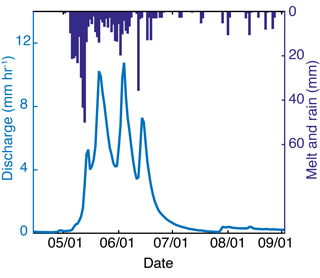
The watershed experiences a continental climate, with 70 % of the 800 mm annual precipitation typically falling as snow from November to May. Growing season length ranges from 45 to 70 days (Schmidt and Friede, 1996), and mean daily summer temperature is 11 ^∘C (Farnes et al., 1995). Peak snowmelt typically occurs between mid-May and mid-June, and the driest months occur in the late summer and fall (Fig. 2). Summer precipitation rarely causes significant streamflow response (Nippgen et al., 2011).

The geology of the Stringer Creek watershed is comprised of Flathead sandstone, Wolsey shale, and granite gneiss. Soils are shallow (< 1 m) typic cryocrepts in the uplands and aquic cryobalfs in the riparian areas. The seasonal dry-down of the upland soils vs. the riparian areas (which typically maintain a shallow water table throughout the year; Jencso et al., 2009) reflects the differentiation in soil types. Upland soils have a sandy loam texture but vary in rock and organic matter content across landscape positions.

Plant communities transition from wet riparian meadows in the valley bottom through drier meadows to the upland conifer forest. The vegetation in the riparian area is predominately grasses (Juncus, Carex, Poa) and willows (Salix) with a mixture of wildflowers (Erigeron, Aster). The forest is primarily comprised of lodgepole pine (Pinus contorta) and subalpine fir (Abies lasiocarpa); Englemann spruce (Picea engelmannii) and whitebark pine (Pinus albicaulis) are also common; and grouse whortleberry (Vaccinium scoparium) is dominant in the understory (Mincemoyer and Birdsall, 2006).

2.2 Landscape characterization

Ten-meter and 3 m digital elevation models (DEMs) were constructed by coarsening 1 m² resolution light detection and ranging (lidar) data. These data were collected in 2005 by the National Center for Airborne Laser Mapping (NCALM). We calculated topographic characteristics that describe both energy availability and relative water availability of each site using DEM landscape analysis methods as described in McGlynn and Seibert (2003). Terrain metrics included in the analysis were aspect (radians), elevation (m), insolation (kWh m⁻²), slope (%), elevation above the creek (EAC, m), distance from creek (DFC, m), gradient to creek (GTC), upslope accumulated area (UAA, m²), and the TWI (Jencso and McGlynn, 2011; Nippgen et al., 2011). Aspect and position-on-slope effects were calculated using the following vector of covariates (Clark, 1990):

$$\begin{array}{}\text{(1)}& u=\left[\begin{array}{c}\cos \mathit{\varphi }\sin \mathit{\theta }\\ \sin \mathit{\varphi }\sin \mathit{\theta }\\ \cos \mathit{\theta }\end{array}\right],\end{array}$$

where ϕ is aspect and θ is percent slope. Potential incoming insolation (from 1 May to 1 September) was calculated in the System for Automated Geoscientific Analyses (SAGA) using 1 h increments averaged over 5-day windows (Böhner and Antonic, 2009). UAA is the watershed area contributing to each point in the landscape and was derived using the MD∞ algorithm (Seibert and McGlynn, 2007). TWI has also been used as an approximation for relative wetness and was calculated using the following equation (Beven and Kirkby, 1978):

$$\begin{array}{}\text{(2)}& \mathrm{TWI}=\ln \left({\displaystyle \frac{a}{\tan \mathit{\theta }}}\right),\end{array}$$

where a is UAA and θ is local slope. All topographic metrics were assessed for relationships with CH₄ and for inclusion in the multivariate model. The riparian area was initially delineated as the area less than 2 m in elevation above the creek using topographically derived flow paths and validated with extensive field surveys (90 transects; Jencso et al., 2010).

We examined the spatial and temporal variability of CH₄ fluxes using data collected across a range of landscape positions in the Stringer Creek watershed. Terrain metrics were used to select 32 sampling sites that span a range of slopes, contributing area, and convergence/divergence in the upper Stringer Creek watershed (Fig. 1). Twenty-five sites were distributed across the uplands, and two transects that cross Stringer creek (with three to four riparian sites each) were selected to characterize the riparian and lower hillslope positions and their transition. The transition zone between the riparian area and the uplands is identified hydrologically as the toe slope position where groundwater tables persist longer than in the uplands but not through the growing season as observed in the riparian area. Measurement sites along the two transects that cross the creek are identified by the side of the creek they are on (east/west) and increase in number away from the creek.

2.3 Soil characterization measurements

Soil cores were collected on 8 and 9 July 2012 within 2 m of each gas sampling site for soil analysis. Soil cores were extracted using a 100 cm³ cylinder that was inserted into the soil, and they were laterally excavated from the organic (0–10 cm) and mineral (22.5–27.5 and 47.5–52.5 cm) soil layers (n= 32 sites). The samples were dried and weighed to calculate bulk density and were analyzed for % carbon (C) and % nitrogen (N), ∂¹³C, and ∂¹⁵N (Kansas State Stable Isotope Mass Spectrometry Laboratory, Thermo Finnigan Delta Plus mass spectrometer and CE 1110 elemental analyzer with ConFlo II Universal Interface for C and N analysis of solids; additional details in Nippert et al., 2013). These data were used to calculate total C_soil (mg cm⁻³), N_soil (mg cm⁻³), and molar C : N ratios. Intact soil cores and bulk soil samples were also collected from 0 to 5 cm on 6 and 7 August 2014 to determine porosity, bulk density, mineral bulk density, and organic content for each site. Porosity was determined by measuring the change in weight between fully saturated and oven-dried intact soil cores (n= 18). The bulk samples were used to corroborate bulk density and particle size distribution following standard procedures.

2.4 Environmental measurements

Weekly measurements of environmental variables were collected in conjunction with gas samples at each site from May to September 2013 between 09:00 and 18:00 UTC. Environmental variables that were measured included volumetric soil water content (VWC), soil temperature (12 cm soil thermometer, Reotemp Instrument Corporation, CA, USA), and barometric pressure (Atmospheric Data Center Pro, Brunton, Boulder, CO, USA). VWC was measured three times at each site during each round of sampling using a Hydrosense II portable soil water content meter (12 cm, Campbell Scientific Inc., UT, USA). The mean of the three samples was used for data analysis. We measured real-time water content hourly at individual riparian (T1E1), transition (T1E2), and hillslope (T1E3) sites using water content probes (CSI model 616, Campbell Scientific Inc., UT, USA) that were inserted from 0 to 12 cm in the soil (Fig. 1).

2.5 Hydrological measurements

Groundwater table data were recorded in wells located along the two riparian–hillslope transects to augment the weekly measurements of near-surface soil water content (Fig. 1). Groundwater wells (created from 3.81 cm diameter polyvinyl chloride (PVC), screened from completion depth to within 10 cm of ground surface) were installed along the riparian–hillslope transects (co-located with gas wells). Capacitance rods (±1 mm, Tru Track, Inc., New Zealand) in each well recorded groundwater level every 30 min. Well completion depths (to the soil bedrock interface) ranged from 0.5 to 1 m in the riparian zones and from 0.8 to 1.5 m on the hillslopes. Installation details can be found in Jencso et al. (2009). Groundwater data were also used to evaluate our initial delineation of sites as riparian vs. upland.

2.6 Soil gas measurements and flux calculations

Soil gas wells constructed of 5.25 cm diameter, 15 cm long sections of PVC were installed to sample soil air for concentration measurements of CH₄, CO₂, and O₂ at 5, 20, and 50 cm depths. Gas wells were buried at completion depths of 20 and 50 cm and capped with a size 11 rubber stopper. These gas wells were open at the bottom to equilibrate with soil gas at their respective depths. Shallow gas wells were designed to measure gas concentrations closer to the soil surface; the bottoms were closed with a PVC cap, and screened openings on the sides enabled equilibration with soil gas at 5 cm depth. All gas wells were outfitted with a closed sampling loop made of PVC tubing (4.8 mm inside diameter, Nalgene 180 clear PVC, Nalgene Nunc International, Rochester, NY, USA) that was passed through the rubber stopper and joined above the ground surface by 6–8 mm HDPE tubing connectors (FisherBrand, Fisher Scientific, USA). Thus, the equilibrium volume was the volume of the PVC well plus that of the tubing.

Weekly gas samples were taken from the closed recirculation loop after observed soil CO₂ concentration stabilized. Soil CO₂ concentration was measured in-line using a Vaisala Carbocap handheld CO₂ meter (GM70, measurement range of either 0–20 000 ppmv or 0–50 000 ppmv) adjusted for local temperature and pressure. Soil % O₂ was also measured in-line using a handheld Apogee O₂ sensor (MO-200, Logan, UT, USA; precision: ±0.1 % O₂). Once the CO₂ concentration reading stabilized, one gas sample was collected from each depth through a brass Swagelok T fitting with a 9.5 mm Cole-Parmer septum (Vernon, IL, USA) sampling port, using a PrecisionGlide needle (22G1, Becton Dickinson & Co, NJ, USA) and 60 mL Luer-Lok syringe (BD, Franklin Lakes, NJ, USA). Gas samples (∼ 50 mL) were transferred to and stored in 150 mL laminated FlexFoil sample bags (SKC, Eighty Four, PA, USA). Prior to sample collection in the field, sample bags were emptied by vacuum, filled with N₂ carrier gas, and evacuated in the lab to avoid sample contamination. This process was done twice for bags that had previously contained gas with concentrations of CH₄ considerably higher than ambient. The sampling syringe was cleared between samples and flushed with 10 mL of air from the gas well three times before slowly taking the sample (to avoid creating any vacuum in the gas well). During snowmelt, saturated soils in the riparian area resulted in flooded wells, preventing gas sampling at those time points.

Gas samples were analyzed for CH₄ at Montana State University using a Hewlett-Packard 5890 Series II gas chromatograph outfitted with a flame ionization detector (FID). The inlet system used a 10-port injection valve with a 1 cm³ sample loop. The injection valve was configured for backflushing of a precolumn (25 cm × 0.32 cm OD, packed with Porapak T 80/100 mesh) to prevent water vapor from reaching the analytical column. The sample loop temperature (ambient) was monitored using a NIST-traceable electronic thermometer, and barometric pressure was obtained from the Montana State University weather station (operated by Dr. Joseph A. Shaw). Two analytical columns (both 183 cm × 0.32 cm OD, one packed with Chromosorb 102 80/100 mesh and the other with Porapak-Q 80/100 mesh) were used in series for gas separation. The temperatures of the column oven and FID were 55 and 240 ^∘C, respectively. The carrier gas was a commercial ultra-high-purity N₂, which was further purified through Molecular Sieve 5A, activated charcoal, and an oxygen scrubber. The carrier flow to the FID was maintained at approximately 30 mL min⁻¹. Under these conditions, CH₄ eluted to the FID at 1.9 min. A certified 51 ppmv CH₄ in air standard (Air Liquide; ±1 % accuracy) was used for instrument calibration, both alone and after dilution into ultra-high-purity N₂ carrier gas; the detector response was linear, and the overall analytical precision was better than ±0.05 ppmv.

Methane fluxes were calculated using the gradient method (Fick's first law) and measured soil concentrations at 5 cm (Eq. 3).

$$\begin{array}{}\text{(3)}& f_{{\mathrm{CH}}_{\mathrm{4}}}=D_{{\mathrm{CH}}_{\mathrm{4}}}\times \left({\displaystyle \frac{d\left[{\mathrm{CH}}_{\mathrm{4}}\right]}{\mathrm{d}z}}\right),\end{array}$$

where $f_{{\mathrm{CH}}_{\mathrm{4}}}$ is the flux of CH₄ out of the soil (µg CH₄- C m⁻² h⁻¹), $D_{{\mathrm{CH}}_{\mathrm{4}}}$ is the CH₄ effective diffusivity (m² h⁻¹), and (d[CH₄]) ∕ dz is the CH₄ gradient from 0.05 m to the soil surface (µg CH₄–C m⁻⁴; the distance from the soil surface, z (m), is defined as positive upward). For determination of (d[CH₄]) ∕ dz , measured mole fractions of CH₄ were converted to mass concentrations assuming ideality of gases and using the measured soil temperature. Although this formulation does not include production or consumption that is occurring between 5 cm and the surface, the CH₄ concentration gradient from shallow depths to the surface is typically relatively linear (Koschorreck and Conrad, 1993), suggesting that determining $f_{{\mathrm{CH}}_{\mathrm{4}}}$ using a linear equation is appropriate. Effective diffusivity was estimated for each sample using an empirical relationship between the measured VWC and the ratio of CH₄ diffusivity to its value in free air at measured temperature and barometric pressure (Massman et al., 1998). This relationship (Fig. 3) was established by measuring methane flux and concentrations across a variety of spatial locations (co-located with gas wells) and time points using a LI-COR 8100A infrared gas analyzer with a 20 cm diameter chamber and an in-line sampling port for collecting discrete time-course CH₄ samples from the chamber. Our exponential model relating effective CH₄ diffusivity to soil water content is mathematically equivalent to an exponential fit of diffusivity to air-filled pore space (Richter et al., 1991) when total porosity is treated as a constant. Our model results were in good agreement with other commonly used physical models of soil gas diffusion for total porosities near 0.6 (Buckingham, 1904; Ghanbarian and Hunt, 2014; Møldrup et al., 2014) and incorporate site-to-site variability due to local VWC. We calculated cumulative seasonal CH₄ flux ($F_{{\mathrm{CH}}_{\mathrm{4}}})$ for each site by summing the linearly interpolated daily fluxes (29 May–12 September). We believe that this parsimonious approach is appropriate to assess how landscape position influences the relative magnitude of seasonal CH₄ fluxes.

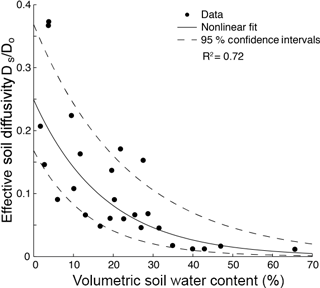
Figure 3 Relationship between effective soil diffusivity for methane D_s (expressed relative to its free-air diffusivity D_o) and soil water content. This empirical relationship was used to estimate 0–5 cm soil CH₄ diffusivity for every sampling event at each site.

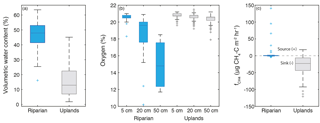
Figure 4 (a) Riparian and upland soil water content. (b) Percent oxygen of riparian and upland landscape positions at 5, 20, and 50 cm. (c) Methane flux in riparian and upland landscape positions. Riparian and upland sample sets were significantly different for all sets of data except for the 5 cm O₂ data (two-sample t test p < 0.01). Riparian measurements n= 53; upland measurements n= 259. Boxes denote 25th, 50th, and 75th percentiles; whiskers represent maximum and minimum values; and crosses denote outliers (greater than 75th percentile times interquartile range, or less than 25th percentile times interquartile range).

2.7 Statistics and modeling

We used two-sample t tests to test for differences between $f_{{\mathrm{CH}}_{\mathrm{4}}}$ and environmental variables across riparian and upland locations. We performed linear regression analysis on the upland CH₄ fluxes to assess relationships between instantaneous upland $f_{{\mathrm{CH}}_{\mathrm{4}}}$ and environmental variables using the R Stats Package (R Core Team, 2016). Further linear regression analysis was performed on natural log-transformed cumulative CH₄ influx (ln$\left|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}\right)$ vs. all terrain metrics, soil properties, and each site's average VWC (VWC_avg) and temperature (T_avg). We log-transformed the absolute value of $F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ to meet linear regression assumptions of homoscedasticity and linearity.

Table 1 Average soil characteristics with 1 standard deviation in parentheses.

We assessed two sets of predictor variables for multiple-regression modeling: (1) both terrain metrics and local soil measurements (VWC_avg, T_avg, and soil properties) and (2) only terrain metrics. We subset the predictor variables to prevent multicollinearity in the final model. If a set of topographic or soil variables had a Pearson's correlation coefficient greater than 0.6 (Dorman et al., 2013), the variable with a lower correlation with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ was removed from the multiple-regression analysis (Fig. A1 and A2). We also assessed the strength of local soil measurements independent of the multiple-regression models to determine which local variables were of most importance. A parameter jack-knife method (Phillips, 2006, 2008) was used to determine the importance of individual variables within each set of data (Fig. A4). We used the Leaps package and the exhaustive search method (Lumley and Miller, 2009) to select the best linear multiple-regression model using terrain metrics and local measurements, and terrain metrics alone in order to create a spatially distributed estimate of ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$. Model assessment was based on the adjusted r² and Bayesian information criterion (BIC; see Sect. 3.5). Given the necessity of using the same dataset to select predictor variables that were used to create the model, we performed a leave-one-out cross validation (LOOCV) using the DAAG package (Maindonald and Braun, 2015) to determine the mean square error of each model.

3 Results

3.1 Terrain analysis

Terrain analysis was performed using both 3 and 10 m DEMs, and although higher-resolution mapping can be beneficial in some scenarios, the 10 m flow accumulation results have been shown to be more reflective of the lateral transport of water in TCEF and were used in this analysis (Jencso et al., 2009). The slopes in the upper Stringer Creek watershed range from moderate (2 %) to steep (66 %). Sampling sites encompassed the range of aspects in the watershed (72–312^∘); however the range of potential incoming solar radiation was relatively narrow over the growing season (1026–1141 kWh m⁻²). Our site selection spanned a range of landscape hydrologic settings with UAAs ranging from 318 m² to 10 667 m² in the uplands, with one site representing a less frequent but much higher UAA (22 981 m²). This site was removed from upland regression analysis due to the strong leverage it had on observed relationships. Riparian sites were not characterized by the 10 m² DEM due to their relatively small extent (less than the grid size) and challenges associated with discerning between down-hillslope and down-valley flow accumulation. A threshold of 2 m in EAC was used to identify riparian areas (Jencso et al., 2009) and was consistent with field observations for five of seven riparian gas well nests. One site (T2W3), located 40 m away from the creek (4.5 m EAC), was heavily influenced by the large upstream riparian extent and gentle local slope, which resulted in it maintaining a groundwater table and high soil water content throughout the season, characteristic of riparian sites. Alternatively, a sampling site that was located within the EAC delineated riparian area (T2W2 1.5 m EAC, 15 m away) no longer had a groundwater table present by late July and had a steady decline in soil water content, which is characteristic of hillslope locations. The hydrologic dynamics of these sites suggested that their CH₄ dynamics could be better characterized by categorizing them based on hydrologic measurements rather than the simple terrain analysis.

3.2 Range and seasonality of environmental variables

Soil molar C : N ratios ranged from 13 to 43 in the shallow soil samples (0–5 cm). Average bulk density was 0.64 g cm⁻³ at riparian sites (n= 7) and 0.75 g cm⁻³ in the uplands (n= 25; Table 1). Average soil porosity in the riparian area (0.76; n= 6) was significantly higher (two-sample t test, p < 0.05) than average soil porosity of the uplands (0.65; n= 12) and agreed well with the estimated landscape-average soil porosity of ∼ 0.6 implicated by the exponential VWC–diffusivity relationship (Fig. 3).

Soil temperatures ranged from 0 to 8 ^∘C across all sampling sites during the first sampling event on 23 May 2013 and reached the seasonal maximum soil temperature (9–20 ^∘C) by mid-July. Soil temperatures declined through August with seasonally intermediate temperatures by 12 September (8–15 ^∘C). The average soil temperature in the riparian area (11.5 ^∘C) was higher than that of the upland soils (10.6 ^∘C), likely due to minimal canopy cover and thus higher insolation in the riparian corridor.

VWC had a strong seasonal pattern and was significantly different between riparian and upland landscape positions (two-sample t test, p < 0.001; Fig. 4a), as shown by real-time water content probes and spatially distributed VWC measurements (Fig. 5). VWC reached a minimum (2–12 % in the uplands and 25–55 % in the riparian area) in late July prior to a sequence of late-season rain events that increased the range of VWC in the uplands to 3–21 % and the riparian area to 29–59 %.

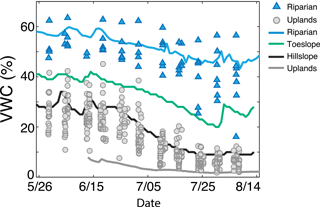
Figure 5 Real-time water content sensors (solid lines) that were distributed across landscape positions during the growing season of 2013 show the seasonal dry-down of the landscape, with a muted signal in the riparian area. These high-frequency sensor data corroborate the distributed volumetric water content (VWC) measurements made at every site during discrete sampling (filled symbols). Riparian sites increase in variability throughout the season, and hillslope positions gradually dry down to low soil moisture conditions.

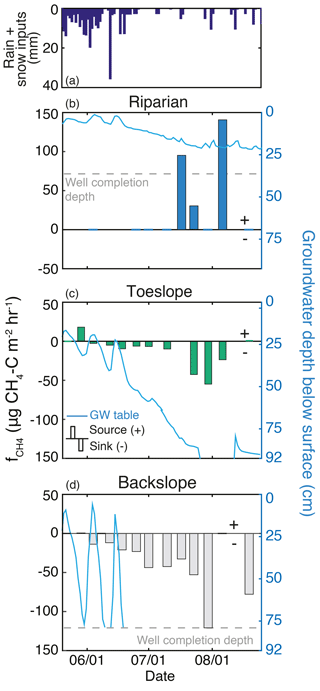
Figure 6 Methane dynamics and the seasonal decline of the groundwater (GW) table at three sites located along a riparian–hillslope transect during the 2013 growing season. (a) Rain and snow inputs for the season. (b) The riparian GW table remained in the soil zone throughout the season, and this location (T1E1) was a source of CH₄. (c) The toe slope position (T1E2) GW table dropped below the soil zone in late July but recovered after a late-season rain event. Early in the season, this landscape position produced CH₄ but gradually increased CH₄ uptake as the GW table declined. (d) The backslope (T1E3) GW table dropped below the soil zone in late June and was a CH₄ sink the entire season, with maximum uptake at the end of July.

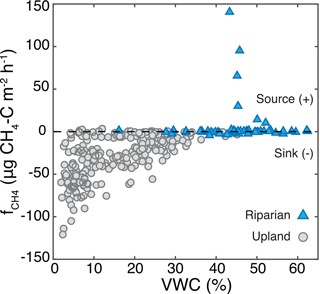
Figure 7 Measurements of CH₄ flux ($f_{{\mathrm{CH}}_{\mathrm{4}}}$) and soil water content across all 32 sites for all sampling dates. Magnitude of $f_{{\mathrm{CH}}_{\mathrm{4}}}$ in the riparian area was not related to VWC, while magnitude and variability of CH₄ uptake in the uplands increased with decreasing VWC.

Groundwater (GW) table dynamics can be described by three general responses that were related to proximity to the creek (Fig. 6). Riparian locations maintained a GW table throughout the season, with near-surface saturation during snowmelt, and GW tables 20–50 cm below the soil surface late in the season. GW wells closest to the stream (T1E1 and T1W1) had a water table within 22–25 cm of the surface throughout the season. Toe slope positions (near the strong break in slope on the east side) responded rapidly to snowmelt, and retained a GW table through late July. Wells in this transition zone (e.g., T1E2, Fig. 6c) had variable GW dynamics, which included GW response to the rain events (up to 11 mm) in the first week of August. At another transition location, a well that was influenced by the large local riparian extent and low local gradient (T2W3) maintained a GW table within 70 cm of the surface throughout the season. Upland positions above the break in slope exhibited transient GW tables during peak snowmelt, and by mid- to late June no longer had GW tables present. During snowmelt these wells had a GW table for up to 28 days, and no wells had a GW table after 26 June.

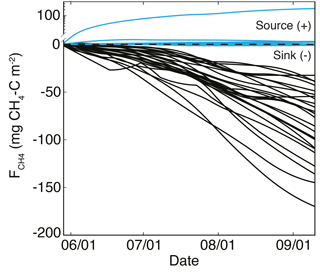
Figure 8 Cumulative CH₄ flux ($F_{{\mathrm{CH}}_{\mathrm{4}}}$) for each site, riparian in blue and uplands in black. Most riparian sites were near neutral, with one location being a source; all upland locations were CH₄ sinks.

The shallow soil was well oxygenated; in the uplands 5 cm O₂ ranged from 19.6 to 21.2 %, and 5 cm riparian O₂ ranged from 18.3 to 21.0 % in the soil atmosphere (Fig. 4b). Upland soils were well oxygenated across all sites and depths (19.2–21.5 % O₂ at 20 cm, 17.9–21.2 % O₂ at 50 cm; Fig. 4b). The only substantial depletion of O₂ was in the 20 and 50 cm samples in the riparian area, which ranged from 10.2 to 20.9 % O₂ at 20 cm and from 11.7 to 18.5 % O₂ at 50 cm (Fig. 4). Median O₂ of riparian sites decreased from 20.5 % at 5 cm to 18.2 % at 20 cm and 16.7 % at 50 cm.

Methane fluxes ($f_{{\mathrm{CH}}_{\mathrm{4}}}$) exhibited a considerable range across the landscape (−121 to 141 µg CH₄–C m⁻² h⁻¹; Fig. 4, Table 2), with significantly different $f_{{\mathrm{CH}}_{\mathrm{4}}}$ between the riparian and upland positions (two-sample t test, p < 0.001). Riparian CH₄ efflux was generally low, and the upland positions were predominately sinks (Table 2). Upland locations did produce small CH₄ fluxes out of the soil (up to 3.5 µg CH₄–C m⁻² h⁻¹) early in the season.

3.3 Environmental influences on measured CH₄ fluxes

Net CH₄ uptake was largest in dry soils, and a transition to net emission occurred around 38–43 % VWC (Fig. 7). Upland $f_{{\mathrm{CH}}_{\mathrm{4}}}$ was significantly correlated with VWC (r²= 0.36, p < 0.001), and the variability in magnitude of CH₄ uptake increased with decreasing VWC. Although soil CH₄ concentrations were not correlated with VWC, the influence of VWC on diffusivity was associated with a significant relationship between upland $f_{{\mathrm{CH}}_{\mathrm{4}}}$ and VWC. Maximum efflux occurred at 43 % VWC, and maximum uptake occurred at 4.7 % VWC. At low VWC substantial $f_{{\mathrm{CH}}_{\mathrm{4}}}$ into the soil occurred. Efflux out of the soil occurred at high VWC (∼ 40–50 %), and near-net-zero $f_{{\mathrm{CH}}_{\mathrm{4}}}$ was measured through the full range of VWC (1.4–64 %; Fig. 7).

Methane fluxes were not significantly correlated with % O₂ at any depth, nor with soil temperature (Fig. A3). CH₄ uptake was constrained to samples with 5 cm O₂ above 19 % and generally increased with increasing 5 cm % O₂, with the largest between 20 and 21 % O₂ (i.e., at approximate atmospheric levels). CH₄ efflux occurred even when 5 cm O₂ was 21 % and up to 19.5 % O₂ at 20 cm. The largest $f_{{\mathrm{CH}}_{\mathrm{4}}}$ (either into or out of the soil) occurred between 8 and 14 ^∘C, and declined with higher or lower temperatures.

Table 2 Methane flux statistics (µg CH₄–C m⁻² h⁻¹); SD stands for standard deviation.

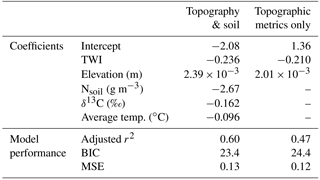
Table 3 Coefficients of the parameters used to model cumulative seasonal influx (ln$\left|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}\right)$, and statistical measures of model performance (all p < 0.01 ). MSE is the mean square error calculated from the leave-one-out cross validation (Methods Sect. 4.8). TWI is unitless, and aspect is scaled from 0 to 1. Model types are differentiated by the inclusion of soil data to show how the lack of soil data in a spatially distributed estimate of upland ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ decreases goodness of model fit.

3.4 Cumulative seasonal CH₄ fluxes and relationships to environmental variables and landscape position

Cumulative seasonal CH₄ fluxes ($F_{{\mathrm{CH}}_{\mathrm{4}}}$) ranged from −170 to −33 mg CH₄–C m⁻² in the uplands and from −0.98 to 3.12 mg CH₄–C m⁻² in the riparian sites, with one riparian location producing a relatively large $F_{{\mathrm{CH}}_{\mathrm{4}}}$ of 232 mg CH₄–C m⁻² (Fig. 8). Rates of upland consumption generally increased through the season and were consistent across sites until July when cumulative fluxes began to diverge (Fig. 8). Although most environmental variables (bulk density, C : N, C_soil, N_soil, T_avg, ∂¹³C, and ∂¹⁵N) were not significantly correlated with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$, the average VWC of each site was negatively correlated with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ (r²= 0.32, p < 0.01).

We assessed the degree to which terrain metrics were correlated with environmental variables and $F_{{\mathrm{CH}}_{\mathrm{4}}}$ in order to understand how the characteristics of a given landscape position could influence environmental variables and resulting total seasonal CH₄ fluxes (cumulative fluxes). Relationships between ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ and terrain metrics were stronger with the 10 m DEM than the 3 m DEM; therefore relationships reported below and remaining analyses were conducted with the 10 m resolution DEM. Cumulative seasonal CH₄ influx (ln$\left|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}\right)$ was regressed against average VWC (VWC_avg) and temperature of each site (T_avg), soil characteristics, and each terrain metric (Figs. A1 and A2). We used the strength of these individual relationships to determine which soil variables and terrain metrics to include in the multiple-regression models. If variables were cross-correlated, the variable with a stronger relationship with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ was retained; therefore individual regressions should not be used as independent predictors. Five of the nine terrain metrics evaluated had significant relationships with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$, including elevation, EAC, DFC, TWI, and UAA (Fig. A1). Elevation, DFC, and EAC showed a positive relationship with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$, meaning locations farther away or higher in elevation above the creek (e.g., toward ridges) had higher ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ than near-creek sites. UAA and TWI had a negative relationship to ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ and were positively related to VWC_avg (UAA r²= 0.27, p < 0.01; TWI r²= 0.43, p < 0.001). The negative influence of soil moisture on ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ resulted in lower ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ in locations with higher TWI or UAA. In summary, both landscape-mediated relative water availability and local VWC explained net uptake of CH₄ across the watershed during the 2013 growing season.

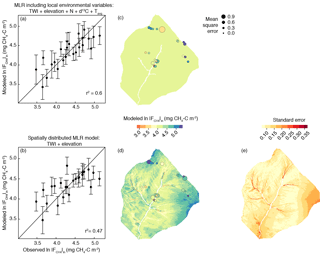
Figure 9 Measured cumulative CH₄ influx (ln$\left|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}\right)$ vs. predicted ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ for (a) the model that includes soil variables and (b) the model that only used topographic variables. 1:1 lines are shown for reference. The associated adjusted r² is shown with each model; details on model fit and coefficients are in Table 3. (c) Sampling locations and associated error for the soils model. (d) Map of ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ across the upper Stringer Creek watershed showing results from the topographic model. Size of site symbols are scaled to their mean square error, and color is associated with predicted flux shown in (a) and (b). (e) Standard error from the topographic model.

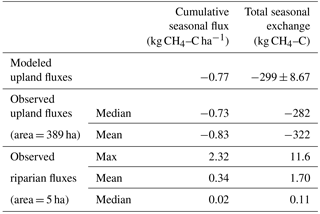
Table 4 Modeled and observed seasonal CH₄ uptake (separated by landscape element), as well as total areally integrated seasonal CH₄ exchange. Observed mean and median of upland $F_{{\mathrm{CH}}_{\mathrm{4}}}$ bracket the estimated average $F_{{\mathrm{CH}}_{\mathrm{4}}}$ from the spatially distributed topographic model. Total estimated riparian CH₄ effluxes are orders of magnitude smaller than uptake in the uplands.

3.5 Multiple-regression model of cumulative upland CH₄ fluxes

Multiple regressions that included soil data explained up to 60 % of the observed variability in ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ (Table 3), showing that, albeit not as readily available, the addition of soil variables can improve modeling results. Although these models cannot be extrapolated to the watershed scale, including N_soil improves the model performance by 12 %, whereas including T_avg and δ¹³C only improves the model by 3 and 2 %, respectively (Fig. A4).

We created a spatially explicit model of upper Stringer Creek ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ using the topographically based model with the best fit (adjusted r²= 0.47, p < 0.001) and lowest BIC (for model selection, where the model with the lowest BIC is preferred; Schwarz, 1978). This model included only TWI and elevation as parameters (Eq. 4, Table 3, Fig. 9). The seasonal CH₄ uptake from the spatial model reached up to 2.1 kg CH₄–C ha⁻¹, averaged 0.77 kg CH₄–C ha⁻¹, and totaled 299 kg CH₄–C for the entire upland area (Table 4). We extrapolated the mean, median, and maximum riparian $F_{{\mathrm{CH}}_{\mathrm{4}}}$ to estimate contributions from riparian area (5 ha), resulting in a range of potential total riparian $F_{{\mathrm{CH}}_{\mathrm{4}}}$ (Table 4). Even when using the maximum riparian CH₄ efflux, the riparian emission offset < 4 % of total upland CH₄ influx, highlighting the strong role of upland uptake in the net landscape CH₄ balance.

$$\begin{array}{}\text{(4)}& \ln \mathrm{|}{F}_{{\mathrm{CH}}_{\mathrm{4}}}{\mathrm{|}}_{\mathrm{in}}=\left(k_{\mathrm{1}}\times \mathrm{TWI}\right)+\left(k_{\mathrm{2}}\times \mathrm{elevation}\right)+k_{\mathrm{3}}\end{array}$$

4 Discussion

We utilized understanding of watershed hydrology processes at TCEF (Jencso et al., 2009, 2010; Kelleher et al., 2017; Nippgen et al., 2015) to design a sampling campaign which captured CH₄ fluxes across environmental gradients that were characterized through topographic analysis, field observation, and hydrological measurements. This approach allowed us to assess environmental influences on CH₄ fluxes: at the point scale, we examined the influence of environmental variables on observed CH₄ fluxes ($f_{{\mathrm{CH}}_{\mathrm{4}}}$); at the intermediate scale, we identified functional landscape elements (riparian, upland, and the transition between them) which related to the direction and persistence of $f_{{\mathrm{CH}}_{\mathrm{4}}}$; and at the landscape scale, we assessed the influence of topographic position on cumulative CH₄ fluxes (ln$\left|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}\right)$ in the uplands. Our observed average $f_{{\mathrm{CH}}_{\mathrm{4}}}$ (−28.5 ± 25.1 µg CH₄–C m⁻² h⁻¹, Table 2) was comparable to those of other temperate forests, which range from −333 to 0.75 µg CH₄–C m⁻² h⁻¹ (mean: 32.9 µg CH₄–C m⁻² h⁻¹, standard error: 18; Dalal et al., 2008). We used observed relationships between ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ and topographic metrics to create multiple-regression models of varying complexity to estimate the total watershed $F_{{\mathrm{CH}}_{\mathrm{4}}}$. The average predicted $F_{{\mathrm{CH}}_{\mathrm{4}}}$ from the spatially distributed model of upland CH₄ fluxes was similar to the extrapolated mean of measured $F_{{\mathrm{CH}}_{\mathrm{4}}}$. This is partially due to our sampling approach which captured a range of landscape positions found at TCEF. It should be noted that simply extrapolating a mean flux from a measurement site or multiple measurement sites does not capture the frequency distribution of similar landscape positions unless this is built into the sampling scheme (Vidon et al., 2015). Thus, we suggest capturing and/or modeling the spatial variability of landscapes is critical to estimating CH₄ consumption or efflux across landscapes.

4.1 How do environmental variables relate to CH₄ flux through the growing season, and how does landscape structure relate to relative magnitude and direction of CH₄ fluxes across the landscape?

Research on soil–atmosphere CH₄ exchange has been conducted across a range of ecosystems (Smith et al., 2000; Castaldi and Fierro, 2005; Dalal and Allen, 2008; Luo et al., 2013), but assessing the spatial and temporal variability of CH₄ fluxes at the landscape scale has been limited. Studies focused on CH₄ oxidation have shown varied responses to commonly measured environmental variables such as soil moisture and temperature (e.g., Adamsen and King, 1993; Bradford et al., 2001; Price et al., 2004), nutrient variability (e.g., N species: Verchot et al., 2000; dissolved organic carbon: Sullivan et al., 2013). In addition to these physiological constraints, soil structure and texture create the physical landscape at the microbial scale by mediating how quickly soils drain and saturate, directly influencing transport and diffusion of substrates and O₂ (Dorr et al., 1993; Czepiel et al., 1995; Ball et al., 1997; von Fischer et al., 2009). Soil nutrient status can be important in understanding the variability of CH₄ dynamics between ecosystems or dominant landscape units (Boeckx et al., 1997; Saari et al., 1998) but did not have a significant influence on CH₄ uptake at the landscape scale. Although we did not find relationships between soil characteristics and CH₄ uptake, small-scale (centimeters to meters) variability in soil structure and organic matter can be particularly relevant in low moisture conditions, where even with similar values of VWC a range of soil moisture conditions (and therefore diffusivity) can occur.

Rates of both soil CH₄ production and consumption have been shown to increase with increasing temperature in laboratory studies (Bowden et al., 1998) and in field studies spanning wetlands, rice paddies (Bartlett and Harriss, 1993; Segers, 1998; Meixner and Eugster, 1999; Yvon-Durocher et al., 2014), spruce forests of Germany (Steinkamp et al., 2001), the Mongolian steppe region (Wu et al., 2010), and alpine grasslands (Wei et al., 2014). However, consensus has not been reached on the relationship between CH₄ flux and temperature across ecosystems (Luo et al., 2013). In fact, several studies have shown limited temperature influence on daily and seasonal variability of CH₄ consumption in upland soils (King and Adamsen, 1992; Del Grosso et al., 2000; Smith et al., 2000; Castaldi and Fierro, 2005; Shrestha et al., 2012; Imer et al., 2013). At TCEF, we did not find a simple relationship between $f_{{\mathrm{CH}}_{\mathrm{4}}}$ and soil temperature. Early in the growing season, when soils were near saturation due to the recent snowmelt, both low soil temperatures and restricted gas-phase transport were likely limiting $f_{{\mathrm{CH}}_{\mathrm{4}}}$. As the season progressed and temperatures increased, the largest range and magnitude of $f_{{\mathrm{CH}}_{\mathrm{4}}}$ was observed, but these conditions coincided with increased diffusivity due to decreasing soil moisture, making the independent effects difficult to ascertain. These compounding seasonal factors in both riparian and upland settings, and the relatively low range of variability in soil temperature suggest our site is not an ideal location for assessing temperature effects on CH₄ fluxes. Given these caveats, our results do agree with findings from a study of temperature and moisture effects on methane consumption across ecosystem types (Luo et al., 2013) which found maximum CH₄ uptake corresponded with average soil temperature (Fig. A3).

Depth to groundwater table, VWC, and O₂ have been used to estimate soil redox conditions that are essential for methanogenesis (Fiedler and Sommer, 2000; Liptzin et al., 2011). As depth to water table increases, the volume in which oxidation can occur increases, thereby decreasing net CH₄ efflux (Moore and Roulet, 1993), yet, similar to Fiedler and Sommer (2000), we found that depth to groundwater table was not sufficient to predict the magnitude of riparian CH₄ efflux in these well-drained soils. High VWC is often associated with O₂ depletion (Silver et al., 1999), yet we measured near-atmospheric O₂ even up to 60 % VWC, similarly to Hall et al. (2012), who suggest that high VWC does not necessarily lead to depleted O₂, even when soil water content is above field capacity. Additionally, Teh et al. (2005) show that laboratory experiments varying O₂ do not result in significant changes in rates of methanogenesis. Based on these findings, we suggest that using VWC as a proxy for O₂ conditions should be done with caution when estimating biogeochemical fluxes reliant on redox conditions, and we highlight the limited support for predictability of the magnitude of CH₄ efflux based on O₂.

Soil moisture has a strong influence on the microbial populations that drive methane cycling (Conrad, 1996; Potter et al., 1996; Smith et al., 2003; Luo et al., 2013; Du et al., 2015), but the differential response of methanotrophs and methanogens to soil moisture status can make it difficult to find simple relationships between net CH₄ flux and VWC. The hydrologic landscape at TCEF is such that the groundwater dynamics are heavily influenced by topography (Jencso et al., 2009, 2010), which creates a range of soil moisture conditions across the uplands and a distinct riparian area that maintains a shallow water table through the growing season (Figs. 5 and 6). We assessed the direction, magnitude, and seasonality of $f_{{\mathrm{CH}}_{\mathrm{4}}}$ and determined that the patterns created by the soil moisture conditions influencing these fluxes functionally corresponded to riparian, transitional, and upland landscape elements.

Riparian zones are often characterized by high rates of biogeochemical cycling due to organic carbon availability, fluctuating water tables, and correspondingly variable redox conditions. At TCEF, soil in the riparian area is saturated during the snowmelt period, and the hydrologic connection to the uplands provides a downslope pulse of dissolved organic carbon (Pacific et al., 2010). This seasonal input of carbon could lead to increased methanogenesis, yet soil CH₄ concentrations remained relatively consistent throughout the growing season (data not shown). Despite this, and the fact that the riparian locations sampled at TCEF maintained a water table throughout the season, these sites often exhibited little to no measurable CH₄ flux (Figs. 6, 7). These low CH₄ fluxes are consistent with observations from other forest riparian areas, where much of the CH₄ produced deeper in the soil is oxidized before reaching the soil surface (humid tropics: Teh et al., 2005; floodplain wetland: Batson et al., 2015; seasonally dry ecosystems: von Fischer and Hedin, 2002; Castaldi et al., 2006; riparian area: Vidon et al., 2015). The few large fluxes observed might be due to limited sampling when gas wells were inundated (potentially missing ebullition events); low temperatures and diffusivity; fluxes of dissolved CH₄ through the groundwater to the stream channel (Itoh et al., 2007); recalcitrance of organic matter (Valentine et al., 1994; Updegraff et al., 1995); or lack of sampling of fluxes from riparian vegetation, which can be an important transport process in wetlands (Whiting and Chanton, 1993; Shannon et al., 1996; Bridgham et al., 2013). Given these caveats, 115 samples over 13 weeks of sampling show that, although riparian areas can be locations of high rates of biogeochemical cycling, large net emissions of CH₄ were not common among the riparian sites sampled at TCEF.

Transition zones or boundaries between landscape elements can exhibit steep gradients in hydrologic conditions and nutrients (Hedin et al., 1998a). We determined that this was also true for CH₄ dynamics, which shifted from CH₄ efflux in the saturated soils of the riparian area to CH₄ uptake in the aerated soils of the uplands. Distinguishing the general boundary between riparian and upland landscape elements can be tractable using terrain metrics (here, the EAC threshold of 2 m), but accurately capturing the shifting spatial extent of the transition zone through time can be challenging (Creed and Sass, 2011). At TCEF, this required direct measurement of the local groundwater table. The near-net-zero $F_{{\mathrm{CH}}_{\mathrm{4}}}$ in these transitional sites was a culmination of both CH₄ efflux and uptake rather than a consistent intermediate VWC that created near-neutral fluxes throughout the season. We did observe near-zero fluxes in the VWC range of 38–43 %, which are in accordance with VWC thresholds (32–44 %) differentiating net CH₄ efflux from net uptake in other upland forests (Sitaula et al., 1995; Luo et al., 2013), but this intermediate VWC is likely a transient state that occurs in some parts of the landscape rather than being characteristic of a landscape position throughout the season. We expect the transition zones could be particularly sensitive to climate variability because the resulting changes in hydrologic dynamics could shift their boundaries and net CH₄ flux behavior.

Flux of CH₄ into the soil ($f_{{\mathrm{CH}}_{\mathrm{4}}}$) was strongly mediated by local soil water content (Figs. 7 and A4), resulting in a seasonal pattern of $f_{{\mathrm{CH}}_{\mathrm{4}}}$ that was reflective of the snowmelt dynamics in this watershed. During and shortly after snowmelt, relatively high upland VWC constrained $f_{{\mathrm{CH}}_{\mathrm{4}}}$ and even resulted in a few small sources of CH₄ (Fig. 6). Low rates of $f_{{\mathrm{CH}}_{\mathrm{4}}}$ could have been due to the combined effects of restricted diffusion of CH₄ (and O₂) into the soil, production of CH₄ deeper in the soil, and/or low temperatures. As the soil moisture state of the watershed decreased, gas-phase transport of CH₄ into the soil increased, microsites of potential methanogenesis decreased, and those combined effects increased CH₄ uptake through the growing season (Fig. 6). Previous studies have suggested that there is an optimum water content range for CH₄ oxidation, below which methanotrophs become water stressed and consume less CH₄ (Adamsen and King, 1993; Torn and Harte, 1996; West and Schmidt, 1998; Dunfield, 2007). Here, we did not find a pronounced decrease in uptake at low water content; in fact, we observed our largest measured influx at an extremely dry site (Fig. 7); we note, however, that this was preceded by a rain event which might have influenced this $f_{{\mathrm{CH}}_{\mathrm{4}}}$ measurement (Lohse et al., 2009). Net CH₄ consumption at low water content has been documented in other systems, most notably in arid environments (savannas: Otter and Scholes, 2000; desert soils: McLain and Martens, 2005; shrublands: Castaldi and Fierro, 2005; in some temperate forests: Castro et al., 1995). At TCEF, the driest sites were not only the locations of the largest measured CH₄ uptake, but they also showed the greatest variability in $f_{{\mathrm{CH}}_{\mathrm{4}}}$, again highlighting the potential influence of small-scale heterogeneity in soil texture and nutrient status.

4.2 Prediction and scaling of CH₄ consumption using terrain analysis

Greenhouse gases have been modeled using a range of frameworks including empirical (data-driven), mechanistic (process-based), and atmospheric inverse modeling (see Blagodatsky and Smith (2012) and Wang et al. (2012) for detailed reviews). Although these modeling efforts have significantly advanced our understanding of GHG dynamics at landscape to regional scales, most of them do not reflect spatial patterns (or variability) in the lateral redistribution of water (Tague and Band, 2001; Groffman, 2012). The spatial patterns of soil properties (Konda et al., 2010), microbial assemblages (Florinsky et al., 2004), and resultant biogeochemistry influenced by landscape position and topography (Creed and Beall, 2009; Riveros-Iregui and McGlynn, 2009; Creed et al., 2013; Anderson et al., 2015) have been investigated and used to scale point observations to the larger landscape in a limited number of studies. Remote sensing and vegetation classification have also been suggested as empirical methods to scale CH₄ effluxes from wetlands to larger areas (Bartlett et al., 1992; Bubier et al., 1995; Sun et al., 2013), but similar remotely sensed scaling of soil CH₄ uptake is currently lacking.

We used an empirical model based on topographic indices to scale CH₄ fluxes from point measurements to the watershed scale. The extensive area of dry uplands consuming CH₄ (98 % of watershed area) and low average production from the small riparian area resulted in a watershed net growing season sink up to 299 ± 8 kg CH₄–C (0.77 kg CH₄–C ha⁻¹). We found higher uncertainty in the near-stream area; this is likely due to the influence of higher TWI in locations that have an EAC above the riparian threshold of 2 m (Fig. 9). These locations might behave more like the transitional areas which are saturated early in the season and no longer have a groundwater table, or saturated conditions, later in the season. These locations highlight two limitations to this methodology: firstly, CH₄ flux dynamics in locations that transition between saturated and aerated conditions will not be captured by a regression using static terrain metrics. Secondly, 10 m resolution digital elevation data are insufficient to resolve topographic variability within our small riparian zone, even though the variable contributing area along the riparian zone influences the timing and delivery of nutrients to the riparian area (Jencso et al., 2010; Pacific et al., 2010).

This spatially distributed model (ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ ∝ TWI and elevation) estimated a total net seasonal CH₄ uptake similar to the CH₄ uptake estimated by extrapolating the mean $F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$. This might partially be because the model did not capture the highest cumulative fluxes well and had higher standard error in the dry, high-elevation locations (Fig. 9). The high frequency of landscape settings that experience drier conditions represents the disproportionate amount of the landscape which exhibits high net CH₄ uptake. Therefore, extrapolating a mean value to the entire watershed can bias estimates across watersheds. The use of central tendency and its effects on estimating GHG fluxes across landscapes was also highlighted with respect to CH₄ by Vidon et al. (2015) and has significant implications for our understanding of the contribution of upland landscapes to regional and global CH₄ inventories.

Terrain analysis reflects the long-term conditions of a given location relative to its landscape setting. Lower VWC (at the point scale) and relative water availability (as represented by TWI at the landscape scale) corresponded to more CH₄ uptake and are the most influential parameters at those respective scales due to their influence on microbial activity and soil diffusivity (Fig. A4). The inclusion of elevation in the model might be due to a combination of factors including its effect on both temperature and incoming insolation, which could lead to higher evapotranspiration and lower soil water content at the high elevations. Elevation could also be capturing the differences in mineral type which result in variable soil chemistry and pH. This could be impacting the soil microbial communities, which have been shown to significantly differ between lower and higher upland soils in the watershed (Du et al., 2015). Our modeling exercise demonstrates soil variables can aid in the explanation of CH₄ uptake (particularly at high CH₄ uptake) and suggests that we might be conservatively estimating CH₄ consumption given the lack of soil parameters in the spatially distributed estimate of CH₄ consumption (Eq. 5).

Consistent with previous research on CO₂ fluxes at TCEF (Riveros-Iregui and McGlynn, 2009) and other studies (Duncan et al., 2013; Vidon et al., 2014), our regression model results suggest that the topographic redistribution of water and the frequency distribution of relevant functional landscape elements should be considered in scaling exercises. These approaches may better reflect CH₄ dynamics in a variety of watersheds, such as locations where the riparian extent is proportionally larger and potentially offsets the upland CH₄ sink to a greater degree (Sakabe et al., 2016). Here, even if the maximum $F_{{\mathrm{CH}}_{\mathrm{4}}}$ from the riparian area were used to estimate net efflux, it would have to comprise over 25 % of the watershed area to offset the net CH₄ consumption in the uplands. As noted in a recent review by Bernhardt et al. (2017), it is critically important to perform these scaling exercises to determine the relative influences of point scale measurements on net watershed balances. These results highlight the importance of accounting for the upland CH₄ sink, which can significantly offset high rates of methane production in riparian areas.

5 Conclusions

The strong gradients of water availability at TCEF impose both a direct (local) and indirect (distal/historic) effect on the microbial communities and physical transport processes regulating biogeochemical fluxes. We implemented a sampling design that utilized these hydrologic gradients to study the influence of landscape heterogeneity on watershed CH₄ fluxes. We determined that soil moisture was the dominant environmental influence on the direction of net CH₄ fluxes, and the magnitude of CH₄ uptake in the uplands due to its influence on soil diffusivity. Low nutrient status and limited range in soil temperature could be responsible for the lack of a direct relationship between C_soil, N_soil, or T_avg and CH₄ uptake but likely contribute to the variability in observed CH₄ fluxes across the landscape.

Landscape elements can be useful in characterizing areas that behave similarly to net sources or sinks of CH₄, but the boundary between elements can shift as the landscape dries down or wets up. Although riparian areas can disproportionally contribute to net landscape biogeochemical fluxes, their area relative to the uplands made them a minor component of the CH₄ balance in upper Stringer Creek. Interestingly, there was limited support for a consistent seasonal trend in CH₄ effluxes in the riparian area, while the uplands increased in sink strength as the growing season progressed.

The effect of soil moisture on CH₄ uptake led to an observable relationship between landscape structure and CH₄ flux. We used these relationships to create empirically derived multiple-regression models with spatially distributed parameters. This allowed us to better visualize spatial patterns of fluxes and to extrapolate from measurement locations the watershed scale. This is preferable to the use of central tendency, which does not incorporate the frequency distribution of landscape settings relative to measurement locations. The importance of specific terrain metrics will vary across watersheds, particularly those that are not in water-limited regions. Further research on the applicability of this method in other locations and the use of higher-resolution DEMs to assess spatial variability in the riparian area is needed. These findings contribute to the literature on the importance of spatial heterogeneity, and the lateral redistribution of water, and suggest that we could be significantly underpredicting net watershed CH₄ sink strength if we do not account for spatial variability.

Appendix A

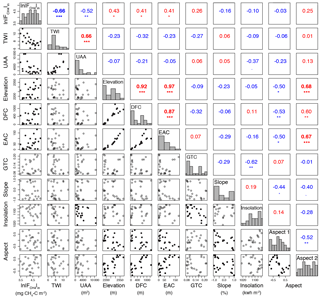
Figure A1 All topographic variables included in initial exploratory data analysis. If a set of topographic variables had a Pearson's correlation coefficient greater than 0.6, then the variable with a lower correlation with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ was removed from the analysis. Significance is denoted by asterisks: ( ) < 1, (*) ≤ 0.05, (**) ≤ 0.01, and (***) ≤ 0.001. Blue text indicates negative relationships and red indicates positive relationships. Histograms of each variable run diagonally and separate the correlation coefficients from the bivariate plots. Bivariate plots with filled symbols denote significant relationships. Aspect parameters were calculated in radians using Eq. (1).

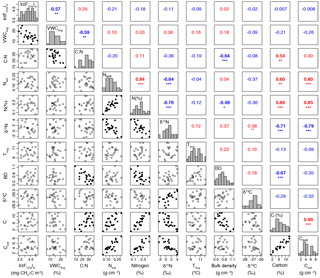
Figure A2 All environmental variables considered in the initial exploratory data analysis. If a set of variables had a Pearson's correlation coefficient greater than 0.6, the variable with a lower correlation with ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$ was removed. Significance is denoted by asterisks: ( ) ≤ 1, (*) ≤ 0.05, (**) ≤ 0.01, and (***) ≤ 0.001. Blue text indicates negative relationships, and red indicates positive relationships. Histograms of each variable run diagonally and separate the correlation coefficients from the bivariate plots. Bivariate plots with filled symbols denote significant relationships.

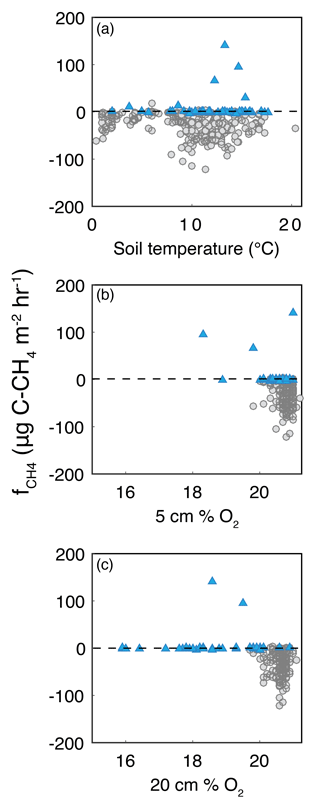
Figure A3 Bivariate plots of CH₄ flux (f_CH4) with (a) soil temperature, (b) 5 cm %O₂, and (c) 20 cm % O₂. Circles are measurements from upland locations, and triangles are from riparian locations.

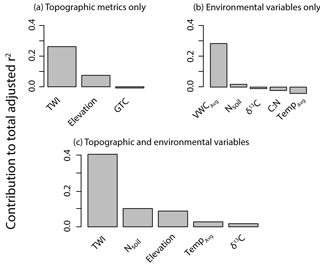
Figure A4 Results from the variable jack-knife analysis to determine which variables were the most important from a given parameter set: (a) topographic metrics (in final MLR), (b) soil variables only, and (c) topographic and soil variables (from grouped MLR). Variables included in each set are shown on the x axis. The y axis indicates the contribution to the total adjusted r² of the model when the variable is included in the model (the larger the number, the more important the variable is to the model, and the higher its relative influence on ln$|F_{{\mathrm{CH}}_{\mathrm{4}}}{|}_{\mathrm{in}}$). Given the penalty to the adjusted r² for additional variables, some variables did not contribute to model performance and were not included in any of the models (e.g., T_avg, C : N).