Evaluation of a new inference method for estimating ammonia volatilisation from multiple agronomic plots

Tropospheric ammonia (NH₃) is a threat to the environment and human health and is mainly emitted by agriculture. Ammonia volatilisation following application of nitrogen in the field accounts for more than 40 % of the total NH₃ emissions in France. This represents a major loss of nitrogen use efficiency which needs to be reduced by appropriate agricultural practices. In this study we evaluate a novel method to infer NH₃ volatilisation from small agronomic plots consisting of multiple treatments with repetition. The method is based on the combination of a set of NH₃ diffusion sensors exposed for durations of 3 h to 1 week and a short-range atmospheric dispersion model, used to retrieve the emissions from each plot. The method is evaluated by mimicking NH₃ emissions from an ensemble of nine plots with a resistance analogue–compensation point–surface exchange scheme over a yearly meteorological database separated into 28-day periods. A multifactorial simulation scheme is used to test the effects of sensor numbers and heights, plot dimensions, source strengths, and background concentrations on the quality of the inference method. We further demonstrate by theoretical considerations in the case of an isolated plot that inferring emissions with diffusion sensors integrating over daily periods will always lead to underestimations due to correlations between emissions and atmospheric transfer. We evaluated these underestimations as −8 % ± 6 % of the emissions for a typical western European climate. For multiple plots, we find that this method would lead to median underestimations of −16 % with an interquartile [−8–22 %] for two treatments differing by a factor of up to 20 and a control treatment with no emissions. We further evaluate the methodology for varying background concentrations and NH₃ emissions patterns and demonstrate the low sensitivity of the method to these factors. The method was also tested in a real case and proved to provide sound evaluations of NH₃ losses from surface applied and incorporated slurry. We hence showed that this novel method should be robust and suitable for estimating NH₃ emissions from agronomic plots. We believe that the method could be further improved by using Bayesian inference and inferring surface concentrations rather than surface fluxes. Validating against controlled source is also a remaining challenge.

1 Introduction

Tropospheric ammonia (NH₃) is mainly emitted by agriculture and has great environmental impacts (atmospheric pollution, eutrophication, reduction of biodiversity), which are increasingly taken into account in European and international regulations (Council, 1996, 2016; UNECE, 2012). Ammonia losses also have great agronomic and economic impacts for farmers, as they reduce nitrogen use efficiency. The varying prices of mineral fertilisers and concerns about environmental and health threats demand improvements in the efficiency of nitrogen utilisation, and especially in recycling nitrogen through organic fertilisation (Sutton et al., 2011). Indeed, NH₃ volatilisation during storage of manure and slurry and following their field application is the main source of NH₃ in Europe (55 % of the emissions) while farm building emissions represent 45 %. In France, crop farming represents 35 % of the emissions and animal farming represents 65 % (CITEPA, 2017; ECETOC, 1994; EUROSTAT, 2012; Faburé et al., 2011). Reducing NH₃ losses from this agricultural sector is therefore a major objective for applied research.

While NH₃ emissions from farm buildings and storage can be handled by engineering solutions, losses during organic fertilisation are much more dependent on the combination of application methods (splash plate, band spreading, pressurised injection, open and close slot injection, trailing hose, and trailing shoe), soil type and occupation, and environmental conditions (soil humidity, air temperature, wind speed, solar radiation) (Sommer et al., 2003). For instance, Sintermann et al. (2012) report NH₃ losses following cattle and pig slurry application in the field ranging from a few percent to 50 % over large fields and up to 100 % over medium fields. Evaluating ammonia losses from field fertilisation over a range of practices and soil and climatic conditions is therefore key in evaluating the best application methods.

However, characterising these emissions at the field scale requires complex experimental design and most of the time also requires the use of large fields (Ferrara et al., 2016, 2012; Flechard and Fowler, 1998; Loubet et al., 2012; Milford et al., 2009; Sintermann et al., 2011b; Spirig et al., 2010; Sun et al., 2015; Whitehead et al., 2008). Especially useful for measuring ammonia losses are methods that can deal with small- and medium-scale fields (20–50 m on the side) that are commonly used in agronomic trials. Indirect estimation methods (soil nitrogen balance or ¹⁵N balance) are not well adapted to evaluate gaseous ammonia losses, mainly because of the soil heterogeneity and also because the method relies on evaluating small variations of large numbers (McGinn and Janzen, 1998). Among existing methods for measuring NH₃ emissions, the integrated horizontal flux method (Wilson and Shum, 1992) is well adapted, but is a subject of debate in its practical application since it seems to be systematically biased towards higher estimates (Häni et al., 2016; Sintermann et al., 2012). Alternatively, enclosure methods proved to be not representative for a sticky compound such as ammonia (Pacholski et al., 2006), but more concerning is the fact that ammonia fluxes result from an air-surface equilibrium which is disturbed by the confined environment offered by the chamber. Inverse dispersion modelling approaches either based on backward Lagrangian stochastic models (Flesch et al., 1995) or Eulerian models (Kormann and Meixner, 2001; Loubet et al., 2001) or based on the Philip equation (Philip, 1959) have been demonstrated to be adapted for estimating NH₃ volatilisation from strong sources (Loubet et al., 2010; Sommer et al., 2005).

These approaches are well adapted to small or medium fields (≤ 50 × 50 m²) but typically require hourly NH₃ concentration measurements. Long-term concentration measurements of NH₃ are now well handled by the use of short-path passive samplers developed by Sutton et al. (2001), or active denuders, which have both been used for concentration monitoring for years (Tang et al., 2001, 2009). These active denuders can be adapted for measuring fluxes based on conditional sampling like the conditional time-averaged gradient method (COTAG) (Famulari et al., 2010), which is a useful method but only adapted for large fields (≥ 0.5 ha). The passive samplers have also been shown to be adapted for inverse modelling estimations of NH₃ sources for large fields (Carozzi et al., 2013b; Ferrara et al., 2014).

In another field of research, solutions to the multiple source inference problem, which consists of inferring multiple sources based on measured concentrations at multiple points in space and time, have been developed especially since 2008 (Crenna et al., 2008; Gao et al., 2008; Gericke et al., 2011; Mukherjee et al., 2015; Vandré and Kaupenjohann, 1998). They have chiefly been used over regional scales (Flesch et al., 2009; Lushi and Stockie, 2010; Yee and Flesch, 2010), and have been shown to be very dependent on the source-sensor geometry (Crenna et al., 2008; Flesch et al., 2009; Wang et al., 2013). Mukherjee et al. (2015) highlighted the dependency of the inferred source on background concentration and plot disposition by means of an inverse footprint approach. Yee et al. (2008) have shown how to retrieve the number, location and intensity of multiple sources with dispersion models coupled with Bayesian inference methods. Yee and Flesch (2010) have evaluated the inversion and inference methods for determining four point sources using several laser transects. Flesch et al. (2009) have shown that source–receptor geometry is critical in determining whether a multiple-source inversion problem can provide realistic solutions or not. Flesch et al. (2009) have moreover shown that if the geometry is well chosen the accuracy of the method for a 15 min integration time can reach 10 to 20 %. These studies have also shown that the multiple source inference problems can be solved if not ill-conditioned (ill-conditioning depends on the location of sources and concentration sensors and is characterised by a conditioning number κ).

In this study, we pose the following research questions: can inverse dispersion modelling approaches be used for inferring NH₃ emissions from multiple small plots (agronomic trials) using passive samplers, and to which degree of accuracy? The answer is given through the investigation of the optimal design in terms of field dimensions, plot location and size, passive sampler locations, and their duration of exposure. Throughout this study, agronomic trials are considered to be multiple small adjacent fields with repetitions of treatments. A typical trial would consist of three repetitions of three treatments. Hence the double challenge that we face in this study is to consider both (i) the multiple-source inference issue (adjacent small fields) and the (ii) time-integration issue (using passive samplers).

To answer these questions, we use a four-step approach: (1) the ammonia emissions are first modelled on each source using prescribed NH₃ emissions potential dynamics coupled with a simple soil–vegetation–atmosphere exchange scheme to mimic realistic seasonal, daily and hourly variations in NH₃ emissions. (2) These prescribed emissions are then used to estimate the concentration at each target location using short-range atmospheric dispersion modelling over half-hourly periods. (3) The obtained concentrations are then averaged over several integration periods to simulate the behaviour of passive samplers. Finally, (4) the sources are evaluated by inference with dispersion modelling based on the averaged concentrations.

Two dispersion models and several inference methodologies are evaluated. The effect of the size of the source, the locations of targets, the dynamics and magnitude of each source, the meteorological conditions, and the background concentration variability are evaluated and discussed. The feasibility of the method is finally evaluated over a real case with two repetitions of three treatments (slurry spreading, injection and a reference without fertilisation).

2 Materials and methods

At first we present the theoretical background of source inference by optimisation for single and multiple sources with time-averaging concentration sensors. Then the method used to generate a realistic ammonia source is introduced before the description of the dispersion models used for both generating the concentration fields and inferring back the sources. The geometry of the sources, sensor locations and the meteorological data used for this analysis are then shown, and finally the real test case used for evaluating the method is detailed.

2.1 The theory of the source inference method

At first we will recall some important theoretical features of the inverse dispersion modelling approach, which is actually an inference method.

2.1.1 Case of a single area source and a single concentration sampler

We first consider the case of a single area source with a single concentration sampler (target). The source varies with time. The method is based upon the general superimposition principle (Thomson et al., 2007), which relates the concentration at a given location C(x,t) to the source strength S(t) and the background concentration C_bgd(t) using a transfer function D(x,t), which has the dimensions of a transfer resistance (s m⁻¹).

$$\begin{array}{}\text{(1)}& {\displaystyle }C(x,t)=D(x,t)\times S\left(t\right)+C_{\mathrm{bgd}}\left(t\right)\end{array}$$

Here x denotes the location of the sensor and t the time. The concentration and source units are in µg N-NH₃ m⁻³ and µg N-${\mathrm{NH}}_{\mathrm{3}}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, respectively. The superimposition principle implies that the studied tracer must be conservative, which is a reasonable hypothesis for NH₃ whose reaction time with acids in the atmosphere is below the transport time for spatial scales below 1000 m (Nemitz et al., 2009). Moreover, in Eq. (1), we assume a spatially homogeneous area source with strength S(t). The spatial homogeneity of the source is less trivial for NH₃ than other gas released in agriculture as the source itself depends on the concentration at the surface. However, Loubet et al. (2010) have shown that the heterogeneity of the source can be neglected as long as the dimension of the source is larger than 20 m. Hence, this study is limited to source areas with fetch larger than 20 m and a spread of the concentration samplers over a domain smaller than 1000 m. Moreover, it is interesting to note that for infinitely spread fields, the transfer resistance is linearly linked to the transfer matrix (see Supplement Sect. S1)

2.1.2 Effect of time-averaging sensors on source inference for a single source

Since we consider time-averaging concentration samplers, we develop the time-averaged equation of Eq. (1) over an integration time period τ:

$$\begin{array}{}\text{(2)}& {\displaystyle }\stackrel{\mathrm{‾}}{C\left(x\right)}=\stackrel{\mathrm{‾}}{D\left(x\right)\times S}+\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}},\end{array}$$

where the overbars denote a time average over the period τ. Similar to turbulent flux calculations, the first part of the right-hand side of Eq. (2) is decomposed using the Reynolds decomposition of a random variable (Kaimal and Finnigan, 1994), giving

$$\begin{array}{}\text{(3)}& {\displaystyle }\stackrel{\mathrm{‾}}{C\left(x\right)}=\stackrel{\mathrm{‾}}{D\left(x\right)}\times \stackrel{\mathrm{‾}}{S}+\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}}+\stackrel{\mathrm{‾}}{D^{\prime }\left(x\right)S^{\prime }},\end{array}$$

where $\stackrel{\mathrm{‾}}{D(x{)}^{\prime }{S}^{\prime }}$ is the time covariance between D(x,t) and S(t). If the averaged background concentration $\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}}$ is a known quantity, Eq. (3) can be easily manipulated to give an estimation of the averaged source strength $\stackrel{\mathrm{‾}}{S}$, the quantity we want to infer:

$$\begin{array}{}\text{(4)}& {\displaystyle }\stackrel{\mathrm{‾}}{S}=\underset{\left(\mathrm{I}\right)}{{\displaystyle \frac{\stackrel{\mathrm{‾}}{C\left(x\right)}-\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}}}{\stackrel{\mathrm{‾}}{D\left(x\right)}}}}-\underset{\left(\mathrm{II}\right)}{{\displaystyle \frac{\stackrel{\mathrm{‾}}{D^{\prime }\left(x\right)\times S^{\prime }}}{\stackrel{\mathrm{‾}}{D\left(x\right)}}}}.\end{array}$$

In the right-hand side of Eq. (4), (I) can be calculated from measured $\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}}$ and $\stackrel{\mathrm{‾}}{C\left(x\right)}$ and $\stackrel{\mathrm{‾}}{D\left(x\right)}$, which is itself calculated with dispersion models. Conversely, (II) is a priori unknown and depends on the correlation between the source strength and the transfer function $\stackrel{\mathrm{‾}}{D(x{)}^{\prime }{S}^{\prime }}$. Hence, if (II) is neglected, the inferred source $\stackrel{\mathrm{‾}}{S}$ is biased. The relative bias of the method is then

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathit{\delta }\stackrel{\mathrm{‾}}{S}}{\stackrel{\mathrm{‾}}{S}}}={\displaystyle \frac{\stackrel{\mathrm{‾}}{D^{\prime }\left(x\right)S^{\prime }}}{\stackrel{\mathrm{‾}}{D\left(x\right)}\times \stackrel{\mathrm{‾}}{S}}}.\end{array}$$

Hence we show in Eq. (5) that time averaging leads to a relative bias which can be quantified by the time covariance between the transfer function and the source strength. However, this quantity is by nature unknown since the dynamics of S(t) is unknown. Determining $\stackrel{\mathrm{‾}}{D(x{)}^{\prime }{S}^{\prime }}$ requires knowledge of the source dynamics, which can be obtained from measurements with a micrometeorological method. It can alternatively be approached by modelling using state-of-the-art ammonia exchange processes as we do here.

In addition to the bias, which is term (II) in Eq. (4), evaluating term (I) is encompassed with errors related to the uncertainties in $\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}}$, $\stackrel{\mathrm{‾}}{C\left(x\right)}$ and $\stackrel{\mathrm{‾}}{D\left(x\right)}$. In particular, cases in which $\stackrel{\mathrm{‾}}{D\left(x\right)}$ is small may lead to large errors in inferring the source term S. This is linked to the conditioning of the inverse problem and is discussed in Supplement Sect. S2.

2.1.3 Case of multiple sources and multiple concentration samplers with time averaging

If we generalise the approach to multiple sources and multiple receptors, then the transfer function becomes a matrix $D(x_i,S_j,t)$, which is the contribution of source S_j to concentration at a target located at x_i. For reading purposes we simplify the matrix notation to D_i,j. Equation (3) then becomes

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\stackrel{\mathrm{‾}}{\left[\begin{array}{c}{C}_{\mathrm{1}}\\ \mathrm{⋮}\\ C_M\end{array}\right]}=\stackrel{\mathrm{‾}}{\left[\begin{array}{ccc}{D}_{\mathrm{1},\mathrm{1}}& \mathrm{\cdots }& D_{\mathrm{1},M}\\ \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ D_{N,\mathrm{1}}& \mathrm{\cdots }& D_{N,M}\end{array}\right]}\times \stackrel{\mathrm{‾}}{\left[\begin{array}{c}{S}_{\mathrm{1}}\\ \mathrm{⋮}\\ S_M\end{array}\right]}\\ \text{(6a)}& {\displaystyle }& {\displaystyle }+\stackrel{\mathrm{‾}}{{\mathit{C}}_{\mathrm{bgd}}}+\stackrel{\mathrm{‾}}{\left[\begin{array}{ccc}{D^{\prime }}_{\mathrm{1},\mathrm{1}}& \mathrm{\cdots }& {D^{\prime }}_{\mathrm{1},M}\\ \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ {D^{\prime }}_{N,\mathrm{1}}& \mathrm{\cdots }& {D^{\prime }}_{N,M}\end{array}\right]\times \left[\begin{array}{c}{S^{\prime }}_{\mathrm{1}}\\ \mathrm{⋮}\\ {S^{\prime }}_M\end{array}\right]},\end{array}$$

which in condensed notation gives

$$\begin{array}{}\text{(6b)}& {\displaystyle }\stackrel{\mathrm{‾}}{\mathit{C}\left(x_i\right)}=\stackrel{\mathrm{‾}}{{\mathbf{D}}_{i,j}}\times \stackrel{\mathrm{‾}}{{\mathit{S}}_j}+\stackrel{\mathrm{‾}}{{\mathit{C}}_{\mathrm{bgd}}}+\stackrel{\mathrm{‾}}{{\mathbf{D}}_{i,j}^{\prime }\times {\mathit{S}}_j^{\prime }}.\end{array}$$

If the number of targets is equal to the number of sources, the problem can be solved by inversion of a linear system. If the number of targets is larger than the number of sources, the problem is a multiple linear regression type with unknowns $\stackrel{\mathrm{‾}}{{\mathit{S}}_j}$ and $\stackrel{\mathrm{‾}}{{\mathit{C}}_{\mathrm{bgd}}}$. The third term on the right-hand side of Eq. (6b) is a bias which is a priori unknown and which we will evaluate in this study.

2.1.4 Source inference methods

The inferred sources, $\stackrel{\mathrm{‾}}{{\mathit{S}}_i^{\mathrm{inferred}}}$, were derived from Eqs. (3) or (6) assuming the covariance term (last term on right-hand side) was null. The method used to infer the source was either a simple division (Eq. 3) or an optimisation of the linear system using the linear model function lm in R (package stats, R version 3.2.3), with either M = 1 (single source) or M = 9 (multiple sources):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\stackrel{\mathrm{‾}}{\left[\begin{array}{ccc}{D}_{\mathrm{1},\mathrm{1}}& \mathrm{\cdots }& D_{\mathrm{1},M}\\ \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ D_{N,\mathrm{1}}& \mathrm{\cdots }& D_{N,M}\end{array}\right]}\times \stackrel{\mathrm{‾}}{\left[\begin{array}{c}{S}_{\mathrm{1}}^{\mathrm{inferred}}\\ \mathrm{⋮}\\ S_M^{\mathrm{inferred}}\end{array}\right]}=\stackrel{\mathrm{‾}}{\left[\begin{array}{c}{C}_{\mathrm{1}}\\ \mathrm{⋮}\\ C_N\end{array}\right]}\\ \text{(7)}& {\displaystyle }& {\displaystyle }-\stackrel{\mathrm{‾}}{{\mathit{C}}_{\mathrm{bgd}}}.\end{array}$$

The bias δS_i was then evaluated as the difference between the inferred sources $\stackrel{\mathrm{‾}}{{\mathit{S}}_i^{\mathrm{inferred}}}$ and the modelled sources $\stackrel{\mathrm{‾}}{{\mathit{S}}_i^{\mathrm{obs}}}$ averaged over each period:

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathit{\delta }{\mathit{S}}_i=\stackrel{\mathrm{‾}}{{\mathit{S}}_i^{\mathrm{inferred}}}-\stackrel{\mathrm{‾}}{{\mathit{S}}_i^{\mathrm{obs}}}.\end{array}$$

As shown in Eqs. (3) and (6) the overall mean bias δS_i contains (i) a bias term due to the inference method which is dependent mainly on the conditioning of the matrix D_i,j (see Supplement Sect. S2) and (ii) a bias term which is intrinsically linked to the covariance between D_i,j and S_j (Eqs. 3 and 6). Thus, with Eq. (8) we evaluate the sum of the two biases without distinction. In order to infer the sources, the elements of the dispersion matrix D_i,j need to be determined. The next part details how these were estimated with a dispersion model.

2.2 The dispersion model used for determining the transfer matrix D_i,j

The elements of the transfer matrix ${\mathbf{D}}_{i,j}=D(x_i,S_j,t)$, which is by definition the concentration at location x_i and time t generated by a source S_j of strength S_j(t)=1, were calculated using a dispersion model. The FIDES-3D model (Loubet et al., 2010), based on the analytical solution of the advection–diffusion equation of Philip (1959) was used for that purpose. This model was first compared with a backward Lagrangian stochastic dispersion model (bLS, the WindTrax software, Thunder Beach Scientific, Nanaimo, Canada; Flesch et al., 1995), and successively tuned to mimic the bLS. The two models and how the FIDES model was tuned are briefly described hereafter and detailed in Supplement Sects. S3 and S4.

The FIDES model is based on the Philip (1959) solution of the advection–diffusion equation, which assumes power law profiles for the wind speed U(z) and the vertical diffusivity K_z(z) at height z. This approach also assumes no chemical reactions in the atmosphere and spatial horizontal homogeneity of roughness length (z₀), wind speed (U), and vertical and lateral diffusivity (K_z and K_y). The dispersion model is detailed in Huang (1979) and Loubet et al. (2010). The details of the model and the way the transfer function $D(x_i,S_j,t)$ was estimated are detailed in Supplement Sect. S2.

The Schmidt number, which is the ratio of momentum to scalar vertical diffusivity $Sc=K{m}_z/K_z$, is key in dispersion modelling, as it determines the vertical diffusion rate of scalars. Wilson (2015) demonstrated that bLS and dispersion models like FIDES give different values of Sc by constitution. In order to assure consistency of the Philip (1959) approach with bLS models, considered as references in dispersion modelling, we chose to tune the Philip (1959) model to get the same Sc number as in WindTrax as described by Flesch et al. (1995). The details are given in Supplement Sect. S4. The comparison showed that the tuned FIDES model gives very similar concentrations to WindTrax at measurement heights lower than 2 m above the source, although slightly overestimated under stable and neutral conditions and slightly underestimated under unstable conditions. The correlation between the two models is however very high ($R^{\mathrm{2}}\ge \sim \mathrm{0}$.96), meaning that using the tuned FIDES model to characterise source inference performance will lead to results comparable to WindTrax. Moreover, since in this study the same model is used for predicting and for inferring the fluxes, the results are self-consistent.

2.3 Ammonia sources from simple SVAT modelling and prescribed emissions potentials

In order to evaluate the bias introduced by time averaging the concentrations when inferring single or multiple sources (third term in Eqs. 3 and 6), we generated NH₃ emissions patterns mimicking the behaviour of real sources as closely as possible. With that goal, we used the SurfAtm-NH₃ model developed by Personne et al. (2009) for two purposes: (i) evaluating the turbulence parameters (the friction velocity u_∗ and the Monin Obukhov length L) from the meteorological datasets to parameterise the dispersion models, and (ii) providing the surface temperature T(z₀) and the surface resistances in order to calculate ammonia emissions patterns.

The SurfAtm-NH₃ model is a one-dimensional, bidirectional surface–vegetation–atmosphere transfer (SVAT) model, which simulates the latent (LE) and sensible (H) heat fluxes, as well as the NH₃ fluxes between the biogenic surfaces and the atmosphere. It is a resistance analogue model separately treating the vegetation layer and the soil layer, and coupling a slightly modified (Choudhury and Monteith, 1988) model of energy balance and the two-layer bidirectional NH₃ exchange model of Nemitz et al. (2000) with a water balance model. Unless otherwise stated, the surface was considered a bare soil with z₀=5 mm, displacement height (d) = 0 m, and leaf area index (LAI) = 0.

The ammonia emissions patterns were modelled using the resistance approach and assuming atmospheric concentration was zero, which is a reasonable assumption following nitrogen application and leads to patterns mimicking reality, which is what we are seeking here:

$$\begin{array}{}\text{(9)}& {\displaystyle }F={\displaystyle \frac{C_{\mathrm{pground}}}{R_{\mathrm{a}}\left(z_{\mathrm{ref}}\right)+R_{{\mathrm{bNH}}_{\mathrm{3}}}}}.\end{array}$$

Here R_a(z_ref) is the aerodynamic resistance at the reference height z_ref=3.17 m, and $R_{{\mathrm{bNH}}_{\mathrm{3}}}$ is the soil boundary layer resistance for ammonia as described in Personne et al. (2009). The ground surface compensation point concentration (C_pground) was expressed as a function of Γ, the ratio of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ to H⁺ concentrations in the soil liquid phase at the surface, as in Loubet et al. (2012):

$$\begin{array}{ll}{\displaystyle }{C}_{\mathrm{pground}}& {\displaystyle }=K_{\mathrm{h}}\left\{T\left(z_{\mathrm{0}}\right)\right\}\times K_{\mathrm{d}}\left\{T\left(z_{\mathrm{0}}\right)\right\}\times \mathrm{\Gamma }\\ \text{(10)}& {\displaystyle }& {\displaystyle }=\mathrm{\Gamma }\times {\mathrm{10}}^{-\mathrm{3.4362}+\mathrm{0.0508}T\left(z_{\mathrm{0}}\right)},\end{array}$$

where K_h and K_d are the Henry and the dissociation constant for NH₃, respectively, and T(z₀) is the soil surface temperature. Since we wanted to evaluate the correlation between the transfer function D_i,j and the source strength S_j, which is the bias in the inference problem (Eq. 6), the NH₃ volatilisation was modelled to reproduce the variety of existing kinetics of NH₃ emissions from fields. With that goal, three Γ patterns were simulated:

1. a constant Γ=Γ₀, which would mimic background NH₃ emissions from soils;

2. an exponentially decreasing $\mathrm{\Gamma }={\mathrm{\Gamma }}_{\mathrm{0}}\exp (-\mathrm{4.6}t/{\mathit{\tau }}_{\mathrm{0}})$, which best represents NH₃ emissions following slurry application;

3. a Gaussian $\mathrm{\Gamma }=\mathrm{N}({\mathrm{\Gamma }}_{\mathrm{0}},{\mathit{\sigma }}_{\mathrm{\Gamma }})$, which would represent the typical NH₃ emissions following urea application.

Here Γ₀ is the maximum Γ during the period, t is the time in days, and τ₀ is the duration of the emissions in days. The factor 4.6 was chosen so that when t=τ₀, Γ goes down to 1 % of Γ₀. The duration of the emissions was chosen to be 4 weeks, τ₀=28 days. The timescale of the exponential decrease we used here was around 6 days, which is twice as large as the one reported by Massad et al. (2010) for slurry application (2.9 days). While these Γ patterns gave the weekly trend of NH₃ emissions, the daily patterns were produced by the thermodynamical and turbulence drivers of NH₃ emissions, which were explicitly taken into account through the compensation point (Eq. 10). To facilitate understanding, in most of the paper only the constant Γ was considered, and the effect of modifying the source strength was evaluated in a sensitivity study.

2.4 Spatial set-up of the sources and concentration sensors

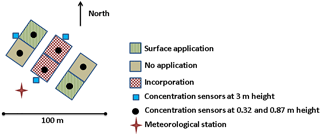
The sources (plots) were considered to be squares with width x_plot and aligned south–north. Two configurations were considered: (1) a single-source configuration and (2) a multiple-source configuration, which mimics typical agronomic trials with nine sources (plots) placed next to each other, with three treatments of three repetitions each. Each treatment was assigned a value of Γ₀ different from the others, while the three repetitions of the same treatment were assigned the same value of Γ. The concentration sensor (receptors) locations, x_i, were set in the middle of each plot, at several heights z_i. (Fig. 1).

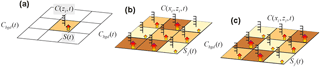
Figure 1 General scheme of the source receptor locations for (a) a single source and (b) multiple sources. (c) “Optimum” plot layout used for the multiple-source configuration.

A number of plot sizes (x_plot=25, 50, 100 and 200 m on the side), and receptor heights (z_i=0.25, 0.5, 1 and 2 m), were tested successively. Several source strengths and dynamics were also tested: Γ was first considered constant with time (pattern 1) in all the plots, and the Γ₀ values of each of the three treatments were either chosen to be significantly different in strength (10⁴, 10⁵, 10⁶), or of the same order of magnitude (1000, 2000, 4000). Then the three Γ patterns (constant, exponential and Gaussian) were randomly assigned to the treatments for each simulation period. The ammonia background concentration, C_bgd, was considered constant and equal to 1 ppb except when studying the sensitivity of the inference method to the background concentration, where it was set as unknown. Throughout this study, an “optimum” block configuration was considered (shown in Fig. 1c), which avoided trivial configurations like aligned blocks and maximised the mean distance between blocks as in a Latin-square design.

2.5 Simulation details

2.5.1 Meteorological data and fertiliser application periods

A range of meteorological conditions were simulated based on the half-hourly meteorological data of the FR-Gri ICOS site in 2008. In total 13 periods of 28 days were considered, which spanned the whole year except the last 2 days of the year. Each period consisted of 1344 half-hourly data.

2.5.2 Concentration sensor integration periods

In order to evaluate the influence of the concentration averaging period on the source inference, several integration periods τ were tested: 0.5 (no integration), 3, 6, 12, 24, 48 and 168 h (7 days). In practice the concentrations were computed at each sensor location using Eq. (6) over 0.5 h: at that timescale, which corresponds to the spectral gap, the covariance term is assumed to be negligible (Van der Hoven, 1957). Then the averaged concentrations were computed for all integration periods.

2.5.3 Sensitivity to inferential method scenarios

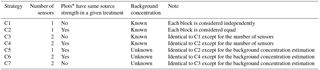
Several scenarios were considered and summarised in Table 1.

1. The background concentration $\stackrel{\mathrm{‾}}{C_{\mathrm{bgd}}}$ was either supposed known and fixed to the prescribed values (C1–C4) or was inferred (C5–C7).

2. The three repetitions of each treatment were either supposed to have the same source strength (C2, C4, C5, C6) or they were inferred independently (C1, C3, C7). In C2, C4, C5 and C6, S_i=S_m for all i and m values belonging to the same treatment. In practice a new dispersion matrix was calculated by averaging together all columns belonging to the same treatment (matrix dimension N × 3). Three strength values of S were inferred to be tested.

3. Either one concentration sensor at each source location (z_i) was considered (C1, C2, C5) or two sensors positioned at two heights were considered (C3, C4, C6, C7). All the measurement heights and their combinations were considered.

Table 1 Scenarios tested for inferring the sources and background concentration.

^* Each treatment has three plots (repetitions).

2.6 Statistical indicators

For each run the mean bias (BIAS) and the normalised mean bias (NBIAS) were calculated as ${\mathrm{BIAS}}_i=\frac{\mathrm{1}}{N_{\mathit{\tau }}}\sum _{\mathit{\tau }}\mathit{\delta }\mathrm{cum}{S}_i$, ${\mathrm{NBIAS}}_i={\mathrm{BIAS}}_i/\phantom{{\mathrm{BIAS}}_i\left(\frac{\mathrm{1}}{N_{\mathit{\tau }}}\sum _{\mathit{\tau }}\mathrm{cum}{S}_i^{\mathrm{obs}}\right)}\left(\frac{\mathrm{1}}{N_{\mathit{\tau }}}\sum _{\mathit{\tau }}\mathrm{cum}{S}_i^{\mathrm{obs}}\right)$, where N_τ is the number of the time-averaged samples over each 28-day period and cumS_i and $\mathrm{cum}{S}_i^{\mathrm{obs}}$ are the inferred and observed cumulated fluxes over the same period. The medians and interquartiles of these statistical indicators were then calculated over the 13 periods of 28 days for 2008.

2.7 Real experimental test case

In order to evaluate the feasibility of the method we applied it to a real test case (Fig. 2). The trial was located at La Chapelle Saint-Sauveur in France ($\mathrm{47}{}^{\circ }{\mathrm{26}}^{\prime }{\mathrm{44.1}}^{\prime \prime }$ N, $\mathrm{0}{}^{\circ }{\mathrm{58}}^{\prime }{\mathrm{50.7}}^{\prime \prime }$ W) and performed from 5 to 26 April 2011. Soil texture was loamy with a pH in water of 6.2 and a bulk density of 1.4 t m⁻³ in the first 15 cm. The experimental unit was composed by six squared subplots 20 m wide with two repetitions of three treatments: (1) surface application of cattle slurry, (2) surface application and incorporation of the same slurry, and (3) no application. Slurry pH was 7.5 with a dry matter (DM) content of 6.05 % and C : N ratio of 10.4 and it contained 38.4 g N kg⁻¹ (DM) as total nitrogen and 13.2 g N-NH₄ kg⁻¹ (DM) as ammoniacal nitrogen. Slurry was applied on 5 April 2011 at a rate of 49 m³ ha⁻¹, which led to 114 kg N ha⁻¹ and 39 kg N-NH₄ ha⁻¹. The application was identical between the two repetitions with a small standard deviation (< 0.2 kg N ha⁻¹). The incorporation was performed in two subplots 1 h after the end of the slurry spreading with a disc harrower at a depth of 0.10 m. The soil humidity between 0 and 5 cm depth was homogeneous over the blocks and decreased from 20 ± 1 to 17 ± 1 % w∕w between the start and the end of the experiment. Meteorological data were measured at less than 50 m from the central plots (Fig. 2). Air temperature, relative humidity, global solar radiation, wind velocity and direction were recorded every 30 min at 2 m height. The turbulence parameters (u_∗ and L), input of the dispersion models, were evaluated with a simple energy balance model of Holtslag and Van Ulden (1983) assuming a Bowen ratio of 0.5 and a deep soil temperature equal to the averaged ambient temperature. Ammonia concentration was measured with diffusive samplers (ALPHA), (Sutton et al., 2001; Tang et al., 2001, 2009), which were placed at the centre of each subplot at two heights (0.32 and 0.87 m from the ground) as well as next to the assay at three locations (5 m away from the plots) at 3 m height. The ALPHA samplers were set in place just after slurry application and incorporation (between 14:20 and 14:50 LT) and left exposed subsequently for 3, 22, 23, 23, 71 h (3 days) and 359 h (15 days), hence spanning 21 days. The diffusive samplers were prepared prior to the experiment, stored at 4^∘ C in a refrigerator and analysed by colorimetry. Since no background concentrations were measured at a reasonable distance from the field, the background concentration was assumed as the minimum over the whole period of the concentrations measured on the 3 m height masts.

Figure 2 Scheme of the real experimental test case performed on six subplots with three treatments and two repetitions. Cattle slurry was either applied on the surface or incorporated. The concentration sensor and meteorological station locations are shown on the scheme.

3 Results and discussion

3.1 Meteorological data range and simulated ammonia sources

The meteorological conditions over the 13 periods represented a good sample of temperate climate conditions. The friction velocity u_∗ varied between 0.024 and 1.181 m s⁻¹, and the stability parameter z∕L at 1 m height varied between −49 and 21 (Fig. 3). It is noticeable that u_∗ showed greater variability during the winter than during the summer, while it was the opposite for z∕L. The surface temperature also showed a structure varying between periods, with a larger temperature range during the summer (from 5.7 to 50.4 ^∘C) than during the winter (from −5.2 to 22.9 ^∘C). This surface temperature variability is an essential feature to representing real-case ammonia sources (Sutton et al., 2009), which shows a variability reflecting both the surface temperature and the resistance variations (Eqs. 9 and 10).

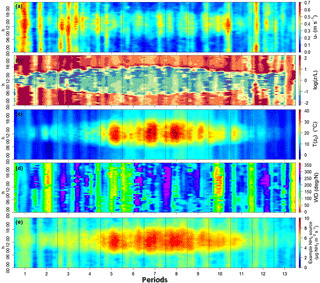
Figure 3 Footprints of measured u_∗ (a), z∕L at 1 m height (b), T(z₀) (c) and wind direction (d) for the hour of the day and the 13 considered periods over the year 2008 at the FR-Gri ICOS site. The modelled ammonia source is also reported (e) according to Eqs. (9) and (10) over the same period with an emissions potential Γ=10 000.

3.2 Example ammonia concentration dynamics modelled with the tuned FIDES model

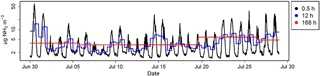
The modelled ammonia concentrations reproduced typical patterns measured above field following nitrogen application well, with maximum concentrations during the day and minimum concentrations at night (Fig. 4). These patterns are a consequence of daily variations of the sources driven by surface temperature combined with variations in the aerodynamic transfer function D_i,j, which behaves similarly to a transfer resistance (see Supplement Sect. S1). The integration periods are also shown in Fig. 4, which illustrates the progressive loss of information of the pattern structure with integration periods. Particularly, it can be seen that the day-to-night variation is captured up to an integration period of 6 h. Moreover, it should be noted that averaging also means overestimating lower concentrations and underestimating higher concentrations.

Figure 4 Example modelled concentration pattern at 1 m above a single 50 m width source for several averaging periods (0.5, 12 and 168 h) for the month of July 2008. The source Γ was set to 10⁵. The y axis is log scaled.

3.3 Evaluation of the inference method for a single source and a single sensor

At first we evaluate the bias of the inference method for the simpler case of a single source and a single sensor placed in the centre of the source field at several heights, assuming we know the background concentration (strategy C1; Fig. 1a). This case has the advantage of having a condition number equal to 1 (Supplement Sect. S2 and Eq. S1) and a bias δS which is well defined and equal to $-{\stackrel{\mathrm{‾}}{D}}^{-\mathrm{1}}\times \stackrel{\mathrm{‾}}{D^{\prime }{S}^{\prime }}$ (Eq. 8). This section hence focuses on evaluating the influence of sensor height, time integration and source dimension on the bias without dealing with the complexity of the interactions between multiple fields.

3.3.1 Example of inferred source dynamics

Figure 5 reports an example source inference, which shows the progressive smoothing of the source with integration period. We first see that the source strength corresponding to Γ=10⁵ leads to ammonia emissions ranging from 0 to ∼ 1 $\mathrm{\mu }\mathrm{g}{\mathrm{NH}}_{\mathrm{3}}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ in the winter, which corresponds to 0.71 kg N ha⁻¹ day⁻¹. Over the entire year, the maximum emissions occur during the hottest days and reach up to 7.1 kg N ha⁻¹ day⁻¹. Regarding the inference method, it can be seen in that example that, up to 24 h, the variability in emissions over the period is captured quite well.

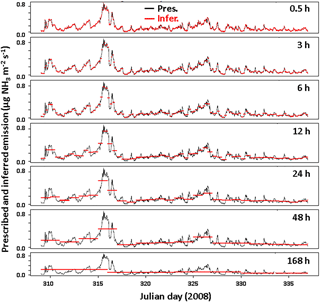
Figure 5 Example source inference for a 25 m width square field and a concentration sensor placed at 0.5 m above ground. Here Γ=10⁵ and is set to constant (pattern 1). The seven integration periods are shown: 0.5 to 168 h. The x axis shows the day of year and corresponds to a span over November. The prescribed source is in black (Obs.) and the inferred one in red (Pred.).

3.3.2 Effect of target height, source dimension and integration period on the bias δS for a single source

In this simpler case shown in Fig. 6, the fractional bias of the inferred emissions is mostly negative for the combination in which the ratio of sensor height to plot dimension is small and integration times are larger than 6 h. According to Eq. (5), this means that the covariance term $\stackrel{\mathrm{‾}}{D^{\prime }{S}^{\prime }}$ is negative for these conditions, meaning that any increase in source strength S at a time t is correlated with a decrease in the transfer function D(t)and vice versa. This is expected as S(t) increases with the surface temperature (Eq. 10) and is proportional to ${\left[R_{\mathrm{a}}\left(z_{\mathrm{ref}}\right)+R_{{\mathrm{bNH}}_{\mathrm{3}}}\right]}^{-\mathrm{1}}$ (Eq. 9), while D(t) is proportional to the aerodynamic resistance R_a(z_ref), as shown in Supplement Sect. S1. Hence, over daily periods, S and D are negatively correlated: S increases during the day and decreases at night (due to temperature and wind speed daily patterns), while D decreases during the day and increases at night (mainly due to wind speed patterns). This is expected to be a general feature for NH₃ surface fluxes as the daily variability reproduced by the model used in this study is representative of most situations from mineral and organic fertilisation to urine patches or seabird colonies (Ferrara et al., 2014; Flechard et al., 2013; Milford et al., 2001; Móring et al., 2016; Personne et al., 2015; Riddick et al., 2014; Sutton et al., 2013).

The median bias δS_i tends to increase in magnitude with the sensor height for large fields (x_plot=100 and 200 m), while it decreases for smaller fields (x_plot=25 and 50) when sensor height gets close to the field boundary layer height. Furthermore, δS_i becomes positive and very large when sensors are above the field boundary layer height (Fig. 6). For large fields, the increase in the magnitude of the bias with lower sensor height is expected as D decreases with height in absolute value. For small fields, the decrease in the bias corresponds to a loss of information as D gets close to zero when the sensor gets closer to the field boundary layer height. For heights above this limit, we observe a change in sign of the bias, which can be explained by the fact that the sensor concentration footprint is not in the source during stable conditions (at night), while it is in the source under unstable conditions during the day. The inference method will hence not work if at least one sensor is not below the plot boundary layer height.

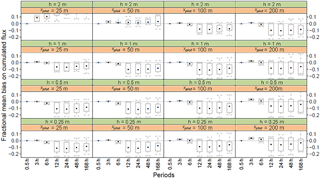
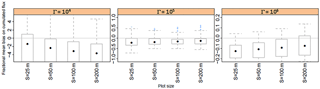
Figure 6 Fractional bias of inferred cumulated ammonia emissions for a single squared field with a lateral dimension of (x_plot) 25, 50, 100 or 200 m and sensor heights (h) 0.25, 0.5, 1 and 2 m, as a function of sensor integrating periods. The points show the median, the boxes the interquartile, and the whiskers the maximum and minimum over the 13 application periods.

We also note that for integration periods equal to or below 3 h, the fractional bias is slightly positive, which can be explained by the positive correlation between S and D at small timescales. This is because of the influence of u_∗ on T(z₀): for a given solar radiation and air temperature over small timescales (< 3 h), an increase in u_∗ leads to a decrease in T(z₀), which leads to an exponential increase in the surface compensation point according to Eq. (10). However, at the same time, R_a(z)⁻¹ decreases, but linearly with u_∗. The resulting ammonia emissions calculated with Eq. (9) nevertheless increases because the exponential effect of temperature overcomes the linear effect of the exchange velocity (data not shown). This effect is more visible for large fields than small fields because over small fields an additional effect is that when u_∗ decreases, the footprint increases and the source “seen” by the targets hence decreases because it incorporates a fraction of zero emissions sources.

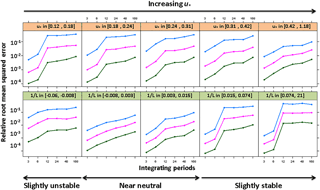
Figure 7 Relative root-mean-squared error as a function of integration period for stability factor and friction velocity classes for a single 25 m side field. Medians and quartiles are given for equally sized bins of u_∗ and 1∕L and for the lowest sensor height (0.25 m). The blue, pink and green curves are the third, second and first quartiles, respectively.

Overall, the median fractional bias for weekly integrated emissions over a 25 m field and sensor heights below 0.5 m was overall −8 % with an interquartile (−14 to −2 %). We can conclude that the bias of the NH₃ emissions is reproducible within ±6 %. We can also conclude that it would be better to place the concentration sensor at a low height to minimise the bias of the method.

3.3.3 Effect of surface boundary layer turbulence on the inference method for a single source

The inference method depends on the turbulence at the site and especially on the main drivers of the dispersion, which are the friction velocity and the stability regime. Indeed, Fig. 7 shows that the relative root-mean-square residual of the inferred source (RRMSR) decreases with increasing u_∗ at long integration periods and is larger in slightly stable than near-neutral or slightly unstable conditions. Figure 7 also shows that under stable conditions or low u_∗ the RRMSR increases by more than an order of magnitude (up to 50 %) when integration periods increase from 6 to 12 h, which catches most of the source variance. We also see that under near-neutral or high u_∗ conditions, the third quartile of the RRMSR remains below 10 % for all integration periods. Finally, we also see that the larger third quartiles at short integration periods are obtained with intermediate u_∗ values or slightly unstable conditions. A similar response of the bias to u_∗ and 1∕L was reported by Fig. 6 in Flesch et al. (2004) and Fig. 3 in Gao et al. (2009) in controlled source experiments. While Gao et al. (2009) attributed the bias of the inference method to parameterisation of the stability dependence of the turbulent parameters (z∕L), in this study this cannot happen since we use the same parameterisation for prescribing the concentration and inferring it. In our case, the interpretation is to be linked with Eq. (5): the smaller u_∗ or the most stable conditions also correspond to the larger time derivatives of source strength (driven by surface temperature and surface exchange resistances) as well as the larger time derivatives of transfer function D. We hence expect that under such conditions, the covariance between the transfer function and the source strength will be larger than under near-neutral conditions. In a more heuristic view, under low turbulence, large time derivatives of concentrations are expected above a source due to low mixing (small changes in mixing lead to large variations in concentrations).

We conclude that the inference method with a long integration period will lead to very moderate biases for locations with near-neutral conditions and high wind speed, but may lead to much larger bias under stable conditions and low wind speed as soon as the integration period reaches 12 h.

3.4 Multiple-source case

In contrast to the single-source case, with multiple sources (see Fig. 1b) the inference method leads to biases at small integration times as can be seen in the example reported in Fig. 8. In that specific case, the emissions of treatments 2 (Γ=10⁵) and 3 (Γ=10⁶) are 10 times and 100 times larger than those of treatment 1 (Γ=10⁴), respectively. This leads to concentrations over plots of treatment 1 (and to a lesser extent over those of treatment 2) being highly correlated to emissions from plots of treatment 3 (and hence less with subplots of treatment 1). As a result, inferring emissions of plots of treatment 1 becomes harder as soon as averaging periods become larger or equal to 3 h. This can be viewed as a progressive loss of information of the treatment 1 contribution to concentrations due to the overweighing contribution of treatment 3 plots. However, we also see that treatments 2 and 3 seem quite correctly inferred for integration times smaller than 48 h.

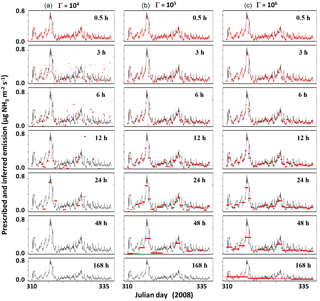
Figure 8 Example result of multiple plot case inference. Black curves: observations; red dots: inferred sources. (a) Treatment 1, Γ=10⁴. (b) Treatment 2, Γ=10⁵. (c) Treatment 3, Γ=10⁶. Missing red dots are out of the y-scale boundaries. Example plots from treatments 1, 2 and 3 are shown from left to right. The period is the same as in Fig. 7 (November 2008 for the FR-Gri ICOS site), and emissions are up to 1, 10 and 100 $\mathrm{\mu }\mathrm{g}{\mathrm{NH}}_{\mathrm{3}}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ for the three emissions potentials. Strategy C7 with target heights 0.25 and 1 m, and source width 25 m on a side.

In the following we will first evaluate the influence of the length of integration periods, sensor heights and plot dimensions on the fractional biases made when inferring the source. Each factor will be evaluated independently of the others in order to understand the processes behind it. For these evaluations background concentration was kept constant at 1 µg NH₃ m⁻³. Strategy C1 was used except when testing sensor heights, for which strategy C3, which uses two targets, was also used. These two strategies assume that the background concentration is known, which avoids any compensating effects between source and background concentration inferences. Then the sensitivity of the methodology to the (i) emissions ratios between two of the three treatments and (ii) the variability in the background concentration were evaluated. Finally, seven inversion strategies were compared to determine which was the most robust (Table 1).

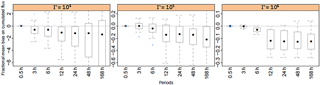
Figure 9 Effect of integration period on source inference in a multiple-plot set-up. The fractional mean bias of the source is shown for each treatment. Inference strategy C1 was used (single sensor, independent blocks, background concentration known). Statistics for runs with target heights 0.25 and 0.5 m and a source width = 25 m are calculated. All application periods are considered. Filled points show medians, boxes show interquartiles, and bars show minimums and maximums. Outliers are points up to 1.5 times away from box limits.

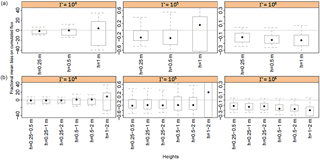
Figure 10 Effect of target heights on source inference in a multiple-plot set-up for integration periods of 1 week (168 h). Same as the case reported for Fig. 9 except that strategies C1 (with a single sensor, top graphs) and C3 (with two heights, bottom graphs) are compared here (the background is assumed known in both strategies).

3.4.1 Effect of integration periods on the bias

We first consider strategy C1, which is the simplest configuration, in which plots are independent, background concentration is known and one target is used above each plot. Figure 9 shows that for the given treatment range (∼ 1–100 µg NH₃ m⁻² s⁻¹), the fractional mean bias is lower than 0.2 in magnitude for the treatment emitting the most (treatment 3, Γ=10⁶), lower than 0.4 for the intermediate treatment (treatment 2, Γ=10⁵) and up to 8 for the treatment emitting the least (treatment 1, Γ=10⁵); here we considered the 0.25–0.75 quantiles. The bias of the highest treatment (treatment 3) actually behaves similarly to a single-source case (Fig. 6), with a median bias around 10 % for 48 h integration periods. This is expected because treatment 1 and treatment 2 have a much smaller emissions strength and hence little influence on the concentration above the treatment 3 plots, which therefore behave in a similar manner to a single source. As a consequence, this bias in treatment 3 is mainly due to the anti-correlation between D and S, which increases with integration periods. The fractional mean bias is very large for treatment 1 even for small integration periods. The bias can either be positive or negative, showing that this method does not allow for a correct estimation of the smallest sources.

Figure 11 Effect of plot size on source inference in a multiple-plot set-up for integration periods of 168 h and target heights of 0.25 and 0.5 m. Same as in Fig. 8.

3.4.2 Effect of target heights on the bias

Figure 10 shows that the bias remains low as long as sensor heights are low enough to catch a sufficient part of the field footprint. When only a single height is used (strategy C1) this means that the sensor should be placed at 0.5 m or below for the field size we have tested here (25 m). The result is similar for a pair of sensors (strategy C3). For the lowest treatment though, the bias (and its variability) remain high whatever the height. It is interesting to notice that the heights which were found to provide an optimal inference of NH₃ sources (below 0.5 m) are smaller than ZINST (the height at which the vertical flux can be approximated by the horizontal flux) reported by Wilson et al. (1982) (which were 0.9 m for 40 m diameter circular sources, and which we estimate as 0.65 m based on a power law extrapolation as in Laubach et al., 2012). It is also important to note that this height should vary with both the roughness length z0 and displacement height as was shown by Wilson et al. (1982) for ZINST.

3.4.3 Effect of plot size on the bias

Increasing the plot size from 25 to 200 m in width reduces the bias of the two highest source treatments for which the median bias reaches values around 10 %, while the interquartiles remain stable (Fig. 11). Conversely, in treatment 1 (Γ=10⁴), the bias increases. It is expected that the bias in a multiple-source configuration never becomes smaller than the bias in a single-source problem, which is a limit linked to the time integration (covariance between the source and the concentration; see Eqs. 3 and 6). It is also expected that the biases remain higher than the single-source case until the source size increases sufficiently so that the concentration generated by a block on the neighbour fields becomes negligible compared to the concentration generated by the source below. This is what we observe in treatment 2 (Γ=10⁵) and treatment 3 (Γ=0⁶), with treatment 2 showing a median bias of −13 % (larger than in the single-source case) for the 200 m wide field, while the bias of the largest source tends to be −10 % [−17 %, −1 %], which is the range observed for a single source.

3.4.4 Sensitivity of the method to ratios of emissions potentials among treatments

A central question is the capability of the inference method to resolve small or large differences in emissions from the nearby blocks. Indeed, we can speculate that small differences will be hard to resolve while large differences will lead to large bias. In order to determine the resolution power of the method, we compared the performance of the inference method with a set of three treatments: the first treatment had Γ=0 to mimic a reference field receiving no nitrogen; the second treatment had a constant Γ=1000 corresponding to a small emissions (0.7 kg N ha⁻¹ day⁻¹), and the third treatment Γ was successively set to increasing values from 1500 to 10⁵ (70 kg N ha⁻¹ day⁻¹). In this section we consider the background to be known (sensitivity to the background concentration will be evaluated in the next section).

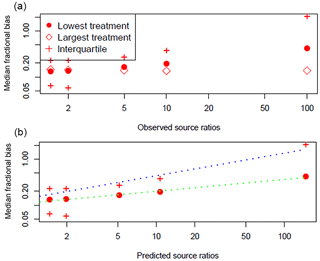
Figure 12 Median fractional bias of cumulated emissions as a function of the ratio of the high-to-low source treatments for a 7-day integration period. (a) Bias as a function of the theoretical source ratios. (b) Bias as a function of the predicted source ratios. Dotted lines show power function regressions on medians (green) and interquartiles (blue). Strategies C1 and C3 are pooled together with all runs including sensor heights 0.25 and 0.5 m.

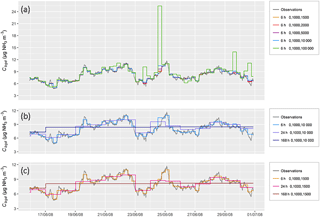
Figure 13 Background concentrations prescribed (Observation) and inferred using strategy C7 and height combination (0.25, 2 m): (a) effect of the treatment contrasts for a short integration period of 6 h (treatments 1, 2 and 3 are given); (b) effect of integration period for contrasted treatments (Γ=0, 1000, 10 000); (c) effect of integration period for similar treatments (Γ=0, 1000, 1500).

Figure 12 shows the median and interquartile biases of the cumulated emissions for the longest integration period of 168 h over the ratio of the high-to-low source treatments. The bias of the largest source always remained around 14 %, which is larger than the single-source case. The bias of the lowest source increased with increasing inter-treatment source ratios from 13 to 40 %. In fact we find that the fractional bias increased approximately as a power function of the ratio of the two predicted sources (dotted lines, 0.11 x^0.256).

3.4.5 Quality of background concentration estimations

As pointed out by Flesch et al. (2004), the knowledge of the background concentration is essential in a source inference problem. Retrieving the background necessitates having at least N_sources+1 sensors. Hence only strategies with two heights per plot or which assume identical emissions in treatment repetitions can be evaluated in their capacity of retrieving the background (strategy C2 to C7). In order to evaluate the sensitivity of the method when the background concentration varies with time, we set a realistic background concentration as a linear combination of u_∗ and air temperature (T_a) with a mean of 6 µg NH₃ m⁻³ and a standard deviation of 0.1 µg NH₃ m⁻³. This test was performed with a range of treatments in order to elucidate the correlations between varying background and varying treatments. We see in Fig. 13 that the concentration, which follows a realistic pattern, is well retrieved even over the longest integration period of 168 h. However, we see that for the treatments with the largest source contrast (Γ=1000 and 10⁵), the background concentration can be overestimated even for small integration periods (6 h). The median residual of the background concentration was smaller in magnitude than 0.05 µg NH₃ m⁻³, except for the case with very large differences among treatments (0, 1000, 10 000), for which the residual reached 0.1 and 0.5 µg NH₃ m⁻³ for the 6 h and 24 h or 168 h integration periods. Furthermore, the background concentrations were overestimated for the largest source ratios and underestimated for the lowest source ratios and longer integration periods (24 and 168 h).

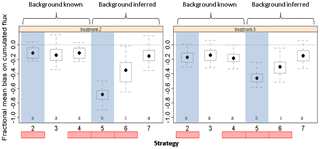
Figure 14 Comparison of biases for all source inference strategies. In strategies C2, C3 and C4 we hypothesise that we have perfect knowledge of the background concentrations, while in strategies C5, C6 and C7 background concentrations are inferred together with the sources. In strategies C2, C4, C5 and C6 (red rectangles) we suppose that plots from the same treatment have the same emissions, while in strategies C3 and C7 we infer each plot separately. In strategies C2 and C5 we assume single sensors are placed above each plot (blue shades), while in strategies C3, C4, C6 and C7 we assume two sensors are placed above each plot.

3.4.6 Identifying the most robust strategy

Finally, to identify which strategy is the most suitable for retrieving the emissions from the multi-plot configuration, we compared all strategies for a simulation with a variable background (set as in the previous section) and two source ratios of 2 and 20 between treatments 2 and 3 (treatment 1 being a zero-source reference). We found, as expected, that strategies with known backgrounds have low biases compared to strategies that calculate the background, except for strategy C7, which provided biases similar to strategy C3, which is the strategy equivalent to C7 but with a known background (Fig. 14). We also see that incorporating some knowledge of the sources by assuming plots from the same treatment have the same emissions gave slightly better estimates when the background is known (strategies C2 and C4 compared to C3). This is however not true when the background is unknown, in which case the magnitude of the bias increases up to a median of 0.7 (strategies C5 and C6 compared to C7). It is due to compensation between background concentration and source strength as we have seen in Fig. 14 that the background concentration was overestimated in such cases. We also see, as expected, that the strategies with two sensors placed at different heights above each plot lead to better evaluations of the emissions. Overall, the strategy based on two sensors above each plot, which also assumes that sources are independent, seems to be the most robust (strategy C7). This strategy does not assume the background is known, nor does it assume the plots have similar emissions, which is more adapted to reality. Indeed, even though the same amount of nitrogen is applied in each repetition plot, the emissions may vary due to soil heterogeneity and advection. We finally obtain a median bias for strategy C7 which is −16 % with an interquartile [−8–22 %]. It is important to stress though that the minimums and maximums are further away, which indicates that under some rarer circumstances, the method may overestimate the sources by 12 % or underestimate them by 40 %. These cases correspond to integration periods with very low wind speeds and stable conditions.

3.5 Application of the methodology to a real test case with multiple treatments

The evaluation of the methodology on a real test case is shown in Figs. 15–17. The concentration measured above the surface-applied slurry (up to 200 µg N-NH₃ m⁻³) is much higher than above the two other treatments (below 50 µg N-NH₃ m⁻³) (Fig. 15).

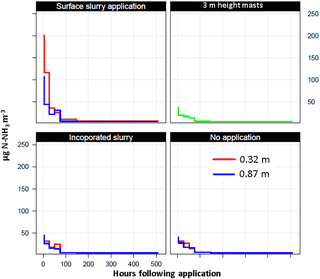
Figure 15 Concentrations measured in a real test case with six blocks composed of three treatments and two repetitions. Here the mean concentration for the repetition and the three replicate ALPHA samplers are shown at two heights above ground. The concentration measured at 3 m height and 5 m away from the plots is also shown in green. The background concentration, evaluated as the minimum of the green curve, was 5 µg N-NH₃ m⁻³.

The inference method gives very consistent results both in terms of comparison between repetitions (B1 and B2) of a given treatment and in terms of comparison between treatments (strategy C7 shown in Fig. 16). Surface slurry application showed the largest emissions: 9 ± 0.3 kg N ha⁻¹ in B1 and 10 ± 0.2 kg N ha⁻¹ in B2 (median and confidence interval). This corresponds to an emissions factor around 24 % of the N-NH₄ applied and 8 % of the total N applied, which is in line with agronomic references (Sintermann et al., 2011a; Sommer et al., 2006). In contrast, the incorporated slurry showed much smaller emissions: 0.3 ± 0.2 kg N ha⁻¹ in B1 and 0.6 ± 0.2 kg N ha⁻¹ in B2. It is noticeable that no application showed slight deposition, especially in B2: −0.26 ± 0.2 kg N ha⁻¹ in B1 and −1.7 ± 0.2 kg N ha⁻¹ in B2.

Comparing the inference strategies is instructive (Fig. 17). We see that in methods which assume a known background (strategies C3 and C4), the inferred emissions are slightly higher than when background is assumed unknown. We should state that we set the background concentration to the minimum concentration measured on the 3 m height masts because these were located too close to the plots to be considered real background masts. This explains why strategies C3 and C4 lead to higher estimates compared to strategies C6 and C7, as the background may have been underestimated. We also find that all methods consistently infer a deposition flux to the blocks with no application, which is consistent with our knowledge of ammonia exchange between the atmosphere and the ground (Flechard et al., 2013). Indeed, the concentration in the atmosphere, which is enriched by the nearby sources is expected to be higher than near the ground due to a low soil pH (6.1), a low nitrogen content in the soil surface (6–9.5 g N kg⁻¹ DM) and a 20 % humid soil surface, hence leading to a flux from the air to the ground.

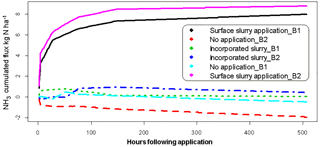
Figure 16 Cumulated fluxes estimated with the inference method on the real test case with strategy C7. Three treatments with two repetitions are compared (B1 and B2).

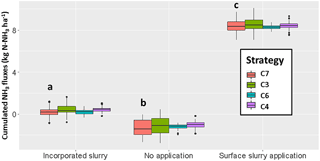
Figure 17 Same as Fig. 16 but grouped by treatments and with additional strategies C4 and C6, which consider that replicates have the same surface flux. The variability in the box plot aggregates the uncertainty on the inference method (the standard deviation on the flux estimate in the least-square model, which accounts for the variability in the replicated concentration measurements), and the variability among the repetitions in each treatment. Letters a, b and c show significant differences among treatments for the C7 strategy, according to a Tukey test (95 % family-wise confidence level).

From our theoretical study we know that strategy C7 should give a bias around −16 % ± ∼ 7 %. Therefore, we could expect that the real flux is the one measured with C7 times 1.15 (±0.08); hence it would be 10.9 ± 1.3 kg N ha⁻¹. This corresponds to 28 ± 3 % of the N-NH₄ applied and ∼ 9 ± 1 % of the total N applied. For the incorporated slurry, the emissions are around 20 times smaller than the emissions from the surface-applied slurry. Under these conditions, the bias on the emissions would be around −20 %, which means that the corrected emissions would range from 0.5 to 2.5 % of the N-NH₄ applied and 0.2 and 0.8 % of the total N applied. We should bear in mind that the theoretical correction is based on the median of the simulations performed with the 2008 dataset in Grignon, which had similar meteorological conditions to this trial. It would be much more relevant though for future developments to evaluate the bias based on the same method as developed here but with emissions and meteorological conditions taken from the real case.

3.6 Comparison with previous work

Several studies have reported methodologies for evaluating multiple sources using dispersion models. These were mostly based on backward Lagrangian modelling (Crenna et al., 2008; Flesch et al., 2009; Gao et al., 2008). There were several inference methods reported: the methods based on the inversion of the dispersion matrix D_i,j or singular value decomposition of least-square optimisation (Flesch et al., 2009), which optimise the conditioning of the dispersion matrix, and one based on Bayesian inference (Yee and Flesch, 2010). Yee and Flesch (2010) showed that the Bayesian approach would avoid unrealistic source estimates that could appear when the matrix conditioning was poor. Unrealistic source estimates were for instance reported by Flesch et al. (2009), with negative emissions sources.

Ro et al. (2011) evaluated the bLS technique to infer two controlled methane surface sources with laser measurements. They found 0.6 recovery ratios (ratio of inferred to known source) if the fields were not in the footprint of the sensor but with adapted filters; they found a high degree of recovery of 1.1 ± 0.2 and 0.8 ± 0.1 for the two sources. They found that in contradiction to Crenna et al. (2008) and Flesch et al. (2009), even with large conditioning numbers they had high recovery rates.

Misselbrook (2005) compared different methodologies and showed that under high concentrations diffusion samplers may lead to overestimation of up to 70 % of the concentration. They suggest potential issues related to the deformation of the Teflon membrane, which would modify the distance between coated filters and the membrane itself, which could cause sampler saturation. There is hence some concern about the quality of diffusion samplers to measure concentrations at heights close to large sources, which would necessitate field validations.

3.6.1 Sensor positioning and conditioning number

Crenna et al. (2008) have clearly shown that the optimal sensor positioning should be so that each sensor preferentially sees a single source, and reversely, each source should preferentially influence a single sensor. In this study the source–sensor geometry was especially designed in a way that minimises the condition number by placing the sensors in the middle of each plot. For the smallest source (x_plot=25 m), the conditioning number ranged from 1.97 to 3.01 (median 2.42) for sensors located at 0.25 m, and increased to 2.6–6.9 (median 3.2) for sensors at 0.5 m, 4.7–150 (median 21) for sensors at 1.0 m, and 40–165 000 (median 640) for sensors at 2 m. This shows that including at least one sensor per block at heights lower than the field width divided by 20 would ensure that the conditioning number remains lower than in most trials reported by Crenna et al. (2008).

By comparing different strategies we have found that the strategies using two sensors over each source systematically led to improved performances (C3 versus C1 and C6 versus C5, Fig. 14). This is also in line with the results of Crenna et al. (2008), who showed that using more sensors separated spatially improves the performance of the inference method. Hence we can conclude that the inference method we used is based on a well-conditioned system which leads to robust results of the least-square optimisation. This is further illustrated by the real-case example (Figs. 15–17), which shows a good reproducibility among block repetitions. Indeed, good reproducibility among repetitions is a check for evaluating the quality of the inference method in real test cases. The use of the Bayesian inference method would however also be valuable in the set-up we propose here.

3.6.2 Effect of time-integrating sensors on the source inference quality

The use of time-averaging sensors for estimating ammonia sources was already reported by Sanz et al. (2010), Theobald et al. (2013), Carozzi et al. (2013a, b), Ferrara et al. (2014) and Riddick et al. (2016a, 2014). All these studies have shown the feasibility of these measurements; however only a few of them allow the estimation of the impact of averaging: Riddick et al. (2014) measured emissions from a bird colony on Ascension Island with WindTrax using both several ALPHA samplers in a transect across the colony and a continuous analyser for ammonia (AiRRmonia, Mechatronics, NL) downwind. They also averaged the continuous sampler concentrations to evaluate the effect of averaging on the emissions estimates. They found as we do here that averaging over monthly periods would lead to systematic underestimations from −9 to −66 %. They also found that estimations from diffusive samplers would lead to average underestimations of −12 %. This is very close to what we find here for a single source over 1 week (Fig. 6). In a similar comparison Riddick et al. (2016b) found that time integration led to slight overestimations with the integration approach, which is within the range of statistics of the bias we have found for the larger area sources (third quartile in Fig. 6).

3.6.3 Dependency on meteorological conditions

We should bear in mind that the use of time-averaging sensors in the inference method is also highly dependent on the surface layer turbulent structure as shown by Fig. 7. We find, as expected, that stable conditions or low wind speed conditions are those that lead to the highest potential bias (as shown by the third quartile under stable conditions at the bottom of Fig. 7). This is a well-known limitation of inverse dispersion modelling which was reported by Flesch et al. (2009, 2004) and which suggested that inverse dispersion would be inaccurate for $u_{\ast }<\mathrm{0}$.15 m s⁻¹ and $|z/L|<\mathrm{1}$. However, both our study and the studies of Riddick et al. (2014, 2016b) show that this is not as much of an issue for ammonia emissions. Indeed, this is due to the fact that ammonia emissions follow a daily cycle with low emissions at night and high emissions during the day. This is firstly because the ground surface compensation point concentration (C_pground) has an exponential dependency on surface temperature as assumed in Eq. (10) based on known thermodynamical equilibrium constants (Flechard et al., 2013). This is secondly due to the fact that ammonia emission is a diffusion-based process which is limited by the surface resistances, as modelled in Eq. (9), which leads to small fluxes when R_a(z_ref) and $R_{{\mathrm{bNH}}_{\mathrm{3}}}$ become large, which happens during low wind speeds (they are both roughly inversely proportional to wind speed) and stable conditions, which also happens at night (Flechard et al., 2013). In real situations, the combination of small turbulence and high surface concentration leads to a further decrease in the flux, which is dependent on the difference between C_pground and the concentration in the atmosphere above (a feature which was not accounted for in this study as this would imply a higher degree of complexity in the modelling approach). This means that the results we found in this study would not apply for species with an emissions pattern with different temporal dynamics (either constant or anti-correlated with surface temperature or wind speed).

4 Conclusions

In this study we have demonstrated that it is possible to infer, with reasonable biases, ammonia emissions from multiple small fields located near each other using a combination of a dispersion model and a set of passive diffusion sensors which integrate over a few hours to weekly periods. We found that the Philip (1959) analytical model in FIDES gave similar concentrations as the backward Lagrangian stochastic model WindTrax at 2 m above a small source, under neutral and stable stratification as long as the stability correction functions used in both models are similar and the Schmidt number is identical (here set to 0.64). Under unstable conditions FIDES gave 20 % smaller concentrations at 2 m compared to WindTrax.

We demonstrated by theoretical considerations that passive sensors always lead to the underestimation of ammonia emissions for an isolated source because of the negative time correlation between the ammonia emissions and the transfer function. Using a yearly meteorological dataset typical of the oceanic climate of western Europe we found that the bias over weekly integration times is typically −8 ± 6 %, which is in line with previous reports. Larger biases are expected for meteorological conditions with stable conditions and low wind speeds as soon as the integration period is larger than 12 h.

We showed that the quality of the inference method for multiple sources was dependent on the number of sensors considered above each plot. The most essential technique to minimise the bias of the method was to place a sensor in the middle of each source within the boundary layer. The quality of the sensor positioning was evaluated using “condition numbers” which ranged from 2 to 3 for a sensor placed at 25 cm above the ground to much higher values (40–1.6 × 10⁵) for a sensor at 2 m above 25 m width sources. Although the lowest sensors have the best condition number, we would rather recommend using heights of 50 cm above the canopy in order to reduce uncertainty in positioning the sensors close to the ground as well as avoid non-diffusive transfer conditions. Similarly, although the highest sensors had low condition numbers, they were shown to improve the robustness of the sources' inference, especially for evaluating the background concentrations. Using replicates of each treatment was found to be essential for evaluating the quality of the inference and derive robust statistical indicators for each treatment.

When considering a system, characteristic of agronomic trials, composed of a low and a high potential source and a reference with no nitrogen application, we found that the fractional bias remained smaller than around 25 % for ratios between the largest and smallest sources lower than a factor of 5 and increased as a power function of the ratio. Furthermore, the dynamics of the emissions were found not to strongly affect the fractional bias. As expected, we also found that the fractional bias decreased with increasing source dimensions, especially for the lowest source strength in a multiple-source trial.

Finally, a test on a practical trial proved the applicability of the method in real situations with contrasted emissions. We indeed calculated ammonia emissions of around 27 ± 3 % of the total ammoniacal nitrogen applied for surface-applied slurry while we found less than 1 % of emissions for the treatments with incorporated slurry.

This method could also be improved by incorporating knowledge of the surface source dynamics into the inference procedure. Further work is required, however, for validating the method, for instance using prescribed emissions, and to evaluate the method for growing crops using real measurements with diffusion samplers close to the ground.