Ammonia emission measurements of an intensively grazed pasture

The quantification of ammonia (NH₃) emissions is still a challenge and the corresponding emission factor for grazed pastures is uncertain. This study presents NH₃ emission measurements of two pasture systems in western Switzerland over the entire grazing season 2016. During the measurement campaign, each pasture system was grazed by 12 dairy cows in an intensive rotational management. The cow herds on the two pastures differed in the energy to protein balance of the diet. NH₃ concentrations were measured upwind and downwind of a grazed subplot with line-integrating open path instruments that were able to retrieve small horizontal concentration differences (< 0.2 µg NH₃ m⁻³). The NH₃ emission fluxes were calculated by applying a backward Lagrangian stochastic (bLS) dispersion model to the difference of paired concentration measurements and ranged from 0 to 2.5 µg N–NH₃ m⁻² s⁻¹. The fluxes increased steadily during a grazing interval from previous non-significant values to reach maximum emissions at the end of the grazing interval. Afterwards they decreased exponentially to near zero-values within 3–5 days. A default emission curve was calculated for each of the two systems and adopted to each rotation in order to account for missing data values and to estimate inflow disturbances due to grazing on upwind paddocks. Dung and cow location were monitored to account for the non-negligible inhomogeneity of cow excreta on the pasture. The average emission (± SD of individual rotation values) per grazing hour was calculated as 0.64±0.11 g N–NH₃ cow⁻¹ h⁻¹ for the herd with the N-balanced diet (system M) and 1.07±0.06 g N–NH₃ cow⁻¹ h⁻¹ for the herd with the protein-rich grass-only diet (system G). Surveys of feed intake, body weight and milk yield of the cow herds were used to estimate the nitrogen (N) excretion by an animal N budget model. Based on that, mean relative emission factors of 6.4±2.0 % and 8.7±2.7 % of the applied urine N were found for the systems M and G, respectively. The results can be used to validate the Swiss national emission inventory and demonstrate the positive effect of an N-balanced diet on pasture NH₃ emissions.

1 Introduction

Agricultural livestock production is the main source of air pollution by ammonia (NH₃; Bouwman et al., 1997). The largest share of emissions is usually assigned to the excretions in the barn with subsequent manure storage and spreading (Kupper et al., 2015). These high emissions are largely responsible for the formation of secondary aerosols in the atmosphere through reactions with nitric and sulfuric acids (Nemitz et al., 2009). This can have a significant effect on human health and can also lead to eutrophication and acidification of the environment through deposition (Sutton et al., 2011).

Grazing is considered one efficient mitigation option to reduce NH₃ volatilisation due to the direct infiltration of urine in the soil before urea is degraded to ammonium and NH₃. According to the Swiss inventory model Agrammon (Kupper et al., 2015; see Fig. 4b therein), grazing livestock produces about 8 times lower emissions compared to indoor housing (including storage and spreading of manure). Emission inventories usually make use of generalised emission factors that relate emissions to the corresponding source of water-soluble nitrogen (urea, ammonium or dissolved NH₃). In the case of grazed pastures the relevant nitrogen (N) source is urine by animal excretion (Petersen et al., 1998). However, the pasture emission factor still has a large uncertainty because corresponding NH₃ emission experiments are rare and the available studies report a large range of emission factors (5 to 25.7 % of excreted urine N; e.g. Jarvis et al., 1989; Bussink, 1992; Laubach et al., 2012, 2013b). Many of the studies used manually applied urine and measured the emissions with chamber or wind tunnel methods. These techniques might lead to questionable results due to the altering of the environment and the high heterogeneity of the emissions (Misselbrook et al., 2005; Sintermann et al., 2012).

Volten et al. (2012) introduced a new open path miniDOAS system that measures line-integrated NH₃ concentrations with a relatively high temporal resolution. Sintermann et al. (2016) adopted and further developed the system to field applicability and suggested that paired miniDOAS systems in combination with a dispersion model can be used to estimate emissions of a pasture. Bell et al. (2017) estimated the NH₃ emission factor based on miniDOAS concentration measurements in combination with a backward Lagrangian stochastic (bLS) dispersion model for a 12-day period and demonstrated the applicability of the miniDOAS–bLS combination for grazing systems. However, no information on the excreta distribution on the pasture was obtained and retrieved emission factors were based on a standard cow and feeding strategy. The relatively short measurement campaign in May also limited the representativeness of the derived emission factor for a full year. For micrometeorological methods a spatially homogenous source area is usually needed (Munger et al., 2012), which is often not the case on grazed pastures (Draganova et al., 2016). However, only very few studies reported on the uncertainty associated with a heterogeneous emission source and those studies usually focused on greenhouse gas emissions (Felber et al., 2015; Peltola et al., 2015).

In the present experiment the miniDOAS systems in combination with bLS modelling were applied to determine NH₃ emissions of two paired rotational grazing systems over a full grazing season. Position monitoring of dung patches with GPS and of cows with a camera system was used to relate the measured emissions to the animal and excreta density. The calculated emission factors were based on actual in situ cow productivity data and feed analyses and were compared to standard emission factors.

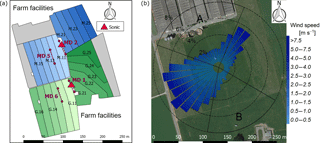
Figure 1 (a) Measurement site with the pastures for the two herds (blue: grass diet with additional maize silage; green: full grazing regime; grey: optional pasture areas) and the division into the paddocks (M.11–M.25, G.11–G.25). Additionally, the locations of the two sonic anemometers and the four miniDOAS systems (MD1–MD6; names based on serial number) are shown. (b) Wind distribution for the northern sonic anemometer with the corresponding sector contributions (black dotted circles) for the period May–October 2016. The areas A and B indicate wind sectors from which advection from the nearby farm building can occur. The wind distribution was overlaid on a Google Earth image of the experimental area (map data: Google, DigitalGlobe).

2 Material and methods

2.1 Site description and experimental design

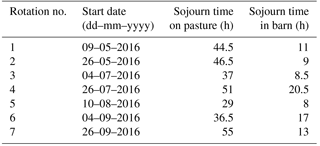
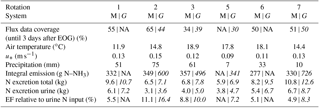
The study site was located in the Prealps of Switzerland at the research farm Agroscope Posieux in the canton of Fribourg (46^∘46^′04${}^{\prime \prime }$ N, 7^∘06^′28${}^{\prime \prime }$ E). The soil is classified as stagnic Anthrosol with a loamy texture (20 % clay, 35 % silt and 45 % sand) and the vegetation consisted mainly of a typical grass–clover mixture (10 % to 50 % Lolium perenne and 7 % to 40 % Trifolium repens) with an increasing clover share during the grazing season. In 2007 the last renovation of the site took place. Since then the site has been used as an intensive pasture for cattle. Averaged over the past years, the average fertiliser application rate was about 120 kg N ha⁻¹ per year, in addition to the excreta of grazing animals. Climate records show an annual average temperature of 8.7 ^∘C and an annual precipitation amount of 1075 mm (MeteoSwiss, 2018). The experiment was conducted at a flat 5.5 ha pasture and the cows were managed in a rotational grazing system (Fig. 1). The whole pasture was divided into two separate systems having different feeding strategies for the cows. The southern system (labelled “G”) represented a full grazing regime without additional feed supplementation. This resulted in a considerable protein surplus for the animals, leading to unnecessarily high N excretion. At the northern system (labelled “M”) cows were provided with additional maize silage (roughly 25 % of the total feed dry matter intake) which has a low protein content and resulted in a more demand-adjusted optimised protein content in the diet (Arriaga et al., 2010; Yan et al., 2006) leading to less N excretion. Each of the two pasture systems was divided into 11 paddocks resulting in a full rotation period of about 20 days, depending on the grass growth conditions. The size of the paddocks was adjusted to the different treatments: 1700 m² for the northern M system and 2200 m² for the southern G system. The grazing rotation was synchronous for the two systems and started in the middle of the fields (on paddocks X.11 with X indicating both fields) in the westerly direction (until paddock X.16) and then from the middle (X.21) to the eastern side of the field (X.25). Twice a day (around 05:00–07:00 and 15:00–17:00 LT) the cows were brought to the nearby barn for milking. However, in cases of high air temperatures in August and the beginning of September the cows spent a longer period in the barn during daytime (typically 11:00–17:00 LT). Due to dry periods during the summer months and subsequent low grass growth additional pasture areas were used for grazing. The herd for each system consisted of 12 dairy cows. The main measurement campaign took place between May and October 2016, and in summary, seven full grazing rotations took place in that period (Table 1). During the measurement campaign, the site was fertilised with ammonium nitrate (28 kg ha⁻¹, end of June) and urea (42 kg ha⁻¹; X.11–X.16 middle of August, X.21–X.25 beginning of September).

Table 1 Summary of grazing rotations in 2016 on paddocks X.11 and X.12 investigated for NH₃ emissions.

2.2 Ammonia emission measurements

2.2.1 Ammonia concentration

Line-integrated NH₃ concentrations were measured using four miniDOAS systems (Sintermann et al., 2016). These open path instruments make use of the differential optical absorption in the UV range (200–230 nm). Two miniDOAS systems (MD5 and MD2; names based on serial number) were installed at system M and two instruments (MD1 and MD6) at system G (Fig. 1a). All instruments were installed at a height of 1.3 m. Each miniDOAS pair (e.g. MD5 and MD2) was separated by a horizontal distance of about 30 m, which allowed for concentration measurements upwind and downwind of a subplot of the paddocks in between. The single light path between the sensor and the retroreflector for the individual devices had a length of 30 to 35 m. The instruments reported NH₃ concentrations at a temporal resolution of 1 min. The 1 min data were processed to 30 min averages for further processing. Due to the predominant wind directions NE and SW one miniDOAS usually reported upwind concentration C_Upwind (µg NH₃ m⁻³) and the other one the downwind concentration C_Downwind (Fig. 1). This setting allowed for the computation of the horizontal concentration gradient ΔC caused by emissions from the area in between. The reference spectrum (Sintermann et al., 2016) for each miniDOAS was determined during a 7-day inter-comparison campaign at the Chaumont, Switzerland (47^∘02^′58${}^{\prime \prime }$ N, 6^∘58^′16${}^{\prime \prime }$ E; 1136 m, 20–27 July 2016). The site is located 30 km north-west of Posieux and is only marginally contaminated by NH₃; it was therefore ideal to compute the reference spectra. The miniDOAS systems were operated in parallel and compared to wet chemical impingers (Häni et al., 2016) in order to retrieve the instrumental offset and absolute concentration.

2.2.2 Turbulence and meteorological parameters

For the characterisation of turbulent mixing the three-dimensional wind velocity (u, v, w) and air temperature were measured at 10 Hz using an ultrasonic anemometer–thermometer (HS-50, Gill Instruments Ltd., UK; hereafter termed sonic anemometer) mounted on a horizontal arm at 2 m above the ground. Each system was equipped with one of those anemometers. The micrometeorological parameters friction velocity (u_∗, m s⁻¹), roughness length (z_o, m) and Obukhov length (L, m) were computed from the 30 min processed eddy covariance data of the sonic anemometer. Further weather parameters were measured with a standard automated weather station (Campell Scientific Ltd., UK). It used a WXT520 (Vaisala, Vantaa, FL) to measure wind speed, precipitation, temperature and barometric pressure and a pyranometer (CNR1, Kipp & Zonen, Delft, NL) to measure global radiation. The station was installed at system M next to the sonic anemometer.

2.2.3 Data filtering

The raw MD concentrations were filtered based on the level of light reaching the spectrometer. This led to a data loss between about 1 % and 4 % for the different MD. An additional filter was applied to account for conditions with low turbulence by u_∗ filtering. As the measurement site is located at the Swiss western plateau, which is known for low wind speeds, especially during the night, a u_∗ threshold of 0.05 m s⁻¹ was applied, leading to a relative data loss of 26 % and 30 % for system M and G, respectively. Flesch et al. (2014) stated that using a u_∗ value of 0.05 m s⁻¹ can be accepted as the data quality does not increase too much by applying higher u_∗ values. The wind sectors facing towards the farm buildings north and south of the fields were removed as well due to unwanted advection from the nearby farm buildings (Figs. 1 and 2). Filtering for u_∗ and wind direction decreased the data by about 44 % and 49 % for system M and G, respectively.

2.2.4 Emission calculation based on dispersion modelling

The emissions were calculated based on inverse dispersion modelling and measurements of NH₃ concentrations upwind and downwind of an emitting source. An open-source version of the bLS model by Häni (2017; based on Flesch et al., 2004) programmed in the statistical software R (R Core Team, 2016) was used. The first-order bLS model assumed horizontally homogenous and vertically inhomogeneous Gaussian turbulence and used the Monin–Obukhov similarity theory to calculate the vertical profiles of wind speed and turbulence. Minor adjustments to the original model (Flesch et al., 2004) are described in Häni et al. (2018). The newly introduced deposition module, which is part of the software package, was not used in this study. The bLS model related the measured 30 min concentration difference ΔC (µg NH₃ m⁻³) to the unknown emission rate E (µg NH₃ m⁻² s⁻¹) of the investigated paddocks (Eq. 1). The coefficient D (s m⁻¹) was determined based on the simulated movement of 25 000 fluid particles released at the location of the concentration sensor line and tracked backwards in time up to a distance of 250 m (extending well beyond the investigated pasture fields). Simulated touchdowns inside the specified source area contribute to the magnitude of D.

$$\begin{array}{}\text{(1)}& E={\displaystyle \frac{C_{\mathrm{Downwind}}-C_{\mathrm{Upwind}}}{D}}\equiv {\displaystyle \frac{\mathrm{\Delta }C}{D}}\end{array}$$

The bLS model used wind and turbulence information measured by the sonic anemometer. In order to calculate a concentration footprint for each 30 min period Δt, averaged data of the wind direction, the standard deviations of the wind components, u_∗ and values representing the surface roughness were used. Additional geometric information of the source area locations and extensions and the position and height of the miniDOAS measurement paths were provided as well. An intrinsic assumption of the bLS model approach is that the model domain has a uniform surface roughness, which is supported by the results of Felber et al. (2015) for the same site, and that the defined emitting area is homogenous concerning its source strength. Thus it is assumed that the monitored pasture paddocks are homogenously grazed and the urine and dung patches, representing the main NH₃ emission sources, are more or less uniformly (or randomly) distributed on the paddock area.

The present inverse dispersion method yields a net NH₃ flux of the investigated paddocks that is in excess of any general background flux (e.g. due to deposition of ambient NH₃; Móring et al., 2017). The resulting flux thus represents the effect (emission) of grazing excreta. However, because the excreta patches only cover a small part of the grazed pasture, the measured net flux may also include some short-range redeposition of the gross excreta NH₃ emission. A partitioning of these effects is beyond the scope of the present study and would require small-scale spatially resolved measurements (e.g. by enclosures) of patch and non-patch surface areas.

2.2.5 Artificial release experiment

In order to test the methodology an additional experiment with an artificial gas release was conducted in June–July 2017 at the field site next to the sonic anemometer of system M. The source consisted of a grid of 14 critical orifices (100 µm diameter, stainless steel, LenoxLaser, USA), which were installed on the ground facing upward with a distance to each other of 2 m. The centre of the line was connected to a distribution unit, which regulated the gas flow with a mass flow controller (red-y smart controller; Vögtlin Instruments, Switzerland). The flow rate, pressure within the grid and the accumulated gas flow were saved to a hard disc within the housing of the distribution unit. A gas mixture with 5±0.1 % NH₃ in 95 % CH₄ (CarbaGas, Switzerland) was used with a release rate of about 3.1 standard L min⁻¹. Two miniDOAS systems (MD2 and MD5) were installed in parallel roughly 6 m north-east and south-west of the source line to account for the predominant wind directions. Both instruments were installed at a height of about 0.6 m due to the close distance to the artificial source.

Table 2 Measured driving parameters and resulting urine N and feces N of the animal N budget model averaged for the individual rotations and for each herd (system M | G). If only one number is given it corresponds to both herds simultaneously. Rotation 4 is not shown due to missing miniDOAS measurements.

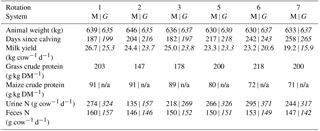
n/a: not applicable. Italic font: system G results.

2.3 Estimation of N excretion on the pasture

The NH₃ emission flux, quantified as described above, is a pasture-area-related quantity. In order to allow a comparison of the results of the present study with literature reports and with emission inventory models, emission factors were derived by relating the measured emissions to the urine N input from the cows. As N input to the pasture cannot easily be measured total N and urine N in the excretions of the cows were estimated with a dairy cow nitrogen budget model based on the official Swiss feeding recommendation for dairy cows (Bracher et al., 2011). Input to the model included information concerning the milk yield and N content, the weight of the cows, the calving date and the crude protein proportional to the N content in the forage (Table 2). Milk yield and body weight were measured for each cow on a daily basis, whereas data on grass protein were only collected and analysed eight times between the end of April and the end of September, but usually close in time to the measurement period. The grass parameters of the systems M and G were averaged for further processing. Crude protein of the maize silage was analysed three times (beginning of May, middle of July, beginning of September). Missing data were linearly interpolated between the measured values. The N in the excretions was finally calculated as a balance between the N input of the feed, N storage due to body weight gain and N in milk and excreta for each cow and each day of the year. The breakdown in urine N and dung N is based on N balance studies by Bracher et al. (2011). Finally, based on the grazing duration the urine N input to the investigated paddocks was computed for each rotation. An associated uncertainty of 15 % was estimated by comparing the N budget model to published results of Swiss N excretion studies (Bretscher, unpublished data).

2.4 Cow and excreta distribution monitoring

The measured concentration difference and thus the derived NH₃ flux is mainly related to the emission of the surface area between the MD sensor paths on each grazing system (according to the main wind directions; Fig. 1). This is only a part of the entire paddock area, which was considered as a uniformly emitting area in the bLS calculations (Sect. 2.2.4) and for which the average urine N input was quantified (Sect. 2.3). On a pasture cows can move freely and therefore the urine and dung patches may not be homogenously distributed on the entire area, which can lead to error-prone emission estimates (Auerswald et al., 2010; Bell et al., 2017; Laubach et al., 2013a).

In order to assess the spatial distribution of the cow excreta on the paddocks X.11 and X.12 as main emission sources in our experiment, we used two different approaches. The number and position of dung patches were determined with a handheld GPS device within the first 3–5 days after grazing. In addition, the cow position on the pasture was monitored with a day–night digital camera system at a temporal resolution of 10 min. The locations of the individual cows were manually marked on the displayed pictures in a post-processing step. However, the night mode often did not yield useful information and therefore images showing the cow positions during night-time were very sparse.

In order to account for inhomogeneity in the excreta distribution within the investigated paddocks, they were divided as shown in Fig. 3a. The middle sections between the paired MD sensor paths represent the main source areas of the measured fluxes. Their excreta density d_X.meas was related to the density of the entire paddocks d_(X.11+X.12) to determine the excreta density correction factor k_d.

$$\begin{array}{}\text{(2)}& k_{\mathrm{d}}={\displaystyle \frac{d_{\left(X.11+X.12\right)}}{d_{X.\mathrm{meas}}}}\end{array}$$

The exemplary dung patch survey in Fig. 3a shows a positive deviation from the average paddock-wide density for both system M (k_d=1.28) and system G (k_d=1.40). However, dung observations were only available for two rotations for paddock M.11, three rotations for G.11 and two rotations for X.12, while daytime cow position observation by camera was available for the whole measurement campaign for system M and from rotation 3 onwards for system G. As cow excreta (mainly in the form of urine) is the main source of NH₃ emissions, missing dung density values were estimated based on a regression analysis (R²=0.98) between parallel surveys of density anomalies for dung patches and cow positions (Fig. 3b).

The k_d factors derived from the combined information of the dung patch and the cow position surveys were used to calculate integral NH₃ emissions E_int for each rotation for the two investigated paddocks X.11 and X.12 (with corresponding areas A) for a time period between the start of grazing and the end of grazing (EOG).

$$\begin{array}{}\text{(3)}& {\displaystyle }{E}_{\mathrm{int}}=\sum _{t=\mathrm{start}\mathrm{of}\mathrm{grazing}}^{\mathrm{EOG}+\mathrm{10}\mathrm{days}}E\left(t\right)\mathrm{\Delta }t\cdot k_{\mathrm{d}}^{-\mathrm{1}}\cdot \left(A_{X.11}+A_{X.12}\right)\end{array}$$

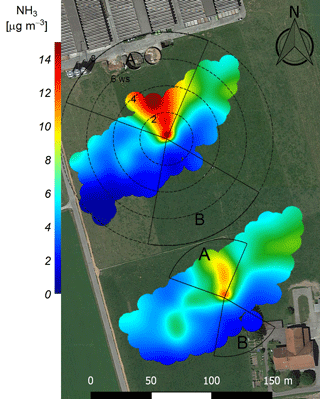
Figure 2 The polar plot shows the averaged NH₃ concentration of the miniDOAS MD5 (top) and MD6 (bottom) depending on wind direction and wind speed (black dotted circles) for the period May–October 2016. The sectors A and B indicate areas with either high NH₃ concentration from farm buildings or otherwise unfavourable wind direction due to the measurement set-up. The polar plots were produced using the R software package openair (Carslaw and Ropkins, 2012) and overlaid on a Google Earth image of the experimental area (map data: Google, DigitalGlobe).

3 Results and discussion

This chapter is organised as follows. The first section (Sect. 3.1) shows the observed NH₃ concentrations during the grazing campaign, whereas the next sections present and discuss the emission fluxes. Sect. 3.2 describes the measured area-related fluxes, including interference correction and gap filling, leading to cumulative emissions over individual grazing events. The corresponding emission uncertainty and its sources are discussed in Sect. 3.3. The area-related emissions were converted to animal-related emissions using cow and dung distribution monitoring results (Sect. 3.4) and further converted to emission factors related to animal urine N (Sect. 3.5). In the final section of the chapter (Sect. 3.6) the advantages and problems of the experimental design are highlighted.

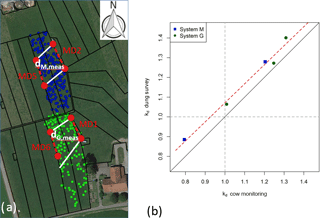
Figure 3 (a) GPS-tagged dung positions recorded after grazing rotation 7 overlaid on a Google Earth image of the experimental area (map data: Google, DigitalGlobe). The positions of the MD ammonia sensors and paths are indicated by the red dots and dotted lines. The white lines enclose the main emission measurement area between the sensors. Their dung patch density d_X.meas was related to the average density over the investigated paddocks according to Eq. (2); (b) comparison of k_d values according to Eq. (2) for dung patch and cow position distributions on system M (blue) and system G (green).

3.1 Ammonia concentrations during grazing season

The NH₃ concentration values observed during the entire measurement campaign had strong temporal and spatial variability. They were typically in the range of 4–15 µg NH₃ m⁻³ with maximum values of about 100 µg NH₃ m⁻³. As shown in Fig. 2 the highest concentrations usually resulted from advection from the nearby farm located in the northern direction of the miniDOAS instruments. This advection is weaker at the southern system G due to the larger distance to the farm. The general concentration pattern is nevertheless very similar for both systems. The highest wind speeds (above 4 m s⁻¹) usually resulted in low NH₃ concentrations due to a good mixing of the atmospheric boundary layer with the lowest concentrations coming from the south-western direction. The higher background concentration from the north-easterly direction is probably a result of a nearby piggery some 350 m away. During the whole measurement period (beginning of May to middle of October) the MD instruments were online between 62 % (MD 6) and 85 % (MD 2) of the time. Power failure and instrument errors were the main reasons for the partial data loss. The measurement campaign at the Chaumont mountain site (Sect. 2.2.1) led to a data loss for the first 3 days during rotation 4. During rotation 1 no data from the MD instruments MD1 and MD6 could be acquired due to instrument errors.

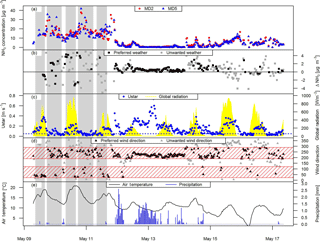
Figure 4 Time series of (a) MD concentration measurements (MD2 and MD5) on pasture system M and (b) the corresponding difference in concentration. The concentration differences during good wind conditions are shown in black, while grey indicates concentration differences during undesirable weather conditions. (c) Time series of u_∗ and global radiation. The blue dashed line indicates the 0.05 m s⁻¹ u_∗ threshold. (d) Time series of wind direction. Wind direction values overlapping the preferred wind sector (avoiding sector A and B; Fig. 2) are shown in black. The preferred wind sectors are indicated by the red area. (e) Time series of air temperature and precipitation. The grey shaded area indicates grazing on the paddocks between MD2 and MD5.

During the grazing period on paddocks X.11 and X.12 the NH₃ concentration difference increased (see example for one rotation in Fig. 4) due to increased excreta on the field, mainly in the form of urine. Concentration differences in the range of about 0–8  µg NH₃ m⁻³ for system M and of about 0–15  µg NH₃ m⁻³ for system G were measured. A few hours after grazing the concentration differences started to decrease significantly. Mostly within the first 3–5 days after the EOG the concentration differences reached values around the accuracy limit of the MD devices (about 0.2 µg NH₃ m⁻³). Typically for the Swiss western plateau wind speed had a strong diurnal pattern with low wind speeds during night-time. This often led to a weak mixing in the boundary layer and subsequently high observed concentrations. In order to avoid error-prone emission estimates the concentration values were filtered according to Sect. 2.2.3. This led to low data availability for emission calculation, especially during night-time conditions. Precipitation events typically resulted in low concentrations and subsequent low concentration differences.

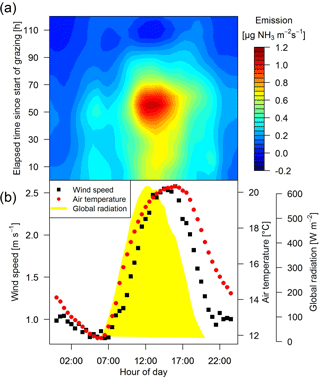
Figure 5 (a) Measured averaged half-hourly fluxes of all rotations for system M depending on hour of day and elapsed time since grazing on the paddocks between MD2 and MD5 started.(b) Half-hourly averaged values of global radiation, wind speed and air temperature measured at system M during May to October 2016.

3.2 Field-scale fluxes

The field-scale fluxes were determined based on the concentration differences of the paired MD systems and the dispersion coefficient D (see Eq. 1) computed by the bLS model. The emissions typically showed a diurnal emission pattern with the highest values occurring between midday and late afternoon, which correlated well with atmospheric driving parameters like air temperature, wind speed and global radiation (Fig. 5, horizontal axis). This emission behaviour can theoretically be explained by higher wind speeds and unstable conditions during daytime leading to a reduction of the aerodynamic resistance at the interface between the atmosphere and the urine patch surface and thus leading to higher emissions. Ammonia fluxes are also based on the thermodynamic equilibrium at this interface leading to higher emissions with increasing temperatures during daytime (Flechard and Sutton, 2013). Beside the diurnal variation, the emissions generally increased during the grazing phase (typical grazing duration: 50–70 h; Table 1) with a fast subsequent decrease afterwards (Fig. 5a, vertical axis). The observed emission fluxes usually decreased to insignificant values within 3–5 days after EOG. This management-related temporal pattern could be parameterised as shown in Fig. 6, in which daytime emission values are plotted against the elapsed time since the start or end of the grazing period. The emissions showed an approximately linear increase during grazing (due to the continuous formation of new excreta patches) and an exponential decay after EOG. The decay or e-folding time of the exponential function was evaluated as 28 and 23 h (37 % of maximum value at the beginning) for the systems M and G, respectively.

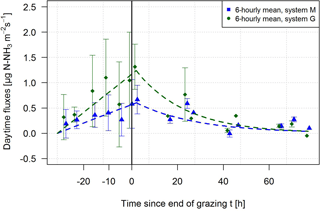
Figure 6 Average temporal pattern of management-related NH₃ emissions for system M (blue) and system G (green) for daytime conditions. Curves with linear increase from the start of grazing until 3 h after the end of grazing and exponential decrease afterwards were fitted to the 6-hourly averaged values of the measured daytime fluxes. These curves were used as a default emission pattern for flux correction and gap filling (see Sect. 3.2). The vertical bars indicate the standard deviation of averaged half-hourly fluxes. The black vertical line indicates the end of grazing. For better readability the data points for the two systems were slightly shifted horizontally.

Due to quality-related data filtering (Sect. 2.2.3) and missing concentration data the emission time series had a considerable share of gaps that needed to be filled in order to calculate cumulative emissions. The following relatively simple gap-filling procedure was applied.

• i.

  Gaps shorter than 3 h were filled by linear interpolation between available measurements.

• ii.

  For longer gaps during daytime, the management-related emission curves in Fig. 6 (linear increase during grazing and subsequent exponential decrease) were fitted to the available daytime data of individual grazing phases. This allowed us to account for different weather and soil effects between the rotations.

• iii.

  Because of the low amount of available night-time data, it was not possible to derive and fit individual curves for longer night-time gaps. Thus it was assumed that the general temporal pattern is similar to daytime conditions (curves in Fig. 6) but with a lower amplitude for night-time. The corresponding reduction factor (=0.39) was based on the overall ratio between mean night-time and daytime emissions during grazing.

Due to the limited amount of measured data and the considerable number of possible environmental driving parameters (air temperature, global radiation, wind speed, precipitation, soil and leaf humidity; Fig. 5, also Bell et al., 2017; Häni et al., 2016; Laubach et al., 2013b; Móring et al., 2016) the emissions were not parameterised as a function of these parameters but only as a function of grazing duration and elapsed time since the start or end of grazing. Nevertheless, a good agreement was found using a linear increase in emissions during the grazing period and an exponential decrease afterwards.

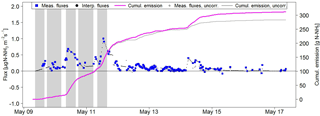
Figure 7 Measured emission of paddocks M.11 and M.12 (between sensors MD2 and MD5; Fig. 1a) during rotation 1. Missing half-hourly flux data were filled based on either linear interpolation or on the default emission curve (Fig. 6) in order to compute the cumulative emissions. For comparison the uncorrected emissions (interference of upwind grazing according to Eq. (4) not considered) are also shown. The shaded time intervals indicate grazing on the investigated paddocks.

The applied flux measurement approach as described in Sect. 2.2 assumes spatially limited emissions between the two measurement paths and negligible emissions upwind of the system. However, upwind paddocks were grazed while the measurement paddocks were in the emission decay phase. In some cases, depending on wind direction, the emission sources on the upwind paddocks can lead to a greater concentration signal of the inflow compared to the outflow instrument. They interfere with the concentration signals of the paddock(s) of interest and can lead to an underestimation of the true emissions. In the strict sense this is a problem of an underdetermined system when fewer concentration detectors are available compared to the emission sources (see also Bell et al., 2017). To estimate the influence of grazed upwind paddocks, a default emission pattern E_def(t) according to the fitted curves in Fig. 6 was used. The effect of each upwind paddock i on the measured concentration difference ΔC in Eq. (1) was calculated from the corresponding bLS dispersion coefficients for both MD systems D_i,Upwind and D_i,Downwind.

$$\begin{array}{}\text{(4)}& \mathrm{\Delta }{C}_{\mathrm{corr}}=\sum _i{E}_{\mathrm{def}}\left(t_i\right)\cdot \left(D_{i,\mathrm{Upwind}}-D_{i,\mathrm{Downwind}}\right)\end{array}$$

This effect was corrected for in the flux calculation (Eq. 1). The resulting measured fluxes during the campaign were within a range of 0 to 2.1 µg N–NH₃ m⁻² s⁻¹ for system M and 0 to 2.3 µg N–NH₃ m⁻² s⁻¹ for system  G.

Table 3 Cumulative emission results for paddocks X.11 and X.12 (combined) of the two pasture systems (M | G) during the individual rotations. The corresponding averaged weather parameters and N excretion input to the paddocks are also listed. Rotation 4 is not shown due to missing miniDOAS data at the beginning of the rotation.

NA: not available. Italic font: system G results.

The cumulative integral emission E_int (Eq. 3) for each system and rotation was calculated based on the gap-filled half-hourly fluxes and the area of the investigated paddocks (see example in Fig. 7). Depending on atmospheric driving parameters (mainly precipitation) about half of the overall emissions occurred during the grazing phase. Precipitation events during that time period led to a significant reduction in emissions with subsequently higher emissions later on (observable especially during rotation 2 and the higher fluxes on 14 May in Fig. 6). Over the entire grazing season, cumulative emissions for the different rotations were retrieved under variable weather conditions with the highest air temperatures recorded during rotation 3 to rotation 6 and the highest precipitation amounts occurring in the first three rotations (Table 3). The highest integral emissions usually occurred at the southern paddock and showed a strong temporal variability depending mainly on the grazing duration (Table 1) and N input (Table 3). The emissions during rotation 7 on system G showed the largest magnitude of all single rotations and fields. This is also in line with the highest N input to the pasture from cow excreta.

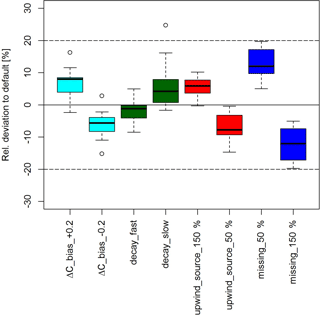
Figure 8 Sensitivity analysis of various error sources on emission results for individual rotations. Each box plot shows the resulting relative effect of a potential systematic error. The investigated effects include the overestimation or underestimation of the offset in concentration measurements (cyan), the exponential decay times of the default emission curves in Fig. 6 (green), and the magnitude of default emission curves used for upwind source interference correction (red) and for gap filling (blue).

3.3 Uncertainty of emission flux measurements

3.3.1 Effect of different error sources

The performance of the miniDOAS devices for concentration measurements was optimised by adjusting the offsets among all four instruments during the 7-day inter-calibration at the Chaumont site between rotation 3 and 4. During that period the instruments were running in parallel and the measured concentrations (mostly 0–2  µg NH₃ m⁻³) were compared to the measurements of wet chemical impingers. It was found that the potential bias between the instruments was below 0.2 µg NH₃ m⁻³ and was therefore similar to the results by Sintermann et al. (2016).

Missing flux data were replaced either by values of the default emission curve (Fig. 6) or by applying a liner interpolation between measurements. The default emission curves were also used to estimate unwanted interferences in the measured concentration differences from emitting upwind paddocks. In order to test the sensitivity of the emission result to uncertainties in the gap-filling method and interferences from upwind grazing, we varied the values of the default emission curve to 50 % and 150 % of the default values. Sensitivity to the exponential decay time of the default emission curve was tested with a systematic increase in the decay time of 50 % (decay_slow) and a reduction of 30 % (decay_fast). We found (Fig. 8) that the relative effect of all simulated errors on the cumulative emissions was generally below 20 % for individual rotations (except for a few outliers). The highest impact on the emission results was due to the uncertainty in the gap filling of missing values that predominantly occurred during night. Since the simulated error sources are independent, they were combined to an overall measurement-related error of 17 % by Gaussian error propagation.

The bLS dispersion modelling is a well-defined approach and was evaluated extensively by Flesch et al. (2005), Harper et al. (2010) and McGinn et al. (2009), who found that the model uncertainty is typically of the order of 20 %. Combining the 20 % uncertainty for the bLS modelling and the 17 % measurement-related uncertainty results in a total mean systemic uncertainty of 26 %.

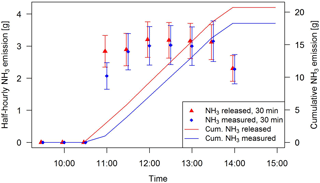
Figure 9 Released (red) and measured (blue) NH₃ emissions during artificial source experiment 3 on 19 June 2017. The measured emissions were quantified using the concentration difference of the miniDOAS systems MD2 and MD5 and the corresponding modelled bLS dispersion coefficient. The error bars indicate the uncertainty of the artificial source (Sect. 3.3.2) and from the measured emissions (bLS dispersion modelling; Sect. 3.3).

3.3.2 Artificial gas release

For an exemplary test of the performance of the applied methodology, tracer gas releases were conducted at the same site in the year after the main experiment in June and July 2017. The gas was only released during stationary westerly winds in order to avoid advection from the nearby barn. Table 4 lists the main meteorological and technical aspects of the individual releases and shows the corresponding results. The duration of the releases strongly depended on the observed wind speed and therefore varied significantly.

Table 4 Artificial source characteristics, environmental conditions, measured MD concentrations and recovery rates during the individual gas release experiments. Averaged values during the release periods are shown. For selected parameters, the standard deviation is given as well.

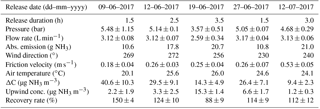
Due to the westerly winds MD2 detected upwind concentrations and MD5 downwind concentrations. All measurements were averaged to 30 min values and the emissions were calculated following Eq. (1) (Fig. 9). In order to check the mass flow controller of the artificial source, the release rate of all single orifices was measured during three releases (release 2, 4 and 5). The observed differences between the summed orifice release rates and the measured mass flow from the gas cylinder varied between −7 % and 9 % with an overall average of only 1 %±8.7 %. The associated uncertainty of the artificial source of 17.4 % was calculated as 2 times the standard deviation.

The quality of the calculated emissions for each source experiment is defined as the recovery rate, which is calculated as the ratio of the measured cumulative emissions of the bLS and the cumulative measured emissions from the flow controller (Table 4). Four out of five releases resulted in a recovery rate above 100 % and four release experiments showed a recovery rate between 88 % and 124 %. Release number 1 had an exceptionally high recovery rate of about 150 %. During that particular release the dynamic pressure within the tubes of the system upstream of the flow controller was higher at the beginning compared to the following ones. Nevertheless, we have no conclusive explanation for this individual result. The overall mean of 111 % and the standard deviation of 18 % was calculated based on all individual half-hourly measurements. As the recovery rates were not significantly different from 100 % we can assume that the inverse dispersion methodology in combination with miniDOAS line sensors is suitable to quantify the NH₃ emissions of the pasture experiment.

3.4 Animal-related emissions

As the bLS approach assumes a homogenous spatial distribution of emission sources within the investigated paddock, the actual distribution of the cow excreta could have a significant influence on the calculated emissions per animal or per excreta input. The relative density of the emitting urine patches was assumed to be proportional to the observed density of dung patches and/or animal positions as described in Sect. 2.4. Figure 10 shows the correction factor k_d (Eq. 2, 3) of the excreta density in the main measurement section (between the MD instruments) from the mean density of the entire paddock area. In the case of a uniform excreta distribution k_d should be 1. However, a considerably heterogeneous distribution was found for the different rotations and paddocks. On the southern pasture (system G) a generally higher excreta density was found between the MD devices in comparison to the averaged field. On the northern pasture (system M) the effect was more variable with negative deviations until rotation 5 and positive deviations towards the end of the grazing season.

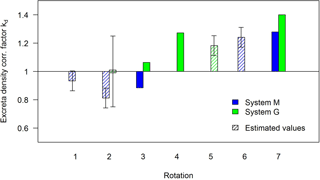
Figure 10 Correction factor k_d (Eqs. 2, 3) of the excreta density for rotations with available emission results (Table 3). For the rotations without dung observations, the corresponding correction factors (hatched bars) were estimated based on a regression analysis between parallel surveys of density anomalies for dung patches and cow positions (Fig. 3b). The error bars show the corresponding uncertainty of estimated k_d values as described in Sect. 3.4.

There is some uncertainty associated with the visual identification (for GPS localisation) of dung patches due to potential double counting or overlooking of dung patches on the paddock and due to the use of the linear relationship between cow and dung density. But these errors are assumed to behave randomly and are thus relatively small, resulting in a combined relative emission uncertainty of about 7 %. This is much smaller compared to the systematic uncertainty of the measured fluxes (Sect. 3.3.1). Since there were no cow nor dung monitoring data available for system G during rotation 2, no correction for inhomogeneous excreta density was applied in this case, but a higher uncertainty (25 %) was attributed to the emissions based on the variability of the dung density of the other rotations (Fig. 10).

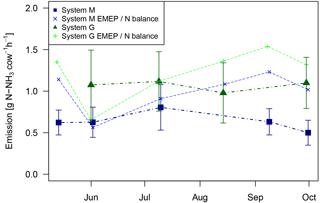
Figure 11 Emissions per cow and grazing hour for system M and system G. Measured values (thick dots and lines) in comparison to estimated values based on urine N amount from the N balance model and the EMEP standard emission factor for NH₃ (10 %; see EMEP/EEA, 2016). The error bars (2σ) were calculated based on the methodological uncertainty (Sect. 3.3.1) and on excreta density uncertainty in the single rotations (Sect. 3.4).

In order to calculate the animal-related emissions and the emission factor for the individual rotations, the derived cumulative emissions were corrected for excreta inhomogeneity (Eq. 3) by applying the excreta density ratios k_d shown in Fig. 10 (see also Eq. 2). The measured emissions per cow and grazing hour (h) stayed rather constant with a value of about 0.64±0.11 g N–NH₃ cow⁻¹ h⁻¹(mean ± 1 standard deviation) for system M and about 1.07±0.12 g N–NH₃ cow⁻¹ h⁻¹ for system G (Fig. 11). For comparison, the application of a 10 % standard emission factor for NH₃ (EMEP/EEA, 2016) results in larger mean values and a larger variability (system M: 0.99±0.24 g N–NH₃ cow⁻¹ h⁻¹; system G: 1.22±0.31 g N–NH₃ cow⁻¹ h⁻¹).

The error bars in Fig. 11 represent the total error of the absolute emissions. This error is predominantly due to systematic effects (Sect. 3.3.1) that are identical (bLS uncertainty) or very similar (gap filling uncertainty) for the two parallel pasture systems. Therefore these systematic errors are not relevant for the comparison of the two systems, for which only the random uncertainty and the instrument bias uncertainty (Fig. 8) have to be considered. The random uncertainty for the seasonal mean was estimated from the variability between rotations. In combination with the bias uncertainty this results in a significant mean difference between the two systems of 0.43±0.13 g N–NH₃ cow⁻¹ h⁻¹, corresponding to a relative reduction effect of the N-balanced diet compared to the grazing-only diet of 40 %.

3.5 Emission factors for the two pasture systems

The EF values for individual rotations in Table 3 are based on the measured cumulative emissions relative to the urine N deposited (excreted) on the two pasture systems for the different rotations. They range within 4.9 %–11.1 % for system M and show generally higher values for system G (range 7.2 %–16 %). The highest EF values were observed during the second rotation. They are mainly driven by the low N content of the grass on pasture, resulting in low estimated urine N excretion (Table 2). The variation in EF is in contrast to the rather stable measured absolute NH₃ emissions as shown in Fig. 11. This may indicate that the analysed grass samples are not fully representative for the selective grazing intake of the cows. On the other hand, an exceptionally high value of the measured emissions is unlikely because a rainfall event started during the second half of the grazing period and lasted almost 2 days with a precipitation amount of about 40 mm (data not shown). Typically, smaller volatilisation of NH₃ is expected during such weather periods (Sommer and Olesen, 2000). A delayed onset of emissions was observed as described in Móring et al. (2016) after the rain event stopped. However, the emissions were small compared to the ones observed during the first grazing day (roughly one-third) and were therefore not able to counterbalance the reduced emissions of the second part of the grazing period.

The annual average pasture EF and its uncertainty was derived from the overall means of NH₃ emission and urine N input and resulted in 6.4 %±2.0 % for system M and 8.7 %±2.7 % for system G. The uncertainty of about one-third mainly stems from the systematic errors discussed in Sects. 3.3.1 and 2.4. The mean EFs are ranked towards the lower end of reported values (5 %–26 % of excreted urine N; e.g. Bussink, 1992; Jarvis et al., 1989; Laubach et al., 2012, 2013b) but are in line with the results (6 %–9 %) of the recent study by Bell et al. (2017). A single emission factor as used in many inventory models (e.g. EMEP/EEA, 2016; Kupper et al., 2015) would not be able to reflect the observed difference of 2.3 % between the two grazing–feeding systems in our experiment. The reduction in EF for system M is not statistically significant but may indicate a non-linear effect of the N input rate on the NH₃ emissions, similar to the findings of the recent literature synthesis study by Jiang et al. (2017), who reported a higher emission factor with increasing fertiliser N application. Thus the optimised N-balanced feeding strategy may decrease the NH₃ emissions even more than expected from the reduced urine N excretion.

3.6 Advantages and problems of experimental set-up

The present field experiment was optimised to measure the NH₃ emissions of two neighbouring pastures managed in an intensive rotation. The periodic high density of animals (55–70 cows ha⁻¹) and fresh excreta on the grazed paddocks resulted in intermittent high fluxes and allowed us to observe the temporal behaviour of the emissions (Figs. 6, 7). This would not be possible on a continuous grazing system with much larger paddock sizes and accordingly smaller excreta densities and emissions. For continuous grazing on large fields other micrometeorological measurement techniques like eddy covariance (Ammann et al., 2012) would be preferable. The small paddock sizes in this study also kept the cow excreta heterogeneity on a moderate level, whereas on larger free-range grazing areas the animals often gather at the same place (Cowan et al., 2015), leading to a more complicated quantification of the EF. While the distribution of dung patches and cows was monitored by means of visual inspection or evaluation of the camera images, a direct localisation of urine patches was not possible in this way. Sensors for urine patch detection exist, but are either still in development (Kumar et al., 2016), relatively expensive (Quin et al., 2016) or unpractical for field-scale experiments (Dodd et al., 2015). Therefore we assumed a similar density distribution of dung and urine patches on the paddock (Auerswald et al., 2010; Luo et al., 2017).

The present set-up with the parallel pastures and accordingly similar micrometeorological conditions constituted an effective way to analyse the difference between the two systems as the main systematic uncertainty source of the single pasture emissions (bLS; Sect. 3.3.1) were cancelled out. However, subsequent grazing on neighbouring upwind paddocks could produce interferences with the measurements that could be corrected only in an approximate way. Another error source arose due to the strong variability of the measured crude protein in the grass with consequently high variability in the estimated N in the urine. It was not directly measured as automated monitoring techniques for urine N on the pasture are not yet mature enough and still have some limitations regarding animal welfare (Misselbrook et al., 2016). Manual measurements of the urine N amount were outside of the scope of this project due to the laborious work involved.

4 Concluding remarks

In a paired field experiment, NH₃ emissions on two pasture systems were measured for an entire grazing season under real practice conditions. The herds of the two pastures were kept in an intensive rotational grazing management with different protein to energy ratios, resulting in different N excretion rates. The fast rotation with a short but high stocking rate and excreta deposition within the grazed paddock allowed us to observe the temporal dynamics of the corresponding NH₃ emissions. Maximum emissions were found at the end of each grazing phase on the investigated area. Afterwards an exponential decay of the emissions led to non-significant low values typically within 3–5 days. A diurnal emission pattern with peaks during the afternoon was observed on all rotations.

Monitoring of the cow and dung density distribution was essential for a quantitative comparison of the two systems. The emissions per cow and grazing hour showed only a very limited variation over the season but a distinct difference (40 %) between the two systems. About half of this difference could be explained by the different urine N excretion rate of the two herds. The resulting average EFs were 6.4 %±2.0 % and 8.7 %±2.7 % for the herd with the N-balanced diet and the herd with the N surplus in the forage, respectively. Thus the experiment showed the large potential of an optimised feeding strategy to reduce NH₃ emissions. The results can also serve as a validation for the Swiss national emission inventory for NH₃ emissions on pastures. It is recommended for further studies to include regular analyses of the N content in the urine in order to overcome the associated uncertainties.