Drivers of future seasonal cycle changes in oceanic pCO₂

Recent observation-based results show that the seasonal amplitude of surface ocean partial pressure of CO₂ (pCO₂) has been increasing on average at a rate of 2–3 µatm per decade (Landschützer et al., 2018). Future increases in pCO₂ seasonality are expected, as marine CO₂ concentration ([CO₂]) will increase in response to increasing anthropogenic carbon emissions (McNeil and Sasse, 2016). Here we use seven different global coupled atmosphere–ocean–carbon cycle–ecosystem model simulations conducted as part of the Coupled Model Intercomparison Project Phase 5 (CMIP5) to study future projections of the pCO₂ annual cycle amplitude and to elucidate the causes of its amplification. We find that for the RCP8.5 emission scenario the seasonal amplitude (climatological maximum minus minimum) of upper ocean pCO₂ will increase by a factor of 1.5 to 3 over the next 60–80 years. To understand the drivers and mechanisms that control the pCO₂ seasonal amplification we develop a complete analytical Taylor expansion of pCO₂ seasonality in terms of its four drivers: dissolved inorganic carbon (DIC), total alkalinity (TA), temperature (T), and salinity (S). Using this linear approximation we show that the DIC and T terms are the dominant contributors to the total change in pCO₂ seasonality. To first order, their future intensification can be traced back to a doubling of the annual mean pCO₂, which enhances DIC and alters the ocean carbonate chemistry. Regional differences in the projected seasonal cycle amplitude are generated by spatially varying sensitivity terms. The subtropical and equatorial regions (40^∘ S–40^∘ N) will experience a ≈30–80 µatm increase in seasonal cycle amplitude almost exclusively due to a larger background CO₂ concentration that amplifies the T seasonal effect on solubility. This mechanism is further reinforced by an overall increase in the seasonal cycle of T as a result of stronger ocean stratification and a projected shoaling of mean mixed layer depths. The Southern Ocean will experience a seasonal cycle amplification of ≈90–120 µatm in response to the mean pCO₂-driven change in the mean DIC contribution and to a lesser extent to the T contribution. However, a decrease in the DIC seasonal cycle amplitude somewhat counteracts this regional amplification mechanism.

1 Introduction

Owing to its large chemical capacity to resist changes in [CO₂] (referred to as buffering capacity), the ocean has absorbed nearly half of the anthropogenic CO₂ produced by fossil fuel burning and cement production since the industrial revolution (Sabine et al., 2004). While the ocean's absorption of CO₂ lowers the atmospheric concentration, it also increases the ocean's [CO₂] and in turn lowers its buffering capacity. This leads to a reduction in the oceanic uptake of CO₂ and an intensification of the pCO₂ seasonal cycle (from now on referred to as δpCO₂) (McNeil and Sasse, 2016; Völker et al., 2002). In a recent key observational study by Landschützer et al. (2018), it was demonstrated that the δpCO₂ amplitude increased at a rate of ≈2–3 µatm per decade from 1982 to 2015.

The pCO₂ already experiences large seasonal fluctuations, which in some regions can reach up to 60 % above and below the annual mean pCO₂ (Takahashi et al., 2002). An intensification of the δpCO₂ amplitude could produce seasonal hypercapnia conditions (McNeil and Sasse, 2016), which together with increased [H⁺] seasonality (Hagens and Middelburg, 2016; Kwiatkowski and Orr, 2018) and aragonite undersaturation events (Hauri et al., 2015; Sasse et al., 2015; Shaw et al., 2013) could expose marine life to harmful seawater conditions earlier than expected if considering only annual mean values. Moreover, a projected amplification of δpCO₂ might increase the net CO₂ uptake in some regions, such as the Southern Ocean, thereby further accelerating the decrease in the buffering capacity in that region (Hauck and Völker, 2015).

The pCO₂ seasonal amplitude is controlled mainly by seasonal changes in temperature (T) and biological activity together with upwelling changes that alter DIC concentrations. Usually, DIC and T changes work in opposite directions (Fay and McKinley, 2017; Sarmiento and Gruber, 2006; Takahashi et al., 2002). In subtropical regions higher pCO₂ values occur in summer when solubility decreases. In subpolar regions, pCO₂ increases in winter when waters upwell that are rich in DIC and when respiration of organic matter takes place. Decreased subpolar pCO₂ occurs in summer when primary productivity is higher and upwelling diminishes. Therefore, we find close relationships of δpCO₂ with the ocean's [CO₂], which controls chemical reactions, and with mean pCO₂, which moderates exchange with the atmosphere. Both factors are related by the solubility constant that depends on temperature and salinity.

Furthermore, the regional differences in the influence of temperature and biology on δpCO₂ are modulated by the ocean's buffering capacity. This is due to the ability of CO₂ to react with seawater to form bicarbonate $\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]$ and carbonate $\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$, leaving only a small portion of dissolved carbon dioxide in the form of aqueous CO₂ ([CO₂(aq)]). [CO₂(aq)] together with carbonic acid ([H₂CO₃]) are defined as [CO₂]. Therefore, it is useful to define the total amount of carbon as DIC, which is the sum of the three carbon species ($\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]$, $\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$, and [CO₂]). At current chemical conditions, most of the DIC is in the form of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, and therefore the buffering capacity is largely controlled by the ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ capable of transforming CO₂ into bicarbonate through the reaction CO₂(aq) + ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ + H₂O = 2${\mathrm{HCO}}_{\mathrm{3}}^{-}$ (Zeebe and Wolf-Gladrow, 2001). The larger the buffering capacity, the larger the pCO₂ ability to resist changes in DIC. To quantify this capacity, we can introduce the sensitivity factor γ_DIC, which is inversely related to the buffering capacity, defined as ${\mathit{\gamma }}_{\mathrm{DIC}}=\partial \ln \left(p{\mathrm{CO}}_{\mathrm{2}}\right)/\partial \mathrm{DIC}$, (Egleston et al., 2010). Other sensitivity factors are related to the total alkalinity (γ_TA), salinity (γ_S), and temperature (γ_T) changes and are defined in a similar way as $\partial \ln \left(p{\mathrm{CO}}_{\mathrm{2}}\right)/\partial \mathrm{TA}$, $\partial \ln \left(p{\mathrm{CO}}_{\mathrm{2}}\right)/\partial S$, and $\partial \ln \left(p{\mathrm{CO}}_{\mathrm{2}}\right)/\partial T$, respectively. It is important to note that the pCO₂ is highly sensitive to temperature due to two factors: first through solubility changes that account for 2 ∕ 3 of the present-day temperature impact, and second through the dissociation constants that control the carbon system reactions (Sarmiento and Gruber, 2006).

While the mechanisms controlling the seasonal cycle of pCO₂ at present day are well documented, the future evolution of these drivers has not been fully elucidated. Current literature suggests that seasonal amplification is a consequence of an increase in the T and DIC contributions to δpCO₂ (Landschützer et al., 2018) and an increased sensitivity of the ocean to these variables (Fassbender et al., 2017).

The aim of our paper is to provide an in-depth analysis of the mechanisms controlling the future strength of δpCO₂ and its regional differences using seven CMIP5 global Earth system models. Our analysis focuses on 21st century evolution using the Representative Concentration Pathway 8.5 (RCP8.5) scenario. We give a comprehensive analysis of the projected evolution of the DIC, TA, T, and S contributions to pCO₂ seasonality. To achieve this goal, we derive explicit analytical expressions for pCO₂ sensitivities in terms of γ_DIC, γ_TA, γ_T, and γ_S, thereby extending previous work done by Egleston et al. (2010).

2 Methodology

2.1 CMIP5 models

For our analysis, pCO₂, DIC, TA, T, and S monthly mean output variables covering the period from 2006–2100 were obtained from future climate change simulations conducted with seven fully coupled Earth system models that participated in the Coupled Model Intercomparison Project, Phase 5 (CMIP5) (Taylor et al., 2012). The following models were selected based on data availability: CanESM2, CESM1-BGC, GFDL-ESM2M, MPI-ESM-LR, MPI-ESM-MR, HadGEM2-ES, and HadGEM2-CC (see the supplementary material of Hauri et al., 2015). For the purpose of this paper, we used the Representative Concentration Pathway 8.5 (RCP8.5) future climate change simulations (IPCC, 2013). The ocean's surface data sets were regridded onto a $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid using climate data operators (CDOs). The Arctic Ocean and the region poleward of 70^∘ S are removed from the analyses because observational data for model validation are scarce.

2.2 Analysis of δpCO₂

To elucidate the underlying dynamical, thermodynamical, biological, and chemical processes controlling δpCO₂ we calculated a first-order Taylor series expansion of δpCO₂ in terms of its four drivers, DIC, TA, T, and S. While T and S are controlled only by physics, DIC and TA are controlled by physical, chemical, and biological processes. Throughout this paper we use salinity-normalized DIC and TA using a mean salinity of 35 psu. This effectively removes the concentration–dilution freshwater effect, following the procedure of Lovenduski et al. (2007). The salinity normalized variables are referred to as DIC_s and TA_s, corresponding to DIC $\cdot S_{\mathrm{0}}/S$ and TA $\cdot S_{\mathrm{0}}/S$, respectively. The freshwater effect on DIC and TA is now included in the S term, renamed as S_fw. For the Taylor series expansion, each variable (X= DIC, TA, T, and S) is decomposed into $X=\stackrel{\mathrm{‾}}{X}+\mathit{\delta }X$. The term $\stackrel{\mathrm{‾}}{X}$ represents the 21-year mean and δX denotes the seasonal cycle (calculated as the monthly mean deviation from the 21-year average). The Taylor expansion is then computed for an initial (2006–2026) and final (2080–2100) period. We use multi-decade means and eventually multi-model ensemble means to remove the effects of interannual variability. The full first-order series expansion is given by

$$\begin{array}{ll}{\displaystyle }\mathit{\delta }p{\mathrm{CO}}_{\mathrm{2}}\approx & {\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{DIC}}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}\mathit{\delta }{\mathrm{DIC}}_{\mathrm{s}}+{\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{TA}}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}\mathit{\delta }{\mathrm{TA}}_{\mathrm{s}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial T}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}\mathit{\delta }T+{\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial S}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}\mathit{\delta }{S}_{\mathrm{fw}}.\end{array}$$

Each term of the right-hand side of Eq. (1) represents the contribution from one of the four drivers of δpCO₂. The analytical expressions for the derivatives (without the salinity normalization) are given by the following.

$$\begin{array}{ll}\text{(2)}& {\displaystyle }& {\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{TA}}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}=\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot {\displaystyle \frac{-{\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}}{\stackrel{\mathrm{‾}}{\mathrm{DIC}}\cdot \mathrm{\Theta }-{\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}^{\mathrm{2}}}}{\displaystyle }& {\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{DIC}}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}=\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{\Theta }}{\stackrel{\mathrm{‾}}{\mathrm{DIC}}\cdot \mathrm{\Theta }-{\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial T}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}=\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{\mathrm{DIC}}\cdot \mathrm{\Theta }-{\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }\left[{\stackrel{\mathrm{‾}}{\mathrm{TA}}}_{\mathrm{c}}\cdot ({\displaystyle \frac{\partial {\mathrm{Alk}}_{\mathrm{c}}}{\partial T}}+{\displaystyle \frac{\partial \left[\mathrm{B}(\mathrm{OH}{)}_{\mathrm{4}}^{-}\right]}{\partial T}}+{\displaystyle \frac{\partial \left[{\mathrm{OH}}^{-}\right]}{\partial T}})\right.\\ \text{(3)}& {\displaystyle }& {\displaystyle }\left.-\mathrm{\Theta }\cdot {\displaystyle \frac{\partial (\mathrm{DIC}-[{\mathrm{CO}}_{\mathrm{2}}\left]\right)}{\partial T}}\right]-{\displaystyle \frac{\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot }{\stackrel{\mathrm{‾}}{K_{\mathrm{0}}}(T,S)}}{\displaystyle \frac{\partial K_{\mathrm{0}}(T,S)}{\partial T}}{\displaystyle }& {\displaystyle \frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial S}}{\mathrm{|}}_{\stackrel{\stackrel{\mathrm{‾}}{\mathrm{TA}},\stackrel{\mathrm{‾}}{\mathrm{DIC}}}{\stackrel{\mathrm{‾}}{T},\stackrel{\mathrm{‾}}{S}}}=\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{\mathrm{DIC}}\cdot \mathrm{\Theta }-{\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }\left[{\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}\cdot ({\displaystyle \frac{\partial {\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}}{\partial S}}+{\displaystyle \frac{\partial \left[\mathrm{B}(\mathrm{OH}{)}_{\mathrm{4}}^{-}\right]}{\partial S}}+{\displaystyle \frac{\partial \left[{\mathrm{OH}}^{-}\right]}{\partial S}})\right.\\ \text{(4)}& {\displaystyle }& {\displaystyle }\left.-\mathrm{\Theta }\cdot {\displaystyle \frac{\partial (\mathrm{DIC}-[{\mathrm{CO}}_{\mathrm{2}}\left]\right)}{\partial S}}\right]-{\displaystyle \frac{\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot }{\stackrel{\mathrm{‾}}{K_{\mathrm{0}}}(T,S)}}{\displaystyle \frac{\partial K_{\mathrm{0}}(T,S)}{\partial S}}{\displaystyle }\end{array}$$

Here, $\mathrm{\Theta }=\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]+\mathrm{4}\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]+\frac{\left[\mathrm{B}\right(\mathrm{OH}{)}_{\mathrm{4}}^{-}]\left[{\mathrm{H}}^{+}\right]}{(k_{\mathrm{b}}+[{\mathrm{H}}^{+}\left]\right)}+\left[{\mathrm{H}}^{+}\right]+\left[{\mathrm{OH}}^{-}\right]$ and ${\stackrel{\mathrm{‾}}{\mathrm{Alk}}}_{\mathrm{c}}=\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]+\mathrm{2}\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$. The explicit T and S partial derivatives are given in the Supplement (Text S1). The first two derivatives coincide with the results of Egleston et al. (2010) and Hagens and Middelburg (2016), with the exception of the sign of [OH⁻] in the Egleston et al. (2010) term S. To verify this approach we compared the sum of the Taylor expansion terms with the full simulated range of δpCO₂ from the model's output. The Taylor expansion reproduces the full seasonal cycle amplitude of the original climate model simulations well (Fig. S1 in the Supplement). The analytical expressions for temperature and salinity presented here are – to our knowledge – the first ones of their kind. Previously the calculation of these terms was based on the approximation given by Takahashi et al. (1993) or on numerical calculations.

To gain more insight into the processes causing the amplification of δpCO₂ we introduce a method based on a second Taylor series expansion described below. Equation (1) can be rewritten using the expressions for the sensitivities γ determined by the relation $\frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}}\frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{X}}={\mathit{\gamma }}_{\mathrm{X}}$. These sensitivities have been historically used to represent the percentage of change in pCO₂ per unit of DIC, TA, T, or S. With this notation, Eq. (1) can be expressed in the following way.

$$\begin{array}{ll}{\displaystyle }\mathit{\delta }p{\mathrm{CO}}_{\mathrm{2}}\approx & {\displaystyle }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot \left({\mathit{\gamma }}_{\mathrm{DIC}}\cdot \mathit{\delta }{\mathrm{DIC}}_{\mathrm{s}}+{\mathit{\gamma }}_{\mathrm{TA}}\cdot \mathit{\delta }{\mathrm{TA}}_{\mathrm{s}}+{\mathit{\gamma }}_{\mathrm{T}}\right.\\ \text{(5)}& {\displaystyle }& {\displaystyle }\left.\cdot \mathit{\delta }T+{\mathit{\gamma }}_{S_{\mathrm{fw}}}\cdot \mathit{\delta }{S}_{\mathrm{fw}}\right)\end{array}$$

Each term in Eq. (5) consists of three parts: $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$, the sensitivity γ_X, and the corresponding seasonal cycle δX. To understand which component is the main driver for δpCO₂ changes, we perform a second Taylor expansion of the end of the century's δpCO₂ around the initial state of the system in 2006–2026.

To maximize mathematical clarity we will introduce some definitions: first, we introduce the symbol Δ to indicate the difference between the period 2080–2100 and 2006–2026. Therefore, the total future change in δpCO₂ is now referred to as ΔδpCO₂. In the same manner, the total changes in sensitivities and seasonal cycles are written as $\mathrm{\Delta }{\mathit{\gamma }}_{\mathrm{DIC}{}_{\mathrm{s}},\mathrm{\Delta }{\mathit{\gamma }}_{\mathrm{TA}{}_{\mathrm{s}}},\mathrm{\Delta }{\mathit{\gamma }}_{\mathrm{T}},\mathrm{\Delta }{\mathit{\gamma }}_{\mathrm{S}{}_{\mathrm{fw}}}}$ and $\mathrm{\Delta }\mathit{\delta }{\mathrm{DIC}}_{\mathrm{s}},\mathrm{\Delta }\mathit{\delta }{\mathrm{TA}}_{\mathrm{s}},\mathrm{\Delta }\mathit{\delta }T,\mathrm{\Delta }\mathit{\delta }{S}_{\mathrm{fw}}$, respectively. Finally, we introduce the vector X formed by the four variables DIC_s, TA_s, T, and S_fw as $\mathit{\{}{X}_{\mathrm{0}},X_{\mathrm{1}},X_{\mathrm{2}},X_{\mathrm{3}}\mathit{\}}=\mathit{\{}{\mathrm{DIC}}_{\mathrm{s}},{\mathrm{TA}}_{\mathrm{s}},T,S\mathit{\}}$. With this notation, we can write an expansion of Eq. (5) of the final state of the system by 2080–2100 named X^f around the initial state $\mathit{X}{}^{\mathrm{i}}=\mathit{\{}{{\mathrm{DIC}}_{\mathrm{s}}}^i,{{\mathrm{TA}}_{\mathrm{s}}}^i,T^i,S_{\mathrm{fw}}^i\mathit{\}}$ by 2006–2026 as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }\mathit{\delta }p{\mathrm{CO}}_{\mathrm{2}}=\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\sum _{k=\mathrm{0}}^{\mathrm{3}}{{\mathit{\gamma }}_{X_k}}^i\cdot \mathit{\delta }{X_k}^i\\ {\displaystyle }& {\displaystyle }+{\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}}^i\sum _{k=\mathrm{0}}^{\mathrm{3}}\mathrm{\Delta }{\mathit{\gamma }}_{X_k}\cdot \mathit{\delta }{X_k}^i\\ {\displaystyle }& {\displaystyle }+{\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}}^i\sum _{k=\mathrm{0}}^{\mathrm{3}}{{\mathit{\gamma }}_{X_k}}^i\cdot \mathrm{\Delta }\mathit{\delta }{X}_k\\ {\displaystyle }& {\displaystyle }+\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\sum _{k=\mathrm{0}}^{\mathrm{3}}\mathrm{\Delta }{\mathit{\gamma }}_{X_k}\cdot \mathit{\delta }{X_k}^i\text{(second-order\hspace{0.17em}\hspace{0.17em}terms)}\\ {\displaystyle }& {\displaystyle }+\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\sum _{k=\mathrm{0}}^{\mathrm{3}}{{\mathit{\gamma }}_{X_k}}^i\cdot \mathrm{\Delta }\mathit{\delta }{X}_k\\ \text{(6)}& {\displaystyle }& {\displaystyle }+{\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}}^i\sum _{k=\mathrm{0}}^{\mathrm{3}}\mathrm{\Delta }{\mathit{\gamma }}_{X_k}\cdot \mathrm{\Delta }\mathit{\delta }{X}_k,\end{array}$$

where the first, second, and third terms represent the contributions to ΔδpCO₂ due to changes in the mean pCO₂ ($\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$), the pCO₂ sensitivities ($\mathrm{\Delta }{\mathit{\gamma }}_{X{}_k}$), and the seasonal cycles (ΔδX_k), respectively; the fourth to sixth rows are the second-order terms. This method is similar to the one used by Landschützer et al. (2018).

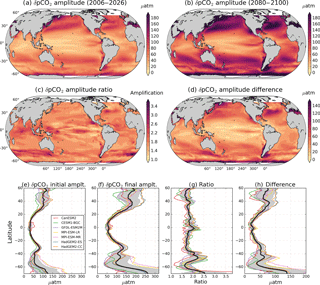
Figure 1 RCP8.5 ensemble mean pCO₂ seasonal cycle amplitude. Amplitude is calculated as climatology maximum minus minimum for (a) initial (2006–2026) and (b) final (2080–2100) periods. Initial and final climatologies were calculated as the monthly deviation from the respective 21-year period mean. (c, d) The ratio and difference between the δpCO₂ amplitudes for 2080–2100 and 2006–2026, respectively. (e)–(h) The zonal means of (a)–(d), respectively, with the individual models shown as colored lines and the ensemble mean overlaid in black. Gray shading represents 1 standard deviation across the models.

3 Results and discussion

3.1 δpCO₂ amplification

Figure 1a shows the ensemble mean δpCO₂ amplitude (calculated as climatological maximum minus minimum) for the initial period 2006–2026. The values range from ≈98 µatm for the high latitudes (40–70^∘ S, 40–60^∘ N) to ≈60 µatm between 40^∘ S and 40^∘ N. The ensemble mean initial seasonal amplitude range is in good agreement with observational estimates calculated for the reference year 2005 (Takahashi et al., 2014b) and for the 1982–2015 period (Landschützer et al., 2017). The agreement between models and observations is remarkably good in the equatorial regions, but the initial amplitude is slightly overestimated in the middle and high latitudes (see Fig. S3 in the Supplement). The higher amplitude in models than observations is expected, as the initial period 2006–2026 already experienced an amplification compared to previous years. Moreover, Tjiputra et al. (2014) found that the ocean's pCO₂ historical trend is larger in models than observations when it is estimated in large-scale areas of the ocean. However, they found that model pCO₂ trends agree with observations when the trends are subsampled to the locations where the observations were taken, and therefore they do a good job of reproducing well-known time series. Moreover, differences are expected as Pilcher et al. (2015) suggested that CMIP5 models perform well in reproducing the seasonal cycle timing, but still show considerable errors in reproducing the seasonal amplitude of pCO₂ due to differences in the mechanisms represented in each model, especially in subpolar biomes.

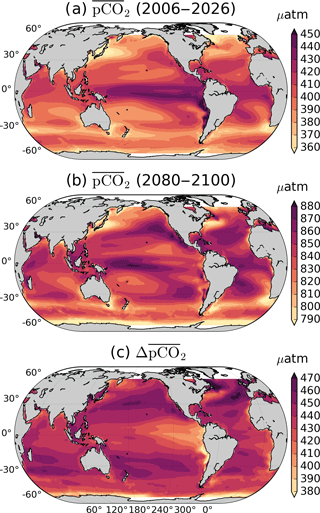
Figure 2 RCP8.5 ensemble mean $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ by (a) 2006–2026 and (b) 2080–2100. (c) Difference between 2080–2100 and 2006–2026. The North Atlantic and subpolar gyres show the largest difference between initial and final periods. The scale is different in each plot to enhance regional features.

By 2080–2100 the annual cycle amplitude attains values of ≈197 and ≈101 µatm in the high and middle to low latitudes, respectively (Fig. 1b). These seasonal variations correspond to 20 % and 18 % of annual $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ for the initial and final periods, respectively. Figure 1c shows that the global ocean δpCO₂ will intensify by a factor of 1.5 to 3 for the 2080–2100 period relative to the 2006–2026 reference period. Figure 1d shows the difference in amplitude (ΔδpCO₂); this pattern differs from the ratio because the ratio overestimates the amplification in areas where the initial amplitude is lower than ≈10 µatm. McNeil and Sasse (2016) used observations and a neural-network clustering algorithm to project that by the year 2100, the δpCO₂ amplitude in some regions could be up to 10 times larger than it was in the year 2000. Our mean amplification factor estimation agrees with the mean threefold amplification found for most of the ocean by McNeil and Sasse (2016). However, the high values in this previous study cannot be reproduced here, mainly because we consider 21-year average ratios instead of single-year ratios, which are strongly affected by interannual variability. Using observations, Landschützer et al. (2018) found an increase of 2.2 µatm per decade, which is smaller than our findings of a total 42 µatm increase by the end of the century between 40^∘ S and 40^∘ N and a global mean change of 81 µatm on the high latitudes. This difference is again possibly due to the higher mean pCO₂ values in models than observations.

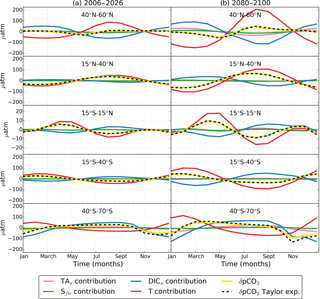
Figure 3 RCP8.5 ensemble mean seasonal cycle (δpCO₂) and its Taylor decomposition. Colored lines indicate the contributions of DIC_s (blue), TA_s (pink), T (red), and S_fw (green) to δpCO₂ reconstructed from its Taylor decomposition (Eq. 1; dashed black). δpCO₂ calculated from monthly pCO₂ (solid yellow) is shown for comparison with the Taylor expansion. Column (a) shows the period 2006–2026 and column (b) shows the period 2080–2100. Each row represents the global zonal average for a different latitudinal band. Temperature dominates all latitudes except the Southern Ocean. In the 40–60^∘ N band, T contribution is largely compensated for by DIC. The TA_s and S_fw effects are rather small in all latitudes.

The global ocean mean amplification factor of δpCO₂ roughly coincides with a doubling of $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ (Fig. 2). The direct relationship between these two is explained in Sect. 3.5. Figure 1e–h show the zonal mean of Fig. 1a–d; in general, towards the end of the century the pCO₂ amplifies more in high latitudes, but so does the standard deviation uncertainty among models. This regional pattern agrees with the observation-based findings of Landschützer et al. (2018), which show that high latitudes have already experienced a larger amplification than middle to low latitudes from 1982 to 2015. Furthermore, the same pattern is projected by CMIP5 models for the seasonal amplification of [H⁺] by the end of the century (Kwiatkowski and Orr, 2018). This is expected from the near-linear relation between pCO₂ and [H⁺]. These regional differences in amplification for pCO₂ can be explained in terms of the relative magnitudes and the phases between the DIC, TA, T, and S contributions, which are explained in subsequent sections.

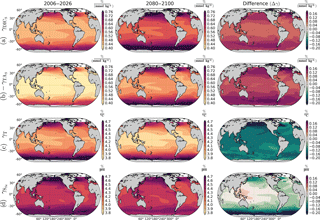
Figure 4 RCP8.5 ensemble mean pCO₂ sensitivities for DIC_s (row a), TA_s (row b), T (row c), and S_fw (row d). Row (b) shows the negative γ_TA. The first and second columns show the sensitivities by 2006–2026 and 2080–2100, respectively. The third column shows the difference between 2080–2100 and 2006–2026 sensitivities. High latitudes show the largest difference between initial and final periods. While DIC_s and TA_s sensitivities increase, the T and S_fw sensitivities decreases, except in the Western Pacific Warm Pool, where ${\mathit{\gamma }}_{S{}_{\mathrm{fw}}}$ increases.

3.2 Present and future drivers of δpCO₂

To understand the driving factors of δpCO₂ and its spatiotemporal differences, we split δpCO₂ into the four different contributions from DIC_s, TA_s, T, and S_fw for the initial and final periods, following Eq. (1). The results are shown in Fig. 3. For most of the ocean, the ensemble mean estimated contributions from DIC_s and T to the present-day δpCO₂ are in good agreement with the data-based estimates of Takahashi et al. (2014b) and Landschützer et al. (2017), particularly in the equatorial regions (see Fig. S3 in the Supplement). However, our T and DIC contributions are slightly larger in middle and high latitudes for the same reasons the pCO₂ seasonal amplitude is overestimated (see Sect. 3.1). Also, differences arise between our DIC_s contribution and the observation-based so-called “nonthermal” contribution because the nonthermal contribution also includes the total alkalinity and salinity effects. Nonetheless, between 40^∘ S and 40^∘ N our ensemble mean shows that δpCO₂ is dominated by changes in temperature that control CO₂ solubility, which decreases in summer, enhancing pCO₂; this is in agreement with observations. The Southern Ocean is controlled by DIC, which responds to changes in upwelling and phytoplankton blooms. Both mechanisms act together to decrease (increase) DIC in summer (winter) (Sarmiento and Gruber, 2006).

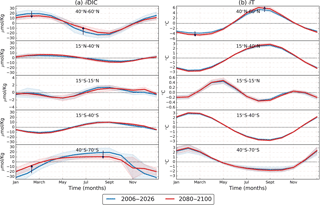
Figure 5 RCP8.5 ensemble zonal mean seasonal cycles of (a) δDIC_s and (b) δT for different latitudinal bands. Blue lines represent the 2006–2026 period, depicted for comparison with the 2080–2100 period shown by red lines. Different panels represent different latitudinal sections. Black arrows point out that while the T seasonal cycle is projected to increase in most of the ocean, global DIC_s is projected to decrease. The shading represents 1 standard deviation across the models. It is important to note that the scale is different for some of the latitudinal bands.

The models show that the δpCO₂ in the 40^∘ N to 60^∘ N band is controlled by T, which disagrees with the abovementioned observations that show a non-temperature dominance in this band. The difference between models and observations arises from two regions: the North Atlantic basin and the northwestern Pacific, specifically near the Oyashio current and the outflows from the Sea of Okhotsk (see Fig. S3 in the Supplement). Most models show a T dominance in the North Atlantic basin; only CESM1-BGC and GFDL-ESM2M show a DIC dominance (see Fig. S4 in the Supplement). The North Atlantic is one of the major sinks of anthropogenic CO₂; however, some models fail to estimate its uptake capacity (Goris et al., 2018). Goris et al. (2018) found that models with an efficient carbon sequestration present a DIC-dominated pCO₂ seasonal cycle in the North Atlantic, but models with low anthropogenic uptake show a T dominance in this region. In the northwestern Pacific, Mckinley et al. (2006) found that coarse models are not able to capture the intricate oceanographic features of this area, and therefore the pCO₂ seasonality is not well captured.

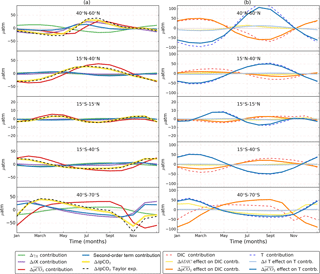
Figure 6 Contribution of seasonalities, sensitivities, and mean pCO₂ changes to ΔδpCO₂. (a) Time series for the terms of Eq. (6) for different latitudinal bands. The Δ symbol represents the total century change calculated as the 2080–2100 value minus the 2006–2026 value. The total change in seasonal pCO₂ (ΔδpCO₂) is depicted as a dashed black. This change is decomposed into changes in seasonalities (ΔδX, purple), sensitivities (Δγ_X, green), mean pCO₂ ($\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$, red), and second-order terms (blue) summed over the four variables that control pCO₂ (DIC, TA, T and S). For comparison with the expansion, ΔδpCO₂ is calculated from model output (yellow). Column (b) shows the total change in DIC (dashed red) and T (dashed blue) contributions. Also shown are two components of the total change in these contributions: the $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ effect on the DIC (solid orange) and T (solid blue) contributions and the ΔδDIC (yellow) and ΔδT (light blue) effects. In column (a), the δpCO₂ change follows the $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ effect. Column (b) shows that, actually, the leading cause of amplification is the $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ effect on the T contribution. It is important note the different scale between column (a) and (b). Also, the scale was reduced in the 15^∘ S–15^∘ N region to highlight its features.

Towards the end of the century (Fig. 3, right column), the amplification of δpCO₂ is caused by an increase in the DIC_s and T contributions and to a lesser extent due to TA_s and S_fw. Only in the high latitudes does the TA_s contribution reinforce the DIC_s effect. The δDIC_s and δT relative phase and magnitude play an important role in causing regional differences of future δpCO₂. For example, between 40 and 60^∘, we find a lower amplification factor than at 30–40^∘ in both hemispheres (Fig. 1c), contrary to what we expected from the general observed larger amplification at higher latitudes. In this band of lower amplification, the warm water from subtropical regions meets the nutrient-rich water from the subpolar regions, but the DIC_s and T effects are almost 6 months out of phase, and therefore their cancellation is larger than in the 30–40^∘ latitude band where, for example, in the North Atlantic, there is 9-month phase difference between the two contributions. A clear illustration of this phase effect is found in the Supplement (Fig. S5).

In the Southern Ocean there is a shift in the maximum δpCO₂ occurring from August–September to March–April (Fig. 3, last row). This shift is generated because the T contribution gains importance over DIC_s due to a reduction of δDIC_s magnitude at the same time that δT increases (Fig. 5). In the equatorial Pacific region (Fig. 5), T dominates over DIC_s but both contributions are small due to their low seasonality. Therefore, this region will experience a low amplification in δpCO₂. In this region some models underestimate the pCO₂ trend (Tjiputra et al., 2014), and therefore the seasonal amplification might be underestimated too. In the following sections we conduct further analysis by decomposing each contribution as the result of three factors: the mean pCO₂ ($\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$), the regional pCO₂ sensitivities (γ_DIC, γ_TA, γ_T, and ${\mathit{\gamma }}_{S_{\mathrm{fw}}}$), and the seasonal cycles (δDIC_s, δTA_s, δT, and δS_fw) as determined in Eq. (5).

3.3 Future pCO₂ sensitivities

The γ_DIC and γ_TA are projected to increase by the end of the century due to a lower ocean buffering capacity produced by increasing temperature and larger background concentrations of DIC (Fassbender et al., 2017). This agrees with our results shown in Fig. 4, which shows that all regions will experience an increase in γ_DIC and γ_TA. Lower buffer factors (higher sensitivities factors) are found in regions where DIC and TA have similar values, and they will decrease (increase) as the DIC ∕ TA ratio in the oceans increases (Egleston et al., 2010). The alkalinity sensitivity is negative, as pCO₂ decreases with increasing alkalinity, but we show here the negative γ_TA for better comparison. γ_TA will increase (with negative values) more than the DIC sensitivity. However, seasonal changes in open-ocean TA_s are small, and therefore the total contribution of alkalinity in our analysis is negligible compared to the DIC_s and T contributions. ${\mathit{\gamma }}_{{\mathrm{S}}_{\mathrm{fw}}}$ decreases everywhere except in the Western Pacific Warm Pool. In this region ${\mathit{\gamma }}_{{\mathrm{S}}_{\mathrm{fw}}}$ increases, probably due to future changes in precipitation that enhance the freshwater effect. In Fig. 4, the sensitivities (γ) are expressed as a percentage change in pCO₂ per unit in DIC, TA, T, and S, respectively. This follows the approach of Takahashi et al. (1993); however, in their paper the authors compute the Revelle factor, which is related to γ_DIC as $R=\mathrm{DIC}\cdot {\mathit{\gamma }}_{\mathrm{DIC}}$. To illustrate the meaning of the sensitivities, we will focus on the subtropical North Pacific in the 15–40^∘ N latitudinal band. In this region γ_DIC indicates an average 0.6 % change in pCO₂ per unit of DIC in 2006–2026. Therefore, for a δDIC_s seasonal cycle amplitude of 40 µmol kg⁻¹ and $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\approx \mathrm{400}$ µatm, the total δpCO₂ amplitude equals 96 µatm. Following the same reasoning, by 2080–2100, γ_DIC increases to 0.7 % and δDIC_s decreases to 30 µmol kg⁻¹; therefore, for a $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ equal to 800 µatm, the δpCO₂ amplitude due to δDIC amounts to 168 µatm.

Temperature sensitivity has been experimentally determined by Takahashi et al. (1993), who found a value of 0.0423, meaning that pCO₂ changes by about 4 % for every ^∘C. This value agrees with our global mean ensemble estimate of 0.0428. However, our analytical expression of γ_T shows that this value varies regionally and, for reasons unknown to us, it might decrease in the future to a global mean value of 0.0415 (Fig. 4c, third column). The T sensitivity is larger in colder regions and lower in the warmer tropics; however, colder regions will experience a larger reduction in γ_T, which locally prevents a larger amplification of the T contribution to δpCO₂. In the next section we show that the T seasonality is projected to increase in high latitudes, strengthening the T contribution.

3.4 Future δDIC_s, δTA_s, δT, and δS_fw

Towards the end of the century, the global mean amplitude of δDIC_s is projected to decrease by ≈26 %–28 % in the high latitudes (Fig.5a), according to all the CMIP5 Earth system model simulations used here. In the middle to low latitudinal band there is no agreement between models; while some show an increase, others project a decrease in amplitude. As suggested by Landschützer et al. (2018), the larger decrease in the Southern Ocean may be the result of changes in the shallow overturning circulation that prevent CO₂ accumulation in this region. This reduction may be counteracted by the predicted increase in productivity owing to a suppression of light and temperature limitations (Bopp et al., 2013; Steinacher et al., 2010).

According to the CMIP5 models, most of the ocean is projected to experience a slight increase in δT, as shown in Fig. 5b. All models show a slight increase in δT; only one model showed a slightly decrease in the southern region, and two models showed a decrease in the equatorial region during October to December. It is important to note that Fig. 5 shows the seasonal values with the mean T removed. Therefore, when considering the positive T trends, the absolute summer values show an increase and the absolute winter values a decrease. This agrees with the results of Alexander et al. (2018), who showed that models project a seasonal intensification of T with larger warm extremes and reduced cold extremes. The authors attributed the T seasonality intensification to an increased oceanic stratification and an overall shoaling of the mixed layer depth, which confines seasonal changes in a reduced volume of water, producing larger changes at the surface. They also showed that the intensification trends are stronger in summer than winter, as the mixed layer depth is shallower in summer. Moreover, ice-covered regions will experience the largest increase in T seasonality due to the loss of sea ice because the ice melting and freezing moderates the surface water temperature seasonality (Carton et al., 2015).

The TA seasonality is also projected to increase in the high latitudes according to all models, except CESM1-BGC, which shows a decrease. For δS (see Fig. S6 in the Supplement) there is no agreement among the different CMIP5 models, except in the Southern Ocean where all the models show a slight decrease. Kwiatkowski and Orr (2018) demonstrated that the seasonality of the drivers is important to determine future changes in [H⁺] seasonality. In the same fashion, our results show that the four δpCO₂ drivers present changes in seasonality, and in particular δDIC_s and δT changes are important to explain future projections of the δpCO₂ amplitude. The increase in δT enhances the δpCO₂ amplification, and the reduction of δDIC_s in the Southern Ocean locally prevents a larger amplification.

3.5 Regional dominant factors

To identify the main cause of the δpCO₂ amplification we use the Taylor series expansion method. With this method we consider the system's final state (δpCO₂ by 2080–2100) as a perturbation of the initial state (δpCO₂ by 2006–2026), as shown in Eq. (6). The expansion is done in three groups of variables: the seasonal cycles of DIC_s, TA_s, T, and S (δX), the sensitivities of pCO₂ to the same four variables (γ_x), and the mean pCO₂ ($\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$). Therefore, each term of the expansion represents how much of the total δpCO₂ change (indicated by ΔδpCO₂ and calculated as the 2080–2100 value minus the 2006–2026 value) is due to the change in each of these factors. We also add the second-order terms that come from their combination. The results are shown in Fig. 6a and they indicate that the leading cause of the δpCO₂ amplification is the change in $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ ($\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$), which confirms previous findings by Landschützer et al. (2018).

It is important to note that our linear Taylor expansion approach neglects one aspect of the highly nonlinear carbonate chemistry of the ocean: it assumes $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ and the sensitivities as independent variables and therefore does not include the positive feedback between larger $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ and increasing γ_DIC (decreasing buffering capacity). Hence in the following, we use changes in $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ and changes in seawater carbonate chemistry synonymously, overall resulting in an enhanced response of δpCO₂ to seasonal changes in DIC, TA, T, and S.

Considering regional differences, we note that amplification increases as we move poleward in spite of decreasing $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ (see Figs. 1 and 2). This characteristic geographical pattern of stronger high-latitude amplification is the result of larger present-day sensitivities (${\mathit{\gamma }}_{\mathrm{DIC}{}_{\mathrm{s}}}$, γ_T) and seasonal amplitudes (δDIC_s, δT) in the high latitudes that amplify the effect of $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ even when its value is small compared to other regions (see Eq. 6, first row term). Some exceptions can be found south of Greenland and near the subtropical gyres, where $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ reaches higher values and therefore also presents large amplification. We also found spatial differences on smaller scales; for example, the western equatorial Pacific presents lower initial δpCO₂ and amplification than the eastern equatorial Pacific (see Fig. 1). This is because the eastern side of the basin has larger DIC_s and T contributions than the western side (see Fig. S2) as a consequence of the upwelling of cold, CO₂-rich waters in the east, which lower the buffering capacity and induce larger δpCO₂ amplitude due to the seasonal effects of productivity and solubility (Valsala et al., 2014).

To further disentangle which of the two main drivers (DIC_s or T) is most affected by $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$, we decomposed the DIC_s and T contributions into their sensitivity, seasonal cycle, and $\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ components. Figure 6b shows the total DIC and T components together with the $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ and seasonal cycle effects on them. The effects from the sensitivities are not depicted, as they only play a minor role. Only the Δγ_DIC term gains importance in the Southern Ocean (not shown). In most of the ocean, the $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ effect on T contribution is the leading cause of amplification. This effect is the result of seasonal solubility changes acting over a larger [CO₂] (Gorgues et al., 2010). In the northern high latitudes, an increase in δT reinforces the amplification. In general, the ΔδT contribution gains importance as we move poleward in both hemispheres and therefore the second-order terms originating from $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}\cdot \mathrm{\Delta }\mathit{\delta }T$ also reinforce the amplification. Interestingly, in the high latitudes, the amplification through second-order terms is as important as the change in the seasonality of the drivers.

The Southern Ocean is an exception to the T dominance; in this region the $\mathrm{\Delta }\stackrel{\mathrm{‾}}{p{\mathrm{CO}}_{\mathrm{2}}}$ effect on the DIC_s contribution dominates, and the regional amplification is reinforced by low values of the mean buffering capacity (high ${\mathit{\gamma }}_{\mathrm{DIC}{}_{\mathrm{s}}}$). This result agrees with the findings of Hauck and Völker (2015). In this area the amplification is counteracted by a reduction in δDIC_s.

4 Conclusions

In this study, we used output from seven CMIP5 global models, subjected to the RCP8.5 radiative forcing scenarios, to provide a comprehensive analysis of the characteristics and drivers of the intensification of the seasonal cycle of pCO₂ between present (2006–2026) and future (2080–2100) conditions. By 2080–2100 the δpCO₂ will be 1.5–3 times larger compared to 2006–2026. The projected amplification by the Earth system models and the possible causes of it are consistent with observation-based amplification for the period from 1982 to 2015 (Landschützer et al., 2018). However, the models slightly overestimate the present-day amplification, probably due to the larger pCO₂ trends in models than observations (Tjiputra et al., 2014).

The models confirm the well-established mechanisms controlling present-day δpCO₂ (Fay and McKinley, 2017; Sarmiento and Gruber, 2006; Takahashi et al., 2002). DIC_s and T contributions are the main counteracting terms dominating the seasonal evolution of δpCO₂. Furthermore, the models show that under future conditions the controlling mechanisms remain unchanged. This result confirms the findings of Landschützer et al. (2018) that identified the same regional controlling mechanism for the past 30 years. The relative role of the DIC and T terms is regionally dependent. High latitudes and upwelling regions, such as the California current system and the coast of Chile, are dominated by DIC_s and the temperate low latitudes are driven by T. Only in the North Atlantic and northwestern Pacific do the models show a dominance of thermal effects over nonthermal effects, which is in disagreement with observations. This further illustrates the urgent need for models to accurately represent regional oceanographic features to accurately reproduce the δpCO₂ characteristics.

In agreement with Landschützer et al. (2018), the model projections towards the end of this century also demonstrate that the global amplification of δpCO₂ is due to the overall long-term increase in anthropogenic CO₂. A higher oceanic background CO₂ concentration enhances the effect of T-driven solubility changes on δpCO₂ and alters the seawater carbonate chemistry, also enhancing the DIC seasonality effect. The spatial differences of δpCO₂ amplification, however, are determined by the regional sensitivities and seasonality of pCO₂ drivers. For example, polar regions show larger sensitivity to DIC and T and larger seasonal cycles of DIC and T. Therefore, these areas present a strong enhancement of δpCO₂ in spite of smaller changes in mean pCO₂.

Moreover, the pCO₂ seasonal cycle amplitude depends on the relative magnitude and phase of the contributions. The models ensemble mean reproduces the highly effective compensation of DIC_s and T contributions when they are 6 months out of phase, confirming previous studies (Landschützer et al., 2018; Takahashi et al., 2002). The compensation of DIC and T prevents a larger amplification of δpCO₂, even when both contributions are largely amplified.

The amplification of the TA and S contributions has a small impact on δpCO₂ in most regions, except in the high latitudes at which the TA contribution complements the DIC one, enhancing the nonthermal effect in this region.

The use of Earth system models allowed us to state the importance of including future changes in driver seasonalities for future δpCO₂ projections. The T seasonality is projected to increase in most of the ocean basins, thereby reinforcing the δpCO₂ amplification. The δT increase is consistent with an increase in stratification that will confine the seasonal changes in net heat fluxes to a shallower mixed layer (Alexander et al., 2018). The DIC_s seasonality decreases in some cold areas and its reduction prevents a larger amplification. For the sensitivities, while γ_DIC increases, γ_T decreases. The latter phenomenon needs further study.

The increasing amplitude of δpCO₂ might have implications for the net air–sea flux of CO₂, in particular in regions where there is an imbalance between winter and summer values (Gorgues et al., 2010). Examples of such behavior can be found in the Southern Ocean (between 50 and 60^∘ S) (Takahashi et al., 2014a) and in the latitude band from 2–40^∘ in both hemispheres (Landschützer et al., 2014). Moreover, seasonal events of high pCO₂ could have an impact on acidification, aragonite undersaturation events (Sasse et al., 2015), and hypercapnia conditions (McNeil and Sasse, 2016). Therefore, understanding the drivers of future δpCO₂ may help to better assess the response of marine ecosystems to future changes in carbonate chemistry. Finally, our complete analytical expansion of δpCO₂ in terms of its four variables provides a practical tool to accurately and quickly diagnose temperature and salinity sensitivities from observational or modeling data sets.