The role of soil pH on soil carbonic anhydrase activity

Carbonic anhydrases (CAs) are metalloenzymes present in plants and microorganisms that catalyse the interconversion of CO₂ and water to bicarbonate and protons. Because oxygen isotopes are also exchanged during this reaction, the presence of CA also modifies the contribution of soil and plant CO¹⁸O fluxes to the global budget of atmospheric CO¹⁸O. The oxygen isotope signatures (δ¹⁸O) of these fluxes differ as leaf water pools are usually more enriched than soil water pools, and this difference is used to partition the net CO₂ flux over land into soil respiration and plant photosynthesis. Nonetheless, the use of atmospheric CO¹⁸O as a tracer of land surface CO₂ fluxes requires a good knowledge of soil CA activity. Previous studies have shown that significant differences in soil CA activity are found in different biomes and seasons, but our understanding of the environmental and ecological drivers responsible for the spatial and temporal patterns observed in soil CA activity is still limited. One factor that has been overlooked so far is pH. Soil pH is known to strongly influence microbial community composition, richness and diversity in addition to governing the speciation of CO₂ between the different carbonate forms. In this study we investigated the CO₂–H₂O isotopic exchange rate (k_iso) in six soils with pH varying from 4.5 to 8.5. We also artificially increased the soil CA concentration to test how pH and other soil properties (texture and phosphate content) affected the relationship between k_iso and CA concentration. We found that soil pH was the primary driver of k_iso after CA addition and that the chemical composition (i.e. phosphate content) played only a secondary role. We also found an offset between the δ¹⁸O of the water pool with which CO₂ equilibrates and total soil water (i.e. water extracted by vacuum distillation) that varied with soil texture. The reasons for this offset are still unknown.

1 Introduction

The build-up of carbon dioxide (CO₂) in the atmosphere is increasing rapidly because of anthropogenic activities (IPCC, 2013). The terrestrial biosphere currently mitigates about 25 % of anthropogenic CO₂ emissions as a result of a small disequilibrium between two large gross CO₂ fluxes, photosynthetic CO₂ uptake and respiratory CO₂ release (Le Quéré et al., 2015). It is clear from recent studies that this disequilibrium is highly variable from year to year with climate and is difficult to measure directly (Ballantyne et al., 2012; Gurney and Eckels, 2011; Poulter et al., 2014; Le Quéré et al., 2015). Currently this disequilibrium is estimated as a residual term in atmospheric budgets of CO₂ after reconciling the various fluxes between the oceans, the atmosphere and anthropogenic emissions (including land use change). These mass budgets rely heavily on coupled climate–carbon models that require accurate representations of how key ecosystem processes such as respiration and stomatal conductance respond to changes in climate and other environmental factors (Friedlingstein et al., 2006). However, it is difficult to evaluate the performance of these models at large scales, as it is difficult to estimate gross CO₂ fluxes directly (Beer et al., 2010; Wingate et al., 2009, 2010). Therefore, additional datasets and tools that can track the behaviour of these processes and bring independent information on how to constrain their representation in models are now urgently required.

One potential approach takes advantage of the observed variability in the oxygen isotope composition of CO₂ molecules in the atmosphere (δ¹⁸O_a) (Ciais et al., 1997; Cuntz, 2003; Farquhar et al., 1993; Francey and Tans, 1987; Welp et al., 2011; Wingate et al., 2009). This variability in δ¹⁸O_a is driven principally by the seasonal and inter-annual variability in the oxygen isotope composition of leaf and soil water pools that are strongly regulated by climate (Welp et al., 2011). Furthermore, large differences between the oxygen isotope composition of soil and leaf water pools exist and can be used to track rapidly the relative contributions of soil and leaf CO₂ exchange (Ciais et al., 1997; Farquhar et al., 1993; Francey and Tans, 1987; Welp et al., 2011; Wingate et al., 2010). This large-scale and rapid hydration of CO₂ by the biosphere is accelerated by the family of carbonic anhydrase enzymes (CAs), which are ubiquitous in bacteria, algae, fungi and plants (Badger, 2003; Elleuche and Poggeler, 2010; Moroney et al., 2001; Smith and Ferry, 2000). In leaves the activity and concentration of CAs are high enough to expect that CO₂ diffusing out of the leaf is in nearly full isotopic equilibrium with leaf water (Farquhar and Cernusak, 2012; Gillon and Yakir, 2001). In soils full isotopic equilibration between CO₂ and water can also occur below a certain depth (Miller et al., 1999; Tans, 1998) but will depend strongly on the distribution and activity of CA in the soil profile (Gangi et al., 2015; Wingate et al., 2009). This is because when the rate of CO₂ diffusion through a soil layer exceeds the CA-catalysed CO₂ hydration rate in that layer, full isotopic equilibration cannot occur (Tans, 1998; Wingate et al., 2008, 2009, 2010). Thus variations in soil CA activity and CO₂ diffusion rates dictate the shallowest depth where full isotopic equilibration between CO₂ and water can occur.

By compiling datasets of depth-resolved soil water δ¹⁸O composition and soil–air CO¹⁸O exchange rates for a range of biomes, Wingate et al. (2009) found a tendency for larger soil CA activities in warmer and drier regions, and proposed three relatively simple but spatially explicit scenarios of soil CA activity at the global scale (Wingate et al., 2009). Subsequently, using the lower range of soil CA activity estimates made by Wingate et al. (2009), an atmospheric CO¹⁸O inversion was performed and led to a surprisingly high rate of global photosynthesis, of ca. 175 GtC yr⁻¹ over the period 1980–2010 (Welp et al., 2011), a surprisingly high value compared to the accepted global estimate of 115–130 GtC yr⁻¹ (Beer et al., 2010; IPCC, 2013). This global-scale estimate of photosynthesis over land was also highly sensitive to the range of soil CA activities used, demonstrating that a better understanding of the environmental and ecological drivers of soil CA activity was key to reduce the uncertainty in large-scale gross CO₂ fluxes using atmospheric CO¹⁸O budgets.

Changes in the abundance and diversity of soil microbial communities were proposed as possible drivers of the observed spatial and temporal changes in soil CA activity (Seibt et al., 2006; Wingate et al., 2008, 2009, 2010). In particular, soil pH is known to strongly influence microbial community composition, richness and diversity (Fierer and Jackson, 2006; Griffiths et al., 2011; Hartman et al., 2008; Lauber et al., 2009) and could thus influence soil CA activity indirectly via changes in the microbial populations that would translate into difference in CA requirements and in the expression of classes of CA with different enzymatic efficiencies. Indeed, α- and β-CA classes are not represented equally in all kingdoms. Very schematically, α-CAs tend to be more abundant in algae and micro-algae while β-CAs are more commonly found in fungi (Elleuche and Poggeler, 2010; Moroney et al., 2001). In addition, α-CAs can be extracellular enzymes unlike β-CAs that are, to our knowledge, only intracellular enzymes. Soil pH should also influence CA-driven CO₂ hydration kinetics directly as CA reactivation is known to be limited by its de-protonation with a pK_a around 7.2 (Rowlett et al., 2002). This may not be true for intracellular CA activity, as it has been shown that soil micro-organisms have the ability to regulate and maintain their intracellular pH within one pH unit near neutral (Krulwich et al., 2011). However, in certain micro-organisms, extracellular CAs have also been found (e.g. Hopkinson et al., 2013) whose activity should be directly affected by external (soil) pH. Thus a direct link between (at least a fraction of) soil CA activity and soil pH should exist.

Actually, part of the reported variations in soil CA activity derived from the isotopic exchange rates between soil water and CO₂ can be explained by differences in soil pH. This is because soil CA activities are often reported as an enhancement factor relative to an un-catalysed CO₂–H₂O isotopic exchange rate, assumed equal to ca. 0.012 s⁻¹ at 25 ^∘C (Miller et al., 1999). However, because soil pH governs the speciation of CO₂ between the different carbonate forms, with dissolved CO₂ being predominant only in acidic environments (pH < 6), the true un-catalysed rate (k_iso,uncat) is not the same for all soils and is strongly reduced in alkaline conditions (Mills and Urey, 1940; Uchikawa and Zeebe, 2012). Thus for the same soil CA activity – or more precisely for the same soil CO₂–water isotopic exchange rate (k_iso) – the enhancement factor should rather be defined relative to the true un-catalysed rate (k_iso ∕ k_iso,uncat) and would then be much greater in alkaline soils than in acidic ones.

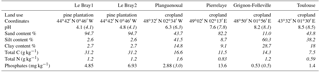
Table 1 Main characteristics of the soils investigated in this study. Numbers in italics indicate literature data (Achat et al., 2014).

The chemical composition of the soil solution is another potentially important factor that should be considered when reporting soil CA activity. Several studies have shown that some anions commonly found in soils could act as CA inhibitors or activators, depending on their ability to exchange protons. For example, at neutral pH, phosphate ions were reported to be activators of bovine α-CA as CO₂ hydration rates increased up to 6.5-fold relative to a solution without phosphates, whilst sulfate ions on the other hand were shown to act as a weak inhibitor on the same α-CA (Rowlett et al., 1991). The presence of these ions also modifies, sometimes dramatically, the pH response of CA activity in vitro (Rowlett et al., 1991), questioning our previous idea that pH might be the only chemical factor controlling soil CA activity.

The aim of this study was to investigate the relationship between soil CA activity and soil pH. For this we used a setup that allowed us to retrieve simultaneously the soil CA activity and the δ¹⁸O of the soil water pool with which CO₂ equilibrates, without destructive sampling. Using six different soils differing in pH by almost 4 pH units, we investigated the influence of soil pH on the CO₂ hydration rate (k_h) and CO₂–H₂O equilibration (k_iso). We also artificially increased the CA concentration in each soil by adding solutions of bovine CA. This CA isoform was chosen because it is well characterised in terms of enzymatic activity (Uchikawa and Zeebe, 2012) and pH response (Rowlett et al., 1991) and it has been demonstrated that its activity was very stable in time even after several hours in solution (Uchikawa and Zeebe, 2012). Thus it was possible to investigate whether CA concentrations and soil pH were the only factors affecting the activity of this exogenous CA. Because of the direct role of pH on CO₂ speciation and CO₂ hydration rate, we hypothesised that exogenous CA activity should be inhibited in acidic soils, but that the native soil phosphate concentration might also influence the activity of CA for soils differing in pH.

2 Material and methods

2.1 Soil sampling

A range of soils that differed naturally in terms of pH, texture, land use and chemical composition were investigated (Table 1). Soil samples from Le Bray, a maritime pine forest located at about 20 km southwest of Bordeaux (France), were collected in November 2014 (LeBray1) and April 2016 (LeBray2). The four other soils were sampled from croplands. The soils from Planguenoual (France, 95 km northwest of Rennes) and Grignon-Folleville (France, 20 km southwest of Paris) were collected in May 2013. More details about these soils can be found in Achat et al. (2014). The soil from Pierrelaye (France, 30 km northwest of Paris) was sampled in October 2014 and May 2016 but mixed in one batch and the soil from Toulouse was sampled once in May 2016.

All soil samples were taken from the soil surface (0–15 cm) after removal of the coarse litter elements. They were sieved with a 4 mm mesh, homogenised and air-dried for several weeks in the laboratory. A first set of experiments was conducted in March 2015 with the soils from LeBray1, Planguenoual and Grignon-Folleville. Prior to gas exchange measurements, 330 to 440 g of soil was repacked in a 500 mL Teflon pot to obtain a common soil depth (ca. 7 cm). For each soil type, we prepared three repacked Teflon pots. Each soil pot was then irrigated with 125 mL of water and allowed to drain for 12 to 24 h at room temperature and light conditions. Drainage was facilitated by a small hole (3 mm inner diameter) drilled at the bottom of the pot to avoid the accumulation of water and anoxic conditions in deeper soil layers. During gas exchange measurements this hole was closed with a Teflon screw. Preliminary results from this first set of experiments indicated substantial evaporation-induced isotopic enrichment of soil water in the top layer, as well as soil-to-soil variations in water-filled pore space (WFPS), which could complicate the interpretation of the results. Thus a second set of experiments was conducted in June 2016 where the WFPS was better controlled and soil evaporation was minimised by allowing the soils to drain prior to measurement inside a dark chamber controlled at 21 ^∘C and with a saturating water vapour generated from an evaporating reservoir filled with the same water that was used for irrigation. The soils from LeBray2, Pierrelaye and Toulouse were chosen for this second set of experiments, to minimise differences between soil texture, whilst keeping a large range of pH (Table 1). Prior to gas exchange measurements, 280 to 300 g of soil was repacked in a 500 mL Teflon pot to a common soil depth of ca. 5–6 cm. Each soil pot was then irrigated in order to reach a WFPS of 25 % and left in the dark chamber for 24 h. All Teflon pots used in the experiment had a constant surface area of 41.85 cm².

2.2 Carbonic anhydrase addition

For a set of gas exchange measurements, lyophilised α-CA powder from bovine erythrocytes (C3934-100MG, Sigma-Aldrich, France) was diluted into the irrigation water. For each set of experiments, CA concentrations of ca. 24 and 80 mg L⁻¹ were used. We chose these concentration because they would correspond to the upper range of CA concentrations expected in natural soils, assuming a cytoplasmic CA concentration of 0.1 mM (Ogée et al., 2016). Apart from this addition of CA into the irrigation water, all other preparation steps of the soil microcosms were kept identical to the ones described above for the microcosms without CA addition.

CA activities from soil microcosms without CA powder addition are qualified hereafter as “native” and CA activities related to the CA addition are called “non-native” and estimated, for a given soil, as the difference between the activities on the CA-added microcosms and their native rates.

2.3 Experimental setup and working sequence

Prior to gas exchange measurements, each soil pot was closed using a screw-tight lid connected to inlet and outlet tubes (Fig. 1) and immersed into a 6.5 L water bath, thermally regulated at 20 ^∘C. An acclimation time of at least 20 min was used to allow the soil column to re-equilibrate to the new air supply CO₂ composition and the new temperature. The soil CO₂ efflux and its oxygen isotopic composition were then measured using the experimental setup illustrated in Fig. 1. To simultaneously retrieve soil CA activity, reported here as the CO₂–H₂O isotopic exchange rate k_iso, and the δ¹⁸O of the soil water pools with which CO₂ equilibrates (δ_sw-eq), we designed a system that allowed us to measure CO₂ isotope fluxes under two, quasi-simultaneous isotopic steady states that only differ in the isotopic composition of the CO₂ entering the soil chamber (Fig. 1). The air supplied to the chamber came directly from a tank containing dry air during the first steady state (SS1) and from a mix of dry, CO₂-free air and a tank of pure CO₂ during the second steady state (SS2). In practice, the air was supplied to the microcosms during SS2 using a compressor (FM2 Atlas Copto, Nacka, Sweden), coupled to a chemical scrub column (Ecodry K-MT6, Parker Hannifin, Cleveland, OH, US) that removed water vapour and CO₂ from the air before being mixed with pure CO₂, with a δ¹⁸O isotopic composition significantly different from the CO₂-in-air mixture used in SS1. During SS2 mixing valves adjusted the CO₂ concentration of the inlet air to maintain it close to the value of the inlet air used in SS1 within acceptable error (423 ± 5 ppm), whilst their oxygen isotope compositions differed markedly (Fig. 2). The transition between SS1 and SS2 was operated by means of a three-way valve (Fig. 1) and a transition period of 20 min was necessary to attain the new steady state (Fig. 2). A full sequence of measurements lasted about 1h (Fig. 2) and consisted of two steady states. During each steady state, the by-pass (i.e. the air entering the soil chamber) and the outlet of the chamber were alternately selected via a manifold connected to a stable isotope CO₂ analyser (Fig. 2). During the first set of experiments each working sequence was repeated three times on each soil and CA treatment (pseudo-replication) at a temperature of 25 ^∘C. During the second set of experiments each soil and CA treatment were made in triplicates but measured only once over a single working sequence (true replication) at a temperature of 21 ^∘C.

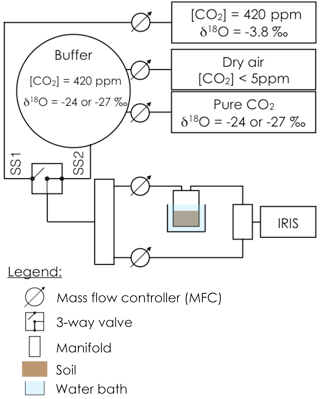
Figure 1 Schematic of the experimental setup used to estimate simultaneously the CO₂–H₂O isotope exchange rate (k_iso) in a soil microcosm and the oxygen isotopic composition of the soil water pool with which the CO₂ equilibrates (δ_sw-eq). The soil microcosm consists of 280–300 g of dry soil previously re-humidified to 25 % of the water holding capacity using mineral water containing different amounts of exogenous CA powder. The soil column is thermally regulated using a 6.5 L water bath and the air entering the chamber is a mixture of CO₂ in dry air whose oxygen isotopic composition is alternatively enriched (steady state 1, −3.8 ‰ VPDB_g) and depleted (steady state 2, between −24 and −27 ‰ VPDB_g, depending on the experiment).

To account for possible non-linearity and drift of the stable isotope analyser during the experiments, gas from two calibration tanks of known CO₂ concentration and isotopic composition was regularly recorded in-between sample measurements (Fig. 2). For both sets of experiments the calibration tanks, whose ¹²C¹⁶O₂ and ¹²C¹⁶O¹⁸O mixing ratios bracketed our measurements, were measured at approximately 16 min intervals, consistent with the expected stability of the analyser (see below).

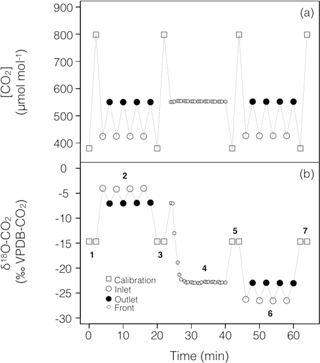
Figure 2 Typical time series of the measured CO₂ mixing ratio and isotope composition (δ¹⁸O) over the course of a working sequence. The sequence is composed of seven steps (indicated in b) to successively measure: (1) two calibration bottles spanning the expected range of CO₂ mixing ratios, (2) inlet and outlet lines of the soil microcosm, measured 4 times consecutively, using a CO₂ with an enriched δ¹⁸O (steady state 1), (3) calibration bottles, (4) the outlet of the chamber during the switch of the air supplying the soil chamber (front), (5) calibration bottles, (6) inlet and outlet lines of the soil chamber, measured 4 times consecutively, using a CO₂ with a depleted δ¹⁸O (steady state 2) and (7) calibration bottles.

2.4 CO₂ mixing ratio and stable isotope measurements

Mixing ratios of ¹²C¹⁶O₂, ¹³C¹⁶O₂ and ¹²C¹⁶O¹⁸O were measured using an Isotope Ratio Infrared Spectrometer (IRIS, Delta Ray, Thermo Fisher Scientific, USA). The cell pressure was controlled and maintained at 100 mbar throughout the experiment. The air sample passed through a multi-pass Herriot cell at a flow of 85 mL min⁻¹ with a total path length of 5 m, leading to a theoretical residence time in the analyser of ca. 35 s. To minimise carry-over effects caused by this residence time, each line (inlet or chamber air or calibration tanks) was measured for 2 min and only the last 40 s of measurements were averaged to provide a single mean and standard deviation.

Calibration tank mixing ratios for the different isotopologues (¹²CO₂, ¹³CO₂ and CO¹⁸O) were averaged as described above (2 min of measurement and only the last 40 s were averaged) and interpolated in time using a spline function. These interpolated time series were then used to perform a two-point calibration regression on the mixing ratios for each sample measurement. Total CO₂ mixing ratio was computed following Wingate et al. (2010):

$$\begin{array}{}\text{(1)}& \left[{\mathrm{CO}}_{\mathrm{2}}\right]={\displaystyle \frac{{[}^{\mathrm{12}}{\mathrm{C}}^{\mathrm{16}}{\mathrm{O}}^{\mathrm{16}}\mathrm{O}]+{[}^{\mathrm{13}}{\mathrm{C}}^{\mathrm{16}}{\mathrm{O}}^{\mathrm{16}}\mathrm{O}]+{[}^{\mathrm{12}}{\mathrm{C}}^{\mathrm{16}}{\mathrm{O}}^{\mathrm{18}}\mathrm{O}]}{\mathrm{0.999179}}},\end{array}$$

where the factor 0.999179 accounts for the presence of ¹²C¹⁶O¹⁷O in the gas mixture. The δ¹⁸O of CO₂ was expressed on the VPDB-CO₂ scale using the formula

$$\begin{array}{}\text{(2)}& {\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}-\mathrm{CO}}_{\mathrm{2}}=\mathrm{0.5}{\displaystyle \frac{{[}^{\mathrm{12}}{\mathrm{C}}^{\mathrm{16}}{\mathrm{O}}^{\mathrm{18}}\mathrm{O}]/{[}^{\mathrm{12}}{\mathrm{C}}^{\mathrm{16}}{\mathrm{O}}_{\mathrm{2}}]}{\mathrm{0.00208835}}}-\mathrm{1},\end{array}$$

where 0.00208835 is the ¹⁸O ∕ ¹⁶O isotope ratio of the VPDB-CO₂ reference standard (Allison et al., 1995) and the factor 0.5 accounts for the fact that there are two oxygen atoms per molecule of CO₂ but only one ¹⁸O atom in ¹²C¹⁶O¹⁸O.

Standard deviations on CO₂ mixing ratios of the different isotopologues were used to compute measurement error on total CO₂ concentration. In contrast, measurement error on the isotope ratios was not calculated using Eq. (2) but computed from the standard deviation over the last 20 s of measurements of the instantaneous ratio [¹²C¹⁶O¹⁸O] ∕ [¹²C¹⁶O₂]. This is because fluctuations in one CO₂ isotopologue was always highly correlated with fluctuations in the other CO₂ isotopologue leading to much smaller fluctuations in their ratios than the one calculated from simple error propagation using Eq. (2). Using this approach, typical errors on [CO₂] and δ¹⁸O-CO₂ values were around 0.1 ppm and 0.3 ‰, respectively.

Under steady-state conditions (i.e. during SS1 or SS2 in Fig. 2), and according to the mass balance of total CO₂ in the chamber headspace, the soil CO₂ efflux is proportional to the total CO₂ concentration difference between the inlet and outlet airstreams:

$$\begin{array}{}\text{(3)}& F={\displaystyle \frac{u_{\mathrm{in}}}{S}}\left(c_{\mathrm{out}}-c_{\mathrm{in}}\right),\end{array}$$

where u_in (mol s⁻¹) is the flow rate of dry air on the inlet of the chamber, S is the soil surface (m²) and c_in and c_out are the mixing ratios of total CO₂ (mol mol⁻¹) in the air entering and leaving the chamber respectively. Because these mixing ratios were determined on a dry air basis (because of the Nafion dryer upstream before the CO₂ isotope analyser) only the flow of dry air on the inlet of the chamber was required to perform the mass balance.

The fluxes of ¹²C¹⁶O₂ (¹⁶F) and ¹²CO¹⁸O (¹⁸F) can be computed using Eq. (3), and the oxygen isotopic signature of the soil CO₂ flux (δ_F = 0.5${}^{\mathrm{18}}F{/}^{\mathrm{16}}F/\mathrm{0.00208835}$ − 1, also expressed on the VPDB-CO₂ scale) can thus be calculated from the ¹²C¹⁶O₂ concentrations and δ¹⁸O of the inlet (¹⁶C_in, ¹⁸δ_in) and outlet (¹⁶C_out, ¹⁸δ_out) air:

$$\begin{array}{}\text{(4)}& {\mathit{\delta }}_F={\displaystyle \frac{{}^{\mathrm{16}}{c}_{\mathrm{out}}^{\mathrm{18}}{\mathit{\delta }}_{\mathrm{out}}{-}^{\mathrm{16}}{c}_{\mathrm{in}}^{\mathrm{18}}{\mathit{\delta }}_{\mathrm{in}}}{{}^{\mathrm{16}}{c}_{\mathrm{out}}{-}^{\mathrm{16}}{c}_{\mathrm{in}}}}.\end{array}$$

For each steady state, three or four inlet/outlet measurements were performed leading to three or four individual values of δ_F from which a mean and standard deviation could be computed.

2.5 Theoretical retrieval of soil CA activity and δ_eq

Assuming uniform soil properties (i.e. uniform soil porosity, moisture and temperature), δ_F can be computed as (Tans, 1998; Wingate et al., 2010)

$$\begin{array}{}\text{(5)}& {\mathit{\delta }}_F={\mathit{\delta }}_{\mathrm{eq}}+{\mathit{\epsilon }}_{\mathrm{D}}+{\displaystyle \frac{V_{\mathrm{inv}}{C}_{\mathrm{a}}}{F}}\left({\mathit{\delta }}_{\mathrm{eq}}-{\mathit{\delta }}_{\mathrm{a}}\right),\end{array}$$

where δ_eq (‰ VPDB-CO₂) is the CO₂ oxygen isotopic composition in equilibrium with soil water, ε_D (−8.7 ‰) is the oxygen isotope fractionation factor during diffusion of CO₂ in air, C_a (mol m⁻³) and δ_a (‰ VPDB-CO₂) are the concentration and δ¹⁸O of CO₂ in the air at the soil–air interface, respectively, F is the soil CO₂ efflux (µmol m⁻² s⁻¹) and V_inv (m s⁻¹) is the piston velocity (i.e. the rate at which a column of air gets pushed into the soil; Tans, 1998). In the following we will assume full mixing inside the chamber so that δ_a = ¹⁸δ_out and C_a = $c_{\mathrm{out}}p/\mathrm{8.3144}/T$, where p (Pa) and T (K) are air pressure and temperature inside the chamber headspace. The piston velocity is a function of soil moisture and temperature and soil CA activity only (Tans, 1998; Wingate et al., 2010) so that it should be the same between the two steady states. Because c_out and F were also maintained constant between the two steady states it was possible to retrieve δ_eq and V_inv from the two steady-state measurements:

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }{\mathit{\delta }}_{\mathrm{eq}}={\displaystyle \frac{-{\mathit{\epsilon }}_{\mathrm{D}}\left({\mathit{\delta }}_{\mathrm{a},\mathrm{1}}-{\mathit{\delta }}_{\mathrm{a},\mathrm{2}}\right)+{\mathit{\delta }}_{F,\mathrm{2}}{\mathit{\delta }}_{\mathrm{a},\mathrm{1}}-{\mathit{\delta }}_{F,\mathrm{1}}{\mathit{\delta }}_{\mathrm{a},\mathrm{2}}}{{\mathit{\delta }}_{\mathrm{a},\mathrm{1}}-{\mathit{\delta }}_{\mathrm{a},\mathrm{2}}+{\mathit{\delta }}_{F,\mathrm{2}}-{\mathit{\delta }}_{F,\mathrm{1}}}},\text{(7)}& {\displaystyle }& {\displaystyle }{V}_{\mathrm{inv}}={\displaystyle \frac{F}{C_{\mathrm{a}}}}{\displaystyle \frac{{\mathit{\delta }}_{F,\mathrm{2}}-{\mathit{\delta }}_{F,\mathrm{1}}}{{\mathit{\delta }}_{\mathrm{a},\mathrm{1}}-{\mathit{\delta }}_{\mathrm{a},\mathrm{2}}}},\end{array}$$

where δ_a,1 and δ_a,2 are δ_a during steady states 1 and 2 and δ_F,1 and δ_F,2 are the corresponding δ_F, computed from Eq. (4).

Strictly speaking, Eq. (5) is valid only for a semi-infinite soil column. In our experiments the soil depths were of a few centimetres only and mass transport was not possible at the bottom of the soil column (i.e. zero CO₂ flux), because the microcosms were closed at the bottom. With this new boundary condition, Eq. (5) should be slightly modified (see Appendix A for a full derivation):

$$\begin{array}{}\text{(8)}& {\mathit{\delta }}_F={\mathit{\delta }}_{\mathrm{eq}}+{\stackrel{\mathrm{̃}}{\mathit{\epsilon }}}_{\mathrm{D}}+{\displaystyle \frac{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{inv}}{C}_{\mathrm{a}}}{F}}\left({\mathit{\delta }}_{\mathrm{eq}}-{\mathit{\delta }}_{\mathrm{a}}\right),\end{array}$$

with ${\stackrel{\mathrm{̃}}{\mathit{\epsilon }}}_{\mathrm{D}}={\mathit{\epsilon }}_{\mathrm{D}}\left(\mathrm{1}-z_{\mathrm{1}}/z_{\max }\tanh \left(z_{\max }/z_{\mathrm{1}}\right)\right)$ and ${\stackrel{\mathrm{̃}}{V}}_{\mathrm{inv}}=V_{\mathrm{inv}}\tanh \left(z_{\max }/z_{\mathrm{1}}\right)$, where z_max is soil depth and $z_{\mathrm{1}}=D_{\mathrm{iso}}/V_{\mathrm{inv}}$ with $D_{\mathrm{iso}}=D_{\mathrm{eff}}/(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{D}})$ and D_eff (m² s⁻¹) the effective diffusivity of gaseous CO₂ through the soil matrix (Tans, 1998; Wingate et al., 2010). The latter was computed using the formulation of Moldrup et al. (2003) for repacked soils: $D_{\mathrm{eff}}=(\mathit{\phi }-\mathit{\theta }{)}^{\mathrm{2.5}}/\mathit{\phi }{D}_{\mathrm{0}}$, where φ (m³ m⁻³) is total soil porosity and D₀ (m² s⁻¹) is the molecular diffusivity of CO₂ in soil air at temperature T_s (K): $D_{\mathrm{0}}=\mathrm{1.381}\times {\mathrm{10}}^{-\mathrm{5}}$ (T_s∕273.15)^1.81 (Massman, 1998). The right-hand side of Eq. (6b) was then used to estimate ${\stackrel{\mathrm{̃}}{V}}_{\mathrm{inv}}$ and V_inv was solved iteratively to satisfy the equation ${\stackrel{\mathrm{̃}}{V}}_{\mathrm{inv}}=V_{\mathrm{inv}}\tanh \left(V_{\mathrm{inv}}{z}_{\max }/D_{\mathrm{iso}}\right)$, from which z₁ and then ${\stackrel{\mathrm{̃}}{\mathit{\epsilon }}}_{\mathrm{D}}$ and δ_eq could be deduced (using Eq. 6b replacing ε_D by ${\stackrel{\mathrm{̃}}{\mathit{\epsilon }}}_{\mathrm{D}})$.

The soil CO₂–H₂O isotopic exchange rate (k_iso, in s⁻¹) was then derived from the piston velocity according to

$$\begin{array}{}\text{(9)}& k_{\mathrm{iso}}={\displaystyle \frac{V_{\mathrm{inv}}^{\mathrm{2}}}{D_{\mathrm{iso}}B\mathit{\theta }}},\end{array}$$

where B (m³ m⁻³) is the solubility coefficient for CO₂ in water (Weiss, 1974) and θ (m³ m⁻³) is the volumetric soil water content.

The soil CO₂–H₂O isotopic exchange rate k_iso was further converted into a CO₂ hydration rate (k_h). Following Uchikawa and Zeebe (2012) we have

$$\begin{array}{}\text{(10)}& k_{\mathrm{h}}=\mathrm{2}{k}_{\mathrm{iso}}{\left\{\mathrm{1}+{\displaystyle \frac{C}{S}}-\sqrt{\mathrm{1}+{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{C}{S}}+{\left({\displaystyle \frac{C}{S}}\right)}^{\mathrm{2}}}\right\}}^{-\mathrm{1}},\end{array}$$

where C (mol m⁻³) is the CO₂ concentration in soil water and S = [H₂CO₃] + [HCO${}_{\mathrm{3}}^{-}$] + [CO${}_{\mathrm{3}}^{\mathrm{2}-}$]. Assuming that the ratio C ∕ S is close to its equilibrium value (this assumption is actually required to derive Eq. 10), the ratio k_h ∕ k_iso is only a function of temperature and pH (Uchikawa and Zeebe, 2012). In acidic soils, this ratio approaches 3 at any temperature, because there are three oxygen atoms in the CO₂–H₂O system and in this pH range, CO₂ is the dominant dissolved inorganic carbon species.

Following the same reasoning as in Ogée et al. (2016) for carbonyl sulfide (OCS) hydrolysis, the soil CO₂ hydration rate can also be expressed as a function of bulk CA concentration [CA] (mol m⁻³):

$$\begin{array}{}\text{(11)}& k_{\mathrm{h}}=k_{\mathrm{h},\mathrm{uncat}}(T,\mathrm{pH})+{\displaystyle \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}}(T,\mathrm{pH})\left[\mathrm{CA}\right],\end{array}$$

where k_h,uncat (s⁻¹) is the un-catalysed CO₂ hydration rate at a given temperature T (K) and pH and k_cat and K_M are the (community-averaged) CA-catalysed maximum hydration rate and Michaelis–Menten constant at the same temperature and pH. The expected pH dependency of k_h and k_iso for different levels of CA concentrations are shown in Fig. 3.

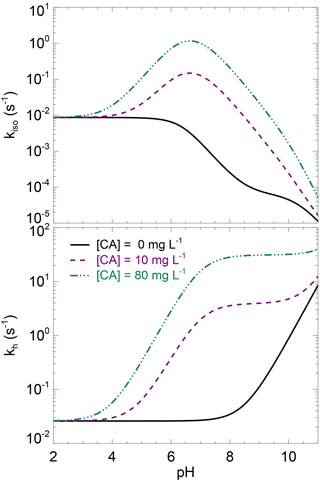
Figure 3 Theoretical rates of CO₂ hydration (k_h) and CO₂–H₂O oxygen isotope exchange (k_iso) as a function of pH, for three levels of carbonic anhydrase concentration. These theoretical curves have been obtained using the un-catalysed rate formula compiled in Uchikawa and Zeebe (2012) and enzymatic parameters of $k_{\text{cat}}/K_{\text{M}}=\mathrm{70}$ s⁻¹ µM⁻¹ and pK_a=7, which are typical values for CA-catalysed CO₂ hydration (Rowlett et al., 2002; Smith and Ferry, 2000). Using enzymatic parameter values more specific to the α-CA powder used here for the CA treatment (i.e. $k_{\mathrm{cat}}/K_{\mathrm{M}}=\mathrm{30}\pm \mathrm{5}$ s⁻¹ µM⁻¹ and $p{K}_{\mathrm{a}}=\mathrm{7.1}\pm \mathrm{0.5}$) would not change qualitatively this figure.

Values of δ_eq were converted into a soil water isotope composition equivalent (δ_sw-eq, in ‰ VSMOW) according to Brenninkmeijer et al. (1983): δ_sw-eq = δ_eq + 0.20 (T_s − 297.15). According to Wingate et al. (2009) this δ_sw-eq should correspond to the soil water δ¹⁸O at a depth z_eq (m) given by

$$\begin{array}{}\text{(12)}& z_{\mathrm{eq}}\approx \mathrm{2}\sqrt{\mathrm{2}\ln \mathrm{2}}{z}_{\mathrm{1}}.\end{array}$$

2.6 Water extraction and isotopic measurements

These estimated profiles of soil water δ¹⁸O were further compared to δ¹⁸O measurements of soil water extracts (δ_sw). For this, after completion of the full gas exchange sequence shown in Fig. 2, soil samples were collected at 1, 2 and 4 cm below the soil surface and stored in Weaton glass jars with Parafilm in a refrigerator. Water from these soil samples was then extracted by vacuum distillation and the extracted water analysed for stable isotope composition using a Triple Isotope Water Analyser (TIWA 45EP; Los Gatos Research Inc., CA, USA) coupled to a liquid auto sampler (PAL System, Switzerland). The δ¹⁸O values of soil water samples were calibrated on the VSMOW-SLAP scale using three internal laboratory water standards that covered the expected range of δ¹⁸O in soil water (−10.16 ± 0.06, −5.59 ± 0.14 and +5.21 ± 0.13 ‰ in 2015 and −10.31 ± 0.06, −4.84 ± 0.06 and +0.62 ± 0.06 ‰ in 2016, on the VSMOW-SLAP scale). Two internal standards (the most depleted and more enriched ones) were used for calibration whilst the third internal standard was used for quality check. These in-house standards were kept in 25 L kegs that were over-pressured with dry air and measured against IAEA standards before and after the experiments, with no drift observed.

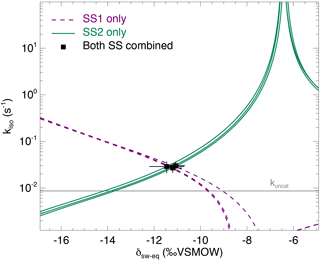
Figure 4 The CO₂–H₂O isotopic exchange rate (k_iso) and isotopic composition of soil water equilibrated with CO₂ (δ_sw) retrieved using the two-steady-state approach described in the main text (Eqs. 6a and 6b), for one single microcosm (LeBray1 with an α-CA addition of 24 mg L⁻¹). Relationships between k_iso and δ_sw for steady state 1 (dotted lines) and steady state 2 (solid lines) are also shown. In this example the microcosm was measured over three consecutive sequences, resulting in three curves for each steady state and three intersection points that coincide well with the two-steady-state solution for each sequence (black squares). The pH-dependent, un-catalysed CO₂–H₂O isotopic exchange rate (Uchikawa and Zeebe, 2012) is indicated by the grey horizontal line.

Both soil water samples and internal working standards were transferred into 2 mL glass vials and the vials were then closed with pre-pierced PTFE caps and silicone septa. Vials with internal standard waters were interspaced every five sample vials following the International Atomic Energy Agency (IAEA) recommendations. A small water volume (0.2–1.0 µL) from each vial was sampled using a 5 µL syringe (SGE Analytical Science, Ringwood, Australia) and injected through a septum in a vaporiser unit maintained at 80 ^∘C to ensure complete vaporisation of the liquid water straight after injection. The vapour was then transferred through a Teflon tube to the pre-evacuated optical cavity of the water isotope analyser. Before each measurement the syringe was rinsed three times in deionised water. Each vial was then measured eight times in total and only the last five measurements, subject to data filtering, were retained and averaged. Based on measurements on the internal standard used for quality check, the accuracy (i.e. the mean absolute difference between calibrated and true δ¹⁸O values) and reproducibility (i.e. the standard deviation of these means) of our δ¹⁸O measurements were always below 0.15 and 0.1 ‰ respectively.

2.7 Phosphate concentration measurements

Because phosphate ions can act as either strong CA activators (Rowlett et al., 1991) or CA inhibitors (Rusconi et al., 2004), total phosphate concentration in the different soils was measured using the water extraction and colorimetric method (Van Veldhoven and Mannaerts, 1987). On 10 g of dry soil we added 99 mL of deionised water and 1 mL of a biocide (Toluene) to stop any microbial activity. Soil suspensions were incubated at 20 ^∘C for 16 h on an agitating roller, then sampled with plastic syringes and filtered through 0.2 mm membrane filters. The filtered solutions were then analysed for phosphate concentrations (mg(P) L⁻¹) using a malachite green colorimetric method (Van Veldhoven and Mannaerts, 1987). Results were then expressed on a dry soil mass basis (mg(P) kg(soil)⁻¹).

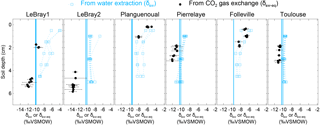
Figure 5 The isotopic composition of soil water at different depths in the replicated soil microcosms from each site, estimated either by vacuum distillation and water isotope analysis (δ_sw, blue squares) or online CO₂–H₂O isotopic exchange using the two-steady-state approach (δ_sw-eq, at depth z_eq, black circles; see text). Profiles for the different CA treatments are plotted together without distinction (because exogenous CA addition should not affect the isotopic composition of soil water). The blue vertical line also indicates the isotopic composition of the irrigation water used for the re-wetting of the air-dried soils. According to Eq. (11), the addition of exogenous CA shifts the gas exchange results (δ_sw-eq) to shallower depths (z_eq).

3 Results

3.1 Illustration of the non-destructive soil CA activity measurement method

From each sequence and steady state, it was possible to compute a relationship between the soil CO₂–H₂O isotopic exchange rate, k_iso and the isotope composition of soil water in equilibration with soil CO₂, δ_sw-eq by combining Eqs. (7) and (8). This approach, when presented graphically, leads to a plot with up to six curves (two curves per sequence; see Fig. 4 in the case of LeBray1 with 24 mg L⁻¹ of exogenous CA addition) that intersect at very similar locations within the k_iso–δ_sw-eq space. Combining the two steady states from the same sequence of measurement (Fig. 2) and using the iterative procedure described above, it is also possible to estimate k_iso and δ_sw-eq numerically, as indicated by the symbols in Fig. 4. These values corresponded closely to the intersection points of the two curves for each steady state in the k_iso–δ_sw-eq space (Fig. 4). Errors on the CO₂ isotope measurements were also algebraically propagated into the equations in order to estimate uncertainties on k_iso and δ_sw-eq. The repeatability of the measurements between the three sequences was very good with a standard deviation equal to or lower than the propagated error on individual estimates (i.e. the spread of the squares in Fig. 4 was always smaller than the error bars on each individual square). Sometimes the intersection between the two lines was not as clearly defined as the one shown in Fig. 4 but the combination of the two steady states always provided very consistent and repeatable estimates of both k_iso and δ_sw-eq between the different sequences. For example, in the experiment shown in Fig. 4, we obtained k_iso values of 0.022 ± 0.005, 0.025 ± 0.006 and 0.025 ± 0.005 s⁻¹ and δ_sw-eq values of −11.3 ± 0.6, −11.5 ± 0.7 and −11.2 ± 0.3 ‰ VSMOW for the three sequences. These estimated values of δ_sw-eq were significantly different (P < 0.05) from the δ¹⁸O of irrigation water (−10.1 ‰ VSMOW) and from the mean cryogenically extracted soil water averaged over the entire soil column and weighted by volumetric soil water content (Fig. 5). Similar results were also observed on LeBray2 where the water pool “seen” by CO₂ had an isotopic composition (δ_sw-eq, black circles in Fig. 5) that was strongly depleted (by about 5 ‰) compared to the cryogenically extracted soil water pool (blue squares in Fig. 5). In contrast, more enriched CO₂-derived δ_sw-eq values and shallower z_eq were found in soils containing a larger clay fraction (i.e. Planguenoual and Folleville; see Table 1), also in much better agreement with the δ¹⁸O profile of cryogenically extracted soil water (Fig. 5).

3.2 Effect of soil pH on soil CA activity

The native (i.e. without any addition of exogenous α-CA during irrigation) isotopic exchange rates (k_iso,native) of the six soils were always higher than the un-catalysed rate (k_iso,uncat) and tended to increase slightly with more alkaline conditions (Fig. 6). These values of native isotopic exchange rates are consistent with what we would theoretically predict using β-CA concentrations between 10 and 80 mg L⁻¹ (Fig. 3).

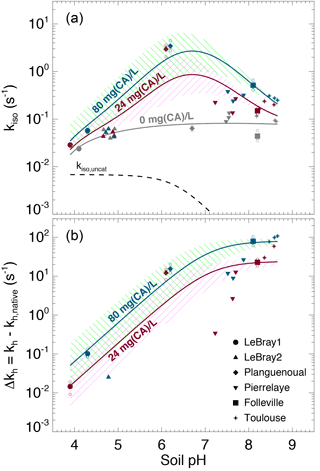
Figure 6 (a) Measured CO₂–H₂O isotopic exchange rates (k_iso) in the different soils for different levels of α-CA addition and (b) associated enhancement hydration rates ($k_{\mathrm{h}}-k_{\mathrm{h},\mathrm{native}})$ caused by the α-CA addition. In (a), the un-catalysed isotope exchange rate (k_iso,uncat; see Uchikawa and Zeebe, 2012) is shown for reference (black dotted curve). The pH dependence of the native isotope exchange rates (grey points in a) is interpolated over the entire pH range explored here using a third-order polynomial fit (grey curve in a). The range of the theoretical rates above this native rate curve that we would expect from α-CA addition of 24 mg L⁻¹ (purple curve and hatched area) and 80 mg L⁻¹ (green curve and hatched area) are also shown and have been obtained using $k_{\mathrm{cat}}/K_{\mathrm{M}}=\mathrm{30}\pm \mathrm{5}$ s⁻¹ µM⁻¹ and $p{K}_{\mathrm{a}}=\mathrm{7.1}\pm \mathrm{0.5}$. For those microcosms that were measured multiple times (several sequences), smaller open symbols are displayed to indicate the results from each individual sequence. In some cases (e.g. LeBray 2), some points could not be displayed in (b) because the k_iso measured after CA addition was smaller than the mean native k_iso, resulting in negative Δk_h values (within the measurement uncertainty).

The addition of exogenous CA generally led to higher k_iso values compared to the native rates, and also enhanced CO₂ hydration rates k_h, with marked differences depending on the pH range (Fig. 6a). On the most acidic soils, the addition of exogenous α-CA barely increased k_h above its native rate (k_h,native), by 0.1 s⁻¹ or less (the native rate was around 0.06 s⁻¹), but within the uncertainties on the measurements. On the other hand for the most alkaline soils (Toulouse, Folleville) k_h increased to about 20 s⁻¹ with 24 mg L⁻¹ of CA added to the irrigation water and up to 65–100 s⁻¹ at 80 mg L⁻¹. Results from the soils with more neutral pH (Planguenoual, Pierrelaye) were intermediate between these two cases with enhanced hydration rates of the order of 10 s⁻¹ or less.

This influence of soil pH on the enhancement of k_h by exogenous CA was anticipated as the k_cat∕K_M (appearing in Eq. 10) is known to be strongly reduced in acidic pH with a pH response of the form (Rowlett et al., 1991)

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}}={\left({\displaystyle \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}}\right)}_{max}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\mathrm{10}}^{p{K}_{\mathrm{a}}-\mathrm{pH}}}}.\end{array}$$

To test whether our results only reflected the pH response of the exogenous α-CA, we rewrote Eq. (10) as follows:

$$\begin{array}{}\text{(14)}& k_{\mathrm{h}}=k_{\mathrm{h},\mathrm{native}}+{\displaystyle \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}}{\left[\mathrm{CA}\right]}_{\mathrm{exogenous}},\end{array}$$

where k_h,native (s⁻¹) represents the native value of k_h and [CA]_exogenous (mol m⁻³) is the concentration of exogenous CA in soil water. For a given pH (and temperature) the difference $\mathrm{\Delta }{k}_{\mathrm{h}}=k_{\mathrm{h}}-k_{\mathrm{h},\mathrm{native}}$ should then be proportional to [CA]_exogenous and the slope of the relationship should be given by k_cat∕K_M and thus be influenced by soil pH. The theoretical pH response of Δk_h at the two CA concentration values used in this study (24 and 80 mg L⁻¹) is shown in Fig. 6b, using Eq. (12) with $p{K}_{\mathrm{a}}=\mathrm{7.1}\pm \mathrm{0.5}$ and ($k_{\mathrm{cat}}/K_{\mathrm{M}}{)}_{\max }=\mathrm{30}\pm \mathrm{7}$ s⁻¹ µM⁻¹ and a molar mass of 30 kg mol⁻¹, typical values for bovine α-CA (Lindskog and Coleman, 1973; Rowlett et al., 1991; Uchikawa and Zeebe, 2012). For LeBray1, Folleville and Toulouse, our results were in very close agreement with Eq. (12) for the two different CA concentrations we tested, but this was not the case for the other soils. For LeBray2 and Pierrelaye, the observed enhanced hydration rates were smaller than the ones predicted by Eq. (12) while for Planguenoual, they were higher.

4 Discussion

4.1 Can we predict the enhancement in soil CA activity associated with exogenous CA addition?

Results presented in Fig. 6b demonstrate that a low (acidic) soil pH clearly inhibits the non-native, additional hydration rate of CO₂ induced by a supply of exogenous CA to the soil water. Our data from three of the soils (LeBray1, Folleville and Toulouse) agreed remarkably well with the pH response described by Eq. (12) and parameterised with k_cat ∕ K_M and pK_a values previously estimated from independent studies on the same α-CA than the one used here (Uchikawa and Zeebe, 2012) or other bovine CA (Rowlett et al., 1991). This indicates that our gas exchange method to estimate CO₂ hydration rates in soil water is robust, despite possible complications caused by CO₂ diffusion through the soil matrix and the potential for heterogeneity in soil water content and pore space in our microcosms. A further possible complication could have arisen because of the necessity to subtract the native hydration rate from our Δk_h calculations. This approach could have introduced a possible bias in our calculations of Δk_h if the native hydration rates were markedly different between soils with and without CA addition – i.e. if the addition of water with exogenous CA over the 12–24 h prior to our gas exchange measurements was enough to induce changes in microbial growth and diversity and/or their CA gene expression compared to soils where only water was added. We estimated the bacterial and fungal abundance using qPCR for some of our microcosms and could not find any clear trend in the number of 16S and 18S DNA gene copies with the amount of exogenous CA added to the soil (not shown). These results suggest that within the timeframe of our experiment, exogenous CA addition did not affect the community structure. However, conservation of the community structure does not necessarily translate into conservation of the native CO₂ hydration rate as microbial communities may have modulated their CA gene expression in response to the availability and activity of exogenous CA. Actually, the observed values of Δk_h were not always consistent with those predicted for three of the soils (LeBray2, Pierrelaye and Planguenoual), which may indicate changes in native CO₂ hydration rates with exogenous CA addition that would have biased our Δk_h estimations.

Another possible reason for these discrepancies between observed and predicted Δk_h could be that the model we are using to derive k_iso and thus k_h from our gas exchange data (Eq. 8) assumes that the soil column is homogeneous in terms of soil water content, temperature, porosity, CA concentration and respiration rate (Tans, 1998; see also Appendix A). Care was taken to remain as close as possible to these conditions: the soils had been sieved and homogenised before being placed into the soil chambers, the irrigation of the soil was performed at least 12 h prior to the gas exchange measurements and the soil microcosms were immersed in a water bath to minimise temperature gradients during the gas exchange measurements. Furthermore, in 2016 we also increased the preparation time to 24 h and minimised soil water evaporation and isotopic enrichment (see Sect. 2). However, despite these precautions, soil water content and its oxygen isotope composition was not always homogeneous throughout the soil column (Fig. 5).

Also, on the most alkaline soils, we noticed that the CO₂ mixing ratio on the outlet of the soil microcosm was not always constant but decreased slightly, indicating that steady state was not reached. This could be explained by the fact that these alkaline soils contain a large pool of total dissolved inorganic carbon that takes much longer to re-equilibrate after a change in the CO₂ concentration in the microcosm headspace, especially if this concentration differed markedly from the CO₂ concentration seen by the soil prior to measurement. On these soils, the acclimation time of 20 min was certainly too short, but was chosen as a compromise in order to minimise other possible artefacts caused by soil evaporation whilst the microcosm was flushed with dry air during the measurements.

In order to explore the possible consequences of the deviations from non-steady state and soil water inhomogeneity on our k_iso estimates, we also used a numerical model that simulates explicitly the transport and rate of change of the different CO₂ isotopologues throughout the soil column and inside the chamber headspace. The model was similar to the one used in Gangi et al. (2015) but with prescribed vertical profiles of soil water content (θ) and isotopic composition (δ_sw). The model was run over the entire sequence shown in Fig. 2 and three model parameters were optimised in order to find the best match between the modelled and observed time series of CO₂ mixing ratio and its carbon and oxygen isotopic composition in the chamber headspace. These model parameters were the ratio k_iso ∕ k_iso,uncat (assumed constant through the soil column), the CO₂ mixing ratio of the air prior to connecting the microcosm to the air supply and a possible offset between δ_sw and δ_sw,eq (also assumed constant throughout the soil column). The latter parameter seemed necessary given the results shown in Fig. 5. Soil CO₂ production rate was assumed to be uniform throughout the soil column and computed iteratively to match the observed CO₂ efflux. Soil temperature was set to the constant value of the water bath and vertical profiles of soil water content and isotopic composition (δ_sw) were prescribed from depth-resolved measurements (Fig. 5). Surprisingly, the results from this numerical model differed only marginally from those shown in Figs. 5 and 6 (see Supplement Fig. S1). Values of Δk_h were slightly affected by non-steady-state effects, either positively (Pierrelaye) or negatively (Planguenoual). Soil water inhomogeneity could also affect Δk_h values slightly both positively (Folleville) or negatively (LeBray1). Overall, the discrepancies between Δk_h estimates and the theoretical predictions (Eq. 12) were only marginally reduced, even after non-steadiness and soil water inhomogeneity had been accounted for.

Another factor that could explain the deviation of Δk_h from theory is the presence of phosphate ions in the soil solution (Table 1) that could either activate or inhibit CA compared to its activity in the absence of such anions (Rowlett et al., 1991; Rusconi et al., 2004). We tested this hypothesis by exploring how the ratio between Δk_h predicted by Eq. (12) (Δk_h,theory) and the observed Δk_h varied with total phosphate concentration (P_i), as well as with the concentrations in mono- and di-hydrogen phosphate ions (HPO${}_{\mathrm{4}}^{\mathrm{2}-}$ and H₂PO${}_{\mathrm{4}}^{-}$ respectively). Although the relationships between Δk_h,theory ∕ Δk_h and the different phosphate ion concentrations were quite dispersed, we could observe a positive trend (not shown). Also, two of the soils with the highest total P_i and H₂PO${}_{\mathrm{4}}^{-}$ molar concentrations (LeBray2 and Pierrelaye) had the largest Δk_h,theory ∕ Δk_h ratio, corresponding to an inhibitory factor of about 10 in Pierrelaye and even higher in LeBray2. This could indicate that phosphate ions act as an inhibitor of the exogenous CA used in our experiments, explaining the reduced response to CA addition in these two soils (Fig. 6).

4.2 With which soil water pool does the CO₂ equilibrate?

Our results also revealed large differences between the isotopic composition of the water pool “seen” by the CO₂ (δ_sw-eq) and that of cryogenically extracted soil water (δ_sw), with significantly (P < 0.05) more depleted δ_sw-eq values compared to δ_sw (Fig. 5 and Table S2 in the Supplement). Interestingly, very similar “offsets” between δ_sw and δ_sw,eq were also predicted by the numerical model (not shown), except for LeBray1 where even larger offsets were found. For a given soil the offset did not seem to vary with soil CA activity (i.e. the difference between δ_sw and δ_sw,eq was the same for soils with and without CA addition; see Table S2) and, at least for the only soil tested, did not seem to be affected by small change in soil water content (similar offsets were observed between LeBray1 and LeBray2). However, in-between the different soils, it seemed that those with the highest CA activity (Planguenoual, Folleville) also had the smallest offset (Table S2). Also for LeBray soil, Jones et al. (2017) showed that the offset between δ_sw and δ_sw-eq decreased when the soil was approaching saturation.

The exact reason for this offset between δ_sw and δ_sw,eq is still unknown. Noting that δ_sw and δ_sw,eq are estimated from measurements coming from different analysers, we verified that the calibrations of the two analysers were consistent with one another. We thus pressurised pure CO₂ into a keg partially full of water of known isotopic composition and let the water–CO₂ mixture equilibrate for several weeks. The pure CO₂ was then diluted into CO₂-free air to reach ambient CO₂ concentrations and the air mixture was analysed with our CO₂ isotope analyser. We found a small difference of about −0.31 ‰ between the δ¹⁸O of the equilibrated CO₂ and the δ¹⁸O of the water in the keg. Clearly, such a bias would only explain a small fraction of the measured offset between δ_sw and δ_sw,eq, down to −6 ‰ on some soils. Also the fact that this offset cancels in soils with high CA activity indicates that our calibration scheme is clearly not the only cause of the existence of such an offset.

A possible explanation for the observed difference between δ_sw and δ_sw,eq could be that, at any given depth, soil water is not isotopically homogeneous and that CO₂ “sees” a different water pool to that extracted during cryogenic distillation, with different thermodynamic and chemical properties between the different soil water pools. This idea has been proposed by several studies already. For example Hsieh et al. (1998) allowed pure CO₂ to equilibrate for several weeks with different soils at different water contents and found that the isotopic composition of equilibrated CO₂ could differ by several ‰ compared to the δ¹⁸O of the soil water extracted by vacuum distillation, even at relatively high (i.e. 32 %) gravimetric water contents. They explained this difference by recognising that soil surfaces contain a lot of ions that could modify the isotopic composition of the “bound” water pool and also the CO₂–H₂O isotopic fractionation factor.

More recently, Chen et al. (2016) performed laboratory experiments that suggest the existence of two isotopically distinct pools of water around hydrophilic materials such as silage, litter or soil organic matter. They found a negative apparent isotopic fractionation between total water (extracted by cryogenic distillation) and unconfined water (estimated by water liquid–vapour equilibration), suggesting a depletion of the water bound to the hydrophilic material. They also found that the magnitude of this apparent fractionation increased with the solid to water ratio. To reconcile these results with ours, we would need to assume that CO₂ equilibrates with bound water, even when exogenous CA is added to the soil. This is somewhat surprising, because once in solution we would expect the exogenous CA to be equally spread between bound and unbound water. Another explanation could be that water around the CA reaction sites is depleted. Chen et al. (2016) found large apparent fractionation factors with water adsorbed onto casein, another protein found in milk. However, according to their theory, at high water contents (or low solid-to-water ratios), the fractionation factor should vanish. In addition, Uchikawa and Zeebe (2012) found that the isotopic equilibration between BaCO₃ and water was not affected by the presence of CA in the solution, thus rejecting the hypothesis of different water composition around the CA reaction sites. Clearly, more experiments on CO₂–H₂O equilibration in soils such as those performed by Hsieh et al. (1998) are needed to better understand the underlying mechanisms leading to this apparent oxygen isotope disequilibrium between soil CO₂ and soil water, even below the equilibrium depth.

5 Conclusion

Our experimental results demonstrate that our two-steady-state approach is robust and sensitive enough to detect changes in the CO₂–H₂O isotope exchange rate when the concentration of CA enzyme in the soil matrix is augmented artificially. We also found that natural variations in soil pH had a strong control over the variability of soil CA activity, with a smaller influence of the phosphate ion concentration, and these variations reassuringly followed similar patterns to those observed in other studies on α-CA activity in buffered solutions. This is a real advancement in our understanding of the spatial variations of soil CA activity across biomes reported by Wingate et al. (2009) and the associated impact on the atmospheric budget of CO¹⁸O. However, our results should still be taken with caution. Although α-CAs may be present in certain soil microbial communities with a high abundance of phototrophs such as cyanobacteria and micro-algae, the majority of microbial CAs in soils are more likely represented by the β-CA class (Smith and Ferry, 2000). In addition, β-CAs are seldom active externally like α-CAs and are rather found in the internal cell components of the microbe, in particular the cytoplasm (e.g. Merlin et al., 2003). Thus, although β-CAs also exhibit a strong dependence of CA activity with pH (Rowlett et al., 2002), it remains to be investigated whether the location and relative abundance of different CAs in soil communities modifies the expected relationship with pH. In addition, it is not clear whether the impact of anions such as phosphate ions will remain important when the CA is active internally. This was beyond the scope of the present study but is an obvious next step to be addressed in future experiments to help understand and model better the spatio-temporal variations in atmospheric CO¹⁸O at large scales.

Appendix A: Derivation of Eq. (7) in the main text

Following Tans (1998) we will assume that the CO₂ concentration profile within the soil column is driven by two processes: respiration, characterised by a production density S (mol m⁻³ s⁻¹) and diffusion, characterised by an effective diffusivity D_eff (m² s⁻¹). At steady state, the mass balance equation (see also Eq. 3 in Tans, 1998) is

$$\begin{array}{}\text{(A1)}& {\displaystyle }{D}_{\mathrm{eff}}{\displaystyle \frac{{\text{d}}^{\mathrm{2}}C}{\text{d}{z}^{\mathrm{2}}}}+S=\mathrm{0},\end{array}$$

where C (mol m⁻³) is the CO₂ concentration at depth z (m) within the soil column. Assuming S constant throughout the soil column (a fair assumption when working on repacked, temperature-controlled soil columns), and with the boundary conditions C=C_a at z=0 and $\text{d}C/\text{d}z=\mathrm{0}$ at $z=z_{max}$, the solution of Eq. (A1) is (see for example Eq. 23a in Tans, 1998)

$$\begin{array}{}\text{(A2)}& {\displaystyle }C\left(z\right)=C_{\mathrm{a}}+{\displaystyle \frac{S}{D_{\mathrm{eff}}}}\left[z{z}_{\max }-{\displaystyle \frac{z^{\mathrm{2}}}{\mathrm{2}}}\right]=\mathrm{0}.\end{array}$$

Denoting by R, R_S and R_eq the ¹⁸O ∕ ¹⁶O ratio of soil air CO₂, soil respired CO₂ and CO₂ in equilibrium with soil water, respectively, the steady-state CO¹⁸O mass balance equation is (see also Eq. 9 in Tans, 1998)

$$\begin{array}{}\text{(A3)}& {\displaystyle }{D}_{\mathrm{iso}}{\displaystyle \frac{{\text{d}}^{\mathrm{2}}RC}{\text{d}{z}^{\mathrm{2}}}}-B\mathit{\theta }{k}_{\mathrm{iso}}C\left(R-R_{\mathrm{eq}}\right)+S{R}_{\mathrm{S}}=\mathrm{0}.\end{array}$$

Defining y=RC, Eq. (A3) becomes

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{z}_{\mathrm{1}}^{\mathrm{2}}{\displaystyle \frac{{\text{d}}^{\mathrm{2}}y}{\text{d}{z}^{\mathrm{2}}}}-y=-y_{\mathrm{S}}-R_{\mathrm{eq}}C\left(z\right)\text{with}\\ \text{(A4)}& {\displaystyle }& {\displaystyle }{z}_{\mathrm{1}}^{\mathrm{2}}={\displaystyle \frac{D_{\mathrm{iso}}}{B\mathit{\theta }{k}_{\mathrm{iso}}}}\text{and}{y}_{\mathrm{S}}={\displaystyle \frac{R_{\mathrm{S}}S}{B\mathit{\theta }{k}_{\mathrm{iso}}}}.\end{array}$$

The general solution of this differential equation is of the form $y\left(z\right)=A{e}^{-z/z_{\mathrm{1}}}+B{e}^{+z/z_{\mathrm{1}}}+Y\left(z\right)$, where A and B are constants to be defined and Y is a particular solution of Eq. (A4). Choosing Y of the form $Y=a{z}^{\mathrm{2}}+bz+c$, the coefficients a, b and c must satisfy Eq. (A4) for any depth z. Using the expression of C(z) from Eq. (A2), this gives

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }Y\left(z\right)=-R_{\mathrm{eq}}{\displaystyle \frac{S}{\mathrm{2}{D}_{\mathrm{eff}}}}{z}^{\mathrm{2}}+R_{\mathrm{eq}}{\displaystyle \frac{S}{D_{\mathrm{eff}}}}{z}_{\max }z+R_{\mathrm{eq}}{C}_{\mathrm{a}}\\ \text{(A5)}& {\displaystyle }& {\displaystyle }+y_{\mathrm{S}}-R_{\mathrm{eq}}{\displaystyle \frac{S}{D_{\mathrm{eff}}}}{z}_{\mathrm{1}}^{\mathrm{2}}.\end{array}$$

With the boundary conditions y=C_aR_a at z=0 and $\text{d}y/\text{d}z=\mathrm{0}$ at $z=z_{max}$, the solution of Eq. (A4) can be found (i.e. constants A and B can be identified) and this gives

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }y\left(z\right)=\left[C_{\mathrm{a}}\left(R_{\mathrm{a}}-R_{\mathrm{eq}}\right)+R_{\mathrm{eq}}{\displaystyle \frac{S{z}_{\mathrm{1}}^{\mathrm{2}}}{D_{\mathrm{eff}}}}-y_{\mathrm{S}}\right]{\displaystyle \frac{e^{-z/z_{\mathrm{1}}}+{\mathit{\xi }}^{\mathrm{2}}{e}^{+z/z_{\mathrm{1}}}}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}\\ \text{(A6)}& {\displaystyle }& {\displaystyle }+Y\left(z\right),\text{with}\mathit{\xi }=e^{-z_{\max }/z_{\mathrm{1}}}.\end{array}$$

The CO₂ and CO¹⁸O fluxes at the soil surface are given by

$$\begin{array}{}\text{(A7)}& {\displaystyle }F=D_{\mathrm{eff}}{\left.{\displaystyle \frac{\mathrm{d}C}{\mathrm{d}z}}\right|}_{z=\mathrm{0}}\text{and}{F}_{\mathrm{iso}}=D_{\mathrm{iso}}{\left.{\displaystyle \frac{\mathrm{d}y}{\mathrm{d}z}}\right|}_{z=\mathrm{0}}.\end{array}$$

From Eq. (A2) we get $F=S{z}_{max}$ and from Eq. (A6) we obtain

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{F}_{\mathrm{iso}}=\left[V_{\mathrm{inv}}{C}_{\mathrm{a}}\left(R_{\mathrm{eq}}-R_{\mathrm{a}}\right)-{\displaystyle \frac{z_{\mathrm{1}}}{z_{\max }}}F\left({\mathit{\alpha }}_{\mathrm{D}}{R}_{\mathrm{eq}}-R_{\mathrm{S}}\right)\right]\\ \text{(A8)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\mathrm{1}-{\mathit{\xi }}^{\mathrm{2}}}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}+{\mathit{\alpha }}_{\mathrm{D}}{R}_{\mathrm{eq}}F,\end{array}$$

where ${\mathit{\alpha }}_{\text{D}}=D_{\mathrm{iso}}/D_{\mathrm{eff}}$. Defining $R_F=F_{\mathrm{iso}}/F$ and using the delta notation (i.e. $\mathit{\delta }=R/R_{\mathrm{std}}$ – 1 where R_std is the ¹⁸O ∕ ¹⁶O ratio of the international standard VPDB_g), Eq. (A8) becomes

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\delta }}_F=\left[{\displaystyle \frac{V_{\mathrm{inv}}{C}_{\mathrm{a}}}{F}}\left({\mathit{\delta }}_{\mathrm{eq}}-{\mathit{\delta }}_{\mathrm{a}}\right)-{\displaystyle \frac{z_{\mathrm{1}}}{z_{\max }}}\left({\mathit{\delta }}_{\mathrm{eq}}+{\mathit{\epsilon }}_{\mathrm{D}}-{\mathit{\delta }}_{\mathrm{S}}\right)\right]\\ \text{(A9)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\mathrm{1}-{\mathit{\xi }}^{\mathrm{2}}}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}+{\mathit{\delta }}_{\mathrm{eq}}+{\mathit{\epsilon }}_{\mathrm{D}},\end{array}$$

where ${\mathit{\epsilon }}_{\mathrm{D}}={\mathit{\alpha }}_{\text{D}}-\mathrm{1}$ and noting that the second-order term ε_Dδ_eq has been discarded. Now, assuming R_S=R_eq (or equivalently δ_S=δ_eq), Eq. (A9) simplifies to Eq. (8) in the main text.