the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Environmental and biological controls on Na∕Ca ratios in scleractinian cold-water corals
Nicolai Schleinkofer
Jacek Raddatz
André Freiwald
David Evans
Lydia Beuck
Andres Rüggeberg
Volker Liebetrau
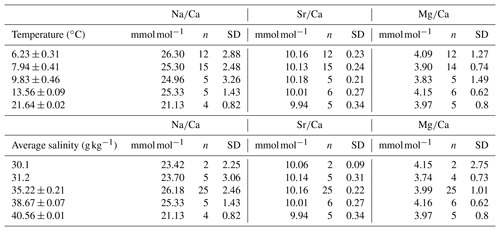
Here we present a comprehensive attempt to correlate aragonitic Na∕Ca ratios from Desmophyllum pertusum (formerly known as Lophelia pertusa), Madrepora oculata and a caryophylliid cold-water coral (CWC) species with different seawater parameters such as temperature, salinity and pH. Living CWC specimens were collected from 16 different locations and analyzed for their Na∕Ca ratios using solution-based inductively coupled plasma-optical emission spectrometry (ICP-OES) measurements.
The results reveal no apparent correlation with salinity (30.1–40.57 g kg−1) but a significant inverse correlation with temperature ( ). Other marine aragonitic organisms such as Mytilus edulis (inner aragonitic shell portion) and Porites sp. exhibit similar results highlighting the consistency of the calculated CWC regressions. Corresponding Na∕Mg ratios show a similar temperature sensitivity to Na∕Ca ratios, but the combination of two ratios appears to reduce the impact of vital effects and domain-dependent geochemical variation. The high degree of scatter and elemental heterogeneities between the different skeletal features in both Na∕Ca and Na∕Mg, however, limit the use of these ratios as a proxy and/or make a high number of samples necessary. Additionally, we explore two models to explain the observed temperature sensitivity of Na∕Ca ratios for an open and semi-enclosed calcifying space based on temperature-sensitive Na- and Ca-pumping enzymes and transport proteins that change the composition of the calcifying fluid and consequently the skeletal Na∕Ca ratio.
- Article
(6219 KB) - Full-text XML
-
Supplement
(403 KB) - BibTeX
- EndNote
Sodium-to-calcium ratios (Na∕Ca) have been proposed as a new tool in paleoceanography to reconstruct seawater salinities. Cultured benthic and planktonic foraminifera as well as living planktonic foraminifera from the Red Sea showed the potential of calcitic Na∕Ca ratios as a salinity proxy (Mezger et al., 2016; Wit et al., 2013). Cold-water corals provide one of the most promising marine paleoenvironmental archives for climatic research due to the potential to reconstruct high-resolution records using the aragonitic skeleton (Druffel, 1997). About half of the known scleractinian coral species do not live in tropical, shallow water (<50 m) but in deeper waters, including deep-sea environments (>200 m) (Roberts et al., 2009). These deep or cold-water corals lack phototrophic symbionts and, therefore, are azooxanthellate. Like their zooxanthellate shallow-water relatives, some azooxanthellate deep-water species, such as Desmophyllum pertusum and Madrepora oculata, are also capable of building large three-dimensional reef frameworks that serve as habitats for thousands of different organisms and constitute biodiversity hotspots in low to high latitudes and from shallower water to the deep seas (Henry and Roberts, 2016; Roberts et al., 2009). The distribution of cold-water corals (CWCs) is controlled by several parameters, amongst which is the density of seawater (Dullo et al., 2008), which appears to correlate with the so-called intermediate nepheloid layers (INLs). These INLs contribute an important source of particulate organic matter (POM) (Kiriakoulakis et al., 2005, 2007) that CWCs feed on. Additionally, it has been suggested, that gamete density restricts the lateral transport to certain density envelopes (Dullo et al., 2008). For D. pertusum, the suitable density envelope amounts to σθ=27.35–27.65 kg m−3 (Dullo et al., 2008), although these values are not applicable to every oceanic region (Flögel et al., 2014; Freiwald et al., 2009; Rüggeberg et al., 2011). Since seawater density is a function of temperature and salinity, these parameters also partly control the spatial distribution of CWCs. Most known CWCs occur in salinities of 35 g kg−1 and mean temperatures of 4–12 ∘C (Freiwald, 2002; Freiwald and Roberts, 2005), although they are also able to thrive at lower and higher temperatures and salinities (e.g., Bett, 2001; Roder et al., 2013; Taviani et al., 2005).
Independent proxies are needed to reconstruct the environment in which CWCs lived in the past to better understand their temperature, salinity or pH tolerances and to study the influence of parameters on their spatial distribution. This would also help to better locate new unknown sites of CWC occurrences. For temperature and pH, different geochemical proxies can be used to calculate these parameters in the geological past. Sr∕Ca and Li∕Mg ratios serve as temperature proxies (Cohen et al., 2006; Gagnon et al., 2007; Mitsuguchi et al., 1996; Montagna et al., 2014; Raddatz et al., 2013, 2014b; Rollion-Bard and Blamart, 2015; Shirai et al., 2005), U∕Ca and boron isotopes serve as proxies of the carbonate system (Anagnostou et al., 2011, 2012; Blamart et al., 2007; McCulloch et al., 2012; Raddatz et al., 2014a, 2016; Rollion-Bard et al., 2011). However, independent geochemical methods to reconstruct past salinities are absent but urgently needed to reconstruct spatial distribution patterns in the past and quantify the effects of ocean acidification on CWCs by researching its effects in the past. Even though CWCs show that they can maintain growth in undersaturated, corrosive waters, the older unprotected parts of the reef are susceptible to dissolution (Büscher et al., 2017; Form and Riebesell, 2012). This weakens the reef integrity and might have severe implications for available microhabitats (Büscher et al., 2017; Roberts, 2006).
Reconstructing past salinities can be accomplished with several different techniques, e.g., diatom and dinoflagellate species composition (Zonneveld et al., 2001), morphology and the size of placoliths from Emiliania huxleyi (Bollmann et al., 2009), Ba∕Ca ratios in foraminiferal calcite (Weldeab et al., 2007), the strontium isotope composition of bivalves (Israelson and Buchardt, 1999), the process length of dinoflagellate cysts (Mertens et al., 2009), the hydrogen isotope composition of alkenones (van der Meer et al., 2007; Schouten et al., 2006), or temperature-corrected (Mg∕Ca, TEX86) oxygen isotopes (Elderfield and Ganssen, 2000). While some of these proxies may yield reliable results (e.g., coupled Mg∕Ca and oxygen isotopes – Elderfield et al., 2012; Lear et al., 2000) others suffer from rather large uncertainties introduced by modeled parameters or require a good knowledge of the regional oceanography (Wit et al., 2013). Others, like Ba∕Ca ratios are more effected by terrestrial runoff and are therefore only applicable in proximal sites. Complications with the existing proxies mean that further methods are desirable; therefore, we explore here whether coral Na∕Ca ratios may be useful in this regard.
The influence of seawater salinity on Na∕Ca ratios are known from Atlantic oysters (Rucker and Valentine, 1961), barnacle shells (Gordon et al., 1970) and inorganically precipitated calcium carbonate (Ishikawa and Ichikuni, 1984). Recently it has been shown that Na incorporation into calcitic planktonic and benthic foraminifera appears to be at least partly controlled by seawater salinity (Allen et al., 2016 (only in Globigerinoides ruber); Mezger et al., 2016; Wit et al., 2013). According to Wit et al. (2013), the incorporation of Na in calcite depends on the activity of Na in the seawater which is a function of salinity. There is strong evidence that Na substitutes for Ca in biogenic aragonite despite its charge difference (Okumura and Kitano, 1986; Yoshimura et al., 2017). However, since Na and Ca compete for the same lattice positions, the calcium concentration and Na∕Ca activity ratio of the surrounding seawater might also control the amount of sodium incorporation (Ishikawa and Ichikuni, 1984; White, 1977). Over longer periods of geological time, when concentrations of some elements in seawater have varied, this would inhibit the use of Na∕Ca ratios as a salinity proxy but might prove useful to reconstruct oceanic calcium concentrations. Recent studies also show that the Na∕Ca ratio in foraminiferal calcite is also mainly controlled by seawater Na∕Ca ratios (Hauzer et al., 2018).
In this study, we investigate the impact of different seawater parameters on the incorporation of Na into the aragonitic skeleton of the scleractinian cold-water coral D. pertusum, M. oculata and a caryophylliid species from the Red Sea. The corals were collected alive from a variety of locations to cover a broad range of temperatures (5.9–21.6 ∘C) and salinities (30.1–40.6 g kg−1).
2.1 Study area and sample collection
The samples were taken from 45 different coral specimens collected from 16 different locations (Table 1). Most of the samples (n=25) were collected during different cruises from the Norwegian margin. The other samples derive from the Irish margin and Bay of Biscay (n=4), the Mediterranean Sea and Gulf of Cadiz (n=7), the Gulf of Mexico and Great Bahama Bank (n=4), and the Red Sea (n=5) (Fig. 1). Conductivity–temperature–depth (CTD) downcast data for water parameters was available for all locations except the Red Sea and the Gulf of Mexico. Where no CTD data were available, the water parameters were retrieved from annual averaged data from the World Ocean Atlas 2013 (WOA13; Locarnini et al., 2013; Zweng et al., 2013). Where available, comparison of in situ CTD and WOA13 data revealed an agreement within 0.15 ∘C in Santa Maria de Leuca and 0.04 ∘C in the Bay of Biscay. The seawater carbonate system data such as pH were taken from the associated cruise report (Flögel et al., 2014), or in case of the Red Sea and the western Atlantic, from Mezger et al. (2016) and CARINA (Carbon in the Atlantic). Flögel et al. (2014) used a WTW Multi 350i compact precision handheld meter to determine pH (Flögel et al., 2014); pH in the Red Sea was calculated from DIC (dissolved inorganic carbon) and TA (total alkalinity), measured during PELAGIA 64PE158 (Mezger et al., 2016), using CO2SYS (Lewis and Wallace, 1998). pH values are reported using the total scale.
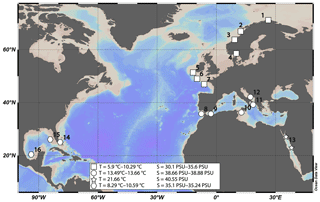
Figure 1Map of sampling locations. Locations are grouped in four areas with similar physical parameters. (1) Lopphavet, Sotbakken, Stjernsund; (2) Traenadjupet; (3) Sula, Nordleksa, Tautra, Røberg; (4) Oslofjord; (5) Galway Mound; (6) Whittard Canyon; (7) Guilvinec Canyon; (8) Meknes Carbonate Mound Province; (9) El Idrissi Bank; (10) Urania Bank; (11) Santa Maria di Leuca (SML) province; (12) Bari Canyon; (13) Red Sea; (14) Great Bahama Bank; (15) southwest Florida; (16) Campeche Bank.
We took 31 samples from different coral colonies and three different species (D. pertusum, M. oculata, a caryophylliid species) that were collected during different cruises. The samples were taken from the uppermost calices after physically cleaning them with a dental drill tool to remove secondary overgrowths. We avoided further cleaning or rinsing with water because studies suggest that structurally substituted Na is readily leached even by distilled water (Ragland et al., 1979). It is possible that organic contents inside the skeleton bias the results as shown in foraminifera (Branson et al., 2016). However, the study on foraminifera shows that the Na∕Ca ratio only significantly varies in POS (primary organic sheet) regions. In corals the COC (centers of calcification) would be an equivalent structure, which we avoided during the sampling process. Furthermore, it has been suggested that these regions only significantly affect bulk sample elemental ratios in very thin-walled foraminifera (Branson et al., 2016). In corals the area of COC is larger (20 % of the total skeleton radius; Rollion-Bard and Blamart, 2015), but the Na∕Ca ratio does not increase in the COC as strongly as it does in the POS areas of foraminifera (Branson et al., 2016; Rollion-Bard and Blamart, 2015). Avoiding the COC areas in bulk samples only reduces the mean Na∕Ca ratio by 0.18 mmol mol−1 (); additional cleaning of organic material is, therefore, not necessary. An additional 14 samples (D. pertusum) were prepared as longitudinal slices through the coral's calice, glued on metal plates. In order to identify elemental heterogeneities within the theca wall, subsamples were taken using a micromill (Merchantec MM-000-134).
2.2 ICP-OES analyses
Elemental ratios were measured by inductively coupled plasma-optical emission spectrometry (ICP-OES). The ICP-OES analysis was carried out with Thermoscientific iCap 6300 dual viewing at Goethe University, Frankfurt. This machine is both capable of measuring axially and radially. Alkali metals (Na) were measured radially on line 589.59 nm, whereas earth alkali metals (Mg, Sr) were measured axially on lines 279.55 and 421.55 nm, respectively. The sample powder (≈140 µg) was dissolved in 500 µL HNO3 (2 %) and 300 µL aliquots were separated. Subsequently 1500 µL of 1.2 mg L−1 yttrium solution was added to each aliquot as an internal standard resulting in 1 mg L−1. The intensity data were background subtracted and standardized internally to Y and normalized to Ca. External standards were mixed from single-element standard solutions to match the typical element concentrations of cold-water corals (cf. Rosenthal et al., 1988). The coral standard JCp-1 (Hathorne et al., 2013; Okai et al., 2002) was measured after every 10th sample to allow for drift correction and monitor measurement quality.
Relative precision of the element/Ca measurements was based on the international calcium-carbonate standard JCp-1 (20 replicates) and amounts to 20.47±0.68 mmol mol−1 Na∕Ca (19.8±0.14 mmol mol−1; Okai et al., 2002), 4.09±0.11 mmol mol−1 Mg∕Ca (4.199±0.065 mmol mol−1; Hathorne et al., 2013; Okai et al., 2002) and 9.36±0.07 mmol mol−1 Sr∕Ca (8.838±0.042 mmol mol−1; Hathorne et al., 2013; Okai et al., 2002). Measurements were conducted in two sessions lasting 10 and 5 h.
2.3 Data processing
Before applying statistics, outliers were removed from the raw data. Outliers were identified by the average±1.5 SD per oceanic region (Norwegian margin, Bay of Biscay–Irish margin, Mediterranean Sea, Red Sea, Gulf of Mexico–Bahamas). The threshold was chosen to eliminate data points <15 mmol mol−1 and >35 mmol mol−1 over a range from 15 to 35 mmol mol−1, which is roughly 5 mmol mol−1 higher and lower than the reported range from a similar study (Rollion-Bard and Blamart, 2015). The profiled samples were additionally checked for values that derive from the COC, which are identifiable through a positively correlating increase in Mg∕Ca and Na∕Ca. The chosen threshold was the mean of the profiled sample + 2 SD of JCp-1. Statistical calculations were conducted with the ORIGIN Pro software suite.
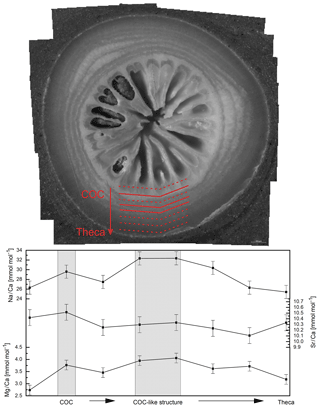
Figure 2Intraindividual element heterogeneities of one sample from Lopphavet (D. pertusum). Shaded gray areas indicate COC and COC-like structures (solid lines in sample picture). Error bars indicate 2 SD of the JCp-1 mean. Within the uncertainty Sr∕Ca ratios show no significant changes throughout the coral, whereas Mg∕Ca and Na∕Ca show variations of 1.25 and 6 mmol mol−1, respectively.
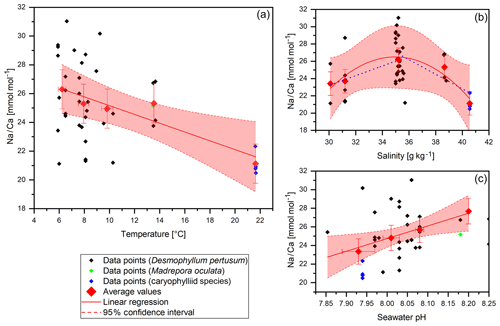
Figure 3Na∕Ca data (without COC) plotted against water temperature, salinity and pH. Red diamonds indicate averaged values for temperature ranges. Temperature ranges are 5–7, 7–9, 9–11, 13–15 and 21–23 ∘C. The x error relates to the SD of the temperature or salinity mean. The y error bars indicate 2 SD of the JCp-1 mean. Red lines are linear regressions of the averaged values with the 95 % confidence interval shaded. Blue dotted lines indicate linear regressions for different salinity ranges.
Spatial distribution patterns show great variations in Na∕Ca ratios through the corals skeleton (Fig. 2). In the COC and COC-like structures (structures that geochemically correspond to COC but morphologically to fibrous deposits) Na∕Ca ratios show significant increases but the amount of increase relative to the mean is not uniform in the sample. Increases range from +2 to +10 mmol mol−1. Mg∕Ca is positively correlated with Na∕Ca in the COC structures but mostly independent from Na∕Ca in the fibrous deposits (FDs). Similar to Na∕Ca, the amplitude of Mg∕Ca in the COC structures is very variable in their amount and ranges from +0.5 to +3 mmol mol−1. Both sodium and magnesium are often enriched in the outermost parts of the theca. Sr∕Ca ratios are mostly stable throughout the theca and seem to be independent from the different skeletal structures. In some samples, there are covariances between Sr∕Ca and Mg∕Ca and Na∕Ca present, but in general they do not appear to be controlled by the skeletal morphology in the same way as Mg∕Ca and Na∕Ca, as shown by their independence from the different skeletal structures.
3.1 Element∕Ca ratios of scleractinian cold-water corals
Na∕Ca ratios vary between 20.49±1.36 (1 SD) mmol mol−1 in the Red Sea and 31.04±1.36 mmol mol−1 in the Norwegian reefs with a mean of 25.22 mmol mol−1 and a standard deviation of 2.8 mmol mol−1 (Fig. 3). The values are in accordance with previous studies on D. pertusum (21.94–28.11 mmol mol−1; Rollion-Bard and Blamart, 2015) but 5 mmol mol−1 higher than reported for zooxanthellate corals (Amiel et al., 1973; Busenberg and Niel Plummer, 1985; Mitsuguchi et al., 2001; Ramos et al., 2004; Swart, 1981). Significant deviations between D. pertusum (n=38), M. oculata (n=2) and the caryophylliid species (n=5) are not observable. A linear correlation between salinity and Na∕Ca over the whole salinity range is not observable, but the present dataset is best described with a second-order polynomial function. Accordingly, there is a positive trend from 30.1 to 35 g kg−1 followed by a negative trend from 35 to 40.5 g kg−1. Linear regressions equal , P=0.072) and , P=0.4). As the P values show, a significant slope is missing in all these regressions. In the case of the polynomial fit the P value shows that the fit is not significantly superior to the .
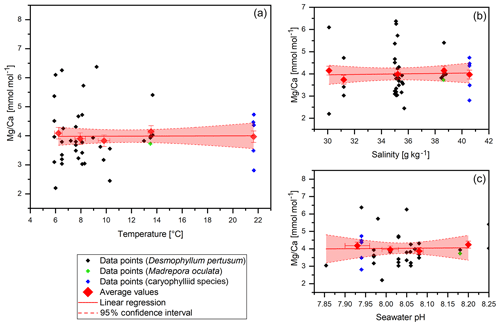
Figure 4Mg∕Ca data (without COC) plotted against water temperature, salinity and pH. Red diamonds indicate averaged values for temperature ranges. Temperature ranges are 5–7, 7–9, 9–11, 13–15 and 21–23 ∘C. The x error relates to the SD of the temperature or salinity mean. The y error bars indicate 2 SD of the JCp-1 mean. Red lines are linear regressions of the averaged values with the 95 % confidence interval shaded.
Na∕Ca and temperature show a significant negative correlation, which is, however, mainly driven by the samples from the highest temperature (Red Sea). The linear regression equals
Temperature and salinity show a positive correlation; accordingly this negative correlation cannot be caused by covariances between salinity and temperature. Corals from the Mediterranean Sea are slightly elevated in their Na∕Ca ratio, but within error they still fit the correlation with both salinity and temperature. Distribution coefficients () at specific temperatures for several different species, including the scleractinian cold-water corals from this study, Porites sp. and M. edulis, show similar values. from this study amounts to , , , and . Distribution coefficients for Porites sp. and M. edulis are (Mitsuguchi et al., 2001) and (Lorens and Bender, 1980), respectively. For comparison, the inorganic distribution coefficient is at 15 ∘C, about 20 % lower (Kinsman, 1970). The results from White (1977) show that the composition of the solution affects the elemental ratios in the precipitate, but in the study from Kinsman (1970) the precipitation happened from seawater. Therefore, it is reasonable to use this data for comparison. A combined regression using the data from this study, the D. pertusum data from Rollion-Bard and Blamart (2015), M. edulis data from Lorens and Bender (1980), and Porites sp. data from Ramos et al. (2004) and Mitsuguchi et al. (2001) equals
Na∕Ca also shows a significant positive correlation with pH of the ambient seawater. Linear regression equals , P=0.017). A negative trend between pH and temperature is visible.
3.2 Mg∕Ca and Sr∕Ca
Mg∕Ca values vary between 2.2±0.2 mmol mol−1 in the Red Sea and 6.38±0.2 mmol mol−1 in the Mediterranean Sea with a mean of 3.99 mmol mol−1 and a standard deviation of 0.97 mmol mol−1 (Fig. 4). Maximum values are higher than the literature states for D. pertusum (2.99–4.72 mmol mol−1; Cohen et al., 2006; Gagnon et al., 2007; Raddatz et al., 2013; Rollion-Bard and Blamart, 2015), but the mean values are well inside the range given in the literature. Significant deviations between D. pertusum, M. oculata and the caryophylliid species are not observable, although there are limited published data for M. oculata and the caryophylliid species. Seawater parameters such as temperature, salinity and pH have no significant effect on Mg∕Ca ratios in the skeleton.
Sr∕Ca values vary between 9.46±0.14 and 10.46±0.14 mmol mol−1 with a mean of 10.1±0.14 mmol mol−1 and a standard deviation of 0.25 mmol mol−1 (Fig. 5). Both maximum and minimum values derive from corals that grew in reefs that are located in the Trondheimfjord. The values are in accordance with previous studies on D. pertusum (9.27–10.05 mmol mol−1; Cohen et al., 2006; Gagnon et al., 2007; Raddatz et al., 2013). Significant deviations between D. pertusum, M. oculata and the caryophylliid species are not observable. Despite the known temperature effect on Sr∕Ca ratios, this effect is not pronounced in this dataset. The correlation shows a strongly deviating slope of −0.015 in comparison to that given in the literature ( ; Raddatz et al., 2013). Linear regressions equal , P=0.03). Sr∕Ca vs. salinity values show a distribution pattern similar to that of Na∕Ca vs. salinity values with the maximum at 35 g kg−1 and descending values at lower and higher salinities, but an AIC (Akaike information criterion) and an F test confirm that a linear fit is better suited. The linear regression equals , P=0.17). P values show that the correlation is not significant.
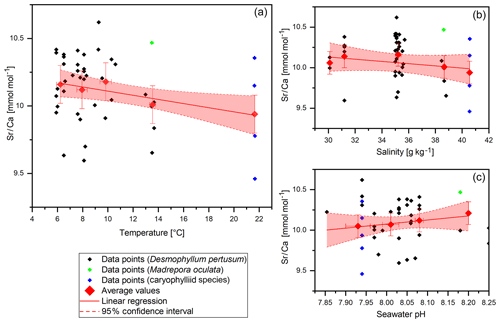
Figure 5Sr∕Ca data (without COC) plotted against water temperature, salinity and pH. Red diamonds indicate averaged values for temperature ranges. Temperature ranges are 5–7, 7–9, 9–11, 13–15 and 21–23 ∘C. The x error relates to the SD of the temperature/salinity mean. The y error bars indicate 2 SD of the JCp-1 mean. Red lines are linear regressions of the averaged values with the 95 % confidence interval shaded.
3.3 Element concentrations in the extracellular calcifying fluid (ECF)
Based on the assumption of a semi-enclosed ECF with seawater leakage and a consequent [Na]ECF similar to [Na]Seawater, it is possible to calculate [Ca]ECF and [Mg]ECF using skeletal Na∕Ca and Mg∕Ca data. Assuming [Na] mmol L−1 (Turekian et al., 2010) and an invariant Na distribution coefficient, [Ca]ECF can be calculated with the following equation:
In order to do so, knowledge of is required. White (1977) reports 1.8– for inorganic aragonite in the four experiments with solution Na∕Ca closest to the natural seawater ratio (∼45 mol mol−1), which would result in predicted aragonite Na∕Ca ratios of 8–18 mmol mol−1, slightly lower than the coral aragonite values we measure. Because this difference may be explained via differences in (e.g.) inorganic and coral aragonite growth rates (Mucci, 1988; White, 1977; Yoshimura et al., 2017) or the presence of organics (Amiel et al., 1973; Cuif et al., 2003; Stolarski, 2003), we adjust our data so that the predicted aragonite Na∕Ca ratios fit our measured ratios by using calculated from the coral samples presented here. As such we cannot presently constrain absolute [Ca]ECF values using this method; however, the aim here is simply to explore whether differences in [Ca]ECF can explain the variance in both our Na∕Ca and Mg∕Ca data. An improved understanding of the inorganic distribution coefficient may enable both precise and accurate ECF reconstructions in the future. Using the method outlined above, we calculate [Ca]ECF values ranging from 7.9 to 12.3 mmol L−1 with a mean of 9.9 mmol L−1. This range is in good agreement with the microsensor studies on Galaxea fascicularis conducted by Al-Horani et al. (2003) (9–11 mmol L−1) by substituting these data into the following equation:
With , calculated from the coral samples presented here, [Mg]ECF can also be calculated. Resulting values range from 32.8 to 104.7 mmol L−1 and a mean of 51.5 mmol L−1 and a median of 46.5 mmol L−1. Results show that the Mg concentration in the ECF is constant with changing Ca concentration.
4.1 Heterogeneities of elemental ratios in scleractinian corals
Ninety percent of the sodium in corals is located in the aragonitic mineral phase, the remaining sodium is bound to organic material and exchangeable sites (Amiel et al., 1973). Magnesium, which covaries with sodium, is not located in the aragonitic phase but either in organic material (20 %–30 %) and a highly disordered inorganic phase such as amorphous calcium carbonate (ACC) (70 %–80 %) (Amiel et al., 1973; Finch and Allison, 2008) or nano domains of Mg-bearing carbonate occluded in the aragonite (Finch and Allison, 2008). A small percentage seems to be also trapped along the (001) surface (Ruiz-Hernandez et al., 2012). Elemental heterogeneities are particularly visible when comparing COC and fibrous deposits (Fig. 2). COC are both chemically and morphologically distinct from the fibrous deposits. While the COC are built by submicron-sized granular crystals (Constantz, 1989), the fibers that build the fibrous zones are not single orthorhombic crystals but elongated composite structures with very fine organo-mineral alternations (Cuif and Dauphin, 1998). Reasons for the different chemical composition are still under debate and include (1) pH variations in the calcifying fluid (Adkins et al., 2003; Holcomb et al., 2009), (2) Rayleigh fractionation (Cohen et al., 2006; Gagnon et al., 2007), (3) kinetic fractionation (McConnaughey, 1989; Sinclair et al., 2006), (4) mixed ion transport through direct seawater transport and ionic pumping (Gagnon et al., 2012), and (5) precipitation from different compartments (Meibom et al., 2004; Rollion-Bard et al., 2010, 2011).
The missing covariance between Sr∕Ca and Mg∕Ca or Na∕Ca ratios excludes Rayleigh fractionation as the main mechanism responsible for the large variances of elemental ratios (Rollion-Bard and Blamart, 2015), as well as mixed ion transport for similar reasons (Rollion-Bard and Blamart, 2015). pH variations and consequent changes in the saturation of the calcifying fluid have been shown to alter Mg∕Ca ratios in corals and abiogenic aragonite (Holcomb et al., 2009) and therefore, could potentially alter Na∕Ca ratios as well. While the pH-elevation at the COC is supported by several studies (McCulloch et al., 2012; Raddatz et al., 2014a; Sinclair et al., 2006), Tambutté et al. (2007) propose that the nanometer-sized spaces between the skeleton and the calicoblastic ectoderm does not allow a modification of the saturation state. Also, studies based on δ11B measurements show that the COC might be an area of lower pH-values compared to the fibrous zones (Blamart et al., 2007; Jurikova et al., 2019; Rollion-Bard et al., 2011). Our data may be explained by different calcification compartments (Meibom et al., 2004; Rollion-Bard et al., 2010, 2011) in combination with kinetic effects caused by rapid calcification rates. Additionally, we propose changing organic contents as a further mechanism that controls elemental ratio differences in the different skeletal parts, visible in the covariance of Mg∕Ca and Na∕Ca ratios throughout the skeleton. However, it is not clear in what way the different precipitation regions are distinct from each other, for example, whether they are characterized by different cell types or different modes of the same cell types (Rollion-Bard et al., 2010). So far, only calicoblasts and desmocytes are known from the aboral ectoderm of corals (Allemand et al., 2011; Tambutté et al., 2007), but calicoblasts show differences in their morphology, ranging from very thin, long and flat to thick and cup like (Tambutté et al., 2007). A major controlling factor on the cell shape is the calcification activity, with flat calicoblasts corresponding to low calcification activity and thick calicoblasts to high calcification activity (Tambutté et al., 2007). These different cell morphologies might be the reason for different types of precipitation: ACC, a proposed precursor phase of aragonite (Von Euw et al., 2017; Rollion-Bard et al., 2010), and granular crystals in the COC regions or organo-mineral fibers in the fibrous deposits. The precipitation of ACC in the COC would certainly explain the enrichment of Mg in these areas, as it is necessary to stabilize the otherwise unstable ACC (Von Euw et al., 2017); however, the relevance of ACC to coral calcification has been questioned as it has so far not been possible to form ACC under carbonate system conditions thought to characterize the calcification space (Evans et al., 2019). Alternatively, the COC are known to be rich in organic material (Cuif et al., 2003; Stolarski, 2003), which would also explain the enrichment of Mg as well as a slight enrichment of Na. However, the amount of Na bound to organic material is not high enough (Amiel et al., 1973) for the enrichment in the COC to be explained solely by high organic contents. Kinetic effects, due to rapid calcification rates, are more likely to be the main control for Na variations in COC and fibrous deposits. Since Na is incorporated into the aragonite lattice by direct substitution with Ca (Okumura and Kitano, 1986; Yoshimura et al., 2017), charge differences occur due to the exchange in divalent Ca with monovalent Na. These charge differences need to be compensated for by lattice defects ( vacancies), which occur more often at higher precipitation rates (Mucci, 1988; White, 1977; Yoshimura et al., 2017). Growth rate effects are also known for the incorporation of Mg into inorganic aragonite, although these effects are more likely to result from crystal surface entrapment of Mg by newly formed aragonite (Gabitov et al., 2008, 2011; Watson, 1996).
Sr∕Ca ratios in the warm-water coral Pocillopora damicornis seem to be largely unaffected by growth rate changes over a range of 1 to over 50 µm d−1 (Brahmi et al., 2012), at least when comparing different skeletal architectures (Fig. 2). This is supported by our data as the observed Sr∕Ca ratios show no significant decrease in the COC or COC-like areas as would be expected from the results of de Villiers et al. (1994) despite the significantly different growth rates in these areas (COC>50–60 µm d−1, FD=1–3 µm d−1; Brahmi et al., 2012). In fact, an increase in the COC is more often but still not regularly visible (Cohen et al., 2006). Consequently, a significant effect of the different skeletal architectures on Sr∕Ca ratios in coralline aragonite can be excluded. Slight increases in the COC, however, can be explained with the great adsorption potential of Sr to organic matter (Chen, 1997; Khani et al., 2012; Kunioka et al., 2006).
4.2 Environmental control on coral Na∕Ca ratios
4.2.1 Salinity
Recently, Na∕Ca ratios in foraminiferal calcite have been suggested as a potential salinity proxy (Allen et al., 2016; Bertlich et al., 2018; Mezger et al., 2016; Wit et al., 2013). Ishikawa and Ichikuni (1984) proposed that the activity of Na in seawater is the primary controlling factor for the incorporation of Na in calcite. However, more recent studies have shown that Na∕Ca in foraminiferal calcite is mainly driven by the seawater Na∕Ca ratio instead of the Na activity when this is the dominant variable (Evans et al., 2018; Hauzer et al., 2018). Species-specific offsets make further biological controls highly plausible.
In this study, no correlation between salinity and Na∕Ca ratios is present (Fig. 3). The positive trend up to 35 g kg−1 followed by a negative trend after 35 g kg−1 can be explained by growth rate changes due to the changing salinity. To our knowledge no studies on the effect of salinity on growth rates have been conducted on D. pertusum, but it is plausible that it shows reduced growth rates in salinities diverging from the biological optimum similar to other marine organisms (e.g., M. edulis; Malone and Dodd, 1967). A specific osmoregulation is probably not needed for CWCs in the mostly salinity-stable habitats they live in (Roberts et al., 2009). Reduced growth rates consequently lower the amount of lattice defects and the amount of possible incorporation sites for sodium (Mucci, 1988; White, 1977; Yoshimura et al., 2017) if bulk extension rates are indeed related to crystal growth rates.
If Na∕Ca ratios in corals are controlled by changes in calcification rate, a calcification rate proxy could be used to correct this effect. Sr∕Ca ratios have been discussed as a possible growth rate proxy (de Villiers et al., 1994) and may be used to determine changes in growth rate. However, our data show that the Sr∕Ca ratios remain constant with changing salinities. Accordingly, concluding from the results of de Villiers et al. (1994), the calcification rate would remain constant over the whole salinity range. It should be noted that higher growth rates do not necessarily imply higher calcification rates or vice versa. A higher growth rate can also be caused by higher organic deposits in the skeleton (Stolarski, 2003). Therefore, a change in calcification cannot necessarily be inferred from changing Sr∕Ca ratios. Still, the effects that growth or calcification rate changes and the different skeletal architectures have on Sr∕Ca ratios in corals are still discussed. There is evidence for positive and negative correlation of Sr∕Ca with growth and calcification rate as well as the different skeletal architectures (Allison and Finch, 2004; Cohen et al., 2006; Kunioka et al., 2006; Raddatz et al., 2013). It still remains unknown why there is no persistent Sr∕Ca variation between the differential skeletal architectures (COC, fibrous deposits) in this study despite being visible in several other studies (Cohen et al., 2006; Gagnon et al., 2007; Raddatz et al., 2013). An explanation could be the low sampling resolution in the profiled samples and possible mixing of COC and fibrous zone material. Further research is needed to evaluate the effects of growth and calcification rates on Sr∕Ca ratios in biogenic carbonates.
4.2.2 Temperature
A temperature control on Na∕Ca ratios has been shown in inorganic precipitated aragonite (White, 1977) and in the planktonic foraminifera G. ruber and G. sacculifer (Mezger et al., 2016), although temperature and salinity covary in that study. Furthermore, Rollion-Bard and Blamart (2015) suggest a possible temperature control on Na∕Ca ratios in the CWC D. pertusum and the warm-water coral Porites sp. However, the temperature sensitivity in inorganically precipitated aragonite is far lower compared to the biogenic aragonite from CWCs including a systematic offset of . Interestingly, other marine carbonates (Porites sp., M. edulis) also fit in the calculated temperature sensitivity. This holds true for biogenic aragonite and biogenic calcite, where M. edulis fits into the temperature sensitivity found by Mezger et al. (2016). A combined regression using the data from Evans et al. (2018), Mezger et al. (2016), and Lorens and Bender (1980) reveals a temperature sensitivity of −0.37 , which is strikingly similar to the sensitivity in aragonite of −0.31 (Fig. 6). The samples that Mezger et al. (2016) used in their study derive from the Red Sea, where a negative correlation between the seawater salinity and seawater temperature exists. They conclude that the salinity effect on Na∕Ca ratios and the covariance between salinity and temperature cause the temperature sensitivity of Na∕Ca ratios. However, it is also possible that the salinity sensitivity is caused by a temperature effect.
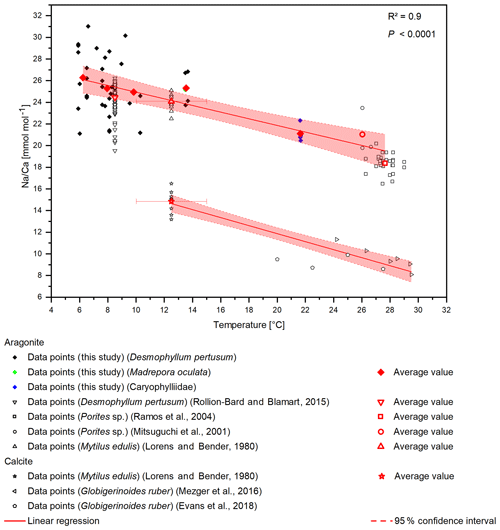
Figure 6Compiled Na∕Ca ratios from different studies. D. pertusum, M. oculata, M. edulis and Porites sp. show a negative linear relation with water temperature. R2 relates only to the aragonitic samples. Calcitic samples from M. edulis and Globigerinoides ruber show the same sensitivity, albeit with an offset of 10 mmol mol−1. Temperature for the data from Lorens and Bender (1980) amounts to the average temperature of the tank the corals were cultivated in, while the error bars show maximum and minimum values.
The apparent offset between inorganically precipitated aragonite and biogenic carbonates further implies a biological control on Na incorporation. In contrast to other elements such as lithium (Montagna et al., 2014), the high correlation between D. pertusum, M. oculata, the caryophylliid species, Porites sp. and M. edulis implies that the Na∕Ca variance introduced by these possibly occurring vital effects appears to be similar for all these species. We suggest that similar Na pathways into the calcifying space exist in foraminifera, mussels and scleractinian warm-water as well as cold-water corals, and temperature exerts a strong control on the activity of these pathways, altering the sodium availability during calcification. Further controls are possibly contributed by temperature-dependent solubility variations in CaCO3 and Na2CO3 and an exothermic Na incorporation mechanism.
Bertlich et al. (2018) proposed that lower temperatures increase the solubility of calcium carbonate and increase the amount of free Ca, leading to higher Na∕Ca ratios at lower temperatures. Yet such a solubility-controlled temperature effect on calcite and aragonite is rather small, whereas the sensitivity to pressure changes is much more pronounced (Pytkowicz and Conners, 1964; Zeebe and Wolf-Gladrow, 2001). Accordingly, the Na∕Ca ratio should also decrease with water depth. Here we do observe a relationship between Na∕Ca ratios and water depth, but at constant temperatures (7.2–7.8 ∘C) there is no effect of water depth (160–280 m) on Na∕Ca ratios. The relationship between depth and Na∕Ca ratios is therefore presumably caused by the positive correlation between water temperature and water depth. A decrease in Na∕Ca ratios with temperatures could also be explained by solubility effects similar to the effects that are discussed to cause the temperature effects on Li∕Ca ratios (Marriott et al., 2004). The solubility of Na2CO3 increases with increasing temperature (Haynes et al., 2016). Again, this would result in decreasing Na∕Ca ratios with increasing temperature because the solubility of Na2CO3 decreases relative to calcium carbonate (Haynes et al., 2016), making it thermodynamically less favorable to incorporate Na. The effects of pressure on the solubility of Na2CO3 cannot be quantified at the moment due to the lack of studies.
Moreover, the temperature effect can also be caused by an exothermic substitution mechanism of Na into the aragonite lattice, similar to the incorporation of Mg in calcite (Mucci and Morse, 1990). If the substitution between Ca and Na is exothermic, consequently the incorporation of Na is favored at lower temperatures. However, there is to our knowledge, no study available that contains enthalpy data for this reaction. While the proposed mechanism by Bertlich et al. (2018) can be excluded as an explanation for the temperature sensitivity of Na∕Ca ratios, the other explanations are equally plausible in terms of the existing studies. Still, the differences in the temperature sensitivity between inorganic precipitated aragonite and biogenic aragonite require further biological controls to explain this deviation.
As an alternative, we explore whether temperature-dependent Na membrane pathways can explain temperature effects on aragonitic Na∕Ca ratios. There are several enzymes and ion pumps known that constitute sodium pathways through the membrane of the calcifying space. ATPase are known from the tropical coral Galaxea fascicularis (Ip and Lim, 1991), Na∕Ca ion pumps are suggested to exist in Galaxea fascicularis and Tubastraea faulkneri (Marshall, 1996). ATPase was found in the bivalve species M. edulis and Limecola balthica (Pagliarani et al., 2006; Wang and Fisher, 1999) as well as Na∕Mg ion pumps in Ruditapes philippinarum and Mytilus galloprovincialis (Pagliarani et al., 2006). Whether these enzymes exist in D. pertusum is unknown, but since corals possess a nervous system (Chen et al., 2008) and D. pertusum shows a reaction to electrical stimulation (Shelton, 1980) at least the existence of ATPase must be assumed. However, it remains unclear if this enzyme participates in the modification of the calcifying fluid. The participation of Na∕Ca ion pumps is also plausible, since it would result in higher Ca concentrations in the calcifying space, which would aid the calcification process due to the high transport capacity (Carafoli et al., 2001). Membrane calcium pumps on the other hand are better suited to transport Ca from a compartment with low Ca concentrations, which is not applicable when considering seawater as the source compartment (Wang et al., 1992). Since the activity of enzymes is a function of temperature (Sizer, 2006), a temperature control of the ion concentration in the calcifying fluid has to be considered. Rising temperatures would increase the activity of the particular enzyme following the Arrhenius equation (Arrhenius, 1896) and consequently lower the Na concentration in the calcifying space. Unfortunately, it is impossible to quantify these effects from the data at hand because the optimum temperature and activation energy is not enzyme specific but further controlled by enzyme and substrate purity and the presence of inhibitors or activators. Specific research is needed to identify the particular enzyme in these corals as well as to determine the rate of ion exchange, although we note that an enzymatic control on aragonitic Na∕Ca ratios does not necessarily imply a temperature control. In addition, besides a temperature control, there is also a pH control on enzyme activity (Trivedi and Danforth, 1966). While a positive correlation between Na∕Ca and seawater pH is present in the samples utilized here, it is not possible to determine if this is caused by pH-controlled enzymatic activity or due to an increased calcification rate. Higher seawater pH would cause higher calcification fluid pH, which would consequently also increase the aragonite saturation in the calcifying fluid (McCulloch et al., 2012). The degree of pH elevation in the coral calcifying space would, therefore, decrease, ultimately conserving energy (≈10 %/−0.1 pHSW), which can be used for ATP (adenosine triphosphate)-dependent transport proteins, pumping more Ca or and leading to faster calcification (McCulloch et al., 2012). It is also possible that the apparent sensitivity of Na∕Ca to pH changes is caused by the negative covariance of pH and temperature.
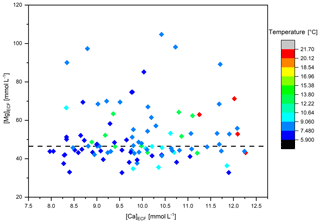
Figure 7Calcium and Magnesium concentration in the ECF of the investigated corals. The color of the data points indicates the ambient water temperature, which increases with increasing Ca concentrations. The dashed line indicates the median of the Mg concentration in the ECF.
Admittedly, the above discussion is only viable under the assumption of a closed calcifying space with a much lower [Na]ECF than [Na]Seawater. In the case of an open or semi-enclosed calcifying space with [Na]ECF close or equal to [Na]Seawater, the amount of Na removed by enzymes or other ion pumps is far too low to cause any significant changes in the composition of the calcifying fluid with regards to Na. In combination with the low distribution coefficient, changes in the Na concentration of the ECF cannot cause the high variability of the skeletal Na∕Ca ratios. Since there is evidence for an at least semi-enclosed calcifying space (Tambutté et al., 2011), we also consider this option. As described in Sect. 3.3 it is possible to calculate the Mg concentration of the ECF under the assumption of seawater leakage into the calcifying space (Adkins et al., 2003; Gagnon et al., 2012) and a resulting approximately constant Na concentration. Based on this hypothesis, and the calculations defined in Eqs. (3) and (4), we show that the Mg concentration in the ECF is constant, but with changing Ca concentration (Fig. 7). There is a large degree of scatter in the [Mg]ECF reconstructions (Fig. 7), which we suggest is unlikely to represent real changes in the ECF [Mg] as it is difficult to envisage a purpose for elevating [Mg]ECF above the [Mg] of seawater given that it plays an inhibitory role in calcium carbonate precipitation by acting antagonistic to the calcium transport (Okazaki, 1956; Swart, 1981; Yamazato, 1966). It may be that the scatter above seawater values is derived from the presence of organic material, as a small positive bias in measured coral Mg∕Ca would result in a large overestimation of [Mg]ECF. Crucially however, we find that [Mg]ECF does not change as a function of [Ca]ECF, with the implication that in this model, changing skeletal Mg∕Ca and Na∕Ca ratios are not caused by changes in the Mg or Na concentration of the ECF but rather are entirely explicable through changes in the Ca concentration. Again, this might be caused by temperature-dependent enzyme or ion-pump activity. Higher temperatures would then cause a higher exchange capacity (Elias et al., 2001), leading to higher Ca- (Fig. 7) and marginally lower Na concentrations in the ECF and consequently lower Mg∕Ca and Na∕Ca ratios. An elevation of [Ca] in the ECF and the calcifying front is also supported by recent studies from Decarlo et al. (2018) and Sevilgen et al. (2019), who conducted Raman spectroscopic, δ11B and microsensor measurements on Pocillopora damicornis, Acropora yongei and Stylophora pistilla. The results furthermore indicate the involvement of transcellular pathways to elevate the Ca concentration in the ECF (Sevilgen et al., 2019).
Even though a clear correlation between temperature and Na∕Ca is present, the usefulness of Na∕Ca ratios is greatly reduced due to the large intraspecies variability. At 6 ∘C Na∕Ca ratios vary by up to 20 % and even up to 10 % in a single polyp. There are several possible reasons for this variability. One is the insufficient removal of the COC during the sampling process. Due to the high growth rate and high organic content in the COC, elements, such as Mg, Na and Li, are enriched, whereas others, like U, are depleted (Gagnon et al., 2007; Raddatz et al., 2013, 2014a; Robinson et al., 2014; Rollion-Bard and Blamart, 2014, 2015). This effect would also explain the high Na∕Ca values in corals from the Mediterranean Sea (T=13.56 ∘C). It is possible that during the sampling process a larger amount of the fibrous deposits was removed in comparison to the other samples. This would cause a greater effect of the enriched COC material and therefore cause higher Na∕Ca ratios. It is therefore preferable to use in situ techniques (laser ablation, EPMA (electron probe microanalyzer), SIMS (secondary ion mass spectrometry)) instead of solution-based chemistry and profile measurements through the theca wall instead of bulk samples because it allows for a better recognition and removal of values that derive from COC or COC-like structures. Seasonality could be also a factor responsible for a percentage of the variation, but the sampled corals originate from depths where seasonality presumably only plays a minor role. An estimated seasonal temperature change of 4 ∘C only suffices to explain 1 mmol mol−1 variation but not the observed variation of 10 mmol mol−1. From this, it can be inferred that there must be other controls on Na∕Ca ratios besides water temperature. Diurnal temperature fluctuations caused by internal waves as found, for example, in the Rockall Trough are also not high enough (3 ∘C) to explain these variations (Mienis et al., 2007). As mentioned in Sect. 4.1, calcification rates constitute a major control on Na∕Ca ratios by controlling the amount of incorporation sites for Na (Kitano et al., 1975; Mucci, 1988; White, 1977; Yoshimura et al., 2017). Therefore, numerous second-order control factors could cause variations in the Na∕Ca ratios by controlling the calcification rate. These second-order controls include nutrient availability and supply, changes in the carbonate system, coral fitness, and many more. Some of these controls (nutrient supply, coral fitness) have the potential to vary with a high spatial resolution and consequently cause great variations in Na∕Ca ratios even if the samples derive from the same colony.
4.3 Na∕Mg ratios to overcome vital effects
Even though a good correlation of R2=0.9 between Na∕Ca and temperature is observable in our data, the samples from the Mediterranean Sea (T=13.54 ∘C) show slightly elevated Na∕Ca ratios. Reasons for this are discussed in Sect. 4.2. Rollion-Bard and Blamart (2015) proposed Na∕Mg ratios to overcome these effects. The basis for this is that Na∕Ca and Mg∕Ca ratios could be controlled by similar vital effects such as growth rate and the amount of organic content. Combining Na∕Ca and Mg∕Ca ratios reduces the impact of these effects, though the temperature sensitivity of Na∕Ca ratios is preserved as Mg∕Ca ratios show no apparent correlation with temperature (Fig. 8). The resulting regression between Na∕Mg and temperature yields the following equation:
The application of Na∕Mg in this study does not significantly improve the regression, as it removes the inverse correlation between 6 and 10 ∘C. This might be caused by covariance between sodium and magnesium. It was shown that magnesium in the parent solution reduces the amount of incorporated sodium (Okumura and Kitano, 1986). However, utilizing Na∕Mg ratios removes the striking irregularity at 13.54 ∘C. The large scatter, however, is not significantly reduced, which implies further vital effects that cannot be resolved with this technique. To overcome this, the mean of at least 10 analyzed samples should be used to obtain reliable results. If these prerequisites are fulfilled, Na∕Mg and Na∕Ca could provide a means of reconstructing temperature. This could prove useful especially for temperature reconstructions in deep time on organisms that are extinct today. In this case the nearest living relative principle is used, which potentially introduces large errors. Further research on different aragonitic and calcitic organisms is necessary to detect further species that show the same temperature sensitivity. If it is shown that Na∕Ca and/or Na∕Mg ratios show no species-specific variations, empirical calibrations could be applied to extinct species for which proxy calibrations are not possible. Still though, when using Na∕Ca for temperature reconstructions, changes in seawater have to be considered that would lead to an underestimation of temperature at high pH. However, Na∕Mg shows no sensitivity to changes in seawater pH, so by combining Na∕Ca and Mg∕Ca ratios, this effect can be ignored.
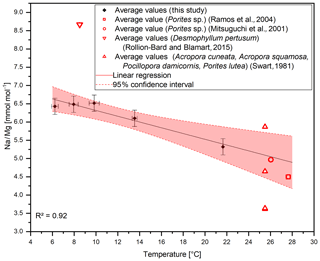
Figure 8Na∕Mg ratios from this study vs. water temperature. Na∕Mg ratios can be used to correct for the sampling of varying proportions of different domains. The y error bars relate to 2 SD of the JCp-1 measurements. The x error bars relate to 1 SD of the temperature mean for the chosen temperature ranges.
The data at hand do not support the utility of Na∕Ca in cold-water corals as a salinity proxy as proposed by Wit et al. (2013) and Mezger et al. (2016) for biogenic calcite. While there is a positive trend between Na∕Ca and salinity when excluding data from the Red Sea samples, it is not statistically significant.
A significant inverse correlation between temperature and Na∕Ca ratios is present, which cannot be explained by a covariance of temperature and salinity (cf. Mezger et al., 2016). Two additional organisms, Porites sp. (Mitsuguchi et al., 2001; Ramos et al., 2004) and M. edulis (Lorens and Bender, 1980) fit in this regression too. The mechanism of sodium incorporation, therefore, appears to be consistent between these three species. We propose temperature-dependent activity in Na ion or Ca ion transport proteins as the underlying mechanism behind the observable correlation. While the intraspecies and intraindividual variation is large, Na∕Ca can be well correlated to environmental variables when based on the averages of several specimens. Therefore, Na∕Ca ratios might provide a temperature proxy that is usable for a wide variety of aragonitic organisms and maybe even calcitic organisms. As proposed by Rollion-Bard and Blamart (2015), Na∕Mg ratios can be used to correct for inconsistencies during the sampling process.
All of the data used are found in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-3565-2019-supplement.
JR and NS designed the experiments and conducted the measurements. JR, AF, LB, AR and VL provided samples and environmental data. NS prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We are grateful to all cruise captains, crew members and cruise participants of research cruises POS325, POS391, POS455, POS 385, M61, POS625, B10-17a/b, 64PE284, M70/1, COR2, MSM20-4, KRSE2013 and RV Gunnerus. Ship time of RV Belgica was provided by BELSPO and RBINS–OD Nature.
FIERCE is financially supported by the Wilhelm and Else Heraeus Foundation, which is gratefully acknowledged. This is FIERCE contribution no. 002.
This research has been supported by the DFG (grant nos. RI 598/4-1, ECHO RA 2516-1), the Swiss National Science Foundation (grant no. 200021_149247) and the Wilhelm and Else Heraeus Foundation.
This paper was edited by Aldo Shemesh and reviewed by William Gray and one anonymous referee.
Adkins, J. F., Boyle, E. A., Curry, W. B., and Lutringer, A.: Stable isotopes in deep-sea corals and a new mechanism for “vital effects”, Geochim. Cosmochim. Ac., 67, 1129–1143, https://doi.org/10.1016/S0016-7037(02)01203-6, 2003.
Al-Horani, F. A., Al-Moghrabi, S. M., and De Beer, D.: The mechanism of calcification and its relation to photosynthesis and respiration in the scleractinian coral Galaxea fascicularis, Mar. Biol., 142, 419–426, https://doi.org/10.1007/s00227-002-0981-8, 2003.
Allemand, D., Tambutté, É., Zoccola, D. and Tambutté, S.: Coral Calcification, Cells to Reefs, in: Coral Reefs: An Ecosystem in Transition, pp. 119–150, Springer, Dordrecht, the Netherlands, 2011.
Allen, K. A., Hönisch, B., Eggins, S. M., Haynes, L. L., Rosenthal, Y., and Yu, J.: Trace element proxies for surface ocean conditions: A synthesis of culture calibrations with planktic foraminifera, Geochim. Cosmochim. Ac., 193, 197–221, https://doi.org/10.1016/j.gca.2016.08.015, 2016.
Allison, N. and Finch, A. A.: High-resolution Sr∕Ca records in modern Porites lobata corals: Effects of skeletal extension rate and architecture, Geochem. Geophy. Geosy., 5, Q05001, https://doi.org/10.1029/2004GC000696, 2004.
Amiel, A. J., Friedman, G. M., and Miller, D. S.: Distribution and nature of incorporation of trace elements in modern aragonitic corals, Sedimentology, 20, 47-64, https://doi.org/10.1111/j.1365-3091.1973.tb01606.x, 1973.
Anagnostou, E., Sherrell, R. M., Gagnon, A., LaVigne, M., Field, M. P., and McDonough, W. F.: Seawater nutrient and carbonate ion concentrations recorded as P∕Ca, Ba∕Ca, and U∕Ca in the deep-sea coral Desmophyllum dianthus, Geochim. Cosmochim. Ac., 75, 2529–2543, https://doi.org/10.1016/j.gca.2011.02.019, 2011.
Anagnostou, E., Huang, K. F., You, C. F., Sikes, E. L., and Sherrell, R. M.: Evaluation of boron isotope ratio as a pH proxy in the deep sea coral Desmophyllum dianthus: Evidence of physiological pH adjustment, Earth Planet. Sc. Lett., 349–350, 251–260, https://doi.org/10.1016/j.epsl.2012.07.006, 2012.
Arrhenius, S.: XXXI. On the influence of carbonic acid in the air upon the temperature of the ground, Dublin Philos. Mag. J. Sci., London, Edinburgh, 41, 237–276, https://doi.org/10.1080/14786449608620846, 1896.
Bertlich, J., Nürnberg, D., Hathorne, E. C., de Nooijer, L. J., Mezger, E. M., Kienast, M., Nordhausen, S., Reichart, G.-J., Schönfeld, J., and Bijma, J.: Salinity control on Na incorporation into calcite tests of the planktonic foraminifera Trilobatus sacculifer – evidence from culture experiments and surface sediments, Biogeosciences, 15, 5991–6018, https://doi.org/10.5194/bg-15-5991-2018, 2018.
Bett, B. J.: UK Atlantic Margin Environmental Survey: Introduction and overview of bathyal benthic ecology, Cont. Shelf Res., 21, 917–56, https://doi.org/10.1016/S0278-4343(00)00119-9, 2001.
Blamart, D., Rollion-Bard, C., Meibom, A., Cuif, J. P., Juillet-Leclerc, A., and Dauphin, Y.: Correlation of boron isotopic composition with ultrastructure in the deep-sea coral Lophelia pertusa: Implications for biomineralization and paleo-pH, Geochem. Geophy. Geosy., 8, 1–11, https://doi.org/10.1029/2007GC001686, 2007.
Bollmann, J., Herrle, J. O., Cortés, M. Y., and Fielding, S. R.: The effect of sea water salinity on the morphology of Emiliania huxleyi in plankton and sediment samples, Earth Planet. Sc. Lett., 284, 320–328, https://doi.org/10.1016/j.epsl.2009.05.003, 2009.
Brahmi, C., Kopp, C., Domart-Coulon, I., Stolarski, J., and Meibom, A.: Skeletal growth dynamics linked to trace-element composition in the scleractinian coral Pocillopora damicornis, Geochim. Cosmochim. Ac., 99, 146–158, https://doi.org/10.1016/j.gca.2012.09.031, 2012.
Branson, O., Bonnin, E. A., Perea, D. E., Spero, H. J., Zhu, Z., Winters, M., Hönisch, B., Russell, A. D., Fehrenbacher, J. S., and Gagnon, A. C.: Nanometer-Scale Chemistry of a Calcite Biomineralization Template: Implications for Skeletal Composition and Nucleation, P. Natl. Acad. Sci. USA, 113, 12934–12939, https://doi.org/10.1073/pnas.1522864113, 2016.
Büscher, J. V., Form, A. U., and Riebesell, U.: Interactive Effects of Ocean Acidification and Warming on Growth, Fitness and Survival of the Cold-Water Coral Lophelia pertusa under Different Food Availabilities, Front. Mar. Sci., 4, 1–14, https://doi.org/10.3389/fmars.2017.00101, 2017.
Busenberg, E. and Niel Plummer, L.: Kinetic and thermodynamic factors controlling the distribution of and Na+ in calcites and selected aragonites, Geochim. Cosmochim. Ac., 49, 713–725, https://doi.org/10.1016/0016-7037(85)90166-8, 1985.
Carafoli, E., Santella, L., Branca, D., and Brini, M.: Generation, control, and processing of cellular calcium signals, Crit. Rev. Biochem. Mol. Biol., 36, 107–260, https://doi.org/10.1080/20014091074183, 2001.
Chen, E., Stiefel, K. M., Sejnowski, T. J., and Bullock, T. H.: Model of traveling waves in a coral nerve network, J. Comp. Physiol. A Neuroethol. Sensory, Neural, Behav. Physiol., 194, 195–200, https://doi.org/10.1007/s00359-007-0305-z, 2008.
Chen, J.-P.: Batch and Contunuous Adsorption of Stontium by Plant Root Tissues, Bioresour. Technol., 60, 185–189, https://doi.org/10.1016/S0960-8524(97)00021-7, 1997.
Cohen, A. L., Gaetani, G. A., Lundälv, T., Corliss, B. H., and George, R. Y.: Compositional variability in a cold-water scleractinian, Lophelia pertusa: New insights into “vital effects”, Geochem. Geophy. Geosy., 7, Q12004, https://doi.org/10.1029/2006GC001354, 2006.
Constantz, B. R.: Skeletal Organization in Caribbean Acropora Spp. (Lamarck), in: Origin, Evolution, and Modern Aspects of Biomineralization in Plants and Animals, pp. 175–199, Springer, Boston, MA, USA, 1989.
Cuif, J.-P. and Dauphin, Y.: Microstructural and physico-chemical characterization of `centers of calcification' in septa of some Recent scleractinian corals, Paläontologische Zeitschrift, 72, 257–270, https://doi.org/10.1007/BF02988357, 1998.
Cuif, J. P., Dauphin, Y. Y., Doucet, J., Salome, M., and Susini, J.: XANES mapping of organic sulfate in three scleractinian coral skeletons, Geochim. Cosmochim. Ac., 67, 75–83, https://doi.org/10.1016/S0016-7037(02)01041-4, 2003.
Decarlo, T., Comeau, S., Cornwall, C., McCulloch, M., and Edward, C.: Coral resistance to ocean acidification linked to increased calcium at the site of calcification, P. Roy. Soc. B-Biol. Sci., 285, 20180564, https://doi.org/10.1098/rspb.2018.0564, 2018.
de Villiers, S., Shen, G. T., and Nelson, B. K.: The Sr∕Ca-temperature relationship in coralline aragonite: Influence of variability in (Sr∕Ca)Seawater and skeletal growth parameters, Geochim. Cosmochim. Ac., 58, 197–208, https://doi.org/10.1016/0016-7037(94)90457-X, 1994.
Druffel, E. R. M.: Geochemistry of corals: Proxies of past ocean chemistry, ocean circulation, and climate, P. Natl. Acad. Sci. USA, 94, 8354–8361, https://doi.org/10.1073/pnas.94.16.8354, 1997.
Dullo, W. C., Flögel, S., and Rüggeberg, A.: Cold-water coral growth in relation to the hydrography of the Celtic and Nordic European continental margin, Mar. Ecol. Prog. Ser., 371, 165–176, https://doi.org/10.3354/meps07623, 2008.
Elderfield, H. and Ganssen, G.: Past temperature and δ18O of surface ocean waters inferred from foraminiferal Mg∕Ca ratios, Nature, 405, 442–445, https://doi.org/10.1038/35013033, 2000.
Elderfield, H., Ferretti, P., Greaves, M., Crowhurst, S. J., McCave, I. N., Hodell, D. A., and Piotrowski, A. M.: Evolution of ocean temperature, Science, 337, 704–709, https://doi.org/10.1594/PANGAEA.786205, 2012.
Elias, C. L., Xue, X. H., Marshall, C. R., Omelchenko, A., Hryshko, L. V., and Tibbits, G. F.: Temperature dependence of cloned mammalian and salmonid cardiac Na(+)/Ca(2+) exchanger isoforms., Am. J. Physiol. Cell Physiol., 281, C993–C1000, https://doi.org/10.1111/j.1432-1033.1984.tb08031.x, 2001.
Evans, D., Müller, W., and Erez, J.: Assessing foraminifera biomineralisation models through trace element data of cultures under variable seawater chemistry, Geochim. Cosmochim. Ac., 236, 198–217, https://doi.org/10.1016/j.gca.2018.02.048, 2018.
Evans, D., Webb, P., Penkman, K. E. H., Kroger, R., and Allison, N.: The characteristics and biological relevance of inorganic amorphous calcium carbonate (ACC) precipitated from seawater, Cryst. Growth Des., 4300–4313, https://doi.org/10.1021/acs.cgd.9b00003, 2019.
Finch, A. A. and Allison, N.: Mg structural state in coral aragonite and implications for the paleoenvironmental proxy, Geophys. Res. Lett., 35, 1–5, https://doi.org/10.1029/2008GL033543, 2008.
Flögel, S., Dullo, W. C., Pfannkuche, O., Kiriakoulakis, K., and Rüggeberg, A.: Geochemical and physical constraints for the occurrence of living cold-water corals, Deep-Sea Res. Pt. II, 99, 19–26, https://doi.org/10.1016/j.dsr2.2013.06.006, 2014.
Form, A. U. and Riebesell, U.: Acclimation to ocean acidification during long-term CO2 exposure in the cold-water coral Lophelia pertusa, Glob. Chang. Biol., 18, 843–853, https://doi.org/10.1111/j.1365-2486.2011.02583.x, 2012.
Freiwald, A.: Reef-Forming Cold-Water Corals, in Ocean Margin Systems, pp. 365–385, Springer, Berlin, Heidelberg, 2002.
Freiwald, A. and Roberts, J. M. (Eds.): Cold-Water Corals and Ecosystems, Springer, Berlin, Heidelberg, 2005.
Freiwald, A., Beuck, L., Rüggeberg, A., Taviani, M., and Hebbeln, D.: The White Coral Community in the Central Mediterranean Sea Revealed by ROV Surveys, Oceanography, 22, 58–74, https://doi.org/10.5670/oceanog.2009.06, 2009.
Gabitov, R. I., Gaetani, G. A., Watson, E. B., Cohen, A. L., and Ehrlich, H. L.: Experimental determination of growth rate effect on U6+ and Mg2+ partitioning between aragonite and fluid at elevated U6+ concentration, Geochim. Cosmochim. Ac., 72, 4058–4068, https://doi.org/10.1016/j.gca.2008.05.047, 2008.
Gabitov, R. I., Schmitt, A. K., Rosner, M., McKeegan, K. D., Gaetani, G. A., Cohen, A. L., Watson, E. B., and Harrison, T. M.: In situ δ7Li, Li∕Ca, and Mg∕Ca analyses of synthetic aragonites, Geochem. Geophys. Geosyst., 12, Q03001, https://doi.org/10.1029/2010GC003322, 2011.
Gagnon, A. C., Adkins, J. F., Fernandez, D. P., and Robinson, L. F.: Sr∕Ca and Mg∕Ca vital effects correlated with skeletal architecture in a scleractinian deep-sea coral and the role of Rayleigh fractionation, Earth Planet. Sc. Lett., 261, 280–295, https://doi.org/10.1016/j.epsl.2007.07.013, 2007.
Gagnon, A. C., Adkins, J. F., and Erez, J.: Seawater transport during coral biomineralization, Earth Planet. Sc. Lett., 329–330, 150–161, https://doi.org/10.1016/j.epsl.2012.03.005, 2012.
Gordon, C. M., Carr, R. A., and Larson, R. E.: the Influence of Environmental Factors on the Sodium and Manganese Content of Barnacle Shells, Limnol. Oceanogr., 15, 461–466, https://doi.org/10.4319/lo.1970.15.3.0461, 1970.
Hathorne, E. C., Gagnon, A., Felis, T., Adkins, J., Asami, R., Boer, W., Caillon, N., Case, D., Cobb, K. M., Douville, E., DeMenocal, P., Eisenhauer, A., Garbe-Schönberg, D., Geibert, W., Goldstein, S., Hughen, K., Inoue, M., Kawahata, H., Kölling, M., Cornec, F. L., Linsley, B. K., McGregor, H. V., Montagna, P., Nurhati, I. S., Quinn, T. M., Raddatz, J., Rebaubier, H., Robinson, L., Sadekov, A., Sherrell, R., Sinclair, D., Tudhope, A. W., Wei, G., Wong, H., Wu, H. C., and You, C.-F.: Interlaboratory study for coral Sr∕Ca and other element/Ca ratio measurements, Geochem. Geophy. Geosy., 14, 3730–3750, https://doi.org/10.1002/ggge.20230, 2013.
Hauzer, H., Evans, D., Müller, W., Rosenthal, Y., and Erez, J.: Calibration of Na partitioning in the calcitic foraminifer Operculina ammonoides under variable Ca concentration: Toward reconstructing past seawater composition, Earth Planet. Sc. Lett., 497, 80–91, https://doi.org/10.1016/j.epsl.2018.06.004, 2018.
Haynes, W. M., Lide, D. R., and Bruno, T. J.: CRC Handbook of chemistry and physics: a ready-reference book of chemical and physical data, CRC Press, Boca Raton, Florida, 2016.
Henry, L.-A. and Roberts, J. M.: Global Biodiversity in Cold-Water Coral Reef Ecosystems, in Marine Animal Forests, pp. 1–21, Springer International Publishing, Cham, 2016.
Holcomb, M., Cohen, A. L., Gabitov, R. I., and Hutter, J. L.: Compositional and morphological features of aragonite precipitated experimentally from seawater and biogenically by corals, Geochim. Cosmochim. Ac., 73, 4166–4179, https://doi.org/10.1016/j.gca.2009.04.015, 2009.
Ip, Y. K. and Lim, A. L. L.: Are calcium and strontium transported by the same mechanism in the hermatypic coral Galaxey fascicularis?, J. Exp. Biol., 159, 507–513, 1991.
Ishikawa, M. and Ichikuni, M.: Uptake of sodium and potassium by calcite, Chem. Geol., 42, 137–146, https://doi.org/10.1016/0009-2541(84)90010-X, 1984.
Israelson, C. and Buchardt, B.: Strontium and oxygen isotopic composition of East Greenland rivers and surface waters: Implication for palaeoenvironmental interpretation, Palaeogeogr. Palaeocl., 153, 93–104, https://doi.org/10.1016/S0031-0182(99)00068-1, 1999.
Jurikova, H., Liebetrau, V., Raddatz, J., Fietzke, J., Trotter, J., Rocholl, A., Krause, S., McCulloch, M., Rüggeberg, A., and Eisenhauer, A.: Boron isotope composition of the cold-water coral Lophelia pertusa along the Norwegian margin: Zooming into a potential pH-proxy by combining bulk and high-resolution approaches, Chem. Geol., 513, 143–152, https://doi.org/10.1016/j.chemgeo.2019.01.005, 2019.
Khani, M. H., Pahlavanzadeh, H., and Alizadeh, K.: Biosorption of strontium from aqueous solution by fungus Aspergillus terreus, Environ. Sci. Pollut. Res., 19, 2408–2418, https://doi.org/10.1007/s11356-012-0753-z, 2012.
Kinsman, D.: Trace cations in aragonite, Abstr. Geol. Soc. Am., 2, 596–597, 1970.
Kiriakoulakis, K., Fisher, E., Wolff, G. A., Freiwald, A., Grehan, A., and Roberts, J. M.: Lipids and nitrogen isotopes of two deep-water corals from the North-East Atlantic: initial results and implications for their nutrition, in: Cold-Water Corals and Ecosystems, pp. 715–729, Springer-Verlag, Berlin/Heidelberg, 2005.
Kiriakoulakis, K., Freiwald, A., Fisher, E., and Wolff, G. A.: Organic matter quality and supply to deep-water coral/mound systems of the NW European Continental Margin, Int. J. Earth Sci., 96, 159–170, https://doi.org/10.1007/s00531-006-0078-6, 2007.
Kitano, Y., Okumura, M., and Idogaki, M.: Incorporation of sodium, chloride and sulfate with calcium carbonate., Geochem. J., 9, 75–84, https://doi.org/10.2343/geochemj.9.75, 1975.
Kunioka, D., Shirai, K., Takahata, N., Sano, Y., Toyofuku, T., and Ujiie, Y.: Microdistribution of Mg∕Ca, Sr∕Ca, and Ba∕Ca ratios in Pulleniatina obliquiloculata test by using a NanoSIMS: Implication for the vital effect mechanism, Geochem. Geophys. Geosyst., 7, Q12P20, doi:10.1029/2006GC001280, 2006.
Lear, C., Elderfield, H., and Wilson, P.: Cenozoic Deep-Sea Temperatures and Global Ice Volumes from Mg∕Ca in Benthic Foraminiferal Calcite, Science, 287, 269–272, https://doi.org/10.1126/science.287.5451.269, 2000.
Lewis, E. and Wallace, D. W.: R: Program developed for CO2 system calculations ORNL/CDIAC-105, Carbon Dioxide Inf. Anal. CentreOak Ridge Natl. Lab. US Dep. Energy, Oak Ridge, Tennessee, 1998.
Locarnini, R. A., Mishonov, A. V, Antonov, J. I., Boyer, T. P., Garcia, H. E., Baranova, O. K., Zweng, M. M., Paver, C. R., Reagan, J. R., Johnson, D. R., Hamilton, M., Seidov, D., and Levitus, S.: World ocean atlas 2013, Volume 1, Temperature, edited by: O. C. L. National Oceanographic Data Center (U.S.) and N. E. S. United States Data, and Information Service, https://doi.org/10.7289/V55X26VD, 2013.
Lorens, R. B. and Bender, M. L.: The impact of solution chemistry on Mytilus edulis calcite and aragonite, Geochim. Cosmochim. Ac., 44, 1265–1278, https://doi.org/10.1016/0016-7037(80)90087-3, 1980.
Malone, P. G. and Dodd, J. R.: Temperature and salinity effects on calcification rate in Mytilus edulis and its paleoecological implications, Limnol. Oceanogr., 12, 432–436, https://doi.org/10.4319/lo.1967.12.3.0432, 1967.
Marriott, C. S., Henderson, G. M., Belshaw, N. S., and Tudhope, A. W.: Temperature dependence of δ7Li, δ44Ca and Li∕Ca during growth of calcium carbonate, Earth Planet. Sc. Lett., 222, 615–624, https://doi.org/10.1016/j.epsl.2004.02.031, 2004.
Marshall, A. T.: Calcification in hermatypic and ahermatypic corals, Science, 271, 637–639, https://doi.org/10.1126/science.271.5249.637, 1996.
McConnaughey, T.: 13C and 18O isotopic disequilibrium in biological carbonates: I. Patterns, Geochim. Cosmochim. Ac., 53, 151–162, https://doi.org/10.1016/0016-7037(89)90282-2, 1989.
McCulloch, M., Trotter, J., Montagna, P., Falter, J., Dunbar, R., Freiwald, A., Försterra, G., López Correa, M., Maier, C., Rüggeberg, A., and Taviani, M.: Resilience of cold-water scleractinian corals to ocean acidification: Boron isotopic systematics of pH and saturation state up-regulation, Geochim. Cosmochim. Ac., 87, 21–34, https://doi.org/10.1016/j.gca.2012.03.027, 2012.
Meibom, A., Cuif, J. P., Hillion, F., Constantz, B. R., Juillet-Leclerc, A., Dauphin, Y., Watanabe, T., and Dunbar, R. B.: Distribution of magnesium in coral skeleton, Geophys. Res. Lett., 31, 1–4, https://doi.org/10.1029/2004GL021313, 2004.
Mertens, K. N., Ribeiro, S., Bouimetarhan, I., Caner, H., Combourieu Nebout, N., Dale, B., De Vernal, A., Ellegaard, M., Filipova, M., Godhe, A., Goubert, E., Grøsfjeld, K., Holzwarth, U., Kotthoff, U., Leroy, S. A. G., Londeix, L., Marret, F., Matsuoka, K., Mudie, P. J., Naudts, L., Peña-Manjarrez, J. L., Persson, A., Popescu, S. M., Pospelova, V., Sangiorgi, F., van der Meer, M. T. J., Vink, A., Zonneveld, K. A. F., Vercauteren, D., Vlassenbroeck, J., and Louwye, S.: Process length variation in cysts of a dinoflagellate, Lingulodinium machaerophorum, in surface sediments: Investigating its potential as salinity proxy, Mar. Micropaleontol., 70, 54–69, https://doi.org/10.1016/j.marmicro.2008.10.004, 2009.
Mezger, E. M., de Nooijer, L. J., Boer, W., Brummer, G. J. A., and Reichart, G. J.: Salinity controls on Na incorporation in Red Sea planktonic foraminifera, Paleoceanography, 31, 1562–1582, https://doi.org/10.1002/2016PA003052, 2016.
Mienis, F., de Stigter, H. C., White, M., Duineveld, G., de Haas, H., and van Weering, T. C. E.: Hydrodynamic controls on cold-water coral growth and carbonate-mound development at the SW and SE Rockall Trough Margin, NE Atlantic Ocean, Deep-Sea Res. Pt. I, 54, 1655–1674, https://doi.org/10.1016/j.dsr.2007.05.013, 2007.
Mitsuguchi, T., Matsumoto, E., Abe, O., Uchida, T., and Isdale, P. J.: Mg∕Ca thermometry in coral skeletons, Science, 274, 961–963, https://doi.org/10.1126/science.274.5289.961, 1996.
Mitsuguchi, T., Uchida, T., Matsumoto, E., Isdale, P. J., and Kawana, T.: Variations in Mg∕Ca, Na∕Ca, and Sr∕Ca ratios of coral skeletons with chemical treatments: implications for carbonate geochemistry, Geochim. Cosmochim. Ac., 65, 2865–2874, https://doi.org/10.1016/S0016-7037(01)00626-3, 2001.
Montagna, P., McCulloch, M., Douville, E., López Correa, M., Trotter, J., Rodolfo-Metalpa, R., Dissard, D., Ferrier-Pagès, C., Frank, N., Freiwald, A., Goldstein, S., Mazzoli, C., Reynaud, S., Rüggeberg, A., Russo, S., and Taviani, M.: Li∕Mg systematics in scleractinian corals: Calibration of the thermometer, Geochim. Cosmochim. Ac., 132, 288–310, https://doi.org/10.1016/j.gca.2014.02.005, 2014.
Mucci, A.: Manganese uptake during calcite precipitation from seawater: Conditions leading to the formation of a pseudokutnahorite, Geochim. Cosmochim. Ac., 52, 1859–1868, https://doi.org/10.1016/0016-7037(88)90009-9, 1988.
Mucci, A. and Morse, J.: Chemistry of low-temperature abiotic calcites: Experimental studies on coprecipitation, stability, and fractionation, Rev. Aquat. Sci., 3, 217–254, 1990.
Okai, T., Suzuki, A., Kawahata, H., Terashima, S., and Imai, N.: Preparation of a New Geological Survey of Japan Geochemical Reference Material: Coral JCp-1, Geostand. Geoanalytical Res., 26, 95–99, https://doi.org/10.1111/j.1751-908X.2002.tb00627.x, 2002.
Okazaki, K.: SKELETON FORMATION OF SEA URCHIN LARVAE. I. EFFECT OF CA CONCENTRATION OF THE MEDIUM, Biol. Bull., 110, 320–333, https://doi.org/10.2307/1538838, 1956.
Okumura, M. and Kitano, Y.: Coprecipitation of alkali metal ions with calcium carbonate, Geochim. Cosmochim. Ac., 50, 49–58, https://doi.org/10.1016/0016-7037(86)90047-5, 1986.
Pagliarani, A., Bandiera, P., Ventrella, V., Trombetti, F., Pirini, M., and Borgatti, A. R.: Response to alkyltins of two Na+-dependent ATPase activities in Tapes philippinarum and Mytilus galloprovincialis, Toxicol. Vitr., 20, 1145–1153, https://doi.org/10.1016/j.tiv.2006.02.006, 2006.
Pytkowicz, R. M. and Conners, D. N.: High pressure solubility of calcium carbonate in seawater, Science, 144, 840–841, https://doi.org/10.1126/science.144.3620.840, 1964.
Raddatz, J., Liebetrau, V., Rüggeberg, A., Hathorne, E., Krabbenhöft, A., Eisenhauer, A., Böhm, F., Vollstaedt, H., Fietzke, J., Correa, M. L., Freiwald, A., and Dullo, W.: Stable Sr-isotope, Sr∕Ca, Mg∕Ca, Li∕Ca and Mg∕Li ratios in the scleractinian cold-water coral Lophelia pertusa, Chem. Geol., 352, 143–152, https://doi.org/10.1016/j.chemgeo.2013.06.013, 2013.
Raddatz, J., Rüggeberg, A., Flögel, S., Hathorne, E. C., Liebetrau, V., Eisenhauer, A., and Dullo, W.-Chr.: The influence of seawater pH on U∕Ca ratios in the scleractinian cold-water coral Lophelia pertusa, Biogeosciences, 11, 1863–1871, https://doi.org/10.5194/bg-11-1863-2014, 2014a.
Raddatz, J., Rüggeberg, A., Liebetrau, V., Foubert, A., Hathorne, E. C., Fietzke, J., Eisenhauer, A., and Dullo, W. C.: Environmental boundary conditions of cold-water coral mound growth over the last 3 million years in the Porcupine Seabight, Northeast Atlantic, Deep-Sea Res. Pt. II, 99, 227–236, https://doi.org/10.1016/j.dsr2.2013.06.009, 2014b.
Raddatz, J., Liebetrau, V., Trotter, J., Rüggeberg, A., Flögel, S., Dullo, W. C., Eisenhauer, A., Voigt, S., and McCulloch, M.: Environmental constraints on Holocene cold-water coral reef growth off Norway: Insights from a multiproxy approach, Paleoceanography, 31, 1350–1367, https://doi.org/10.1002/2016PA002974, 2016.
Ragland, P. C., Pilkey, O. H., and Blackwelder, B. W.: Diagenetic changes in the elemental composition of unrecrystallized mollusk shells, Chem. Geol., 25, 123–134, https://doi.org/10.1016/0009-2541(79)90088-3, 1979.
Ramos, A. A., Inoue, Y., and Ohde, S.: Metal contents in Porites corals: Anthropogenic input of river run-off into a coral reef from an urbanized area, Okinawa, Mar. Pollut. Bull., 48, 281–294, https://doi.org/10.1016/j.marpolbul.2003.08.003, 2004.
Roberts, J. M.: Reefs of the Deep: The Biology and Geology of Cold-Water Coral Ecosystems, Science, 312, 543–547, https://doi.org/10.1126/science.1119861, 2006.
Roberts, J. M., Wheeler, A., Freiwald, A., and Cairns, S.: Cold-Water Corals, Cambridge University Press, Cambridge, 2009.
Robinson, L. F., Adkins, J. F., Frank, N., Gagnon, A. C., Prouty, N. G., Brendan Roark, E., and van de Flierdt, T.: The geochemistry of deep-sea coral skeletons: A review of vital effects and applications for palaeoceanography, Deep-Sea Res. Pt. II, 99, 184–198, https://doi.org/10.1016/j.dsr2.2013.06.005, 2014.
Roder, C., Berumen, M. L., Bouwmeester, J., Papathanassiou, E., Al-Suwailem, A., and Voolstra, C. R.: First biological measurements of deep-sea corals from the Red Sea, Sci. Rep.-UK, 3, 2802, https://doi.org/10.1038/srep02802, 2013.
Rollion-Bard, C. and Blamart, D.: SIMS method and examples of applications in coral biomineralization, in: Biomineralization sourcebook: Characterization of Biominerals and Biomimetic Materials, edited by: DiMasi, E. and Gower, L., pp. 321–336, Taylor & Francis Group, Abingdon, 2014.
Rollion-Bard, C. and Blamart, D.: Possible controls on Li, Na, and Mg incorporation into aragonite coral skeletons, Chem. Geol., 396, 98–111, https://doi.org/10.1016/j.chemgeo.2014.12.011, 2015.
Rollion-Bard, C., Blamart, D., Cuif, J. P., and Dauphin, Y.: In situ measurements of oxygen isotopic composition in deep-sea coral, Lophelia pertusa: Re-examination of the current geochemical models of biomineralization, Geochim. Cosmochim. Ac., 74, 1338–1349, https://doi.org/10.1016/j.gca.2009.11.011, 2010.
Rollion-Bard, C., Blamart, D., Trebosc, J., Tricot, G., Mussi, A., and Cuif, J. P.: Boron isotopes as pH proxy: A new look at boron speciation in deep-sea corals using11B MAS NMR and EELS, Geochim. Cosmochim. Ac., 75, 1003–1012, https://doi.org/10.1016/j.gca.2010.11.023, 2011.
Rosenthal, Y., Field, M. P., and Sherrell, R. M.: Precise Determination of Element/Calcium Ratios in Calcareous Samples Using Sector Field Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 71, 3248–3253, https://doi.org/10.1021/ac981410x, 1999.
Rucker, J. B. and Valentine, J. W.: Salinity response of trace element concentration in Crassostrea virginica, Nature, 190, 1099–1100, https://doi.org/10.1038/1901099a0, 1961.
Rüggeberg, A., Flögel, S., Dullo, W. C., Hissmann, K., and Freiwald, A.: Water mass characteristics and sill dynamics in a subpolar cold-water coral reef setting at Stjernsund, northern Norway, Mar. Geol., 282, 5–12, https://doi.org/10.1016/j.margeo.2010.05.009, 2011.
Ruiz-Hernandez, S. E., Grau-Crespo, R., Almora-Barrios, N., Wolthers, M., Ruiz-Salvador, A. R., Fernandez, N., and De Leeuw, N. H.: Mg∕Ca partitioning between aqueous solution and aragonite mineral: A molecular dynamics study, Chem.-A Eur. J., 18, 9828–9833, https://doi.org/10.1002/chem.201200966, 2012.
Schouten, S., Ossebaar, J., Schreiber, K., Kienhuis, M. V. M., Langer, G., Benthien, A., and Bijma, J.: The effect of temperature, salinity and growth rate on the stable hydrogen isotopic composition of long chain alkenones produced by Emiliania huxleyi and Gephyrocapsa oceanica, Biogeosciences, 3, 113–119, https://doi.org/10.5194/bg-3-113-2006, 2006.
Sevilgen, D. S., Venn, A. A., Hu, M. Y., Tambutté, E., de Beer, D., Planas-Bielsa, V., and Tambutté, S.: Full in vivo characterization of carbonate chemistry at the site of calcification in corals, Sci. Adv., 5, eaau7447, https://doi.org/10.1126/sciadv.aau7447, 2019.
Shelton, G. A. B.: LOPHELIA pertusa (l.): Electrical conduction and behaviour in a deep-water coral, J. Mar. Biol. Assoc. UK, 60, 517–528, https://doi.org/10.1017/S0025315400028538, 1980.
Shirai, K., Kusakabe, M., Nakai, S., Ishii, T., Watanabe, T., Hiyagon, H., and Sano, Y.: Deep-sea coral geochemistry: Implication for the vital effect, Chem. Geol., 224, 212–222, https://doi.org/10.1016/j.chemgeo.2005.08.009, 2005.
Sinclair, D. J., Williams, B., and Risk, M.: A biological origin for climate signals in corals – Trace element “vital effects” are ubiquitous in Scleractinian coral skeletons, Geophys. Res. Lett., 33, 1–5, https://doi.org/10.1029/2006GL027183, 2006.
Sizer, I. W.: Effects of temperature on enzyme kinetics, in: Advances in Enzymology and Related Areas of Molecular Biology, pp. 35–62, Wiley-Blackwell, Hoboken, 2006.
Stolarski, J.: Three-dimensional micro- and nanostructural characteristics of the scleractinian coral skeleton: A biocalcification proxy, Acta Palaeontol. Pol., 48, 497–530, 2003.
Swart, P. K.: The strontium, magnesium and sodium composition of recent scleractinian coral skeletons as standards for palaeoenvironmental analysis, Palaeogeogr. Palaeocl., 34, 115–136, https://doi.org/10.1016/0031-0182(81)90060-2, 1981.
Tambutté, E., Allemand, D., Zoccola, D., Meibom, A., Lotto, S., Caminiti, N., and Tambutté, S.: Observations of the tissue-skeleton interface in the scleractinian coral Stylophora pistillata, Coral Reefs, 26, 517–529, https://doi.org/10.1007/s00338-007-0263-5, 2007.
Tambutté, S., Holcomb, M., Ferrier-Pagès, C., Reynaud, S., Tambutté, É., Zoccola, D., and Allemand, D.: Coral biomineralization: From the gene to the environment, J. Exp. Mar. Bio. Ecol., 408, 58–78, https://doi.org/10.1016/j.jembe.2011.07.026, 2011.
Taviani, M., Remia, A., Corselli, C., Freiwald, A., Malinverno, E., Mastrototaro, F., Savini, A., and Tursi, A.: First geo-marine survey of living cold-water Lophelia reefs in the Ionian Sea (Mediterranean basin), Facies, 50, 409–417, https://doi.org/10.1007/s10347-004-0039-0, 2005.
Trivedi, B. and Danforth, W. H.: Effect of pH on the kinetics of frog muscle phosphofructokinase, J. Biol. Chem., 241, 4110–4112, https://doi.org/10.2196/jmir.1752, 1966.
Turekian, K. K., Steele, J. H., and Thorpe, S. A.: Marine Chemistry & Geochemistry, A Derivative Of Encyclopedia Of Ocean Sciences, Academic Press, Cambridge, Massachusetts, 2010.
van der Meer, M. T. J., Baas, M., Rijpstra, W. I. C., Marino, G., Rohling, E. J., Sinninghe Damsté, J. S., and Schouten, S.: Hydrogen isotopic compositions of long-chain alkenones record freshwater flooding of the Eastern Mediterranean at the onset of sapropel deposition, Earth Planet. Sc. Lett., 262, 594–600, https://doi.org/10.1016/j.epsl.2007.08.014, 2007.
Von Euw, S., Zhang, Q., Manichev, V., Murali, N., Gross, J., Feldman, L. C., Gustafsson, T., Flach, C., Mendelsohn, R., and Falkowski, P. G.: Biological control of aragonite formation in stony corals, Science, 356, 933–938, https://doi.org/10.1126/science.aam6371, 2017.
Wang, K., Villalobo, A., and Roufogalis, B.: The plasma membrane calcium pump: a multiregulated transporter, Trends Cell Biol., 2, 46–52, 1992.
Wang, W. X. and Fisher, N. S.: Effects of calcium and metabolic inhibitors on trace element uptake in two marine bivalves, J. Exp. Mar. Bio. Ecol., 236, 149–164, https://doi.org/10.1016/S0022-0981(98)00195-6, 1999.
Watson, E. B.: Surface enrichment and trace-element uptake during crystal growth, Geochim. Cosmochim. Ac., 60, 5013–5020, https://doi.org/10.1016/S0016-7037(96)00299-2, 1996.
Weldeab, S., Lea, D. W., Schneider, R. R., and Andersen, N.: Centennial scale climate instabilities in a wet early Holocene West African monsoon, Geophys. Res. Lett., 34, 1–6, https://doi.org/10.1029/2007GL031898, 2007.
White, A. F.: Sodium and potassium coprecipitation in aragonite, Geochim. Cosmochim. Ac., 41, 613–625, https://doi.org/10.1016/0016-7037(77)90301-5, 1977.
Wit, J. C., de Nooijer, L. J., Wolthers, M., and Reichart, G. J.: A novel salinity proxy based on Na incorporation into foraminiferal calcite, Biogeosciences, 10, 6375–6387, https://doi.org/10.5194/bg-10-6375-2013, 2013.
Yamazato, K.: Calcification in a solitary coral, Fungia scutaria Lamarck in relation to environmental factors, Bulletin of Science & Engineering Division, University of Ryukyus, Mathematics & natural sciences, 13, 59–122, 1966.
Yoshimura, T., Tamenori, Y., Suzuki, A., Kawahata, H., Iwasaki, N., Hasegawa, H., Nguyen, L. T., Kuroyanagi, A., Yamazaki, T., Kuroda, J., and Ohkouchi, N.: Altervalent substitution of sodium for calcium in biogenic calcite and aragonite, Geochim. Cosmochim. Ac., 202, 21–38, https://doi.org/10.1016/j.gca.2016.12.003, 2017.
Zeebe, R. E. and Wolf-Gladrow, D. A.: CO2 in seawater?: equilibrium, kinetics, isotopes, available at: http://epic.awi.de/4276/ (last access: 22 August 2018), 2001.
Zonneveld, K. A. F., Hoek, P. R., Brinkhuis, H., and Willems, H.: Geographical distributions of organic-walled dinoflagellate cysts in surficial sediments of the Benguela upwelling region and their relationship to upper ocean conditions, Prog. Oceanogr., 48, 25–72, https://doi.org/10.1016/S0079-6611(00)00047-1, 2001.
Zweng, M. M., Reagan, J. R., Antonov, J. I., Locarnini, R. A., Mishonov, A. V, Boyer, T. P., Garcia, H. E., Baranova, O. K., Johnson, D. R., Seidov, D., Biddle, M. M., and Levitus, S.: World ocean atlas 2013. Volume 2, Salinity, edited by: O. C. L. National Oceanographic Data Center (U.S.) and N. E. S. United States Data, and Information Service, https://doi.org/10.7289/V5251G4D, 2013.