Isotopic fractionation of carbon during uptake by phytoplankton across the South Atlantic subtropical convergence

The stable isotopic composition of particulate organic carbon (δ¹³C_POC) in the surface waters of the global ocean can vary with the aqueous CO₂ concentration ([CO_2(aq)]) and affects the trophic transfer of carbon isotopes in the marine food web. Other factors such as cell size, growth rate and carbon concentrating mechanisms decouple this observed correlation. Here, the variability in δ¹³C_POC is investigated in surface waters across the south subtropical convergence (SSTC) in the Atlantic Ocean, to determine carbon isotope fractionation (ε_p) by phytoplankton and the contrasting mechanisms of carbon uptake in the subantarctic and subtropical water masses. Our results indicate that cell size is the primary determinant of δ¹³C_POC across the Atlantic SSTC in summer. Combining cell size estimates with CO₂ concentrations, we can accurately estimate ε_p within the varying surface water masses in this region. We further utilize these results to investigate future changes in ε_p with increased anthropogenic carbon availability. Our results suggest that smaller cells, which are prevalent in the subtropical ocean, will respond less to increased [CO_2(aq)] than the larger cells found south of the SSTC and in the wider Southern Ocean. In the subantarctic water masses, isotopic fractionation during carbon uptake will likely increase, both with increasing CO₂ availability to the cell, but also if increased stratification leads to decreases in average community cell size. Coupled with decreasing δ¹³C of [CO_2(aq)] due to anthropogenic CO₂ emissions, this change in isotopic fractionation and lowering of δ¹³C_POC may propagate through the marine food web, with implications for the use of δ¹³C_POC as a tracer of dietary sources in the marine environment.

1 Introduction

The marine environment is undergoing rapid changes as atmospheric carbon dioxide increases, with the greatest change occurring in the upper ocean (Gruber et al., 1999; Sabine and Tanhua, 2010). Anthropogenic carbon inputs and the increase of greenhouse gases in the atmosphere are causing ocean warming (Cheng et al., 2019), changes to upper ocean stratification (Bopp et al., 2001; Capotondi et al., 2012), and altered distributions of nutrients and carbon (Khatiwala et al., 2013; Quay et al., 2003; Gruber et al., 2019). Marine phytoplankton are diverse, and are already responding to ocean warming, including changes to productivity (Behrenfeld et al., 2006; Arrigo and van Dijken, 2015), the length of growing season (Henson et al., 2018) and phytoplankton cell size (Finkel et al., 2010). Alterations to phytoplankton diversity and/or productivity will likely have knock-on effects on marine food web dynamics. Investigating such changes in remote marine environments requires tracers that can pinpoint shifts in dietary sources. The δ¹³C of organic carbon in marine plants and animals can provide information on carbon sources to the base of the food web (Peterson and Fry, 1987). Improved understanding of ¹³C systematics will lead to reliable use of this proxy in future predictions.

During photosynthesis, marine phytoplankton take up aqueous CO₂ ([CO_2(aq)]) and convert it into organic carbon. In this process the lighter isotope (¹²C) is preferentially consumed, leaving the residual aqueous pool increasingly enriched in the heavier isotope. The stable carbon isotopic composition of marine phytoplankton is determined by the uptake fractionation (ε_p), which is influenced by ambient environmental conditions and phytoplankton cell physiology. Therefore, the δ¹³C of marine plankton can indicate the controlling mechanisms behind carbon uptake which led to its use as a potential proxy for reconstructing the surface water [CO_2(aq)] of past climates (Freeman and Hayes, 1992; Jasper et al., 1994).

The δ¹³C of particulate organic carbon (δ¹³C_POC) varies over relatively large oceanic areas and has been found to inversely correlate with [CO_2(aq)] (the principal carbon source) in surface waters (Rau et al., 1991; Sackett et al., 1965). High [CO_2(aq)] can lead to greater discrimination against ¹³C during phytoplankton uptake. The low-temperature waters of the Southern Ocean and their high [CO_2(aq)] lead to negative δ¹³C excursions in marine plankton in this region (Sackett et al., 1964). Although this relationship holds true to first order over global datasets (Rau et al., 1989), in many marine environments the local variability in δ¹³C_POC can be attributed to other mechanisms.

Phytoplankton growth rate, cell size and cell geometry are also important controls on δ¹³C_POC in surface waters (Bidigare et al., 1997; Francois et al., 1993; Popp et al., 1998; Laws et al., 1995; Villinski et al., 2000). These ecophysiological factors decouple the observed relationship between δ¹³C_POC and [CO_2(aq)], limiting the reliability of δ¹³C_POC as a palaeoproxy. This is particularly true in areas where [CO_2(aq)] is lower or less variable, as other factors have been found to be more important for determining the degree of isotopic fractionation (Henley et al., 2012; Lourey et al., 2004; Popp et al., 1998). In field studies, smaller-sized phytoplankton have been measured with lower δ¹³C_POC compared with larger cells such as diatoms, particularly in fast growing blooms (Hansman and Sessions, 2016; Rau et al., 1990). These findings indicate that the factors determining δ¹³C_POC may vary as one transitions contrasting marine environments.

The carbon fixation pathway can vary amongst phytoplankton species through the assimilation of bicarbonate via active transport as opposed to diffusive CO₂ uptake. In general, more negative excursions in δ¹³C_POC are associated with diffusive entry of CO₂, whereas carbon concentrating mechanisms (CCMs) or diffusive limitation of carbon supply lead to more positive δ¹³C_POC (Raven et al., 2008). When [CO_2(aq)] falls below a critical level, the active transport of CO₂ into the cell can enrich δ¹³C_POC, but this has been found to be proportional to carbon demand or growth rate (Popp et al., 1998). CCMs occur in most cyanobacteria, increasing CO₂ at the site of rubisco activity (Raven et al., 2008).

All of the processes that alter the uptake fractionation of [CO_2(aq)] will ultimately determine the isotopic variability in carbon at the base of the marine food web. Thus, the factors that are sensitive to ongoing climate change need to be better understood in order to accurately use δ¹³C_POC as a tracer of dietary sources and in food web studies.

In this study we investigate the mechanisms for isotopic fractionation in δ¹³C_POC resulting from carbon uptake and biological production in the upper ocean. We report data from a full transect across the south subtropical convergence (SSTC) in the Atlantic Basin, which captures a region of productive open ocean. The cruise sampled both subantarctic and subtropical regimes with contrasting limiting nutrient environments and community structure (Browning et al., 2014). The [CO_2(aq)] and δ¹³C_DIC (stable isotopes of carbon in dissolved inorganic carbon) parameters, along with chlorophyll a and other diagnostic phytoplankton pigments are used collectively to disentangle the processes that fractionate δ¹³C_POC as a response to the algal uptake of [CO_2(aq)] across this region. We find the community cell size, as estimated using the phytoplankton pigment composition, to be the primary determinant of δ¹³C_POC across the SSTC, with smaller cell sizes increasing the carbon availability for fixation. The results from the field study are used to understand/infer how δ¹³C_POC in this region may change into the future with ongoing climate change.

2 Methods

2.1 Carbon concentrations and isotopic measurements

Samples were collected onboard the RRS James Cook between December 2011 and February 2012 (JC068), as part of the GEOTRACES A10 transect of the South Atlantic. An east to west transect was conducted with upper ocean sampling at each station. Standard CTD measurements and water sampling were performed using a stainless steel rosette equipped with a full sensor array and 24×20 L OTE bottles. Salinity, temperature and depth were measured using a CTD system (Seabird 911+), and salinity was calibrated on-board with discrete samples using an Autosal 8400B salinometer (Guildline).

Measurements of total CO₂ (TCO₂) and total alkalinity (TA) were carried out at sea within 24 h of collection. Samples were warmed in a water bath at 25 ^∘C for 1 h before analysis. A set volume of the sample was acidified by addition of excess 10 % phosphoric acid, which converts all inorganic C species to CO₂. This is carried into the coulometric cell by an inert carrier gas (CO₂-free N₂ that is first passed through a magnesium perchlorate and Ascarite II scrubber), and a coulometric titration determines the amount of CO₂, which is equal to TCO₂. Small increments of 0.1 M hydrochloric acid are added to a separate subsample and the amount added to reach the carbonic acid equivalence point is equal to the TA (Humphreys, 2015). Regular measurements of both TCO₂ and TA were made from batch 114 certified reference material (CRM) from Andrew G. Dickson (Scripps Institution of Oceanography; Dickson et al., 2003) and used to calibrate the results. To obtain the final results in micromoles per kilogram ( µmol kg⁻¹), a correction for density (ρ) due to salinity variation was then applied using salinity measured from Niskin bottle samples (Zeebe et al., 2001). Duplicate samples were taken from the same Niskin bottle and analysed consecutively.

[CO_2(aq)] was calculated from measured TA and DIC using CO₂SYS v1.1 (Lewis and Wallace, 1998; van Heuven et al., 2011). Equilibrium constants were evaluated following Mehrbach et al. (1973) for carbonic acid and Dickson (1990) for bisulfate, and the boron : chlorinity ratio of Lee et al. (2010) was used.

Samples for the measurement of the stable isotopes of carbon in dissolved inorganic carbon (δ¹³C_DIC) were collected from the stainless steel rosette. Samples were taken into 250 mL glass bottles with ground glass stoppers. Water was drained directly into the sample bottle using silicone tubing to the bottom of the bottle to eliminate bubble formation. The bottle and cap were rinsed once with water from the rosette bottle before overflowing the sample bottle by at least one bottle volume before withdrawing the silicone tube, carefully avoiding bubble formation. Next, the stopper was placed in the bottle and then removed so that 2.5 mL of sample could be removed to allow for thermal expansion, and 50 µL of 100 % HgCl₂ was added to halt any biological activity. The stoppers and the inside of the neck of the bottles were dried before the stopper, coated with vacuum grease, was replaced and secured with a foam insert and plastic cover. The samples were then shaken to disperse the HgCl₂ and stored at 4 ^∘C until analysis. Samples were measured using a Thermo MAT253 stable isotope mass spectrometer. ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ was determined from δ¹³C_DIC and absolute temperature (T_k), using ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}={\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{DIC}}+\mathrm{23.644}-\mathrm{9701.5}/T_k$ (Rau et al., 1996).

Particulate samples were collected onto ashed, pre-weighed GF/F microfibre filters (0.7 µm pore size, 25 mm diameter). Two to four litres of water was collected from the biological rosette in the surface 400 m depending on the chlorophyll levels detected by the CTD fluorometer. The samples were pressure-filtered simultaneously using an eight-way manifold system. Once the total volume for each depth was filtered, the filters were extracted from the filter holder, placed in labelled aluminium foil and dried at 50^∘ for ∼12 h. Once dried, filters were folded and stored in plastic sample bags at −20 ^∘C. To remove carbonates prior to analysis, filters were wetted with Milli-Q water, fumed with 70 % HCl for 48 h in a desiccator, dried at 50 ^∘C and then folded into tin capsules. The filters were analysed using a Carlo Erba NA 2500 elemental analyser in-line with a VG PRISM III isotope ratio mass spectrometer for elemental POC/PN as well as δ¹³C_POC and δ¹⁵N_PN. All δ¹³C_POC data presented in this study are in the delta per mil notation vs. V-PDB (‰_VPDB).

2.2 Cell size calculations

Phytoplankton pigments were analysed by high-performance liquid chromatography (HPLC) analysis. Between 500 and 2000 mL of seawater was filtered through 25 mm GF/F filters. The filters were placed in 2 mL cryovials and flash frozen in liquid nitrogen. Next, filters were transferred to a −80 ^∘C freezer for longer-term storage. Pigment extracts were analysed with a reverse-phase HPLC column using a Thermo Finnigan HPLC instrument at the National Oceanography Centre Southampton (Gibb et al., 2000). Phytoplankton pigments were extracted in 3 to 5 mL of 90 % acetone by ultrasonication and centrifugation. Extracts were loaded into a chilled autosampler prior to injection into the HPLC system. Pigments were detected by absorbance at 440 nm and identified by diagnostic retention times. The resulting pigment assemblage was used to estimate the fractional contribution of the three size classes (micro-, nano- and picophytoplankton) to the total chlorophyll a pigment concentration (Bricaud et al., 2004; Uitz et al., 2008).

3 Results

3.1 Oceanographic setting

The SSTC is characterized by the convergence of contrasting biogeochemical regimes. In the colder Subantarctic Surface Waters (SASW), located south of the SSTC, concentrations of macronutrients are elevated and primary production is primarily limited by iron availability (Browning et al., 2014). The subtropical waters to the north of the SSTC are associated with the South Atlantic subtropical gyre and are principally macronutrient limited, or possibly macronutrient–iron co-limited (Browning et al., 2014, 2017). The three subtropical water masses, the Agulhas Current (AC), the South Atlantic Central Water (SACW) and the Brazil Current (BC), can be readily identified by warmer temperatures and higher salinities; the influence of the Malvinas Current (MC) separates the core of the SACW and BC (Fig. 1).

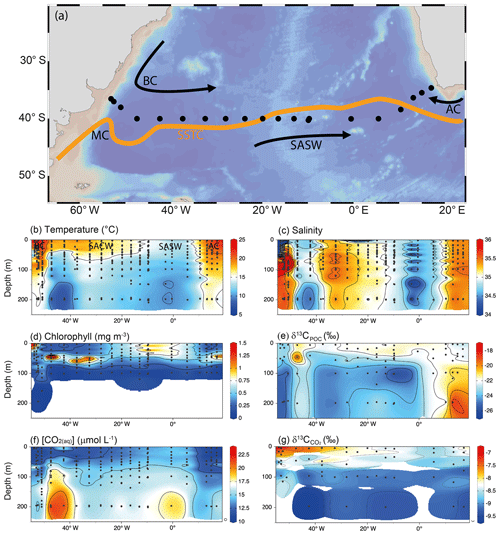
Figure 1 Map and longitudinal transects across the south subtropical convergence. (a) Map of the study region, in which the orange line depicts the subtropical front (SST = 16 ^∘C, from Browning et al., 2014). Longitudinal transects of (b) temperature, (c) salinity, (d) chlorophyll, (e) δ¹³C_POC, (f) [CO_2(aq)] and (g) ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ in the upper 250 m. The water masses are identified in (b): BC refers to the Brazil Current, SACW refers to the South Atlantic Central Water, SASW refers to the Subantarctic Surface Water and AC refers to the Agulhas Current. The interpolation in (b)–(g) was produced using ODV-weighted average gridding (Schlitzer, 2018).

Higher [CO_2(aq)] is associated with the lower temperatures of the SASW. Across the zonal transect, higher ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ is associated with lower [CO₂(aq)] and warmer temperatures of the subtropical water masses (Fig. 1). ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ is highest on the western boundary in the BC and in the Rio de la Plata outflow. δ¹³C_POC across 40^∘ S ranges from −25 ‰ to −20 ‰ indicating a predominantly marine source (e.g. Rau et al., 1989).

Satellite images of surface chlorophyll concentrations across this region indicate elevated standing stocks of phytoplankton in comparison with the South Atlantic gyre and subantarctic waters further south (Browning et al., 2014). Chlorophyll concentrations peak between austral spring and summer, and the south subtropical convergence (SSTC) moves south as a result of the expansion of the Agulhas and Brazil currents. Depth profiles showed that the subantarctic waters have elevated and uniform chlorophyll concentrations (0.2–0.9 mg m⁻³). Conversely, in the subtropical waters, a deep chlorophyll maximum is formed, with low surface concentrations of chlorophyll (<0.2 mg m⁻³) and macronutrients (Tuerena et al., 2015).

3.2 δ¹³C_POC variability

If δ¹³C_POC is principally determined by changing ambient [CO_2(aq)] and is not influenced by cell physiology, such as growth rates and cell size, the δ¹³C_POC can often be predicted by sea surface temperature variability (Rau et al., 1989). In this study, δ¹³C_POC is compared to a model from Rau et al. (1996), which predicts the carbon isotope fractionation (ε_p) and δ¹³C_POC where photosynthesis is strictly based on the passive diffusion of CO₂ into marine phytoplankton cells.

Modelled δ¹³C_POC was calculated using the diffusion model of Rau et al. (1996), where

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{POC}}=& {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}-{\mathit{\epsilon }}_{\mathrm{f}}+\left({\mathit{\epsilon }}_f-{\mathit{\epsilon }}_{\mathrm{d}}\right){\displaystyle \frac{Q_{\mathrm{s}}}{\left[{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}\right]}}\\ & \left({\displaystyle \frac{r}{D_T\left(\mathrm{1}+\frac{r}{r_k}\right)}}+{\displaystyle \frac{\mathrm{1}}{P}}\right).\end{array}\end{array}$$

Here ε_f represents intracellular enzymatic isotope fractionation (‰), ε_d represents diffusive isotope fractionation of CO_2(aq) in seawater (‰), Q_s represents CO₂ uptake rate per unit cell surface area (mol C m⁻² s⁻¹), [CO_2(aq)] refers to ambient CO_2(aq) concentration (mol m⁻³), r is the cell radius (m), D_T is the temperature dependent diffusion rate of CO₂ (m² s⁻¹), r_k is the reacto-diffusive length (m) and P represents the cell wall permeability to CO₂ (m s⁻¹). Q_s was determined from

$$\begin{array}{}\text{(2)}& Q_{\mathrm{s}}={\displaystyle \frac{\left({\mathit{\gamma }}_{\mathrm{c}}{\mathit{\mu }}_i\right)}{\mathrm{4}\mathit{\pi }{r}^{\mathrm{2}}}},\end{array}$$

where γ_c is the carbon content per cell (mol C), and μ_i is the cell growth rate (s⁻¹).

Using this model we tested how δ¹³C_POC and ε_p vary as a function of [CO_2(aq)], temperature, growth rate and cell size. For each of these parameters we used the base values of Rau et al. (1996) unless specified otherwise.

ε_p for measured and modelled δ¹³C was calculated as follows:

$$\begin{array}{}\text{(3)}& {\mathit{\epsilon }}_{\mathrm{p}}={\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{POC}}.\end{array}$$

To understand under the conditions under which the ambient [CO_2(aq)] plays a dominant role in the determination of δ¹³C_POC in surface waters across the frontal region, the relationships between δ¹³C_POC, ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ and CO_2(aq) were compared to modelled estimates for passive diffusion (Fig. 2). SASW samples fall close to the modelled estimates, and subtropical samples decouple from the modelled trend to a much higher degree. In Fig. 2a, [CO_2(aq)] and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ in the SASW have a significant negative correlation ($r=-\mathrm{0.77}$, n=12, p=0.003), and correspond to the model trends, with lower concentrations resulting in higher δ¹³C_DIC and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$. There are no significant correlations between δ¹³C_POC and [CO_2(aq)] or ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ in the subtropical or subantarctic water masses (Fig. 2, p>0.05). These data suggest that although [CO_2(aq)] may play a role in determining the δ¹³C_POC in the SASW, other factors cause deviation away from a significant correlation, with the relationship increasingly decoupled in subtropical waters.

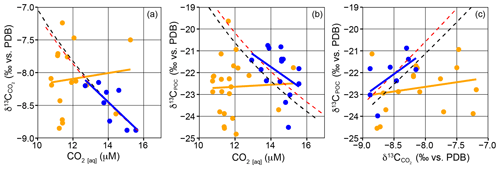
Figure 2 Correlations between [CO_2(aq)], δ¹³C_POC and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ in surface waters. (a) ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ vs. [CO_2(aq)], (b) δ¹³C_POC vs. [CO_2(aq)] and (c) δ¹³C_POC vs. ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$. Blue points represent SASW samples, and orange points represent subtropical samples. A linear regression for each region is shown in the respective colours; all regressions were insignificant (p>0.05), apart from SASW samples in (a) where $r=-\mathrm{0.77}$, n=12 and p=0.003. The dashed lines display the expected trend due to diffusive uptake of carbon by phytoplankton using temperature and not cell size, red refers to atmospheric CO₂ 350 ppm, 1.7 ‰, (Rau et al., 1996), black is 390 ppm, 1.3 ‰ (representative of this study).

To investigate the spatial variability across the SSTC, [CO_2(aq)], and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ were plotted against longitude and compared to model estimates (Rau et al., 1996; Supplement), where we used the model constants for cell size (10 µm) and reconstructing [CO_2(aq)] from temperature variability across the transect (Fig. 3a, b). Temperature can predict the spatial variability in [CO_2(aq)], and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$, but ambient [CO_2(aq)] is lower and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ is higher than model estimates, resulting from biological production and the isotopic disequilibrium between the ocean and atmosphere (Gruber et al., 1999). δ¹³C_POC is predicted using ambient temperature as well as measurements of [CO_2(aq)] and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ (Fig. 3c). There is no correlation between measured and modelled δ¹³C_POC across the transect, suggesting that there are other controlling factors which determine the δ¹³C_POC variability.

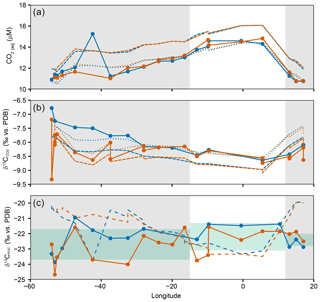
Figure 3 Distribution of (a) [CO_2(aq)], (b) ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ and (c) δ¹³C_POC vs. longitude. Closed circles and solid lines show measured values and trends, orange lines and points equal 5 m and blue lines and points equal 20 m. In (a) and (b), dashed lines are modelled estimates using temperature only (Rau et al., 1996). Long dashes refer to an atmospheric CO₂ of 390 ppm, and dotted lines refer to atmospheric CO₂ of 350 ppm. In (c), dashed lines are modelled estimates using temperature, [CO_2(aq)] and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$. Grey shaded areas highlight the stations sampled north of the SSTC. Green shaded bars represent 2σ for the SACW, SASW and AC regions of the transect.

To test whether cell size (and thus the cellular surface area to volume ratio) plays an important role in determining δ¹³C_POC, we estimated the change in phytoplankton size classes across the transect. Using phytoplankton pigment data we calculated the relative proportion of pico-, nano- and microphytoplankton size fractions to total chlorophyll a biomass (Bricaud et al., 2004; Uitz et al., 2008). Picophytoplankton were more abundant in the subtropical environments than in the SASW, contributing between 30 % and 40 % of the pigment biomass at the core of these water masses (Fig. 4). In contrast, nano- and microphytoplankton were more dominant in the SASW and close to the Rio de la Plata outflow.

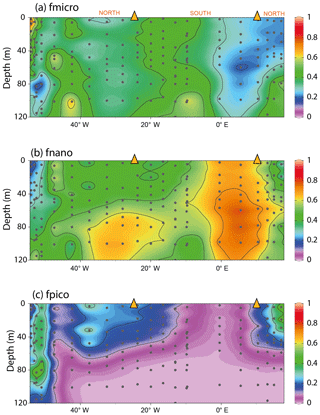
Figure 4 The fractional contribution of phytoplankton size classes to total chlorophyll as estimated from phytoplankton pigments. The size classes are defined as pico (<2 µm), nano (2–20 µm) and micro (20–200 µm). “f” signifies the fractional contribution to the chlorophyll a concentration. Size class estimates were calculated following (Uitz et al., 2008). The interpolation was produced using ODV-weighted average gridding (Schlitzer, 2018).

An estimate of the approximate average community cell size was calculated by defining a specific cell size for each of the three defined size classes (picophytoplankton were defined as 1 µm, nanophytoplankton were defined as 5 µm and microphytoplankton were defined as 50 µm; Bricaud et al., 2004). The central size values for each class were divided by two to approximate the average community cell radius (picophytoplankton were 0.5 µm, nanophytoplankton were 2.5 µm and microphytoplankton were 25 µm). This method only provides a rough indicator of the community cell radius, as size class is represented by one unique size for each algal group; however, this enables one single parameter to be used to characterize the size structure of the algal population, which is important for the purposes of this study.

Estimated average cell radii were generally smaller at the core of the subtropical water masses compared with the SASW (Fig. 5; depth range <40 m, subtropical, >20 ^∘C, 6.5 µm ±0.8, n=17; subantarctic, <18 ^∘C, 10.4 µm ±2.3, n=31). Increasing the average cell size (and thus decreasing SA : V) has the potential to reduce carbon isotope fractionation during uptake by passive diffusion and, thus, increase δ¹³C_POC by reducing the ability of the cell to discriminate between the two isotopes. This has been found in modelled, experimental and environmental studies (Popp et al., 1998; Pancost et al., 1997; Rau et al., 1990, 1996).

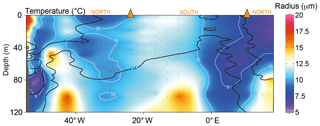
Figure 5 The estimated average phytoplankton community cell radius. The average radius (white contour lines) was calculated using the proportions of pico-, nano- and microplankton in Fig. 4. We estimate the average radius using assumed cellular radii of 0.5, 2.5 and 25 µm for pico-, nano- and microplankton, respectively. The black contour lines show the 14 and 18 ^∘C isotherms. The interpolation was produced using ODV-weighted average gridding (Schlitzer, 2018).

When δ¹³C_POC is modelled using temperature, SASW measurements fall between model estimates for a cell radius of 10–15 µm (Fig. 6a). Conversely, the subtropical samples have higher proportions of picoplankton (<2 µm), and decrease to lower δ¹³C_POC than those predicted using temperature alone, demonstrating that cell size is likely a controlling factor in δ¹³C_POC determination. The average community cell radius in open ocean samples was compared to δ¹³C_POC (Fig. 6b), and a significant positive correlation was observed (r=0.74, n=30, p<0.001).

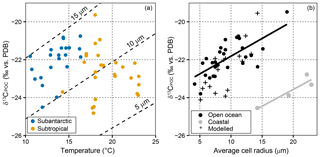
Figure 6 δ¹³C_POC variability and model predictions with temperature and cell size. (a) δ¹³C_POC vs. temperature, with the modelled estimates for cell radii of 5, 10 and 15 µm. Blue circles refer to SASW, and orange circles refer to subtropical waters. (b) δ¹³C_POC vs. cell radius as derived from pigment data. Samples from the eastern and western margin are excluded from correlation estimates. Rio de la Plata: r=0.92, df=2, p=0.075; open ocean: r=0.72, df=30, p<0.001. Modelled δ¹³C_POC is estimated using measured temperature and cell size and an assumed constant cell growth rate of 1.1 d⁻¹. Black crosses in show modelled results. The average cell radius is calculated from microplankton (25 µm), nanoplankton (2.5 µm) and picoplankton (0.5 µm). There are fewer data points in (b), as we did not have corresponding cell size data for all of the δ¹³C_POC measurements.

The samples with a larger estimated community cell size on both the east and western margins were not included in this correlation analysis as they show a significant offset from this relationship (Fig. 6b). These samples have a larger estimated cell size compared with measured δ¹³C_POC and suggest that there is a possible terrestrial influence, either with the supply of allochthonous material, the presence of grazers and/or significant shifts in the species assemblage to a higher abundance of microplankton (Browning et al., 2014). The significant positive correlation between cell size and δ¹³C_POC for open ocean waters suggests that cell size is the primary factor influencing δ¹³C_POC in the surface waters across the SSTC. We further test the relationship between δ¹³C_POC and cell size by predicting changes in δ¹³C_POC using temperature and cell size measurements (black crosses in Fig. 6b). We find good agreement between modelled and measured data points, demonstrating the importance of cell size in estimating δ¹³C_POC.

South of the SSTC, the phytoplankton community is dominated by haptophytes (Browning et al., 2014). A lower species diversity south of the front may explain the closer alignment between [CO_2(aq)] and δ¹³C_POC, as other factors are less significant in influencing ε_p. Recent work has highlighted the interspecies differences in carbon uptake fractionation and their influence on bulk δ¹³C_POC (Hansman and Sessions, 2016). Our results suggest a changing community cell size deviates δ¹³C_POC from expected trends with [CO_2(aq)]. In this open ocean environment, using estimates of cell size in addition to [CO_2(aq)], we can predict variability in δ¹³C_POC.

4 Discussion

4.1 Carbon uptake fractionation across the 40^∘ S transect

The biological fractionation of carbon isotopes during uptake by phytoplankton can be estimated using ${\mathit{\epsilon }}_{\mathrm{p}}\sim {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{POC}}$ (Freeman and Hayes, 1992). This fractionation comprises both the CO₂ fixation during photosynthesis, which utilizes the enzyme rubisco ($\sim -\mathrm{22}$ ‰ to −31 ‰), and is also determined by the factors which limit the external supply of CO₂ to the enzyme. Therefore, the more CO₂-limited the cell, the less the isotopic fractionation of CO₂ fixation will be expressed. These limiting factors include ambient [CO_2(aq)] (Baird et al., 2001), growth rates (Laws et al., 1995; Popp et al., 1998), cell size or geometry (Popp et al., 1998), light availability and day length (Laws et al., 1995; Burkhardt et al., 1999), utilization of HCO${}_{\mathrm{3}}^{-}$ in replacement of CO₂ (Sharkey et al., 1985) and species variability (Falkowski, 1991).

Empirical estimates of ε_p range between 10 ‰ and 18 ‰, with the highest fractionation observed in the Southern Ocean where [CO_2(aq)] is highest, increasing to over 20 µM in surface waters (Young et al., 2013). Over the Atlantic SSTC we measure an ε_p range of 12 ‰–17 ‰. In the subtropical water masses north of the SSTC, the average ε_p is 1 ‰ higher than in the SASW despite lower [CO_2(aq)] (Fig. 7). Our data contrast the global observed variability (of high ε_p in high [CO_2(aq)] regions such as the Southern Ocean) but are comparable to results from previous work in frontal regions where higher ε_p has been observed in lower [CO_2(aq)] subtropical water masses (Bentaleb et al., 1998; Francois et al., 1993).

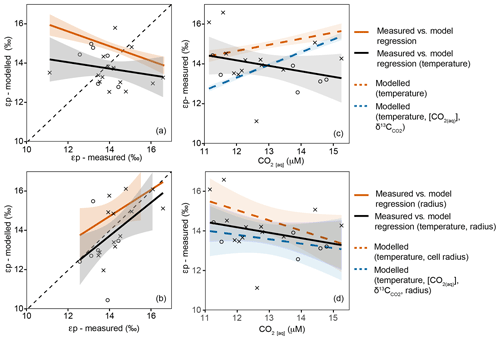
Figure 7 Variation in modelled and measured ε_p in the upper 60 m with changing [CO_2(aq)]. Black points and lines show measured ε_p, circles represent SASW and crosses represent subtropical water masses. (a, c) The regressions for modelled and measured ε_p; (b, d) modelled and measured ε_p against [CO_2(aq)]. Panels (a) and (b) explore the predicted ε_p using temperature, [CO_2(aq)] and ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$. Panels (c) and (d) explore the predicted ε_p using temperature, [CO_2(aq)], ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ and cell size.

We predict the variability in ε_p using temperature, [CO_2(aq)], ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$ and changes in community cell size across the region. If [CO_2(aq)] was the controlling mechanism behind ε_p, increases in [CO_2(aq)] would result in increased ε_p. There is no significant trend between modelled ε_p (temperature, [CO_2(aq)]) and measured ε_p (Fig. 7a). In contrast, when cell size is included, there is a significant positive correlation (Fig. 7c; r=0.72, p=0, df=18). These results indicate that there is an inverse trend between modelled ε_p and [CO_2(aq)] in this region: ε_p increases with decreasing [CO_2(aq)], which can be best attributed to the variability in the gross size structure of the phytoplankton assemblage across the SSTC (Fig. 7).

If the flow of [CO_2(aq)] into and out of a cell is determined by gas diffusion, then the flow is proportional to the cell surface area. A decrease in cell radius leads to an increase in cell surface area to volume ratio (SA : V), increasing the amount of [CO_2(aq)] diffusing across the cell membrane relative to the total carbon within the cell, and allowing greater fractionation and higher ε_p. Thus, ε_p has been found to be negatively correlated with phytoplankton cell size, with larger cells such as diatoms showing less isotopic fractionation compared with smaller phytoplankton (Popp et al., 1998; Hansman and Sessions, 2016). These cell size trends are observed across our open ocean transect, with the largest cell sizes having lower ε_p and higher δ¹³C_POC.

The influence of cell size on the expression of ε_p is likely to have a greater effect with increasing growth rate (Rau et al., 1996; Popp et al., 1998). A higher growth rate, such as in spring/summer blooms increases the range of ε_p expressed across cell sizes. For instance in fast growing blooms, larger cell sizes may have higher relative δ¹³C_POC and lower ε_p than smaller cell sizes, compared with low growth periods (e.g. Fry and Wainwright, 1991). The SSTC is a dynamic nutrient environment (Ito et al., 2005), with the convergence of N-limited subtropical waters (Eppley et al., 1979), with the iron-limited Antarctic Circumpolar Current (ACC) waters (Boyd et al., 2000; Browning et al., 2014). The convergence of contrasting regimes potentially increases nutrient availability to phytoplankton whilst also contributing to the thermal stability of the upper water column (Longhurst, 1998), thus having the potential to elevate growth rates. Therefore, the expression of cell size on ε_p is intuitive in this environment. An increase in ε_p with decreasing cell size has been noted in previous work (Goericke and Fry, 1994) and may be the primary driver for community ε_p in the SSTC during spring and summer, when growth rates are high.

4.2 Regional and global factors influencing uptake fractionation

The changing [CO_2(aq)] is the principal determinant of δ¹³C_POC across the global ocean (Sackett et al., 1965; Rau et al., 1989; Goericke and Fry, 1994). A modelling study found that the inter-hemispheric differences in δ¹³C_POC could be explained by the inter-hemispheric asymmetry in [CO_2(aq)] (Hofmann et al., 2000). Poleward of ∼50^∘ S, [CO_2(aq)] ranges between 15 and 25 µM, δ¹³C_POC between −30 ‰ and −24 ‰, and ε_p is greatest of anywhere in the global ocean (Fig. 8). The fractionation during carbon fixation (rubisco) is highly expressed on ε_p and other factors are less influential.

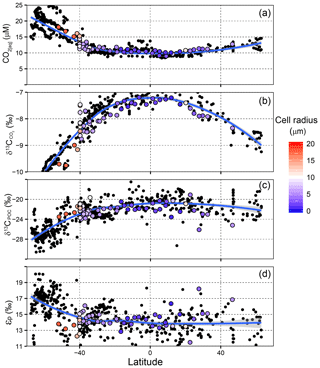
Figure 8 Global distributions of (a) [CO_2(aq)], (b) ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}}}$, (c) δ¹³C_POC and (d) ε_p in surface waters, plotted against latitude. Data include samples from the δ¹³C_POC compilation in Young et al. (2013) and data from this study. Coloured points show cell radius estimates (AMT3, AMT18 and this study). Blue lines in each panel show a loess fitted curve for the dataset.

In the low-latitude ocean, previous studies have shown that this trend becomes decoupled: [CO_2(aq)] decreases, growth rates are more variable and community structure and seasonal dynamics decouple the observed correlation of fractionation with temperature (e.g. Francois et al., 1993; Bentaleb et al., 1998). Previous studies of ε_p at the SSTC found decoupling between δ¹³C_POC and [CO_2(aq)], attributed to changing physical processes across the frontal region (Francois et al., 1993; Bentaleb et al., 1998). The variable water mass movements decouple trends, and it has been suggested that δ¹³C_POC variability in water masses can result from the local phytoplankton assemblage (Fontugne and Duplessy, 1978). Strong seasonal variations in δ¹³C_POC can also result from changes in biological parameters such as cell radius, cell membrane permeability and growth rate (Francois et al., 1993; Goericke and Fry, 1994; Jasper et al., 1994; Laws et al., 1995; Popp et al., 1998). Phytoplankton assemblage-derived changes in ε_p have been observed in other changing environments, such as the seasonal sea ice zone (Dehairs et al., 1997; Popp et al., 1999) and in major frontal regions (Dehairs et al., 1997; Popp et al., 1999; this study).

The results from our field study demonstrate that the phytoplankton assemblage has a key role in determining ε_p and δ¹³C_POC from their cell size and physiology, likely linked to the high growth rates in this frontal region. We test whether cell size variability presents a control over ε_p across meridional transects (Fig. 8). We find no relatable trend on a global scale, and latitudinal trends demonstrate an increase in ε_p with an increase in [CO_2(aq)]. However, increased cell size reduces the expression of a high ε_p (as shown by the higher δ¹³C_POC and lower ε_p in Fig. 8c and d), which is particularly evident between 30 and 60^∘ S.

Thus, regions where frequent physical changes stimulate variable and diverse phytoplankton assemblages may be more likely to have a decoupled relationship between ε_p and [CO_2(aq)]. We suggest that the high growth rates across this region play an important role in driving this change – we sampled across the SSTC in summer (high light levels), which may further promote the importance of cell size in determining δ¹³C_POC.

4.3 Changes to uptake fractionation and δ¹³C_POC in response to climate change

Ambient [CO_2(aq)] is increasing in the global ocean. A recent study found that ε_p has increased significantly since the 1960s in the subtropical Atlantic, whereas no notable change has been detected in polar regions (Young et al., 2013). Our results suggest that a change in the community cell size would impact ε_p, with a decrease in cell radius leading to increased ε_p. Thus, a changing community structure with the onset of climate change may further impact the ε_p and δ¹³C_POC, and have implications for our understanding of carbon isotope variability at the base of the food web.

Observational studies show rapid warming in the world's oceans in response to climate change, and that most of the ocean heat uptake is stored in the upper 75 m (Cheng et al., 2019). Predicted ocean warming trends are variable in different regions, with a greater rate of increase predicted in the polar regions (IPCC, 2013). Warming at the ocean surface promotes thermal stratification, which, in the Southern Ocean may decrease light limitation, whereas in the subtropics it is likely to promote further nutrient limitation (Sarmiento et al., 2004). Thus, climate change will promote varying responses from phytoplankton communities and their physiology across the global ocean (Rousseaux and Gregg, 2015).

In the oligotrophic gyres, ocean–atmosphere global climate models project increased stratification and decreases in net primary productivity with the onset of climate change (Boyd and Doney, 2002; Capotondi et al., 2012; Le Quere et al., 2003). Nutrients are already the limiting factor for net primary productivity and small cells are readily adapted to these oligotrophic environments, where recycled nutrients such as ammonium are the main nutrients available to phytoplankton (Fawcett et al., 2011). Many studies observe a shift to phytoplankton communities dominated by picoplankton as the water column becomes stratified and increasingly nutrient depleted (Atkinson et al., 2003; Bouman et al., 2003; Latasa and Bidigare, 1998; Lindell and Post, 1995; Irwin and Oliver, 2009). These observations suggest that the average community cell size may decrease further with ongoing climate change.

There may be large-scale shifts in community structure, including the physiological dependencies of phytoplankton on light and nutrients and their ecological diversity (Bouman et al., 2005; Behrenfeld et al., 2005; Siegel et al., 2005). A decrease in cell size may lead to a faster pace of metabolism (Brown et al., 2004). However, recent work suggests that CO₂ fixation and respiration rates are unlikely to increase under nutrient limiting conditions (Maranon et al., 2018). Therefore, subtropical regions may simultaneously experience warming, decreases in nutrient supply, increases in CO₂ availability, decreases in cell size and changes to community structure.

At higher latitudes, models predict increases in net primary production with improved light availability in the mixed layer and an extended growing season (Bopp et al., 2001; Sarmiento et al., 2004). Warming and reduction in sea ice is likely to initiate an earlier onset of bloom with a predicted 5–10 d shift per decade (Henson et al., 2018). Therefore, in the subantarctic ocean we may expect decreased light limitation, higher growth rates and decreases in community cell size. The results from this study demonstrate the different physiology of phytoplankton across the SSTC and the expression of carbon uptake on δ¹³C fixed into the phytoplankton cell. We find that δ¹³C_POC can be predicted using variability in cell size and [CO_2(aq)]. Furthermore, the subtropical and subantarctic uptake fractionation may respond differently with changing ambient [CO_2(aq)] and temperature with predicted future climate warming scenarios.

We use the results from this study to predict how the isotopic fractionation during carbon uptake may alter with increased [CO_2(aq)] as a response to climate change. To do so, we alter the model inputs to increase atmospheric CO₂ from 400 to 500 ppm, thereby increasing [CO_2(aq)] in the surface ocean, which we calculate using the solubility coefficients of CO₂ in seawater (Fig. 9, Weiss, 1974). We test variability from an average cell radius of 5, 10 and 20 µm and investigate the changes over the temperature range of the ocean. Although a smaller cell size (radius 5 µm) fractionates δ¹³C to a greater degree than a larger cell, there is only a 1 ‰ increase in ε_p with a 100 ppm increase in atmospheric CO₂ concentrations (Fig. 9a). Therefore, changing the CO₂ concentration alone may not have a large effect on δ¹³C_POC in subtropical environments. Instead, a trend to smaller average cell size would have a much greater impact on the δ¹³C_POC which is observed and predicted in the oligotrophic gyres.

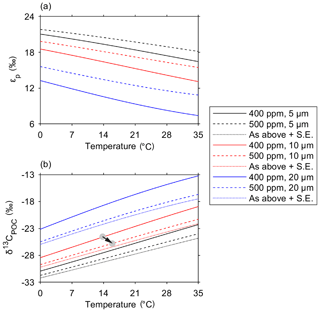
Figure 9 Projected changes in ε_p and δ¹³C_POC due to ongoing anthropogenic emission and upper ocean uptake of CO₂ for different temperatures and cell sizes. Variation in ε_p with seawater temperature for CO₂ partial pressures of 400 ppm (solid line) and 500 ppm (dashed line) and average community cell radii of 5 µm (black), 10 µm (red) and 20 µm (blue). (b) Variation in δ¹³C_POC under the same conditions as in (a), also showing the additional isotopic change driven by the Suess effect (labelled “S.E.” and represented using dotted lines). CO_2(aq) is calculated using the atmospheric CO₂ concentration and the solubility of CO₂ in seawater (Weiss, 1974). The arrow in (b) indicates how a 100 ppm increase in CO₂ and a projected 2 ^∘C increase in temperature would impact δ¹³C (with no change in cell size).

In the subantarctic waters, although predicted ε_p is lower in the larger cell sizes expected south of the SSTC, an increase in ambient CO₂ concentrations would have a much larger effect on ε_p. There is an observed 3 ‰ increase in ε_p in larger phytoplankton (radius 20 µm) with a 100 ppm increase in atmospheric CO₂ concentration. The changing conditions in the subantarctic ocean with the onset of climate change are also likely to promote the success of smaller-sized phytoplankton, as the light conditions improve and the upper ocean becomes increasingly stratified in summer months (Bopp et al., 2001). A decrease in community cell size could also increase ε_p and produce lower δ¹³C_POC. These results indicate that the subantarctic ocean, which has a relatively larger cell size in comparison with the subtropical ocean and is predicted to become increasingly stratified, may experience a greater change in the δ¹³C_POC produced during photosynthesis over the upcoming decades.

The sensitivity of δ¹³C_POC to increases in anthropogenic carbon is determined by the change in [CO_2(aq)] and also its isotopic signature. Enhanced diffusion of anthropogenic CO₂ between the atmosphere and the ocean's surface increases concentrations of [CO_2(aq)] in the ocean (Friedli et al., 1986; Francey et al., 1999). Anthropogenic CO₂ is enriched in the lighter ¹²C isotope, so its invasion into the ocean decreases δ¹³C_DIC in a phenomenon known as the Suess effect (Keeling, 1979), which has been observed across the ocean over the last decade (Quay et al., 2003). The uptake of anthropogenic CO₂ by the world's oceans has led to a decrease in δ¹³C_DIC of 0.025 % yr⁻¹ (Gruber et al., 1999). The increase in seawater pCO₂ from 400 to 500 µatm shown in Fig. 9 corresponds to DIC increasing by between 30 and 50 µmol kg⁻¹ (with a greater DIC increase at higher temperatures). Assuming a ratio of anthropogenic CO₂ invasion to δ¹³C_DIC change (i.e. ΔRC) of about −0.016 ‰ (µmol kg${}^{-\mathrm{1}}{)}^{-\mathrm{1}}$ in this region (Heimann and Maier-Reimer, 1996; McNeil et al., 2001), the associated Suess effect could decrease δ¹³C_DIC – and therefore δ¹³C_POC – by an extra 0.5 ‰ to 0.8 ‰, consistently across all cell sizes (Fig. 9b). This decrease would be in addition to, and independent from, any change due to fractionation, and consistent in magnitude for every cell size.

Seawater warming, which is expected to accompany future increases in [CO_2(aq)], independently modulates the marine carbonate system (Humphreys, 2017) and the fractionation model of Rau et al. (1996). In this case, simultaneous warming would oppose the increase in ε_p (and therefore decrease in δ¹³C_POC) driven by increasing [CO_2(aq)], as shown by the negative line gradients in Fig. 9a (and positive gradients in Fig. 9b). However, this is expected to have a relatively small impact overall, as the following back-of-the-envelope calculation illustrates. Given an equilibrium climate sensitivity (i.e. the equilibrium warming of Earth's near-surface resulting from a doubling of atmospheric pCO₂) of 1.5 to 4.5 ^∘C (Stocker et al., 2013), an increase in pCO₂ from 400 to 500 ppm would drive 0.5 to 1.5 ^∘C of global mean warming. For 10 µm cells, the pCO₂ change alone would increase ε_p by ∼1.8 ‰, while this warming alone would decrease ε_p by only 0.1 to 0.4 ‰, according to the model of Rau et al. (1996).

Stable isotope analysis of organic matter has emerged as the primary means of examining marine food web structure and variability (Middelburg, 2014). Carbon isotope signatures in particulate organic carbon vary substantially from the relative influence of terrestrial and marine carbon, carbon uptake pathways and the influence of carbon concentrating mechanisms (Jasper and Gagosian, 1990; Ganeshram et al., 1999). In contrast to nitrogen isotopes, there is negligible fractionation of carbon isotopes through trophic levels, which allows for the accurate estimation of dietary sources of carbon (Minagawa and Wada, 1984). Therefore, the factors that contribute to variability at the base of the food web need to be well understood in order to accurately comprehend marine food web dynamics (Peterson and Fry, 1987). These findings could also have implications for the distribution of δ¹³C_POC in the deep ocean via organic matter sinking and burial (e.g. Cavagna et al., 2013).

This study highlights the importance of cell size as a primary determinant of the extent of isotopic fractionation in particulate organic carbon during uptake and the subsequent signature imparted at the base of the food web. Our findings support previous work predicting increases in ε_p and decreases in δ¹³C_POC in the future (Young et al., 2013). However, we suggest that increasing ε_p may predominantly result from shifts in community structure towards smaller-sized phytoplankton. Changes in phytoplankton assemblages are being detected globally (Rousseaux and Gregg, 2015), in addition to possible declines in phytoplankton biomass (Boyce et al., 2010). Our detailed study of the subtropical and subantarctic environments predict greater relative decreases in δ¹³C_POC in polar regions than in the subtropics in response to changing [CO_2(aq)]. If increased stratification proceeds in the subantarctic, this may also lead to decreases in average cell size and, thus, even greater decreases in δ¹³C_POC.

5 Conclusions

δ¹³C_POC measurements from the SSTC in the Atlantic Ocean are compared to model predictions to determine the factors which control δ¹³C variability and carbon uptake fractionation (ε_p). Our results contrast global trends in marine waters, where δ¹³C_POC is lower in high CO₂ environments as a result of increased carbon uptake fractionation. Instead we find the δ¹³C_POC and ε_p are largely determined by community cell size variability, which we estimate using phytoplankton pigment composition. We measured a greater ε_p in the subtropical water masses where smaller-sized phytoplankton are more dominant and can fractionate δ¹³C to a greater degree by the increased CO₂ availability to the enzyme rubisco as a result of their enhanced increase surface area to volume ratio. Our results suggest a greater variability in δ¹³C and ε_p as a result of community cell size than previously predicted and highlight the need to understand the phytoplankton community structure.

We use our results from the field study to understand how increased CO₂ availability in the future will affect the carbon isotope fractionation in phytoplankton. Our findings suggest that larger-celled phytoplankton in the subantarctic may respond more to changes in the carbon concentration. However, shifts in algal assemblages towards smaller phytoplankton will also have a large effect on the community ε_p expressed. These results suggest that decreasing cell size and increased CO₂ availability to phytoplankton will increase ε_p and decrease δ¹³C_POC. Our study illustrates that phytoplankton cell size changes in response to warming may alter δ¹³C at the base of the food chain, and need to be taken into account along with the Suess effect when using δ¹³C as a food source tracer.