the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Trees do not always act their age: size-deterministic tree ring standardization for long-term trend estimation in shade-tolerant trees
Rachel Dietrich
Madhur Anand
With increasing awareness of the consequences of climate change for global ecosystems, the focus and application of tree ring research have shifted to reconstruction of long-term climate-related trends in tree growth. Contemporary methods for estimating and removing biological growth trends from tree ring series (standardization) are ill-adapted to shade-tolerant species, leading to biases in the resultant chronologies. Further, many methods, including regional curve standardization (RCS), encounter significant limitations for species in which accurate age estimation is difficult. In this study we present and test two tree ring standardization models that integrate tree size in the year of ring formation into the estimation of the biological growth trend. The first method, dubbed size-deterministic standardization (SDS), uses tree diameter as the sole predictor of the growth trend. The second method includes the combined (COMB) effects of age and diameter. We show that both the SDS and COMB methods reproduce long-term trends in simulated tree ring data better than conventional methods; this result is consistent across multiple species. Further, when applied to real tree ring data, the SDS and COMB models reproduce long-term, time-related trends as reliably as traditional RCS and more reliably than other common standardization methods (i.e. C-method, basal area increments, conservative detrending). We recommend the inclusion of tree size in the year of ring formation in future tree ring standardization models, particularly when dealing with shade-tolerant species, as it does not compromise model accuracy and allows for the inclusion of unaged trees.
- Article
(1038 KB) - Full-text XML
-
Supplement
(464 KB) - BibTeX
- EndNote
Tree rings have long-served as a record of environmental change in forest ecosystems. Early dendrochronological studies used tree ring chronologies from climate-sensitive species to elucidate the dynamics of growth–climate relationships and reconstruct climate anomalies from periods before the existence of instrumental records. However, with increasing awareness of the consequences of climate change for global ecosystems, the focus and application of tree ring research have shifted to reconstruction of low-frequency climate-related trends in tree growth (Gedalof and Berg, 2010; Boisvenue and Running, 2006; Jacoby and D'Arrigo, 1997). As it stands, previous optimism regarding the benefits of carbon fertilization for forest growth (Battipaglia et al., 2013; Norby et al., 2005) has been quelled by a lack of consistent evidence in real forests. While many studies have noted increases in long-term growth rates over time in temperate forests (Gedalof and Berg, 2010; Huang et al., 2007; Martinelli, 2004), others suggest no change (Giguère-Croteau et al., 2019; Camarero et al., 2015; Granda et al., 2014; Silva et al., 2010; Peñuelas et al., 2011). Further, in boreal and drought-prone species, growth decline (Chen et al., 2018; Dietrich et al., 2016; Girardin et al., 2011; Silva and Anand, 2013) and increased mortality (Herguido et al., 2016; Liang et al., 2016) in response to climate stress have been prevalent. Central to all of these studies is the assumption that long-term growth trends can be accurately and unbiasedly estimated from tree ring data.
As it stands, accurate estimation of long-term growth trends in forests may be limited by poorly adapted tree ring standardization (age trend removal) methods (Briffa et al., 1996) and inappropriate sampling methods (Nehrbass-Ahles et al., 2014; Brienen et al., 2012). Early standardization methods (i.e. conservative detrending) were designed to maintain high-frequency variation in tree ring series and discard long-term, low-frequency variation. It is accepted that these methods are inappropriate for estimating long-term, climate-related growth trends (Briffa et al., 1992); however, they are still used in situations where contemporary standardization methods are not applicable due to restrictive data requirements (e.g. Villalba et al., 2012; Gedalof and Berg, 2010; Wang et al., 2006).
Modern standardization methods are designed to estimate biological age- and size-related effects on tree growth independent of time-related variance, thus theoretically maintaining long-term trends in the final chronologies. Among these, the conversion of tree ring widths to basal area increments (BAIs), and the closely related C-method (Biondi and Qeadan, 2008), as well as the use of regional curve standardization (RCS; Briffa et al., 1992), and its many variants (see Helama et al., 2017), have become commonplace (Peters et al., 2015). Traditional RCS relies on the assumption that the species-specific biological growth trend of local trees can be estimated, and thus removed, from a sufficiently large sample of trees using tree age alone. Alternatively, the BAI method assumes that the biological growth trend is sufficiently related to basal area accrued in a given year and, as such, chronologies presented as BAI (instead of raw ring width) contain minimal biological effects. In practice, it is unlikely that this strict relationship accounts for all the variation in ring width that is related to biological size and age effects. As such, some studies have proposed explicit models of BAI that attempt to include variables related to tree age and size or environmental conditions (i.e. tree density, soil fertility, etc.; see, e.g. Linares et al., 2009; Nock et al., 2011). Similarly, the C-method (CM) assumes that tree-wise BAI (tree ring area) distributed over a growing surface in time is constant and as such, annual deviations from this trend can represent the standardized chronology (free from biological trend, Biondi and Qeadan, 2008). Both BAI and CM are best suited to open-growth, shade-intolerant trees, where the strict relationship between annual growth and expected BAI is not impeded by early competition for light.
However, due to the difficulties in separating climate-related trends that vary on long timescales from those related to biological tree growth and/or succession-related environmental change, none of these methods are likely to produce accurate estimates of external forcing when trees from only a single age or size class are sampled (Brienen et al., 2012; Briffa and Melvin, 2011). It follows that studies which only sample even-aged stands or dominant trees are likely to produce biased estimates of long-term growth. While increased awareness of sample biases has led to better prescriptions for study design (see Nehrbass-Ahles et al., 2014; Brienen et al., 2012), systematic tests of the ability of these models to accurately reproduce long-term trends are still limited (e.g. Sullivan et al., 2016; Peters et al., 2015; Esper et al., 2003).
Despite these limitations, RCS remains the standard method for estimating long-term growth trends in tree ring data (Helama et al., 2017). However, the standard RCS approach encounters large limitations for many species in which accurate age estimation is difficult. Additionally, we suggest the inherent assumption of RCS that biological growth trends are sufficiently determined by tree age may not be appropriate in all species. More specifically, this assumption is problematic for shade-tolerant trees. Shade-tolerant species exhibit relatively low low-light mortality and thus can persist in forest understories for variable amounts of time before release from overstory light suppression. In these cases, traditional age-deterministic models exhibit high variance, and thus low precision, in the period following tree establishment and leading up to the age when most trees have been released from suppression (Fig. 1). This period of ill-fit means that trees that are released relatively early (or late) from light suppression will exhibit inflated (or deflated) growth relative to the chronology. As a result, the final chronology will show less agreement than would be expected in a shade-intolerant species. Even more problematically, if trees are sampled according to minimum size thresholds, the youngest trees in the chronology are likely to be early-release trees, leading to an artificial inflation of modern growth rates in the final chronology. While modifications to traditional RCS that address variance in contemporaneous growth rates and regional environmental conditions have been prevalent in shade-intolerant species (see Helama et al., 2017) there has been little to no focus on the improvement of standardization techniques specific to shade-tolerant tree species.
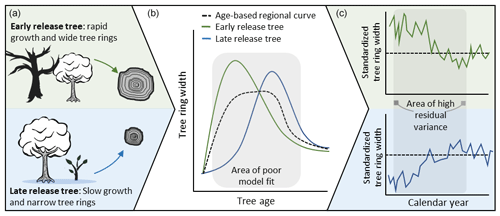
Figure 1(a) In shade-tolerant species, young trees are stochastically released from low-light suppression in the understory. (b) Since release from suppression is not strictly related to tree age, widely used communal age trend models (RCS) poorly model tree growth in the period following establishment and leading up to the age when most trees have been released from suppression. (c) Poor model fit in this period implies that the biological growth trend is not entirely removed from individual series and leads to high residual variance when standardized tree ring series are aligned according to calendar year.
Alternatively, in the field of forest growth and yield modelling, size-deterministic, rather than age-deterministic, predictive growth models are ubiquitous. It is well-understood that tree size regulates the capacity for resource acquisition, namely, light (Canham et al., 2004), water and nutrients (Homann et al., 2000), resource allocation (Lehnebach et al., 2018), and metabolic costs (West et al., 2001). As such, the notion of radial growth being deterministic according to size rather than age is logical from both a physiological and ecological perspective. Tree size in a given year is dependent on its previous size and annual growth, so shade-tolerant trees that have yet to be released from overstory light suppression remain small as they grow older. This relaxes the period of “ill-fit” that would be observed in an age-based model. Accordingly, we propose that a size-deterministic model for tree ring standardization may be more appropriate than traditional RCS for shade-tolerant tree species. The application of size-deterministic models has been limited, with few examples of tree size in a given year being incorporated into BAI models (e.g. Marqués et al., 2016; Camarero et al., 2015; Nock et al., 2011; Martínez-Vilalta et al., 2008) and even fewer of uniquely size-based tree ring models (e.g. Bontemps and Esper, 2011; Gavin et al., 2008). Further, there have been no systematic evaluations of the ability of size-based models to accurately estimate long-term trends in tree ring series.
We present two tree ring standardization models that integrate tree size in the year of ring formation into estimation of the biological growth trend. The first model uses tree diameter as the sole predictor of the communal growth trend while the second includes the combined effects of both age and diameter. It follows that the objective of this study is to determine the efficacy of both models in estimating long-term growth trends in their resultant tree ring chronologies. First, we use modelled tree ring data from shade-tolerant and shade-intolerant species to make the inappropriateness of age-based models explicit for shade-tolerant trees. Further, we investigate the performance of size-based models relative to contemporary standardization methods in the presence of size thresholds in tree sampling. Last, we apply the developed models to tree ring data from shade-tolerant temperate species to evaluate model performance relative to contemporary methods, on the basis of accurate reconstruction of known long-term time-related trends in the series.
2.1 Model formulation
Traditional RCS makes two assumptions about tree growth: first, that trees of the same species in a given region exhibit a common growth trend as they age, and, second, that growth of an individual tree in a given year is thus a product of its age and common climatic or environmental forcing in that year (Esper et al., 2003; Briffa et al., 1992). We present a variant of the RCS method that uses tree size, measured by diameter at breast height (DBH), in the year of ring formation as the primary determinant of the common biological growth trend. As with RCS we assume that the relationship between expected growth and tree size is non-linear and can be approximated for a region from a sufficiently large sample of trees from the species in question. Further, we assume that using a sample of trees from a range of size and age classes ensures estimation of the common trend is not confounded by underlying low-frequency climate or environmental forcing in the chronology (Brienen et al., 2012). The size-based regional curve model, hereafter referred to as the size-deterministic standardization (SDS) model, takes the following form:
where E(RWyi) represents the expected ring width of a given tree (i) in year (y), and f1 represents a non-linear function relating DBH of a given tree (i) in year (y) to E(RWyi). As in RCS, the communal non-linear relationship is estimated communally for all local trees of interest. In our study we estimate f1 with a penalized thin plate regression spline in a generalized additive model (GAM); however, this relationship could be estimated by a number of different spline-fitting or non-linear regression techniques (i.e. ffcsaps function in dplR, Bunn et al., 2018, time-varying splines, Melvin et al., 2007). Under this paradigm the model residuals (eyi) represent individual standardized ring width indices and, by extension, individual tree response to climatic or environmental forcing. Annual model residuals subject to a robust mean thus represent the final standardized chronology. This approach differs slightly from traditional RCS, whereby standardized ring width indices are occasionally produced by division of raw measurements by the expected value. Calculation of standardized ring width indices by subtraction from the expected value, as in the case of residuals, is now commonly used, as it tends to reduce bias in the resultant chronology (Helama et al., 2004) and eases in the formulation of more complex tree ring standardization models. However, unlike division methods, the subtraction method does not provide any stabilization of variance in the resulting residuals; as such, it may be necessary to use a stabilization procedure (i.e. log transformation, power transformation) on raw ring width data beforehand.
Tree size in a given year can be estimated by outside-in or inside-out techniques. If the pith of a tree is present in the core (or reasonably close to) DBHy is a simple summation of all previous ring widths since the year of origin, multiplied by two. Alternatively, if the pith is missed, DBHy can be calculated via subtraction of more modern ring widths (multiplied by two) from the inside-bark diameter. In this case, inside-bark diameter is calculated as measured DBH minus bark thickness (multiplied by two), where bark thickness can be directly measured or estimated using species-specific allometric equations (e.g. Stayton and Hoffman, 1970).
Similar to the model formulation for SDS, RCS models were estimated with GAMs of the following form:
where Ageyi is the age of an individual tree in a given year and the resultant standardized tree ring indices are derived from model residuals (eyi).
In addition, a more complex model that integrated independent size and age effects was also evaluated for comparison. This model, hereafter referred to as the combined model (COMB), took the following form:
In a large variety of long-lived tree species, accurate age estimation (pith sampling) is difficult or impossible; rendering traditional RCS or combined models inappropriate for all trees sampled. To address this issue, the above model can incorporate unaged trees. Here f1 represents the non-linear function relating age to expected ring width for the subset of all trees that are aged (ia). In this model, ring widths from unaged trees are assigned arbitrary ages that do not contribute to the linear approximation of the smooth term for age (i.e. ) but these trees still contribute to the smooth term for size f2(DBHyi). Syntax for missing data in GAMs follows the protocol provided in mgcv (Wood, 2011). In this study all GAMs were fit using the mgcv package (Wood, 2011) in the R statistical program (v.3.5.0).
In addition to the models presented above we investigated three additional standardization methods: conservative detrending (CD), CM, and BAI. Conservative detrending describes functions (i.e. negative exponentials, straight lines) or flexible splines fit to individual tree ring series (see Cook and Kairiukstis, 2013). In this study we use spline-fitting techniques rather than modified negative exponentials as they are more appropriate for shade-tolerant tree species. As above, the individual standardized tree ring width indices are derived from model residuals. The C-method estimates tree-specific expected ring widths by assuming constant annual basal area increment (tree ring area) over the life span of the tree (see Biondi and Qeadan, 2008). Annual deviations from expected values thus represent standardized ring width indices. For consistency, the standard CM approach in dplR (Bunn et al., 2018) was modified in order to calculate indices via subtraction (residuals) instead of division. Tree ring widths were converted to BAI using the dplR package in R (Bunn et al., 2018). R code for worked examples of all standardization procedures used in this study is available (https://doi.org/10.5281/zenodo.3565813).
2.2 Simulated tree ring data
We simulated tree ring data using a well-established gap-phase model. The SORTIE-ND model was chosen over other similar gap-phase models as it better emulates understory light conditions and low-light mortality, both of which are central to the notion of age being an inappropriate determinant of growth in shade-tolerant species. In SORTIE, annual radial tree growth is calculated as an asymptotic function of light availability and previous tree diameter. As such, the underlying growth trend in SORTIE-simulated data should be well-approximated by a flexible curve estimated on the basis of tree size (SDS). As such, we use this analysis solely to elucidate the problematic nature of age-based standardization methods for shade-tolerant species and not to confirm the efficacy of size-based standardization methods.
For simplicity, a stand 100 % dominated by sugar maple (Acer saccharum) was simulated, as sugar maple is a model shade-tolerant species that grows in self-replacing stands. All living trees (>5 cm DBH; n=3657) in the final year of the model run were used for further analysis. Additionally, to elucidate our claim that age-deterministic growth estimation is more problematic in shade-tolerant species, we completed a similar SORTIE simulation for the shade-intolerant species white pine (Pinus strobus). Again, the stand was 100 % white pine, standard model parameters were used, and the simulation was run for 1000 years. All living trees (>5 cm DBH; n=7362) in the final year of the model run were used for further analysis. Additional details regarding model parameters for the SORTIE simulations are provided in the Supplement (Sect. S1).
To simulate a low-frequency climate-related growth trend, a logistic trend was added to raw tree ring width of individual trees produced by both SORTIE simulations. The logistic trend simulated an initial rapid increase in growth and subsequent levelling off that aimed to represent a period of carbon fertilization and eventual acclimation. The logistic model was applied to the last 100 years of growth and took the following form, where RWtyi represents ring widths with the simulated long-term trend and RWryi are raw ring widths:
The logistic trend parameters (r=0.12, k=0.629, a=20) were chosen such that increases in individual tree growth averaged approximately 5 % per decade. Additionally, we tested the standardization models in their ability to detect simulated negative trends in tree growth, as previous studies have noted a failure of contemporary methods to accurately reproduce declining growth trends (Peters et al., 2015). The simulated negative logistic trend took the form of Eq. (4) with parameters (r=0.12, , a=20) chosen such that decreases in growth averaged 5 % per decade. For completeness, we also simulated positive and negative linear trends. Results of those analyses are provided in the Supplement (Sect. S3).
A total of 60 trees were randomly selected, without replacement, from the simulated tree populations and subject to each of the six standardization methods (SDS, RCS, COMB, CD, BAI, CM). Model residuals (in the case of RCS, SDS, COMB, CD and CM) or transformed (BAI) tree ring widths were compiled into an annual mean chronology using Tukey's biweight robust mean. The resultant chronologies were then tested for significant correlation with the imposed trends using Spearman's rank correlation coefficient. This process was bootstrap resampled (with replacement) 100 times, in order to produce confidence intervals for the resultant mean chronologies and their respective correlation coefficients.
To examine the effect of minimum size sampling thresholds on the accuracy of long-term trend reconstruction by each of the standardization methods, we completed the same analysis on trees from the simulated populations that exceeded certain size thresholds. The thresholds employed were 10 cm DBH, which represented a practical minimum size threshold for sampling, and 30 and 50 cm DBH which represented thresholds for mature and dominant trees, respectively. The CD method was only applied when size thresholds exceeded 10 cm DBH due to the troublesome nature of fitting splines to excessively short time series. The mean Spearman's rho for all detrending methods and sampling thresholds were compared using two-way ANOVA and post hoc tests.
2.3 Real tree ring data
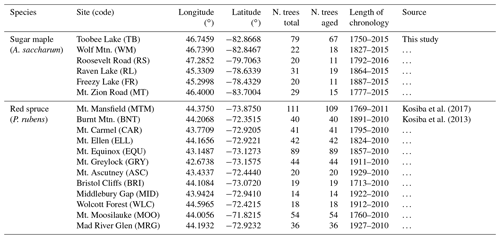
Additionally, we evaluated the performance of the six standardization methods in real tree ring data from shade-tolerant species. We collected tree ring data from seven mature sugar maple-dominated stands in Ontario, Canada (Table 1). Further, tree ring data sets from the shade-tolerant species red spruce (Picea rubens) were obtained from the DendroEcological Network database (https://www.uvm.edu/femc/dendro, last access: 6 December 2019; Table 1). Red spruce was chosen as it had sufficient replication across studies in the database. Descriptions of the sampling strategies and data-processing methods for all sites considered are provided in either the Supplement (Sect. S3) or in their respective references (i.e. Kosiba et al., 2013, 2017). Data were considered suitable for this study if age and DBH estimates were provided and if a minimum 10 trees per site and species were sampled and accurately aged. All cores in which pith offset was estimated to be greater than 10 years were considered unaged. To simplify comparisons of the resultant chronologies, unaged trees were not included in the models.
Prior to model application, a time-deterministic thin plate regression spline was applied to all raw ring widths from each site. This ensured there was no underlying time trend present in the data. Since trees of multiple ages/sizes were sampled in each study we assume the removed time trend is therefore independent of biological trends in the series. For each site, residuals from the regression spline were centred according to the site-wise mean and standard deviation of raw ring widths prior to analysis.
Table 1Location, sample size, chronology length, and source of tree ring data sets used in this study.
Again, increasing and decreasing logistic trends (Eq. 4), as well as linear trends (Supplement, Sect. S3), were added to the (recentred) tree ring residuals. Trend parameters were chosen such that the increase (or decrease) in tree growth averaged 5 % per decade over the last 50 years of growth (r=0.12, k=0.276, a=20, positive trend; r=0.12, , a=20, negative trend). For each site all trees were subject to each of the six standardization methods (SDS, RCS, COMB, CD, BAI, and CM). Model residuals (in the case of RCS, SDS, COMB, CD, and CM) or transformed (BAI) tree ring widths were compiled into an annual mean chronology using Tukey's biweight robust mean. The resultant chronologies were then tested for significant correlation with the imposed trends using Spearman's rank correlation coefficient. In both species (sugar maple and red spruce) one-way ANOVA and Tukey post hoc comparisons were used to test for significant differences in model performance, as estimated by chronology correlation with the imposed trend.
3.1 Comparisons of methods in simulated data
In order to evaluate the efficacy of each standardization method we calculated correlations between chronologies produced by each method and a variety of imposed trends in simulated sugar maple and white pine tree ring data. Bootstrapped confidence intervals for chronologies from each of the standardization methods are provided in Fig. 2a and b for sugar maple and red pine, respectively. Distributions of the respective Spearman's rank correlation coefficients between the chronologies and the imposed trends are provided in Fig. 3a for sugar maple and Fig. 3b for white pine.
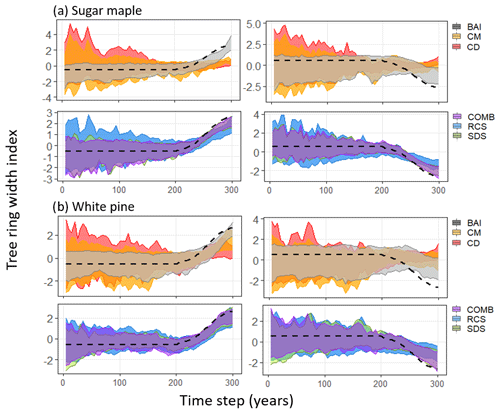
Figure 2The 95 % confidence intervals for standardized chronologies produced by each standardization method (legend on the right side) applied to SORTIE-simulated (a) sugar maple and (b) white pine tree ring data. Confidence intervals obtained via bootstrap resampling (rep = 100) of 60 trees (>10 cm DBH) from the SORTIE-simulated populations. Dotted lines indicate the standardized positive (left side) or negative (right side) logistic trend that was added to the raw tree ring data.
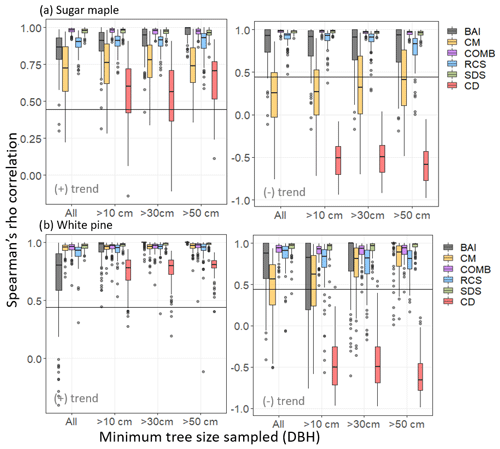
Figure 3Spearman's rho correlation between chronologies produced by each of the five standardization methods and the imposed positive (left column) or negative (right column) logistic trend in SORTIE-simulated (a) sugar maple and (b) white pine tree ring data. Correlation distribution created by bootstrap resampling 60 trees (rep = 100) from SORTIE-simulated tree populations. The horizontal axis denotes minimum tree size (DBH) thresholds for sampling from the population. Horizontal lines indicate threshold for significant Spearman's rho (a=0.05) for correlation between chronologies and the imposed trend.
3.2 Simulated sugar maple tree ring data
In the simulated sugar maple data, two-way ANOVA suggested a significant effect of both the standardization model (p<0.001) and minimum size sampling threshold (p<0.001) on average correlation with the positive logistic trend. Alternatively, for the negative logistic trend there was a significant effect of the standardization model (p<0.001) but not of the size sampling threshold. For both positive and negative logistic trends SDS (, , respectively) and COMB (, , respectively) models produced chronologies with significantly higher correlations than all other models (p<0.001 for all) but that were not significantly different from each other (p=0.998, p=1.000, respectively). For the positive imposed trend, BAI () and RCS () produced chronologies with correlations significantly higher than CD () and CM () (with p<0.001 for all examples) but that were not significantly different from each other (p=0.996). Notably, correlations exhibited by BAI chronologies were dependent on size sampling thresholds with BAI chronologies performing best when size thresholds exceeded 50 cm DBH (Fig. 3a). At this threshold BAI chronologies produced significantly higher correlations than when all trees were sampled (p=0.003) and when trees >10 cm DBH were sampled (p<0.001). The CD method produced chronologies that exhibited the lowest average correlation with the imposed positive trend of all models (p<0.001 for all).
Alternatively, when considering negative imposed trends, BAI () chronologies performed significantly worse than RCS (, p<0.001) but still better than CD () and CM () (p<0.001 for both). Again, CD chronologies exhibited significantly lower correlations than all other models (p<0.001 for all). Notably, RCS chronologies produced at the 50 cm DBH sampling threshold exhibited significantly lower correlations than all other sampling thresholds (p<0.001; Fig. 3a). All other models exhibited similar correlation distributions across the various size thresholds used for sampling.
3.3 Simulated white pine tree ring data
In simulated white pine data, two-way ANOVA suggested a significant effect of both standardization model (p<0.001) and minimum size sampling threshold (p<0.001) on average correlations for both the positive and negative logistic trend analyses. For the positive trend, chronologies produced by SDS (), RCS (), COMB (), and CM () produced high correlations across all sampling thresholds, with SDS performing significantly better than CM (p=0.006) and RCS (p=0.001). All four models produced significantly higher correlations than those produced by BAI () or CD () chronologies, with CD producing the lowest correlations of all models. Contrasts suggested that the significant effect of minimum size threshold was driven by significant differences in correlations from BAI chronologies across sample thresholds, whereby BAI chronologies exhibited significantly lower correlations when no minimum size thresholds (i.e. all trees sampled) were employed (p<0.001 in all cases; Fig. 3b).
When examining negative imposed trends, SDS () and COMB () models produced chronologies with significantly higher correlations than all the other models but that are not significantly different from each other (p=0.594). BAI () and RCS () produced chronologies with correlations significantly higher than CD () and CM () (p<0.001 for all) but that were not significantly different from each other (p=1.00). CD chronologies exhibited significantly lower correlations than all other models (p<0.001 for all). Contrasts suggested that the significant effect of minimum size threshold was driven by significant difference in correlations of chronologies produced by BAI and CM among sampling thresholds. As evident in Fig. 3b, BAI chronologies performed significantly better when sampling thresholds exceeded 50 cm DBH, and CM chronologies performed best when sampling thresholds exceeded 30 cm DBH.
3.4 Comparisons of methods in real tree ring data
Standardization methods were evaluated on the basis of correlations between their resultant chronologies and known time-related trends in tree ring series from shade-tolerant species.
Confidence intervals surrounding chronologies produced from each of the standardization methods applied to the tree ring series from six sugar maple stands are provided in Fig. 4a for both positive and negative logistic trends. The corresponding distributions of Spearman's rank correlation coefficients are provided in Fig. 5a with significant differences (p<0.05) being denoted by letters. Chronologies and corresponding correlation coefficients for the identical analysis performed on 12 red spruce stands are provided in Figs. 4b and 5b.
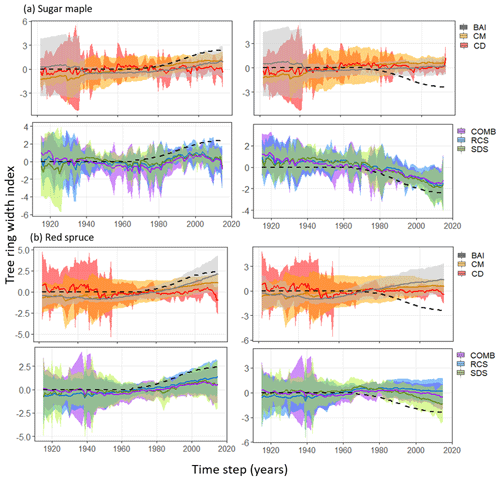
Figure 4Standardized chronologies produced by each standardization method (legend on the right side) applied to tree ring series from (a) sugar maple (n=6) and (b) red spruce (n=12) stands. Solid lines represent the resultant model-wise mean chronologies across all stands considered, while ribbons represent respective 95 % confidence intervals. Dotted lines indicate the standardized positive (left side) or negative (right side) logistic trend that was added to the raw tree ring data.
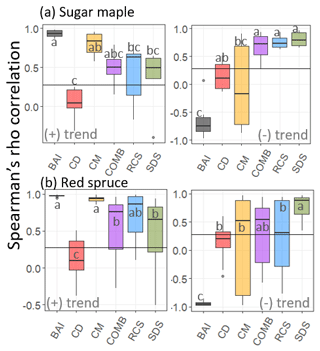
Figure 5Standardized chronologies produced by each standardization method applied to tree ring series from (a) sugar maple (n=6) and (b) red spruce (n=12) stands. Solid lines represent the resultant model-wise mean chronologies across all stands considered while ribbons represent respective 95 % confidence intervals. Dotted lines indicate the standardized positive (left side) or negative (right side) logistic trend that was added to the raw tree ring data.
Regardless of trend direction, RCS, COMB, and SDS chronologies exhibited comparable and consistent results across both species (Fig. 5). In general, chronologies produced by all three methods exhibited conservative but reliable estimations of the imposed trends (Fig. 4). SDS produced chronologies with correlations as high or higher (Fig. 5b, negative trend) than traditional RCS chronologies. Notably, the BAI and CM methods produced strong positive correlations between chronologies and the imposed trend only when the imposed trend was increasing (Figs. 4, 5) but both consistently failed to reproduce negative trends (Fig. 4). Finally, across both species, CD chronologies exhibited low correlations with the imposed trend regardless of direction (Figs. 4, 5).
4.1 Size-deterministic vs. age-deterministic models for long-term trend reconstruction
Using simulated tree ring data from the shade-tolerant species sugar maple, we have shown that standardization models that include tree size in the year of ring formation (SDS, COMB) produced chronologies that retain long-term and low-frequency variation better than those produced by models that only included age as a predictor (RCS). Alternatively, in the shade-intolerant white pine species, chronologies produced by the RCS and COMB models showed no significant difference in their estimation of long-term trends, though SDS chronologies slightly outperformed RCS chronologies. As discussed previously, the finding that size-based standardization models perform well in simulated tree ring data is not surprising given that the SORTIE model calculates annual tree growth as function of tree size. Thus, the underlying growth trend would be well-approximated by a flexible curve estimated on the basis of tree size. As such, we use these results solely to elucidate the problematic nature of age-based standardization methods for shade-tolerant species. SORTIE's use of diameter, rather than age, as a determinant of tree growth is not arbitrary; it is well-established that tree metabolic processes are directly related to size (West et al., 2001). Additionally, there is little evidence for a unique effect of age on tree growth that is independent of size (Munné-Bosch, 2007). With the exception of dendrochronological models, the vast majority of individual tree growth and process models are indeed size-based. It follows that the ubiquitous use of age or calendar year in tree ring standardization methods (RCS, signal-free standardization, CD, Hugershoff curves) is a practice born out of convenience rather than physiological consideration. As such, we agree with previous accounts that this assumption may be especially problematic in shade-tolerant trees where age and size may not be perfectly correlated (Peters et al., 2015; Bontemps and Esper, 2011).
Unfortunately, all systematic comparisons of tree ring standardization methods in real tree ring data (e.g. Sullivan et al., 2016) are limited by their inability to validate long-term trends estimated by chronologies. In this study we evaluate standardization methods on their ability to reconstruct artificial trends in tree ring data. We show that SDS and COMB models are as reliable as the traditional RCS method in accurately detecting long-term trends in shade-tolerant species. Further, SDS appears to provide more reliable reconstructions when the underlying trend is negative. To our knowledge, only one other study has evaluated size-deterministic models on the basis of long-term trend reconstruction in chronologies. Bontemps and Esper (2011) compared RCS and SDS chronologies in common beech (Fagus sylvatica L.) and conclude that both exhibit similar variations, with the magnitude of difference varying between 3 % and 7 %. However, other studies have examined the influence tree size in explicit models of BAI. In tropical tree species of varying shade-tolerance, Nock et al. (2011) note that linear mixed models of BAI that included tree diameter had more support than those that included age. This result is corroborated by analyses of mixed models of BAI in Mediterranean pine species that suggest that the effect of DBH on BAI is more important than the effect of tree age (Marqués et al., 2016). In line with discussion above, Nock et al. (2011) attribute this finding to size being a more important determinant of light capture as it relates to tree height and crown size (King et al., 2005).
The resultant chronologies are indeed more likely to be influenced by the sample of the underlying tree population than by choice of standardization model. Tree age can be difficult or impossible to accurately estimate for some trees. In contrast, annual tree size can be reliability estimated from DBH and tree ring measurements more ubiquitously. We note that in this study only 66 % of sugar maple trees could be accurately aged. Since unaged trees are likely to be the oldest trees in the chronology, it follows that RCS chronologies may exhibit poor sample replication (especially in early years) and may be significantly shorter than those typically produced by SDS or COMB models. This has obvious implications for data quality and suitability. Considerably problematic is the “segment length curse”, whereby almost all standardization methods are ill-equipped to estimate long-term trends on timescales greater than or equal to the length of the chronology itself (Cook et al., 1995). Excessively short RCS chronologies are therefore limited in their application. A large advantage of SDS and COMB models is that they can incorporate otherwise inadmissible tree ring data.
This study does not explicitly test the efficacy of COMB models relative to SDS in the presence of unaged trees. We have also not provided evidence to suggest that the added complexity of COMB models relative to SDS is beneficial to accurate reconstruction of trends in the resultant chronologies. Given the merit the of size-deterministic models presented here, we suggest that future research explores the implications of the trade-off between model information and complexity in the presence of unaged trees.
4.2 BAI, CM, and CD methods for long-term trend reconstruction
The finding that CD did not produce accurate long-term trends in simulated tree ring data is consistent with our expectations (Peters et al., 2015; Briffa et al., 1992). We maintain CD should be avoided if the goal is long-term reconstruction from tree ring data. More interestingly, we have shown that CM and BAI, although designed for shade-intolerant open growth trees, do not reliably reconstruct negative long-term trends in simulated white pine tree ring data. Further, our analysis suggests BAI is less reliable when small and young trees are sampled. This result is corroborated in our study by a failure of both methods to reconstruct negative trends in real sugar maple and red spruce tree ring data. Further, this finding is in line with Peters et al. (2015), who note low reliability of BAI and that BAI is likely to produce erroneous trends when the underlying trend is of low signal, as would be the case for young and small trees that have low BAI rates and low climate sensitivity.
Both BAI and CM impart a strict relationship between tree size and growth. It has been suggested that this relationship may not account for the entire biological growth trend, leading to the maintenance of erroneous long-term trends in the resultant chronologies (Peters et al., 2015). Erroneous increasing trends are indeed noted in both sugar maple (Fig. 4a) and red spruce (Fig. 4b) chronologies produced by BAI and CM in our study. Accordingly, we caution future studies in their interpretation of BAI and CM trends in low-signal tree ring series.
Other studies have explicitly modelled size and/or age effects on BAI using a mixed-effect modelling approach (e.g. Marqués et al., 2016; Camarero et al., 2015; Nock et al., 2011; Martínez-Vilalta et al., 2008). We suggest this approach may better account for species- and site-specific factors that influence expected growth rates, leading to more accurate estimates of long-term trends in the resultant chronology. While our findings regarding the importance of inclusion of size in tree ring standardization models are presented in the context of raw tree ring width models, they are also directly relevant to explicit models of BAI.
A more thorough discussion of the limitations of the CD, BAI, and CM methods, as relevant to reconstruction of long-term trends, is beyond the scope of this study. The interested reader is directed to Peters et al. (2015).
4.3 Other considerations and future research
It is important to note that the goal of this study was not to explicitly test the effect of sample biases (i.e. modern sample bias, selection bias, etc.) on trend reconstruction but instead to assess reliability across different underlying sampling distributions. Accordingly, our results do not suggest that any of the discussed standardization methods are immune to sample biases (i.e. big tree selection bias, slow grower survivorship bias), as our study is not designed to detect and isolate the effects of contemporaneous differences in growth among trees that produce these biases. There is now substantial evidence to suggest that the long-standing practice of sampling only dominant trees or trees exceeding a minimum size threshold within a stand leads to considerable bias in the resultant chronology (Nehrbass-Ahles et al., 2014; Brienen et al., 2012; Briffa and Melvin, 2011). This bias is consistent across standardization methods (Duchesne et al., 2019; Nehrbass-Ahles et al., 2014). We maintain that in cases of long-term trend reconstruction, stands should be sampled according to the underlying stand age and size distribution, either through use of fixed-plots or random tree selection, regardless of the standardization procedure used.
Given the underlying physiological justification of the models presented here, we have no reason to suggest they are not broadly applicable to species of all shade-tolerance levels. We recommend future studies investigate the applicability of SDS and COMB models to both tree ring width and BAI data in a wider range of species. That said, shade-tolerant and broadleaf species and their applicable standardization procedures are underrepresented in dendrochronological studies (Zhao et al., 2019). Further, the applicability of enhanced tree ring standardization models (including traditional RCS and BAI) to global tree ring data sets are limited by widely unavailable metadata (i.e. tree age and DBH) in tree ring databases. Accordingly, we recommend more stringent requirements on the inclusion of applicable metadata in global databases in order to accommodate more complicated standardization models. We advocate for continued refinement of tree ring standardization procedures that are relevant to the ecological questions they aim to address.
Tree ring data collected in this study are available at https://doi.org/10.17632/3jh73nmxf2.1 (Dietrich, 2019). Additionally, this study uses data tree ring data collected by Kosiba et al. (2013) and Kosiba et al. (2017); these data sets are available through the FEMC DendroEcological Network at https://www.uvm.edu/femc/dendro/project/14 (last access: 9 December 2019) and https://www.uvm.edu/femc/dendro/project/13 (last access: 9 December 2019), respectively.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-4815-2019-supplement.
RD collected the data, conceived and designed the analysis, performed the analysis, and wrote the paper. MA supervised the project and provided critical feedback that helped shape research and analysis.
The authors declare that they have no conflict of interest.
We are grateful to the two anonymous reviewers, whose thoughtful and thorough comments greatly improved the impact and intelligibility of this paper. We are also grateful to the staff of the Ontario Forest Research Institute, who supported fieldwork for this study, particularly F. Wayne Bell. Further, we thank Ontario Parks and the Haliburton Forest Reserve for providing access to field sites.
This research has been supported by the Natural Sciences and Engineering Research Council of Canada (grant nos. 400453 and 519655) and the Ministry of Natural Resources and Forestry.
This paper was edited by Sebastiaan Luyssaert and reviewed by two anonymous referees.
Battipaglia, G., Saurer, M., Cherubini, P., Calfapietra, C., McCarthy, H. R., Norby, R. J., and Francesca Cotrufo, M.: Elevated CO2 increases tree-level intrinsic water use efficiency: insights from carbon and oxygen isotope analyses in tree-rings across three forest FACE sites, New Phytol., 197, 544–554, 2013.
Boisvenue, C. and Running, S. W.: Impacts of climate change on natural forest productivity–evidence since the middle of the 20th century, Glob. Change Biol., 12, 862–882, 2006.
Bontemps, J. D. and Esper, J.: Statistical modelling and RCS detrending methods provide similar estimates of long-term trend in radial growth of common beech in north-eastern France, Dendrochronologia, 29, 99–107, 2011.
Brienen, R. J., Gloor, E., and Zuidema, P. A.: Detecting evidence for CO2 fertilization from tree-ring studies: The potential role of sampling biases, Global Biogeochem. Cy., 26, GB1025, https://doi.org/10.1029/2011GB004143, 2012.
Biondi, F. and Qeadan, F.: A theory-driven approach to tree-ring standardization: defining the biological trend from expected basal area increment, Tree-Ring Res., 64, 81–97, 2008.
Briffa, K. R. and Melvin, T. M.: A closer look at regional curve standardization of tree-ring records: justification of the need, a warning of some pitfalls, and suggested improvements in its application, in: Dendroclimatology, 113–145, Springer, Dordrecht, 2011.
Briffa, K. R., Jones, P. D., Bartholin, T. S., Eckstein, D., Schweingruber, F. H., Karlen, W., Zetterberg, P., and Eronen, M.: Fennoscandian summers from AD 500: temperature changes on short and long timescales, Clim. Dynam., 7, 111–119, 1992.
Briffa, K. R., Jones, P. D., Schweingruber, F. H., Karlén, W., and Shiyatov, S. G.: Tree-ring variables as proxy-climate indicators: problems with low-frequency signals, in: Climatic variations and forcing mechanisms of the last 2000 years, 9–41, Springer, Berlin, Heidelberg, 1996.
Bunn, A., Korpela, M., Biondi, F., Campelo, F., Mérian, P., Qeadan, F., Zang, C., Pucha-Cofrep, D., and Wernicke, J.: dplR: Dendrochronology Program Library in R. R package version 1.6.9, available at: https://github.com/AndyBunn/dplR (last access: 6 December 2019), 2018.
Canham, C. D., LePage, P. T., and Coates, K. D.: A neighborhood analysis of canopy tree competition: effects of shading versus crowding, Can. J. Forest Res., 34, 778–787, 2004.
Camarero, J. J., Gazol, A., Tardif, J. C., and Conciatori, F.: Attributing forest responses to global-change drivers: limited evidence of a CO2-fertilization effect in Iberian pine growth, J. Biogeogr., 42, 2220–2233, 2015.
Cook, E. R. and Kairiukstis, L. A. (Eds.): Methods of dendrochronology: applications in the environmental sciences, Springer Science & Business Media, 2013.
Cook, E. R., Briffa, K. R., Meko, D. M., Graybill, D. A., and Funkhouser, G.: The “segment length curse” in long tree-ring chronology development for palaeoclimatic studies, Holocene, 5, 229–237, 1995.
Chen, L., Huang, J. G., Dawson, A., Zhai, L., Stadt, K. J., Comeau, P. G., and Whitehouse, C.: Contributions of insects and droughts to growth decline of trembling aspen mixed boreal forest of western Canada, Glob. Change Biol., 24, 655–667, 2018.
Dietrich, R.: Data for: When trees don't act their age: size-deterministic tree ring standardization for long-term trend estimation in shade tolerant tree, Mendeley Data, v1, https://doi.org/10.17632/3jh73nmxf2.1, 2019.
Dietrich, R., Bell, F. W., Silva, L. C., Cecile, A., Horwath, W. R., and Anand, M.: Climatic sensitivity, water-use efficiency, and growth decline in boreal jack pine (Pinus banksiana) forests in Northern Ontario, J. Geophys. Res.-Biogeo., 121, 2761–2774, 2016.
Duchesne, L., Houle, D., Ouimet, R., Caldwell, L., Gloor, M., and Brienen, R.: Large apparent growth increases in boreal forests inferred from tree-rings are an artefact of sampling biases, Sci. Rep.-UK, 9, 6832, https://doi.org/10.1038/s41598-019-43243-1, 2019.
Esper, J., Cook, E. R., Krusic, P. J., Peters, K., and Schweingruber, F. H.: Tests of the RCS method for preserving low-frequency variability in long tree-ring chronologies, Tree-Ring Res., 59, 81–98, 2003.
Gavin, D. G., Beckage, B., and Osborne, B.: Forest dynamics and the growth decline of red spruce and sugar maple on Bolton Mountain, Vermont a comparison of modeling methods, Can. J. Forest Res., 38, 2635–2649, 2008.
Gedalof, Z. E. and Berg, A. A.: Tree-ring evidence for limited direct CO2 fertilization of forests over the 20th century, Global Biogeochem. Cy., 24, GB3027, https://doi.org/10.1029/2009GB003699, 2010.
Giguère-Croteau, C., Boucher, É., Bergeron, Y., Girardin, M. P., Drobyshev, I., Silva, L. C., Hélie, J. F., and Garneau, M.: North America's oldest boreal trees are more efficient water users due to increased [CO2], but do not grow faster, P. Natl. Acad. Sci. USA, 116, 2749–2754, https://doi.org/10.1073/pnas.1816686116, 2019.
Girardin, M. P., Bernier, P. Y., Raulier, F., Tardif, J. C., Conciatori, F., and Guo, X. J.: Testing for a CO2 fertilization effect on growth of Canadian boreal forests, J. Geophys. Res.-Biogeo., 116, G01012, https://doi.org/10.1029/2010JG001287, 2011.
Granda, E., Rossatto, D. R., Camarero, J. J., Voltas, J., and Valladares, F.: Growth and carbon isotopes of Mediterranean trees reveal contrasting responses to increased carbon dioxide and drought, Oecologia, 174, 307–317, 2014.
Helama, S., Lindholm, M., Timonen, M., and Eronen, M.: Detection of climate signal in dendrochronological data analysis: a comparison of tree-ring standardization methods, Theor. Appl. Climatol., 79, 239–254, 2004.
Helama, S., Melvin, T. M., and Briffa, K. R.: Regional curve standardization: State of the art, Holocene, 27, 172–177, 2017.
Herguido, E., Granda, E., Benavides, R., García-Cervigón, A. I., Camarero, J. J., and Valladares, F.: Contrasting growth and mortality responses to climate warming of two pine species in a continental Mediterranean ecosystem, Forest Ecol. Manage., 363, 149–158, 2016.
Homann, P. S., McKane, R. B., and Sollins, P.: Belowground processes in forest-ecosystem biogeochemical simulation models, Forest Ecol. Manage., 138, 3–18, 2000.
Huang, J. G., Bergeron, Y., Denneler, B., Berninger, F., and Tardif, J.: Response of forest trees to increased atmospheric CO2, CRC Cr. Rev. Plant Sci., 26, 265–283, 2007.
Jacoby, G. C. and D'Arrigo, R. D.: Tree-rings, carbon dioxide, and climatic change, P. Natl. Acad. Sci. USA, 94, 8350–8353, 1997.
King, D. A., Davies, S. J., Supardi, M. N., and Tan, S.: Tree growth is related to light interception and wood density in two mixed dipterocarp forests of Malaysia, Funct. Ecol., 19, 445–453, 2005.
Kosiba, A. M., Schaberg, P. G., Hawley, G. J., and Hansen, C. F.: Quantifying the legacy of foliar winter injury on woody aboveground carbon sequestration of red spruce trees, Forest Ecol. Manage., 302, 363–371, https://doi.org/10.1016/j.foreco.2013.03.006, 2013 (data available at: https://www.uvm.edu/femc/dendro/project/14, last access: 6 December 2019).
Kosiba, A. M., Schaberg, P. G., Rayback, S. A., and Hawley, G. J.: Comparative growth-trends of five northern hardwood and montane tree species reveal divergent trajectories and response to climate, Can. J. Forest Res., 47, 743–754, https://doi.org/10.1139/cjfr-2016-0308, 2017 (data available at: https://www.uvm.edu/femc/dendro/project/13, last access: 6 December 2019).
Lehnebach, R., Beyer, R., Letort, V., and Heuret, P.: The pipe model theory half a century on: a review, Ann. Bot.-London, 121, 773–795, 2018.
Liang, E., Leuschner, C., Dulamsuren, C., Wagner, B., and Hauck, M.: Global warming-related tree growth decline and mortality on the north-eastern Tibetan plateau, Climatic Change, 134, 163–176, 2016.
Linares, J. C., Delgado-Huertas, A., Julio Camarero, J., Merino, J., and Carreira, J. A.: Competition and drought limit the response of water-use efficiency to rising atmospheric carbon dioxide in the Mediterranean fir Abies pinsapo, Oecologia, 161, 611–624, 2009.
Marqués, L., Camarero, J. J., Gazol, A., and Zavala, M. A.: Drought impacts on tree growth of two pine species along an altitudinal gradient and their use as early-warning signals of potential shifts in tree species distributions, Forest Ecol. Manage., 381, 157–167, 2016.
Martinelli, N.: Climate from dendrochronology: latest developments and results, Global Planet. Change, 40, 129–139, 2004.
Martínez-Vilalta, J., López, B. C., Adell, N., Badiella, L., and Ninyerola, M.: Twentieth century increase of Scots pine radial growth in NE Spain shows strong climate interactions, Glob. Change Biol., 14, 2868–2881, 2008.
Melvin, T. M., Briffa, K. R., Nicolussi, K., and Grabner, M.: Time-varying-response smoothing, Dendrochronologia, 25, 65–69, 2007.
Munné-Bosch, S.: Aging in perennials, Crit. Rev. Plant Sci., 26, 123–138, 2007.
Nehrbass-Ahles, C., Babst, F., Klesse, S., Nötzli, M., Bouriaud, O., Neukom, R., Dobbertin, M., and Frank, D.: The influence of sampling design on tree-ring-based quantification of forest growth, Glob. Change Biol., 20, 2867–2885, 2014.
Nock, C. A., Baker, P. J., Wanek, W., Leis, A., Grabner, M., Bunyavejchewin, S., and Hietz, P.: Long-term increases in intrinsic water-use efficiency do not lead to increased stem growth in a tropical monsoon forest in western Thailand, Glob. Change Biol., 17, 1049–1063, 2011.
Norby, R. J., DeLucia, E. H., Gielen, B., Calfapietra, C., Giardina, C. P., King, J. S., Ledford, J., McCarthy, H. R., Moore, D. J. P., Ceulemans, R., De Angelis, P., Finzi, A. C., Karnosky, D. F., Kubiske, M. E., Lukac, M., Pregitzer, K. S., Scarascia-Mugnozza, G. E., Schlesinger, W. H., and Oren, R.: Forest response to elevated CO2 is conserved across a broad range of productivity, P. Natl. Acad. Sci. USA, 102, 18052–18056, 2005.
Peñuelas, J., Canadell, J. G., and Ogaya, R.: Increased water-use efficiency during the 20th century did not translate into enhanced tree growth, Global Ecol. Biogeogr., 20, 597–608, 2011.
Peters, R. L., Groenendijk, P., Vlam, M., and Zuidema, P. A.: Detecting long-term growth-trends using tree-rings: a critical evaluation of methods, Glob. Change Biol., 21, 2040–2054, 2015.
Silva, L. C. and Anand, M.: Probing for the influence of atmospheric CO2 and climate change on forest ecosystems across biomes, Global Ecol. Biogeogr., 22, 83–92, 2013.
Silva, L. C., Anand, M., and Leithead, M. D: Recent widespread tree growth decline despite increasing atmospheric CO2, PloS one, 5, e11543, https://doi.org/10.1371/journal.pone.0011543, 2010.
Stayton, C. L. and Hoffman, M.: Estimating sugar maple bark thickness and volume, USDA Forest Service Research Paper NC-38, St. Paul, Minnesota, USA, 1970.
Sullivan, P. F., Pattison, R. R., Brownlee, A. H., Cahoon, S. M., and Hollingsworth, T. N.: Effect of tree-ring detrending method on apparent growth-trends of black and white spruce in interior Alaska, Environ. Res. Lett., 11, 114007, https://doi.org/10.1088/1748-9326/11/11/114007, 2016.
Villalba, R., Lara, A., Masiokas, M. H., Urrutia, R., Luckman, B. H., Marshall, G. J., Mundo, I. A., Christie, D. A., Cook, E. R., Neukom, R., Allen, K., Fenwick, P., Boninsegna, J. A., Srur, A. M., Morales, M. S., Araneo, D., Palmer, J. G., Cuq, E., Aravena, J. C., Holz, A., and LeQuesne, C.: Unusual Southern Hemisphere tree growth patterns induced by changes in the Southern Annular Mode, Nat. Geosci., 5, 793, https://doi.org/10.1038/ngeo1613, 2012.
Wang, G., Chhin, S., and Bauerle, W. L.: Effect of natural atmospheric CO2 fertilization suggested by open-grown white spruce in a dry environment, Glob. Change Biol., 12, 601–610, 2006.
West, G. B., Brown, J. H., and Enquist, B. J.: A general model for ontogenetic growth, Nature, 413, 628, https://doi.org/10.1038/35098076, 2001.
Wood, S. N.: Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models, J. R. Stat. Soc. B, 73, 3–36, 2011.
Zhao, S., Pederson, N., D'Orangeville, L., HilleRisLambers, J., Boose, E., Penone, C., Bauer, B., Jiang, Y., and Manzanedo, R. D.: The International Tree-Ring Data Bank (ITRDB) revisited: Data availability and global ecological representativity, J. Biogeogr., 46, 355–368, 2019.





