Modeling anaerobic soil organic carbon decomposition in Arctic polygon tundra: insights into soil geochemical influences on carbon mineralization

Rapid warming of Arctic ecosystems exposes soil organic matter (SOM) to accelerated microbial decomposition, potentially leading to increased emissions of carbon dioxide (CO₂) and methane (CH₄) that have a positive feedback on global warming. Current estimates of the magnitude and form of carbon emissions from Earth system models include significant uncertainties, partially due to the oversimplified representation of geochemical constraints on microbial decomposition. Here, we coupled modeling principles developed in different disciplines, including a thermodynamically based microbial growth model for methanogenesis and iron reduction, a pool-based model to represent upstream carbon transformations, and a humic ion-binding model for dynamic pH simulation to build a more versatile carbon decomposition model framework that can be applied to soils under varying redox conditions. This new model framework was parameterized and validated using synthesized anaerobic incubation data from permafrost-affected soils along a gradient of fine-scale thermal and hydrological variabilities across Arctic polygonal tundra. The model accurately simulated anaerobic CO₂ production and its temperature sensitivity using data on labile carbon pools and fermentation rates as model constraints. CH₄ production is strongly influenced by water content, pH, methanogen biomass, and presence of competing electron acceptors, resulting in high variability in its temperature sensitivity. This work provides new insights into the interactions of SOM pools, temperature increase, soil geochemical feedbacks, and resulting CO₂ and CH₄ production. The proposed anaerobic carbon decomposition framework presented here builds a mechanistic link between soil geochemistry and carbon mineralization, making it applicable over a wide range of soils under different environmental settings.

1 Introduction

The northern permafrost region contains 1400–1800 Pg soil carbon (C), which is more than twice as much C as is currently contained in the atmosphere (Tarnocai et al., 2009; McGuire et al., 2012). Persistent cold and saturated soil conditions have limited C decomposition in this reservoir. However, rapid warming and permafrost thaw expose previously frozen organic carbon to accelerated microbial decomposition, potentially leading to emissions of carbon dioxide (CO₂) and methane (CH₄) that have a positive feedback on global warming (Zimov et al., 2006; Schuur et al., 2009, 2015). How quickly frozen soil organic matter (SOM) will be mineralized, and how much permafrost C will be released to the atmosphere following thaw, is highly uncertain. Earth system models project 27–508 Pg carbon release from the permafrost zone by 2100 under current climate forcing (Zhuang et al., 2006; Koven et al., 2015; MacDougall et al., 2012; Schaefer et al., 2014). Understanding environmental dependencies of SOM decomposition is therefore essential for reducing model uncertainties and improving predictions of future climate change.

Disagreement in model projections for the northern permafrost region could be due to differences in model structure, model initialization, or parameters used in simulations. Despite increasingly detailed process representations in many models that simulate terrestrial CO₂ and CH₄ fluxes, important geochemical and metabolic constraints might still be poorly represented, oversimplified, or missing in current biogeochemical models (Xu et al., 2016). The northern permafrost region is rapidly changing in response to the changing climate. Rising temperatures not only release more labile carbon from permafrost for decomposition but also create thermal and hydrological heterogeneity that further affects biogeochemical processes. Here, we examine two mechanisms that substantially affect SOM turnover in permafrost-affected soils. First, rising temperature alters the kinetics of biogeochemical reactions (Segers, 1998). This effect is more pronounced at subzero temperature (Bore et al., 2017), and the process rate increase is higher at lower temperature ranges (Davidson and Janssens, 2006). Microbial communities also change with temperature, compounding effects on process rates (Karhu et al., 2014). Models address this temperature effect using empirical functions and parameters (Tuomi et al., 2008; Xu et al., 2016), which might be highly biased depending on model assumptions and original curve-fitting techniques, generating large uncertainties. Second, heterogeneity in permafrost thaw and related hydrological responses creates geochemical gradients in soils. Models use different levels of detail to simulate effects of water saturation (Meng et al., 2012; Xu et al., 2016). Soil moisture limits gas transport, and it is often used as an implicit control on heterotrophic respiration and methanogenesis. However, the explicit processes resulting from soil oxygen depletion (e.g., soil redox status and pH dynamics) are not widely represented (Riley et al., 2011; Meng et al., 2012; Xu et al., 2015).

The extent of SOM decomposition and gas emissions depends upon soil geochemical characteristics beyond temperature and O₂ availability. Among the wide range of environmental variables, pH emerges as a primary control on decomposition by regulating both microbial communities and microbial metabolic activities (Zhalnina et al., 2015; Bethke et al., 2011; Jin and Kirk, 2018). pH affects microbial metabolism by modulating the thermodynamics and kinetics of redox reactions. Redox reactions produce or consume protons, and thus their free energy yields vary with pH (Bethke et al., 2011; Jin and Bethke, 2007). The Gibbs free energy available to anaerobic microorganisms that degrade simple organic molecules generally increases (becomes less favorable) with increasing pH (Bethke et al., 2011). Notably, iron [Fe(III)] reduction is highly proton consuming and becomes less favorable at higher pH (Fig. S1 in the Supplement). Previous studies identified iron reduction as a major process in anoxic Arctic soils (Lipson et al., 2010, 2013), which increases local pH and might favor co-occurring methanogenesis (Tang et al., 2016; Wagner et al., 2017). However, the influence of iron reduction on methanogenesis rates in different soils is rarely investigated. The reactivity of iron and its pH feedback impose additional complexity on the controls of SOM decomposition and associated CH₄ production.

Despite the importance of pH in controlling redox reactions and resulting C emissions, pH change is not explicitly represented in biogeochemical models. Most of the current biogeochemical models apply a single initial pH value for redox reactions without considering proton production and consumption during the processes. Traditional decomposition models use landscape position, soil moisture content, or other proxies for O₂ concentration to determine the form of C release. Scalars on aerobic respiration (Riley et al., 2011; Lawrence et al., 2015) or empirical ratios of CO₂ and CH₄ (Koven et al., 2015) are often used to inform the extent of C decomposition and partitioning of CO₂ and CH₄ production. Reactions that produce or consume protons and the resulting pH changes or ion exchange reactions are not considered in these empirical models. Some process-rich models explicitly include details of methanogen populations and their interactions with substrates and other environmental factors, but these models still lack the capability to simulate pH changes during long-term carbon decomposition. Instead, constant pH is often assumed within bell-shaped pH response functions (Meng et al., 2012; Tian et al., 2010; Xu et al., 2015). Without underlying proton exchange and pH buffering mechanisms, a significant error may occur when rate calculations depend heavily upon the initial choice of a single optimal pH value for various reactions.

In this study, we developed a new anaerobic carbon decomposition model framework with explicit representation of aqueous-phase geochemistry to allow pH and thermodynamic calculations. By coupling three different models, including a thermodynamically based microbial growth model, a substrate pool-based model, and a humic ion-binding model, we built a process-rich carbon decomposition model that allows simultaneous thermodynamic and pH calculations. Results from anoxic incubations of permafrost-affected soils along a hydrological gradient were synthesized to parameterize and validate this new model framework. The main objectives of this study were to (i) examine the role of soil geochemical variables in controlling anaerobic carbon decomposition and carbon release (as both CO₂ and CH₄); (ii) develop a common set of parameters in the new anaerobic carbon decomposition framework to capture variabilities in CO₂ and CH₄ production; and (iii) evaluate model uncertainties in responses to both soil heterogeneity and model parameterization, emphasizing effects of soil saturation, pH, and temperature response.

2 Materials and methods

2.1 Anaerobic carbon decomposition model

The anaerobic carbon decomposition framework was developed with explicit representation of fermentation, methanogenesis, and iron reduction, which were identified as key mechanisms for anaerobic CO₂ and CH₄ production (Roy Chowdhury et al., 2015; Yang et al., 2016; Zheng et al., 2018b). The main structure of this framework included two major components: a simplified Community Land Model with prognostic carbon and nitrogen (CLM-CN) decomposition cascade (converging trophic cascade, or CTC) (Thornton and Rosenbloom, 2005) to facilitate parameterization of the upstream carbon flow entering the aqueous-phase dissolved organic carbon (DOC) pool (Fig. 1, process 1), and an aqueous phase to facilitate calculations of thermodynamics and redox-reaction-associated acid–base chemistry. An empirical approach was used to represent non-aqueous-phase soil organic carbon (SOC) decomposition. Additionally, mechanistic representations of methanogenesis and iron reduction were developed in this work based on aqueous-phase thermodynamic calculations.

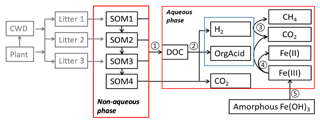
Figure 1 Conceptual diagram showing key processes in the anaerobic carbon decomposition framework, beginning with plant material and coarse wood debris (CWD). The numbers indicate different processes. 1. SOM degradation from soil organic carbon pools with increasing turnover time produces dissolved organic carbon (DOC) and CO₂. 2. Fermentation of DOC into organic acids, H₂, and CO₂. 3. Methanogenesis from organic acids or H₂. 4. Fe(III) reduction from organic acids or H₂. 5. Fe(OH)₃ dissolution.

The simplified CTC cascade included four SOM pools to represent bulk SOC with different levels of complexity. Changes of these SOM pools followed modified first-order decay (see the Supplement for details). We modified the original respiration fraction (Thornton and Rosenbloom, 2005; Koven et al., 2013) into direct and indirect fractions. Thus, for each SOM pool, the direct respiration fraction represented CO₂ lost as originally defined, while the indirect respiration fraction was labile C produced from bulk C entering the aqueous-phase carbon pool (DOC pool, Fig. 1).

The large biomolecules in the DOC pool went through multiple hydrolysis and fermentation steps to produce low-molecular-weight organic acids that would further respire into CO₂ and CH₄ (Boye et al., 2017; Zheng and Graham, 2018; Yang et al., 2016; Roy Chowdhury et al., 2015). Under anoxic conditions, hydrolysis of polysaccharides was considered the rate-limiting step for downstream methanogenesis (Glissmann and Conrad, 2002). Polysaccharide hydrolysis has a favorable free energy, due to increased entropy, but cannot be readily coupled to biological energy transduction outside of the cell. We previously measured a rapid decrease in reducing sugar concentrations in pore water during tundra soil incubations, which indicated that hydrolysis limits decomposition (Yang et al., 2016). At low temperatures (below 15 ^∘C), the microbial degradation of cellulose was considerably diminished, while other polymers, such as starch or proteins, were degraded much faster at low temperature, resulting in the accumulation of organic acids, primarily acetic, propionic, and butyric acids (Kotsyurbenko, 2005; Yang et al., 2016). These low-molecular-weight organic acids further fueled microbial mineralization reactions that led to production of CH₄ and CO₂. Given that most anaerobic lignocellulose degraders also fermented sugars following hydrolysis (Blumer-Schuette et al., 2014), we assumed the turnover of DOC into low-molecular-weight organic acids was a single lumped fermentation process (Fig. 1, process 2), in which labile DOC (C₆H₁₂O₆) was fermented into acetate, H₂, and CO₂ (Appendix A, Reaction AR1, and Table S1 in the Supplement). This assumption gave a fixed stoichiometry ratio: one-third of the fermented carbon was oxidized to CO₂.

Redox reactions including methanogenesis and iron reduction were represented using a thermodynamically based approach (Istok et al., 2010), with unique microbial growth kinetics incorporated into energy-yielding redox reactions. In this thermodynamically based approach, the growth equations of methanogens and iron reducers were derived from paired electron donor (acetate or H₂) and electron acceptor half reactions and a biomass synthesis equation (Istok et al., 2010). Using a constant molecular formula as biomass (C₅H₇O₂N) and ammonium (${\mathrm{NH}}_{\mathrm{4}}^{+}$) as the nitrogen source for biosynthesis, we derived the growth equations for methanogenesis and iron reduction (Appendix A, Reactions AR2–AR5). Rate calculations followed the generalized Monod rate law (Jin and Bethke, 2007) with an additional thermodynamic factor representing the thermodynamic driving force. The thermodynamic factor f(G) is calculated using Eq. (1) (Jin and Bethke, 2003):

$$\begin{array}{}\text{(1)}& f\left(G\right)=\mathrm{1}-\exp \left(-{\displaystyle \frac{-\mathrm{\Delta }G-m\mathrm{\Delta }{G}_{\mathrm{p}}}{\mathit{\chi }RT}}\right),\end{array}$$

where ΔG (kJ (mol reaction)⁻¹) is the free energy change of the redox reaction. ΔG depends on the standard Gibbs free energy change (ΔG⁰) and the concentrations of chemical species involved in the reaction. ΔG_p is the phosphorylation potential, i.e., the energy required to synthesize adenosine triphosphate (ATP) from adenosine diphosphate (ADP) and dihydrogen phosphate in the cell's cytoplasm. ΔG_p is about 45 kJ (mol ATP)⁻¹ (Jin and Kirk, 2018). m is the number of ATP molecules synthesized per redox reaction. χ is the average stoichiometric number (Jin and Kirk, 2018), R is the gas constant (kJ mol⁻¹ K⁻¹), and T is the absolute temperate (K). The factor f(G) ranges from 0 to 1, where the reaction is thermodynamically favorable when f(G)>0.

Both methanogenesis and iron reduction contribute to pH change. Reactions such as ferrihydrite reduction substantially increase alkalinity (Appendix A, Reactions AR4, AR6). Furthermore, the solubility of CO₂ and the composition of dissolved CO₂ and bicarbonate vary significantly over typical soil pH values, affecting all C mineralization processes. In the organic-rich soils modeled here, SOM rather than minerals provides most buffering capacity. Therefore, we used the humic ion-binding model to describe pH buffering during carbon decomposition. A simplified parameterization of proton binding is available in the Windermere Humic Aqueous Model (WHAM; Tipping, 1994, 1998), which has been extensively calibrated to represent the acid–base chemistry of “average” humic and fulvic acids, and benchmarked with heterogeneous natural organic matter (Atalay et al., 2009). We adopted the WHAM parameterization to represent proton-binding characteristics (pH buffering) provided by SOM (Tang et al., 2016). Using representative binding constants provided by WHAM, the pH buffering capacity can be directly adjusted by altering the number of proton-binding sites, which is assumed to be linearly correlated with the total amount of SOM (see the Supplement for details).

2.2 Model implementation and initialization

The above model structure was implemented using the open-source geochemical program PHREEQC 3.0 (Charlton and Parkhurst, 2011) with a new database describing SOC decomposition cascade, redox reaction kinetics, and pH buffering (redox.dat, available at https://github.com/jianqiuz/decomposition, last access: January 2019). This model assumed thermodynamic equilibrium of aqueous chemical speciation, mineral dissolution/precipitation, and ion sorption/desorption based on the updated PHREEQC thermodynamic database (phreeqc.dat; Charlton and Parkhurst, 2011). The database was modified to include WHAM pH buffering and reaction kinetics for SOM pools decay and reaction kinetics for fermentation, methanogenesis, and iron reduction. The kinetic rate constants and microbial biomass growth and decay rates were adopted from former thermodynamically based studies (Istok et al., 2010) and previously tested with low-center polygon Arctic soils (Tang et al., 2016).

The model initialization was based on both the incubation conditions and soil geochemical characterizations (Fig. S2). The initial partitioning of SOM pools was assumed to be at fixed ratios due to the limitation of short-term incubation data. Under the experimental conditions, we assumed SOM1 and SOM2 pools with relatively shorter turnover rates (τ=14 days and 70 days, respectively) were most relevant in the model. On the other hand, SOM3 and SOM4 pools were relatively inert (τ>2 years for both pools). We started with the relative fractions of SOM pools at approximately 10 %, 40 %, 10 %, and 40 % of SOC in organic and mineral soils for SOM1–4. We further assessed the bias of this assumption with sensitivity analysis. Sizes of SOM1 and SOM2 pools were reduced by 90 % for permafrost to better account for the overall low levels of carbon degradation.

All other variables required were initialized using measurements based upon 10 to 15 g of wet soil incubated in 60 to 70 mL sealed bottles. Total SOC, total water (TOTW), total organic acid carbon (TOAC), pH, and the initial concentration of Fe(II) were specified in the model based on measurements (Table S2). The DOC pool in the model was initialized using the measured water-extractable organic carbon (WEOC) expressed as a fraction of SOC (f_doc). On average, WEOC accounts for approximately 2 % of SOC based on our synthesized data (see Sect. 3.1). This value is consistent with previous long-term incubations, which suggested less than 5 % of SOC was fast-decomposing carbon in permafrost-affected soils at a standardized temperature of 4–5 ^∘C (Knoblauch et al., 2013; Schädel et al., 2014). The starting biomass of methanogens and iron reducers was assumed to be within the range of 10⁻³ to 10⁻⁵ g C g SOC⁻¹ for organic soils, 10⁻⁴ to 10⁻⁶ g C g SOC⁻¹ for mineral soils, and 10⁻⁷ to 10⁻⁹ g C g SOC⁻¹ for permafrost (Table S2). This stratified microbial biomass distribution was used to represent the vertical gradient in the relative abundance of microbial communities (Yang et al., 2017).

The lumped fermentation process was the rate-limiting step in the model and was fitted individually with data from each soil microcosm. Based upon reaction stoichiometry, the fermentative conversion of each mole of labile C led to two-thirds of mole of organic acids and one-third of a mole of CO₂. Organic acids were mineralized via methanogenesis or iron reduction to convert approximately 49 % to 88 % of C in organic acids into CO₂. This estimation was based on reaction stoichiometry of Reactions (AR2) and (AR4), and a fraction of the C was incorporated into microbial biomass. Therefore, the percentage of respired C would be less than 100 % even if all organic acids were respired as CO₂. If we assume all fermentation products were mineralized into CH₄ and CO₂, we could estimate the fermentation rate (R_fer) from measured CO₂ production. Thus, R_fer was estimated using the initial CO₂ production rate in the incubation data,and further optimized using the least squares method by fitting with observed CO₂ production values (Table S3).

Temperature and pH response functions were used to further constrain model simulations (Fig. S2). A temperature effect was parameterized using the CLM-CN temperature response function (Appendix B, Eq. B1). Additional temperature response functions were evaluated by sensitivity analysis (see Sect. 2.4). The effect of pH on biological reaction rates is modulated by bell-shaped pH response functions (Tang et al., 2016; Xu et al., 2016). Here, we used the Dynamic Land Ecosystem Model (DLEM) pH response function (Appendix B, Eq. B5), since it generated the least variation in parameter perturbation tests (Tang et al., 2016).

2.3 Incubation data synthesis for model validation

Incubation data from Utqiaġvik (Barrow) Alaska soil cores that represent the microtopographic heterogeneity of polygonal tundra were synthesized to validate the new anaerobic carbon decomposition model. The selected datasets represent fine-scale variabilities in thermal and hydrological regimes across the gradient of soil microtopographic positions (Herndon et al., 2015). The synthesized data contain complete sets of soil geochemical descriptions for organic, mineral, transition zone (if identified), and permafrost layers from each microtopographic feature (see the Supplement for details). Levels of total soil organic carbon, WEOC, and TOAC were available before and after soil incubation. Besides CH₄ and CO₂ production during low-temperature soil decomposition, data on Fe(II) concentrations and pH changes were also available for model initialization and validation.

2.4 Model parameter uncertainty

This model was designed as a generic framework to simulate anaerobic carbon decomposition across a range of soil physiochemical conditions. Two types of sensitivity analysis were conducted to evaluate model performance. First, possible bias and variations associated with model initialization variables (soil geochemical attributes) were assessed using perturbation simulations. Variations of ±25 % and ±50 % (+100 % and 200 % for some variables) were applied to these variables, and the resulting changes in cumulative CO₂ and CH₄ production were evaluated by comparison with reference simulations. This evaluation helps to identify critical measurements needed for initializing the model. Second, parameters specifically benchmarked in this study and parameters adopted from empirical relationships were also evaluated with perturbation simulations. This test helps to apportion the model prediction uncertainties into different sources, including model input, parameters, or model structure.

3 Results

3.1 Meta-analysis to validate model assumptions

Incubation data used in this study were generated from soils representing different microtopographic features with a wide range of moisture and SOC contents and reported elsewhere (Roy Chowdhury et al., 2015; Zheng et al., 2018b). Correlation analysis revealed a close relationship between soil moisture and organic carbon pools (measured as SOC, WEOC, and TOAC) among examined soil microtopographic features and across soil depth (p<0.01, Table S4). All these soil properties significantly correlated with cumulative CO₂ and CH₄ production (p<0.05), suggesting the important role of initial soil geochemical properties in controlling carbon degradation.

Although various levels of carbon mineralization were measured as CO₂ and CH₄ production during incubations, changes in WEOC and TOAC were consistent among treatments with distinct patterns. WEOC represents 0.3 % to 2.6 % of total SOC among all test soils, and this ratio remained constant before and after anoxic incubations (Fig. S3). On the other hand, TOAC showed much more dynamic changes among different soils and different incubation temperatures. TOAC generally increased in soils from the organic layer, transition zone, and permafrost. In contrast, TOAC drastically decreased by up to 90 % in mineral soils. These results indicate that WEOC was in a steady state among examined soils, while TOAC varied substantially due to microbial mineralization processes, supporting the model assumption of lumped fermentation (the conversion of WEOC to TOAC) as the rate-limiting step.

Both CO₂ and CH₄ production rates responded strongly to rising incubation temperature (p=0.02 and p=0.04, respectively; Fig. S4, Tables S5 and S6). The estimated Q₁₀ values of CO₂ production showed a relatively narrow range, while methanogenesis had much larger variation in estimated Q₁₀ values ranging from 1.6 to 48.1. Using Q₁₀ values to simulate the temperature dependence of processes might work for CO₂ production but could generate significant errors in predicting CH₄ production.

Figure 2 Comparison between modeled and observed production of CO₂ (a) and CH₄ (b). Averaged measurements of triplicate microcosms at each time point from each incubation temperature were calculated as observed values.

3.2 Modeled CO₂ and CH₄ production using observed parameters

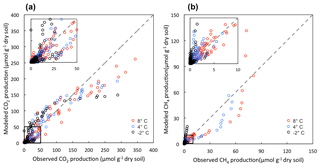
The model performed well in simulating CO₂ and CH₄ dynamics across a range of moisture and SOC gradients and among different soil types (Figs. S5 and S6). Variations in gas production among different conditions, including microtopographic features, soil layers, and different incubation temperatures, were well captured (Fig. S7). The comparisons between modeled and observed CO₂ and CH₄ production are shown in Fig. 2. The model slightly underestimates CO₂ production towards the end of the incubations but still maintains a good agreement between modeled and observed CO₂ production (R²=0.89). The underestimation of CO₂ production is likely due to substrate limitations caused by the initial distribution of different carbon pools. Model-predicted CH₄ production also showed good agreement with observations (R²=0.79). More variation between modeled and observed CH₄ production suggests a systematic pattern in the model parameterization of methanogenesis: the model underestimates CH₄ production at 4 and 8 ^∘C, and overestimates CH₄ production at −2 ^∘C.

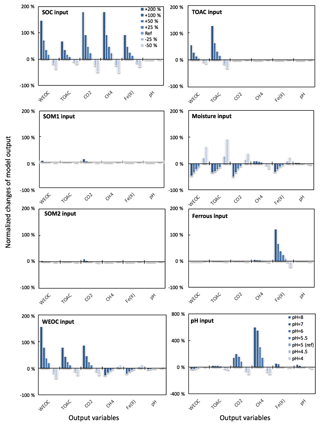
Figure 3 Perturbations of initial soil geochemical conditions differentially affected model predictions (including CH₄, CO₂, Fe(II), TOAC, WEOC, and pH) during anaerobic carbon decomposition. For example, when the initial pH decreased by 8 % and 17 %, CH₄ production decreased by 40 % and 80 %, respectively. Normalized changes in model output were calculated as the ratio of changes caused by perturbation simulations (differences between perturbation and reference runs) to reference simulation output after 60 days of anaerobic decomposition at 8 ^∘C. To test model sensitivity in response to initial pH, the reference run started with pH 6, and up to 1 pH unit changes were applied in perturbation simulations to represent a realistic pH range for soils. Reference simulations were based on soils with 30 % SOC (water content of 2 g g⁻¹ dwt, and pH = 5).

To assess the model sensitivity to initial model inputs, we compared model predictions in response to varying initial model inputs via perturbation simulations. First, we examined the influence of the partitioning of different carbon pools. Significant changes in model predictions of CO₂ and CH₄ were observed in response to perturbations of initial input of SOC and WEOC but not TOAC (Fig. 3). SOC determines the size of different carbon pools in the model, and it further influences the predictions of WEOC, TOAC, CO₂, and CH₄. For example, predicted CO₂ and CH₄ production increased by about 200 % when +200 % changes were applied to initial SOC input. This trend is consistent with correlation analysis of incubation results, described above (Table S4). Perturbations in initial WEOC strongly altered the predictions of TOAC and CO₂, consistent with the model assumption of the conversion of WEOC to TOAC (fermentation process) as the rate-limiting step. The model also predicted increases in CH₄ and Fe(II) accumulation in response to lower WEOC. Lower WEOC significantly reduced organic acid accumulation and thus increased system pH and accelerated rates of both methanogenesis and iron reduction. The starting level of TOAC showed minimal influence on model predictions of CO₂ and CH₄, suggesting other factors rather than substrate availability were limiting carbon mineralization. The initial sizes of SOM1 and SOM2 pools showed very slight changes in model predictions of WEOC and CO₂, and minimal influence on CH₄ prediction, further supporting the assumption that downstream fermentation is the rate-limiting step in the model. Additional soil geochemical factors, including soil moisture, Fe(II), and pH, also significantly influence model output. In particular, initial soil pH showed a dramatic effect on predicted CO₂ and CH₄ production. With initial soil pH increasing from 5 (reference simulation) to 6, the model predicted 160 % and 308 % increases in CO₂ and CH₄ production, respectively. Perturbations in initial soil pH had the strongest effect on the prediction of CH₄ by assigning different values in f_pH that were directly proportional to the methanogenesis rates. The above results of perturbation simulations demonstrated the high sensitivity of this model in response to varying soil geochemical properties.

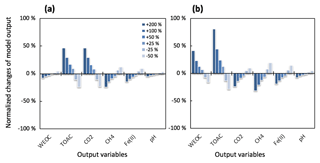
Figure 4 Simulated changes in model predictions (including CH₄, CO₂, Fe(II), TOAC, WEOC, and pH) during anaerobic carbon decomposition in response to perturbations of (a) fermentation rate and (b) fermentation stoichiometry (acetate : CO₂ is 1:1 for reference simulation). Normalized changes in model output were calculated as the ratio of perturbation simulation output to reference simulation output after 60 days of anaerobic decomposition at 8 ^∘C. Reference simulations were based on soils with 30 % SOC (water content of 2 g g⁻¹ dwt, and pH = 6).

3.3 Model sensitivity to parameterization uncertainties

To further validate the model, we performed additional sensitivity analysis to justify model assumptions and estimate the uncertainties generated from model parameterizations. One major assumption of this modeling framework is to lump multiple fermentation processes into one reaction stoichiometry, controlled by one reaction rate constant. It is critical to evaluate how this simplified structure influences model performance and contributes to model output uncertainties. The model parameter sensitivity analysis indicated the TOAC pool was most sensitive to changes in the fermentation rate (R_fer) and reaction stoichiometry (Fig. 4). Downstream reactions were less affected by the uncertainties of the two tested parameters. These results supported our assumption of lumped fermentation with fixed stoichiometry, indicating the robustness of the model structure presented here.

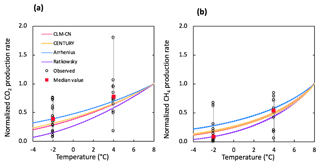
Figure 5 Comparison of simulated and observed temperature responses for the production of CO₂ (a) and CH₄ (b). Results were all normalized to CO₂ or CH₄ production rates at 8 ^∘C for direct comparison. Observations at −2 and 4 ^∘C were plotted in black dots and the median values were marked in red. The shaded area represents output uncertainties generated from rate estimations within 60±5 days. Reference simulations were based on soils with 30 % SOC (water content of 2 g g⁻¹ dwt, and pH = 5).

The selection of temperature response functions represents one of the major sources of model uncertainties. A sensitivity analysis was performed by comparing four different temperature response functions (Appendix B). In our simulations, the quadratic temperature response function proposed by Ratkowsky et al. predicted much higher CO₂ and CH₄ production rates at higher temperature, and the lowest rates of both CO₂ and CH₄ at temperatures below 0 ^∘C, giving the highest temperature response among tested response functions (Fig. 5). In contrast, the Arrhenius equation predicted much lower temperature response for both CO₂ and CH₄. Empirical functions used in the CLM-CN and CENTURY models gave similar temperature responses for both CO₂ and CH₄. Variations in low-temperature CO₂ production are well constrained by established temperature response functions, while CH₄ production at −2 ^∘C showed a much wider range of temperature response, and the median value is best simulated using the Ratkowsky function. This sensitivity analysis is consistent with model output of CO₂ and CH₄ production, where CO₂ is well constrained by the model, but CH₄ is significantly overestimated at −2 ^∘C using the CLM-CN temperature response function. A unified temperature response function for all reactions under different biotic or abiotic constraints substantially contributes to the disagreement between model output and observations.

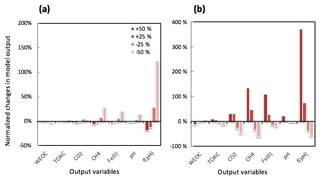
Figure 6 Simulated changes in model predictions (including CH₄, CO₂, Fe(II), TOAC, WEOC, pH, and f_pH) during anaerobic carbon decomposition in response to perturbations of (a) pH buffering capacity and (b) pH response function. Normalized changes in model output were calculated as the ratio of perturbation simulation output to reference simulation output after 60 days of anaerobic decomposition at 8 ^∘C. Reference simulations were based on soils with 30 % SOC (water content of 2 g g⁻¹ dwt, and pH = 5).

Redox reactions contribute to proton production or consumption, and the resulting pH alters the value of the pH response function (f_pH) that directly controls reaction kinetic functions, creating a feedback loop. pH buffering capacity (BC) provided by SOM with proton-binding sites and f_pH represent two major sources of uncertainties in this feedback loop. Thus, we performed perturbation simulations to characterize the sensitivity of model output to variations in BC and f_pH (Fig. 6). Higher BC stabilized system pH during prolonged incubations, while lower BC permitted a pH increase by up to 0.71 pH unit compared to the reference simulation. This 14 % pH increase led to a 123 % increase in f_pH, accelerating both methanogenesis and Fe(III) reduction rates substantially. Perturbations on the pH response function were directly reflected in the slopes of pH response curves (Fig. S8). We found up to 372 % change in the value of f_pH during a 60-day simulation, as a steeper increase in f_pH accelerated both methanogenesis and iron reduction (Reactions AR2–AR5), which contributed to pH rise that further accelerated f_pH increase. Correspondingly, both CH₄ and Fe(II) increased by more than 100 % after the simulation. While BC is an important factor controlling both redox reactions and pH fluctuations, a unified f_pH for all reactions may impose significant variations in model output.

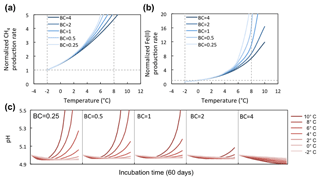
Figure 7 Temperature response of CH₄ and Fe(II) production rates at varying soil pH buffering capacities (BCs). Varying BCs with respect to the reference simulation (BC = 1) creates strong feedback to rates of methanogenesis and iron reduction. Reference simulations were based on soils with 30 % SOC (water content of 2 g g⁻¹ dwt, and pH = 5).

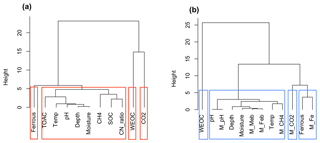
Figure 8 Cluster analysis of soil geochemical properties related to CO₂ and CH₄ production using Ward's linkage method. (a) Cluster analysis of measured soil geochemical characteristics and observed CO₂ and CH₄ production (n=42); (b) cluster analysis of modeled results (n=42). Model-simulated CO₂, CH₄, and Fe(II) production, and final pH values are labeled as M_CO2, M_CH4, M_Fe, and M_pH, respectively. Biomasses of methanogens and iron reducers were tracked in the model and labeled M_Meb and M_Feb, respectively.

BC is an intrinsic soil property simulated with a simplified linear relationship to soil SOM. However, it generates a strong nonlinear response in the simulations of methanogenesis and Fe(III) reduction (Fig. 7a). Simulations with varying soil BC revealed dynamic pH change at lower BC (Figs. 8 and 9, with BC = 1 as the reference simulation) and stabilized pH at higher BC. At constant temperature, rates of both methanogenesis and Fe(III) reduction increased significantly at lower BC due to pH control. At lower BC, when pH change is not well buffered, higher pH accelerated CH₄ and Fe(II) production rates (Fig. 7), giving much higher apparent temperature responses, while at higher BC with stabilized pH in the system, apparent temperature responses of these redox processes were significantly lower than the reference simulation (BC = 1). Variations in pH buffering capacity generated large variations in apparent temperature responses of methanogenesis and Fe(III) reduction due to this pH feedback loop.

4 Discussion

4.1 Synthesized soil geochemistry and model validation

Soil geochemical characteristics represent important abiotic controls on anaerobic carbon decomposition and subsequent CO₂ and CH₄ production. SOC content, soil pH, water table position, C:N ratio, and landscape position were all suggested to contribute to the variability in anaerobic CO₂ and CH₄ production (Lee et al., 2012; Schädel et al., 2014; Treat et al., 2015). We synthesized incubation data for gelisol soils from different pedons and soil moisture regimes representing heterogeneity across the Barrow Environmental Observatory (BEO). This coordinated dataset allowed us to focus on individual factors and their roles in relation to anaerobic CO₂ and CH₄ production.

Carbon released as CO₂ and CH₄ during anoxic incubations decreased with depth. Permafrost was associated with low levels of CO₂ production and very low CH₄ production, consistent with a previous synthesis (Treat et al., 2015). Nevertheless, permafrost TOAC, WEOC, and SOC concentrations were all comparable to organic soils, suggesting high substrate availability but low microbial activity. This trend is consistent with previous studies (Walz et al., 2017; Treat et al., 2015), where highest microbial abundance and diversity were observed in surface soil, and permafrost contained low microbial abundance (Treat et al., 2014; Waldrop et al., 2010). Among surface soils, higher moisture in low-centered polygon soils significantly promoted CO₂ and CH₄ production and the accumulation of fermentation products (measured as TOAC), emphasizing the importance of soil SOC content and moisture as strong environmental drivers for carbon decomposition. Given the bias in correlation analysis created by the skewed distribution of CO₂ and CH₄ production in our dataset, additional cluster analysis was performed based on data similarity rather than correlations. High similarity of soil attributes (depth, moisture, pH, C:N ratio, SOC, TOAC) with CH₄ production (Fig. 8a) was found, suggesting methanogenesis is potentially controlled by a set of soil geochemical characteristics in the local microenvironment.

These synthesized observations support the major assumptions of our model development: (1) the coupled hydrolysis and fermentation processes converting macromolecular SOM into low-molecular-weight organic acids are the rate-limiting step; and (2) different rates of CO₂ and CH₄ production from different soil layers can be attributed to variations in microbial activity manifested as differences in initial microbial biomass or growth rates. Additional observations of substantial Fe(III) reduction and associated pH increases during anaerobic decomposition (Fig. S9) confirmed the need to simulate pH variations associated with redox reactions and corresponding microbial responses. This anaerobic carbon decomposition framework adequately modulated the involved biotic and abiotic interactions by splitting the carbon flow to different redox reactions and simulating pH buffering capacity to mediate associated changes in acidity or alkalinity.

The model presented here identified fermentation, acetoclastic methanogenesis, and acetotrophic iron reduction as key mechanisms for anaerobic CO₂ and CH₄ production (Vaughn et al., 2016; Lipson et al., 2010). Although denitrification, ammonification, and sulfate reduction are all thermodynamically more favorable, low nitrate and sulfate concentrations in BEO soils limit flux through these pathways (Newman et al., 2015). We performed another cluster analysis on the model output (Fig. 8b), where we not only simulated fermentation, methanogenesis and iron reduction rates, and associated pH changes but also tracked the biomass of methanogens (M_Meb) and iron reducers (M_Feb). A dendrogram depicting data similarity showed four distinct clusters consisting of WEOC, CO₂ (CO₂ prediction), ferrous (Fe(II) prediction), and CH₄ (CH₄ prediction) that closely associated with soil geochemical properties and incubation temperature. This result is similar to the cluster analysis of synthesized data, demonstrating that the proposed model structure captured major relationships between carbon mineralization and soil geochemical attributes. Predicted CH₄ production is strongly influenced by incubation temperature, soil pH, soil moisture, and depth which determine the size of the methanogen population. This model prediction is consistent with previous studies on the vertical distribution of methanogen population (Waldrop et al., 2010). Environmental factors, such as labile organic matter, water table depth, and soil redox status, soil alkalinity, and salinity (Wachinger et al., 2000; Rivkina et al., 2007; Høj et al., 2006; Yang et al., 2017) are all likely to contribute to the variabilities in the distribution and abundance of methanogens and subsequent methane production.

4.2 Temperature and pH response of anaerobic carbon decomposition

Rising temperature promotes anaerobic carbon decomposition, resulting in increased rates of anaerobic CO₂ and CH₄ production (Treat et al., 2014; Lupascu et al., 2012). It is widely recognized that methanogenesis is more sensitive to temperature than respiration (Yvon-Durocher et al., 2012, 2014), and it is usually associated with large variations. Segers estimated the Q₁₀ value of methanogenesis ranged from 1.5 to 28 among 1043 incubation experiments using wetland soils (Segers, 1998). Our data synthesis revealed higher temperature sensitivity than other reported values. High estimated temperature sensitivity across the freezing point of water has previously been documented (Waldrop et al., 2010) and further attributed to limited water availability for microbial activities at subzero temperature (Tilston et al., 2010). Ratkowsky et al. proposed a quadratic relationship for the temperature dependence of microbial growth rates that modeled low-temperature growth better than the Arrhenius law (Ratkowsky et al., 1982). Our simulations suggest better prediction of methanogenesis with this temperature response function, possibly due to a more suitable representation of growth limitation of methanogens at subzero temperature. Methanogenesis rates are also influenced by the availability of alternative electron acceptors and carbon source. Processes contributing to the accumulation or consumption of carbon substrates and competing electron acceptors may respond differently to temperature change, which could further complicate the temperature sensitivity of methanogenesis. Current modeling approaches heavily depend upon empirical temperature response functions, which may be associated with large uncertainties due to variations in the selection of data and curve-fitting methods. Extrapolation of carbon decomposition rates, particularly methanogenesis rates, into a future warmer climate remains uncertain. More accurate simulations will require additional information on geochemical properties that contribute to the variations of methanogens distribution and methanogenesis activity.

pH values impose fundamental physiological restrictions on microbial activities. Soil pH ranges from acidic to circumneutral (pH 4–7.5) in northern Alaska and varies substantially through the soil profile and along the microtopographic gradient. Accumulation of organic acids in anoxic soils leads to pH decline (Jones et al., 2003), while consumption of organic acids by methanogenesis and iron reduction increases the alkalinity of the system via the production of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and OH⁻ (Drake et al., 2015; Roy Chowdhury et al., 2015; Howell et al., 1998). The interplay of these processes leads to strong nonlinear pH feedbacks in the system, and previous studies have observed up to 1–2 pH unit changes during short-term anoxic incubations (Xu et al., 2015; Drake et al., 2015; Roy Chowdhury et al., 2015). These relationships between pH and organic carbon decomposition can vary in sign and magnitude. Our model simulations with mechanistic pH evolution indicate that constant pH assumed in previous models may cause significant errors in simulating long-term anaerobic CO₂ and CH₄ production. The intrinsic soil pH buffering capacity plays a large role in stabilizing soil pH and may be heterogeneous depending upon solution acidity or alkalinity, cation exchange capacity and residual acidity or mineral dissolution. These properties derive from SOM characteristics, moisture, mineral content, and additional geochemical properties, leading to complex correlations between soil pH and SOC decomposition rate that require future investigation.

4.3 Fast-decomposing carbon pool

Substrate availability is a primary determinant of potential CO₂ and CH₄ production (Lee et al., 2012; Schuur et al., 2015; Tarnocai et al., 2009). Total SOC is composed of heterogeneous C pools characterized by different turnover times. Carbon release during short-term incubation originates from the C pool with relatively rapid turnover. The size and turnover time of this quickly metabolized carbon pool are usually estimated by two-pool or three-pool conceptual models with a maximum likelihood solution using time series of CO₂ data (Schädel et al., 2013). A previous study on Siberian permafrost soils using a two-pool model estimated a turnover time of 0.26 years for the fastest-responding pool (Knoblauch et al., 2013). A three-pool model was applied using more extensive incubation datasets collected from 23 high-latitude ecosystems, yielding an estimate of a 0.35-year mean turnover time for the fastest-responding carbon pool (Schädel et al., 2014).

In our synthesis study, we directly quantified WEOC and assumed it represented the fast-decomposing labile carbon pool. The size of the labile carbon pool is constant during anaerobic decomposition, while total CO₂ and CH₄ release represent up to 194 % of the labile carbon pool, indicating continuous replenishment of the labile carbon pool from non-labile carbon pools within the hierarchy. The replenishment of the labile carbon pool can be attributed mostly to decomposition of SOM1 and SOM2 pools with faster turnover (Koven et al., 2013). Overall, we estimated the fast-decomposed carbon pool is approximately 2 %–4 % of total SOC, similar to previous estimates. The turnover time calculated from the fermentation rate was comparable to estimates of the turnover time of the fastest-responding carbon pool in previous studies (Fig. 9), suggesting these quantifications and parameterization in the anaerobic carbon decomposition framework apply broadly.

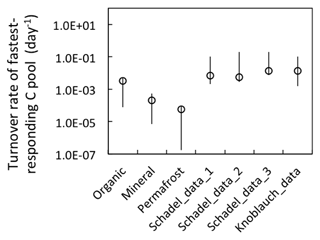
Figure 9 Model-estimated turnover rates of the fastest-decomposing carbon pool. Organic, mineral, and permafrost labels represent estimations from our model simulations (rates estimated at 4 ^∘C). Schadel data represent turnover rates estimated via a three-pool model from pooled anaerobic incubations with normalized incubation temperature of 5 ^∘C (tags 1, 2, and 3 represent pool estimation from different soil types: 1. organic, 2. mineral <1 m, 3. mineral >1 m). Knoblauch data are rate estimates (at 4 ^∘C) made via a two-pool model (Schädel et al., 2014; Knoblauch et al., 2013). Open symbols represent the average values, and the vertical lines represent the estimated range.

4.4 Key features of the anaerobic model framework and future considerations

Here, we present an anaerobic carbon decomposition framework by combining three well-known modeling approaches developed in different disciplines. A pool-based model to represent upstream carbon transformations and replenishment of a DOC pool, a thermodynamically based model to calculate rate kinetics and biomass growth for methanogenesis and Fe(III) reduction, and a humic ion-binding model for aqueous-phase speciation and pH calculation are implemented into the open-source geochemical model PHREEQC (Charlton and Parkhurst, 2011). The model framework presented here has several unique features. First, this model is built upon a thermodynamically based approach, which allows consistent parameterization of individual reactions along the redox ladder. Such a model structure is particularly useful in circumstances when function-specific microbial growth is difficult to quantify and parameterize. Second, calculations of free energy changes of redox couples are used to modulate redox reaction hierarchy. Considering the difficulty in obtaining growth-associated parameters for every functional group, a thermodynamically based approach significantly decreases the number of parameters that are difficult to measure. In addition, proton production and consumption during redox reactions are incorporated into a dynamic pH calculation, allowing various simulations on aqueous solubility and reactivity of different elements. The anaerobic carbon decomposition framework presented here holds a significant advantage over traditional models in simulating carbon decomposition process within a wide range of environmental settings.

In permafrost-affected regions, studies consistently identify iron reduction, denitrification, and sulfate reduction (Lipson et al., 2010, 2013; Ernakovich et al., 2017; Hansen et al., 2007) as alternative anaerobic pathways, which are recognized as energetically more favorable processes than methanogenesis. Fe reduction makes a significant contribution to total respiration (Roy Chowdhury et al., 2015; Herndon et al., 2015), and adding Fe reduction simulations to a baseline model (without Fe reduction or dynamic pH calculations) caused faster decreases in TOAC and WEOC pools and increased CO₂ production as expected (Fig. S10). More indirect feedbacks were revealed when dynamic pH calculation was enabled. With dynamic pH simulation during anaerobic decomposition, the model revealed strong pH dynamics that are counterbalanced by Fe reduction. By including both Fe reduction and dynamic pH calculations, the model accurately reproduced the initial pH drop and subsequent pH rise during incubations, which were commonly observed in permafrost-affected soils (Roy Chowdhury et al., 2015; Herndon et al., 2015). The new model framework presented here provides a basis for a deeper understanding of carbon decomposition under oxygen-limited conditions where the importance of accounting for alternative election acceptors and pH feedbacks becomes more pronounced. Future fine-scale experiments on carbon decomposition using alternative electron acceptors would be beneficial for more comprehensive parameterization of this model framework. Additional observations on temperature and pH sensitivity of specific redox reactions would also be quite useful in reducing large uncertainties generated by the current representation of temperature and pH responses. Application of such a modeling framework at the field scale requires close coupling with hydrology models to facilitate estimations of aqueous-phase concentrations. Additional assumptions on vertical mixing and gas diffusion in the soil column should also be considered.

5 Conclusions

Microbial processes are the driving forces for biogeochemical cycling of soil carbon and are subjected to environmental constraints beyond temperature and organic substrate availability. The present study incorporated microbial redox reactions and mechanistic pH evolution to simulate anaerobic carbon decomposition in Arctic soils with depth and across soil moisture gradients. Our data synthesis and modeling results quantify direct effects of temperature on anaerobic carbon decomposition, as well as indirect effects of soil geochemistry that cause strong redox reaction–pH feedback. We identified substantial pH feedbacks on the predicted CO₂ and CH₄ production. The anaerobic carbon decomposition framework presented in this study provided the essential model structure to incorporate redox reactions of alternative electron acceptors for accurate simulation of CO₂ and CH₄ production. Soil geochemistry imposes critical constraints on SOM decomposition and further regulates permafrost carbon feedback in response to changing climate.

Appendix A: Anaerobic carbon decomposition model

This section lists reactions used in the anaerobic carbon decomposition model. Under anaerobic conditions, dissolved organic carbon is converted to low-molecular-weight organic acids via fermentation. One simplified fermentation reaction is used to represent this lumped fermentation process, where one-third of the fermented organic carbon is converted to CO₂ (Tang et al., 2016; Xu et al., 2015):

$$\begin{array}{}\text{(AR1)}& {\displaystyle }{\mathrm{C}}_{\mathrm{6}}{\mathrm{H}}_{\mathrm{12}}{\mathrm{O}}_{\mathrm{6}}+\mathrm{4}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \mathrm{2}{\mathrm{CH}}_{\mathrm{3}}{\mathrm{COO}}^{-}+\mathrm{2}{\mathrm{HCO}}_{\mathrm{3}}^{-}+\mathrm{4}{\mathrm{H}}^{+}+\mathrm{4}{\mathrm{H}}_{\mathrm{2}}.\end{array}$$

This fermentation reaction generates protons and decreases pH in the system. Fermentation products acetate and H₂ are further consumed via methanogenesis and iron reduction. The growth equations of methanogenesis and iron reduction were derived for each group using a thermodynamically based approach, in which biomass synthesis is included in paired electron donor and electron acceptor half reactions. A general molecular formula (C₅H₇O₂N) is used for microbial biomass, and the growth equations are written as (Istok et al., 2010)

$$\begin{array}{ll}\text{(AR2)}& {\displaystyle }& {\displaystyle }\mathrm{1.5}{\mathrm{H}}^{+}+\mathrm{98.2}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{NH}}_{\mathrm{4}}^{+}+\mathrm{103.7}{\mathrm{CH}}_{\mathrm{3}}{\mathrm{COO}}^{-}{\displaystyle }& {\displaystyle }\to {\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+\mathrm{101.2}{\mathrm{HCO}}_{\mathrm{3}}^{-}+{\mathrm{CH}}_{\mathrm{4}}\end{array}$$

$$\begin{array}{ll}\text{(AR3)}& {\displaystyle }& {\displaystyle }\mathrm{84.9}{\mathrm{H}}^{+}+{\mathrm{NH}}_{\mathrm{4}}^{+}+\mathrm{85.9}{\mathrm{HCO}}_{\mathrm{3}}^{-}+\mathrm{333.5}{\mathrm{H}}_{\mathrm{2}}{\displaystyle }& {\displaystyle }\to {\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+\mathrm{255.6}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{80.9}{\mathrm{CH}}_{\mathrm{4}}\end{array}$$

$$\begin{array}{ll}\text{(AR4)}& {\displaystyle }& {\displaystyle }\mathrm{72.1}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{NH}}_{\mathrm{4}}^{+}+\mathrm{150.2}{\mathrm{Fe}}^{\mathrm{3}+}+\mathrm{21.3}{\mathrm{CH}}_{\mathrm{3}}{\mathrm{COO}}^{-}{\displaystyle }& {\displaystyle }\to {\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+\mathrm{150.2}{\mathrm{Fe}}^{\mathrm{2}+}+\mathrm{167.4}{\mathrm{H}}^{+}+\mathrm{37.5}{\mathrm{HCO}}_{\mathrm{3}}^{-}\end{array}$$

$$\begin{array}{ll}\text{(AR5)}& {\displaystyle }& {\displaystyle }\mathrm{5}{\mathrm{HCO}}_{\mathrm{3}}^{-}+{\mathrm{NH}}_{\mathrm{4}}^{+}+\mathrm{114.8}{\mathrm{Fe}}^{\mathrm{3}+}+\mathrm{57.4}{\mathrm{H}}_{\mathrm{2}}{\displaystyle }& {\displaystyle }\to {\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+\mathrm{114.8}{\mathrm{Fe}}^{\mathrm{2}+}+\mathrm{110.8}{\mathrm{H}}^{+}+\mathrm{13}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}.\end{array}$$

In addition, Fe(III) concentration was calculated based on the dissolution of representative amorphous ferric hydroxides (Reaction AR6), with a solubility constant K_s0=10^3.96. This process consumes many protons and contributes to pH increases.

$$\begin{array}{}\text{(AR6)}& {\displaystyle }\mathrm{Fe}(\mathrm{OH}{)}_{\mathrm{3}\left(\mathrm{s}\right)}+\mathrm{3}{\mathrm{H}}^{+}\leftrightarrow {\mathrm{Fe}}^{\mathrm{3}+}+\mathrm{3}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

A complete set of rate constants used in this model can be found in Table S1.

Appendix B: Temperature and pH response functions

We used the CLM-CN temperature response function (Eq. B1) in our simulations (Thornton and Rosenbloom, 2005). Additional tested temperature response functions included Eq. (B2), which is used by the CENTURY model (Grosso et al., 2005), the Arrhenius equation (Eq. B3) used in ecosys (Grant, 1998), and the quadratic Eq. (B4) (Ratkowsky et al., 1982). T_ref is set at 25 ^∘C, E_a is the activation energy (J mol⁻¹), and R is the universal gas constant (J K⁻¹ mol⁻¹). T_m used in Ratkowsky's model represents a conceptual temperature of no metabolic significance and is set at −8 ^∘C in this study.

$$\begin{array}{}\text{(B1)}& {\displaystyle }\ln f\left(T\right)=\mathrm{308.56}\times \left({\displaystyle \frac{\mathrm{1}}{\mathrm{71.02}}}-{\displaystyle \frac{\mathrm{1}}{T-\mathrm{227.13}}}\right)\end{array}$$

$$\begin{array}{}\text{(B2)}& {\displaystyle }f\left(T\right)=\mathrm{0.56}+\mathrm{0.465}\arctan \left[\mathrm{0.097}\left(T-\mathrm{15.7}\right)\right]\end{array}$$

$$\begin{array}{}\text{(B3)}& {\displaystyle }f\left(T\right)=e^{\frac{-E_{\mathrm{a}}}{R}\left(\frac{\mathrm{1}}{T}-\frac{\mathrm{1}}{T_{\mathrm{ref}}}\right)}\end{array}$$

$$\begin{array}{}\text{(B4)}& {\displaystyle }f\left(T\right)={\left({\displaystyle \frac{T-T_{\mathrm{m}}}{T_{\mathrm{ref}}-T_{\mathrm{m}}}}\right)}^{\mathrm{2}}\end{array}$$

The discontinuous bell-shaped pH response function from the DLEM model was used here (Eq. B5; Tian et al., 2010):

$$\begin{array}{}\text{(B5)}& {\displaystyle }f\left(\text{pH}\right)={\displaystyle \frac{\mathrm{1.02}}{\mathrm{1.02}+{\mathrm{10}}^{\mathrm{6}}\exp (-\mathrm{2.5}\text{pH})}}\left(\mathrm{0}\mathit{<}\text{pH}\mathit{<}\mathrm{7}\right)\end{array}$$

$$\begin{array}{}\text{(B6)}& {\displaystyle }f\left(\text{pH}\right)={\displaystyle \frac{\mathrm{1.02}}{\mathrm{1.02}+{\mathrm{10}}^{\mathrm{6}}\exp (-\mathrm{2.5}\left(\mathrm{14}\text{-pH}\right))}}\left(\mathrm{7}\mathit{<}\text{pH}\mathit{<}\mathrm{14}\right).\end{array}$$