Causes and consequences of pronounced variation in the isotope composition of plant xylem water

Stable isotopologues of water are widely used to derive relative root water uptake (RWU) profiles and average RWU depth in lignified plants. Uniform isotope composition of plant xylem water (δ_xyl) along the stem length of woody plants is a central assumption of the isotope tracing approach which has never been properly evaluated.

Here we evaluate whether strong variation in δ_xyl within woody plants exists using empirical field observations from French Guiana, northwestern China, and Germany. In addition, supported by a mechanistic plant hydraulic model, we test hypotheses on how variation in δ_xyl can develop through the effects of diurnal variation in RWU, sap flux density, diffusion, and various other soil and plant parameters on the δ_xyl of woody plants.

The hydrogen and oxygen isotope composition of plant xylem water shows strong temporal (i.e., sub-daily) and spatial (i.e., along the stem) variation ranging up to 25.2 ‰ and 6.8 ‰ for δ²H and δ¹⁸O, respectively, greatly exceeding the measurement error range in all evaluated datasets. Model explorations predict that significant δ_xyl variation could arise from diurnal RWU fluctuations and vertical soil water heterogeneity. Moreover, significant differences in δ_xyl emerge between individuals that differ only in sap flux densities or are monitored at different times or heights.

This work shows a complex pattern of δ_xyl transport in the soil–root–xylem system which can be related to the dynamics of RWU by plants. These dynamics complicate the assessment of RWU when using stable water isotopologues but also open new opportunities to study drought responses to environmental drivers. We propose including the monitoring of sap flow and soil matric potential for more robust estimates of average RWU depth and expansion of attainable insights in plant drought strategies and responses.

1 Introduction

The use of the stable isotope composition of water has strengthened ecohydrology studies by providing insights into phenomena that are otherwise challenging to observe, such as relative root water uptake depth (RWU depth) (Rothfuss and Javaux, 2017), belowground water competition, and hydraulic lift (Hervé-Fernández et al., 2016; Meunier et al., 2017). Compared to root excavation, the technique is far less destructive and labor intensive. This makes it more flexible for studying multiple individuals across spatial and temporal scales (i.e., individual to ecosystem, daily to seasonal) (Dawson et al., 2002). Moreover, the study of stable isotope composition of xylem water measures the real effects of RWU at different depths, whereas excavation yields only root distribution and architecture. The advantages and wide applicability of this method make it a popular technique that pushes the boundaries of ecohydrology (Dawson et al., 2002; Lanning et al., 2020; Rothfuss and Javaux, 2017; Yang et al., 2010)

A variety of methods are used to infer average RWU depth from the isotope composition of plant xylem water (δ_xyl), but all rely on a direct relationship between the isotopic compositions of plant xylem and soil water (Ehleringer and Dawson, 1992). All have two key assumptions. The first is that the isotope composition of plant xylem water remains unchanged during transport from root uptake to evaporative sites (e.g., leaves and non-lignified green branches). Hence, isotopic fractionation – i.e., processes that cause a shift in the relative abundances of the water isotopologues, driven by their differences in molecular mass – does not occur during the transport from the uptake to the evaporative site (Dawson et al., 2002; Dawson and Ehleringer, 1991; Walker and Richardson, 1991; Wershaw et al., 1966; White et al., 1985; Zhao et al., 2016; Zimmermann et al., 1967). Second, all methods assume that xylem water provides a well-mixed isotope composition of water from different soil layers; sampled xylem water instantaneously reflects the distribution and water uptake of the roots independent of the timing or height of sampling.

The first assumption is relatively well supported. Isotopic fractionation at root level does not raise concerns for most RWU assessments using water isotopologues (Rothfuss and Javaux, 2017) except for kinetic fractionation that might occur during water transport across the root membrane in extreme environments (Lin and Sternberg, 1993; Ellsworth and Williams, 2007; Zhao et al., 2016). Similarly, isotopic fractionation of water within an individual plant, although possible, is generally not considered a serious problem (Cernusak et al., 2005; Dawson and Ehleringer, 1993; Mamonov et al., 2007; Yakir, 1992; Zhao et al., 2016), but this perception was recently contested by Barbeta et al. (2020). However, the second assumption of time and space invariance of the isotope composition of xylem water has, to our knowledge, never been assessed.

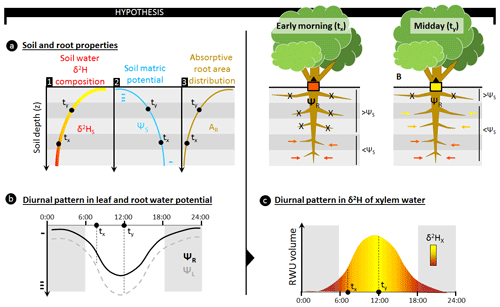
Figure 1 The use of stable water isotopes (δ²H and δ¹⁸O) to assess the relative depth of root water uptake (RWU) requires a depth gradient in isotopic composition of soil water (δ²H_S) to be present (a, sub-panel 1) as only then can the relative contribution of different soil layers to the isotopic composition in a plant's xylem water (δ²H_X) be derived. These δ²H_S gradients occur naturally as the result of evaporative soil drying during drought conditions; however, these conditions also result in the formation of a gradient in soil matric potential (Ψ_S), ensuring an increasing Ψ_S with depth (a, sub-panel 2). RWU and sap flow in plants are passive processes in which water flows in the direction of decreasing water potentials. Specifically for RWU, this implies that water influx through the absorptive root area (A_R; a, sub-panel 3) of a plant's root is facilitated whenever the water potential in the root (Ψ_R) is more negative than the surrounding Ψ_S. As A_R and Ψ_S are generally not uniform with soil depth (z), the relative contribution of a specific soil layer to RWU will depend on (i) the difference between Ψ_S and Ψ_R in that soil layer and (ii) the relative amount of absorptive root area in that soil layer. Stable water isotope techniques assume that the δ²H_X reflects the contribution of δ²H_S from all soil layers. However, this does not account for the diurnal fluctuations in Ψ_R which are invoked by the diurnal patterns in a plant's transpiratory water demands (b). Typically, more negative Ψ_R values are observed when water demands are high, i.e., around midday. However, a decrease in Ψ_R will result in higher RWU and alter the contribution of different soil layers to RWU. Specifically, dryer and shallower soil layers, with more negative Ψ_S, could start contributing to RWU as Ψ_R decreases (c). For example, in the early morning (situation t_x) when Ψ_R is high, only deeper soil layers where Ψ_S is greater than Ψ_R contribute to the overall δ²H composition of the RWU flux. As Ψ_L and Ψ_R decrease towards midday (situation t_y), more water can be absorbed from shallower soil layers. As the A_R in these shallow soil layers is high, they strongly affect the relative contribution of δ²H_S entering the plant. Hence, diurnal fluctuations in Ψ_R will result in fluctuating mixtures of δ²H_S entering the plant. As these δ²H_S mixtures are transported along the xylem pathway, they produce variances in δ²H_X which could complicate RWU assessments via stable water isotope analysis.

Various plant physiological processes, ranging from very simple to more complex mechanisms, could have an influence within plant variation in δ_xyl at short timescales, i.e., sub-daily to sub-hourly. For instance, plant transpiration during the day is regulated by stomata according to water supply and atmospheric demand and follows well-known diurnal patterns (Epila et al., 2017; Steppe and Lemeur, 2004). This results in a changing water potential gradient between soil and leaves throughout the day (Fig. 1a, b) which in turn affects the depth of the average RWU (Doussan et al., 2006; Goldstein et al., 1998; Huang et al., 2017). Hence, shifts in a plant's capacity to take up water at different soil layers during the day can generate diurnal variation in the mixture of isotope composition from water taken up from various depths (Fig. 1c). Subsequently, this water mixture moves up along the xylem with the velocity of the sap flux density. As these sap flux densities depend on species and individual-specific hydraulic traits and on their responses to atmospheric water demand and soil moisture availability, complex dynamics in isotopic composition will emerge and propagate through the plant. The above hypothesis, if true, would make the comparison of isotopic data among individuals, species, and studies difficult.

In this study, we provide a critical assessment of the assumption of δ_xyl invariance along the length of woody plant stems and over short time periods. We first show that variation in δ_xyl along the length of lignified plants exceeds the expected measurement error using three independent datasets including (i) canopy trees and lianas sampled at different heights in French Guiana, (ii) plant species in northwestern China (Zhao et al., 2014), and (iii) European beech and silver firs in southwest Germany (Magh et al., 2020). Second, we build a simple mechanistic model that incorporates basic plant hydraulic transport processes. The model predicts that diurnal changes in water potential gradient between soil and roots result in shifting sources of water absorption that differ in their isotope composition.

2 Materials and methods

2.1 Part A: empirical exploration

2.1.1 Field data French Guiana: variation in δ_xyl with plant height

Six canopy trees and six canopy lianas were sampled during 2 subsequent dry days (24–25 August 2017) at the Laussat Conservation Area in northwestern French Guiana (05^∘28.604^′ N, 053^∘34.250^′ W). The stem xylem tissue of individual plants was sampled at different heights (1.3, 5, 10, 15, and 20 m when possible) at the same radial position of the stem between 09:00 and 15:00 LT (all times are in local time). Stem samples were stripped of bark and phloem tissues. Soil samples were collected at different depths (0.05, 0.15, 0.30, 0.45, 0.60, 0.90, 1.20, and 1.80 m) with a soil auger and in close vicinity to the sampled individuals. Samples were placed in glass collection vials, sealed with a cap, and frozen awaiting cryogenic vacuum distillation (CVD; 4 h at 105 ^∘C). When the weight loss of a sample resulting from the extraction process was below 98 %, the sample was excluded (based on Araguás-Araguás et al., 1998) (see Fig. S1 in the Supplement).

The isotope composition of the water in the samples was measured with a wavelength-scanned cavity ring-down spectrometer (WS-CRDS; L2120-i, Picarro, California, USA) coupled with a vaporizing module (A0211 high-precision vaporizer) and a micro combustion module to avoid organic contamination (Martin-Gomez et al., 2015; Evaristo et al., 2016). Post-processing of raw δ readings into calibrated δ values (in ‰; V-SMOW) was performed using SICalib (version 2.16; Gröning, 2011). More details on the sampling site and sampling procedure can be found in Supplement methods A.

2.1.2 Field data China: temporal variation in δ_xyl

Plant δ_xyl was sampled at high temporal resolution in the Heihe River Basin (HRB), northwestern China. Four distinct study locations differing in altitude, climatological conditions, and ecosystem types were selected. At each location, the dominant tree, shrub, and/or herb species were considered for sampling. In August 2009, Populus euphratica was sampled in the Qidaoqiao riparian forest (42^∘01^′ N, 101^∘14^′ E) and Reaumuria soongarica in the Gobi Desert ecosystem (42^∘16^′ N, 101^∘ 17^′ E; 906–930 m a.s.l., above sea level). In June–September 2011, Picea crassifolia, Potentilla fruticosa, Polygonum viviparum, and Stipa capillata were measured in the Pailugou forest ecosystem (38^∘33^′ N, 100^∘18^′ E; 2700–2900 m a.s.l.). All species were sampled every 2 h over multiple days (3–4), except for P. crassifolia, which was measured hourly. Stem samples were collected for trees and shrubs, while root samples were obtained for the herb species. More details are available in Zhao et al. (2014).

Upon collection, all samples were placed in 8 mL collection bottles and frozen in the field stations before transportation to the laboratory for water extraction via CVD (Zhao et al., 2011). Both δ¹⁸O and δ²H were assessed with a Euro EA3000 element analyzer (Eurovector, Milan, Italy) coupled with an Isoprime isotope ratio mass spectrometer (Isoprime Ltd, UK) at the Heihe Key Laboratory of Ecohydrology and River Basin Science, Cold and Arid Regions Environmental and Engineering Research Institute. Internal laboratory references were used for calibration, resulting in a measurement precision of ±0.2 ‰ and ±1.0 ‰ for δ¹⁸O and δ²H, respectively.

2.1.3 Field data Germany: high temporal variation in δ_xyl

A δ_xyl monitoring campaign studying mature silver firs (Abies alba; n=3) and European beeches (Fagus sylvatica; n=3) was conducted during progressing drought conditions (6–11 July 2017) at the Freiamt field site in southwest Germany. Isotopic composition of xylem water was obtained from branch samples, which were collected every 2 h between 07:00 and 21:00 at the same height and canopy orientation in the sun crown. Branches were stripped of bark and phloem tissue. A Scholander pressure chamber (Scholander, 1966), which allowed concomitant registration of water potential of the sampled branches, was used to extract xylem water directly in the field (Rennenberg et al., 1996). Both δ¹⁸O and δ²H of branch samples were determined with a wavelength-scanned cavity ring-down spectrometer (L2130-i, Picarro, California, USA), followed by data correction using ChemCorrect™ (Picarro, 2010). For more details, see Magh et al. (2020).

2.1.4 Field data normalization

To aid visual comparisons, we use normalized δ_xyl values (β²H_X and β¹⁸O_X) which describe the deviation of an individual sample from the average isotopic composition (a) along the height h of the stem or (b) over 1 day:

$$\begin{array}{}\text{(1)}& {\mathit{\beta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{X}}={\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{X}}-{\displaystyle \frac{\mathrm{1}}{N}}\sum _{j=\mathrm{1}}^N{{\mathit{\delta }}^{\mathrm{2}}\mathrm{H}}_{\mathrm{X},j},\end{array}$$

where N is the number of sampled heights or time steps during 1 day.

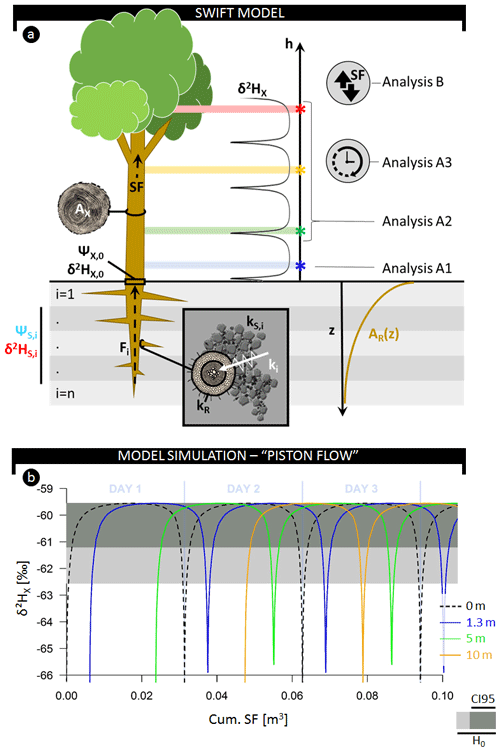
Figure 2 (a) Schematic representation of the model and considered analysis detailed in the text. (b) Simulated fluctuations in δ²H composition of plant xylem water as a function of the cumulative sap flow volume measured at various heights: stem base (0 m, dashed black), 1.3 m (blue), 5 m (green), and 10 m (red). The horizontal gray-colored envelope delineates the acceptable variance from the stem mean according to the null model (H₀), i.e., assuming no variance along the length of a lignified plant aside from the potential extraction error (i.e., 3 ‰). Herein, the dark gray envelope indicates the confidence interval comprising 95 % of potential extraction error (CI95).

2.2 Part B: model exploration

2.2.1 Model derivation

The expected δ_xyl at different stem heights within a tree during the course of the day can be derived from plant and physical properties such as root length density, total fine root surface area, water potential gradients, and the isotope composition of soil water (Fig. 2). We call this the SWIFT model (i.e., Stable Water Isotopic Fluctuation within Trees). To derive the SWIFT model, we first describe the establishment of δ_xyl entering the tree at the stem base via a multisource mixing model (Phillips and Gregg, 2003). We subsequently consider vertical water transport within the tree, which relates to the established sap flow pattern.

To ensure consistency and clarity in variable declarations, we maintain the following notation in the subscripts of variables: uppercase roman to distinguish the medium through which water travels (X for xylem, R for root, and S for soil) and lowercase for units of time and distance (h for stem height, t for time, and i for soil layer index). A comprehensive list of variables, definitions, and units is given in Table 1. A schematic representation of the model is provided in Fig. 2a. Note that the model presented here focuses on hydrogen isotopes (i.e., ²H∕¹H) but can easily be used to study oxygen isotopes (i.e., ¹⁸O∕¹⁶O).

Isotope composition of plant xylem water at stem base

The δ²H composition of xylem water of an individual plant at stem base (δ²H${}_{\mathrm{X},\mathrm{0},t}$) (i.e., height zero; h=0 m; Fig. 2a) at time t can theoretically be derived by calculating a weighted average of water taken up from different soil depths (Phillips and Gregg, 2003). The root zone is divided into n discrete soil layers of equivalent thickness Δz. Here, we assume a constant δ²H composition of soil water (δ²H_S,i) over time in each soil layer, a reasonable assumption when isotopic measurements are conducted during rain-free periods, allowing the expression of δ²H${}_{\mathrm{X},\mathrm{0},t}$ to be as follows:

$$\begin{array}{}\text{(2)}& {{\mathit{\delta }}^{\mathrm{2}}\mathrm{H}}_{\mathrm{X},\mathrm{0},t}={\sum }_{i=\mathrm{1}}^n{f}_{i,t}\times {{\mathit{\delta }}^{\mathrm{2}}\mathrm{H}}_{\mathrm{S},i},\end{array}$$

where f_i,t is the fraction of water taken up at the ith soil layer (Fig. 2a) defined as the following:

$$\begin{array}{}\text{(3)}& f_{i,t}={\displaystyle \frac{{\text{RWU}}_{i,t}}{{\sum }_{i=\mathrm{1}}^n{\text{RWU}}_{i,t}}},\end{array}$$

where RWU_i,t is the net amount of water entering and leaving the roots at time t in the ith soil layer (RWU_i,t is defined positively when entering the root). The current representation of the model does not account for water loss via the root system nor for the mixing of the extracted water from different soil layers within the roots until the water enters the stem base. When tree capacitance is neglected, the sum of RWU_i,t across the entire root zone is equal to the instantaneous sap flow at time t (SF_t):

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& {\text{SF}}_t={\sum }_{i=\mathrm{1}}^n{\text{RWU}}_{i,t}=\sum _{i=\mathrm{1}}^n-k_i\times A_{\mathrm{R},i}\\ & \times \left[{\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}-({\mathrm{\Psi }}_{\mathrm{S},i,t}-z_i)\right],\end{array}\end{array}$$

where k_i is the plant-specific total soil-to-root conductance over soil layer i, ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ is the water potential (i.e., the hydraulic head) at the base of the plant stem, and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ is the soil matric potential at the ith soil layer (Fig. 2a). Total plant water potential is generally defined as the sum of the solute, pressure, gravity, and matric potential. As long-distance water transport through the xylem is studied, the osmotic potential and the kinetic energy head can be assumed negligible (Früh and Kurth, 1999). The xylem pressure potential is represented by ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$. The term z_i is the gravimetric water potential necessary to lift the water from depth z_i to the base of the stem, assuming a hydrostatic gradient in the transporting roots. The model considers z_i to be a positive value (zero at the surface); thus z_i is subtracted from ${\mathrm{\Psi }}_{\mathrm{S},i,t}$. A_R,i is the absorptive root area distribution over soil layer i (Fig. 2a). This parameter, A_R,i, can be derived from plant allometric relations with stem diameter (Čermák et al., 2006) and subsequently distributed over the different soil layers, considering the power-law distribution of Jackson et al. (1995).

The total soil-to-root conductance is calculated assuming that the root and soil resistances are connected in series (Fig. 2a):

$$\begin{array}{}\text{(5)}& k_i={\displaystyle \frac{k_{\mathrm{R}}\times k_{\mathrm{S}}}{k_{\mathrm{R}}+k_{\mathrm{S}}}},\end{array}$$

where k_R is the effective root radial conductivity (assumed constant and uniform) and $k_{\mathrm{S}}=K_{\mathrm{S},i}/l$ is the conductance associated with the radial water flow between soil and root surface. The equation $l=\mathrm{0.53}/\sqrt{\mathit{\pi }\times B_i}$ represents the effective radial pathway length of water flow between bulk soil and root surface (De Jong van Lier et al., 2008; Vogel et al., 2013) with B_i giving the overall root length density distribution per unit of soil. K_S,i is the soil hydraulic conductivity for each soil depth. K_S,i depends on soil water moisture and thus relates to the soil matric potential ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ of the soil layer where the water is extracted. K_S,i is computed using the Clapp and Hornberger (1978) formulation:

$$\begin{array}{}\text{(6)}& K_{\mathrm{S},i}=K_{\text{s,max}}\times {\left({\displaystyle \frac{{\mathrm{\Psi }}_{\text{sat}}}{{\mathrm{\Psi }}_{\mathrm{S},i,t}}}\right)}^{\mathrm{2}+\frac{\mathrm{3}}{b}},\end{array}$$

where K_s,max is the soil conductivity at saturation and b and Ψ_sat are empirical constants that depend on soil type (here considered constant over all soil layers).

Subsequently, f_i,t can be restructured as follows:

$$\begin{array}{}\text{(7)}& f_{i,t}={\displaystyle \frac{k_i\times A_{\mathrm{R},i}\times \mathrm{\Delta }{\mathrm{\Psi }}_{i,t}}{{\sum }_{i=\mathrm{1}}^n{k}_i\times A_{\mathrm{R},i}\times \mathrm{\Delta }{\mathrm{\Psi }}_{i,t}}},\end{array}$$

where the root water to soil matric potential gradient is represented as $\mathrm{\Delta }{\mathrm{\Psi }}_{i,t}={\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}-({\mathrm{\Psi }}_{\mathrm{S},i,t}-z_i$).

Combining Eqs. (2) and (7) then allows the derivation of ${\mathit{\delta }}^{\mathrm{2}}{H}_{\mathrm{X},\mathrm{0},t}$ as follows:

$$\begin{array}{}\text{(8)}& {\mathit{\delta }}^{\mathrm{2}}{H}_{\mathrm{X},\mathrm{0},t}=\sum _{i=\mathrm{1}}^n\left({\displaystyle \frac{k_i\times A_{\mathrm{R},i}\times \mathrm{\Delta }{\mathrm{\Psi }}_{i,t}}{{\sum }_{j=\mathrm{1}}^n{k}_j\times A_{\mathrm{R},j}\times \mathrm{\Delta }{\mathrm{\Psi }}_{j,t}}}\times {\mathit{\delta }}^{\mathrm{2}}{H}_{\mathrm{S},i}\right).\end{array}$$

This equation requires estimates of ΔΨ_i,t, which is preferably measured instantaneously in the field (i.e., via stem and soil psychrometers for ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ respectively). However, as measurements of ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ are not always available, estimated ${\widehat{\mathrm{\Psi }}}_{\mathrm{X},\mathrm{0},t}$ can be derived from sap flow by reorganizing Eq. (4) into

$$\begin{array}{}\text{(9)}& {\widehat{\mathrm{\Psi }}}_{\mathrm{X},\mathrm{0},t}={\displaystyle \frac{\sum _{i=\mathrm{1}}^n\left[k_i\times A_{\mathrm{R},i}\times \left({\mathrm{\Psi }}_{\mathrm{S},i,t}-z_i\right)\right]-{\text{SF}}_t}{\sum _{i=\mathrm{1}}^n{k}_i\times A_{\mathrm{R},i}}},\end{array}$$

which then allows the replacement of ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ with ${\widehat{\mathrm{\Psi }}}_{\mathrm{X},\mathrm{0},t}$ in Eq. (8).

Height-dependent isotope composition of plant xylem water

In our model, the water isotopologues simply move upwards from the stem base with the sap flow velocity. Assuming negligible diffusion, the δ²H isotope composition in xylem water at height h and time t (δ²H${}_{\mathrm{X},h,t}$) is then the isotope composition of xylem water at stem base at time t−τ:

$$\begin{array}{}\text{(10)}& {{\mathit{\delta }}^{\mathrm{2}}\mathrm{H}}_{\mathrm{X},h,t}={{\mathit{\delta }}^{\mathrm{2}}\mathrm{H}}_{\mathrm{X},\mathrm{0},t-\mathit{\tau }},\end{array}$$

where τ is the lag before δ²H${}_{\mathrm{X},\mathrm{0},t}$ reaches stem height h (Fig. 2a), which depends on the true sap flux density in the xylem (SF_V). True sap flux density indicates the real speed of vertical water displacement within a plant and is derived by dividing SF_t over the lumen area of the plant (A_x; Fig. 2a) i.e., the total cross-sectional area of the vessels. The τ value can be obtained from the mass conservation equality:

$$\begin{array}{}\text{(11)}& h\times A_x=\underset{t-\mathit{\tau }}{\overset{t}{\int }}{\text{SF}}_t\mathrm{d}t.\end{array}$$

Note that since most scientific studies express sap flux density as the sap flow over the total sapwood area (SF_S) rather than over the total vessel lumen area (SF_V), for consistency, we will present the model outputs as functions of SF_S.

Note that SF_V presents the sap flux density normalized over the total vessel lumen area, and, as vessel lumen area correlates with plant diameter at breast height (DBH), there is no need for explicit consideration of DBH in the model for comparison among field measurements.

Model analyses show that the impact of the mutual diffusion coefficient of heavy water in normal water on the transport flux is negligible for plants with high sap flux densities, which is the case for the theoretical examples below. However, in plants with low sap flow densities, consideration of diffusion might be required. Diffusion might also be generated by water passing through a complex network of vessels, analogous to diffusion in a porous medium (see Supplement methods B for some analytical results and simulated cases of and a detailed discussion on the role of diffusion). SWIFT was implemented in R version 3.4.0 (R Core Team, 2017) and is publicly available (see GitHub repository HannesDeDeurwaerder/SWIFT).

Model parameterization and analyses

The model's primary purpose is to gain insight into (1) which processes are capable of generating δ_xyl variance and (2) how sensitive the variance in δ_xyl along the stem is in response to the modeled plant hydraulic processes. To this end, we adopted the basic plant parameters from Huang et al. (2017) who studied soil–plant hydrodynamics of loblolly pine (Pinus taeda L.) during a 30 day extended dry down period (Table S1 in the Supplement). We started with synthetic basal sap flow patterns and volumes extracted from the model runs of Huang et al. (2017) for a typical drought day (day 11). Both basal sap flow patterns and volumes are repeated over the studied period as no variation between days is assumed. Sap flow follows the plant's water demand which is the result of daily cycles of transpiration driven by photosynthetic active solar radiation (PAR), vapor pressure deficit (VPD), and optimal stomatal response (Epila et al., 2017). Secondly, both the soil matric potential $({\mathrm{\Psi }}_{\mathrm{S},i,t}$) and δ²H composition of soil water (δ²H_S,i) profiles with soil depth were adopted from Meißner et al. (2012) (Fig. S8; see Table S1 for equations) as driver data of the model and were assumed to stay constant over time. Since the measurements of Meißner et al. (2012) were conducted at a silt loam plot in the temperate climate of central Germany, corresponding soil parameters were selected from Clapp and Hornberger (1978). Subsequently, the following model simulations were executed (see Fig. 2a).

1. Analysis A1 studies the impact of temporal SF_t variation on the isotope composition of xylem water at a fixed stem height. Temporal patterns in δ²H isotope composition in xylem water (δ²H_X) are evaluated for a typical situation, i.e., measurement at breast height (h=1.30 m) (e.g., White et al., 1985; Meinzer et al., 1999; Goldsmith et al., 2012; Hervé-Fernández et al., 2016; De Deurwaerder et al., 2018; Muñoz-Villers et al., 2020).

2. Analysis A2 studies the impact of temporal SF_t variation at different tree heights and temporal patterns in δ²H_X within a tree at various sampling heights (5, 10, and 15 m).

3. Analysis A3 studies the impact of temporal SF_t variation on the isotope composition of xylem water and the timing of sampling. The representation of the profile of δ²H_X along the full height of a tree is measured at different sampling times (09:00 and 11:00) with the standard parameterization given in Table S1.

4. Analysis B studies the variation in δ²H_X due to differences in absolute daily average sap flow speed and diurnal patterns in the δ²H_X in trees that differ solely in daily averaged SF_V, which is set to 0.64, 0.42, and 0.19 m h⁻¹ corresponding to SF_S values of 0.09, 0.06, and 0.03 m h⁻¹, respectively.

All parameters of the four analyses are given in Table S1. The model simulations for each analysis were compared with a null model.

The null model

The null model adopts the standard assumption of zero variation in δ_xyl along the length of the plant body but allows for potential measurement errors related to the extraction protocol. In reality, empirically obtained data will have some variation as observed values (Obs.δ_xyl) are the sum of the true δ_xyl values and their extraction error (error_extraction):

$$\begin{array}{}\text{(12)}& \text{Obs.}{\mathit{\delta }}_{\mathrm{xyl}}=\text{True}{\mathit{\delta }}_{\mathrm{xyl}}+{\text{error}}_{\text{extraction}}.\end{array}$$

Hence, the null model attributes any variance in isotopic composition to extraction errors with maximum extraction error ranges of 3 ‰ for δ²H samples (0.3 ‰ for δ¹⁸O) expected for water extraction recovery rates higher than 98 % (e.g., Orlowski et al., 2013). These extraction errors are negatively skewed following the Rayleigh distillation model which predicts that extraction error for incomplete water recovery will be negative and therefore Obs. δ_xyl≤ True δ_xyl. The null model represents this error_extraction by a negative skew normal distribution (with location parameter ξ=0 ‰, the scale ω=3 ‰ for δ²H or 0.3 ‰ for δ¹⁸O, and shape $\mathit{\alpha }=-\mathrm{\infty }$) (Azzalini, 2013).

2.2.2 Estimation of average RWU depth

Average RWU depths (i.e., the weighted mean of the depths of RWU with the uptake fractions at the different depths as weights) were derived from the simulated δ²H_X values through the use of both the direct inference method and the end-member mixing analysis method. Together, these techniques represent 96 % of the applied methods in the literature (Rothfuss and Javaux, 2017), and the reader is referred to Rothfuss and Javaux (2017) for a complete discussion of both techniques. In line with the general approach assessing RWU with stable water isotopes, the average RWU depth is obtained by relating the δ²H_X with the δ²H_S,i depth profile. We compared average RWU depth estimates obtained from simulated δ²H_X, as described in the analyses above, with the true average RWU depth. Here, the true average RWU depth was defined as the depth corresponding to the daily weighted average δ²H_X and calculated as the weighted sum of δ²H${}_{\mathrm{X},i,t}$ and the relative fraction of water taken up at each depth.

2.2.3 Transport dynamics and sensitivity analysis

We perform a basic model validation of our model assumption that the propagation of an isotopic signature is driven by diurnal sap flow dynamics and diffusion alone. In essence, the model assumes that once water with a given isotopic signature enters the stem, it moves upwards with the speed of sap flow and changes only due to the effect of diffusion. The effects of capacitance on δ²H_X dynamics by the release of storage water in the xylem flow can be ignored. To validate this assumption we compare model predictions against observed δ²H_X dynamics monitored within a pine tree (Pinus pinea L.) following ²H-enrichment in a controlled greenhouse experiment, as detailed in Marshall et al. (2020). δ²H_X was measured at two heights (0.15 and 0.65 m) using a novel in situ technique, the borehole equilibration method. The model simulations performed consider the absolute ranges of sap flux densities during the entire monitoring campaign with the account of tree tapering effects on sap flux densities over the studied stem length (Supplement method C). Validation of diurnal variation in δ²H_X requires high temporal resolution monitoring of δ²H_X dynamics in plant stems with simultaneous high temporal resolution monitoring and characterization of sap flow, soil water potential, and isotopic composition. Such data do not yet exist to the best of our knowledge.

In addition, we performed two sensitivity analyses to assess the relative importance of each parameter in generating variance in δ²H_X along the length of a plant. In both sensitivity analyses, we varied model parameters one at a time to assess the local sensitivity of the model outputs for soil type, sap flux density, root properties, and sampling strategies. The sensitivity analysis provides insight into possibilities for improving the design of field protocols by revealing potential key measurements and caveats in field setups. More details on the performed sensitivity analysis and validation of transport dynamics are available in Supplement method C.

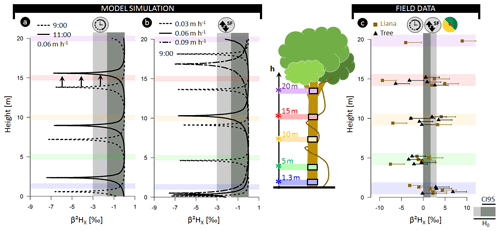
Figure 3 (a) Model outputs for model analysis A3 representing the normalized δ²H composition of xylem water (β²H_X) as a function of the tree height simulated for different sampling times (09:00 and 11:00). The modeled tree has an average daily sap flux density of 0.06 m h⁻¹ (SF_S; approximate daily true sap flux density SF_V=0.42 m h⁻¹). (a) Model outputs for model analysis B where β²H_X in relation to stem height is shown at 09:00 LT but parameterized with distinct SF_S, i.e., 0.09, 0.06, and 0.03 m h⁻¹ (corresponding to SF_V values of 0.64, 0.42, and 0.19 m h⁻¹, respectively). The standard parameterization used for both study analyses is detailed in Table S1. (c) Field measurements of β²H_X for six lianas () and six trees (). Error whiskers are the combination of potential extraction and measurement errors of the isotope analyzer. A species-specific breakdown of the field data is provided in Fig. S2. The horizontal gray-colored envelope in all panels delineates the acceptable variance from the stem mean according to the null model (H₀), i.e., assuming no variance along the length of a lignified plant aside from the potential extraction error (i.e., 3 ‰). Herein, the dark gray envelope indicates the confidence interval comprising 95 % of potential extraction error (CI95).

3 Results

3.1 Part A: empirical exploration

The null model assumes the constant isotopic composition of root water uptake with only limited variance in isotopic composition introduced by extraction errors (β²H_X < 3 ‰; δ¹⁸O_X < 0.3 ‰). However, pronounced δ²H_X variance within individual plants exceeding the null model ranges, are observed in all three independent datasets. The normalized δ²H composition in xylem water (β²H_X) along the stem length of lianas and trees in French Guiana exceeded the null model by a factor of 3.2 and 4.3, respectively (Figs. 3c, S2). Differences of up to 13.1 ‰ and 18.3 ‰ in δ²H and 1.3 ‰ and 2.2 ‰ in δ¹⁸O were observed in individuals of trees and lianas, respectively (Supplement method A, Table A).

Similarly, diurnal intraindividual δ²H_X variances were found for all considered plant growth forms, i.e., trees, shrubs, and herbs, monitored in China (Figs. 4b–d, S3). Observed daily maximum differences in δ²H_X were 18.0 ‰, 21.0 ‰, and 25.2 ‰ for trees, shrubs, and herbs, respectively (2.8 ‰, 6.8 ‰, and 6.5 ‰ in δ¹⁸O_X in Fig. S4). The expected null model variance was exceeded for each species during its measurement period.

Finally, pronounced intraindividual δ²H_X variance was also observed for all monitored firs and beeches in Germany (Figs. 4e, S5). Here, daily maxima differences in δ²H_X were 8.2 ‰ and 14.2 ‰ for Abies alba and Fagus sylvatica, respectively (2.0 ‰ and 4.2 ‰ in δ¹⁸O_X in Fig. S6).

3.2 Part B: model exploration

Isotope composition of xylem water at stem base and basic model behavior

At the stem base, simulated δ²H${}_{\mathrm{X},\mathrm{0},t}$ displays a diurnal fluctuation (Figs. 2b, S7) that corresponds to the daily sap flow pattern (Fig. S7). This pattern is caused by a shifting diurnal average RWU depth. Early in the morning, when transpiration is low, most of the RWU occurs in deeper layers where soil matric potential is less negative and where soil water is more depleted in ²H compared to the soil layers above (Fig. S8a–b). As transpiration increases during the day, a significant proportion of RWU can now be extracted from the drier, shallower layers where the soil water is enriched in ²H, i.e.,, having a higher δ²H. In the afternoon, as transpiration declines, the isotopic composition reflects again the composition of the more depleted soil water in the deeper soil layers, and it remains constant throughout the night because apart from diffusion, SWIFT does not consider mixing of the internal stem water. The mixing effects of diffusion are only noticeable at low sap flow speeds (Fig. 3b).

The highest δ²H_X values (approx. −59 ‰) are found in alignment with the diurnal minimum of ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ (approx. −0.85 MPa; Fig. S7). At this moment, the difference between ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ is at a maximum, enabling water extraction from the upper and driest soil layers. Most root biomass is located near the surface (cf. Jackson et al., 1995; Fig. S8c), and uptake in these layers will result in relatively high contributions to the total RWU.

In contrast, differences between ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ are smaller in the early morning and late afternoon causing root water uptake in the upper soil layers to halt. The decreasing absolute range of ΔΨ_i,t translates into higher proportions of RWU originating from deeper, more depleted soil layers. This causes δ²H_X to drop to a baseline of approx. −67 ‰. This afternoon depletion of δ²H_X will henceforth be referred to as the δ²H_X-baseline drop.

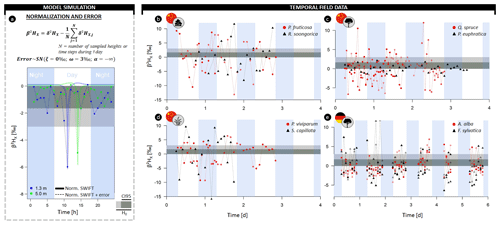
Figure 4 (a) Illustrative example of model simulations transformed in the normalized δ²H composition of xylem water (β²H_X) at 1.3 (blue) and 5 m (green) sampling heights with the formula provided. Thicker lines indicate model simulations without error, and lines connected by dots indicate a scenario of hourly sampling with consideration of the extraction error (i.e., a negative skew normal distribution; ξ=0 ‰, the scale ω=3 ‰, and shape $\mathit{\alpha }=-\mathrm{\infty }$). (b–e) High temporal field measurements of β²H_X of (b) two shrubs, (c) two trees, and (d) two herb species sampled in the Heihe River Basin (northwestern China) and (e) two tree species sampled in the Freiamt field site in southwest Germany. The horizontal gray-colored envelope in all panels delineates the acceptable variance from the stem mean according to the null model (H₀), i.e., assuming no variance along the length of a lignified plant aside from the potential extraction error (i.e., 3 ‰). Herein, the dark gray envelope indicates the confidence interval comprising 95 % of potential extraction error (CI95). A breakdown of the field data on species and individual level is provided in the Supplement figures (Figs. S3–S6).

Isotope composition of xylem water at different times, heights, and SF_V

Temporal fluctuation in δ²H_X within a tree at 1.3 m (i.e., the standard sampling height; analysis A1; Fig. 2a) and other potential sampling heights (e.g., branch collection; analysis A2; Fig. 2a) are provided in Figs. 2b and 3a. Both analyses show that fluctuations in δ²H_X depend on the height of measurement and the corresponding time needed to move the water along the xylem conduits. Note that the selected temporal resolution depends on whether the δ²H_X-baseline drop at a given height equals the (stem base) minimum (here 1 min; see Fig. S12). In addition to sampling height, analysis A3 depicts the importance of sampling time (Fig. 3a). Outputs of analysis B predict that the occurrence and width of the δ²H_X-baseline drop are a function of the sap flow velocity SF_V (Fig. 3b). To aid model interpretation and comparability with field data, we (i) provide an illustrative example of normalized δ²H isotope composition of model-simulated xylem water (β²H_X) with consideration of extraction error (Fig. 4a) and (ii) display the relation between δ²H_X variance and cumulative sap flow volumes, for which the piston flow dynamics in SWIFT originate from the lateral translation of the δ²H_X fluctuation at δ²H${}_{\mathrm{X},\mathrm{0},t}$ (Fig. 2b).

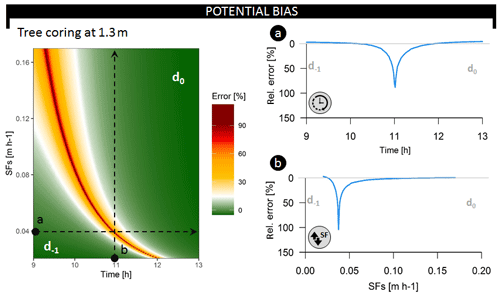
Figure 5 Relative error on the inferred average root water uptake depth (i.e., bias between the average daily and the instantaneously derived average RWU depth) at a coring height of 1.3 m throughout the common sampling period (09:00 until 13:00) and over a range of potential SF_S values (in m h⁻¹), corresponding to an SF_V range of 0.15–1.25 m h⁻¹. Both dotted lines describe test scenarios evaluated in the breakup panels. Respectively, d₋₁ and d₀ indicate whether the derived average RWU depth error corresponds to the previous or current day of measurement. The dynamics in relative error are when sampling (a) over different time steps and restricting sap flux density at 0.04 m h⁻¹ (i.e., SF_V=0.28 m h⁻¹) or (b) over different SF_S values when restricting sampling time to 11:00 LT each day.

3.2.1 Potential biases in average RWU depth estimation

Both the timing of measurement (Fig. 5a) and SF_V (Fig. 5b) influence average RWU depth estimates derived via the direct inference and end-member mixing analysis method (Fig. S9). Collection of tree samples at 1.30 m can result in erroneous estimation, deviating by up to 104 % from the average daily RWU depth (Fig. 5). Plotting the relative error in average RWU depth as a function of time and SF_V (Fig. 5) shows that it is possible to time δ²H_X measurements in a fashion that captures unbiased estimates of the average RWU depth. Xylem water sampling should be timed to capture the δ²H_X that corresponds to water extracted at peak RWU, and the expected sampling time can be derived by considering the time needed for the water to reach the point of measurement (i.e., at 1.30 m in Fig. 5).

3.2.2 Transport dynamics and sensitivity analysis

Our sensitivity analyses show that the expected absolute error in average RWU depth assessment is directly related to both (1) maximum variance in and (2) the probability of sampling nonrepresentative δ²H_X values. The maximum variance depends on the height, while the probability of sampling nonrepresentative areas depends on the width of the δ²H_X-baseline drop (defined above). Hence, variation in δ²H_X is determined by several factors, including the sampling strategy (timing and height of sampling), sap flow velocity (Fig. S10), and the belowground biophysical parameter (Fig. S11). We summarized the most important variables as predicted by SWIFT which should be considered in subsequent RWU studies.

Plants on loamy soils show larger diurnal δ²H_X variances in comparison to those on clay soils for a similar prevailing isotope gradient across the soil profile. Larger variances correspond to potentially larger errors, but the steeper slope of the δ²H_X curve results in a thinner δ²H_X-baseline drop. Hence, loamy soil can result in the potentially large error, but this is mediated by a lower probability of sampling nonrepresentative δ²H_X values during the day.

The volume of water taken up by the plant (SF_t; Fig. S11b) affects xylem water potential of the plant at stem base (${\widehat{\mathrm{\Psi }}}_{\mathrm{X},\mathrm{0},t}$). Higher SF_t requires more negative ${\widehat{\mathrm{\Psi }}}_{\mathrm{X},\mathrm{0},t}$, enabling the plant to access the enriched soil water of more shallow soil layers. Therefore, an increase in SF_t results in the increase in maximum δ²H_X values (increased maximum error) but also results in a smaller width of the baseline drop (Fig. 2–3). Lower SF_t results in smaller errors but a larger probability of sampling a nonrepresentative area (Fig. 3b).

Root properties, i.e., root membrane permeability (Fig. S11c), strongly influence both the total range of δ²H_X variance and the width of the δ²H_X-baseline drops. Decreasing root membrane permeability but with no alterations to the sap flow volumes results in thinner δ²H_X-baseline drops but higher maximum δ²H_X variance.

In addition, the true sap flow velocity (SF_t per unit of lumen area) will determine the relative importance of diffusion on the δ²H_X dynamics. Diffusion can cause a smoothing of the peak and a consequent increase in the width of the δ²H_X-baseline drop. However, as diffusion is proportional to the time that water isotopologues remain in the xylem, its absolute impact on δ²H_X is negligible in plants with a high true sap flow velocity. In contrast, the impact of diffusion on δ²H_X dynamics is substantial for plants with very low velocities, where water takes many days to pass from roots to leaves (see Supplement method B).

The role of diffusion was investigated using a stepwise ²H enrichment experiment in Marshall et al. (2020) (Fig. 6). Analytical solutions of an advection–diffusion equation show that at 0.15 cm, a relatively small diffusivity was required to reproduce the initial increase in xylem isotope signature with values comparable to these reported for diffusivity of heavy water (Meng et al., 2018). However, at 65 cm, the value of diffusivity required to match the observed initial increase was much higher, suggesting other processes besides molecular diffusivity might contribute to the isotope transport (e.g., variable flow velocities within vessels and among vessels of the xylem network). Note also that the analytical solutions were not able to recover the second part of the curve where the isotope reaches the asymptotic enriched value, which is more gradual in the observations (Fig. 6). This also suggests a complex transport of δ²H_X in the xylem.

4 Discussion

4.1 Dynamic diurnal isotope compositions of xylem water along plant stems

Empirical field data show pronounced δ_xyl variance along the stem length (Fig. 3) and over a sub-daily time period (Fig. 4). Our model explorations suggest that basic plant hydraulic functioning can result in shifting mixtures of δ²H_X entering the plant (Figs. 2–3). Daily ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ fluctuations interact with the ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ profile causing different parts of the root distribution to be active during the day. The fluctuations in δ²H_X at the stem base propagate along the xylem with a velocity proportional to the sap flow, and this produces variability in sampled δ²H_X that is much larger than the expected measuring error. Consequently, rather than being static, δ²H_X values along the height of a plant should be envisioned as a dynamic diurnal process.

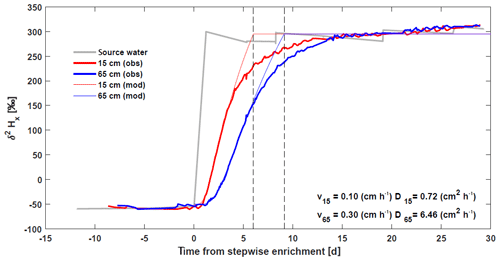
Figure 6 Basic model validation comparing continuous in situ δ²H_X measurements of a stepwise ²H enrichment experiment (Marshall et al., 2020) with analytical solutions of an advection–diffusion equation at heights 0.15 m () and 0.65 m () on a pine tree (Pinus pinea L.). The source water of the intact-root, isotopic-enrichment greenhouse experiment is presented in gray. Model parameters, velocity, and diffusion were fitted by visual inspection independently for the two heights to match the initial increase in isotope signature (values reported in the bottom right).

Importantly, we show that high variance in δ²H_X can result in an incorrect assessment of differences in average RWU depths between plants. Differences do not necessarily result from variability in average RWU depth but may result from monitoring plants at different heights (Figs. 2–3) and at different times (Fig. 3a) or by comparing individuals which have different SF_V (Fig. 3b) and xylem anatomical properties. For example, depending on SF_V and the lumen area, the isotopic signal can take hours or days to travel from roots to leaves – as was also observed experimentally (Magh et al., 2020; Marshall et al., 2020; Steppe et al., 2010).

Low SF_V allows multiple δ²H_X-baseline drops over the length of a single tree. Sampled δ²H_X can reflect the soil isotopic composition of the past several days. Our sensitivity analysis reveals that various soil and plant characteristics have an important role in determining both the daily maximum δ²H_X variance, as well as the width of the δ²H_X-baseline drop. These two characteristics directly impact (i) the expected maximum bias in estimates of average RWU depth and (ii) the chance of measuring δ²H_X values that do not represent a mixture of all rooting layers during peak RWU (i.e., measurements in the baseline drop). Ultimately, these factors will challenge the use of stable water isotopes to study the terrestrial water fluxes, as recently reviewed by Penna et al. (2018). We additionally advocate that future research should explore the minimum set of (bio)physiological drivers and processes that require quantification to correctly interpret δ²H_X along the hydraulic pathway length of a plant.

4.2 General applicability of model and results

A necessary condition for diurnal shifts in RWU is the existence of water potential differences, e.g., more negative water potentials in the upper layers where trees usually have higher root density, which can cause a disproportional partitioning of diurnal RWU between deep and shallow roots over a diurnal course. The pronounced variance in δ_xyl identified in this study is intrinsic to the isotopic tracing technique for RWU assessment as this method relies on the existence of a soil water isotopic profile. Such profiles are the result of soil evaporation, a process inextricably coupled to water potential heterogeneity, and hence to variance in δ²H_X.

Plant transpiration results from a complex interaction between atmospheric demands (i.e., driven by VPD and radiation) and stomatal conductance that depends on tolerance for drought stress and soil moisture content. We may expect that diurnal fluctuation in radiation and VPD, and hence in water transport and depth of water absorption as modeled here, is a general phenomenon in nature. Moreover, much greater fluctuations in VPD and radiation should be expected under more natural conditions than the diurnal cycle described here, and these will increase the variability of transpiration fluxes, leading to even more complex dynamics of ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$. Specifically, the model simulations suggest that intraindividual variability of δ²H_X will reflect the past changes in RWU dynamics, including RWU dynamics driven by changes in environmental demands. For instance, a changing degree in cloud cover that impacts sap flow dynamics can influence ${\mathrm{\Psi }}_{\mathrm{X},\mathrm{0},t}$ rather abruptly (e.g., in lianas; Chen et al., 2015) and lead to instantaneous changes in the δ²H composition of the water mixture taken up at the root level. This can complicate the comparison of different plants sampled at different heights and times.

Note that, based on our model, we expect that soil isotopic enrichment experiments will generate extensive δ²H_X variation along the length of trees whenever diurnal RWU fluctuations cause water extraction to shift between labeled and unlabeled soil layers. Furthermore, when enrichment experiments target trees with different hydraulic properties (such as SF_V) care should be taken to determine when and where to sample these trees to assess a potential ²H enrichment in xylem water (Fig. 6, but see Magh et al., 2020;).

4.3 Alternative causes of δ_xyl fluctuation

The SWIFT model provides a simple traceable and mechanistic explanation, using diurnal variations in SF_t and RWU, for the pronounced variance and dynamic nature of the δ_xyl fluctuations with plant height and time of field samples (e.g., Figs. 3–4) and elsewhere (Cooper et al., 1991). However, several other processes might contribute to generate variability, while others can act to dampen this variability. In the next section, we will discuss alternative causes, complementary and antagonistic, that contribute to the observed intraindividual δ_xyl variances.

Fractionation at root or stem level

An increasing body of observations shows the occurrence of isotopic fractionation at the root level governed by root membrane transport (Lin and Sternberg, 1993; Vargas et al., 2017) or by unknown reasons (Zhao et al., 2016). Brinkmann et al. (2019) hypothesize that root level fractionation causes disparity when average RWU depth calculations based on δ²H_X measurements are compared with those of δ¹⁸O_X. However, it is difficult to imagine a scenario where root fractionation by itself can explain the observed diurnal fluctuations in δ_xyl with height and time. Even if root fractionation significantly contributed to variation in δ_xyl, we would still need to take into account diurnal fluctuation in RWU to explain the observed patterns. Isotopic enrichment of xylem water along the stem length was observed in association with stem transpiration (Barnard et al., 2006; Dawson and Ehleringer, 1993). However, this phenomenon is generally restricted to non-suberized plants and in woody branches in close vicinity to the evaporative surface of the plant (Dawson and Ehleringer, 1993). Isotopic enrichment can, therefore, not explain the variances in δ_xyl observed in our empirical data, which were sampled within the main stem (data French Guiana) or from lignified branch segments distant from evaporative surfaces (data China and Germany).

Temporal and spatial soil dynamics

Soil water content can be extremely heterogeneous in the three spatial dimensions, as well as in time with complex dynamics of soil water movement. For example, hydraulic lift vertically redistributes soil water through the roots (Dawson and Ehleringer, 1993), which may change the water isotopic composition of the water mixture in the rhizosphere that is taken up by roots. Specifically, hydraulic lift redistributes and mixes the isotopic signal of depleted soil water in deeper layers with the enriched soil water signal in the rhizosphere in shallower layers. This should lead to lower variation in the soil water accessible to the plant, and hence less variation along plant height. Horizontal heterogeneity of water content may also affect δ_xyl variance as soil water potentials and the isotope composition of soil water are interlinked. Under these conditions, it is important to understand how much the radial distribution of roots will naturally average out soil heterogeneity. However, note that heterogeneity in the soil does not automatically translate into variability in the xylem. Differential root water uptake driven by the diurnal fluctuation in water potential gradients in the soil–plant interface is still required to generate variability in the xylem isotopic signature.

Storage tissue and phloem enrichment

Storage tissues release water and sugars into the xylem conduits on a daily basis to support water transpiration demand (Goldstein et al., 1998; Morris et al., 2016; Secchi et al., 2017) or to repair embolism (Salleo et al., 2009; Secchi et al., 2017). Both water and sugars are transported in and out of storage tissue via symplastic pathways using plasmodesmata and aquaporins (Knipfer et al., 2016; Secchi et al., 2017), a pathway that has been linked to isotopic fractionation in roots (Ellsworth and Williams, 2007). Moreover, phloem transports photosynthetic assimilates that were produced in the leaves and are therefore potentially affected by transpiration fractionation (Gessler et al., 2013). Hence, these metabolic molecules might show higher values of δ²H and δ¹⁸O compared to RWU. Water release from storage or phloem tissue might locally alter δ_xyl (White et al., 1985). Additionally, the time between water storage and release could bridge multiple days, and corresponding isotopic composition may reflect soil conditions preceding a dry spell when the isotopic signature of soil was less vertically stratified. It is evident that such dynamics are complex, and it is hard to predict how storage tissue and phloem enrichment affect observed δ_xyl patterns. Importantly, xylem isotopic sampling cannot differentiate between water resulting from RWU or storage, and therefore we cannot exclude the possibility that tissue and phloem enrichment play a role. At a minimum this adds further uncertainty to RWU assessment. Water derived from storage tissues might also be present in larger fractions in higher parts of the plants, especially branches, as contamination accumulates as water moves upwards.

Unfortunately, to our best knowledge, empirical data on the isotopic composition of storage tissue and its spatiotemporal dynamics are absent in the literature. Future research should target the impact assessment of storage water on intraindividual δ_xyl, allowing proper implementation in the model.

Diffusion processes

Diffusion is a process of net movement of molecules from a region of higher concentration to a region of lower concentration. Consequently, diffusion dampens δ_xyl variability both in time and space within water xylem. Although the mutual diffusion coefficient of heavy water in normal water is very small and flow within vessels is laminar, other processes might still contribute to generating diffusion along the xylem. For example, as the water moves through the complex network of vessels, differences in velocities between vessels of different sizes cause some particles to move faster or slower than the average flow. According to the Hagen–Poiseuille law, the flow in each vessel is proportional to the fourth power of the vessel radius and the mean velocity is proportional to the square of the radius, thus potentially generating large differences in particle velocities depending on the vessel size distribution and other anatomical properties. Even within a single vessel, velocity is parabolic with a maximum flow velocity in the center and zero at the vessel walls.

4.4 A way forward

The observed large δ_xyl variance and temporal dynamics in the empirical data suggest the need for a critical assessment of the stable isotope tracer technique for RWU studies. However, it also creates new opportunities. Since δ_xyl variance and temporal dynamics herein likely relate to various plant physiological processes, the monitoring of variation in δ_xyl can allow a more integrated understanding of plant water transport and hydraulic properties.

Combining a plant hydraulic model with in situ SF_V, δ²H_S,i and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ can also help improve the robustness of RWU assessment and interpretation. Measurements of δ²H_S,i and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ at multiple depths, i.e., by installing soil water suction cups working in a vacuum (i.e., Rennenberg et al., 1996) and multiple soil matric potential sensors that measure at a high temporal frequency, should be especially valuable since the SWIFT model showed high sensitivity to alterations of this variable and these can be directly supplied as model inputs. At the same time, the availability of SF_t measurements allows for the identification of the moment when water uptake from all root layers is at its maximum, which can be used to determine the optimal timing of sampling at a given height providing a more robust estimation of average RWU depth and uptake.

Alongside the modeling approach presented here, new ways to study δ²H_X at a high temporal scale are strongly encouraged, for example, the pioneering work of Volkmann et al. (2016) in the development of an in situ continuous isotope measurement technique that offers the possibility for monitoring δ_xyl at a sub-hourly resolution. This technique holds strong promise for further elucidating the natural δ²H_X variances found within plants and the physiology processes from which these variances result. Such a high temporal resolution of isotope measurements, coupled with in situ monitoring of various environmental and plant biophysical metrics, is needed for both model improvement and further validation. Moreover, these seem inevitable to eventually differentiate all causal mechanisms of the observed intraindividual δ_xyl variance.

5 Conclusions

A collection of empirical field data show pronounced variance and high temporal fluctuations in δ_xyl. Moreover, these high temporal fluctuations in δ_xyl emanate from basic plant hydraulic functioning, as model explorations show. We expect the observed δ_xyl variance, and sub-daily fluctuations result, for a large part, from the mechanisms considered here, though various other physiological processes could also affect δ_xyl.

Our theoretical explorations warn that variability in the isotope composition of plant xylem water can result in erroneous average RWU depth estimation and will complicate the interpretation and comparison of data; samples taken at different heights and times or plants differing in SF_V may incorrectly show differences in average RWU depth. We further predict that various soil parameters and plant hydraulic parameters affect (i) the absolute size of the error and (ii) the probability of measuring δ_xyl values that do not represent the well-mixed values during the plants' peak RWU. Hydraulic models, such as SWIFT, could help us to design more robust sampling regimes that enable improved comparisons between studied plants. We advocate the addition of SF_t, which indirectly reflects diurnal RWU fluctuations, and ${\mathrm{\Psi }}_{\mathrm{S},i,t}$ monitoring as a minimum in future RWU assessments since these parameters were predicted to be the predominant factors introducing variance in δ_xyl from the SWIFT model exploration. However, soil texture and root permeability are also key measurements especially when comparing across species and sites.

Our findings do not exclude additional factors that impact the observed intraindividual δ_xyl variance and temporal fluctuation as many processes can act simultaneously and are not mutually exclusive. Therefore, we strongly emphasize the need for more research. Directed studies that validate and quantify the relative impact of other plant physiological processes towards variance in δ_xyl are a prerequisite before improved modeling tools can be developed.

Appendix A: Nomenclature