the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The climate benefit of carbon sequestration
Susan E. Crow
Martin Heimann
Holger Metzler
Ernst-Detlef Schulze
Ecosystems play a fundamental role in climate change mitigation by photosynthetically fixing carbon from the atmosphere and storing it for a period of time in organic matter. Although climate impacts of carbon emissions by sources can be quantified by global warming potentials, the appropriate formal metrics to assess climate benefits of carbon removals by sinks are unclear. We introduce here the climate benefit of sequestration (CBS), a metric that quantifies the radiative effect of fixing carbon dioxide from the atmosphere and retaining it for a period of time in an ecosystem before releasing it back as the result of respiratory processes and disturbances. In order to quantify CBS, we present a formal definition of carbon sequestration (CS) as the integral of an amount of carbon removed from the atmosphere stored over the time horizon it remains within an ecosystem. Both metrics incorporate the separate effects of (i) inputs (amount of atmospheric carbon removal) and (ii) transit time (time of carbon retention) on carbon sinks, which can vary largely for different ecosystems or forms of management. These metrics can be useful for comparing the climate impacts of carbon removals by different sinks over specific time horizons, to assess the climate impacts of ecosystem management, and to obtain direct quantifications of climate impacts as the net effect of carbon emissions by sources versus removals by sinks.
- Article
(2769 KB) - Full-text XML
- BibTeX
- EndNote
Terrestrial ecosystems exchange carbon with the atmosphere at globally significant quantities, thereby influencing Earth's climate and potentially mitigating warming caused by increasing concentrations of CO2 in the atmosphere. Carbon fixed during the process of photosynthesis remains stored in the terrestrial biosphere over a range of timescales, from days to millennia – timescales of relevance for affecting the concentration of greenhouse gases in the atmosphere (Archer et al., 2009; IPCC, 2014; Joos et al., 2013). During the time carbon is stored in the terrestrial biosphere, it is removed from the radiative forcing effect that occurs in the atmosphere; thus, it is of scientific and policy relevance to understand the timescale of carbon storage in ecosystems, i.e., for how long newly fixed carbon is retained in an ecosystem before it is released back to the atmosphere.
Timescales of element cycling and storage are unambiguously characterized by the concepts of system age and transit time (Bolin and Rodhe, 1973; Rodhe, 2000; Rasmussen et al., 2016; Sierra et al., 2017; Lu et al., 2018). In a system of multiple interconnected compartments, system age characterizes the time that the mass of an element observed in the system has remained there since its entry. Transit time characterizes the time that it takes element masses to traverse the entire system, from the time of entry until they are released back to the external environment (Sierra et al., 2017). Both metrics are excellent system-level diagnostics of the dynamics and timescales of ecosystem processes. Because system age and transit time both can be reported as mass or probability distributions, they provide different information about an ecosystem over a wide range in the time domain.
System age and transit time are closely related to the complexity of the ecosystem and its process rates, which are affected by the environment (Luo et al., 2017; Rasmussen et al., 2016; Sierra et al., 2017; Lu et al., 2018). Mean system ages of carbon are consistently greater than mean transit time (Lu et al., 2018; Sierra et al., 2018b), suggesting that once a mass of carbon enters an ecosystem a large proportion gets quickly released back to the atmosphere, but a small proportion remains for very long times. Furthermore, differences in transit times across ecosystems suggest that not all carbon sequestered in the terrestrial biosphere spends the same amount of time stored; e.g., one unit of photosynthesized carbon is returned back to the atmosphere faster in a tropical than in a boreal forest (Lu et al., 2018). Therefore, not all carbon drawn down from the atmosphere should be treated equally for the purpose of quantifying the climate mitigation potential of sequestering carbon in ecosystems as it is currently recommended in accounting methodologies (IPCC, 2006).
Global warming potentials (GWPs; see definition in Sect. 2) quantify the radiative effects of greenhouse gases emitted to the atmosphere (Fig. 1) but do not consider the avoided radiative effect of storing carbon in ecosystems (Neubauer and Megonigal, 2015). GWPs are computed using the age distribution of CO2 and other greenhouse gases in the atmosphere (Rodhe, 1990; Joos et al., 2013) but do not consider age or transit times of carbon in ecosystems in the case of sequestration. Transit time distributions, in particular, can better inform us about the time newly sequestered carbon will be removed from radiative effects in the atmosphere.
For more comprehensive accounting of the contribution of carbon sequestration to climate change mitigation, it is necessary to quantify the avoided warming effects of sequestered carbon in ecosystems over the timescale the carbon is stored. The GWP metric is inappropriate to quantify avoided warming potential as a result of sequestration. A metric that can capture this avoided warming effect could have applications for (1) comparing different carbon sequestration activities considering the time carbon is stored in ecosystems and (2) providing better accounting methods for the effect of removals by sinks in climate policy. Currently, the Intergovernmental Panel on Climate Change (IPCC) recommends that countries and project developers report only emissions by sources and removals by sinks of greenhouse gases (GHGs), treating all removals equally in terms of their fate (IPCC, 2006).
Problems with applying GWPs to compute climate benefits of sequestering carbon in ecosystems are well documented (Moura Costa and Wilson, 2000; Fearnside et al., 2000; Brandão et al., 2013; Neubauer and Megonigal, 2015). Several approaches have been proposed to deal with the issue of timescales (Brandão et al., 2013), many of which deal with time as some form of delay in emissions. However, to our knowledge, no solution proposed thus far explicitly accounts for the time carbon is sequestered in ecosystems, from the time of photosynthetic carbon fixation until it is returned back to the atmosphere by autotrophic and heterotrophic respiration, and fires.
Therefore, the main objective of this paper is to introduce a metric to assess the climate benefits of carbon sequestration while accounting for the time carbon is stored in ecosystems. We first present the theoretical framework for the development of the metric, then provide simple examples for its computation, and discuss potential applications for ecosystem management and for climate change mitigation.
2.1 Absolute global warming potential (AGWP)
The direction of carbon flow, into or out of ecosystems, is of fundamental importance to understand and quantify their contribution to climate change mitigation. The absolute global warming potential (AGWP) of carbon dioxide quantifies the radiative effects of a unit of CO2 emitted to the atmosphere during its life time – in the direction land → atmosphere. It is expressed as (Lashof and Ahuja, 1990; Rodhe, 1990)
where is the radiative efficiency or greenhouse effect of one unit of CO2 (in mole or mass) in the atmosphere at time t, and Ma(t) is the amount of gas present in the atmosphere at time t (Rodhe, 1990; Joos et al., 2013). The AGWP quantifies the amount of warming produced by CO2, while it stays in the atmosphere since the time the gas is emitted at time t0 over a time horizon T. The function Ma(t) quantifies the fate of the emitted carbon in the atmosphere and can be written in general form as
where ha(t−t0) is the impulse response function of atmospheric CO2 released into the atmosphere, Ma(t0) is the content of atmospheric CO2 at time t0, and Q(τ) is the perturbation of new incoming carbon to the atmosphere between t0 and t.
For a pulse, or instantaneous emission of CO2, Ma(t0)=E0, and
assuming no additional carbon enters the atmosphere after the pulse. If the pulse is equivalent to 1 kg or mole of CO2, then E0=1 and . For a pulse emission of any arbitrary size, and assuming constant radiative efficiency (see details about this assumption in Sect. 2.2),
The AGWP can be computed for any other greenhouse gas using their respective radiative efficiencies and fate in the atmosphere (impulse response function). To compare different gases, the global warming potential (GWP) is defined as the AGWP of a particular gas divided by the AGWP of CO2 (Shine et al., 1990; Lashof and Ahuja, 1990). Our interest in this paper is on carbon fixation and respiration in the form CO2; therefore, we primarily concentrate here on AGWP.
The impulse response function ha(t−t0) plays a central role within the AGWP framework. The function encodes information about the fate of a gas once it enters the atmosphere and determines for how long the gas will remain. Therefore, it can be interpreted as a density distribution for the transit time of a gas, since the time of emission until it is removed by natural sinks (e.g., CO2) or by chemical reactions (e.g., CH4).
The function typically is assumed to be static; i.e., the time at which the gas enters the atmosphere is not relevant, only the time it remains there (t−t0). However, this function can be time-dependent, expressing different shapes depending on the time the gas enters the atmosphere, i.e., . For example, when natural sinks saturate, faster accumulation of CO2 and longer transit times of carbon in the atmosphere are observed (Metzler et al., 2018). In this situation, the specific time of an emission would lead to different response functions in the atmosphere. Because current research on impulse response functions primarily considers the static time-independent case (see Millar et al., 2017, for an exception), we will consider only the static case for the remainder of this paper.
2.2 The radiative efficiency of CO2 and its impulse response function
The radiative efficiency of CO2 is a function of the concentration of this gas and the concentration of other gases in the atmosphere with overlapping absorption bands (Lashof and Ahuja, 1990; Shine et al., 1990). Therefore, changes as the concentration of GHGs change in the atmosphere. For most applications however, the radiative efficiency of CO2 has been assumed constant in the limit of a small perturbation at a specific background concentration (Lashof and Ahuja, 1990; Shine et al., 1990; Joos et al., 2013; Myhre et al., 2013).
Here, we use a constant value of W m−2 per megagram of carbon based on results reported by Joos et al. (2013) for an atmospheric background of 389 ppm (∼ present day). This radiative efficiency represents the change in radiative forcing caused by a change of 1 Mg of carbon in the atmosphere in the form of CO2 in units of rate of energy transfer (watt) per square meter of surface.
Joos et al. (2013) have also derived impulse response functions (IRFs) of CO2 in the atmosphere using coupled carbon–climate models that include multiple feedbacks among Earth system processes. One function was obtained by emitting a pulse of 100 Gt of carbon to a pre-industrial atmosphere with a background concentration of 280 ppm (PI100 function from here on), and another function was obtained by emitting 100 Gt of carbon to a present-day atmosphere with a background of 389 ppm (PD100 from here on). The functions they report are averages from the numerical output of multiple models fitted to a sum of exponential functions that include an intercept term. This intercept implies that a proportion of the added CO2 never leaves from the atmosphere–ocean–terrestrial system to long-term geological reservoirs. Following Millar et al. (2017), we added a timescale of 1 million years that corresponds to the intercept term in the IRFs. The addition of this timescale has no effect on the results presented here, which are focused on much shorter timescales, but they avoid the mathematical problem that the integrals of the original functions go to infinity with time (Lashof and Ahuja, 1990; Millar et al., 2017).
2.3 Carbon sequestration CS and the climate benefit of carbon sequestration (CBS)
GWPs are useful to quantify the climate impacts of increasing or reducing emissions of GHGs to the atmosphere. However, it is also necessary to quantify the climate benefits of carbon flows in the opposite direction, atmosphere → land. Furthermore, it is also important to quantify not only how much and how fast carbon enters ecosystems, but also for how long the carbon stays (Körner, 2017).
Carbon taken up from the atmosphere through the process of photosynthesis is stored in multiple ecosystem reservoirs for a particular amount of time. Carbon sequestration can be defined as the process of capture and long-term storage of CO2 (Sedjo and Sohngen, 2012). We define here carbon sequestration CS over a time horizon T as
where Ms(t−t0) represents the fate of a certain amount of carbon S0 taken up by the sequestering system at a time t0. Notice that this definition of carbon sequestration is very similar to that of AGWP for an emission, with the exception that the radiative efficiency term is omitted.
To obtain the fate of sequestered carbon over time, we represent carbon cycling and storage in ecosystems using the theory of compartmental dynamical systems (Luo et al., 2017; Sierra et al., 2018a). In their most general form, we can write carbon cycle models as
where x(t)∈ℝn is a vector of n ecosystem carbon pools, is a time-dependent vector-valued function of carbon inputs to the system, and is a time-dependent compartmental matrix. The latter two terms can depend on the vector of states, in which case the compartmental system is considered nonlinear. In case the input vector and the compartmental matrix have fixed coefficients (no time dependencies), the system is considered autonomous, and it is considered non-autonomous otherwise (Sierra et al., 2018a). This distinction of models with respect to linearity and time dependencies (autonomy) is fundamental to distinguish important properties of models. For instance, models expressed as autonomous linear systems have a steady-state solution given by , where x∗ is a vector of steady-state contents for all ecosystem pools. Non-autonomous models have no steady-state solution.
The fate of the fixed carbon for the general nonlinear non-autonomous case can be obtained as
where β(t0)S0=u(t0), and β(t0) is an n-dimension vector representing the partitioning of the total sequestered carbon among n ecosystem carbon pools (Ceballos-Núñez et al., 2020). The n×n matrix Φ(t,t0) is the state-transition operator, which represents the dynamics of how carbon moves in a system of multiple interconnected compartments (see details in Appendix B). Throughout this document, we use the symbol to denote the 1-norm of a vector, i.e., the sum of the absolute values of all elements in a vector.
Because ecosystems and most reservoirs are open systems, the sequestered carbon S0 returns back to the atmosphere, mostly as CO2 due to ecosystem respiration and fires. Carbon release r(t) from ecosystems can be obtained according to
where 1⊺ is the transpose of the n-dimensional vector containing only 1s. The state-transition matrix captures the entire fate and dynamics of the sequestered carbon, from the time it enters t0 until release at any t.
The link between the time it takes sequestered carbon S0 to appear in the release flux r(t) is established by the concept of transit time (Metzler et al., 2018). In particular, we define the forward transit time (FTT) as the age that fixed carbon will have at the time it is released back to the atmosphere, or how long a mass fixed now will stay in the system. The backward transit time (BTT) is defined as the age of the carbon in the output flux since the time it was fixed, or how long the mass leaving the system now had stayed. This implies that
where is the backward transit time distribution of carbon leaving the system at time t with an age t−t0, while is the forward transit time distribution of carbon entering the system at time t0 and leaving with an age t−t0. For systems in equilibrium, both quantities are equal (Metzler et al., 2018). For systems not in equilibrium, semi-explicit formulas for their distributions are given in Appendix B.
For the atmosphere, carbon sequestration is a form of negative emission, and we can represent its fate in the atmosphere as
where the prime symbol represents a perturbed atmosphere as an effect of sequestration. The first term in the right-hand side represents the response of the atmosphere to an instantaneous sequestration S0 at t0, and the second term represents the perturbation in the atmosphere of the carbon returning back from the terrestrial biosphere. Notice that the integral in this equation can be written as a convolution (ha⋆r)(t) between the impulse response function of atmospheric CO2 and the carbon returning from ecosystems to the atmosphere.
We define now the climate benefit of sequestration for a pulse of CO2 into an ecosystem as
This metric integrates over a time horizon T the radiative effect avoided by sequestration of an amount of carbon S0 taken up at time t0 by an ecosystem. It captures the timescale at which the carbon is stored and gradually returns back to the atmosphere. It can also be interpreted as the atmospheric response to carbon sequestration in the form of a negative emission of CO2 during a time horizon of interest. It relies on knowledge of the atmospheric response to perturbations in the form of an impulse response function and the transit time of carbon in an ecosystem.
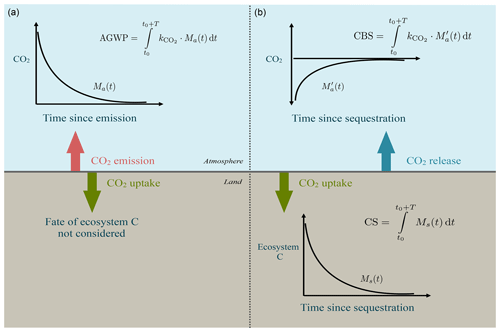
Figure 1Contrast between current approach to quantification of climate effects of emissions and sequestration (a), and the proposed approach for sequestration (b). Plots and equations represent the concepts of absolute global warming potential (AGWP) of an emission of CO2, carbon sequestration (CS), and climate benefits of sequestration (CBS). AGWP integrates over a time horizon T the fate of an instant emission at time t0 of a gas (Ma(t)) and multiplies by the radiative efficiency k of the gas. A similar idea can be used to define CS as the integral of the fate Ms(t) of an instant amount of carbon uptake S0 over T. The CBS captures the atmospheric disturbance caused by CO2 uptake and subsequent release by respiration as the integral over T of the fate of sequestered carbon multiplied by the radiative efficiency of CO2.
2.4 Ecosystems in equilibrium: the linear, steady-state case
The computation of CS and CBS is simplified for systems in equilibrium. For linear systems at a steady state, the time at which the carbon enters the ecosystem is irrelevant (Kloeden and Rasmussen, 2011; Rasmussen et al., 2016); one only needs to know for how long the carbon has been in the system to predict how much of it remains. Mathematically, this implies
Therefore, for linear systems at a steady state, we have the special cases
and
where Ms1 represents the fate of one unit of fixed carbon, which can also be interpreted as the proportion of carbon remaining after the time of fixation.
The amount of released carbon returning to the atmosphere is therefore
which for one unit of fixed carbon is equal to the transit time density distribution f(τ) of a linear system (Metzler and Sierra, 2018, see also Appendix B)
where r1(a)=f(τ), with mean (expected value) transit time given by
We can now derive the steady-state expression of CS as
Furthermore, it is possible to find a closed-form expression for this integral:
where is the identity matrix. Similarly, for one unit of carbon entering a steady-state system at any time, we define CS1 as
which by integration gives
These steady-state expressions can be very useful to compare different systems or changes to a particular system if the steady-state assumption is justified. Furthermore, it can be shown that in the long term, as the time horizon T goes to infinity (∞), the term converges to −I, and therefore Eq. (19) converges to the expression
which means that the total amount of carbon at a steady state is equal to the long-term carbon sequestration of an instantaneous amount of fixed carbon at an arbitrary time.
Similarly, for one unit of carbon entering a system at a steady state, the long-term CS1 from Eq. (21) can be obtained simply as
by using the definition of mean transit time of Eq. (17). This means that long-term sequestration of one unit of CO2 converges to the mean transit time of carbon in an ecosystem.
2.5 Dynamic ecosystems out of equilibrium: the continuous sequestration and emissions case
In addition of considering isolated pulses of emissions E0 or sequestrations S0, we can also consider permanently ongoing emissions and sequestration , respectively. Hence,
where
Here s(τ) is a scalar flux of sequestration at time τ. This leads to
The fate of sequestered carbon, for the atmosphere in the form of a balance between simultaneous sequestration and return of carbon, can now be obtained as
We can now define the climate benefit of sequestration for a dynamic ecosystem with continuous sequestration and respiration as
This expression of CBS accounts for the dynamic behavior of inputs and outputs of carbon in ecosystems, and it can be used to represent time dependencies resulting from environmental changes and disturbances or produced by emission scenarios or scheduled management activities. This time-dependent CBS is computed for a time horizon T starting at any initial time t0. In other words, it can be used to analyze specific time windows of interest, accounting for the fate of all carbon sequestered during specific time intervals.
3.1 The fate of a pulse of inputs through the system
A simple ecosystem carbon model, the terrestrial ecosystem model (TECO), will now demonstrate an application of the theory to compute CS and CBS assuming a linear system at a steady state (i.e., in equilibrium). We used a modified version of the TECO model, originally described by Weng and Luo (2011) with parameter values obtained through data assimilation using observations from the Duke Forest in North Carolina, USA. It contains eight main compartments: foliage x1, woody biomass x2, fine roots x3, metabolic litter x4, structural litter x5, fast soil organic matter (SOM) x6, slow SOM x7, and passive SOM x8 (Fig. 2). The model represents the dynamics of carbon at a temperate forest dominated by loblolly pine. We chose this model due to its simplicity and tractability, but the framework presented in Sect. 2 can be applied to more complex models and for other ecosystems (see reference in Sect. “Executable research compendium (ERC)” for an example with a nonlinear model). In addition to its simplicity and tractability, there are two advantages of using this model over others: (1) it provides reasonable predictions of net ecosystem carbon fluxes and biometric pool data (Weng and Luo, 2011); (2) it is commonly used to express complex ecosystem-level concepts such as the matrix generalization of carbon cycle models, their traceability, and transient behavior (e.g., Luo and Weng, 2011; Luo et al., 2012; Xia et al., 2013; Luo et al., 2017; Sierra, 2019).
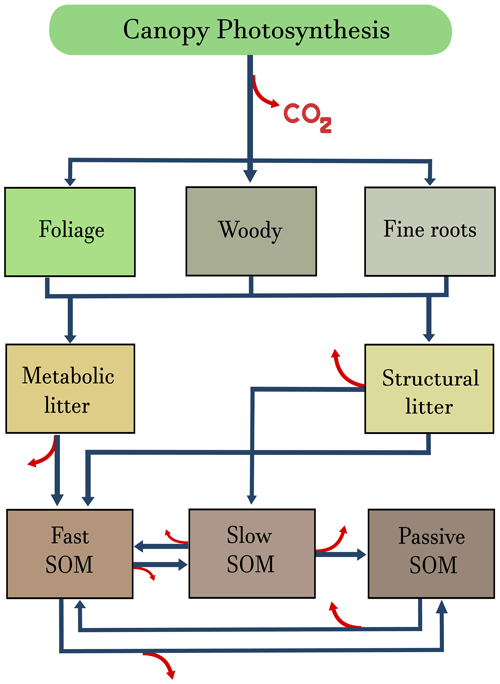
Figure 2Graphical representation of the terrestrial ecosystem model (TECO) described in Weng and Luo (2011) and Luo et al. (2012). Carbon enters the ecosystem through canopy photosynthesis and is allocated to three biomass pools: foliage, woody biomass, and fine roots. From these pools, carbon is transferred to metabolic and structural litter pools, from where it can be respired as CO2 or transferred to the soil organic matter (SOM) pools. Blue arrows represent transfers among compartments, and red arrows release to the atmosphere in the form of CO2.
The model is commonly expressed as
where X is a vector of ecosystem carbon pools, C is a diagonal matrix with cycling rates for each pool, A is a matrix of transfer coefficients among pools, and b is a vector of allocation coefficients to plant parts. We modified the entries of matrix A to allow autotrophic respiration to be computed from the vegetation pools and not from the GPP flux as in the original model (see details in Appendix C). The function U(t) determines the carbon inputs to the system as gross primary production (GPP), and ξ(t) is a time-dependent function that modifies ecosystem cycling rates according to changes in the environment.
For this steady-state example, we assume constant inputs (U(t)=U) and constant rates (ξ(t)=1). Furthermore, defining , and u:=bU, we can write this model as a linear, autonomous compartmental system of the form
with values for B and u as described in Appendix C.
The fate of a pulse of carbon input entering the ecosystem at an arbitrary time when the system is in equilibrium can be obtained by applying Eqs. (13) and (14) (Fig. 3). Carbon enters the ecosystem through foliage, wood, and fine-root pools. A large proportion of this carbon is quickly transferred from these pools to the fine and metabolic litter pools. Subsequently, the carbon moves to the SOM pools with important respiration losses during these transfers. Most carbon is returned back to the atmosphere with a mean transit time of 30.4 years for the whole system. Half of the sequestered carbon is returned back to the atmosphere in 7.6 years and 95 % in 124 years.
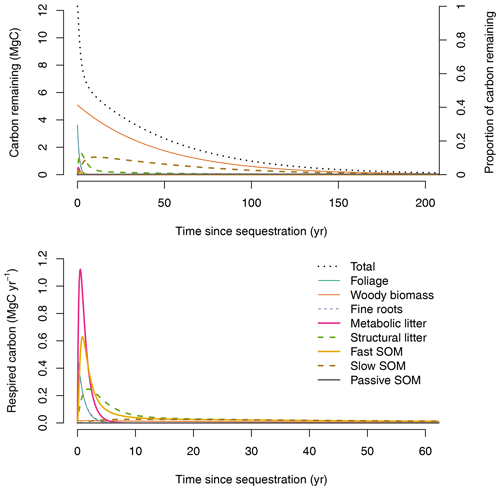
Ecosystem-level CS, i.e., the area under the curve of the amount of remaining carbon over time (area under dotted line in Fig. 3, upper panel), increases towards an asymptote as the time horizon of integration increases (Fig. 4a). Here, CS is reported in units of Mg C ha−1 yr, because this is the amount of carbon retained in organic matter over a fixed time horizon. For relevant time horizons of 50, 100, 500, and 1000 years, CS was 233.51, 317.68, 371.64, and 373.42 Mg C ha−1 yr, respectively. In the long term (i.e., as the time horizon goes to infinity), CS converges to the steady-state carbon stock predicted by the model of 373.67 Mg C ha−1.
A similar computation can be made for one unit of fixed carbon (CS1). In this case CS1 was 18.98, 25.83, 30.21, and 30.36 years for time horizons of 50, 100, 500, and 1000 years, respectively. In the long term, CS1 converges to the mean transit time of carbon: 30.4 years (Fig. 4b).
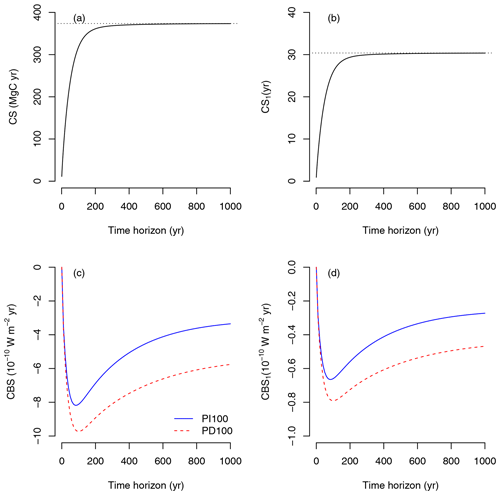
Figure 4Carbon sequestration (CS) and climate benefit of sequestration (CBS) for instantaneous carbon uptake at any given time. (a) CS due to the uptake of 12.3 Mg C ha−1, which corresponds to GPP of 1 year. (b) CS due to the uptake of one unit of carbon (CS1). (c) CBS due to the uptake of 12.3 Mg C ha−1 for two different impulse response functions (pre-industrial atmosphere with a pulse of 100 Gt of carbon: PI100, and present-day atmosphere with a pulse of 100 Gt of carbon: PD100). (d) CBS due to the uptake of one unit of carbon (CBS1) for two different impulse response function. Dotted lines in (a) and (b) represent steady-state carbon storage and mean transit time, respectively.
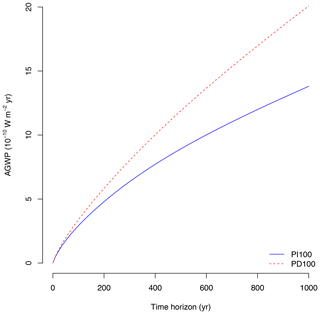
Figure 5Absolute global warming potential (AGWP) due to the emission of 1 Mg of CO2–C to the atmosphere for the two different IRFs (pre-industrial atmosphere with a pulse of 100 Gt of carbon: PI100, and present-day atmosphere with a pulse of 100 Gt of carbon: PD100) reported by Joos et al. (2013).
Due to sequestration at t0, the CBS shows a rapid negative increase in radiative forcing, which decreases as the time horizon increases due to the return of carbon to the atmosphere as an effect of respiration (Fig. 4c). The shape of the curve, however, depends strongly on the IRF for atmospheric CO2. CBS is larger over the long term (>200 years) for the present-day (PD100) curve proposed by Joos et al. (2013) than for the pre-industrial curve (PI100). During the pre-industrial period, perturbations of CO2 in the atmosphere are lower than in the present-day period due to higher uptake of carbon from the oceans and the land biosphere (Joos et al., 2013). Therefore, the benefits of carbon sequestration are larger under present-day conditions based on these IRF curves. Impulse response functions depend strongly on the magnitude and timing of the pulse (Joos et al., 2013; Millar et al., 2017). Therefore, estimates of climate impacts of emissions (AGWP, Fig. 5) and climate benefits of sequestration (CBS, Fig. 4c, d) depend strongly on the choice of the IRF. For the purpose of this paper, we will use the present-day curve (PD100) from here on.
Because AGWP and CBS are based on similar concepts and share similar units, it becomes possible to directly compare one another (Fig. 6) and obtain an estimate of the climate impact of emissions versus sequestration. This can be done either as the ratio of the absolute value of CBS to AGWP, i.e., (unitless), or as the net radiative balance CBS + AGWP (W m−2 yr). It is possible to compute these relations using the CBS for one unit of sequestered carbon, which provides a direct estimate of the impact of one unit of sequestration versus one unit of emission, or corresponding to the amount of GPP sequestered in 1 year (12.3 Mg C ha−1 yr−1 for Duke Forest).
In our example, the emission of 1 Mg of carbon to the atmosphere has a predominant warming effect that cannot be compensated for by the sequestration of 1 Mg of carbon at the Duke Forest (Fig. 6). However, the sequestration of the equivalent of GPP in 1 year can have a significant climate benefit compared to the emission of 1 Mg of carbon, depending on the time horizon of analysis. When one integrates in time horizons lower than 200 years, CBS outweighs AGWP in this example. However, because the lifetime of an emission of CO2 is much longer in the atmosphere than the transit time of carbon through a forest ecosystem, AGWP outweighs CBS on longer timescales.
The time of integration in the computation of GWP has been a heavily debated topic in the past, and this is related to the topic of “permanence” of sequestration in carbon accounting and climate policy (Moura Costa and Wilson, 2000; Noble et al., 2000; Sedjo and Sohngen, 2012). One problem in these previous debates is that the timescale of carbon in ecosystems was not considered explicitly while the timescale of carbon in the atmosphere was. With the approach proposed here, both are explicitly taken into account and can better inform management and policy debates about sequestration of carbon in natural and man-made sinks.
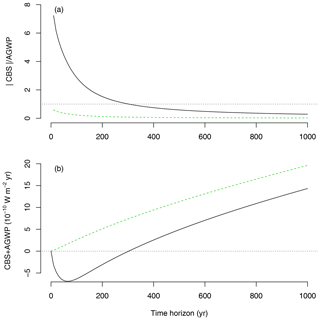
Figure 6Relations between CBS and AGWP for the IRF PD100 as a function of time horizon T. (a) Ratio between the absolute value of CBS and AGWP, based on a total sequestration of 12.3 Mg of carbon (back line, GPP equivalent for 1 ha and 1 year at Duke Forest) versus a sequestration of 1 Mg of carbon (dashed green line). (b) Radiative balance (net difference) between CBS and AGWP for the sequestration of 12.3 Mg of carbon (black line) and 1 Mg of carbon (dashed green line).
3.2 Carbon management to maximize the climate benefit of carbon sequestration
In the context of climate change mitigation, management of ecosystems may be oriented to increase carbon sequestration and its climate benefit. In the recent past, scientists and policy makers have advocated increasing the amount of inputs to ecosystems as an effective form of carbon management (e.g., Silver et al., 2000; Grace, 2004; Lal, 2004; Chabbi et al., 2017; Minasny et al., 2017). Although increases in carbon inputs can increase the amount of stored carbon in an ecosystem with related climate benefits, it does not necessarily increase the amount of time the sequestered carbon will stay in the system. Therefore, strategies that focus on increasing carbon inputs alone do not take full advantage of the potential of ecosystems to mitigate climate change.
We can conceptualize any management activity that increases or reduces carbon inputs to an ecosystem by a factor γ, so the new inputs are given by the product γ u. For example, if we increase carbon inputs to an ecosystem by 10 %, γ=1.1. Increasing carbon inputs by a proportion γ>1 increases carbon storage at a steady state by an equal proportion since
Similarly, a decrease in carbon inputs by a proportion γ<1 decreases steady-state carbon storage by an equal proportion. However, the time carbon requires to travel through the ecosystem is still the same since the transit time does not change, as we can see from the mean transit time expression
Both the transit time distribution (Eqs. B4 and 16) and the mean transit time (Eq. 17) only take into account the proportional distribution of the carbon inputs to the different pools but not the total amount of inputs. Therefore, a unit of carbon that enters an ecosystem stays there for the same amount of time independent of how much carbon is entering the system. Although these results only apply to linear systems at a steady state, they provide some intuition about what might be the case in systems out of equilibrium.
Carbon management can also be oriented to modify process rates in ecosystems as encoded in the matrix B. A proportional decrease in process rates by a factor ξ<1 not only increases carbon storage as
but also increases the mean transit time as
A proportional change in the opposite direction (ξ>1) causes the opposite effect; a proportional increase in process rates decreases carbon storage and decreases mean transit time.
Based on these results, it is now clear that carbon management to increase carbon inputs alone can only increase CS but not CS1; i.e., the new carbon inputs have a sequestration benefit only through increase of carbon storage but not through a longer transit time in ecosystems. Management to decrease process rates, on the contrary, can increase both CS and CS1 because the new carbon entering the system stays there for longer.
We can see these effects of carbon management on CS by running simulations using the TECO model at a steady state (Fig. 7). Now, we modified carbon inputs and process rates by either increasing them by 10 % and 50 % (γ, ξ=1.1, 1.5) or decreasing them by 10 % and 50 % (γ, ξ=0.9, 0.5). The simulations showed that increasing or decreasing carbon inputs increase or decrease CS for any time horizon (Fig. 7a), but it does not modify the behavior of one unit of sequestered carbon (CS1) (Fig. 7b). On the contrary, decreasing or increasing process rates increase or decrease both CS (Fig. 7c) and CS1 (Fig. 7d).
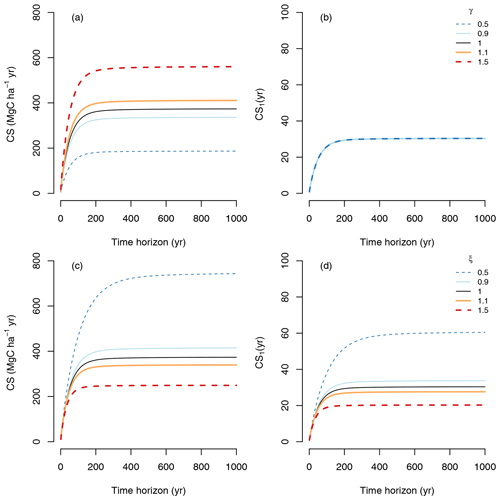
Figure 7Different carbon management strategies and their effect on the CS and CS1. Management to increase or decrease carbon inputs in the vector u by specific proportions γ is shown in panel (a) and (b). Management to increase or decrease process rates in the matrix B by a proportion ξ is shown in panels (c) and (d). Since CS1 quantifies carbon sequestration of one unit of carbon, management of the amount of carbon inputs does not modify CS1 in panel (b), and all lines overlap.
The resultant effects of changes in management of inputs or process rates on CBS can differ substantially. Increases or decreases of carbon inputs have similar proportional effects on CBS, but differences in processes rates are not equally proportional. While an increase in inputs by 50 % would increase CBS by 50 %, a decrease in process rates by 50 % would have an increase in CBS by more than 100 % for time horizons longer than 300 years (Fig. 8). Similarly, while a decrease in inputs by 50 % would reduce CBS by 50 %, an increase in process rates by 50 % would decrease CBS by only ∼ 40 %.
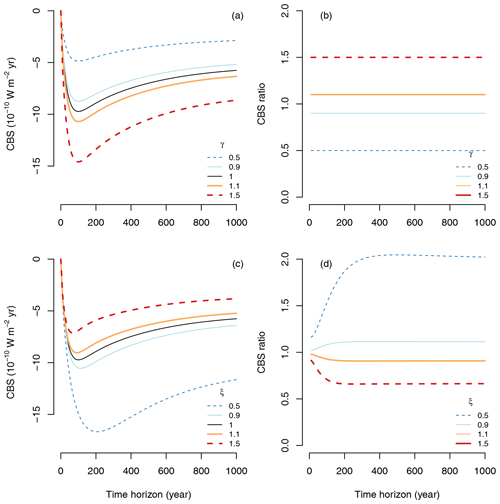
Figure 8Effects of different management strategies on CBS. (a) Effect of increasing or decreasing carbon inputs by a proportion γ on CBS; (b) same effect of γ expressed as a ratio with respect to the reference case of γ=1. (c) Effects of decreasing or increasing process rates in the matrix B by a proportion ξ on CBS; (d) same effect of ξ expressed as a ratio with respect to the reference case ξ=1.
These results show that management of transit time, e.g., by decreasing process rates, may lead to stronger climate benefits than managing carbon inputs alone. Furthermore, one could think about optimization scenarios in which both inputs and transit times are managed to achieve larger climate benefits given certain constraints. The concept of CBS is thus a useful mathematical framework to formally pose such an optimization problem.
We can also use these results to infer differences in CS and CBS for different ecosystem types. Without management, we would expect large variability of CS and CBS in the terrestrial biosphere. Inputs and process rates vary considerably for terrestrial ecosystems as previously reported in other studies. For instance, gross primary productivity can range from about 1 to >30 Mg C ha−1 yr−1 from high- to low-latitude ecosystems (Jung et al., 2020). Based on simulations from the CABLE model, Lu et al. (2018) found a range of mean transit times between 13 and 341 years from low- to high-latitude ecosystems. These large ranges of variability for GPP and mean transit time suggest that CS and CBS may vary among ecosystems by large proportions (>20 times larger or smaller depending on the ecosystems being compared).
4.1 Pulses entering at different times and experiencing different environments
The steady-state examples above are useful to gain some intuition about potential long-term patterns in CS and CBS, but for real-world applications it is necessary to consider systems out of equilibrium and driven by specific time-dependent signals. We will consider now the case of the temperate ecosystem of our previous example driven by increases in atmospheric CO2 concentrations that lead to higher photosynthetic uptake and increasing temperatures that lead to faster cycling rates. We will thus consider a non-autonomous version of the TECO model that follows the general form
where the time-dependent function γ(t) incorporates the effects of temperature and atmospheric CO2 on primary production, and the function ξ(t) incorporates the effects of temperature on respiration rates. Specific shapes for these functions were taken from Rasmussen et al. (2016) and are described in detail in Appendix C. When applied to the CASA model in Rasmussen et al. (2016), these functions predicted an increase in primary production and an increase in process rates, which resulted in a decrease in transit times over a simulation of 600 years.
We used the same simulation setup here starting from an empty system (x(0)=0) and obtained similar results in terms of primary production and transit times as in Rasmussen et al. (2016). We used these simulation results to compute CS and CBS for carbon entering the ecosystem at different times during the simulation window. In particular, we considered the case of the amount of carbon sequestered at years 100 and 300 after the start of the simulation; i.e., we considered the cases t0=100 and t0=300 (Fig. 9a) and computed the fate of this carbon (), its carbon sequestration (CS) and the climate benefit of sequestration (CBS) for different time horizons T.
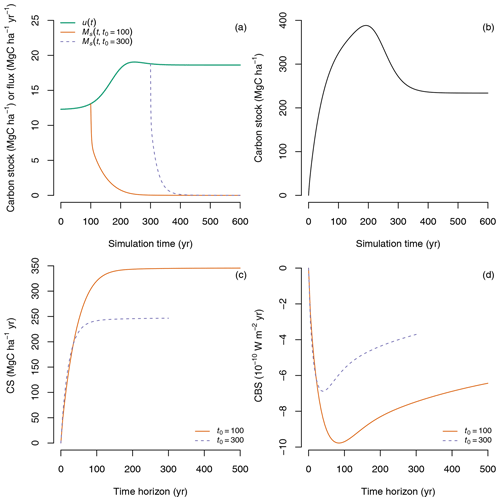
Figure 9Prediction of CS and CBS for a non-steady-state case with time-dependent inputs u(t) controlled by CO2 fertilization and temperature and process rates controlled by temperature modified by a time-dependent factor ξ(t). (a) Predicted time-dependent inputs u(t), and the fate of carbon entering the ecosystem at simulation year 100 () and simulation year 300 (). (b) Predicted carbon accumulation in the ecosystem () for the entire simulation period. (c) Carbon sequestration for the amount of inputs entering at simulation years 100 and 300 calculated for different time horizons T. (d) Climate benefit of sequestration for carbon entering the ecosystem at simulation years 100 and 300 integrated for different time horizons T.
Although more carbon enters the ecosystem at simulation year 300 than at year 100 due to the CO2 fertilization effect, it is lost much faster because of higher temperatures that result in faster transit times for simulation times above 300 years (Fig. 9a). The slower transit times experienced by the carbon that enters at year 100 due to lower temperature result then in much higher values of CS for time horizons T>100 years (Fig. 9c). Similarly for CBS, where differences are evident much earlier, lower temperatures lead to higher values of CBS for time horizons T>50 years (Fig. 9d).
This simple example highlights the importance of time-dependent transit times in determining CS and CBS. If changes in climate lead to faster carbon processing rates, we would thus expect carbon to transit faster through the ecosystem, returning faster to the atmosphere, and therefore with lower values for carbon sequestration and its climate benefit.
4.2 Continuous inputs into a changing environment
In the previous example, we considered the case of two single pulses entering the ecosystem at different times under changing environmental conditions during a simulation. A consolidated view can be obtained by taking all single pulses and integrating them continuously in time to compute CS and CBS using Eqs. (24) and (28), respectively. In this case, CS increases monotonically, and CBS decreases monotonically with time horizon (Fig. 10, continuous black lines), which is somewhat obvious because as the ecosystem accumulates carbon, more of it is retained in the ecosystem and is isolated from atmospheric radiative effects. However, this simulation only considers carbon that enters the ecosystem from the beginning of the simulation until the end of the time horizon, from t0 to t0+T. An important aspect to consider is the role of carbon already present in the ecosystem at t0.
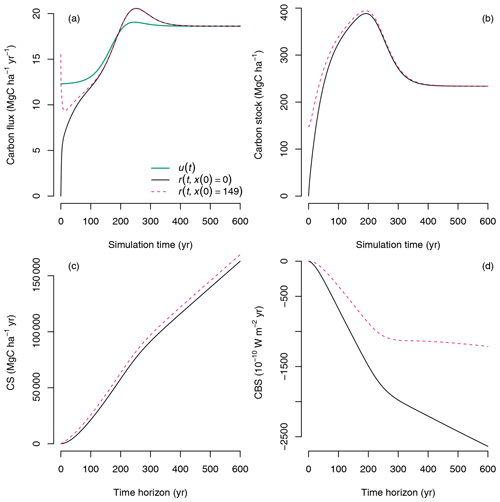
Figure 10Computation of CS and CBS for continuous inputs and release of carbon in simulations with different initial conditions x0: in one simulation the ecosystem develops from empty pools (x(0)=0, i.e., bare ground, black lines), and in the second simulation the ecosystem develops from existing litter and SOM pools but empty biomass pools ( Mg C ha−1, dashed magenta color lines). (a) Inputs u(t) and release fluxes r(t) along the simulation time. (b) Carbon stocks predicted by the model along the simulation time. (c) Carbon sequestration CS for a sequence of time horizons. (d) Climate benefit of sequestration CBS for a sequence of time horizons.
We will consider now the case of continuous sequestration and release of carbon with differences in the initial conditions in the simulation, which can vary according to land use changes. For example, when changing land use from agriculture to forest, or from natural forest to plantation, there are carbon legacies that have an influence on future carbon trajectories (Harmon et al., 1990; Janisch and Harmon, 2002; Sierra et al., 2012). These carbon legacies are usually dead biomass and detritus, which cause ecosystems to lose carbon via decomposition before photosynthesis from new biomass compensates for the losses. In these initial stages of recovery, ecosystems are usually net carbon sources, but they still may store more carbon than an ecosystem developing from bare ground.
The CS and CBS concepts can be very useful to compare contrasting trajectories of ecosystem development and assess their role in terms of carbon sequestration alone and their climate impact. For this purpose, we performed an additional simulation in which at the starting time there is no living biomass, but the detritus pools and the SOM pools are 1.5 and 1.0 times as large as in the equilibrium case, respectively ( Mg C ha−1). In this simulation, the ecosystem losses a significant amount of carbon in the early stages of development, and respiration is much larger than primary production () (Fig. 10a, dashed magenta line). Because soils are already close to an equilibrium value, the ecosystem already has a large amount of carbon stored; therefore in the computation of the fate of carbon Ms(t,t0) there is already a larger amount of carbon to consider, which causes CS to be larger for the land-use-change case than for the bare ground case (Fig. 10c). On the contrary, because there are more emissions from the ecosystem in early development stages, CBS is lower for the land-use-change case than for the bare ground case (Fig. 10d).
These contrasting results between CS and CBS for the continuous case with contrasting initial conditions can be very useful to address debates and controversies about the role of land use change and baselines in carbon accounting. The results show that carbon sequestration can still be high in ecosystems where emission fluxes are large, but climate impacts can differ significantly. By using two different metrics, these two different aspects of carbon sequestration can be discussed separately.
The metrics introduced here, carbon sequestration (CS) and the climate benefit of sequestration (CBS), integrate both the amount of carbon entering an ecosystem and the time it is stored there, thus avoiding radiative effects in the atmosphere. Disproportionate attention is given to quantifying sources and sinks of carbon in ongoing debates about the role of ecosystems in climate change mitigation, with much less attention paid to the fate of carbon once it enters an ecosystem. The time carbon remains in an ecosystem, encapsulated in the concept of transit time, is critical for climate change mitigation because during this time carbon is removed from radiative effects in the atmosphere.
The CS and CBS concepts unify atmospheric and ecosystem approaches to quantifying the greenhouse effect. The CBS concept builds on that of the absolute global warming potential (AGWP) of a greenhouse gas. The main difference is that CBS quantifies avoided warming during the time carbon is stored in an ecosystem, while AGWP quantifies potential warming when the carbon enters the atmosphere. Both metrics rely on the quantification of the fate of carbon (or other GHGs for AGWP) once it enters the particular system. For atmospheric systems, a significant amount of work has been done in determining the fate of GHGs once they enter the atmosphere after emissions (e.g., Rodhe, 1990; O'Neill et al., 1994; Prather, 1996; Archer et al., 2009; Joos et al., 2013). For terrestrial ecosystems; however, robust methods to quantify the fate of carbon as it flows through terrestrial system components have been developed only recently (Rasmussen et al., 2016; Metzler and Sierra, 2018; Metzler et al., 2018).
Global warming potential (GWP), or the climate impact of an emission of a certain gas in relation to the impact of an emission of CO2, is often used to assess climate impacts of actions, e.g., avoided deforestation, land use change, and even enhanced carbon sequestration. However, this metric has two limitations when applied to carbon sequestration and in comparison to the combined use of CBS and AGWP we advocate here: (1) it only quantifies the climate effects of emissions but not of sequestration and treats all fixed carbon equally independent of its transit time in the ecosystem and (2) it is a relative measure with respect to the emission of CO2. GWPs are commonly reported in units of CO2 equivalents, which only address indirectly the effect of a gas in producing warming. In contrast, CBS quantifies the effects of avoided warming in units of W m−2 over the period of time carbon is retained.
Other concepts have been proposed in the past to account for the temporary nature of carbon sequestration (see review by Brandão et al., 2013, and references therein), with special interest in accounting for credits in carbon markets. In fact, “ton-year” accounting methods (Noble et al., 2000) resemble our definition of carbon sequestration; however, none of these previous concepts explicitly considers the time carbon is retained in the ecosystem. Instead, these approaches relate carbon sequestration to delay in fossil fuel emissions (Fearnside et al., 2000), or as the equivalence of the amount of carbon storage to AGWP (Moura Costa and Wilson, 2000). The concepts of sustained global warming potential (SGWP) and sustained global cooling potential (SGCP) proposed by Neubauer and Megonigal (2015) are notable exceptions. The CBS concept captures some of the ideas of the SGCP concept but differs in some fundamental assumptions related to the interpretation of the impulse response functions, the treatment of time-dependent fluxes and rates, and reporting. While SGCP reports values in reference to CO2 as is commonly done for GWP, we report CBS for individual gases as it is done for AGWP. Appendix A elaborates on other aspects of the SGWP and SGCP concepts.
The concept of CBS improves our ability to address some of the existing debates about the role of ecosystems in mitigating climate change and enhances our potential to provide decision support. In combination with quantifications of AGWP, CBS provides the net climate effect of an ecosystem or some management. For example, CBS can be used to better understand the climate impacts of storing carbon in long-term reservoirs such as soils and wood products, as well as the climate benefits of increasing the transit time in these systems. CBS can be used to better quantify the climate benefits of using biofuels as fossil fuel substitution by computing the CBS of the whole bioenergy production system and adding the negative AGWP attributed to the avoided emission. Similarly, it can be incorporated in assessments of sequestration in industrial systems with associated carbon capture and storage.
Carbon management of ecosystems can maximize CS and/or CBS by not only increasing carbon inputs, but also by increasing the transit time of carbon. There are many ways in which the transit time of carbon can be increased – for instance, by increasing transfers of carbon to slow cycling pools such as the case of increasing wood harvest allocation to long-duration products (Schulze et al., 2019), or addition of biochar to soils, or by reducing cycling rates of organic matter such as the case of soil flipping (Schiedung et al., 2019). Independently of the management activity, CS and CBS can be powerful metrics to quantify their climate benefits, make comparisons among them, and compare against baselines or no-management scenarios.
The examples we provided in this paper illustrate the use and interpretation of CS and CBS metrics under the assumptions of linearity, steady state, or time dependencies in carbon cycle dynamics with subsequent consequences for carbon sequestration and its climate benefits. The computation of the CBS relies on a model, which can be as simple as a one-pool model or a state-of-the-science land surface model. The TECO model is an excellent tool to illustrate ecosystem-level concepts because of its simplicity and tractability, but other models with more accurate parameterizations and including more processes should be considered for practical applications. The formulas and formal theory developed in Sect. 2 are general enough to deal with the non-steady-state case as well as with models with nonlinear interactions among state variables. In Sierra (2020), we provide an example in the form of a Jupyter Notebook to compute CS and CBS for a nonlinear model (see Sect. “Executable research compendium (ERC)” for details).
The concepts of CS and CBS present improvements to the current guidelines for carbon inventories that treat all carbon removals by sinks equally (IPCC, 2006) by explicitly considering the transit time of carbon in ecosystems. Therefore, these new concepts have potential for being incorporated in revised policies for carbon accounting in the context of international climate agreements and carbon markets. CS and CBS can aid in the economic valuation of carbon by adding economic incentives to sequestration activities that retain carbon in ecosystems for longer times. In addition, the concepts can help in dealing with the issue of permanence of carbon by explicitly quantifying climate benefits of sequestration that can be compared directly with the climate impacts of emissions on a similar time horizon.
Two potential limitations to apply the concepts of CS and CBS are that they rely (1) on a model that tracks the fate of the fixed carbon and (2) on an impulse response function of CO2 in the atmosphere. Reliable models may not be available for certain types of ecosystems or may include large uncertainties that propagate to CS and CBS estimates. Also, estimates of impulse response functions for atmospheric CO2 seem to also have uncertainties, particularly related to the size of the emission pulse, the atmospheric background at which the pulse is applied, and the long-term behavior of the curve for timescales longer than 1000 years (Archer et al., 2009; Lashof and Ahuja, 1990; Joos et al., 2013; Millar et al., 2017). However, one advantage of the functions proposed by Joos et al. (2013) is that they are derived from coupled climate–carbon models that include multiple feedbacks. Therefore, when computing CS and CBS for small perturbations of the carbon cycle, it is not necessary to explicitly compute carbon–climate feedbacks. Also, when comparing two different systems with a CBS ratio as in Fig. (8) or a ratio CBS to AGWP (Fig. 6), uncertainties in the IRFs would tend to cancel each other out. Nevertheless, advances in our understanding of the fate of emitted CO2 to the atmosphere will consequently derive better estimates of the climate benefits of carbon sequestration.
Analyses of carbon sequestration for climate change mitigation purposes must consider both the amount of carbon inputs and the transit time of carbon. Both concepts are encapsulated in the unifying concepts of carbon sequestration (CS) and climate benefit of sequestration (CBS) that we propose. Carbon management can be oriented to maximize CS and CBS, which can be achieved by managing both rates of carbon input and process rates in ecosystems. We believe the use of these metrics can help to better deal with current discussions about the role of ecosystems in mitigating climate change, provide better estimates of avoided or human-induced warming, and have the potential to be included in accounting methods for climate policy.
Neubauer and Megonigal (2015) proposed two metrics, the sustained global warming potential (SGWP) and the sustained global cooling potential (SGCP), to overcome issues with GWP. However, there is an important misconception in their study that we would like to address here. In particular, these authors state “… GWPs requires the implicit assumption that greenhouse gas emissions occur as a single pulse; this assumption is rarely justified in ecosystem studies”. The use of pulse emissions in computing AGWP, as shown in Eq. (3), is done with the purpose of obtaining a representation of the fate of a unit of emissions under the assumption that the system is in equilibrium. This is a mathematical property of linear time-invariant dynamical systems by which an impulse response function can provide a full characterization of the dynamics of the system (Hespanha, 2009). In other words, the emission pulse is a mathematical method to obtain a description of the fate of incoming mass into the system, but it is not an assumption imposed on the system.
To use impulse response functions, it is necessary to assume that a system is in equilibrium and that all rates remain constant for all times. It is this assumption that is problematic and difficult to impose on ecosystems and not the pulse emission because it is simply a method. Therefore, we are of the opinion that the sustained-flux global warming potential metric proposed by these authors is unjustified on the argument that it removes the assumption of pulse emissions.
One interesting characteristic of the study of Neubauer and Megonigal (2015) is that it uses a model that couples an ecosystem compartment with the atmosphere, and their computation of SGWP and SGCP captures the interactions between these two reservoirs similarly as in the framework described here in Sect. 2. The SGCP is very similar in spirit to the CBS. However, their approach differs from the approach we present here in that our mathematical framework is general enough to deal with ecosystem models of any level of complexity and not restricted to a one-pool model and constant parameters and sequestration rates. Furthermore, we abstain from proposing a metric that is relative to CO2. We are rather interested in an absolute metric that quantifies the effect of CO2 sequestration on radiative forcing and not in equivalents to sequestration or emissions of other gases.
Carbon cycling in the terrestrial biosphere is well characterized by a particular type of dynamical systems called compartmental systems (Anderson, 1983; Jacquez and Simon, 1993). These systems of differential equations generalize mass-balanced models and therefore generalize element and carbon cycling models in ecosystems (Rasmussen et al., 2016; Luo et al., 2017; Sierra et al., 2018a). In their most general form, we can write carbon cycle models as
where x(t)∈ℝn is a vector of ecosystem carbon pools, is a time-dependent vector-valued function of carbon inputs to the system, and is a time-dependent compartmental matrix. The latter two terms can depend on the vector of states, in which case the compartmental system is considered nonlinear. In case the input vector and the compartmental matrix have fixed coefficients (no time dependencies), the system is considered autonomous, and it is considered non-autonomous otherwise (Sierra et al., 2018a). At a steady state, the autonomous linear system has the general solution .
The probability density function (pdf) for system age of linear autonomous models at a steady state can be computed by the following expression (Metzler and Sierra, 2018)
where a is the random variable age, 1⊺ is the transpose of the n-dimensional vector containing ones, ea⋅B is the matrix exponential computed for each value of a, and is the sum of the stocks of all pools at a steady state.
The mean, i.e., the expected value, of the age pdf can be computed by the expression
The pdf of the transit time variable τ for linear autonomous systems in equilibrium is given by (Metzler and Sierra, 2018)
and the mean transit time by
For the most general case of nonlinear non-autonomous systems, we follow the approach described in Metzler et al. (2018). For these systems, the age distribution of mass is given by
where Φ is a state-transition matrix, and f0 is an initial age density distribution at initial time t0. We obtain Φ by taking advantage of an existing numerical solution x(t), which we plug into the original system, obtaining a new compartmental matrix and a new input vector . Then, the new linear non-autonomous compartmental system,
has the unique solution y(t)=x(t), which emerges from the fact that both systems are identical. The solution of the system is then given by
where is the initial vector of carbon stocks. We obtain the state-transition matrix as the solution of the following matrix differential equation:
with initial condition
where is the identity matrix. For the special case in which the time-dependent matrix can be expressed as a product between a time-dependent scalar factor ξ(t) and a constant value matrix B, i.e., B(t)=ξ(t)B, we obtain the state-transition matrix as
These formulas can be applied to any carbon cycle model represented as a compartmental system to obtain the fate of carbon once it enters the ecosystem as well as timescale metrics such as age and transit time distributions.
Computation of the mass remaining in the system
From Eq. (B7), we can see from the first term that the initial amount of carbon in the system x0 changes over time according to the term Φ(t,t0) x0. Rasmussen et al. (2016) showed that, under certain circumstances, Eq. (B7) is exponentially stable as long as B is invertible, and the state-transition operator acts as a term that exponentially “decomposes” the initial amount of carbon. Furthermore, the state-transition operator tracks the dynamics of the incoming carbon and how it is transferred among the different pools before it is respired. Therefore, this operator can be used to compute the fate of an amount of carbon sequestered at time ts as
Similarly, the fate of one unit of sequestered carbon at time ts can be computed as
where the subscript 1 denotes that the function predicts the fate of one unit of carbon.
The terrestrial ecosystem model (TECO) described in Weng and Luo (2011) and Luo et al. (2012) has eight pools to simulate ecosystem-level carbon dynamics, with a parameterization for the Duke Forest, a temperate forest in North Carolina, USA. The annual amount of photosynthetically fixed carbon predicted by the model in this forest (GPP) is U=12.3 Mg C ha−1 yr−1. The vector of carbon allocation is given by
which shows that from all photosynthetically fixed carbon, 14 % is allocated to foliage, 26 % to woody biomass, and 14 % to roots.
Each pool in the model cycles at annual rates given by the diagonal elements of the matrix
with a matrix of transfer coefficients as
Matrix A was modified from the original publication (Luo et al., 2012) by decreasing the proportion that is transferred from vegetation to litter pools in a proportion consistent with the proportions of carbon that are respired by autotrophic respiration. In other words, autotrophic respiration is not computed here as in the original publication where the inputs enter the ecosystem in the form of net primary production, i.e., U = GPP − Ra. We compute autotrophic respiration as the proportion that leaves the autotrophic pools and that is not transferred to the litter pools. In this way, U = GPP, and all carbon that is fixed enters the vegetation pools from where it is subsequently respired or added to the litter pools.
Defining B:=AC and u=bU, we obtained the steady-state solution as
For the simulation with initial conditions as in a land-use-change case, the initial conditions x0 of the simulation were set as
where the symbol ∘ represents entry-wise multiplication.
For the transient simulations, we derived time-dependent modifiers for inputs γ(t) and for process rates ξ(t) following the approach described in Rasmussen et al. (2016). Atmospheric CO2 concentrations increase following a sigmoid curve given by
and surface air temperature increases with CO2 concentrations according to
The combined effect of CO2 concentrations and air surface temperature on primary production is then computed as
with
where β(xa(t),Ts(t)) is the sensitivity of primary production with respect to atmospheric CO2 and air surface temperature, and ρ=0.65 is the ratio of intracellular CO2 to xa(t). The response function with respect to temperature Γ(Ts(t)) is given by
The separate effect of air surface temperatures on process rates is computed with a power function of the form
with ξb=2.
Code to reproduce all results has been permanently stored and can be found in Sierra (2020, https://doi.org/10.5281/zenodo.4399181). The file TECO.R contains all code to reproduce all examples in this paper. The file nonlinear_CS_CBS.ipynb is a Jupyter Notebook that contains code with an example for computing CS and CBS for a nonlinear model out of equilibrium.
CAS conceived the idea and wrote the paper, SEC and EDS contributed the examples, and MH and HM helped to develop the mathematical framework. All authors contributed to writing the paper.
The authors declare that they have no conflict of interest.
Funding was provided by the Max Planck Society and the German Research Foundation (Emmy-Noether Programme SI 1953/2-2). We would like to thank Mark Harmon, Yiqi Luo, and Susan Trumbore for useful comments on previous versions of this paper.
This research has been supported by the German Research Foundation (grant no. SI 1953/2-2).
The article processing charges for this open-access
publication were covered by the Max Planck Society.
This paper was edited by Jens-Arne Subke and reviewed by Alexey Shiklomanov and two anonymous referees.
Anderson, D. H.: Compartmental modeling and tracer kinetics, Springer-Verlag, Berlin, Germany, 1983. a
Archer, D., Eby, M., Brovkin, V., Ridgwell, A., Cao, L., Mikolajewicz, U., Caldeira, K., Matsumoto, K., Munhoven, G., Montenegro, A., and Tokos, K.: Atmospheric Lifetime of Fossil Fuel Carbon Dioxide, Annu. Rev. Earth Pl. Sc., 37, 117–134, https://doi.org/10.1146/annurev.earth.031208.100206, 2009. a, b, c
Bolin, B. and Rodhe, H.: A note on the concepts of age distribution and transit time in natural reservoirs, Tellus, 25, 58–62, 1973. a
Brandão, M., Levasseur, A., Kirschbaum, M. U. F., Weidema, B. P., Cowie, A. L., Jørgensen, S. V., Hauschild, M. Z., Pennington, D. W., and Chomkhamsri, K.: Key issues and options in accounting for carbon sequestration and temporary storage in life cycle assessment and carbon footprinting, The Int. J. Life Cycle Ass., 18, 230–240, https://doi.org/10.1007/s11367-012-0451-6, 2013. a, b, c
Ceballos-Núñez, V., Müller, M., and Sierra, C. A.: Towards better representations of carbon allocation in vegetation: a conceptual framework and mathematical tool, Theor. Ecol., 13, 317–332, https://doi.org/10.1007/s12080-020-00455-w, 2020. a
Chabbi, A., Lehmann, J., Ciais, P., Loescher, H. W., Cotrufo, M. F., Don, A., SanClements, M., Schipper, L., Six, J., Smith, P., and Rumpel, C.: Aligning agriculture and climate policy, Nat. Clim. Change, 7, 307–309, https://doi.org/10.1038/nclimate3286, 2017. a
Fearnside, P. M., Lashof, D. A., and Moura-Costa, P.: Accounting for time in Mitigating Global Warming through land-use change and forestry, Mitig. Adapt. Strat. Gl., 5, 239–270, https://doi.org/10.1023/A:1009625122628, 2000. a, b
Grace, J.: Understanding and managing the global carbon cycle, J. Ecol., 92, 189–202, 2004. a
Harmon, M. E., Ferrell, W. K., and Franklin, J.: Effects on carbon storage of conversion of old-growth forests to young forests, Science, 247, 699–702, 1990. a
Hespanha, J. P.: Linear Systems Theory, Princeton University Press, Princeton, NJ, USA, 2009. a
IPCC: General guidance and reporting, in: 2006 IPCC guidelines for national greenhouse gas inventories, edited by: Eggleston, S., Buendia, L., Miwa, K., Ngara, T., and Tanabe, K., Institute for Global Environmental Strategies, Hayama, Japan, 2006. a, b, c
IPCC: Climate Change 2013, The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9781107415324, 2014. a
Jacquez, J. A. and Simon, C. P.: Qualitative Theory of Compartmental Systems, SIAM Review, 35, 43–79, https://doi.org/10.1137/1035003, 1993. a
Janisch, J. and Harmon, M.: Successional changes in live and dead wood carbon stores: implications for net ecosystem productivity, Tree Physiol., 22, 77–89, 2002. a
Joos, F., Roth, R., Fuglestvedt, J. S., Peters, G. P., Enting, I. G., von Bloh, W., Brovkin, V., Burke, E. J., Eby, M., Edwards, N. R., Friedrich, T., Frölicher, T. L., Halloran, P. R., Holden, P. B., Jones, C., Kleinen, T., Mackenzie, F. T., Matsumoto, K., Meinshausen, M., Plattner, G.-K., Reisinger, A., Segschneider, J., Shaffer, G., Steinacher, M., Strassmann, K., Tanaka, K., Timmermann, A., and Weaver, A. J.: Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis, Atmos. Chem. Phys., 13, 2793–2825, https://doi.org/10.5194/acp-13-2793-2013, 2013. a, b, c, d, e, f, g, h, i, j, k, l, m
Jung, M., Schwalm, C., Migliavacca, M., Walther, S., Camps-Valls, G., Koirala, S., Anthoni, P., Besnard, S., Bodesheim, P., Carvalhais, N., Chevallier, F., Gans, F., Goll, D. S., Haverd, V., Köhler, P., Ichii, K., Jain, A. K., Liu, J., Lombardozzi, D., Nabel, J. E. M. S., Nelson, J. A., O'Sullivan, M., Pallandt, M., Papale, D., Peters, W., Pongratz, J., Rödenbeck, C., Sitch, S., Tramontana, G., Walker, A., Weber, U., and Reichstein, M.: Scaling carbon fluxes from eddy covariance sites to globe: synthesis and evaluation of the FLUXCOM approach, Biogeosciences, 17, 1343–1365, https://doi.org/10.5194/bg-17-1343-2020, 2020. a
Kloeden, P. E. and Rasmussen, M.: Nonautonomous dynamical systems, American Mathematical Society, Providence, USA, 2011. a
Körner, C.: A matter of tree longevity, Science, 355, 130–131, https://doi.org/10.1126/science.aal2449, 2017. a
Lal, R.: Soil carbon sequestration impacts on global climate change and food security, Science, 304, 1623–1627, 2004. a
Lashof, D. A. and Ahuja, D. R.: Relative contributions of greenhouse gas emissions to global warming, Nature, 344, 529–531, https://doi.org/10.1038/344529a0, 1990. a, b, c, d, e, f
Lu, X., Wang, Y.-P., Luo, Y., and Jiang, L.: Ecosystem carbon transit versus turnover times in response to climate warming and rising atmospheric CO2 concentration, Biogeosciences, 15, 6559–6572, https://doi.org/10.5194/bg-15-6559-2018, 2018. a, b, c, d, e
Luo, Y. and Weng, E.: Dynamic disequilibrium of the terrestrial carbon cycle under global change, Trends Ecol. Evol., 26, 96–104, 2011. a
Luo, Y., Weng, E., and Yang, Y.: Ecosystem Ecology, in: Encyclopedia of Theoretical Ecology, edited by: Hastings, A. and Gross, L., University of California Press, Berkeley, CA, USA, 219–229, 2012. a, b, c, d
Luo, Y., Shi, Z., Lu, X., Xia, J., Liang, J., Jiang, J., Wang, Y., Smith, M. J., Jiang, L., Ahlström, A., Chen, B., Hararuk, O., Hastings, A., Hoffman, F., Medlyn, B., Niu, S., Rasmussen, M., Todd-Brown, K., and Wang, Y.-P.: Transient dynamics of terrestrial carbon storage: mathematical foundation and its applications, Biogeosciences, 14, 145–161, https://doi.org/10.5194/bg-14-145-2017, 2017. a, b, c, d
Metzler, H. and Sierra, C. A.: Linear Autonomous Compartmental Models as Continuous-Time Markov Chains: Transit-Time and Age Distributions, Math. Geosci., 50, 1–34, https://doi.org/10.1007/s11004-017-9690-1, 2018. a, b, c, d
Metzler, H., Müller, M., and Sierra, C. A.: Transit-time and age distributions for nonlinear time-dependent compartmental systems, P. Natl. Acad. Sci., 115, 1150–1155, https://doi.org/10.1073/pnas.1705296115, 2018. a, b, c, d, e
Millar, R. J., Nicholls, Z. R., Friedlingstein, P., and Allen, M. R.: A modified impulse-response representation of the global near-surface air temperature and atmospheric concentration response to carbon dioxide emissions, Atmos. Chem. Phys., 17, 7213–7228, https://doi.org/10.5194/acp-17-7213-2017, 2017. a, b, c, d, e
Minasny, B., Malone, B. P., McBratney, A. B., Angers, D. A., Arrouays, D., Chambers, A., Chaplot, V., Chen, Z.-S., Cheng, K., Das, B. S., Field, D. J., Gimona, A., Hedley, C. B., Hong, S. Y., Mandal, B., Marchant, B. P., Martin, M., McConkey, B. G., Mulder, V. L., O'Rourke, S., de Forges, A. C. R., Odeh, I., Padarian, J., Paustian, K., Pan, G., Poggio, L., Savin, I., Stolbovoy, V., Stockmann, U., Sulaeman, Y., Tsui, C.-C., Vågen, T.-G., van Wesemael, B., and Winowiecki, L.: Soil carbon 4 per mille, Geoderma, 292, 59–86, https://doi.org/10.1016/j.geoderma.2017.01.002, 2017. a
Moura Costa, P. and Wilson, C.: An equivalence factor between CO2 avoided emissions and sequestration – description and applications in forestry, Mitig. Adapt. Strat. Gl., 5, 51–60, https://doi.org/10.1023/A:1009697625521, 2000. a, b, c
Myhre, G., Shindell, D., Bréon, F.-M., Collins, W., Fuglestvedt, J., Huang, J., Koch, D., Lamarque, J.-F., Lee, D., Mendoza, B., Nakajima, T., Robock, A., Stephens, G., Takemura, T., and Zhang, H.: Anthropogenic and natural radiative forcing, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T., Qin, D., Plattner, G.-K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P., Cambridge University Press, Cambridge, UK, 658–740, 2013. a
Neubauer, S. C. and Megonigal, J. P.: Moving Beyond Global Warming Potentials to Quantify the Climatic Role of Ecosystems, Ecosystems, 18, 1000–1013, https://doi.org/10.1007/s10021-015-9879-4, 2015. a, b, c, d, e
Noble, I., Apps, M., Houghton, R., Lashof, D., Makundi, W., Murdiyarso, D., Murray, B., Sombroek, W., and Valentini, R.: Implications of Different Definitions and Generic Issues, in: Land Use, Land Use Change, and Forestry, edited by: Watson, R. T., Noble, I. R., Bolin, B., Ravindranath, N. H., Verardo, D. J., and Dokken, D. J., Cambridge University Press, Cambridge, UK, 53–156, 2000. a, b
O'Neill, B. C., Gaffin, S. R., Tubiello, F. N., and Oppenheimer, M.: Reservoir timescales for anthropogenic CO2 in the atmosphere, Tellus B, 46, 378–389, https://doi.org/10.1034/j.1600-0889.1994.t01-4-00004.x, 1994. a
Prather, M. J.: Time scales in atmospheric chemistry: Theory, GWPs for CH4 and CO, and runaway growth, Geophys. Res. Lett., 23, 2597–2600, https://doi.org/10.1029/96GL02371, 1996. a
Rasmussen, M., Hastings, A., Smith, M. J., Agusto, F. B., Chen-Charpentier, B. M., Hoffman, F. M., Jiang, J., Todd-Brown, K. E. O., Wang, Y., Wang, Y.-P., and Luo, Y.: Transit times and mean ages for nonautonomous and autonomous compartmental systems, J. Math. Biol., 73, 1379–1398, https://doi.org/10.1007/s00285-016-0990-8, 2016. a, b, c, d, e, f, g, h, i, j
Rodhe, H.: A Comparison of the Contribution of Various Gases to the Greenhouse Effect, Science, 248, 1217–1219, https://doi.org/10.1126/science.248.4960.1217, 1990. a, b, c, d
Rodhe, H.: Modeling biogeochemical cycles, in: Earth system science: from biogeochemical cycles to global change, edited by: Jacobson, M. C., Charlson, R. J., Rodhe, H., and Orians, G. H., Academic Press, London, UK, 62–84, 2000. a
Schiedung, M., Tregurtha, C. S., Beare, M. H., Thomas, S. M., and Don, A.: Deep soil flipping increases carbon stocks of New Zealand grasslands, Glob. Change Biol., 25, 2296–2309, https://doi.org/10.1111/gcb.14588, 2019. a
Schulze, E. D., Stupak, I., and Hessenmöller, D.: The climate mitigation potential of managed versus unmanaged spruce and beech forests in Central Europe, in: Bioenergy with Carbon Capture and Storage, edited by: Pires, J. C. M. and Gonçalves, A. L. D. C., Academic Press, London, UK, 131–149, https://doi.org/10.1016/B978-0-12-816229-3.00007-7, 2019. a
Sedjo, R. and Sohngen, B.: Carbon Sequestration in Forests and Soils, Annu. Rev. Resour. Econ., 4, 127–144, https://doi.org/10.1146/annurev-resource-083110-115941, 2012. a, b
Shine, K., Derwent, R., Wuebbles, D., and Morcrette, J.: Radiative Forcing of Climate, in: Climate Change – The IPCC Scientific Assessment, edited by: Houghton, J., Jenkins, G., and Ephraums, J., Cambridge Cambridge University Press, Cambridge, UK, 1990. a, b, c
Sierra, C., del Valle, J., and Restrepo, H.: Total carbon accumulation in a tropical forest landscape, Carbon Balance and Management, 7, 12, https://doi.org/10.1186/1750-0680-7-12, 2012. a
Sierra, C. A.: Approaches to Model Processes at the Ecosystem Level, in: Plant Ecology, edited by: Schulze, E.-D., Beck, E., Buchmann, N., Clemens, S., Müller-Hohenstein, K., and Scherer-Lorenzen, M., Springer, Berlin and Heidelberg, Germany, 513–527, https://doi.org/10.1007/978-3-662-56233-8_15, 2019. a
Sierra, C. A.: The Climate Benefit of Carbon Sequestration (Version 1.1), https://doi.org/10.5281/zenodo.4399181, 2020. a, b
Sierra, C. A., Müller, M., Metzler, H., Manzoni, S., and Trumbore, S. E.: The muddle of ages, turnover, transit, and residence times in the carbon cycle, Glob. Change Biol., 23, 1763–1773, https://doi.org/10.1111/gcb.13556, 2017. a, b, c
Sierra, C. A., Ceballos-Núñez, V., Metzler, H., and Müller, M.: Representing and Understanding the Carbon Cycle Using the Theory of Compartmental Dynamical Systems, J. Adv. Model. Earth Sy., 10, 1729–1734, https://doi.org/10.1029/2018MS001360, 2018a. a, b, c, d
Sierra, C. A., Hoyt, A. M., He, Y., and Trumbore, S. E.: Soil Organic Matter Persistence as a Stochastic Process: Age and Transit Time Distributions of Carbon in Soils, Glob. Biogeochem. Cy., 32, 1574–1588, https://doi.org/10.1029/2018GB005950, 2018b. a
Silver, W., Ostertag, R., and Lugo, A. E.: The potential of carbon sequestration through reforestation of abandoned tropical agricultural and pasture lands, Restor. Ecol., 8, 394–407, 2000. a
Weng, E. and Luo, Y.: Relative information contributions of model vs. data to short- and long-term forecasts of forest carbon dynamics, Ecol. Appl., 21, 1490–1505, https://doi.org/10.1890/09-1394.1, 2011. a, b, c, d
Xia, J., Luo, Y., Wang, Y.-P., and Hararuk, O.: Traceable components of terrestrial carbon storage capacity in biogeochemical models, Glob. Change Biol., 19, 2104–2116, https://doi.org/10.1111/gcb.12172, 2013. a
- Abstract
- Introduction
- Theoretical framework
- Example 1: CS and CBS for linear systems in equilibrium
- Example 2: CS and CBS for dynamic systems out of equilibrium
- Discussion
- Conclusions
- Appendix A: Comment on Neubauer and Megonigal (2015)
- Appendix B: Fate and timescales of carbon in compartmental systems
- Appendix C: Detailed representation of the TECO model and the transient simulations used in examples
- Executable research compendium (ERC)
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Theoretical framework
- Example 1: CS and CBS for linear systems in equilibrium
- Example 2: CS and CBS for dynamic systems out of equilibrium
- Discussion
- Conclusions
- Appendix A: Comment on Neubauer and Megonigal (2015)
- Appendix B: Fate and timescales of carbon in compartmental systems
- Appendix C: Detailed representation of the TECO model and the transient simulations used in examples
- Executable research compendium (ERC)
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References




