the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Accelerate coccolith size separation via repeated centrifugation
Hongrui Zhang
Chuanlian Liu
Luz María Mejía
Heather Stoll
Coccolithophores play a key role in the marine carbon cycle and ecosystem. The carbonate shells produced by coccolithophore, named as coccolith, could be well preserved in the marine sediment for millions of years and become an excellent archive for paleoclimate studies. The micro-filtering and sinking–decanting methods have been successfully designed for coccolith separation and promoted the development of geochemistry studies on coccolith, such as the stable isotopes and Sr Ca ratio. However, these two methods are still not efficient enough for the sample-consuming methods. In this study, the trajectory of coccolith movement during a centrifugation process was calculated in theory and carefully tested by separations in practice. We offer a MATLAB code to estimate the appropriate parameter, angular velocity at a fixed centrifugation duration, for separating certain coccolith size fractions from bulk sediment. This work could improve the efficiency of coccolith separation, especially for the finest size fraction, and make it possible to carry out the clumped isotope and radio carbon analyses on coccoliths in sediment.
- Article
(1104 KB) - Full-text XML
-
Supplement
(452 KB) - BibTeX
- EndNote
Coccolithophores are a group of marine calcifying eukaryotic phytoplankton, whose calcite exoskeletons (i.e., coccolith) contribute significantly to the particulate inorganic carbon (PIC) export from the euphotic zone into the deep ocean (Young and Ziveri, 2000). Coccoliths preserved in marine sediment are also excellent archives for paleo-productivity reconstruction (Beaufort et al., 1997). The element ratio Sr Ca in coccoliths is correlated with the growth rate of calcite crystals (Stoll et al., 2002), thereby becoming a competitive candidate for coccolithophore growth rate, which is an essential parameter in the paleo-CO2 reconstruction by alkenone carbon isotope. However, the coccolith geochemical analyses are limited by the difficulty of separating coccoliths from bulk sediment. To solve this problem, different separating methods have been proposed in the past over a few decades (Paull and Thierstein, 1987; Stoll and Ziveri, 2002; Minoletti et al., 2008).
Most of them, in general, could be categorized into two groups: the first one is micro-filtering and the second is the sinking–decanting technique. The micro-filtering method relies heavily on the specifications of micro-filter membrane (such as 3, 5 and 8 µm pore sizes), which are highly effective at separation of the larger-size coccoliths but useless for coccoliths smaller than 2 µm. The sinking–decanting method, on the other hand, could offer more freedom in coccolith size by adjusting the sinking durations, thereby separating both small and large coccoliths. However, because of the slow sinking speed, a single separation of particles smaller than 2 µm may take more than 10 h in settling. Moreover, operations should be repeated about 6–8 times, which means a full separation may take at most 1 week. Hence, it is necessary to improve this method by reducing the time cost in coccolith separation.
Based on the Stokes sinking equation, the sinking rate of a certain particle increases with the increase of density difference between particle and liquid, decrease of the liquid viscosity, and the increase of gravity. Changing the physical property of liquid often leads to an organic and toxic solvent which could lead to potential contamination for further geochemistry analyses. A better way to accelerate coccolith sinking speed is changing the gravity or the acceleration speed of the reference system, which can be easily achieved by centrifugation. One study has mentioned the usage of centrifugation in coccolith separation, but only centrifugation settings for a special case were provided (Hermoso et al., 2015). Here in this study, the separation of coccoliths by centrifugation method is introduced systemically. We first calculate the trajectory of coccolith movement in centrifugation processes and show how to estimate the centrifugation parameters in different situations. After that, two tests are performed to confirm the robustness of our calculations. Ultimately, a sample containing coccoliths ranging from 2 to 12 µm is selected for a separation case in practice.
The movement of coccoliths under centrifugation is similar to that under the gravity. Previously, we have calculated the separation ratio variation with time during the settling (Zhang et al., 2018). All calculations in this study are with an assumption that the coccolith is in force balance all the time during both settling and centrifugation for a convenience of calculation. Here we offer a brief proof for this assumption based on spherical particles (the sink speeds of spherical particles are ∼ 30 % higher than those of coccoliths of the same size) and give a quick review of the derivation we did before.
Based on Newton's second law, the force balance of a spherical object during sinking can be described by the following equation:
where F is the joint force of particle, which is equal to zero in force balance; r is the radius of sphere; ρp and ρl are the density of particle and liquid, respectively; η is the velocity of liquid; v is the particle sinking speed; and is the particle acceleration speed, which can be also denoted as a. On the right-hand side of the first equal to sign, the first term is the gravity force, the second term is buoyancy and the third term is the dragging force from liquid. By transforming Eq. (1), we can obtain the expression of accelerated speed () of a sphere as Eq. (2):
Given that the initial value of sinking speed is equal to zero at the initial time (t=0), we can solve the differential equation (Eq. 2) and obtain the variation of velocity with time as the following equation:
When the value of t is large enough, the first term of the numerator in Eq. (3) is close to zero, which means the sinking velocity is close to the terminal sinking velocity described in the Stocks equation (Eq. 4).
Given a spherical calcite carbonate particle with a 5 µm radius and density of 2.7 g cm−3, the density of water being equal to 1.0 g cm−3, and when t is equal to 10−7 s, then the first term of the numerator is m s−2 and small enough to be neglected compared with the second term, which is 6.3 m s−2. The timescale in coccolith separation is minutes for centrifugation and hours for settling; Therefore, we suggest that it is reasonable to assume that the coccolith sinks with the “terminal speed” from the very beginning.
The only difference between the terminal speed under centrifugation and under gravity is the acceleration speed. If g in Eqs. (1)–(4) is adapted by a, which is the acceleration speed of the coccolith during centrifugation, these four equations above can also describe the sphere's movement in the centrifugation if we adapt the gravity to centripetal acceleration (ca). Here we define a new parameter named sinking parameter (sp):
The physical meaning of sp is the influence of coccolith shape and liquid property (density and viscosity) on sinking velocity without considering the effect of gravity (or the acceleration rate of the reference system). The sinking speed of the coccolith in water during a centrifugation (v′) can be described as follows:
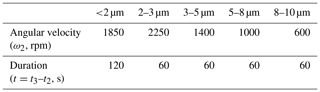
where the ca is centripetal acceleration during centrifugation, ω is angular velocity of the centrifuge, (L+D) is the rotation radius as illustrated in Fig. 1. Parameter L is a fixed value for a certain type of centrifuge, and D depends on the position of the coccolith in the tube. Here we should note two issues. The first one is that the rotation radius is varying when coccolith is moving in the centrifuge tube; in other words, D is always changing. This effect could be ignored when L is much larger than D, but, unfortunately, most centrifuges employed in geochemistry laboratories are not large enough. The second one is that angular velocity is dynamic when the centrifuge is accelerating and decreasing. To solve these two dynamic parameters, Eq. (6) was transformed into a form of differential equation as Eq. (7) for the convenience of integration in the next step.
For all centrifugation steps, there are three stages: the acceleration stage (t1 to t2 in Fig. 1), the constant angular velocity stage (t2 to t3 in Fig. 1) and the deceleration stage (t3 to t4 in Fig. 1). The durations of the acceleration stage and deceleration stage can usually be controlled and the angular velocity is changing with a constant speed. For those machines where the angular velocity dynamic (ω=f(t)) is unknown, we should measure it manually.
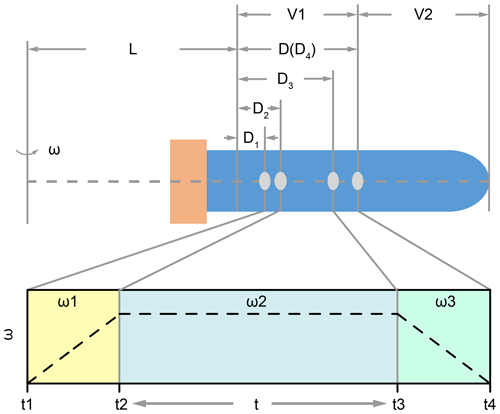
Figure 1The position of coccolith and the variation of ω in the three centrifuging stages: L represents the minimum rotation radius, and V1 and V2 represent the volumes of the two parts; in the first stage, the angular velocity increases from zero to ω1 (it could be linear or cubic, which depends on the machine). Meanwhile, the coccolith moves a distance of D2–D1; similarly, the coccolith moves a distance of D3–D2 in the second stage, and it moves a distance of D4–D3 in the last stage.
After knowing the angular velocity curve, integrate D over t in Eq. (7) by three steps from t1 to t4:
Adding Eqs. (8)–(10) together gives
Set D4 equal to D, which represents the maximum distance that a coccolith can move in the upper suspension V1. Now we can use the coccolith sinking property, sp, and centrifugation settings to describe the coccolith position after centrifugation D1:
The meaning of D1 is that all coccoliths with an initial position on the right side of D1 in Fig. 1 will move to the right side of D4 and then be kept in the suspension after pumping, while the coccoliths on the left side of D1 will be removed by pumping.
In our previous publication (Zhang et al., 2018), we defined a parameter named separation ratio (R), which represents the percentage of coccolith removed in one separation if we pump the upper V1 volume suspension out of (V1+V2) suspension in total.
Replacing the D1 in Eq. (15) with Eq. (12) gives the separation ratio (R) as a function of centrifugation settings:
The R can be employed in estimating the centrifugation parameters for separating one type of coccoliths from another. For example, if we want to separate a group of coccolith (marked as CoccolithA, with sinking parameter spA) from another group of coccolith (marked as CoccolithB, with sinking parameter of spB and spA < spB), the R of CoccolithB should be set as zero, which means all CoccolithB in the section V1 have sunk into V2 after centrifugation; therefore, all coccolith pumped out should be CoccolithA. To solve the angular velocity (ω2) and centrifugation duration (t=t3–t2) in Eq. (14), we need to fix at least one of them. Usually the duration could be safely set as 1 min or 2 min, and then we solve the suitable angular velocity with known parameters V1, V2, D and L. The MATLAB code for the parameter estimation is in the Supplement. After repeating these “centrifugation–pumping” routines several times, CoccolithA could be fully separated from CoccolithB.
3.1 Experimental design
To test the robustness of our estimation in the last section, we performed two groups of experiments comparing the observed with predicted separation ratios. Here we select two different coccoliths, Florisphaera profunda and small Gephyrocapsa, with small size and thereby slow sinking speed, sampled from ODP 807 and IODP U1304, respectively. Most of the small Gephyrocapsa employed in this study are smaller than 3 µm with a mixture of G. muellerae less than 10 %. Two centrifuges from Anting Company, TDL-40B and DL-5B, were selected to perform the tests. The angular velocity of DL-5B can be set as linear increased or decreased with time in the acceleration or deceleration stages, while the angular velocity of TDL-40B was measured manually by reading the number on the instrument panel. The centrifugation duration can only be adapted by a step of 1 min on both of these machines. The slowest angular velocities of these two machines is 500 revolutions per minute (rpm). If we selected water as dispersion agent, most of the coccoliths we used will sink to the tube bottom after 2 min even with the slowest angular velocity. Hence, to slow down the coccolith sinking speed in these tests, glycerol solution was employed in this equation test, which can be dissolved with water in any proportion and washed away from carbonate calcite particles conveniently. The density and viscosity data can be found in Table 1.
All calculations above are for the situation that particles are sinking in water or diluted solution, the physical property of which is close to water. However, in this case, the property of glycerol is significantly different from water. Here we define a new parameter, τ, to transform the sinking speed in water to that in different liquid. The physical meaning of τ is a ratio turning the sinking velocity in water (v) into the velocity in any liquid with different density and viscosity (v′):
Based on the definition of Stokes equation, the term τ can be calculated as follows:
where the ρp, ρl and ρw are densities of particle, liquid (in this study is glycerol solution) and water, respectively. ηl and ηw are the viscosity of liquid and water, respectively.
Combining Eqs. (14)–(16) forms the separation ratio as a function of centrifugation settings in different liquid:
In this test, the calculated R by Eq. (17) will be compared with the measured one. To perform these tests, about 100 mg of bulk sediment was scattered into 30 mL 0.5 % ammonia, and after that, particles larger than 20 µm were removed by a mesh. In this test, we should obtain suspensions with nearly monospecific coccoliths. To achieve this, in the test with F. profunda, coccoliths larger than 3 µm were removed by the sinking method described in Zhang et al. (2018), and coccoliths larger than 5 µm were removed by the same method in the test with small Gephyrocapsa. Briefly, the suspension was (1) set in a 100 mL reagent bottle, sinking freely for a few hours, and then (2) pumped out of the upper 2 cm. These two steps were repeated 5–8 times until coccoliths were purified. The sinking duration was 2 h for the F. profunda sample and 1.25 h for the small Gephyrocapsa sample, respectively.
Then 50 mL tubes with 45 mL coccolith suspensions were mounted in the centrifuge and run with the settings shown in Table 1. After centrifugation, the upper 30 mL supernatant was pumped out by pipette and then filtered onto a 0.4 µm polycarbonate membrane filter with a vacuum pump. The coccoliths on the polycarbonate membrane were resuspended into 20 mL diluted ammonia again, and coccolith number in the suspension was measured with the same method described in our previous work (Zhang et al., 2018). Finally, the separation ratio, R, was calculated by the coccolith number in the upper 30 mL suspension and divided by the total coccolith number. All the centrifuging experiments were carried out in the laboratory with temperature controlled to be around 20 (± 1) ∘C to avoid variation of physical properties, especially the viscosity, with temperature.
Table 1The settings of two tests: the density and viscosity of glycerol at 20 ∘C; data are from Dorsey (1940); the parameters of the centrifuge employed in this study are the following: Fp and G60 represent the experiments carried out with F. profunda in 70 % glycerol and small Gephyrocapsa (< 3 µm) in 60 % glycerol, respectively; L represents the minimum rotation radius of centrifugation, which represents the distance between the shaft and top of suspension as illustrated in Fig. 1. A, B and C are the terms on the left-hand side of the equal to sign in Eqs. (8)–(10).

3.2 Result of experiments
In the test, a 30 mL suspension was pumped out from a 45 mL suspension, leading to the result that the initial R should be 60 %. However, the intercept of calculated R is smaller than 60 % as the gravity settling in Zhang et al. (2018), because the time in the x axis of Fig. 2 is the period in which angular velocity remains constant. In other words, even though the time is set as zero, the centrifuge will still do the acceleration and deceleration processes, and coccoliths will move toward the bottom. The results of observed R (dots in Fig. 2) are close to the theoretical values (dash lines in Fig. 2), although a few measured results are lower than the prediction. We suggest that this difference may be caused by coccolith loss during harvesting of the coccolith from glycerol solutions into ammonia solution.
So far, we have obtained the coccolith movement equation in the centrifugation and proved its correctness. In the next section, a case of coccolith separation by the centrifuging method will be carried out giving an example of separation.
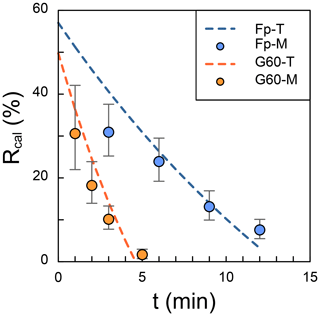
Figure 2The comparison of theoretical and measured separation ratio (R): the dots represent the measured values, and dashed lines are theoretical calculations. The error bars represent 95 % error based on the assumption that the error of counting coccolith follows the Poisson distribution. The orange dots represent the measured R in small Gephyrocapsa test with 60 % glycerol (G60-M), and the blue ones represent the measured R in F. profunda text with 70 % glycerol (Fp-M). The dashed orange line is the theoretical values for small Gephyrocapsa test with 60 % glycerol(G60-T), and the blue one is the theoretical values for F. profunda test with 70 % glycerol (Fp-T). Raw pictures for coccolith counting are shown in Figs. S1 and S2.
4.1 Separation steps
The aim of this section is to separate a sample in practice using the centrifugation method. A sample form ODP 982B (56X Section 5 5–9 cm) dated around mid-Miocene (nannofossil zone NN4) was selected in this test. The coccolithophore Reticulofenestra spp. dominated in the assemblage, with long-axis length ranging from 2 µm to more than 12 µm, offering an ideal sample to test the coccolith separation method. Calcidiscus spp. (4–10 µm), Helicosphaera spp. (5–10 µm) and Coccolithus spp. (6–8 µm) were also found in this sample, which contributed less than 10 % to all coccoliths together. The preservation of fossil was moderate with many coccolith fragments but no evidence of dissolution in the raw sample. The detailed operations are the following:
-
Step 1. Weigh about 40 mg bulk sediment, scatter with 45 mL 0.5 % ammonia solution and transfer the suspension into a 50 mL centrifuging tube;
-
Step 2. Calculate the centrifugation parameters (angular velocity and duration). Here we did not measure coccolith sinking velocities but employ the length–velocity relationship in the previous study directly: sinking rate at 25∘ = 0.0982 × length2 (Zhang et al., 2018). Based on this length-velocity equation and the centrifuge properties listed in Table 1, we estimated that the angular velocity and duration for separating coccolith with a length of 2, 3, 5, 8 and 10 µm should be 1850 rpm for 2 min, 2250, 1400, 1000 and 600 rpm for 1 min, respectively. The MATLAB code for calculating the angular velocity at fixed centrifugation duration (1 or 2 min) is in the Supplement.
-
Step 3. Mount the tube into the centrifuge and balance weight; set the angular velocity to 1850 rpm and the duration to 2 min and start the machine;
-
Step 4. Pump out the upper 30 mL from each suspensions and release it into a beaker (500 mL or larger beaker, depends on how many times this step is repeated) and drop about 100 µL onto a glass coverslip. Dry the suspension on glass coverslip and mount the coverslip on a slide. The details of this step follow Bordiga et al. (2015);
-
Step 5. Repeat step 2–5 with different centrifugation parameters listed in Table 2;
-
Step 6. Take pictures of coccoliths in each slide on the microscope and measure the coccolith size on the computer with the method described by Fuertes et al. (2014).
4.2 Coccolith length in each fraction
The coccolith size distribution harvested from different centrifugation settings are shown in Fig. 3 (the coccolith size was measured in a circular-polarizing microscope, and coccoliths under a cross-polarizing microscope are shown in Figs. S3–S9 for species identification). The results show that the separated coccolith size increased with the decrease of angular velocity, and the differences of mean coccolith lengths are significant between each size fraction. However, we should also note that there is still overlap of coccolith sizes between two neighboring fractions. With the centrifugation parameters set as 2250 rpm and 2 min, the coccoliths harvested have long-axis lengths around 2–4 µm, and when the centrifugation parameters were varied to 1400 rpm and 1 min, the coccolith long-axis size ranges from 3 to 7 µm, which means coccoliths with a length between 3–4 µm appear in two fractions. Such situations may also happen in both settling and micro-filtering methods, but the range of overlap seems to be larger for the centrifugation method compared with the size fractions harvested by other methods.
Figure 3The coccolith size in different fractions after centrifuge separation: the yellow, red, green and blue dots represent 2250 rpm for 2 min, 1400, 1000 and 600 rpm for 1 min, respectively.
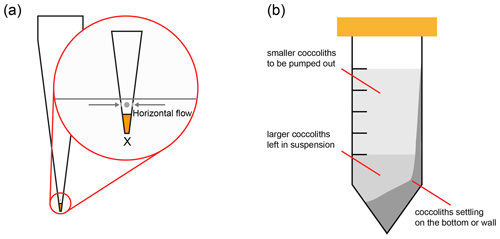
Figure 4Two methods to reduce the coccolith size overlapping. (a) Adaption of pipette tip: the orange part on the tip is sealed by solidified glue, and the gray parts mean that small holes should be drilled allowing the suspension to flow in horizontally; (b) choose a proper pumping position to avoid extracting the coccolith on the tube wall. The lightest gray part in the tube represents the suspension in which the smaller coccolith floats; most of the larger coccoliths are in the lower part of the suspension and the tube bottom.
4.3 Troubleshooting
The first potential reason leading to overlap may be that the repeating times are not enough. This could be the main problem for settling under gravity, since the time costs for separation under gravity are much larger than the centrifugation method. Bolton et al. (2012) suggested that separations done 4–6 times are enough for fossil extraction, and in our separations we repeated separations more than 8 times for a certain centrifugation setting. Considering these facts, we suggest that this overlapping was not caused by the separation times.
Another reason could be that larger coccoliths, which are supposed to sink into the lower suspension, are pumped out after centrifugation. When the upper suspension was pumped out, the pumping speed could be too fast, drawing up larger coccoliths from the lower suspension. This problem could be solved by reducing the pumping speed. Hoverer, in practice, the pumping speed of a pipette is difficult to control. Here we recommend to modify the tips of pipettes as follows: (1) suck a drop of glue into the top of pipette tips (the Norland optical adhesive 74 was employed in this study), (2) solidify the glue with ultraviolet light to seal the top of tips, and (3) drill holes above the glue horizontally. After this modification, the suspension will go into tips horizontally instead of vertically (Fig. 4a) to avoid mixing larger coccoliths with smaller ones.
The size overlapping could also be caused by the centrifugation tube not remaining perfectly horizontal during centrifugation. In our calculations, the tubes are assumed to be perfectly horizontal during all centrifugation processes; thereby, it was assumed that there should be no collisions between coccoliths or the tube wall. However, in practice, the tubes in a centrifuge are not always horizontal and even a few degrees slope of the tubes can lead some coccoliths will knock and stick on the tube wall forming a significant coccolith layer on one side of the tube wall as illustrated in Fig. 4b. These coccoliths on tube wall will be pumped out after centrifugation, causing the coccolith length overlapping among two fractions. To avoid this problem, before the step of pumping out suspension, we should observe the tube carefully. If a coccolith layer can be found on the tube wall, the pipette tip should be placed on the opposite of the coccolith layer to reduce the size overlapping.
In this study, we described the method of separating coccolith from bulk sediment by centrifuging. The rotation speed for separating coccoliths within a certain range of length could be solved after measuring the rotations radius (property of centrifuge) and fixing the centrifugation duration.
The centrifugation method is not perfectly accurate and could still mix different species of coccolith as other traditional separating methods. The size overlapping of this method could be reduced by adapting the pipette tips and avoiding pumping out the coccolith on tube wall. However, this method is more efficient in separating the finest particle (smaller than 3 µm) out of bulk sediment, which is always the time-consuming step in micro-filtering and sinking methods. Thereby, this method can be widely used in the sample preparation for analyses needing a large amount of material, such as coccolith clumped isotope and radioactive carbon isotope measurements. Moreover, the centrifugation method can be combined with other separation steps, for example using the centrifugation method to remove the finest particles followed by micro-filtering with different sizes of membranes. This method could largely reduce the time cost in sample preparation for coccolith geochemistry analyses and has the potential for wide use in the future.
The code for calculating centrifuging parameter is contained in the Supplement.
All necessary data are included in Table 1 and in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-18-1909-2021-supplement.
This study was conceived by HZ and CL Measurements and calculations were conducted by HZ. HZ, HS and LMM wrote the paper.
The authors declare that they have no conflict of interest.
This study was funded by the National Science Foundation of China (41930536, to Chuanlian Liu), ETH core funding (to Heather Stoll), European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement (795053 to Luz María Mejía) and the Chinese Scholarship Council (CSC) with a scholarship to Hongrui Zhang. We thank the Integrated Ocean Drilling Program (IODP) for providing the samples. We thank Guodong Jia for providing two centrifuges to test our work and Xinquan Zhou for identification the Miocene nannofossils.
This research has been supported by the National Natural Science Foundation of China (grant no. 41930536), the ETH core funding, the Chinese Scholarship Council (grant no. 201706260032), and Marie Skłodowska-Curie (grant no. 795053).
This paper was edited by Hiroshi Kitazato and reviewed by two anonymous referees.
Beaufort, L., Lancelot, Y., Camberlin, P., Cayre, O., Vincent, E., Bassinot, F., and Labeyrie, L.: Insolation cycles as a major control of equatorial Indian Ocean primary production, Science 278, 1451–1454, https://doi.org/10.1126/science.278.5342.1451, 1997.
Bolton, C. T., Stoll, H. M., and Mendez-Vicente, A.: Vital effects in coccolith calcite: Cenozoic climate-pCO2drove the diversity of carbon acquisition strategies in coccolithophores?, Paleoceanography, 27, https://doi.org/10.1029/2012pa002339, 2012.
Bordiga, M., Bartol, M., and Henderiks, J.: Absolute nannofossil abundance estimates: Quantifying the pros and cons of different techniques, Rev. Micropaleontol., 58, 155–165, https://doi.org/10.1016/j.revmic.2015.05.002, 2015.
Dorsey, N. E.: Properties of ordinary water-substance, Reinhold Publishing Corporation, New York, 1940.
Fuertes, M.-Á., Flores, J.-A., and Sierro, F. J.: The use of circularly polarized light for biometry, identification and estimation of mass of coccoliths, Mar. Micropaleontol. 113, 44–55, https://doi.org/10.1016/j.marmicro.2014.08.007, 2014.
Hermoso, M., Candelier, Y., Browning, T. J., and Minoletti, F.: Environmental control of the isotopic composition of subfossil coccolith calcite: Are laboratory culture data transferable to the natural environment?, GeoResJ, 7, 35–42, https://doi.org/10.1016/j.grj.2015.05.002, 2015.
Minoletti, F., Hermoso, M. and Gressier, V. Separation of sedimentary micron-sized particles for palaeoceanography and calcareous nannoplankton biogeochemistry, Nat. Protoc., 4, 14–24, https://doi.org/10.1038/nprot.2008.200, 2009
Paull, C. K. and Thierstein, H. R.: Stable isotopic fractionation among particles in Quaternary coccolith-sized deep-sea sediments, Paleoceanography 2, 423–429, https://doi.org/10.1029/PA002i004p00423, 1987.
Stoll, H. M. and Ziveri, P.: Separation of monospecific and restricted coccolith assemblages from sediments using differential settling velocity. Mar. Micropaleontol., 46, 209–221, https://doi.org/10.1016/S0377-8398(02)00040-3, 2002.
Stoll, H. M., Rosenthal, Y., and Falkowski, P.: Climate proxies from Sr Ca of coccolith calcite: calibrations from continuous culture of Emiliania huxleyi, Geochim. Cosmochim. Ac., 66, 927–936, https://doi.org/10.1016/S0016-7037(01)00836-5, 2002.
Young, J. R. and Ziveri, P.: Calculation of coccolith volume and it use in calibration of carbonate flux estimates, Deep Sea Res. Pt. II, 47, 1679–1700, https://doi.org/10.1016/S0967-0645(00)00003-5, 2000.
Zhang, H., Stoll, H., Bolton, C., Jin, X., and Liu, C.: Technical note: A refinement of coccolith separation methods: measuring the sinking characteristics of coccoliths, Biogeosciences, 15, 4759–4775, https://doi.org/10.5194/bg-15-4759-2018, 2018.
- Abstract
- Introduction
- Trajectory of coccoliths during centrifugation
- Test of the correctness of calculations
- Separation of coccoliths in practice
- Summary
- Code availability
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Trajectory of coccoliths during centrifugation
- Test of the correctness of calculations
- Separation of coccoliths in practice
- Summary
- Code availability
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement