the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Multi-compartment kinetic–allometric (MCKA) model of radionuclide bioaccumulation in marine fish
Roman Bezhenar
Kyeong Ok Kim
Govert de With
Kyung Tae Jung
A model of the radionuclide accumulation in fish taking into account the contribution of different tissues and allometry is presented. The basic model assumptions are as follows. (i) A fish organism is represented by several compartments in which radionuclides are homogeneously distributed. (ii) The compartments correspond to three groups of organs or tissues: muscle, bones and organs (kidney, liver, gonads, etc.) differing in metabolic function. (iii) Two input compartments include gills absorbing contamination from water and digestive tract through which contaminated food is absorbed. (iv) The absorbed radionuclide is redistributed between organs or tissues according to their metabolic functions. (v) The elimination of assimilated elements from each group of organs or tissues differs, reflecting differences in specific tissues or organs in which elements were accumulated. (vi) The food and water uptake rates, elimination rate, and growth rate depend on the metabolic rate, which is scaled by fish mass to the power. The analytical solutions of the system of model equations describing dynamics of the assimilation and elimination of 134Cs, 57Co, 60Co, 54Mn and 65Zn, which are preferably accumulated in different tissues, exhibited good agreement with the laboratory experiments. The developed multi-compartment kinetic–allometric model was embedded into the box model POSEIDON-R (Maderich et al., 2018b), which describes transport of radionuclides in water, accumulation in the sediment and transfer of radionuclides through the pelagic and benthic food webs. The POSEIDON-R model was applied for the simulation of the transport and fate of 60Co and 54Mn routinely released from Forsmark Nuclear Power Plant (NPP) located on the Baltic Sea coast of Sweden and for calculation of 90Sr concentration in fish after the accident at Fukushima Dai-ichi NPP. Computed concentrations of radionuclides in fish agree with the measurements much better than calculated using standard whole-body model and target tissue model. The model with the defined generic parameters could be used in different marine environments without calibration based on a posteriori information, which is important for emergency decision support systems.
- Article
(4260 KB) - Full-text XML
-
Supplement
(368 KB) - BibTeX
- EndNote
Accumulation of radionuclides in marine organisms is a complicated process that is governed by uptake of radionuclides from water, sediment and food as well as by depuration. In turn, these processes depend on the chemical properties of elements, their roles in metabolic processes, the positions of organisms in the food web and marine environmental parameters. In the case of chronic exposure, the radiological assessment models often assumed an equilibrium approach (Carvalho, 2018), in which concentration in the organism relates to the concentration in water using a biological accumulation factor (BAF). However, to describe highly time-dependent transfer processes resulting from accidental releases, dynamic models for the uptake and retention of activity in marine organisms are necessary (Vives i Batlle et al., 2016). According to Takata et al. (2019), the effective half-lives of post-Fukushima Dai-ichi Nuclear Power Plant (FDNPP) accident disequilibrium of 137Cs in biota ranged from 100 to 1100 d. The most commonly used bioaccumulation models are the whole-body models, where the organism is represented as a single box in which contamination is evenly distributed (e.g. Fowler and Fisher, 2004; Vives i Batlle et al., 2016). However, the distribution of radionuclides in organisms, and in particular in fish, is non-uniform. For example, the highest concentration of radiocaesium in fish is observed in the muscle, while the highest concentrations of the actinides, plutonium and americium, are measured in specific organs (Coughtrey and Thorne, 1983). Moreover, Vives i Batlle (2012) noted that elimination of activity from organisms occurred with different rates that can be interpreted as elimination from different tissues or organs with different metabolism. In a first approximation, this is used in the “target tissue” approach (Heling et al., 2002; Tateda et al., 2013; Maderich et al., 2014a, b; Bezhenar et al., 2016), where radionuclides are grouped into several classes depending on the type of tissues in which a specific radionuclide accumulates preferentially (target tissue). However, the contribution of other tissues with greater mass than the mass of the target tissue can be commensurate with the contribution of the target tissue to the amount of radioactivity in the body. Distribution of accumulated activities of isotopes Cs, Sr and Co in muscle, bone and liver estimated from previously reported data (Yankovich, 2003; Yankovich et al., 2010) are shown in Fig. 1. The accumulated activity in a given tissue was calculated as a ratio of tissue mass fraction (%) (Yankovich, 2003) to body-to-tissue concentration ratio (Yankovich et al., 2010). As seen in Fig. 1, the accumulated activity of Sr in muscle is not negligible in comparison with accumulated activity in bones, whereas the accumulated activity of Co is redistributed between muscle, bone and liver.
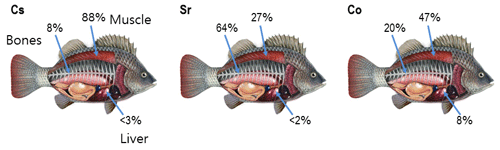
Figure 1Distribution of accumulated activities of isotopes Cs, Sr and Co in muscle, bone and liver estimated from data (Yankovich, 2003; Yankovich et al., 2010).
A more general approach to the description of the radionuclide accumulation in the tissues of fish is using the physiologically based pharmacokinetic (PBPK) models (Barron et al., 1990; Thomann et al., 1997; Garnier-Laplace et al., 2000; Otero-Muras et al., 2010; Grech et al., 2019). In the PBPK models, the fish organism is represented as three groups of compartments: absorption compartments simulating uptake of contaminants, distribution compartments simulating tissues and organs, and excretion compartments. The exchange of contaminants between compartments is limited by blood flux perfusing compartments. However, these models require a significant number of parameters depending on elements, fish species and marine environments. They must be determined from laboratory experiments (Thomann et al., 1997) or by optimization procedures (Otero-Muras et al., 2010). Note that, with the exception of model Grech et al. (2019), PBPK fish models do not include scaling (allometric) relationships between metabolic rates and organism mass (West et al., 1997; Higley and Bytwerk, 2007; Vives i Batlle et al., 2007; Beresford et al., 2016). Therefore, there is a need to develop a generic model of intermediate complexity between the one-compartment model and the PBPK model taking into account (i) the heterogeneity of the distribution of contamination in fish tissues and (ii) the allometric relationships between metabolic rates and organism mass. Such a model can be used for accidental release simulations without local calibration, which is a complicated task in the circumstances of the accident.
In this paper, a new approach for predicting radionuclide accumulation in fish by taking into account the contributions of different tissues and allometry is presented. The developed multi-compartment kinetic–allometric (MCKA) model is embedded into the box model POSEIDON-R (Lepicard et al., 2004; Maderich et al., 2014a, b; 2018b; Bezhenar et al., 2016), which describes transport of radionuclides in water, accumulation in the sediment, and transfer of radionuclides through the pelagic and benthic food webs. The paper is organized as follows. The MCKA model is described in Sect. 2. The comparison with laboratory experiments is given in Sect. 3. The results of simulation of several radionuclides in the marine environment for regular and accidental releases are described in Sect. 4. The conclusions are presented in Sect. 5.
2.1 Model equations
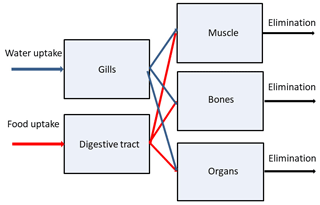
Here, a simple multi-compartmental model to simulate kinetics of radionuclides in the fish is described. The basic assumptions are as follows: (i) a fish organism is represented by several compartments in which radionuclides are homogeneously distributed; (ii) the compartments correspond to three groups of organs or tissues differing in metabolic function: muscle, bones and organs (kidney, liver, gonads, etc.); (iii) two input compartments include gills which absorb contamination from water and digestive tract through which contaminated food is absorbed; (iv) the absorbed radionuclide is redistributed between organs or tissues according to their metabolic functions; (v) the elimination of assimilated elements from each group of organs or tissues differs, reflecting differences in the specific tissues or organs in which elements were accumulated; and (vi) the food and water uptake rates, elimination rate, and growth rate depend on the metabolic rate, which is scaled by fish mass to the power following general theory (West et al., 1997). A schematic representation of the model is shown in Fig. 2.
The equation for concentration of radionuclide C1 [Bq kg−1] wet weight (WW) in the gill compartment (i=1) is written as
The equation for concentration of unabsorbed radionuclide C2 [Bq kg−1] (WW) in the digestive tract compartment (i=2) is
The equations for concentrations of radionuclide Ci [Bq kg−1] (WW) in the muscle (i=3), bones (i=4) and organs (i=5) are
Here, t is time; mi is the mass of the ith tissue; m [kg] is the total mass of fish; Cw [Bq m−3] is the concentration of radionuclide in water; Cf [Bq kg−1] (WW) is the concentration of radionuclide in food; Kw [m3(kg d)−1] is a water uptake rate per unit fresh weight of fish and Kf [kg(kg d)−1] is a food uptake rate per unit fresh weight of fish; λ1 is a loss rate from gills to water [d−1]; k1, k1i, k2, and k2i [d−1] are transfer rates between tissues; and λ2 [d−1] is the egestion rate from the digestive tract; λi [d−1] is the absorbed radionuclide elimination rate from different tissues or organs ().
The activity concentration in the food Cf is expressed by the following equation, summing for a total of n prey types
where Cprey,j is the activity concentration in prey of type , Pj is preference for prey of type j, drwpred is the dry weight fraction of fish and drwprey,j is the dry weight fraction of prey of type j. The mean whole-body concentration of activity in the organism Cwb and whole-body activity Awb [Bq] are calculated as
where μi represents weighting factors .
Transfer rates k1 and k2 are related with tissue transfer rates k1i and k2i as
Summing Eqs. (1) to (3) yields the equation for total concentration of activity in fish Cwb as
where λg is the organism growth rate, defined as
The growth dilution can be ignored in the model calculations when λg≪λi. For short-lived radionuclides, λi should be corrected by taking into account the physical decay. The assimilation efficiencies of elements from water AEw and food AEf (Pouil et al., 2018) can be introduced, assuming that uptake from water and food is equilibrated by loss to the water from gills and through egestion. The corresponding relations are
Taking into account the relations Eqs. (9)–(10) for constant AEw and AEf, Eq. (7) will be similar to the standard whole-body single-compartment equation
if elimination terms in Eq. (7) are replaced by a single term λwbCwb, assuming that λwb is a single whole-body elimination rate (Fowler and Fisher, 2004).
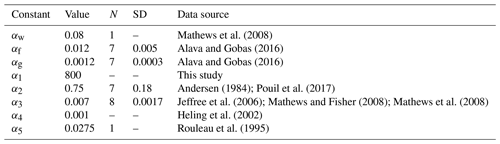
Table 1Parameters in allometric relations, standard deviation (SD) of parameters and number of measurements N.
The food and water uptake rates, elimination rate, and growth rate depend on the metabolic rate, which in turn is known to scale by the organism mass. Here, we employed quarter-power scaling for uptake, elimination and growth rates derived from general theory (West et al., 1997). This theory predicts for all organisms the power law for metabolic rates. It describes transport of essential materials through space-filling fractal networks of branching tubes assuming that the energy dissipation is minimized and that the terminal branch of the network is size invariant. The scaling relations are
where () are constants. These parameters can also depend on temperature, salinity and fish age (e.g. Belharet et al., 2019; Heling and Bezhenar, 2009). Notice that a number of laboratory experiments (Thomas and Fisher, 2010) showed that temperature exerts no major influence on uptake and elimination, whereas the effect of salinity varies for elements (Heling and Bezhenar, 2009; Jeffree et al., 2017). Here, we did not analyse these factors requiring separate consideration. The values of constants () estimated from laboratory experiments and marine data are provided in Table 1, whereas values of weighting factors μ1=0.01, μ2=0.01, μ3=0.78, μ4=0.12, and μ5=0.08 were chosen using estimates from Yankovich (2003).
2.2 Kinetics in equilibrium state
The model parameters can be estimated using measurement data and applying the kinetic equations under equilibrium conditions. Equations (1)–(3) rewritten for radionuclide concentrations in the equilibrium state are
Then, using Eqs. (13)–(14), the assimilation efficiencies of elements from water AEw and food AEf are rewritten as
When λ1≫λg and λ2≫λg, we determine from Eqs. (16) and (12), approximately, that
This assumption also imposes a requirement on the modelling of radionuclides with decay constant λ≪λi. Eq. (17) relations are used to relate kinetic coefficients of the model with experimentally determined parameters AEw, AEf, λ1 and λ2. Eq. (15) can be rewritten as
where AEwi and AEfi are assimilation efficiencies for tissue i,
The assimilation efficiencies are expressed through kinetic coefficients as
We define the bioconcentration factor (BCF) as a ratio of whole body of fish to water concentrations with no dietary intake, bioaccumulation factor (BAF) as ratio of whole body of fish to water concentrations with dietary intake, and body-to-tissue concentration ratio (CRi) as the ratio of whole body to ith tissue concentrations, whereas the ratio of food to water concentrations is indicated as BAFfood. The parameters BAF, CRi and BAFfood are described as
Values of BAF for different radionuclides are named as CF (Concentration Factor) in IAEA (2004). Yankovich et al. (2010) provide CRi based on aggregate experimental data for marine fish. We assume that the kinetics of assimilation in fish tissues are similar for radionuclides absorbed from water and food; i.e.
Notice that assimilation for some elements can be considered route dependent (Reinfelder et al., 1999), and so Eq. (22) is only a first approximation. Inserting Eq. (22) into Eq. (18) yields
Summing Eq. (23) for yields
Using Eqs. (23) and (24), the ratio AEfi AEf can be written as
The values of kinetic coefficients k1 and k2 and assimilation efficiencies for tissues AEfi were calculated from Eqs. (17) and (25) using assimilation efficiencies from experimental data (Pouil et al., 2018). The values of AEfi for several radionuclides are given in Table 2.
Table 2The food assimilation efficiency AEf (Pouil et al., 2018), assimilation efficiency of elements from water AEw, tissue assimilation efficiencies AEfi and trophic transfer factor (TTF) for several elements.
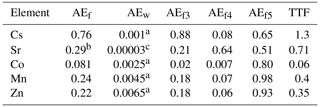
a The values were estimated from experiments by Mathews and Fisher (2008). b The value was estimated using BAF from IAEA (2004). c Heling and Bezhenar (2009) for seawater environment.
Equation (24) can be rearranged to express the ratio of BAFwb to BAFfood by taking into account dominance of dietary intake over water intake (Mathews and Fisher, 2009). This ratio is the trophic transfer factor (TTF), written as
TTF > 1 indicates possible biomagnification, and TTF < 1 indicates that biodiminution is likely. As follows from Eq. (26), the TTF value does not depend on the mass of fish. The TTF values calculated by using Eq. (26) are given in Table 2. Among the considered elements, only caesium (TTF > 1) may be biomagnified in the food chain, in agreement with Kasamatsu and Ishikawa (1997), where it was found that the BAF of 137Cs increased with increasing trophic level. The concentrations of other radionuclides in Table 2 decreased with the increase of trophic level (TTF < 1), which is consistent with the findings presented by Cardwell et al. (2013), where an inverse relationship was obtained between trophic levels and the concentration of inorganic metals in water chains.
Notice that values of AEf, AEw and BAF do not depend on the fish mass. The literature data reveal diverse relationships between fish mass and both radionuclide bioconcentration (BCF) and bioaccumulation (BAF) factors. In particular, data of laboratory experiments (Mathews et al., 2008) showed that there is no significant relationship between bioconcentration factor BCF and fish size for most studied aqueous metals. The BAF in larger and older fish of the same species can differ from smaller and younger fish due to the change of habitat and diet with age (e.g. Kasamatsu and Ishikawa, 1997; Ishikawa et al., 1995; Kim et al., 2019); however, in this study we did not consider the change of prey preference along the fish growth.
3.1 Depuration of radionuclides after pulse-like feeding
Retention of absorbed elements in fish after single feeding was often used to estimate AEf and depuration rate (e.g. Jeffree et al., 2006; Mathews and Fisher, 2008; Mathews et al., 2008; Pouil et al., 2017). According to Goldstein and Elwood (1971), single feeding can be approximated by a delta function δ(t) at t=0 as
where Af is the total amount of ingested activity. The solutions of Eqs (1)–(3) for activities A2=m2C2 and Ai=miCi and for initial conditions are
As follows from these solutions, the decay of activity in the fish organisms includes a fast component with decay constant representing transfer of activity to the fish body and unabsorbed element egestion from the digestive tract, along with a slow component which is governed by elimination constants for i tissues. These solutions are generalized solutions of the equations of the sequentially linked two-compartment model by Goldstein and Elwood (1971), whereas in the D-DAT model (Vives i Batlle et al., 2008) an organism was represented by two boxes with parallel kinetics, also describing “slow” and “fast” exchange processes.
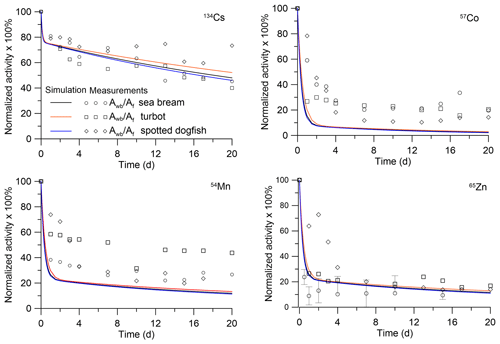
The analytical solutions (Eqs. 28–29) can be compared with laboratory experiments in which depuration of metals from the fish after single feeding was studied. In the experiment by Mathews and Fisher (2008), the retention of several radioisotopes in juvenile sea bream (Sparus auratus) was considered. The average wet weight of the fish was 0.0001 kg. These fish were fed radiolabelled Artemia salina nauplii. The fish were allowed to feed for 1 h, after which metal retention was observed in clean water over a 15 d period. The solutions with parameters corresponding to the fish mass and metal AE (Pouil et al., 2018) were compared with experimental data for 134Cs, 60Co, 54Mn, and 65Zn in Fig. 3. As seen in Fig. 3, both model and experiments showed two phases (fast and slow) of radionuclide elimination. Most of the activity is contained in muscle; however, the first 5 d after feeding the concentrations of 60Co and 54Mn in organs are much greater than in the muscle.
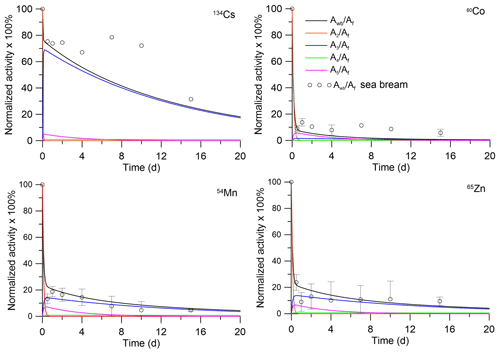
Figure 3Retention of radionuclides in whole body and tissues of juvenile sea bream (Sparus auratus). The simulations are compared with whole-body measurements by Mathews and Fisher (2008).
The solutions were also compared with laboratory experiments for predator fish (Mathews et al., 2008). In these experiments, the retention of several radioisotopes in sea bream (Sparus auratus), turbot (Psetta maxima) and spotted dogfish (Scyliorhinus canicula) was studied. Immature S. auratus (wet weight 0.012 kg), P. maxima (wet weight 0.027 kg) and S. canicula (wet weight 0.008 kg) were fed radiolabelled prey fish (juvenile S. auratus). After this feeding, fish were fed unlabelled prey fish for 3 weeks. In Fig. 4, the solutions Eqs. (28)–(29) were compared with the laboratory experiments in which prey fish were labelled by 134Cs, 57Co, 54Mn and 65Zn. The analytical solutions (Eqs. 28–29) and experiment agreed, demonstrating general dependence of the depuration process on fish mass. Differences between experimental data for different species may be due to differences in anatomy and physiology, as discussed by Jeffree et al. (2006) for P. maxima and S. canicula. The model, unlike the situation for prey fish (Fig. 3), underestimates the total concentrations of 57Co and 54Mn in comparison with experiments, which is probably due to the neglect of other factors, except body weight, for the bioaccumulation kinetics. Parameters of the MCKA model for fish from experiments (Mathews and Fisher, 2008; Mathews et al., 2008) are given in Table S1, whereas Tables S2–S4 show dependence on radionuclides of the transfer rates k2,i in different fishes.
3.2 Bioconcentration of dissolved radionuclides from sea water
Uptake and absorption in fish of elements from water were studied in several laboratory experiments (e.g. Jeffree et al., 2006; Mathews and Fisher, 2008; Mathews et al., 2008). The modelling of the absorption of elements can be used to estimate an assimilation efficiency AEw. An analytical solution of Eqs. (1) and (3) with initial conditions Ci=0 at t=0 is written as
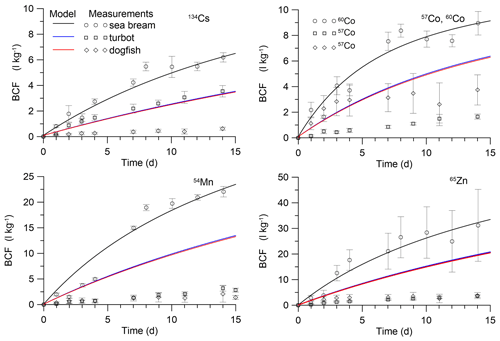
Figure 5Simulated BCF in marine fish during the period of exposition in water. The simulations are compared with isotope measurements by Mathews et al. (2008) in juvenile sea bream (Sparus auratus) and measurements by Jeffree et al. (2006) in turbot (Psetta maxima) and spotted dogfish (Scyliorhinus canicula).
These solutions were compared with laboratory experiments for prey fish (Mathews et al., 2008) and for predator fish (Jeffree et al., 2006). In the experiment by Mathews et al. (2008), the uptake of several radioisotopes by juvenile S. auratus (wet weight 0.0002 kg) was studied during 25 d of exposure, whereas in experiments by Jeffree et al. (2006) immature P. maxima (wet weight 0.0061 kg) and S. canicula (wet weight 0.0067 kg) were used for study during a 15 d period. Parameters of the MCKA model for these fishes are given in Table S5, whereas Tables S6–S8 show dependence on radionuclides of the transfer rates k1,i in different fishes. The comparison of the analytical solutions (Eqs. 30–31) with experimental data with respect to bioconcentration factor (BCF = C [L kg−1]) is presented in Fig. 5. The values of AEw were selected to approximate the experiment for small prey fish (Mathews et al., 2008). They differ for different metals. For 134Cs, the value of AEw was 0.001, whereas for 57Co and 60Co, 54Mn, and 65Zn, these values were 0.0025, 0.0045, 0.0065, respectively. This contrasted with AEf, which is larger for 134Cs than for 57Co, 60Co, 54Mn, and 65Zn (Pouil et al., 2017). The estimated values of AEw are presented in Table 2. The above-mentioned values of AEw were used to calculate BCF for larger predator fish in experiments by Jeffree et al. (2006). As seen in Fig. 5, values of AEw for considered elements are of the order 10−3, which is in agreement with most models. However, comparison with larger fish highlighted some differences between species of fish, as discussed by Jeffree et al. (2006), and differences between model and experiment for a constant value of AEw. At the same time, it is known that dietary intake of metals dominates over water intake (Mathews and Fisher, 2009). Therefore, deviations in values of AEw would not be significantly affected by the full uptake of elements from the marine environment.
The parameter α1 can be estimated from the relations Eqs. (13) and (16) according to the experimental data for equilibrium conditions. An average value of gill BCF1 is approximately 10 L kg−1 for 58Co, 54Mn, 134Cs and 65Zn (Jefferies and Heweit,1971; Pentreath, 1973). Then for AEw=0.001, we obtained α1=800. With the selected value of α1, the process of adaptation of the gill tissue to changes in the concentration of radioactivity in water is much faster than for other tissues of the fish. In addition, as follows from the analytical solutions (Eqs. 30–31) at λ1≫λi, the contribution of gill contamination to the whole-body contamination is small.
3.3 Simplification of the model based on the results of analytical solutions and laboratory experiments
Comparison of the model against laboratory experiments on the retention of absorbed elements in fish after single feeding demonstrated the need to include the kinetic characteristics of the digestive tract in the model when highly non-equilibrium transfer dynamics are expected. However, for modelling of food uptake in marine environment with multiple feedings the simple equilibrium assumption Eq. (14) can be used. At the same time, the analytical solution describing the bioconcentration due to the uptake and absorption of elements from water in fish, as well as the results of the laboratory experiment, shows that the contribution to the gills (Eq. 13) is negligible. Therefore, for modelling of uptake from water, the equilibrium assumption can also be used as it is shown above. The corresponding simplified equations for muscle, bone and organs can be rewritten as
The uncertainty in calculations using Eq. (32) arises due to (i) limited experimental data to define allometry constants αf, αw, α3, α4, α5; (ii) large intervals in the values of known AEf coefficients; (iii) unknown AEf values for many radionuclides; (iv) a lack of experimental data about AEw; and (v) limited experimental data for whole-body to tissue concentration ratios, CRi, in the marine fish. Therefore, a sensitivity analysis is necessary to estimate uncertainty of the simulation results. We estimated the effects of variations in above parameters in the Eq. (24) on the value of BAF in equilibrium state. The simple local sensitivity analysis and the one-at-a-time method (Pianosi et al., 2016) were used. The sensitivity of model output was estimated using a sensitivity index (SI) calculated following Hamby (1994) as
where Dmax and Dmin are the outputs corresponded to maximal and minimal input parameter values, respectively. Similarly to Bezhenar et al. (2016), the range for every parameter was defined as follows: minimum value was set to half the reference value and maximum value was set to twice the reference value. Calculated SI for three radionuclides, which are preferably accumulated in different tissues (137Cs, 90Sr and 60Co), are given in Fig. S1.
The results of the sensitivity study suggest that model results are most sensitive to variations of AEf and αf for 137Cs and 60Co, whereas for 60Co they are almost not sensitive to variations of AEw and αw. Note that model results are also sensitive to the variations of parameters related to tissues where the radionuclide is mainly accumulated: α3 and CR3 for 137Cs and α5 and CR5 for 60Co. For 90Sr, the model results are moderately sensitive to the variations of most above-considered parameters.
4.1 Modified POSEIDON-R box model
In order to predict the accumulation of radionuclides in fish in the marine environment using the MCKA model described above, it is necessary to calculate changes in concentration in water and in bottom sediments and to calculate the transport of radionuclides through food chains. The POSEIDON-R box model (Lepicard et al., 2004; Maderich et al., 2014a, b; 2018b; Bezhenar et al., 2016) can be used to simulate the marine environment as a system of 3D boxes for the water column, bottom sediment and food web. The water column box is vertically subdivided into layers. The suspended matter settles in the water column. The bottom sediment box is divided into three layers (Fig. S2). The downward burial processes operate in all three sediment layers. Maderich et al. (2018b) described the POSEIDON-R model in detail.
A food web model that includes pelagic and benthic food chains is implemented within the POSEIDON-R box model (Bezhenar et al., 2016). In the food web model, marine organisms are grouped into classes according to trophic level and species type (Fig. S3). The food chains differ between the pelagic zone and the benthic zone. Pelagic organisms comprise primary producers (phytoplankton) and consumers (zooplankton, non-piscivorous (forage) fish and piscivorous fish). In the benthic food chain, radionuclides are transferred from algae and contaminated bottom sediments to deposit-feeding invertebrates, demersal fish and benthic predators. Bottom sediments include both organic and inorganic components. Radioactivity is assumed to be assimilated by benthic organisms from the organic components of the bottom deposits. Other food web components are crustaceans (detritus feeders), molluscs (filter feeders) and coastal predators, which feed throughout the water column in shallow coastal waters. All organisms take in radionuclides both via the food web and directly from the water. Table S9 in the Supplement contains food preferences for organisms in the food web which are used in the model. Details of the transfer of radiocaesium through the marine food web are presented by Bezhenar et al. (2016) and Maderich et al. (2018b).
The POSEIDON-R model can handle different types of radioactive releases: including atmospheric fallout and point sources associated with routine releases from nuclear facilities located directly on the coast or point sources associated with accidental releases (Lepicard et al., 2004). For coastal discharges occurring in the large (“regional”) boxes, “coastal” release boxes are nested into the regional box system. The intermediary boxes between coastal and regional boxes are called “inner” boxes.
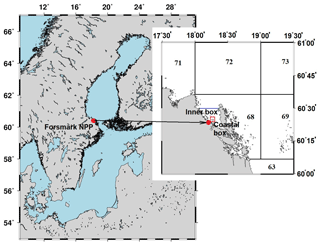
Figure 6Box system around the Forsmark NPP. The numbers denote regional boxes in the box system of the Baltic Sea (Bezhenar et al., 2016). An additional “Inner box” is separated from regional box 68 by the blue line. The coastal box (red rectangle) surrounds the area where cooling water from NPP is discharged.
4.2 Release of radionuclides during normal operation of the Forsmark Nuclear Power Plant
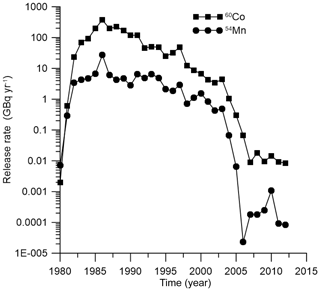
This section presents the simulation results of 60Co and 54Mn routine release into the marine environment from Forsmark NPP, located on the Baltic Sea coast of Sweden. The POSEIDON-R model with embedded food web MCKA model, one-compartment fish model and bioaccumulation factor (equilibrium) model was customized for the Baltic Sea, as described by Bezhenar et al. (2016) and Maderich et al. (2018a). The nested boxes (inner and coastal boxes) inside the regional box no. 68 in the Baltic Sea box system were added to resolve the radionuclide concentration in the near field (Fig. 6). Parameters of the inner and coastal boxes are based on data from Aquilonius (2010). The main parameters of boxes when zooming in to the NPP are presented in Table S10 in the Supplement. The simulation results for 60Co and 54Mn were compared with measurements for the smallest coastal box, where measurement data for bottom sediments and fish were available (Forsmark, 2014). The measurement data were compared with simulations for two species of fish: herring (Clupea harengus membras) as a non-piscivorous fish and pike (Esox lucius) as a coastal predator. There is no information on the mass of fish caught in the vicinity of Forsmark NPP. Therefore, we used estimates of the masses typical for prey and predatory fish, which are given in Table S11. In the one-compartment model, two parameters must be prescribed: assimilation efficiency and biological half-life . Assimilation efficiency (see Table 2) was obtained from Pouil et al. (2018). Baudin et al. (1997) used T0.5=21 d for 60Co in the one-compartment model. The average value for T0.5 in predatory marine fish is 40 d (Beresford et al., 2015). Therefore, for 60Co, we used T0.5=20 d for prey fish and T0.5=40 d for predatory fish. There are very limited data for T0.5 values in marine fish for 54Mn. According to Beresford et al. (2015), T0.5 is in the range between 20 and 40 d. Therefore, we used the same values of T0.5 for 54Mn, as for 60Co. According to Jeffree et al. (2017), the uptake and depuration kinetics of 60Co and 54Mn for fish species in marine, brackish and freshwater environments are very similar. Therefore, we can apply the model parameters defined for marine environment (see Table S11) to reconstruct the herring and pike contamination by the above-mentioned radionuclides in the area near the Forsmark NPP with low salinity (3–5 PSU, denoting practical salinity unit).
The release rates of 60Co from the Forsmark NPP (Forsmark, 2014) are plotted in Fig. 7.
As seen in Fig. 8a, the results of simulation for the concentration of 60Co in the bottom sediments are in good agreement with the measurements (Forsmark, 2014) in the coastal box for the wide range of employed values of sediment distribution coefficient Kd: from L kg−1 for margin seas to L kg−1 for open ocean (IAEA, 2004). The benthic food web (Bezhenar et al., 2016a), which describes the transfer of radioactivity from bottom sediments to deposit-feeding invertebrates and finally to fish, is quite important in this range of Kd values. The results from the POSEIDON-R calculations obtained with the MCKA model are compared (Fig. 8b, c) with measurements and results of calculations obtained with a one-compartment model and with an equilibrium approach using a standard BAF value (IAEA, 2004). Whereas one-compartment and equilibrium models underestimated the concentration of 60Co in fish, the MCKA model using generic parameters yields better agreement with measurements for both non-piscivorous fish (Fig. 8b) and coastal predator feeding by pelagic and benthic organisms in the coastal area (Fig. 8c).
Similarly, the behaviour of 54Mn in the marine environment near the Forsmark NPP is modelled. The release rate of 54Mn from the NPP is also plotted in Fig. 7 using data from Forsmark (2014). Comparison of the simulated concentration of 54Mn in bottom sediments with measurements (Forsmark, 2014) for the Forsmark coastal box is given in Fig. 8d. Good agreement was obtained when a standard value of L kg−1 for 54Mn in margin seas (IAEA, 2004) was used. This means that, as in the case of 60Co, a significant fraction of radionuclide is deposited at the bottom, and the benthic food web should be considered. Similarly to the 60Co case, obtained results of simulation are also compared with results obtained using the one-compartment model and equilibrium approach. Again, the MCKA model yields the best agreement with measurements for both non-piscivorous fish (Fig. 8e) and coastal predators (Fig. 8f); however, this agreement is slightly worse than in the 60Co case. Notice that the BAF in the equilibrium approach can be locally estimated using a posteriori data. However, the MCKA model provided good agreement with measurements using only a priori information, which is important in the case of accidents, as considered in the next section.
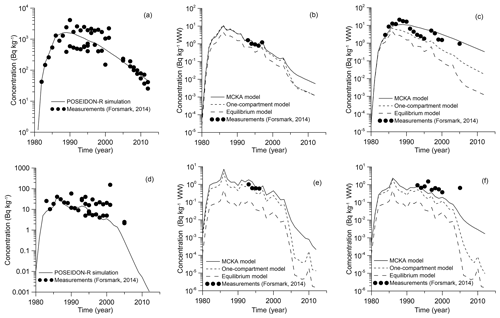
Figure 8Comparison between calculated and measured 60Co (Forsmark, 2014) concentrations in bottom sediment (a), non-piscivorous fish (herring) (b) and coastal predator fish (pike) (c) and 54Mn concentrations in bottom sediment (d), non-piscivorous fish (herring) (e) and coastal predator fish (pike) (f) for the coastal box.
4.3 Accumulation of 90Sr in the fish after the Fukushima Dai-ichi accident
Following caesium, 90Sr is the second most important radiologically long-lived radionuclide released as a result of the FDNPP accident. It is highly soluble in water and exhibits a relatively high ability for assimilation by marine organisms due to similar chemical properties with calcium. The atmospheric deposition of 90Sr is usually not taken into account due to its low volatility. Most of the 90Sr released from the FDNPP was directly released to the ocean, with estimates of total inventory in the range from 0.04 to 1.0 PBq (Buesseler et al., 2017). Here, we extended the simulation by Maderich et al. (2014b) of transfer and fate of 90Sr resulting from the FDNPP accident using the POSEIDON-R model complemented by the food web model (Bezhenar et al., 2016) and MCKA fish model.
The POSEIDON-R model was customized for the north-western Pacific and adjacent seas (the East China Sea, the Yellow Sea, and the East Sea or Sea of Japan) as in (Maderich et al., 2018a). A total of 188 boxes covered this region. The boxes around the FDNPP are shown in Fig. 9 with an additional 4 km×4 km coastal box in the vicinity of FDNPP. The coastal box was included for the model validation with 90Sr measurements conducted in this specific area. Details of customization are given in Maderich et al. (2014a, b; 2018a).
The historical contamination due to global atmospheric deposition in the period from 1945–2010 was simulated according to Maderich et al. (2014b) with data from the Marine Radioactivity Information System database (MARIS, 2020). The value of the accidental release was estimated as 160 TBq (16 TBq d−1 during 10 d) that was consistent with the range reported by Buesseler et al. (2017). In the post-accidental period, the continuous leakage of 90Sr due to groundwater transport of radioactivity from the NPP site was monitored (Castrillejo et al., 2016). Therefore, in the simulation the conservative scenario was used for release of 90Sr in the post-accidental period (Fig. 9); the release of 90Sr was assumed equal to 137Cs release (Maderich et al. (2018a).
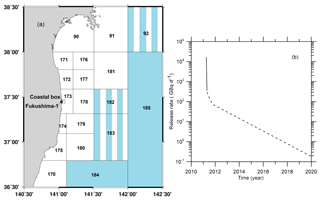
Figure 9(a) Boxes along the eastern coast of Japan with fine resolution in the area around the FDNPP (Maderich et al., 2018a). Deep boxes with three vertical layers in the water column are coloured by blue, boxes with two vertical layers are marked by vertical stripes, and shallow one-layer boxes are white. (b) Release rates of 90Sr in the accidental (bold line) and post-accidental (dashed line) periods.
Comparison between calculated and measured 90Sr concentrations in water, bottom sediment and piscivorous fish for the coastal box and box no. 173 are shown in Fig. 10. Measured concentrations of 90Sr in the water and bottom sediments before the accident were obtained from the MEXT database (MEXT, 2020). Concentrations of 90Sr after the accident at TEPCO (Tokyo Electric Power Company) sampling points near the discharging canals (T-1 and T-2) and at different distances offshore (TD-5 inside the coastal box area and T-7, TD-1 and TD-9 for outer box no. 173) are available in the NRA (Japan Nuclear Regulation Authority) database (NRA, 2020). The results of simulation show that the concentration of 90Sr in the seawater reaches the maximum just after the accidental release (Fig. 10a, d). Notice that the box model gives the average concentrations for each box, which means that local concentrations may be larger or smaller than the average (Fig. 10). Especially large differences can occur during the accidental release under strongly non-equilibrium conditions. Further large dispersion of measured concentrations shows that non-equilibrium conditions remained for a long time in the area close to NPP (Fig. 10a). The agreement between calculated and measured concentrations (Fig. 10a, d) could be a confirmation of the correctness of estimation of the source term. This is also confirmed by agreement of measured and simulated concentrations of 90Sr in the bottom sediment (Fig. 10b, e). Notice that there is no measurement data for bottom sediment in box no. 173 (Fig. 10e).
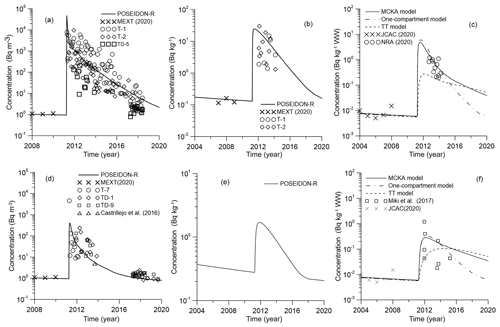
Figure 10Comparison between calculated and measured 90Sr concentrations in water (a), bottom sediment (b) and piscivorous fish (c) for the coastal box and in water (d), bottom sediment (e) and piscivorous fish (f) for box no. 173.
The calculated concentration of 90Sr in piscivorous fish was compared with measurement data for fat greenling (Hexagrammos otakii) before the accident (JCAC, 2020) and with data from NRA (2020) and Miki at al. (2017) after the accident. The NRA data for 90Sr are very limited. Therefore, different species of piscivorous fish were considered, such as sharks (Triakis scyllium, Squatina japonica), rockfish (Sebastes cheni) and sea bass (Lateolabrax japonicus). Parameters of the MCKA model for these fishes are given in Table S11. The simulation results with the MCKA model agree well with the experimental observations (Fig. 10c, f), while the target tissue (TT) approach underestimates the concentration of 90Sr in the fish.
Comparison of the Eqs. (1)–(3) and (7) of the MCKA model and Eq. (11) of the standard whole-body model demonstrates that the main difference is found in the description of the whole-body elimination rate λwb. Whereas in the whole-body model the value of λwb is constant, in the MCKA model it is the ratio of activity-weighted tissue elimination rates to whole-body activity:
Therefore, in the MCKA model, the value of λwb can vary over time, depending on the uptake of radionuclide and the tissue elimination rates. The time variation of λwb computed from Eq. (34) is shown in Fig. 11 for three different cases: (a) pulse-like feeding experiment (Mathews and Fisher, 2008), (b) release of 60Co during normal operation of the Forsmark NPP and (c) accumulation of 90Sr in the fish due to the FDNPP accident. As seen in the plots, λwb varies considerably when there is non-equilibrium, such as in the case of a pulse-like feeding or an accident. Even in case of a routine release, λwb follows any changes in the release rate (Fig. 11b).
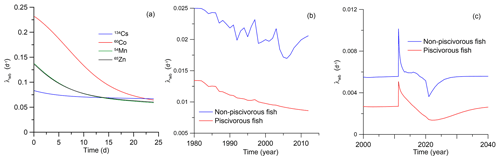
Figure 11The calculated λwb for three scenarios: (a) the pulse-like feeding experiment (Mathews, Fisher (2008), (b) the release of 60Co during normal operation of the Forsmark NPP and (c) the accumulation of 90Sr in the fish due to the FDNPP accident.
In case of the FDNPP accident, the calculated λwb shows some tendency towards an equilibrium value, but after a pulse-like release of 90Sr in 2011, λwb doubled following the release of activity and then slowly converged to the quasi-equilibrium state governed by the global deposition. Notice that in this case we extended the simulation period to 2040 by extrapolating deposition data and FDNPP release data in Fig. 9b. Therefore, the whole-body model with a constant λwb, which is calibrated using observational data, cannot correctly describe such transient processes in the organism. This is confirmed in Fig. 10 by comparing the results from the MCKA model and the one-compartment model. Here the AE value in both models are the same, whereas the equilibrium value λwb was calculated in the MCKA model using the value before 2011 for piscivorous fish (λwb=0.0027 d−1). The one-compartment model simulation results using parameters from the MCKA model are close to the MCKA model results at the initial stage of accidental release. However, over time, the concentration of 90Sr in fish tends to equilibrium faster than the MCKA model predicts, which is explained by the time-dependent behaviour of λwb in the MCKA model. These results suggest also that the MCKA model could be effectively used to find equivalent parameters for the one-compartment model as was done here.
A new approach to predicting the accumulation of radionuclides in fish by taking into account heterogeneity of distribution of contamination in the organism and dependence of metabolic process rates on the fish mass was developed. The fish organism was represented by compartments for three groups of tissues or organs (muscle, bone, organs) and two input compartments representing gills and the digestive tract. The absorbed elements are redistributed between organs or tissues and then eliminated according to their metabolic function. The food and water uptake rates, elimination rate, and growth rate depend on the metabolic rate, which is scaled by the fish mass to the power, but they do not depend on the radionuclide. At the same time, the activity is distributed between the different tissues and organs according to the tissue assimilation efficiencies, which differ per radionuclide (Table 2), but do not depend on fish mass. Therefore, the transfer rates can be associated with a specific radionuclide and fish mass as shown, for example, in Tables S2–S4 and S6–S8. The position of the fish species in the trophic level also affects the concentration of activity in the organism.
This model is of intermediate complexity and provides an alternative for the basic/simplistic whole-body models and the highly advanced PBPK models. The main difference between the MCKA and whole-body models was found in the description of the whole-body elimination rate λwb. Whereas in the whole-body model the value of λwb is constant, in the MCKA model it is the ratio of activity-weighted tissue elimination rates to whole-body activity as described by Eq. (34). The elimination rate λwb varies considerably in non-equilibrium state of fish, such as in the case of a pulse-like feeding or an accident.
The trophic transfer factors (TTF) were calculated for five elements using assimilation efficiencies AEf obtained from laboratory data. Among considered elements, only the caesium (Cs) level may elevate in the predator fish of the food chain (TTF > 1). This is in agreement with measurements. The concentrations of other elements (Sr, Co, Mn, Zn) decrease with the increase of trophic level (TTF <1). The kinetics of the assimilation and elimination of 134Cs, 57Co, 60Co, 54Mn and 65Zn, which are preferably accumulated in different tissues, were analysed using the analytical solutions of a system of model equations. These solutions exhibited good agreement with the laboratory experiments for the depuration process after single feeding of fish with radiolabelled prey and with respect to uptake of activity from water. Notice that for relatively slow processes in the marine environment, transfer processes in the gills and digestive tract can be close to equilibrium, which allows for consideration of only a three-compartment (muscle, bone, organs) version of the model.
The developed MCKA model was embedded into the box model POSEIDON-R, which describes the transfer of radionuclides through the pelagic and benthic food webs. The POSEIDON-R model was applied for the simulation of the transport and fate of 60Co and 54Mn routinely released from Forsmark NPP located on the Baltic Sea coast of Sweden and for calculation of 90Sr concentration in fish after the accident at Fukushima Dai-ichi NPP. Predicted concentrations of radionuclides in fish agreed well with the measurements in both case studies. It is shown that the MCKA model with the defined generic parameters could be used in different marine environments without calibration based on a posteriori information, which is important for emergency decision support systems (Periáñez et al., 2019).
POSEIDON-R code is a part of the decision support system JRODOS for off-site emergency management after nuclear accidents. https://resy5.iket.kit.edu/JRODOS/index.html
Data used in the study are freely available in MARIS, JCAC, MEXT and NRA databases, and in several publications.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-18-2591-2021-supplement.
RB, VM and KOK conducted the literature review and designed the study. RB, VM and KTJ developed the model and performed modelling of laboratory experiments. GdW and KOK collected data for case studies. RB, VM and KOK performed the simulations for case studies. RB, VM, KTJ and GdW analysed results of simulations and wrote the initial article. All authors edited and approved the final article text.
The authors declare that they have no conflict of interest.
Authors are grateful to three anonymous reviewers for useful suggestions that helped to improve the article.
This research has been supported by the Korea Institute of Ocean Science and Technology (grant no. PE99912), the National Research Foundation of Ukraine (Ukraine) (grant nos. 2020.02/0048 and 2020.01/0421) and the International Atomic Energy Agency (grant no. CRP K41017).
This paper was edited by Kenneth Rose and reviewed by three anonymous referees.
Alava, J. and Gobas, F.: Modeling 137Cs bioaccumulation in the salmon-resident killer whale food web of the Northeastern Pacific following the Fukushima Nuclear Accident, Sci. Tot. Environ., 544, 56–67, 2016.
Andersen, N. G.: Depletion rates of gastrointestinal content in common goby (Pomatoschistus microps (Kr.)). Effects of temperature and fish size, Dana, 3, 31–42, 1984.
Aquilonius, K.: The marine ecosystems at Forsmark and Laxemar-Simpevarp. SR-Site Biosphere, Sweden, SKB, 495. pp., 2010.
Barron, M. G., Stehly, G. R., and Hayton, W. L.: Pharmacokinetic modeling in aquatic animals. Models and concepts, Aquat. Toxicol., 17, 187–212, 1990.
Baudin, J. P., Veran, M. P., Adam, C., and Garnier-Laplace, J.: Co-60 transfer from water to the rainbow trout (Oncorhynchus mykiss Walbaum), Archives of Environmental Contamination and Toxicology, 33, 230–237, 1997.
Belharet, M., Charmasson, S., Tsumune, D., Arnaud, M., and Estournel, C.: Numerical modeling of 137Cs content in the pelagic species of the Japanese Pacific coast following the Fukushima Dai-ichi Nuclear Power Plant accident using a size structured food-web model, PLoS ONE, 14, e0212616, https://doi.org/10.1371/journal.pone.0212616, 2019.
Beresford, N. A., Beaugelin-Seiller, K., Burgos, J., Cujic, M., Fesenko, S., Kryshev, A., Pachal, N., Real, A., Su, B. S., Tagami, K., Vives i Batlle, J., Vives-Lynch, S., Wells, C., and Wood, M. D.: Radionuclide biological half-life values for terrestrial and aquatic wildlife, J. Environ. Rad., 150, 270–276, 2015.
Beresford, N.A.,Wood, M.D., Vives i Batlle, J., Yankovich, T.L., Bradshaw, C., and Willey, N.: Making the most of what we have: application of extrapolation approaches in radioecological wildlife transfer models, J. Environ. Rad., 151, 373-386, 2016.
Bezhenar, R., Jung, K. T., Maderich, V., Willemsen, S., de With, G., and Qiao, F.: Transfer of radiocaesium from contaminated bottom sediments to marine organisms through benthic food chains in post-Fukushima and post-Chernobyl periods, Biogeosciences, 13, 3021–3034, https://doi.org/10.5194/bg-13-3021-2016, 2016.
Buesseler, K., Dai, M., Aoyama, M., Benitez-Nelson, C., Charmasson, S., Higley, K., Maderich, V., Masque, P., Morris, P. J., Oughton, D., and Smith, J. N.: Fukushima Daiichi-derived radionuclides in the Ocean: transport, fate, and impacts, Annu. Rev. Mar. Sci., 9, 173–203, https://doi.org/10.1146/annurev-marine-010816-060733, 2017.
Cardwell, R. D., DeForest, D. K., Brix, K. V., and Adams, W. J.: Do Cd, Cu, Ni, Pb and Zn biomagnify in aquatic ecosystems? Reviews of Environmental Contamination and Toxicology, 226, 101–122, 2004.
Carvalho, F. P.: Radionuclide concentration processes in marine organisms: A comprehensive review, J. Environ. Radioactiv., 186, 124–130, 2018.
Castrillejo, M., Casacuberta, N., Breier, C. F., Pike, S. M., Masque, P., and Buesseler, K. O.: Reassessment of 90Sr, 137Cs and 134Cs in the coast off Japan derived from the Fukushima Dai-ichi Nuclear Accident, Environ. Sci. Tech., 50, 173–180, 2016.
Coughtrey, P. J. and Thorne, M. C.: Radionuclide distribution and transport in terrestrial and aquatic ecosystems: A critical review of data, Vol 2, edited by: Balkema A. A., Rotterdam, 500 pp., 1983.
Forsmark: Forsmark omgivningsdata utdrag ur databas 20140113.xlsx, Forsmark, Sweden, 2014.
Fowler, S. W. and Fisher, N. S.: Radionuclides in the biosphere, Ch. 6. in: Marine Radioactivity, Radioactivity in environment, edited by: Livingston, H. D., v.6. Elsevier, 167–203, 2004.
Garnier-Laplace, J., Adam, C., Lathuilliere, T., Baudin, J., and Clabaut, M.: A simple fish physiological model for radioecologists exemplified for 54Mn direct transfer and rainbow trout ( Oncorhynchus mykiss W.), J. Environ. Radioactiv., 49, 35–53, 2006.
Goldstein, R. A. and Elwood, J. W.: A Two-compartment, three-parameter model for the absorption and retention of ingested elements by animals, Ecology, 52, 935–939, 1971.
Grech, A., Tebb, C., Brochot, C., Bois, F. Y., Bado-Nilles, A., Dorne, J. L., Quignot, N., and Beaudouin, R.: Generic physiologically-based toxicokinetic modelling for fish: Integration of environmental factors and species variability, Sci. Tot. Environ., 651, 516–531, 2019.
Hamby, D. M.: A review of techniques for parameter sensitivity analysis of environmental models, Environ. Monit. Assess., 32, 135–154, 1994.
Higley, K. A. and Bytwerk, D. P.: Generic approaches to transfer, J. Environ. Radioactiv., 98, 4–23, 2007.
Heling, R., Koziy, L., and Bulgakov, V.: On the dynamical uptake model developed for the uptake of radionuclides in marine organisms for the POSEIDON-R model system, Radioprotection 37, 833–838, 2002.
Heling, R. and Bezhenar, R.: Modification of the dynamic radionuclide uptake model BURN by salinity driven transfer parameters for the marine food web and its integration in POSEIDON-R., Radioprotection, 44, 741–746, 2009.
IAEA (International Atomic Energy Agency): Sediment distribution coefficients and concentration factors for biota in the marine environment, Technical Report Series No 422, IAEA, Vienna, Austria, 95 pp., 2004.
Ishikawa, Y., Yamada, K., Nonaka, N., Marumo, K., and Ueda, T.: Size-dependent concentrations of radiocesium and stable elements in muscles of flathead flounder Hippoglossoides dubius, Fish Sci (Tokyo), 61, 981–985, 1995.
Jefferies, D. F. and Heweit, C. J.: The accumulation and excretion of radioactive caesium by the plaice and thornback ray, J. Mar. Biol. Ass. UK, 51, 411–422, 1971.
Jeffree, R. A., Warnau, M., Teyssie, J.-L., and Markich, S. J.: Comparison of the bioaccumulation from seawater and depuration of heavy metals and radionuclides in the spotted dogfish Scyliorhinus canicula (Chondrichthys) and the turbot Psetta maxima (Actinopterygii: Teleostei), Sci. Total Environ., 368, 839–852, 2006.
Jeffree, R. A., Markich, S., Oberhansli, F., and Teyssie, J. L.: Radionuclide biokinetics in the Russian sturgeon and phylogenetic consistencies with cartilaginous and bony marine fishes, J. Environ. Radioactiv., 202, 25–31, 2017.
JCAC (Japan Chemical Analysis Center): Environmental Radioactivity Database, available at: https://www.jcac.or.jp/, last access: 26 October 2020.
Kim, S. H., Lee, H., Lee, S. H., and Kim, I.: Distribution and accumulation of artificial radionuclides in marine products around Korean Peninsula, Mar. Pollut. Bull., 146, 521–531, 2019.
Kasamatsu, F. and Ishikawa, Y.: Natural variation of radionuclide 137Cs concentration in marine organisms with special reference to the effect of food habits and trophic level, Mar. Ecol. Prog. Ser., 160, 109–120, 1997.
Lepicard, S., Heling, R., and Maderich, V.: POSEIDON-R/RODOS models for radiological assessment of marine environment after accidental releases: application to coastal areas of the Baltic, Black and North Seas, J. Environ. Radioactiv., 72, 153–161, 2004.
Maderich, V., Bezhenar, R., Heling, R., De With, G., Jung, K. T., Myoung, J. G., Cho, Y.-K., Qiao, F., and Robertson, L.: Regional long-term model of radioactivity dispersion and fate in the Northwestern Pacific and adjacent seas: application to the Fukushima Dai-ichi accident, J. Environ. Radioactiv., 131, 4–18, 2014a.
Maderich, V., Jung, K. T., Bezhenar, R., de With, G., Qiao, F., Casacuberta, N., Masque, P., and Kim, Y. H.: Dispersion and fate of 90Sr in the Northwestern Pacific and adjacent seas: global fallout and the Fukushima Dai-ichi accident, Sci. Total Environ., 494, 261–271, 2014b.
Maderich, V., Bezhenar, R., Tateda, Y., Aoyama, M., and Tsumune, D.: Similarities and differences of 137Cs distributions in the marine environments of the Baltic and Black seas and off the Fukushima Dai-ichi nuclear power plant in model assessments, Mar. Pollut. Bull., 135, 895–906, 2018a.
Maderich, V., Bezhenar, R., Tateda, Y., Aoyama, M., Tsumune, D., Jung, K. T., and de With, G.: The POSEIDON-R compartment model for the prediction of transport and fate of radionuclides in the marine environment, MethodsX, 5, 1251–1266, 2018b.
MARIS (Marine Radioactivity Information System) (2020): Data available at https://maris.iaea.org/home,last access: 26 October 2020.
Mathews, T. and Fisher, N. S.: Trophic transfer of seven trace metals in a four-step marine food chain, Mar. Ecol. Prog. Ser., 367, 23–33, 2008.
Mathews, T., Fisher, N. S., Jeffree, R. A., and Teyssie, J.-L.: Assimilation and retention of metals in teleost and elasmobranch fishes following dietary exposure, Mar. Ecol. Prog. Ser., 360, 1–12, 2008.
Mathews, T. and Fisher, N. S.: Dominance of dietary intake of metals in marine elasmobranch and teleost fish, Sci. Tot. Environ., 407, 5156–5161, 2009.
MEXT: (Japanese Ministry of Education, Culture, Sports, Science and Technology): Environmental radiation database, available at: http://search.kankyo-hoshano.go.jp/servlet/search.top, last access: 26 October 2020.
Miki, S., Fujimoto, K., Shigenobu, Y., Ambe, D., Kaeriyama, H., Takagi, K., Ono, T., Watanabe, T,., Sugisaki, H., and Morita, T.: Concentrations of 90Sr and 137Cs/90Sr activity ratios in marine fishes after the Fukushima Dai-ichi Nuclear Power Plant accident, Fish. Oceanog., 26, 221–233, 2017.
NRA (Monitoring information of environmental radioactivity level, Japan): Monitoring information of environmental radioactivity level, available at: http://radioactivity.nsr.go.jp/en/list/205/list-1.html, last access: 26 October 2020.
Otero-Muras, I., Franco-Uria, A., Alonso, A. A., and Balsa-Canto, E.: Dynamic multi-compartmental modelling of metal bioaccumulation in fish: Identifiability implications, Environ. Modell. Softw., 25, 344–353, 2010.
Pentreath, R. J.: The accumulation from sea water of 65Zn, 54Mn, 58Co,and 59Fe, by the thornback ray, Raja clavata l, J. Exp. Mar. Biol. Ecol., 12, 327–334, 1973.
Periáñez, R., Bezhenar, R., Brovchenko, I., Duffa, C., Iosjpe, M., Jung, K.T., Kim, K.O., Kobayashi, T., Liptak, L., Little, A., Maderich, V., McGinnity, P., Min, B. I., Nies, H., Osvath, I., Suh, K. S., and de With, G.: Marine radionuclide transport modelling: Recent developments, problems and challenges, Environ. Modell. Softw., 122, 104523, https://doi.org/10.1016/j.envsoft.2019.104523, 2019.
Pianosi, F., Beven, K., Freer, J., Hall, J. W., Rougier, J., Stephenson, D. B., and Wagener, T.: Sensitivity analysis of environmental models: A systematic review with practical workflow, Environ. Modell. Softw., 79, 214–232, 2016.
Pouil, S., Warnau, M., Oberhansli, F., Teyssie, J.-L., Bustamante, P., and Metian, M.: Comparing single-feeding and multi-feeding approaches for experimentally assessing trophic transfer of metals in fish, Environ. Toxicol. Chem., 36, 1227–1234, 2017.
Pouil, S., Bustamante, P., Warnau, M., and Metian, M.: Overview of trace element trophic transfer in fish through the concept of assimilation efficiency, Mar. Ecol. Prog. Ser., 588, 243–254, 2018.
Reinfelder, J. R., Fisher, N. S., Luoma, S. N., Nichols, J. W., and Wang, W.-X.: Trace element trophic transfer in aquatic organisms: a critique of the kinetic model approach, Sci. Tot. Environ., 219, 117–135, 1998.
Rouleau, C., Tjalve, H., Gottofrey, J., and Pelletier, E.: Uptake, distribution and elimination of 54Mn(II) in the brown trout (Salmo Trutta), Environ. Toxicol. Chem., 14, 483–490, 1995.
Takata, H., Johansen, M. P., Kusakabe, M., Ikenoue, T., Yokota, M., and Takaku, H.: A 30-year record reveals re-equilibration rates of 137Cs in marine biota after the Fukushima Dai-ichi nuclear power plant accident: Concentration ratios in pre-and post-event conditions, Sci. Tot. Environ., 675, 694–704, 2019.
Tateda, Y., Tsumune, D., and Tsubono, T.: Simulation of radioactive cesium transfer in the southern Fukushima coastal biota using a dynamic food chain transfer model, J. Environ. Radioactiv., 124, 1–12, 2013.
Thomann, R. V., Shkreli, F., and Harrison, S.: A pharmacokinetic model of cadmium in rainbow trout, Environ. Toxicol. Chem., 16, 2268–2274, 1997.
Thomas, D. M. and Fisher, N. S.: Evaluation of body size and temperature on 137Cs uptake in marine animals, J. Environ. Radioactiv., 202, 25–31, 2019.
Vives i Batlle, J., Wilson, R. C., and McDonald, P.: Allometric methodology for the calculation of biokinetic parameters for marine biota, Sci. Tot. Environ., 388, 256–269, 2007.
Vives i Batlle, J., Wilson, R. C., Watts, S. J., Jones, S. R., McDonald, P., and Vives-Lynch, S.: Dynamic model for the assessment of radiological exposure to marine biota, J. Environ. Radioactiv., 99, 1711–1730, 2008.
Vives i Batlle, J.: Radioactivity in the Marine Environment, in: Encyclopedia of Sustainability Science and Technology, edited by: Meyers, R. A., Springer, New York, 8387–8425, 2012.
Vives i Batlle, J., Beresford, N.A., Beaugelin-Seiller, K., Bezhenar, R., Brown, J., Cheng, J.-J., Ćujić, M., Dragović, S., Duffa, C., Fiévet, B., Hosseini, A., Jung, K.T., Kamboj, S., Keum, D.-K., Kobayashi, T., Kryshev, A., LePoire, D., Maderich, V., Min, B.-I., Periáñez, R., Sazykina, T., Suh, K.-S., Yu, C., Wang, C., and Heling, R.: Inter-comparison of dynamic models for radionuclide transfer to marine biota in a Fukushima accident scenario, J. Environ. Radioactiv., 153, 31–50, 2016.
West, G. B., Brown, J. H., and Enquist, B. J.: A general model for the origin of allometric scaling laws in biology, Science 276, 122–126, 1997.
Yankovich T. L.: Towards an improved ability to estimate internal dose to non-human biota: development of conceptual models for reference non-human biota, Proceedings of third international symposium on the protection of the environment from ionising radiation, IAEA, Vienna, Austria, 365–373, 2003.
Yankovich, T., Beresford, N., Wood, M., Aono, T., Anderson, P., Barnett, C. L., Bennett, P., Brown, J. E., Fesenko, S., Fesenko, J., Hosseini, A., Howard, B. J., Johansen, P., Phaneuf, M. M., Tagami, K., Takata, H., Twining, J. R., and Uchida, S.: Whole-body to tissue-specific concentration ratios for use in biota dose assessments for animals, Radiation Environ, Biophysics, 49, 549–565, 2010.