the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A triple tree-ring constraint for tree growth and physiology in a global land surface model
Jonathan Barichivich
Philippe Peylin
Thomas Launois
Valerie Daux
Camille Risi
Jina Jeong
Sebastiaan Luyssaert
Annually resolved tree-ring records extending back to pre-industrial conditions have the potential to constrain the responses of global land surface models at interannual to centennial timescales. Here, we demonstrate a framework to simultaneously constrain the representation of tree growth and physiology in the ORCHIDEE global land surface model using the simulated variability of tree-ring width and carbon (Δ13C) and oxygen (δ18O) stable isotopes in six sites in boreal and temperate Europe. We exploit the resulting tree-ring triplet to derive integrative constraints for leaf physiology and growth from well-known mechanistic relationships among the variables. ORCHIDEE simulates Δ13C (r=0.31–0.80) and δ18O (r=0.36–0.74) better than tree-ring width (r<0.55), with an overall skill similar to that of a tree-ring model (MAIDENiso) and another isotope-enabled global vegetation model (LPX-Bern). The comparison with tree-ring data showed that growth variability is not well represented in ORCHIDEE and that the parameterization of leaf-level physiological responses (stomatal control) to drought stress in the temperate region can be constrained using the interannual variability of tree-ring stable isotopes. The representation of carbon storage and remobilization dynamics emerged as a critical process to improve the realism of simulated growth variability, temporal carryover, and recovery of forest ecosystems after climate extremes. Simulated forest gross primary productivity (GPP) correlates with simulated tree-ring Δ13C and δ18O variability, but the origin of the correlations with tree-ring δ18O is not entirely physiological. The integration of tree-ring data and land surface models as demonstrated here should guide model improvements and contribute towards reducing current uncertainties in forest carbon and water cycling.
- Article
(1983 KB) - Full-text XML
- BibTeX
- EndNote
A major challenge for the land surface model (LSM) component of Earth system models is to accurately simulate the historical and future dynamical coupling between the global biosphere and climate (Friedlingstein et al., 2014). Although LSMs are skillful at reproducing short-term (<20 years) contemporary observations of plant water and carbon cycling, their simulated responses to environmental changes at longer timescales from decades to centuries are still highly uncertain and contribute to the spread in current climate change projections (Ciais et al., 2013; Friedlingstein et al., 2014). Some of these models project that the terrestrial biosphere will continue behaving as a carbon sink of anthropogenic emissions during the course of the century, while others simulate that it will turn into an additional carbon source to the atmosphere that will accelerate climate change (Friedlingstein et al., 2006; Jones et al., 2013; Friedlingstein et al., 2014). The uncertainties in simulated long-term trends are also evident for the water cycle and over the historical period (Frank et al., 2015; Phillips et al., 2019). The lack of a general agreement on the historical and future long-term responses of the terrestrial biosphere in land surface models thus limits confidence in future climate projections (Ciais et al., 2013).
The development, parameterization, and evaluation of current land surface models have been based on a handful of manipulative experiments (Ainsworth and Long, 2005; Smith et al., 2015; Andresen et al., 2016; Song et al., 2019), a quasi-global network of eddy-covariance observations (Baldocchi, 2019), Earth observations (Orth et al., 2017), and forest inventories (Bellassen et al., 2011) covering the last few decades. Most of these data streams are not able to reveal the temporal evolution of plant responses to global change factors at multi-decadal and longer timescales, where mechanistic understanding on how trees perish or adapt to environmental change is still limited (McDowell et al., 2008; Cailleret et al., 2018). Tree-ring width and their carbon (δ13C) and oxygen (δ18O) stable isotope data are increasingly being used to address the lack of direct observations on long-term changes in plant physiology and growth with global change (Huang et al., 2007; Frank et al., 2015; Girardin et al., 2016; Babst et al., 2018; de Boer et al., 2019; Lavergne et al., 2020) and could provide the much needed long-term benchmark for land surface models (Zuidema et al., 2018).
In recent decades, some dendrochronological and forest process-based models have successfully integrated the simulation of tree-ring width with stable isotopes in order to interpret measurements and improve simulated tree water status, photosynthesis, and growth (Fritts et al., 1999; Hemming et al., 2001; Ogée et al., 2009; Eglin et al., 2010; Danis et al., 2012; Wei et al., 2014; Ulrich et al., 2019). Radial growth is represented with decreasing complexity from tree to stand-level models, considering different degrees of integration of controls from sources (photosynthesis and allocation) and sinks (cell growth) of carbon in the trees (Vaganov et al., 2011; Körner, 2015). The tree-ring community has developed a detailed source–sink representation of radial growth for conifers as the product of daily cambial dynamics and wood formation (i.e., cell division, enlargement, and wall thickening), coupled or not to a full representation of tree-level photosynthesis and carbon allocation (Fritts et al., 1999; Hemming et al., 2001; Vaganov et al., 2011; Drew and Downes, 2015). Stand-level forest models parameterize radial growth of conifers and angiosperms as a direct dependency of photosynthesis, using the allocation of photosynthates and tree allometry (Deleuze et al., 2004; Misson, 2004; Sato et al., 2007; Li et al., 2014). A well-known stand-level tree-ring model using this approach is MAIDENiso (Danis et al., 2012; Lavergne et al., 2017), which has the unique triple capability to simulate radial growth and oxygen and carbon isotopic ratios in tree rings.
The representation of tree biomass growth in global land surface models is still rudimentary and is one of the critical areas where much improvement is needed (Fatichi et al., 2014; Körner, 2015; Jones et al., 2020). Like stand-level models, most global models represent growth using a simple carbon-source approach and consider it to be the difference between instantaneous photosynthetic carbon assimilation and respiration. Sink processes of wood formation, emphasized in tree-level models (Vaganov et al., 2011), are neglected (Fatichi et al., 2014). Reserve pools of labile carbon have only recently been considered because of the need to realistically represent continued forest growth when photosynthesis is suppressed by environmental stresses (Naudts et al., 2015; Vuichard et al., 2019; Jones et al., 2020). Currently there is no global land surface model with the capability to explicitly simulate tree-ring width. Nevertheless, tree-ring width data have been used as an indirect benchmark for the interannual variability of simulated net primary productivity in some global land surface models (Rammig et al., 2015; Churakova et al., 2016). In contrast to ring width, tree-ring δ13C or δ18O stable isotopes have already been incorporated in some global land surface models such as FOREST-BGC (Panek and Waring, 1997), ORCHIDEE (Shi et al., 2011; Churakova et al., 2016; Risi et al., 2016), JULES (Bodin et al., 2013), LPX-Bern (Saurer et al., 2014; Keel et al., 2016; Keller et al., 2017), and CLM4.5 (Raczka et al., 2016; Keller et al., 2017).
An enormous benefit of explicitly modeling tree-ring width and stable isotopes in the global land surface models is the ability to directly compare readily available tree-ring data to modeled data. Thus, the global models can be evaluated and improved with freely available worldwide tree-ring data found, for example, in the International Tree-ring Data Bank (ITRDB) and tree-ring laboratories around the world. Furthermore, the interpretation of these tree-ring data can be supported by model simulations. The comparison of simulated δ13C and derived physiological indicators such as the carbon isotopic discrimination (Δ13C) by plants and the intrinsic water use efficiency (iWUE) with direct tree-ring isotopic measurements has helped benchmark stomatal responses to drought stress and rising atmospheric CO2 concentrations in the global models (Panek and Waring, 1997; Bodin et al., 2013; Saurer et al., 2014; Keller et al., 2017). Simulated δ18O has been used to evaluate the representation of hydrological processes along the soil–plant–atmosphere continuum (Risi et al., 2016) and interpret the variability in tree-ring δ18O data in terms of climatic drivers and source water δ18O (Shi et al., 2011; Keel et al., 2016; Churakova et al., 2016). The interannual variability of tree-ring δ13C and δ18O has been shown to correlate with local eddy-covariance measurements of forest productivity (Belmecheri et al., 2014; Tei et al., 2019). A recent study showed that the relationship holds at a regional scale and is stronger for δ18O than δ13C and tree-ring width (Levesque et al., 2019), suggesting that tree-ring isotopic variability might integrate large-scale physiological signals useful to evaluate global carbon cycle models. Yet, stable isotope–productivity relationships have not been studied in this type of model.
Empirical tree-ring studies frequently combine δ18O and δ13C as a means to mechanistically interpret plant physiological responses (Saurer et al., 1997; Scheidegger et al., 2000; Barnard et al., 2012; Roden and Farquhar, 2012; Szejner et al., 2020). In contrast, most of the studies with land surface models have focused on the simulation and evaluation of a single tree-ring variable (Saurer et al., 2014; Keel et al., 2016; Keller et al., 2017). Key developments in the ORCHIDEE global land surface model now allow the explicit simulation of radial growth (Bellassen et al., 2010; Naudts et al., 2015; Jeong et al., 2020) and carbon and oxygen composition in tree-ring cellulose (Risi et al., 2016) as done in the MAIDENiso tree-ring model (Danis et al., 2012). This offers the opportunity to explore how multiple tree-ring variables can be used to constrain the long-term plant responses simulated by global land surface models and identify processes that need to be better represented or parameterized.
The aims of this study are to (i) integrate key developments and identify the critical processes to concurrently simulate the interannual variability of tree-ring width and its carbon (Δ13C) and oxygen stable isotopes in the ORCHIDEE global land surface model, (ii) develop a conceptual triple tree-ring constraint for simulated growth and physiology that exploits the mechanistic relationships among tree-ring variables, and (iii) evaluate the simulated relationships between productivity and tree-ring carbon and oxygen stable isotopes. We first assess and compare the ability of ORCHIDEE and MAIDENiso models to simulate 20th century tree-ring width and isotopic variability and their inter-relationships in the Fontainebleau forest in France. Then, we run ORCHIDEE in five other sites along a climate gradient from boreal Finland to temperate France, and we compare its ability to simulate δ18O variability in the gradient with that of the LPX-Bern global vegetation model (Keel et al., 2016). The simulated relationships between isotopic variability and productivity in ORCHIDEE are also evaluated along the gradient.
2.1 Model description
The global land surface model ORCHIDEE (Krinner et al., 2005) is the terrestrial component of the IPSL (Institut Pierre Simon Laplace) Earth system model (Dufresne et al., 2013; Boucher et al., 2020). ORCHIDEE simulates the half-hourly exchange of energy, carbon, and water between the terrestrial biosphere and the atmosphere, either coupled with the LMDz (Laboratoire de Météorologie Dynamique Zoom) general circulation model (Hourdin et al., 2006) or forced by observed meteorology.
The global forests are represented by eight plant functional types (PFTs) described by a common set of governing equations with specific parameter values, with the only exception being some PFT-specific phenology representations (Krinner et al., 2005). Canopy photosynthesis is based on the leaf-level photosynthesis formulation of Farquhar et al. (1980), and together with respiration, the energy balance and hydrological processes are simulated at a half-hourly time step, which is the typical resolution of eddy-covariance measurements of carbon and water fluxes (Baldocchi et al., 2001). Leaf gas exchange is simulated by coupling the photosynthesis model with the stomatal conductance model of Ball et al. (1987). The CO2 demand is determined as the minimum of Rubisco carboxylation and RuBP regeneration, while CO2 supply depends on the difference in CO2 concentration between the air outside the leaf and the carboxylation sites. Carbon allocation to the different vegetation pools, phenology, and mortality are calculated at a daily time step.
Soil hydrology is modeled using a surface and a deep reservoir (Choisnel et al., 1995). Water enters the surface layer via throughfall, snowmelt, and dew and frost. Water can leave the soil reservoir through transpiration, bare soil evaporation, surface runoff, and drainage. Plant water stress is calculated at half-hourly time steps as a function of soil water content (McMurtrie et al., 1990) weighted by root mass. Water stress reduces transpiration through a direct reduction of stomatal conductance as soil moisture depletes.
The key developments used for simulating tree-ring parameters include the addition of a forest management module (Bellassen et al., 2010) and the simulation of oxygen stable isotope ratios along the soil–plant–atmosphere continuum (Risi et al., 2016). The model code used in this study (SVN r898 version) precedes the current code that merged the nitrogen cycle and canopy structure in ORCHIDEE r5698 (Naudts et al., 2015; Vuichard et al., 2019), where the tree-ring functionality will also be reported (Jeong et al., 2020).
2.1.1 Tree-ring width
The forest management module explicitly simulates the temporal trajectory of stem growth of trees in a size-structured forest stand. The size structure of the stand is prescribed by defining a starting density of trees per hectare distributed across a number of stem diameter size classes, typically following an inverted-J distribution. Initial tree height and biomass are obtained by allometric relationships with stem diameter (Bellassen et al., 2010). For each PFT, photosynthesis and net primary production (NPP) are computed at the stand level at half-hourly and daily steps, respectively.
At the end of the year, accumulated woody NPP increment is allocated across the different diameter classes following an empirical competition rule for evenly aged stands (Deleuze et al., 2004). A greater NPP share is allocated to larger dominant trees compared to smaller less vigorous trees, emulating the competition for light and resources within the stand. The absolute annual stem growth increment in the allocation rule is determined by a parameter (λ) that defines the slope between the fraction of NPP allocated to each diameter class and the mean diameter of the class. A second parameter (σ) represents a diameter threshold below which less vigorous trees receive only a fixed part of the yearly stand NPP increment. The stem growth of the largest and smallest trees is tracked individually through the entire simulation (Bellassen et al., 2010).
Simulated tree-ring width (i.e., radial growth) for each diameter class was computed from annual increments in stem circumference as follows:
where TRWt is the annual tree-ring width in millimeters for the year t, and Circt and Circt−1 are the stem circumferences for the current year and the previous year, respectively. The annual ring widths simulated in this scheme account for the size-related trend in stem growth increment and PFT-specific tree allometry, providing a mean representation of radial growth for trees across a range of sizes that can be meaningfully compared with measured tree-ring width data. However, in this formulation tree-ring width variability depends only on direct GPP allocation (i.e., it is a carbon-source-driven process) and does not consider the dynamics of carbon storage or wood formation processes that can account for a large fraction of observed interannual tree-ring width variation (Misson, 2004).
2.1.2 Tree-ring carbon isotopes
To eliminate the effect of δ13C of atmospheric CO2 and preserve only the effects of plant metabolic processes, the 13C enrichment of plant organic material is usually expressed in terms of the carbon isotope discrimination (Δ13C). Differences between the 13C enrichment of atmospheric CO2 and plant material are attributed to discriminatory processes during photosynthesis.
Photosynthetic carbon isotope discrimination was estimated at half-hourly time steps using the simple formulation of Farquhar et al. (1982) for C3 plants:
where a (4.4 ‰) is the kinetic discrimination associated with diffusion between free air and the stomatal cavity, b (27 ‰) is the fractionation during CO2 fixation by the Rubisco enzyme (Farquhar et al., 1982; Cernusak et al., 2013), ci is the leaf internal CO2 concentration simulated by ORCHIDEE, and ca is the atmospheric CO2 concentration prescribed from measurements. Annual tree-ring carbon discrimination (Δ13CR) was then calculated as the mean of the half-hourly discrimination values in the above-ground biomass weighted by gross primary productivity (GPP) between the start (SOS) and the end (EOS) of the growing season:
This formulation for carbon discrimination is commonly used as a simple approximation for discrimination derived from measured δ13C in tree-ring cellulose (Francey and Farquhar, 1982). For simplicity, it assumes that further post-photosynthetic fractionation during photo- and dark-respiration and carbohydrate remobilization and storage is negligible. Although these processes normally have an important impact on whole-ring cellulose isotopic composition (Gessler et al., 2009; Werner et al., 2012), at least the impact of carbon remobilization is minimal in the latewood component of tree rings (Helle and Schleser, 2004). The ci term in Eq. (2) integrates the gas exchange dynamics (i.e., stomatal conductance and photosynthesis) simulated by the model as a complex function of micrometeorological variability, seasonal water stress, and the long-term warming and increase in ca. Hence, despite its simplicity, simulated carbon discrimination using Eq. (2) has been shown to be valuable to constrain the integrated environmental response of land surface models using carbon discrimination derived from tree-ring δ13C measurements (e.g., Bodin et al., 2013; Churakova et al., 2016; Keel et al., 2016).
2.1.3 Tree-ring oxygen isotopes
The δ18O signature in tree-ring cellulose primarily reflects the isotopic composition of soil water and the evaporative enrichment of leaf water due to transpiration, but other mixing and biochemical fractionation processes during water transport along the soil–plant–atmosphere continuum also contribute to the final δ18O signature (Gessler et al., 2014). The δ18O isotopic composition of the source water used by plants may originate from rainfall or groundwater, while the δ18O isotopic enrichment of leaf water depends strongly on vapor pressure deficit (i.e., the ratio of the vapor pressure in the atmosphere and the intercellular spaces of the leaves) or relative humidity (Farquhar et al., 1998; Scheidegger et al., 2000).
The δ18O fractionation and mixing processes in all water pools and fluxes along the soil–plant–atmosphere continuum (Risi et al., 2016) are represented following a similar formulation as in other isotope-enabled global land surface models (Aleinov and Schmidt, 2006; Haese et al., 2013). The isotopic composition of precipitation and near-surface water vapor have to be prescribed monthly when running the model stand-alone or are simulated by the LMDz general circulation model in coupled simulations. Precipitation reaching the soil surface or intercepting the canopy fractionates during evaporation according to the Craig and Gordon equation (Craig and Gordon, 1965), which generically describes the preferential evaporation of the lighter isotope of a free water body at steady state.
The resulting isotopic composition of soil water and mixing are parameterized as a vertical profile to overcome the limitation of depth resolution in the two-layer representation of soil in the model. No isotopic fractionation is assumed to occur during absorption of soil water by roots, and thus the isotopic signature of xylem water is the same as that of soil water. The isotopic composition of leaf water at the evaporation sites (δ18Oe) is diagnosed by inverting the Craig and Gordon (1965) equation:
where δ18Osw is the isotopic composition of soil water taken up by the roots integrating older soil water and recent precipitation, δ18Ov is the isotopic composition of atmospheric water vapor, α is the equilibrium fractionation due to the phase change from liquid water to vapor, αk is the kinetic fractionation due to diffusion of vapor into unsaturated air, and h is the relative humidity normalized to surface temperature.
Isotopic enrichment of leaf water in the mesophyll (δ18Olw) results from mixing between isotopically enriched leaf water at the evaporative site and depleted xylem water (δ18Oxw) through the so-called Péclet effect:
where is a coefficient that decreases as the Péclet effect increases, with as the Péclet parameter. E is the transpiration rate per leaf area, L is the effective diffusion length, and W is the leaf water content per leaf volume. In order to keep the model as simple as possible, L was set to 8 mm and W was assumed to be 103 kg m−3 for all PFTs following Risi et al. (2016). Admittedly, constant L is a major assumption and source of uncertainty for global models (Keel et al., 2016; Risi et al., 2016) since it is highly variable between species and also depends on climate conditions and leaf anatomy, morphology, and age (Barnard et al., 2007; Roden et al., 2015). The value used for L was obtained from an optimization of simulated diurnal isotopic cycles against observations at mid-latitude sites (Risi et al., 2016).
Half-hourly tree-ring cellulose isotopic composition (δ18Ocell) is calculated from the isotopic composition of leaf water (δ18Olw) and xylem water (δ18Oxw) following the formulation of Anderson et al. (2002):
where f0 is the fraction of exchange with xylem water prior to cellulose synthesis, which reduces the imprint of leaf water on cellulose. For δ18O this exchange is estimated to be 0.42 based on the best-fit relationship under controlled experiments (Roden et al., 2000). The parameter ϵ is the biochemical fractionation factor during cellulose formation associated with water carbonyl interactions and is estimated to be 27 ‰ (DeNiro and Epstein, 1979; Stenberg and DeNiro, 1983).
An estimate of growing season tree-ring isotopic composition (δ18OR) is obtained by weighting δ18Ocell by GPP as done for Δ13CR in Eq. (3):
A model evaluation across a network of 10 sites in Europe and North America shows that this representation is able to reproduce the main features of the seasonal and vertical variations in soil water isotope content, as well as the seasonal isotopic signals in stem and leaf water (Risi et al., 2016). The isotopic variability simulated by ORCHIDEE has been used to interpret local climatic signals in tree-ring δ18O records (Shi et al., 2011; Churakova et al., 2016) and to investigate regional and global isotopic signatures of continental recycling (Risi et al., 2013).
2.2 Tree-ring data
Six previously published tree-ring datasets in northern and western Europe with simultaneous measurements of ring width and δ13C and δ18O compositions were used to evaluate the skill of the model along a climate gradient (Table 1). The three northernmost sites are located in the temperature-limited boreal region in Finland and have chronologies of ring width and δ13C and δ18O composition for Scotch pine (Kessi and Sivakkovaara; Hilasvuori et al., 2009) and pedunculate oak (Bromarv; Hilasvuori and Berninger, 2010). The remaining three sites are located in France and represent moisture-sensitive temperate forests of sessile oak (Fontainebleau; Etien et al., 2009) and pedunculate oak (Rennes and Annecy; Raffalli-Delerce et al., 2004; Danis et al., 2006). In all sites, except Annecy, the available ring width and δ13C and δ18O chronologies cover the common period 1960–2000.
The tree-ring width measurement series available for each site were standardized by dividing each series by its mean ring width (Cook et al., 1990). The resulting series of tree-ring width indices were averaged together to produce a mean site chronology composed by 7 to 28 trees (Table 1). This simple standardization method allows the computation of average tree-ring chronologies without the average being dominated by the faster growing trees with wider rings. Depending on the site, four to nine trees were selected to develop carbon (δ13CR) and oxygen (δ18OR) stable isotope chronologies by pooling rings from the selected trees (Table 1) and using standard methods for cellulose extraction and measurement of the isotopic ratios (McCarroll and Loader, 2004; Daux et al., 2018). For oaks, earlywood and latewood sections were separated, but only latewood was processed. For pine, the carbon and oxygen isotopic compositions were measured for the whole ring.
Tree-ring carbon discrimination was computed by subtracting the stable carbon isotope composition of the atmosphere (δ13Ca) from the measurements using the expression of Farquhar et al. (1982):
Data for δ13Ca were obtained from McCarroll and Loader (2004) for the period 1901–2000.
2.3 Simulations
The model was run at each tree-ring site over the period 1901–2000 using as meteorological forcing the nearest 0.5∘ grid of the 6-hourly CRU-NCEP dataset (Viovy, 2014). This gridded forcing dataset is a statistical merging of the monthly CRU TS station-based dataset of the Climate Research Unit (New et al., 2000) with the atmospheric reanalysis from the National Centers for Environmental Prediction (NCEP). The corresponding soil type and vegetation PFT were prescribed for the sites (Table 1). Monthly δ18O composition of precipitation (δ18Op) and water vapor (δ18Ov) was obtained from the nearest grid of a global simulation of the isotope-enabled LMDz general circulation model nudged by an atmospheric reanalysis over the period 1890–2007 (Risi et al., 2010).
Biomass and soil carbon pools were initialized to steady-state equilibrium by a 5000-year spinup obtained by cycling over the meteorology for the period 1901–1910. The model was then run over the period 1901–2000 using observed CO2 and an initial tree density of 1000 trees per hectare to approach current forest age and density following tree mortality over time due to self-thinning.
In order to benchmark the triple tree-ring ability of ORCHIDEE, a simulation of the MAIDENiso tree-ring model for the Fontainebleau forest was obtained from an earlier study (Danis et al., 2012). The model simulates tree-ring δ13C and δ18O stable isotopes using the formulation of Lloyd and Farquhar (1994) and the Craig–Gordon model (Craig and Gordon, 1965), respectively. Ring width is parameterized as the annual stem growth increment based on daily carbon allocation to leaves, stem, roots, and storage as a function of climate, soil water balance, and atmospheric CO2. Growth is decoupled from instantaneous photosynthesis by a labile carbon pool, which allows the model to reproduce the temporal autocorrelation in tree rings (Misson, 2004). The simulation was produced using a site-specific calibration and includes tree-ring width, δ13C, and δ18O over the period 1953–2000 as described in Danis et al. (2012). The daily δ18Op and δ18Ov forcings were obtained by using a linear regression based on daily mean air temperature and precipitation from two nearby stations as predictors, with coefficients obtained from the nearest isotopic observations in Saclay.
In addition, tree-ring δ18O simulated with the LPX-Bern Dynamic Global Vegetation Model (Keel et al., 2016) was extracted for each site from a published global simulation available for the period 1960–2012 at (dataset available at https://www.climate.unibe.ch, last access: 18 June 2021). This simulation was obtained by forcing LPX-Bern with monthly soil water δ18O (δ18Osw), δ18Ov, and relative humidity data from a simulation with the coupled atmosphere–land surface model ECHAM5-JSBACH driven by observed sea surface temperature (Haese et al., 2013; Keel et al., 2016). LPX-Bern uses the Péclet modified Craig–Gordon model to calculate daily δ18O in leaf water together with the formulation of Roden–Lin–Ehleringer (Roden et al., 2000) to determine δ18O in tree-ring cellulose.
2.4 Model–data comparison
The ability of ORCHIDEE to simulate the interannual variability of the three tree-ring parameters over the course of the 20th century was first evaluated in the Fontainebleau forest (Table 1). Fontainebleau is a well-studied tree-ring site in France (Michelot et al., 2011, 2012; Daux et al., 2018) and it has been used to evaluate the MAIDENiso tree-ring model (Danis et al., 2012). We compared our simulation of ring width, Δ13C, and δ18O for this site with the simulation of MAIDENiso over the period 1953–2000. Then, the evaluation was conducted for the rest of the sites over the common period 1960–2000, except in Annecy where a shorter span of the observations limited the model–data comparison to the period 1971–2000.
A simulated tree-ring width chronology was derived for each site by dividing the simulated tree-ring width series of the largest model tree by its mean. Since growth allocation in the model increases almost linearly with stem size, the absolute annual ring width varies among stem size classes, but its interannual variability remains similar across all size classes; thus the choice of size class does not affect the standardized variability. The standardization removes the effect of stem size class and conserves the interannual and longer variability but does not remove the juvenile effect in tree-ring width. However, the juvenile trend in simulated and observed ring width does not affect the evaluation period (1960–2000) because at this time trees were already mature canopy individuals with their radial growth fluctuating around the mean.
Simulated δ18O and Δ13C tree-ring chronologies were obtained by averaging the simulated half-hourly isotopic variability between May and August. Using just the summer season (June–August) improves results for Δ13C but substantially degrades results for δ18O; thus May was included as a compromise in order to use a common season for the isotopes and ensure comparability across sites. Late May and early June correspond to the seasonal peak in transpiration and photosynthesis of oak in Fontainebleau, which is closely followed by the transition between earlywood and latewood (Michelot et al., 2011). A mean δ18O series was created from the nearest LPX-Bern grid () and corresponding PFT to each evaluation site for a comparison with the observations and ORCHIDEE over the common period 1960–2000.
Since the focus of our evaluation is on the interannual variability and not on the absolute values, correlation and the normalized standard deviation (i.e., the standard deviation of simulated tree-ring parameters divided by the standard deviation of the observations) were used to quantitatively evaluate the skill of the models to simulate the variability in tree-ring width and stable isotopes. Differences in the temporal persistence (i.e., carryover effect) in the observed and simulated tree-ring parameters were evaluated using the first-order autocorrelation of the time series.
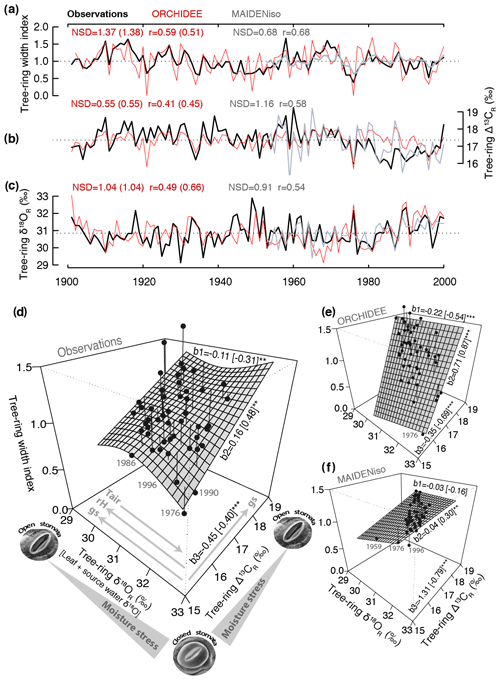
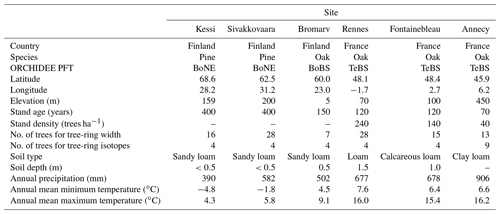
Figure 1Comparison of simulated and observed tree-ring width and isotopic variability in Fontainebleau and the triple tree-ring constraint to assess the integrated model responses. (a–c) Comparison of tree-ring width and latewood Δ13CR and δ18OR variability simulated by ORCHIDEE (red) and MAIDENiso (gray) with observations (black). The normalized standard deviation (NSD) and Pearson correlation (r) are indicated in each case. The mean of the simulations was set to that of the observations for each parameter. (d–f) Bivariate response surface of tree-ring width as a function of δ18OR and Δ13CR variability based on observations and on ORCHIDEE and MAIDENiso simulations over the common period 1953–2000. The individual years are indicated by the black dots, and their vertical distance to the surface is represented by the lines. The most extreme years with low growth and high moisture stress are labeled in each panel. The regression slopes between the tree-ring variables are indicated along the edges of each surface: tree-ring width vs. δ18OR (b1), tree-ring width vs. Δ13CR (b2), and Δ13CR vs. δ18OR (b3) as predictand vs. predictor order. In each case, the linear correlation is indicated in brackets. The asterisks denote the significance levels of the slopes and correlations: * p<0.1, p<0.05, and p<0.001. In panel (d), the relationship between stomatal aperture and moisture stress is indicated along the isotopic axes together with the expected changes in stomatal conductance (gs) and relative humidity (RH) according to the dual isotope model (Scheidegger et al., 2000). The expected enrichment of source water δ18O with increasing air temperature (Tair) is also indicated.
The integrated growth–isotope responses simulated by ORCHIDEE and MAIDENiso models in Fontainebleau were qualitatively compared with observations using a bivariate response surface between tree-ring width variability and the joint variability of the two isotopes. A smoothed response surface was fitted using a data-adaptive bivariate generalized additive model (GAM) implemented with the “mgcv” package (Wood, 2017) in the R environment (R Core Team, 2020). This visualization device extends the dual isotope conceptual model of Scheidegger et al. (2000) to illustrate the mechanistic information content of the triple tree-ring constraint for models introduced in this study. It neatly reveals the complex association of tree growth with gas exchange inferred from stable isotopes in both observations and models.
To disentangle the relative importance of source water (δ18Osw) and leaf water enrichment above source water () between May and August in determining the variability of δ18OR simulated by ORCHIDEE and LPX-Bern, we used the Lindeman–Merenda–Gold (LMG) method (Grömping, 2006). This linear decomposition method quantifies the contribution of different correlated regressors (here δ18Osw and Δ18Olw) to the total r2 of a multiple linear regression model.
3.1 A triple tree-ring constraint for ORCHIDEE and MAIDENiso in Fontainebleau
3.1.1 Interannual and decadal tree-ring variability
ORCHIDEE shows a significant skill in simulating the interannual and multidecadal variability of oak tree-ring width (r=0.59, p<0.01) and latewood Δ13CR (r=0.41, p<0.01) and δ18OR (r=0.49, p<0.01) over the 20th century in Fontainebleau (Fig. 1a–c). The magnitude of the interannual variability of δ18OR is well simulated (NSD = 1.04) but that of tree-ring width is overestimated by 37 % (NSD = 1.37), while that of Δ13CR is underestimated by about a similar magnitude (NSD = 0.55). Δ13CR is systematically overestimated since 1980, when the observations show a decrease by about 1 ‰ (Fig. 1b). Overall, the model simulates 35 % of the observed tree-ring width variability and 17 %–24 % of latewood isotopic variability over the 20th century.
The first-order autocorrelation or carryover in observed tree-ring width is significant (rlag1=0.54, p<0.001) and its magnitude indicates that ring width in the previous year explains up to 30 % of current year tree-ring width variability. In contrast, simulated tree-ring width has no first-order autocorrelation (rlag1=0.02, p>0.1) because of the direct coupling of growth with carbon source from photosynthesis in the model. As a result, in years with extreme summer drought conditions like in 1921 and 1976 the model does not simulate any stem growth because photosynthesis is strongly suppressed (Fig. 1a). The simulated growth recovery after these extremes occurs too fast compared with the observations. The first-order autocorrelation in the isotopic observations is significant only for Δ13CR (rlag1=0.37, p<0.001), while in the simulations it is marginally significant for both Δ13CR (rlag1=0.18, p<0.1) and δ18OR (rlag1=0.27, p<0.01).
The skill of ORCHIDEE compares well with that of the MAIDENiso tree-ring model (Fig. 1a–c), specifically calibrated for the site over the period 1953–2000. Over this period, MAIDENiso is able to simulate between 30 % and 46 % of the total variability of the observations of tree-ring width and isotopes, which compares to the 20 % to 44 % of the total observed variance simulated by ORCHIDEE over the same period with standard parameterization. MAIDENiso is considerably better than ORCHIDEE at simulating tree-ring width (r=0.68 vs. r=0.51) and Δ13CR (r=0.58 vs. r=0.45) variability, but despite simulating the amplitude of Δ13CR and δ18OR well (NSD = 0.91–1.16), it substantially underestimates the amplitude of tree-ring width (NSD = 0.68). Unlike ORCHIDEE, it is able to simulate a significant first-order autocorrelation in tree-ring width (rlag1=0.45, p<0.01) with a magnitude similar to that of the observations (rlag1=0.50, p<0.01). This carryover effect accounts for up to 25 % of current-year tree-ring width variability in the observations (1953–2000) and is thus an important component of the growth variability captured by the carbon remobilization dynamics of the model.
MAIDENiso is able to simulate the observed decrease in Δ13CR since 1980 better than ORCHIDEE (Fig. 1b). The amount and amplitude of δ18OR variability is slightly better simulated by ORCHIDEE (r=0.66, p<0.001; NSD = 1.04) than by MAIDENiso (r=0.54, p<0.001; NSD = 0.91; Fig. 1c). The partitioning of the r2 of a multiple linear regression shows that source water (δ18Osw) and leaf water enrichment above source water (Δ18Olw) account for 56 % and 37 % of the total variability of δ18OR simulated by ORCHIDEE over the period 1953–2000, respectively. We could not quantify the contributions of δ18Osw and Δ18Olw in MAIDENiso because these simulated data were not available. The forcing series of δ18Op used to drive MAIDENiso and ORCHIDEE are different and are not significantly correlated over the May–August period (, p>0.1). Nevertheless, δ18OR simulated by the two models is significantly correlated (r=0.56, p<0.001), suggesting a similarity of simulated Δ18Olw variability.
3.1.2 The growth–isotope tree-ring triplet
So far the evaluation statistics used above only describe the unidimensional skill of the models and do not evaluate their ability to simulate the joint relationships that exist among tree-ring width, Δ13CR, and δ18OR. The strength of the correlations between the actual tree-ring width and isotopic chronologies in Fontainebleau indicates that oak radial growth has 10 % and 24 % of common variance with latewood δ18OR and Δ13CR, respectively (Fig. 1d). In turn, the isotopes have 16 % of common variability. The interpretation of these three-way relationships (correlations) can be aided by visualizing the bivariate surface response of tree-ring width as a function of the dual latewood isotope variability (Fig. 1d). The resulting surface provides, at a glance, insights into causal and non-causal (indirect) relationships between environmental variability (temperature and drought stress) and stomatal responses and growth (see axes in Fig. 1d). The main geometry of the surface can be described by three regression slopes: b1: tree-ring width in relation to δ18OR, b2: tree-ring width in relation to Δ13CR, and b3: Δ13CR in relation to δ18OR (Fig. 1d). These slopes can be used to compare the surface of the observations with those simulated by models.
The bivariate surface response in Fontainebleau shows that in the observations, ring width has a consistent positive and significant linear relationship with latewood Δ13CR (b2=0.16, r=0.48, p<0.01), whereas its relationship with δ18OR is highly non-linear and with an overall negative slope (, , p<0.05; Fig. 1d). The scatter of the observation points across the surface depicts a negative and significant linear relationship between carbon and oxygen isotopic ratios (, , p<0.01; Fig. 1d). The two models qualitatively simulate different growth–isotope surface responses, and none are able to capture the observed non-linear relationship between tree-ring width and δ18OR (Fig. 1e–f). The surface simulated by ORCHIDEE is more consistent with the observations (Fig. 1e). It captures the sign and significance of the relationships between tree-ring width and δ18OR (, p<0.001) and Δ13CR (r=0.87, p<0.001), and also between the isotopic ratios (, p<0.001). However, the corresponding slopes b1 (−0.22) and b2 (0.71) are respectively 2 and 4 times higher than in the observations (Fig. 1e). The slope b3 (−0.35) is slightly smaller than observed (−0.45), but still the correlation between δ18OR and Δ13CR is overestimated. Therefore, ORCHIDEE captures important features of the observed tree-ring triplet, but it substantially overestimates the coupling between growth and isotopic variability (29 %–50 % of common variance) and between isotopes (48 % of common variance).
The growth–isotope surface response of MAIDENiso is rather flat and considerably different from the surfaces derived from the observations and ORCHIDEE (Fig. 1f). It reveals a decoupling between growth and isotopic variability with slopes b1 (−0.03) and b2 (0.04) close to zero. Yet, the model simulates a strong coupling between isotopic ratios ( and 62 % of common variance, p<0.001), which is 3 times higher than in the observations and ORCHIDEE. The large slope b3 in MAIDENiso results from the overestimation of the simulated Δ13CR variability (NSD = 1.16) combined with underestimated δ18OR variability (NSD = 0.91). This demonstrates that the good performance of the model in simulating individual tree-ring variables (Fig. 1a–c) does not necessarily translate into a realistically simulated tree-ring triplet (Fig. 1f).
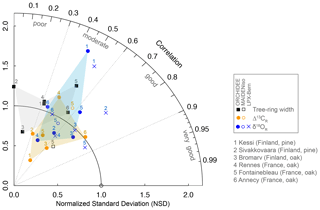
Figure 2Taylor diagram showing the correlation (angular coordinate) and normalized standard deviation (NSD; radial coordinate) of the simulated tree-ring parameters (ORCHIDEE, MAIDENiso, and LPX-Bern) with respect to the observations for the six sites used in this study (see Table 1). Tree-ring width is denoted by square symbols and Δ13CR and δ18OR by orange and blue circles, respectively. The models are denoted by solid symbols (ORCHIDEE), open symbols (MAIDENiso in Fontainebleau or site 5), and blue crosses (LPX-Bern). The statistics were computed over the common period 1960–2000, except in Annecy (site 6) where data availability limited the comparison to the period 1971–2000. The target point (NSD and correlation equal to 1) is represented by a circle. The gray, blue, and orange shading denotes the range of the performance statistics covered by ORCHIDEE for tree-ring width, Δ13CR, and δ18OR, respectively. Four qualitative areas of performance in terms of the magnitude of correlations or simulated variance are indicated as a visual aid.
3.2 Model performance across sites
The performance of ORCHIDEE for tree-ring width, Δ13CR and δ18OR varies substantially across sites (Fig. 2), with no clear pattern along the climate gradient from Finland to France or between species for any parameter. However, it is clear that the isotopic variability is better simulated than tree-ring width and also that δ18OR is the tree-ring variable better simulated. Tree-ring width is well simulated (25 %–30 % of the observed variability) at only two out of six sites. In the remaining sites, the simulations account for less than 10 % (r<0.32) of the observed variability, falling mostly in the region of poor performance in Fig. 2.
Figure 3Drivers of simulated δ18OR variability and consistency between isotopic forcings and simulations of ORCHIDEE and LPX-Bern across the climate gradient from boreal Finland (left) to temperate France (right). (a) Simulated contributions of source water (δ18Osw; turquoise) and leaf water enrichment (Δ18Olw; green) signals to δ18OR variability during 1960–2000. The percentage of explained variance (r2) is indicated in each bar. (b) Correlation between the isotopic composition of precipitation (δ18Op; light gray) and air vapor (δ18Ov; dark gray) used to force the models and the resulting δ18Osw (turquoise), Δ18Olw (green), and δ18OR (dark blue) simulated by ORCHIDEE and LPX-Bern during 1960–2000. All variables were averaged over the period May–August. Significance at the 95 % confidence level is indicated by the black dots.
Although ORCHIDEE is able to simulate about 10 %–64 % (r=0.31–0.80) of the observed Δ13CR variability, it tends to underestimate its amplitude by 30 %–60 %, particularly in the northernmost sites of pine (Kessi and Sivakkovaara) where the isotopic ratios were measured over the whole ring (Fig. 2). With the exception of the northernmost site, the amplitude of δ18OR variability is simulated within ± 20 % and the simulations account for 13 %–55 % (r=0.36–0.74) of the variance of the observations, with all the sites falling in the region of moderate to good performance in Fig. 2.
The δ18OR simulations of the LPX-Bern global model are systematically better than the simulations of ORCHIDEE in terms of correlations and amplitude of the interannual variability (Fig. 2). In Fontainebleau LPX-Bern simulates 74 % (r=0.86) of the observed δ18OR variability. In this site, ORCHIDEE and MAIDENiso are able to simulate only 40 % (r=0.63) and 34 % (r=0.58) of the observed variability, respectively. Three sites (Kessi, Sivakkovaara, and Fontainebleau) exceed the range of performance of ORCHIDEE (blue shading in Fig. 2), mostly due to the good skill of the LPX-Bern simulation in terms of correlation with the observations.
In order to understand the origin of the differences between ORCHIDEE and LPX-Bern, it is necessary to compare their isotopic drivers and the relative contributions of the isotopic composition of source water (δ18Osw) and leaf water enrichment () to simulated δ18OR variability in each model. In contrast to LPX-Bern, ORCHIDEE simulates a much stronger contribution of δ18Osw (46 %–85 %) than Δ18Olw (14 %–53 %) to δ18OR variability (Fig. 3a). The δ18OR variability simulated by LPX-Bern is dominated by the Δ18Olw (42 %–78 %) isotopic signal (Fig. 3b). ORCHIDEE does not simulate any clear latitudinal pattern for the relative importance of δ18Osw and Δ18Olw. In contrast, LPX-Bern simulates an increasing importance of Δ18Olw toward the north, except at the coolest northernmost site where δ18OR is dominated by the signature of δ18Osw in the two models.
The isotopic signatures of precipitation (δ18Op) and vapor (δ18Ov) from the LMDz atmospheric model used to drive ORCHIDEE are poorly correlated with those produced by the ECHAM5 atmospheric model that underlay δ18Osw used to force LPX-Bern (Fig. 3c). In spite of this lack of agreement, the soil-integrated δ18Osw variability simulated by ORCHIDEE and JSBACH (coupled with ECHAM5) land surface models is significantly correlated. The strength of the correlations increases for the resulting Δ18Olw and δ18OR variability simulated by ORCHIDEE and LPX-Bern (Fig. 3c). This pattern of correlations indicates that, in models, seasonal differences in the isotopic composition of precipitation are strongly buffered by water mixing in the soil profile, resulting in coherent isotopic variations in source water and thereby contributing to the correlation of the δ18OR signals simulated by the models. The significant resemblance of simulated Δ18Olw between the models points to similarities in the response of leaf evaporative enrichment and meteorological forcings (i.e., vapor pressure deficit, VPD). Taken together, the analysis of the isotopic forcings and contributions of source water and leaf enrichment suggests that the better performance of LPX-Bern derives from the higher contribution of leaf enrichment to simulated δ18OR variability.
ORCHIDEE overestimates the correlation between δ18OR and Δ13CR in the temperate sites in France, but it simulates the magnitude of the isotopic coupling observed in the boreal oak and pine sites in Finland very well (Fig. 4a). This means that the simulated stomatal control and responses to atmospheric humidity are overestimated in the temperate deciduous PFT, as is apparent in a stronger correlation between simulated isotopic ratios and VPD in these sites compared with the observations (Fig. 4b–c).
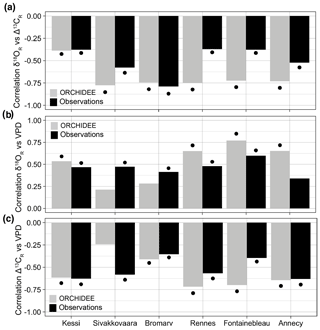
Figure 4Observed and simulated isotopic coupling and response to VPD across the climate gradient during 1960–2000. (a) Correlation between δ18OR and Δ13CR in simulations (gray) and observations (black). (b–c) Correlations between growing season VPD and simulated (gray) and observed (black) δ18OR and Δ13CR variability, respectively. For Annecy the period of analysis is 1971–2000. Significance at the 95 % confidence level is indicated by the black dots.
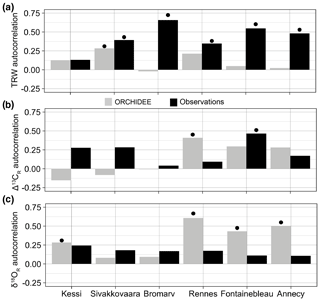
Figure 5First-order autocorrelation in observed (black) and simulated (gray) tree-ring variables over the period 1960–2000. (a) Tree-ring width. (b) Δ13CR. (c) δ18OR. For Annecy the period of analysis is 1971–2000. Significance at the 95 % confidence level is indicated by the black dots.
Measured latewood or whole-ring isotopic ratios have no significant first-order autocorrelation in the sites (Fig. 5b–c), with the exception of Δ13CR in Fontainebleau. However, ORCHIDEE simulates substantial autocorrelation in δ18OR variability in the three temperate sites in France and also in the northernmost boreal site in Finland (Fig. 5c), likely as a result of autocorrelation in the isotopic composition of source water. In contrast, simulated Δ13CR has significant autocorrelation only in Rennes, although it is nearly significant as well in Fontainebleau (Fig. 5b).
3.3 Simulated relationship between productivity and isotopic variability
Growing season (May–August) GPP is significantly correlated with the simulated isotopic variability across all sites (Fig. 6a). The relationship is more consistent with δ18OR ( to −0.73) than with Δ13CR ( to 0.85) along the climate gradient. The strength of the correlations between δ18OR and GPP ( to −0.73) appears to increase from the boreal to the temperate region. This empirical relationship is driven by a synergistic effect of source water and leaf water enrichment because both variables correlate negatively with GPP (Fig. 6b). Leaf water enrichment tends to correlate with GPP more strongly than source water, though in the northernmost pine site only source water is correlated with GPP. Simulated tree-ring width is highly correlated with simulated GPP because of its direct dependency on it (Fig. 6a).
4.1 Uncertainties and critical processes for modeling tree-ring width and isotopic ratios in a global model
Our evaluation in Fontainebleau and the other five sites across a boreal-to-temperate climate gradient in Europe showed that ORCHIDEE better simulates the interannual variability of tree-ring stable isotopes than ring width (30 %–64 % and <30 % of the observed variability, respectively), with a general performance for the stable isotopes similar to MAIDENiso and slightly lower than LPX-Bern (Figs. 1 and 2). The lower skill for tree-ring width results primarily from the inability of ORCHIDEE to simulate the significant temporal autocorrelation observed in ring width variability (Fig. 6a). Temporal carryover is characteristic of tree-ring width (Fritts, 1976; Cook, 1985) and varies considerably with species and location, accounting for 20 %–25 % of current-year ring width variability (Breitenmoser et al., 2014). Several developmental and physiological processes involved in tree growth can produce carryover, including primarily remobilization of non-structural carbohydrates from previous years (Kagawa et al., 2006; Keel et al., 2006; Carbone et al., 2013), cambial dynamics (Vaganov et al., 2011), leaf lifespan (LaMarche and Stockton, 1974; Monserud and Marshall, 2001), and environmental cycles or slowly varying crown and root dynamics that affect tree water and carbon balance across several years (Fritts, 1976; Rocha et al., 2006). The carryover of ring width observations can be removed through statistical prewhitening (Cook, 1985). A data–model comparison using prewhitened observations results in slightly higher correlations with simulated ring width variability in the three French sites (e.g., increase in r from 0.50 to 0.56 in Fontainebleau) but not in the Finnish sites (not shown), where autocorrelation was lower (Fig. 6a).
The ORCHIDEE version used in this study (r898) lacks a labile carbon pool and like most other global land surface models (Fatichi et al., 2014; Jones et al., 2020) is unable to simulate growth carryover. As a result, simulated growth depends directly on instantaneous photosynthesis, and thereby it reflects only current-year GPP variability (see Fig. 6a). This simplified representation of growth is currently the major limitation of the model to simulate tree-ring width variability (Figs. 1a and 2). Nevertheless, in Fontainebleau ORCHIDEE still simulates 26 % of the observed interannual variability but overestimates its amplitude and the speed of recovery from drought extremes like 1976 (Fig. 1a). Legacy effects of reduced growth following drought events can persist for 1 to 4 years in drought-sensitive ecosystems (Anderegg et al., 2015; Cailleret et al., 2018). Such prolonged legacy effects are typically not simulated by global carbon cycle models that lack the representation of the significant dependency of interannual tree growth on carbon remobilization from storage in their carbon allocation schemes (Anderegg et al., 2015). Recent developments to improve the realism of growth variability in land surface models have added a module of labile carbon storage and its utilization to decouple growth from instantaneous photosynthesis (Naudts et al., 2015; Vuichard et al., 2019; Jeong et al., 2020; Jones et al., 2020). This allows reproduction of growth carryover and realistically sustains growth from storage during periods of environmental stress that might suppress photosynthesis, such as severe or prolonged drought (Jones et al., 2020). The newest version of ORCHIDEE (r5698) includes a pool of labile carbon that should contribute to a more realistic simulation of tree-ring width variability and ecosystem recovery from climate extremes (Vuichard et al., 2019; Jeong et al., 2020).
MAIDENiso explicitly represents the autocorrelation in tree-ring width through its carbon storage pool and utilization scheme (Misson, 2004; Danis et al., 2012). However, the calibrated model overestimated the magnitude of the observed autocorrelation, which led to muted interannual variability in simulated tree-ring width (NSD = 0.68). Because of the simulated carryover, it was able to capture the enduring effect of the extreme drought of 1976 in Fontainebleau (Fig. 1a). In this extreme year, photosynthesis was strongly reduced, and carbon expenditure to growth and respiration in the model was sustained by stored carbon at the cost of partially depleting the pool. The carbon pool then took several years to recover, mimicking the observed slow recovery of growth after the drought (Fig. 1a).
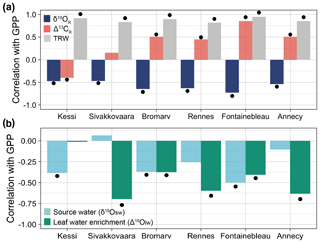
Figure 6Correlations between the simulated tree-ring variables at each site and simulated May–August gross primary productivity (GPP) over the evaluation period 1960–2000. (a) Correlations of δ18OR (dark blue), Δ13CR (light red), and tree-ring width (gray) with GPP. (b) Correlations of soil and leaf water δ18O components of δ18OR with GPP. For Annecy the period of analysis is 1971–2000. Significance at the 95 % confidence level is indicated by the black dots.
ORCHIDEE was able to simulate 30 %–64 % of the observed Δ13CR variability along the climate gradient, but the amplitude of the interannual variations was underestimated by 30 %–60 % (Fig. 2), and it failed to capture the decrease in Δ13CR since 1980 in Fontainebleau (Fig. 1b). An earlier study with ORCHIDEE found a similar underestimation of the interannual variability of Δ13CR for larch in northeastern Yakutia, where the model simulated 26 % (r=0.51) of the observed variability (Churakova et al., 2016). The low amplitude of the simulated variability can be related to missing post-photosynthetic fractionation and mixing processes in the simple representation used for Δ13CR (Eq. 2). However, the same formulation has been shown to reproduce the observations in earlier studies in Europe with the LPX-Bern and CLM4.5 global land surface models (Keller et al., 2017). The representation of water stress and processes that affect ci could also explain the lower performance of ORCHIDEE. A simple parameter sensitivity test in Fontainebleau (not shown) indicated that the amplitude of Δ13CR in ORCHIDEE is very sensitive to soil depth and maximum photosynthetic capacity (Vcmax). This suggests that Δ13CR simulated by Eq. (2) and the associated drought and stomatal responses can be better parameterized by using tree-ring data as an observational constraint to optimize model parameters. Nevertheless, besides an improved parameterization, using a more complete formulation for carbon discrimination (Lloyd and Farquhar, 1994) combined with a scheme of carbohydrate mixing of isotopic signatures from old stored carbon and new photosynthetic carbon (Hemming et al., 2001; Danis et al., 2012) should contribute to improve the simulation of Δ13CR and stomatal responses in the latest version of ORCHIDEE (Jeong et al., 2020).
Modeling the fractionation processes of δ18O along the soil–plant–atmosphere continuum is complicated by interactions between environmental factors and physiological responses (Gessler et al., 2009; Werner et al., 2012; Gessler et al., 2014). As a result, δ18OR is arguably one of the tree-ring variables most difficult to interpret (Roden and Siegwolf, 2012; Barbour and Song, 2014) and to simulate in a global model. Our results show that despite this complexity and uncertainties, global models like ORCHIDEE and LPX-Bern can simulate the amplitude of δ18OR within ± 20 % and account for up to 74 % of the observed interannual variability (Fig. 2). Disentangling the effect of isotopic signatures from source water and leaf evaporative enrichment revealed that the better performance of LPX-Bern in simulating δ18O variability was due to its higher sensitivity to leaf evaporative enrichment compared with ORCHIDEE (Fig. 3a), which is predominantly sensitive to source water δ18O (Fig. 3b). This implies that the observations support a dominant control of leaf evaporative enrichment on δ18OR in our study sites. A similar result was found with MAIDENiso for species in Canada and Patagonia (Lavergne et al., 2017). We could not verify if this is also the case in the MAIDENiso simulation used for Fontainebleau (Danis et al., 2012) because simulated δ18Osw and δ18Olw were not available. A previous tree-ring study using ORCHIDEE with the same parameterization in the Tibetan Plateau found that δ18Olw accounted for 66 % of the variability of simulated δ18OR (Shi et al., 2011), which although dominant still shows the considerable sensitivity of the model to δ18Osw (i.e., 34 % of the variance).
Given the support for a larger relative importance of δ18O evaporative enrichment of leaf water with transpiration in LPX-Bern and MAIDENiso, uncertainties in the parameterization of leaf physiology and mixing of source (xylem) and leaf water will have a large impact on the overall skill of the models when compared with the observations. LPX-Bern and ORCHIDEE have a similar representation of the Péclet effect (Eq. 5) and isotopic mixing during cellulose production (Eq. 6; Keel et al., 2016), which is reflected in the significant correlation of simulated Δ18Olw (Fig. 3c). The main difference in the parameterization of the Péclet effect is for the path length L. LPX-Bern used a value of 3 mm for all PFTs (Keel et al., 2016), while we used a fixed value of 8 mm for all PFTs obtained from tuning against seasonal observations in a few midlatitude sites (Risi et al., 2016). Equation (5) shows that the almost 3 times higher L in ORCHIDEE should result in a larger Péclet effect, which increases (decreases) the contribution of xylem water (evaporative enrichment) to the δ18O signature of leaf water. In addition, we assumed the common value 0.42 for the parameter f0 (fraction of exchange with xylem water prior to cellulose synthesis) in Eq. (6), while a value of 0.4 was used in LPX-Bern (Keel et al., 2016). These parameter differences enhanced the imprint of the isotopic signature of xylem water in δ18OR simulated by ORCHIDEE. Future studies should evaluate model sensitivity to these parameters and constrain them with tree-ring observations.
The seasonal and interannual variability in the δ18O composition of precipitation and air vapor at tree-ring sites is a source of uncertainty for modeling tree-ring δ18O (Evans, 2007; Danis et al., 2012; Lavergne et al., 2017; Keel et al., 2016). However, the dampening effect of soil water mixing considerably reduces the impact of the seasonal variability in δ18O of precipitation on the more integrated δ18Osw signal (Danis et al., 2012). Our results showed that even when precipitation δ18O from two atmospheric models does not correlate, the resulting δ18Osw variability might be consistent and significantly correlated (Fig. 3c). The current parameterization of the Péclet effect (L) and exchange with xylem water (f0) in ORCHIDEE make it more sensitive to uncertainties in precipitation δ18O forcing data. A dedicated model intercomparison study for tree-ring δ18O using the same meteorological and isotopic forcing will help to evaluate uncertainties and attribute differences to forcing data, parameters, and model structure.
4.2 Constraining model processes with the growth–isotope tree-ring triplet
The enhanced information content obtained by combining multiple and complementary tree-ring variables has long been recognized in multi-proxy dendroclimatology (McCarroll et al., 2003; Schollaen et al., 2013; Loader et al., 2015) and dendroecology (Guerrieri et al., 2009; Savard, 2010; Shestakova and Martínez-Sancho, 2021), but its potential remained largely untapped in ecological modeling. The novel simulation of the growth–isotope tree-ring triplet in a global land surface model (Fig. 1e) enables application of known mechanistic relationships between isotopes (Scheidegger et al., 2000) and between growth and carbon isotopes in the same ring (Francey and Farquhar, 1982; Cernusak and English, 2015; Shestakova et al., 2017) to benchmark the physiological responses of the model. This brings a new perspective to data–model comparisons beyond the traditional use of the interannual variability or trends (Panek and Waring, 1997; Danis et al., 2012; Bodin et al., 2013; Churakova et al., 2016; Keel et al., 2016; Keller et al., 2017; Ulrich et al., 2019).
The relationship between Δ13CR (or δ13CR) and δ18OR is the basis of the well-known dual isotope conceptual model (Saurer et al., 1997; Scheidegger et al., 2000), which is widely used as a physiological constraint of leaf-level plant responses to environmental variability (Barnard et al., 2012). δ18OR variation is interpreted as a proxy for stomatal conductance (gs), assuming that it reflects only changes in leaf water enrichment caused by variation in air relative humidity, whereas changes in Δ13CR are interpreted as an integrated measure of photosynthesis (A) relative to stomatal conductance, that is the intrinsic water use efficiency (iWUE). A negative relationship between δ18OR and Δ13CR, as seen across the diagonal of the tree-ring triplet in Fontainebleau (slope b3 in Fig. 1d), would indicate that plants have a strong stomatal control of gas exchange, and stomatal conductance (rather than photosynthetic rate) drives variations in Δ13CR and iWUE.
Depending on regional climate, the slope between tree-ring width and δ18OR (b1 in Fig. 1d) can capture the seasonally integrated response of trees to air temperature and environmental moisture (Rebetez et al., 2003; Liu et al., 2017). However, the shape and nature of the relationship alone might be difficult to interpret without separating the effects of oxygen isotopic fractionation in leaves and source water variability on δ18OR (Barnard et al., 2012; Roden and Siegwolf, 2012; Sargeant et al., 2019). But when ring width variations are simultaneously negatively related to δ18OR and positively to Δ13CR variations, as observed in Fontainebleau (Fig. 1d), it can be established with confidence that tree growth is modulated by leaf physiology through the stomatal limitation of CO2 supply to photosynthesis as a response to air and soil humidity constraints (see axes in Fig. 1d).
The slope between tree-ring width and Δ13CR (b2 in Fig. 1d) provides a robust indication of the main climatic and carbon assimilation drivers (i.e., supply of CO2 by stomatal conductance or demand of CO2 by photosynthesis) associated with wood biomass growth variability (Voelker et al., 2014; Shestakova et al., 2017, 2019). In Mediterranean and temperate climates with moisture-limited tree growth, the slope or correlation between ring width and Δ13CR is positive (Shestakova et al., 2019), as seen in Fontainebleau (Fig. 1d). This means that tree growth and leaf physiology are both similarly driven by soil moisture constraints through a limitation of CO2 supply to photosynthesis due to reduced stomatal conductance to avoid dehydration. In the boreal region north of the Arctic circle, where tree growth and function are controlled by low temperatures and radiation, the slope and correlation between ring width and Δ13CR turn negative (Shestakova et al., 2019). Under these conditions, the main control of Δ13CR is assimilation rate, and therefore lower Δ13CR is associated with increased photosynthesis and growth. The growth–Δ13CR coupling will be stronger when tree growth variability is driven by concurrent climate and photosynthetic rates. In contrast, it will be weaker when growth relies more on stored carbohydrates and other processes that contribute to growth carryover and isotopic mixing.
The growth–isotope relationships can change over time with increased drought and warming (Shestakova et al., 2017, 2019) and are clearer during climate extremes. For instance, in a temperate location such as Fontainebleau it is expected that dry summer conditions would associate with narrow tree rings, decreased Δ13CR, and increased oxygen isotope enrichment in leaf water (thus higher δ18OR) because trees would close their stomata to reduce stomatal conductance and avoid dehydration at the expense of photosynthesis. Precipitation and soil water δ18O would also be enriched because of higher temperatures, further increasing δ18OR. Consistent with this expectation, our bivariate response surface shows that years with extremely narrow rings like 1976, 1990, and 1996 are associated with low Δ13CR and high δ18OR in latewood (Fig. 1d). The opposite occurs during moist years with wider rings, when conditions for stomatal aperture are optimal. Depending on the climatic region, the paleo-temperature signals carried by δ18OR could be used to disentangle changes in the climatic forcing of past growth anomalies and physiological responses inferred from the growth–isotope triplet under pre-industrial and current climate conditions.
The growth–isotope triplet of the observations can be directly compared with the simulated triplet to mechanistically constrain the realism of model responses. The geometry of the tree-ring triplet simulated by ORCHIDEE r898 (Fig. 1e) demonstrates that the model is able to simulate more realistic physiological responses to environmental variability than MAIDENiso in Fontainebleau (Fig. 1f). However, the simulated growth–Δ13CR and Δ13CR–δ18OR relationships in ORCHIDEE are much stronger than in the observations. Removing the δ18Osw effect from simulated δ18OR to highlight the effect of leaf water enrichment in Fontainebleau further increased the strength of the coupling between δ18OR and Δ13CR (not shown). The correlation between stable isotopes and their correlations with VPD are also substantially overestimated in the other temperate sites (Rennes and Annecy; Fig. 4a–b). These model–data mismatches indicate that the model overestimates drought stress and the limitation of photosynthetic carbon assimilation by stomatal control in the temperate region, where stomatal regulation strongly drives variability in plant water use efficiency (Frank et al., 2015; Shestakova et al., 2019).
The implication of such a strong stomatal constraint for land–atmosphere interactions in ORCHIDEE r898 is an overestimation of energy partitioning towards sensible heat and an underestimation of transpiration and carbon uptake per unit of leaf area in the temperate region. In the boreal region (Kessi, Sivakkovaara, and Bromarv), where stomatal control is not the main driver of Δ13CR (Shestakova et al., 2019), ORCHIDEE simulated a level of correlation between stable isotopes (Fig. 4b) and sensitivity to VPD (Fig. 4c) in good agreement with the observations, indicating a better gas exchange parameterization for the boreal broadleaf summergreen and needleleaf evergreen PFTs (Table 1). The parameterization of the temperate broadleaf summergreen PFT of the model could be improved by assimilating tree-ring data together with other ecosystem observations (e.g., eddy covariance, forest inventories, earth observations) using a data assimilation technique (Peylin et al., 2016; Thum et al., 2017).
The poor realism of the growth–isotope triplet simulated by MAIDENiso (Fig. 1f) is related to the low amplitude of simulated ring width variability (NSD = 0.68) due to excessive carryover from carbon remobilization, which decouples growth from current photosynthesis and leads to small growth–isotope slopes (b1 and b2). Although MAIDENiso was calibrated against the tree-ring observations in Fontainebleau (Danis et al., 2006), it still simulates a stomatal control even stronger than in ORCHIDEE, as indicated by a higher correlation between δ18OR and Δ13CR (r=0.79, p<0.001). These issues demonstrate that the statistical calibration of growth and physiological processes separately does not necessarily lead to an improved realism of simulated tree responses to environmental variability. An integrative constraint such as the tree-ring triplet presented here provides a way forward to improve the representation and parameterization of the biology of tree growth and function in models. If only one tree-ring variable is simulated, it is easier to tune a model to fit the data. But if the growth–isotope triplet is to be fit, the constraint is stronger and mechanistically informed.
4.3 Simulated relationship between isotopic variability and productivity
Our results showed that the simulated interannual variability in δ18OR was significantly and negatively correlated with GPP across all sites in the climate gradient ( to −0.73, p<0.01) because both source water (δ18Osw) and leaf water enrichment (Δ18Olw) related negatively with GPP (Fig. 6). Although Δ18Olw dominates the correlation in most sites, it is the synergistic effect of δ18Osw variations that contributes to the apparent spatial consistency of the δ18OR–GPP correlation. The negative sign of the correlations of GPP with both components of δ18OR points to temperature as their underlying cause. On the one hand, higher temperatures during the growing season result in enriched δ18O in precipitation and further enrich δ18Osw through evaporation. On the other hand, higher temperatures also lead to increased VPD, which increases leaf water enrichment and reduces GPP because of stomatal closure (Fig. 1d).
An earlier study attributed the correlation between δ18OR variability and satellite-based estimates of net primary productivity (NPP) at large spatial scales to the common but opposite effect of VPD on leaf water enrichment and NPP, without considering the possible effect of source water (Levesque et al., 2019). Our findings suggest that δ18OR–productivity correlations should be interpreted with caution because they are not entirely driven by leaf physiology, and source water is often an important driver of δ18OR (Fig. 3a–b).
The simulated interannual variability in Δ13CR also correlated with GPP in most sites, but the relationship was less spatially consistent since its significance and sign varied across the boreal-to-temperate climate gradient (Fig. 6a). A positive correlation between simulated Δ13CR and GPP in all temperate and boreal oak sites (r=0.45 to 0.85, p<0.01) is coherent with a stomatal limitation of carbon assimilation (Shestakova et al., 2019). In the two boreal pine sites, correlations were weaker and only the northernmost site had a significant negative correlation (, p<0.01). In such a cool and moist environment, internal leaf CO2 concentration and water use efficiency are controlled by photosynthetic rate, which is limited by temperature and sunshine (McCarroll and Loader, 2004; Hilasvuori et al., 2009).
This contrast in Δ13CR–GPP correlations between the temperate and boreal region mirrors a shift from a positive to a negative relationship between Δ13CR and tree-ring width due to a change from water-limited to temperature-limited leaf physiology (Shestakova et al., 2019). These model-based isotope–GPP relationships are consistent with recent findings showing that tree-ring δ18O correlates with satellite-based NPP over large spatial scales, whereas Δ13C has a more spatially variable correlation with GPP (Belmecheri et al., 2014; Levesque et al., 2019; Tei et al., 2019) and ring width (Shestakova et al., 2017, 2019).
We demonstrated the potential of a tree-ring triplet based on tree-ring width and Δ13C and δ18O stable isotopes to constrain the representation of tree growth and physiology in the global land surface model ORCHIDEE (r898), bridging the long-standing gap between the tree-ring and land surface modeling communities. The comparisons with tree-ring data and the MAIDENiso and LPX-Bern models showed that the parameterization of leaf-level physiological responses (stomatal control) of ORCHIDEE can be mechanistically constrained using the simulated tree-ring isotopic variability, but the representation of tree growth requires improvement. The lack of carbon remobilization from storage in the model is currently a major limitation for a realistic simulation of the interannual coupling between tree physiology and growth and the enduring legacy effects of climate extremes on ecosystem dynamics. This calls for an updated representation of the biology of tree growth beyond the simple carbon-source approach, considering the effects of carbon storage and controls from wood tissue formation.
The use of the growth–isotope tree-ring triplet showed that good performance of a model in simulating individual tree-ring variables does not necessarily translate into realistically simulated tree responses to environmental variability. Because the tree-ring triplet integrates the response of the soil–plant–atmosphere system to environmental variability, it is a powerful mechanistic constraint for tree growth and physiology in the context of modeling forest–atmosphere interactions. Consistent with recent observational studies, interannual variations in simulated forest productivity (GPP) correlated significantly with simulated variations in tree-ring Δ13C and δ18O stable isotopes. However, correlations between tree-ring δ18O and productivity are not entirely driven by leaf physiology and should be interpreted with caution because of the significant and often large contribution of source water δ18O to the relationship. These results establish the foundations for improving the simulation of tree rings in ORCHIDEE (Jeong et al., 2020) and a forthcoming optimization of model parameters using tree-ring data together with other short-term ecosystem observations (e.g., remote sensing, eddy-covariance, forest inventories) in a formal data assimilation technique (Peylin et al., 2016). Such advances should contribute to reduce current uncertainties in historical and future changes in forest carbon and water cycling.
The latest ORCHIDEE model code is archived at https://doi.org/10.14768/20200228001.1 (Luyssaert, 2019). All the tree-ring data and ORCHIDEE tree-ring simulations used in this study are available at https://doi.org/10.5281/zenodo.4992981 (Barichivich, 2021).
JB, PP, TL, and VD designed the research. TL conducted the simulations with the support of CR. JJ and SL contributed to model development and research design. JB revised the model, analyzed the data, and wrote the manuscript. All the authors contributed to data interpretation and commented on the manuscript.
The authors declare that they have no conflict of interest.
This research is part of a post-doctoral grant to Jonathan Barichivich from the presidential program “Make Our Planet Great Again” (MOPGA) conducted through the Centre National de la Recherche Scientifique (CNRS) of France. We thank Joel Guiot for sharing the simulations of MAIDENiso for Fontainebleau, Fortunat Joos, and Martin Werner for kindly sharing the isotopic forcing used for their LPX-Bern simulations and Manuel Gloor and Roel Brienen for discussions on isotopic theory. We also thank John Marshall and the two other anonymous reviewers for their constructive comments that improved the paper.
This research has been supported by the VERIFY grant from the European Commission, Horizon 2020 framework program (grant no. 776810).
This paper was edited by Christopher Still and reviewed by John Marshall and two anonymous referees.
Ainsworth, E. A. and Long, S. P.: What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2, New Phytol., 165, 351–372, 2005. a
Aleinov, I. and Schmidt, G.: Water isotopes in the GISS ModelE land surface scheme, Glob. Planet. Change, 51, 108–120, 2006. a
Anderegg, W. R. L., Schwalm, C., Biondi, F., Camarero, J. J., Koch, G., Litvak, M., Ogle, K., Shaw, J. D., Shevliakova, E., Williams, A. P., Wolf, A., Ziaco, E., and Pacala, S.: Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models, Science, 349, 528–532, 2015. a, b
Anderson, W., Bernasconi, S., McKenzie, J., Saurer, M., and Schweingruber, F.: Model evaluation for reconstructing the oxygen isotopic composition in precipitation from tree ring cellulose over the last century, Chem. Geol., 182, 121–137, 2002. a
Andresen, L. C., Müller, C., De Dato, G., Dukes, J. S., Emmett, B. A., Estiarte, M., Jentsch, A., Kröel-Dulay, G., Lüscher, A., Niu, S., Peñuelas, J., Reich, P.B., Reinschk, S., Ogaya, R., Schmidt, I.K., Schneider, M.K., Sternberg, M., Tietema, A., Zhu, K., and Bilton, M. C.: Shifting impacts of climate change: Longterm 60 patterns of plant response to elevated CO2, drought, and warming across ecosystems, in: Advances in Ecological Research, Elsevier, London, Vol. 55, 437–473, 2016. a
Babst, F., Bodesheim, P., Charney, N., Friend, A. D., Girardin, M. P., Klesse, S., Moore, D. J., Seftigen, K., Björklund, J., Bouriaud, O., Dawson, A., DeRose, R. J., Dietze, M. C., Eckes, A. M., Enquist, B., Frank, D. C., Mahecha, M. D., Poulter, B., Record, S., Trouet, V., Turton, R. H., Zhang, Z., and Evans, M. E. K.: When tree rings go global: challenges and opportunities for retro-and prospective insight, Quaternary Sci. Rev., 197, 1–20, 2018. a
Baldocchi, D., Falge, E., Gu, L., Olson, R., Hollinger, D., Running, S., Anthoni, P., Bernhofer, C., Davis, K., Evans, R., Fuentes, J., Goldstein, A., Katul, G., Law, B., Lee, X. H., Malhi, Y., Meyers, T., Munger, W., Oechel, W., Paw, K. T., Pilegaard, K., Schmid, H. P., Valentini, R., Verma, S., Vesala, T., Wilson, K., and Wofsy, S.: FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities, Bull. Am. Meteorol. Soc., 82, 2415–2434, 2001. a
Baldocchi, D. D.: How eddy covariance flux measurements have contributed to our understanding of Global Change Biology, Glob. Change Biol., 26, 242–260, 2019. a
Ball, J. T., Woodrow, I. E., and Berry, J. A.: A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions, in: Progress in Photosynthesis Research, Springer, Dordrecht, 221–224, 1987. a
Barbour, M. M. and Song, X.: Do tree-ring stable isotope compositions faithfully record tree carbon/water dynamics?, Tree Physiol., 34, 792–795, 2014. a
Barichivich, J.: Triple tree-ring constraint for models (data and code), Zenodo [Dataset], https://doi.org/10.5281/zenodo.4992981, last access: 19 June 2021.
Barnard, R. L., Salmon, Y., Kodama, N., Sörgel, K., Holst, J., Rennenberg, H., Gessler, A., and Buchmann, N.: Evaporative enrichment and time lags between δ18O of leaf water and organic pools in a pine stand, Plant Cell Environ., 30, 539–550, 2007. a
Barnard, H., Brooks, J., and Bond, B.: Applying the dual-isotope conceptual model to interpret physiological trends under uncontrolled conditions, Tree Physiol., 32, 1183–1198, 2012. a, b, c
Bellassen, V., Le Maire, G., Dhôte, J.-F., Ciais, P., and Viovy, N.: Modelling forest management within a global vegetation model – Part 1: Model structure and general behaviour, Ecol. Model., 221, 2458–2474, 2010. a, b, c, d
Bellassen, V., Le Maire, G., Guin, O., Dhôte, J.-F., Ciais, P., and Viovy, N.: Modelling forest management within a global vegetation model – Part 2: Model validation from a tree to a continental scale, Ecol. Model., 222, 57–75, 2011. a
Belmecheri, S., Maxwell, R. S., Taylor, A. H., Davis, K. J., Freeman, K. H., and Munger, W. J.: Tree-ring δ13C tracks flux tower ecosystem productivity estimates in a NE temperate forest, Environ. Res. Lett., 9, 074011, https://doi.org/101088/1748-9326/9/7/074011, 2014. a, b
Bodin, P. E., Gagen, M., McCarroll, D., Loader, N. J., Jalkanen, R., Robertson, I., R Switsur, V., Waterhouse, J. S., Woodley, E. J., Young, G. H., and Alton, P. B.: Comparing the performance of different stomatal conductance models using modelled and measured plant carbon isotope ratios (δ13C): implications for assessing physiological forcing, Glob. Change Biol., 19, 1709–1719, 2013. a, b, c, d
Boucher, O., Servonnat, J., Albright, A. L., Aumont, O., Balkanski, Y., Bastrikov, V., Bekki, S., Bonnet, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Caubel, A., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., D’Andrea, F., Davini, P., de Lavergne, C., Denvil, S., Deshayes, J., Devilliers, M., Ducharne, A., Dufresne, J.-L., Dupont, E., Éthé, C., Fairhead, L., Falletti, L., Flavoni, S., Foujols, M.-A., Gardoll, S., Gastineau, G., Ghattas, J., Grandpeix, J.-Y., Guenet, B., Guez, L., Guilyardi, É., Guimberteau, M., Hauglustaine, D., Hourdin, F., Idelkadi, A., Joussaume, S., Kageyama, M., Khodri, M., Krinner, G., Lebas, N., Levavasseur, G., Lévy, C., Li, L., Lott, F., Lurton, T., Luyssaert, S., Madec, G., Madeleine, J.-B., Maignan, F., Marchand, M., Marti, O., Mellul, L., Meurdesoif, Y., Mignot, J., Musat, I., Ottle, C., Peylin, P., Planton, Y., Polcher, J., Rio, C., Rochetin, N., Rousset, C., Sepulchre, P., Sima, A., Swingedouw, D., Thiéblemont, R., Traore, A. K., Vancoppenolle, M., Vial, J., Vialard, J., Viovy, N., and Vuichard, N. N.: Presentation and evaluation of the IPSL-CM6A-LR climate model, J. Adv. Model. Earth Syst., 12, 1–52, 2020. a
Breitenmoser, P., Brönnimann, S., and Frank, D.: Forward modelling of tree-ring width and comparison with a global network of tree-ring chronologies, Clim. Past, 10, 437–449, https://doi.org/10.5194/cp-10-437-2014, 2014. a
Cailleret, M., Dakos, V., Jansen, S., Robert, E. M., Aakala, T., Amoroso, M. M., Antos, J. A., Bigler, C., Bugmann, H., Caccianiga, M., Camarero, J.-J., Cherubini, P., Coyea, M., Das, A., Davi, H., Gea-Izquierdo, G., Gillner, S., Haavik, L., Hartmann, H., Heres ̧, A.-M., Hultine, K., Janda, P., Kane, J., Kharuk, V., Kitzberger, T., Klein, T., Levanic, T., Linares, J.-C., Lombardi, F., Mäkinen, H., Meszaros, I., Metsaranta, J., Oberhuber, W., Papadopoulos, A., Petritan, A. M., Rohner, B., Sanguesa- Barreda, G., Smith, J., Stan, A., Stojanovic, D., Suarez, M.-L., Svoboda, M., Trotsiuk, V., Villalba, R., Westwood, A., Wyckoff, P., and Martinez-Vilalta, J.: Early-warning signals of individual tree mortality based on annual radial growth, Front. Plant Sci., 9, 1964, https://doi.org/10.3389/fpls.2018.01964, 2018. a, b
Carbone, M. S., Czimczik, C. I., Keenan, T. F., Murakami, P. F., Pederson, N., Schaberg, P. G., Xu, X., and Richardson, A. D.: Age, allocation and availability of nonstructural carbon in mature red maple trees, New Phytol., 200, 1145–1155, 2013. a
Cernusak, L. A. and English, N. B.: Beyond tree-ring widths: stable isotopes sharpen the focus on climate responses of temperate forest trees, Tree Physiol., 35, 1–3, 2015. a
Cernusak, L. A., Ubierna, N., Winter, K., Holtum, J. A., Marshall, J. D., and Farquhar, G. D.: Environmental and physiological determinants of carbon isotope discrimination in terrestrial plants, New Phytol., 200, 950–965, 2013. a
Choisnel, E., Jourdain, S., and Jacquart, C.: Climatological evaluation of some fluxes of the surface energy and soil water balances over France, Ann. Geophys., 13, 666–674, 1995. a
Churakova, O. V., Shashkin, A. V., Siegwolf, R. T., Spahni, R., Launois, T., Saurer, M., Bryukhanova, M. V., Benkova, A. V., Kuptsova, A. V., Peylin, P., Vaganov, E. A., Masson-Delmotte, V., and Roden, J.: Application of eco-physiological models to the climatic interpretation of δ13C and δ18O measured in Siberian larch tree-rings, Dendrochronologia, 39, 51–59, 2016. a, b, c, d, e, f, g
Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J., Chhabra, A., DeFries, R., Galloway, J., Heimann, M., Jones, C., Le Quéré, C., Myneni, R., Piao, S., and Thornton, P.: Carbon and Other Biogeochemical Cycles, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 465–570, 2013. a, b
Cook, E., Briffa, K., Shiyatov, S., and Mazepa, V.: Tree-Ring Standardization and Growth-Trend Estimation, in: Methods of Dendrochronology: Applications in the Environmental Sciences, edited by: Cook, E. and Kairiukstis, L., Kluwer, Dordrecht, 104–123, 1990. a
Cook, E. R.: A time series analysis approach to tree ring standardization, PhD Dissertation, The University of Arizona, Graduate College, Tucson, 1985. a, b
Craig, H. and Gordon, L. I.: Deuterium and oxygen-18 variations in the ocean and the marine atmospheres, in: Proceedings of a Conference on Stable Isotopes in Oceanographic Studies and Palaeotemperature, edited by: Tongiorgi, E., Lischi and Figli, Pisa, Italy, 9–130, 1965. a, b, c
Danis, P., Masson-Delmotte, V., Stievenard, M., Guillemin, M., Daux, V., Naveau, P., and Von Grafenstein, U.: Reconstruction of past precipitation δ18O using tree-ring cellulose δ18O and δ13C: a calibration study near Lac d'Annecy, France, Earth Planet. Sc. Lett., 243, 439–448, 2006. a, b
Danis, P.-A., Hatté, C., Misson, L., and Guiot, J.: MAIDENiso: a multiproxy biophysical model of tree-ring width and oxygen and carbon isotopes, Can. J. Forest Res., 42, 1697–1713, 2012. a, b, c, d, e, f, g, h, i, j, k, l
Daux, V., Michelot-Antalik, A., Lavergne, A., Pierre, M., Stievenard, M., Bréda, N., and Damesin, C.: Comparisons of the performance of δ13C and δ18O of Fagus sylvatica, Pinus sylvestris, and Quercus petraea in the record of past climate variations, J. Geophys. Res.-Biogeo., 123, 1145–1160, 2018. a, b
de Boer, H. J., Robertson, I., Clisby, R., Loader, N. J., Gagen, M., Young, G. H., Wagner-Cremer, F., Hipkin, C. R., and McCarroll, D.: Tree-ring isotopes suggest atmospheric drying limits temperature–growth responses of treeline bristlecone pine, Tree Physiol., 39, 983–999, 2019. a
Deleuze, C., Pain, O., Dhôte, J.-F., and Hervé, J.-C.: A flexible radial increment model for individual trees in pure even-aged stands, Ann. Forest Sci., 61, 327–335, 2004. a, b
DeNiro, M. J. and Epstein, S.: Relationship between the oxygen isotope ratios of terrestrial plant cellulose, carbon dioxide, and water, Science, 204, 51–53, 1979. a
Drew, D. M. and Downes, G.: A model of stem growth and wood formation in Pinus radiata, Trees, 29, 1395–1413, 2015. a
Dufresne, J.-L., Foujols, M.-A., Denvil, S., Caubel, A., Marti, O., Aumont, O., Balkanski, Y., Bekki, S., Bellenger, H., Benshila, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., De Noblet, N., Duvel, J.-P., Éthé, C., Fairhead, L., Fichefet, T., Flavoni, S., Friedlingstein, P., Grandpeix, J.-Y., Guez, L., Guilyardi, É., Hauglustaine, D., Hourdin, F., Idelkadi, A., Ghattas, J., Joussaume, S., Kageyama, M., Krinner, G., Labetoulle, S., Lahellec, A., Lefebvre, M.-P., Lefèvre, F., Lévy, C., Li, Z., Lloyd, J., Lott, F., Madec, G., MANCIP, M., Marchand, M., Masson, S., Meurdesoif, Y., Mignot, J., Musat, I., Parouty, S., Polcher, J., Rio, C., Schulz, M., Swingedouw, D., Szopa, S., Talandier, C., Terray, P., Viovy, N., and Vuichard, N.: Climate change projections using the IPSL-CM5 Earth System Model: from CMIP3 to CMIP5, Clim. Dynam., 40, 2123–2165, 2013. a
Eglin, T., Francois, C., Michelot, A., Delpierre, N., and Damesin, C.: Linking intra-seasonal variations in climate and tree-ring δ13C: a functional modelling approach, Ecol.l Model., 221, 1779–1797, 2010. a
Etien, N., Daux, V., Masson-Delmotte, V., Mestre, O., Stievenard, M., Guillemin, M., Boettger, T., Breda, N., Haupt, M., and Perraud, P.: Summer maximum temperature in northern France over the past century: instrumental data versus multiple proxies (tree-ring isotopes, grape harvest dates and forest fires), Climatic Change, 94, 429–456, 2009. a
Evans, M.: Toward forward modeling for paleoclimatic proxy signal calibration: A case study with oxygen isotopic composition of tropical woods, Geochem. Geophy. Geosy., 8, Q07008, https://doi.org/10.1029/2006GC001406, 2007. a
Farquhar, G., Barbour, M., and Henry, B.: Interpretation of oxygen isotope composition of leaf material, in: Stable isotopes: integration of biological, ecological, and geochemical processes, edited by: Griffiths, H., Bios Scientific, London, 27–48, 1998. a
Farquhar, G. D., von Caemmerer, S., and Berry, J. A.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, 1980. a
Farquhar, G. D., O'Leary, M. H., and Berry, J. A.: On the relationship between carbon isotope discrimination and the intercellular carbon dioxide concentration in leaves, Funct. Plant Biol., 9, 121–137, 1982. a, b, c
Fatichi, S., Leuzinger, S., and Körner, C.: Moving beyond photosynthesis: from carbon source to sink-driven vegetation modeling, New Phytol., 201, 1086–1095, 2014. a, b, c
Francey, R. and Farquhar, G.: An explanation of 13C 12C variations in tree rings, Nature, 297, 28–31, 1982. a, b
Frank, D., Poulter, B., Saurer, M., Esper, J., Huntingford, C., Helle, G., Treydte, K., Zimmermann, N. E., Schleser, G., Ahlström, A., Ciais, P., Friedlingstein, P., Levis, S., Lomas, M., Sitch, S., Viovy, N., Andreu-Hayles, L., Bednarz, Z., Berninger, F., Boettger, T., d’Alessandro, C., Daux, V., Filot, M., Grabner, M., Gutierrez, E., Haupt, M., Hilasvuori, E., Jungner, H., Kalela-Brundin, M., Krapiec, M., Leuenberger, M., Loader, N., Marah, H., Masson-Delmotte, V., Pazdur, A., Pawelczyk, S., Pierre, M., Planells, O., Pukiene, R., Reynolds-Henne, C., Rinne, K., Saracino, A., Sonninen, E., Stievenard, M., Switsur, V., Szczepanek, M., Szychowska-Krapiec, E., Todaro, L., Waterhouse, J. S., and Weigl, M.: Water-use efficiency and transpiration across European forests during the Anthropocene, Nat. Clim. Change, 5, 579–583, 2015. a, b, c
Friedlingstein, P., Cox, P., Betts, R., Bopp, L., von Bloh, W., Brovkin, V., Cadule, P., Doney, S., Eby, M., Fung, I., Bala, G., John, J., Jones, C., Joos, F., Kato, T., Kawamiya, M., Knorr, W., Lindsay, K., Matthews, H., Raddatz, T., Rayner, P., Reick, C., Roeckner, E., Schnitzler, K.-G., Schnur, R., Strassmann, K., Weaver, A., Yoshikawa, C., and Zeng, N.: Climate–carbon cycle feedback analysis: results from the C4 MIP model intercomparison, J. Clim., 19, 3337–3353, 2006. a
Friedlingstein, P., Meinshausen, M., Arora, V. K., Jones, C. D., Anav, A., Liddicoat, S. K., and Knutti, R.: Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks, J. Clim., 27, 511–526, 2014. a, b, c
Fritts, H. C.: Tree Rings and Climate, Academic Press, London, 1976. a, b
Fritts, H. C., Shashkin, A., and Downes, G. M.: A simulation model of conifer ring growth and cell structure, in: Tree Ring Analysis: Biological, Methodological and Environmental Aspects, edited by: Wimmer, R. and Vetter, R. E., Wallingford, UK, CABI Publishing, Wallingford, 1999. a, b
Gessler, A., Brandes, E., Buchmann, N., Helle, G., Rennenberg, H., and Barnard, R. L.: Tracing carbon and oxygen isotope signals from newly assimilated sugars in the leaves to the tree-ring archive, Plant Cell Environ., 32, 780–795, 2009. a, b
Gessler, A., Ferrio, J. P., Hommel, R., Treydte, K., Werner, R. A., and Monson, R. K.: Stable isotopes in tree rings: towards a mechanistic understanding of isotope fractionation and mixing processes from the leaves to the wood, Tree Physiol., 34, 796–818, 2014. a, b
Girardin, M. P., Bouriaud, O., Hogg, E. H., Kurz, W., Zimmermann, N. E., Metsaranta, J. M., de Jong, R., Frank, D. C., Esper, J., Büntgen, U., Guo, X. J., and Bhatti, J.: No growth stimulation of Canada’s boreal forest under half-century of combined warming and CO2 fertilization, P. Natl. Acade. Sci. USA, 113, E8406–E8414, 2016. a
Grömping, U.: Relative importance for linear regression in R: the package relaimpo, J. Stat. Softw., 17, 1–27, 2006. a
Guerrieri, M., Siegwolf, R., Saurer, M., Jäggi, M., Cherubini, P., Ripullone, F., and Borghetti, M.: Impact of different nitrogen emission sources on tree physiology as assessed by a triple stable isotope approach, Atmos. Environ., 43, 410–418, 2009. a
Haese, B., Werner, M., and Lohmann, G.: Stable water isotopes in the coupled atmosphere–land surface model ECHAM5-JSBACH, Geosci. Model Dev., 6, 1463–1480, https://doi.org/10.5194/gmd-6-1463-2013, 2013. a, b
Helle, G. and Schleser, G.: Beyond CO2-fixation by Rubisco–an interpretation of 13C 12C variations in tree rings from novel intra-seasonal studies on broad-leaf trees, Plant Cell Environ., 27, 367–380, 2004. a
Hemming, D., Fritts, H., Leavitt, S., Wright, W., Long, A., and Shashkin, A.: Modelling tree-ring δ13C, Dendrochronologia, 19, 23–28, 2001. a, b, c
Hilasvuori, E. and Berninger, F.: Dependence of tree ring stable isotope abundances and ring width on climate in Finnish oak, Tree Physiol., 30, 636–647, 2010. a
Hilasvuori, E., Berninger, F., Sonninen, E., Tuomenvirta, H., and Jungner, H.: Stability of climate signal in carbon and oxygen isotope records and ring width from Scots pine (Pinus sylvestris L.) in Finland, J. Quaternary Sci., 24, 469–480, 2009. a, b
Hourdin, F., Musat, I., Bony, S., Braconnot, P., Codron, F., Dufresne, J.-L., Fairhead, L., Filiberti, M.-A., Friedlingstein, P., Grandpeix, J.-Y., Krinner, G., Levan, P., Li, Z.-X., and Lott, F.: The LMDZ4 general circulation model: climate performance and sensitivity to parametrized physics with emphasis on tropical convection, Clim. Dynam., 27, 787–813, 2006. a
Huang, J.-G., Bergeron, Y., Denneler, B., Berninger, F., and Tardif, J.: Response of forest trees to increased atmospheric CO2, Crit. Rev. Plant Sci., 26, 265–283, 2007. a
Jeong, J., Barichivich, J., Peylin, P., Haverd, V., McGrath, M. J., Vuichard, N., Evans, M. N., Babst, F., and Luyssaert, S.: Using the International Tree-Ring Data Bank (ITRDB) records as century-long benchmarks for land-surface models, Geosci. Model Dev. Discuss. [preprint], https://doi.org/10.5194/gmd-2020-29, in review, 2020. a, b, c, d, e, f
Jones, C., Robertson, E., Arora, V., Friedlingstein, P., Shevliakova, E., Bopp, L., Brovkin, V., Hajima, T., Kato, E., Kawamiya, M., Liddicoat, S., Lindsay, K., Reick, C. H., Roelandt, C., Segschneider, J., and Tjiputra, J.: Twenty-first-century compatible CO2 emissions and airborne fraction simulated by CMIP5 Earth system models under four representative concentration pathways, J. Clim., 26, 4398–4413, 2013. a
Jones, S., Rowland, L., Cox, P., Hemming, D., Wiltshire, A., Williams, K., Parazoo, N. C., Liu, J., da Costa, A. C. L., Meir, P., Mencuccini, M., and Harper, A. B.: The impact of a simple representation of non-structural carbohydrates on the simulated response of tropical forests to drought, Biogeosciences, 17, 3589–3612, https://doi.org/10.5194/bg-17-3589-2020, 2020. a, b, c, d, e
Kagawa, A., Sugimoto, A., and Maximov, T. C.: 13CO2 pulse-labelling of photoassimilates reveals carbon allocation within and between tree rings, Plant Cell Environ., 29, 1571–1584, 2006. a
Keel, S. G., Siegwolf, R. T., and Körner, C.: Canopy CO2 enrichment permits tracing the fate of recently assimilated carbon in a mature deciduous forest, New Phytol., 172, 319–329, 2006. a
Keel, S. G., Joos, F., Spahni, R., Saurer, M., Weigt, R. B., and Klesse, S.: Simulating oxygen isotope ratios in tree ring cellulose using a dynamic global vegetation model, Biogeosciences, 13, 3869–3886, https://doi.org/10.5194/bg-13-3869-2016, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m
Keller, K. M., Lienert, S., Bozbiyik, A., Stocker, T. F., Churakova (Sidorova), O. V., Frank, D. C., Klesse, S., Koven, C. D., Leuenberger, M., Riley, W. J., Saurer, M., Siegwolf, R., Weigt, R. B., and Joos, F.: 20th century changes in carbon isotopes and water-use efficiency: tree-ring-based evaluation of the CLM4.5 and LPX-Bern models, Biogeosciences, 14, 2641–2673, https://doi.org/10.5194/bg-14-2641-2017, 2017. a, b, c, d, e, f
Körner, C.: Paradigm shift in plant growth control, Curr. Opin. Plant Biol., 25, 107–114, 2015. a, b
Krinner, G., Viovy, N., de Noblet-Ducoudré, N., Ogée, J., Polcher, J., Friedlingstein, P., Ciais, P., Sitch, S., and Prentice, I. C.: A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system, Global Biogeochem. Cy., 19, 1–34, 2005. a, b
LaMarche Jr., V. C. and Stockton, C. W.: Chronologies from termperature-sensitive bristlecone pines at upper treeline in Western United States, Tree-Ring Bull., 21–44, 1974. a
Lavergne, A., Gennaretti, F., Risi, C., Daux, V., Boucher, E., Savard, M. M., Naulier, M., Villalba, R., Bégin, C., and Guiot, J.: Modelling tree ring cellulose δ18O variations in two temperature-sensitive tree species from North and South America, Clim. Past, 13, 1515–1526, https://doi.org/10.5194/cp-13-1515-2017, 2017. a, b, c
Lavergne, A., Voelker, S., Csank, A., Graven, H., de Boer, H. J., Daux, V., Robertson, I., Dorado-Liñán, I., Martínez-Sancho, E., Battipaglia, G., Bloomfield, K., Still, C., Meinzer, F., Dawson, T., Julio Camarero, J., Clisby, R., Fang, Y., Menzel, A., Keen, R., Roden, J., and Prentice, I. C.: Historical changes in the stomatal limitation of photosynthesis: empirical support for an optimality principle, New Phytol., 225, 2484–2497, 2020. a
Levesque, M., Andreu-Hayles, L., Smith, W. K., Williams, A. P., Hobi, M. L., Allred, B. W., and Pederson, N.: Tree-ring isotopes capture interannual vegetation productivity dynamics at the biome scale, Nat. Commun., 10, 1–10, 2019. a, b, c
Li, G., Harrison, S. P., Prentice, I. C., and Falster, D.: Simulation of tree-ring widths with a model for primary production, carbon allocation, and growth, Biogeosciences, 11, 6711–6724, https://doi.org/10.5194/bg-11-6711-2014, 2014. a
Liu, X., Zhang, X., Zhao, L., Xu, G., Wang, L., Sun, W., Zhang, Q., Wang, W., Zeng, X., and Wu, G.: Tree ring δ18O reveals no long-term change of atmospheric water demand since 1800 in the northern Great Hinggan Mountains, China, J. Geophys. Res.-Atmos., 122, 6697–6712, 2017. a
Lloyd, J. and Farquhar, G. D.: 13C discrimination during CO2 assimilation by the terrestrial biosphere, Oecologia, 99, 201–215, 1994. a, b
Loader, N., Street-Perrott, F., Daley, T., Hughes, P., Kimak, A., Levanic, T., Mallon, G., Mauquoy, D., Robertson, I., Roland, T., van Bellen, S., Ziehmer, M., and Leuenberger, M.: Simultaneous determination of stable carbon, oxygen, and hydrogen isotopes in cellulose, Anal. Chem., 87, 376–380, 2015. a
Luyssaert, S.: ORCHIDEE_CN_CAN revision 5698, [Dataset], https://doi.org/10.14768/20200228001.1 (last access: 19 June 2021), 2019.
McCarroll, D. and Loader, N. J.: Stable isotopes in tree rings, Quaternary Sci. Rev., 23, 771–801, 2004. a, b, c
McCarroll, D., Jalkanen, R., Hicks, S., Tuovinen, M., Gagen, M., Pawellek, F., Eckstein, D., Schmitt, U., Autio, J., and Heikkinen, O.: Multiproxy dendroclimatology: a pilot study in northern Finland, The Holocene, 13, 829–838, 2003. a
McDowell, N., Pockman, W. T., Allen, C. D., Breshears, D. D., Cobb, N., Kolb, T., Plaut, J., Sperry, J., West, A., Williams, D. G., and Yepez, E.: Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought?, New Phytol., 178, 719–739, 2008. a
McMurtrie, R., Rook, D., and Kelliher, F.: Modelling the yield of Pinus radiata on a site limited by water and nitrogen, Forest Ecol. Manage., 30, 381–413, 1990. a
Michelot, A., Eglin, T., Dufrene, E., LELARGE-TROUVERIE, C., and Damesin, C.: Comparison of seasonal variations in water-use efficiency calculated from the carbon isotope composition of tree rings and flux data in a temperate forest, Plant Cell Environ., 34, 230–244, 2011. a, b
Michelot, A., Bréda, N., Damesin, C., and Dufrêne, E.: Differing growth responses to climatic variations and soil water deficits of Fagus sylvatica, Quercus petraea and Pinus sylvestris in a temperate forest, Forest Ecol. Manage., 265, 161–171, 2012. a
Misson, L.: MAIDEN: a model for analyzing ecosystem processes in dendroecology, Can. J. Forest Res., 34, 874–887, 2004. a, b, c, d
Monserud, R. A. and Marshall, J. D.: Time-series analysis of δ13C from tree rings, I. Time trends and autocorrelation, Tree Physiol., 21, 1087–1102, 2001. a
Naudts, K., Ryder, J., McGrath, M. J., Otto, J., Chen, Y., Valade, A., Bellasen, V., Berhongaray, G., Bönisch, G., Campioli, M., Ghattas, J., De Groote, T., Haverd, V., Kattge, J., MacBean, N., Maignan, F., Merilä, P., Penuelas, J., Peylin, P., Pinty, B., Pretzsch, H., Schulze, E. D., Solyga, D., Vuichard, N., Yan, Y., and Luyssaert, S.: A vertically discretised canopy description for ORCHIDEE (SVN r2290) and the modifications to the energy, water and carbon fluxes, Geosci. Model Dev., 8, 2035–2065, https://doi.org/10.5194/gmd-8-2035-2015, 2015. a, b, c, d
New, M., Hulme, M., and Jones, P.: Representing twentieth-century space–time climate variability, Part II: Development of 1901–96 monthly grids of terrestrial surface climate, J. Clim., 13, 2217–2238, 2000. a
Ogée, J., Barbour, M. M., Wingate, L., Bert, D., Bosc, A., Stievenard, M., Lambrot, C., Pierre, M., Bariac, T., Loustau, D., and Dewar, R.: A single-substrate model to interpret intra-annual stable isotope signals in tree-ring cellulose, Plant Cell Environ., 32, 1071–1090, 2009. a
Orth, R., Dutra, E., Trigo, I. F., and Balsamo, G.: Advancing land surface model development with satellite-based Earth observations, Hydrol. Earth Syst. Sci., 21, 2483–2495, https://doi.org/10.5194/hess-21-2483-2017, 2017. a
Panek, J. A. and Waring, R. H.: Stable carbon isotopes as indicators of limitations to forest growth imposed by climate stress, Ecol. Appl., 7, 854–863, 1997. a, b, c
Peylin, P., Bacour, C., MacBean, N., Leonard, S., Rayner, P., Kuppel, S., Koffi, E., Kane, A., Maignan, F., Chevallier, F., Ciais, P., and Prunet, P.: A new stepwise carbon cycle data assimilation system using multiple data streams to constrain the simulated land surface carbon cycle, Geosci. Model Dev., 9, 3321–3346, https://doi.org/10.5194/gmd-9-3321-2016, 2016. a, b
Phillips, T. J., Bonfils, C. J., and Zhang, C.: Model consensus projections of US regional hydroclimates under greenhouse warming, Environ. Res. Lett., 14, 014005, https://doi.org/10.1111/j.1365-3040.2009.01989.x, 2019. a
R Core Team: R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 19 June 2021), 2020. a
Raczka, B., Duarte, H. F., Koven, C. D., Ricciuto, D., Thornton, P. E., Lin, J. C., and Bowling, D. R.: An observational constraint on stomatal function in forests: evaluating coupled carbon and water vapor exchange with carbon isotopes in the Community Land Model (CLM4.5), Biogeosciences, 13, 5183–5204, https://doi.org/10.5194/bg-13-5183-2016, 2016. a
Raffalli-Delerce, G., Masson-Delmotte, V., Dupouey, J.-L., Stievenard, M., Breda, N., and Moisselin, J.: Reconstruction of summer droughts using tree-ring cellulose isotopes: a calibration study with living oaks from Brittany (western France), Tellus B, 56, 160–174, 2004. a
Rammig, A., Wiedermann, M., Donges, J. F., Babst, F., von Bloh, W., Frank, D., Thonicke, K., and Mahecha, M. D.: Coincidences of climate extremes and anomalous vegetation responses: comparing tree ring patterns to simulated productivity, Biogeosciences, 12, 373–385, https://doi.org/10.5194/bg-12-373-2015, 2015. a
Rebetez, M., Saurer, M., and Cherubini, P.: To what extent can oxygen isotopes in tree rings and precipitation be used to reconstruct past atmospheric temperature? A case study, Climatic Change, 61, 237–248, 2003. a
Risi, C., Bony, S., Vimeux, F., and Jouzel, J.: Water-stable isotopes in the LMDZ4 general circulation model: Model evaluation for present-day and past climates and applications to climatic interpretations of tropical isotopic records, J. Geophys. Res.-Atmos., 115, D12118, https://doi.org/10.1029/2009jd013255, 2010. a
Risi, C., Noone, D., Frankenberg, C., and Worden, J.: Role of continental recycling in intraseasonal variations of continental moisture as deduced from model simulations and water vapor isotopic measurements, Water Resour. Res., 49, 4136–4156, 2013. a
Risi, C., Ogée, J., Bony, S., Bariac, T., Raz-Yaseef, N., Wingate, L., Welker, J., Knohl, A., Kurz-Besson, C., Leclerc, M., Zhang, G., Buch- mann, N., Santrucek, J. J., Hronkova, M., David, T., Peylin, P., and Guglielmo, F.: The water isotopic version of the land-surface model ORCHIDEE: Implementation, evaluation, sensitivity to hydrological parameters, Hydrol. Curr. Res., 7, 1000258, https://doi.org/10.4172/2157-7587.1000258, 2016. a, b, c, d, e, f, g, h, i, j
Rocha, A. V., Goulden, M. L., Dunn, A. L., and Wofsy, S. C.: On linking interannual tree ring variability with observations of whole-forest CO2 flux, Glob. Change Biol., 12, 1378–1389, 2006. a
Roden, J. and Siegwolf, R.: Is the dual-isotope conceptual model fully operational?, Tree Physiol., 32, 1179–1182, 2012. a, b
Roden, J., Kahmen, A., Buchmann, N., and Siegwolf, R.: The enigma of effective path length for 18O enrichment in leaf water of conifers, Plant Cell Environ., 38, 2551–2565, 2015. a
Roden, J. S. and Farquhar, G. D.: A controlled test of the dual-isotope approach for the interpretation of stable carbon and oxygen isotope ratio variation in tree rings, Tree Physiol., 32, 490–503, 2012. a
Roden, J. S., Lin, G., and Ehleringer, J. R.: A mechanistic model for interpretation of hydrogen and oxygen isotope ratios in tree-ring cellulose, Geochim. Cosmochim. Ac., 64, 21–35, 2000. a, b
Sargeant, C. I., Singer, M. B., and Vallet-Coulomb, C.: Identification of source-water oxygen isotopes in trees toolkit (ISO-Tool) for deciphering historical water use by forest trees, Water Resour. Res., 55, 10954–10975, 2019. a
Sato, H., Itoh, A., and Kohyama, T.: SEIB–DGVM: A new Dynamic Global Vegetation Model using a spatially explicit individual-based approach, Ecol. Model., 200, 279–307, 2007. a
Saurer, M., Aellen, K., and Siegwolf, R.: Correlating δ13C and δ18O in cellulose of trees, Plant Cell Environ., 20, 1543–1550, 1997. a, b
Saurer, M., Spahni, R., Frank, D. C., Joos, F., Leuenberger, M., Loader, N. J., McCarroll, D., Gagen, M., Poulter, B., Siegwolf, R., Andreau- Hayles, L., Boettger, T., Dorado Linan, I., Fairchild, I., Friedrich, M., Guiterrez, E., Haupt, M., Hilasvuori, E., Heinrich, I., Helle, G., Grudd, H., Jalkanen, R., Levanic, T., Linderholm, H., Robertson, I., Sonninen, E., Treydte, K., Waterhouse, J., Woodley, E., Wynn, P., and Young, G.: Spatial variability and temporal trends in water-use efficiency of European forests, Glob. Change Biol., 20, 3700–3712, 2014. a, b, c
Savard, M. M.: Tree-ring stable isotopes and historical perspectives on pollution – An overview, Environ. Pollut., 158, 2007–2013, 2010. a
Scheidegger, Y., Saurer, M., Bahn, M., and Siegwolf, R.: Linking stable oxygen and carbon isotopes with stomatal conductance and photosynthetic capacity: a conceptual model, Oecologia, 125, 350–357, 2000. a, b, c, d, e, f
Schollaen, K., Heinrich, I., Neuwirth, B., Krusic, P. J., D'Arrigo, R. D., Karyanto, O., and Helle, G.: Multiple tree-ring chronologies (ring width, δ13C and δ18O) reveal dry and rainy season signals of rainfall in Indonesia, Quaternary Sci. Rev., 73, 170–181, 2013. a
Shestakova, T. A. and Martínez-Sancho, E.: Stories hidden in tree rings: a review on the application of stable carbon isotopes to dendrosciences, Dendrochronologia, 125789, https://doi.org/10.1016/j.dendro.2020.125789, 2021. a
Shestakova, T. A., Camarero, J. J., Ferrio, J. P., Knorre, A. A., Gutierrez, E., and Voltas, J.: Increasing drought effects on five European pines modulate δ13C-growth coupling along a Mediterranean altitudinal gradient, Funct. Ecol., 31, 1359–1370, 2017. a, b, c, d
Shestakova, T., Voltas, J., Saurer, M., Berninger, F., Esper, J., Andreu-Hayles, L., Daux, V., Helle, G., Leuenberger, M., Loader, N., Masson- Delmotte, V., Saracino, A., Waterhouse, J., Schleser, G., Bednarz, Z., Boettger, T., Dorado-Liñán, I., Filot, M., Frank, D., Grabner, M., Haupt, M., Hilasvuori, E., Jungner, H., Kalela-Brundin, M., Kra ̧piec, M., Marah, H., Pawełczyk, S., Pazdur, A., Pierre, M., Planellis, O., Pukiene ̇, R., Reynolds-Henne, C., Rinne-Garmston, K., Rita, A., Sonninen, E., Stiévenard, M., Switsur, V., Szychowska- Kra ̧piec, E., Szymaszek, M., Todaro, L., Treydte, K., Vitas, A., Weigl, M., Wimmer, R., and Gutiérrez, E.: Spatio-temporal patterns of tree growth as related to carbon isotope fractionation in European forests under changing climate, Glob. Ecol. Biogeogr., 28, 1295–1309, 2019. a, b, c, d, e, f, g, h, i
Shi, C., Masson-Delmotte, V., Risi, C., Eglin, T., Stievenard, M., Pierre, M., Wang, X., Gao, J., Bréon, F.-M., Zhang, Q.-B., and Daux, V.: Sampling strategy and climatic implications of tree-ring stable isotopes on the southeast Tibetan Plateau, Earth Planet. Sc.e Lett., 301, 307–316, 2011. a, b, c, d
Smith, M. D., La Pierre, K. J., Collins, S. L., Knapp, A. K., Gross, K. L., Barrett, J. E., Frey, S. D., Gough, L., Miller, R. J., Morris, J. T., Rustad, L. E., and Yarie, J.: Global environmental change and the nature of aboveground net primary productivity responses: insights from long-term experiments, Oecologia, 177, 935–947, 2015. a
Song, J., Wan, S., Piao, S., Knapp, A. K., Classen, A. T., Vicca, S., Ciais, P., Hovenden, M. J., Leuzinger, S., Beier, C., Kardol, P., Xia, J., Liu, Q., Ru, J., Zhou, Z., Luo, Y., Guo, D., Langley, J. A., Zscheischler, J., Dukes, J. S., Tang, J., Chen, J., Hofmockel, K. S., Kueppers, L. M., Rustad, L., Liu, L., Smith, M. D., Templer, P. H., Thomas, R. Q., Norby, R. J., Phillips, R. P., Niu, S., Fatichi, S., Wang, Y., Shao, P., Han, H., Wang, D., Lei, L., Wang, J., Li, X., Zhang, Q., Li, X., Su, F., Liu, B., Yang, F., Ma, G., Li, G., Liu, Y., Liu, Y., Yang, Z., Zhang, K., Miao, Y., Hu, M., Yan, C., Zhang, A., Zhong, M., Hui, Y., Li, Y., and Zheng, M.: A meta-analysis of 1,119 manipulative experiments on terrestrial carbon-cycling responses to global change, Nat. Ecol. Evolut., 3, 1309–1320, 2019. a
Stenberg, L. and DeNiro, M. J.: Biogeochemical implications of the isotopic equilibrium fractionation factor between the oxygen atoms of acetone and water, Geochim. Cosmochim. Ac., 47, 2271–2274, 1983. a
Szejner, P., Belmecheri, S., Ehleringer, J. R., and Monson, R. K.: Recent increases in drought frequency cause observed multi-year drought legacies in the tree rings of semi-arid forests, Oecologia, 192, 241–259, 2020. a
Tei, S., Sugimoto, A., Kotani, A., Ohta, T., Morozumi, T., Saito, S., Hashiguchi, S., and Maximov, T.: Strong and stable relationships between tree-ring parameters and forest-level carbon fluxes in a Siberian larch forest, Polar Sci., 21, 146–157, 2019. a, b
Thum, T., MacBean, N., Peylin, P., Bacour, C., Santaren, D., Longdoz, B., Loustau, D., and Ciais, P.: The potential benefit of using forest biomass data in addition to carbon and water flux measurements to constrain ecosystem model parameters: case studies at two temperate forest sites, Agr. Forest Meteorol., 234, 48–65, 2017. a
Ulrich, D. E., Still, C., Brooks, J. R., Kim, Y., and Meinzer, F. C.: Investigating old-growth ponderosa pine physiology using tree-rings, δ13C, δ18O, and a process-based model, Ecology, 100, e02656, https://doi.org/10.1002/ecy.2656, 2019. a, b
Vaganov, E. A., Anchukaitis, K. J., and Evans, M. N.: How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics, in: Tree Rings and Climate: Sharpening theFocus, Developments in Environmental Research, Vol. 11, edited by: Hughes, M. and Swetnam, T. W., and Diaz, H., 37–75, Springer, 2011. a, b, c, d
Viovy, N.: CRUNCEP v4 (CRU TS 3.21), available at: http://dods.extra.cea.fr/data/p529viov/cruncep (last access: 7 November 2020), 2014. a
Voelker, S. L., Meinzer, F. C., Lachenbruch, B., Brooks, J. R., and Guyette, R. P.: Drivers of radial growth and carbon isotope discrimination of bur oak (Quercus macrocarpa M ichx.) across continental gradients in precipitation, vapour pressure deficit and irradiance, Plant Cell Environ., 37, 766–779, 2014. a
Vuichard, N., Messina, P., Luyssaert, S., Guenet, B., Zaehle, S., Ghattas, J., Bastrikov, V., and Peylin, P.: Accounting for carbon and nitrogen interactions in the global terrestrial ecosystem model ORCHIDEE (trunk version, rev 4999): multi-scale evaluation of gross primary production, Geosci. Model Dev., 12, 4751–4779, https://doi.org/10.5194/gmd-12-4751-2019, 2019. a, b, c, d
Wei, L., Marshall, J. D., Link, T. E., Kavanagh, K. L., Du, E., Pangle, R. E., Gag, P. J., and Ubierna, N.: Constraining 3-PG with a new δ13C submodel: a test using the δ13C of tree rings, Plant Cell Environ., 37, 82–100, 2014. a
Werner, C., Schnyder, H., Cuntz, M., Keitel, C., Zeeman, M. J., Dawson, T. E., Badeck, F.-W., Brugnoli, E., Ghashghaie, J., Grams, T. E. E., Kayler, Z. E., Lakatos, M., Lee, X., Máguas, C., Ogée, J., Rascher, K. G., Siegwolf, R. T. W., Unger, S., Welker, J., Wingate, L., and Gessler, A.: Progress and challenges in using stable isotopes to trace plant carbon and water relations across scales, Biogeosciences, 9, 3083–3111, https://doi.org/10.5194/bg-9-3083-2012, 2012. a, b
Wood, S.: Generalized Additive Models: An Introduction with R, Chapman and Hall/CRC, 2 Edn., 2017. a
Zuidema, P. A., Poulter, B., and Frank, D. C.: A wood biology agenda to support global vegetation modelling, Trends Plant Sci., 23, 1006–1015, 2018. a