the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Common ambiguities in plant hydraulics
Christian Frankenberg
Plant hydraulics gains increasing interest in plant ecophysiology and vegetation modeling. However, the hydraulic properties and profiles are often improperly represented, thus leading to biased results and simulations, e.g., the neglection of gravitational pressure drop results in overestimated water flux. We highlight the commonly seen ambiguities and/or misunderstandings in plant hydraulics, including (1) the distinction between water potential and pressure, (2) differences among hydraulic conductance and conductivity, (3) xylem vulnerability curve formulations, (4) model complexity, (5) stomatal-model representations, (6) bias from analytic estimations, (7) whole-plant vulnerability, and (8) neglected temperature dependencies. We recommend careful thinking before using or modifying existing definitions, methods, and models.
- Article
(1811 KB) - Full-text XML
- BibTeX
- EndNote
Plant hydraulics gains increasing interest in understanding plants' responses and acclimation/adaptation to the environment (Santiago et al., 2004; McDowell et al., 2008; McDowell, 2011; Meinzer et al., 2010; Allen et al., 2010; Anderegg et al., 2012, 2016; Gleason et al., 2016; Wang et al., 2021a; Liu et al., 2021) and modeling canopy carbon and water fluxes within vegetation and land surface models (Buckley and Mott, 2013; Manzoni et al., 2013; McDowell et al., 2013; Sperry et al., 2017; Kennedy et al., 2019; Liu et al., 2020; Wang et al., 2020, 2021b; Sabot et al., 2022). However, xylem hydraulic properties and flow pressure profile are often improperly represented, due to the ambiguities and misunderstandings of various plant hydraulics parameters, though the plant hydraulics models used in topical research are already dramatically simplified compared to a complicated hydraulic architecture (Tyree and Ewers, 1991). For instance, distinctions between (a) water potential and pressure, (b) hydraulic conductance and conductivity, and (c) division and derivative are often not recognized. Further, the pursuit of simplicity, analytical solution, and novelty consequently results in modifications of known and well-tested functional forms. However, while researchers should be encouraged to try “new” approaches, it is important to keep in mind whether these changes or new methods (a) are correct and (b) need to be tested before moving forward. Any research violating the two principles would be unwarranted, no matter how “reasonable” they appear to be.
For example, regarding the modeling of plant hydraulics, since Wolf et al. (2016) and Sperry et al. (2017) advanced the stomatal optimization theory (Cowan and Farquhar, 1977) by quantifying hydraulic risk under a general gain–risk optimization framework, an increasing number of new models or variants have been developed (e.g., Anderegg et al., 2018; Dewar et al., 2018; Eller et al., 2018; Wang et al., 2020, 2021a; Chen et al., 2022), and many plant-hydraulics-based models show predictive skills comparable to statistical methods (Anderegg et al., 2018; Venturas et al., 2018; Eller et al., 2020; Wang et al., 2020; Sabot et al., 2022). Nevertheless, these tested models are not always replicated correctly, as researchers tend to mutate the formulations and sometimes hypotheses, such as the neglect of the rhizosphere component that plays an important role in drought stress conditions (Sperry et al., 1998; Sperry and Love, 2015; Sperry et al., 2016; Wang et al., 2020). Although the modifications often resemble tested models, they are often used without being thoroughly tested. Reasons behind the lack of model testing include the following: (a) there is not yet a well-established method or database to conveniently benchmark the new model variants; (b) research that focuses on varying the formulations and testing the variants is not encouraged by reviewers due to lack of novelty; and (c) one may not recognize the changes or differences that have been made. Here, we list some common ambiguities and misunderstandings in plant hydraulics and recommend careful thinking before using or modifying existing definitions, methods, and models.
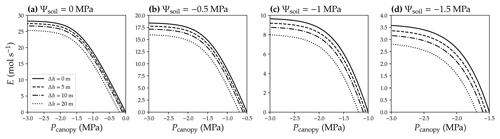
Water movement in xylem conduits includes mass flow through xylem conduits and diffusion between xylem conduits and capacitance tissues. Water mass flow (from site 1 to 2) in xylem is driven by the net force at the target plane per area (driving pressure, DP; see Table 1 for the list of symbols), which is as in Fig. 1a. Dissolved ions only play a role in liquid water density but do not contribute to the driving pressure for long-distance transport in the xylem because the distance involved is too long for diffusion and thus chemical potential to be an important contributor. Water diffusion across the cell membrane (from xylem conduit to the cell) is driven by the potential difference, which is as in Fig. 1a, and the dissolved ions play a role through the osmotic potential.
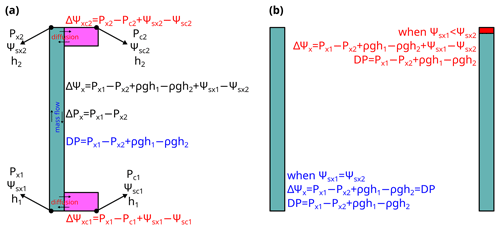
Figure 1Diagram for the difference between potential and pressure in plant hydraulics. (a) Difference among pressure difference (ΔP), potential difference (ΔΨ), and mass flow driving pressure (DP). Ψ is the sum of water pressure (Px for xylem and Pc for cell), osmotic potential (Ψsx for xylem and Ψsx for cell), and gravitational potential related to height (ρgh). (b) Example when ΔΨ differs from ΔP. In scenario 1 (left), where Ψsx2=Ψsx1 (labeled in blue), ΔΨ=DP. In scenario 2 (right), where Ψsx2<Ψsx1 (labeled in red), ΔΨ>DP. See Table 1 for the list of symbols.
As ion concentration in xylem conduit is very low, the osmotic potential in xylem conduit (Ψsx) is often ignored. Therefore, water potential is imperceptibly used in place of mass flow driving pressure (i.e., DP) because of the gravity term in it. To date, many people have used water potential rather than water pressure when modeling and describing mass water flow. This, though it may be easier for people to understand in most scenarios, is not correct. For example, in Fig. 1b, if the osmotic potential at the bottom and top are the same, the driving pressure and water potential difference are the same. However, if the osmotic potential at the top is more negative than at the bottom (for example, via adding a very thin layer of high-concentration salt solution), the driving pressure will be lower than the water potential difference. Besides the fact that the values of DP and water potential difference are not always equal, the primary reason for not misusing them is that water potential describes the tendency for water to move between adjacent phases (where water molecules will diffuse), whereas pressure is more relevant to bulk water movement. Thus, using potential difference for water mass flow is technically incorrect, and it is necessary to clarify the terminology to distinguish them.
Water potential and pressure used in plant hydraulics are both defined as a difference from a reference value: water potential (often denoted as Ψ or ψ in literature) is typically defined as the difference from the potential of pure water in the soil, and water pressure (often denoted as P or p) is typically defined as the difference from the environmental air pressure. Water pressure difference between xylem water and surrounding air is responsible for air-seeded conduit cavitation (Sperry and Tyree, 1988; Tyree and Sperry, 1989), which occurs when the pressure difference exceeds the capillary pressure at the air–water interface. Thus, using water potential to describe the xylem vulnerability curve should be avoided. Although the Δ values of the two are interchangeable in many scenarios (e.g., when there is no height change or external air pressure and osmotic potential in the xylem is zero), one needs to be cautious to avoid ambiguity by
-
using pressure in xylem cavitation,
-
using pressure in water mass flow,
-
using potential in water diffusion across the cell membrane (e.g., water exchange between xylem and living cell).
We note that water transport in plants also includes mass flow within the apoplastic spaces (e.g., in roots and leaves; Aloni et al., 1998) and through plasmodesmata (e.g., between bundle sheath and phloem; Schulz, 2015), liquid water diffusion among living cells, and gaseous vapor phase diffusion among water–air interfaces (e.g., vapor diffusion within the stomatal chamber; Buckley, 2015; Buckley et al., 2017). As recommended, it is more accurate to use potential for diffusion and pressure for mass flow.
A commonly seen mistake is the use of leaf water potential to describe measurements from the pressure chamber method (Scholander et al., 1964; Boyer, 1967), which gives a decent estimate of xylem water pressure. People often refer to the measurement as leaf water potential, as (a) xylem conduit water has very low solute content; (b) the gravity term is often negligible compared to the very negative leaf xylem water pressure; and (c) if the water has reached equilibrium internally prior to the pressure chamber measurement, xylem water potential should equal that in the mesophyll. However, it is always more accurate to treat it as an equivalent pressure or a balance pressure (at the end of xylem). Similar logic applies to xylem water potential and xylem water pressure and so does the thermocouple psychrometer method (Boyer and Knipling, 1965; Boyer, 1968). It is recommended to refer to the measurement as leaf or xylem water pressure or balance pressure in the future, rather than leaf or xylem water potential that is not directly measurable.
Hydraulic conductance (k) and conductivity (K) are also often confused in the literature (e.g., Kannenberg et al., 2019; Cardoso et al., 2020; Li et al., 2021). Hydraulic conductance (flow rate divided by driving pressure) is an extensive property (depends on the extent/size of the system), whereas hydraulic conductivity is an intensive property that is supposed to represent different xylem anatomy. The most widely used definitions for conductance and conductivity are the following: (a) hydraulic conductance (namely k) is the ratio between flow rate through the segment (Q) and driving pressure (ΔP−ρgΔh) (an extensive parameter depending on segment length and cross-section area); (b) hydraulic conductivity (namely K) is the ratio between flow rate and driving pressure gradient (an extensive parameter depending on segment cross-section area); (c) sapwood-area-specific hydraulic conductivity (KS) is the ratio between hydraulic conductivity and xylem sapwood area (AS); and (d) leaf-area-specific hydraulic conductivity (KL) is the ratio between hydraulic conductivity and leaf area the xylem supports (AL):
Note that only KS and KL are per unit conducting area and thus can be treated as “intrinsic” properties for comparison purposes: KS for sapwood water permeability and KL for leaf water supply capability. However, KL may not best describe leaf water supply capability. For example, if two branches have the same KS, leaf area, and sapwood area but differ in their length, the computed K and KL would be the same for the two branches even though the actual leaf water supply capabilities differ. In comparison, conductance of the entire branch divided by leaf area of the branch, i.e., leaf-area-specific hydraulic conductance (kL) as inspired by leaf-area-specific whole-plant hydraulic conductance, would be a better measure for leaf water supply. kL can be estimated using
where kbranch is hydraulic conductance of the entire branch (not a stem segment).
Various formulas have been used to represent xylem VC, and the three most common ones are the Weibull cumulative probability function (Eq. 6) (e.g., Sperry et al., 2016; Love et al., 2019), logistic function (Eq. 7) (e.g., Feng et al., 2018; Huber et al., 2019), and power function (Eq. 8) (e.g., Eller et al., 2018; Liu et al., 2020):
where B, C, a, b, m, and n are vulnerability function parameters and P50 is the water pressure at which the tissue loses 50 % of its conductance. Note that there are also more complex VC formulations based on the three, such as the double Weibull function used in hydraulic fiber bridge (Cai et al., 2014; Pan and Tyree, 2019) and cavitation fatigue (Feng et al., 2015; Zhang et al., 2018).
We should be aware that the logistic VC function (Eq. 7 or a formulation based on it) does not always start from 1 when P=0. This problem is minor for sigmoidal VCs (s-shaped); however, the offset at P=0 could introduce bias if the VC becomes more exponential (r-shaped; see Fig. 5 of Huber et al., 2019, for an example). In this case, fitting VC using Eq. (7) would result in overestimated kmax and less negative P50. Thus, Eq. (7) should be rescaled to minimize the bias, and the modified formulation is
Plant hydraulics models have various complexities depending on the various aims of research and difficulties in model parameterization (Tyree and Ewers, 1991; Tyree and Zimmermann, 2002). In terms of flow profiles, the models can be categorized to steady-state and non-steady-state models. The steady-state models use a constant flow rate within roots, stem, and leaves. The non-steady-state models employ a changing flow rate within or among different tissues given the water exchange between xylem and capacitance tissues. In terms of the model complexity, the models range from a single element to a xylem network (say multiple roots and multiple canopy layers). Further, hydraulic conductance of an element may change with the growth of plants; for example, the drought legacy, maximum hydraulic conductance, and VC vary with the stack of new tree rings (McCulloh and Sperry, 2005; Cai and Tyree, 2010). Although more complex models may better represent the water flow and pressure profiles within the plants, increasing difficulties in model parameterization makes these more complex models less appealing to users. However, inappropriate model selection could result in biased results, for instance, modeling plant hydraulics at a steady state for plants with high water capacity and ignoring a vessel-tapering effect when modeling xylem growth. Thus, it is important to select plant hydraulics models with adequate complexity in topical research. See the section below for a detailed example of how reduced model complexity (ignoring VC segmentation) may bias the modeled hydraulic risk and thus stomatal responses.
Plant-hydraulics-based stomatal models are gaining increasing interest in the vegetation and land modeling communities (e.g., Kennedy et al., 2019; Sabot et al., 2020) as they predict stomatal closure at dry environmental conditions without employing an arbitrary tuning factor (often known as the β factor) (Powell et al., 2013). For instance, the recently developed optimality-theory-based models propose that plants should balance the gain and risk associated with stomatal functioning (Wolf et al., 2016; Sperry et al., 2017). When plants open their stomata more, plants gain more photosynthetic carbon but lose more water and have higher risk in hydraulic failure; therefore, plants are supposed to find a sweet spot to maximize the difference between the gain and risk. These optimality theory models, particularly those weighing the risk based on plant hydraulics, show comparable or better predictive skills compared to the statistical approaches (Anderegg et al., 2018; Eller et al., 2018; Venturas et al., 2018; Wang et al., 2020; Sabot et al., 2022). However, a common mistake when using plant-hydraulics-based models is that one does not follow the original model formula or hypothesis. For example, the Sperry et al. (2017) model defines the risk associated with stomatal functioning (Θ) as
where Amax is the maximal achievable photosynthetic rate at the given setting, Pcanopy is the water pressure at the end of leaf xylem, kcanopy,ref is the maximum kcanopy when the transpiration rate is 0, kcrit is kcanopy when the transpiration rate reaches the maximum transport capacity of the xylem, and E is the transpiration rate. kcrit by definition is 0, as a minimum incremental transpiration rate results in infinity increase in xylem pressure (the in Fig. 2). Thus, in the subsequent research where Sperry et al. (2017) was tested (Venturas et al., 2018; Wang et al., 2020), the model has been reformulated to
Note here that kcanopy is the derivative of a water supply curve at given soil water potential and canopy water pressure, and is different from the (a) relative conductance of root, stem, or leaf xylem (i.e., , where kref is the maximum k at a reference xylem pressure) and (b) relative whole-plant hydraulic conductance (). However, model descriptions from various sources may be contrasting: Sperry et al. (2017) expressed their risk in derivative form; Eller et al. (2018) expressed their risk calculations in three completely different ways including division (their Eq. 2.3), derivative (their Eq. 2.6), and point estimation (their Eq. 2.8); Mencuccini et al. (2019) interpreted the two models based on kplant; and Wang et al. (2020) interpreted the two models based on the derivative forms. See Fig. 2 for how the three quantities differ.
Figure 2Difference between quantities used in plant hydraulics. The simulation is done for a plant with soil water potential of −0.5 MPa, no gravity term, and no drought legacy effect from previous xylem embolism. See Table 1 for the list of symbols.
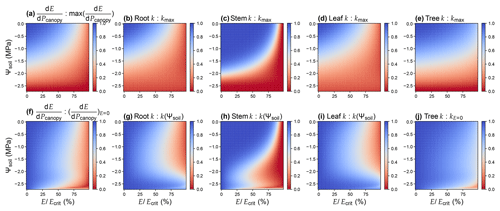
Figure 3Comparison of different risk measures of stomatal opening. (a)–(e) Values are relative to the maximum when soil water potential is 0 and the transpiration rate is 0. (f)–(j) Values are relative to the maximal when the transpiration rate is 0 at the given soil water potential. The simulation is done assuming there is no drought legacy effect from previous xylem embolism. For the simulation, the plant has a root : stem : leaf resistance ratio of 2 : 1 : 1; root and stem height change are 1 and 10 m, respectively; VCs are represented using a Weibull function; Weibull B and C are 1.879 MPa and 2.396 for root, 2.238 MPa and 9.380 for stem, and 1.897 MPa and 2.203 for leaf (data from Wang et al., 2019). See Table 1 for the list of symbols.
For a xylem that does not have height change or VC segmentation, . Otherwise, using k(P) to proxy could result in biases, particularly when gravity is not negligible and when tissue VCs differ dramatically (Sperry et al., 2016; McCulloh et al., 2019). Using the parameters of a real plant as an example (data from Wang et al., 2019), it is obvious that none of the root, stem, leaf, or whole-plant hydraulic conductance is a good proxy (Fig. 3). Therefore, researchers should test the models that differ from the original forms. Note that the primary reason that Sperry et al. (2017) used was to account for the VC segmentation. Using stem VC (easiest to measure; typically more resistant than roots and leaves) to proxy root and leaf VCs in stomatal models would likely result in less sensitive stomatal response to environmental stimuli such as soil moisture (Fig. 3).
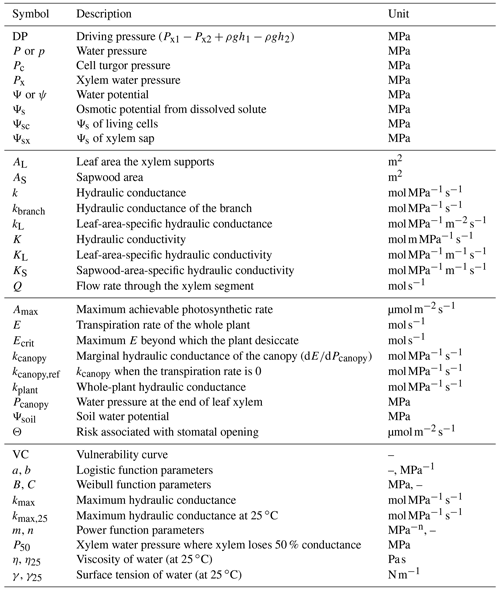
The pursuit of simplicity and analytic solution often leads to biased results, for example, using leaf or stem VC as a proxy for (e.g., Fig. 3) and ignoring the impact of gravity (e.g., Fig. 4). As a result, it is important to distinguish true analytic solution from analytic estimation. For example in a xylem water supply curve, when gravitational pressure drop is neglected, flow rate at a given canopy water pressure will be overestimated (Fig. 4). The greater the height changes are, the more E is overestimated (Fig. 4). The absolute value of E overestimation decreases with more negative soil water potential, whereas the relative E overestimation increases with more negative soil water potential (Fig. 4). Thus, given the potentially great biases, it is recommended to verify any analytic or numerical estimations against a true numerical solution before using them in research.
The ideas of whole-plant conductance and VC largely advance the understanding of how plant traits coordinate, as they provide a simple way to correlate different traits (see McCulloh et al., 2019, for an overview). Whole-plant hydraulic conductance (kplant) depends on not only the upstream water potential (namely Ψsoil) but also the downstream water pressure (Pcanopy): . However, one should be aware of the hidden assumptions when using the term whole-plant hydraulic conductance (or any similar terms): upstream water potential (soil water potential in this scenario) is the same everywhere, and driving pressure is the same everywhere, regardless of plant height, canopy light conditions, and the root–stem–leaf network. Therefore, in the practice of modeling or research, the two assumptions are barely met. Further, note that kplant is an extensive parameter from root to leaves, and xylem water pressure and xylem hydraulic conductance are profiles rather than being constant along the flow path. Therefore, by definition, there is not a whole-plant vulnerability curve; instead, f(Ψsoil,Pcanopy) is a whole-plant vulnerability surface (Fig. 5). It is obvious that neither Ψsoil, Pcanopy, nor a mean pressure can predict a unique kplant (although the change in kplant is relatively smaller for the mean pressure; dotted line in Fig. 5). Further, the drought legacy effect from previous non-refillable xylem embolism (Anderegg et al., 2015) would further complicate the scenario as the “surface” changes with drought legacy. Therefore, it is not recommended to use the term whole-plant vulnerability curve in research.
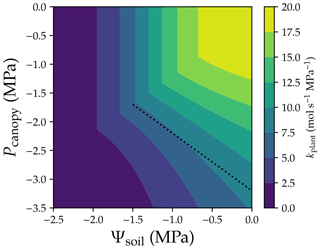
Figure 5Whole-plant vulnerability surface. Whole-plant hydraulic conductance is computed using . The dotted line plots the scenario when mean xylem water pressure is −1.6 MPa. The simulation is done assuming there is no drought legacy effect from previous xylem embolism. See Table 1 for the list of symbols.
When modeling plant hydraulics, the temperature effects on viscosity (η), surface tension (γ), and osmotic potential are typically ignored. However, when water temperature decreases from 25 to 10 ∘C (298.15 to 283.15 K), (1) viscosity of water increases by 43.8 %, meaning a > 40 % increase in pressure drop along the flow path for a given flow rate; (2) surface tension of water increases by 3.1 %, meaning that the capillary force withholding the air–water interface at the pit membrane increases by 3.1 % for a given curvature radius (xylem becomes more resistant to cavitation) and that soil metric potential becomes 3.1 % more negative for a given soil water content; and (3) soil osmotic water potential would be 5.0 % less negative for a given ion concentration. Therefore, a more reasonable way to describe a xylem VC (e.g., using Weibull function) should be
where the subscript 25 denotes the values are at a reference temperature of 25 ∘C. In other words, kmax needs to be scaled to , and P needs to be scaled to .
Plant hydraulics is often improperly represented in research, potentially resulting in ambiguities to those who are not familiar with the terminologies. This paper documents differences among commonly seen ambiguous and miscellaneous terms that are often not recognized and the mistakes and misunderstandings researchers may make when using established methods and models. The mathematics and visualizations of the documented items will help researchers in their research and teaching associated with plant hydraulics.
Simulations of the results in Figs. 2–5 were done using a registered Julia package PlantHydraulics.jl (v0.2.13). Code used for the simulations can be found at CaltechDATA (https://doi.org/10.22002/g862k-ahh79, Wang, 2022).
No data sets were used in this article.
YW conceived the idea. YW and CF prepared the results and wrote the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We gratefully acknowledge the generous support of Eric and Wendy Schmidt (by recommendation of the Schmidt Futures) and the Heising-Simons Foundation. We benefit from the discussion with Tom Buckley on the proper usages of water potential and water pressure.
This research has been supported by the National Aeronautics and Space Administration (Carbon Cycle Science, grant no. 80NSSC21K1712).
This paper was edited by Andreas Ibrom and reviewed by two anonymous referees.
Allen, C. D., Macalady, A. K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., Kitzberger, T., Rigling, A., Breshears, D. D., Hogg, E. T., Gonzalez, P., Fensham, R., Zhang, Z., Castro, J., Demidova, N., Lim, J.-H., Allard, G., Running, S. W., Semerci, A., and Cobb, N.: A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests, Forest Ecol. Manage., 259, 660–684, 2010. a
Aloni, R., Enstone, D. E., and Peterson, C. A.: Indirect evidence for bulk water flow in root cortical cell walls of three dicotyledonous species, Planta, 207, 1–7, 1998. a
Anderegg, W. R. L., Berry, J. A., Smith, D. D., Sperry, J. S., Anderegg, L. D., and Field, C. B.: The roles of hydraulic and carbon stress in a widespread climate-induced forest die-off, P. Natl. Acad. Sci. USA, 109, 233–237, 2012. a
Anderegg, W. R. L., Schwalm, C., Biondi, F., Camarero, J. J., Koch, G., Litvak, M., Ogle, K., Shaw, J. D., Shevliakova, E., Williams, A., Wolf, A., Ziaco, E., and Pacala, S.: Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models, Science, 349, 528–532, 2015. a
Anderegg, W. R. L., Klein, T., Bartlett, M., Sack, L., Pellegrini, A. F. A., Choat, B., and Jansen, S.: Meta-analysis reveals that hydraulic traits explain cross-species patterns of drought-induced tree mortality across the globe, P. Natl. Acad. Sci. USA, 113, 5024–5029, 2016. a
Anderegg, W. R. L., Wolf, A., Arango-Velez, A., Choat, B., Chmura, D. J., Jansen, S., Kolb, T., Li, S., Meinzer, F. C., Pita, P., Resco de Dios, V., Sperry, J. S., Wolfe, B. T., and Pacala, S.: Woody plants optimise stomatal behaviour relative to hydraulic risk, Ecol. Lett., 21, 968–977, 2018. a, b, c
Boyer, J. S.: Leaf water potentials measured with a pressure chamber, Plant Physiol., 42, 133–137, 1967. a
Boyer, J. S.: Relationship of water potential to growth of leaves, Plant Physiol., 43, 1056–1062, 1968. a
Boyer, J. S. and Knipling, E. B.: Isopiestic technique for measuring leaf water potentials with a thermocouple psychrometer, P. Natl. Acad. Sci. USA, 54, 1044–1051, 1965. a
Buckley, T. N.: The contributions of apoplastic, symplastic and gas phase pathways for water transport outside the bundle sheath in leaves, Plant Cell Environ., 38, 7–22, 2015. a
Buckley, T. N. and Mott, K. A.: Modelling stomatal conductance in response to environmental factors, Plant Cell Environ., 36, 1691–1699, 2013. a
Buckley, T. N., John, G. P., Scoffoni, C., and Sack, L.: The sites of evaporation within leaves, Plant Physiol., 173, 1763–1782, 2017. a
Cai, J. and Tyree, M. T.: The impact of vessel size on vulnerability curves: Data and models for within-species variability in saplings of aspen, Populus tremuloides Michx., Plant Cell Environ., 33, 1059–1069, 2010. a
Cai, J., Li, S., Zhang, H., Zhang, S., and Tyree, M. T.: Recalcitrant vulnerability curves: Methods of analysis and the concept of fibre bridges for enhanced cavitation resistance, Plant Cell Environ., 37, 35–44, 2014. a
Cardoso, A. A., Visel, D., Kane, C. N., Batz, T. A., García Sánchez, C., Kaack, L., Lamarque, L. J., Wagner, Y., King, A., Torres-Ruiz, J. M., Corso, D., Burlett, R., Badel, E., Cochard, H., Delzon, S., Jansen, S., and McAdam, S. A. M.: Drought-induced lacuna formation in the stem causes hydraulic conductance to decline before xylem embolism in Selaginella, New Phytol., 227, 1804–1817, 2020. a
Chen, C., Riley, W. J., Prentice, I. C., and Keenan, T. F.: CO2 fertilization of terrestrial photosynthesis inferred from site to global scales, P. Natl. Acad. Sci. USA, 119, e2115627119, https://doi.org/10.1073/pnas.2115627119, 2022. a
Cowan, I. R. and Farquhar, G. D.: Stomatal function in relation to leaf metabolism and environment, Sym. Soc. Exp. Biol., 31, 471–505, 1977. a
Dewar, R., Mauranen, A., Mäkelä, A., Hölttä, T., Medlyn, B., and Vesala, T.: New insights into the covariation of stomatal, mesophyll and hydraulic conductances from optimization models incorporating nonstomatal limitations to photosynthesis, New Phytol., 217, 571–585, 2018. a
Eller, C. B., Rowland, L., Oliveira, R. S., Bittencourt, P. R. L., Barros, F. V., da Costa, A. C. L., Meir, P., Friend, A. D., Mencuccini, M., Sitch, S., and Cox, P.: Modelling tropical forest responses to drought and El Niño with a stomatal optimization model based on xylem hydraulics, Philos. T. Roy. Soc. B, 373, 20170315, https://doi.org/10.1098/rstb.2017.0315, 2018. a, b, c, d
Eller, C. B., Rowland, L., Mencuccini, M., Rosas, T., Williams, K., Harper, A., Medlyn, B. E., Wagner, Y., Klein, T., Teodoro, G. S., Oliverira, R. S., Matos, I. S., Rosado, B. H. P., Fuchs, K., Wohlfahrt, G., Montagnani, L., Meir, P., Sitch, S., and Cox, P. M.: Stomatal optimization based on xylem hydraulics (SOX) improves land surface model simulation of vegetation responses to climate, New Phytol., 226, 1622–1637, 2020. a
Feng, F., Ding, F., and Tyree, M. T.: Investigations concerning cavitation and frost fatigue in clonal 84K poplar using high-resolution cavitron measurements, Plant Physiol., 168, 144–155, 2015. a
Feng, X., Ackerly, D. D., Dawson, T. E., Manzoni, S., Skelton, R. P., Vico, G., and Thompson, S. E.: The ecohydrological context of drought and classification of plant responses, Ecol. Lett., 21, 1723–1736, 2018. a
Gleason, S. M., Westoby, M., Jansen, S., Choat, B., Hacke, U. G., Pratt, R. B., Bhaskar, R., Brodribb, T. J., Bucci, S. J., Cao, K.-F., Cochard, H., Delzon, S., Domec, J.-C., Fan, Z.-X., Field, T. S., Jacobsen, A. L., Johnson, D. M., Lens, F., Maherali, H., Martinez-Vilalta, J., Mayr, S., McCulloh, K. A., Mencuccini, M., Mitchell, O. J., Morris, H., Nardini, A., Pittermann, J., Plavcova, L., Schreiber, S., Sperry, J. S., Wright, I. J., and Zanne, A. E.: Weak tradeoff between xylem safety and xylem-specific hydraulic efficiency across the world's woody plant species, New Phytol., 209, 123–136, 2016. a
Huber, A. E., Melcher, P. J., Piñeros, M. A., Setter, T. L., and Bauerle, T. L.: Signal coordination before, during and after stomatal closure in response to drought stress, New Phytol., 224, 675–688, 2019. a, b
Kannenberg, S. A., Novick, K. A., and Phillips, R. P.: Anisohydric behavior linked to persistent hydraulic damage and delayed drought recovery across seven North American tree species, New Phytol., 222, 1862–1872, 2019. a
Kennedy, D., Swenson, S., Oleson, K. W., Lawrence, D. M., Fisher, R., Lola da Costa, A. C., and Gentine, P.: Implementing plant hydraulics in the community land model, version 5, J. Adv. Model. Earth Syst., 11, 485–513, 2019. a, b
Li, S., Fang, L., Hegelund, J. N., and Liu, F.: Elevated CO2 modulates plant hydraulic conductance through regulation of PIPs under progressive soil drying in tomato plants, Front. Plant Sci., 12, 666066, https://doi.org/10.3389/fpls.2021.666066, 2021. a
Liu, H., Ye, Q., Gleason, S. M., He, P., and Yin, D.: Weak tradeoff between xylem hydraulic efficiency and safety: climatic seasonality matters, New Phytol., 229, 1440–1452, 2021. a
Liu, Y., Kumar, M., Katul, G. G., Feng, X., and Konings, A. G.: Plant hydraulics accentuates the effect of atmospheric moisture stress on transpiration, Nat. Clim. Change, 10, 691–695, 2020. a, b
Love, D. M., Venturas, M. D., Sperry, J. S., Brooks, P. D., Pettit, J. L., Wang, Y., Anderegg, W. R. L., Tai, X., and Mackay, D. S.: Dependence of aspen stands on a subsurface water subsidy: Implications for climate change impacts, Water Resour. Res., 55, 1833–1848, 2019. a
Manzoni, S., Vico, G., Palmroth, S., Porporato, A., and Katul, G.: Optimization of stomatal conductance for maximum carbon gain under dynamic soil moisture, Adv. Water Resour., 62, 90–105, 2013. a
McCulloh, K. A. and Sperry, J. S.: Patterns in hydraulic architecture and their implications for transport efficiency, Tree Physiol., 25, 257–267, 2005. a
McCulloh, K. A., Domec, J.-C., Johnson, D. M., Smith, D. D., and Meinzer, F. C.: A dynamic yet vulnerable pipeline: Integration and coordination of hydraulic traits across whole plants, Plant Cell Environ., 42, 2789–2807, 2019. a, b
McDowell, N., Pockman, W. T., Allen, C. D., Breshears, D. D., Cobb, N., Kolb, T., Plaut, J., Sperry, J., West, A., Williams, D. G., and Yepez, E. A.: Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought?, New Phytol., 178, 719–739, 2008. a
McDowell, N. G.: Mechanisms linking drought, hydraulics, carbon metabolism, and vegetation mortality, Plant Physiol., 155, 1051–1059, 2011. a
McDowell, N. G., Fisher, R. A., Xu, C., Domec, J.-C., Hölttä, T., Mackay, D. S., Sperry, J. S., Boutz, A., Dickman, L., Gehres, N., Limousin, J. M., Macalady, A., Martinez-Vilalta, J., Mencuccini, M., Plaut, H. A., Ogee, J., Panglem, R. E., Rasse, D. P., Ryan, M. G., Sevanto, S., Waring, R. H., Williams, A. P., Yepez, E. A., and Pockman, W. T.: Evaluating theories of drought-induced vegetation mortality using a multimodel–experiment framework, New Phytol., 200, 304–321, 2013. a
Meinzer, F. C., McCulloh, K. A., Lachenbruch, B., Woodruff, D. R., and Johnson, D. M.: The blind men and the elephant: the impact of context and scale in evaluating conflicts between plant hydraulic safety and efficiency, Oecologia, 164, 287–296, 2010. a
Mencuccini, M., Manzoni, S., and Christoffersen, B.: Modelling water fluxes in plants: From tissues to biosphere, New Phytol., 222, 1207–1222, 2019. a
Pan, R. and Tyree, M. T.: How does water flow from vessel to vessel? Further investigation of the tracheid bridge concept, Tree Physiol., 39, 1019–1031, 2019. a
Powell, T. L., Galbraith, D. R., Christoffersen, B. O., Harper, A., Imbuzeiro, H., Rowland, L., Almeida, S., Brando, P. M., Costa, A. C. L., Costa, M. H., and Moorcroft, P. R.: Confronting model predictions of carbon fluxes with measurements of Amazon forests subjected to experimental drought, New Phytol., 200, 350–365, 2013. a
Sabot, M. E., De Kauwe, M. G., Pitman, A. J., Medlyn, B. E., Verhoef, A., Ukkola, A. M., and Abramowitz, G.: Plant profit maximization improves predictions of European forest responses to drought, New Phytol., 226, 1638–1655, 2020. a
Sabot, M. E., De Kauwe, M. G., Pitman, A. J., Medlyn, B. E., Ellsworth, D. S., Martin-StPaul, N., Wu, J., Choat, B., Limousin, J.-M., Mitchell, P. J., Rogers, A., and Serbin, S. P.: One Stomatal Model to Rule Them All? Towards Improved Representation of Carbon and Water Exchange in Global Models, J. Adv. Model. Earth Syst., 14, e2021MS002761, https://doi.org/10.1029/2021MS002761, 2022. a, b, c
Santiago, L. S., Goldstein, G., Meinzer, F. C., Fisher, J. B., Machado, K., Woodruff, D., and Jones, T.: Leaf photosynthetic traits scale with hydraulic conductivity and wood density in Panamanian forest canopy trees, Oecologia, 140, 543–550, 2004. a
Scholander, P. F., Hammel, H., Hemmingsen, E., and Bradstreet, E.: Hydrostatic pressure and osmotic potential in leaves of mangroves and some other plants, P. Natl. Acad. Sci. USA, 52, 119–125, 1964. a
Schulz, A.: Diffusion or bulk flow: how plasmodesmata facilitate pre-phloem transport of assimilates, J. Plant Res., 128, 49–61, 2015. a
Sperry, J. S. and Love, D. M.: What plant hydraulics can tell us about responses to climate-change droughts, New Phytol., 207, 14–27, 2015. a
Sperry, J. S. and Tyree, M. T.: Mechanism of water stress-induced xylem embolism, Plant Physiol., 88, 581–587, 1988. a
Sperry, J. S., Adler, F. R., Campbell, G. S., and Comstock, J. P.: Limitation of plant water use by rhizosphere and xylem conductance: Results from a model, Plant Cell Environ., 21, 347–359, 1998. a
Sperry, J. S., Wang, Y., Wolfe, B. T., Mackay, D. S., Anderegg, W. R. L., McDowell, N. G., and Pockman, W. T.: Pragmatic hydraulic theory predicts stomatal responses to climatic water deficits, New Phytol., 212, 577–589, 2016. a, b, c
Sperry, J. S., Venturas, M. D., Anderegg, W. R. L., Mencuccini, M., Mackay, D. S., Wang, Y., and Love, D. M.: Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost, Plant Cell Environ., 40, 816–830, 2017. a, b, c, d, e, f, g
Tyree, M. T. and Ewers, F. W.: The hydraulic architecture of trees and other woody plants, New Phytol., 119, 345–360, 1991. a, b
Tyree, M. T. and Sperry, J. S.: Vulnerability of xylem to cavitation and embolism, Annu. Rev. Plant Biol., 40, 19–36, 1989. a
Tyree, M. T. and Zimmermann, M. H.: Xylem structure and the ascent of sap, 2nd edn., Springer Berlin, Heidelberg, https://doi.org/10.1007/978-3-662-04931-0, 2002. a
Venturas, M. D., Sperry, J. S., Love, D. M., Frehner, E. H., Allred, M. G., Wang, Y., and Anderegg, W. R. L.: A stomatal control model based on optimization of carbon gain versus hydraulic risk predicts aspen sapling responses to drought, New Phytol., 220, 836–850, 2018. a, b, c
Wang, Y.: Code for research papers (Version 1), CaltechDATA [data set], https://doi.org/10.22002/g862k-ahh79, 2022. a
Wang, Y., Sperry, J. S., Venturas, M. D., Trugman, A. T., Love, D. M., and Anderegg, W. R. L.: The stomatal response to rising CO2 concentration and drought is predicted by a hydraulic trait-based optimization model, Tree Physiol., 39, 1416–1427, 2019. a, b
Wang, Y., Sperry, J. S., Anderegg, W. R. L., Venturas, M. D., and Trugman, A. T.: A theoretical and empirical assessment of stomatal optimization modeling, New Phytol., 227, 311–325, 2020. a, b, c, d, e, f, g
Wang, Y., Anderegg, W. R., Venturas, M. D., Trugman, A. T., Yu, K., and Frankenberg, C.: Optimization theory explains nighttime stomatal responses, New Phytol., 230, 1550–1561, 2021a. a, b
Wang, Y., Köhler, P., He, L., Doughty, R., Braghiere, R. K., Wood, J. D., and Frankenberg, C.: Testing stomatal models at the stand level in deciduous angiosperm and evergreen gymnosperm forests using CliMA Land (v0.1), Geosci. Model Dev., 14, 6741–6763, https://doi.org/10.5194/gmd-14-6741-2021, 2021b. a
Wolf, A., Anderegg, W. R. L., and Pacala, S. W.: Optimal stomatal behavior with competition for water and risk of hydraulic impairment, P. Natl. Acad. Sci. USA, 113, E7222–E7230, 2016. a, b
Zhang, W., Feng, F., and Tyree, M. T.: Seasonality of cavitation and frost fatigue in Acer mono Maxim., Plant Cell Environ., 41, 1278–1286, 2018. a
- Abstract
- Introduction
- Water potential and pressure
- Hydraulic conductance and conductivity
- Xylem vulnerability curve (VC)
- Hydraulic-model complexity
- Stomatal-model representation
- Analytic solution and estimation
- Whole-plant vulnerability “curve”
- Temperature effects
- Conclusions
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Water potential and pressure
- Hydraulic conductance and conductivity
- Xylem vulnerability curve (VC)
- Hydraulic-model complexity
- Stomatal-model representation
- Analytic solution and estimation
- Whole-plant vulnerability “curve”
- Temperature effects
- Conclusions
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References