Isotopomer labeling and oxygen dependence of hybrid nitrous oxide production

Nitrous oxide (N₂O) is a potent greenhouse gas and ozone depletion agent, with a significant natural source from marine oxygen-deficient zones (ODZs). Open questions remain, however, about the microbial processes responsible for this N₂O production, especially hybrid N₂O production when ammonia-oxidizing archaea are present. Using ¹⁵N-labeled tracer incubations, we measured the rates of N₂O production from ammonium (NH${}_{\mathrm{4}}^{+}$), nitrite (NO${}_{\mathrm{2}}^{-}$), and nitrate (NO${}_{\mathrm{3}}^{-}$) in the eastern tropical North Pacific ODZ and the isotopic labeling of the central (α) and terminal (β) nitrogen (N) atoms of the N₂O molecule. We observed production of both doubly and singly labeled N₂O from each tracer, with the highest rates of labeled N₂O production at the same depths as the near-surface N₂O concentration maximum. At most stations and depths, the production of ⁴⁵N₂O^α and ⁴⁵N₂O^β were statistically indistinguishable, but at a few depths there were significant differences in the labeling of the two nitrogen atoms in the N₂O molecule. Implementing the rates of labeled N₂O production in a time-dependent numerical model, we found that N₂O production from NO${}_{\mathrm{3}}^{-}$ dominated at most stations and depths, with rates as high as 1600 ± 200 pM N₂O d⁻¹. Hybrid N₂O production, one of the mechanisms by which ammonia-oxidizing archaea produce N₂O, had rates as high as 230 ± 80 pM N₂O d⁻¹ that peaked in both the near-surface and deep N₂O concentration maxima. Based on the equal production of ⁴⁵N₂O^α and ⁴⁵N₂O^β in the majority of our experiments, we infer that hybrid N₂O production likely has a consistent site preference, despite drawing from two distinct substrate pools. We also found that the rates and yields of hybrid N₂O production were enhanced at low dissolved oxygen concentrations ([O₂]), with hybrid N₂O yields as high as 20 % at depths where [O₂] was below detection (880 nM) but nitrification was still active. Finally, we identified a few incubations with [O₂] up to 20 µM where N₂O production from NO${}_{\mathrm{3}}^{-}$ was still active. A relatively high O₂ tolerance for N₂O production via denitrification has implications for the feedbacks between marine deoxygenation and greenhouse gas cycling.

1 Introduction

Nitrous oxide (N₂O) is one of the lesser-known greenhouse gases, yet its potential to warm the environment on a per-molecule basis is immense. N₂O has a global warming potential 273 times that of carbon dioxide (Smith et al., 2021), and its atmospheric mixing ratio is increasing at a rate of 0.85 ± 0.03 ppb yr⁻¹ (Tian et al., 2020). In the ocean, hotspots of N₂O production and flux to the atmosphere occur in marine oxygen-deficient zones (ODZs), where steep redox gradients allow multiple N₂O production processes to overlap (Codispoti and Christensen, 1985). ODZs have expanded over the last 60 years (Breitburg et al., 2018; Stramma et al., 2008) and will likely continue to do so as the oceans warm (Oschlies et al., 2018), although the fate of the anoxic cores of ODZs ([O₂] ≤ 20 µmol kg⁻¹) remains uncertain (Bianchi et al., 2018; Busecke et al., 2022; Cabré et al., 2015). Without a clear picture of N₂O cycling in these regions, it is impossible to predict how climate change will impact the marine emissions of this powerful greenhouse gas.

Much of the N₂O cycling in ODZs is linked to denitrification. In low-oxygen waters, denitrifying organisms produce N₂O as an intermediate during organic matter remineralization (Dalsgaard et al., 2014; Naqvi et al., 2000; Zumft, 1997). Both direct rate measurements (Frey et al., 2020; Ji et al., 2015, 2018) and natural abundance isotope measurements (Casciotti et al., 2018; Kelly et al., 2021; Monreal et al., 2022; Toyoda et al., 2023) indicate that N₂O production directly from nitrate (NO${}_{\mathrm{3}}^{-}$), i.e., without exchange with extracellular nitrite (NO${}_{\mathrm{2}}^{-}$) or nitric oxide (NO) pools, is the primary source of N₂O in ODZs. N₂O production from extracellular NO${}_{\mathrm{2}}^{-}$, meanwhile, tends to occur at lower rates (Frey et al., 2020; Ji et al., 2015, 2018). Historically, N₂O production from denitrification was thought to cease at dissolved oxygen concentrations above 2–3 µM (Dalsgaard et al., 2014), but more recent data suggest that N₂O production from NO${}_{\mathrm{3}}^{-}$ can occur at ambient oxygen levels as high as 30 µM (Frey et al., 2020; Ji et al., 2018). N₂O consumption via denitrification is more sensitive to oxygen than N₂O production via denitrification, leading to an oxygen window in which denitrification is a source but not a sink of N₂O (Babbin et al., 2015; Dalsgaard et al., 2014; Farías et al., 2009; Frey et al., 2020), although the oxygen inhibition constant for N₂O consumption remains difficult to define (Sun et al., 2021a). N₂O may also be consumed through N₂O fixation, although the importance of N₂O fixation in the ocean has yet to be determined (Farías et al., 2013; Si et al., 2023).

Nonetheless, a significant fraction of the N₂O in the oxyclines above and below ODZs may be derived from archaeal nitrification. When NO${}_{\mathrm{2}}^{-}$ is present, isotopic evidence continues to suggest that ammonia-oxidizing archaea can produce N₂O via a hybrid mechanism that combines nitrogen (N) derived from NO${}_{\mathrm{2}}^{-}$ and ammonium (NH${}_{\mathrm{4}}^{+}$) to form the N₂O molecule (Frame et al., 2017; Frey et al., 2020, 2023; Stieglmeier et al., 2014; Trimmer et al., 2016). New evidence indicates that ammonia-oxidizing archaea can produce N₂O both as a by-product of hydroxylamine oxidation and via hybrid N₂O production and that the ratio of these processes depends on the ratio of NH${}_{\mathrm{4}}^{+}$ to NO${}_{\mathrm{2}}^{-}$ available to the archaea (Wan et al., 2023b). The exact mechanism and enzymology of archaeal N₂O production remains unknown (Carini et al., 2018; Stein, 2019) but may involve a reaction between hydroxylamine and NO, which occur as intermediates during archaeal ammonia oxidation (Kozlowski et al., 2016; Lancaster et al., 2018; Martens-Habbena et al., 2015; Vajrala et al., 2013). In anaerobic conditions, ammonia-oxidizing archaea are also capable of NO dismutation to O₂ and N₂, which may involve N₂O as an intermediate (Kraft et al., 2022). Ammonia-oxidizing bacteria, more common in regions that are nutrient-replete, produce N₂O as a byproduct of hydroxylamine oxidation (Cohen and Gordon, 1979) and via nitrifier denitrification as oxygen concentrations decline (Goreau et al., 1980; Stein and Yung, 2003; Wrage et al., 2001) and nitrite concentrations rise (Frame and Casciotti, 2010).

The stable natural abundance nitrogen and oxygen isotopes of N₂O can provide quantification of – and distinction among – potential N₂O cycling mechanisms (Kim and Craig, 1990; Rahn and Wahlen, 2000; Toyoda and Yoshida, 1999). For example, natural abundance N₂O isotopocule studies have indicated that the high near-surface N₂O accumulations in the eastern tropical North Pacific (ETNP) ODZ are 80 % derived from denitrification and 20 % derived from nitrification (Kelly et al., 2021). The isotopic content of the individual N and oxygen (O) atoms in the N₂O molecule are expressed in delta notation, defined as δ(¹⁵N) or δ(¹⁸O) = ($R_{\mathrm{sample}}/R_{\mathrm{standard}}-\mathrm{1}$), where R_standard for δ(¹⁵N) and R_standard for δ(¹⁸O) are the ratios ¹⁵N $/$ ¹⁴N of air and ¹⁸O $/$ ¹⁶O of Vienna Standard Mean Ocean Water (VSMOW), respectively (Kim and Craig, 1990; Rahn and Wahlen, 2000; Toyoda and Yoshida, 1999). In addition to the bulk N and O isotope ratios in N₂O, we can measure the isotopic content of the inner (α) N atom and the outer (β) N atom in N₂O (Brenninkmeijer and Röckmann, 1999; Toyoda and Yoshida, 1999). The difference in the ¹⁵N content of these two atoms is often referred to as the “site preference” and is defined as $\mathit{\delta }{(}^{\mathrm{15}}{\mathrm{N}}^{\mathrm{sp}})=\mathit{\delta }{(}^{\mathrm{15}}{\mathrm{N}}^{\mathit{\alpha }})-\mathit{\delta }{(}^{\mathrm{15}}{\mathrm{N}}^{\mathit{\beta }})$. In natural abundance studies, δ(¹⁵N^sp) is particularly useful because it exhibits distinct values for different N₂O production processes, which are independent of the isotopic value of the substrate (Frame and Casciotti, 2010; Sutka et al., 2003, 2004, 2006; Toyoda et al., 2002, 2005). This allows partitioning between different N₂O sources and has been used extensively to quantify N₂O cycling in the ocean (Bourbonnais et al., 2017, 2023; Casciotti et al., 2018; Farías et al., 2009; Kelly et al., 2021; Monreal et al., 2022; Popp et al., 2002; Toyoda et al., 2002, 2005, 2019, 2021, 2023; Westley et al., 2006; Yamagishi et al., 2007). As we elaborate upon in the discussion, however, the premise that δ(¹⁵N^sp) exhibits a unique and consistent value depends on the assumption that both N atoms in N₂O are derived from a singular substrate pool. Thus, hybrid N₂O production may complicate traditional interpretations of natural abundance N₂O isotopocules.

Previous studies have used ¹⁵N tracer experiments to measure N₂O production rates in ODZs (Frey et al., 2020, 2023; Ji et al., 2015, 2018). These studies used the accumulation of ⁴⁵N₂O and ⁴⁶N₂O resulting from the addition of ¹⁵N-labeled substrates such as ¹⁵N–NH${}_{\mathrm{4}}^{+}$ and ¹⁵N–NO${}_{\mathrm{2}}^{-}$ to measure N₂O production rates. To our knowledge, the isotopomer measurement has never been applied to ¹⁵N tracer experiments to track ¹⁵N from different substrates into the α and β positions of the N₂O molecule. Here, we present data showing the production of N₂O isotopomers with ¹⁵N in the α position (⁴⁵N₂O^α) and ¹⁵N in the β position (⁴⁵N₂O^β) from ¹⁵N-labeled NH${}_{\mathrm{4}}^{+}$, NO${}_{\mathrm{2}}^{-}$, and NO${}_{\mathrm{3}}^{-}$. Measuring the production of ⁴⁵N₂O^α and ⁴⁵N₂O^β creates an additional constraint on N₂O production mechanisms and thus allows us to quantify different source processes more precisely and accurately. We employed these measurements to (a) validate previous ¹⁵N tracer studies of N₂O production rates in the ETNP; (b) uncover that the hybrid pathway dominates production by nitrification; (c) establish the insignificance of production solely from NH${}_{\mathrm{4}}^{+}$ except the surface; and (d) infer a constant δ(¹⁵N^sp) for hybrid N₂O, despite drawing from two substrate pools. We also use these results to confirm inferences from natural abundance N₂O isotopocules measured in the same system (Kelly et al., 2021).

2 Methods

2.1 Sampling sites

Experiments were performed at three stations in the eastern tropical North Pacific on the R/V Sally Ride in March–April 2018 (Fig. 1). Station PS1 (10° N, 113° W) was on the edge of the oxygen-deficient region, station PS2 (16° N, 105° W) was near the geographic center of the ODZ, and station PS3 (18° N, 102° W) was 19 km from the coast of Mexico (Fig. 1). Samples were collected from 30 L Niskin bottles mounted on a 12-place rosette with a conductivity–temperature–depth profiler and sensors for chlorophyll a fluorescence and dissolved O₂ (Sea-Bird SBE 43 oxygen sensor). The cruise took place during a weak La Niña event (Ocean Niño Index = −0.6 °C; NOAA/National Weather Service, 2020).

Ambient [NO${}_{\mathrm{2}}^{-}$] and [NH${}_{\mathrm{4}}^{+}$] were measured shipboard with standard colorimetric (Grasshoff et al., 1999) and fluorometric methods (Grasshoff et al., 1999; Holmes et al., 1999), respectively. Ambient [NO${}_{\mathrm{3}}^{-}$] was measured at Stanford University using a Westco SmartChem 200 Discrete Analyzer (detection limit 83 nM, precision 0.6 µM). Ambient [N₂O] was measured via an isotope ratio mass spectrometer (IRMS) at the Stanford Stable Isotope Biogeochemistry Laboratory as part of a prior study (Kelly et al., 2021).

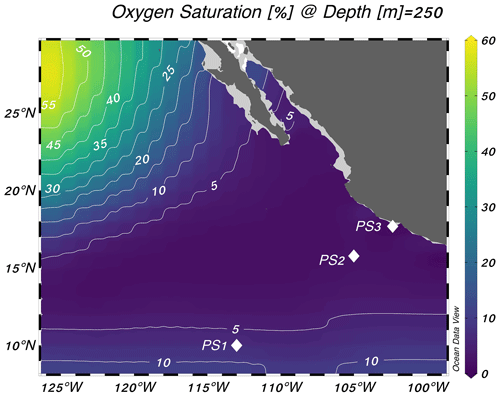
Figure 1 Locations of the three stations sampled for this study. Stations are plotted on top of World Ocean Atlas oxygen saturation ( %) at 250 m depth (World Ocean Atlas, 2013). Schlitzer, Reiner, Ocean Data View, https://odv.awi.de, last access: 25 October 2023.

2.2 Sample collection

Incubation depths were chosen to target prominent hydrographic features: the primary NO${}_{\mathrm{2}}^{-}$ maximum, shallow and deep oxyclines, oxic–anoxic interfaces above and below the ODZ, secondary chlorophyll a maximum, and secondary NO${}_{\mathrm{2}}^{-}$ maximum (Table S1). Incubation samples were filled directly from Niskin bottles into 160 mL glass serum bottles (WHEATON) using Tygon tubing. Incubation bottles were overflowed three times before being capped and sealed bubble-free, with no headspace, using gray butyl rubber septa (National Scientific) and aluminum crimp seals. To minimize oxygen contamination during sampling, incubation bottles were overflowed in a secondary container filled with suboxic water from the same depth, and Niskin bottles were vented with carbon dioxide gas to displace the withdrawn water. The butyl rubber stoppers were deoxygenated in a He-flushed anaerobic chamber for ∼ 1 week prior to sampling.

After sample collection, a 2 mL He headspace was created in each bottle by displacing the 2 mL sample from the bottle with He. At most (all but two) anoxic depths at stations PS2 and PS3, samples were sparged with He gas for 90 min at a flow rate of at least 100 mL min⁻¹, equivalent to 56 volume exchanges, to remove potential oxygen contamination introduced during sampling. Depths with low but non-zero ambient dissolved oxygen were not purged with He gas. After sparging, 100 µL of 1030 ppm N₂O in He (4 nmol N₂O) in gaseous form was introduced back into each bottle for a final concentration of 26 nM to provide a constant background of N₂O for later isotopic analysis (Fig. S4a). The isotopic content of this N₂O carrier, measured independently via IRMS (Kelly et al., 2023; McIlvin and Casciotti, 2010), was δ(¹⁵N^α) $=-\mathrm{1.5}$ ± 0.2 ‰, δ(¹⁵N^β) = 0.2 ± 0.4 ‰, δ(¹⁵N^bulk) = −0.65 ± 0.08 ‰, and δ(¹⁸O) = 37.4 ± 0.3 ‰.

Time series were constructed by sacrificing triplicate bottles over a time course, rather than by resampling the incubation bottles over time. A total of 27 incubation samples were thus produced at each experimental depth, comprised of triplicate samples for each of the three time points and three tracers. For each station and depth, nine samples were amended with ¹⁵NH₄Cl (98.8 atm % ¹⁵N; Sigma-Aldrich) to a final concentration of 0.501 µM and with Na¹⁴NO₂ to a final concentration 1.01 µM. Nine samples were amended with Na¹⁵NO₂ (98.8 atm % ¹⁵N; Sigma-Aldrich) to a final concentration of 5.00 µM and with ¹⁴NH₄Cl to a final concentration of 0.510 µM. Finally, nine samples were amended with K¹⁵NO₃ (98.8 atm % ¹⁵N; Sigma-Aldrich) to a final concentration of 1.00 µM, plus 1.01 µM Na¹⁴NO₂ and 0.510 µM ¹⁴NH₄Cl. Note that the Na¹⁵NO₂ tracer was added at a higher concentration than the other tracers or the Na¹⁴NO₂ carrier; this discrepancy was due to a miscalculation that was caught midway through the cruise, but the high tracer addition was retained for the sake of consistency. The NO${}_{\mathrm{2}}^{-}$ and NH${}_{\mathrm{4}}^{+}$ tracer and carrier additions were confirmed via [NO${}_{\mathrm{2}}^{-}$] and [NH${}_{\mathrm{4}}^{+}$] measurements of sample aliquoted from each bottle immediately before samples were measured for N₂O isotopic content, using colorimetric and fluorometric techniques (Grasshoff et al., 1999; Holmes et al., 1999). The Na¹⁴NO₂ and ¹⁴NH₄Cl amendments served two purposes: (1) to provide enough total NO${}_{\mathrm{2}}^{-}$ for isotopic analysis of ¹⁵NO${}_{\mathrm{2}}^{-}$ produced from ¹⁵NH${}_{\mathrm{4}}^{+}$ and (2) to minimize isotope dilution of the substrate pool, which can cause underestimation of rates with low substrate additions. The final atm % ¹⁵N of the substrate pools was thus 56 %–100 % for ¹⁵N–NH${}_{\mathrm{4}}^{+}$, 65 %–100 % for ¹⁵N–NO${}_{\mathrm{2}}^{-}$, and 2 %–92 % for ¹⁵N–NO${}_{\mathrm{3}}^{-}$ experiments. Three samples for each tracer were terminated immediately after tracer addition with the addition of 100 µL saturated mercuric chloride (HgCl₂) solution. These also served as abiotic controls. The remaining samples were incubated at 12 °C in the dark; three samples per tracer were terminated at 12 h and at 24 h with 100 µL saturated HgCl₂. All samples were incubated at 12 °C, which was chosen as an intermediate temperature that approximated subsurface conditions. After termination, samples were stored at room temperature (∼ 20 °C) in the dark until isotope analysis.

2.3 Chemiluminescent optode oxygen measurements

Eight 160 mL glass serum bottles were prepared with a chemiluminescent oxygen optode spot (PyroScience) affixed to the inner glass wall with silicone glue. These bottles were incubated alongside experimental bottles to monitor dissolved [O₂] during incubations. At stations PS2 and PS3, two optode bottles per depth were filled, purged, amended with the N₂O carrier, and incubated without the addition of tracer or HgCl₂. At each time point, [O₂] was measured in each sensor bottle for at least 10 min using fiber-optic cables paired to the oxygen optode spot mounted inside the bottle (PyroScience). The fiber-optic cables were calibrated with a two-point measurement of (1) a sodium sulfite solution (30 g L⁻¹ in DI, or 0.24 M) and (2) surface seawater saturated with air at 12 °C (270 µM [O₂], based on a salinity of 35 psu and a temperature of 12 °C) (Garcia and Gordon, 1992). The two calibration bottles, each containing its own optode spot, were used to calibrate all four of the fiber-optic cables, effectively correcting them to the same scale. Differences in detection limit between sensor spots were accounted for by first performing this two-point calibration procedure to correct for differences between fiber-optic cables and then by measuring the minimum oxygen concentration measured by each sensor spot in purged seawater (purged at 100 mL min⁻¹. for 90 min, equal to 56 volume exchanges). Those detection limits were specific to each optode spot and varied from 146–880 nM [O₂].

The optode [O₂] measurements were adjusted for the detection limit specific to each sensor spot; optode [O₂] for each experiment was calculated as the mean measured [O₂] at each of the three time points. No optode measurements were made at station PS1, since this station lacked a secondary NO${}_{\mathrm{2}}^{-}$ maximum; thus incubations performed at low-oxygen depths were not expected to occur under functional anoxia. Optical oxygen sensors are susceptible to interference from NO, which could result in an overestimate of [O₂] in experiments with especially high rates of NO production (Kraft et al., 2022). Given maximum ammonia oxidation rates of 4.68 ± 0.07 nM N d⁻¹, the release of equivalent amounts of NO would result in an [O₂] overestimate of 0.745 nM during a 24 h incubation, based on the interference curve calculated by Kraft et al. (2022) ([O₂] overestimate = 0.159 × [NO]). Because of this small potential error and the lack of relevant NO measurements, no correction was applied for NO interference.

Optode [O₂] generally agreed with ambient [O₂] measured by the Sea-Bird oxygen sensor attached to the rosette (Fig. S1). Two important exceptions were in the experiments at the base of the ODZ and the deep ODZ core at station PS2, which were not purged before tracer addition. As a result, the ambient [O₂] at these depths was below detection on the Sea-Bird sensor, but the optode [O₂] measurements in the incubation bottles from these depths were 17.7 ± 0.1 and 19.2 ± 0.8 µM, respectively (Fig. S1, Table S1). Additionally, two depths that were suboxic (and thus not sparged prior to tracer addition) had higher optode [O₂] than ambient [O₂]: in the deep oxycline at station PS2, ambient [O₂] was 6.8 µM and optode [O₂] was 14.8 ± 0.2 µM; at the oxic–anoxic interface at station PS2, ambient [O₂] was 6.5 µM and optode [O₂] was 9.48 ± 0.09 µM (Fig. S1, Table S1). Because of these few exceptions, we always report both optode and ambient [O₂] in the following figures and text.

2.4 Nitrous oxide isotopocule measurements

Two steps were taken to prepare incubation samples for N₂O isotopocule analysis immediately prior to measurement. Firstly, a 5 mL aliquot was removed from each sample by syringe and replaced with He gas. These aliquots were refrigerated until analysis for [NO${}_{\mathrm{2}}^{-}$] and [NH${}_{\mathrm{4}}^{+}$] to check tracer and carrier additions, as mentioned above. After this aliquot was removed, 100 µL of ¹⁴NH₄Cl, Na¹⁴NO₂, or K¹⁴NO₃ carrier was added to each sample at final concentrations of 54, 262, or 27 µM, respectively, to bring ¹⁵N tracer levels below 5000 ‰. Note that these carrier additions were different from the ¹⁴N carrier added to each incubation alongside the ¹⁵N tracer; the purpose of the later carrier additions was to prevent exposure of the IRMS system to highly ¹⁵N-enriched substrates.

Samples were measured for N₂O concentrations and ¹⁵N isotopocules on a custom-built purge and trap system coupled to a Thermo Finnigan DELTA V Plus IRMS, which was run in continuous flow mode and configured to measure $m/z$ 30, 31, 44, 45, and 46 (McIlvin and Casciotti, 2010). These measurements were made under normal operating conditions, using an ionization energy of 124 eV, emission current of 1.50 mA, and accelerating voltage of 3 kV. Samples were analyzed alongside reference materials (B6, S2, and atmosphere-equilibrated seawater) to calibrate the IRMS for scrambling in the ion source with the pyisotopomer software package in Python (Kelly et al., 2023). The number ratios of isotopomers ¹⁴N¹⁵NO and ¹⁵N¹⁴NO were calculated as in Kelly et al. (2023), with the following modifications to account for the contribution of ¹⁵N¹⁵NO to the molecular ion number ratios $\mathrm{46}/\mathrm{44}$ (⁴⁶R) and $\mathrm{31}/\mathrm{30}$ (³¹R), which, while negligible at natural abundance, becomes important in tracer experiments.

In natural abundance samples, pyisotopomer solves the following four equations to obtain ¹⁵R^α and ¹⁵R^β:

$$\begin{array}{}\text{(1)}& {}^{\mathrm{45}}R={}^{\mathrm{15}}{R}^{\mathit{\alpha }}+{}^{\mathrm{15}}{R}^{\mathit{\beta }}+{}^{\mathrm{17}}R\text{(2)}& {}^{\mathrm{46}}R=\left({}^{\mathrm{15}}{R}^{\mathit{\alpha }}+{}^{\mathrm{15}}{R}^{\mathit{\beta }}\right){}^{\mathrm{17}}R+{}^{\mathrm{18}}R+{}^{\mathrm{15}}{R}^{\mathit{\alpha }}{}^{\mathrm{15}}{R}^{\mathit{\beta }}\text{(3)}& {}^{\mathrm{17}}R/{}^{\mathrm{17}}{R}_{\mathrm{VSMOW}}={\left({}^{\mathrm{18}}R/{}^{\mathrm{18}}{R}_{\mathrm{VSMOW}}\right)}^{\mathit{\beta }}\left[\mathrm{\Delta }\left({}^{\mathrm{17}}\mathrm{O}\right)+\mathrm{1}\right]\text{(4)}& {}^{\mathrm{31}}R={\displaystyle \frac{\begin{array}{c}\left(\mathrm{1}-\mathit{\gamma }\right){}^{\mathrm{15}}{R}^{\mathit{\alpha }}+\mathit{\kappa }{}^{\mathrm{15}}{R}^{\mathit{\beta }}+{}^{\mathrm{15}}{R}^{\mathit{\alpha }}{}^{\mathrm{15}}{R}^{\mathit{\beta }}\\ +{}^{\mathrm{17}}R\left[\mathrm{1}+\mathit{\gamma }{}^{\mathrm{15}}{R}^{\mathit{\alpha }}+(\mathrm{1}-\mathit{\kappa }){}^{\mathrm{15}}{R}^{\mathit{\beta }}\right]\end{array}}{\mathrm{1}+\mathit{\gamma }{}^{\mathrm{15}}{R}^{\mathit{\alpha }}+(\mathrm{1}-\mathit{\kappa }){}^{\mathrm{15}}{R}^{\mathit{\beta }}}},\end{array}$$

where ⁴⁵R, ⁴⁶R, and ³¹R are the molecular ion number ratios $\mathrm{45}/\mathrm{44}$, $\mathrm{46}/\mathrm{44}$, and $\mathrm{31}/\mathrm{30}$. ¹⁵R^α, ¹⁵R^β, ¹⁷R, and ¹⁸R denote the number ratios of ¹⁴N¹⁵N¹⁶O, ¹⁵N¹⁴N¹⁶O, ¹⁴N${}_{\mathrm{2}}^{\mathrm{17}}$O, and ¹⁴N${}_{\mathrm{2}}^{\mathrm{18}}$O, respectively, to ¹⁴N${}_{\mathrm{2}}^{\mathrm{16}}$O. Here, Δ(¹⁷O) was assumed to be equal to zero. In these equations, the term (¹⁵R^α)(¹⁵R^β) represents the statistically expected contribution of ¹⁵N¹⁵N¹⁶O to the ⁴⁶R and³¹R ion number ratios, based on the probabilities of forming ¹⁵N¹⁵N¹⁶O. The probability of getting ¹⁵N in N^α is given by ¹⁵R^α, and the probability of getting ¹⁵N in N^β is given by ¹⁵R^β; furthermore, the two probabilities are assumed to be independent, so the probability of getting ¹⁵N in both positions would be (¹⁵R^α)(¹⁵R^β) (Kaiser et al., 2004). Predicting the concentration of ¹⁵N¹⁵N¹⁶O from the distribution of ¹⁵N in the singly labeled molecules (¹⁵R^α and ¹⁵R^β) is a reasonable assumption for natural abundance samples, where the concentration of ¹⁵N¹⁵N¹⁶O is extremely low (Kantnerová et al., 2022; Magyar et al., 2016).

For ¹⁵N-labeled samples, however, we cannot predict ¹⁵N¹⁵N¹⁶O from the singly labeled molecules (¹⁵R^α and ¹⁵R^β). This is because the relationship between the formation of ¹⁵N¹⁵N¹⁶O, ¹⁴N¹⁵N¹⁶O, and ¹⁵N¹⁴N¹⁶O depends on production mechanism and the atom fraction of the substrate. For example, in ¹⁵N–NO${}_{\mathrm{2}}^{-}$ experiments with denitrification occurring, there may be far more ¹⁵N¹⁵N¹⁶O molecules produced than the amount predicted from the production of ¹⁴N¹⁵N¹⁶O and ¹⁵N¹⁴N¹⁶O. To account for this, we added a term to the equations for ⁴⁶R and ³¹R to account for the potential of excess ¹⁵N¹⁵N¹⁶O production (¹⁵N¹⁵N¹⁶O_excess) in tracer experiments:

$$\begin{array}{}\text{(5)}& {\displaystyle }\begin{array}{rl}{}^{\mathrm{46}}R& =\left({}^{\mathrm{15}}{R}^{\mathit{\alpha }}+{}^{\mathrm{15}}{R}^{\mathit{\beta }}\right){}^{\mathrm{17}}R+{}^{\mathrm{18}}R\\ & +{\left({}^{\mathrm{15}}{R}^{\mathit{\alpha }}{}^{\mathrm{15}}{R}^{\mathit{\beta }}\right)}_{t\mathrm{0}}{+}^{\mathrm{15}}{\mathrm{N}}^{\mathrm{15}}{\mathrm{N}}^{\mathrm{16}}{\mathrm{O}}_{\mathrm{excess}}\end{array}\text{(6)}& {}^{\mathrm{31}}R={\displaystyle \frac{\begin{array}{c}\left(\mathrm{1}-\mathit{\gamma }\right){}^{\mathrm{15}}{R}^{\mathit{\alpha }}+\mathit{\kappa }{}^{\mathrm{15}}{R}^{\mathit{\beta }}+{\left({}^{\mathrm{15}}{R}^{\mathit{\alpha }}{}^{\mathrm{15}}{R}^{\mathit{\beta }}\right)}_{t\mathrm{0}}\\ {+}^{\mathrm{15}}{\mathrm{N}}^{\mathrm{15}}{\mathrm{N}}^{\mathrm{16}}{\mathrm{O}}_{\mathrm{excess}}\\ +{}^{\mathrm{17}}R\left[\mathrm{1}+\mathit{\gamma }{}^{\mathrm{15}}{R}^{\mathit{\alpha }}+(\mathrm{1}-\mathit{\kappa }){}^{\mathrm{15}}{R}^{\mathit{\beta }}\right]\end{array}}{\mathrm{1}+\mathit{\gamma }{}^{\mathrm{15}}{R}^{\mathit{\alpha }}+(\mathrm{1}-\mathit{\kappa }){}^{\mathrm{15}}{R}^{\mathit{\beta }}}}.\end{array}$$

To quantify ¹⁵N¹⁵N¹⁶O_excess in tracer samples, we assumed that any increase in ⁴⁶R over the course of the experiment is due to added ¹⁵N¹⁵N¹⁶O, i.e., that δ(¹⁸O) remains constant. This should be a reasonable assumption – while denitrification and N₂O consumption could cause natural-abundance-level increases in δ(¹⁸O) and thus ⁴⁶R (10s of per mil), N₂O production from ¹⁵N-labeled substrates are expected to cause much greater increases in ⁴⁶R (100s to 1000s of per mil). We calculated the term ¹⁵N¹⁵N¹⁶O_excess by subtracting the mean ⁴⁶R at t₀ from the measured ⁴⁶R at later time points using the pyisotopomer template designed for tracer experiments (Kelly, 2023). Then, we used the “Tracers” function in pyisotopomer, which takes this ¹⁵N¹⁵N¹⁶O_excess into account, to calculate ¹⁵R^α and ¹⁵R^β.

The concentration of ⁴⁴N₂O in each sample was calculated from $m/z$ 44 peak area and from a linear conversion factor divided by the sample volume (McIlvin and Casciotti, 2010). The concentrations of ⁴⁵N₂O^α, ⁴⁵N₂O^β, and ⁴⁶N₂O were finally calculated by multiplying ¹⁵R^α, ¹⁵R^β, and ⁴⁶R by the average [⁴⁴N₂O] across all time points for that tracer experiment. Average values of [⁴⁴N₂O] were used to avoid aliasing random variability in [⁴⁴N₂O] over increases in ¹⁵R^α, ¹⁵R^β, and ⁴⁶R. The analytical precisions for N₂O isotopocule measurements, based on the pooled standard deviations of reference materials run alongside samples, were δ(¹⁵N^α)= 4.4 ‰, δ(¹⁵N^β)= 3.4 ‰, δ(¹⁵N^bulk)= 3.5 ‰, and δ(¹⁸O) = 2.1 ‰. The analytical precision was poorer than that in a similar natural abundance dataset (Kelly et al., 2021) due to minor ¹⁵N carry-over in some of the standards analyzed immediately following highly enriched samples.

2.5 Nitrite and nitrate isotope measurements

After N₂O analysis, approximately 2 mL of sample remained in each bottle, which was prepared for the analysis of δ(¹⁵N–NO${}_{\mathrm{2}}^{-}+$ NO${}_{\mathrm{3}}^{-}$), δ(¹⁵N–NO${}_{\mathrm{3}}^{-}$), or δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$), to determine the rates of NH₃ oxidation, NO${}_{\mathrm{2}}^{-}$ oxidation, and NO${}_{\mathrm{3}}^{-}$ reduction, depending on the tracer experiment. Samples incubated with ¹⁵N–NH${}_{\mathrm{4}}^{+}$ were prepared for δ(¹⁵N–NO${}_{\mathrm{2}}^{-}+$NO${}_{\mathrm{3}}^{-}$) analysis using the denitrifier method (Casciotti et al., 2002; Sigman et al., 2001), with updates from McIlvin and Casciotti (2011), to determine rates of NH₃ oxidation. These samples were run on a Thermo Finnigan DELTA^PLUS XP IRMS alongside a process blank and reference materials USGS32, USGS34, and USGS35 (Böhlke et al., 2003) to obtain δ(¹⁵N–NO${}_{\mathrm{2}}^{-}+$NO${}_{\mathrm{3}}^{-}$).

Samples incubated with ¹⁵N–NO${}_{\mathrm{2}}^{-}$ were first treated with 5 % sulfamic acid (weight by volume, or 10 mM final concentration) to remove ¹⁵N–NO${}_{\mathrm{2}}^{-}$ (Granger and Sigman, 2009) then prepared with the denitrifier method for δ(¹⁵N–NO${}_{\mathrm{3}}^{-}$) analysis (Casciotti et al., 2002; McIlvin and Casciotti, 2011; Sigman et al., 2001) to determine rates of NO${}_{\mathrm{2}}^{-}$ oxidation. For these analyses, reference materials USGS32, USGS34, and USGS35 (Böhlke et al., 2003) were also treated with 5 % sulfamic acid and prepared with the denitrifier method alongside samples. Incubations with low ambient [NO${}_{\mathrm{3}}^{-}$] had high t₀δ(¹⁵N) values (> 1000 ‰; Fig. S2). This is likely because NO${}_{\mathrm{3}}^{-}$ is produced when sulfamic acid is added to NO${}_{\mathrm{2}}^{-}$ (Granger and Sigman, 2009), so the sulfamic treatment probably chemically converted some ¹⁵N–NO${}_{\mathrm{2}}^{-}$ tracer to ¹⁵N–NO${}_{\mathrm{3}}^{-}$; additionally, ¹⁵N–NO${}_{\mathrm{3}}^{-}$ is a possible contaminant of the ¹⁵N–NO${}_{\mathrm{2}}^{-}$ tracer solutions. Regardless, this would have shifted all three time points equally and thus should not introduce a bias into the slope of δ(¹⁵N–NO${}_{\mathrm{3}}^{-}$) with time and the rates calculated from there.

Finally, samples incubated with ¹⁵N–NO${}_{\mathrm{3}}^{-}$ were prepared for δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$) isotopic analysis with the azide method (McIlvin and Altabet, 2005) to determine rates of NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$. The 2 mL of remaining sample was transferred into 20 mL vials, where it was prepared alongside reference materials RSIL-N23, -N7373, and -N10219 (Casciotti et al., 2007). Reference materials were diluted from 200 mM working stocks into 3 mL NO${}_{\mathrm{2}}^{-}$-free seawater in 5 and 10 nmol quantities of NO${}_{\mathrm{2}}^{-}$ to correct for the contribution of a consistent blank to a range of sample sizes. The analytical precisions for δ(¹⁵N–NO${}_x^{-}$), δ(¹⁵N–NO${}_{\mathrm{3}}^{-}$), and δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$) were 0.9 ‰, 1.2 ‰, and 0.4 ‰, respectively. The δ(¹⁵N) analytical precision for the denitrifier and azide methods is typically better (McIlvin and Altabet, 2005; Sigman et al., 2001), but tracer measurements tend to have lower analytical precision than natural abundance measurements.

The rates of NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{2}}^{-}$ oxidation were calculated using a weighted least-squares linear regression through product ¹⁵N vs. incubation time (Fig. S3). Each sample was weighted by its uncertainty, which was calculated based on the slope and intercept of the calibration curve, blank peak area, and sample peak area (Appendix A). Although using this uncertainty calculation is complex, it allows the assessment of relative error and the inclusion of low-peak-area samples that had high enough δ(¹⁵N) enrichments such that the relative error remained below 10 % (and in most cases 1 %). A weighted least-squares regression was used in place of an ordinary least-squares regression to prevent samples with high uncertainties from biasing the slope estimate (e.g., two samples in Fig. S3b). Then, the rate was calculated by

$$\begin{array}{}\text{(7)}& \mathrm{rate}\left(\mathrm{nM}\mathrm{N}{\mathrm{d}}^{-\mathrm{1}}\right)={\displaystyle \frac{m\left({}^{\mathrm{15}}{F}_{\mathrm{product}}\right)\left[P\right]}{{}^{\mathrm{15}}{F}_{\mathrm{substrate}}}},\end{array}$$

where m(¹⁵F_product) is the slope of the atom fraction of ¹⁵N in the product vs. incubation time, [P] is the mean product concentration (e.g., NO${}_{\mathrm{3}}^{-}$ in an NO${}_{\mathrm{2}}^{-}$ oxidation experiment), and ¹⁵F_substrate is the atom fraction of ¹⁵N in the substrate (e.g., NO${}_{\mathrm{2}}^{-}$ in an NO${}_{\mathrm{2}}^{-}$ oxidation experiment). Our method of estimating individual uncertainties was developed to deal with low NH₃ oxidation rates, which generated low peak areas in δ(¹⁵N–NO${}_{\mathrm{3}}^{-}$) samples. Since the rates of NO${}_{\mathrm{3}}^{-}$ reduction were generally much higher than the rates of NH₃ oxidation (Table S2), a parallel method was not needed to estimate individual uncertainties in samples measured with the azide method, i.e., δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$) measurements, so rates of NO${}_{\mathrm{3}}^{-}$ reduction were with an ordinary least-squares regression in Eq. (7) instead of a weighted least-squares regression.

2.6 Modeling N₂O production mechanisms

A time-dependent model was constructed to infer the rates and mechanisms of N₂O production from the measured isotopocule time courses in each incubation experiment. While it is possible to calculate rates of hybrid and bacterial N₂O production with linear regressions of ⁴⁵N₂O and ⁴⁶N₂O with time (Trimmer et al., 2016), these calculations cannot take into account ¹⁵N transfer between substrates and, more importantly, produce separate rate estimates for separate tracer experiments. They also do not leverage the additional information provided by N₂O isotopomers. We sought to solve for a common set of N₂O production rate constants across the three parallel tracer experiments at a given station and depth, wherein the only differences between each tracer experiment were the starting concentrations of ¹⁴N and ¹⁵N in NH${}_{\mathrm{4}}^{+}$, NO${}_{\mathrm{2}}^{-}$, and NO${}_{\mathrm{3}}^{-}$ (Fig. 2). The model encoded four different N₂O-producing pathways: (1) production solely from NH${}_{\mathrm{4}}^{+}$, which includes N₂O from hydroxylamine oxidation (referred to as Pathway 1 in Wan et al., 2023b), hybrid production using cellular NO${}_{\mathrm{2}}^{\mathit{\_}}$ (referred to as Pathway 2 in Wan et al., 2023b), and nitrifier denitrification using cellular NO${}_{\mathrm{2}}^{-}$; (2) hybrid production using extracellular NO${}_{\mathrm{2}}^{-}$ (referred to as Pathway 3 in Wan et al., 2023b); (3) production from NO${}_{\mathrm{2}}^{-}$, i.e., denitrification or nitrifier denitrification using extracellular NO${}_{\mathrm{2}}^{-}$; and (4) production from NO${}_{\mathrm{3}}^{-}$, i.e., denitrification using cellular NO${}_{\mathrm{2}}^{-}$ (Fig. 2). Using this model, the relative importance of each of these pathways was determined at each incubation depth based on the production of ¹⁵N-labeled N₂O isotopocules in parallel experiments supplied with different ¹⁵N substrates.

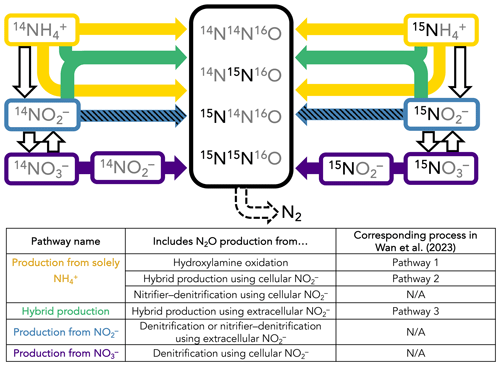
Figure 2 Schematic of the forward-running model used to solve for rates of N₂O production. Horizontal arrows represent processes whose rates are solved for, while vertical arrows represent processes whose rates are prescribed based on our experimental results. The model solves for second-order rate constants for four N₂O-producing processes: (1) production solely from NH${}_{\mathrm{4}}^{+}$ (yellow horizontal arrows), which includes N₂O from hydroxylamine oxidation (Wan et al., 2023, Pathway 1), hybrid production using cellular NO${}_{\mathrm{2}}^{-}$ (Wan et al., 2023, Pathway 2), and nitrifier denitrification using cellular NO${}_{\mathrm{2}}^{-}$; (2) hybrid production using NH${}_{\mathrm{4}}^{+}$ and extracellular NO${}_{\mathrm{2}}^{-}$ (green arrows; Wan et al., 2023, Pathway 3); (3) production from NO${}_{\mathrm{2}}^{-}$, i.e., denitrification or nitrifier denitrification using extracellular NO${}_{\mathrm{2}}^{-}$ (hatched blue horizontal arrows); and (4) production from NO₃, i.e., denitrification or nitrifier denitrification using cellular NO${}_{\mathrm{2}}^{-}$ (indigo horizontal arrows). The model also solves for f, the proportion of N^α derived from NO${}_{\mathrm{2}}^{-}$ during hybrid N₂O production. NH₃ oxidation (yellow vertical arrows), NO${}_{\mathrm{2}}^{-}$ oxidation (hatched blue vertical arrows), and NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ (indigo vertical arrows) are modeled as first-order rates to account for ¹⁵N transfer between substrate pools, as described in the main text. Finally, N₂O consumption (dashed black arrow) is modeled as first order to N₂O. It is assumed that, while the distribution of ¹⁵N in each tracer experiment at a given station and depth is different, the overall rates and mechanisms of N₂O production are the same regardless of which substrate is labeled. The model is optimized against the observed ⁴⁶N₂O, ⁴⁵N₂O^α, ⁴⁵N₂O^β, and ⁴⁴N₂O at each time point in each tracer experiment (black box).

The concentration of each nitrogen species was modeled as

$$\begin{array}{}\text{(8)}& N_{t+\mathrm{1}}=N_t+\mathrm{\Delta }t\left(\sum _{n=\mathrm{1}}^i{J}_n^{\mathrm{source}}-\sum _{n=\mathrm{1}}^k{J}_n^{\mathrm{sink}}\right),\end{array}$$

where N_t is the concentration of a given N species (e.g., NH${}_{\mathrm{4}}^{+}$, NO${}_{\mathrm{2}}^{-}$, NO${}_{\mathrm{3}}^{-}$, or N₂O) at time t, N_t+1 is its concentration at time t+1, Δt represents the model time step (days), $\sum _{n=\mathrm{1}}^i{J}_n^{\mathrm{source}}$ is the sum of i individual source processes of that species (nM d⁻¹), and $\sum _{n=\mathrm{1}}^k{J}_n^{\mathrm{sink}}$ is the sum of k individual sink processes of that species (nM d⁻¹).

The pattern of N₂O isotopocule production for a given process was set by the total rate J of N₂O production for that process multiplied by the probability of forming each isotopocule from a given pair of substrates. The probabilities of forming each isotopocule were based on the atom fractions of the two substrates from which the nitrogen atoms in N₂O are derived:

$$\begin{array}{}\text{(9)}& {\displaystyle }P\left({}^{\mathrm{46}}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\right)=\left({}^{\mathrm{15}}{F}_{\mathrm{1}}\right)\left({}^{\mathrm{15}}{F}_{\mathrm{2}}\right)\text{(10)}& {\displaystyle }\begin{array}{rl}P\left({}^{\mathrm{45}}{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}^{\mathit{\alpha }}\right)& =f\left({}^{\mathrm{15}}{F}_{\mathrm{1}}\right)\left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{2}}\right)\\ & +\left(\mathrm{1}-f\right)\left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{1}}\right)\left({}^{\mathrm{15}}{F}_{\mathrm{2}}\right)\end{array}\text{(11)}& {\displaystyle }\begin{array}{rl}P\left({}^{\mathrm{45}}{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}^{\mathit{\beta }}\right)& =\left(\mathrm{1}-f\right)\left({}^{\mathrm{15}}{F}_{\mathrm{1}}\right)\left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{2}}\right)\\ & +f\left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{1}}\right)\left({}^{\mathrm{15}}{F}_{\mathrm{2}}\right)\end{array}\text{(12)}& {\displaystyle }P\left({}^{\mathrm{44}}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\right)=\left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{1}}\right)\left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{2}}\right),\end{array}$$

where P(⁴⁶N₂O), P(⁴⁵N₂O^α), P(⁴⁵N₂O^β), and P(⁴⁴N₂O) are the probabilities of forming each isotopocule; ¹⁵F₁ is the atom fraction of ¹⁵N in substrate 1; ¹⁵F₂ is the atom fraction of ¹⁵N in substrate 2; f is the proportion of N^α derived from substrate 1; and 1 – f is the proportion of N^α derived from substrate 2. Assuming a 1:1 pairing of substrates 1 and 2, f also represents the proportion of N^β derived from substrate 2 and 1 – f represents the proportion of N^β derived from substrate 1. Processes that derive both nitrogen atoms from the same substrate pool are a special case of Eqs. (9)–(12), where ¹⁵F₁=¹⁵F₂. Measuring bulk ⁴⁵N₂O production instead of individual isotopomers (Trimmer et al., 2016) is also a special case of Eqs. (9)–(12), where P(⁴⁵N₂O) = P(⁴⁵N₂O^α)+ P(⁴⁵N₂O^β) and f cancel out.

To represent each N₂O-producing J term in the model, the rates of N₂O production were modeled as second order:

$$\begin{array}{}\text{(13)}& J_i=k_i\left[{\mathrm{substrate}}_{\mathrm{1}}\right]\left[{\mathrm{substrate}}_{\mathrm{2}}\right],\end{array}$$

where J_i is the rate of N₂O production process i in nM N d⁻¹, k_iis a second-order rate constant for that process, [substrate₁] is the concentration of substrate 1 for process i, and [substrate₂] is the concentration of substrate 2 for process i. Each rate constant k_i was optimized in the model for each station and depth. Again, N₂O production processes that draw both nitrogen atoms from the same substrate are a special case, where [substrate₁] = [substrate₂]. J was multiplied by $\mathrm{1}/\mathrm{2}$ to convert the rate from nM N d⁻¹ to nM N₂O d⁻¹, which was then multiplied by Eqs. (9)–(12) to obtain the rates of production of each isotopocule (note that rates are reported in pM d⁻¹). For example, the rate of hybrid ⁴⁶N₂O production was represented as

$$\begin{array}{}\text{(14)}& J_{\mathrm{hybrid}}^{{}^{\mathrm{46}}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}}=\mathrm{1}/\mathrm{2}\left(k_{\mathrm{hybrid}}\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]\left[{\mathrm{NO}}_{\mathrm{2}}^{-}\right]\right)\left({}^{\mathrm{15}}{F}_{{\mathrm{NH}}_{\mathrm{4}}^{+}}\right)\left({}^{\mathrm{15}}{F}_{{\mathrm{NO}}_{\mathrm{2}}^{-}}\right),\end{array}$$

where $J_{\mathrm{hybrid}}^{{}^{\mathrm{46}}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}}$ is the rate of ⁴⁶N₂O production via hybrid production in nM N₂O d⁻¹.

To relate the J terms to consumption of the substrate pools (NH${}_{\mathrm{4}}^{+}$, NO${}_{\mathrm{2}}^{-}$, and NO${}_{\mathrm{3}}^{-}$), J draws upon the ¹⁵N and ¹⁴N substrate pools according to the atom fractions of ¹⁵N in each substrate:

$$\begin{array}{}\text{(15)}& J_i^{\mathrm{15}}=J_i{\cdot }^{\mathrm{15}}{F}_{\mathrm{substrate}}\text{and}{J}_i^{\mathrm{14}}=J_i\cdot \left(\mathrm{1}{-}^{\mathrm{15}}{F}_{\mathrm{substrate}}\right),\end{array}$$

where $J_i^{\mathrm{15}}$ and $J_i^{\mathrm{14}}$ are the rates of consumption of the ¹⁵N and ¹⁴N substrate pools by N₂O-producing process i, J_i is the rate in nM N d⁻¹ calculated in Eq. (13) for N₂O production process i, and ¹⁵F_substrate is the atom fraction of ¹⁵N in the given substrate pool (NH${}_{\mathrm{4}}^{+}$, NO${}_{\mathrm{2}}^{-}$, and NO${}_{\mathrm{3}}^{-}$). Essentially, Eq. (15) relates how each rate J_i draws from the ¹⁵N and ¹⁴N substrate pools, while Eqs. (9)–(12) determine the ¹⁵N and ¹⁴N distribution in the product N₂O. For example, the rate of ¹⁵NH${}_{\mathrm{4}}^{+}$ consumption by hybrid N₂O production was represented as

$$\begin{array}{}\text{(16)}& J_{\mathrm{hybrid}}^{{}^{\mathrm{15}}{\mathrm{NH}}_{\mathrm{4}}^{+}}=\left(k_{\mathrm{hybrid}}\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]\left[{\mathrm{NO}}_{\mathrm{2}}^{-}\right]\right)\left({}^{\mathrm{15}}{F}_{{\mathrm{NH}}_{\mathrm{4}}^{+}}\right),\end{array}$$

where $J_{\mathrm{hybrid}}^{{}^{\mathrm{15}}{\mathrm{NH}}_{\mathrm{4}}^{+}}$ is the rate of ¹⁵N–NH${}_{\mathrm{4}}^{+}$ consumption via hybrid production in nM N d⁻¹. Equation (16) does not contain the factor of $\mathrm{1}/\mathrm{2}$ in Eq. (14) because the units are nM N d⁻¹, not nM N₂O d⁻¹. Rates of ¹⁵N and ¹⁴N transfer between substrate pools via NH₃ oxidation, NO${}_{\mathrm{2}}^{-}$ oxidation, and NO${}_{\mathrm{3}}^{-}$ reduction were also included in the model. The model solves for N₂O production rates, given a set of NH₃ oxidation, NO${}_{\mathrm{2}}^{-}$ oxidation, and NO${}_{\mathrm{3}}^{-}$ reduction rates calculated in Sect. 2.5, Eq. (7) (Table S2). These rates were represented in the model as first order:

$$\begin{array}{}\text{(17)}& J^{\mathrm{15}}={\displaystyle \frac{k}{\mathit{\alpha }}}\left[{}^{\mathrm{15}}\mathrm{N}\right]\text{and}{J}^{\mathrm{14}}=k\left[{}^{\mathrm{15}}\mathrm{N}\right],\end{array}$$

where J¹⁵ and J¹⁴ represent the rates of ¹⁵N and ¹⁴N transformation via NH₃ oxidation, NO${}_{\mathrm{2}}^{-}$ oxidation, or NO${}_{\mathrm{3}}^{-}$ reduction; k is a first-order rate constant derived from measured rates; α is a fractionation factor (Table S3); [¹⁵N] is the concentration of the ¹⁵N species; and [¹⁴N] is the concentration of the ¹⁴N species. N₂O consumption was modeled as first order to the concentration of each isotopocule, based on the [O₂]-corrected rates of N₂O consumption measured on the same cruise (Sun et al., 2021a).

The model was optimized against isotopocule data at each time step in each tracer experiment (Fig. S4). The parameters being optimized (inputs to the cost function) were the second-order rate constants k_i for N₂O production solely from NH${}_{\mathrm{4}}^{+}$, N₂O production from NO${}_{\mathrm{2}}^{-}$ via denitrification or nitrifier denitrification, N₂O production from NO${}_{\mathrm{3}}^{-}$ via denitrification, hybrid N₂O production using extracellular NO${}_{\mathrm{2}}^{-}$, and f (Fig. 2). In the model, these are all separate processes that operate independently. The model was optimized using the Nelder–Mead simplex algorithm (Nelder and Mead, 1965), implemented in the SciPy optimization library (Virtanen et al., 2020), which has been used successfully for natural abundance N₂O isotopocule models (Monreal et al., 2022). Model error was estimated by optimizing the model at each station and depth with 100 combinations of model parameters, randomly varying the initial concentrations of each ¹⁵N and ¹⁴N substrate and rate constants for NH₃ oxidation, NO${}_{\mathrm{2}}^{-}$ oxidation, and NO${}_{\mathrm{3}}^{-}$ oxidation by up to 25 %.

To ground-truth the model, rates of N₂O production obtained from the model were compared to the measured net rates of ⁴⁶N₂O production (Fig. S5). For processes drawing both nitrogen atoms from the same substrate pool (i.e., not hybrid production), the modeled rates of N₂O production from each substrate should correspond roughly to the net rate of ⁴⁶N₂O production from the same ¹⁵N-labeled substrate. Higher modeled rates of N₂O production solely from NH${}_{\mathrm{4}}^{+}$ generally corresponded to higher net rates of ⁴⁶N₂O production from ¹⁵N–NH${}_{\mathrm{4}}^{+}$ (Fig. S5a). Since the model cannot produce negative rates, negative net rates of ⁴⁶N₂O production from ¹⁵N–NH${}_{\mathrm{4}}^{+}$ corresponded to modeled N₂O production rates equal to zero (Fig. S5a). Modeled rates of N₂O production from NO${}_{\mathrm{2}}^{-}$ and NO${}_{\mathrm{3}}^{-}$ via denitrification also corresponded to higher measured rates of ⁴⁶N₂O production from ¹⁵N–NO${}_{\mathrm{2}}^{-}$ and ¹⁵N–NO${}_{\mathrm{3}}^{-}$, respectively (Fig. S5b, c).

3 Results

3.1 Depth distributions of oxygen, nitrite, and nitrous oxide

Station PS1, which was at the edge of the ODZ, represented a “background” station with no secondary NO${}_{\mathrm{2}}^{-}$ maximum and a less-pronounced minimum in [N₂O] below the oxycline (Fig. S6; Kelly et al., 2021). At station PS1, the oxic–anoxic interface, defined in this study as the depth just above the ODZ, occurred at the base of the mixed layer at 100 m depth (Fig. S6). Station PS2 was near the geographic center of the oxygen-deficient region and had a secondary NO${}_{\mathrm{2}}^{-}$ maximum of 2.2 µM, indicating functional anoxia (Fig. S6). The oxic–anoxic interface at station PS2 occurred at 92 m depth (Fig. S6). Below the oxic–anoxic interface, [N₂O] declined to 4.5 ± 0.3 nM before increasing again at the base of the secondary NO${}_{\mathrm{2}}^{-}$ maximum and reaching a local maximum around 800 m depth. Station PS3 was approximately 19 km from the coast of Mexico and had a shallow oxic–anoxic interface that moved up and down on timescales of days: on 10 April, the oxic–anoxic interface occurred at 40 m depth; 2 d later, the oxic–anoxic interface had deepened to 62 m depth. Experiments were performed at the oxic–anoxic interface on both days and are designated with the abbreviations “Interface” and “Interface2” in the experimental metadata (Table S1). The chemical profiles from 11 April (Fig. S6), on which the near-surface [N₂O] maximum occurred at 61 m (Kelly et al., 2021), are displayed along with the rate data in this study. Station PS3 had a pronounced secondary NO${}_{\mathrm{2}}^{-}$ maximum of 2.8 µM at 161 m depth (Fig. S6) and an NH${}_{\mathrm{4}}^{+}$ maximum of 400 nM at 15 m depth (not shown). On 11 April, [N₂O] reached a maximum of 195 ± 13 nM at the oxic–anoxic interface and declined below this depth. Below 600 m depth, [N₂O] began to increase again to 44 ± 3 nM. At every station, a deep secondary chlorophyll a maximum was observed near the oxic–anoxic interface, where photosynthetically active radiation was much reduced and [NO${}_{\mathrm{3}}^{-}$] was abundant (Travis et al., 2023). This secondary chlorophyll a maximum tended to develop between the depths of the oxic–anoxic interface and the secondary NO${}_{\mathrm{2}}^{-}$ maximum (Travis et al., 2023).

3.2 Nitrification and nitrate reduction rates

NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ occurred at rates ranging from 0.54 ± 0.04 to 33.2 ± 0.1 nM N d⁻¹ (Table S2). There was a small, significant rate of NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ in apparently aerobic waters near the surface at station PS1 (Fig. 3a). The highest rates of NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ occurred in the deep, anoxic waters at station PS2 (33.24 ± 0.01 nM N d⁻¹; Fig. 3d) and in the secondary chlorophyll maximum at station PS3 (19.2 ± 0.1 nM N d⁻¹; Fig. 3g).

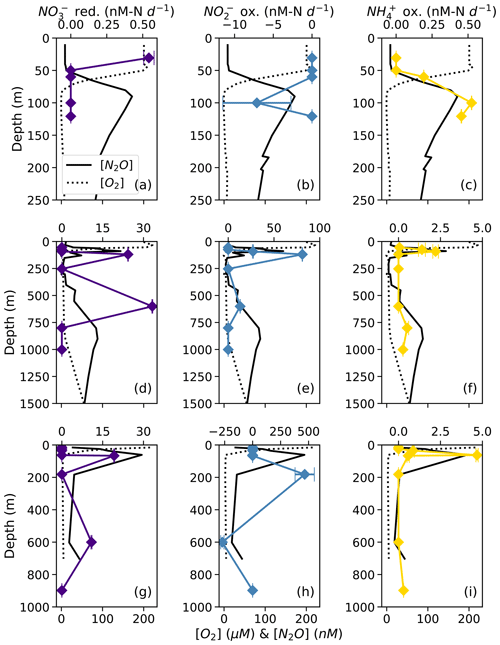
Figure 3 Rates of NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ (a, d, g; indigo), NO${}_{\mathrm{2}}^{-}$ oxidation to NO${}_{\mathrm{3}}^{-}$ (b, e, h; blue), and NH₃ oxidation to NO${}_{\mathrm{2}}^{-}+$ NO${}_{\mathrm{3}}^{-}$ (c, f, i; yellow) at stations PS1 (a–c), PS2 (d–f), and PS3 (g–i). Rates are plotted over depth profiles of dissolved [O₂] (dashed lines) and [N₂O] (solid lines; from Kelly et al., 2021). Error bars represent rate error, calculated from the error of the slope of product ¹⁵N vs. time. Note the different x-axis scales for rate measurements (top x axes) and [O₂] and [N₂O] (bottom x axes).

NO${}_{\mathrm{2}}^{-}$ oxidation rates ranged from 13.05 ± 0.08 to 465 ± 86 nM N d⁻¹ (Table S2). The highest rates of NO${}_{\mathrm{2}}^{-}$ oxidation occurred within apparently oxygen-deficient waters at 81.0 ± 0.2 nM N d⁻¹ in the secondary chlorophyll a maximum at station PS2 and at 465 ± 86 nM N d⁻¹ in the secondary NO${}_{\mathrm{2}}^{-}$ maximum at station PS3 (Fig. 3e, h; Table S2). Note that these are potential rates, since the ¹⁵N addition was generally much greater than the ambient concentration (Lipschultz, 2008). In some cases, NO${}_{\mathrm{2}}^{-}$ oxidation rates appeared negative due to a decrease in ¹⁵N–NO${}_{\mathrm{3}}^{-}$ vs. incubation time (Fig. 3b, h), which was likely an artifact of the elevated t₀ δ(¹⁵N) values in some of our ¹⁵N–NO${}_{\mathrm{2}}^{-}$ treatments (discussed above). We chose, however, not to left-censor the data.

NH₃ oxidation to NO${}_{\mathrm{2}}^{-}$ occurred at small but significant rates ranging from 0.19 ± 0.0004 to 4.68 ± 0.07 nM N d⁻¹ (Table S2). At every station, rates of NH₃ oxidation peaked near the base of the mixed layer at the same depth as the near-surface [N₂O] maximum (Fig. 3c, f, i). At station PS2, NH₃ oxidation showed a secondary peak at the same depth as the deep [N₂O] maximum (Fig. 3f). At station PS3, there was also a small, significant rate of NH₃ oxidation (0.303 ± 0.005 nM N d⁻¹) at 898 m, which was close to the bottom depth (Fig. 3i). Rates of NH₃ oxidation were generally lower than NO${}_{\mathrm{2}}^{-}$ oxidation and undetectable in oxygen-deficient waters (Fig. 3c, f, i).

3.3 Net production rates of ⁴⁵N₂O^α, ⁴⁵N₂O^β, and ⁴⁶N₂O (measured net rates)

At each station, the observed rates of net ⁴⁶N₂O (Fig. 4), ⁴⁵N₂O^α, and ⁴⁵N₂O^β (Fig. 5) production from ¹⁵N–NH${}_{\mathrm{4}}^{+}$, ¹⁵N–NO${}_{\mathrm{2}}^{-}$, and ¹⁵N–NO${}_{\mathrm{3}}^{-}$ all peaked at or just below the oxic–anoxic interface, where the near-surface [N₂O] maximum was found. There were also relatively higher rates of net ⁴⁶N₂O production from ¹⁵N–NO${}_{\mathrm{2}}^{-}$ and ¹⁵N–NO${}_{\mathrm{3}}^{-}$ within the secondary NO${}_{\mathrm{2}}^{-}$ maximum (253 m) at station PS2 (Fig. 4d–e). Relatively high rates of net ⁴⁵N₂O^α and ⁴⁵N₂O^β production also occurred in the secondary NO${}_{\mathrm{2}}^{-}$ maximum at stations PS2 (253 m; Fig. 5d–e) and PS3 (182 m; Fig. 5g–h). The net rates of ⁴⁵N₂O^α and ⁴⁵N₂O^β production varied in concert at almost every station and depth, with a few exceptions (Fig. 5).

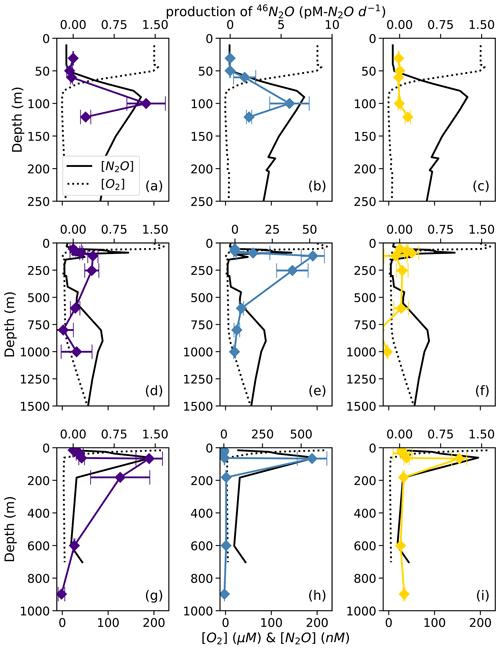
Figure 4 Net ⁴⁶N₂O production from ¹⁵N–NO${}_{\mathrm{3}}^{-}$ (a, d, g; indigo), ¹⁵N–NO${}_{\mathrm{2}}^{-}$ (b, e, h; blue), and ¹⁵N–NH${}_{\mathrm{4}}^{+}$ (c, f, i; yellow) at stations PS1 (a–c), PS2 (d–f), and PS3 (g–i). N₂O production rates are plotted over depth profiles of dissolved [O₂] (dashed lines) and [N₂O] (solid lines; from Kelly et al., 2021). Error bars are calculated from the linear regression slope error of ⁴⁶N₂O vs. incubation time. Note the different x-axis scales for ⁴⁶N₂O production (top x axes) and [O₂] and [N₂O] (bottom x axes) .

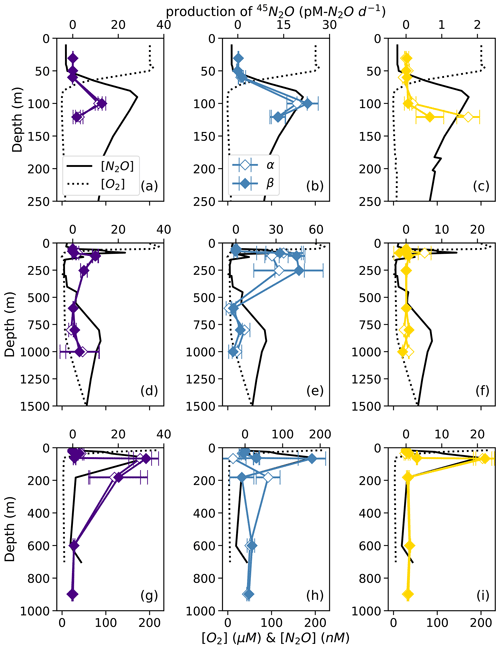
Figure 5 Net ⁴⁵N₂O^α (open symbols) and ⁴⁵N₂O^β (closed symbols) production from ¹⁵N–NO${}_{\mathrm{3}}^{-}$ (a, d, g; indigo), ¹⁵N–NO${}_{\mathrm{2}}^{-}$ (b, e, h; blue), and ¹⁵N–NH${}_{\mathrm{4}}^{+}$ (c, f, i; yellow) at stations PS1 (a–c), PS2 (d–f), and PS3 (g–i). N₂O production rates are plotted over depth profiles of dissolved [O₂] (dashed lines) and [N₂O] (solid lines; from Kelly et al., 2021). Error bars are calculated from the linear regression slope error of ⁴⁵N₂O vs. incubation time. Note the different x-axis scales for ⁴⁵N₂O production (top x axes) and [O₂] and [N₂O] (bottom x axes) .

For example, in the secondary NO${}_{\mathrm{2}}^{-}$ maximum (182 m) at station PS3, in the ¹⁵N–NO${}_{\mathrm{2}}^{-}$ experiment, the production of ⁴⁵N₂O^α was 60 ± 30 pM N₂O d⁻¹ (p=0.09) and there was no significant production of ⁴⁵N₂O^β (Fig. 5h). In the parallel ¹⁵N–NH${}_{\mathrm{4}}^{+}$ experiment, the production of ⁴⁵N₂O^β was 0.7 ± 0.3 pM N₂O d⁻¹ (p=0.06) and there was no significant production of ⁴⁵N₂O^α. At this station and depth, f (the proportion of N^α derived from NO${}_{\mathrm{2}}^{-}$) was equal to 0.9 ± 0.2 (Table S4). The second experiment in which labeling was unequal occurred at the oxic–anoxic interface (92 m) at station PS2, where, in the ¹⁵N–NH${}_{\mathrm{4}}^{+}$ experiment, the production of ⁴⁵N₂O^α was 5 ± 2 pM N₂O d⁻¹ (p=0.02) and there was no significant production of ⁴⁵N₂O^β (Fig. 5f). Here, f was equal to 0.2 ± 0.1. Finally, at the mid-oxycline depth (25 m) at station PS3, in the ¹⁵N–NH${}_{\mathrm{4}}^{+}$ experiment, the production of ⁴⁵N₂O^α was 0.23 ± 0.8 pM N₂O d⁻¹ (p=0.02) and there was no significant production of ⁴⁵N₂O^β. Here, f was statistically indistinguishable from zero.

At many stations and depths, the net production of ⁴⁵N₂O^α and ⁴⁵N₂O^β exceeded the values expected from ⁴⁶N₂O production for a process that draws both nitrogen atoms from the same substrate pool (Fig. S7). This expected value is calculated from the atom fraction of ¹⁵N in the substrate and from a binomial distribution of the isotopocules of N₂O during N₂O production (Trimmer et al., 2016):

$$\begin{array}{}\text{(18)}& p_{\mathrm{expected}}^{\mathrm{45}}={\displaystyle \frac{p^{\mathrm{46}}}{{\left({}^{\mathrm{15}}F\right)}^{\mathrm{2}}}}\mathrm{2}\left({}^{\mathrm{15}}F\right)\left(\mathrm{1}{-}^{\mathrm{15}}F\right)={\displaystyle \frac{p^{\mathrm{46}}}{{}^{\mathrm{15}}F}}\mathrm{2}\left(\mathrm{1}{-}^{\mathrm{15}}F\right),\end{array}$$

where $p_{\mathrm{expected}}^{\mathrm{45}}$ is the expected production of ⁴⁵N₂O^α and ⁴⁵N₂O^β from a process that draws both nitrogen atoms from the same substrate pool, p⁴⁶ is the net production rate of ⁴⁶N₂O, and ¹⁵F is the atom fraction of ¹⁵N in the substrate pool (for example, NO${}_{\mathrm{2}}^{-}$ in a ¹⁵N–NO${}_{\mathrm{2}}^{-}$ experiment). Then, excess production of ⁴⁵N₂O is any ⁴⁵N₂O production above and beyond this expected rate:

$$\begin{array}{}\text{(19)}& p_{\mathrm{excess}}^{\mathrm{45}}=p^{\mathrm{45}}-p_{\mathrm{expected}}^{\mathrm{45}}=p^{\mathrm{45}}-{\displaystyle \frac{p^{\mathrm{46}}}{{}^{\mathrm{15}}F}}\mathrm{2}\left(\mathrm{1}{-}^{\mathrm{15}}F\right),\end{array}$$

where $p_{\mathrm{excess}}^{\mathrm{45}}$ is the excess production of ⁴⁵N₂O above and beyond that expected for a process drawing both nitrogen atoms from the same pool and p⁴⁵ is the measured net production of ⁴⁵N₂O. The equations for ⁴⁵N₂O^α and ⁴⁵N₂O^β are the same as Eq. (19), except for a factor of 2. In many of the ¹⁵N–NH${}_{\mathrm{4}}^{+}$ experiments, there was significant excess ⁴⁵N₂O^α and ⁴⁵N₂O^β production (Fig. S7a). Similarly, there was significant excess ⁴⁵N₂O^α and ⁴⁵N₂O^β production in many of the ¹⁵N–NO${}_{\mathrm{2}}^{-}$ experiments, although this was harder to discern due to the wider range of atom fractions in these experiments (Fig. S7b). In a few experiments, excess ⁴⁵N₂O^α and ⁴⁵N₂O^β production diverged.

3.4 N₂O production mechanisms and yields (model results)

Based on model results, the rates of N₂O production from NO${}_{\mathrm{3}}^{-}$ (denitrification using cellular NO${}_{\mathrm{2}}^{-}$; Fig. 2) were the highest among the N₂O production processes measured in this study. At suboxic to anoxic depths, the rates of N₂O production from NO${}_{\mathrm{3}}^{-}$ were orders of magnitude higher than all the other N₂O production rates (Fig. 6). N₂O production from NO${}_{\mathrm{3}}^{-}$ reached its maximum value (1600 ± 400 pM N₂O d⁻¹; Table S4) at the depth of the near-surface [N₂O] maximum at every station (Fig. 6a, e, i), where there were also high rates of NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ at stations PS2 and PS3 (Fig. 6e, i). N₂O production from NO${}_{\mathrm{2}}^{-}$ (denitrification using extracellular NO${}_{\mathrm{2}}^{-}$; Fig. 2) exhibited lower rates, with a maximum of 510 ± 30 pM N₂O d⁻¹ (Table S4). At stations PS1 and PS3, N₂O production from NO${}_{\mathrm{2}}^{-}$ peaked at the depth of the near-surface [N₂O] maximum (Fig. 6b, j); at station PS2, N₂O production from NO${}_{\mathrm{2}}^{-}$ was observed in the near-surface [N₂O] maximum but peaked in the secondary NO${}_{\mathrm{2}}^{-}$ maximum (253 m; Fig. 6f).

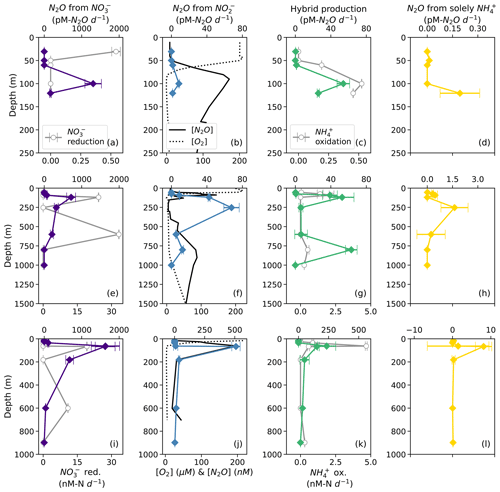
Figure 6 N₂O production from NO${}_{\mathrm{3}}^{-}$ (a, e, i; indigo diamonds), N₂O production from NO${}_{\mathrm{2}}^{-}$ (b, f, j; blue diamonds), hybrid N₂O production (c, g, k; green diamonds), and N₂O production solely from NH${}_{\mathrm{4}}^{+}$ (d, h, l; yellow diamonds) at stations PS1 (a–d), PS2 (e–h), and PS3 (i–l). Panels (a), (e), and (i) also show rates of NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ (open circles). Panels (b), (f), and (j) show depth profiles of dissolved [O₂] (dashed lines) and [N₂O] (solid lines; from Kelly et al., 2021). Panels (c), (g), and (k) show rates of NH₃ oxidation (gray circles). N₂O production rate error bars are calculated from 100 model optimizations, varying key parameters by up to 25 %. Note the different x-axis scales for NO${}_{\mathrm{3}}^{-}$ reduction to NO${}_{\mathrm{2}}^{-}$ (a, e, i; bottom), N₂O production (top), [O₂] and [N₂O] (b, f, j; bottom), and NH₃ oxidation (c, g, k; bottom).

Hybrid N₂O production occurred at a similar rate to N₂O production from NO${}_{\mathrm{2}}^{-}$, ranging from 0.061 ± 0.005 to 230 ± 80 pM N₂O d⁻¹. Hybrid N₂O production peaked within the near-surface [N₂O] maximum at all stations (Fig. 6c, g, k). At station PS2, hybrid N₂O production exhibited the highest rates at the same depths as NH₃ oxidation, with a secondary peak in the deep [N₂O] maximum (Fig. 6g). At station PS3, hybrid N₂O production, like NH₃ oxidation, exhibited a small, significant rate at 898 m, which was very close to the bottom depth at station PS3 (Table S4).

N₂O production solely from NH${}_{\mathrm{4}}^{+}$ occurred at the smallest rates overall, ranging from 0.010 ± 0.004 to 8 ± 2 pM N₂O d⁻¹ (Table S4). N₂O production solely from NH${}_{\mathrm{4}}^{+}$ peaked around the near-surface [N₂O] maximum at each station (Fig. 6d, h, l) and in the secondary NO${}_{\mathrm{2}}^{-}$ maximum at station PS2 (Fig. 6h).

The percentage of N₂O production from NH${}_{\mathrm{4}}^{+}$ comprised of hybrid N₂O was calculated as

$$\begin{array}{}\text{(20)}& \mathit{\%}\mathrm{hybrid}={\displaystyle \frac{\mathrm{hybrid}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)}{\begin{array}{c}{\mathrm{N}}_{\mathrm{2}}\text{O from hydroxylamine}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\\ +{\text{hybrid N}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\end{array}}}.\end{array}$$

On average, hybrid N₂O production was 86 ± 28 % of N₂O production from NH${}_{\mathrm{4}}^{+}$. Hybrid N₂O production was > 75 % of the total N₂O production from NH${}_{\mathrm{4}}^{+}$ at all stations and depths except for the top of the oxycline at station PS1 (Fig. 7a), the middle of the oxycline at station PS2 (Fig. 7b), and the top of the oxycline at station PS3 (Fig. 7c), where it comprised 0 %, 68 %, and 19 % of N₂O production from NH${}_{\mathrm{4}}^{+}$, respectively. Hybrid production as a percentage of total N₂O production from NH${}_{\mathrm{4}}^{+}$ declined with increasing dissolved oxygen (Fig. S8), although more measurements are needed to fully evaluate this trend.

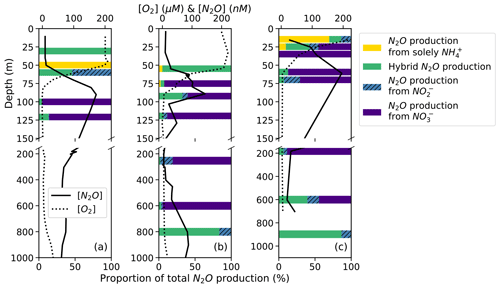
Figure 7 N₂O production solely from NH${}_{\mathrm{4}}^{+}$ (yellow bars), hybrid N₂O production (green bars), N₂O production from NO${}_{\mathrm{2}}^{-}$ (hatched blue bars), and N₂O production from NO${}_{\mathrm{3}}^{-}$ (indigo bars) as proportions of total N₂O production at stations PS1 (a), PS2 (b), and PS3 (c). Data are plotted over depth profiles of dissolved [O₂] (dashed lines) and [N₂O] (solid lines; from Kelly et al., 2021). Note broken y axes and different x-axis scales for [O₂] and [N₂O] (top) and for proportions (bottom).

The percentage of hybrid N₂O production as a proportion of total N₂O production was more variable and tended to decline with decreasing dissolved oxygen as production from NO${}_{\mathrm{3}}^{-}$ increased (Fig. 7). Hybrid N₂O production was greater than 75 % of total N₂O production only at the surface at station PS1 (Fig. 7a), at the top of the oxycline and in the deep [N₂O] maximum at station PS2 (Fig. 7b), and in the deep [N₂O] maximum at station PS3 (Fig. 7c).

N₂O production from NO${}_{\mathrm{3}}^{-}$ comprised a much greater proportion of total N₂O production overall (Fig. 7). In the near-surface [N₂O] maximum at station PS1, N₂O production was predominantly (95.4 %) from NO${}_{\mathrm{3}}^{-}$, with smaller contributions from hybrid production (4.0 %) and denitrification from NO${}_{\mathrm{2}}^{-}$ (0.6 %; Fig. 7a). In the near-surface [N₂O] maximum at station PS2, N₂O production was 60.2 % from NO${}_{\mathrm{3}}^{-}$, 32.1 % from hybrid production, 7.3 % from NO${}_{\mathrm{2}}^{-}$, and 0.4 % solely from NH${}_{\mathrm{4}}^{+}$ (Fig. 7b). In the near-surface [N₂O] maximum at station PS3, N₂O production was 87.0 % from NO${}_{\mathrm{3}}^{-}$, 12.4 % from hybrid production, 0.5 % from NO${}_{\mathrm{2}}^{-}$, and 0.1 % solely from NH${}_{\mathrm{4}}^{+}$ (Fig. 7c).

3.5 Oxygen dependence of N₂O production

The oxygen dependencies of N₂O production pathways were determined by fitting model-derived N₂O production pathways vs. [O₂] using the following rate law:

$$\begin{array}{}\text{(21)}& \mathrm{rate}=a{e}^{-b\left[O_{\mathrm{2}}\right]}.\end{array}$$

In this analysis, both ambient [O₂] measured by the Sea-Bird sensor mounted on the rosette (“ambient [O₂]”) and [O₂] measured by chemiluminescent optodes mounted inside incubation bottles (“incubation [O₂]”) were examined. The rate dependencies on ambient and incubation [O₂] reflect both preconditioning (i.e., the ambient [O₂] in which the microbial community was living before the incubation experiment) and the response to perturbation (i.e., the experimental conditions inside the incubation bottles, if different from the environment). Those incubations that had higher incubation [O₂] than the ambient [O₂] had received small oxygen perturbations.

N₂O production via denitrification exhibited an exponentially declining relationship with dissolved O₂, where N₂O production from NO${}_{\mathrm{2}}^{-}$ was more inhibited by dissolved O₂ than N₂O production from NO${}_{\mathrm{3}}^{-}$ was (Fig. 8). When looking at the oxygen dependence of denitrification, we found several instances of N₂O production from NO${}_{\mathrm{3}}^{-}$ via denitrification with dissolved [O₂] greater than 3 µM (Fig. 8a–b). For example, at the oxic–anoxic interface at station PS2, where ambient [O₂] was 6.49 µM and incubation [O₂] was 6.29 ± 0.07 µM (Table S1), N₂O production from NO${}_{\mathrm{3}}^{-}$ was 70 ± 10 pM N₂O d⁻¹ (Fig. 6e, Table S4). N₂O production from NO${}_{\mathrm{2}}^{-}$ at the same station and depth was 8.9 ± 0.2 pM N₂O d⁻¹ (Fig. 6f, Table S4). Similarly, at the oxic–anoxic interface of station PS3, where ambient [O₂] was 12.48 µM and incubation [O₂] was 6.64 ± 0.03 µM (Table S1), N₂O production from NO${}_{\mathrm{3}}^{-}$ was 120 ± 20 pM N₂O d⁻¹ (Fig. 6i, Table S4). There were also two anoxic depths at station PS2 that were not sparged with He before tracer addition (“base of ODZ” and “deep ODZ core”), where ambient [O₂] was below detection but incubation [O₂] was significantly elevated (17.7 ± 0.1 and 19.2 ± 0.8 µM, respectively; Table S1). At these depths, N₂O production from NO${}_{\mathrm{2}}^{-}$ was 12 ± 1 and 5.2 ± 0.4 pM N₂O d⁻¹, respectively (Fig. 6f, Table S4). N₂O production from NO${}_{\mathrm{3}}^{-}$ at the “deep ODZ core” depth was 210 ± 40 pM N₂O d⁻¹ (Table S4).

Hybrid N₂O production rates also decreased exponentially with increasing dissolved [O₂] (Fig. 9a–b). Fitting hybrid rates vs. ambient [O₂] produced a rate (Eq. 21) with a=65.83 and b=0.17 (Fig. 9a); hybrid rates vs. incubation [O₂] produced fits with a=76.26 and b=0.067 (Fig. 9b).

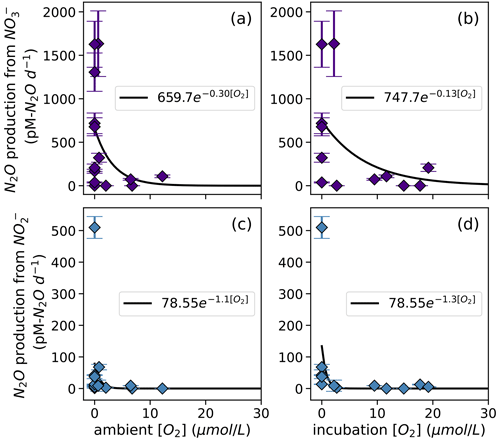
Figure 8 N₂O production from NO${}_{\mathrm{3}}^{-}$ via denitrification (a, b) and from NO${}_{\mathrm{2}}^{-}$ via denitrification (c, d), measured at a range of [O₂] measured by a Seabird sensor (a, c) or by chemiluminescent optodes mounted inside incubation bottles (b, d). Curves of form, $\mathrm{yield}=a{e}^{-{\mathrm{O}}_{\mathrm{2}}b}$, are fit through the data (black lines); values of a and b are shown in white boxes in each plot.

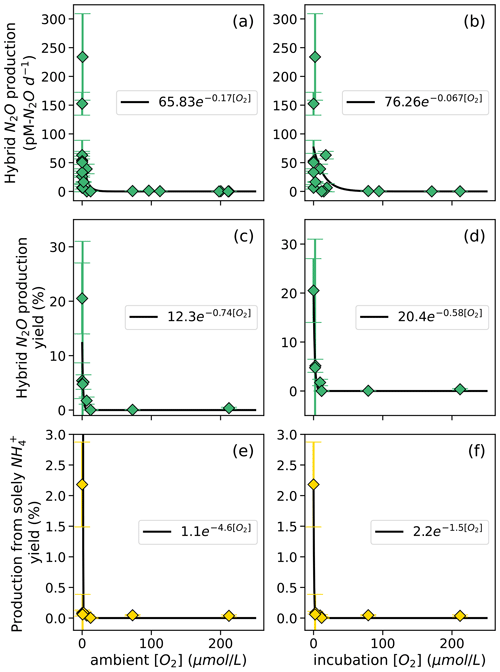
Figure 9 Hybrid N₂O production rates (a, b), N₂O yield (%) during hybrid production (c, d), and N₂O yield ( %) during production solely from NH${}_{\mathrm{4}}^{+}$ (e, f) along a range of ambient [O₂] measured by a Seabird sensor for the Niskin bottles from which samples were taken (a, c, e) and of [O₂] measured by chemiluminescent optodes mounted inside incubation bottles (b, d, f). Error bars are calculated from 100 model optimizations, varying key parameters by up to 25 %. Yields are only calculated at stations and depths where rates of NH₃ oxidation are greater than 0. Curves of form, $\mathrm{rate}=a{e}^{-b\left[{\mathrm{O}}_{\mathrm{2}}\right]}$, are fit through the data (black lines); values of a and b are shown in white boxes in each plot.

The rate of N₂O production solely from NH${}_{\mathrm{4}}^{+}$ also decreased exponentially with increasing dissolved [O₂]. The highest rates of N₂O production solely from NH${}_{\mathrm{4}}^{+}$ occurred in the secondary chlorophyll maximum at station PS3 (Table S4), where dissolved oxygen was below detection. N₂O yield during production solely from NH${}_{\mathrm{4}}^{+}$ also exhibited exponentially decreasing relationships with dissolved [O₂] (Fig. 9e–f). To ensure mass balance in terms of NH${}_{\mathrm{4}}^{+}$ consumption (Fig. S9), N₂O yield (%) during production solely from NH${}_{\mathrm{4}}^{+}$ was calculated as

$$\begin{array}{}\text{(22)}& \mathrm{yield}\left(\mathit{\%}\right)={\displaystyle \frac{\mathrm{2}\left[{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\mathrm{solely}\mathrm{from}{\mathrm{NH}}_{\mathrm{4}}^{+}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\right]}{\begin{array}{c}\mathrm{2}\left[{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\mathrm{solely}\mathrm{from}{\mathrm{NH}}_{\mathrm{4}}^{+}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\right]\\ +\mathrm{hybrid}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\\ +{\mathrm{NH}}_{\mathrm{3}}\mathrm{oxidation}\left(\mathrm{nM}\mathrm{N}{\mathrm{d}}^{-\mathrm{1}}\right)\end{array}}},\end{array}$$

where N₂O production solely from NH${}_{\mathrm{4}}^{+}$ is in units of nM N₂O d⁻¹, hybrid N₂O production is in units of nM N₂O d⁻¹, and NH₃ oxidation to NO${}_{\mathrm{2}}^{-}$ is in units of nM N d⁻¹. This assumes that the formation of N₂O solely from NH${}_{\mathrm{4}}^{+}$ draws two nitrogen atoms from the NH${}_{\mathrm{4}}^{+}$ pool, while hybrid N₂O production and the oxidation of NH${}_{\mathrm{4}}^{+}$ to NO${}_{\mathrm{2}}^{-}$ each draw one atom from the NH${}_{\mathrm{4}}^{+}$ pool (Fig. S9). Following the same convention, N₂O yield (%) during hybrid production was calculated as

$$\begin{array}{}\text{(23)}& \mathrm{yield}\left(\mathit{\%}\right)={\displaystyle \frac{\mathrm{hybrid}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)}{\begin{array}{c}\mathrm{2}\left[{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\mathrm{solely}\mathrm{from}{\mathrm{NH}}_{\mathrm{4}}^{+}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\right]\\ +\mathrm{hybrid}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{nM}{\mathrm{N}}_{\mathrm{2}}\mathrm{O}{\mathrm{d}}^{-\mathrm{1}}\right)\\ +{\mathrm{NH}}_{\mathrm{3}}\mathrm{oxidation}\left(\mathrm{nM}\mathrm{N}{\mathrm{d}}^{-\mathrm{1}}\right)\end{array}}}.\end{array}$$

The maximum N₂O yield from hybrid production was 21 ± 7 % (Fig. 9c, d). while the maximum N₂O yield during production solely from NH${}_{\mathrm{4}}^{+}$ was 2.2 ± 0.7 % (Fig. 9e, f). The N₂O yield during production solely from NH${}_{\mathrm{4}}^{+}$ declined more sharply with increased O₂ than the N₂O yield during hybrid production did (Fig. 9c–f).

4 Discussion

In this study, we found that N₂O production from denitrification was the dominant source of N₂O both within the ODZ and in the upper oxycline. Hybrid N₂O production was a smaller but significant contributor to N₂O in the upper oxycline, and the primary source of N₂O in the deep oxycline. N₂O production solely from NH${}_{\mathrm{4}}^{+}$ (which includes N₂O from hydroxylamine oxidation, hybrid production with cellular NO${}_{\mathrm{2}}^{-}$, and nitrifier denitrification with cellular NO${}_{\mathrm{2}}^{-}$) was negligible everywhere except surface waters. Our findings of equal formation of ⁴⁵N₂O^α and ⁴⁵N₂O^β in most experiments indicate that N^α retains an equal proportion of NO${}_{\mathrm{2}}^{-}$ and NH${}_{\mathrm{4}}^{+}$-derived N during hybrid production, which may imply that hybrid N₂O production exhibits a constant δ(¹⁵N^sp). All of the processes measured in this study exhibited a strong dependence on dissolved oxygen, although denitrification was less inhibited by dissolved oxygen than previous work would suggest.

4.1 Rates of N₂O production via denitrification

Based on our rate data, N₂O production from NO${}_{\mathrm{3}}^{-}$ is the dominant source of N₂O in both the near-surface [N₂O] maximum and the anoxic ODZ core. This agrees well with natural abundance isotopocule measurements in the ETNP, which indicate that the near-surface [N₂O] maximum is likely to comprise ∼ 80 % N₂O produced via denitrification and ∼ 20 % N₂O produced via nitrification or archaeal N₂O production, producing a local minimum in δ(¹⁵N^sp) (Kelly et al., 2021). Natural abundance isotopomer work has shown that N₂O production from NO${}_{\mathrm{3}}^{-}$ could be an important source of N₂O in the anoxic core of ODZs, as long as it has a positive δ(¹⁵N^sp) (Casciotti et al., 2018; Kelly et al., 2021; Monreal et al., 2022). While denitrification is generally accepted to produce N₂O with δ(¹⁵N^sp)≈ 0 ‰ (Sutka et al., 2006; other refs), some strains of denitrifying bacteria can produce N₂O with δ(¹⁵N^sp)=10 ‰–22 ‰ (Toyoda et al., 2005; Wang et al., 2023) and denitrifying fungi produce N₂O with δ(¹⁵N^sp)=35 ‰–37 ‰ (Lazo-Murphy et al., 2022; Rohe et al., 2014; Sutka et al., 2008; Yang et al., 2014). Here, the dominance of N₂O production from ¹⁵N–NO${}_{\mathrm{3}}^{-}$, combined with parallel natural abundance isotopomer studies, suggest that strains of denitrifying bacteria and fungi that produce N₂O with a high site preference may be important contributors to N₂O in the core of ODZs. The importance of N₂O production from NO${}_{\mathrm{3}}^{-}$ also presents an important exception to the modular view of the microbial nitrogen cycle network, which holds that intermediates are passed externally from one cell to the next, rather than being held internally (Kuypers et al., 2018). N₂O production from NO${}_{\mathrm{3}}^{-}$ that utilizes an internal NO${}_{\mathrm{2}}^{-}$ pool is currently left out of most biogeochemical models of nitrogen cycling in and around oxygen-deficient zones (Bianchi et al., 2023), and modeling work that includes this as a source of N₂O is needed.

4.2 Pathways of hybrid N₂O production and implications for hybrid δ(¹⁵N^sp)

Hybrid N₂O production peaked at the same depths as NH₃ oxidation (Fig. 6c, g, k), which were also the depths at which ammonia-oxidizing archaea were most abundant (Frey et al., 2023), consistent with N₂O production associated with ammonia-oxidizing archaea. At most stations and depths, the production of ⁴⁵N₂O^α and ⁴⁵N₂O^β in both the ¹⁵N–NO${}_{\mathrm{2}}^{-}$ and ¹⁵N–NH${}_{\mathrm{4}}^{+}$ experiments were roughly equal. From this we conclude that, during hybrid formation, N^α and N^β each retained nitrogen atoms derived from both NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{2}}^{-}$. The equal formation of ⁴⁵N₂O^α and ⁴⁵N₂O^β led to values off within an error of 0.5 in most of our experiments (Table S4), and the mean value of f across all stations and depths was 0.5 ± 0.2. This means that, during hybrid N₂O production, half of the N^α atoms were derived from NO${}_{\mathrm{2}}^{-}$ and half were derived from NH${}_{\mathrm{4}}^{+}$ (likewise for N^β).

Although our data do not allow us to comment directly on the enzymatic machinery of hybrid N₂O formation, our data can be used to theorize hypothetical pathways for hybrid N₂O production. Firstly, we see much higher rates of hybrid production using ambient NO${}_{\mathrm{2}}^{-}$ (Pathway 3 in Wan et al., 2023b) than hybrid production using cellular NO${}_{\mathrm{2}}^{-}$ (Pathway 2 in Wan et al., 2023b). Again, this agrees with the results of Wan et al. (2023b), who see higher rates of hybrid formation from extracellular NO${}_{\mathrm{2}}^{-}$ within the range of [¹⁵N–NH${}_{\mathrm{4}}^{+}$]/[NO${}_{\mathrm{2}}^{-}$] covered by our experiments. In our model, hybrid N₂O production is operationally defined as a 1:1 combination of N derived from NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{2}}^{-}$, which is generally consistent with previous work (Stieglmeier et al., 2014). Any combination of N derived from NO${}_{\mathrm{2}}^{-}$ with a second N derived from NO${}_{\mathrm{2}}^{-}$ would be included in the modeled quantity of N₂O production from NO${}_{\mathrm{2}}^{-}$; likewise, any combination of N derived from NH${}_{\mathrm{4}}^{+}$ with a second N derived from NH${}_{\mathrm{4}}^{+}$ would be included in the N₂O production solely from NH${}_{\mathrm{4}}^{+}$. The question, then, is what reaction would be specific enough to have one N derived from each substrate but not specific enough to govern ¹⁵N placement in the resulting N₂O? One such reaction could be the combination of NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{2}}^{-}$ to form a symmetrical intermediate such as hyponitrous acid (HONNOH, or hyponitrite ⁻ONNO⁻ in its deprotonated form), which has been discussed as a possible intermediate in hybrid nitrous oxide formation (Wei et al., 2019). Hyponitrous acid may react to form N₂O via breakage of one of the N–O bonds, resulting in N₂O that contains a 1:1 ratio of NH${}_{\mathrm{4}}^{+}$:NO${}_{\mathrm{2}}^{-}$. With a precursor such as hyponitrite or hyponitrous acid, equal formation of ⁴⁵N₂O^α and ⁴⁵N₂O^β could be achieved with non-selective N–O bond breakage.

These findings of equal ⁴⁵N₂O production have important implications for the natural abundance δ(¹⁵N^sp) of N₂O produced by the hybrid N₂O process. Assuming that hybrid N₂O production proceeds through a symmetrical intermediate in which NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{2}}^{-}$ are paired in a 1:1 ratio, we can model δ(¹⁵N^sp) as

$$\begin{array}{}\text{(24)}& \begin{array}{rl}\mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}^{\mathrm{sp}}\right)& =\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}^{\mathit{\alpha }}\right)-\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}^{\mathit{\beta }}\right)\\ & =\left[f\mathit{\delta }\left({}^{\mathrm{15}}\mathrm{N}-{\mathrm{NO}}_{\mathrm{2}}^{-}\right)+\left(\mathrm{1}-f\right)\mathit{\delta }\left({}^{\mathrm{15}}\mathrm{N}-{\mathrm{NH}}_{\mathrm{4}}^{+}\right)\right]\\ & -\left[\left(\mathrm{1}-f\right)\mathit{\delta }\left({}^{\mathrm{15}}\mathrm{N}-{\mathrm{NO}}_{\mathrm{2}}^{-}\right)+f\mathit{\delta }\left({}^{\mathrm{15}}\mathrm{N}-{\mathrm{NH}}_{\mathrm{4}}^{+}\right)-\mathit{\epsilon }\right]\end{array},\end{array}$$

where f is the proportion of the α nitrogen derived from NO${}_{\mathrm{2}}^{-}$ and the proportion of the β nitrogen derived from NH${}_{\mathrm{4}}^{+}$ and ε is the fractionation factor associated with N^β–O bond breakage. If $f\ne \mathrm{1}/\mathrm{2}$, hybrid δ(¹⁵N^sp) retains a dependence on the δ(¹⁵N) of the substrates – or, more accurately, the difference in δ(¹⁵N) of the two substrates; if the δ(¹⁵N) of the substrates is equal, it will cancel out regardless of f. If δ(¹⁵N–NH${}_{\mathrm{4}}^{+}$) >δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$), as is generally the case in the secondary nitrite maximum (Buchwald et al., 2015; Casciotti, 2016), then low values of f should produce high hybrid δ(¹⁵N^sp) and high values of f should produce low hybrid δ(¹⁵N^sp) (Fig. 10). If, however, $f=\mathrm{1}/\mathrm{2}$, as was the case for most experimental depths in this study, hybrid δ(¹⁵N^sp) should depend only on ε and not on the isotopic composition of each substrate. This means that a δ(¹⁵N^sp) endmember could potentially be established for hybrid N₂O production, even though hybrid N₂O production draws from different substrate pools. Wei et al. (2019) discuss possible pathways or endmembers of hybrid N₂O formation, i.e., via cis-hyponitrous acid, trans-hyponitrous acid, and nitramide, all leading to N₂O with different δ(¹⁵N^sp) values. More studies are needed to determine the δ(¹⁵N^sp) of N₂O produced by ammonia-oxidizing archaea under a range of conditions.

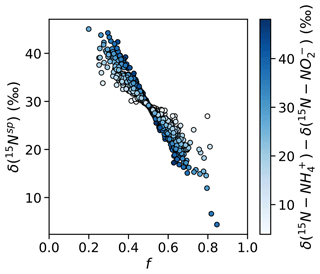
Figure 10 Simulated values of δ(¹⁵N^sp) calculated with a range of f (the proportion of N^α derived from NO${}_{\mathrm{2}}^{-}$ during hybrid N₂O production) and δ(¹⁵N–NH${}_{\mathrm{4}}^{+}$)–δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$), assuming ε=30.3 ‰ (Santoro et al., 2011). Results are shaded by δ(¹⁵N–NH${}_{\mathrm{4}}^{+}$) – δ(¹⁵N–NO${}_{\mathrm{2}}^{-}$). When f is less than or greater than $\mathrm{1}/\mathrm{2}$, there is the potential for δ(¹⁵N^sp) to depend on the isotopic compositions of each substrate.

The unequal production of ⁴⁵N₂O^α and ⁴⁵N₂O^β observed at certain depths led to values of f significantly different from 0.5 (Table S4). At these depths, N^α retained a different proportion of nitrogen derived from NO${}_{\mathrm{2}}^{-}$ and NH${}_{\mathrm{4}}^{+}$ than N^β did, causing ⁴⁵N₂O^α and ⁴⁵N₂O^β to diverge. The depths with f≠0.5 anchored significant relationships between f and ambient [O₂] (R²=0.84, p<0.001; Fig. S10a) and potential density anomaly (σ_θ) (R²=0.72, p<0.001; Fig. S10b). The oxygen and potential density gradients may be proxies for changing archaeal community compositions at different depths in the water column, which may exhibit different patterns of incorporation of NO${}_{\mathrm{2}}^{-}$-derived N and NH${}_{\mathrm{4}}^{+}$-derived N into N^α and N^β. It is also possible that we sampled a different “hybrid” N₂O-producing process at these depths, such as fungal co-denitrification (Shoun et al., 2012), which may proceed via a different pathway from archaeal hybrid N₂O production.

4.3 Rates of nitrification and N₂O production solely from NH${}_{\mathrm{4}}^{+}$

The rates of N₂O production from NH${}_{\mathrm{4}}^{+}$ in this study (i.e., the sum of hybrid N₂O production and N₂O production solely from NH${}_{\mathrm{4}}^{+}$) peaked at 240 ± 80 pM N₂O d⁻¹ (Table S4). These were similar to those measured on the same cruise by Frey et al. (2023), who measured rates of N₂O production from NH${}_{\mathrm{4}}^{+}$ in the oxycline of 28–149 pM N₂O d⁻¹ (Frey et al., 2023). The low rates of NH₃ oxidation to NO${}_{\mathrm{2}}^{-}$ in this study (0.05–4.68 nM N d⁻¹) were also similar to those measured by Frey et al. (2023), who measured NH₃ oxidation rates of 1.0–11.7 nM d⁻¹ in the oxycline. NH₃ oxidation rates in this study were smaller than those measured on the same cruise by Travis et al. (2023), who measured NH₃ oxidation rates as high as 90 ± 2 nM d⁻¹ in fully oxygenated incubations at station PS3. The highest rates of NO${}_{\mathrm{2}}^{-}$ oxidation we observed occurred at anoxic depths at stations PS2 and PS3 (Fig. 3e, h), which agrees with mounting evidence suggesting the importance of NO${}_{\mathrm{2}}^{-}$ oxidation in apparently anoxic regions (Sun et al., 2017, 2021b).

When [O₂] was less than 10 µM, the rates of hybrid N₂O production (6–230 pM N₂O d⁻¹) were orders of magnitude greater than the rates of N₂O production solely from NH${}_{\mathrm{4}}^{+}$ at the same depths (0–8 pM N₂O d⁻¹) (Fig. 6). Indeed, at the upper oxic–anoxic interface, the rates of hybrid N₂O production were on a similar order of magnitude to N₂O production from NO${}_{\mathrm{2}}^{-}$ via denitrification (8–510 pM N₂O d⁻¹). These results agree with previous work showing that hybrid N₂O formation represents a high percentage of total N₂O production from NH${}_{\mathrm{4}}^{+}$ in the ETNP and eastern tropical South Pacific (ETSP) (Frey et al., 2020, 2023). The results in this study also agree with recent culture work: the ¹⁵N–NH${}_{\mathrm{4}}^{+}$ experiments in this study fell along a range of [¹⁵N–NH${}_{\mathrm{4}}^{+}$] $/$ [NO${}_{\mathrm{2}}^{-}$] of 0.14–0.5, in which Wan et al. (2023b) found that hybrid N₂O production occurred at a rate 2 to 4 times greater than N₂O production via hydroxylamine oxidation (N derived solely from NH${}_{\mathrm{4}}^{+}$) in cultures of Nitrosopumilus maritimus.

We found three depths near the surface where hybrid production comprised a smaller percentage (0 %–68 %) of total N₂O production from NH${}_{\mathrm{4}}^{+}$ (Fig. 7a–c). Previous work in the ETNP found that hybrid N₂O production always comprised > 90 % of N₂O production from NH${}_{\mathrm{4}}^{+}$ (Frey et al., 2023), and, where our samples overlapped with this previous work, we observed similarly high proportions of hybrid production (Fig. 5). The depths where we observed a smaller proportion of hybrid production had not been sampled previously; it is possible that we sampled different microbial communities there, acclimated to different levels of NH${}_{\mathrm{4}}^{+}$, NO${}_{\mathrm{2}}^{-}$, and dissolved oxygen. We also found that hybrid N₂O formation generally comprised a small proportion of total N₂O production, which was dominated by N₂O production from NO${}_{\mathrm{3}}^{-}$, especially at suboxic depths (Fig. 7d–h). This is similar to previous findings from the ETSP, which showed that hybrid formation comprised 0 %–95 % of total N₂O production from NO${}_{\mathrm{2}}^{-}$ along the natural [O₂] gradient (Frey et al., 2020). This large range is due to the large range of rates of N₂O production from NO${}_{\mathrm{2}}^{-}$, which can occur at orders of magnitude higher or lower than hybrid N₂O production.

4.4 Oxygen dependence of N₂O production rates and yields

N₂O production from NO${}_{\mathrm{2}}^{-}$ and NO${}_{\mathrm{3}}^{-}$ exhibited exponential dependence on dissolved oxygen, albeit with smaller maximum rates than those found in the ETSP (Frey et al., 2020; Ji et al., 2015). Most surprising were the significant rates of N₂O production via denitrification at [O₂] > 3 µM (Fig. 8a–d), which has previously been suggested as the threshold above which denitrification ceases (Dalsgaard et al., 2014). These observations are particularly evident in the plots of N₂O production from NO${}_{\mathrm{3}}^{-}$ vs. incubation [O₂] (Fig. 8b), where positive, significant rates of N₂O production from NO${}_{\mathrm{3}}^{-}$ were evident in incubations containing [O₂] as high as 19.2 ± 0.8 µM (PS2 deep ODZ core experiment). One explanation for N₂O production via denitrification at such high levels of ambient dissolved oxygen is particle-associated denitrification (Bianchi et al., 2018; Smriga et al., 2021; Wan et al., 2023a). Fungal denitrification may also have contributed to these fluxes, since denitrifying fungi can tolerate a higher level of oxygen than their bacterial counterparts. Additionally, denitrifying microbial communities acclimatized to lower ambient [O₂] may be able to continue to produce N₂O when [O₂] is suddenly increased.

These results showed that N₂O production from NO${}_{\mathrm{3}}^{-}$ can occur in [O₂] as high as 19.2 ± 0.8 µM, which is similar to results from the ETSP showing that N₂O production from NO${}_{\mathrm{3}}^{-}$ in manipulated [O₂] can be as high as 30 µM (Frey et al., 2020). The volume of suboxic water in the ocean has been increasing over the last 50 years and will likely continue to expand over the 21st century (Oschlies et al., 2018; Schmidtko et al., 2017; Stramma et al., 2008), although the extent of this deoxygenation remains uncertain (Bianchi et al., 2018; Busecke et al., 2022; Cabré et al., 2015). Constraining the window of oxygen concentrations under which denitrification leads to N₂O production will be key to understanding how marine deoxygenation and N₂O cycling will interact.

While this study and others have found that hybrid N₂O production represents a consistent percentage of N₂O production from NH${}_{\mathrm{4}}^{+}$ along a range of ambient [O₂] (Frey et al., 2020, 2023), the rate of hybrid N₂O production followed a clear exponential dependence on dissolved oxygen (Fig. 9). The differences in ambient and incubation [O₂] resulted in slight differences in the coefficients for each yield curve; nevertheless, hybrid rates plotted along both ambient and incubation [O₂] gradients exhibited remarkably similar [O₂] inhibition curves, with the highest rates at [O₂] < 7 µM. These results are similar to those of Frey et al. (2023), who showed a decrease in N₂O production from NH${}_{\mathrm{4}}^{+}$ with increasing [O₂].

The maximum N₂O yield for hybrid production (21 %; Fig. 8c, d) was 1 order of magnitude higher than previous estimates of N₂O yields during NH₃ oxidation from ETSP and ETNP, which did not include hybrid N₂O production (Ji et al., 2018). These high yields occurred at the oxic–anoxic interface at station PS1 and just below the oxic–anoxic interface at station PS3, where ambient [O₂] was below detection but NH₃ oxidation still occurred (Fig. 3). This indicates the potential for extremely high yields of N₂O from hybrid production where NH₃ oxidation is active in suboxic to anoxic environments.

N₂O yields during production solely from NH${}_{\mathrm{4}}^{+}$ also increased with decreasing [O₂] (Fig. 9b), as previously reported (Frey et al., 2020; Goreau et al., 1980; Ji et al., 2018; Nevison et al., 2003). N₂O yields during production solely from NH${}_{\mathrm{4}}^{+}$ increased sharply with decreasing [O₂] along both ambient and incubation [O₂] gradients but were much smaller than the yields from hybrid N₂O production (Fig. 8c–d). The maximum yields during production solely from NH${}_{\mathrm{4}}^{+}$ were similar to the maximum yields found by another study in the ETNP, which were around 3 % (Frey et al., 2023), and much higher than yields from ammonia-oxidizing archaea in soils and culture (up to 0.03 %) (Hink et al., 2017a, b).

4.5 Experimental artifacts

Care was taken to minimize the effects of experimental setup on the microbial communities in each sample. In addition to the steps taken to prevent oxygen contamination (described in Sect. 2: Methods), a relatively short 24 h incubation period was selected to minimize bottle effects and shifts in the microbial community composition over the course of each incubation. Nonetheless, sample collection, preparation, and incubation conditions could have affected the microbial communities in several ways. Firstly, samples were frequently collected from depths where the water temperature was cooler than that of the laboratory, and, while samples were returned to a cool temperature during incubation (12 °C), they were exposed to warmer temperatures (> 20 °C) during the 2 h in which they underwent collection and manipulation prior to incubation. Likewise, during this interval, samples were exposed to higher light levels before being returned to the dark for incubation. While oxygen contamination was minimized during sample collection, it was not eliminated entirely, and a temporary oxygen intrusion before sparging may have poisoned certain anaerobic processes. The 90 min sparge also likely removed carbon dioxide in addition to oxygen and N₂O, increasing the pH of each sample. Finally, the NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{2}}^{-}$ tracer and carrier additions exceeded the ambient concentrations of these substrates, potentially stimulating the rates of processes that rely on these substrates. All of these perturbations, while common among incubation studies, may have affected the microbial community differentially in each sample. Thus, the results presented here represent processes able to withstand these perturbations to ambient environmental conditions. Any abiotic reactions between the HgCl₂ preservative and the NO${}_{\mathrm{2}}^{-}$ tracer and carrier would have shifted all three time points equally and thus should not introduce a bias into the slopes of ¹⁵N-labeled N₂O with time and the rates calculated from there.

4.6 Alternative sources of N₂O

Other processes may have contributed to N₂O production in our samples. A complementary set of experiments found that fungal denitrification comprised 50 % of total N₂O production via denitrification at the secondary chlorophyll a maximum depths discussed here (Peng and Valentine, 2021). Additionally, since our samples were unfiltered, particle-associated N₂O production and consumption may have occurred in some of our experiments, especially in experiments at the highly productive coastal station. We cannot rule out any of these alternative sources of N₂O in our samples, so we regard these processes as potential contributors to the bulk denitrifying flux discussed here.

5 Conclusions

We applied N₂O isotopocule measurements to ¹⁵N tracer incubations to measure N₂O production rates and mechanisms in the ETNP. We found that N₂O production rates peaked at the oxic–anoxic interface above the ODZ, with the highest rates of N₂O production from NO${}_{\mathrm{3}}^{-}$. Hybrid N₂O production peaked in both the shallow and deep oxyclines, where NH₃ oxidation was also active, and exhibited yields as high as 21 % of ammonia oxidation.

Based on the equal production of ⁴⁵N₂O^α and ⁴⁵N₂O^β in the vast majority of our experiments, we posit a two-step process for hybrid N₂O production involving an initial bond-forming step that draws nitrogen atoms from each substrate to form a symmetric intermediate and a second bond-breaking step that breaks an N–O bond in the symmetric intermediate to form N₂O. From this, we infer that hybrid N₂O production likely has a consistent δ(¹⁵N^sp), despite drawing from two distinct substrate pools. This has important implications for the interpretation of natural abundance isotopocule measurements, since it implies that it may be possible to define a δ(¹⁵N^sp) endmember for hybrid N₂O formation. More culture experiments are needed to quantify the δ(¹⁵N^sp) of N₂O produced by ammonia-oxidizing archaea under different temperatures, oxygen levels, and ratios of NH${}_{\mathrm{4}}^{+}$ $/$ NO${}_{\mathrm{2}}^{-}$.

N₂O production rates and yields of every process examined here were inhibited by dissolved oxygen. The N₂O yield from hydroxylamine oxidation was most sensitive to O₂, followed by the rates of N₂O production from NO${}_{\mathrm{2}}^{-}$ via denitrification, hybrid N₂O production, and N₂O production from NO${}_{\mathrm{3}}^{-}$ via denitrification. Indeed, we measured positive, significant rates of N₂O production from NO${}_{\mathrm{3}}^{-}$ at ambient [O₂] as high as 12.5 µM and at manipulated [O₂] as high as 19.2 µM. These denitrifying fluxes may have derived partially from fungal N₂O production, since fungal denitrifiers can tolerate higher oxygen levels than bacteria (Peng and Valentine, 2021) or particle-associated denitrification (Bianchi et al., 2018; Smriga et al., 2021). These results suggest that a broad window of [O₂] could support net N₂O accumulation, and additional studies are needed to further constrain this window and the resulting feedbacks between denitrification and marine deoxygenation.

Appendix A: Estimating uncertainties for nitrate isotope analyses from tracer samples

Since only 2 mL of sample was available for preparation and analysis of nitrate isotopes using the denitrifier method, it was not possible to always achieve consistent peak areas. Instead of discarding low-peak-area samples, however, we wanted to establish a method to estimate the uncertainties associated with individual samples based on their peak area. This uncertainty arises from a correction scheme for δ(¹⁵N) that assumes constant blank : sample quantity ratios. What follows is a method for estimating this uncertainty, using the slope and intercept of the calibration curve and blank peak area.

In brief, the first step of this method is to calculate the peak area and δ(¹⁵N) of the blank for an individual run (batch of bacteria) using the slope and intercept of the nitrate isotope calibration curve (Casciotti et al., 2002). Then, a range of theoretical measured δ(¹⁵N) is calculated for a set of dummy samples based on a range of “actual” δ(¹⁵N), a range of theoretical peak areas, and the peak area and δ(¹⁵N) of the blank. Then, we correct each of these theoretical measured δ(¹⁵N) values with the calibration curve, as one would do normally, to obtain δ(¹⁵N_corrected) for each dummy sample. We estimate the error for each dummy sample by comparing the δ(¹⁵N_corrected) we have calculated to the δ(¹⁵N_sample) we have assigned to it. Then, for each run (and associated blank), we can fit a function through these errors, their corresponding peak areas, and the corresponding δ(¹⁵N_sample). We can then feed this function the peak area and measured δ(¹⁵N) of actual samples in that run to estimate their uncertainties.

Figure A1 δ(¹⁵N_error) vs. peak area for a range of dummy samples with measured peak areas from 0.5 to 10 Vs, based on a blank peak area of 0.15 Vs and δ(¹⁵N_blank) of −69.3 ‰.

Figure A2 δ(¹⁵N_error) vs. peak area and δ(¹⁵N_sample) for a range of dummy samples with peak areas from 0.5 to 10 Vs and δ(¹⁵N_sample) from −20 ‰ to 180 ‰, based on a blank peak area of 0.15 Vs and δ(¹⁵N_blank) of −69.3 ‰.

In practice, we start with a simple mass balance that states that the measured δ(¹⁵N) is a function of the sample δ(¹⁵N), sample peak area A_sample, blank δ(¹⁵N), and blank peak area A_blank:

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}\mathit{\delta }\left({}^{\mathrm{15}}{N}_{\mathrm{measured}}\right)\left(A_{\mathrm{measured}}\right)& =\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}_{\mathrm{sample}}\right)\left(A_{\mathrm{sample}}\right)\\ & +\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}_{\mathrm{blank}}\right)\left(A_{\mathrm{blank}}\right),\end{array}\end{array}$$

where δ(¹⁵N_measured) is the measured δ(¹⁵N), A_measured is the measured peak area, δ(¹⁵N_sample) is the actual sample δ(¹⁵N), A_sample is the peak area attributable to sample N, δ(¹⁵N_blank) is the δ(¹⁵N) of the blank, and A_blank is the peak area attributable to blank N. Dividing through by A_measured,

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}\mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{measured}}\right)& =\mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{sample}}\right)\left({\displaystyle \frac{A_{\mathrm{sample}}}{A_{\mathrm{measured}}}}\right)\\ & +\mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{blank}}\right)\left({\displaystyle \frac{A_{\mathrm{blank}}}{A_{\mathrm{measured}}}}\right).\end{array}\end{array}$$

Equation (A2) can be expressed as a linear equation, $y=mx+b$, where m is the slope of δ(¹⁵N_measured) vs. δ(¹⁵N_sample) and b is the y intercept. Thus

$$\begin{array}{}\text{(A3)}& {\displaystyle }m=\left({\displaystyle \frac{A_{\mathrm{sample}}}{A_{\mathrm{measured}}}}\right)\text{(A4)}& {\displaystyle }b=\mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{blank}}\right)\left({\displaystyle \frac{A_{\mathrm{blank}}}{A_{\mathrm{measured}}}}\right).\end{array}$$

We can obtain the mean blank peak area A_blank from the slope and the mean peak area of the measured reference materials (A_measured):

$$\begin{array}{}\text{(A5)}& {\displaystyle }\left({\displaystyle \frac{A_{\mathrm{blank}}}{A_{\mathrm{measured}}}}\right)=\mathrm{1}-\left({\displaystyle \frac{A_{\mathrm{sample}}}{A_{\mathrm{measured}}}}\right)=\mathrm{1}-\left(m\right)\text{(A6)}& {\displaystyle }{A}_{\mathrm{blank}}=\left[\mathrm{1}-\left(m\right)\right]\left(A_{\mathrm{measured}}\right).\end{array}$$

Finally, we obtain δ(¹⁵N_blank) from

$$\begin{array}{}\text{(A7)}& \mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{blank}}\right)=b/\left({\displaystyle \frac{A_{\mathrm{blank}}}{A_{\mathrm{measured}}}}\right)={\displaystyle \frac{b}{\mathrm{1}-\left(m\right)}}.\end{array}$$

We assign the dummy samples a range of theoretical measured peak areas, A_measured. The ratio of the blank peak area to the measured peak areas for a given sample is given by dividing A_blank (calculated from Eq. A6) by this theoretical peak area to obtain $\left(\frac{A_{\mathrm{blank}}}{A_{\mathrm{measured},i}}\right)$, where A_measured,i is the theoretical peak area for that sample. Then, the ratio of sample peak area to measured peak area for a given theoretical sample is given by

$$\begin{array}{}\text{(A8)}& \left({\displaystyle \frac{A_{\mathrm{sample}}}{A_{\mathrm{measured},i}}}\right)=\mathrm{1}-\left({\displaystyle \frac{A_{\mathrm{blank}}}{A_{\mathrm{measured},i}}}\right).\end{array}$$

As a first example, we assign all of the theoretical samples the same δ(¹⁵N_sample) of 180 ‰. Then, to obtain a range of theoretical measured δ(¹⁵N_measured), we plug the δ(¹⁵N_blank) calculated from Eq.  (A7), the range of theoretical peak areas A_measured,i, and this δ(¹⁵N_sample) into Eq. (A2):

$$\begin{array}{}\text{(A9)}& \begin{array}{rl}\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}_{{\mathrm{measured}}_i}\right)& =\mathrm{180}\mathrm{‰}\cdot \left({\displaystyle \frac{A_{\mathrm{sample}}}{A_{\mathrm{measured},i}}}\right)\\ & +\mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{blank}}\right)\left({\displaystyle \frac{A_{\mathrm{blank}}}{A_{\mathrm{measured},i}}}\right)\end{array}.\end{array}$$

We correct the range of $\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}_{{\mathrm{measured}}_i}\right)$ calculated from Eq. (A9) with the slope and intercept of the calibration curve δ(¹⁵N_sample) vs. δ(¹⁵N_measured):

$$\begin{array}{}\text{(A10)}& \mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}_{{\mathrm{corrected}}_i}\right)=m\left({\displaystyle \frac{A_{\mathrm{sample}}}{A_{\mathrm{measured},i}}}\right)+b.\end{array}$$

Then we calculate the error associated with each dummy sample using

$$\begin{array}{}\text{(A11)}& \mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{error}}\right)=\left|\mathit{\delta }\left({{}^{\mathrm{15}}\mathrm{N}}_{{\mathrm{corrected}}_i}\right)-\mathrm{180}\mathrm{‰}\right|.\end{array}$$

Following this exercise with a range of theoretical peak areas from 0.5 to 10 Vs produces the following curve (Fig. A1). It shows that these theoretical errors increase as peak area decreases, reflecting the basis of the error.

Repeating this exercise with a range of δ(¹⁵N_sample) values from −20 ‰ to 180 ‰ produces a 3D version of this curve (Fig. A2). This shows that the estimated uncertainty is highest for samples with δ(¹⁵N_sample) most divergent from δ(¹⁵N_blank) and for the peak areas most divergent from the reference materials.

Finally, we fit a function of the following form through these theoretical data:

$$\begin{array}{}\text{(A12)}& \mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{error}}\right)=a\cdot e^{c\cdot A_{\mathrm{sample}}}+d\cdot \mathit{\delta }\left({}^{\mathrm{15}}{\mathrm{N}}_{\mathrm{sample}}\right),\end{array}$$

where a, c, and d are constants, A_sample is the measured peak areas of the theoretical samples, and δ(¹⁵N_sample) is the assigned value for the dummy samples.

This procedure was repeated for each denitrifier run to produce coefficients a, c, and d specific to that set of analyses. Then, to estimate the uncertainty associated with each measurement, we used the corrected δ(¹⁵N) for each sample's δ(¹⁵N_sample) and its measured peak area for A_sample in Eq. (A12).