Effects of grain size and seawater salinity on magnesium hydroxide dissolution and secondary calcium carbonate precipitation kinetics: implications for ocean alkalinity enhancement

Understanding the impacts that mineral grain size and seawater salinity have on magnesium hydroxide (Mg(OH)₂) dissolution and secondary calcium carbonate (CaCO₃) precipitation is critical for the success of ocean alkalinity enhancement. We tested Mg(OH)₂ dissolution kinetics in seawater using three Mg(OH)₂ grain sizes (<63, 63–180 and >180 µm) at three salinities (∼36, ∼28 and ∼20). While Mg(OH)₂ dissolution occurred more quickly the smaller the grain size, salinity did not significantly impact measured rates. Our results also demonstrate that grain size can impact secondary CaCO₃ precipitation, suggesting that an optimum grain size exists for ocean alkalinity enhancement (OAE) using solid Mg(OH)₂. Of the three grain sizes tested, the medium grain size (63–180 µm) was optimal in terms of delaying secondary CaCO₃ precipitation. We hypothesise that in the lowest-grain-size experiments, the higher surface area provided numerous CaCO₃ precipitation nuclei, while the slower dissolution of bigger grain sizes maintained a higher alkalinity and pH at the surface of particles, increasing CaCO₃ precipitation rates and making them observable much more quickly than for the intermediate grain size. Salinity also played a role in CaCO₃ precipitation, where the decrease in magnesium (Mg) allowed secondary precipitation to occur more quickly, similar in effect size to another known inhibitor, i.e. dissolved organic carbon (DOC). In summary, our results suggest that OAE efficiency as influenced by CaCO₃ precipitation depends not only on seawater composition but also on the physical properties of the alkaline feedstock used.

1 Introduction

The concentration of carbon dioxide (CO₂) in the atmosphere remained in a relatively narrow band from ∼180 to ∼280 ppmv for 800 000 years but has risen rapidly over the last 250 years to approximately 420 ppmv today (Lüthi et al., 2008; Monnin et al., 2001; Siegenthaler et al., 2005). This is the result of increasing utilisation of fossil fuels, cement production and land-use change, driving subsequent global climate change (IPCC, 2021). While about 42 % of CO₂ emissions remain in the atmosphere and are mainly responsible for global warming, about 26 % are currently absorbed by the oceans, leading to ocean acidification (Friedlingstein et al., 2022; IPCC, 2021). To mitigate the effects of ocean acidification locally and slow down the increase in the Earth's global temperature, CO₂ reduction efforts are not sufficient, and carbon dioxide removal (CDR) strategies have become necessary as a supplement to emission reduction (Hoegh-Guldberg et al., 2019).

One emerging marine CDR approach is ocean alkalinity enhancement (OAE). Over long timescales, the natural CO₂-facilitated weathering of alkaline rocks supplies alkalinity to the oceans, influencing their CO₂ uptake potential and storage. OAE builds upon this weathering feedback in the Earth system and can be accomplished by actively spreading pulverised alkaline minerals in and around marine environments or by electrochemically removing acidity from seawater (Eisaman et al., 2023). In both cases, the seawater total alkalinity (A_T) is increased, thereby increasing the atmospheric CO₂storage capacity of seawater (GESAMP, 2019; Kheshgi, 1995). On local scales around areas where the OAE perturbation is performed, the increases in alkalinity and pH may also mitigate ocean acidification (Hartmann et al., 2013).

Recent studies have investigated the carbonate chemistry changes following OAE, and a major outcome was the risk of runaway calcium carbonate (CaCO₃) precipitation (Fuhr et al., 2022; Hartmann et al., 2023; Moras et al., 2022). There are several inorganic CaCO₃ precipitation mechanisms that have been described in the literature (Morse et al., 2007; Pytkowicz, 1965). CaCO₃ can precipitate homogeneously in the absence of solid or soluble organic and inorganic particles, pseudo-homogeneously in the presence of organic surfaces, and heterogeneously in the presence of mineral solids (Marion et al., 2009). The key parameter that governs whether precipitation occurs is the calcium carbonate saturation state (Ω), which is calculated from seawater Ca²⁺ and ${{\mathrm{CO}}_{\mathrm{3}}}^{\mathrm{2}-}$ concentrations as

$$\begin{array}{}\text{(1)}& \mathrm{\Omega }={\displaystyle \frac{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]\left[{{\mathrm{CO}}_{\mathrm{3}}}^{\mathrm{2}-}\right]}{K_{\text{sp}}}},\end{array}$$

where Ca²⁺ and ${{\mathrm{CO}}_{\mathrm{3}}}^{\mathrm{2}-}$ are the concentrations of calcium and carbonate in solution, respectively, and K_sp the solubility product of CaCO₃ in the solution. Ω is therefore closely related to the composition of the solution and its salinity but is also highly temperature dependent (Zeebe and Wolf-Gladrow, 2001). For aragonite, the CaCO₃ morphotype that inorganically precipitates in modern seawater, the saturation state (Ω_A) has to be higher than 12.3 for pseudo-homogeneous precipitation to occur in water with a salinity of 35 and at 25 °C (Marion et al., 2009). Homogeneous precipitation will occur at much higher Ω_A values, while heterogeneous precipitation will occur at much lower Ω_A but depends on the actual lattice compatibility of CaCO₃ with the mineral particles present (Morse et al., 2007; Zhong and Mucci, 1989). Another important aspect is that once precipitation becomes measurable, it will continue in a “runaway” fashion, i.e. quickly ramping up until it slows down once Ω_A approaches 1 again.

Several studies have reported such behaviour after the addition of alkaline minerals (Fuhr et al., 2022; Hartmann et al., 2023; Moras et al., 2022), with a critical threshold of Ω_A = ∼7.0 for the two calcium-based OAE minerals – calcium oxide (CaO) and calcium hydroxide (Ca(OH)₂) – and report precipitation stopping at Ω_A values of 1.8–2.0 (Moras et al., 2022). Precipitation has also been observed for magnesium-based minerals such as brucite or reagent-grade magnesium hydroxide – Mg(OH)₂ – but actual thresholds have not been determined (Hartmann et al., 2023). Furthermore, the effect of grain size, the determining factor for the surface area available for mineral dissolution and CaCO₃ precipitation, has not been studied. Similarly, the effect of potential CaCO₃ precipitation inhibitors, such as seawater magnesium (Mg) concentrations governed by salinity and dissolved organic carbon (DOC), are relatively unknown (Chave and Suess, 1970; Millero et al., 2001; Pan et al., 2021; Zhong and Mucci, 1989). This study focuses on the impact of Mg(OH)₂ grain size on its dissolution kinetics in natural seawater as well as the impact of salinity. Furthermore, the subsequent runaway CaCO₃ precipitation that is triggered, along with its kinetics, are reported. Finally, the effects of increased Mg and DOC in seawater on the CaCO₃ precipitation process is explored.

2 Material and methods

2.1 Seawater collection and experimental setup

Using 25 L jerrycans, seawater was collected at Broken Head, New South Wales, Australia ($\mathrm{25}\mathit{°}{\mathrm{42}}^{\prime }{\mathrm{12}}^{\prime \prime }$ S, $\mathrm{153}\mathit{°}{\mathrm{37}}^{\prime }{\mathrm{03}}^{\prime \prime }$ E), about 200 m from the shore to avoid sampling sand and suspended particles. The collected seawater was stored in the dark at 4 °C for 3 d to reduce microbial activity and to allow particles to settle to the bottom, facilitating filtration. The entire contents of the jerrycans were then sterile filtered using a peristaltic pump and a 0.2 µm Whatman Polycap 75 AS filter before being stored in cleaned and autoclaved 25 L polycarbonate bottles. Prior to conducting the experiments, each seawater batch was equilibrated to laboratory air pCO₂ by bubbling it with H₂O-saturated air for at least a week (Moras et al., 2023). This ensured comparable starting conditions for the various experiments, with a calculated starting pCO₂ of 420.6 ± 28.6 µatm in all experiments. All experiments utilised reagent grade Mg(OH)₂ (>98 %, supplied by Atlas Materials) that had been ground in a pulveriser laboratory mill.

2.2 Grain size and salinity experiments

Approximately 1.5 L of seawater was placed in a clean 2 L borosilicate 3.3 beaker surrounded by a water jacket set to 21 °C and controlled by a TK-1000 tank chiller line. A floating lid with three ports was placed on the water surface, allowing concurrent Mg(OH)₂ addition, pH measurement and water sampling. After Mg(OH)₂ addition, the seawater was incubated for 18 h to allow for full Mg(OH)₂ dissolution. Thereafter the beaker contents were transferred to a clean 1 L borosilicate 3.3 Schott bottle that was tightly closed without any headspace to minimise CO₂ ingassing. The bottle was placed in a dark room on a stirring platform at 200 rpm at room temperature (24.8 ± 1.3 °C). All grain size and salinity treatments were run in triplicate for up to 34 d.

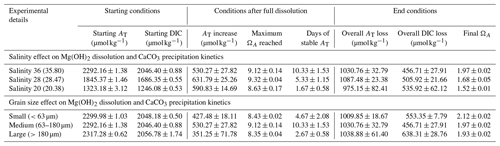
For the grain size experiments, three grain size ranges were produced using two stainless steel sieves with 63 and 180 µm mesh sizes. The medium range, i.e. 63–180 µm, was also used for the salinity experiments at ∼36, ∼28 and ∼20. The lower-salinity seawater was produced by mixing natural seawater with MilliQ water. Exact salinities of the 200 mL of seawater samples equilibrated to room temperature in a gas-tight polycarbonate container were determined by measuring conductivity and temperature with a 914 pH/conductometer and converting to salinity using the 1978 practical salinity scale (Lewis and Perkin, 1981). For all experiments, Mg(OH)₂ additions were adjusted to yield an Ω_A of ∼9 (Table 1) to allow for a significant A_T increase and secondary CaCO₃ precipitation, based on previously found thresholds for CaO and Ca(OH)₂ and with the assumption that the CaCO₃ inhibition role of Mg²⁺ requires a higher Ω_A for CaCO₃ precipitation within days (Moras et al., 2022). Varying amounts of Mg(OH)₂ were used in the salinity experiments. The decrease in dissolved Ca following dilution with MilliQ led to higher amounts of Mg(OH)₂ being added with decreasing salinity to reach a similar Ω_A of about 9. Furthermore, preliminary tests conducted with the Mg(OH)₂ powder used for these experiments, despite the powder having reagent-grade properties (>98 % pure), have shown that only about 75 % of the theoretical maximum A_T was generated. Therefore, the Mg(OH)₂ additions were adjusted accordingly, with additions varying from 23.3 mg kg⁻¹ in the salinity 36 experiments (and all grain size experiments) to 30.2 mg kg⁻¹ in the salinity 20 experiments.

Table 1 Summary of the main experimental parameters for each of the incubations investigating the salinity and grain size effects on Mg(OH)₂ dissolution and CaCO₃ precipitation kinetics. “Days of stable A_T” encompasses the time between maximum ΔA_T recorded and the start of CaCO₃ runaway precipitation.

In all experiments, the first 18 h of reaction were monitored by measuring the pH on the free scale (pH_F) with an Aquatrode Plus with Pt1000 (Metrohm) connected to an 888 Titrando (Metrohm) before transferring the contents of the 2 L beaker into the clean 1 L Schott bottles. A sample for A_T and dissolved inorganic carbon (DIC) measurements was taken before Mg(OH)₂ addition and after 18 h. The temperature and pH_F were then recorded twice a day until a sudden drop in pH_F was observed, linked to CaCO₃ precipitation. A new sample for A_T and DIC measurements was then taken. The time at which CaCO₃ runaway precipitation was deemed to have started was considered to be the last stable pH_F measurement before the sudden drop. A_T and DIC samples were taken at varying intervals during CaCO₃ precipitation (see Figs. 2 and 4) to cover most of the CaCO₃ precipitation process, and at least 300 mL of water was reserved for two A_T and DIC samples at the end of the experiment. Between 9 and 10 A_T and DIC samples per experiment were collected to monitor the changes in DIC and A_T over time. Their decrease in a 2:1 ratio was further used to reconstruct A_T and DIC from pH measurements in the experiments on the effect of Mg and DOC on CaCO₃ precipitation (see below for details).

2.3 Manipulation of dissolved organic carbon and magnesium

Seawater dilution with MilliQ to decrease salinity also decreased the concentration of various seawater components, such as Mg and DOC. To disentangle a potentially general effect of salinity on Mg(OH)₂ dissolution and secondary precipitation kinetics from reductions in Mg and DOC concentrations, two additional experiments were designed. In the first, the experiments at a salinity of 20 were replicated, but the Mg concentration was increased to a concentration representative of a salinity of 35, i.e. 52.8 mmol kg⁻¹ (Dickson et al., 2007), by the addition of magnesium chloride (MgCl₂) from a 3 M stock solution (molarity verified by inductively coupled plasma mass spectrometer measurements). This experiment was run in triplicate. For the second experiment, a DOC-enriched seawater solution at a salinity of 20 was produced by ultrafiltration (molecular weight cutoff of 2000 Daltons, Vivaflow200 Hydrosart, Sartorius). A DOC gradient was then created in five bottles by mixing the DOC-enriched salinity 20 seawater with the MilliQ-diluted seawater. The DOC concentrations ranged from approximately 120 to approximately 325 µmol kg⁻¹.

In both the Mg and DOC experiments, dissolution and secondary CaCO₃ precipitation kinetics were mainly monitored using pH_F measurements, although a sample for A_T and DIC measurement was also taken before Mg(OH)₂ addition and at the end of each treatment. These samples, coupled with the pH_F measurements, allowed the changes in A_T and DIC to be estimated over time. The reconstruction occurred in two steps, where the increase in pH following Mg(OH)₂ was assumed to be linked to an increase in A_T at constant DIC. Then, any decrease in pH was assumed to be due to CaCO₃ precipitation, so the estimated A_T and DIC loss after Mg(OH)₂ dissolution decreased in a 2:1 ratio, as observed in the salinity and grain size experiments. Finally, to account for CO₂ ingassing over time, the difference between estimated maximum A_T and final measured A_T was used as a proxy. Half of the difference, representing CaCO₃ precipitation, was used to estimate the theoretical DIC loss. Once compared to the final measured DIC, an ingassing rate was estimated.

2.4 Analytical procedures

The pH electrode was calibrated using three Metrohm buffer solutions (pH 4, 7 and 9), corresponding to a pH measurement on the free scale. A_T analyses were conducted using a potentiometric titration with an 848 Titrino Plus coupled to an 869 Compact Sample Changer from Metrohm. A 0.05 M HCl solution with the ionic strength adjusted to 0.72 mol kg⁻¹ (representative of a salinity of 35) using NaCl was used as the titrant (Dickson et al., 2007). The DIC concentration was measured using an Automated Infra-Red Inorganic Carbon Analyzer (AIRICA) coupled to a LI-COR Li7000 Infra-Red detector (Gafar and Schulz, 2018). Both A_T and DIC measurements were corrected against in-house reference material (previously calibrated against certified reference material), with measurement uncertainties of ±2.20 and ±1.98 µmol kg⁻¹ (Moras et al., 2023). Ω_A and carbonate chemistry speciation were calculated from measured A_T and DIC, providing temperature and salinity measurements, using CO2SYS (Sharp et al., 2021). To do so, the boric acid dissociation constant from Uppström (1974), the carbonic acid dissociation constant from Lueker et al. (2000) and the sulfuric acid dissociation constant from Dickson (1990) were selected.

For scanning electron microscopy (SEM), discrete samples of about 10 mL of A_T-enriched seawater were filtered through 0.2 µm polycarbonate filters (Whatman Cyclopore). These filters were rinsed with 20 mL of MilliQ to remove salts and dried overnight at 60 °C. Once dried, the filters were kept in a desiccator until analysis. The filters were attached to double-sided carbon tabs and placed on aluminium mounts before being coated with gold. SEM analysis was performed using a tabletop Scanning Electron Microscope TM4000 Plus from Hitachi coupled to an Energy Dispersive X-Ray (EDX) Analyser, allowing us to determine the elemental composition of observed particles.

The concentration of the MgCl₂ stock solution was measured by inductively coupled plasma mass spectrometer (ICP-MS) measurements using an Agilent 7700 ICP-MS coupled to a laser ablation unit (NWR213, Electro Scientific Industries, Inc.). Seawater reference materials from the National Research Council of Canada NASS-6 were used to correct the measurements. The DOC concentration of the DOC-enriched stock solution was determined using a Thermo Fisher Flash Elemental Analyzer after acidifying the sample with nitric acid (Carvalho, 2023).

3 Results

3.1 Grain size effects on Mg(OH)₂ dissolution kinetics

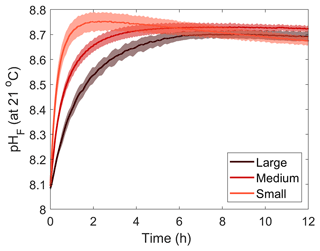
Three Mg(OH)₂ grain sizes were dissolved in seawater at a salinity of ∼36 (Fig. 1). The starting pH_F was similar for all incubations, at 8.11 ± 0.03, 8.09 ± 0.01 and 8.07 ± 0.03 for the small (<63 µm), medium (63–180 µm) and large (>180 µm) grain sizes, respectively. Upon dissolution, pH_F increased quite rapidly, reaching a maximum after about 2 h for the small-particle-size experiments and about 6 to 8 h in the medium- and large-particle-size experiments (Fig. 1). In each incubation, a logarithmic trend in pH_F was observed, with the dissolution being much quicker for smaller grain sizes. After 2 h, the maximum pH_F recorded for the smaller grain size was 8.76 ± 0.04, which continuously decreased to 8.68 ± 0.00 between 11 and 12 h after the addition of Mg(OH)₂. In contrast, the pH_F for the medium and larger grain size increased to 8.72 ± 0.00 and 8.68 ± 0.03, respectively, after about 8 h and remained stable thereafter (Fig. 1).

Figure 1 Changes in pH_F at 21 °C following dissolution of three Mg(OH)₂ grain sizes in natural seawater over 12 h. Each grain size was run in triplicate, with the averages presented as the solid lines and the standard deviation ranges as the transparent areas.

3.2 Grain size effect on CaCO₃ precipitation kinetics

The pH increase was reflected by increasing A_T, measured prior to the Mg(OH)₂ addition and 18 h later, by about 430, 530 and 350 µmol kg⁻¹, in the small-, medium- and large-grain-size incubations, respectively (Fig. 2). A_T remained stable for 3–7, 9–12 and 2–3 d before dropping in each grain size treatment (small, medium and large). In all incubations, A_T concentrations decreased in a similar fashion, with a strong drop in the first 2 d before slowly decreasing for another week and stabilising. The overall A_T loss for the duration of the experiments was ∼1035 µmol kg⁻¹ in the medium- and large-grain-size incubations, while the A_T dropped by about 1010 µmol kg⁻¹ in the small-grain-size incubations (Table 1).

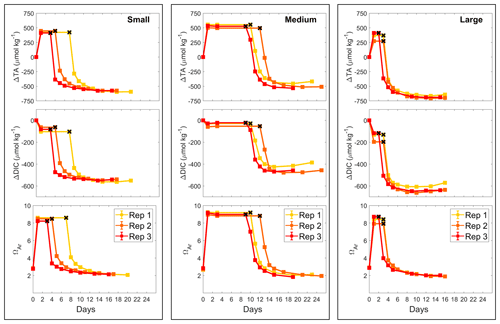
Figure 2 Changes in A_T, DIC and Ω_A during dissolution of three Mg(OH)₂ grain sizes in natural seawater over a maximum of 25 d. Three replicates were conducted for each grain size and are represented in red, orange and yellow. The last stable A_T and DIC conditions estimated by pH_F measurements are represented by black crosses.

The changes in Ω_A followed a similar pattern as those in A_T, increasing from ∼2.8 on average to ∼9.1 in the medium-grain-size incubation and to ∼8.4 in the small- and large-grain-size experiments. Ω_A decreased at the same time as A_T in the respective experiments, stabilising around ∼2.0 in all experiments.

Finally, a small drop in DIC was observed after Mg(OH)₂ addition in all experiments, of about 80, 30 and 140 µmol kg⁻¹ in the small-, medium- and large-grain-size incubations, respectively. The DIC then remained relatively stable until the rapid A_T drop, where the overall DIC drops for the small-, medium- and large-grain-size incubations were calculated at ∼550, ∼455 and ∼640 µmol kg⁻¹, respectively. While A_T and Ω_A remained stable after this drop, DIC increased slightly, which was particularly obvious in the medium- and large-grain-size incubations.

3.3 Salinity effect on Mg(OH)₂ dissolution kinetics

To test the effects of salinity on Mg(OH)₂ dissolution and CaCO₃ precipitation kinetics, three sets of experiments were conducted at three different salinities, i.e. 20.38, 28.47 and 35.80, using medium-grain-size Mg(OH)₂. From here on, the salinities of 20.38, 28.47 and 35.80 will be referred to as salinities of 20, 28 and 36, respectively. Similarly to the grain size experiments, the dissolution of Mg(OH)₂ occurred rapidly at all three salinities, with the maximum pH_F recorded after approximately 8 h (Fig. 3). Starting pH_F values were slightly different, recorded at 7.99 ± 0.05, 8.06 ± 0.01 and 8.09 ± 0.01 in the salinity 20, 28 and 36 incubations and increasing to a maximum of 9.19, ±0.00, 8.91 ± 0.00 and 8.72 ± 0.00, respectively. In all incubations, similar logarithmic trends were observed for pH_F (Fig. 3).

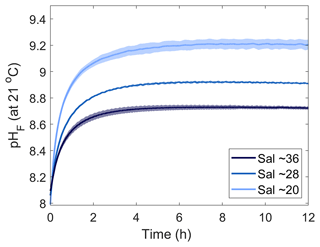
Figure 3 Changes in pH_F at 21 °C following Mg(OH)₂ dissolution in three different seawater salinities over 12 h. Each salinity has been run in triplicate, with the averages presented as the solid lines and the standard deviation ranges as the transparent areas. Please note that different maximum pH levels were reached because of increasing Mg(OH)₂ addition with decreasing salinity to reach a similar Ω_A.

3.4 Salinity effect on CaCO₃ precipitation kinetics

In all incubations, A_T increased as was suggested by the pH_F trends, by ∼590, ∼630 and ∼530 µmol kg⁻¹ in the salinity 20, 28 and 36 incubations, respectively (Fig. 4). A_T remained stable for different periods of time in each treatment: 1–2 d in the salinity 20 incubations, 4–6 d in the salinity 28 incubations and 9–12 d in the salinity 36 incubations. Thereafter, A_T dropped quickly for the first 2 d in all incubations and stabilised quickly in the salinity 20 experiments. In the salinity 28 incubations, A_T slowly decreased over 5 d after the first strong drop and then stabilised, while in the salinity 36 experiments, the A_T decreased slowly over 7 d after the initial drop before finally stabilising. The overall A_T losses for the salinity 20, 28 and 36 experiments were estimated at ∼975, ∼1090 and ∼1030 µmol kg⁻¹, respectively (Table 1).

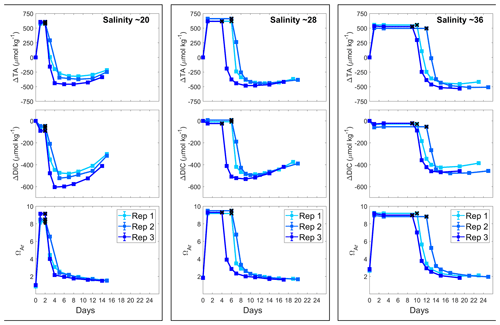
Figure 4 Changes in A_T, DIC and Ω_A during Mg(OH)₂ dissolution in three different salinities over a maximum of 25 d. Three replicates were conducted for each salinity and are represented in shades of blue. The last stable A_T and DIC conditions estimated by pH_F measurements are represented by black crosses.

Ω_A values followed a similar pattern as A_T in all experiments. The starting Ω_A values were different, varying from 1.0 for the salinity 20 incubations to 2.0 and 2.8 for the salinity 28 and 36 incubations, respectively. Similarly, following Mg(OH)₂ addition, Ω_A quickly increased to reach 8.6, 9.3 and 9.1 with increasing salinity. Together with A_T, Ω_A eventually started dropping and then stabilised at different values, around 1.5 for a salinity of 20, around 1.7 for a salinity of 28 and around 2.0 for a salinity of 36.

Finally, DIC also decreased after Mg(OH)₂ addition. An initial DIC drop was observed directly after Mg(OH)₂ addition: about 60 µmol kg⁻¹ at the lowest salinity and 30 µmol kg⁻¹ at the highest salinity. At a salinity of 28, a much smaller DIC drop was observed in one replicate. After a period of stable DIC conditions, DIC also dropped in a similar fashion as A_T, with an overall DIC loss of about 535, 505 and 455 µmol kg⁻¹ from the lower- to higher-salinity incubations. While no DIC increase was observed towards the end of the experiment in the salinity 36 incubations, strong DIC increases were observed in the salinity 28 incubations and even more prominent ones in the salinity 20 incubations.

3.5 Magnesium and DOC effects on CaCO₃ precipitation

A similar pattern was observed for the salinity 20 experiments at natural and increased Mg concentrations, i.e. a rapid increase in A_T reaching a maximum on day 1, followed by a steady decline over the next 2 weeks (Fig. 5). The maximum ΔA_T reached was slightly different, with about 600 µmol kg⁻¹ of A_T increase in the salinity 20 experiment and nearly 800 µmol kg⁻¹ in the salinity 20+MgCl₂ incubations. Another interesting difference is the slower A_T decrease with MgCl₂ compared to that at a salinity of 20. After about 18 d, the lowest ΔA_T was reached, while it only took about 6 d for the salinity 20 ΔA_T to reach the minimum. Similarly, DIC appeared to decrease less rapidly when MgCl₂ was present, and Ω_A followed a similar trend after the initial strong increase.

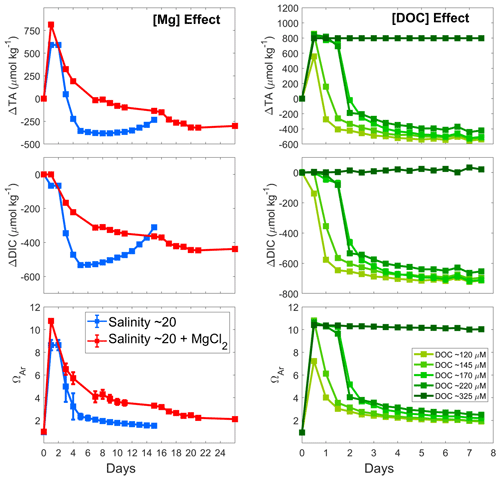
Figure 5 Comparison of the calculated A_T, DIC and Ω_A changes at 21 °C following Mg(OH)₂ addition to seawater with a salinity of 20 (blue), to seawater with a salinity of 20 and Mg concentration equal to a salinity of 35 (red), and to seawater with varying DOC concentrations (green). Values reported in the Mg effect panels represent the average of triplicate experiments run at a salinity of 20 and a salinity of 20+MgCl₂, with standard deviations represented by the error bars.

Out of the five DOC experiments, four incubations showed a drop in A_T (Fig. 5). Similar maximum ΔA_T values were reached in most experiments, with a ΔA_T of ∼800 µmol kg⁻¹. However, in the incubation with ∼120 µmol kg⁻¹ DOC, A_T increased by only ∼600 µmol kg⁻¹. Following this increase, A_T decreased within a day in both the 120 and 145 µmol kg⁻¹ DOC incubations and stayed stable until day 3 in incubations with 170 and 220 µmol kg⁻¹. These four incubations also show a similar levelling pattern over time, even though it appears that in the higher DOC incubations the total loss in A_T was lower than for the lower DOC incubations. ΔDIC also followed a similar trend to ΔA_T, with an early drop at 120 µmol kg⁻¹ of DOC, a drop after 1 d at 145 µmol kg⁻¹ of DOC, and a slow decrease from day 1 and a stronger drop on day 2 at 170 and 220 µmol kg⁻¹ of DOC. Ω_A followed a very similar pattern to ΔA_T, with higher final Ω_A in the experiments with higher DOC concentrations. Finally, in the experiment with the highest DOC concentration, i.e. 325 µmol kg⁻¹, no drop in A_T, DIC or Ω_A was observed (the experiment was run for 42 d).

4 Discussion

4.1 Grain size and salinity effects on Mg(OH)₂ dissolution

Maximum Mg(OH)₂ dissolution directly after its addition was negatively correlated with grain size (Figs. 1 and 3). The smaller the grain size, the faster the maximum pH_F was reached, indicative of complete dissolution. This can be explained by the fact that smaller particles have a larger surface area per gram of material than larger particles do. The increasing dissolution rate with decreasing particle size is particularly noticeable when A_T changes were estimated using the pH_F data and starting DIC measurements (Fig. 6). Assuming a constant DIC over the first 30 min of reaction, i.e. no significant CaCO₃ precipitation and/or CO₂ ingassing, A_T can be reconstructed using CO2SYS. The maximum ΔA_T reached with the larger particle size occurred within 8 h, while it only took about 2 h for the ΔA_T to reach a maximum with the small particle size. The initial dissolution rate, i.e. within the first 30 min, was also significantly different between the various grain sizes. The A_T generation of smaller grain size particles was estimated at about 796.5 ± 7.1 µmol A_T mg⁻¹ min⁻¹. The medium particles dissolved about twice as slowly over the first 30 min, estimated at 391.6 ± 2.6 µmol A_T mg⁻¹ min⁻¹, while the larger grain sizes dissolved more than 4 times more slowly, at about 168.7 ± 6.9 µmol A_T mg⁻¹ min⁻¹. Another important difference between the smaller-grain-size experiments and the two others is the constant decrease in pH_F observed right after reaching the maximum pH_F value (Fig. 1). This decrease in pH_F can only be linked to either CaCO₃ precipitation decreasing A_T and ultimately pH_F or CO₂ ingassing increasing the dissolved CO₂ concentration and ultimately decreasing the pH_F. The constant and linear trend suggests that the latter is responsible for the decrease. If CaCO₃ precipitation was responsible for these pH_F changes, the changes would follow a similar pattern to a negative exponential function. This is due to the fact that the more CaCO₃ nucleates, the more surface area becomes available for further nucleation (Zhong and Mucci, 1989). However, in our case, the changes appear to be linear. Such a pattern is indicative of CO₂ ingassing at an early stage, i.e. before the ingassing starts plateauing, dictated by the difference between atmospheric and seawater pCO₂. Such ingassing is also occurring in the other experiments but is likely hidden by the pH_F increase occurring during the longer dissolution of Mg(OH)₂ with a bigger grain size.

For salinity, there was a difference in initial dissolution rates within the range of salinities tested, with dissolution rates for salinities of 36, 28 and 20 estimated at 391.6 ± 2.6, 359.8 ± 0.2 and 301.9 ± 0.3 µmol A_T mg⁻¹ min⁻¹, respectively. While these differences are not as significant as those in the grain size experiments, the dissolution rate decreased by about 23 % between salinities of 36 and 20. Overall, the A_T generation potential of smaller-grain-size Mg(OH)₂ (<63 µm) at a salinity of 36 was similar to that of Ca(OH)₂ (Moras et al., 2022) which was also sieved through a 63 µm filter. Assuming the same molar A_T generation potential, the same maximum Ω_A should have been reached. However, for Ca(OH)₂ it was ∼7.4, while our small-grain-size Mg(OH)₂ incubations reached a maximum Ω_A of ∼8.4. Such a difference is likely due to the difference in the starting conditions and experimental settings. In the experiments shown here, the starting Ω_A was ∼2.8, while it was about ∼2.5 in Moras et al. (2022). This is explained by the differences in the starting water composition and salinity ultimately affecting the final Ω_A despite similar A_T increases. Furthermore, higher amounts of Mg(OH)₂ were added compared to Moras et al. (2022), leading to a higher Ω_A and a higher theoretical ΔA_T if no early CaCO₃ nucleation occurred. However, dissolution kinetics appear to differ between the minerals, with Ca(OH)₂ dissolving within 20–30 min, while it took 2 h for Mg(OH)₂ to dissolve. These two minerals still dissolve at a relatively quick pace compared to other OAE feedstock, for instance olivine (Montserrat et al., 2017). Olivine took much longer to dissolve, with a maximum increase in recorded pH of ∼0.15 units within 4–9 d. Ca(OH)₂ and Mg(OH)₂ additions required ∼20 mg of materials, while to obtain such olivine results, more than 30 g of olivine were added per kg of filtered seawater, meaning that the A_T generation potential is several orders of magnitude lower.

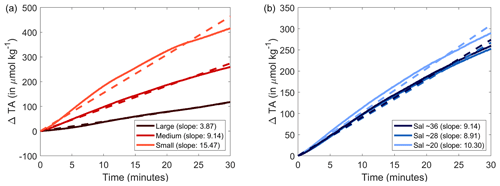
Figure 6 Normalised changes in calculated A_T over the first 30 min following the addition of Mg(OH)₂ with three different grain sizes to natural seawater (a) and to three different salinities (b). A linear fit was calculated and is represented by the dashed line, and each slope is reported in the legend in parentheses.

4.2 Grain size and salinity effects on CaCO₃ precipitation

In all experiments, Mg(OH)₂ additions were chosen to reach an Ω_A at which secondary CaCO₃ precipitation would be expected based on our experience with CaO and Ca(OH)₂ (Moras et al., 2022). Based on our suspicion that CaCO₃ might precipitate onto magnesium-rich particles less easily than onto calcium-rich particles, we chose a saturation state of ∼9, slightly higher than the level of ∼7 observed for CaO and Ca(OH)₂ (Moras et al., 2022). Precipitation kinetics were similar for all grain sizes; i.e. after the first precipitation was observed, a new steady state was achieved in about 2 weeks. Precipitation seemingly stopped at Ω_A values close to 2.0 in experiments with seawater at a salinity of 36, similar to observations made by Moras et al. (2022) using CaO and Ca(OH)₂. For the smallest grain size, A_T was stable for 3–7 d, which is longer than what has been observed for CaO and Ca(OH)₂ of the same size (Moras et al., 2022). This could be related to higher lattice compatibility of CaCO₃ for calcium-based minerals when it comes to precipitation onto mineral surfaces (Lioliou et al., 2007). Interestingly, however, the rate at which CaCO₃ precipitated was similar to that of CaO and Mg(OH)₂, while Ca(OH)₂ took almost twice as long to reach a new steady state (compare Fig. 1 to Fig. 2 in Moras et al., 2022).

A_T remained stable for longer, i.e. 9–12 d when using medium grain size. However, similarly to the smaller-grain-size experiments, A_T was also less stable with at a larger grain size, i.e. 2–3 d. As such, there appears to be an optimum grain size for keeping A_T stable for longer. To explain this, there must be two opposing processes at work. As discussed earlier, smaller particles have larger surface areas per gram of material than larger ones; i.e. smaller particles in our experiments had on average more than 23 times the area of larger particles for the same amount of material, assuming round particles of 63 and 180 µm, respectively. Hence, heterogeneous precipitation will be quicker for smaller particles (Zhong and Mucci, 1989). In contrast, the mechanism that could favour quicker precipitation for larger particles with smaller surface areas remains to be understood. Here, it could be higher pH levels and hence Ω_A that is reached at a particle's surface with larger diffusive boundary layer. Hence, pH and Ω_A levels are likely to be much higher and remain higher for longer due to the slower dissolution of larger particles at the site of CaCO₃ nucleation, which positively affects CaCO₃ precipitation rates.

At varying salinities, CaCO₃ precipitation became noticeable at different points in time: earlier at low salinity and later at higher salinity. While the first assumption was that at lower salinity the decrease in Ca would prevent early CaCO₃ precipitation, it appears that another mechanism is at play. The natural CaCO₃ inhibition potential of seawater due to dissolved Mg and DOC concentrations was affected during MilliQ dilution. It now appears that at a lower salinity, the decrease in inhibition allowed CaCO₃ precipitation to occur despite a decrease in Ca and starting Ω_A. Under such circumstances, early CaCO₃ nucleation onto yet-to-be-dissolved Mg(OH)₂ particles would occur at a faster rate at a lower salinity, which could be explained by the early drops in DIC after the addition of Mg(OH)₂. The absence of such a decrease in the salinity 28 experiments is an interesting outcome but could be explained by early CO₂ ingassing. The increase in DIC through CO₂ ingassing could have compensated for the DIC decrease from early CaCO₃ formation.

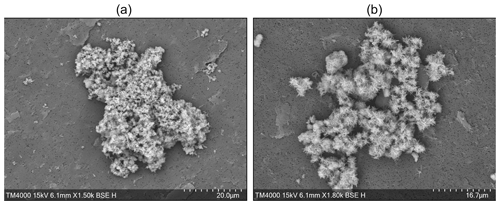
While EDX analysis did not, to our surprise, reveal significant magnesium concentrations in early precipitated aragonite crystals, i.e. ∼18 h after Mg(OH)₂ addition, some aragonite crystals were observed early on. The presence of Mg could have been expected if CaCO₃ precipitated heterogeneously onto Mg(OH)₂ particles (Fig. 7). The absence of Mg after EDX analysis suggests that while some Mg(OH)₂ could have been used as precipitation nuclei for CaCO₃ early on, it completely dissolved within the first 18 h. Only the freshly precipitated CaCO₃ would then remain in suspension, eventually acting as precipitation nuclei for runaway CaCO₃ precipitation. Finally, it is interesting to highlight that some traces of early aragonite crystals were present in all experiments and that the needle-shaped crystals were 2 to 3 times smaller in the larger-grain-size experiments than those sampled at the end of the medium-grain-size experiments (Fig. 7). One explanation that supports the previously mentioned boundary layer theory is that the larger-grain-size particles dissolving at a slower pace maintained an Mg-rich environment, while CaCO₃ started nucleating. The presence of this Mg during nucleation could have ultimately prevented CaCO₃ from fully forming bigger, needle-like crystals. However, these are speculations that are hard to prove or disprove.

Figure 7 SEM images of aragonite crystals sampled ∼18 h after the addition of larger-grain-size Mg(OH)₂ (a) and sampled at the end of the medium-grain-size incubations (b).

4.3 The role of dilution and potential effects of Mg and DOC concentrations

The role of Mg in inhibiting CaCO₃ nucleation is well known (Morse et al., 2007; Pan et al., 2021; Pytkowicz, 1965). Another known CaCO₃ nucleation inhibitor is organic matter, particularly dissolved organic matter (Chave and Suess, 1970). While the role of organic matter is not as well understood as that of Mg, both have been linked to a decrease in CaCO₃ nucleation and precipitation rates.

In our experiments involving dilution with MilliQ water, all dissolved components of the seawater were diluted, including Mg and DOC. Such decreases could explain the quicker CaCO₃ precipitation in the salinity 20 experiments compared to a salinity of 36, as lower Mg and DOC concentrations did not inhibit precipitation as they did in the higher-salinity treatments. To test this, a new salinity 20 batch was prepared in triplicate and Mg was added to raise the total Mg concentration to ∼52 mmol kg⁻¹, similar to the Mg concentration in natural seawater at a salinity of 35. The Mg increase did affect CaCO₃ precipitation kinetics, as shown by changes in A_T (Fig. 5): it was slightly slower and apparently reached a new steady state at higher ΔA_T and Ω_A. Furthermore, it is important to highlight that despite CaCO₃ precipitation being triggered at a similar time, i.e. within 1 to 2 d, a difference was observed regarding the maximum ΔA_T reached. In the salinity 20+MgCl₂ experiments, the maximum ΔA_T value was higher than the one in the salinity 20 experiments. This suggests that with a higher dissolved Mg concentration, less CaCO₃ is precipitated early on. Following this early precipitation, an overall slower precipitation rate is observed until reaching a steady state (Fig. 5).

However, the slightly reduced CaCO₃ precipitation rate due to decreased Mg concentration alone cannot explain such stark differences in A_T stability between the salinity 36 and 20 experiments (Fig. 4). It is most likely linked to the decrease in both Mg and DOC concentrations when diluting with MilliQ. The gradient of five salinity 20 replicates with increasing DOC concentrations clearly showed that secondary CaCO₃ precipitation could be delayed by modifying the DOC concentrations alone. For instance, secondary precipitation became measurable after 12 h at DOC concentrations of 120 µmol kg⁻¹, i.e. a salinity of 35 diluted to 20, but there was almost no secondary precipitation at a DOC concentration of 325 µmol kg⁻¹, i.e. about 1.5 times higher than in the salinity 35 experiment. CaCO₃ precipitation was delayed by about 2 d when doubling the DOC concentration and completely prevented at even higher levels (Fig. 5) within the time frame of the experiment (1 week). Together, these data suggest that seawater DOC and Mg act in synergy when it comes to inhibiting CaCO₃ precipitation.

Another interesting finding was the new steady state reached after runaway CaCO₃ precipitation. In natural seawater at a salinity of 36, the equilibrated Ω_A was estimated around 2.0, which is about 0.8 units lower than the starting conditions (Fig. 4). The decrease in Ω_A after runaway precipitation has important implications for OAE: when CaCO₃ precipitates in a runaway fashion, seawater can become more acidic than it was prior to mineral dissolution and less able to sequester atmospheric CO₂ (Moras et al., 2022). While further work is required to understand these carbonate chemistry mechanisms at lower salinities, we can note that after runaway precipitation in seawater at a salinity of 20, the final Ω_A was higher than the starting one. Such a difference is likely due to the lower starting Ca²⁺ concentration at a lower salinity.

5 Conclusions

One main objective of this research was to assess the dissolution of Mg(OH)₂ in seawater at varying salinities using different mineral grain sizes and report on the subsequent CaCO₃ precipitation kinetics. The dissolution of Mg(OH)₂ in natural seawater occurred at a much faster rate when using grain sizes lower than 63 µm due to the higher surface area in contact with seawater. In contrast, bigger particles (>63 µm) took about 4 times as long to fully dissolve. In all experiments, CaCO₃ precipitation occurred in a runaway fashion; i.e. after a period of seeming stability, A_T decreased rapidly before a new steady state was reached at which A_T concentrations were far lower than prior to the Mg(OH)₂ addition. Such a pattern was also observed for Ca-rich minerals but at lower Ω_A. While further research is required to precisely determine the critical Ω_A for both Ca- and Mg-rich minerals, the longer time for the initiation of CaCO₃ runaway precipitation and the overall higher Ω_A may suggest that Mg(OH)₂ is a safer alkaline feedstock for OAE. One major finding of this research was that two processes seem to occur during CaCO₃ precipitation in relation to grain size, where in one process the higher surface area of smaller particles could increase precipitation rates, while the second may maintain higher pH around larger particles due to a larger diffusive boundary layer compared to smaller particles, which increased precipitation rates. Hence, there appears to be an optimum grain size to minimise secondary CaCO₃ precipitation. The second objective of this research was to understand the role of salinity in Mg(OH)₂ dissolution and CaCO₃ precipitation kinetics. While no obvious changes in dissolution were observed, CaCO₃ precipitation differed, with quicker precipitation observed at lower salinities. The decrease in Mg concentrations was identified as the root cause, although in our experiments it was also linked to the lowered DOC concentration, an artefact of low-salinity seawater preparation when diluted with MilliQ. Nevertheless, this highlights the importance of DOC in modifying CaCO₃ precipitation kinetics and hence A_T stability.