the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Bias in calculating gross nitrification rates in forested catchments using the triple oxygen isotopic composition (Δ17O) of stream nitrate
Urumu Tsunogai
Fumiko Nakagawa
A novel method has been proposed and applied in recent studies to quantify gross nitrification rate (GNR) in forested catchments using the triple oxygen isotopic composition (Δ17O) of stream nitrate. However, the equations used in these calculations assume that the Δ17O value of nitrate consumed through assimilation or denitrification in forest soils is equal to the Δ17O value of stream nitrate. The GNR estimated from the Δ17O value of stream nitrate was significantly higher than the GNRs in our simulated calculations for a forested catchment where the soil nitrate had Δ17O values higher than those the stream nitrate. Given that most reported soil nitrate in forested catchments showed Δ17O values higher than those of the stream nitrate, we concluded that the GNR estimated from the Δ17O value of stream nitrate was, to an extent, an overestimate of the actual GNR.
- Article
(875 KB) - Full-text XML
-
Supplement
(381 KB) - BibTeX
- EndNote
Nitrate () is an important nitrogen nutrient for primary production in soils. Nitrification is the microbial process that produces in forested ecosystems. Thus, quantifying the nitrification rate can assist in the evaluation of the present and future states of forested ecosystems. The net nitrification rate can be estimated from an increase in concentration during a certain period. However, the gross nitrification rate (GNR), which includes the net nitrification rate plus the consumption rate of (e.g., through plant assimilation or denitrification), reflects the internal N cycling better than the net nitrification rate (Bengtsson et al., 2003), especially in forested ecosystems. Although the net nitrification rate is often negligible (Stark and Hart, 1997), the consumption rate is significant in forested ecosystems, such that the GNR often exceeds the net nitrification rate by several orders of magnitude (Verchot et al., 2001).
Recent studies have successfully estimated the GNR in aquatic environments, such as lakes, using the Δ17O values of as a conservative tracer to determine the mixing ratio between atmospheric nitrate () and biologically produced nitrate () (Tsunogai et al., 2011, 2018). The is deposited in the water environment, while is produced through nitrification. The always shows a Δ17O value close to 0 ‰ because its oxygen atoms are derived from either terrestrial O2 or H2O through nitrification. Contrarily, the always displays an anomalous enrichment in 17O with Δ17O value being approximately ‰ in Japan (Tsunogai et al., 2010, 2016; Ding et al., 2022, 2023) because of oxygen transfers from atmospheric ozone (Michalski et al., 2003; Nelson et al., 2018). Additionally, Δ17O is almost stable during “mass-dependent” isotope fractionation processes (Michalski et al., 2004; Tsunogai et al., 2016). This is because possible variations in the δ17O and δ18O values during the processes of biogeochemical isotope fractionation follow the relation of δ17O ≈ 0.5 δ18O, which cancels out the variations in the Δ17O value. Thus, regardless of the partial consumption through denitrification or assimilation after deposition in a water column, the Δ17O can be used as a conservative tracer of to calculate the mixing ratio of to total () in a water column using the following equation:
where the Δ17Oatm and Δ17O denote the Δ17O values of and dissolved in the water environment, respectively. Using the ratio estimated from the Δ17O value of in a lake water column and the deposition rate of into the lake, the GNR (i.e., production rate of ) can be successfully estimated. This approach works because the ratios are homogeneous in the water column due to the active vertical mixing; thus, we can constrain the ratios of consumed in the lake water column (Tsunogai et al., 2011, 2018).
In addition to applications in water environments, the Δ17O method has been applied to forested catchments to determine GNR (Fang et al., 2015; Hattori et al., 2019; Huang et al., 2020). Using the deposition flux of into the catchment and the leaching flux of unprocessed and via streams, the GNR in a forested catchment was estimated similarly to the estimation for water environments (Fang et al., 2015). However, unlike in water environments, where the ratio of nitrate consumed in the water column can be easily measured, it is often difficult to determine the ratio of consumed in soil layers. Consequently, past studies have approximated these values as equal to those of stream leached from forested catchments without actual observation (Fang et al., 2015; Hattori et al., 2019; Huang et al., 2020). Such an approximation should be used with extreme caution, as the ratios (Δ17O values) of soil are not always equal to those of stream (Hattori et al., 2019; Rose, 2014; Nakagawa et al., 2018). To clarify the details of the approximation and its impact on the final estimated GNR, we present an accurate relationship between the Δ17O of soil and the GNR using basic isotope mass balance equations. Thereafter, we present a possible range of variation in the GNRs estimated for a forested catchment, using parameters such as Δ17O values of stream reported in a past study. Finally, we compared the GNRs estimated in this study with those obtained from the Δ17O values of stream .
The total mass balance equation of including the GNR in catchments can be expressed as follows:
where , GNR, , , and GDR denote the deposition flux of into the catchment, GNR in the catchment, leaching flux of from the catchment, uptake rate of in the catchment, and gross denitrification rate in the catchment, respectively.
The isotope mass balance for each Δ17O value of in the catchment can be expressed using a similar equation:
where , , , , and denote the Δ17O value of deposited into the catchment, that of the produced through nitrification, that of the leached from the catchment, that of the assimilated by plants and other organisms in the catchment, and that of the decomposed through denitrification in the catchment, respectively.
If the Δ17O values of the in the forested soil layers, where the was consumed through assimilation or denitrification, are equal to the Δ17O value of in the stream, we could obtain Eq. (4):
Consequently, by combining Eqs. (3) and (4), we could obtain Eq. (5):
We could estimate the GNR using Eq. (6) obtained from Eqs. (2) and (5) because we can approximate the Δ17O values of produced through nitrification () to 0 (Michalski et al., 2003; Tsunogai et al., 2010):
Equation (6) corresponds to the equations used in previous studies to quantify the GNR in the forested catchments (Eq. 4 in Fang et al., 2015; Eq. 8 in Hattori et al., 2019; Eq. 4 in Huang et al., 2020).
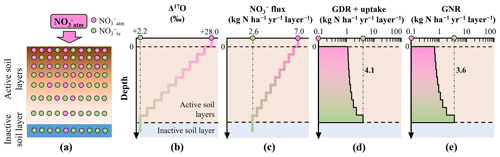
Figure 1Distribution of in the simulated forested soil with heterogeneous distribution of Δ17O values of (a). Vertical distribution of the following parameters in the forested soil: assumed Δ17O values of (b), assumed leaching flux of (c), estimated consumption rate (GDR + uptake) (d), and estimated GNR (e).
The Δ17O values of in forested soil layers should be equal to those of stream in Eq. (6), as presented in Eq. (4) to obtain Eq. (6). While the number of simultaneous observations of the oxygen isotopes of in soil and stream in a given forested catchment is limited (Hattori et al., 2019; Osaka et al., 2010; Rose, 2014; Nakagawa et al., 2018), the observations showed that the oxygen isotopic ratios of soil are often heterogeneous. In addition, the oxygen isotopic ratios of soil mostly exceeded those of stream . Different from water environments, vertical mixing of water and soil is limited in forested soil, so the Δ17O values of soil are often heterogeneous. For example, Hattori et al. (2019) found a decreasing Δ17O trend in soil with depth, ranging from over +20 ‰ at the surface to less than +3 ‰ at depths of 25–90 cm. Additionally, more than 60 % of the soil samples exhibited Δ17O values significantly higher than those of stream determined simultaneously ( + 1 to +3 ‰). A similar trend in the vertical distribution was observed in the δ18O values of in another forested catchment, from above +35 ‰ at the surface soil to less than +10 ‰ at depths of 30–50 cm from the soil surface (Osaka et al., 2010). In addition, most of the soil also exhibited δ18O values higher than those of the stream (Osaka et al., 2010). Rose (2014) monitored the horizontal distribution of the Δ17O of soil by randomly setting 15 tension-free lysimeters at depths of 0–10 cm in a 39 ha forested catchment. They reported significantly higher Δ17O values in soil ( 5.8 ‰ on average) than those of stream (+0.5 ‰ on average) leached from the forested catchment. As most fine roots and root biomass are concentrated in the top 10 cm of the soil in forested catchments (Jackson et al., 1996; Li et al., 2020), most assimilation (uptake reactions) of should occur in that top 10 cm of soil. Consequently, the significant difference in the Δ17O values between soil and stream , particularly in surface soil layers, implies that the estimated GNRs in forested catchments obtained from Eq. (6) were inaccurate.
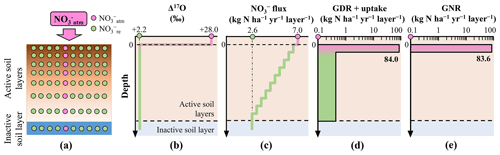
Figure 2Distribution of in the simulated forested soil with homogeneous distribution of Δ17O values of (a). Vertical distribution of the following parameters in the forested soil: assumed Δ17O values of (b), assumed leaching flux of (c), estimated consumption rate (GDR + uptake) (d), and estimated GNR (e).
To demonstrate the impact of this approximation on GNR estimation, we simulated GNR for two different forest soils within the same catchment. In the first scenario, soil exhibited a Δ17O value close to that of at the surface, which decreased to the Δ17O of stream at depth (heterogeneous soil) (Fig. 1a and b). In the second scenario, soil had Δ17O values equal to those of stream throughout the soil profile (homogeneous soil) (Fig. 2a and b).
To simulate the forested catchment studied by Hattori et al. (2019), we used the same parameter values for the current calculation, including 7.0 for , 2.6 for , +28.0 ‰ for , and +2.2 ‰ for . All symbols (e.g., GNR) are consistent with those used by Hattori et al. (2019).
To estimate GNR in each forest soil type, we divided the soils into 10 vertical layers (i.e., 10 steps). In the heterogeneous soil, the Δ17O values of gradually decreased with depth, from +28.0 ‰ to +2.2 ‰, at a rate of −2.58 ‰ per step (Fig. 1b). In the homogeneous soil, Δ17O values of were constant at +2.2 ‰ across all layers (Fig. 2b). Note that the y axes in the models were layers, not depths (Tables S1–S3 in the Supplement). While the Δ17O values of soil always showed decreasing trends with depth irrespective of the season, Δ17O values of soil showed significant temporal variation at each depth (Hattori et al., 2019). This was the reason why the layers were adopted for the y axes in our models instead of depths. As a result, the specific depth of each layer varies over time. In addition, the relation between depth and layer is not always linear. The temporal variation found in the vertical distributions of Δ17O values in the forested catchment (Hattori et al., 2019) can be explained by our model as well without contradiction because the Δ17O values of soil , while showing large temporal variation at each depth, always showed decreasing trend with depth throughout their observation (Hattori et al., 2019).
To estimate GNR in each layer, both the Δ17O value and the flux in soil are required. While Hattori et al. (2019) reported soil concentrations for each layer, indicating little vertical variation within the forested catchment, they did not measure the catchment water flux. Consequently, it is difficult to constrain the flux for each layer of forest soil. Nevertheless, was 7.0 and was 2.6 in the catchment (Hattori et al., 2019). Additionally, because water fluxes decrease gradually with depth in various forest settings (e.g., Christiansen et al., 2006), we assumed a gradual decrease in flux from 7.0 to 2.6 at a rate of −0.44 per layer (Figs. 1c and 2c). Similar trends in the flux of soil have been observed in other forested catchments (Callesen et al., 1999; Inoue et al., 2021).
Applying the total mass balance and isotope mass balance equations (Eqs. 2 and 3) to each layer, we estimated GNR (Figs. 1e and 2e) and the total consumption rate of (GDR + uptake) (Figs. 1d and 2d) in each layer. In this calculation, we made the following assumptions: (1) Δ17O values of were constant in each layer, (2) vertical flow of in soil layers proceeds downward from the surface to the final layer (no. 10), and (3) GNR and the consumption rate (GDR + uptake) are 0 in layers beyond the final layer. By summing the GNR determined for each layer, we estimated the total GNR in the forested catchment.
The total GNR estimated for the catchment with the homogeneous Δ17O values in soil (homogeneous soil) was 83.6 kg of (Fig. 2e), exactly equal to that estimated by Hattori et al. (2019) using Eq. (6). This result allows us to further verify that past studies estimating GNR using Eq. (6) implicitly approximated that Δ17O values of soil consumed in forested catchments were homogeneous and always equal to those of stream . However, the total GNR estimated for the catchment with heterogeneous Δ17O values in soil (heterogeneous soil) was considerably lower (13.0 kg of ; Fig. 1e), while the same parameters were used for , , , and .
As we increased the number of layers in the forest soils to 20, 30, 50, 100, and 1000, the estimated GNR for the heterogeneous soil decreased to 11.4, 11.0, 10.5, 10.3, and 10.1 , respectively. Moreover, when we changed the calculation method from stepwise summation to integration, the estimated GNR was 11.2 . Furthermore, even if we assumed nonlinear variation for the leaching flux of soil , in which the leaching flux of soil increased with soil depth from layers 1 to 5 with an increasing rate of 0.44 per layer, while the leaching flux decreased with soil depth from layers 6 to 10 with a decreasing rate of 1.32 per layer (Table S3), the newly estimated total GNR (19.1 ) was still comparable with that estimated for the forested catchment with the heterogeneous soil shown by Fig. 1 (13.0 ). As a result, we concluded that the differences in the Δ17O values of the soil consumed in a forested catchment from that of stream resulted in a significant deviation in the GNR estimated using Eq. (6) from the actual GNR. In addition, the most important parameter to determine GNR was the Δ17O values of consumed in soil layers. That is, the other parameters, such as the number of layers and the vertical changes in the leaching flux of soil , had little impact on total GNR.
By combining the total mass balance and isotope mass balance shown in Eqs. (2) and (3), Eq. (7) was obtained to accurately estimate the total GNR:
where denotes the “average” Δ17O of consumed through assimilation or denitrification in the forested catchment. Most of the soil measured to date exhibited Δ17O values higher than those of stream leached from the catchments (Hattori et al., 2019; Rose, 2014). Consequently, the total GNR estimated from stream using Eq. (6) exceeded the total GNR estimated from soil using Eq. (7) to an extent. Therefore, the total GNR estimated from Eq. (6) was overestimated to an extent.
If we can estimate the downward water flux at each soil layer, along with the concentration and Δ17O value of in each soil layer, using, e.g., a tension-free lysimeter (Inoue et al., 2021), we could estimate the vertical change in the flux for each soil layer, along with the Δ17O values of soil . Thereafter, applying Eq. (6) to each layer, we can more accurately estimate the total GNR for the forested catchment by integrating the GNR estimated for each soil layer together with the consumption rate in the forested catchment.
Past studies have proposed the Δ17O method for determining the GNR in forested catchments. The equations used in the calculation implicitly assumed that the Δ17O values of consumed in forested soils are homogeneous and equal to those of the stream . However, the values are often heterogeneous and do not always equal those of the stream in forested soils. It is essential to clarify and verify the Δ17O values of in forested soils and streams before applying the Δ17O values of stream to estimate the total GNR.
All data are presented in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-21-4717-2024-supplement.
WD, UT, and FN designed the study. WD and UT performed data analysis and wrote the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We thank Joel Bostic, Lucy Rose and the three anonymous referees for their valuable remarks on an earlier version of this paper. We are grateful to the members of the Biogeochemistry Group, Nagoya University, for their valuable support throughout this study.
This research has been supported by the Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science, and Technology of Japan (grant nos. 22H00561, 17H00780, and 22K19846); the Grant-in-Aid for Japan Society for the Promotion of Science Fellows (grant no. 23KJ1088); the Yanmar Environmental Sustainability Support Association; the River Fund of the River Foundation, Japan; the Reiwa Environmental Foundation; and Nagoya University and the Japan Science and Technology Agency (grant no. JPMJFS2120).
This paper was edited by Frank Hagedorn and reviewed by three anonymous referees.
Bengtsson, G., Bengtson, P., and Månsson, K. F.: Gross nitrogen mineralization-, immobilization-, and nitrification rates as a function of soil ratio and microbial activity, Soil Biol. Biochem., 35, 143–154, https://doi.org/10.1016/S0038-0717(02)00248-1, 2003.
Callesen, I., Raulund-Rasmussen, K., Gundersen, P., and Stryhn, H.: Nitrate concentrations in soil solutions below Danish forests, Forest Ecol. Manag., 114, 71–82, https://doi.org/10.1016/S0378-1127(98)00382-X, 1999.
Christiansen, J. R., Elberling, B., and Jansson, P.-E.: Modelling water balance and nitrate leaching in temperate Norway spruce and beech forests located on the same soil type with the CoupModel, Forest Ecol. Manag., 237, 545–556, https://doi.org/10.1016/j.foreco.2006.09.090, 2006.
Ding, W., Tsunogai, U., Nakagawa, F., Sambuichi, T., Sase, H., Morohashi, M., and Yotsuyanagi, H.: Tracing the source of nitrate in a forested stream showing elevated concentrations during storm events, Biogeosciences, 19, 3247–3261, https://doi.org/10.5194/bg-19-3247-2022, 2022.
Ding, W., Tsunogai, U., Nakagawa, F., Sambuichi, T., Chiwa, M., Kasahara, T., and Shinozuka, K.: Stable isotopic evidence for the excess leaching of unprocessed atmospheric nitrate from forested catchments under high nitrogen saturation, Biogeosciences, 20, 753–766, https://doi.org/10.5194/bg-20-753-2023, 2023.
Fang, Y., Koba, K., Makabe, A., Takahashi, C., Zhu, W., Hayashi, T., Hokari, A. A., Urakawa, R., Bai, E., Houlton, B. Z., Xi, D., Zhang, S., Matsushita, K., Tu, Y., Liu, D., Zhu, F., Wang, Z., Zhou, G., Chen, D., Makita, T., Toda, H., Liu, X., Chen, Q., Zhang, D., Li, Y., and Yoh, M.: Microbial denitrification dominates nitrate losses from forest ecosystems, P. Natl. Acad. Sci. USA, 112, 1470–1474, https://doi.org/10.1073/pnas.1416776112, 2015.
Hattori, S., Nuñez Palma, Y., Itoh, Y., Kawasaki, M., Fujihara, Y., Takase, K., and Yoshida, N.: Isotopic evidence for seasonality of microbial internal nitrogen cycles in a temperate forested catchment with heavy snowfall, Sci. Total Environ., 690, 290–299, https://doi.org/10.1016/j.scitotenv.2019.06.507, 2019.
Huang, S., Wang, F., Elliott, E. M., Zhu, F., Zhu, W., Koba, K., Yu, Z., Hobbie, E. A., Michalski, G., Kang, R., Wang, A., Zhu, J., Fu, S., and Fang, Y.: Multiyear Measurements on Δ17O of Stream Nitrate Indicate High Nitrate Production in a Temperate Forest, Environ. Sci. Technol., 54, 4231–4239, https://doi.org/10.1021/acs.est.9b07839, 2020.
Inoue, T., Nakagawa, F., Shibata, H., and Tsunogai, U.: Vertical Changes in the Flux of Atmospheric Nitrate From a Forest Canopy to the Surface Soil Based on Δ17O Values, J. Geophys. Res.-Biogeo., 126, 1–18, https://doi.org/10.1029/2020JG005876, 2021.
Jackson, R. B., Canadell, J., Ehleringer, J. R., Mooney, H. A., Sala, O. E., and Schulze, E. D.: A global analysis of root distributions for terrestrial biomes, Oecologia, 108, 389–411, https://doi.org/10.1007/BF00333714, 1996.
Li, F. L., McCormack, M. L., Liu, X., Hu, H., Feng, D. F., and Bao, W. K.: Vertical fine-root distributions in five subalpine forest types shifts with soil properties across environmental gradients, Plant Soil, 456, 129–143, https://doi.org/10.1007/s11104-020-04706-x, 2020.
Michalski, G., Scott, Z., Kabiling, M., and Thiemens, M. H.: First measurements and modeling of Δ17O in atmospheric nitrate, Geophys. Res. Lett., 30, 3–6, https://doi.org/10.1029/2003GL017015, 2003.
Michalski, G., Meixner, T., Fenn, M., Hernandez, L., Sirulnik, A., Allen, E., and Thiemens, M.: Tracing Atmospheric Nitrate Deposition in a Complex Semiarid Ecosystem Using Δ17O, Environ. Sci. Technol., 38, 2175–2181, https://doi.org/10.1021/es034980+, 2004.
Nakagawa, F., Tsunogai, U., Obata, Y., Ando, K., Yamashita, N., Saito, T., Uchiyama, S., Morohashi, M., and Sase, H.: Export flux of unprocessed atmospheric nitrate from temperate forested catchments: a possible new index for nitrogen saturation, Biogeosciences, 15, 7025–7042, https://doi.org/10.5194/bg-15-7025-2018, 2018.
Nelson, D. M., Tsunogai, U., Ding, D., Ohyama, T., Komatsu, D. D., Nakagawa, F., Noguchi, I., and Yamaguchi, T.: Triple oxygen isotopes indicate urbanization affects sources of nitrate in wet and dry atmospheric deposition, Atmos. Chem. Phys., 18, 6381–6392, https://doi.org/10.5194/acp-18-6381-2018, 2018.
Osaka, K., Ohte, N., Koba, K., Yoshimizu, C., Katsuyama, M., Tani, M., Tayasu, I., and Nagata, T.: Hydrological influences on spatiotemporal variations of δ15N and δ18O of nitrate in a forested headwater catchment in central Japan: Denitrification plays a critical role in groundwater , J. Geophys. Res.-Biogeo., 115, 0148–0227, https://doi.org/10.1029/2009jg000977, 2010.
Rose, L. A.: Assessing the nitrogen saturation status of appalachian forests using stable isotopes of nitrate, PhD thesis, University of Pittsburgh, https://d-scholarship.pitt.edu/22783/ (last access: 26 April 2024), 2014.
Stark, J. M. and Hart, S. C.: High rates of nitrification and nitrate turnover in undisturbed coniferous forests, Nature, 385, 61–64, https://doi.org/10.1038/385061a0, 1997.
Tsunogai, U., Komatsu, D. D., Daita, S., Kazemi, G. A., Nakagawa, F., Noguchi, I., and Zhang, J.: Tracing the fate of atmospheric nitrate deposited onto a forest ecosystem in Eastern Asia using Δ17O, Atmos. Chem. Phys., 10, 1809–1820, https://doi.org/10.5194/acp-10-1809-2010, 2010.
Tsunogai, U., Daita, S., Komatsu, D. D., Nakagawa, F., and Tanaka, A.: Quantifying nitrate dynamics in an oligotrophic lake using Δ17O, Biogeosciences, 8, 687–702, https://doi.org/10.5194/bg-8-687-2011, 2011.
Tsunogai, U., Miyauchi, T., Ohyama, T., Komatsu, D. D., Nakagawa, F., Obata, Y., Sato, K., and Ohizumi, T.: Accurate and precise quantification of atmospheric nitrate in streams draining land of various uses by using triple oxygen isotopes as tracers, Biogeosciences, 13, 3441–3459, https://doi.org/10.5194/bg-13-3441-2016, 2016.
Tsunogai, U., Miyauchi, T., Ohyama, T., Komatsu, D. D., Ito, M., and Nakagawa, F.: Quantifying nitrate dynamics in a mesotrophic lake using triple oxygen isotopes as tracers, Limnol. Oceanogr., 63, S458–S476, https://doi.org/10.1002/lno.10775, 2018.
Verchot, L. V., Holmes, Z., Mulon, L., Groffman, P. M., and Lovett, G. M.: Gross vs net rates of N mineralization and nitrification as indicators of functional differences between forest types, Soil Biol. Biochem., 33, 1889–1901, https://doi.org/10.1016/S0038-0717(01)00095-5, 2001.





