Evaluating adsorption isotherm models for determining the partitioning of ammonium between soil and soil pore water in environmental soil samples

Ammonium in soil pore water is thought to participate in bidirectional exchange with the atmosphere; however, common soil nutrient analysis methods determine the bulk quantity of ammonium associated with the soil particles rather than determining the aqueous ammonium concentration. Previous works have applied the Langmuir and Freundlich isotherm equations to ammonium-enriched soils to estimate partitioning, but this may not be representative of conditions in natural, unmanaged soils. In this work, environmental soil samples were collected from green spaces in Toronto and used to evaluate several commonly used adsorption isotherm equations, including the Langmuir, Freundlich, Temkin and Toth equations, to determine their applicability in lightly managed and non-fertilized soils. We then compare ammonia emission potentials (a quantity predicting the propensity of ammonia to volatilize from a liquid reservoir) determined using a conventional high-salt extraction procedure to determine the soil ammonium content to that modelled using the Temkin and Langmuir equations and demonstrate that conventional approaches may overestimate emission potentials from soils by a factor of 5–20.

1 Introduction

1.1 Contextualizing the significance of ammonium partitioning in soils

Globally, emissions of reduced nitrogen compounds (NH₃) make up as much as half of the global atmospheric reactive nitrogen sources (Flechard et al., 2013). Of the NH₃ budget, approximately two-thirds of emissions are related to anthropogenic agricultural activities, with natural sources being responsible for only 15 %–20 % of emissions (Bouwman et al., 1997; Sutton et al., 2008, 2013; Van Aardenne et al., 2001). Following emission, NH₃ tends to partition into fine particulate matter or deposit via wet or dry deposition on a timescale of hours to days. NH₃ is understood to engage in bidirectional exchange throughout the earth system, with NH₃ depositing or volatilizing depending on local environmental conditions (Farquhar et al., 1980; Flechard et al., 1999, 2013; Guo et al., 2022; Nemitz et al., 2000; Sutton et al., 1995; Walker et al., 2023; Wentworth et al., 2014; Zhang et al., 2010). The bidirectional exchange of NH₃ between soils and the atmosphere has been considered important to its overall budget, particularly in remote areas, but research on the mechanisms of NH₃ partitioning in soils between adsorbed (inaccessible) and aqueous (accessible) NH₃ often focuses on fertilized croplands with substantial concentrations of NH₃ present (Venterea et al., 2015; Vogeler et al., 2011). Consequently, NH₃ volatilization models may parameterize all or most of the soil NH₃ as being readily able to exchange with the atmosphere, which may be reasonable for recently fertilized soils but not for unmanaged soils (Massad et al., 2010; Pleim et al., 2013; Zhu et al., 2015). However, cropland is estimated to make up less than 15 % of the Earth's land area, while unfertilized or irregularly fertilized natural, semi-natural or pastoral land reflects nearly three-quarters of terrestrial surfaces (Ellis et al., 2020). The short atmospheric lifetime of NH₃ makes it important for understanding the exchange of NH₃ over all types of surfaces despite agricultural cropland being the most globally significant source.

1.2 Importance of developing an ammonium adsorption partitioning model

The propensity for ammonia to volatilize from liquid reservoirs is parameterized by the emission potential (Γ), which is calculated as the ratio of aqueous NH${}_{\mathrm{4}}^{+}$ to H⁺. However, NH${}_{\mathrm{4}}^{+}$ in soils is present not only as NH${}_{\mathrm{4}}^{+}$_(aq) in soil pore water, but also as NH${}_{\mathrm{4}}^{+}$_(ads) adsorbed to soil particles. Because soils tend to exist with both permanent and pH-dependent negative charges (Bache, 1976), NH${}_{\mathrm{4}}^{+}$ ions compete for adsorption against other cations in solution. The total quantity of cations that can adsorb to the soil particles is termed the cation exchange capacity (CEC, typically reported as centimoles positive charge per kilogram). Traditional methods for determining NH${}_{\mathrm{4}}^{+}$ in soil – intended for nutrient analysis in which the total ammoniacal nitrogen is more important than the partitioning between NH${}_{\mathrm{4}}^{+}$_(ads) and NH${}_{\mathrm{4}}^{+}$_(aq) – use high-concentration salt solutions to displace all cations from the soil. As a result, these approaches do not distinguish between NH${}_{\mathrm{4}}^{+}$_(aq) and NH${}_{\mathrm{4}}^{+}$_(ads) (Li et al., 2012) and therefore likely overestimate the emission potential of soils. In this paper, we explore a variety of adsorption isotherm models with the goal of identifying a simple approach to relate the total quantity of NH${}_{\mathrm{4}}^{+}$ in soil to the aqueous fraction of NH${}_{\mathrm{4}}^{+}$_(aq) that can participate in bidirectional exchange with the atmosphere.

1.3 Adsorption isotherm equations

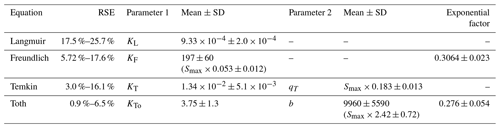
The adsorption behaviour of molecules to surfaces is complex and dependent on the properties of both the surface and the adsorbed molecules. Numerous adsorption equations have been proposed, based on both theoretical and empirical models; however, as the partitioning of NH${}_{\mathrm{4}}^{+}$ between soil pore water and soil particles is complex and influenced by many other simultaneous equilibria, we consider each of the examined equations as being empirically determined only rather than based on a theoretical treatment of the system. Previous studies have sought to develop an adsorption model for NH${}_{\mathrm{4}}^{+}$ in soils based on the Langmuir (Alnsour, 2020; Venterea et al., 2015) and Freundlich equations (Vogeler et al., 2011) but have focused on croplands and other agricultural soils. In this work, in addition to the Langmuir and Freundlich equations, we also investigate the application of the Temkin and Toth adsorption equations to NH${}_{\mathrm{4}}^{+}$ sorption in soils. Each of these equations (as formulated in Table 1) represents the adsorbed NH${}_{\mathrm{4}}^{+}$ concentration (S, mg kg⁻¹) in terms of the NH${}_{\mathrm{4}}^{+}$ concentration in solution (C, mg L⁻¹). Except for the Freundlich equation, each of these equations incorporates a saturation point or maximum adsorption capacity (S_max, mg kg⁻¹); this work treats S_max as an empirically measured property, equivalent to the CEC (converted to milligrams of NH${}_{\mathrm{4}}^{+}$ kg⁻¹ soil), rather than as a calculated fitting parameter.

Table 1 Adsorption isotherm equations applied in this work and their parameters.

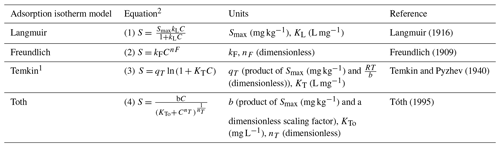
¹ The Temkin model is also given as $\mathrm{S}=\frac{RT}{b}\ln K_{\mathrm{T}}C$ (see Chu, 2021, for this formulation). ² Where S is the concentration of NH${}_{\mathrm{4}}^{+}$ adsorbed to soil particles (mg kg⁻¹), C is the concentration of NH${}_{\mathrm{4}}^{+}$ in solution (mg L⁻¹), and S_max is the maximum adsorption capacity (mg kg⁻¹), which was determined empirically as equivalent to the measured cation exchange capacity of the soil. This work treats the remaining parameters as empirical constants only.

2 Methods

2.1 Soil collection

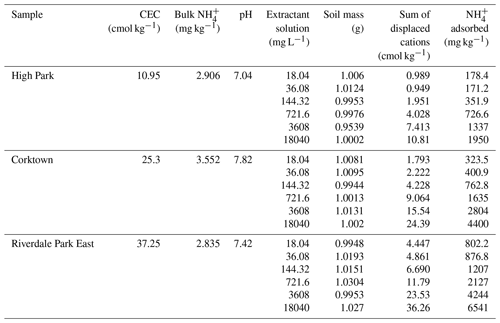
Soil samples were collected from 24 green space (parks, urban forest, roadside sites, etc.) locations across Toronto. Samples were collected only on days preceded by at least 2 d without precipitation and were collected by inserting a 7.5 cm internal diameter steel tube into the ground to a depth of 5–10 cm and recovering a soil core by removing the tube from the ground. The soil cores were mixed and sieved immediately and transported back to the lab for analysis. Samples analyzed for NH${}_{\mathrm{4}}^{+}$ content were always analyzed immediately to avoid potential artefacts from freezing, and samples analyzed for CEC or adsorption curves were frozen for storage prior to analysis. Soil samples were collected from eight locations in fall 2021 as a training set for developing the model. A subsequent 16 soil samples from across Toronto were collected in spring/summer 2023 to be used to evaluate the effectiveness of applying the model to uncharacterized soils and to determine the impact on soil emission potentials.

2.2 Soil analysis

2.2.1 Cation exchange capacity determination

The CEC was determined using the inductively coupled plasma optical emission spectroscopy (ICP-OES) cation sum method (Bache, 1976). Briefly, 1 g of soil was measured out and mixed with 25 mL of 1 M NH₄Cl, shaken, and refrigerated for 36–48 h to settle. The supernatant was filtered using 0.2 µm syringe filters, diluted 50-fold using volumetric glassware and analyzed for the common soil-associated exchangeable cations Na⁺, K⁺, Mg²⁺ and Ca²⁺. The ICP-OES (iCAP Pro, Thermo Fisher Scientific, Waltham, USA) was calibrated using a commercially available mixed standard of six cations (Li⁺, Na⁺, NH${}_{\mathrm{4}}^{+}$, K⁺, Mg²⁺, Ca²⁺) (Dionex Cation II, Thermo Fisher Scientific, Waltham, USA). Another soil-associated cation that can contribute to CEC is Al³⁺; our initial measurements screened for Al, but we did not detect it in solution. The CEC was determined for all 24 collected samples and used to select 3 of the soil samples from the 16 collected in 2023 to be used as a test set for the developed model.

2.2.2 Adsorption curve characterization

The determination of the adsorption behaviour of NH${}_{\mathrm{4}}^{+}$ was performed using a modified version of the procedure described by Venterea et al. (2015), combined with the ICP-OES cation sum method (Bache, 1976). Briefly, a series of batch equilibrium samples was prepared by mixing 1 g of soil with 25 mL aliquots of NH₄Cl solutions with concentrations ranging from 2.5–1000 mM. The samples were shaken, refrigerated for 36–48 h to settle, filtered with 0.2 µm syringe filters, diluted 50-fold with volumetric glassware and analyzed using ICP-OES. The quantity of NH${}_{\mathrm{4}}^{+}$ adsorbed onto each soil was inferred based on the displaced Na⁺, Mg²⁺, Ca²⁺ and K⁺ ions measured in solution. In the cation sum method, the total quantity of adsorbable cations is determined by saturating the soil with an index cation (in this procedure, and generally, NH${}_{\mathrm{4}}^{+}$ from NH₄Cl), which displaces the exchangeable cations on the soil's adsorption sites. Thus, the displaced cations measured for each NH₄Cl solution concentration are representative of the quantity of NH${}_{\mathrm{4}}^{+}$ adsorbing onto the soil. Adsorption curves were determined for the original eight soil samples in the training set, as well as the three selected soil samples for the test set.

2.2.3 pH and NH${}_{\mathrm{4}}^{+}$ determination

The pH and the NH${}_{\mathrm{4}}^{+}$ content was determined for the 16 soil samples collected in 2023. The pH was determined for each soil by mixing soil with ultra-pure (18 MΩ cm) water (DIW) in a 1:2 ratio and then measuring the pH of the slurry by immersing a pH electrode (Hach Company, Loveland, USA) until a stable pH reading was obtained. NH${}_{\mathrm{4}}^{+}$ was extracted from the soil using a 2 M KCl extraction solution. A total of 2.5 g of soil was mixed with 25 mL of the extraction solution, shaken and refrigerated for 36 h to allow suspended solids to settle out of solution. Afterward, the supernatant was filtered using 0.2 µm PES membrane syringe filters. The soil NH${}_{\mathrm{4}}^{+}$ was quantified using the indophenol-blue salicylate method (Kempers and Zweers, 1986). Briefly, two reagent solutions, A and B, were prepared: reagent A consisted of a solution of 1 M sodium salicylate and 100 mg L⁻¹ sodium nitroprusside, while reagent B consisted of a solution of 1 M NaOH and 0.12 % by volume of 5 % available chloride NaOCl. Soil extracts were prepared for analysis by adding 0.6 mL of reagent A to 2 mL of soil extract, followed by the addition of 1.4 mL of reagent B. The mixtures were then stored for 2 h in the dark for colour development and then quantified using UV–Vis spectrometry (Lambda 365, PerkinElmer, Waltham, USA) at 649 nm.

Conventionally, the soil emission potential is calculated as a function of the soil pH (H${}_{\mathrm{DIW}}^{+}$) and salt-solution-extracted NH${}_{\mathrm{4}}^{+}$ (NH${}_{\mathrm{4}}^{+}$_SALT). In addition to investigating whether adsorption isotherm equations could be applied to estimate NH${}_{\mathrm{4}}^{+}$_(aq) from the total soil NH${}_{\mathrm{4}}^{+}$, we investigated the impact of calculating the emission potential using a “like-with-like” ratio of H${}_{\mathrm{DIW}}^{+}$ with NH${}_{\mathrm{4}}^{+}$ extracted using DIW as the solvent, as well as the ratio of NH${}_{\mathrm{4}}^{+}$_SALT to H⁺ determined from a salt-solution and soil slurry. Consequently, the pH was also determined as described above but using a 0.01 M CaCl₂ solution in place of DIW, while soil NH${}_{\mathrm{4}}^{+}$ was also determined as described above but using DIW as the solvent.

2.3 Data analysis

2.3.1 Characterizing adsorption parameters using a training and a test set

Curve-fitting was done in R using the nls function to fit our experimental data for the eight samples in our training set to the Langmuir, Freundlich, Temkin and Toth equations. Goodness of fit was evaluated by calculating the Akaike information criterion (AIC) using the AIC function from the R stats package. The AIC is calculated using Eq. (1):

$$\begin{array}{}\text{(1)}& \mathrm{AIC}=\mathrm{2}K-\mathrm{2}\ln \left(L\right),\end{array}$$

where K is the number of independent variables, and L is the log-likelihood estimate. The log-likelihood estimate can be extracted directly from nls objects fitted in R using the AIC function.

Fitting parameters for each equation were determined by pooling all the experimental data, standardizing each adsorption curve by the maximum adsorption achieved (i.e. all curves went from 0 to 1) and then fitting each equation from Table 1 to those curves.

To validate the effectiveness of these equations when applied to uncharacterized soil samples, we selected 3 soil samples from the 16 soil samples collected in 2023 to form a test set; these samples were selected by choosing the soil samples with the lowest (10.9) and highest CECs (37.2) and a soil with an average CEC (25.3). As the original training set mostly consisted of samples with CECs from 20–30 (with two samples with CECs of 7.6 and 16), we chose two samples that were significantly different than the average training set sample as well as one similar sample to determine whether the fitting parameters could be used for “extreme” samples or only for samples similar to the training set. The test set was characterized in the same way as the training set and was then modelled using three approaches:

• i.

  using the average CEC for all the soil samples of 25 cmol kg⁻¹ (S_max of 4500 mg kg⁻¹) and the training set parameters

• ii.

  using the measured CEC for each soil sample to calculate S_max and the training set parameters

• iii.

  using the fitting algorithm as described in Sect. 2.3.1 to determine the least-squares fit for each equation to the experimental data.

2.3.2 Emission potential determination

The NH₃ emission potential is a quantity calculated as the ratio of aqueous NH${}_{\mathrm{4}}^{+}$ to H⁺ (Eq. 2).

$$\begin{array}{}\text{(2)}& \mathrm{\Gamma }={\displaystyle \frac{\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]}{\left[{\mathrm{H}}^{+}\right]}}\end{array}$$

Commonly, for soils this would be calculated using the total NH${}_{\mathrm{4}}^{+}$ (determined using a salt solution extraction) and the pH measured using an extraction with deionized water. We denote this as Γ_STD, corresponding to $\frac{{\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]}_{\mathrm{salt}}}{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{DIW}}}$. The pH may also be measured in a (less concentrated) salt solution, which we denote as Γ_SALT, corresponding to $\frac{{\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]}_{\mathrm{salt}}}{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{salt}}}$. Similarly, though we are not aware of this as a common method, NH${}_{\mathrm{4}}^{+}$ could be determined using a DIW extraction solution, resulting in a third parameterization of the emission potential as Γ_DIW, representing $\frac{{\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]}_{\mathrm{DIW}}}{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{DIW}}}$. Lastly, by applying one of the adsorption isotherm models, the total soil NH${}_{\mathrm{4}}^{+}$ can be partitioned into NH${}_{\mathrm{4}}^{+}$_(ads) (S) and NH${}_{\mathrm{4}}^{+}$_(aq) (C), and the emission potential can be calculated using only the NH${}_{\mathrm{4}}^{+}$ in solution (C). These versions of the emission potential are denoted as Γ_{equation name} (e.g. as Γ_Langmuir, Γ_Temkin).

3 Results

3.1 Performance of adsorption isotherm equations applied to an environmental soil training and test set

We evaluated the ability of the Langmuir, Freundlich, Temkin and Toth equations to model the exchange of NH${}_{\mathrm{4}}^{+}$ between adsorbed and aqueous forms. An adsorption curve was characterized for each soil, and the data from each soil adsorption experiment were pooled and then fit using the R nls function. The adsorption curves and fitting parameters are shown in Fig. 1 and Table 2. Additionally, as our interest is ultimately in the performance of these adsorption equations at the lower concentration limit, we refit each equation using only the extraction solutions ≤680 mg L⁻¹ NH₄Cl. The adsorption curves and fitting parameters under those conditions are shown in Fig. 2 and Table 3.

While the Langmuir (Alnsour, 2020; Guo et al., 2022; Venterea et al., 2015) and Freundlich (Vogeler et al., 2011) equations have been previously reported as being effective at modelling NH${}_{\mathrm{4}}^{+}$ adsorption in soils, we found them to be the least effective of the equations we examined for the full adsorption curves, both over- and underestimating the adsorbed NH${}_{\mathrm{4}}^{+}$ concentrations (Fig. 1), while the Temkin and Toth equations better fit the experimental data. Computing the Akaike information criterion for these equations results in an AIC of −138, −190, −222 and −249 for the Langmuir, Freundlich, Temkin and Toth equations, respectively. The absolute value of the AIC is not important, but for a set of models, the model with the lowest AIC is considered the best at fitting the experimental data, indicating an order of Toth > Temkin > Freundlich > Langmuir for model effectiveness. However, fitting only the lower range of the adsorption curves (0–40 mM) slightly changed these results: the Toth equation could not be fit by our algorithm, and the resulting AIC values were −93, −157 and −152 for the Langmuir, Freundlich and Temkin equations, respectively, indicating that the Freundlich equation best fit the experimental data. (Note that AIC values for models fit to different datasets should not be directly compared to one another.)

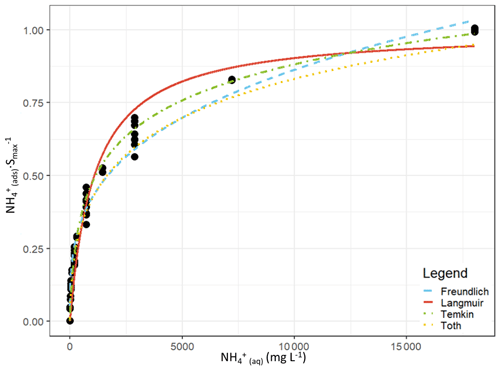
Figure 1 Curve-fitting comparison between the Langmuir (red, solid), Freundlich (blue, – – –), Temkin (green, ⋅ – ⋅ –) and Toth (orange, ⋅ ⋅ ⋅) equations. The curves are plotted using the experimental data from all eight soil adsorption experiments, and the y axis is normalized to the maximum adsorption achieved during each experiment.

Table 2 Comparison of goodness of fit and fitting parameters for the selected adsorption equations.

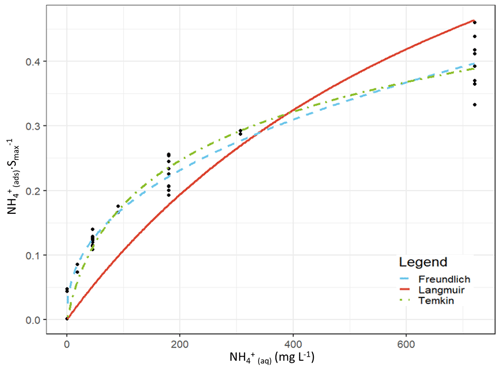
Figure 2 Curve-fitting comparison between the Langmuir (red, solid), Freundlich (blue, – – –) and Temkin (green, ⋅ – ⋅ –) equations. The curves are plotted using the experimental data from all eight soil adsorption experiments but only using the extraction solutions of ≤40 mM NH${}_{\mathrm{4}}^{+}$ for fitting, and the y axis is normalized to the maximum adsorption achieved during each experiment. The Toth equation could not be fit to the experimental data under these conditions.

Table 3 Comparison of goodness of fit and fitting parameters for the selected adsorption equations. Data fit only for the ≤40 mM NH${}_{\mathrm{4}}^{+}$ solutions.

With our objective being to evaluate how well each equation can fit soils without going through the full characterization procedure, we analyzed the adsorption curves of the low-CEC, medium-CEC and high-CEC soils in our test set (i) using a “typical” CEC of 25 and the fitting parameters from Table 2, (ii) using the measured CEC and the fitting parameters from Table 2, and (iii) by fitting the equations using the least-squares fitting algorithm. Using the first approach, we found that none of the equations could reasonably fit the experimental data when using an incorrect CEC and that each of the equations fit the experimental data reasonably well using the average parameters and the correct CEC (Fig. 3). The relative goodness of fit for each equation was the same for the test set as for the training set, i.e. Toth > Temkin > Freundlich > Langmuir. We also tested an alternative approach for calculating each equation's fitting parameters, in which, rather than pooling the normalized data and then fitting each curve, the curves were fit to each soil adsorption curve separately and the resulting fitting parameters were then pooled. A full summary of the alternative fitting parameters and the test set characterization is given in Fig. A1 and Tables A1–A3.

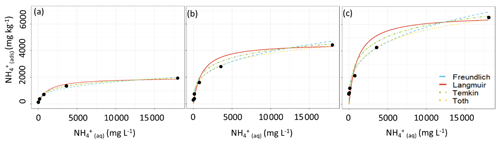
Figure 3 Curve-fitting comparison between the unfitted Langmuir (red, solid), Freundlich (blue, – – –), Temkin (green, ⋅ – ⋅ –) and Toth (orange, ⋅ ⋅ ⋅) equations using the fitting parameters from Table 3 applied to the test set of the (a) low-CEC, (b) moderate-CEC and (c) high-CEC samples (method ii).

Overall, we find that the Toth and Temkin equations best fit the full adsorption curves, while the Freundlich and Temkin equations best fit the low-range adsorption curves. However, both the Freundlich and Toth equations seem to be less robust when applied to this system than the Temkin equation. Firstly, the Freundlich equation, as formulated in Tables 2 and 3, has an intrinsic dependence on the CEC, which is contrary to the theoretical basis of the Freundlich equation. Using the alternative fitting approach, the Freundlich equation does not require a CEC dependence, but in that case, it has high error when fitting uncharacterized soils. Similarly, for the Toth equation, the alternative approach results in a significantly different set of fitting parameters, which resulted in the Toth equation quite poorly fitting the non-characterized soils. Additionally, while this may be a limitation of the fitting algorithm we selected, we found the Toth equation to be more difficult to consistently fit to our experimental data, with no solution being found for the low-range concentrations. Consequently, taking all of these factors into consideration, we find that the Temkin equation is most suitable for evaluating NH${}_{\mathrm{4}}^{+}$ adsorption from uncharacterized soil samples. For comparison with previous studies, in which the Langmuir equation is the most frequently used adsorption equation, we will continue to analyze it in subsequent sections despite it performing much worse than the Temkin equation for both the low-range and full-range data.

3.2 Determining aqueous NH${}_{\mathrm{4}}^{+}$ concentrations using the Langmuir and Temkin equations

To relate the total NH${}_{\mathrm{4}}^{+}$ measured ($m_{{\mathrm{NH}}_{\mathrm{4}}}$) to the adsorbed portion (S) and the aqueous portion (C), we define Eq. (3):

$$\begin{array}{}\text{(3)}& m_{{\mathrm{NH}}_{\mathrm{4}}}=S+{\displaystyle \frac{wC}{\mathit{\rho }}},\end{array}$$

where $m_{{\mathrm{NH}}_{\mathrm{4}}}$ is the total mass of NH${}_{\mathrm{4}}^{+}$ per kilogram soil (mg kg⁻¹), w the volumetric moisture content of the soil (liter water per liter soil) and ρ the bulk density of the dry soil (kg L⁻¹). By substituting the Langmuir or Temkin equations into Eq. (3), $m_{{\mathrm{NH}}_{\mathrm{4}}}$ can be expressed in terms of C:

$$\begin{array}{}\text{(4)}& {\displaystyle }{m}_{{\mathrm{NH}}_{\mathrm{4}}}={\displaystyle \frac{S_{\max }{k}_{\mathrm{L}}C}{\mathrm{1}+k_{\mathrm{L}}C}}+{\displaystyle \frac{wC}{\mathit{\rho }}},\text{(5)}& {\displaystyle }{m}_{{\mathrm{NH}}_{\mathrm{4}}}=q_T\ln \left(\mathrm{1}+K_{\mathrm{T}}C\right)+{\displaystyle \frac{wC}{\mathit{\rho }}},\end{array}$$

where S_max is the maximum adsorption capacity (mg kg⁻¹), q_T is the product of S_max and an empirical fitting constant (mg kg⁻¹), and K_L (L mg⁻¹) and K_T (L mg⁻¹) are empirical fitting constants.

To solve for C, we inverted these equations using Wolfram Mathematica (https://www.wolfram.com/mathematica/, last access: 11 November 2023), yielding Eq. (6) (Langmuir) and Eq. (7) (Temkin).

$$\begin{array}{}\text{(6)}& {\displaystyle }C={\displaystyle \frac{\begin{array}{c}-S_{\max }\cdot K_{\mathrm{L}}+K_{\mathrm{L}}\cdot m_{{\mathrm{NH}}_{\mathrm{4}}}-Z\\ +\sqrt{\mathrm{4}{K}_{\mathrm{L}}\cdot Z\cdot m_{{\mathrm{NH}}_{\mathrm{4}}}+{\left(S_{\max }\cdot K_{\mathrm{L}}-K_{\mathrm{L}}\cdot m_{{\mathrm{NH}}_{\mathrm{4}}}+Z\right)}^{\mathrm{2}}}\end{array}}{\mathrm{2}{K}_{\mathrm{L}}\cdot Z}},\text{(7)}& {\displaystyle }C={\displaystyle \frac{-Z+K_{\mathrm{T}}\cdot q_T\cdot \mathbf{W}\left(e^{\frac{Z}{K_{\mathrm{T}}\cdot q_T}+\frac{m_{{\mathrm{NH}}_{\mathrm{4}}}}{q_T}}\cdot Z\right)}{K_{\mathrm{T}}\cdot \mathrm{Z}}},\end{array}$$

where W(x) is the Lambert W function, and Z= $\frac{w}{\mathit{\rho }}$.

If it is assumed that $m_{{\mathrm{NH}}_{\mathrm{4}}}\approx S$, then these equations can be simplified to Eqs. (8) and (9), respectively.

$$\begin{array}{}\text{(8)}& {\displaystyle }C={\displaystyle \frac{m_{{\mathrm{NH}}_{\mathrm{4}}}}{k_{\mathrm{L}}(S_{\max }-m_{{\mathrm{NH}}_{\mathrm{4}}})}}\text{(9)}& {\displaystyle }C={\displaystyle \frac{e^{\frac{m_{{\mathrm{NH}}_{\mathrm{4}}}}{q_T}}-\mathrm{1}}{K_{\mathrm{T}}}}\end{array}$$

We tested this assumption and found that, for our unfertilized soil samples, the simplified equations have a positive bias of only 0.57 %–1.5 % for the aqueous concentration (C) and that, for most soils fertilized with the equivalent of up to 300 kg N ha⁻¹, the simplified equations should have a positive bias of less than 5 %. Consequently, we used the simplified equations for our analysis.

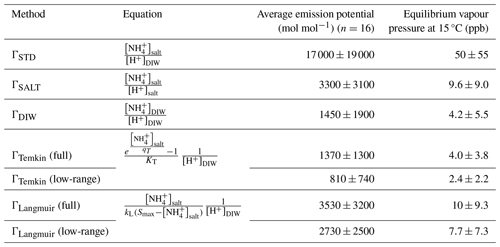
Table 4 Comparison of emission potentials determined using the standard, Langmuir, Temkin, salt extraction and DIW extraction methods. Standard deviations represent the underlying variability in the collected soil samples.

Figure 4 Soil emission potentials using the standard, salt extraction, Temkin, Langmuir and DIW extraction approaches, arranged by CEC.

3.3 Determining environmental soil emission potentials

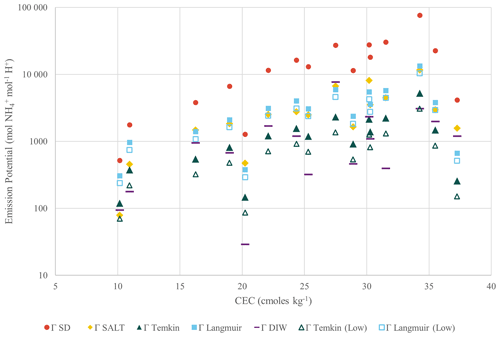
Soil emission potentials were then calculated using the approaches described in Sect. 2.3.3, corresponding to the “standard” approach, two approaches based on matching the NH${}_{\mathrm{4}}^{+}$ and pH extraction solutions, and two approaches based on applying the Langmuir and Temkin equations to the measured extract concentrations and pH values. The adsorption equations were calculated using both the low-range and full curve fitting parameters. For the Langmuir calculations, the fit parameters were $K_{\mathrm{L}}=\mathrm{9.29}\times {\mathrm{10}}^{-\mathrm{4}}$ L mg⁻¹(full) and $K_{\mathrm{L}}=\mathrm{1.20}\times {\mathrm{10}}^{-\mathrm{3}}$ L mg⁻¹ (low-range), and S_max was calculated as the equivalent of the CEC in units of milligrams per kilogram (mg kg⁻¹). For the Temkin calculations, the fit parameters were $K_{\mathrm{T}}=\mathrm{1.33}\times {\mathrm{10}}^{-\mathrm{2}}$ L mg⁻¹ and q_T (mg kg⁻¹) $=\mathrm{0.180}\times S_{\max }$ (full) and $K_{\mathrm{T}}=\mathrm{3.40}\times {\mathrm{10}}^{-\mathrm{2}}$ L mg⁻¹ and q_T (mg kg⁻¹) $=\mathrm{0.120}\times S_{\max }$ (low-range). Among the approaches, Γ_STD results in the highest estimate for the emission potential (17 000±19 000 mol mol⁻¹), followed by Γ_Langmuir and Γ_SALT (2730–3530 mol mol⁻¹) and Γ_Temkin and Γ_DIW (810–1450 mol mol⁻¹) (Table 4). Emission potential is linearly related to equilibrium vapour pressure; at a temperature of 15 °C, these emission potentials correspond to equilibrium concentrations of 2.4–50 ppb. Although CEC is inversely related to the proportion of NH${}_{\mathrm{4}}^{+}$ present in the aqueous phase, the emission potentials increase exponentially as a function of the CEC due to the strong positive correlation between soil pH and CEC (Fig. 4).

4 Discussion

The conventional approach for calculating emission potentials in soils lacks a solid theoretical foundation and ought to be applied with caution. Empirically, this approach has performed poorly, with several studies reporting that calculated values of Γ_STD are unrealistically high and do not correspond well to measured or modelled emission fluxes (Cooter et al., 2010; Flechard et al., 2013; Neftel et al., 1998; Nemitz et al., 2001; Xu et al., 2022). Our assessment that the conventional method overestimates the soil emission potential by at least a factor of 5 is similar to findings reported by Nemitz et al. (2001) and Cooter et al. (2010), who reported needing to reduce their soil emission potentials by a factor of 6.66 and 2–3, respectively, for their modelled predictions to match their flux observations. We believe that our empirical treatment of this system with the Langmuir and Temkin equations provides a more reasonable approach to estimate the soil emission potential. Additionally, in our view, the “like-with-like” extraction approach (e.g. Γ_SALT or Γ_DIW) has a more mechanistic basis than the conventional approach involving dissimilar extraction solutions. A few recent studies have reported on a similar approach using a Langmuir adsorption model (Alnsour, 2020; Guo et al., 2022), as well as by matching the NH${}_{\mathrm{4}}^{+}$ and pH extraction solutions (Wu et al., 2023), showing that these methods can be feasibly implemented into an environmental sampling campaign. Venterea et al. (2015) reported that soil NH${}_{\mathrm{4}}^{+}$ partitioning could be effectively modelled using a modified version of the Langmuir isotherm equation of the form $S=\frac{S_{\max }C}{K+C}$, where K (mg L⁻¹) is the aqueous concentration at which $S=\mathrm{1}/\mathrm{2}{S}_{\max }$. The Venterea equation is equivalent to the Langmuir isotherm when $K=\frac{\mathrm{1}}{K_{\mathrm{L}}}$; for the parameters determined in this study, $\mathrm{1}/\mathrm{2}$ the saturation capacity is reached at exactly $C=\frac{\mathrm{1}}{K_{\mathrm{L}}}=K$, indicating that for our analysis the Langmuir and Venterea equations are equivalent.

How does this approach compare to the implementation of bidirectional exchange of NH₃ in chemical transport models? Widely used models such as GEOS-CHEM and the EPA's CMAQ model soil emission potentials mechanistically rather than being based on emission potentials prescribed using land-use categories (Bash et al., 2013; Pleim et al., 2013, 2019; Zhu et al., 2015). In both models, the exchangeable soil NH₃ has been parameterized as the volumetric molar concentration of NH${}_{\mathrm{4}}^{+}$ in the top 1–5 cm divided by the volumetric water content in the soil, or $\left[{\mathrm{NH}}_{\mathrm{4}}^{+}\right]=\frac{{\mathrm{NH}}_{\mathrm{4}}^{+}\mathrm{mol}{\mathrm{m}}^{-\mathrm{3}}}{\mathit{\theta }{\mathrm{m}}^{\mathrm{3}}{\mathrm{m}}^{-\mathrm{3}}}$ (Massad et al., 2010). In this parameterization, the entire soil NH${}_{\mathrm{4}}^{+}$ content of the top layer of soil is treated as being dissolved into the soil water, and thus a lower water content would result in a higher concentration of NH${}_{\mathrm{4}}^{+}$ and consequently a higher emission potential. (The parameter used by these models for the resistance to NH₃ emissions from soil is inversely proportional to soil moisture such that the actual emission of NH₃ from soil would still be proportional to soil water content (Pleim et al., 2013).) In our model of the system, most NH${}_{\mathrm{4}}^{+}$ present is adsorbed to soils, with the aqueous concentration controlled by the equilibrium between adsorbed and aqueous NH${}_{\mathrm{4}}^{+}$; increasing the soil water content would thus allow more NH${}_{\mathrm{4}}^{+}$ to enter the aqueous phase to maintain the equilibrium concentration. (Increased water content could also result in nutrient runoff, reducing the soil NH${}_{\mathrm{4}}^{+}$ content, or increased mineralization, increasing the soil NH${}_{\mathrm{4}}^{+}$ content.) In the subsequent development of the bidirectional model coupled with an agricultural ecosystem model, Pleim et al. (2019) noted that reducing the NH₃ available for emission by implementing the Langmuir adsorption isotherm approach proposed by Venterea et al. (2015) appeared to lead to unexpectedly low fractions of NH₃ available for exchange. It may be that for recently fertilized soils, the applied fertilizer is not in contact with sufficient soil for this equilibrium relation to apply. An updated version of CMAQ (v5.2.1) uses a Langmuir-derived approach described in Venterea et al. (2015) to predict NH₃ bidirectional exchange, and Kelly et al. (2019) explore its indirect impact on PM_2.5 composition across the US, suggesting that the reduced emission potential from our approach is compatible with atmospheric agro-ecosystem modelling.

5 Conclusions

This work evaluated the Langmuir, Freundlich, Temkin and Toth adsorption isotherm equations as applied to environmental soil samples and NH${}_{\mathrm{4}}^{+}$ partitioning. We determined that under ideal conditions the Toth equation was the most effective of these equations at fitting soil adsorption curves but that the Temkin equation was most effective at predicting the adsorption behaviour of soil samples with minimal additional characterization required and was effective over both low concentration ranges and the saturation concentration range. Applying this method to a series of environmental soil samples, we determined that the conventional method for directly measuring soil emission potentials may overestimate them by a factor of 5–20 (relative to using the Langmuir and Temkin equations). Of the two adsorption equations, the Temkin equation fit the data better, with a significantly lower AIC (−222 vs. −138 for the Langmuir equation). Comparing these empirical equations with an alternative approach for determining emission potential based on extracting NH${}_{\mathrm{4}}^{+}$ and pH with the same extraction solutions (i.e. DIW : DIW or salt : salt) showed that the Temkin equation fit using the full adsorption range agreed well with the DIW : DIW ratio method but was significantly different when using the low-range fitting parameters.

Appendix A

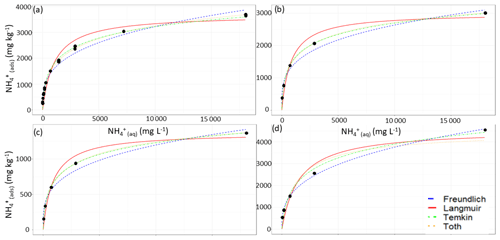
Figure A1 Curve-fitting comparison between the Langmuir (red, solid), Freundlich (blue, – – –), Temkin (green, ⋅ – ⋅ –) and Toth (orange, ⋅ ⋅ ⋅) equations for soil samples collected from (a) King's College Circle, (b) the University of Toronto Scarborough forest, (c) High Park and (d) Queen's Park.

Table A1 Comparison of the residual standard errors, as well as the range of fitted parameters for adsorption curves fit to the un-pooled data. Parameters given in parentheses are reported for comparison with the parameters in Table 2. Goodness of fit is reported using the residual standard error (RSE) rather than AIC to avoid confusion between ranges of AICs for each equation.

Table A2 Residual standard errors when applying average fit parameters from the pooled and (separately fit) training data to the test set soil samples for (i) a CEC of 25, (ii) the experimentally measured CEC and (iii) when the data are fit using the fitting algorithm.

Table A3 Sample information for the adsorption test set.