No increase is detected and modeled for the seasonal cycle amplitude of δ¹³C of atmospheric carbon dioxide

Measurements of the seasonal cycle of δ¹³C of atmospheric CO₂ (δ¹³C_a) provide information on the global carbon cycle and the regulation of carbon and water fluxes by leaf stomatal openings on ecosystem and decadal scales. Land biosphere carbon exchange is the primary driver of δ¹³C_a seasonality in the Northern Hemisphere (NH). We use isotope-enabled simulations of the Bern3D-LPX (Land surface Processes and eXchanges) Earth system model of intermediate complexity and fossil fuel emission estimates with a model of atmospheric transport to simulate atmospheric δ¹³C_a at globally distributed monitoring sites. Unlike the observed growth of the seasonal amplitude of CO₂ at northern sites, no significant temporal trend in the seasonal amplitude of δ¹³C_a was detected at most sites, consistent with the insignificant model trends. Comparing the preindustrial (1700) and modern (1982–2012) periods, the modeled small-amplitude changes at northern sites are linked to the near-equal increase in background atmospheric CO₂ and the seasonal signal of the net atmosphere–land δ¹³C flux in the northern extratropical region, with no long-term temporal changes in the isotopic fractionation in these ecosystems dominated by C₃ plants. The good data–model agreement in the seasonal amplitude of δ¹³C_a and in its decadal trend provides implicit support for the regulation of stomatal conductance by C₃ plants towards intrinsic water use efficiency growing proportionally to atmospheric CO₂ over recent decades. Disequilibrium fluxes contribute little to the seasonal amplitude of the net land isotope flux north of 40° N but contribute near equally to the isotopic flux associated with growing season net carbon uptake in tropical and Southern Hemisphere (SH) ecosystems, pointing to the importance of monitoring δ¹³C_a over these ecosystems. We propose applying seasonally resolved δ¹³C_a observations as an additional constraint for land biosphere models and underlying processes for improved projections of the anthropogenic carbon sink.

1 Introduction

The seasonal variations in the carbon exchange fluxes between the atmosphere and the surface cause a seasonal cycle in atmospheric CO₂ (C_a) (Keeling et al., 1996; Graven et al., 2013; Masarie et al., 2014) and its stable isotopic signature (δ¹³C_a) (Keeling, 1960; Keeling et al., 1984, 1989, 2005; GLOBALVIEW-CO2C13, 2009), with δ¹³C defined as δ¹³C = $[R_{\mathrm{sample}}/R_{\mathrm{std}}-\mathrm{1}]\times \mathrm{1000}$, where R_sample and R_std are the ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}$ abundance ratios of the sample and the carbonate standard Pee Dee Belemnite (PDB; 0.0112372), respectively (Craig, 1957). Observations of the atmospheric seasonal cycles in background tropospheric air provide large-scale information on the carbon fluxes between the atmosphere, ocean, and land (Heimann et al., 1989, 1998) and constraints for models used to project C_a and global warming.

The additional information of δ¹³C data in comparison to carbon data stems from differences in fractionation for different carbon fluxes. Carbon isotopic fractionation describes the preferential transfer of light ¹²C compared to heavier ¹³C. The degree of fractionation is different for the different physical, chemical, and biological processes (Mook, 1986), causing differences in the isotopic composition of carbon reservoirs and fluxes. The seasonal δ¹³C_a variations result from the combination of carbon and isotopic fluxes from fossil fuel burning, land use, and the exchange of the atmosphere with the ocean and land biosphere. Comparing results of carbon-isotope-enabled models with observations of δ¹³C_a is useful to assess whether the mix of carbon and isotopic sink and source fluxes is represented consistently in comparison with the observations. δ¹³C_a observations offer, therefore, a benchmark for evaluating and improving Earth system models.

Fractionation is particularly large during the assimilation of CO₂ from the atmosphere by plants following the C₃ photosynthesis pathway, which are responsible for most of the global productivity (Still et al., 2003). Importantly, changes in isotopic fractionation by C₃ plants are indicative of changes in stomatal conductance, regulating the leaf-internal CO₂ mole fraction and thus photosynthesis (Farquhar, 1989; Saurer and Voelker, 2022; Cernusak and Ubierna, 2022). Photosynthesis, the associated water loss, and evaporative cooling are key characteristics of ecosystem function that are central to the cycles of carbon, nitrogen, water, and energy (Keenan et al., 2013; Knauer et al., 2017) and to the land sink of anthropogenic carbon. Acquisition of CO₂ for photosynthesis is accompanied by the loss of water through the stomatal pores that govern, by their conductance, the diffusion of these two gases between the leaf interior and the atmosphere. A key question is how ecosystems adjust their overall conductance and, thereby, co-regulate carbon uptake and plant growth, regulating water loss and evaporative cooling under rising C_a, growing nitrogen inputs to ecosystems, and increasing water vapor deficits under global warming. Many studies relying on multi-decadal- to century-scale tree-ring δ¹³C records and free-air CO₂ enrichment (FACE) experiments suggest that small changes in isotopic fractionation and intrinsic water use efficiency, the ratio of assimilation to conductance, grow roughly proportionally with C_a (Voelker et al., 2016; Saurer et al., 2014; Kauwe et al., 2013; Peñuelas et al., 2011; Keller et al., 2017; Frank et al., 2015). In contrast, Battipaglia et al. (2013) and Keenan et al. (2013) suggest a scenario where conductance and the flows of carbon and water are downregulated under increasing C_a. Keeling et al. (2017), analyzing decadal-scale change in seasonally detrended δ¹³C_a and the annual atmospheric budgets of carbon and ¹³C, find a decrease in isotopic fractionation of global mean net primary production; the change is attributed to changes in fractionation associated with mesophyll conductance and photorespiration of C₃ plants, and intrinsic water use efficiency is inferred to grow proportionally with C_a. Conflicting results for 20th-century changes in fractionation and intrinsic water use efficiency are also found in global land biosphere models (Keller et al., 2017).

The observational records from globally distributed monitoring sites (Keeling et al., 1996; Graven et al., 2013; Masarie et al., 2014) demonstrate a significant growth trend in the seasonal cycle amplitude (SA) of C_a (Bacastow et al., 1985; Keeling et al., 1996; Graven et al., 2013; Barlow et al., 2015; Piao et al., 2018) driven by changes in the seasonality of net land carbon uptake (Graven et al., 2013; Forkel et al., 2016). The observed seasonal cycle and amplitude growth of C_a are widely used to evaluate carbon cycle models and system understanding by transporting fluxes from terrestrial, oceanic, and fossil fuel sources with a model of atmospheric transport to obtain local C_a anomalies (Heimann et al., 1998; Dargaville et al., 2002; Scholze et al., 2008; Peng et al., 2015; Lienert and Joos, 2018). Studies address the role of different climatic drivers and terrestrial carbon cycle processes such as drought, land use, warming, productivity, and soil respiration (Heimann et al., 1989, 1998; Graven et al., 2013; Forkel et al., 2016; Ito et al., 2016; Bastos et al., 2019; Wang et al., 2020) and surface-to-atmosphere C fluxes (e.g., Peylin et al., 2013). SAs(C_a) and their temporal trends at different monitoring sites are used for constraining an ensemble of land biosphere model simulations (Lienert and Joos, 2018).

Comparable studies analyzing the temporal trends in SA(δ¹³C_a) and the seasonal cycle of δ¹³C_a are scarce. While seasonally resolved atmospheric δ¹³C_a measurements are available (GLOBALVIEW-CO2C13, 2009; Keeling et al., 2001), these seasonally resolved records are yet to be fully utilized in the context of process-based carbon cycle models. Heimann et al. (1989) simulated the spatiotemporal distribution of δ¹³C_a and C_a with an atmospheric transport model using estimates of net primary production (NPP) and heterotrophic respiration based on satellite data and surface temperature and prescribed surface ocean CO₂, demonstrating the dominant role of land biosphere fluxes for Northern Hemisphere (NH) seasonality and finding relevant signals from the ocean and land in the Southern Hemisphere (SH). Van der Velde et al. (2018) applied their CarbonTracker Data Assimilation System for CO₂ and ¹³CO₂ by varying the net exchange fluxes of CO₂ and ¹³CO₂ in ocean and terrestrial biosphere models and propagating the fluxes through an atmospheric transport model to solve for weekly adjustments to fluxes and isotopic terrestrial discrimination, minimizing differences between observed and estimated mole fractions. They identified a decrease in stomatal conductance on a continent-wide scale during a severe drought. Ballantyne et al. (2011) applied an analytical regression approach to analyze the differences in isotopic signatures between Northern Hemisphere site data and free-troposphere background data from Niwot Ridge to infer seasonal variations in the source signature of the net atmosphere–land biosphere flux and to evaluate models of stomatal conductance. Observations of δ¹³C_a seasonal cycles were used to investigate isotopic fractionation (Ballantyne et al., 2010) and trends in the phenology of northern terrestrial ecosystems (Gonsamo et al., 2017) but to our knowledge have not been used for analyzing trends in SA(δ¹³C_a) globally.

This study addresses the following main questions:

1. Is the seasonal cycle of δ¹³C_a observed at a network of globally distributed sites represented well in model simulations? How large are the contributions of ocean, land, and fossil fuel fluxes to δ¹³C_a seasonality?

2. What are the temporal trends in SA(δ¹³C_a) in the observational records, and are the modeled trends in SA(δ¹³C_a) consistent with the observed trends?

3. What are the different drivers of SA(δ¹³C_a) versus SA(C_a) and of their temporal trends? Is a model scenario with intrinsic water use efficiency growing proportional with C_a consistent with δ¹³C_a seasonality data?

We simulate atmospheric δ¹³C_a and C_a at 19 globally distributed sites using the matrix representation of an atmospheric transport model and net atmosphere-to-surface fluxes of CO₂ and δ¹³(CO₂) from an Earth system model of intermediate complexity (EMIC) alongside gridded fossil fuel emission estimates and changes in land use and the distribution of C₃ and C₄ crops. We compare model results to observations and analyze trends in SA(δ¹³C_a) using the records of the Scripps CO₂ program (Keeling et al., 2001) and the Cooperative Global Atmospheric Data Integration Project (2013) product. We discuss the implications of our results for changes in the fractionation by C₃ plants, their stomatal controls, and associated carbon and water fluxes. We develop a theoretical framework to explain the trends in SA(δ¹³C_a) and decompose net carbon and isotope land biosphere fluxes into underlying component fluxes and changes in carbon fluxes and fractionation. The framework could serve future studies, e.g., studies applying an ensemble of different models for multi-model evaluation, and provide more robust conclusions in comparison to using a single model chain.

2 Methods

2.1 Bern3D-LPX Earth system model of intermediate complexity

Spatially resolved surface-to-atmosphere CO₂ and ¹³CO₂ fluxes are simulated with the Bern3D-LPX (Land surface Processes and eXchanges) Earth system model of intermediate complexity. Here, the ocean–atmosphere model Bern3D (Jeltsch-Thömmes and Joos, 2020; Battaglia and Joos, 2018; Ritz et al., 2011) is coupled to the dynamic global vegetation model (DGVM) framework of the Land surface Processes and eXchanges (LPX) model, LPX-Bern v1.4 (Lienert and Joos, 2018). The Bern3D model features a 41 × 40 horizontal ocean grid (about 9° × 4.5°) with 32 depth layers coupled to a single-layer energy–moisture balance atmosphere (Ritz et al., 2011). In Bern3D, carbon and its isotopes are implemented as tracers with fractionation for air–sea and sea–air gas exchange, aquatic chemistry, and the production of organic material and CaCO₃ as a function of surface ocean temperature, aqueous CO₂, and the speciation of dissolved inorganic carbon, as described by Jeltsch-Thömmes and Joos (2023). LPX-Bern simulates the coupled cycling of carbon, nitrogen, and water (Xu-Ri and Prentice, 2008; Wania et al., 2009a, b; Stocker et al., 2014) and vegetation dynamics using plant functional types (Sitch et al., 2003). It is run here at a 3.75° × 2.5° resolution. Grid cells are subdivided into different land use classes (mineral soil, wetlands, crop, pasture, urban). Carbon isotopes were added (Scholze et al., 2003) using a photosynthetic fractionation scheme (Lloyd and Farquhar, 1994) and without further isotopic fractionation during the transfer through the vegetation, litter, soil, and product pools. The scheme neglects fractionation by boundary layer transport and ternary effects associated with the interaction of CO₂, water, and air (Farquhar and Cernusak, 2012), and fractionation by dark-day respiration is set to zero, while fractionation by the following terms is explicitly considered: stomatal conductance (with a scaling factor of 4.4 ‰), dissolution and liquid transport (1.8 ‰), carboxylation (27.5 ‰), and photorespiration (8 ‰ and the CO₂ compensation point that would occur in the absence of dark respiration, Γ^*, increases with temperature) (Lloyd and Farquhar, 1994). The signature of respired carbon reflects the signature of carbon assimilated at previous times; the lag times between assimilation and respiration are dictated by the turnover timescales of the various pools, depending on temperature and soil moisture. Land carbon and isotope fluxes respond to altered climate, which influences, for example, photosynthesis through temperature and water limitation, fire frequency, and autotrophic and heterotrophic respiration rates; respond to increasing C_a, which stimulates photosynthesis and affects water use efficiency (“CO₂ fertilization”); respond to land use (Strassmann et al., 2008), which causes, for example, transfer of tree carbon to the atmosphere, litter, and product pools after deforestation and shifts from natural vegetation to C₃ and C₄ crops and pasture; and respond to altered nitrogen deposition and the addition of nitrogen fertilizer on managed land alleviating nitrogen limitation.

Bern3D and LPX-Bern were spun up individually, followed by a 500-year coupled spinup to preindustrial equilibrium (1700 CE; 276.3 ppm, −6.27 ‰). A transient simulation, E_standard, from 1700 to 2020 is driven by annual fossil fuel carbon emissions (including the contribution from cement production) (Friedlingstein et al., 2020), net land use area changes (Hurtt et al., 2020), and non-CO₂ radiative forcing. δ¹³C of the fossil fuel emissions follows Andres et al. (2017) for 1751–2014 and is set to the value for 1751 before. For 2014–2020, signatures of major source categories (coal, oil, gas, cement) are assumed to be constant and combined with the emission sources from Friedlingstein et al. (2020), following the approach of Andres et al. (2000). Here, we explicitly distinguish land use classes for C₃ and C₄ crops and prescribe their extent, and net land use area changes are based on the Land-Use Harmonization 2 dataset (Hurtt et al., 2020). Nitrogen deposition and nitrogen fertilization are taken from the Global N₂O Model Intercomparison Project (Tian et al., 2018). Nitrogen (N) is a limiting nutrient in LPX, and plant growth is downregulated under N stress, which tends to reduce plant growth and plant growth responses to rising C_a compared to a model with absent N cycling. The monthly wind stress climatology from the NCEP/NCAR Reanalysis produced by the National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) (Kalnay et al., 1996) is prescribed to the ocean. Climatic Research Unit (CRU) Time Series (TS) version 4.05 high-resolution gridded data of month-by-month variation in climate (CRU TS v4.05) (Harris et al., 2020) are used for the land model. For 1700–1900 and the spinup, the climate of 1901–1931 is recycled. A baseline is provided by a control simulation, termed E_control, without anthropogenic CO₂ emissions; absent radiative forcing from non-CO₂ species (e.g., from CH₄, N₂O, ozone); and with land use, nitrogen deposition, and nitrogen fertilization at the 1700 level, as well as recycling the 1901–1931 land climate. C_a and δ¹³C_a evolve freely in all simulations presented and remain at their preindustrial values in E_control.

2.2 Atmospheric transport model TM3 and the seasonal cycles of C_a and δ¹³C_a

We employ the transport matrices of the global atmospheric tracer model TM3, a three-dimensional transport model (Heimann and Körner, 2003; Kaminski et al., 1998; Schürmann et al., 2016), to translate surface–atmosphere fluxes from Bern3D-LPX and fossil fuel emissions into C_a and δ¹³C_a anomalies at 19 measurement sites across the globe. Before transport, the fluxes are remapped to the TM3 grid with 72 × 48 grid cells (5° × 3.75°). Here, the matrices span 1982 to 2012 and are only available if there is also a CO₂ measurement available at the corresponding site. Each matrix represents the sensitivity of the local atmospheric concentration for a given month to the local surface fluxes of the previous period, spanning up to 48 months. The transport model is initialized with equal C_a and δ¹³C_a at all sites.

For ¹³C, the signature-weighted net atmosphere-to-surface flux is

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}(\mathit{x},t)=f_{\mathrm{as},\mathrm{net}}(\mathit{x},t)\cdot {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as},\mathrm{net}}(\mathit{x},t).\end{array}$$

δ¹³f_as,net is in units of mol ‰ m⁻² yr⁻¹. x indicates location and t time at the monthly and spatial (5° × 3.75°) resolution of TM3. The net carbon fluxes (f_as,net; mol m⁻² yr⁻¹); their signatures (δ¹³C_as,net); and, therefore, δ¹³f_as,net, are readily available for fossil fuel emissions, including cement production (Andres et al., 2009a, b). Bern3D-LPX simulates two-way exchange of CO₂ and ¹³CO₂ from and to the ocean and land surface. Net transfer rates are determined by the difference in these gross fluxes to yield the atmosphere-to-surface net fluxes, f_as,net and δ¹³f_as,net, of Bern3D-LPX.

The matrices are applied with f_as,net to compute anomalies in C_a and with δ¹³f_as,net to compute anomalies in ¹³CO₂. We get δ¹³C_a from ${}^{\mathrm{13}}{\mathrm{CO}}_{\mathrm{2}}/{\mathrm{C}}_{\mathrm{a}}$. This method of transporting signature-weighted net fluxes was chosen instead of separately transporting ¹³CO₂ and ¹²CO₂. Both approaches were tested and showed very similar results, except for numerical issues in months having very small local ¹²CO₂ anomalies for the second approach.

Ocean, land, and fossil fuel fluxes from the standard simulation are transported separately to quantify the contributions of these individual components to the seasonal variations in C_a and δ¹³C_a. For E_control, fossil fuel fluxes are not transported, consistent with the model setup. A limitation is that transport matrices are only available for the period of 1982 to 2012, limiting the analysis period and direct model–data comparison to 3 decades only.

2.3 Site data

Background CO₂ from 19 monitoring sites for which transport matrices are available is used for comparison with simulated C_a and δ¹³C_a and to determine observation-based trends in their SAs. The Cooperative Global Atmospheric Data Integration Project (2013) product is used for C_a. For δ¹³C_a, the records of the Scripps CO₂ program (Keeling et al., 2001) for Alert, Mauna Loa, and the South Pole from monthly averaged flask data are used. These records span a longer period than the available transport matrices. For the remaining 16 sites, the shorter (1994 to 2009) records of GLOBALVIEW-CO2C13 (2009) are used. In the main paper, we focus on 3 out of the 19 available transport sites: Alert (82.5° N, Canada), Mauna Loa (19.5° N, Hawaii), and the South Pole (90° S, Antarctica). Results for the other sites are shown in the Supplement and Table 1. The Scripps and GLOBALVIEW-CO2C13 data are on slightly different scales (Lueker et al., 2020); this does not affect our analysis of seasonal anomalies. The δ¹³C_a records of GLOBALVIEW-CO2C13 (2009) span the order of a decade and are, therefore, not used for trend detection, although we evaluated trends from the simulations for the GLOBALVIEW sites (Table 2, excluding Key Biscayne). We require at least 10 monthly values for a year to be included in the linear regression.

Additional δ¹³C_a monthly flask data from the Scripps CO₂ program (Keeling et al., 2001) are used for analyzing temporal trends in the SA(δ¹³C_a). We focus on eight sites with more than 20 years of data: Alert (ALT, 82° N), Nuvuk (formerly Point Barrow) (PTB, 71° N), La Jolla (LJO, 33° N), Mauna Loa Observatory (MLO, 20° N), Cape Kumukahi (KUM, 20° N), Christmas Island (CHR, 2° N), Samoa (SAM, 14° S), and the South Pole (SPO, 90° S). The data are provided as (i) monthly samples, (ii) a fit to these monthly samples, and (iii) the monthly samples but with missing values replaced by fitted values. We also used the original, non-gap-filled data and years with at least 9, 10, or 11 monthly values per year in the regression.

3 The influence of carbon and isotope fluxes on the seasonal cycles of C_a and δ¹³C_a: a conceptual framework

We develop a simplified conceptual framework to qualitatively explore the influence of carbon and isotope fluxes on the seasonal cycles of C_a and δ¹³C_a. For illustration, the atmosphere is considered to be well-mixed in this section; the atmospheric transport operator is linear, and the findings may qualitatively also apply to spatially resolved fluxes. The budgets for the atmospheric inventories of carbon and ¹³C are approximated (Tans et al., 1993) as

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{N}_{\mathrm{a}}=-F_{\mathrm{as},\mathrm{net}}\text{(3)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}(N_{\mathrm{a}}\cdot {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}})& =\left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{N}_{\mathrm{a}}\right)\cdot {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}+N_{\mathrm{a}}\cdot \left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}\right)\\ & =-F_{\mathrm{as},\mathrm{net}}\cdot \stackrel{\mathrm{‾}}{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as},\mathrm{net}}}.\end{array}\end{array}$$

N_a and N_a⋅δ¹³C_a are the atmospheric inventories of carbon and (approximately) of ¹³C (in mol ‰). F_as,net and $F_{\mathrm{as},\mathrm{net}}\cdot \stackrel{\mathrm{‾}}{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as},\mathrm{net}}}$ are the globally integrated net atmosphere-to-surface carbon and ¹³C flux; $\stackrel{\mathrm{‾}}{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as},\mathrm{net}}}$ is the signature of the global net carbon flux. We set $N_{\mathrm{a}}=c\cdot {\mathrm{C}}_{\mathrm{a}}$, where c is a unit conversion factor. Solving Eqs. (2) and (3) for the changes in C_a and δ¹³C_a yields

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\mathrm{C}}_{\mathrm{a}}={\displaystyle \frac{-\mathrm{1}}{c}}\cdot F_{\mathrm{as},\mathrm{net}}\text{(5)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}={\displaystyle \frac{-\mathrm{1}}{c\cdot {\mathrm{C}}_{\mathrm{a}}}}\cdot {\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*},\end{array}$$

with ${\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*}$ being the global integral of

$$\begin{array}{}\text{(6)}& {\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}=f_{\mathrm{as},\mathrm{net}}\cdot \left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as},\mathrm{net}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}\right).\end{array}$$

The superscript ^* indicates that the ¹³C fluxes (e.g., in units of mol ‰ yr⁻¹ m⁻² for ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}$) are referenced to the atmospheric signature. Equation (6) corresponds to Eq. (1) for the net atmosphere-to-surface isotopic flux but is now referenced to the atmospheric signature instead of the signature of 0 ‰ of the Vienna Pee Dee Belemnite standard as in Eq. (1). In this way, a positive (negative) flux causes a negative (positive) change in δ¹³C_a.

Equations (4) and (5) are readily integrated over the growing season from the intra-annual maximum to the minimum (subscripts indicate max and min) in C_a and the corresponding beginning, t_beg, and end, t_end, of the growing season to get the seasonal cycle amplitude (SA) for the two tracers and (cumulative) net fluxes (see Appendix A for calculation of SA for a flux):

$$\begin{array}{}\text{(7)}& {\displaystyle }\underset{\mathrm{SA}\left({\mathrm{C}}_{\mathrm{a}}\right)}{\underbrace{{\mathrm{C}}_{\mathrm{a},\max }-{\mathrm{C}}_{\mathrm{a},\min }}}={\displaystyle \frac{\mathrm{1}}{c}}\underset{\mathrm{SA}\left(F_{\mathrm{as},\mathrm{net}}\right)}{\underbrace{\underset{t_{\mathrm{beg}}}{\overset{t_{\mathrm{end}}}{\int }}{F}_{\mathrm{as},\mathrm{net}}\left(t\right)\mathrm{d}t}}\text{(8)}& {\displaystyle }\underset{\mathrm{SA}\left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}\right)}{\underbrace{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a},\max }-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a},\min }}}={\displaystyle \frac{-\mathrm{1}}{c\cdot {\mathrm{C}}_{\mathrm{a}}}}\underset{\mathrm{SA}\left({\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*}\right)}{\underbrace{\underset{t_{\mathrm{beg}}}{\overset{t_{\mathrm{end}}}{\int }}{\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*}\left(t\right)\mathrm{d}t}}.\end{array}$$

Equations (5) and (8) provide important insights. First, changes in δ¹³C_a and its seasonal cycle are driven by ${\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*}$; seasonal changes in C_a, the denominator in Eq. (5), are small compared to C_a, and C_a is considered constant within a given year (the error associated with this approximation is less than 3 %). Second, the background CO₂ mole fraction, C_a, modulates the magnitude of the δ¹³C_a seasonal cycle. SA(δ¹³C_a) would be larger under low preindustrial C_a than under modern C_a for equal seasonal variations in ${\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*}$. Correspondingly, SA(δ¹³C_a) does not change over time as long as the relative changes in SA(${\mathit{\delta }}^{\mathrm{13}}{F}_{\mathrm{as},\mathrm{net}}^{*}$) and in C_a are equal. Equations (7) and (8) were derived for a globally well-mixed atmosphere and global fluxes but analogously also apply for the tracer seasonality at individual sites, with the integral on the right-hand side of Eqs. (7) and (8) representing the integral of (transport-weighted) fluxes over the region influencing tracer seasonality at the site. We recall that the above equations and conclusions were derived by assuming a well-mixed atmosphere, while in reality spatial flux patterns and transport and their changes influence seasonal cycles at individual atmospheric sites. Further, the start and end of the growing season are assumed to coincide with the switch in the sign of the isotopic flux; this is the case in our model for zonally integrated fluxes. These seasonal fluxes will be presented in Sect. 4.3. Equations (2) to (8) are for illustrating the influence of carbon and carbon isotope fluxes on the seasonal cycles of C_a and δ¹³C_a; they were not used for calculating numerical results.

The notation and sign convention introduced above are applied in this paper. In brief, f_i,j defines a one-way flux from the source reservoir i to the receiving reservoir j and is positive. The isotopic signature of this flux is δ¹³C_i,j. The net flux from reservoir i to reservoir j is $f_{i,j,\mathrm{net}}$ and is the difference between the corresponding one-way fluxes; e.g., $f_{i,j,\mathrm{net}}=f_{i,j}-f_{j,i}$. $f_{i,j,\mathrm{net}}$ is positive if the net flux results in the transfer of mass from i to j.

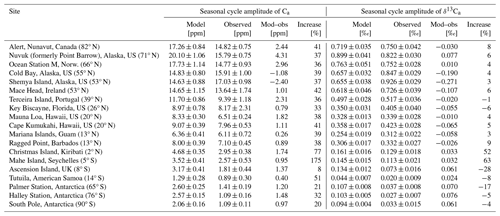
Table 1 The seasonal cycle amplitude of C_a and δ¹³C_a from the standard simulation (mod; E_standard) and observations (obs) for 19 monitoring sites and the period of 1982–2012. The increase over the industrial period is estimated from the difference between the standard simulation and the preindustrial control ($\mathrm{100}\cdot (E_{\mathrm{standard}}-E_{\mathrm{control}})/E_{\mathrm{control}}$).

4 Results

4.1 Seasonal cycles of atmosphere–surface fluxes, C_a, and δ¹³C_a

The Bern3D-LPX model simulates (E_standard) large seasonal variations in the net land biosphere–atmosphere exchange of CO₂ and ¹³CO₂, whereas seasonal variations in ocean–atmosphere fluxes are much smaller (Fig. 1). This seasonality is broadly consistent with estimates of regional air–land carbon flux seasonality from an atmospheric inversion (Gurney et al., 2004) and air–sea flux seasonality from surface ocean pCO₂ observations (Landschützer et al., 2014; Takahashi et al., 2009; Fay et al., 2021), except in the Southern Ocean and in the northern subpolar gyres. The LPX land biosphere model shows the expected uptake of isotopically depleted carbon, resulting in positive f_as,net and negative ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}$ during the summer and vice versa in winter.

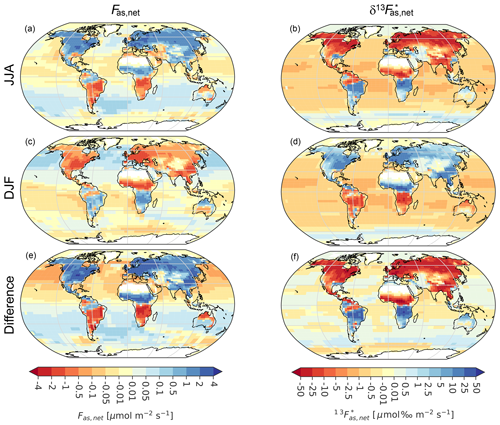
Figure 1 Net seasonal atmosphere-to-surface fluxes. Fluxes are for (a, c, e) carbon and (b, d, f) the δ¹³C-weighted carbon flux, ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}$ (see Sect. 3), from the standard simulation (E_standard) and are averaged over 1982–2012 for (a, b) June, July, and August (JJA); (c, d) December, January, and February (DJF); and (e, f) JJA minus DJF. Note the non-linear color bars with blue colors in panels (a) to (d) indicating a lowering in atmospheric CO₂ and δ¹³C.

The Bern3D ocean model shows a negative ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}$ in the low latitudes and midlatitudes, small modern fluxes in the northern subpolar gyres, and a positive flux in the Southern Ocean in both seasons (Fig. 1). These modern Bern3D fluxes are driven by the atmosphere–ocean isotopic disequilibrium, here defined as the isotopic signature of the atmosphere-to-surface carbon flux minus the signature of the surface-to-atmosphere flux (δ_dis,as; Eq. A2), with a negative δ_dis,as in the low latitudes and midlatitudes, a small modern disequilibrium in northern high latitudes, and a positive δ_dis,as south of 50° S, consistent with observations (Menviel et al., 2015; Quay et al., 2017; Becker et al., 2018).

The preindustrial δ_dis,as and ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}$ are negative in the low latitudes and midlatitudes and positive in high-latitude ocean regions (not shown), mainly driven by the temperature dependency of isotopic fractionation during air–sea exchange and the cycling of marine biological matter (see Fig. 1 of Menviel et al., 2015, to compare Bern3D and LOVECLIM results for δ_dis,as). Fossil fuel emissions cause a negative flux perturbation worldwide, shifting the net isotopic fluxes to more negative values over the industrial period.

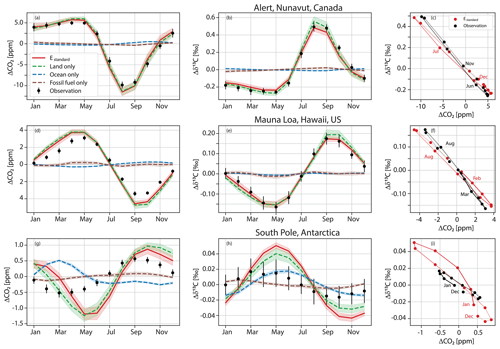
Figure 2 The simulated (red) seasonal cycle of atmospheric C_a (left, a, d, g) and its signature δ¹³C_a (middle, b, e, h) compared to observations (black dots). In the rightmost panels (c, f, i) the seasonal anomalies (Δ) of C_a are plotted against those of δ¹³C_a, with lines connecting the monthly values (dots) fading from January to December. Results are for Alert, northern Canada (a, b, c); Mauna Loa, Hawaii (d, e, f); and the South Pole (g, h, i). Simulated values are from transporting net TM3 fluxes of the Bern3D-LPX E_standard simulation from all (red, E_standard), terrestrial (green, dashed), oceanic (blue, dashed), and fossil fuel sources (brown, dashed). The observational and model anomalies are computed from monthly values between 1982 and 2012 if both the measurements and transport matrices are available. Error bars and shading correspond to the standard deviation from the interannual variability in monthly values.

Figure 2 compares the mean seasonal cycles of C_a and δ¹³C_a from E_standard with measurements from 1982 (at Alert from 1985) to 2012 at three sites and with factorial simulations, where the fluxes of the land (dashed green line), ocean (dashed blue line), and fossil fuel emissions (dashed brown lines) were considered individually (see Table 1 and Figs. S1 and S2 in the Supplement for additional sites). For the Northern Hemisphere (NH) sites of Alert (top panels) and Mauna Loa (middle panels), the seasonal variations are dominated by the terrestrial biosphere fluxes, with minor contributions from ocean fluxes and fossil fuel emissions.

Both the timing and amplitude of the observed seasonal cycle of C_a and δ¹³C_a are captured reasonably well by E_standard (Fig. 2). The simulated SA(C_a) and its interannual variability (IAV) are overestimated compared to observations at Alert (17.3 ± 0.84 ppm versus 14.8 ± 0.75 ppm) and Mauna Loa (8.3 ± 0.30 ppm versus 6.5 ± 0.24 ppm). SA(δ¹³C_a) matches the observations (ALT – 0.72 ± 0.035 ‰ versus 0.75 ± 0.042 ‰; MLO – 0.34 ± 0.013 ‰ versus 0.33 ± 0.028 ‰). Good model–data agreement in the phasing of the seasonal cycle of C_a relative to δ¹³C_a is demonstrated for Alert in panel (c), where monthly anomalies in δ¹³C_a are plotted versus anomalies in C_a. Both the observations and the model show hysteresis throughout the year, with the loop rotating clockwise. At Mauna Loa, the rotation direction of the hysteresis loop is clockwise in the simulation and counterclockwise in the observations (panel f). Still, the observed hysteresis is small, with offsets of less than 0.03 ‰. The hysteresis arises as the ratio between the rate of change in δ¹³C_a versus the rate of change in C_a varies over the year (Keeling et al., 1989; Heimann et al., 1989). This non-linearity in the atmospheric tracer relationship originates from seasonally varying transport in combination with spatially and temporally varying relationships of atmosphere–surface δ¹³C to CO₂ flux. For example, the isotopic signature of the growing season net atmosphere-to-land carbon flux δ¹³C_al,net is −13.4 ‰ for the northern high-latitude region (>40° N) but only −10.7 ‰ for the region 10–40° N, and the signal observed at any measurement site results from varying contributions from these and other latitudinal bounds given intra-annually varying winds and hence transport.

Results for the South Pole are different than for the NH sites (Fig. 2g, h, i). Neither the timing nor the amplitude of C_a (2.1 ± 0.16 ppm simulated versus 1.1 ± 0.11 ppm observed) and δ¹³C_a (0.094 ± 0.004 ‰ versus 0.033 ± 0.015 ‰) agrees with observations. SA(C_a) and SA(δ¹³C_a) at the South Pole are observed to be 14 and 23 times smaller than at Alert, respectively. The absolute data–model mismatches are therefore not as drastic as the relative mismatches. The disagreement between simulation and observational estimates is also apparent when considering the scatter plot in panel (i). The model shows a complex hysteresis relationship, whereas the observations display a clockwise loop.

The remote Antarctic sites (the South Pole, Palmer, and Halley) show an expected relatively larger dependence on the ocean, but the terrestrial contribution still dominates in the model (Figs. 2, S1, and S2). The C_a seasonal cycle resulting from atmosphere–ocean flux is shifted by up to 6 months compared to observations at the South Pole and the other two Antarctic sites (Palmer, Halley; blue lines versus black dots in Fig. S1), pointing to biases in the Bern3D ocean flux. Observation-based analyses indicate stronger ocean CO₂ uptake in summer than in winter in the Southern Ocean (Jin et al., 2024; Long et al., 2021; Fay et al., 2021) in contrast to results from Bern3D (Fig. 1) and more complex ocean models (Hauck and Völker, 2015) and several Earth system models from CMIP5 (Majkut et al., 2014) and CMIP6 (Joos et al., 2023). The simulated amplitude and phasing of the δ¹³C_a seasonal cycle resulting from the ocean are broadly in line with observations at the Antarctic sites (Fig. S2). The air–sea isotopic disequilibrium is large in the Southern Ocean, and the two-way air–sea and sea–air exchange fluxes yield a substantial net isotopic flux, even under low net carbon flux. Temperature-dependent fractionation is higher in winter than in summer, and the air–sea gas exchange piston velocity and, in turn, the isotope fluxes are larger under high winds in winter than in summer in the modeled Southern Ocean, consistent with the observed seasonal phasing of δ¹³C_a at the Antarctic sites. Errors in modeled Southern Ocean fluxes are expected to have a minor impact on simulated SA(C_a) and SA(δ¹³C_a) at NH sites, where the influence of land fluxes dominates by far (Figs. 2, S1, S2).

Considering all extratropical Northern Hemisphere sites, model–data mismatches are less than 30 % for SA(C_a) and SA(δ¹³C_a) and their root-mean-square errors (RMSEs) are 2.6 ppm and 0.14 ‰, respectively. For the tropical and SH sites, large relative data–model deviations of up to 140 % for SA(C_a) and up to 290 % for SA(δ¹³C_a) are evident, although absolute deviations are less than 1.8 ppm, and 0.18 ‰ and the corresponding RMSEs are 1.2 ppm and 0.05 ‰ (Table 1).

Interannual variability in simulated SA(δ¹³C_a) compares reasonably well with observations at sites in the NH subtropics and extratropics (average of the 1σ standard deviation of 12 sites is 0.031 ‰ in E_standard versus 0.031 ‰ in observations) and in the tropics and SH (0.009 ‰ versus 0.013 ‰) (Table 1). Similar agreement between simulated and observation-derived IAV holds for SA(C_a) (NH extratropics –0.75 versus 0.96 ppm; tropics and SH – 0.29 versus 0.30). This suggests that the variability in the seasonal amplitude of the carbon and isotope fluxes is reasonably represented by LPX-Bern. The correct simulation of variability can be challenging and van der Velde et al. (2013) report too low an interannual variability in the annually integrated isotopic disequilibrium flux for their model.

4.2 Temporal trends in the seasonal cycle amplitude of δ¹³C_a and C_a

Detection of trends in SA(δ¹³C_a) may be hampered by interannual-to-decadal variability, short record lengths, and a small SA(δ¹³C_a) in comparison to measurement uncertainty and variability, as is typical at Southern Hemisphere sites. For example, dividing SA(δ¹³C_a) by 2 standard deviations of IAV yields a signal-to-noise ratio (Keller et al., 2014) below 2.7 at SH sites and as low as 1.1 at the South Pole and on American Samoa (Table 1). Thus, SA(δ¹³C_a) would need to roughly double over the observational period for a trend in SA(δ¹³C_a) to emerge from the noise of IAV at these two sites. The situation is more favorable for trend detection at NH extratropical sites (Table 1), where the signal-to-noise ratio ranges between 9 and 16, and changes of 6 % to 11 % in SA(δ¹³C_a) would emerge.

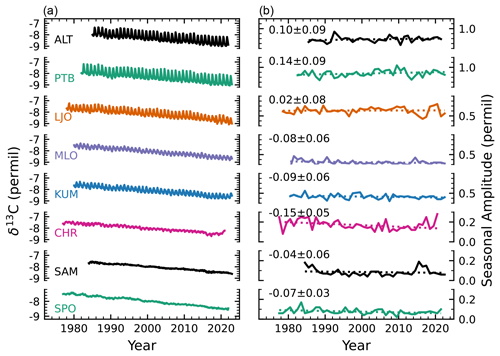
Figure 3 Temporal evolution of δ¹³C_a (a) and its seasonal amplitude (b) from data of the Scripps network (Keeling et al., 2001). Gap-filled data provided by Scripps are used for the eight sites. The slope and its standard error from a linear regression through the seasonal amplitude data (dotted) are given in ‰ per century. Trends are not different from zero based on a two-sided t test and a significance level of 5 %, except at Christmas Island (CHR) and the South Pole (SPO). Sites are ordered according to latitude (Alert (ALT, 82° N), Nuvuk (formerly Point Barrow) (PTB, 71° N), La Jolla (LJO, 33° N), Mauna Loa Observatory (MLO, 20° N), Cape Kumukahi (KUM, 20° N), Christmas Island (CHR, 2° N), Samoa (SAM, 14° S), and the South Pole (SPO, 90° S)).

Table 2 Temporal trends in the seasonal cycle amplitude of C_a and δ¹³C_a from the standard simulation (E_standard) and observations for 19 monitoring sites from 1982 to 2012. Observational data of C_a are from the GLOBALVIEW-CO₂ product and are fitted for the period of 1982–2012, while the data for δ¹³C_a are from Scripps and are fitted as shown in Fig. 3. The seasonal cycle amplitude of a given year is only computed if at least 10 monthly values are available. The number of years included in the trend calculation for SA(C_a) and model-based SA(δ¹³C_a) is given in parentheses. The observed trend for C_a is affected by anomalous values at Key Biscayne, which is not included. Over the period of 1982–2012, significant trends (two-sided t test at 5 % significance) are only found for Alert, Nuvuk (formerly Point Barrow), Ocean Station M, and Mahe Island for observed C_a; for Mariana Islands, Mahe Island, Palmer, Halley, and the South Pole for simulated C_a; and for Ascension, Mahe Island, and the South Pole for simulated δ¹³C_a. The decadal-scale trends are given per century for better readability.

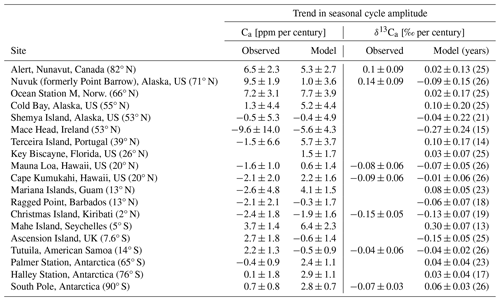
Temporal trends in SA(δ¹³C_a) from the Scripps gap-filled data are not statistically different from zero, except at the tropical site Christmas Island and at the South Pole (Fig. 3). Averaging the trends across all eight sites yields −0.0038 ± 0.026 ‰ per century (mean ± 1 SD of the mean), and averaging the trends for the extratropical sites ALT, PTB, and LJO yields +0.09 ± 0.06 ‰ per century, with both averaged trends not statistically different from zero. The trend for the NH extratropical sites translates into a change in SA(δ¹³C_a) of around 5 ± 3 % over the 40-year observational period. For the fitted data, trends are statistically different from zero only at two sites (La Jolla and Christmas Island). This is consistent with Gonsamo et al. (2017), who did not detect a temporal trend in SA(δ¹³C_a) and seasonal phasing by fitting Scripps daily flask data from the four sites of Alert, Nuvuk (formerly Point Barrow), La Jolla, and Mauna Loa. In summary, observed temporal trends in SA(δ¹³C_a) are small (≤ 0.15 ‰per century) and are not statistically different from zero (at p<0.05) at individual sites. A significant negative trend is found for the tropical site Christmas Island, and detection of trends is difficult at the Southern Hemisphere sites, where SA(δ¹³C_a) is small.

Simulated trends in SA(δ¹³C_a) are small (often less than 0.01 ‰ per decade) and statistically insignificant (5 % level) except at three SH sites (Ascension, Mahe, the South Pole) with a small seasonal cycle amplitude (Table 2). Observed relative trends in SA(C_a) are larger than in SA(δ¹³C_a) in the northern high latitudes and are statistically significant at Alert, Nuvuk (formerly Point Barrow), Ocean Station, and Mahe Island but insignificant at all other sites over the 1982–2012 analysis period. Simulated trends in SA(C_a) are insignificant, except at four SH sites and on the Mariana Islands.

We compare model (m) and observed (o) slopes (β) to probe model–observation agreement. Under the null hypothesis of no slope difference, the $T=({\mathit{\beta }}_m-{\mathit{\beta }}_o)/\sqrt{s_{{\mathit{\beta }}_m}^{\mathrm{2}}+s_{{\mathit{\beta }}_o}^{\mathrm{2}}}$ statistic (where s_β is the standard error in the β slope estimate) is Student's t distributed (Welch, 1947). Trends are different when the T values are larger than the 0.975 quantile of a t distribution with ν degrees of freedom ($T>\sim \mathrm{2}$). Modeled and observed trends are different at one site, the South Pole, for SA(δ¹³C_a) and at one site (Nuvuk, formerly Point Barrow) for SA(C_a). As will become clear in the next section, the largest surface–atmosphere isotope fluxes and temporal changes in these fluxes are simulated in the region north of 40° N. We are therefore interested in quantifying how well the model represents temporal changes in SA(C_a) in this region and over a 40-year period, representative of the δ¹³C_a observational record. For the five NH high-latitude sites with more than 20 years of data, uncertainties in the temporal changes in SA(C_a) range between 5 % and 13 % at individual sites over a 40-year period. The average trend in SA(C_a) for these five NH sites (Alert, Nuvuk (formerly Point Barrow), Ocean Station M, Cold Bay, Shemya Island) is 4.8 ± 1.6 ppm per century (31 ± 10 % per century) from observations and 3.8 ± 1.8 ppm per century (22 ± 11 % per century) from the model. These estimates translate into a relative change in SA(C_a) of around 4 % to 5 % over a 40-year period. This suggests that our model chain accurately represents the observed temporal changes in SA(C_a) in the NH extratropical atmosphere.

Given the mostly insignificant trends at individual sites over the model analysis period of 1982–2012, the question of whether larger trends are detected when considering longer timescales arises. Century-scale trends, or their absence, can be readily estimated in the simulations by comparing SA(C_a) and SA(δ¹³C_a) for the modern period (1982–2012) (E_standard) and the preindustrial control (E_control) (Table 1; solid red versus dashed blue lines in Figs. S3 and S4). For C_a, a growth in SA is clearly visible (12.2 to 17.25 ppm at Alert, 6 to 8.3 ppm at Mauna Loa, 1.7 to 2.1 ppm at the South Pole). Across all 19 sites, SA(C_a) has grown by 44 % ± 35 % (mean ± standard deviation) from 1700 CE to 1982–2012. The growth in SA(C_a) ranges between 33 % and 42 % across the 12 extratropical NH sites (Table 1).

For δ¹³C_a, E_control and E_standard exhibit an almost identical SA averaged across all 19 sites (2 % ± 16 % lower in E_control than in E_standard). The change in SA(δ¹³C_a) from the preindustrial (E_control) to modern (E_standard) periods ranges between −6 % and 9 % across the 12 extratropical NH sites, whereas more diverse results (−28 % to +63 %) are simulated at the tropical and SH sites (Fig. S4, Table 1). The change in SA(δ¹³C_a), $S=E_{\mathrm{standard}}-E_{\mathrm{control}}$, does not emerge from the noise of variability (N = 2 standard deviations from IAV of E_standard), except at one tropical (Christmas Island) and three SH sites (Ascension Island, Mahe Island, Palmer Station); we require $\left|S\right|/N>\mathrm{1}$ for the signal S to emerge (Keller et al., 2014). The fact that trends in SA(C_a) and the near-zero trends in SA(δ¹³C_a) are better identified by the difference between the modern and preindustrial periods than by regression over the modern period motivates us to focus on the comparison between E_standard versus E_control in the remaining result sections.

4.3 Zonal decomposition of seasonal land–biosphere fluxes

4.3.1 Changes in the seasonal amplitude of land–biosphere fluxes and δ¹³C_a over the historical period

Next, we address the near-absent temporal trends in SA(δ¹³C_a) at NH sites by analyzing the zonally averaged cumulative growing season flux of $\left|{\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}\right|$, i.e., SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) (Fig. 4). The northern midlatitude to high-latitude ecosystem fluxes exhibit the largest seasonal cycle, followed by tropical rain-green forests and savannahs in E_standard. This flux pattern contributes to the larger SA(δ¹³C_a) in the NH extratropics versus tropical and SH sites. A similar latitudinal flux pattern holds for E_control.

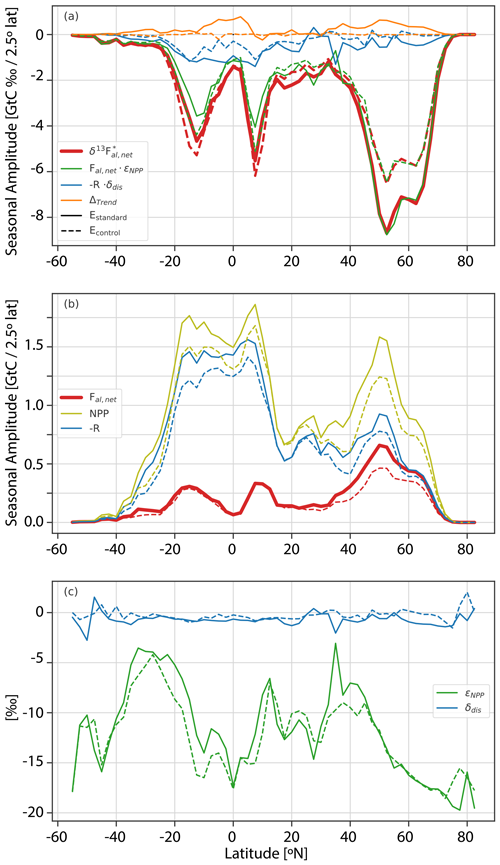
Figure 4 The seasonal amplitude per 2.5° latitude band of the signature-weighted, detrended net atmosphere–land flux, ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$, in the period of 1982–2012 is shown in (a) in red (see Eq. 8). This quantity is the sum of three constituent seasonal amplitudes (Eq. 9 and Appendix A): net land–atmosphere flux weighted with photosynthetic fractionation ($f_{\mathrm{al},\mathrm{net}}\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}$, green) plus release fluxes weighted with the disequilibrium signature ($R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$, blue) plus the contribution to the seasonal amplitude by the underlying trend of ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ (Δ_trend, orange) (sign convention – green + blue + orange = red). In (b), the seasonal amplitudes of (non-detrended) net carbon fluxes are shown. The net atmosphere–land flux (f_al,net, red) is split into net primary productivity (NPP, olive) and release flux (R, blue). In (c) the corresponding fractionation of photosynthesis ε_NPP and the disequilibrium signature δ_dis,la are shown. All values are for the period with ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ smaller than zero (∼ growing season). The results from the standard simulation (E_standard, solid lines) are compared to the preindustrial control simulation (E_control, dashed lines).

Turning to the change over the historical period, SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) is 28 % larger for the region north of 15° N (30 % larger for > 40° N and 20 % larger for 15–40° N) for E_standard than for E_control. This growth is comparable to the observed increase in C_a of 32 % from the preindustrial period to the reference period of 1982–2012. In contrast, E_control sometimes exhibits larger SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) than E_standard in the tropical and SH ecosystems (Fig. 4). Following Eq. (8), the near-proportional growth in the SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) and in annual mean C_a in the NH extratropics is consistent with the absence of any major long-term change in SA(δ¹³C_a) at extratropical NH sites (Table 1 and Fig. S4). SA(δ¹³C_a) and its change at extratropical NH sites is dominated by the large SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) in the northern extratropics (Fig. 4), and transport from low-latitude regions is less important. On the other hand, the large extratropical SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) influences SA(δ¹³C_a) and its temporal changes at lower latitudes. Without this influence, we would, based on Eq. (8), expect a decrease in SA(δ¹³C_a) outside the extratropics, given that the relative increase in annual mean C_a is larger than the increase in SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) in these regions.

Factorial simulations with an individual forcing kept at preindustrial levels show small individual contributions by climate change, fossil fuel emissions, and land use to the industrial period growth in SA(δ¹³C_a) at northern extratropical sites (Figs. S3 and S4). This suggests that the statistically insignificant trend in SA(δ¹³C_a) at northern extratropical sites is not caused by offsetting impacts of climate change versus increasing C_a. Fossil fuel emissions cause an increase and land use change a reduction in SA(δ¹³C_a) at low-latitude and southern sites (Figs. S3 and S4). We attribute the dampening influence of land use change to the replacement of C₄ plants by C₃ crops, causing a general shift in the fractionation during photosynthesis to less negative values south of ∼ 45° N (Fig. 4c). This damping influence highlights the importance of considering spatiotemporal variations in C₃ and C₄ plant distributions when analyzing δ¹³C_a. In summary, the results suggest that the near-proportional growth in SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) and in C_a is mainly responsible for the statistically insignificant trend in SA(δ¹³C_a) at high-northern-latitude sites and contributes to the statistically insignificant trend in SA(δ¹³C_a) at other NH sites via atmospheric transport.

For CO₂, the amplitude of the modeled zonally averaged net atmosphere-to-land CO₂ flux, SA(f_al,net), shows the largest values in the NH extratropics and a large increase over the historical period of 33 % in the region 15–90° N (15–40° N – 26 %; 40–90° N – 37 %) driven by a larger increase in NPP than release fluxes (R), whereas SA(f_al,net) is smaller in the tropics and SH and shows hardly any changes from the preindustrial (E_control) to modern (E_standard) periods south of 20° N. These results are consistent with previous studies showing northern ecosystems progressively taking up more carbon during the growing season (Graven et al., 2013; Forkel et al., 2016; Piao et al., 2018; Bastos et al., 2019). For example, using carbon fluxes from two atmospheric inversions and 11 land models, Bastos et al. (2019) find a positive trend in SA(f_al,net) north of 40° N and small or no growth in SA(f_al,net) between 25 and 40° N.

4.3.2 The coupling between the seasonal amplitude of C_a and δ¹³C_a

SA(C_a) and SA(δ¹³C_a) are partly coupled by the underlying carbon fluxes. The question to which extent SA(δ¹³C_a) holds information independent from SA(C_a) arises. We decompose ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ in a contribution linked to the net atmosphere-to-land carbon flux, $f_{\mathrm{al},\mathrm{net}}=\mathrm{NPP}-R$, and an isotopic disequilibrium flux (see Appendix A and Sect. 3 for notation; f_al,net is positive for a flux into the land biosphere):

$$\begin{array}{}\text{(9)}& {\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}=\underset{f_{\mathrm{al},\mathrm{net}}}{\underbrace{(\text{NPP}-R)}}\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}-R\cdot \underset{{\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}}{\underbrace{\left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_R-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{NPP}}\right)}}.\end{array}$$

NPP is the net primary productivity of all plants within a grid cell. R is the sum of all land biosphere release fluxes to the atmosphere, such as those from heterotrophic respiration, fire, mortality, and product pools, except autotrophic respiration. δ¹³C_R is the signature of R, and δ¹³C_NPP is the signature of NPP, with ε_NPP (or ε_al) representing the (flux-weighted) fractionation by NPP. The difference in signatures of R and NPP is the isotopic disequilibrium, δ_dis,la. Here, as in LPX-Bern, we have assumed that the uptake difference between gross primary production (GPP) and NPP is released on short timescales and without further carbon isotope fractionation.

Equation (9), together with Eqs. (7) and (8), provides insights into the driving factors for the seasonal amplitudes. Putting the ocean aside (Heimann et al., 1989), SA(C_a) is driven by the spatiotemporal pattern of NPP−R , whereas SA(δ¹³C_a) is additionally influenced by seasonal variations in ε_NPP, and the disequilibrium flux ($-R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$). The latter is indicative of the transit time of carbon through the land biosphere.

The decomposition of zonally averaged SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) into the amplitude of constituent fluxes and their isotopic signatures is displayed in Fig. 4 and Table S1 in the Supplement. On the global average, SA($f_{\mathrm{al},\mathrm{net}}\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}$) contributes to SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) with a fraction of 90 % for both E_standard and E_control. For the region north of 40° N, SA($-R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$) contributes only 7 % to SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) in E_standard and is almost negligible in E_control (2 %). In E_control, SA($-R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$) and δ_dis,la, albeit to a smaller extent than in E_standard, are not negligible due to the lagged response of the respiration signatures to natural changes in ε_NPP. A small contribution (Δ_trend) to the isotopic flux seasonality in E_standard arises from the long-term increase in flux (Fig. 4; see Appendix A). The small contribution of the disequilibrium flux ($-R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$) relative to the net flux ($f_{\mathrm{al},\mathrm{net}}\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}$; Eq. 9) arises as the seasonal amplitude of the carbon release flux R is similar in magnitude to that of the net land carbon uptake f_al,net in the northern extratropics (blue versus red lines in Fig. 4b), while the disequilibrium δ_dis,la is an order of magnitude smaller than ε_NPP (Fig. 4c). Thus in LPX, SA(δ¹³C_a) is dominated by the growing season net carbon uptake flux in northern high latitudes, suggesting that SA(δ¹³C_a) holds little information on the isotopic disequilibrium at high-latitude sites. Rather, the additional information of SA(δ¹³C_a) compared to SA(C_a) is on the magnitude of ε_NPP at northern high-latitude sites. In contrast, the contribution by the disequilibrium flux SA($-R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$) and the contribution by the net carbon flux SA($f_{\mathrm{al},\mathrm{net}}\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}$) are nearly equal in the tropics (10° S–10° N) and the SH (Fig. 4, Table S1), suggesting that SA(δ¹³C_a) potentially holds additional information on R and carbon turnover in these regions in comparison to SA(C_a).

The zonal variation in (growing season) photosynthetic fractionation ε_NPP is mainly due to differences in vegetation composition, with C₄ plants having considerably lower photosynthetic fractionation than C₃ plants (Fig. 4c). Land use and the evolving distribution of C₃ and C₄ crops are prescribed in the model, and C₄ grasses are more prevalent than C₃ grasses in low-latitude dryland ecosystems. Accordingly, maxima in flux-weighted, zonal-mean ε_NPP are simulated at 35° N, 12° N, and broadly around 30° S. Minima are simulated for the C₃-dominated high-latitude ecosystems and tropical rainforest zone. In E_standard, ε_NPP is generally less negative than in E_control and increased by 1.18 ‰ (9 % in relative units) on the global average (SA(NPP)-weighted), mainly due to the increase in the prevalence of C₄ plants, while ε_NPP remains time-invariant in the C₃-dominated ecosystems north of 45° N (Fig. 4c). To estimate the influence of the increase in C₄ prevalence on global mean ε_NPP (but not on global GPP), we run a factorial simulation, $E_{{\mathrm{C}}_{\mathrm{3}}}$, with the fractionation formulation for all C₄ plants replaced by that for C₃ plants. The difference between E_standard and $E_{{\mathrm{C}}_{\mathrm{3}}}$, i.e., the change in fractionation attributable to C₄ plants, amounts to about 1.5 ‰ on a global average (1982–2012 versus 1720–1750) (Fig. S5), pointing again to the importance of C₃ and C₄ plant distribution changes for δ¹³C_a.

Keeling et al. (2017) analyzed the atmospheric budgets of carbon and ¹³C using seasonally detrended data, using a three-box land model with time-invariant overturning timescales, using globally uniform isotopic fractionation, and neglecting changes in C₃ and C₄ distribution in their standard setup. They found that global mean ε_NPP decreased by 0.66 ± 0.34 ‰ from 1975 to 2005 and attributed this change to changes in fractionation associated with mesophyll conductance and photorespiration of C₃ plants. It appears challenging to detect and attribute changes in the fractionation of global mean NPP with a box model, given uncertainties in NPP (Graven et al., 2024) and changes in C₃ versus C₄ plant distribution.

While the influence of the gross exchange flux and the isotopic disequilibrium on δ¹³C_a seasonality is modeled to be small at northern sites of today, it remains to be explored how global warming will change these parameters, e.g., due to changes in fire frequency and tree mortality, and affect δ¹³C_a and the information provided by continued δ¹³C_a observations. We may also expect different disequilibrium fluxes and, in turn, δ¹³C_a seasonality if the global carbon sink is driven by a stimulation of NPP, e.g., by CO₂ fertilization (Walker et al., 2021) as in LPX-Bern, versus a change in tree longevity (Bugmann and Christof, 2011; Körner, 2017). It remains to be investigated, e.g., by applying perturbed-parameter ensembles and sensitivity simulations, whether such differences indeed significantly affect δ¹³C_a seasonality.

Monitoring C_a and δ¹³C_a over tropical and SH land regions could potentially provide valid information to disentangle NPP, respiration, and net carbon fluxes, given the substantial contribution of the disequilibrium flux to SA(${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$). However, the seasonality of δ¹³C_a and C_a at the tropical background monitoring sites analyzed in this study is strongly influenced by long-range transport, adding uncertainty to the interpretation of seasonal signals at background sites. Ideally, seasonally resolved observations are taken in air masses influenced primarily by regional land biosphere fluxes – thereby minimizing uncertainties from long-range transport – and interpreted with the help of atmospheric transport and land biosphere models (Botía et al., 2022). For example, the data may be assimilated into atmospheric transport models applied in inverse mode to infer surface carbon and isotope fluxes or assimilated into isotope-enabled land biosphere models combined with atmospheric transport to optimize parameters governing modeled carbon and isotope fluxes (Peylin et al., 2016; van der Velde et al., 2018; Castro-Morales et al., 2019).

4.4 Implications for stomatal conductance and water use

Our result of a time-invariant ε_NPP in northern extratropical regions holds implications for carbon and water fluxes and evaporative cooling. The good agreement between observations and model results for SA(δ¹³C_a) and its temporal trend at northern sites provides implicit support for regulation of stomatal conductance by C₃ plants towards a constant ratio of the CO₂ mole fraction in the leaf intercellular space (c_i) and ambient atmospheric air (c_a) on the continental scale. Following Farquhar (1989) and Cernusak et al. (2013), ε_NPP is approximately proportional to $c_{\mathrm{i}}/c_{\mathrm{a}}$:

$$\begin{array}{}\text{(10)}& {\mathit{\epsilon }}_{\mathrm{NPP}}=-\left(a+(b-a)\cdot {\displaystyle \frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}\right),\end{array}$$

with a (4.4) and b (27) being constants. Two contrasting scenarios are published for the regulation of leaf stomatal conductance for C₃ plants. First, many site studies (Voelker et al., 2016; Saurer et al., 2014; Kauwe et al., 2013; Peñuelas et al., 2011; Frank et al., 2015; Keller et al., 2017) suggest a regulation of stomatal conductance towards a constant $c_{\mathrm{i}}/c_{\mathrm{a}}$ and, hence, suggest that c_i grows proportionally to c_a. An absent temporal trend in $c_{\mathrm{i}}/c_{\mathrm{a}}$ translates into an absent trend in ε_NPP and vice versa (Eq. 10). Focusing on regions north of > 40° N, where carbon fluxes are largest and C₃ plants dominate, LPX-Bern simulates a small role of isotopic disequilibrium fluxes and a dominant influence of net atmosphere–surface fluxes on SA(δ¹³C_a) (Fig. 4, green versus blue lines). Importantly, LPX-Bern simulates small temporal changes in the (flux-weighted) fractionation of the zonally and seasonally integrated NPP at northern sites (Fig. 4c, green lines) and a stomatal regulation towards constant $c_{\mathrm{i}}/c_{\mathrm{a}}$. In turn, the good model–data agreement in the temporal trends of SA(C_a) and SA(δ¹³C_a) implies consistency with the observational evidence for this scenario towards constant $c_{\mathrm{i}}/c_{\mathrm{a}}$.

In contrast, Battipaglia et al. (2013) and Keenan et al. (2013) suggest a regulation of stomatal conductance towards a constant c_i and a decreasing ratio of $c_{\mathrm{i}}/c_{\mathrm{a}}$ under rising C_a. Evaluating Eq. (10) for 1980–2022, the period with δ¹³C_a measurements, yields a decrease in ε_NPP of 15 % (−3.0 ‰ to −3.8 ‰) for an initial $c_{\mathrm{i}}/c_{\mathrm{a}}$ ratio in the range of 0.7 to 0.9 and constant c_i. We argue that the good observation–model agreement in the simulated trends in SA(C_a) implies that the influence of the simulated net atmosphere–land carbon flux is realistic, and SA(δ¹³C_a) would decrease if ε_NPP decreases. A decrease in SA(δ¹³C_a) of 15 % would emerge from the noise of variability at individual northern sites. Taken together, we suggest that the scenario towards constant $c_{\mathrm{i}}/c_{\mathrm{a}}$ is consistent with the observations, whereas the scenario towards constant c_i appears less likely. However, uncertainties remain, and our conclusions for the two scenarios of stomatal regulation await confirmation by other modeling studies.

The two scenarios imply large differences in water fluxes (Knauer et al., 2017). The intrinsic water use efficiency (iWUE), the ratio between assimilation of CO₂ by photosynthesis (A) and conductance of CO₂ (g), is, as ε_NPP, a function of c_i and c_a:

$$\begin{array}{}\text{(11)}& \mathrm{iWUE}={\displaystyle \frac{A}{g}}=c_{\mathrm{a}}\cdot \left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}\right).\end{array}$$

iWUE would have increased from 1980 to 2022 by 23 % for constant $c_{\mathrm{i}}/c_{\mathrm{a}}$ but by 77 % to 231 % for constant c_i, assuming an initial $c_{\mathrm{i}}/c_{\mathrm{a}}$ of 0.7 to 0.9. In the latter scenario, stomatal conductance and correspondingly water loss per stomatal pore would have decreased strongly over the last decades.

Equation (10) is an approximation (Farquhar et al., 1982; Lloyd and Farquhar, 1994; Farquhar and Cernusak, 2012; Cernusak et al., 2013) considered to be sufficient for many applications by Cernusak et al. (2013) and applied in the publications cited in the previous two paragraphs. However, there are four contributions only implicitly considered by choosing parameter b in Eq. (10), and these may contribute small temporal trends to ε_NPP. In turn, inferred $c_{\mathrm{i}}/c_{\mathrm{a}}$ would also have a temporal trend for a constant ε_NPP. We estimate the trend contribution of these additional terms to be of small magnitude (<1 ‰) in comparison to the 3 ‰ to 3.8 ‰ difference estimated for our two scenarios (see Appendix B for details).

5 Conclusions

We explored the global-scale mechanisms driving the observed seasonal cycles of δ¹³C of atmospheric CO₂ (δ¹³C_a) and of atmospheric CO₂ at 19 monitoring sites using atmosphere–surface fluxes from the Bern3D-LPX Earth system model of intermediate complexity and fossil fuel emissions in combination with transport matrices from the TM3 atmospheric transport model. We find good data–model agreement at northern and tropical sites. No significant trends are detected or modeled in the seasonal cycle amplitude of δ¹³C_a at most monitoring sites, in contrast to the positive trends in the seasonal amplitude of CO₂. We attribute the statistically insignificant trend in the seasonal amplitude of δ¹³C_a to a near-equal percentage increase in the growing season net carbon uptake and isotope flux and in the background atmospheric CO₂ in the northern extratropical land regions. Over the industrial period and at low-latitude and SH sites, land use change has a dampening influence on δ¹³C_a seasonality through the replacement of C₃ plants by C₄ crops. Modeled isotopic disequilibrium fluxes have a small influence on the seasonal signal of δ¹³C_a at NH sites but play an important role in tropical and SH ecosystems, suggesting that monitoring the δ¹³C_a seasonality over tropical and SH land would provide valuable information on gross carbon exchange fluxes and the timescales of carbon turnover in the land biosphere. Our results, based on a single model chain, provide implicit support for a regulation of the stomatal conductance of C₃ plants towards a constant $c_{\mathrm{i}}/c_{\mathrm{a}}$ ratio on biome scales and for intrinsic water use efficiency to grow proportionally to atmospheric CO₂ over recent decades, with implications for carbon and water fluxes. More generally, the results suggest that observations of the δ¹³C_a seasonal cycle offer highly useful information on carbon and water cycle processes. We recommend seasonally resolved δ¹³C_a observations as a constraint for land biosphere models used to simulate the terrestrial sink of anthropogenic carbon and land use emissions, for example, using perturbed parameter ensembles in Bayesian approaches (Lienert and Joos, 2018; van der Velde et al., 2018). Future studies may employ an ensemble of isotope-enabled models and perturbed parameter ensembles to elucidate whether our findings are robust and to show which models or process assumptions are compatible or incompatible with δ¹³C_a data for improved projections of atmospheric CO₂ and global warming.

Appendix A: Decomposition of ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}$ and the calculation of seasonal amplitudes

We reformulate the net isotope flux in terms of net and gross carbon fluxes, isotopic fractionation, and isotopic disequilibrium (e.g., Mook, 1986; Joos and Bruno, 1998) to diagnose their influence on the seasonal cycles.

The fractionation for a gross flux, e.g., from the atmosphere to the surface, is

$$\begin{array}{}\text{(A1)}& {\mathit{\epsilon }}_{\mathrm{as}}\cong ({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}),\end{array}$$

with δ¹³C_as the signature of the gross flux from a to s (f_as) and δ¹³C_a the signature of the source. The isotopic disequilibrium (or difference) between atmosphere–surface gross fluxes is

$$\begin{array}{}\text{(A2)}& {\mathit{\delta }}_{\mathrm{dis},\mathrm{sa}}=-{\mathit{\delta }}_{\mathrm{dis},\mathrm{as}}=\left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{sa}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as}}\right).\end{array}$$

The net carbon and isotope fluxes are the differences between the gross fluxes:

$$\begin{array}{}\text{(A3)}& {\displaystyle }{f}_{\mathrm{as},\mathrm{net}}=f_{\mathrm{as}}-f_{\mathrm{sa}}\text{(A4)}& {\displaystyle }\begin{array}{rl}{\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}& =f_{\mathrm{as}}\cdot \left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}\right)\\ & -f_{\mathrm{sa}}\cdot \left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{sa}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}\right).\end{array}\end{array}$$

Rearranging yields

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}{\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{as},\mathrm{net}}^{*}& =f_{\mathrm{as},\mathrm{net}}\cdot \underset{{\mathit{\epsilon }}_{\mathrm{as}}}{\underbrace{\left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{a}}\right)}}\\ & -f_{\mathrm{sa}}\cdot \underset{{\mathit{\delta }}_{\mathrm{dis},\mathrm{sa}}}{\underbrace{\left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{sa}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{as}}\right)}}.\end{array}\end{array}$$

For the land biosphere (l), it follows from Eqs. (A3) and (A5) that

$$\begin{array}{}\text{(A6)}& {\displaystyle }{f}_{\mathrm{al},\mathrm{net}}=\mathrm{NPP}-R\text{(A7)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}=f_{\mathrm{al},\mathrm{net}}\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}-R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}},\end{array}$$

with

$$\begin{array}{}\text{(A8)}& {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}={\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_R-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{NPP}}.\end{array}$$

NPP is the net primary productivity of all plants within a grid cell. R is the sum of all release fluxes to the atmosphere, such as those from heterotrophic respiration, fire, mortality, and product pools, except autotrophic respiration. δ¹³C_R is the signature of R, and δ¹³C_NPP is the signature of NPP, with ε_NPP (or ε_al) representing the (flux-weighted) fractionation by NPP.

The seasonal amplitudes of ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ and its components are calculated as follows. The time series of ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ is detrended and normalized to zero. The trend is computed by a rolling 12-month mean of ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$. Then, the resulting trend curve is subtracted from ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ (disregarding the first and last 6 months of the original series) to get a detrended curve. Finally, the detrended curve is normalized by subtracting its period mean. Δ_trend (e.g., in units of mol ‰ yr⁻¹ m⁻²) is the difference between ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ after and before this detrending and normalizing procedure. We define a seasonal mask to compute seasonal amplitudes of fluxes and their signatures. For each model year, we identify months in which detrended ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ is negative or equal to zero (roughly corresponding to the growing season). The sum of fluxes of these months is then termed the seasonal amplitude in a given year. For ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$, this procedure is consistent with considering the difference between maximum and minimum values of the detrended cumulative sum of ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$. Accordingly, the seasonal amplitudes of the component fluxes contributing to ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ are computed by summation over months where ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ is less than or equal to zero within a given year. Component fluxes are [$(\mathrm{NPP}-R)\cdot {\mathit{\epsilon }}_{\mathrm{NPP}}$], [$R\cdot {\mathit{\delta }}_{\mathrm{dis},\mathrm{la}}$], [Δ_trend] and, further, [NPP], [R], and [NPP−R] (Fig. 4). These component fluxes are not detrended to readily calculate the signatures δ_dis,la and ε_NPP by division of the seasonal amplitude isotopic flux with the corresponding seasonal amplitude carbon flux.

We note that the annual climatological mean values of the isotopic disequilibrium (δ_dis,la), the net carbon flux (f_al,net), and the net isotopic flux (${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$) vanish by definition for the preindustrial equilibrium. However, this does not hold for their seasonal amplitudes. Further, detrending ${\mathit{\delta }}^{\mathrm{13}}{f}_{\mathrm{al},\mathrm{net}}^{*}$ before the computation of its seasonal amplitude is consistent with the calculation of the C_a and δ¹³C_a seasonal amplitude from the detrended atmospheric time series.

The seasonal cycles of C_a or δ¹³C_a are computed from observations and the TM3 results using the following procedure for either C_a or δ¹³C_a. Months with missing values in either the observations or the TM3 simulation are masked in the TM3 and observational time series. Then the time series are detrended using a 12-month rolling mean, and the overall mean of the series is set to zero to get (for year, y, and month, m) seasonal anomalies ΔC_a(y,m) and Δδ¹³C_a(y,m). Finally, the period means for each calendar month, $\stackrel{\mathrm{‾}}{\mathrm{\Delta }{\mathrm{C}}_{\mathrm{a}}\left(m\right)}$ and $\stackrel{\mathrm{‾}}{\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{13}}{\text{C}}_{\mathrm{a}}\left(m\right)}$, are computed by averaging over all corresponding monthly values. Additionally, the standard deviation is computed for each calendar month to inform about the interannual variability in the seasonality. The period-mean SA is computed as the difference between the month with the highest ($\stackrel{\mathrm{‾}}{m_{max}}$) and lowest ($\stackrel{\mathrm{‾}}{m_{min}}$) value in $\stackrel{\mathrm{‾}}{\mathrm{\Delta }{\text{C}}_{\mathrm{a}}\left(m\right)}$ and $\stackrel{\mathrm{‾}}{\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{13}}{\text{C}}_{\mathrm{a}}\left(m\right)}$, respectively. For individual years, we computed SA by the difference from the extreme monthly values of each year.

Appendix B: Uncertainties in the relationship between ε_NPP and $c_{\mathrm{i}}/c_{\mathrm{a}}$

In Sect. 4.4, we applied a simplified expression for fractionation of C₃ plants during photosynthesis (ε_NPP) and used this expression to translate trends in ε_NPP to trends in $c_{\mathrm{i}}/c_{\mathrm{a}}$ and in iWUE. The potential contributions to trends in ε_NPP from neglected ternary effects, dark-day respiration, and transport through the mesophyll and photorespiration are discussed in this appendix.

The isotopic fraction for C₃ photosynthesis is framed as a multi-step process considering the transport of CO₂ and the underlying gradients in CO₂ mole fractions from the ambient air (mole fraction – c_a) to the leaf surface (c_s) in the intercellular air spaces (c_i) and the sites of carboxylation (c_c), as well as the fractionation during carboxylation, dark-day respiration, R_d, and photorespiration (Cernusak, 2013). The transport of CO₂ equals the consumption of CO₂ by assimilation, A: $A=g(c_{\mathrm{a}}-c_{\mathrm{i}})=g_{\mathrm{m}}(c_{\mathrm{i}}-c_{\mathrm{c}})$, with g being the conductance of the stomatal pores and the boundary layer and g_m the mesophyll conductance. The relationship can be rewritten as $A/\left(g{c}_{\mathrm{a}}\right)=(\mathrm{1}-c_{\mathrm{i}}/c_{\mathrm{a}})=g_{\mathrm{m}}/g(c_{\mathrm{i}}/c_{\mathrm{a}}-c_{\mathrm{c}}/c_{\mathrm{a}})$. If A increases in proportion to c_a and g and g_m is assumed to be constant, then it follows that $c_{\mathrm{i}}/c_{\mathrm{a}}$ and $c_{\mathrm{c}}/c_{\mathrm{a}}$ are also constant. In turn, the fractionation associated with the boundary layer and stomatal conductance ($-a(\mathrm{1}-c_{\mathrm{i}}/c_{\mathrm{a}}$); a=4.4 ‰), mesophyll conductance ($-a_{\mathrm{m}}(c_{\mathrm{i}}/c_{\mathrm{a}}-c_{\mathrm{c}}/c_{\mathrm{a}}$); a_m=1.8 ‰), and carboxylation ($-b\times c_{\mathrm{c}}$) remain constant. The overall influence of mesophyll transport on ε_NPP can also be written as $(b-a_{\mathrm{m}})/g_{\mathrm{m}}\times A/c_{\mathrm{a}}$ (Keeling et al., 2017).

Keeling et al. (2017) assumed that $A/c_{\mathrm{a}}$ decreases over time, with A increasing by 45 % for a doubling of CO₂, and that therefore fractionation by the mesophyll contribution would change by −0.006 ‰ ppm⁻¹, i.e., a change in ε_NPP of 0.47 ‰ for the CO₂ increase of 78 ppm from 1980 to 2022. On the other hand, Campbell et al. (2017) observationally constrained the growth in gross primary production over the 20th century to be 31 ± 5 %, larger than the increase in c_a of 25 %. Accordingly, $A/c_{\mathrm{a}}$ increases, and the mesophyll trend contribution is positive. With the central parameter values of Keeling et al. (2017) (A=9 µmol m⁻² s⁻¹, g_m=0.2 mol m⁻² s⁻¹, CO₂ = 355 ppm), the contribution is +0.002 ‰ ppm⁻¹. Keeling et al. (2017) also estimated changes in fractionation associated with photorespiration ($-f\times {\mathrm{\Gamma }}^{*}/c_{\mathrm{a}}$; f=12 ‰) to be −0.004 ‰ ppm⁻¹ assuming a constant CO₂ compensation point, Γ^*. The real sensitivity must be smaller, as Γ^* increases with temperature and because Keeling et al. (2017) applied an estimate for the CO₂ compensation point in the presence of R_d (43 ppm) instead of the absence of R_d (${\mathrm{\Gamma }}^{*}=\mathrm{31}$ ppm). Further, fractionation during day respiration is $-e\times c_{\mathrm{c}}/c_{\mathrm{a}}\times R_d/V_{\mathrm{c}}$ (Cernusak et al., 2013), roughly about 0 to −0.3 ‰ for e in the range of 0 ‰ to 5 ‰; we apply RuBisCO carboxylation rates, V_c, of 11 µmol m⁻² s⁻¹ derived from the value of A=9 µmol m⁻² s⁻¹ by Keeling et al. (2017), (R_d=1 µmol m⁻² s⁻¹ and $c_{\mathrm{c}}/c_{\mathrm{a}}=\mathrm{0.6}$). Finally, ternary effects of about −0.7 ‰ (0.024 × b) increase with water vapor deficit (Farquhar and Cernusak, 2012). Given the small amplitudes of these two contributions, their temporal trends have also been small over recent decades.