The triple oxygen isotope composition of phytoliths as a proxy of continental atmospheric humidity: insights from climate chamber and climate transect calibrations

Continental atmospheric relative humidity (RH) is a key climate parameter. Combined with atmospheric temperature, it allows us to estimate the concentration of atmospheric water vapor, which is one of the main components of the global water cycle and the most important gas contributing to the natural greenhouse effect. However, there is a lack of proxies suitable for reconstructing, in a quantitative way, past changes of continental atmospheric humidity. This reduces the possibility of making model–data comparisons necessary for the implementation of climate models. Over the past 10 years, analytical developments have enabled a few laboratories to reach sufficient precision for measuring the triple oxygen isotopes, expressed by the ¹⁷O-excess (¹⁷O-excess = ln (δ¹⁷O + 1) – 0.528 × ln (δ¹⁸O + 1)), in water, water vapor and minerals. The ¹⁷O-excess represents an alternative to deuterium-excess for investigating relative humidity conditions that prevail during water evaporation. Phytoliths are micrometric amorphous silica particles that form continuously in living plants. Phytolith morphological assemblages from soils and sediments are commonly used as past vegetation and hydrous stress indicators. In the present study, we examine whether changes in atmospheric RH imprint the ¹⁷O-excess of phytoliths in a measurable way and whether this imprint offers a potential for reconstructing past RH. For that purpose, we first monitored the ¹⁷O-excess evolution of soil water, grass leaf water and grass phytoliths in response to changes in RH (from 40 to 100 %) in a growth chamber experiment where transpiration reached a steady state. Decreasing RH from 80 to 40 % decreases the ¹⁷O-excess of phytoliths by 4.1 per meg/% as a result of kinetic fractionation of the leaf water subject to evaporation. In order to model with accuracy the triple oxygen isotope fractionation in play in plant water and in phytoliths we recommend direct and continuous measurements of the triple isotope composition of water vapor. Then, we measured the ¹⁷O-excess of 57 phytolith assemblages collected from top soils along a RH and vegetation transect in inter-tropical West and Central Africa. Although scattered, the ¹⁷O-excess of phytoliths decreases with RH by 3.4 per meg/%. The similarity of the trends observed in the growth chamber and nature supports that RH is an important control of ¹⁷O-excess of phytoliths in the natural environment. However, other parameters such as changes in the triple isotope composition of the soil water or phytolith origin in the plant may come into play. Assessment of these parameters through additional growth chambers experiments and field campaigns will bring us closer to an accurate proxy of changes in relative humidity.

1 Introduction

Continental atmospheric relative humidity (RH) is a key climate parameter. Combined with atmospheric temperature, it allows scientists to estimate the concentration of atmospheric water vapor, which is one of the main components of the global water cycle and the most important gas contributing to the natural greenhouse effect (e.g., Held and Soden, 2000; Dessler and Davis, 2010; Chung et al., 2014). However, global climate models (GCMs) have difficulties in properly capturing continental humidity conditions (Sherwood et al., 2010; Risi et al., 2012; Fischer and Knutti, 2013). Although tropospheric RH results from a subtle balance between different processes (including air mass origins and trajectories, large-scale radiative subsidence, evaporation of falling precipitation, detrainment of convective system, evapotranspiration), it is usually depicted as rather constant in GCMs, in agreement with thermodynamic coupling between atmospheric water vapor and sea surface temperature (Bony et al., 2006; Stevens et al., 2017). A model–data comparison approach is thus essential to progress on this issue. This approach has to be applicable beyond the instrumental period to make use of past changes in atmospheric water vapor conditions.

There are multiple ways to reconstruct past continental temperature and precipitation, for instance from pollen (Bartlein et al., 2010; Herbert and Harrison, 2016; Wahl et al., 2012) or tree ring data (Labuhn et al., 2016; Lavergne et al., 2017). However, there is a serious lack of proxies suitable for reconstructing, in a quantitative way, past variations in continental atmospheric RH. Indeed, the stable isotopes of oxygen and hydrogen (δ¹⁸O and δD) of tree rings can be influenced by several parameters other than humidity (precipitation source, temperature). This limits the interpretation of tree ring isotope series in terms of humidity changes to places where variations of these other parameters are well constrained (Grießinger et al., 2016; Wernicke et al., 2015). A promising method relies on the δ¹⁸O and δD of plant biomarkers (e.g., n-alkanes and fatty acids from leaf waxes) recovered from soils (or buried soils) and sediments. It allows for an estimate in changes in plant water deuterium-excess (d-excess $=\mathit{\delta }\mathrm{D}-\mathrm{8.0}\times \mathit{\delta }$¹⁸O), linked to changes in precipitation sources and RH. This method under development can however be biased by factors other than climatic ones, such as plant functional types and selective degradation of the biomarkers (e.g., Rach et al., 2017; Schwab et al., 2015; Tuthorn et al., 2015).

Phytoliths are micrometric amorphous silica (SiO₂, nH₂O) particles that form continuously in living plants. Silicon is actively absorbed by the roots (Ma and Yamaji, 2006) and is translocated in the plant tissues where it polymerizes inside the cells, in the cell walls and in extracellular spaces of stems and leaves. Silica polymerization appears to be an active physiological process, which does not only depends on transpiration (Kumar et al., 2017). In grasses, which are well known silica accumulators, silica accounts for several % of dry weight (d.w.) and is mainly located in the stem and leaf epidermis. Phytolith morphological assemblages from soils and sediments are commonly used as past vegetation and hydrous stress indicators (e.g., Aleman et al., 2012; Backwell et al., 2014; Bremond et al., 2005a, b; Contreras et al., 2014; Nogué et al., 2017; Piperno, 2006). The potential of the δ¹⁸O signature of phytoliths (δ¹⁸O_Phyto) from grasses for paleoclimate reconstruction has been investigated through growth chamber and North American Great Plains calibrations. It has been shown that the δ¹⁸O_Phyto of grass stems weakly affected by transpiration correlated with the δ¹⁸O signature of soil water (δ¹⁸O_SW) and the atmospheric temperature, as expected for a polymerization of silica in isotope equilibrium with the plant water (Webb and Longstaffe, 2000, 2002, 2003, 2006). It has also been shown that δ¹⁸O_Phyto from grass leaves correlated with RH, as expected for an evaporative kinetic isotope enrichment of the leaf water (e.g., Cernusak et al., 2016) imprinted on δ¹⁸O_Phyto. However, because grass stem and leaf phytoliths have the same morphology and are mixed in soil and sedimentary samples, these calibrations were not sufficient for using δ¹⁸O_Phyto of grassland phytolith assemblages as a paleoclimatic signal. In tropical trees, silica is found in leaves, bark and wood and accounts for a few % d.w. (e.g., Collura and Neumann, 2017). In the wood, silica polymerizes in the secondary xylem supposedly unaffected by transpiration, in the form of Globular granulate phytolith types (Madella et al., 2005; Scurfield et al., 1974; ter Welle, 1976). These phytoliths make up more than 80 % of tropical humid forest and rainforest phytolith assemblages found in soils and sediments (Alexandre et al., 1997; Alexandre et al., 2012). Examination of the δ¹⁸O_Phyto of rainforest assemblages showed correlations with the δ¹⁸O of precipitation (δ¹⁸O_Pre) and the atmospheric temperature (Alexandre et al., 2012). However, in this case, the use of δ¹⁸O_Phyto did not further develop because it was applicable only to forested areas and humid climatic periods, which is a major drawback for paleoclimatic reconstructions.

The triple isotope composition of oxygen in the water molecule represents an alternative for investigating RH conditions prevailing during water evaporation. In the triple isotope system, the mass-dependent fractionation factors between A and B (¹⁷α_A−B and ¹⁸α_A−B) are related by the exponent θ_A−B (${}^{\mathrm{17}}{\mathit{\alpha }}_{\mathrm{A}-\mathrm{B}}=$ ${}^{\mathrm{18}}{\mathit{\alpha }}_{\mathrm{A}-\mathrm{B}}^{\mathit{\theta }}$ or ${\mathit{\theta }}_{\mathrm{A}-\mathrm{B}}=$ ln¹⁷α_A−B/ln¹⁸α_A−B). The exponent can also be expressed as ${\mathit{\theta }}_{\mathrm{A}-\mathrm{B}}={\mathrm{\Delta }}^{\prime }$¹⁷O${}_{\mathrm{A}-\mathrm{B}}/{\mathrm{\Delta }}^{\prime }$¹⁸O_A−B with Δ^′17O_A−B $={\mathit{\delta }}^{\prime }$¹⁷O${}_{\mathrm{A}}-{\mathit{\delta }}^{\prime }$¹⁷O_B, Δ^′18O${}_{\mathrm{A}-\mathrm{B}}={\mathit{\delta }}^{\prime }$¹⁸O${}_{\mathrm{A}}-{\mathit{\delta }}^{\prime }$¹⁸O_B, δ^′17O = ln (δ¹⁷O + 1) and δ^′18O = ln (δ¹⁸O + 1). In the δ^′17O vs. δ^′18O space, λ_A−B represents the slope of the data alignment during mass-dependent fractionation between A and B. Whereas θ_A−B is linked to a particular physical process (equilibrium or kinetic), λ_A−B is empirically measured between two groups of materials and is not related to a well-understood single process (Pack and Herwartz, 2014). It has been recently estimated that θ equals 0.529 for liquid-vapor equilibrium (θ_equil; Barkan and Luz, 2005) and 0.518 for vapor diffusion in air (Barkan and Luz, 2007). It has additionally been shown that meteoric waters plot along a trend with a slope λ of 0.528 ± 0.001. The departure from this trend is conventionally called ¹⁷O-excess (¹⁷O-excess = δ'¹⁷O − 0.528 × δ¹⁸O) (Luz and Barkan, 2010). In case of mass-dependent fractionation processes, the magnitudes of the ¹⁷O-excess in waters and minerals are very small and measurement of the ¹⁷O-excess, expressed in per meg (10⁻³ ‰), requires very high analytical precisions.

In the water cycle, the ¹⁷O-excess variations mainly result from diffusion processes, while equilibrium fractionation does not lead to important departure from the meteoric water mean trend. Theoretical and empirical estimations have shown that in contrast to d-excess, and except at very high latitudes, changes in water ¹⁷O-excess are not significantly impacted by temperature (∼ 0.1 per meg/^∘C; Uemura et al., 2010) and much less sensitive to distillation processes (Angert et al., 2004; Barkan and Luz, 2007; Landais et al., 2008; Uemura et al., 2010; Steig et al., 2014). Changes in water ¹⁷O-excess are thus essentially controlled by evaporative kinetic fractionation. The ¹⁷O-excess decreases in the evaporating water and increases in the vapor phase when RH decreases at evaporative sites (e.g., sea surface, lake surface, soil surface or leaf surface). Over the last 10 years, a few studies have used the ¹⁷O-excess of water to interpret ice core archives in climatic terms (Guillevic et al., 2014, Schoeneman et al., 2014; Winkler et al., 2012; Landais et al., 2008, 2012). They supported that ¹⁷O-excess is a marker of RH, sea-ice extent at the moisture source, and air mass mixing (Risi et al., 2010) except at the very high latitudes of East Antarctica where temperature can have a significant influence. The observed variations of ¹⁷O-excess in Greenland ice cores of ∼ 20 per meg maximum were thus interpreted as variations of RH or sea-ice extent in the source region and coincide with variations in the low- to mid-latitude water cycle as recorded by other proxies (such as CH₄ or δD of CH₄) (Guillevic et al., 2014). An even smaller number of studies measured or attempted to model the ¹⁷O-excess of rainwater at low and temperate latitudes (Affolter et al., 2015; Landais et al., 2010b; Li et al., 2015; Luz and Barkan, 2010; Risi et al., 2013). The observed variations in ¹⁷O-excess, partly explained by convective processes and re-evaporation of precipitation, were on the order of 30–40 per meg, either during a rainy event or along climatic gradients. Only a few studies focused on open surface waters, and showed that variations of the ¹⁷O-excess ranged from tens to hundreds of per meg when the surface water underwent strong evaporative enrichment (Surma et al., 2015, 2018; Luz and Barkan, 2010), in agreement with the Craig and Gordon (1965) formulation. The most important variations in ¹⁷O-excess occur at the plant-atmosphere interface. In leaf water, variations higher than 200 per meg were encountered (Landais et al., 2006; Li et al., 2017). Difference in ¹⁷O-excess between leaf water subject to evaporation (LW) and stem water (SW) not subject to evaporation, increased with decreasing RH (from 100 to 30 %), as expected for processes dominated by kinetic fractionation. When measuring a sequence of LW–SW couples sampled under different climatic conditions, the slope of the line linking their triple isotope composition and named λ_transp, equivalent to λ_LW−SW, was found to change with RH. This pattern was influenced neither by the plant species nor by the environmental conditions (e.g., atmospheric temperature, soil water conditions) (Landais et al., 2006). However, opposite trends of λ_transp with RH were observed from one study to another (Landais et al., 2006; Li et al., 2017). This discrepancy was attributed to the possibility that steady state is not always reached during sampling and to likely differences in isotope composition of the ambient vapor, a parameter of the Craig and Gordon model that is often not measured but estimated (Li et al., 2017).

While ¹⁷O-excess measurements of waters were expanding, analyses of the triple oxygen isotope composition of minerals (mostly silicates and carbonates) were also developed, allowing estimates of fractionation during polymerization and providing constraints on both temperature and isotope composition of the water source (Pack and Herwartz, 2014; Levin et al., 2014; Passey et al., 2014; Herwartz et al., 2015; Miller et al., 2015; Sharp et al., 2016). Variations of ¹⁷O-excess on the order of tens to hundreds of per meg were reported from one mineral to another. For most of the studies cited above, the objective was to discriminate between high and low temperature formation processes or to decipher from which type of water the mineral formed (i.e., seawater, hydrothermal water, meteoric or surface water). The ¹⁷O-excess of biogenic and sedimentary carbonates was also investigated as a potential record of evaporating water sources (Passey et al., 2014). With regard to silicate–water fractionation, the relationship between the three oxygen isotopes defined by ${\mathit{\theta }}_{{\mathrm{SiO}}_{\mathrm{2}}-\mathrm{water}}$ was estimated between 0.521 and 0.528, increasing logarithmically with temperature (Sharp et al., 2016).

In the present study, in the light of the recent findings cited above, we examined whether changes in atmospheric RH imprint the ¹⁷O-excess of phytoliths (¹⁷O-excess_Phyto) in a measurable way and whether this imprint offers a potential for reconstructing past RH. For that purpose, we first monitored the ¹⁷O-excess evolution of soil water, grass leaf water and grass phytoliths in response to changes in RH in a growth chamber experiment. Then, we measured the ¹⁷O-excess_Phyto from 57 phytolith assemblages collected in soil tops along a RH and vegetation transect in inter-tropical West and Central Africa. Relationships between ¹⁷O-excess_Phyto and RH were looked for and assessed on the basis of previous quantifications of kinetic isotope enrichment of leaf water and equilibrium fractionation between water and silica. Results from the natural sampling were compared to the ones from the growth chamber experiment to evaluate the importance of RH in controlling ¹⁷O-excess_Phyto in natural environment.

2 Materials and methods

2.1 Samples from the growth chamber experiment

Festuca arundinacea, commonly referred to as tall fescue, is widely distributed globally as forage and an invasive grass species (Gibson and Newman, 2001) and can adapt to a wide range of conditions. In 2016, F. arundinacea (Callina RAGT Semences) was grown in three chambers under three conditions of RH (ca. 40, 60 and 80 %) kept constant using wet air introduction and ultrasonic humidifier. We checked that the humidifiers did not lead to any isotope fractionation between the water in their reservoirs and the vapor delivered. Temperature and light intensity were kept constant at 25 ± 0.6 (standard deviation, SD) ^∘C and 293 ± 14 (SD) mmol m⁻² s⁻¹, respectively.

In a 35 L tank ($\mathrm{53}\times \mathrm{35}\times \mathrm{22}$ cm), 20 kg of dried commercial potting soil were packed above a 1.6 cm layer of quartz gravel. A porous cup for water extraction was placed in the soil with its extraction tube hermetically extending outside of the tank walls. The soil was irrigated with 10 L of the same water as the one used for the humidifier. Four grams of seeds were sown along four rows in each tank, resulting in about 6000 seedlings. Each tank was then placed in a chamber and was irrigated from a Mariotte bottle (25 L) placed next to it. The Mariotte system was set so that a water saturated level of 5 cm remained constant at the base of the tank. The irrigation water was supplemented with 105 mg L of SiO₂ (in the form of SiO₂ K₂O). Ten days after germination, agar-agar (polysaccharide agarose) was spread on the soil surface around the seedlings (about 8 cm tall), to prevent any evaporation (Alexandre et al., 2016).

A fourth tank was kept at 100 % of RH thanks to the installation of a 20 cm high plexiglass cover, in a forth chamber set at 80 % of RH. In this case no agar-agar was added and the vapor around F. arundinacea came from evaporation and transpiration of the soil water. Otherwise the treatment was the same as in the other chambers.

For each humidity condition, three to four harvests were made at intervals of 10–14 days. The 20–25 cm long leaves were cut at two cm above the soil level and weighed. From the first to the fourth sampling, the harvested wet leaves increased from 15–20 g (10 days of growth) to 40–60 g (14 days of growth). Three to five g of leaves were put in glass gastight vials and kept frozen for bulk leaf water extraction. The remaining leaves were dried for phytolith extraction. Forty mL of irrigation water from the Mariotte bottle, and of soil water from the porous cup, were kept at 5 ^∘C before analyses.

After each harvest, the tanks were left in their chamber of origin but the 40, 60 and 80 % RH treatments were rotated between the growth chambers so that the four replicates of a given RH treatment would come from at least two different chambers. The 100 % humidity was set up in a unique chamber during the entire duration of the experiment. The harvested leaves in this treatment were often covered by condensation drops which were blotted between two sheets of wiping paper, rapidly after harvesting. The experimental setup details and the harvest list are given in Table 1.

2.2 Samples from the natural climate transects

Fifty-seven top soil samples were collected during several field trips along vegetation and humidity transects in Mauritania and Senegal (Bremond et al., 2005b; Lézine, 1988; Pasturel, 2015) Gabon (Lebamba et al., 2009) and Congo (Alexandre et al., 1997) in the Saharan, Sahelian, Sudanian, guinean and Congolian bioclimatic zones, respectively (White et al., 1983). Samplings, phytolith extractions and phytolith morphological assemblages descriptions are given in the above-mentioned studies, except for the samples of Gabon from which phytoliths were chemically treated and counted in the frame of the present study.

The sampled site location as well as the associated climatic and oxygen isotope variables are given in Table 2. The vegetation overlying the sampled soils was categorized into savanna (Mauritania, Senegal), wooded savanna (Senegal), humid forest (Gabon and Congo) and enclosed savanna (Gabon). For each sampled site, yearly climate average were calculated from the monthly means of temperature, precipitation, RH and diurnal temperature, extracted from the Climate Research Unit (CRU) 1961–1990 time series (10' spatial resolution; http://www.cru.uea.ac.uk (last access: 23 May 2018), Harris et al., 2013, CRU 2.0). Mean annual precipitation (MAP), mean annual temperature (MAT) and mean annual RH range from 49 to 2148 mm, 24.3 to 29.8 ^∘C and 40.2 to 82.5 %, respectively. In addition, in order to get a proxy of RH during wet months, likely those of the grass growing season, averaged RH monthly means for months with at least 1 day with precipitation higher than 0.1 mm (RH-rd0 > 1) was calculated. It ranges from 56.3 to 82.5 %. As maximum transpiration is supposed to be reached around 15:00 UTC we also calculated RH and RH-rd0 > 1 at 15:00 (RH15 and RH15-rd0 > 1, respectively) according to New et al. (2002) and Kriticos et al. (2012). For each sampling site, estimates of δ^′18O of precipitation for the months with at least 1 day with precipitation higher than 0.1 mm (δ^′18O_{Pre−rd0 > 1}) were calculated from δ¹⁸O of precipitation extracted from The Online Isotopes in Precipitation Calculator-version OIPC2-2 (http://www.waterisotopes.org (last access: 23 May 2018); Bowen and Revenaugh, 2003; Bowen and Wilkinson, 2002; Bowen et al., 2005) and weighted by the amount of precipitation. The estimates range from −1.51 to −4.46 ‰. There is currently no data on the ¹⁷O-excess of precipitation (¹⁷O-excess_Pre) at these sites.

2.3 Phytolith chemical extractions

Phytoliths from soils were extracted following Crespin et al. (2008) using HCl, H₂O₂, C₆H₅Na₃O₇ and Na₂O₄S3–H₂O at 70 ^∘C, and a ZnBr₂ heavy liquid separation. It has been shown that up to a temperature of 70 ^∘C the extraction has no effect on the δ¹⁸O (Crespin et al., 2008). We verified that it did not have any effect on the ¹⁷O-excess either, using our internal standard MSG extracted at 60 and 70 ^∘C (Crespin et al., 2008). The obtained ¹⁷O-excess values were similar (−211 and −243 per meg, respectively) given our reproducibility of ±34 per meg (see Sect. 2.6.1). Phytoliths from Festuca arundinaceae were thus extracted using a high purity protocol with HCl, H₂SO₄, H₂O₂, HNO₃, KClO₃ and KOH at 70 ^∘C following Corbineau et al. (2013).

2.4 Phytolith counting

Phytolith assemblages from the humidity transects were mounted on microscope slides in Canada Balsam, for counting, at a 600× magnification. More than 200 identifiable phytoliths with a diameter greater than 5 µm and with a taxonomic significance were counted per sample. Three repeated counting gave an error of ±3.5 % (SD). Phytoliths were named using the International Code for Phytolith Nomenclature 1.0 (Madella et al., 2005) and categorized as Globular granulate type produced by the wood (Scurfield et al., 1974; Kondo et al., 1994), palm Globular echinate type and grass types comprising Acicular, Bulliform, Elongate psilate, Elongate echinate, Bulliform cells, and Grass Short Cells types. For each sample from the natural transects, the phytolith index d∕p, a proxy of tree cover density (Alexandre and Bremond, 2009; Bremond et al., 2005b), was calculated. It is the ratio of Globular granular phytolith category (Madella et al., 2005) formed in the secondary xylem of the dicotyledon (d) wood to the grass short cell phytolith category formed in the epidermis of grasses or Pooideae (p) (Collura and Neumann, 2017; Scurfield et al., 1974; ter Welle, 1976). Those two categories make up most of the phytolith assemblages recovered from inter-tropical soils (Bremond et al., 2005a, b; Alexandre et al., 1997, 2013).

Phytolith assemblages from the F. arundinacea samples were also mounted and counted. The phytolith types were categorized according to their cell of origin in the epidermis into Epidermal short cell, Epidermal long cell, Bulliform cell and Hair acicular.

2.5 Leaf and soil water extraction

Leaf water was extracted using a distillation line. Leaves were introduced in a glass tube connected to the distillation line, and frozen through immersion of the glass tube in liquid nitrogen. While keeping the sample frozen, the distillation line was pumped to reach a vacuum higher than 5 × 10⁻² mbar. The pumping system was then isolated and the glass sample tube warmed to 80 ^∘C. Meanwhile, at the other end of the distillation line, a glass collecting tube was immersed in liquid nitrogen to trap the extracted water. To avoid condensation, the line between the sample tube and the collection tube was heated with a heating wire. The distillation was completed after 6 h. In order to remove volatiles from the extracted water, a few granules of activated charcoal were added and the water slowly stirred for 12 h.

Soil water was extracted using a 31 mm porous ceramic cup. Brown- or yellow-colored samples were filtered at 0.22 µm, but remained colored after filtration, indicating the presence of soluble compounds.

2.6 Isotope analyses

The oxygen isotope results are expressed in the standard δ-notation relative to VSMOW.

2.6.1 Phytoliths

Phytolith samples of 1.6 mg were dehydrated and dehydroxylated under a flow of N₂ (Chapligin et al., 2010) and oxygen extraction was performed using the IR Laser-Heating Fluorination Technique at CEREGE (Aix-en-Provence, France) (Alexandre et al., 2006; Crespin et al., 2008; Suavet et al., 2010). The purified oxygen gas (O₂) was passed through a −114 ^∘C slush to refreeze gases interfering with the mass 33 (e.g., NF), potentially produced during the fluorination of residual organic N, before being sent to the dual-inlet mass spectrometer (ThermoQuest Finnigan Delta Plus). The composition of the reference gas was determined through the analyses of NBS28 for which isotope composition has been set to δ¹⁸O = 9.60 ‰, δ¹⁷O = 4.99 ‰ and ¹⁷O-excess = −65 per meg. During the measurement period, reproducibility (SD) of the analyses of the working quartz standard (Boulangé 2008) against which the isotope composition of the sample gas was corrected on a daily basis (three quartz standards were analyzed per day) was ±0.20 ‰, ±0.11 ‰ and ±22 per meg for δ¹⁸O, δ¹⁷O and ¹⁷O-excess, respectively (n=63; one run of eight dual inlet measurements). For every session of measurement, the effectiveness of the entire dehydration and IR–laser–fluorination–IRMS procedure was checked through the analysis of a working phytolith standard (MSG60) with δ¹⁸O $=\mathrm{36.90}\pm \mathrm{0.78}$ ‰, δ¹⁷O $=\mathrm{19.10}\pm \mathrm{0.40}$ ‰ and ¹⁷O-excess $=-\mathrm{215}\pm \mathrm{34}$ per meg (n=29). For comparison, the inter-laboratory pooled value for MSG60 is δ¹⁸O = 37.0 ± 0.8 ‰ (Chapligin et al., 2011). Recent measurements of the silicate reference materials UWG-2 garnet (Valley et al., 1995) and San Carlos (SC) olivine gave the following values: δ¹⁸O${}_{\mathrm{UWG}-\mathrm{2}}=\mathrm{5.72}\pm \mathrm{0.12}$ ‰, δ¹⁷O${}_{\mathrm{UWG}-\mathrm{2}}=\mathrm{2.95}\pm \mathrm{0.06}$ ‰, ¹⁷O-excess${}_{\mathrm{UWG}-\mathrm{2}}=$ −68 ± 27 per meg (n=5), δ¹⁸O_SC= 4.95 ± 0.22 ‰, δ¹⁷O${}_{\mathrm{SC}}=\mathrm{2.56}\pm \mathrm{0.12}$ ‰, ¹⁷O-excess_SC= −49 ± 24 per meg (n=3). For comparison, silicate analyses presented in Sharp et al. (2016) are normalized to a δ¹⁸O value for San Carlos Olivine of 5.3 ‰ and a ¹⁷O-excess value of −54 per meg. As previously discussed in Suavet et al. (2010), a large scatter is often observed for SC olivine δ¹⁸O and δ¹⁷O values measured in a given laboratory or from a laboratory to another. This is probably attributable to the heterogeneity of the analyzed samples. At CEREGE, the internal standard of SC olivine is prepared from a number of millimetric crystals with possibly different oxygen isotope composition. The δ¹⁸O and δ¹⁷O values from Suavet et al. (2010), Tanaka and Nakamura (2013), Pack et al. (2016), Sharp et al. (2016) and the present study average 5.29 ± 0.23 (1 SD) ‰ and 2.72 ± 0.12 (1 SD) ‰, respectively. Nevertheless, despite the large SD on ¹⁸O and δ¹⁷O measurements, the SC olivine ¹⁷O-excess appears relatively constant (−71 ± 23 (1 SD)) per meg.

2.6.2 Leaf water

Leaf water was analyzed at LSCE (Gif-sur-Yvette, France) following the procedure previously detailed in Landais et al. (2006). In summary, a fluorination line was used to convert water to oxygen using CoF₃ heated at 370 ^∘C in a helium flow. The oxygen was then trapped in a tube immersed in liquid helium before being analyzed by dual inlet IRMS (ThermoQuest Finnigan MAT 253 mass spectrometer) against a reference oxygen gas. All measurements were run against a working O₂ standard calibrated against VSMOW. The resulting precisions (2 runs of 24 dual inlet measurements) were 0.015 ‰ for δ¹⁷O, 0.010 ‰ for δ¹⁸O and 5 per meg for ¹⁷O-excess.

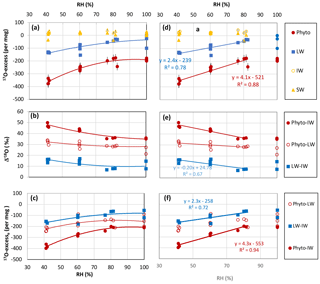
Figure 1 Growth chamber experiment: (a) ¹⁷O-excess vs. relative humidity (RH) of irrigation water (IW), soil water (SW), leaf water (LW) and phytolith (Phyto). Error bars show standard deviation (SD) on the replicates. They are smaller than the symbol when not shown. (b) ¹⁸O-enrichment from irrigation water to leaf water (Δ^′18O_LW−IW), from irrigation water to phytolith (Δ^′18O_Phyto−IW) and from leaf water to phytolith (Δ^′18O_Phyto−LW). (c) ¹⁷O-excess associated with the enrichment from irrigation water to leaf water (¹⁷O-excess_e LW−IW), from irrigation water to phytolith (¹⁷O-excess_{e Phyto−IW}), and from leaf water to phytolith (¹⁷O-excess_{e Phyto−LW}). (d), (e) and (f) linear correlations for the 40–80 % RH range extracted from (a), (b) and (c), respectively.

2.6.3 Irrigation and soil waters

Figure 2 Growth chamber experiment: phytolith types extracted from Festuca arundinaceae and observed in natural light microscopy: epidermal long cell (LC), epidermal short cell (SC).

Irrigation and soil water were analyzed at the Ecotron of Montpellier (France) with an isotope laser analyzer (Picarro L2140i) operated in ¹⁷O-excess mode using an auto-sampler and a high-precision vaporizer. Each water sample was used to fill three vials randomly dispatched in four groups of six samples (three replicates per sample). Each sample group was bracketed by three working standards (Giens-1, Iceberg-1 and Eco-1). Ten injections were performed for each vial, and the results of the first six injections were discarded to account for memory effects. Following IAEA recommendations (IAEA, 2013), each liquid measurement sequence was started with two vials of deionized water for instrument conditioning.

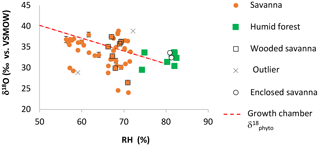
Figure 3 Natural West and Central African transect: δ^′18O of phytoliths (δ^′18O_Phyto) vs. relative humidity RH-rd0 > 1 (see Fig. 4 for explanation). Error bars show standard deviation (SD) on the replicates. When not shown, they are smaller than the symbol.

The isotope compositions of each sample group were calibrated using the three interpolated mean values obtained for the bracketing working standards (Delattre et al., 2015). All isotope ratios were normalized on the VSMOW2/SLAP2 scale, with an assigned SLAP2 ¹⁷O-excess value of zero, following the recommendations of Schoenemann et al. (2013). The resulting precisions (three replicates) were 0.02 ‰, 0.01 ‰ and 10 per meg for δ¹⁷O, δ¹⁸O and ¹⁷O-excess (n=31).

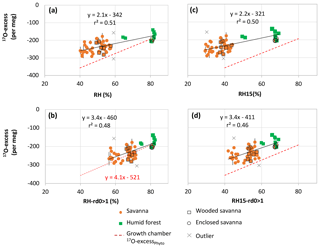
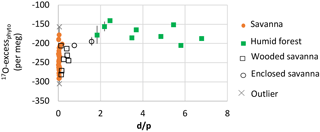
Figure 4 Natural West and Central African transect: ¹⁷O-excess vs. relative humidity (RH) of phytolith assemblages from soil tops collected under savanna, wooded savanna, humid forest and enclosed savanna along a humidity gradient (Table 1). The growth chamber ¹⁷O-excess_Phyto vs. RH correlation line is displayed for comparison. (a) RH-Av: yearly average of monthly means; (b) RH-rd0 > 1: yearly average of monthly means for months with at least 1 day with precipitation higher than 0.1 mm; (c) RH15: RH at 15:00 UTC; (d) RH15-rd0 > 1: RH-rd0 > 1 at 15:00 UTC.

The three working standards were also analyzed using the fluorination/IRMS technique used for leaf water analyses at LSCE. The ¹⁷O-excess maximum difference was 6.4 per meg, which is lower than the analytical precision obtained using the laser spectrometer (Table S1a in the Supplement).

In order to assess whether soluble organic compounds present in some soil water samples did not impact the laser analyzer isotope measurements (Martín-Gómez et al., 2015), a representative set of colored samples were analyzed with and without the Picarro micro combustion module (MCM) set up between the high-precision vaporizer and the analyzer inlet. This system was designed to partly remove organic volatile compounds using a catalytic process. The obtained isotope compositions were not significantly different (Table S1b), suggesting that organic compounds were either in low concentration, and/or did not interfere in the spectral window used by the analyzer. Therefore, the other soil water samples were analyzed without the MCM.

Figure 5 Natural West and Central African transect: ¹⁷O-excess of phytoliths (¹⁷O-excess_Phyto) vs. d∕p.

3 Results

3.1 Growth chamber experiment

δ^′18O and ¹⁷O-excess of the irrigation water (respectively δ^′18O_IW and ¹⁷O-excess_IW) average −5.59 ± 0.00 ‰ and 26 ± 5 per meg, respectively. δ^′18O and ¹⁷O-excess of the soil water (respectively δ^′18O_SW and ¹⁷O-excess_SW) average −2.89 ± 0.19 ‰ and 16 ± 8 per meg, respectively (Table S2). The isotope difference is thus significant for δ^′18O, less significant for ¹⁷O-excess, according to the analytical error. Although evaporative kinetic fractionation of the top soil water suctioned by the porous cup under vacuum cannot be ruled out, isotopic exchanges between the soil water and oxygen-bearing phases of the rhizosphere may also have impacted the soil water isotopic composition (Bowling et al., 2017; Chen et al., 2016; Oerter et al., 2014; Orlowski et al., 2016). Hereinafter, we consider the isotope signatures of the water absorbed by the roots of F. arundinacea to be equivalent to the irrigation water that fed the saturation level at the base of the tank. This water was reached by the deepest roots, as observed on a cross section of the soil after the end of the experiment, and likely reached the upper roots by capillarity.

The transpiration of F. arundinacea increases rapidly from 0.03 to 0.6 L day⁻¹ from 100 to 60 % RH and more slowly from 60 to 40 % RH, where it reaches 0.61 L day⁻¹ (averages of the replicates, Table 1). In response to decreasing RH, δ^′18O (Table S2) and ¹⁷O-excess (Fig. 1a) values of the bulk leaf water (δ^′18O_LW and ¹⁷O-excess_LW) show clear increasing and decreasing trends, respectively. The averaged ¹⁸O-enrichment of bulk leaf water relatively to irrigation water (Δ^′18O_LW−IW) increases from 100 to 60 % of RH and seems to be stabilizing from 60 to 40 % RH (Fig. 1b; Table 1). For 100 % RH, the high standard deviations (SD) associated with δ¹⁸O_LW (Table S2), and consequently with Δ^′18O_LW−IW (Table 1), are due to the very high δ¹⁸O_LW value of sample P3-100-10-05-16. However, as we do not have any explanation for this high value, these data were not excluded from further calculation. The ¹⁷O-excess values associated with the enrichment Δ^′18O_LW−IW (or ¹⁷O-excess${}_{\mathrm{e}\mathrm{LW}-\mathrm{IW}}={\mathrm{\Delta }}^{\prime }$¹⁷O${}_{\mathrm{LW}-\mathrm{IW}}-\mathrm{0.528}\times$ Δ^′18O_LW−IW) are scattered for a given RH. The averaged value however follows a clear pattern (Fig. 1c; Table 1): it decreases slowly from 100 to 80 % RH (from −88 ± 48 to −75 ± 20 per meg,) and more rapidly from 80 to 40 % RH where it reaches −159 ± 9 per meg. When the relationship is linearized, the slope of the line between ¹⁷O-excess_e LW−IW and 40 to 80 % RH is 2.3 per meg/% (Fig. 1f). The raw values of λ_LW−IW do not show any significant trend with RH and average 0.519 ± 0.002 (Table 1).

Table 1 Growth chamber experiment: experimental setup, phytolith content and morphological characteristics, isotope enrichments (${{\mathrm{\Delta }}^{\prime }}^{\ast }{\mathrm{O}}_{\mathrm{A}-\mathrm{B}}$ = ${{\mathit{\delta }}^{\prime }}^{\ast }{\mathrm{O}}_{\mathrm{a}}$ − ${{\mathit{\delta }}^{\prime }}^{\ast }{\mathrm{O}}_{\mathrm{b}}$), associated ¹⁷O-excess_e (¹⁷O-excess_e = Δ^′ 17O − $\mathrm{0.528}\times {\mathrm{\Delta }}^{\prime }{}^{\mathrm{18}}\mathrm{O}$), θ ($\mathit{\theta }={\mathrm{\Delta }}^{\prime }{}^{\mathrm{17}}\mathrm{O}/{\mathrm{\Delta }}^{\prime }{}^{\mathrm{18}}\mathrm{O}$) and λ values of phytoliths compared to either leaf water or irrigation water and of leaf water compared to irrigation water. Av: average; n: number of replicates; SD: standard deviation calculated on the replicates; n.v.: no value; d: (day), T (^∘C), Transp. (l day⁻¹), Bio, C. (% d.w.) and LC (%) stands for duration, temperature, transpiration, biomass, phytolith concentration and long cell abundance in the phytolith morphological assemblage expressed in % of counted phytoliths with taxonomic significance, respectively. Samples are named according to the climate chamber no. they were collected in (e.g., P1, P2), the set relative humidity (e.g., 40, 60) and the date of sampling (e.g., 29-04-16 for dd/mm/yy).

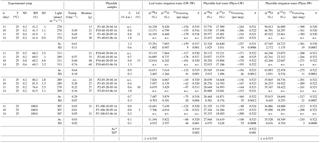
^*Calculated on the raw values.

The average phytolith content ranges from 1.1 to 0.1 % d.w. Silicification of the leaf blade of F. arundinacea increases with increasing transpiration and decreasing humidity (Table 1). Phytolith morphological identification shows that they formed preferentially in the epidermal short cell and to a smaller extent in the epidermal long cells (Fig. 2). The proportion of silicified long cells increases with increasing transpiration and decreasing RH (Table 1). Some hair and bulliform cells were also silicified, but in much smaller quantities. δ^′18O and ¹⁷O-excess of phytoliths (δ^′18O_Phyto and ¹⁷O-excess_Phyto, respectively) show the same general trends with RH as δ^′18O_LW and ¹⁷O-excess_LW (Fig. 1a, Table S2).

The average value of the ¹⁸O-enrichment of phytoliths relative to the bulk leaf water (Δ^′18O_Phyto−LW) increases slowly (from 27.97 ± 6.97 to 28.47 ± 0.38 ‰) when RH decreases from 100 to 80 % and more rapidly from 80 to 40 % where it reaches 32.32 ± 1.92 ‰ (Fig. 1b, Table 1). With regard to the enrichment of phytoliths relative to the irrigation water, Δ^′18O_Phyto−IW shows the same trend with RH as Δ^′18O_LW−IW (Fig. 1b, Table 1). ¹⁷O-excess_Phyto and ¹⁷O-excess_{e Phyto−IW} shows the same decreasing trend with RH as ¹⁷O-excess_e LW−IW (Fig. 1c, Table 1). When the relationships of ¹⁷O-excess_Phyto and ¹⁷O-excess_{e Phyto−IW} with 40 to 80 % RH are linearized, the slopes of the lines are 4.1 and 4.3 per meg/%, respectively (Fig. 1d, f). A Student's t-test (relevant when the variance of two data sets are equal; Andrade and Estévez-Pérez, 2014), calculated on the ¹⁷O-excess_e LW−IW vs. RH and ¹⁷O-excess_{e Phyto−IW} vs. RH data sets shows that the slopes of the lines are not statistically different for a 75 % confidence interval. Thus, the link between ¹⁷O-excess_{e Phyto−IW} and RH is mainly due to the leaf water ¹⁷O-excess dependency on RH. The raw values of λ_Phyto−LW appears constant, averaging 0.522 ± 0.001 (Table 1).

3.2 Natural samples

Values of δ^′18O_Phyto and ¹⁷O-excess_Phyto range, respectively, from 23.79 to 38.16 ‰ and from −140 to −290 per meg (Table 2). The variations are on the same order of magnitude as for the growth chamber experiment. The estimates of δ¹⁸O_Pre vary little along the sampled transect (from −4.46 to −3.22 ‰). No relationship is observed between δ^′18O_Phyto or the ¹⁸O enrichment of phytoliths relative to precipitation (Δ^′18O_Phyto−Pre) and MAP, MAT or RH (Fig. 3, Table 2).

Although scattered, the ¹⁷O-excess_Phyto values show a significant positive linear correlation with RH (Fig. 4), regardless of which RH variable is taken into account. After excluding two outliers, the slopes of the correlation lines are 2.1 and 2.2 when RH and RH15 are taken into account, and 3.4 when either RH-rd0 > 1 or RH15-rd0 > 1 are considered. The relationship obtained between ¹⁷O-excess_Phyto and RH-rd0 > 1 (i.e., RH of the wet months during which plants grow) is the closest to the one obtained between ¹⁷O-excess_Phyto and RH in the growth chambers (Fig. 4b). It can be expressed as follows (Eq. 1):

$$\begin{array}{ll}{\displaystyle }{}^{\mathrm{17}}\mathrm{O}\text{-}{\mathrm{excess}}_{\mathrm{Phyto}}& {\displaystyle }=\mathrm{3.4}\times \text{RH-rd0}>\mathrm{1}\\ \text{(1)}& {\displaystyle }& {\displaystyle }-\mathrm{460}(r^{\mathrm{2}}=\mathrm{0.48};p<\mathrm{0.001}),\end{array}$$

where ¹⁷O-excess_Phyto is expressed in per meg and RH in %.

Table 2 Natural West and Central African phytolith samples: coordinates, climatic parameters, calculated phytolith index d∕p, measured δ^′18O_Phyto, δ^′17O_Phyto, ¹⁷O-excess_Phyto, calculated δ^′18O of phytolith forming water (δ¹⁸O_PhytoFW) and precipitation-weighted δ^′18O${}_{\mathrm{Pre}-\mathrm{rd}\mathrm{0}>\mathrm{1}}$. Average and standard deviation (SD) are given for replicates. MAP: Mean Annual Precipitation; MAT: Mean Annual Temperature; RH: mean annual relative humidity; RH15: RH at 15:00 UTC; RH-rd0 > 1: relative humidity average for months with at least 1 day with precipitation higher than 0.1 mm; RH15-rd0 > 1: RH-rd0 > 1 at 15:00 UTC. See text for data source and calculation.

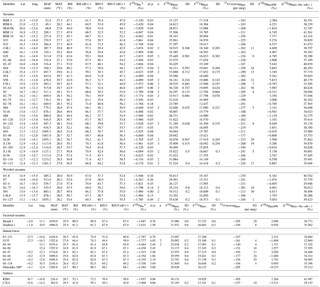
^*Amount-weighted average for months with at least 1 day with precipitation > 0.1 mm.

The excluded outliers (Table 3) are RIM1 and C3L4. RIM1 presents a very low ¹⁷O-excess (−305 per meg) relative to the ¹⁷O-excess of the samples with close RH-rd0 > 1, i.e., from 71 to 74 % (average of $-\mathrm{237}\pm \mathrm{32}$ per meg for 82–78, 83–116 and 83–115). C3L4 is located next to C4L3 and under similar averaged RH but presents a ¹⁷O-excess higher by 133 per meg. RIM1 and C3L4 show morphological patterns very similar to the other assemblages with the same range of RH. Thus, the discrepancies may lie either in the fact that local RH variations may not be reflected in RH averaged estimates for 10' (≈ 185 km²) or in the particularity of the isotope composition of the local soil water (see discussion below).

The phytolith index d∕p ranges from 0.01 to 0.08 in savanna, from 0.14 to 0.49 in wooded savanna, from 0.76 to 1.58 in enclosed savanna and from 1.84 to 6.78 in humid forests (Table 2). This unambiguous increase in d∕p with tree cover density is in agreement with previous calibrations performed for the West African area (Bremond et al., 2005b). Interestingly, under high RH conditions, humid forest and enclosed savanna that are characterized by a large range of d∕p represent a small range of ¹⁷O-excess. Conversely, under lower RH conditions, savanna and wooded savanna that are characterized by a small range of d∕p represent a large range of ¹⁷O-excess (Fig. 5). This absence of a relationship between ¹⁷O-excess and tree cover density is also mirrored in Fig. 4, where phytolith samples from different vegetation types (i.e., savanna vs. wooded savanna or humid forests vs. enclosed savanna), that have developed under the same RH conditions, have the same range of ¹⁷O-excess.

4 Discussion

4.1 Imprint of changes in atmospheric RH on the ¹⁷O-excess of leaf water

In the bulk leaf water, the trends observed between Δ^′18O_LW−IW or ¹⁷O-excess_e LW−IW and RH are in agreement with an evaporative kinetic fractionation that increases when RH decreases, as expected from previous studies on the δ¹⁸O or ¹⁷O-excess evolution of leaf water (e.g., Cernusak et al., 2016; Landais et al., 2006; Li et al., 2017). The average value of λ_LW−IW (0.519) is close to the value of θ_diff calculated for the diffusion of vapor in air (0.518; Barkan and Luz, 2007). As schematically described in Landais et al. (2016), λ_transp (equivalent to λ_LW−IW) represents the interplay among three processes in the leaf boundary layer: (1) the equilibrium fractionation, which is only temperature-dependent (Majoube, 1971) and drives the isotope composition of leaf water along the equilibrium water line (θ_equil=0.529); (2) the diffusion transport leading to increasing kinetic fractionation with decreasing relative humidity along the diffusion line; (3) the isotope exchange of leaf water with atmospheric water vapor, decreasing from turbulent to laminar and molecular leaf boundary layer vapor transport conditions (e.g., Buhay et al., 1996). In the case of the growth chamber experiment, the fact that λ_LW−IW is close to θ_diff supports that the increasing diffusion of vapor in air when RH decreases or transpiration increases is the main process controlling the evolution of ¹⁷O-excess_LW. At high humidity (80–100 % RH), the kinetic fractionation likely reaches its minimum as the diffusion process becomes limited.

The δ¹⁸O_LW is commonly modelled as a function of the isotope composition of absorbed water, the isotope composition of water vapor, and RH (Craig and Gordon, 1965). The Craig and Gordon simple approach overestimates δ¹⁸O_LW and different corrections have been proposed to take into account the diffusion of the evaporating water back to the leaf lamina and the advection of less evaporated stem water (i.e., the Péclet effect, Buhay et al., 1996; Helliker and Ehleringer, 2000; Roden et al., 2000; Farquhar and Gan, 2003; Farquhar and Cernusak, 2005; Ripullone et al., 2008; Treydte et al., 2014). In the growth chamber experiment, where water availability, relative humidity, and temperature were kept constant, we assume that transpiration rapidly reached a steady state and that the isotope composition of transpired water was the same as that of the irrigation water entering the plant (e.g., Welp et al., 2008). A tentative estimate of the theoretical value of Δ^′18O_LW−IW, Δ^′17O_LW−IW and ¹⁷O-excess_e LW−IW was performed using the equations proposed for ¹⁸O-enrichment by Cernusak et al. (2016) (Table S3). For calculating the Δ¹⁷_LW−IW we used for the equilibrium and kinetic fractionations (respectively ¹⁷α_eq and ¹⁷α_k in Table S3) ${}^{\mathrm{17}}{\mathit{\alpha }}_{\mathrm{eq}}{=}^{\mathrm{18}}{\mathit{\alpha }}_{\mathrm{eq}}^{\mathrm{0.529}}$ and ¹⁷α_k= ${}^{\mathrm{18}}{\mathit{\alpha }}_k^{\mathrm{0.518}}$. As expected, the predicted Δ^′18O_LW−IW values were all higher than the observed values by several ‰. Helliker and Ehleringer (2000) proposed, for monocotyledonous species characterized by a vertical parallel veinal structure, to use instead of the Craig and Gordon model the Gat and Bowser (1991) equation describing the movement of water through a sequence of pools in series. However, this model would further increase the estimates of Δ^′18O_LW−IW. The predicted ¹⁷O-excess_e displayed in Table S3 was either higher or lower than the observed ¹⁷O-excess_e LW−IW. Predicted λ_LW−IW increased with RH from 0.521 to 0.529 which is far from the observed values averaging 0.519. The predicted value of 0.529 at 100 % RH reflects pure equilibrium in a situation where irrigation water and water vapor are assumed to have similar isotope composition since irrigation water is directly vaporized into the chamber (Table S3), without any fractionation. Sensitivity tests show that regardless of the model chosen (Buhay et al., 1996; Cernusak et al., 2016; Li et al., 2017), estimations of λ_LW−IW are very dependent on the isotope compositions of the water vapor (Li et al., 2017), not measured either in our experiment or in previous studies (Landais et al., 2006; Li et al., 2017). In the natural environment, a first-order approximation for the isotope composition of water vapor is to consider equilibrium with precipitation. As a result of water-vapor equilibrium fractionation and soil water ¹⁸O-enrichment, this can lead to a water vapor ¹⁸O-depleted by 10–13 ‰ compared to the soil water (Landais et al., 2006; Lehmann et al., 2018). In this case the predicted λ_transp (equivalent to λ_LW−SW) decreases with increasing humidity. Finally, because wrong values of the isotope compositions of the water vapor may affect significantly the calculation of Δ^′18O_LW−IW, Δ^′17O-excess_e LW−IW and λ_LW−SW, we call for vapor isotope measurements as a prerequisite to accurately model the leaf water triple oxygen isotope evolution with RH. However, overall, despite the uncertainties on the predicted evolution of λ_LW−SW with RH, the predicted value of ¹⁷O-excess_e LW−IW decreases when RH increases, which is also observed, as well as reflected in the triple isotope composition of phytoliths, as discussed below.

4.2 Imprint of changes in atmospheric RH on the ¹⁷O-excess of phytoliths

Polymerization of silica is supposed to occur in isotope equilibrium with the forming water, and, therefore, to be only governed by temperature and the isotope composition of the forming water. Almost a dozen temperature-dependent relationships have been empirically established between the δ¹⁸O of quartz, sinters, cherts, diatoms or phytoliths and the δ¹⁸O of their forming water (δ¹⁸O_PhytoFW). Although the obtained fractionation coefficients are close (from −0.2 to −0.4 ‰ ^∘C⁻¹), the range of fractionation (Δ¹⁸O_{Phyto−PhytoFW}) is large (see synthesis in Alexandre et al., 2012). The Δ¹⁸O_{Phyto−PhytoFW} values obtained in the frame of the growth chamber experiment (ranging from 27.9 ± 7.2 to 32.3 ± 2.2 ‰) encompass the Δ¹⁸O_{Phyto−PhytoFW} of 31.1 ‰ calculated from the Dodd and Sharp (2010) relationship for 25 ^∘C. It is lower than the values of 36.4 and 36 ‰ at 25 ^∘C, calculated from Sharp et al. (2016) and Alexandre et al. (2012). Whereas Alexandre et al. (2012) and Sharp et al. (2016) generally estimated the forming-water δ¹⁸O values, Dodd and Sharp (2010) measured the the δ¹⁸O values of the water samples. The proximity of the obtained range of Δ¹⁸O_Phyto−LW values to the Δ¹⁸O_{Phyto−PhytoFW} calculated from Dodd and Sharp (2010) suggests that phytoliths formed in equilibrium with a water of isotope composition close to that of the bulk leaf water. This is additionally supported by the obtained averaged value of λ_Phyto−LW (0.522 ± 0.001) close to the ${\mathit{\theta }}_{{\mathrm{SiO}}_{\mathrm{2}}-\mathrm{water}}$ equilibrium value of 0.524 calculated for 25 ^∘C from Sharp et al. (2016).

Evolution of the triple isotope composition of bulk leaf water and phytoliths can be illustrated by plotting δ^′17O vs. δ^′18O, or ¹⁷O-excess vs. δ^′18O (Fig. 6) which is more appropriate to evidence small variations. Figure 6 shows that the leaf water evolved from the irrigation water pool, becomes increasingly subject to kinetic fractionation when RH decreased. This evolution follows a single leaf water line reflecting ${\mathit{\lambda }}_{\mathrm{LW}-\mathrm{IW}}=\mathrm{0.519}$ (Table 1). Then, if phytoliths polymerized from the bulk leaf waters, at 25 ^∘C, according to a constant equilibrium fractionation, their expected isotope signature should follow a line parallel to the leaf water line. This is the case for phytoliths formed at RH higher than 40 %. However, the isotope signature of phytoliths formed at 40 % RH suggests a forming water more evaporated than the bulk leaf water. The Péclet effect, which is known to scale with transpiration (e.g., Barnard et al., 2007), can explain this discrepancy. Advection of less evaporated stem water may decrease δ^′18O_LW and increase ¹⁷O-excess_LW relative to δ^′18O and ¹⁷O-excess of the epidermal water prone to evaporation and from which phytoliths formed. At this point, the data scattering prevents further discussion but the possibility that when RH is low, or when transpiration is high, the phytolith forming-water is different from the bulk leaf water must be investigated in future research developments.

With regard to the natural samples, whereas no relationship was found between δ^′18O_Phyto and RH, a clear positive linear dependency of ¹⁷O-excess_Phyto on RH was shown, equivalent to 2.1 per meg/% when the annual RH average was taken into account, or to 3.4 per meg/% when the average of the growing season (RH-rd0 > 1) was taken into account (Fig. 4). These coefficients are close to the slope of the lines obtained for the growth chamber experiment between ¹⁷O-excess_Phyto, ¹⁷O-excess_e LW−IW and ¹⁷O-excess_{e Phyto−IW} and 80 to 40 % RH (Fig. 1a, e and f). This consistency represents a major positive step in examining whether changes in atmospheric RH imprint the ¹⁷O-excess of natural phytolith assemblages in a predictable way. Without taking into account the two outliers, the linear regression between RH-rd0 > 1 and ¹⁷O-excess_Phyto for a 95 % confidence interval can be expressed as follows:

$$\begin{array}{ll}{\displaystyle }\mathrm{RH}\text{-rd0}>\mathrm{1}& {\displaystyle }=\mathrm{0.14}\pm \mathrm{0.02}(\mathrm{S}.\mathrm{E}.)\times {}^{\mathrm{17}}\mathrm{O}\text{-}{\mathrm{excess}}_{\mathrm{phyto}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }+\mathrm{100.5}\pm \mathrm{4.7}(\mathrm{S}.\mathrm{E}.),\end{array}$$

where ¹⁷O-excess_Phyto is expressed in per meg and RH in %, r²=0.48, and p < 0.001. S.E. stands for standard error. The S.E. of the predicted RH-rd0 > 1 value is ±5.6 %. However, the data scattering (Fig. 4) calls for assessing additional parameters that can contribute to changes in ¹⁷O-excess_Phyto, besides RH, before using the ¹⁷O-excess_Phyto for quantitative RH reconstruction.

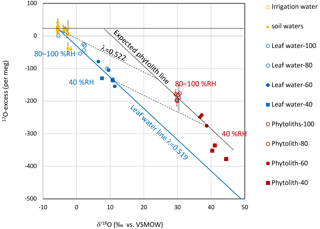
Figure 6 Growth chamber experiment: ¹⁷O-excess vs. δ^′18O of irrigation water (IW), soil water (SW), bulk leaf water (LW) and phytolith (Phyto). Error bars show standard deviation (SD) on the replicates. The leaf water line (blue) represents how the triple oxygen isotope composition of the bulk leaf water of Festuca arundinacea evolves from an irrigation water signature to a more evaporated water signature when RH decreases. Assuming that phytoliths precipitate from the bulk leaf water, the expected phytolith line (black) should be parallel to the leaf water line as the equilibrium fractionation between phytolith and leaf water is constant at constant temperature (25 ^∘C). In the investigated case this fractionation, represented by the black dotted line, is equivalent to λ=0.522 (Table 1). The isotope signature of phytoliths formed at RH higher than 40 % follow the expected phytolith line. However, the isotope signature of phytoliths formed at 40 % RH suggest a forming water more evaporated than the bulk leaf water.

One can expect that the isotope composition of the soil water taken up by the roots will impact ¹⁷O-excess_Phyto. In tropical dry and humid areas, evaporative kinetic fractionation can lead to a ¹⁸O-enrichment of the soil water of several ‰, in the first dm depth (e.g., Gaj et al., 2016; Liu et al., 2010). Spatial variability in the composition of the rainfall feeding the upper soil water may also intervene. However, the amount-weighted values of δ^′18O_Pre along the sampled transect vary little (Table 2). With regard to ¹⁷O-excess, changes in soil water evaporation rather than the small variations expected for ¹⁷O-excess_Pre (Landais et al., 2010b; Li et al., 2015) should impact the evolution of ¹⁷O-excess_Phyto, although, here, the lack of measurements only allows for speculation.

The vegetation type and the plant part from which phytoliths come from may also bring some noise to the relationship between ¹⁷O-excess_phyto and RH. In grasses, leaf water is expected to be more prone to evaporative enrichment than stem water, and inside the leaf itself, the heterogeneity of evaporative sites repartition and water movements can lead to a significant heterogeneity in the δ¹⁸O signatures of water and phytoliths (Cernusak et al., 2016; Helliker and Ehleringer, 2000; Webb and Longstaffe, 2002). However, soil top phytolith assemblages likely record several decades of annual bulk phytolith production and their isotope composition is expected to be an average. This would explain the consistency of the ¹⁷O-excess_Phyto data obtained from bulk grass phytoliths from climate chambers and the bulk phytolith assemblages from natural vegetation. Further investigation on the extent of the heterogeneity of ¹⁷O-excess in water and phytoliths in mature grasses would help to verify this assumption. In trees, the Globular granulate phytolith is assumed to come from the non-transpiring secondary xylem of the wood. Thus Globular granulate phytoliths should present an isotope signature closer to that of the soil water, or less impacted by kinetic fractionation than grass phytoliths. However, for a given range of RH, samples with significant representations of both phytolith categories (i.e., wooded savanna and enclosed savanna samples with d∕p from 0.1 to 1.6) present ¹⁷O-excess values close to the values obtained by samples with very low or very high d∕p (Figs. 4 and 5). To further assess the significance of the Globular granulate isotope signature, we calculated δ^′18O_PhytoFW values (Table 2) using the Dodd and Sharp (2010) fractionation factor and compared it to the precipitation-weighted δ^′18O${}_{\mathrm{Pre}-\mathrm{rd}\mathrm{0}>\mathrm{1}}$ average. For the humid forest assemblages, δ^′18O_PhytoFW values are higher than δ^′18O${}_{\mathrm{Pre}-\mathrm{rd}\mathrm{0}>\mathrm{1}}$ by 4.6 ± 1.5 ‰. This difference is larger than the range of ¹⁸O-enrichment observed for the upper 10 cm depth of soil water under tropical humid forests (2–3 ‰; Liu et al., 2008; Stahl et al., 2013), suggesting that evaporative isotope signatures of both soils and leaf water imprinted the Globular granulate phytolith type. This is in line with recent ¹⁸O-labelling experiment showing that the ¹⁸O-enriched oak phloem water may exchange with xylem water under low transpiration rates (Lehmann et al., 2018). Complementary examination of the isotope signature of phytolith assemblages from forests growing under different RH conditions (i.e., dry forests, humid forests, rainforests), as well as further investigation of the anatomical origin of the Globular granulate phytolith type, are now required to further discuss the meaning of the ¹⁷O-excess signal brought by wooded savanna and tropical forest phytolith assemblages.

Biases due to the calibration methodology may also be responsible for the data scattering. Imperfect adequacy between the space scales recorded by the soil top phytolith assemblages and the RH variables may come into play. Phytolith assemblages represent a mixture of local and wind-transported phytoliths. In the open Saharan, Sahelian and Sudanian zones of West Africa the winter low-altitude northeasterly trade winds may transport phytoliths southward, reducing differences between assemblages from different biogeographic zones and increasing differences among assemblages of a given biogeographic zone (Bremond et al., 2005b). Additional samples from other geographic zones are thus needed to increase the robustness of the relationship. With regard to the recorded timescales, the CRU RH 30-year averages are in agreement with the several decades of phytolith production.

5 Conclusions

The present combination of growth chamber and in situ transect calibrations lay the groundwork for further examination of the robustness of the ¹⁷O-excess_Phyto as a proxy of changes in RH. The growth chamber experiment demonstrated that change in RH imprints ¹⁷O-excess_Phyto (by 4.1 per meg/% between 40 and 80 % RH) or the ¹⁷O-excess_{e Phyto−IW} (by 4.3 per meg/%, between 40 and 80 % RH) through its imprint on ¹⁷O-excess_e LW−IW. As the isotope composition of the irrigation water was stable, and transpiration likely reached a steady state, the positive correlation between ¹⁷O-excess_LW and RH was only governed by the kinetic fractionation occurring in the leaf epidermis water subject to evaporation, as supported by the averaged value of λ_LW−IW of 0.519, close to θ_diff.

In order to model the triple oxygen isotope fractionation in play at the soil/plant/atmosphere interface we require direct and continuous measurements of the triple isotope composition of water vapor. Such measurements should develop in the near future through the use of isotope ratio infrared analyzers (e.g., Berkelhammer et al., 2013; Schmidt et al., 2010). We also suggest to constrain as much as possible the isotope composition of the soil water taken up by the roots. Stem water is usually used as an analogue of soil water when modelling δ^′17O_LW and δ^′18O_LW (Landais et al., 2006; Li et al., 2017). However, in the stem, water in the phloem that is bidirectional (moves up and down the plant's stem) receives the contribution of evaporating leaf water, and water in the xylem that is unidirectional (moves up the plant's stem) may exchange with phloem waters (Lehmann et al., 2018). Consequently one may expect the isotope composition of stem water to be slightly different than that of soil water (Berkelhammer et al., 2013; Treydte et al., 2014).

When plotting ¹⁷O-excess_Phyto vs. RH, the samples collected along the West and Central African relative humidity transect define a correlation coefficient ranging from 2.1 to 3.4 per meg/% (depending on the RH variable taken into account) and lay close to the growth chamber ¹⁷O-excess_Phyto line. This supports that RH is an important control of ¹⁷O-excess_Phyto in natural environment, even if phytolith assemblages come from different vegetation types. However, other parameters such as changes in the triple isotope composition of the soil water, vegetation source or imperfect adequation between the space scales recorded by the soil top phytolith assemblages and the RH variables may come into play and explain the scattering of ¹⁷O-excess_Phyto. Assessment of these parameters through additional growth chambers experiments and field campaigns will bring us closer to an accurate proxy of changes in relative humidity.