Inferring the effects of sink strength on plant carbon balance processes from experimental measurements

The lack of correlation between photosynthesis and plant growth under sink-limited conditions is a long-standing puzzle in plant ecophysiology that currently severely compromises our models of vegetation responses to global change. To address this puzzle, we applied data assimilation to an experiment in which the sink strength of Eucalyptus tereticornis seedlings was manipulated by restricting root volume. Our goals were to infer which processes were affected by sink limitation and to attribute the overall reduction in growth observed in the experiment to the effects on various carbon (C) component processes. Our analysis was able to infer that, in addition to a reduction in photosynthetic rates, sink limitation reduced the rate of utilization of nonstructural carbohydrate (NSC), enhanced respiratory losses, modified C allocation and increased foliage turnover. Each of these effects was found to have a significant impact on final plant biomass accumulation. We also found that inclusion of an NSC storage pool was necessary to capture seedling growth over time, particularly for sink-limited seedlings. Our approach of applying data assimilation to infer C balance processes in a manipulative experiment enabled us to extract new information on the timing, magnitude and direction of the internal C fluxes from an existing dataset. We suggest that this approach could, if used more widely, be an invaluable tool to develop appropriate representations of sink-limited growth in terrestrial biosphere models.

1 Introduction

Almost all mechanistic models of terrestrial vegetation function are based on the carbon (C) balance: plant growth is represented as the difference between C uptake (through photosynthesis) and C loss (through respiration and turnover of plant parts). This approach to modeling plant growth dates back to early crop and forest production models (McMurtrie and Wolf, 1983; de Wit and van Keulen, 1987; de Wit, 1978) and now provides the fundamental quantitative framework to integrate our scientific understanding of plant ecosystem function (Makela et al., 2000).

However, C balance models have been criticized for being “source focused” (Fatichi et al., 2014). Most C balance models predict growth from the environmental responses of photosynthesis (“source limitation”). In contrast to this assumption, many experimental studies demonstrate that growth is directly limited by environmental conditions (“sink limitation”) rather than the availability of photosynthate. For example, growth is more sensitive to water limitation than is photosynthesis (Bradford and Hsiao, 1982; Müller et al., 2011; Mitchell et al., 2014); low temperatures are considerably more limiting to cell division than to photosynthesis (Körner et al., 2014); nutrient limitation may slow growth without reducing photosynthesis (Reich, 2012; Crous and Ellsworth, 2004); and physical sink limitation may reduce growth with a decline in photosynthetic capacity and an accumulation of leaf starch (Arp, 1991; Campany et al., 2017; Poorter et al., 2012a; Paul and Foyer, 2001).

How can we move to models that include both source and sink limitation? There is ongoing discussion about realistic implementations of nonstructural carbohydrates (NSCs) in vegetation models; because of their multiple roles in plant functioning, such an implementation provides a buffer against discrepancies in source and sink activity. Some C balance models include a “storage” pool of NSC (Running and Gower, 1991; Bossel, 1996; Thornley and Cannell, 2000), but most of these models make the assumption that the NSC pool acts merely as a buffer between C sources and sinks, balancing out seasonally or at least over several seasons (Fatichi et al., 2014; Friend et al., 2014; De Kauwe et al., 2014; Schiestl-Aalto et al., 2015). There is mounting evidence that the NSC plays a more active role in tree physiology (Buckley, 2005; Sala et al., 2012; Wiley and Helliker, 2012; Hartmann et al., 2015). For example, NSC accumulation can lead to downregulation of photosynthesis (Nikinmaa et al., 2014). Therefore, the need to quantify the NSC pool and to better understand the prioritization of storage vs. growth is of great importance.

An understanding of the dynamics of storage is also essential to correctly represent the C balance in models (Hartmann and Trumbore, 2016). If, for example, a direct growth limitation is implemented into models, how should the surplus of accumulated photosynthates be treated? In their proof-of-concept sink-limited model, Fatichi et al. (2014) allowed reserves to accumulate indefinitely. Alternatively, some models (e.g., CABLE; Law et al., 2006, O-CN; Zaehle and Friend, 2010) increase respiration rates when excess labile C accumulates. Both approaches can be seen as model-oriented solutions to maintain C balances that are unsatisfactory because they are not based on empirical data. Experiments in which sink strength is manipulated may provide the key to improving our understanding of C balance processes under direct growth limitation.

Efforts have been made to understand the physiological and morphological changes in response to belowground C sink limitation by manipulating rooting volume in tree seedlings (Arp, 1991; Campany et al., 2017; Poorter et al., 2012a). These experiments often reveal photosynthetic downregulation and accumulation of leaf starch and reductions in growth (Arp, 1991; McConnaughay and Bazzaz, 1991; Gunderson and Wullschleger, 1994; Sage, 1994; Poorter et al., 2012a; Robbins and Pharr, 1988; Maina et al., 2002; Campany et al., 2017). In a recent study with eucalyptus seedlings, Campany et al. (2017) showed that the reduction in seedling growth when rooting volume was restricted could not be completely explained by the negative effects of sink limitation on photosynthesis, suggesting that other components of the C balance were affected in the process. However, Campany et al. (2017) could not accurately quantify all components of tree C balance, i.e., photosynthesis, carbohydrate storage, biomass partitioning and respiration.

Quantifying all components of C balance is not an easy task given that not all processes are measured with equal fidelity, and data gaps will always occur. Klein and Hoch (2015) used a C mass balance approach with a tabular process flowchart to decipher C components and provide a full description of tree C allocation dynamics. Here, rather than using a manual process, we used a data assimilation modeling (DA-modeling) framework, which has been proven to be a powerful tool in analyzing complex C balance problems (Williams et al., 2005; Richardson et al., 2013). For example, Richardson et al. (2013) use DA to discriminate among alternative models for the dynamics of nonstructural carbon (NSC), finding that a model with two NSC pools, fast and slow, performed best; Rowland et al. (2014) applied DA to experimental observations of ecosystem C stocks and fluxes to infer seasonal shifts in C allocation and plant respiration in an Amazon forest; and Bloom et al. (2016) used DA to constrain a C balance model with satellite-derived measurements of leaf C to simulate continental-scale patterns in C cycle processes.

Our goal in this paper was to use DA to quantify the impact of sink limitation on C balance processes. We utilized data from an experiment in which sink limitation was induced by restricting the rooting volume of Eucalyptus tereticornis seedlings over the course of 4 months (Campany et al., 2017). We assimilated photosynthesis and growth measurements from the experiment into a simple C balance model to infer the effects of sink limitation on the main C balance processes, namely respiration, carbohydrate utilization, allocation and turnover.

Although in reality plants do have a storage component, it is not necessarily the case that including such a storage component in the model leads to model improvement. Hence, it is important to test whether or not adding the storage component improves the performance of the model enough to justify the additional complexity. Therefore, we first tested two null hypotheses.

• H1:

  There is no need to consider storage in the model: growth can be adequately predicted from current-day photosynthate.

• H2:

  There is no effect of sink limitation on C balance processes other than via a reduction of photosynthesis.

We were then interested to test the following specific hypotheses about the impact of sink limitation on C balance.

• H3:

  We hypothesized that the rate of utilization of carbohydrate for plant growth would be lower under sink limitation, causing growth rates to slow and nonstructural carbohydrate to accumulate.

• H4:

  We hypothesized that under sink limitation a larger proportion of C would be lost to growth respiration and less used for production. We have dubbed this the “wasteful plant” hypothesis; this hypothesis corresponds to the assumption embedded in some models that respiration is upregulated when labile C accumulates; e.g., CABLE, O-CN (Law et al., 2006; Zaehle and Friend, 2010).

• H5:

  We hypothesized that foliage and root C allocation fractions would be reduced in favor of wood allocation. Sink limitation induced by nutrient and/or water stress often results in a shift in C allocation away from foliage and towards fine roots (Poorter et al., 2012b). However, for this experiment, the physical restriction of root growth limits the potential for root allocation. Hence, we predicted that both foliage and fine root allocation would decrease.

2 Materials and methods

2.1 Experiment description

The site and experimental setup have been described in detail by Campany et al. (2017), so we only provide a brief description here. The experiment was carried out at the Hawkesbury Forest Experiment site (33^∘37^′ S, 150^∘44^′ E) in Richmond, NSW, Australia. The site is located in the subhumid temperate region and experiences warm summers and cool winters. The seedlings were planted on 21 January 2013 (mid-summer) and harvested on 21 May 2013 (late autumn). Mean daily temperatures ranged from 22.8 to 46.4 ^∘C (monthly mean of 32.1 ^∘C) in January 2013, which was the warmest month of the year, and cooled down in May 2013 with an average of 21 ^∘C (BoM, 2017).

From a single local Cumberland plain cohort, 20-week-old Eucalyptus tereticornis seedlings in tube stock were chosen. A total of 10 seedlings were harvested at the start of the experiment to measure initial leaf area and dry mass of foliage, woody components and roots. There were 49 seedlings used in the main experiment, allocated to seven treatments. The plants were grown in containers of differing volume set into the ground (5, 10, 15, 20, 25 or 35 L) or were planted directly into soil (free seedlings, used as the control). All plants were grown in the open under field conditions, but were watered regularly to avoid moisture stress.

2.2 Experimental data acquisition

Full details of all measurements are given in Campany et al. (2017). The mass of each pool (foliage, wood, root, storage) was estimated over time as follows. The initial dry mass of leaves, woods and roots was measured for 10 seedlings at the start of the experiment using the harvesting procedure described in Campany et al. (2017). The dry mass of all experimental plants was measured at the end of the experiment following the same procedure. Seedling growth was tracked during the 4 months of the experiment by measuring stem height (h), diameter at 15 cm height (d) and number of leaves on a weekly basis. These measurements were used to estimate the time course of wood and foliage biomass: for root total C we used only initial and final harvest measurements. Initial root C was estimated by averaging all 10 harvested seedlings.

We estimated weekly total C in wood (C_s,w) from the measurements of stem height and diameter by using an allometric model fitted to initial and final harvest data.

$$\begin{array}{}\text{(1)}& \log \left({\mathrm{C}}_{\mathrm{t},\mathrm{w}}\right)=b_{\mathrm{1}}+b_{\mathrm{2}}\log \left(d\right)+b_{\mathrm{3}}\log \left(h\right)\end{array}$$

For each seedling, the total leaf area (LA) and foliage total C (C_t,f) over time (t) were estimated based on harvested data (T = time of harvest) and weekly leaf counts (LCs) over time.

$$\begin{array}{}\text{(2)}& {\displaystyle }\text{LA}\left(t\right)={\displaystyle \frac{\text{LA}\left(T\right)}{\text{LC}\left(T\right)}}\text{LC}\left(t\right)\text{(3)}& {\displaystyle }{\mathrm{C}}_{\mathrm{t},\mathrm{f}}\left(t\right)={\displaystyle \frac{M_{\mathrm{f}}\left(T\right)}{\text{LC}\left(T\right)}}\text{LC}\left(t\right)\end{array}$$

Fully expanded new leaves were sampled for total nonstructural carbohydrate (NSC) concentration on a fortnightly basis. These concentrations were multiplied by leaf biomass to estimate the foliage TNC pool (C_n,f) at each time point. The partitioning of the nonstructural C amongst foliage, wood and root tissues according to empirically determined fractions was then used to estimate the wood and root components of the total TNC pool. Structural C mass for each component was estimated by subtracting nonstructural C mass from total C mass.

Only foliage nonstructural C (C_n,f) was measured, so to estimate the partitioning of the nonstructural C among different organs, we used data from a different experiment on similar-sized seedlings of a related species (Eucalyptus globulus), which were grown in 5 L pots until 4 months of age (Duan et al., 2013). We used data from the ambient well-watered control treatments. In that experiment, foliage, wood and root NSC were measured repeatedly over 2 months. There was no statistically significant change over time in the NSC distribution, so we used the mean distribution for mass-specific C_n over time, which was calculated to be a ratio of 75 : 16 : 9 among foliage, wood and root pools.

We estimated daily GPP from leaf-level gas exchange measurements and a simple canopy scaling scheme, as described in Campany et al. (2017) and summarized below. Measurements of photosynthesis were made fortnightly throughout the experiment on one fully expanded leaf per plant (Campany et al., 2017). Photosynthetic CO₂ response (ACi) curves and leaf dark respiration rates (R) were measured on two occasions, 13–14 March 2013 (when new leaves were first produced) and 14–15 May 2013 (prior to the final harvest). The ACi curves were used to estimate photosynthetic parameters (the maximum rate of Rubisco carboxylation, V_cmax and the maximum rate of electron transport for RuBP regeneration under saturating light, J_max) using the biochemical model of Farquhar et al. (1980) and fit with the “plantecophys” package (Duursma, 2015) in R. The parameter g₁, reflecting the sensitivity of stomatal conductance (g_s) to the photosynthetic rate, was estimated by fitting the optimal stomatal conductance model of Medlyn et al. (2011) to measured stomatal conductance data.

Treatment effects on photosynthesis were detected immediately on newly produced (fully expanded) leaves and Campany et al. (2017) did not observe variation over time in photosynthetic rates. Hence, the photosynthesis parameters were assumed not to change over time but were specific for each treatment. Therefore, daily net C assimilation per unit leaf area (C_day) was estimated by using a coupled photosynthesis–stomatal conductance model (Farquhar et al., 1980; Medlyn et al., 2011) using mean photosynthetic parameters (J_max, V_cmax, g₁ and R_d) for each treatment and meteorological data from the on-site weather station. The daily GPP was estimated by multiplying C_day, total leaf area (LA) and a self-shading factor. The self-shading factor, which is a linear function of LA, is calculated via simulation with a detailed radiative transfer model, using R package YplantQMC version 0.6-6 by Duursma and Cieslak (2014) for individual treatment. The leaf maintenance respiration rate (R_m, $\mathrm{g}\mathrm{C}{\mathrm{g}}^{-\mathrm{1}}\mathrm{C}\mathrm{plant}{\mathrm{day}}^{-\mathrm{1}}$) was calculated for each seedling by scaling the measured rate (R) to air temperature using a Q₁₀ value of 1.86 (Campany et al., 2017). The daily total maintenance respiration, R_m,tot, is calculated as a temperature-dependent respiration rate, R_m, multiplied by plant biomass. We assumed the same tissue-specific dark respiration rates for leaf, woody and root tissues for these seedlings, as was observed for seedlings of this species by Drake et al. (2017).

2.3 Carbon balance model (CBM)

We used a DA-modeling framework similar to that used by Richardson et al. (2013). This approach uses a simple carbon balance model shown in Fig. 1. The model is driven by daily input of gross primary production (GPP), which directly enters into a nonstructural C pool (C_n). The daily total maintenance respiration, R_m,tot, is subtracted from C_n pool. The pool is then utilized for growth at a rate k (i.e., kC_n). Of the utilization flux, a fraction Y is used in growth respiration (R_g), and the remaining fraction (1−Y) is allocated to structural C pools (C_s) among foliage, wood and root (C_s,f, C_s,w, C_s,r). The foliage pool is assumed to turn over with rate s_f. We assume there is neither wood or root turnover as the seedlings in the experiment were young.

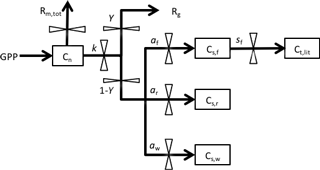
Figure 1 Structure of the carbon balance model. Pools are shown as boxes: C_n, nonstructural storage C; C_s,f, structural C in foliage; C_s,r, structural C in roots; C_s,w, structural C in wood. Fluxes, denoted by arrows, include the following: GPP, gross primary production; R_m,tot, total maintenance respiration; R_g, growth respiration; C_t,lit, structural C in leaf litterfall. Fluxes are governed by six key parameters: k, storage utilization coefficient; Y, growth respiration fraction; a_f, allocation to foliage; a_w, allocation to wood; a_r, allocation to roots; s_f, leaf turnover rate. a_r is defined as $\mathrm{1}-a_{\mathrm{f}}-a_{\mathrm{w}}$.

The dynamics of the four carbon pools are described by four difference equations:

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{\mathrm{C}}_{\mathrm{n}}=\text{GPP}-R_{\mathrm{m}}\left({\mathrm{C}}_{\mathrm{t},\mathrm{f}}+{\mathrm{C}}_{\mathrm{t},\mathrm{w}}+{\mathrm{C}}_{\mathrm{t},\mathrm{r}}\right)-k{\mathrm{C}}_{\mathrm{n}},\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{\mathrm{C}}_{\mathrm{s},\mathrm{f}}=k{\mathrm{C}}_{\mathrm{n}}\left(\mathrm{1}-Y\right)a_{\mathrm{f}}-s_{\mathrm{f}}{\mathrm{C}}_{\mathrm{s},\mathrm{f}},\text{(6)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{\mathrm{C}}_{\mathrm{s},\mathrm{w}}=k{\mathrm{C}}_{\mathrm{n}}\left(\mathrm{1}-Y\right)a_{\mathrm{w}},\text{(7)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{\mathrm{C}}_{\mathrm{s},\mathrm{r}}=k{\mathrm{C}}_{\mathrm{n}}\left(\mathrm{1}-Y\right)a_{\mathrm{r}},\end{array}$$

where GPP is the gross primary production ($\mathrm{g}\mathrm{C}{\mathrm{plant}}^{-\mathrm{1}}{\mathrm{day}}^{-\mathrm{1}}$); R_m is the maintenance respiration rate ($\mathrm{g}\mathrm{C}{\mathrm{g}}^{-\mathrm{1}}\mathrm{C}{\mathrm{day}}^{-\mathrm{1}}$); C_t,f, C_t,w and C_t,r are the total C in foliage, wood and root, respectively (g C plant⁻¹); k is the storage utilization coefficient ($\mathrm{g}\mathrm{C}{\mathrm{g}}^{-\mathrm{1}}\mathrm{C}{\mathrm{day}}^{-\mathrm{1}}$); Y is the growth respiration fraction; a_f, a_w and a_r are the allocation to foliage, wood and root, respectively; and s_f is the leaf turnover rate ($\mathrm{g}\mathrm{C}{\mathrm{g}}^{-\mathrm{1}}\mathrm{C}{\mathrm{day}}^{-\mathrm{1}}$). a_r is defined as $\mathrm{1}-a_{\mathrm{f}}-a_{\mathrm{w}}$.

The nonstructural (storage) C pool (C_n) is assumed to be divided amongst foliage, wood and root tissues (C_n,f, C_n,w, C_n,r) according to an empirically determined ratio of 75 : 16 : 9. Total carbon in each tissue (C_t) is then calculated as the sum of nonstructural carbon (C_n) and structural carbon (C_s) for that tissue.

$$\begin{array}{}\text{(8)}& {\displaystyle }& {\displaystyle }{\mathrm{C}}_{\mathrm{t},\mathrm{f}}=\mathrm{0.75}\times {\mathrm{C}}_{\mathrm{n}}+{\mathrm{C}}_{\mathrm{s},\mathrm{f}}\text{(9)}& {\displaystyle }& {\displaystyle }{\mathrm{C}}_{\mathrm{t},\mathrm{w}}=\mathrm{0.16}\times {\mathrm{C}}_{\mathrm{n}}+{\mathrm{C}}_{\mathrm{s},\mathrm{w}}\text{(10)}& {\displaystyle }& {\displaystyle }{\mathrm{C}}_{\mathrm{t},\mathrm{r}}=\mathrm{0.09}\times {\mathrm{C}}_{\mathrm{n}}+{\mathrm{C}}_{\mathrm{s},\mathrm{r}}\end{array}$$

Table 1 Summary of the three model simulation sets.

2.4 Application of data assimilation (DA) algorithm

DA was used to estimate the six parameters (k, Y, a_f, a_w, a_r, s_f) of the CBM for this experiment. All parameters were allowed to vary quadratically with time; i.e., each parameter was represented as

$$\begin{array}{}\text{(11)}& p=p_{\mathrm{1}}+p_{\mathrm{2}}t+p_{\mathrm{3}}{t}^{\mathrm{2}}.\end{array}$$

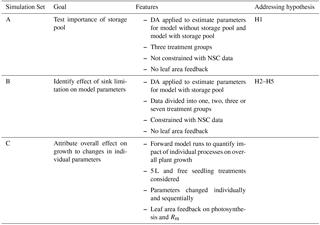
Quadratic variation over time was found to yield significantly better model fits than either constant parameter values or linear variation over time (see Supplement Sect. S1). We executed three distinct sets of model simulations (Table 1), with the goals of (1) testing the need for a storage pool; (2) determining the effect of sink limitation on model parameters; and (3) attributing the overall effect of sink limitation on growth to the change in individual parameters.

For each set of model simulations, GPP and R_m were used as inputs to the DA framework, and the measurements of the total C mass of each of the plant components and foliage NSC concentrations were used to constrain the parameter values. The set of constraints included 18 measurements of C_t,f and C_t,w, two measurements of C_t,r (start and end of the experiment) and six measurements of foliage NSC. There were 5 quadratically varying parameters to determine for each treatment, summing to a total of 15 (3×5) coefficients to determine, compared with total 44 data measurements available, for each treatment.

We used the Metropolis algorithm (Metropolis et al., 1953) as implemented by Zobitz et al. (2011), with broad prior probability density functions (PDFs) for the parameters (Table 2). Values of k, a_f, a_r and s_f were allowed to vary within the maximum possible range, while parameter Y was constrained according to the literature on growth respiration (Villar and Merino, 2001). Parameter a_r was calculated from a_f and a_w with a check on a_r to ensure that it had reasonable values ($\mathrm{0}<a_{\mathrm{r}}<\mathrm{1}$). Standard error (SE) was used as an estimate of uncertainty on the assimilated data (Rowland et al., 2014; Richardson et al., 2010) and was calculated based on six replicate measurements. When combining errors, the errors were assumed to be uncorrelated (Hughes and Hase, 2010).

Model parameters were assumed to be real, positive and to have a lognormal probability distribution (Rowland et al., 2014). Therefore, all processes of parameter selection and the acceptance and rejection of parameters in relation to prior ranges were performed in lognormal space (Knorr and Kattge, 2005). We performed the first iteration starting from the prior set of parameters. To generate subsequent values for each parameter, a new point was generated by varying all vector elements by some step chosen with a Gaussian-distributed random number generator having a mean of 0 and an SD of 0.005 in lognormal space. We adjusted the step length for each parameter to values that lead to an average acceptance rate of the new points of around 35–40 %. We confirmed the chain convergence, having 3000 iterations to adequately explore the posterior parameter space, by visual inspection of the trace plots of different parameters as suggested by Van Oijen (2008). The trace plots show how the chain moves through parameter space for each individual parameter. The parameter vectors sampled during the first phase of the chain were not representative and therefore the first 10 % of the chain was discarded from the posterior sample.

Table 2 Prior parameter PDFs (with uniform distribution) and the starting point of the iteration for all parameters.

2.4.1 Importance of storage pool

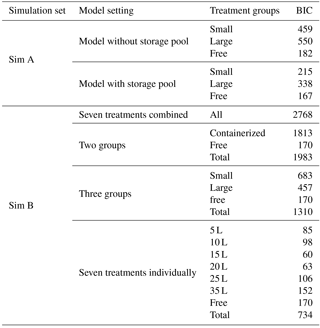
We tested the hypothesis (H1) on the importance of including a nonstructural C storage pool in CBM by contrasting fits of the full model with fits of a simplified model without the nonstructural C pool (Simulation Set A, Table 1). The simplified model omits the nonstructural C pool (C_s) from the full model (Fig. 1) and assumes that all available C is utilized for growth each day. We applied the DA framework to both model options and calculated the Bayesian information criterion (BIC; Schwarz, 1978) to determine the better model structure. BIC measures how well the model predicts the data based on a likelihood function and compares model performance taking into account the number of fitted parameters, with the lowest BIC number indicating the best model setting. For this comparison, both models were fit to the biomass data only, not leaf NSC data, in order to ensure that both models were fit to the same number of data points.

2.4.2 Effects of sink limitation on model parameters

The effects of sink limitation on C balance were investigated by applying the DA framework to data from all treatments combined and then subsets of treatments (Simulation Set B, Table 1). Considering all treatments pooled together gives the same parameters for all the treatments and effectively assumes no effect of sink limitation. On the other hand, taking more subsets of treatments produces more parameter sets (one for each subset) and allows for parameters to vary according to the degree of sink limitation. We first fitted the model to all data ignoring treatment differences, then considered two treatment groups (free seedling/5–35 L containerized seedlings), three groups (free/5–15/20–35 L) and four groups (free/5–10/15–20/25–35 L). We also fitted the model to each of the seven treatments individually, with the parameter set for each treatment being unique. The BIC values were compared across treatment groupings.

2.4.3 Attribution analysis

We performed a sensitivity analysis to quantify the impact of the response of each individual process to sink limitation on overall plant growth (Simulation Set C, Table 1). This analysis consisted of forward runs of the model, including a leaf area feedback to GPP. That is, rather than taking GPP based on measured LA (Eq. 9) as input, in this version of the model we calculated daily GPP using the modeled LA, the photosynthesis rate and corresponding self-shading factor. Adding the LA feedback to the model was necessary to quantify how the treatment effect on individual model parameters affects final seedling biomass through its effect on foliage mass, and consequently GPP, over time.

LA in each time step is estimated from NSC-free specific leaf area (SLA_nonsc) and the predicted foliage structural carbon (C_s,f) in that time step. SLA_nonsc is calculated at harvest, discarding the foliage NSC portion, and is assumed to be constant for a given treatment throughout the experiment.

$$\begin{array}{}\text{(12)}& \text{LA}={\text{SLA}}_{\mathrm{nonsc}}\times {\mathrm{C}}_{\mathrm{s},\mathrm{f}}\end{array}$$

Once the LA feedback was implemented in the CBM, we ran the model with the inputs and modeled parameters from the smallest pot seedling (5 L), then changed the parameters to those for the free seedling sequentially in order to quantify the effect of each parameter on the final seedling biomass. The parameters we considered for this attribution analysis were daily photosynthetic rate per unit leaf area (C_day), maintenance respiration rate (R_m), C allocation fractions to biomass (a_f, a_w, a_r), growth respiration rate (Y), foliage turnover rate (s_f) and utilization coefficient (k). We additionally carried out a sensitivity analysis in which we varied each parameter from its baseline value separately.

3 Results

3.1 Importance of storage pool

First, we tested the null hypothesis (H1) that there is no need for a nonstructural carbohydrate storage pool in the carbon balance model. We compared BIC values for model structures with and without a storage pool. Table 3 (Simulation Set A) shows the results for model fits with the optimal grouping strategy (three treatment groups). BIC values were consistently lower for the model including the storage pool; the improvement in model fit is most noticeable for the containerized seedlings. This analysis demonstrates that the model does need to include a storage pool to correctly represent the experimental data. In all remaining analyses, the full CBM (with nonstructural C pool) is applied to data from all four plant C pools (NSC, foliage, wood and root biomass).

Table 3 BIC values from model fits. The lowest BIC values indicate the best performing parameter settings for any particular simulation. Note that for Sim A, leaf NSC data were not used to constrain either model to ensure that both models were fit to the same dataset, resulting in lower BICs compared to Sim B. Treatment groups are as follows: “small” – 5, 10 and 15 L containers; “large” – 20, 25 and 25 L containers; “free” – freely rooted seedlings; “All” – all data; “containerized” – all plants in containers.

3.2 Sink limitation effect on C balance processes

We addressed our second null hypothesis (H2) that there is no effect of sink limitation on carbon balance processes by comparing BIC values obtained for model fits when all treatments were combined vs. separating the treatments into subgroups. If there was no effect of sink limitation, the BIC value when all treatments are fit together would be similar to that obtained when treatments are separated into groups. The BIC values shown in Table 3 (Simulation Set B) decrease strongly as the number of treatment groups increases, indicating a clear effect of sink limitation on carbon balance processes. Although the BIC values continue to decrease as more treatment groups are considered, we also found that interpreting parameter changes became more difficult as the number of groups increased. Hence, further analyses in this paper used unique parameter sets for three treatment groups: small containers, large containers and free seedlings.

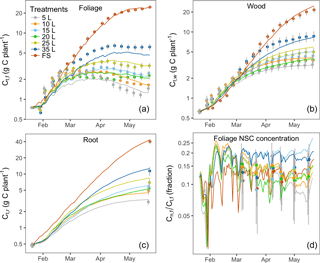
Figure 2 C stocks (lines) with the inferred parameter set and corresponding observations (symbols): (a) total C mass in foliage C_t,f, (b) total C mass in wood C_t,w, (c) total C mass in root C_t,r and (d) foliage NSC concentration (C_n,f ∕ C_t,f). Note that the carbon pools and foliage NSC concentration (y axes) are plotted on log scale to visualize the changes at the beginning of the experiment. Error bars (1 SE, n=6) are shown for each observation.

3.3 Analysis of carbon stock dynamics

Figure 2 shows the correspondence between modeled C pools and data. The model reproduced the key features of biomass growth over time in response to treatment. Biomass growth (Fig. 2a, b and c) and the foliage storage pool (Fig. 2d) were very clearly impacted by sink limitation: biomass growth was strongly reduced for containerized seedlings, which was very well mimicked by the model. Foliage growth in the free seedlings slowed towards the end of the experiment. Wood and root growth continued throughout the experiment in freely rooted seedlings but slowed down during the second half of the experiment in containerized seedlings. NSC concentrations (C_n,f ∕ C_t,f) in seedlings in small containers were higher compared those in free seedlings at the beginning of the season but all treatments had similar concentrations after 4 months (Fig. 2d). In March, at the time of the first leaf NSC measurements, the foliage storage pool (Supplement Fig. S1) was similar in size across all treatments, but it increased over time in the free seedlings as these plants continued to grow and decreased over time in the plants in small containers.

Modeled C stocks for all seven treatments closely tracked their corresponding observations (Fig. 2) as most of the predicted biomass values were within 1 standard error of the measurements. The exception is the 35 L container treatment, which is underestimated slightly because the grouping of 20, 25 and 35 L treatments into one group makes it difficult for the model to fit all treatments in this group.

3.4 Parameter estimates

Data assimilation indicated significant treatment effects on all five fitted parameters (Fig. 3). There was a large effect of sink limitation on the utilization coefficient (k). In agreement with our hypothesis H3, the free seedlings had the highest k, and the seedlings in small containers (most sink limited) had the lowest k (Fig. 3a). As the experiment progressed, the utilization rate of free seedlings began to decrease (Fig. 3a). In contrast to the free seedlings, the potted seedlings had relatively low utilization rates initially (k close to 0.5) and the utilization rates slowed down abruptly with time, most significantly in the smallest container treatments (Fig. 3a).

In agreement with hypothesis H4, the estimated growth respiration rate (Y) varied according to the sink strength of the treatment groups and was highest in the lowest sink strength treatments (Fig. 3b). Moreover, Y did not vary significantly over time for the sink-limited treatment groups. However, the rate of growth respiration for the free seedlings slowed down over time.

The data assimilation process also indicated that the growth allocation fractions vary among treatments and over time. Consistent with hypothesis H5, the wood allocation fraction was highest in the smallest container treatments and lowest in the free seedlings (Fig. 3d). For the free seedlings, allocation was initially highest to foliage and roots (Fig. 3c–e); over time, the plants reduced allocation to foliage and increased it to wood and roots. In the containerized seedlings, allocation was initially highest to wood and foliage; over time, foliage allocation decreased to almost zero and root allocation increased.

The estimated leaf turnover rate, s_f, was also notably higher for sink-limited treatments compared to free seedlings (Fig. 3f). The large value of modeled leaf litterfall for sink-limited treatments is consistent with observations during the experiment that containerized seedlings had relatively large leaf litterfall, beyond normal senescence. Estimated s_f increased over time for all treatment groups (most notably in free seedlings) due to a combination of ontogeny, seasonal change and growth restriction in the sink-limited seedlings.

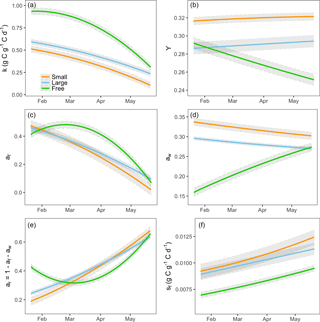
Figure 3 Modeled final parameters for three groups of treatments during the experiment period (21 January to 21 May 2013): (a) storage utilization coefficient, k; (b) growth respiration fraction, Y; (c) allocation to foliage, a_f; (d) allocation to wood, a_w; (e) allocation to roots, a_r; and (f) leaf turnover rate, s_f. a_r is defined as $\mathrm{1}-a_{\mathrm{f}}-a_{\mathrm{w}}$. The gray shaded area shows the 95 % confidence intervals of modeled parameters.

3.5 Carbon budget

The model was used to partition total GPP (g C plant⁻¹) from the entire experiment period into different C pools (growth respiration, maintenance respiration, nonstructural carbon, structural foliage, wood and root carbon, and litterfall) for all seven treatments (Fig. 4). Total GPP was considerably lower for the containerized seedlings, owing to lower photosynthetic rates per unit leaf area, C_day (Fig. 5a), and lower total leaf area (LA) per plant. Though starting with the same total LA of 0.016 m², the 5 L containerized and free seedlings had total LA of 0.031 and 0.516 m², respectively, after 4 months of treatment. Simultaneously, the partitioning of GPP changed considerably across different treatments.

Small container seedlings (5, 10, 15 L) had a higher fraction of GPP lost in leaf litterfall compared to other seedlings (Fig. 4), consistent with observations during the experiment. The proportion of GPP in final foliage mass was extremely low in sink-limited treatments (also shown in Fig. 2a). The allocation of GPP to final foliage and root biomass was highest in the free seedlings, although interestingly allocation to final wood biomass was similar across treatments. The final allocation to storage was also higher in free seedlings. The sink-limited seedlings had a higher proportional C lost through maintenance respiration. Tissue-specific respiration rates were similar in free and containerized seedlings, so the ∼ 35 % reduction in photosynthetic rate for the smallest containerized seedlings led to a higher overall R_m,tot ∕ GPP fraction. In summary, the estimated total respiration ($R_{\mathrm{m},\mathrm{tot}}+R_{\mathrm{g}}$) to GPP ratio was considerably lower for the free seedlings compared to the sink-limited treatments. The carbon use efficiency (CUE) remained relatively constant and high over time for free seedlings (∼ 0.65), whereas CUE in the smallest container treatments showed a sharp reduction over time down to ∼ 0.25 (Supplement Fig. S2).

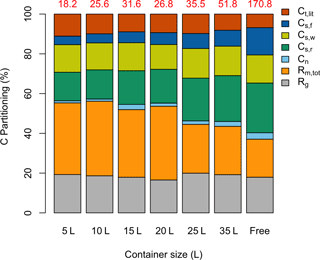
Figure 4 Simulated proportional C partitioning for the whole experimental period. The total accumulated GPP (g C plant⁻¹) for individual treatments is shown (in red) at the top of each column. “Free” stands for free seedling. Different C partitions are in the color legend: total litterfall, C_t,lit; foliage structural C, C_s,f; wood structural C, C_s,w; root structural C, C_s,r; nonstructural C pool, C_n; total maintenance respiration, R_m,tot; and growth respiration, R_g.

3.6 Attribution analysis

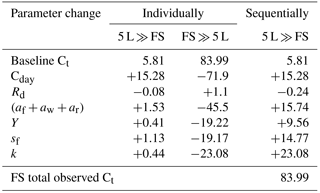
Sink limitation affected biomass growth via a range of processes, namely reduction in photosynthesis and variation in the utilization rate, growth respiration, leaf litterfall and C allocations to foliage, wood and root across various treatment groups. We quantified the contribution of each of these process responses separately by running the CBM with parameter inputs changing both sequentially and individually (one at a time). Table 4 presents the effect of the parameters changing individually from the value of the smallest container treatment (5 L) to that of free seedlings (FS) and the other way around, resetting the previous parameter to the baseline value. The final biomass values in Table 4 indicate the contribution of each individual parameter separately and sequentially. Photosynthetic capacity had the largest individual effect on total plant growth (+15.28 and −71.9 g C) compared to the rest of the parameters. However, the allocation pattern and utilization rate also had a sizeable effect on final biomass (Table 4).

Figure 5 shows how biomass (M_f, M_w and M_r) is predicted to change when each parameter is changed sequentially from the parameter set derived from DA on the 5 L observations (gray line, Fig. 5) to that of the parameters obtained when using the free seedlings as a constraint of the model (red line, Fig. 5). Daily net C assimilation per unit leaf area (C_day), which was 30 % higher for free seedlings compared to the 5 L container treatment (Fig. 5a), had a large impact on plant growth (final total biomass was increased by 11 g; Table 4 and Fig. 5g–i, gray to orange). Maintenance respiration rate (R_m) did not vary significantly across treatments (Fig. 5b), in line with the data presented in Campany et al. (2017), and consequently its impact was insignificant (the final total biomass is reduced by only 0.24 g; Table 4 and Fig. 5g–i, orange to light blue). The modeled biomass allocation fractions (a_f, a_w and a_r) in Fig. 5c had important but mixed effects on C stocks. The final foliage mass was increased from 3.4 to 9.6 g due to the increase in C allocation to foliage (Fig. 5g, light blue to green), which has a positive feedback on GPP. Concomitant changes in C allocation to wood and root resulted in smaller changes to these biomasses as shown in Fig. 5h–i (2.5 and 7.0 g rise, respectively). Overall, the change in allocation pattern resulted in an increase in final total biomass by 15.74 g (Table 4). Growth respiration rate (Y) was ∼ 20 % lower in free seedlings (Fig. 5d), which had a considerable impact on C budgets (the final total biomasses were increased by 9.56 g; Table 4 and green to yellow Fig. 5g–i). Leaf turnover, s_f, was low in the free seedlings compared to the 5 L container treatment (Fig. 5e), which had a large positive effect on final C pools (Fig. 5g–i, yellow to blue). The foliage mass was increased by 5.6 g; the wood and root masses were also further increased (3.4 and 5.8 g, respectively) due to the increase in GPP when foliage is retained for longer. Finally, the utilization coefficient, k, was higher in free seedlings (Fig. 5f), causing a 20–30 % positive feedback on C budgets (total biomass increased by 23.08 g; Table 4 and Fig. 5g–i, blue to red).

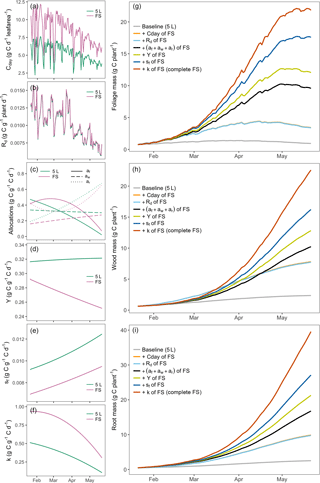
Figure 5 Attribution analysis. Left column (a–f): changes in inferred parameters. Right column (g–i): associated impacts on C budgets due to sequential parameter changes from 5 L container treatment to that of free seedlings (right column, g–i). Different colors in the figure indicate the parameter shifts (left column, a–f) and their associated impacts on C budgets (right column, g–i). Legend: 5 L, highly sink-limited treatment with a container size of 5 L; FS, free seedlings without any sink limitation. Note that the orange line is overlain by the light blue line; the small change in maintenance respiration results in a very minor effect on biomass growth.

Table 4 Estimates of final biomass due to parameter change (individual and sequential), showing the contribution of each parameter separately and successively to biomass changes. All values in g C plant⁻¹. +/− indicates biomass increase or decrease due to particular parameter change. The final column corresponds to the changes shown in Fig. 5.

4 Discussion

4.1 Effects of sink limitation on C balance

Our DA model analysis of this root volume restriction experiment provided significant new insights into the response of key C balance processes to sink limitation. We were able to infer that, in addition to a reduction in photosynthetic rates, sink limitation reduced NSC utilization rates, increased growth respiration, modified allocation patterns and enhanced senescence. Our attribution analysis indicated that all of these process responses contributed significantly to the overall reduction in biomass observed under low rooting volume.

We first tested the null hypothesis (H1) that seedling growth rates could be adequately predicted from current-day photosynthate. This hypothesis was rejected, with a storage pool being necessary to simulate growth, particularly for containerized seedlings (Sim A, Table 3). The approach of simulating growth from current-day photosynthate is commonly used in models, particularly for evergreen plants (e.g., Jain and Yang, 2005; Law et al., 2006; Thornton et al., 2007), but several authors have proposed the need for a storage pool to balance the C sources and sinks in the short term, as well as to simulate the effects of photosynthetic downregulation in the long term (Pugh et al., 2016; Richardson et al., 2013; Fatichi et al., 2016). Our results support the need for an NSC pool in CBMs.

We then tested the second null hypothesis (H2) that there was no effect of treatment on the parameters of the C balance model. This hypothesis was also rejected: fitting the DA model framework simultaneously to all treatments with one set of parameters (ignoring sink limitation effect) gave a low goodness of fit (Sim B, Table 1). This result is consistent with the finding of Campany et al. (2017) that the observed effects of sink limitation on photosynthesis in this experiment were insufficient to explain the large reduction in biomass. Instantaneous photosynthetic rates were reduced 20–30 % by sink limitation. Our DA analysis indicated that several other processes contributed to the reduction in biomass growth, including carbohydrate utilization, growth respiration, allocation patterns and turnover.

Our results suggested a significant effect of sink limitation on the carbohydrate utilization rate, k (Fig. 3a). The modeled k values were approximately twice as large in free seedlings compared to the small containers. This result supports the hypothesis (H3) that plants would have the lowest utilization rate under sink-limited conditions. At the start of the measurement period, the free seedlings were utilizing almost all C produced immediately in growth (k close to 1.0; Fig. 3a). The utilization coefficient of the free seedlings decreased over time, causing a buildup in C storage (Fig. 2d). This decrease in utilization rate could potentially be an ontogenetic effect, with free seedlings initially allocating all carbon to growth during establishment but increasing storage with increasing size. However, ontogenetic effects are confounded with season in this experiment, such that decreasing utilization rates over time could also be a result of decreasing temperatures moving into autumn. There is a real need to quantify how the carbohydrate utilization rate varies with environmental conditions and ontogeny; data assimilation of experiments in which photosynthesis and growth rates have been monitored over time offer one means to do so.

Although the carbohydrate utilization rate was highest in the free seedlings, leaf carbohydrate concentrations were not lower in these plants at the end of the experiment. As shown in the final C budget analysis (Fig. 4), there was a higher total C allocation to the NSC pool in free seedlings than sink-limited treatments. Final carbohydrate storage was high in free seedlings despite high k because the carbohydrate pool was recharged throughout the experiment (Fig. 2d), as the free seedlings had high photosynthetic rates but no higher maintenance respiration requirement. In contrast, NSC was depleted for the smallest pot treatments after mid-March (Fig. 2d) when demand exceeded supply due to both the limited production of photoassimilates and enhanced leaf litterfall (Fig. 3f).

The modeled rate for growth respiration, Y, was larger for sink-limited treatments than the free seedlings (Fig. 3b). Overall, there was lower C utilization (i.e., CUE) in plant structural growth in sink-limited treatments (∼ 45 %) compared to free seedlings (∼ 60 %). This finding supports the “wasteful plant” hypothesis H4. Inferred Y remained constant over time for the containerized treatments, implying a fixed portion of C loss due to growth respiration despite seasonal variation. However, a reduction in Y over time was inferred for the free seedlings, suggesting a possible ontogenetic effect. However, it is important to note that we have inferred growth respiration from the CBM framework. Therefore, these estimates could possibly also include C losses via other pathways. Direct measurements of growth respiration rates would be useful to confirm the inferred effects of sink limitation and investigate potential underlying mechanisms.

We also demonstrated that the allocation fractions among organs change in sink-limited conditions, with sizeable consequences for plant growth rates. Previous analyses of pot-size experiments have generally only been able to estimate changes in final biomass partitioning (e.g., Poorter et al., 2012a). Campany et al. (2017) analyzed final biomass partitioning in the experiment and did not find any significant difference in biomass partitioning in sink-limited seedlings compared to free seedlings once ontogenetic drift was taken into account. Our analysis adds to that of Campany et al. (2017) by calculating the dynamics of allocation over time and taking estimated foliage loss into account. Our analysis showed that modeled allocation fractions vary significantly over time (Fig. 3c, d and e). In the free seedlings, allocation to foliage decreased, and allocation to both wood and roots increased, reflecting the ontogenetic effects mentioned by Campany et al. (2017). However, our analysis also highlights significant variations among treatments in the modeled C allocation fractions to foliage, wood and root that are not ontogenetic. At the beginning of the experiment, foliage allocation fractions were similar for all treatment groups, but wood allocation was higher and root allocation lower in the containerized seedlings compared to the free seedlings. For the containerized seedlings, changes over time also differed from those in the free seedlings: wood allocation decreased marginally rather than increasing, foliage allocation declined steeply over time and root allocation increased steeply. These allocation patterns in seedlings supported our hypothesis H5 that sink limitation due to root restriction would favor allocation to wood over foliage or fine roots. Calculating dynamic allocation patterns over the course of an experiment thus provides additional insights beyond analysis of the final biomass outcome.

4.2 Application of DA to infer C balance processes

We have demonstrated that the DA approach can be an invaluable tool for quantifying C fluxes in experimental systems, enabling us to extract important new information from existing datasets to inform carbon balance models, such as the rate and timing of the transfer of photosynthate to and from storage pools. The DA-modeling approach is able to draw together the experimental data to estimate all the components of C balance, including photosynthesis, respiration, NSC, biomass partitioning and turnover. This approach could readily be applied to other experiments to derive new information, allowing for a better representation of C balance processes in vegetation models.

Applying this approach requires a range of measurements to constrain the key C balance processes. Here, we used estimated daily C assimilation and maintenance respiration rate as model inputs and constrained the model with measurements of biomass pools (foliage, wood, root) and foliage NSC concentrations. We used fortnightly foliage and wood biomass measurements; the DA framework would work with fewer data observations, but parameters would be estimated with less accuracy. Informal exploration of the model suggested that measurements of foliage turnover would have been particularly useful to better constrain the model. Any experiment having estimates of GPP, maintenance respiration and structural biomass could potentially be investigated with this framework. However, additional measurements of storage and turnover would be highly beneficial for the performance of the simulation. Repeated observations over time are also useful, particularly for young plants, to account for variations in parameter values over time. We found significant changes in parameter values during the course of the 4-month experiment, which may be linked to both ontogeny and seasonal variation in temperature.

One major caveat to our results is that belowground carbon cycling processes were not well characterized. For practical reasons, processes such as root growth, respiration, turnover and exudation are rarely well quantified in empirical studies. Here, we had access to initial and final estimates of root biomass. Root respiration was estimated; root turnover and exudation were assumed to be zero. There is evidence that stress can increase rates of root exudation: for example, Karst et al. (2017) demonstrate increased exudation rates in seedlings exposed to cold soils. They also showed that stressed plants may exude C beyond that predicted by simple concentration gradients in NSC between root and soil. The loss of C independent of NSC in roots suggests that exudation may be actively enhanced once plant growth is limited (Hamilton et al., 2008; Karst et al., 2017). As our CBM does not include this process, it would attribute any C loss through root exudation to another process removing C from the plant, such as growth respiration. The increase in growth respiration that we inferred may thus potentially include root exudation. We have reasonable confidence, from the combination of measurements available, in our inference that the C loss term was increased with sink limitation. However, direct measurements of one or both processes would be required to determine the role of root exudation.

In addition, we did not have access to estimates of root or wood NSC. We used data measured in a previous experiment on 4-month-old E. globulus seedlings (Duan et al., 2013) to estimate these values from foliage NSC. It would have been useful to obtain these values, particularly since wood and root tissue can act as storage organs, and the timing of storage development would be extremely useful to quantify. The concentration of NSC in plant roots measured by Duan et al. (2013) was relatively small compared to that of foliage (mean 2.15 %). However, fine root NSC values in a nearby experiment on 17-month-old E. parramattensis saplings were even lower (0.78 %; Morgan E. Furze et al., unpublished data, 2016). It is possible that these very fast-growing eucalypt species only start to accumulate root reserves when they are established. Further research is needed to quantify the trade-off between allocation to growth and storage during establishment.

4.3 Implications for modeling plant growth under sink-limited conditions

The goal of our study was to examine how carbon balance models should be modified to represent the sink limitation of growth while maintaining mass balance. Our results demonstrate that several process representations need to be modified. Firstly, we demonstrate a clear need to incorporate a carbohydrate storage pool with a dynamic utilization rate for growth. We demonstrate that the utilization rate is slowed by sink limitation and may also vary with ontogeny. Targeted experimental work is needed to better quantify this variation in utilization rates. Secondly, in addition to a feedback on photosynthetic rates, other plant processes including growth respiration, turnover and allocation are also affected by sink limitation. Applying a DA-modeling framework to experimental data with rooting volume restriction has allowed us to quantify these effects in this experiment. Applying this approach more broadly would potentially allow us to identify general patterns that could then be formulated for inclusion into models.

The inferences on carbohydrate dynamics from seedling studies could be used to infer mature tree responses that can subsequently be integrated at ecosystem level and beyond using the concepts of Hartmann et al. (2018). We are enthusiastic to see the approach applied to other experiments, but there are likely to be gaps in the datasets to constrain the key C balance processes. Fortunately, the DA approach does not require continuous measurements of all of the C stocks and fluxes. In the absence of measurements, the model can be relied upon to project the time evolution of missing stocks and fluxes, although of course the precision of model estimates and insights that can be gained increases with data availability. DA can also be applied at ecosystem scale. There are several successful examples of DA being applied to forest growth, albeit without a focus on storage (e.g., Van Oijen, 2008; Williams et al., 2005; Bloom et al., 2016; Quaife et al., 2008; Pinnington et al., 2016). Overall, this approach provides important insights into the regulation of carbohydrate storage and would significantly advance our ability to predict the impacts of environmental changes on plant growth and vulnerability to stress.