the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Carbon exchange in an Amazon forest: from hours to years
Marcos Longo
Marielle N. Smith
Natalia Restrepo-Coupe
Raphael Tapajós
Rodrigo da Silva
David R. Fitzjarrald
Plinio B. Camargo
Lucy R. Hutyra
Luciana F. Alves
Bruce Daube
J. William Munger
Kenia T. Wiedemann
Scott R. Saleska
Steven C. Wofsy
In Amazon forests, the relative contributions of climate, phenology, and disturbance to net ecosystem exchange of carbon (NEE) are not well understood. To partition influences across various timescales, we use a statistical model to represent eddy-covariance-derived NEE in an evergreen eastern Amazon forest as a constant response to changing meteorology and phenology throughout a decade. Our best fit model represented hourly NEE variations as changes due to sunlight, while seasonal variations arose from phenology influencing photosynthesis and from rainfall influencing ecosystem respiration, where phenology was asynchronous with dry-season onset. We compared annual model residuals with biometric forest surveys to estimate impacts of drought disturbance. We found that our simple model represented hourly and monthly variations in NEE well (R2=0.81 and 0.59, respectively). Modeled phenology explained 1 % of hourly and 26 % of monthly variations in observed NEE, whereas the remaining modeled variability was due to changes in meteorology. We did not find evidence to support the common assumption that the forest phenology was seasonally light- or water-triggered. Our model simulated annual NEE well, with the exception of 2002, the first year of our data record, which contained 1.2 MgC ha−1 of residual net emissions, because photosynthesis was anomalously low. Because a severe drought occurred in 1998, we hypothesized that this drought caused a persistent, multi-year depression of photosynthesis. Our results suggest drought can have lasting impacts on photosynthesis, possibly via partial damage to still-living trees.
- Article
(6075 KB) - Full-text XML
-
Supplement
(197 KB) - BibTeX
- EndNote
The Amazon's tropical forests are pivotal to global climate, exchanging large, globally important quantities of energy and matter, including atmospheric carbon (Betts et al., 2004). Amazon forests contain 10 %–20 % of Earth's biomass carbon (Houghton et al., 2001). Increased emissions of the forest's carbon can therefore accelerate climate change, and attention is now focused on how vulnerable this large reservoir of carbon will be to a potentially drier future climate (de Almeida Castanho et al., 2016; Farrior et al., 2015; Duffy et al., 2015; Longo et al., 2018; McDowell et al., 2018). Characterizing the response of present-day Amazon rain forest carbon balance to climate and drought disturbance is a necessary step to improving predictions of future vulnerability.
Eddy covariance CO2 flux measurements are a powerful tool for quantifying net ecosystem exchange of carbon (NEE) (Baldocchi, 2003). NEE is the difference between uptake from gross ecosystem productivity (GEP) and emission from ecosystem respiration (RE). The magnitudes of these gross fluxes are influenced both by exogenous environmental conditions such as light, moisture, and temperature (Collatz et al., 1991; Bolker et al., 1998; Fatichi et al., 2014; Kiew et al., 2018) and by endogenous biophysical properties such as canopy structure, phenology, and community composition (Barford et al., 2001; Melillo et al., 2002; Dunn et al., 2007; Doughty and Goulden, 2008; Stark et al., 2012; Frey et al., 2013; Morton et al., 2016; Wu et al., 2016).
Partitioning the exogenous and endogenous influences upon eddy covariance NEE is possible using statistical modeling (Barford et al., 2001; Yadav et al., 2010; Wu et al., 2017). To partition influences upon NEE in a 20-year eddy flux record in a temperate New England forest, Urbanski et al. (2007) used a statistical modeling approach: by representing hourly NEE merely as response to exogenous meteorology and annually integrating their results, they concluded that meteorology did not explain the accelerated uptake seen in annually integrated NEE. They hypothesized that residual uptake was due to long-term forest regrowth and succession, a hypothesis that was corroborated by biometric measurements of increasing canopy foliage and accelerating mid-successional tree biomass accrual. This novel partitioning framework for NEE has not previously been applied to any tropical forest, in part because long-term eddy covariance coverage of tropical forests is lacking (Zscheischler et al., 2017). A simple statistical framework may allow tropical forest CO2 flux measurements to better inform model development and improvement.
On seasonal timescales, tropical evergreen forests undergo endogenous changes in GEP via the phenology of leaf flush and abscission (Doughty and Goulden, 2008; Restrepo-Coupe et al., 2013; Wu et al., 2016). The seasonal dependency of productivity has motivated the development of rooting depth and phenology sub-models in dynamic global vegetation models (DVGMs) (Verbeeck et al., 2011; De Weirdt et al., 2012; Kim et al., 2012). These sub-models have led to complexity in the modeled mechanisms controlling the GEP seasonal cycle without necessarily improving accuracy. It is necessary to quantify the magnitude and timing of phenology's effect on the GEP seasonal cycle after accounting for the integrated hourly response to sunlight.
On interannual to decadal timescales, endogenous changes in forest NEE can arise from disturbance and recovery (Nelson et al., 1994; Moorcroft et al., 2001; Chambers et al., 2013; Espírito-Santo et al., 2014; Anderegg et al., 2015). The km67 eddy flux site in the Tapajós National Forest (TNF) presents a unique opportunity to study the potential legacy of disturbance caused by drought. This eastern Brazilian Amazon forest lies on the dry end of the rainfall spectrum for tropical evergreen forests (Saleska et al., 2003; Hutyra et al., 2005). A severe El Niño drought in 1997–1998 was followed by disturbance, evidenced by a large and heavily respiring coarse woody debris (CWD) pool in 2001. Subsequent NEE measurements showed a 4-year transition from being a net carbon source in 2002 to nearly carbon-neutral in 2004 and 2005 (Hutyra et al., 2007). The observed disequilibrium state led researchers to the hypothesis that RE was high but dissipating and that the forest will continue to transition into equilibrium, becoming a sink throughout the decade (Pyle et al., 2008). Conversely, this hypothesis implies that any new disturbance should drive the forest back into disequilibrium, becoming a source again. We test these predictions using meteorological records; forest inventories of aboveground biomass (AGB) and CWD; and an additional 3.5 years of eddy flux data, resumed after a 2.5-year interruption, collected since prior studies.
In this study, we test hypotheses related to controls of NEE on multiple timescales at an eastern Amazon rain forest. Specifically, we seek to answer the following questions: (1) what were the effects of exogenous meteorology upon NEE across hourly to yearly timescales? (2) What is the seasonal effect of canopy phenology upon NEE? Is phenology synchronized with wet/dry seasonality? (3) Major basin-wide droughts occurred in 1998 before eddy flux measurements began, and they were reported again in 2005 and 2010 (Zeng et al., 2008; Philips et al., 2009; Lewis et al., 2011; Doughty et al., 2015) during the span of measurements. Did any of these basin-wide droughts affect the TNF in particular? What was the impact of drought upon interannual variability and the decadal trend in NEE? Furthermore, which NEE component, GEP or RE, was perturbed most by drought? Overall, we statistically partitioned the multiple influences on NEE across timescales from hours to an entire decade of eddy flux and forest inventory measurements.
2.1 Site description
The Tapajós National Forest (TNF) is located to the southeast of the convergence of the Tapajós and Amazon rivers in Pará, Brazil. The forest site is on the dry end of the spectrum of evergreen tropical forests, receiving 1918 mm of annual rainfall and experiencing a 5-month-long dry season from July 15 to December 14, defined by average monthly precipitation of less than 100 mm (Hutyra et al., 2007). Temperature and humidity average 25 ∘C and 85 %, respectively (Rice et al., 2004). The forest has a closed canopy with a height of roughly 40 m (Stark et al., 2012) and emergent trees up to 55 m (Rice et al., 2004). The forest has fast turnover rates, with much of the population consisting of small-diameter trees (Pyle et al., 2008) but many larger trunks, an uneven age distribution, many epiphytes, and emergent trees; the forest may be considered primary or “old growth” (Goulden et al., 2004). Soils are predominantly nutrient-poor clay oxisols with some sandy utisols (Rice et al., 2004), both of which have low organic content and cation exchange capacity. The forest terrain is 75 m upland on a plateau adjacent to the nearby Tapajós River, with a deep water table accessed by roots sometimes more than 12 m deep (Hutyra et al., 2007). The flux tower that provided flux and meteorological data is located near km 67 of the Santarém–Cuiabá highway. The tower and site are designated by site ID “BR-Sa1” in the FLUXNET data system but are herein referred to simply as “km67”.
2.2 Eddy covariance measurements
Hourly fluxes of NEE were calculated using the sum of hourly turbulent eddy fluxes plus the hourly change in height-weighted average CO2 concentration in the canopy air column (Saleska et al., 2015). Our measurements covered two contiguous periods: one from January 2002 to January 2006 (period 1) and another from July 2008 to December 2011 (period 2). The tower fell in January 2006 when a tree snapped a supporting guy-wire. Measurements resumed in July of 2008 when the tower was rebuilt and equipment repaired. Measurements ceased again in 2012 when electrical failures damaged measurement and calibration systems. Some data collection has resumed since 2015, although gaps in these data were much larger than those in periods 1 and 2, precluding calculating annual carbon balance after 2011.
2.3 Flux data processing, quality control, and gap filling
Nighttime NEE measurements were filtered for low turbulence. We used a turbulence threshold filter of to ensure consistency with previous studies (Saleska et al., 2003; Hutyra et al., 2008). The absolute magnitude of nighttime respiration and resulting carbon balance was highly sensitive to the selection of (Saleska et al, 2003; Miller et al., 2004). However, the interannual variability and trend remained the same regardless of the choice of (Saleska et al., 2003). Errors in total annual NEE therefore do not reflect potentially large error and should be interpreted as errors in the differences between years, not errors in the annual magnitude of the carbon source/sink. Coverage of hourly NEE was substantial for both periods in the total eddy covariance record. After quality control and outlier detection, period 1 (2002–2006) had 80 % and period 2 (mid 2008–2011) had 75 % data coverage for all hours. Filtering for u∗ below the threshold of 0.22 m s−1 left 48 % and 42 % coverage of period 1 and 2, respectively.
We used established gap-filling models to obtain annual NEE totals. Gross ecosystem productivity (GEP) was gap-filled using a hyperbolic fit curve between GEP and photosynthetically active radiation (PAR) (Waring et al., 1995). For RE, we adapted the method by Hutyra et al. (2007), who calculated missing, filtered, and daytime hours using 50 u∗-filtered nighttime hour bins; we used a running average of 50 u∗-filtered nighttime hours, allowing us to capture the onset of semiannual seasonal transitions in RE. Consistent with other tropical forest sites, temperature was not used in our gap filling, because temperature variability at tropical forests is low, which results in weak and insignificant correlations with RE (Carswell et al., 2002). We calculated annual errors as 95 % bootstrap confidence intervals by resampling similar hours with replacement (NEE conditions for the same month, time of day, and similar PAR conditions), instead of resampling all hourly NEE, so that resampling did not capture diurnal and long-term nonstationary.
2.4 Meteorological measurements
Meteorological variables measured at km67 included PAR, temperature, and specific humidity. Downward drifts in PAR data due to a degrading sensor were corrected by de-trending a time series of midday PAR observations in the top 95th percentile of each month (Longo, 2014). This threshold included substantial information about the sunniest hours, throughout which intensity should remain constant between years for any given month. We scaled the radiation time series using the proportion between the fitted trend and the initial fitted value. Simultaneous total incoming shortwave-radiation measurements allowed us to partially fill missing periods of PAR data using a relationship derived from linear regression in simultaneously measured hours (R2=0.98).
Rainfall measurements were greatly underestimated at this site because of a faulty tipping bucket rain gauge. We discarded site-based data and calculated a distance-weighted synthetic hourly rainfall time series from a network of nearby meteorological stations, with locations ranging from 10 to 110 km away from km67. More information on the meteorological network is available in Fitzjarrald et al. (2008). Detailed information about the subsequent calculations of the synthetic precipitation data set and PAR drift correction are available in Longo (2014).
Additionally, the Brazil National Institute of Meteorology (INMET) has a station at Belterra, located 25 km away from km67, with daily precipitation totals dating back to 1971, which were used to corroborate the seasonal and long-term trends at km67. Correlation between these two monthly data sets for the years 2001–2012 was R2=0.88. Altogether there were three data sets: the local tower-based meteorology, the mesoscale network meteorology data interpolated to km67, and the INMET meteorology. Further information regarding the robustness of these three data sets, and correlations amongst them, can be found in Longo (2014). The three data sets provided us with at least two redundant estimates for all meteorological variables at km67.
2.5 Coarse woody debris and mortality
To assess how disturbance coincided with changes in NEE, we conducted surveys of coarse woody debris (CWD). These surveys capture the magnitude and dynamics of the respiring pool of dead tree biomass. Transect subplots were surveyed in 2001 for pieces greater than 10 cm in diameter (Rice et al., 2004). Bootstrapped confidence intervals were quantified by resampling subplot totals (n=321) with replacement. Additionally, in 2006, pieces only greater than 30 cm in diameter were surveyed. Lastly, we conducted an additional CWD survey in 2012 using the line-intercept method (Van Wagner, 1968) throughout all transects for a total length of 4 km to minimize sampling uncertainty. Bootstrap confidence intervals were quantified by resampling line segment totals (n=40) with replacement. These two different methodologies have previously produced consistent simultaneous results within measurement uncertainties, which were 20 % larger for line-intercept sampling than plot-based sampling (Rice et al., 2004).
Because CWD surveys were conducted infrequently, we inferred mortality from aboveground biometry surveys in 1999, 2001, 2005, 2008, 2009, 2010, and 2011. Trees larger than 10 cm diameter at breast height were surveyed and were converted to biomass using non-species-specific equations (Chambers et al., 2001a) based on sampling previously established protocols for this site (Rice et al., 2004; Pyle et al., 2008). Mortality biomass was inferred by tallying biomass of dead trees that were alive in the prior survey. Sometimes, trees were missed by the census surveyors before they could be confirmed dead or were found again. In 2012 we assigned missing trees that were not later found alive an equal probability of dying in all surveyed years in which they had been missing (Longo, 2014). We used tree mortality to model CWD over time using a simple box model with a first-order rate equation:
where M is the mortality rate input to the CWD pool (MgC ha−1 yr−1) and k is the decay loss rate of 0.124 yr−1. The loss rate is derived from measurements of respiring CWD in Manaus, Amazonas (Chambers et al., 2001b), and snag density measurements taken at km67 (Rice et al., 2004). The box model initial condition was the 2001 survey of total CWD. This model allowed us to assess whether disturbances after 2001 were sufficient to cause an increase in CWD or whether disturbances after 2001 were minimal and the CWD pool respired and depleted gradually. The final time step of the model was validated against the second and final full measurement of CWD made in 2012.
2.6 Empirical NEE model
Our low-parameter empirical model represents the mean response of NEE to hourly and seasonal changes in exogenous meteorology and seasonal changes in phenology throughout the decade. We used our model to diagnose interannual nonstationarity in model residuals, which correspond to endogenous ecosystem changes in photosynthesis and respiration rates between years, give or take random measurement error and unaccounted for model terms. We fit the model to the entire 7.5-year interrupted eddy covariance record of raw, u∗-filtered hourly NEE (NEEobs):
where NEEModel is the modeled hourly NEE. The models were fit in two steps: first, the two model parameters that represent RE, a0 and a1, were fit to nighttime data; then the remaining three GEP parameters were fit to daytime data. Parameter a0 is the wet-season intercept for RE. Parameter a1 is an adjustment of the ecosystem respiration during the rainfall-defined dry season (factor variable sR, defined in detail below). Parameters a2 and a3 are the Michaelis–Menten light response parameters. We also include a simple scaling factor for endogenous changes in phenology: a time-varying binary factor variable spheno represents timing in changes to the intrinsic light use efficiency (LUE ) within an average seasonal cycle. The purpose of this simplistic scaling factor was to determine when the timing of endogenous seasonal shifts in LUE that were not explained by light and moisture were most pronounced.
Atmospheric moisture and diffuse radiation, in addition to radiation, are also known to affect photosynthesis at tropical sites on short timescales (Kiew et al., 2018), by affecting stomatal closure and hence controlling the degree to which photosynthetic uptake saturates at high PAR. We tested a higher-parameter model based on a light and moisture model representing exogenous changes to LUE from Wu et al. (2017) to examine whether these meteorological variables added explanatory power to our model at monthly and longer timescales. This model adjusts LUE by multiplying terms that account for effects of vapor pressure deficit (VPD: 1−kVPD) and cloudiness index (CI: ), a statistical proxy for diffuse radiation. To determine whether this model was parsimonious, we evaluated the Bayesian information criteria (BIC) of the data–model mean monthly residuals for the model in Eq. (2) and the higher-parameter light and moisture model. We found that the higher-parameter model was not parsimonious because the additional parameters did not improve the goodness of fit at monthly timescales. We explain these results further in Sect. 3.4.2 and discuss their implications further in Sect. 4.1 and 4.2.
This forest site has coincident deficits in rainfall and ecosystem RE during the dry season (Saleska et al., 2003; Goulden et al., 2004) due to desiccation of dead wood, leaf litter, and other substrates for heterotrophic respiration (Hutyra et al., 2008). To depict this reduced dry-season RE, we set dry-season sR≡1 and wet-season sR≡0, fitting a1 to the mean dry-season RE. We defined the dry-season onset as the period during which rainfall is below 50 mm per half-month, consistent with previous definitions of tropical forest dry season as 100 mm month−1 (e.g. Saleska et al., 2016). We defined the wet-season onset as the first in a series of three or more semi-monthly periods with rainfall greater than 50 mm; this definition allows for sporadic dry-season downpour while ensuring that there is not more than one dry season per year. Although a1 does not vary across years, our meteorologically defined sR permits the duration of the dry season to vary interannually. A longer dry season in a given year would therefore result in less RE (more net uptake) when NEEExo is integrated over that full year.
We tested three different seasonal timings for the phenology factor variable: (1) spheno≡0 year-round (no phenology), (2) spheno≡1 during the dry season and spheno≡0 during the wet season, and (3) spheno≡1 during the peak of leaf flush (15 June to 14 September) (Hutyra et al., 2007) and spheno≡0 all other times of the year. In scenario 2, the timing of phenology varies interannually, but in scenarios 1 and 3, modeled phenology does not differ between years and therefore does not influence interannual variability in modeled GEP or NEE.
After subtracting hourly NEEModel from NEEobs, the annually integrated residuals reflect changes in the ecosystem's efficiency irrespective of the aggregate response to meteorology, plus or minus random error and unaccounted-for meteorological controls. Upper-level soil moisture, for instance, exerts seasonal controls upon NEE at various tropical sites differently depending on terrain (Hayek et al., 2018; Kiew et al., 2018) but is not included in the model because it was insignificantly associated with GEP (Wu et al., 2017) or RE at this site after we controlled for other variables, including wet- and dry-season onset, in our model. Examples of a change in intrinsic ecosystem efficiency may occur in the aftermath of a drought – during which leaf stomates close, causing the ecosystem to sequester less CO2 per unit incident PAR than average – or a storm inducing widespread mortality and a pulse of CWD during which RE would be higher than average for a given season or year. In both scenarios, we would expect residuals to be positive during or after the event, because the ecosystem would sequester less and emit more CO2 relative to other years. To assess which aggregated annual residuals were significantly different from zero, we quantified 95 % confidence intervals in annual NEE residuals due to random error using bootstrapping (Sect. 2.3).
We partitioned both NEEobs and NEEModel into RE and GEE (gross ecosystem exchange) (GEE = −GEP, to keep the same sign convention as eddy flux NEE) to determine which of the two components was more adequately represented by our model. For observations of NEE, RE, and GEE, we used hours during which a direct u∗-filtered measurement of NEE occurred. Observations of RE are nighttime hours during which NEE was measured; observations of GEE are daytime hours during which the 50 h running average RE was subtracted from measured NEE. Partitioned GEE is not a direct observation but represents the lowest-parameter approximation of a direct measurement (GEE = NEE − RE; see Wu et al., 2017). Our GEE and RE results are limited by not accounting for partitioning bias.
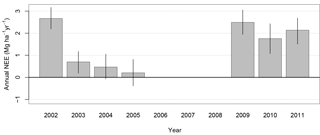
Figure 1Annual sums of NEE in kg ha−1 yr−1. Error bars are 95 % confidence intervals. Positive values indicate a source of CO2 to the atmosphere. Net emission of carbon to the atmosphere during every year in the time series was possibly due to choice of (Fig. S2 for annual NEE time series derived from an alternative choice of flux bias correction).
3.1 Eddy covariance measurements of CO2 fluxes
NEE has a large diurnal cycle relative to its mean seasonal cycle, with a mean diel range of 25.05 µmol m−2 s−1. The range of the mean seasonal cycle is 2.46 µmol m−2 s−1, or 10 % of the mean diel range. Annual totals of NEE are presented in Fig. 1. For period 1, the first 4 years, annual NEE is similar to that reported previously by Hutyra et al. (2007), despite using slightly modified gap-filling procedures here (Sect. 2.3). The previously reported trend remains: a moderate source in 2002 of 2.7 MgC ha−1 yr−1 (±0.595 % bootstrap confidence intervals) tapering off to nearly carbon-neutral totals in the following years, within confidence limits of 0.5 (±0.6) MgC ha−1 yr−1 in 2004 and 0.2 (±0.6) MgC ha−1 yr−1 in 2005. During the three subsequent years that comprise period 2, 2009–2011, the forest returned to being a moderate source of carbon, with a range of 1.8±0.6 MgC ha−1 yr−1 in 2010 to 2.5±0.5 MgC ha−1 yr−1 in 2009. We examined measurements of rainfall, CWD, and AGB for indications of drought or other disturbance during 2002–2011 to explain these patterns seen in annual NEE totals.
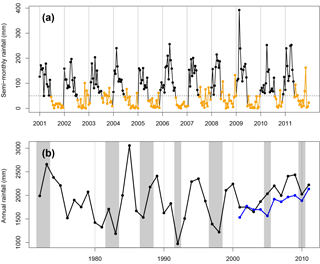
Figure 2(a) Semi-monthly dry-season rainfall totals for wet season (black) and dry season (orange). Hourly rainfall was estimated by objective analysis (Eq. 1) from meteorology stations near 67 km. The horizontal dashed line shows the dry-season threshold of 50 mm per half-month. (b) Yearly totals of rainfall from Belterra INMET station (black), 25 km away from km67, and km67 rainfall estimated by objective analysis (blue). Recent El Niño anomalies (gray shaded areas) coincide with droughts in the 1990s but not in the 2000s (blue points) at this site, when annual rainfall was within the long-term historical variability.
3.2 Meteorological measurements and drought
We examined our distance-weighted interpolated estimate of km67 rainfall for trends and droughts. Our precipitation estimate was consistent with previous estimates of precipitation for this site and region, with a minimum of 1595 mm in 2005 and maximum of 2137 mm in 2011 (Saleska et al., 2003; Nepstad et al., 2007). While 2005 annual precipitation was a minimum, no previous groundwater deficits in carbon exchange, latent heat flux, or sensible heat fluxes were observed during this year (Hutyra et al, 2007). Our measurements did not indicate that any drought occurred during or immediately preceding period 2 of NEE measurements. In fact, period 2 annual rainfall totals increased on average by 20 % relative to period 1. The dry season in 2009 was longer than average, lasting 6 months (Fig. 2a). Mean annual radiation was expectedly anti-correlated with annual rainfall. Accordingly, period 2 experienced 4 % less mean annual PAR than period 1.
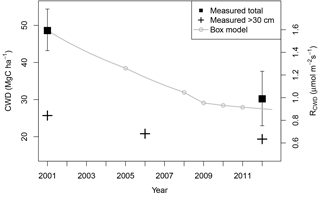
Figure 3Measurements of total CWD (black squares with 95 % bootstrapped CI error bars) and subsets of CWD ≥30 cm diameter (black crosses) show a decrease over time. CWD box model (gray line) also shows a gradual decrease in CWD over time. The initial condition is the 2001 measurement of CWD; the source is input from mortality inferred by biometry census (census times represented by gray circles), and the sink is an empirical respiration rate of 0.124 yr−1 (Pyle et al., 2008). Left axis shows the CWD respiration flux (RCWD), corresponding to the equivalent amount of CWD on the right axis.
Our synthetic decade-long rainfall record corresponded closely with the nearby INMET Belterra measurements, although INMET Belterra had on average 220 mm of rainfall more per year, likely due to differences in circulation and convection between the km67 forest and Belterra pasture land surface (Fitzjarrald et al., 2008). Annual rainfall totals throughout the decade of eddy flux measurements of 2002–2011 lay well within the historical variability of annual rainfall since 1972, which experienced a range of 974 to 3057 mm of annual precipitation (Fig. 2b). The second- and third-lowest annual precipitation totals (1391 and 1218 mm, respectively) occurred during 1997–1998, during a major El Niño event, which persisted from June of 1997 to June of 1998 (Ross et al., 1998) and corresponded with a 9-month-long dry season, the longest in the historical record.
3.3 Coarse woody debris and mortality
We examined measurements of CWD over time to assess whether a disturbance might have impacted the period 2 carbon balance. Compared to CWD stocks in 2001 of 48.6 (±5.9) MgC ha−1, CWD stocks in 2012 were significantly lower at 30.5 MgC ha−1 (±7.4) (Fig. 3). Errors in the 2012 pool were 25 % larger. The larger magnitude of error is consistent with higher uncertainty for line-intercept sampling relative to area-based sampling at the TNF (Rice et al., 2004). Because CWD measurements were sparse in time, we included an additional measurement in 2006 of large CWD, with a diameter greater than or equal to 30 cm, totaling 20.8±12.8 MgC ha−1. We compared this measurement with similarly sized CWD from other surveys (Fig. 3). Total large CWD was 25.7±11.4 MgC ha−1 in 2001 and 19.8±11.9 MgC ha−1 in 2012. Differences in large CWD between 2001 and 2006 and between 2006 and 2012 are small relative to their uncertainties, but they still show a qualitative downward trend over time.
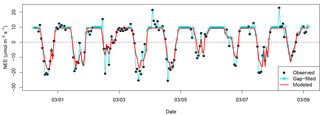
Figure 4Example time series of NEEobs and NEEModel for 9 days of the wet season in 2008. Pearson correlation coefficient between NEEobs and NEEModel is R=0.90 over the entire 7.5-year time series.
Table 1Model parameter values (95 % confidence intervals in parentheses) and R2 fit. Parameters have the following units: a0, a1, and a2: µmol CO2 m−2 s−1; a3: µmol photons m−2 s−1; kpheno: unitless.

A box model of CWD (Eq. 2) allowed us to estimate the transient behavior of the CWD pool throughout years in which it was not directly measured (Fig. 3). The CWD mortality input rates M were derived from forest inventory surveys. The box model shows no large spikes from mortality events outweighing the respiration rate, and its derivative is negative throughout time, predicting a continuously depleting CWD pool. The box model estimate for 2012 CWD is 26.2 MgC ha−1 and lies well within the uncertainty of the concurrent 2012 measurement. We see no evidence via increased CWD that disturbance has occurred since the start of measurements.
Assuming that the large initial CWD pool arose from a past disturbance, hypothetically following the 1997–1998 El Niño drought, we ran the CWD box model (Eq. 2) backward in time to estimate the magnitude of such a disturbance. We assumed that the disturbance occurred in 1998 because 1999 and 2000 were not characterized by below-average rainfall. Severe drought events have been accompanied by increased mortality and canopy turnover rates in intact Amazon forests (Leitold et al., 2018). Because the CWD measurement was made in July of 2001, we calculated the box model CWD value to the end of the El Niño drought in June 1998 using the same respiration rate, k, and the mean mortality, M, for all surveys, and we applied this rate to the mean and 95 % bootstrapped confidence intervals of the 2001 measurement (48.6±5.9 MgC ha−1). Our estimate of the CWD pool immediately following the drought was thus 63.7±8.1 MgC ha−1. Subtracting the 2012 measurement of 30.2±7.3 MgC ha−1 from this number, which is our best estimate of equilibrium CWD that may have existed before the 1997–1998 El Niño drought, we estimate drought-induced mortality to be 33.5±15.4 MgC ha−1, or 12 %–31 % of present AGB.
3.4 Empirical NEE Model
3.4.1 Hourly variability in NEE
Optimized parameter values for our model are included in Table 1. Our model predicted 81 % of the variance in observed hourly NEE and captured 94 % of the amplitude of the diurnal cycle. The only hourly independent variable in the model was PAR; hourly NEE in our model was therefore predominantly driven by changes in sunlight. Modeled hourly variability frequently captured the difference in magnitude in NEE between high- and low-uptake events (example time series shown in Fig. 4).
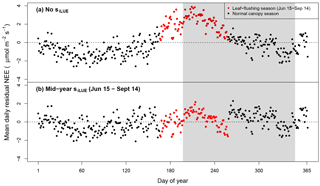
Figure 5Mean daily data–model residuals averaged over all 7.5 years: (a) lacks an adjustment for phenological change in LUE. Leaf-flush period only partially overlaps the dry season (gray shaded area). (b) The best-fitting parameterization of the model contained a midyear phenology scaling factor (; Table 2), which was asynchronous with the dry season (red points).
3.4.2 Seasonal variability in NEE
In our best-fitting model parameterization, phenology was asynchronous with the dry season (Table 2). Over the mean seasonal cycle, removing this seasonal phenology parameterization resulted in positive residual NEE from 15 June to 14 September, hence overpredicting uptake during this time (Fig. 5a). Our final model, however, simplistically corrects for this positive anomaly, adjusting NEE by 16 % (Fig. 5b; Table 2). Although this seasonal transition appears to be more gradual over the season, our simplistic, low-parameter phenology representation was chosen for parsimony. While the seasonal timing of respiration, sR, varied by meteorological inputs (semi-monthly total rainfall < 50 mm), we could not identify a similar seasonal meteorological trigger for phenology and therefore used set calendar dates.
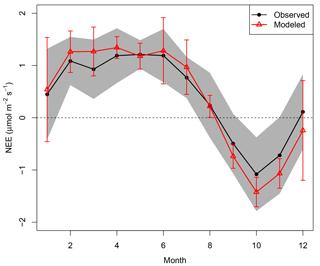
Figure 6Mean seasonal cycle of NEEobs (black dots) and NEEModel (red triangles). Gray shaded areas are standard deviations of interannual variability for the mean NEEobs for each respective month. Error bars are standard deviations of the interannual variability in monthly mean NEEModel.
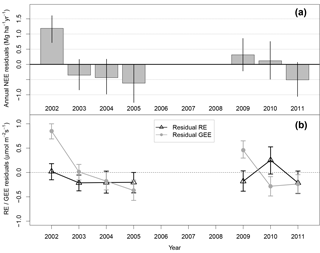
Figure 7(a) Annually summed model residuals. Error bars are 95 % bootstrapped confidence intervals. Annual residual NEE in 2002 is statistically different from 0 within random NEE measurement error; all other years are not. (b) Residuals of model representation of partitioned GEE (gray circles) and RE (black triangles).
Our model predicted monthly mean NEE well (R2=0.59 across all months). Hourly changes in PAR were integrated over monthly and seasonal time periods. Therefore, seasonal variability in our model was controlled by precipitation, sunlight, and a simplistic parametric representation of phenology (Eq. 2; Table 1).
Part of the remaining seasonal variability was explained by random measurement error: 95 % bootstrap confidence intervals representing hourly measurement errors in monthly mean NEE had an average range of 1.07 µmol m−2 s−1, 47 % of the mean NEE seasonal cycle's range. The model slightly overpredicted the mean seasonal cycle's magnitude, albeit well within the model and measurement interannual variability (Fig. 6). The model attributed the greatest sink to October, because (1) October rainfall was low enough each year to be classified as part of the dry season; (2) PAR was consistently high due to sunny conditions after the dry-season onset; and (3) the phenology scaling factor () returned to 1 after 14 September, increasing the October LUE and pushing the carbon balance further towards a sink.
A higher-parameter model with VPD and diffuse radiation from Wu et al. (2017) explained additional variance in hourly NEE but not in monthly NEE (Table S1 in the Supplement). The BIC score for this model (−31.4) was greater (more negative) than that from our main model (−35.6; Eq. 2), because it did not improve the goodness of fit but contained additional parameters. The BIC results imply that VPD and diffuse radiation do not explain significant additional variance relative to our model (Eq. 2) at monthly and greater timescales.
3.4.3 Interannual variability in NEE
Hourly changes in PAR and seasonal changes in precipitation were integrated annually to determine yearly sums of modeled NEE. Therefore, interannual variability was controlled by precipitation and sunlight. Phenology did not vary interannually; therefore it did not affect interannual variability in modeled NEE.
We disaggregated the meteorological influence on NEE, represented by our model (Eq. 2), from long-term changes in forests' ecological efficiency by examining the annually integrated hourly model residuals. In 2002, there was a total of 1.2 MgC ha−1yr−1 of excess emissions unaccounted for by the modeled mean response to meteorology (Fig. 7a). The correlation between modeled and measured yearly NEE was low and insignificant (R2=0.17; p = 0.37) owing to the 2002 anomaly; if 2002 is excluded as an outlier, the correlation is high and significant (R2=0.81; p = 0.014). All other years were not significantly different from zero within random measurement error, represented by 95 % bootstrap confidence intervals, indicating that these years are well predicted by meteorological variability, including the relatively higher emission/lower uptake in period 2 (Fig. 1).
On average, period 2 saw a 20 % increase in annual precipitation relative to period 1. Abbreviated dry-season lengths and lack of radiation from increased cloudiness in period 2 resulted in less modeled net uptake relative to period 1.
We partitioned observed and modeled NEE into RE and GEE. Interannual variations in RE were accurately represented as changes in wet- and dry-season length (Fig. S1 in the Supplement). The range in annual residual RE is therefore small compared to that of annual residual GEE (Fig. 7b). In 2002, mean model GEE had 0.85 µmol m−2 s−1 more uptake than observations. Therefore, the 1.2 MgC ha−1 yr−1 residual emissions in 2002 were more likely due to anomalously low photosynthesis rather than high RE.
4.1 Hourly and seasonal changes in NEE and implications for modeling phenology
Hourly changes in NEE were due predominantly to changes in sunlight (Fig. 4). Phenology only played a small role in modeled hourly variability, improving the fit of our model by only 1 % relative to a model that only used meteorology and lacked a phenology parameterization (Table 2).
Seasonal changes, on the other hand, were due to a combination of sunlight, rainfall inputs, and phenology (Fig. 6). The model parameterization contained a seasonal decrease in respiration (a1) that was synchronous with the dry season, a timing that was consistent with other tropical forest sites but can exert the opposite influence depending on terrain, drainage, and inundation (Kiew et al., 2018). A phenological LUE decrease in GEP (1−kpheno) was asynchronous with the dry season (Eq. 5; Table 2). Modeled phenology explained 26 % of the variability in observed monthly NEE (Table 2).
VPD and diffuse radiation do not explain significant additional variance in NEE relative to our model (Eq. 2) at monthly timescales (Tables 1, S1). The relative importance of phenology at monthly timescales, compared to that of VPD and diffuse radiation, is consistent with other findings regarding GEP at our research site: moving from finer to coarser temporal resolution, the influence of exogenous meteorology becomes outweighed by that of exogenous ecosystem changes such as those in phenology (Wu et al., 2017).
Seasonal changes in LUE are well explained by canopy leaf age and demography both at this site and at a comparatively wetter forest site in Manaus, showing good agreement with a model informed by camera and trap-based observations of leaf flushing and shedding (Wu et al., 2016). Our single midyear parameter simplistically upshifts the trough in a more continuous seasonal oscillation between low and high LUE (Fig. 5) because we lacked independent variables explaining the seasonal oscillation.
The seasonally asynchronous nature of phenology-mediated LUE establishes a middle ground in debates over whether the eastern Amazon canopy is enhanced or “greens up” during the dry season (Huete et al., 2006; Myneni et al, 2007; Samanta et al., 2012; Morton et al., 2014; Bi et al., 2015; Guan et al., 2015; Saleska et al., 2016). Changes to the canopy's LUE do indeed occur, but not synchronously with the dry season at our site (Fig. 5). Evidence from previous studies at the TNF suggests that changes in phenological LUE result from carbon allocation shifting from stem allocation to the turnover and production of new leaves (Goulden et al., 2004), supporting the prevailing hypothesis that tropical trees have been selected to coordinate new leaf production ahead of dry-season peaks of irradiance (Wright and van Schaik, 1994). The GEP seasonal cycles at additional evergreen Amazon forest sites are not well described by sunlight alone (Restrepo-Coupe et al., 2013). Averaging over seasonal windows is therefore likely to miss a potential inter-seasonal depletion and enhancement of canopy LUE if additional regions of evergreen Amazon forest similarly exhibit seasonally asynchronous phenology.
Interannual variation in phenology is represented mechanistically in phenology and LUE sub-models, which have been optimized using km67 eddy flux data but nonetheless fail to reproduce the observed midyear GEP decrease at this site. Kim et al. (2012) present a light-triggered phenology scheme, which assumes higher modeled leaf turnover rates and higher maximum leaf photosynthesis during the dry season, and hence produced higher dry-season GEP. Their model produced leaf-flushing rates that lagged behind observations and contradicted observations that light-controlled GEP decreases midyear at km67 (Fig. 5). Another phenology scheme has been developed by De Weirdt et al. (2012), which attributes excess leaf allocation to the turnover of new, more efficient leaves but nevertheless overpredicted midyear GEP at km67 relative to their prior model. Wu et al. (2016), on the other hand, successfully represent the GEP seasonal cycle using their model of leaf age and demography but relied on observations of canopy leaf fluxes. Their model, however, does not provide a meteorologically triggered mechanism for seasonal leaf shedding and flushing. Therefore, until such a trigger can be identified, models that mechanistically represent phenology are primed to make erroneous predictions about the interannual and long-term consequences of changing seasonal lengths for the Amazon carbon balance.
4.2 Interannual variability in NEE
Annual totals of measured NEE exhibited an unpredicted trend: despite previous hypotheses that the years after period 1 would continue to trend downward towards more uptake (Hutyra et al., 2007; Pyle et al., 2008), the ecosystem returned to a moderate carbon source in all 3 years of period 2 (Fig. 1). We examined whether the reversal of the period 1 trend throughout period 2 could be explained by exogenous changes in climate or an endogenous biophysical change. We developed the model selection framework to partition these two sources of variability.
Our model represented NEE well across a variety of timescales (Figs. 4, 5, 7). On yearly timescales, interannual differences in NEEModel were due to exogenous meteorology, as phenology did not vary interannually. The model predicted annual NEE accurately within 95 % confidence limits of random measurement error for 6 out of 7 years (Fig. 7a), including period 2, during which the forest returned to a carbon source (Fig. 1). The model representation of the period 2 source was due to lower radiation and higher rainfall relative to period 1, consistent with findings of light limitation in Amazon forests derived from satellite observations of climate and vegetation activity (Nemani et al., 2003).
The overall magnitude of the carbon source/sink, however, was highly sensitive to the choice of u∗ filter, consistent with previous findings (Saleska et al., 2003; Miller et al., 2004; Hayek et al., 2018). We therefore applied a novel correction to the long-term magnitude of NEE that is independent of the u∗ filter (Hayek et al., 2018), which indicated that the ecosystem may in fact be a slight sink but that the interannual variability, which our model represents, remained the same (Fig. S2). The overall magnitude of the carbon source/sink therefore does not affect our results concerning the variability between years. The least net uptake still occurred in 2002, from which NEE remained insignificantly different in 2009 and 2011.
We examined the possibility that a systematically high bias in 2002 PAR could result in an overprediction of 2002 GEP and erroneously cause a positive 2002 residual. We found that PAR was appropriately drift-corrected by corroboration with Rnet, which was not affected by drifts. Additionally, we note that rainfall was not atypical in 2002 relative to 2003–2005 (Fig. 2).
Additional meteorological variables such as the VPD and diffuse radiation did not appear to explain residual NEE in 2002. A model including these variables did not explain the positive NEE and GEE anomaly in 2002 (Fig. S3). The annual means of both VPD and CI in 2002 lay within their decadal range, making high VPD or low diffuse radiation an unlikely explanation for low photosynthetic uptake. These meteorological factors did not appear to significantly impact interannual changes in NEE, consistent with previous findings regarding GEP at this site (Wu et al., 2017).
We cannot rule out that the 2002 source may be a measurement artifact, caused for example by disturbance following tower construction. We note, however, that tower construction was completed almost a year before the measurements we used, with preliminary data collection occurring during 2001 (Saleska et al., 2003). We examine the possibility that 1998 drought-based disturbance impacted forest GEP through 2002 in Sect. 4.2.2.
4.2.1 Temporal and spatial heterogeneity of droughts
Our multiple records of meteorology adjacent to our research site (Fig. 2), which we used to inform our simple model of NEE, can also shed light on the larger discussion of recent droughts in the Amazon. Previous reports of 21st-century droughts in this region are inconsistent. For the 2010 Amazon drought, Lewis et al. (2011) show that water deficits were minimal in the eastern Amazon region, consistent with our findings. However, Doughty et al. (2015) report ubiquitous detrimental effects of the 2010 drought basin-wide, including a −3 MgC ha−1 GEP anomaly overlying the TNF. Our results contradict these findings: we did not find anomalously low water inputs, nor a concurrent GEP or NEE anomaly (Fig. 7b), in 2010. For the 2005 Amazon drought, Zeng et al. (2008) claim that tropical North Atlantic warming in the dry July–October quarter led to rainfall reductions everywhere in the Amazon, a result not borne out by our precipitation analysis. The two supposedly basin-wide droughts in 2005 and 2010 did not appear to affect the region in which this particular site lies. Measurements and empirical modeling of CWD over time support this finding because no interim disturbances were detected between 2001 and 2011 (Fig. 3). The spatial extent and severity with which a more recent 2015–2016 El Niño drought impacted Amazon forests, however, remains to be quantified.
4.2.2 Legacy impacts of drought on ecosystem function
Our model overpredicted photosynthetic uptake in 2002 but predicted RE well (Figs. 7b, S1), suggesting that a drought disturbance in 1998 persistently affected forest GEP, not RE, through 2002. These findings contradict a previously established hypothesis that legacy effects of a prior drought disturbance increased RE in 2002 via increased CWD respiration (RCWD) and related pathways of decomposition (Saleska et al., 2003; Rice et al, 2004; Hutyra et al., 2007; Pyle et al., 2008).
CWD measurements from the km67 site suggest that there was major disturbance before measurements of CO2 eddy fluxes began. Three years after the 1998 drought, there was a large pool of CWD (48.6 MgC ha−1 in 2001), implying that a drought-based disturbance had occurred in the past. By 2012, the CWD pool respired faster than it could accrue additional necromass from mortality (Fig. 3), implying that no additional impactful disturbance occurred at this site between 2002 and 2012. Although RCWD was in fact higher in 2002 than 2005, this difference accounted for only 0.2 µmol m−2 s−1 (Fig. 3) of respiration. Changes in RCWD therefore explain the small differences in annual RE (Fig. S1) but inadequately account for the full 1.3 µmol m−2 s−1 (2.4 MgC ha−1 yr−1) difference in NEE between these years (Figs. 1, 7).
Identifying the cause of the reduced 2002 GEP is beyond the scope of this statistical modeling study. It is possible that the 1997–1998 El Niño drought not only killed entire trees but also damaged living trees through hydraulic failure and partial limb death, affecting canopy photosynthesis for subsequent years. An analysis of over 1000 temperate forest census sites suggests that recovery of live tree biomass accumulation may be delayed by up to 4 years after drought (Anderegg et al., 2015). Following the 2005 and 2010 western droughts, findings from forest inventories (Brienen et al., 2015) and remote sensing (Saatchi et al., 2013) suggested that legacy effects from tropical forest droughts can also persist for 4 years or more. Drought cavitation due to xylem embolisms reduces hydraulic conductivity, leading to whole-tree mortality (Choat et al., 2012), initiating a classic disturbance-recovery scenario in which felled trees generate canopy gaps for early successional seedlings and saplings to immediately capitalize on newly available light, causing CO2 sources to approximately balance sinks (Chambers et al., 2004). However, cavitation is also known to cause branch dieback in still-living trees (Koch et al., 2004), reducing canopy foliage partially but not completely forfeiting light resources to the understory. Drought-induced limb diebacks therefore potentially prolong forest recovery relative to immediate disturbances such as windfall. We hypothesize that partial drought damage to surviving trees can persistently affect whole-forest photosynthesis. Our findings, that a 1997–1998 drought disturbance was followed by reduced photosynthesis in 2002, emphasize the need to better mechanistically understand multi-year legacy impacts following droughts in evergreen Amazon forests.
The decade-long record of eddy flux at km67 in the TNF demonstrated unpredicted trends in 7.5 years of measured NEE. Our simple, low-parameter empirical model could represent interannual differences in NEE as integrated continuous responses to changes in meteorology, with the exception of the first year, suggesting that increased moisture and decreased sunlight, not an interim disturbance, were responsible for the elevated period 2 carbon source. Although overall magnitude of the carbon source/sink was highly sensitive to the specific choice of u∗ filter, the interannual variability, which was predicted by the model, remained the same. Contrary to some reports, no major drought was apparent in concurrent rainfall records, nor was a major concurrent disturbance apparent in biometry surveys of this site from 2001 through 2011.
Our model represented a seasonal midyear decline in GEP. Our representation of phenology follows set calendar dates and cannot distinguish between various hypotheses concerning the environmental trigger for seasonal leaf shedding and flushing. DVGMs and other numerical simulation ecosystem models that represent phenology as a response to light-triggered leaf flushing or root water constraints do not tend to represent the seasonal cycle of GEP accurately and are therefore in danger of overpredicting the future response of photosynthesis to longer dry seasons resulting from climate change.
Our finding that reduced photosynthesis, not increased respiration, contributed to the high NEE source in 2002 modifies the previous hypothesis that the 1997–1998 El Niño drought disturbance affected NEE via respiration. Our findings support a corollary hypothesis that partial drought-induced damage to still-living trees can impact whole-ecosystem photosynthesis adversely for multiple years, which is consistent with findings from regional- and global-scale forest biometric studies (Anderegg et al., 2015; Brienen et al., 2015). In order to understand how drought disturbance uniquely impacts forest recovery, observational studies and plot-based manipulation experiments are needed in conjunction with models. Such future research is needed to determine the return times for droughts at which persistent forest biomass loss and collapse may occur.
The eddy flux data used in this study are available online via the Lawrence Berkeley National Laboratory (LBNL) AmeriFlux network database at http://ameriflux.lbl.gov/sites/siteinfo/BR-Sa1 (Saleska et al., 2015).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-15-4833-2018-supplement.
MNH and SCW designed the study. MNH performed the statistical analysis. ML and JW conducted post-processing of meteorology data. MNS, LFA, and PBC conducted forest biometric surveys and provided data. RT, RdS, and DRF provided auxiliary meteorological data. NRC, LRH, BD, JWM, KTW, SRS, and SWC conducted measurements and eddy covariance data pre-processing. All authors contributed to writing the manuscript.
The authors declare that they have no conflict of interest.
This work was supported by funding from a National Science Foundation
PIRE fellowship (OISE 0730305) and a US Department of Energy grant
(DE-SC0008311).
Edited by: Paul Stoy
Reviewed by: two anonymous referees
Anderegg, W. R. L., Schwalm, C., Biondi, F., Camarero, J. J., Koch, G., Litvak, M., Ogle, K., Shaw, J. D., Shevliakova, E., Williams, A. P., Wolf, A., Ziaco, E., and Pacala, S.: Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models, Science, 349, 528–532, https://doi.org/10.1126/science.aab1833, 2015.
Baldocchi, D. D.: Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future, Glob. Change Biol., 9, 479–492, https://doi.org/10.1046/j.1365-2486.2003.00629.x, 2003.
Barford, C. C., Wofsy, S. C., Goulden, M. L., Munger, J. W., Pyle, E. H., Urbanski, S. P., Hutyra, L., Saleska, S. R., Fitzjarrald, D., and Moore, K.: Factors Controlling Long- and Short-Term Sequestration of Atmospheric CO2 in a Mid-latitude Forest, Science, 294, 1688–1691, https://doi.org/10.1126/science.1062962, 2001.
Betts, R. A., Cox, P. M., Collins, M., Harris, P. P., Huntingford, C., and Jones, C. D.: The role of ecosystem-atmosphere interactions in simulated Amazonian precipitation decrease and forest dieback under global climate warming, Theor. Appl. Climatol., 78, 157–175, https://doi.org/10.1007/s00704-004-0050-y, 2004.
Bi, J., Knyazikhin, Y., Choi, S., Park, T., Barichivich, J., Ciais, P., Fu, R., Ganguly, S., Hall, F., Hilker, T., Huete, A., Jones, M., Kimball, J., Lyapustin, A. I., Mõttus, M., Nemani, R. R., Piao, S., Poulter, B., Saleska, S. R., Saatchi, S. S., Xu, L., Zhou, L., and Myneni, R. B.: Sunlight mediated seasonality in canopy structure and photosynthetic activity of Amazonian rainforests, Environ. Res. Lett., 10, 64014, https://doi.org/10.1088/1748-9326/10/6/064014, 2015.
Bolker, B. M., Pacala, S. W., and Parton, W. J.: Linear analysis of soil decomposition: Insights from the Century model, Ecol. Appl., 8, 425–439, https://doi.org/10.1890/1051-0761(1998)008[0425:LAOSDI]2.0.CO;2, 1998.
Brienen, R. J. W., Phillips, O. L., Feldpausch, T. R., Gloor, E., Baker, T. R., Lloyd, J., Lopez-Gonzalez, G., Monteagudo-Mendoza, A., Malhi, Y., Lewis, S. L., Vásquez Martinez, R., Alexiades, M., Álvarez Dávila, E., Alvarez-Loayza, P., Andrade, A., Aragão, L. E. O. C., Araujo-Murakami, A., Arets, E. J. M. M., Arroyo, L., Aymard C, G. A., Bánki, O. S., Baraloto, C., Barroso, J., Bonal, D., Boot, R. G. A., Camargo, J. L. C., Castilho, C. V, Chama, V., Chao, K. J., Chave, J., Comiskey, J. A., Cornejo Valverde, F., da Costa, L., de Oliveira, E. A., Di Fiore, A., Erwin, T. L., Fauset, S., Forsthofer, M., Galbraith, D. R., Grahame, E. S., Groot, N., Hérault, B., Higuchi, N., Honorio Coronado, E. N., Keeling, H., Killeen, T. J., Laurance, W. F., Laurance, S., Licona, J., Magnussen, W. E., Marimon, B. S., Marimon-Junior, B. H., Mendoza, C., Neill, D. A., Nogueira, E. M., Núñez, P., Pallqui Camacho, N. C., Parada, A., Pardo-Molina, G., Peacock, J., Peña-Claros, M., Pickavance, G. C., Pitman, N. C. A., Poorter, L., Prieto, A., Quesada, C. A., Ramírez, F., Ramírez-Angulo, H., Restrepo, Z., Roopsind, A., Rudas, A., Salomão, R. P., Schwarz, M., Silva, N., Silva-Espejo, J. E., Silveira, M., Stropp, J., Talbot, J., ter Steege, H., Teran-Aguilar, J., Terborgh, J., Thomas-Caesar, R., Toledo, M., Torello-Raventos, M., Umetsu, R. K., van der Heijden, G. M. F., van der Hout, P., Guimarães Vieira, I. C., Vieira, S. A., Vilanova, E., Vos, V. A., and Zagt, R. J.: Long-term decline of the Amazon carbon sink., Nature, 519, 344–348, https://doi.org/10.1038/nature14283, 2015.
Carswell, F. E., Costa, A. L., Palheta, M., Malhi, Y., Meir, P., Costa, J. D. P. R., Ruivo, M. D. L., Leal, L. D. S. M., Costa, J. M. N., Clement, R. J., and Grace, J.: Seasonality in CO2 and H2O flux at an eastern Amazonian rain forest, J. Geophys. Res.-Atmos., 107, 8076, https://doi.org/10.1029/2000JD000284, 2002.
Chambers, J. Q., Santos, J. Dos, Ribeiro, R. J., and Higuchi, N.: Tree damage, allometric relationships, and above-ground net primary production in central Amazon forest, Forest Ecol. Manag., 152, 73–84, https://doi.org/10.1016/S0378-1127(00)00591-0, 2001a.
Chambers, J. Q., Schimel, J. P., and Nobre, A. D.: Respiration from coarse wood litter in central Amazon forests, Biogeochemistry, 52, 115–131, https://doi.org/10.1023/A:1006473530673, 2001b.
Chambers, J. Q., Higuchi, N., Teixeira, L. M., dos Santos, J., Laurance, S. G., and Trumbore, S. E.: Response of tree biomass and wood litter to disturbance in a Central Amazon forest, Oecologia, 141, 596–611, https://doi.org/10.1007/s00442-004-1676-2, 2004.
Chambers, J. Q., Negron-Juarez, R. I., Marra, D. M., Di Vittorio, A., Tews, J., Roberts, D., Ribeiro, G. H. P. M., Trumbore, S. E., and Higuchi, N.: The steady-state mosaic of disturbance and succession across an old-growth Central Amazon forest landscape, P. Natl. Acad. Sci. USA, 110, 3949–3954, https://doi.org/10.1073/pnas.1202894110, 2013.
Choat, B., Jansen, S., Brodribb, T. J., Cochard, H., Delzon, S., Bhaskar, R., Bucci, S. J., Feild, T. S., Gleason, S. M., Hacke, U. G., Jacobsen, A. L., Lens, F., Maherali, H., Martínez-Vilalta, J., Mayr, S., Mencuccini, M., Mitchell, P. J., Nardini, A., Pittermann, J., Pratt, R. B., Sperry, J. S., Westoby, M., Wright, I. J., and Zanne, A. E.: Global convergence in the vulnerability of forests to drought, Nature, 491, 752–755, https://doi.org/10.1038/nature11688, 2012.
Collatz, G. J., Ball, J. T., Grivet, C., and Berry, J. A.: Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer, Agr. Forest Meteorol., 54, 107–136, https://doi.org/10.1016/0168-1923(91)90002-8, 1991.
de Almeida Castanho, A. D., Galbraith, D., Zhang, K., Coe, M. T., Costa, M. H., and Moorcroft, P.: Changing Amazon biomass and the role of atmospheric CO2 concentration, climate, and land use, Global Biogeochem. Cy., 30, 18–39, https://doi.org/10.1002/2015GB005135, 2016.
De Weirdt, M., Verbeeck, H., Maignan, F., Peylin, P., Poulter, B., Bonal, D., Ciais, P., and Steppe, K.: Seasonal leaf dynamics for tropical evergreen forests in a process-based global ecosystem model, Geosci. Model Dev., 5, 1091–1108, https://doi.org/10.5194/gmd-5-1091-2012, 2012.
Doughty, C. E. and Goulden, M. L.: Seasonal patterns of tropical forest leaf area index and CO2 exchange, J. Geophys. Res.-Biogeo., 113, G00B06, https://doi.org/10.1029/2007JG000590, 2008.
Doughty, C. E., Metcalfe, D. B., Girardin, C. A. J., Amézquita, F. F., Cabrera, D. G., Huasco, W. H., Silva-Espejo, J. E., Araujo-Murakami, A., da Costa, M. C., Rocha, W., Feldpausch, T. R., Mendoza, A. L. M., da Costa, A. C. L., Meir, P., Phillips, O. L., and Malhi, Y.: Drought impact on forest carbon dynamics and fluxes in Amazonia, Nature, 519, 78–82, https://doi.org/10.1038/nature14213, 2015.
Duffy, P. B., Brando, P., Asner, G. P., and Field, C. B.: Projections of future meteorological drought and wet periods in the Amazon, P. Natl. Acad. Sci. USA, 112, 13172–13177, https://doi.org/10.1073/pnas.1421010112, 2015.
Dunn, A. L., Barford, C. C., Wofsy, S. C., Goulden, M. L., and Daube, B. C.: A long-term record of carbon exchange in a boreal black spruce forest: means, responses to interannual variability, and decadal trends, Glob. Change Biol., 13, 577–590, https://doi.org/10.1111/j.1365-2486.2006.01221.x, 2007.
Espírito-Santo, F. D. B. B., Gloor, M., Keller, M., Malhi, Y., Saatchi, S., Nelson, B., Junior, R. C. O., Pereira, C., Lloyd, J., Frolking, S., Palace, M., Shimabukuro, Y. E., Duarte, V., Mendoza, A. M., López-González, G., Baker, T. R., Feldpausch, T. R., Brienen, R. J. W. W., Asner, G. P., Boyd, D. S., and Phillips, O. L.: Size and frequency of natural forest disturbances and the Amazon forest carbon balance, Nat. Commun., 5, 1–6, https://doi.org/10.1038/ncomms4434, 2014.
Farrior, C. E., Rodriguez-Iturbe, I., Dybzinski, R., Levin, S. A., and Pacala, S. W.: Decreased water limitation under elevated CO2 amplifies potential for forest carbon sinks, P. Natl. Acad. Sci. USA, 112, 7213–7218, https://doi.org/10.1073/pnas.1506262112, 2015.
Fatichi, S., Leuzinger, S., and Körner, C.: Moving beyond photosynthesis: from carbon source to sink-driven vegetation modeling, New Phytol., 201, 1086–1095, https://doi.org/10.1111/nph.12614, 2014.
Fitzjarrald, D. R., Sakai, R. K., Moraes, O. L. L., De Oliveira, R. C., Acevedo, O. C., Czikowsky, M. J., and Beldini, T.: Spatial and temporal rainfall variability near the amazon-tapajós confluence, J. Geophys. Res.-Biogeo., 114, G00B11, https://doi.org/10.1029/2007JG000596, 2008.
Frey, S. D., Lee, J., Melillo, J. M., and Six, J.: The temperature response of soil microbial efficiency and its feedback to climate, Nat. Clim. Change, 3, 395–398, https://doi.org/10.1038/nclimate1796, 2013.
Goulden, M. L., Miller, S. D., Da Rocha, H. R., Menton, M. C., De Freitas, H. C., E Silva Figueira, A. M., and Dias De Sousa, C. A.: Diel and seasonal patterns of tropical forest CO2 exchange, Ecol. Appl., 14, 42–54, https://doi.org/10.1890/02-6008, 2004.
Guan, K., Pan, M., Li, H., Wolf, A., Wu, J., Medvigy, D., Caylor, K. K., Sheffield, J., Wood, E. F., Malhi, Y., Liang, M., Kimball, J. S., Saleska, S. R., Berry, J., Joiner, J., and Lyapustin, A. I.: Photosynthetic seasonality of global tropical forests constrained by hydroclimate, Nat. Geosci., 8, 284–289, https://doi.org/10.1038/ngeo2382, 2015.
Hayek, M. N., Wehr, R., Longo, M., Hutyra, L. R., Wiedemann, K., Munger, J. W., Bonal, D., Saleska, S. R., Fitzjarrald, D. R., and Wofsy, S. C.: A novel correction for biases in forest eddy covariance carbon balance, Agr. Forest Meteorol., 250–251, 90–101, https://doi.org/10.1016/j.agrformet.2017.12.186, 2018.
Houghton, R. A., Lawrence, K. T., Hackler, J. L., and Brown, S.: The spatial distribution of forest biomass in the Brazilian Amazon: a comparison of estimates, Glob. Change Biol., 7, 731–746, https://doi.org/10.1046/j.1365-2486.2001.00426.x, 2001.
Huete, A. R., Didan, K., Shimabukuro, Y. E., Ratana, P., Saleska, S. R., Hutyra, L. R., Yang, W., Nemani, R. R., and Myneni, R.: Amazon rainforests green-up with sunlight in dry season, Geophys. Res. Lett., 33, 2–5, https://doi.org/10.1029/2005GL025583, 2006.
Hutyra, L. R., Munger, J. W., Nobre, C. A., Saleska, S. R., Vieira, S. A., and Wofsy, S. C.: Climatic variability and vegetation vulnerability in Amazônia, Geophys. Res. Lett., 32, L24712, https://doi.org/10.1029/2005GL024981, 2005.
Hutyra, L. R., Munger, J. W., Saleska, S. R., Gottlieb, E., Daube, B. C., Dunn, A. L., Amaral, D. F., de Camargo, P. B., and Wofsy, S. C.: Seasonal controls on the exchange of carbon and water in an Amazonian rain forest, J. Geophys. Res.-Biogeo., 112, G03008, https://doi.org/10.1029/2006JG000365, 2007.
Hutyra, L. R., Munger, J. W., Hammond-Pyle, E., Saleska, S. R., Restrepo-Coupe, N., Daube, B. C., de Camargo, P. B., and Wofsy, S. C.: Resolving systematic errors in estimates of net ecosystem exchange of CO2 and ecosystem respiration in a tropical forest biome, Agr. Forst Meteorol., 148, 1266–1279, https://doi.org/10.1016/j.agrformet.2008.03.007, 2008.
Kiew, F., Hirata, R., Hirano, T., Wong, G. X., Aeries, E. B., Musin, K. K., Waili, J. W., Lo, K. S., Shimizu, M., and Melling, L.: CO2 balance of a secondary tropical peat swamp forest in Sarawak, Malaysia, Agr. Forest Meteorol., 248, 494–501, https://doi.org/10.1016/j.agrformet.2017.10.022, 2018.
Kim, Y., Knox, R. G., Longo, M., Medvigy, D., Hutyra, L. R., Pyle, E. H., Wofsy, S. C., Bras, R. L., and Moorcroft, P. R.: Seasonal carbon dynamics and water fluxes in an Amazon rainforest, Glob. Change Biol., 18, 1322–1334, https://doi.org/10.1111/j.1365-2486.2011.02629.x, 2012.
Koch, G. W., Sillett, S. C., Jennings, G. M., and Davis, S. D.: The limits to tree height, Nature, 428, 851–854, https://doi.org/10.1038/nature02417, 2004.
Leitold, V., Morton, D. C., Longo, M., dos-Santos, M. N., Keller, M., and Scaranello, M.: El Niño drought increased canopy turnover in Amazon forests, New Phytol., 219, 959–971, https://doi.org/10.1111/nph.15110, 2018.
Lewis, S. L., Brando, P. M., Phillips, O. L., van der Heijden, G. M. F., and Nepstad, D.: The 2010 Amazon Drought, Science, 331, 554–554, https://doi.org/10.1126/science.1200807, 2011.
Longo, M.: Amazon Forest Response to Changes in Rainfall Regime: Results from an Individual-Based Dynamic Vegetation Model, Doctoral dissertation, Harvard University, 2014.
Longo, M., Knox, R. G., Levine, N. M., Alves, L. F., Bonal, D., Camargo, P. B., Fitzjarrald, D. R., Hayek, M. N., Restrepo-Coupe, N., Saleska, S. R., da Silva, R., Stark, S. C., Tapajós, R. P., Wiedemann, K. T., Zhang, K., Wofsy, S. C., and Moorcroft, P. R.: Ecosystem heterogeneity and diversity mitigate Amazon forest resilience to frequent extreme droughts, New Phytol., 219, 914–931, https://doi.org/10.1111/nph.15185, 2018.
McDowell, N., Allen, C. D., Anderson-Teixeira, K., Brando, P., Brienen, R., Chambers, J., Christoffersen, B., Davies, S., Doughty, C., Duque, A., Espirito-Santo, F., Fisher, R., Fontes, C. G., Galbraith, D., Goodsman, D., Grossiord, C., Hartmann, H., Holm, J., Johnson, D. J., Kassim, A. R., Keller, M., Koven, C., Kueppers, L., Kumagai, T., Malhi, Y., McMahon, S. M., Mencuccini, M., Meir, P., Moorcroft, P., Muller-Landau, H. C., Phillips, O. L., Powell, T., Sierra, C. A., Sperry, J., Warren, J., Xu, C., and Xu, X.: Drivers and mechanisms of tree mortality in moist tropical forests, New Phytol., 219, 851–859, https://doi.org/10.1111/nph.15027, 2018.
Melillo, J. M., Steudler, P. A., Aber, J. D., Newkirk, K., Lux, H., Bowles, F. P., Catricala, C., Magill, A., Ahrens, T., and Morrisseau, S.: Soil warming and carbon-cycle feedbacks to the climate system, Science, 298, 2173–2176, https://doi.org/10.1126/science.1074153, 2002.
Miller, S. D., Goulden, M. L., Menton, M. C., Da Rocha, H. R., De Freitas, H. C., E Silva Figueira, A. M., and De Sousa, C. A. D.: Biometric and micrometeorological measurements of tropical forest carbon balance, Ecol. Appl., 14, 114–126, https://doi.org/10.1890/02-6005, 2004.
Moorcroft, P. R., Hurtt, G. C., and Pacala, S. W.: a Method for Scaling Vegetation Dynamics: the Ecosystem Demography Model, Ecol. Monogr., 71, 557–586, https://doi.org/10.1890/0012-9615(2001)071[0557:AMFSVD]2.0.CO;2, 2001.
Morton, D. C., Nagol, J., Carabajal, C. C., Rosette, J., Palace, M., Cook, B. D., Vermote, E. F., Harding, D. J., and North, P. R. J.: Amazon forests maintain consistent canopy structure and greenness during the dry season, Nature, 506, 221–224, https://doi.org/10.1038/nature13006, 2014.
Morton, D. C., Rubio, J., Cook, B. D., Gastellu-Etchegorry, J. P., Longo, M., Choi, H., Hunter, M., and Keller, M.: Amazon forest structure generates diurnal and seasonal variability in light utilization, Biogeosciences, 13, 2195–2206, https://doi.org/10.5194/bg-13-2195-2016, 2016.
Myneni, R. B., Yang, W., Nemani, R. R., Huete, A. R., Dickinson, R. E., Knyazikhin, Y., Didan, K., Fu, R., Negrón Juárez, R. I., Saatchi, S. S., Hashimoto, H., Ichii, K., Shabanov, N. V, Tan, B., Ratana, P., Privette, J. L., Morisette, J. T., Vermote, E. F., Roy, D. P., Wolfe, R. E., Friedl, M. A., Running, S. W., Votava, P., El-Saleous, N., Devadiga, S., Su, Y., and Salomonson, V. V: Large seasonal swings in leaf area of Amazon rainforests, P. Natl. Acad. Sci. USA, 104, 4820–4823, https://doi.org/10.1073/pnas.0611338104, 2007.
Nelson, B. W., Kapos, V., Adams, J. B., Oliveira, W. J., and Oscar, P. G.: Forest Disturbance by Large Blowdowns in the Brazilian Amazon, Ecology, 75, 853–858, 1994.
Nemani, R. R., Keeling, C. D., Hashimoto, H., Jolly, W. M., Piper, S. C., Tucker, C. J., Myneni, R. B., and Running, S. W.: Climate-driven increases in global terrestrial net primary production from 1982 to 1999, Science, 300, 1560–1563, https://doi.org/10.1126/science.1082750, 2003.
Nepstad, D. C., Tohver, I. M., Ray, D., Moutinho, P., and Cardinot, G.: Mortality of large trees and lianas following experimental drought in an Amazon forest, Ecology, 88, 2259–69, 2007.
Phillips, O. L., Aragão, L. E. O. C., Lewis, S. L., Fisher, J. B., Lloyd, J., López-gonzález, G., Malhi, Y., Monteagudo, A., Peacock, J., Quesada, C. A., Heijden, G. Van Der, Almeida, S., Amaral, I., Arroyo, L., Aymard, G., Baker, T. R., Bánki, O., Blanc, L., Bonal, D., Brando, P., Chave, J., Cristina, Á., Oliveira, A. De, Cardozo, N. D., Czimczik, C. I., Feldpausch, T. R., Freitas, M. A., Gloor, E., Higuchi, N., Jiménez, E., Lloyd, G., Meir, P., Mendoza, C., Morel, A., Neill, D. A., Nepstad, D., Patiño, S., Peñuela, M. C., Prieto, A., Ramírez, F., Schwarz, M., Silva, J., Silveira, M., Thomas, A. S., Steege, H., Stropp, J., Vásquez, R., Zelazowski, P., Dávila, E. A., Andelman, S., Andrade, A., Chao, K., Erwin, T., Fiore, A. Di, C, E. H., Keeling, H., Killeen, T. J., Laurance, W. F., Cruz, A. P., Pitman, N. C. A., Vargas, P. N., Ramírez-angulo, H., Rudas, A., and Salamão, R.: Drought Sensitivy of the Amazon Rainforest, Science, 323, 1344–1347, https://doi.org/10.1126/science.1164033, 2009.
Pyle, E. H., Santoni, G. W., Nascimento, H. E. M., Hutyra, L. R., Vieira, S., Curran, D. J., van Haren, J., Saleska, S. R., Chow, V. Y., Carmago, P. B., Laurance, W. F., and Wofsy, S. C.: Dynamics of carbon, biomass, and structure in two Amazonian forests, J. Geophys. Res.-Biogeo., 113, G00B08, https://doi.org/10.1029/2007JG000592, 2008.
Restrepo-Coupe, N., da Rocha, H. R., Hutyra, L. R., da Araujo, A. C., Borma, L. S., Christoffersen, B., Cabral, O. M. R., de Camargo, P. B., Cardoso, F. L., da Costa, A. C. L., Fitzjarrald, D. R., Goulden, M. L., Kruijt, B., Maia, J. M. F., Malhi, Y. S., Manzi, A. O., Miller, S. D., Nobre, A. D., von Randow, C., Sá, L. D. A., Sakai, R. K., Tota, J., Wofsy, S. C., Zanchi, F. B., and Saleska, S. R.: What drives the seasonality of photosynthesis across the Amazon basin? A cross-site analysis of eddy flux tower measurements from the Brasil flux network, Agr. Forest Meteorol., 182/183, 128–144, https://doi.org/10.1016/j.agrformet.2013.04.031, 2013.
Rice, A. H., Pyle, E. H., Saleska, S. R., Hutyra, L., Palace, M., Keller, M., de Camargo, P. B., Portilho, K., Marques, D. F., and Wofsy, S. C.: Carbon Balance and Vegetation Dynamics in an Old-Growth Amazonian Forest, Ecol. Appl., 14, 55–71, https://doi.org/10.1890/02-6006, 2004.
Ross, T., Lott, N., McCown, S., and Quinn, D.: The El Nino Winter of '97–'98, NOAA Natl. Clim. Data Cent. Tech. Reports 98-02, 1–28, 1998.
Saatchi, S., Asefi-Najafabady, S., Malhi, Y., Aragao, L. E. O. C., Anderson, L. O., Myneni, R. B., and Nemani, R.: Persistent effects of a severe drought on Amazonian forest canopy, P. Natl. Acad. Sci. USA, 110, 565–570, https://doi.org/10.1073/pnas.1204651110, 2013.
Saleska, S. R., Miller, S. D., Matross, D. M., Goulden, M. L., Wofsy, S. C., da Rocha, H. R., de Camargo, P. B., Crill, P., Daube, B. C., de Freitas, H. C., Hutyra, L., Keller, M., Kirchhoff, V., Menton, M., Munger, J. W., Pyle, E. H., Rice, A. H., and Silva, H.: Carbon in Amazon forests: unexpected seasonal fluxes and disturbance-induced losses, Science, 302, 1554–1557, https://doi.org/10.1126/science.1091165, 2003.
Saleska, S. R., Hayek, M. N., Wiedemann, K., Longo, M., Hutyra, L. R., Daube, B. C., Munger, J. W., and Wofsy, S. C.: AmeriFlux BR-Sa1 Santarem-Km67-Primary Forest, https://doi.org/10.17190/AMF/1245994 (last access: 12 January 2017), 2015.
Saleska, S. R., Wu, J., Guan, K., Restrepo-Coupe, N., Nobre, A. D., Araujo, A., and Huete, A. R.: Dry-season greening of Amazon forests, Nat. Br. Commun. Aris., 531, E4–E5, https://doi.org/10.1038/nature16457, 2016.
Samanta, A., Knyazikhin, Y., Xu, L., Dickinson, R. E., Fu, R., Costa, M. H., Saatchi, S. S., Nemani, R. R., and Myneni, R. B.: Seasonal changes in leaf area of Amazon forests from leaf flushing and abscission, J. Geophys. Res.-Biogeo., 117, G01015, https://doi.org/10.1029/2011JG001818, 2012.
Stark, S. C., Leitold, V., Wu, J. L., Hunter, M. O., de Castilho, C. V, Costa, F. R. C., McMahon, S. M., Parker, G. G., Shimabukuro, M. T., Lefsky, M. A., Keller, M., Alves, L. F., Schietti, J., Shimabukuro, Y. E., Brandão, D. O., Woodcock, T. K., Higuchi, N., de Camargo, P. B., de Oliveira, R. C., Saleska, S. R., and Chave, J.: Amazon forest carbon dynamics predicted by profiles of canopy leaf area and light environment, Ecol. Lett., 15, 1406–14, https://doi.org/10.1111/j.1461-0248.2012.01864.x, 2012.
Urbanski, S., Barford, C., Wofsy, S., Kucharik, C., Pyle, E., Budney, J., McKain, K., Fitzjarrald, D., Czikowsky, M., and Munger, J. W.: Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res.-Biogeo., 112, G02020, https://doi.org/10.1029/2006JG000293, 2007.
Van Wagner, C. E.: The Line Intersect Method in Forest Fuel Sampling, For. Sci., 14, 20–26, 1968.
Verbeeck, H., Peylin, P., Bacour, C., Bonal, D., Steppe, K., and Ciais, P.: Seasonal patterns of CO2 fluxes in Amazon forests: Fusion of eddy covariance data and the ORCHIDEE model, J. Geophys. Res.-Biogeo., 116, G02018, https://doi.org/10.1029/2010JG001544, 2011.
Waring, R. H., Law, B. E., Goulden, M. L., Bassow, S. L., McCreight, R. W., Wofsy, S. C., and Bazzaz, F. A.: Scaling gross ecosystem production at Harvard Forest with remote sensing: A comparison of estimates from a constrained quantum-use efficiency modei and eddy correlation, Plant Cell Environ., 18, 1201–1213, https://doi.org/10.1111/j.1365-3040.1995.tb00629.x, 1995.
Wright, S. J. and van Schaik, C. P.: Light and the Phenology of Tropical Trees, Am. Nat., 143, 192–199, https://doi.org/10.1086/285600, 1994.
Wu, J., Albert, L. P., Lopes, A. P., Restrepo-Coupe, N., Hayek, M., Wiedemann, K. T., Guan, K., Stark, S. C., Christoffersen, B., Prohaska, N., Tavares, J. V., Marostica, S., Kobayashi, H., Ferreira, M. L., Campos, K. S., Silva, R. da, Brando, P. M., Dye, D. G., Huxman, T. E., Huete, A. R., Nelson, B. W., and Saleska, S. R.: Leaf development and demography explain photosynthetic seasonality in Amazon evergreen forests, Science, 351, 972–977, https://doi.org/10.1126/science.aad5068, 2016.
Wu, J., Guan, K., Hayek, M., Restrepo-Coupe, N., Wiedemann, K. T., Xu, X., Wehr, R., Christoffersen, B. O., Miao, G., da Silva, R., de Araujo, A. C., Oliviera, R. C., Camargo, P. B., Monson, R. K., Huete, A. R., and Saleska, S. R.: Partitioning controls on Amazon forest photosynthesis between environmental and biotic factors at hourly to interannual timescales, Glob. Change Biol., 23, 1240–1257, https://doi.org/10.1111/gcb.13509, 2017.
Yadav, V., Mueller, K. L., Dragoni, D., and Michalak, A. M.: A geostatistical synthesis study of factors affecting gross primary productivity in various ecosystems of North America, Biogeosciences, 7, 2655–2671, https://doi.org/10.5194/bg-7-2655-2010, 2010.
Zeng, N., Yoon, J.-H., Marengo, J. A., Subramaniam, A., Nobre, C. A., Mariotti, A., and Neelin, J. D.: Causes and impacts of the 2005 Amazon drought, Environ. Res. Lett., 3, 14002, https://doi.org/10.1088/1748-9326/3/1/014002, 2008.
Zscheischler, J., Mahecha, M. D., Avitabile, V., Calle, L., Carvalhais, N., Ciais, P., Gans, F., Gruber, N., Hartmann, J., Herold, M., Ichii, K., Jung, M., Landschützer, P., Laruelle, G. G., Lauerwald, R., Papale, D., Peylin, P., Poulter, B., Ray, D., Regnier, P., Rödenbeck, C., Roman-Cuesta, R. M., Schwalm, C., Tramontana, G., Tyukavina, A., Valentini, R., van der Werf, G., West, T. O., Wolf, J. E., and Reichstein, M.: Reviews and syntheses: An empirical spatiotemporal description of the global surface–atmosphere carbon fluxes: opportunities and data limitations, Biogeosciences, 14, 3685–3703, https://doi.org/10.5194/bg-14-3685-2017, 2017.






