Bipolar carbon and hydrogen isotope constraints on the Holocene methane budget

Atmospheric methane concentration shows a well-known decrease over the first half of the Holocene following the Northern Hemisphere summer insolation before it started to increase again to preindustrial values. There is a debate about what caused this change in the methane concentration evolution, in particular, whether an early anthropogenic influence or natural emissions led to the reversal of the atmospheric CH₄ concentration evolution. Here, we present new methane concentration and stable hydrogen and carbon isotope data measured on ice core samples from both Greenland and Antarctica over the Holocene. With the help of a two-box model and the full suite of CH₄ parameters, the new data allow us to quantify the total methane emissions in the Northern Hemisphere and Southern Hemisphere separately as well as their stable isotopic signatures, while interpretation of isotopic records of only one hemisphere may lead to erroneous conclusions. For the first half of the Holocene our results indicate an asynchronous decrease in Northern Hemisphere and Southern Hemisphere CH₄ emissions by more than 30 Tg CH₄ yr⁻¹ in total, accompanied by a drop in the northern carbon isotopic source signature of about −3 ‰. This cannot be explained by a change in the source mix alone but requires shifts in the isotopic signature of the sources themselves caused by changes in the precursor material for the methane production. In the second half of the Holocene, global CH₄ emissions increased by about 30 Tg CH₄ yr⁻¹, while preindustrial isotopic emission signatures remained more or less constant. However, our results show that this early increase in methane emissions took place in the Southern Hemisphere, while Northern Hemisphere emissions started to increase only about 2000 years ago. Accordingly, natural emissions in the southern tropics appear to be the main cause of the CH₄ increase starting 5000 years before present, not supporting an early anthropogenic influence on the global methane budget by East Asian land use changes.

1 Introduction

Atmospheric methane (CH₄) is a potent greenhouse gas and its concentrations are strongly coupled to the Earth's climate system. Due to the human influence on the Earth system, the CH₄ concentration ([CH₄]) in the atmosphere has increased by a factor of 2.5 (relative to the preindustrial level) over the last centuries and contributes significantly to the human-induced radiative forcing (Etheridge et al., 1998; Dlugokencky et al., 2005). Today both anthropogenic CH₄ sources (rice agriculture, livestock, fossil fuel production, anthropogenic biomass burning, and landfills) and natural CH₄ sources (natural wetlands, wildfires, geologic emissions, wild animals (including termites), and marine CH₄ hydrates) contribute to the global CH₄ emissions (Kirschke et al., 2013). The main mechanism removing CH₄ from the atmosphere is the chemical reaction of CH₄ with OH radicals in the troposphere. Together with the other sink processes (such as stratospheric loss, reaction with Cl radicals in the marine boundary layer, and soil uptake) the OH sink determines the recent atmospheric lifetime of CH₄, which is 9.1±0.9 years (Prather et al., 2012).

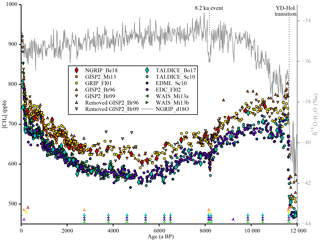
Figure 1 CH₄ concentration data compilation. Discrete [CH₄] data over the Holocene used for the CH₄ data compilation on synchronised gas age scales and corrected for offsets among data sets (references are listed in Table 1). The δ¹⁸O-H₂O data from the layer-counted NGRIP ice core have been used as an absolute time marker for fast climatic changes (e.g. the Younger Dryas–Holocene transition and the 8.2 ka event) assuming an essentially synchronous change in rapid temperature variations and atmospheric CH₄. The markers at the bottom of the plot indicate the tie points of the synchronised age scales (see Table 3).

Despite the fact that the total CH₄ emissions today are well known, there is still considerable debate about the individual contributions of (in particular small) CH₄ sources and their variability, e.g. evidenced by the mismatch of bottom-up and top-down estimates of the total CH₄ emissions (Kirschke et al., 2013; Crill and Thornton, 2017; Saunois et al., 2016). Moreover, a long-standing debate exists whether long-term Holocene CH₄ trends are naturally caused by wetland emissions (Singarayer et al., 2011) or whether an anthropogenic influence started already 4000–5000 years ago with early human land use changes (Ruddiman, 2003) (see below). To better assess the human influence on the global methane cycle, robust estimates of the natural (pre-anthropogenic) CH₄ emissions and their climate-coupled variations are required. Only polar ice cores can provide this information as they represent a direct, albeit (through the bubble enclosure process in the firn) low-pass-filtered, archive of trapped air and therefore offer the possibility to investigate the atmospheric composition of the past. With such ice core measurements the millennial to centennial evolution of the atmospheric [CH₄] has been determined back to 800 000 years before present (ka BP), where present refers to the year 1950, using the Antarctic EPICA Dome C (EDC) ice core showing glacial–interglacial variations in atmospheric [CH₄] by a factor of about 2 (Loulergue et al., 2008). More important for the assessment of the human influence on CH₄ levels are their variations during the Holocene, i.e. our current interglacial that started about 10 000 years ago. In this time period [CH₄] decreased by about 100 parts per billion (ppb) until about 5000 years ago (Fig. 1) after an early maximum during the Preboreal period (about 11.5–10 ka BP) (Blunier et al., 1995; Brook et al., 1996; Flückiger et al., 2002; Schilt et al., 2010). CH₄ values started to slowly increase again in the mid-Holocene until the fast anthropogenic increase resulting from industrialisation started around 200 years ago (MacFarling Meure et al., 2006). High-resolution CH₄ measurements on the West Antarctic Ice Sheet (WAIS) and Greenland GISP2 (Greenland Ice Sheet Project 2) ice cores (Mitchell et al., 2013) over the last 2800 years also show centennial CH₄ variations of 20–30 ppb superimposed on the long-term increase, reflecting natural variability in CH₄ emissions.

With the trend reversal in the mid-Holocene leading to a “bowl shape” (Blunier et al., 1995) of [CH₄], the Holocene differs from many previous interglacials, where the [CH₄] steadily dropped to glacial levels concurrently with the Northern Hemisphere summer insolation. One hypothesis postulates that CH₄ emissions caused by early human land use were responsible for the CH₄ turnaround at about 5 ka BP (Ruddiman and Thomson, 2001; Ruddiman, 2003). According to these authors, early farming activities, mainly rice agriculture in the eastern part of China, led to significant releases of CH₄ long before the industrial era (Ruddiman et al., 2008) and thus the authors propose that the bowl was shaped by human activities. Another explanation supported by a model-based study explains the late Holocene CH₄ rise by calling upon increased emissions from southern tropical wetlands due to an insolation-driven strengthening of the monsoon in western Amazonia (Singarayer et al., 2011). Accordingly, this model is able to produce a global [CH₄] rise in the Holocene driven by changes in the orbital forcing only. Note that due to the different orbital configuration during the last interglacial (MIS5.5), this model is also able to reproduce the steadily declining [CH₄] during MIS5.5, when strongly declining boreal CH₄ emissions overcompensate for increasing southern tropical wetland emissions.

An important point is that the two scenarios explain the Holocene CH₄ rise with additional emissions taking place in different geographic regions. By measuring the [CH₄] on ice cores from both polar regions (Greenland and Antarctica), the interpolar difference (IPD) can be calculated. This quantity can be used to draw conclusions about the hemispheric distribution of the CH₄ emissions (Brook et al., 2000; Chappellaz et al., 1997; Mitchell et al., 2013; Yang et al., 2017). Another tool to investigate the processes involved in the CH₄ cycle are measurements of the stable isotope signature in ice core CH₄. The CH₄ released by the various sources is associated with typical hydrogen and carbon isotopic signatures δD-CH₄ (D representing deuterium or ²H) (Quay et al., 1999; Walter et al., 2008; Whiticar, 1993; Whiticar and Schaefer, 2007) and δ¹³C-CH₄ (Whiticar, 1993; Quay et al., 1999; Whiticar and Schaefer, 2007; Etiope et al., 2008; Walter et al., 2008). In addition, the sink processes lead to a strong fractionation (Snover and Quay, 2000; Feilberg et al., 2005; Whiticar and Schaefer, 2007; Levine et al., 2011b), which leaves atmospheric CH₄ strongly enriched in heavy isotopes relative to the isotopic emission signatures. Changes of the relative contributions in sources lead to an alteration of the atmospheric CH₄ isotopic composition. CH₄ isotope measurements in ice cores therefore allow us to deduce the role the different processes related to the CH₄ cycle played in the past. By measuring both δD-CH₄ and δ¹³C-CH₄ from the Greenland GISP2 ice core over the Holocene, Sowers (2010) was able to provide first evidence of possible changes in the CH₄ precursor material due to a shift in the C3 to C4 plant ratio but could not unambiguously answer the question about the Holocene CH₄ anomaly.

In this study we combined for the first time comprehensive information on the CH₄ IPD and measurements of the bipolar carbon and hydrogen stable isotopic signature of CH₄ by measuring all three parameters – [CH₄], δD-CH₄, and δ¹³C-CH₄ – on ice samples from both polar regions with high analytical precision and improved resolution. Furthermore, we use a two-box model approach, which allows us to deconvolve the atmospheric signal and to calculate the total emissions and their isotopic signatures in each hemisphere.

As mentioned above, changes in the sinks leave an imprint on the isotopic composition of CH₄ in the atmosphere. However, while minor changes in the relative importance of the sink processes cannot be ruled out, in general, atmospheric chemistry models point to small changes in total lifetime (Kaplan et al., 2006; Levine et al., 2011a) and we also assume the relative contribution of individual sinks to be rather constant over the Holocene when relatively stable climate conditions prevailed. Therefore, the discussion of this study centres around CH₄ source processes and hence emissions of different CH₄ source categories.

2 Method

2.1 Measurements

The stable isotope data (δD-CH₄ and δ¹³C-CH₄) presented in this study were measured at the University of Bern on samples from the NGRIP (North Greenland Ice Core Project) ice core from Greenland. Antarctic samples from the EDML (EPICA Dronning Maud Land) and the TALDICE (TALos Dome Ice CorE) ice cores were analysed for δD-CH₄ and δ¹³C-CH₄, respectively (Bock et al., 2017). Note that for both parameters the samples from Greenland and Antarctica were measured during the same time interval with the same measurement system by the same operators and in randomised order. This procedure is crucial to avoid any systematic error (e.g. due to a long-term drift of the system) and ensures unbiased results in our source inversion.

The two isotopic parameters were measured at the University of Bern on two independent measurement systems designed for this specific purpose as described in detail in previous publications (Bock et al., 2010, 2014; Schmitt et al., 2014). They follow the same principal procedure: the air is (i) extracted from the ice sample by purging the meltwater with He; (ii) water vapour, CO₂, and the major air compounds (N₂, O₂, and Ar) are removed from the gas sample; (iii) CH₄ is separated from other trace gases using gas chromatography (GC); (iv) CH₄ is pyrolysed to H₂ or combusted to CO₂ in the δD and δ¹³C systems, respectively; and (v) the isotopic composition of H₂ and CO₂ is measured using an isotope-ratio mass spectrometer (IRMS). For both systems effects of interfering masses, specifically krypton, in the mass spectrometer are avoided by technical adaptations (Schmitt et al., 2013). In the case of δD-CH₄, the focussed H₂ peak is separated from other components using a second GC separation (post-pyrolysis trapping) (Bock et al., 2014). In the δ¹³C-CH₄ system, the CH₄-derived CO₂ is captured and delayed using a fused silica trap (at −196 ^∘C) after the combustion oven and thereby separated from krypton (Schmitt et al., 2014). Note that many δD-CH₄ and δ¹³C-CH₄ values based on such a gas chromatography–mass spectrometry method reported in the literature are not corrected for this effect, leading to significant offsets, especially for low CH₄ concentrations.

The δD-CH₄ values are determined relative to our primary air standard Air Controlé, a recent clean air ([CH₄] $=\mathrm{1971}\pm \mathrm{7}$ ppb), which has been cross-referenced to $-\mathrm{93.6}\pm \mathrm{2.2}$ ‰ with respect to Vienna Standard Mean Ocean Water (VSMOW) using Alert 2002/11, an air collected at Alert Station, Canada (Bock et al., 2014). The latter was referenced by Poss (2003) to be $-\mathrm{82.15}\pm \mathrm{0.3}$ ‰ with respect to VSMOW, which anchors our δD values to the isotope scale of the University of Heidelberg (Bock et al., 2010, 2014). Note that so far no internationally uniform δD-CH₄ standardisation scale has been established, leading to systematic inter-laboratory offsets as described in Umezawa et al. (2018). The δD-CH₄ measurement precision (1σ) of 2.3 ‰ was derived by calculating the pooled standard deviation of multiple NGRIP replicate (vertically neighbouring samples) measurements. The reference gas for the δ¹³C-CH₄ measurements is Boulder, an ambient air diluted with CH₄-free air ([CH₄] $=\mathrm{1508.18}\pm \mathrm{0.17}$ ppb) calibrated by the National Oceanic and Atmospheric Administration (NOAA) to a δ¹³C-CH₄ value of $-\mathrm{47.34}\pm \mathrm{0.02}$ ‰ with respect to Vienna Pee Dee Belemnite (VPDB) (Schmitt et al., 2014; Umezawa et al., 2018). The δ¹³C-CH₄ measurement precision (1σ) derived from replicate measurements is better than 0.15 ‰ for ice core samples.

2.2 Monte Carlo spline approximation of millennial CH₄ changes

To compare values from different ice core data sets (with different and variable temporal resolutions and measurement precisions) interpolation of the data to a common age scale is needed. Additionally, the records have to be low-pass filtered to the same (millennial) timescales that can be resolved in the isotope records. Therefore, in this study smoothing splines following Enting (1987) are used to calculate a continuous low-pass-filtered record from the discretely measured values. The stiffness of the spline curve is characterised by its cut-off period. A Python (http://www.python.org/, last access: 11 October 2018) routine was developed to calculate splines in a Monte Carlo manner, in which the data points are varied within a normal distribution within their standard deviation defined by the individual uncertainty of the measured values. This procedure allows for the calculation of the average of the splines representing the best-guess mean evolution of the data on the timescale resolved by the spline. Furthermore, using the standard deviation of all splines, the spread of the individual splines can be translated to an uncertainty of the mean spline. This spline calculation is used for various purposes in this study. The choice of the cut-off period has a large influence on the outcome of the spline and is therefore always documented wherever it is selected manually. For some applications (e.g. in the routines described in Sect. 2.3.2 and 2.3.3), however, we apply an objective criterion to define an appropriate cut-off period for a data set: wherever the cut-off period is not specified explicitly, it is set to 8 times the median of the data resolution.

Table 1 Data sets used for CH₄ data compilation. The CH₄ offset correction is added to the data to correct for inter-laboratory and time-period-related offsets (see Sect. 2.3.2). Additional data sets used for the time matching (e.g. covering the rapid CH₄ increase after 1850 CE or the Younger Dryas–Holocene transition) are listed.

^∗ GRIP data compilation performed by Jacqueline Flückiger in 2001 containing data from various publications, e.g. Blunier et al. (1995) and Chappellaz et al. (1993, 1997).

If the sampling rate in some parts of a data set is much higher than in others, this part has a larger impact on the spline than other more coarsely resolved sections. For short periods of large signal change (e.g. the 8.2 ka event for CH₄) such an oversampling relative to other parts of the data set may lead to significant artefacts in the calculated spline. Wherever this might be an issue, an additional step was introduced into the spline calculation routine, in which the data were down-sampled in a randomised way within the Monte Carlo loop (i.e. for each individual spline) to end up with a subset of a prescribed number of data points, for which the chance of data points to get picked is inversely proportional to the local data density. The down-sampled data are still unequally distributed, but on average the data density is similar over the whole time period studied.

2.3 Data correction and compilation

For further analysis of our new data, we complemented our [CH₄] records with data from other studies from the GRIP (Greenland Ice Core Project), GISP2, TALDICE, EDML, WAIS (West Antarctic Ice Sheet), and EDC ice cores shown in Table 1. However, combining different data sets introduces various challenges. In the following paragraphs we describe how these difficulties have been addressed.

2.3.1 Timescale synchronisation

All ice cores have individually determined gas age scales, which allow us to assign an age to each sample. Since we compare values from different ice cores (and from both hemispheres), small deviations in the age calculations have significant consequences for the interpretation (e.g. artefacts in the box model inversion; see Sect. 2.4). In an attempt to synchronise the different data sets, we linearly stretched and compressed the individual age scales between manually chosen tie points in three steps.

1. Wherever possible, we tied the data sets of each of the cores to the same reference age scale. For CH₄ data sets that reach far enough to the present, the fast CH₄ increase of the last centuries was used to synchronise the timescales. As a reference we used [CH₄] data from the Law Dome ice core (MacFarling Meure et al., 2006) and an atmospheric [CH₄] history derived from NEEM firn air (Buizert et al., 2012) representing the CH₄ evolution in Antarctica and in Greenland, respectively. Both records cover the entire anthropogenic CH₄ increase and overlap with recent atmospheric measurements (CSIRO, 2017; Dlugokencky et al., 2017). For the early Holocene the layer-counted NGRIP δ¹⁸O-H₂O record was used as reference timescale. Where the CH₄ data show strong signals such as at the 8.2 ka event and the Younger Dryas–Holocene transition, these were synchronised to the corresponding δ¹⁸O signal, assuming that there is no significant lag between the temperature changes recorded in δ¹⁸O and the response of CH₄ source to this change (Baumgartner et al., 2014).

2. With the use of splines of different cut-off periods and their time derivatives we were looking for typical features and signals in the [CH₄] evolution of the different data sets within the same hemisphere to define additional tie points and synchronise the data sets for each hemisphere. However, within each hemisphere the temporal alignments of all the distinguishable CH₄ features were already within the limitation of the data resolution. Therefore, no additional tie points could be defined at this stage, within each hemisphere.

3. In the third synchronisation step we aligned the data of both hemispheres after applying the offset corrections (see Sect. 2.3.2). Additional time corrections (for the Southern Hemisphere data) could be defined by looking at the fine structure of the [CH₄] evolution (e.g. the mid-Holocene [CH₄] minimum (around 5400 a BP) or the local [CH₄] maximum before the early Holocene decrease (around 9850 a BP)). Over the late Holocene period Mitchell et al. (2013) provided already synchronised data for the GISP2 and the WAIS ice core based on decadal to centennial variability; we retained their timescale over this period.

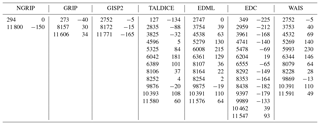
Table 2 lists the original age scales of the different ice cores. The tie points (original age and age correction) used to achieve an optimal temporal synchronisation among the CH₄ data sets are shown in Table 3. Temporal shifts to data with ages younger than the first tie point and older than the last tie point were chosen to be identical to those of the first and last tie points, respectively. Please note that for the ice cores, where the primary age scales provide an age uncertainty, all but three tie point corrections (GRIP: 273 years; TALDICE: 127 years and 6042 years) lie within the 1σ range of the uncertainty given for the individual age scales.

Table 2 Ice cores and age scales. Short names of the ice cores and initial gas age scales used for the CH₄ compilation.

Table 3 Time synchronisation. Tie points of the reference timescale for the individual ice cores (left column, in yr BP) and time corrections (right column, in years) applied with respect to the core-dependent timescale listed in Table 2. The correction values are linearly interpolated among the tie points and held constant before the earliest and after the latest tie points.

2.3.2 Offset correction

Another issue that can complicate compiling multiple data sets is concentration offsets. The CH₄ data sets we use to complement our new data were measured with different methods, in different labs, and at different times over the last decades. If we use the information about the relative evolution of the methane concentration documented by other measurement series, we have to be aware that the absolute level might show an offset from our data due to calibration and extraction issues. Therefore, we correct all data sets for such potential offsets. To do so, we calculated residuals defined as the difference between the spline values of the CH₄ data from other labs evaluated at the age of our data and the CH₄ mixing ratios of our data. A least-squares optimisation routine was used to find the offsets for the spline values of the different data sets. The offset corrections applied to the data are shown in Table 1. The GISP2 and WAIS data sets by Mitchell et al. (2013) are treated as a single data set, as they were measured in the same lab and during the same measurement campaign, and their difference (Greenland minus Antarctica) represents the true IPD. In Fig. 1 the synchronised and offset-corrected CH₄ time series as used in this study are shown.

2.3.3 Outlier detection

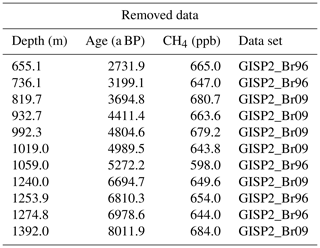
The GISP2 data sets from Brook et al. (1996) and Brook (2009) show an increased incidence of anomalously high [CH₄] values (relative to other data sets) in the mid-Holocene. As this ice is from the brittle ice zone (the zone where air bubbles and clathrates coexist in the ice, and which is prone to bad core quality due to the pressure and temperature relaxation process after the core was brought to the surface) this is probably due to infiltration of modern air into the ice samples in (micro)cracks in the ice after core retrieval (Gow et al., 1997; Neff, 2014). To avoid artificial elevation of the splined signal, which would result in a significant increase in the IPD, we identified and removed such outliers within the depth interval of 650–1400 m of the GISP2 ice core (equivalent to the time window 2.7–8.1 ka BP). To do so we used an iterative elimination approach. In each step, first the two GISP2 data sets were corrected for offsets relative to each other (Brook et al., 1996, was shifted to fit with Brook, 2009, by 36 ppb) and combined to one data set. Thereafter, for each GISP2 data point the difference between its value and the spline of all other GISP2 data in the brittle zone was calculated and divided by the 1σ uncertainty of the Monte Carlo spline at its age. If the largest (positive) relative residual exceeded the threshold value of 4, the corresponding data point was removed. This procedure was repeated until no outliers could be found any more. Table 4 shows the data points that were identified and eliminated through this method (also shown in Fig. 1). In total 15 out of 95 data points (within this depth range) were removed, reflecting the bad core quality in this depth interval. Note that in this outlier detection routine we make the assumption that the [CH₄] evolution in the atmosphere is relatively smooth. As we focus only on millennial changes in the data here, this assumption does not affect our conclusions. In the following discussion we assume that the corrected GISP2 data and the CH₄ data from the GRIP and NGRIP ice cores over this time interval are not affected anymore by modern air intrusion in the brittle ice. If this assumption does not hold, the true Northern Hemisphere CH₄ concentration would be lower and so would Northern Hemisphere emissions at that time.

Table 4 GISP2 outliers. Data points that were removed from the two GISP2 data sets by Brook et al. (2009) and Brook (1996) due to elevated CH₄ values probably due to contamination related to the ice sample quality in the brittle zone. Please note that the age and the concentration values are corrected for the age shift and the CH₄ correction, respectively.

2.3.4 Isotope data corrections

All stable isotope data have been corrected for gravitational enrichment. This process takes place in the firn column and leads to an enrichment of the heavier isotopes at the depth at which the air bubbles are finally closed off and the gas is trapped in the ice (Schwander, 1996). Using δ¹³⁶Xe data, which come as a side product during the δ¹³C-CH₄ measurement of the Bern δ¹³C system, and additional published δ¹⁵N-N₂ data (Landais et al., 2006; Capron et al., 2013; Eggleston et al., 2016), we experimentally derived this gravitational enrichment and directly correct the CH₄ stable isotope data, as this gravitational enrichment is only dependent on the mass difference between the two isotopes considered. The correction for the TALDICE δ¹³C values decreases from the early Holocene to the present from 0.39 ‰ to 0.28 ‰. The NGRIP δ¹³⁶Xe data do not show a systematic change. Thus, a constant value of 0.32 ‰ is subtracted from the NGRIP isotope values. Only very few δ¹⁵N-N₂ data points in the early Holocene were available to correct the EDML δD-CH₄ record. Since in the case of δD-CH₄ the measurement error and the observed signal are much larger than the gravitational enrichment, it is adequate to assume that this correction is also constant over time without any consequences for the interpretation of the data. For the EDML δD-CH₄ record a correction of 0.46 ‰ was applied.

Due to the relatively constant climatic conditions and slow [CH₄] changes occurring over the Holocene, thermal diffusion (Severinghaus et al., 1998) and diffusive fractionation (Buizert et al., 2013) – other processes potentially leading to an artefact in the stable isotope signature – are not considered in this study.

2.4 Box model inversion

Our box model inversion is a tool to disentangle the different processes involved in the atmospheric methane cycle. More precisely, it allows us to obtain quantitative information about the emission processes that led to the tropospheric CH₄ concentration changes recorded in the ice cores in the past. In other similar studies different approaches of varying complexity and with different boundary conditions have been presented (Fischer et al., 2008; Baumgartner et al., 2012; Mitchell et al., 2013). For this study we use a two-box model in which the boxes represent the northern and southern tropospheric hemispheres.

The following six inversion equations allow us to use the six measured parameters (the tropospheric [CH₄] (c_x) and the two stable isotope ratios (ⁱR_x)) for each hemisphere to calculate the emissions (E_x) and their isotope ratios (${}^i{R}_{E_x}$) for both boxes analytically (with x and y representing north and south and i the mass numbers 2 or 13 for deuterium and ¹³C):

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{E}_x=m^{\ast }\cdot \left({\displaystyle \frac{r_x\cdot c_x}{{\mathit{\tau }}_x}}+{\displaystyle \frac{c_x}{\mathrm{2}\cdot \mathit{\theta }}}-{\displaystyle \frac{c_y}{\mathrm{2}\cdot \mathit{\theta }}}\right),\text{(2)}& {\displaystyle }& {}^i{R}_{E_x}={\displaystyle \frac{m^{\ast }}{E_x}}\cdot \left({\displaystyle \frac{r_x\cdot c_x}{{\mathit{\tau }}_x}}{\cdot }^i{R}_x{\cdot }^i{\mathit{\alpha }}_x+{\displaystyle \frac{c_x}{\mathrm{2}\cdot \mathit{\theta }}}{\cdot }^i{R}_x-{\displaystyle \frac{c_y}{\mathrm{2}\cdot \mathit{\theta }}}{\cdot }^i{R}_y\right).\end{array}$$

The first term in Eqs. (1) and (2) represents the loss due to the CH₄ sinks, and the other two terms represent the interpolar mixing (out of and into the box, with θ being the mixing time between the poles as explained in more detail below). The parameter $m^{\ast }=\frac{m_{\mathrm{0}}}{c_{\mathrm{0}}}$ translates atmospheric concentrations (ppb) to total atmospheric inventories (Tg) using the mean atmospheric concentration value c₀=1650 ppb of the year 1987. Here we use the corresponding global CH₄ burden m₀=4800 Tg by Steele et al. (1992) that was also used in previous ice core studies (Fischer et al., 2008; Baumgartner et al., 2012). Note that this value is 7 %–10 % higher than more recent estimates (Dalsøren et al., 2016) and accordingly the derived absolute emissions may be 7 %–10 % overestimated. However, we focus our interpretation on relative emission changes, which are not affected by this scaling factor. The transport between the boxes is quantified by the interpolar exchange time θ=1.56 yr, which is determined through a model calibration using recent sulfur hexafluoride (SF₆) data (described in Sect. 2.4.1).

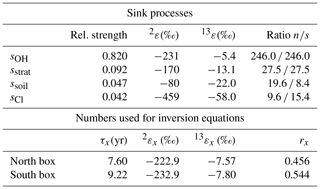
Table 5 Values used in our box model inversion. Relative strengths, isotopic fractionations (²ε and ¹³ε) (Cantrell et al., 1990; Tyler et al., 1994; Brenninkmeijer et al., 1995; Irion et al., 1996; Gierczak et al.,1997; Quay et al., 1999; Feilberg et al., 2005), the north–south ratio of the individual sink processes (ratio n∕s), and the parameters for each hemisphere used in our CH₄ box model inversion.

Note that the sizes of the two well-mixed boxes are not equal; the sizes are defined by the global mean annual latitude of the inter-tropical convergence zone (ITCZ) φ_ITCZ=5^∘ N (Marshall et al., 2014), which acts as a barrier to the hemispheric exchange of air masses. The inequality of the box sizes is reflected in Eqs. (1) and (2) by

$$\begin{array}{}\text{(3)}& {\displaystyle }{r}_x={\displaystyle \frac{V_x}{V_{\mathrm{atm}}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}\mp \sin \left({\mathit{\phi }}_{\mathrm{ITCZ}}\right)\right),\end{array}$$

the ratio of the box volume relative to the total atmospheric volume (r_n=0.456, r_s=0.544 for φ_ITCZ=5^∘ N). The global mean lifetime of CH₄ quantifies the total methane sink and is set to τ=8.4 yr (as in the four-box model used in Fischer et al., 2008, and in Bock et al., 2017). Again, using other estimates of the atmospheric lifetime (Prather et al., 2012; Naik et al., 2013) changes the absolute emission estimates but does not affect our conclusions on relative emission changes. According to the relative importance given by Kirschke et al. (2013) (average of bottom-up estimates of all three time intervals shown in their study) the sink is proportionally divided into the four different sink processes (s_OH, s_strat, s_soil, s_Cl) shown in Table 5. While s_OH and s_strat are thought to be equally distributed north and south of the ITCZ and therefore are the same in the two boxes, s_soil and s_Cl are partitioned according to the area ratios of land and open water, respectively, derived from a 0.5^∘ × 0.5^∘ resolution land-cover database (Channan et al., 2014). The lifetime of CH₄ in each box,

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\tau }}_x=\mathit{\tau }\cdot {\displaystyle \frac{\sum s_{\mathrm{tot}}}{\sum s_x}}\cdot r_x,\end{array}$$

is determined by the north–south distribution of the sinks and the relative box sizes. The chosen values for the atmospheric CH₄ lifetime and the strengths and the distribution of the sinks represent a best-guess based on the cited literature. Hence, other studies end up with slightly different values. Note also that we assume the model parameters to remain temporally unchanged over the Holocene.

The different sink processes lead to strong fractionations in both isotopes (Cantrell et al., 1990; Quay et al., 1999; Houweling et al., 2000; Snover and Quay, 2000, and references therein; Saueressig et al., 2001; Feilberg et al., 2005) and yield the hemispheric isotope fractionation factors ${}^i{\mathit{\alpha }}_x=\mathrm{1}{+}^i{\mathit{\epsilon }}_x$, with the fractionations ⁱε_x shown in Table 5. As in our model with only two tropospheric boxes s_strat is applied to the total tropospheric CH₄ inventory instead of the isotopically more depleted stratospheric CH₄, the literature values for the stratospheric sink fractionation have to be adjusted to ${}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{strat}}=-\mathrm{170}$ ‰ and ${}^{\mathrm{13}}{\mathit{\epsilon }}_{\mathrm{strat}}=-\mathrm{13.1}$ ‰. These values have been empirically derived to match the tropospheric isotopic signature of the forward four-box model described by Fischer et al. (2008), which contains two stratospheric boxes. Using the identical CH₄ emission set-up in both models, the north–south air mass exchange of the two-box model has been increased to equal the tropospheric [CH₄] values (IPD) of those of the four-box model. In a second step, the fractionations of the stratospheric sink ⁱε_strat in the two-box model have been adjusted to match the tropospheric δD-CH₄ and δ¹³C-CH₄ values of the two models.

The sink fractionation values used for the four-box model analysis by Bock et al. (2017) are very similar to the values we used in this study. Note that the numbers for the sink fractionation caused by stratospheric loss and by soils were accidentally swapped in the printed version of Table S3 by Bock et al. (2017) for both δ¹³C and δD. However, their model runs and therefore the results are based on the correct values.

As the individual data points from ice core [CH₄] and isotope measurements are subject to uncertainty in both time and magnitude even after our homogenisation procedure, we only use the millennial variations in CH₄, δD-CH₄, and δ¹³C-CH₄ in our box model inversion. To this end we calculated low-pass-filtered versions of the measured data using the Monte Carlo spline approximations described in Sect. 2.2, which allow us to quantify the mean and the uncertainty of the millennial variations. The uncertainty of the splines of the tropospheric values are introduced into the emission values using Gaussian error propagation. Due to the mentioned limitations we refrain from analysing shorter-scale variability.

2.4.1 SF₆ calibration of the two box model

The same approach used to set up the CH₄ inversion described in the previous section (Eqs. 1 and 2) allows us to formulate the general equations for the change of the concentration of any trace gas species in the two hemisphere boxes:

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}{c}_x}{\mathrm{d}t}}\cdot r_x\cdot m^{\ast }=E_x-S_x-{\displaystyle \frac{m^{\ast }}{\mathrm{2}\cdot \mathit{\theta }}}\left(c_x-c_y\right),\end{array}$$

with $\frac{\mathrm{d}{c}_x}{\mathrm{d}t}$ representing the rate of change of the hemispheric concentration, m^∗ the translation factor linking a concentration to an atmospheric inventory, E_x and S_x the emissions and the sinks in box x, and r_x the ratio of the box volumes depending on the mean annual latitude of the ITCZ φ_ITCZ as described above, where x and y stand for north and south (or vice versa).

SF₆ is a strong greenhouse gas with a lifetime of more than 1000 years, is solely of anthropogenic origin, and is mainly emitted in the Northern Hemisphere ($r_{E{}_{\mathrm{n}}}=\mathrm{95}$ %, $r_{E{}_{\mathrm{s}}}=\mathrm{5}$ %) (Geller et al., 1997, p. 6; Kovács et al., 2017; Levin et al., 2010). NOAA/ESRL (2017) measurements taken at Alert Station (Canada), Summit (Greenland), Palmer Station (Antarctica), and South Pole (Antarctica) record the SF₆ evolution in both polar regions over the last decades. Since the target in this study is the long-time trend and not seasonal variations, the NOAA/ESRL data are smoothed using a smoothing spline with a cut-off period of 2 years. For every year in the recorded period (1996–2008 CE) the annual SF₆ increase ($\frac{\mathrm{d}{c}_x}{\mathrm{d}t}$) and the mean concentration (c_x and c_y) are calculated. The records of the global emissions (E_tot), the global atmospheric mean SF₆ concentration (c_tot), and the total atmospheric inventory (m_tot) published by Levin et al. (2010) are used to calculate the hemispheric emissions $E_x=r_{E_x}\cdot E_{\mathrm{tot}}$ and the translation factor $m^{\ast }=\mathrm{mean}\left(\frac{m_{\mathrm{tot}}}{c_{\mathrm{tot}}}\right)=\mathrm{25.7}\frac{Gg{\mathrm{SF}}_{\mathrm{6}}}{\mathrm{ppt}}$. With the approximation of a negligible sink term (since lifetime exceeds the timescale of interest by 2–3 orders of magnitude), Eq. (1) can be solved for the interpolar exchange time:

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathit{\theta }={\displaystyle \frac{m^{\ast }\left(c_x-c_y\right)}{\mathrm{2}\left(\frac{\mathrm{d}{c}_x}{\mathrm{d}t}\cdot r_x\cdot m^{\ast }-r_{E_x}\cdot E_{\mathrm{tot}}\right)}},\end{array}$$

where c_x and c_y are the SF₆ concentrations at high latitudes. Note that with this calibration we effectively define the exchange time between the northern and southern polar regions, which is somewhat longer than the mean interhemispheric exchange time. As we use θ later for our inversion of polar CH₄ concentrations measured in the ice cores, we effectively correct for the difference in polar and mean hemispheric CH₄ concentration using this SF₆ calibration. We use the term interpolar exchange time throughout the paper. Using Eq. (2) the interpolar exchange time can be calculated for each year. With φ_ITCZ=5.0^∘ N we get the average value of $\mathit{\theta }=\mathrm{1.56}\pm \mathrm{0.17}$ yr.

Another valid strategy to cope with the ice core data representing polar tropospheric values would be to correct the data to represent mean hemispheric (φ_ITCZ=5.0^∘ N) values (similarly to how it has been carried out by Etheridge et al. (1998) and by Schaefer et al. (2016) to derive a global average signal from ice core CH₄ and δ¹³C-CH₄ data) based on the knowledge about the modern CH₄ concentration distribution (e.g. as provided by Dlugokencky et al., 2017). However, using the corrected data for the box model inversion also requires the corresponding calculation of θ (to represent the hemispheric mixing time) using mean hemispheric SF₆ concentrations. The lower spatial resolution of the SF₆ concentration data (especially in the low latitudes) biases the mean hemispheric SF₆ values and thus does not allow a satisfying calculation of a hemispheric exchange time. Therefore, we decided not to follow this approach and use polar values in combination with the polar exchange time (as explained above) for our inversion study.

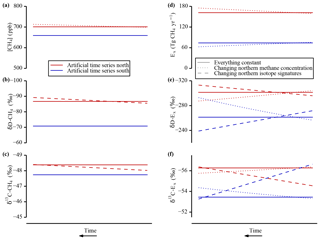
Figure 2 Artificial time series and inversion results. Artificial tropospheric [CH₄] (a) and stable isotope time series (b, c) used as input for the box model inversion. The calculated mean hemispheric CH₄ emission strengths (d) and their isotopic signatures (e, f) show the dependence on the different input parameters. Three experiments are performed: all input values constant (solid lines), all constant but the northern tropospheric CH₄ isotope values varied (dashed lines), and all constant but [CH₄] varied (dotted lines). To be consistent with the wording in the text, time runs from right to left. Note the inverted y axes in panels (b), (c), (e), and (f).

2.4.2 Inversion of artificial time series

The interpretation of the output of our inversion model is challenging and not always intuitive. To get a better understanding of the model output, some simplified experiments using artificial time series have been performed and are shown in this study for didactic reasons. In a first approach all six parameters are held constant over time. In the panels on the left in Fig. 2 the tropospheric [CH₄] (a) and the isotopic signatures δD-CH₄ (b) and δ¹³C-CH₄ (c) are shown for the northern box in red and for the southern box in blue. The constant values (solid lines) represent the levels of the splines of our measurements at 2 ka BP and serve as input to the inversion model. The panels on the right show the inversion results, i.e. the integrated emissions (d) and their mean isotopic signatures (e, f) that are emitted into the two hemisphere boxes according to our model. As the input parameters are constant, the emission signal must be constant in all parameters as well. However, although the Northern Hemisphere concentrations are only 6 % larger than the southern ones, a large difference in the emission strengths ($E_{\mathrm{n}}\approx \mathrm{2.2}\cdot E_{\mathrm{s}}$) is needed to maintain the IPD in the [CH₄], compensating for the air mass exchange between the atmospheres. Also note that due to the sink fractionation the isotopic signature of atmospheric CH₄ is strongly enriched in the heavy isotopes compared to the emissions (see Table 5).

For the second experiment (dashed lines in Fig. 2), the IPDs of the tropospheric isotope signatures (IPD_δD and IPD_δ13C) were changed, while the concentrations remained unchanged. By altering the northern stable isotope signal the isotopic IPDs are changed within the range observed in the splined ice core records (dashed lines in Fig. 2b and c). This leads to changes in the calculated isotope signatures of the emissions, whereas the emission strengths are unaffected. As shown (dashed lines) in Fig. 2e and f, the isotopic signature for both the Northern Hemisphere and the Southern Hemisphere emissions needs to be altered to yield the given atmospheric values of constant [CH₄] and isotopic signatures changing only in one hemisphere. To achieve the declining isotope signal in the northern troposphere, the isotope signatures of emissions from the Northern Hemisphere have to become isotopically more depleted in heavy isotopes (later on conveniently referred to as isotopically “lighter”, equivalent to lower δ values) over time. At the same time the isotopically lighter CH₄ mixed from the northern into the southern box requires the southern box emissions to become more enriched in the heavy isotope (isotopically “heavier”, equivalent to higher δ values) over time. Since the southern source is much weaker than the northern source (more northern-sourced CH₄ is mixed from north to south than southern-sourced CH₄ is mixed from south to north), the change in the isotopic signatures of the emissions turns out to be even larger in the Southern Hemisphere.

The dotted line in panel (a) in Fig. 2 shows a third scenario, in which all tropospheric parameters are kept constant except for the [CH₄] in the Northern Hemisphere. Similar to the former experiment, the [CH₄] in the northern box is varied between values representing the minimal and the maximal measured IPD${}_{{\mathrm{CH}}_{\mathrm{4}}}$. The dotted curves in the right panels (d–f) in Fig. 2 indicate that this change has an influence on all six emission parameters of our model. The emission strength in the northern box increases to produce the rising [CH₄]. Declining emission strength in the Southern Hemisphere compensates for the increasing CH₄ north-to-south flux due to the rising IPD${}_{{\mathrm{CH}}_{\mathrm{4}}}$. The CH₄ that enters a box by atmospheric mixing is already fractionated by the sinks and isotopically heavier than the newly emitted CH₄. If the relative amount of CH₄ input by mixing is decreased for the northern (increased for the southern) box, the emission signatures become less (more) depleted in heavy isotopes to maintain the tropospheric CH₄ isotopic signatures.

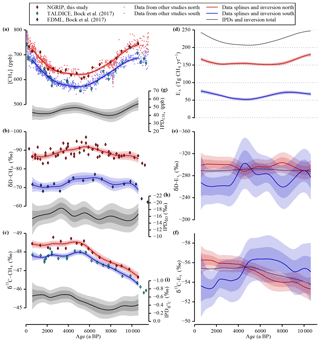
Figure 3 Data and inversion. The panels on the left (a–c) show the concentration and the two stable isotope signatures of CH₄ measured in ice cores representing the tropospheric values over the Holocene. The concentration data are complemented with data from other studies (see Table 1). All three parameters were measured on ice cores from Greenland (red) and from Antarctica (blue and cyan) representing the northern and the southern polar troposphere, respectively. A spline function with a cut-off period of 3000 years has been used to calculate the smoothed evolution of the tropospheric signals represented by the lines and the 1σ and 2σ error bands. The panels (g), (h), and (i) show the IPDs of all three parameters also with their 1σ and 2σ error bands. A box model inversion is used to calculate the hemispheric CH₄ emissions shown in the panels on the right. In panel (d) the emission strengths are shown for both hemisphere boxes together with the total CH₄ emissions. Panels (e) and (f) show the mean isotopic signatures of the emissions for both stable isotopes of CH₄. All the error bands represent 1σ and 2σ uncertainties. Note the inverted y axes in panels (b), (c), (e), (f), (h), and (i). Red refers to Northern Hemisphere records and blue to Southern Hemisphere records throughout the paper.

Since the variations for both experiments were performed based on a reasonable range (observed changes in IPDs), the span for the calculated values of the emission parameters also provides a range for the changes that are needed to alter the measured tropospheric IPDs in the Holocene. Note, however, that the variation scenarios (e.g. a full decoupling of atmospheric concentration and the isotopic composition of CH₄) do not represent changes we expect to observe in nature and are presented for illustrative reasons only.

3 Results

The homogenised tropospheric data (this study complemented with published [CH₄] data from Chappellaz et al., 1993, 1997; Blunier et al., 1995; Brook et al., 1996; Brook, 2009; Flückiger et al., 2002; Schilt et al., 2010; Mitchell et al., 2013; see Sect. 2.3, Fig. 1, and Table 1) are shown in Fig. 3 in the left-hand panels. The smoothing splines, which are all calculated with the same cut-off period of 3000 years, are shown including their 1σ and 2σ uncertainty bands. In Fig.3a the composite of the time-synchronised and offset-corrected CH₄ data is shown over the Holocene. The diamond-shaped symbols represent the NGRIP and TALDICE data of this study measured during the δ¹³C-CH₄ measurement campaign. Overall, our data compilation after the above-mentioned corrections supports previous trends: after high concentrations in the Preboreal (ca. 11.5–10 ka BP) the data show a decline of the atmospheric [CH₄] over the first half of the Holocene followed by a reversal of this trend and an accelerating increase from the mid-Holocene to the late Holocene. The preindustrial level is comparable to the [CH₄] during the Preboreal warm period. The splines emphasise this long-term evolution nicely but, deliberately, do not reproduce the fine structure in the data (see for example Mitchell et al., 2013). The difference between the [CH₄] values in the Northern Hemisphere and Southern Hemisphere (the IPD${}_{{\mathrm{CH}}_{\mathrm{4}}}$) is shown in Fig. 3g. The concentration measured in ice cores from Greenland (red) is on average 45 ppb higher than the values derived from Antarctic ice cores (blue), which agrees with the result of Chappellaz et al. (1997).

In Fig. 3b the δD-CH₄ values measured in ice from the NGRIP and the EDML ice cores are shown. As additionally illustrated in Fig. 3h we find a pronounced difference of −16.3 ‰ between northern and southern δD-CH₄ values, which is rather stable over the whole period of investigation. Limited by the coarser resolution of the EDML δD-CH₄ data, the smoothed curves and the error bands illustrate the probable evolution of the true tropospheric signals only on millennial timescales and longer. Compared to the large [CH₄] changes, the δD-CH₄ signal over the Holocene is relatively small and similar in the two data sets. The values become isotopically lighter in the first half of the Holocene and heavier again in the second half. Note that our NGRIP δD-CH₄ data differ significantly from the data set from the GISP2 ice core published by Sowers (2010) (see Fig. 4). First, there is a difference of the mean level between the two data sets of 10 to 15 ‰, which can be attributed to an inter-laboratory difference (Bock et al., 2014; Umezawa et al., 2018). Second, the GISP2 data suggested a shift of about 20 ‰ towards heavier values from 5 to 1 ka BP, which is not confirmed by our data. This disagreement, however, may be largely attributed to the much larger scattering of the GISP2 data set, which did not yet allow the quantification of an unambiguous trend in δD-CH₄.

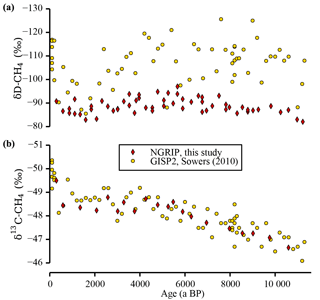
Figure 4 Comparison of stable CH₄ isotope data. This study's stable CH₄ isotope values of the NGRIP ice cores are shown together with the data published by Sowers (2010) using the GISP2 ice core. The δD-CH₄ data sets (a) differ in the absolute level and the variance, whereas the δ¹³C-CH₄ data (b) are in good agreement. Note that all data are corrected for gravitational fractionation in the firn column. All data of this study are free of krypton interference, whereas the GISP2 δ¹³C-CH₄ record has been subsequently corrected for it (Schmitt et al., 2013). Note the inverted y axes.

In Fig. 3c the δ¹³C-CH₄ measured on ice from the NGRIP and TALDICE ice cores are shown. Both data sets show a gradual trend towards lighter values over the first half of the Holocene and almost constant values over the second half. The point of inflection is well defined at about 5 ka BP. As shown in Fig. 3f, at about the same time the IPD${}_{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}$ changes quickly from −0.35 ‰ to −0.63 ‰, which is rather constant before and after the point of inflection. Our NGRIP δ¹³C-CH₄ record is well in line with the GISP2 data by Sowers (2010) (see Fig. 4), which have been subsequently corrected for the analytical krypton interference (Schmitt et al., 2013).

Our inversion model calculates the emissions that led to the measured tropospheric signals shown in the panels on the left in Fig. 3. In Fig. 3d the strength of the integrated emissions (in Tg CH₄ per year) in each of the two troposphere boxes are shown. Additionally, the total CH₄ global emissions (sum of north and south) are shown in grey. Note that the uncertainty (1σ and 2σ) in emission fluxes is very small and much smaller than the long-term changes in the emission fluxes over the Holocene indicated by the spline average. This uncertainty reflects only the error in emission fluxes for changes on millennial timescales that are resolved in our spline. As indicated in high-resolution data (for example Mitchell et al., 2013) the centennial variability in atmospheric CH₄ is high and the uncertainties of reconstructed emission fluxes on such shorter timescales would be significantly higher as well.

The following observations can be made from the inversion results: the CH₄ emissions into the northern box are more than 2 times higher than the emissions into the southern box. After a decrease of roughly 30 Tg CH₄ yr⁻¹ in the early Holocene the northern emissions remain relatively constant between 8 and 2 ka BP before increasing by 15 Tg CH₄ yr⁻¹. In the Southern Hemisphere the emissions suggest a slight increase in the first 2000 years of the record followed by a significant 22 Tg CH₄ yr⁻¹ decrease until 4–5 ka BP after which emissions increase by 25 Tg CH₄ yr⁻¹ in the second half of the Holocene.

The weighted averaged δD signature of all the integrated CH₄ emissions is shown in Fig. 3e for each hemisphere. With values of about −295 ‰ the northern emission δD signature is on average 30 ‰ lighter than the Southern Hemisphere emissions. Before 7.5 ka BP and around 4.5 ka BP the δD-E_x signal shows long-term variations around the Holocene mean that are in antiphase between the Northern Hemisphere and Southern Hemisphere, whereas the global mean δD-E (grey line) remains essentially constant. Based on these two observations and the knowledge from our experiments with artificial time series (see Sect. 2.4.2) showing that a change in the isotopic signature in one hemisphere has a large influence of different sign on the emission isotope signal in the other hemisphere (Fig. 2), we attribute the δD-E_x fluctuations to the measurement uncertainty of the individual data points of the low-resolution δD-CH₄ EDML record which affect the spline reconstruction. The absence of a long-term trend in δD-E_x over the Holocene despite the significant changes in the atmospheric [CH₄] is remarkable and a strong constraint on the average Holocene CH₄ budget. However, the large uncertainty in δD-E_x does not allow us to make robust conclusions about millennial variations in the hydrogen isotopic signature of CH₄ emissions.

The δ¹³C-CH₄ values of the emissions shown in Fig. 3f indicate a significant shift of the northern emissions to heavier values over the Holocene, which is especially pronounced in the time interval before 4 ka BP. In the south, δ¹³C-E_s also shows a slight negative trend over the first half of the Holocene, which, however, is still well within the 1σ inversion uncertainty. A stronger positive trend, however, occurs during the second half of the Holocene, which, however, is still within the 2σ uncertainty of the reconstruction. The global mean of the isotopic emission signatures reflects the coherent trends in the measured atmospheric values, with a strong negative trend of −1.8 ‰ over the first 5000 years of the Holocene.

3.1 Sensitivity studies

The size ratio of the two boxes of the box model inversion is defined by the annual mean latitude of the ITCZ φ_ITCZ. In fact, there is evidence from different proxies of a southward migration of the ITCZ during the Holocene (Haug et al., 2001; Zhao and Harrison, 2012; McGee et al., 2014). Since it is not possible to deduce robust numbers for the position and the movement of the global mean ITCZ from local studies, φ_ITCZ has been kept constant over time at a reasonable Holocene value in our standard inversion (described in Sect. 2.4). However, sensitivity runs have been performed to quantify the impact of this assumption on the conclusions drawn from our inversion results.

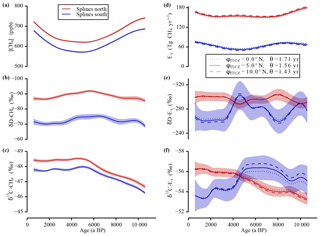
Figure 5 Sensitivity study “SF₆ calibration”. In panels (a–c) the data splines with the 1σ uncertainty bands of the measured tropospheric values are shown. In panels (d–f) the calculated strengths and the isotopic signature of the emissions are shown for the three different φ_ITCZ and θ set-ups to investigate the sensitivity of the inversion to the SF₆ calibration. Note the inverted y axes in panels (b), (c), (e), and (f).

As described in Sect. 2.4.1, SF₆ calibration has been used to determine the interpolar exchange time θ associated with different values of φ_ITCZ. For the first sensitivity study these two parameters have always been fitted in parallel to ensure that the different model configurations all fit the SF₆ constraint in an optimum way. In Fig. 5 the splines of the Holocene data (left panels) and the corresponding emission values derived by the inversion (right panels) are shown. In the sensitivity runs, the inversion equations have been solved using other (φ_ITCZ, ε) couples with φ_ITCZ moving from 0.0 to 10.0^∘ N. In all six emission parameters, these variations only lead to small changes relative to the total signal variability. For the isotopic signatures of the emissions, all curves lie well within the 1σ error of the 5.0^∘ N results.

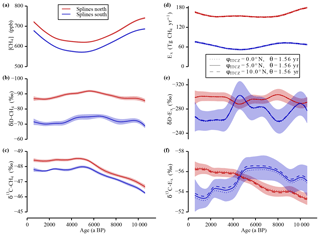
Figure 6 Sensitivity study “ITCZ position”. In panels (a–c) the data splines with the 1σ uncertainty error bands of the measured tropospheric values are shown. In panels (d–f) the calculated strengths and the isotopic signature of the emissions are shown for the three different φ_ITCZ set-ups and the best-guess value for θ to investigate the sensitivity of the inversion to a shift of the ITCZ. Note the inverted y axes in panels (b), (c), (e), and (f).

A change of the mean annual position of the ITCZ also has an influence on the box sizes. This has a direct impact on the north–south partitioning of the individual CH₄ sinks and thus on all six inversion parameters. Therefore, another sensitivity run was carried out, in which only φ_ITCZ was varied and θ kept constant at the best guess value. As shown in Fig. 6, the sensitivity of the inversion to a change of φ_ITCZ is very low if θ is kept constant. Note that the southward migration of the ITCZ over the Holocene is thought to be smaller than 1^∘ (McGee et al., 2014). The results of this second set of experiments in which only one parameter was changed (i.e. the constraints of the SF₆ calibration were not fulfilled) also shows that on average variations in φ_ITCZ and θ contribute a similar amount to the deviation from our standard run (φ_ITCZ=5^∘ N) (see Fig. 6).

4 Discussion

The main goal of this study is to profit from the improved CH₄ multi-parameter data set using our inversion model in order to evaluate the different scenarios and to constrain the global CH₄ budget over the Holocene. To this end, we consider the early, mid-Holocene, and late Holocene separately.

4.1 Early Holocene (11–8 ka BP)

The significant early drop in the northern emission strength together with the slight shift towards isotopically lighter carbon emissions in the Northern Hemisphere from 11 to 8 ka BP is challenging to account for. One potential solution to account for the observed concentration shift would be a general weakening of the boreal CH₄ sources as a result of the decreasing northern summer insolation (Berger and Loutre, 1991). However, this should lead to a trend in both isotope emission signatures towards heavier values in the Northern Hemisphere, as in general the high-latitude CH₄ emissions from wetlands are isotopically light in both isotopes (Whiticar and Schaefer, 2007; Walter et al., 2008). Accordingly, this conflicts with the stable isotope results from our inversion. For δD-E_n the inversion might be affected by one single measurement point (EDML δD-CH₄) at 8.19 ka BP, forcing the emission signature curves of the two hemispheres apart and indicating that δD-E_n becomes lighter. Nevertheless, even if this single data point is removed, the inversion signal would be constant over this period but would not show a trend towards heavier values as expected from a decline in boreal emissions.

Based on ¹⁴C dating, Walter et al. (2007) estimated the CH₄ emissions from thermokarst lakes to decrease from 26 to 5 Tg CH₄ yr⁻¹ in the period from 11 to 8 ka BP in line with the decreasing trend in Northern Hemisphere emissions in our inversion. To match the result of the isotope inversion, another isotopically heavy northern source (e.g. biomass burning) has to be reduced simultaneously to compensate for the lack of isotopically light thermokarst CH₄ emissions. However, charcoal records from sediments do not indicate a decline of wild fires in the Northern Hemisphere but rather point to the opposite during the Holocene (Daniau et al., 2012).

Part of the answer of this puzzle may lie in the combined temporal evolution of the strengths and isotopic signature of the boreal wetlands. Due to land ice and permafrost retreat in the early Holocene, minerotrophic fens, characterised by relatively high CH₄ emissions which are not as strongly depleted in ¹³C, turn into ombrotrophic bogs over time with more ¹³C-depleted but also much weaker CH₄ emissions (Ding et al., 2005; Sowers, 2010; Hornibrook, 2013; Yu et al., 2013). This reduction of CH₄ emissions in the course of conversion of fens to bogs requires a very depleted ¹³C source signature of the bogs to quantitatively explain our inversion results and may therefore not suffice to explain the δ¹³C-E_n shift towards lighter values in the early Holocene. Furthermore, an enrichment trend in δD-E_n (of about 5 ‰) would be expected if the δD-depleted high-latitude emissions became relatively less important, while – if at all – we see a 20 ‰ depletion in δD-E_n from 10 to 8 ka BP. Also the isotopic signature of the water used in methanogenesis has a direct imprint on the hydrogen isotopic signature of the emitted CH₄ (Whiticar and Schaefer, 2007). Speleothem δ¹⁸O records confirm an isotopic shift towards lighter values in the meteoric water in the summer monsoon regions of the Northern Hemisphere from 11 to 8 ka BP (Wang et al., 2014) and an inverse relationship in the Southern Hemisphere, in line with our inversion. However, the speleothem records also suggest opposite trends over the rest of the Holocene, which are not seen in our inversion results. In addition, isotopically light meltwater from the retreating Northern Hemisphere ice sheets (for example in proglacial lakes) may contribute to a depletion in the hydrogen isotopic signature of boreal CH₄ source in the early Holocene.

4.2 Mid-Holocene (8–5.5 ka BP)

Our inversion results show that the decrease in atmospheric CH₄ concentrations over this interval is mainly caused by declining Southern Hemisphere emissions. This decrease in the Southern Hemisphere CH₄ emission from 8 to 5.5 ka BP – during the time of the strongest increase in austral summer insolation (Berger and Loutre, 1991) – appears counterintuitive but is in line with the model results by Singarayer et al. (2011), in which this is caused by changes in tropical rainfall location. This is also the period when the ITCZ is thought to have started moving southward as a response to the change in the orbital forcing (Haug et al., 2001; Zhao and Harrison, 2012; McGee et al., 2014), having an influence on the hemispheric CH₄ source distributions. CH₄ emissions from regions that were attributed to the Southern Hemisphere box in the early Holocene may now contribute CH₄ to the Northern Hemisphere due to the shift of the ITCZ. Note that such a change has an influence not only on the spatial emission distribution but also on other parameters (such as θ), which are relevant for the inversion model, in which the box sizes were kept constant over time. Our sensitivity studies (see Sect. 3.1) show, however, that a movement of the ITCZ in the model has only a small effect on the inversion results.

As discussed above, the δD signal of the CH₄ emissions is mostly constant in both hemispheres. This is expected if one hemisphere box gains emissions from tropical wetlands, characterised by stable isotope signatures close to the integrated source mix, at the cost of the other box. The rather constant charcoal wildfire reconstructions for the Northern Hemisphere in this time window (Daniau et al., 2012) do not support a decline in biomass burning CH₄ emissions being responsible for the 1.5 ‰ depletion in δ¹³C-E_n between 7 and 5.5 ka BP. The δ¹³C shift of the emissions could be related to a shift in the ratio of C3 to C4 plants as suggested by Sowers (2010), while a further evolvement of northern fens to bogs is incompatible with the relatively constant emissions in the Northern Hemisphere. Under Holocene climate conditions, with high availability of humidity and CO₂, C₃ plants successfully compete against the relatively ¹³C-enriched C₄ plants and thereby alter the carbon isotopic signature of the precursor material of methanogenesis (Farquhar et al., 1989). This process was also suggested by Möller et al. (2013) to explain the close correlation of the δ¹³C-CH₄ signal with atmospheric CO₂ and the decoupling from the [CH₄] in the glacial period.

4.3 Late Holocene (5.5–1 ka BP)

The early anthropogenic influence hypothesis (Ruddiman and Thomson, 2001) calls upon increasing emissions from rice paddies mainly in eastern Asia. In our box model such emissions would be located in the Northern Hemisphere box and therefore lead to an increase in northern emissions after 5 ka BP. However, the box model inversion shows no significant increase in E_n before 2 ka BP. In contrast, at 5.5 ka BP, at the time when all six presented tropospheric records imply a change in the global CH₄ cycle, the inversion indicates an amplification of Southern Hemisphere CH₄ emissions. This clearly supports the idea of a natural Holocene wetland CH₄ emission increase as suggested by Singarayer et al. (2011). In contrast, a southern anthropogenic source can be excluded since the Southern Hemisphere was barely populated in the mid-Holocene (Kaplan et al., 2011). The observed shift in δD-E_s and especially δ¹³C-E_s towards heavier values in this interval cannot be explained simply by increased tropical wetland emissions in the Amazon region but also requires an enhancement of a Southern Hemisphere CH₄ source strongly enriched in ¹³C. Using a simple mass balance approach ($E_{\mathrm{total}}{\cdot }^i{\mathit{\delta }}_{\mathrm{total}}=E_{\mathrm{initial}}{\cdot }^i{\mathit{\delta }}_{\mathrm{initial}}+E_{\mathrm{additional}}{\cdot }^i{\mathit{\delta }}_{\mathrm{additional}}$) allows us to determine a δ¹³C signature of the additional CH₄ emissions of 19 Tg CH₄ yr⁻¹ to be about −45.5 ‰, which is isotopically heavier than tropical wetland CH₄ emissions (−56.8 ‰ according to Whiticar and Schaefer, 2007). Note, however, that this quantitative approach is based on the assumption of unchanged carbon isotopic signatures of the initial CH₄ emissions and therefore needs to be taken with care. Increasing emissions from tropical and subtropical wild fires in the Southern Hemisphere, which are also documented in charcoal records (Daniau et al., 2012), could have become increasingly important, e.g. due to enhanced fuel production or higher CH₄ emission efficiency (more smoldering fires), both caused by wetter climatic conditions, and would readily explain the joint information derived from inversion results on Southern Hemisphere CH₄ emissions and their stable isotopic signatures. Other isotopically heavy sources such as geological emissions and marine CH₄ hydrates are unlikely to dramatically gain importance in the mid-Holocene and only in one hemisphere and can therefore be ruled out as important players driving the observed CH₄ changes.

5 Conclusions

Our new records of [CH₄], δD-CH₄, and δ¹³C-CH₄ measured on samples from polar ice cores from both hemispheres provide valuable insights into the Holocene CH₄ cycle. A significant IPD for δ¹³C and δD, as already documented for [CH₄], exists over the entire period of investigation. While the [CH₄] data confirm the well-known Holocene evolution, the two stable isotope records provide additional insights. This shows the value of our multi-isotope approach in order to avoid drawing wrong conclusions. A two-box model approach has been used to translate the measured signals into emissions. The calculated hemispheric CH₄ emission signatures, characterised by different trends in the two hemispheres for δ¹³C and no statistically significant variation in δD, show a decoupling of the emission signatures of the two analysed isotopes. Therefore, we attribute the long-term changes of the atmospheric CH₄ isotopes over the first half of the Holocene to shifts in the isotopic source signatures of individual CH₄ sources rather than to changes in the global CH₄ source mix.

In the early Holocene (11–8 ka BP) we associate the decline of Northern Hemisphere emissions and the δ¹³C trend towards lower values with the natural evolution of high-latitude wetlands from fens (high CH₄ emissions) to bogs (lower but strongly ¹³C-depleted CH₄ emissions). An alternative explanation calling upon a significant decrease in CH₄ emissions from thermokarst lakes would require compensation by other processes to fulfil the δ¹³C constraint, e.g. a substantial decline of wild fire activity in the Northern Hemisphere. In the mid-Holocene (8–5.5 ka BP) the inversion shows a decline of the Southern Hemisphere CH₄ emissions and an ongoing shift of the δ¹³C emission signatures towards lighter values, which might be related to the southward migration of the ITCZ and the change of the C3-to-C4 plant ratio altering the carbon isotopic composition of the precursor material for CH₄ production. During the second half of the Holocene (5.5–1 ka BP), which shows a major increase in CH₄ emissions accompanied by a shift towards higher δ¹³C signatures in the Southern Hemisphere, our results favour the CH₄ rise to be caused by natural CH₄ emissions (both wetlands and wildfires) in the southern tropics rather than by early rice agriculture in east Asia.

The CH₄ stable isotope data provide a powerful constraint on the Holocene CH₄ system (e.g. to benchmark CH₄ emission models); however, the relatively large uncertainty ranges in the calculated emission parameters still limit our ability to draw more robust conclusions on temporal variations. The inversion would benefit from an increased temporal resolution in the Southern Hemisphere δD-CH₄ record. However, since the concentration data have a large influence on all six inversion parameters, we see the largest potential to better constrain the Holocene CH₄ emissions by actually improving the [CH₄] records. Better IPD${}_{{\mathrm{CH}}_{\mathrm{4}}}$ data measured on the same analytical system during the same measurement campaign in high temporal resolution, which ensures an accurate synchronisation (such as the data by Mitchell et al. (2013) for the last 2800 years), would bring us a large step forward in further constraining the Holocene CH₄ cycle. This is especially true for the Greenland ice cores within the brittle ice zone, e.g. GISP2 records for depths between 650 and 1400 m, equivalent to the time window 2.7–8.1 ka BP when individual samples subject to modern air intrusion may compromise the Greenland CH₄ record. The new EGRIP ice core currently drilled in northeast Greenland has much lower accumulation; hence a brittle ice zone located at older ages may help to improve the CH₄ record in this time interval in the future. Alternatively, a high-accumulation ice core from Greenland where ice older than 2.7 ka BP is found below the brittle ice zone would circumvent this issue and allow for uncompromised CH₄ measurements over the Holocene.