Southern Ocean controls of the vertical marine δ¹³C gradient – a modelling study

δ¹³C, the standardised ¹³C ∕ ¹²C ratio expressed in per mille, is a widely used ocean tracer to study changes in ocean circulation, water mass ventilation, atmospheric pCO₂, and the biological carbon pump on timescales ranging from decades to tens of millions of years. δ¹³C data derived from ocean sediment core analysis provide information on δ¹³C of dissolved inorganic carbon and the vertical δ¹³C gradient (i.e. Δδ¹³C) in past oceans. In order to correctly interpret δ¹³C and Δδ¹³C variations, a good understanding is needed of the influence from ocean circulation, air–sea gas exchange and biological productivity on these variations. The Southern Ocean is a key region for these processes, and we show here that Δδ¹³C in all ocean basins is sensitive to changes in the biogeochemical state of the Southern Ocean. We conduct a set of idealised sensitivity experiments with the ocean biogeochemistry general circulation model HAMOCC2s to explore the effect of biogeochemical state changes of the Southern and Global Ocean on atmospheric δ¹³C, pCO₂, and marine δ¹³C and Δδ¹³C. The experiments cover changes in air–sea gas exchange rates, particulate organic carbon sinking rates, sea ice cover, and nutrient uptake efficiency in an unchanged ocean circulation field. Our experiments show that global mean Δδ¹³C varies by up to about ±0.35 ‰ around the pre-industrial model reference (1.2 ‰) in response to biogeochemical change. The amplitude of this sensitivity can be larger at smaller scales, as seen from a maximum sensitivity of about −0.6 ‰ on ocean basin scale. The ocean's oldest water (North Pacific) responds most to biological changes, the young deep water (North Atlantic) responds strongly to air–sea gas exchange changes, and the vertically well-mixed water (SO) has a low or even reversed Δδ¹³C sensitivity compared to the other basins. This local Δδ¹³C sensitivity depends on the local thermodynamic disequilibrium and the Δδ¹³C sensitivity to local POC export production changes. The direction of both glacial (intensification of Δδ¹³C) and interglacial (weakening of Δδ¹³C) Δδ¹³C change matches the direction of the sensitivity of biogeochemical processes associated with these periods. This supports the idea that biogeochemistry likely explains part of the reconstructed variations in Δδ¹³C, in addition to changes in ocean circulation.

1 Introduction

The vertical marine δ¹³C gradient (Δδ¹³C) is the surface-to-deep difference in δ¹³C of dissolved inorganic carbon (DIC), where the standardised ¹³C ∕ ¹²C ratio (δ¹³C) is expressed in per mille (Zeebe and Wolf-Gladrow, 2001):

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=\left({\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}/{}^{\mathrm{12}}\mathrm{C}}{{\left({}^{\mathrm{13}}\mathrm{C}/{}^{\mathrm{12}}\mathrm{C}\right)}_{\mathrm{standard}}}}-\mathrm{1}\right)\times \mathrm{1000}\mathrm{‰}.\end{array}$$

Here, ¹³C ∕ ¹²C_standard is the Pee Dee Belemnite standard (0.0112372) (Craig, 1957). ¹³C is slightly heavier than the ¹²C isotope, which causes a fractionation effect during air–sea gas exchange and photosynthesis, thereby changing δ¹³C and Δδ¹³C (Laws et al., 1997; Zhang et al., 1995; Mackenzie and Lerman, 2006). Photosynthetic fractionation increases the ¹³C ∕ ¹²C ratio of surface ocean DIC (i.e. a δ¹³C increase) due to the preferred uptake of the lighter ¹²C into biogenic matter (which therefore has a low δ¹³C). The deep sea DIC has a relatively low δ¹³C signature as a result of the remineralisation of low-δ¹³C biogenic matter at depth. The resulting vertical δ¹³C gradient is in addition influenced by air–sea gas exchange and circulation (Zeebe and Wolf-Gladrow, 2001; Emerson and Hedges, 2008; Ziegler et al., 2013). Both deep sea and surface ocean δ¹³C signatures are archived in the calcareous shells of foraminifera in the sediments. Such records of δ¹³C from planktic and benthic foraminiferal shell material cover tens of millions of years (Hilting et al., 2008). Using this archive, δ¹³C and Δδ¹³C have been used to reconstruct, for example, atmospheric CO₂ concentration, ocean circulation, and the strength of the biological pump (Broecker, 1982; Shackleton and Pisias, 1985; Zahn et al., 1986; Oppo et al., 1990; Hollander and McKenzie, 1991; Keir, 1991; Crucifix, 2005; Curry and Oppo, 2005; Lisiecki, 2010; Broecker and McGee, 2013; Ziegler et al., 2013; Hoogakker et al., 2015; Bauska et al., 2016). Δδ¹³C is independent of whole-ocean δ¹³C shifts (due to terrestrial influences), because such influences would affect δ¹³C equally everywhere. This makes Δδ¹³C a valuable proxy to study the marine carbon cycle independent of changes in carbon storage on land. Besides the use of δ¹³C for understanding the past ocean, contemporary measurements of δ¹³C of DIC support the quantification of anthropogenic carbon uptake by the oceans as well as the study of the effects of biology and ocean circulation on tracer distributions (Kroopnick, 1980, 1985; Gruber and Keeling, 2001; Quay et al., 2003; Holden et al., 2013; Eide et al., 2017b). However, major uncertainties remain in the interpretation of foraminiferal δ¹³C records and Δδ¹³C (Oliver et al., 2010; Broecker and McGee, 2013) as well as in the interpretation of the present-day δ¹³C data (Eide et al., 2017b).

This article addresses part of these uncertainties by exploring the pre-industrial sensitivity of δ¹³C and Δδ¹³C to biogeochemical change in idealised model experiments. By doing so we can investigate a number of biogeochemical mechanisms that could explain (part of) the observed changes in δ¹³C and Δδ¹³C. We focus on the Southern Ocean (SO), the ocean south of 45^∘ S, because the SO plays an important role in the global carbon cycle by regulating atmospheric CO₂ concentrations and uptake of anthropogenic CO₂ (Broecker and Maier-Reimer, 1992; Heinze, 2002; Marinov et al., 2006) as well as influencing the global efficiency of the biological pump, global primary production, and preformed nutrients (Primeau et al., 2013).

Variations in Δδ¹³C over the past few 100 000 years show that Δδ¹³C is generally increased during glacial periods, due to a higher contrast of deep δ¹³C with surface and mid-depth δ¹³C (Broecker, 1982; Shackleton and Pisias, 1985; Boyle, 1988; Charles et al., 2010; Oliver et al., 2010). Long-term δ¹³C and Δδ¹³C variations have been explained by ocean circulation changes (Duplessy et al., 1988; Jansen, 2017; Oppo et al., 1990; Toggweiler, 1999; Menviel et al., 2016). However, Δδ¹³C variability cannot be explained by ocean stratification or circulation changes alone: an interaction between biogeochemical and physical processes must be at play (Keir, 1991; Boyle, 1988; Mulitza et al., 1998; Charles et al., 2010; Ziegler et al., 2013; Schmittner and Somes, 2016). Δδ¹³C has been used in different ways over time: in earlier studies as the contrast between surface and deep water δ¹³C, derived from planktic versus benthic foraminifera (Broecker, 1982; Boyle, 1988; Shackleton et al., 1983; Duplessy et al., 1988), and now increasingly as the contrast of deep ocean (benthic) δ¹³C with thermocline or intermediate ocean δ¹³C (Mulitza et al., 1998; Charles et al., 2010; Lisiecki, 2010).

Here, we explore the sensitivity of δ¹³C and Δδ¹³C to changes in the biogeochemical state of the Global Ocean and Southern Ocean under a constant circulation field, to support the paleo-oceanographic interpretation of δ¹³C and Δδ¹³C as well as to improve the understanding of the SO role in global carbon cycling and its variability and sensitivity. In order to study biogeochemical mechanisms that could influence δ¹³C and Δδ¹³C, a set of sensitivity experiments is conducted with the ocean biogeochemistry general circulation model HAMOCC2s (Heinze et al., 2016). We first estimate the contribution of biology versus air–sea gas exchange to marine δ¹³C of DIC (Sect. 3.2). The experiments focus on one or more of the biogeochemical aspects assumed to be important for δ¹³C and Δδ¹³C, e.g. the biological pump efficiency and/or equilibration at the air–sea interface (Sect. 3.3.1–3.3.4). Together these experiments provide a broad spectrum of biogeochemical changes that could influence local and global δ¹³C and Δδ¹³C. The modelling results of Sect. 3.3.1–3.3.4 are discussed in context of observational data from sediment cores (Sect. 3.4). As δ¹³C and Δδ¹³C are used to study changes in atmospheric pCO₂ ($p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$), a final section will cover the relationship between atmospheric δ¹³C, Δδ¹³C, and $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ under different marine biogeochemical states (Sect. 3.5).

2 Methods

In this study we employ the ocean biogeochemistry general circulation model HAMOCC2s (Heinze et al., 1999, 2016), which simulates the inorganic and organic carbon cycle in the water column and in the sediments. The horizontal resolution of the model is $\mathrm{3.5}{}^{\circ }\times \mathrm{3.5}{}^{\circ }$ and there are 11 depth layers in the ocean. HAMOCC2s has an annual time step and an annually averaged fixed circulation field, as well as a one-layer atmosphere component (permitting exchange of O₂, ¹³CO₂, and CO₂ with the ocean component), which is assumed to be longitudinally well-mixed. The model is computationally very economic and thus an ideal tool for sensitivity experiments over long integration times. Biogenic particulate matter in the model is represented as particulate organic carbon (POC), calcium carbonate (CaCO₃), and biogenic silica (opal). These biogenic particles are only modelled as export production due to the annual time step of the model. POC and opal export production are described by Michaelis–Menten kinetics for nutrient uptake, limited by phosphate and silicic acid respectively (Sect. 1A in the Supplement). CaCO₃ export production depends on the ratio between opal and POC production. POC is carried as a tracer as well as transported downwards according to a set of mass balance equations that describe POC gain through surface-layer POC production and POC losses through constant sinking and remineralisation rates (Sect. 1A in the Supplement). This is done similarly for opal and CaCO₃ sinking and dissolution. As the model has an annual time step, sea ice is always present south of ∼60^∘ S and north of ∼70^∘ N in the control run (Fig. S1 in the Supplement). A more detailed model description is provided in previous studies using a similar configuration of HAMOCC2s (Heinze, 2002; Heinze et al., 2016), as well as in Sect. 1A in the Supplement.

Fractionation between ¹³C and ¹²C during photosynthesis is set to a constant value of −20 ‰ (Lynch-Stieglitz et al., 1995; Tagliabue and Bopp, 2008), as model results are little influenced by the chosen parameterisation (Schmittner et al., 2013; Jahn et al., 2015). The fractionation during air–sea gas exchange depends on temperature according to $\mathit{\epsilon }=-\mathrm{9.483}\times {\mathrm{10}}^{\mathrm{3}}/T$ + 23.89 ‰, where temperature (T) is measured in Kelvin (K) (Mook, 1986), causing stronger fractionation at lower temperatures (i.e. at high latitudes). Fractionation during CaCO₃ formation is omitted from the model, as was done in previous studies (Lynch-Stieglitz et al., 1995; Marchal et al., 1998; Schmittner et al., 2013), as its size is uncertain but likely minor (∼1 ‰) and effects on δ¹³C and Δδ¹³C are small (Shackleton and Pisias, 1985). In the version of HAMOCC2s used in this study, a fixed weathering input is used for ¹³C to tune the ocean inventory to values comparable to observations. The weathering flux of ¹³C into the ocean was determined by an iterative procedure: The model was run over 100 000 years, replacing the weathering rate with the diagnosed burial rate for ¹³C continuously. After this, the model ¹³C inventory was recalibrated such that the atmospheric value for δ¹³C arrived at −6.5 ‰. This procedure was repeated over three iterations. Afterwards, the weathering rate of ¹³C was fixed to the last diagnosed value (0.36 Tmol ¹³C yr⁻¹) – which results in a weathering flux δ¹³C of DIC of −11 ‰ . Another 100 000-year run was carried out with this constant input rate in order to check whether the global ¹³C distribution was stable in all reservoirs. The sensitivity experiments were then re-started from the result of that run. Weathering fluxes are added homogeneously over the first ocean layer as dissolved matter and in a fixed stoichiometric ratio for CaCO₃, organic carbon, ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$, alkalinity, and Si. Annual weathering fluxes (Tmol) are 27 for CaCO₃, 5 for organic carbon, 5/r_C : P for ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$, 2 × CaCO₃-r_N : P × ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ for alkalinity, and 4.5 for Si (with $r_{\mathrm{C}:\mathrm{P}}=\mathrm{122}$ and $r_{\mathrm{N}:\mathrm{P}}=\mathrm{16}$). These values are within the uncertainties of observational estimates for Si (5.6 Tmol yr⁻¹; Tréguer, 2002), CaCO₃ (∼32 Tmol yr⁻¹; Milliman and Droxler, 1996), and organic carbon (4 Tmol yr⁻¹; Broecker and Peng, 1987) and have been adjusted to improve the fit of the respective modelled marine tracer distributions as well as burial fluxes to observational estimates. The spin-up procedure described here created a model set-up with close-to-observed marine and atmospheric δ¹³C (δ¹³C^atm) values and freely evolving atmospheric pCO₂ and δ¹³C. This equilibrated model version is referred to as the “control run” in the remainder of this article. We define the vertical δ¹³C gradient (Δδ¹³C) as follows:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}={\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{surface}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{deep}},\end{array}$$

where δ¹³C_surface and δ¹³C_deep are the volume-weighted mean δ¹³C of DIC in the surface ocean (< 50 m depth, i.e. the model photic zone) and the deep ocean (lowermost wet layer in the model, if the top of the layer is > 3 km depth), respectively. By doing so, we can compare the Δδ¹³C summarised as one number between the different sensitivity experiments.

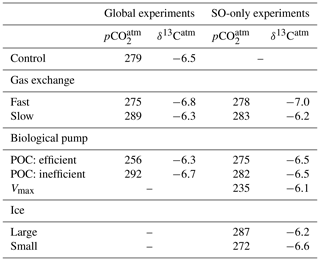
Table 1 Description of the sensitivity experiments. The sensitivity experiments on the CO₂ gas exchange rate and the biological pump have been done twice, once for the Global Ocean and once only making changes in the Southern Ocean (south of 45^∘ S).

We conducted a set of sensitivity experiments to explore changes in air–sea gas exchange rate, sea ice extent (influencing both biological production and the air–sea gas exchange of carbon), and the efficiency of the biological pump through the POC sinking rate and nutrient uptake rate (Table 1). We employ the term “efficiency of the biological pump” as a measure of the success of phytoplankton to maintain low nutrient concentrations in the surface ocean. All experiments are run for 2000 model years starting from the end of the spin-up. These runtimes allowed for atmospheric quasi-equilibrium to establish (Fig. S5), with an exception for the long-term effects caused by POC sinking rate changes (as studied in more detail by Roth et al., 2014). The equilibration timescale of Δδ¹³C is much shorter than that of atmospheric δ¹³C: this is the case because (1) the long-term weathering-burial equilibration of δ¹³C affects the whole ocean reservoir simultaneously – thus keeping Δδ¹³C constant – and (2) the processes that potentially influence Δδ¹³C (changes in biological production and air–sea gas exchange) affect Δδ¹³C on shorter (centennial to millennial) timescales. In order to compare effects of SO change and global change, the gas exchange rate and POC sinking rate experiments are done twice – once changing the respective model parameter for the Global Ocean and once for the Southern Ocean only (SO-only). The model parameters were changed in a way that marine biogeochemical tracer distributions (e.g. ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$, δ¹³C) remained reasonable but did provide an estimate of the sensitivity of the respective tracer to biogeochemical change. The model has a constant sea ice cover (Fig. S1), which permits gas transfer through the ice depending on ice cover thickness (the transfer rate is divided by ice thickness in centimetres) while light transfer is inhibited at ice thicknesses over 0.01 cm. The maximum and minimum sea ice cover experiments (“ice large” and “ice small”, Table 1) approximate the Last Glacial Maximum winter extent and the modern summer extent of SO sea ice, respectively (Crosta, 2009 and Fig. A22 therein) and assume full inhibition of gas and light transfer through ice for simplicity. The experiment on nutrient drawdown (V_max) alters the Michaelis–Menten kinetics of POC production by changing the maximum nutrient (i.e. ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$) uptake rate ($V_{\max }^{\mathrm{POC}}$ in Sect. 1A in the Supplement). The gas exchange experiments alter the specific gas exchange rate k_w, as described in more detail in Sect. 1B in the Supplement. The POC sinking rate experiments change the sinking velocity constant w_POC in the POC mass balance equations (Sect. 1A in the Supplement).

The contribution of biological processes versus air–sea gas exchange to δ¹³C is calculated using the method of Broecker and Maier-Reimer (1992) as done for observations by Eide et al. (2017b) and in a modelling context by Sonnerup and Quay (2012):

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}\left[\mathrm{‰}\right]={\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{photo}}}{\stackrel{\mathrm{‾}}{\mathrm{DIC}}}}\times r_{\mathrm{C}:\mathrm{P}}\times \left({\mathrm{PO}}_{\mathrm{4}}-\stackrel{\mathrm{‾}}{{\mathrm{PO}}_{\mathrm{4}}}\right)+\stackrel{\mathrm{‾}}{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}},\end{array}$$

where ${\mathit{\epsilon }}_{\mathrm{photo}}=-\mathrm{20}\mathrm{‰}$, $r_{\mathrm{C}:\mathrm{P}}=\mathrm{122}$ and the following model control run mean values are used: $\stackrel{\mathrm{‾}}{\mathrm{DIC}}$ =2332.284 µmol kg⁻¹, $\stackrel{\mathrm{‾}}{{\mathrm{PO}}_{\mathrm{4}}}=\mathrm{2.409}$ µmol kg⁻¹ and $\stackrel{\mathrm{‾}}{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}=\mathrm{0.656}$ ‰. These values result in the modelled δ¹³C_bio : ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship δ¹³C_bio$=\mathrm{3.18}-\mathrm{1.05}\times$ ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$. The constant 3.18 is somewhat higher than estimated for observed δ¹³C, for which a constant of 2.8 was found by Eide et al. (2017b). This higher constant originates from the over-prediction of the model mean δ¹³C and ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ at depth, as seen in other models (Sonnerup and Quay, 2012). Equation (3) assumes a constant biological fractionation as well as a constant r_C : P ratio, and these assumptions will introduce some error in the partition of biological and air–sea gas exchange signatures derived from observed δ¹³C to ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ ratios (e.g. Eide et al. 2017b). For the purpose of determining δ¹³C_bio in our model, these assumptions are unproblematic, since r_C : P and ε_photo are actually taken to be constant in the model formulation. The air–sea gas signature δ¹³C_AS is approximated as the residual (δ¹³C_AS = ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{model}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}).{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{AS}}$ is 0 ‰ when δ¹³C_model = δ¹³C_bio, i.e. when the δ¹³C can be explained by biology only. We express δ¹³C_bio as a percentage to aid interpretation of the results (denoted ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$), because the values of δ¹³C_bio in per mille depend strongly on the chosen “reference” values, i.e. mean DIC, ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$, and δ¹³C (compare Broecker and Maier-Reimer, 1992; Lynch-Stieglitz et al., 1995; Sonnerup and Quay, 2012; Schmittner et al., 2013; Eide et al., 2017b). The conversion from δ¹³C_bio to a percentage is calculated as follows:

$$\begin{array}{}\text{(4)}& {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}\left(\mathit{\%}\right)={\displaystyle \frac{\left|{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}\right|}{\left|{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}\right|+\left|{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{AS}}\right|}}\times \mathrm{100}\mathit{\%}.\end{array}$$

In our analysis, we define the total amount of air–sea carbon exchange as $F_{\mathrm{u}+\mathrm{d}}=F_{\mathrm{up}}+F_{\mathrm{down}}$, with F_up as the upward annual carbon flux from the ocean into the atmosphere and F_down its downward counterpart (Sect. 1B in the Supplement and Heinze and Maier-Reimer, 1999). F_u+d is relevant for understanding the sensitivity of δ¹³C. The net carbon exchange is defined as $F_{\mathrm{net}}=F_{\mathrm{up}}-F_{\mathrm{down}}$. The sign of F_net indicates whether a region is a source or a sink for carbon and is relevant for understanding changes in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$.

Figure 1 Modelled δ¹³C of DIC (‰) distribution for the model control run: (a) δ¹³C at 25 m depth, (b) Pacific transect of δ¹³C, (c) zonal transect of δ¹³C at 26^∘ S, and (d) Atlantic transect of δ¹³C.

3 Results and discussion

3.1 Model control run

The model reproduces the main features of observed marine δ¹³C, as shown in Figs. 1 and S2. The modelled global mean surface ocean δ¹³C_surface of DIC is higher (1.88 ‰) than deep ocean δ¹³C_deep (0.67 ‰), creating a mean ocean Δδ¹³C of 1.21 ‰. In the North Atlantic and SO, Δδ¹³C is the least pronounced (0.9 ‰ and 0.8 ‰ respectively) due to vertical mixing between surface and deep water during deep water formation and upwelling (Duplessy et al., 1988). Δδ¹³C increases with water mass age as expected from the increased imprint of remineralisation on δ¹³C. The mean modelled ocean δ¹³C is higher by 0.16 ‰ relative to observations (Eide et al., 2017b), which is especially pronounced in the oldest water masses (Fig. S2). This is observed in other models as well and attributed to the model's relative contribution of deep water production in the North Atlantic and Southern Ocean (Sonnerup and Quay, 2012). The modelled global export POC production is 9.6 Gt C yr⁻¹, of which 18 % is produced in the SO, which is within the uncertainty of observational estimates (MacCready and Quay, 2001; Schlitzer, 2002; Dunne et al., 2007; Lutz et al., 2007; Nevison et al., 2012). The atmosphere has a modelled equilibrium $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of 279 ppm and a δ¹³C^atm of −6.50 ‰ , which developed in the model from the “best-fit” weathering value $F_{\mathrm{eq}}^{\mathrm{w}}$ as described above in Sect. 2. Net air–sea gas exchange is close to zero (ventilating $\sim \mathrm{2}\times {\mathrm{10}}^{-\mathrm{7}}$ Gt of carbon to the atmosphere annually). The resulting drift of the model control over 2000 years is $\mathrm{7}\times {\mathrm{10}}^{-\mathrm{7}}$ ‰ for δ¹³C^atm, and $+\mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ ppm for $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$.

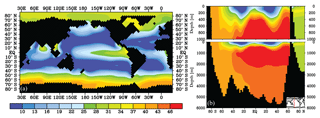
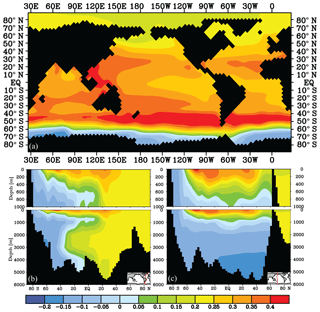
Figure 2 ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$, the contribution of biology to the local δ¹³C signal (%), as calculated using Eq. (4) at (a) 25 m depth and (b) a Pacific transect. The remainder of 100 % is attributed to air–sea gas exchange. The δ¹³C_bio and δ¹³C_AS values in per mille are very similar to the values found by Schmittner et al. (2013).

3.2 Air–sea gas exchange versus biology

The contribution of biology based on Eqs. (2) and (3) to the δ¹³C distribution is presented in Fig. 2, broadly in agreement with previous studies (Kroopnick, 1985; Schmittner et al., 2013). The contribution of biology to the modelled δ¹³C distribution is generally below 45 % and has a steep gradient from the surface to the deep ocean. The (thermodynamic) fractionation effect of air–sea gas exchange on δ¹³C is strongly impeded by the long equilibration time of ¹³C, which leaves room for biological processes to contribute significantly to δ¹³C and Δδ¹³C (Lynch-Stieglitz et al., 1995; Murnane and Sarmiento, 2000; Schmittner et al., 2013; Eide et al., 2017a). In the ocean below 250 m, the influence of biology increases to 35 %–45 % due to the remineralisation of POC, with the exception of the Arctic Ocean, where no POC production is modelled due to the sea ice cover (Figs. 2b and S1). ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$ is close to 50 % around 1000 m depth in the northern Pacific and Indian oceans, due to the old water masses located there, which have accumulated a large fraction of remineralised DIC. At the surface, air–sea gas exchange dominates the δ¹³C signature of DIC, as is visible from the low ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$ (Fig. 2a). The only exception at the surface is in upwelling regions, where a relatively high ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$ is expected due to high POC production and upwelled remineralised carbon. High ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$generally corresponds to a low-δ¹³C water mass (compare Figs. 1 and 2), as expected from the upwelling of ¹³C-depleted DIC and modelled and observed close to the Antarctic continent (Fig. 1a and observations by Eide et al., 2017a). The results presented in Fig. 2 appear to be quite robust as ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$ typically does not change by more than 5 %–10 % for the wide range of biogeochemical states, as is explored in the sensitivity experiments presented below.

3.3 Sensitivity of Δδ¹³C and δ¹³C

3.3.1 Air–sea gas exchange of carbon

Atmospheric and marine carbon isotopic ratios are generally in thermodynamic disequilibrium due to their relatively long equilibration timescales compared to the time of contact of a water parcel with the atmosphere. CO₂ equilibration through the air–sea interface takes ∼4 months (Jones et al., 2014) and is inversely related to the Revelle buffer factor, and slowed down by a factor of ∼20 compared to inert gases due to carbon speciation (i.e. the adjustment of the bicarbonate pool). Again ∼10 times slower than CO₂, the air–sea equilibration of the atmospheric isotope ratio ¹³CO₂ ∕ ¹²CO₂ (i.e. δ¹³C^atm) with marine DI¹³C ∕ DI¹²C (i.e. δ¹³C) takes ∼4 years (Jones et al., 2014). The equilibration timescale of the carbon isotopes is not facilitated by the buffering reaction of CO₂ with H₂O, but instead depends on the DIC : CO₂ ratio of seawater (Broecker and Peng, 1974; Jones et al., 2014; Galbraith et al., 2015). Over 90 % of the surface ocean δ¹³C signature is set by air–sea gas exchange outside of upwelling regions across the world's oceans (Fig. 2), making the equilibration across the air–sea interface important for surface ocean δ¹³C. Understanding the effects of equilibration across the air–sea interface is thus key to understanding global surface ocean δ¹³C signatures. Here we explore two extreme cases, very slow but non-zero gas exchange (“gas slow”, gas exchange rate divided by 4) and very fast gas exchange to bring the air–sea equilibration close to equilibrium (“gas fast”, gas exchange rate multiplied by 4).

Our results show that the effects of changes in air–sea gas exchange on δ¹³C mainly depend on the prior disequilibrium δ¹³C_diseq (δ¹³C_diseq = δ¹³C-δ¹³C_eq, where δ¹³C_eq represents the δ¹³C value a water parcel would have had if it would have fully equilibrated with the atmosphere; see also Gruber et al., 1999). Full isotopic equilibrium with the atmosphere results in a δ¹³C_surface of ∼0.5 to ∼4 ‰ at low and high latitudes, respectively (Menviel et al., 2015), where the range is caused by the temperature-dependent fractionation (Mook et al., 1986; Zhang et al., 1995). In this study, modelled ε is between 7.7 ‰ and 11 ‰ . This thermodynamic effect increases the difference between δ¹³C_surface and δ¹³C_eq at the poles (Menviel et al., 2015), thus increasing the potential of high-latitude surface water to be affected by air–sea gas exchange fluxes.

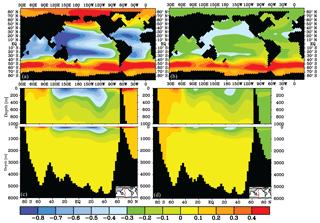
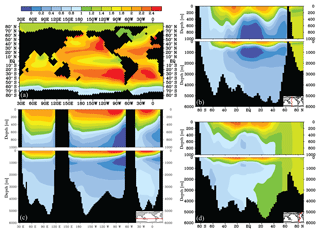
Figure 3 δ¹³C of DIC (‰) difference after 2000 years for the fast gas exchange experiments (experiment − control): global experiments (a, c) and SO-only experiments (b, d), at 25 m depth (a, b) and as a Pacific transect of δ¹³C difference (c, d).

Our gas exchange experiments (Table 1) show a transient phase where the net global air–sea gas exchange flux F_net is non-zero, which affects $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ until a new quasi-equilibrium is established (Fig. S3). We find an increase in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ by 10 ppm (slow gas exchange) and a decrease by 4 ppm (fast gas exchange) after 2000 years, respectively. If gas exchange is only changed in the SO (i.e. for 22 % of the global ice-free ocean area), an effect of 3.7 and −0.7 ppm is found after 2000 years (Table 2). Gas exchange in the SO can thus cause a disproportionate response (∼30 % of the sensitivity) in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. These changes occur in the first ∼600 years of the sensitivity experiments (Fig. S3), with the strongest changes occurring after ∼100 years. The air–sea pCO₂ difference is smaller at increased gas exchange rates and larger at reduced gas exchange rates (Fig. S4). δ¹³C^atm decreases by 0.3 ‰ during fast gas exchange and increases by 0.2 ‰ when the gas exchange rate is reduced. This is explained by the increase in the global amount of air–sea gas exchange F_u+d in the fast gas exchange experiment (4 times more, at 542 Gt C yr⁻¹). Such an increase leads to a smaller thermodynamic disequilibrium, which increases the mean marine δ¹³C and lowers δ¹³C^atm. Slow gas exchange reduces F_u+d (by 73 % to 36 Gt C yr⁻¹), thus decreasing the role of air–sea gas exchange on surface ocean δ¹³C. This results in an increased contrast between atmospheric and surface ocean δ¹³C, which explains the increase in δ¹³C^atm. Moreover, our SO-only experiments show that these effects on δ¹³C^atm are more pronounced if gas exchange only changes in the SO. This indicates that the remainder of the ocean offsets part of the atmospheric sensitivity to SO change.

Table 2 Results of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (ppm) and δ¹³C^atm (‰) for all sensitivity experiments.

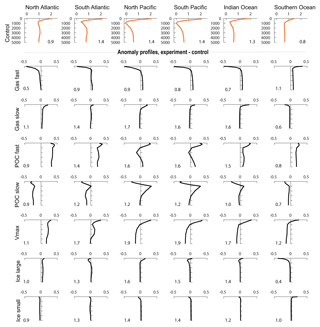
Figure 4 Volume-weighted basin mean anomaly profiles of δ¹³C after 2000 years, with respect to the control profiles (upper row). Δδ¹³C denoted per basin in the lower right (control) and lower left (sensitivity experiments) corner of each subgraph. Results are presented for the global gas exchange and POC sinking experiments. Basin extent is visualised in Fig. S8.

δ¹³C shows a different response in high latitudes compared to the lower latitudes in the surface ocean (Figs. 3a and S5): an increased air–sea gas exchange rate lowers the surface ocean δ¹³C of DIC by 0.2 ‰ to 0.9 ‰ at the lower latitudes and increases surface ocean δ¹³C at high latitudes by 0.2 ‰–0.5 ‰ (Figs. 3 and 4). The direction of the response indicates whether δ¹³C_diseq is positive or negative, and is in line with previous studies (Schmittner et al., 2013; Galbraith et al., 2015) that show that the disequilibrium is negative (δ¹³C < δ¹³C_eq) at high latitudes and in low-latitude upwelling regions, and positive elsewhere. The sign of δ¹³C_diseq, and thus the direction of the δ¹³C response, is understood from the difference between the natural δ¹³C distribution (Fig. 1) and the δ¹³C_eq, which depends on thermodynamic fractionation (Sect. 2). At increased gas exchange rates (i.e. closer to equilibrium), δ¹³C has to increase in cool high-latitude surface waters and has to decrease in warm low-latitude surface waters in order to get closer to equilibrium (Menviel et al., 2015; Murnane and Sarmiento, 2000). The net effect of a slower gas exchange rate on surface ocean δ¹³C is less pronounced than the effect of an increased gas exchange rate (Figs. S5, 3). The smaller effects seen for slow gas exchange indicate that the control model ocean is a “slow ocean”, i.e. closer to (very) slow gas exchange than to thermodynamic equilibrium (infinitely fast gas exchange).

The effect of the gas exchange rate on marine δ¹³C is mostly established in the top 250 to 1000 m of the water column (Figs. 3c, d, 4). Recording this air–sea gas exchange signal thus strongly depends on the reliability of planktic δ¹³C-based δ¹³C_surface reconstructions and knowledge of the living depth represented by the planktic foraminifera. The signal penetrates deepest (to ∼2000 m depth) into the North Atlantic (Fig. 4), where δ¹³C is strongly influenced by air–sea gas exchange (Fig. 2a). However, the interpretation of variations in North Atlantic benthic δ¹³C as coming partly from air–sea gas exchange (Lear et al., 2016) is not supported by our experiment. Due to the limited export of the δ¹³C signal to depth, the sensitivity of Δδ¹³C to the gas exchange rate mainly comes from surface ocean δ¹³C. Globally, the Δδ¹³C is weakened to 0.87 ‰ when the thermodynamic disequilibrium is decreased (i.e. “Gas fast”, Fig. 5) and Δδ¹³C strengthens to 1.32 ‰ when the thermodynamic disequilibrium is increased (“Gas slow”, Fig. 5). The extent to which thermodynamic equilibrium can develop is thus an efficient way to change the biologically induced Δδ¹³C (Murnane and Sarmiento, 2000); however, this is only true at lower latitudes where δ¹³C_diseq is positive: the direction of the high-latitude SO Δδ¹³C sensitivity mirrors the sensitivity of the low-latitude regions (Fig. 4) as well as the global mean due to its negative δ¹³C_diseq.

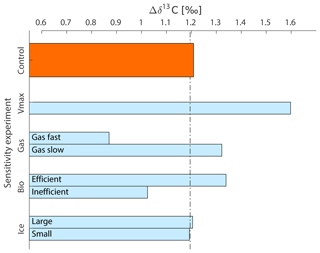
Figure 5 Global mean Δδ¹³C after 2000 years for the different sensitivity experiments (Table 1). “Bio – Efficient” represents the high POC sinking rate experiment, “Bio – Inefficient” the slow POC sinking rate experiment. The results for the Southern Ocean-only experiments (Sect. 2) are described in the text.

3.3.2 The biological pump: POC sinking rate

The net effect of a regionally changed biological pump efficiency depends on the sequestration efficiency, which depends on the interplay between the biological pump and ocean circulation (DeVries et al., 2012). A more efficient biological pump (here, a higher POC sinking rate) leads to a loss of carbon to the sediments, which affects $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and δ¹³C^atm on millennial timescales. Here we present results from a 2000-year simulation (as for the other experiments), which are thus transient results. A full equilibrium of the system could take as long as 200 000 years (Roth et al., 2014). On these long timescales other processes and feedbacks would occur (Tschumi et al., 2011), which complicates the attribution of changes to a primary trigger. A fast POC sinking rate leads to a $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ decrease of 23 ppm and higher (+0.2 ‰) atmospheric δ¹³C after 2000 years (Table 2, Fig. S3) as well as an increase in mean ocean δ¹³C of 0.15 ‰ , caused by the transient sediment burial of low-δ¹³C POC. The transient imbalance between weathering and burial fluxes can thus cause profound changes in both marine and atmospheric δ¹³C, and moreover provides an important feedback for the long-term marine carbon cycle (Tschumi et al., 2011; Roth et al., 2014). In our experiment, an efficient biological pump leads to a global ∼6 % decrease in the amount of air–sea gas exchange F_u+d because of efficient export of carbon to depth, thereby lowering the net upward advection of carbon. A mirrored but weaker response is modelled for a decrease in biological pump efficiency: halving the POC sinking rate leads to a 13 ppm increase in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (of which 23 % can be explained by the SO) and a more negative atmospheric δ¹³C (−6.7 ‰ ) and 7 % increased F_u+d (Table 2, Fig. S3).

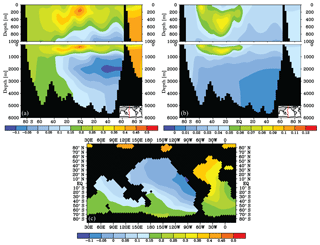
Figure 6 δ¹³C of DIC (‰) difference after 2000 years for the POC sinking rate experiments (experiment − control): (a) the global efficient biological pump (high POC sinking rate) experiment for a Pacific transect and (b) the SO-only efficient biological pump experiment for a Pacific transect and (c) the global efficient biological pump experiment at 3000 m depth. Note the different scales.

Surface ocean δ¹³C is mostly influenced by the changes in productivity and the vertical displacement of the POC remineralisation depth. The deepening of the remineralisation depth has been extensively discussed in the literature (Boyle, 1988; Keir, 1991; Mulitza et al., 1998; Roth et al., 2014) and likely explains lowered mid-depth glacial δ¹³C together with changes in ocean circulation (for example, Toggweiler, 1999). POC sinking removes nutrients and preferentially light ¹²C carbon from the surface ocean, while exporting them to the deep ocean. If POC sinking rates are high, this increases the mean surface ocean δ¹³C (contributing to the δ¹³C^atm increase) by 0.12 ‰ and lowers mean deep ocean δ¹³C by 0.01 ‰ (Fig. 6) – with values corrected for the overall 0.15 ‰ increase in marine δ¹³C, which occurs due to transient imbalance between weathering and sediment burial. Therefore, even though the absolute export production is globally reduced by 26 %, the biological pump is more efficient as any new nutrients in the surface ocean will immediately be used and exported. With a halving of the POC sinking rate, the remineralisation is confined closer to the surface ocean (Fig. 4). The net effect is that surface ocean δ¹³C is reduced (by a mean of 0.21 ‰ – corrected for the mean ocean change of 0.04 ‰) throughout the ocean (Fig. 4), because the fractionation effect during photosynthesis is counteracted by the remineralisation of POC (which would normally have occurred at depth). The SO plays a relatively minor role in the sensitivity to the POC experiments (Fig. 6b). Changes in deep ocean δ¹³C depend on the water mass age (Fig. 6c): old water (North Pacific) has a larger remineralisation signal when the biological pump is efficient. Independent of the biological pump efficiency, the relatively young waters of the deep North Atlantic generally adopt about the same δ¹³C signal as the surface ocean δ¹³C, which is set by air–sea gas exchange. This is in agreement with a relatively low ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$ estimate for the deep North Atlantic (∼30 %).

The sensitivity of Δδ¹³C to changes in POC sinking rate depends strongly on location (Figs. 4 and 6). In general, the Δδ¹³C is strengthened for an increased biological pump efficiency (Fig. 5), and this effect is stronger with water mass age (Figs. 6c and 4). The downward shift of the remineralisation depth of low-δ¹³C POC drives this increase in Δδ¹³C, a mechanism discussed by Boyle (1988) and Mulitza et al. (1998), among others, to understand glacial Δδ¹³C increase. Our results show that the vertical displacement of the δ¹³C profile is most pronounced in the North and South Pacific (Fig. 4). The North Atlantic Δδ¹³C is much less affected as these waters are mostly influenced by air–sea gas exchange. Instead, the entire North Atlantic profile is shifted more than in the other ocean basins (Fig. 4). Δδ¹³C weakens for a reduced biological pump efficiency (Figs. 4 and 5), especially in older water where ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{bio}}^{\mathrm{perc}}$ is higher (Fig. 2a). It is worth noting, however, that the changes in Δδ¹³C in the SO are comparably small because the vertical mixing in the SO of the low-δ¹³C deep water mostly causes shifts in the entire δ¹³C profile, not a change in the gradient (Fig. 4).

Figure 7 δ¹³C of DIC (‰) difference after 2000 years for the V_max nutrient depletion experiment (experiment − control): (a) at 25 m depth and for (b) an Atlantic transect and (c) a Pacific transect.

3.3.3 The biological pump: SO nutrient depletion

Consistent with previous studies (Sarmiento et al., 2004; Marinov et al., 2006; Primeau et al., 2013), we find a large atmospheric impact of our SO nutrient depletion experiment. The high SO nutrient uptake efficiency (i.e. an efficient biological pump) causes a 44 ppm reduction in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ after 2000 years. The V_max experiment reaches quasi-equilibrium after ∼800 years, as seen from the time evolution of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and δ¹³C^atm (Fig. S3). δ¹³C^atm increases to −6.1 ‰ due to the increased surface ocean δ¹³C (Fig. 7a). This 0.4 ‰ increase is high compared to the results of Menviel et al. (2015), who found a δ¹³C^atm sensitivity of 0.1 ‰–0.2 ‰ in response to changes in SO nutrient utilisation. The different development time compared to the fast POC sinking rate experiment is explained by the absence of long-term loss of carbon to the sediments in the V_max experiment, because transport and water-column remineralisation within the SO limits an increase in POC burial there. In the SO, net carbon uptake (F_net) increases fourfold to 1.5 Gt C yr⁻¹ (Fig. S6) because the high nutrient and carbon consumption transport carbon into the ocean interior and do not permit CO₂ to escape to the atmosphere.

SO export production of POC is increased (Fig. S7) by a factor of 2.4, causing global POC export production to increase by 15 %, albeit reducing lower-latitude productivity (non-SO up to ∼35^∘ N) by 13 %. This relocation of global POC export production in response to SO increased nutrient uptake efficiency is in agreement with earlier studies (Marinov et al., 2006; Primeau et al., 2013). The increased surface ocean δ¹³C signature everywhere north of the SO sea ice edge (Fig. 7a) is in the SO attributed to increased POC export production counteracted by a decreased F_u+d (which would reduce δ¹³C_surface in the SO because of the negative δ¹³C_diseq; Figs. 3 and S5). At lower latitudes, the decreased F_u+d (which increases δ¹³C_surface in lower latitudes because of the positive δ¹³C_diseq; Figs. 3 and S5) dominates the effect of the 13 % lower POC export production on δ¹³C_surface. At depth and under the sea ice in the Antarctic, where deep water upwells, the imprint of additional POC remineralisation at depth decreases δ¹³C of DIC (Fig. 7). This decrease in δ¹³C is only visible in water masses downstream of the SO (Fig. 7b and c) and is most pronounced in the deep North Pacific (Fig. 7c). The increased nutrient uptake rate in the SO increases global mean Δδ¹³C by 0.4 ‰ (Fig. 5) as well as increasing Δδ¹³C in all ocean basins (Fig. 4), as seen for the fast POC sinking rate experiment. Δδ¹³C is affected more in older waters, where a more pronounced remineralisation imprint has developed (Fig. 4). Besides effects on the δ¹³C distribution (Fig. 7), the O₂ and ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ distributions change as well: the O₂ distribution is reorganised such that surface ocean O₂ is increased (by up to 20 µmol kg⁻¹, with largest changes in the SO), while deep ocean O₂ is reduced downstream of the SO (by up to 40 µmol kg⁻¹). Surface ocean ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ is reduced mostly in the SO (by up to 0.8 µmol kg⁻¹). This signal is, however, too small to significantly increase mean deep ocean ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$. This implies a reduction in global preformed phosphate governed by the efficient nutrient uptake in the SO; see also Primeau et al. (2013). SO nutrient drawdown can thus cause negligible mean (deep) ocean ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ and δ¹³C changes, despite causing large changes in local δ¹³C and Δδ¹³C through the interplay between biology and air–sea gas exchange. Interesting in light of glacial proxy interpretation, the fit to the δ¹³C : ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship is improved throughout the ocean for the V_max experiment, similar to the effects of the “Gas slow” experiment (Fig. 8). Changes in the goodness of fit of δ¹³C and ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ data to the δ¹³C : ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship (i.e. δ¹³C_bio $=\mathrm{3.18}-\mathrm{1.05}\times$ ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$, Sect. 2) are usually interpreted as changes in ventilation or air–sea gas exchange (Lear et al., 2016; Eide et al., 2017b). However, here we show that changes in the fit represent the relative importance of biology and air–sea gas exchange in determining δ¹³C, as both changes in δ¹³C_diseq (i.e. gas exchange rate experiments) and changes in the biological pump can affect the goodness of fit to the δ¹³C : ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship (Fig. 8).

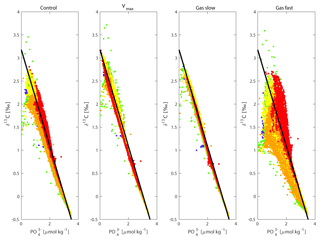
Figure 8 δ¹³C versus ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ for the control, V_max, “gas slow” and “gas fast” experiments for all ocean basins except the Nordic Seas (i.e. basins A to F in Fig. S8). Dark blue = A/North Atlantic, Light blue = B/South Atlantic, Red = C/Southern Ocean, Yellow = D/South Pacific, Green = E/North Pacific, Orange = F/Indian Ocean. The black line is the δ¹³C_bio $=\mathrm{3.18}-\mathrm{1.05}\times$ ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship, i.e. the relationship between δ¹³C and ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ expected if only biology affected δ¹³C (Sect. 2). Deviations from the black line represent the relative importance of air–sea gas exchange compared to biology for δ¹³C.

3.3.4 Southern Ocean sea ice cover

The sea ice cover of the SO changes considerably over glacial–interglacial cycles, as well as on seasonal timescales (Crosta, 2009) and Fig. A22 therein). In general, the model sea ice cover will inhibit light penetration into the surface ocean and limit air–sea gas exchange based on its thickness (Sect. 2). In the sensitivity experiments we assume complete inhibition of both light and air–sea carbon exchange by the sea ice. In this section we thus explore the effect of both biological production and air–sea gas exchange in two extreme cases, (i) the largest realistic sea ice cover based on the glacial maximum winter extreme (50^∘ S) and (ii) the smallest sea ice cover based on the contemporary summer minimum sea ice extent (70^∘ S). Note that there is a constant sea ice cover about north of 70^∘ N and south of 60^∘ S in the control run of the model. Therefore, the strongest marine δ¹³C change is expected south of 60^∘ S for a decreased sea ice cover and between 50 and 60^∘ S for an increased sea ice cover, as this is the area where ice cover is altered relative to the control run. Ocean circulation changes that could result from a changed sea ice cover are not taken into account, as we want to study the potential isolated effect of sea ice on δ¹³C through biological and air–sea gas exchange changes.

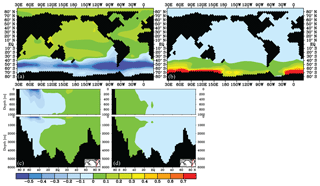
Figure 9 δ¹³C of DIC (‰) difference after 2000 years for the Antarctic sea ice cover experiments (experiment − control): the effect of a large (a, c) and small (b, d) Antarctic sea ice cover, for 25 m depth (a, b) and an Atlantic transect (c, d).

Both local and global air–sea carbon fluxes are influenced by a change in the SO sea ice cover, which results in changes in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and δ¹³C^atm. In our experiment, $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ increases by 9 ppm for an increased sea ice cover and decreases by 6 ppm for a decreased sea ice cover (Table 2, Fig. S3). As noted in Sect. 3.3.1, a change in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is governed by a transient change in the net air–sea gas exchange flux F_net until a new equilibrium is established. An extended ice cover causes more CO₂ to remain in the atmosphere because the additional ice covers a part of the SO that is a sink for CO₂ (Fig. S4 – Control). As the net global air–sea gas exchange F_net approaches equilibrium, the non-SO ocean therefore becomes a smaller source for carbon. This reduces the net gas exchange F_net inside and outside of the SO by ∼40 %–50 %. Our results show that the effects of a changed sea ice cover on $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ are yet to be fully understood: Stephens and Keeling (2000) for example modelled a strong decrease in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in response to an increased sea ice cover south of the Antarctic Polar Front, because they mostly cover a part of the SO that is a source of carbon to the atmosphere. In our study, the reduction in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ by 6 ppm due to a reduced sea ice cover is attributable to the POC production in the previously ice-covered area between ∼60 and 70^∘ S. In a sensitivity experiment where the ice cover influences air–sea gas exchange only, the sea ice retreat leads to an increase in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ because the region below the ice is strongly supersaturated in carbon with respect to the atmosphere. The increased sea ice cover leads to a complete suppression of air–sea gas exchange south of 50^∘ S. Since this region is in negative carbon isotopic disequilibrium with the atmosphere (δ¹³C < δ¹³C_eq), the ice cover inhibits a δ¹³C flux into the ocean. As a result, $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ increases to −6.2 ‰ , while the opposite happens for a reduced sea ice cover, leading to a lowered $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (−6.6 ‰).

The increased sea ice cover over the SO results in a surface ocean δ¹³C reduction relative to the control of −0.5 ‰ to −0.1 ‰ in the SO (Figs. 4 and 9), while δ¹³C increases outside of the SO by 0 ‰–0.2 ‰ (Fig. 9a). The reduction is especially pronounced between 40 and 60^∘ S. The ∼40 % reduced POC export production in the SO due to light inhibition by the sea ice cover causes a major part of the SO surface δ¹³C reduction, as the absence of photosynthesis will cause lower surface ocean δ¹³C. Next to that, the reduced air–sea gas exchange F_u+d in the SO also leads to a lowered surface ocean δ¹³C signature. About the opposite happens when we simulate a strongly decreased sea ice cover (only ice south of 70^∘ S): a small reduction of δ¹³C is modelled outside the SO, but the SO δ¹³C_surface locally becomes up to ∼0.8 ‰ higher relative to the control (Fig. 9b) as the increased amount of air–sea gas exchange F_u+d decreases the carbon isotopic disequilibrium and increases POC production in the newly exposed area, both acting to increase δ¹³C of DIC.

The effect of a changed ice cover on deep ocean δ¹³C is less than ∼0.1 ‰ (Fig. 9c, d) as the surface signal is diluted while it follows the general ocean circulation. As for air–sea gas exchange (Sect. 3.3.1), no pronounced deep ocean δ¹³C signal is found outside of the SO due to sea ice cover changes (this is opposed to interpretations by Lear et al., 2016). Global mean Δδ¹³C is not significantly affected by changes in the SO sea ice cover (Fig. 5) because the low- and high-latitude effects on δ¹³C_surface cancel each other out. The SO Δδ¹³C, however, weakens considerably to 0.4 ‰ when the 50–60^∘ S region becomes covered with sea ice and strengthens to 1 ‰ if the sea ice is removed between 60 and 70^∘ S (Fig. 4). The presence or absence of a sea ice cover should thus be clearly visible in especially planktic SO δ¹³C sediment records. The effect on Δδ¹³C spreads downstream of the SO, where Δδ¹³C is increased by up to 0.2 ‰ in the Pacific Ocean for an increased SO sea ice cover (Fig. 4).

3.4 Modelled versus observed Δδ¹³C variations

The variations in Δδ¹³C on glacial–interglacial timescales provide researchers with a tracer to study the biogeochemical state of the past global ocean, under the condition that we can interpret (variations in) Δδ¹³C. The idealised perturbations made to the (Southern) Ocean in this study show that global mean Δδ¹³C is particularly sensitive to an increased gas exchange rate and changes in the efficiency of the biological pump. Global mean Δδ¹³C varies by up to about ±0.35 ‰ around the pre-industrial model reference (1.2 ‰ ) in response to biogeochemical change (Fig. 5) – under the assumption of a constant ocean circulation. However, the sensitivity of Δδ¹³C to biogeochemical changes depends strongly on location for all sensitivity experiments (Fig. 4), possibly explaining part of the incoherency of reconstructed planktic and benthic foraminiferal δ¹³C from sediment cores (Oliver et al., 2010). In general, such Δδ¹³C reconstructions show Δδ¹³C variations in ∼1 ‰ over the past 350 000 years (Shackleton et al., 1983; Shackleton and Pisias, 1985; Boyle, 1988; Charles et al., 2010; Oliver et al., 2010; Ziegler et al., 2013). Ocean circulation changes explain at least part of these variations in Δδ¹³C (Oppo et al., 1990; Heinze et al., 1991; Heinze and Hasselmann, 1993; Toggweiler 1999; Charles et al., 2010; Jansen, 2017). However, the changes in the biogeochemical state of the ocean imposed in our experiments show that variations in Δδ¹³C could be strongly influenced by (SO) biogeochemistry as well. Δδ¹³C is increased during glacials and reduced during interglacials across a large set of sediment cores (Boyle, 1988; Charles et al., 2010; Oliver et al., 2010; Ziegler et al., 2013). Rapid and large changes have been documented for SO Δδ¹³C records (Ziegler et al., 2013), and here we show that biogeochemical changes in the SO affect Δδ¹³C globally. Our results show that an increase in mean Δδ¹³C could biogeochemically result from slower gas exchange, increased POC sinking rates, or an increased nutrient uptake rate in the SO (Figs. 4 and 5). Such biogeochemical changes have been associated with glacial periods (for example, Ziegler et al., 2013) and are potential candidates to explain part of the Δδ¹³C increase in interplay with stronger ocean stratification. Sediment-core reconstructions of Δδ¹³C show that an increased Δδ¹³C can originate from a downward shift of the metabolic imprint of low-δ¹³C POC, which would increase shallow δ¹³C (Boyle, 1988; Mulitza et al., 1998; Toggweiler, 1999; Charles et al., 2010), and/or a deep ocean δ¹³C decrease (Broecker, 1982; Boyle, 1988; Oliver et al., 2010), with little variation recorded for surface ocean δ¹³C. The absence of a clear surface δ¹³C signal could in the SO be the net effect of an increased sea ice cover (locally decreasing δ¹³C; Figs. 4 and 9a) and an increased biological pump efficiency (locally increasing δ¹³C_surface; Figs. 6a and b, 7a) or increased SO thermodynamic equilibrium (Fig. 3a and b) – if these opposing signals get mixed. A pronounced deep ocean δ¹³C decrease is associated with an efficient biological pump and older water masses in our study (Fig. 4). Interestingly, large local changes in deep ocean δ¹³C and Δδ¹³C do not necessarily imply changes in mean deep ocean ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ (Sect. 3.3.3).

The local character of the Δδ¹³C sensitivity (Fig. 4) implies that correlations between sediment core Δδ¹³C ∕ δ¹³C variations and global parameters (e.g. pCO₂) are not easily extrapolated to other sediment cores over large distances. Analysis of SO Δδ¹³C reconstructions from sediment cores, at 42 and 46^∘ S (Charles et al., 2010) for example, shows that there is a strong correlation between these cores and Northern Hemisphere climate fluctuations. We expect that this strong correlation does not exist for cores further south in the SO because our results indicate that the SO south of ∼50–60^∘ S often has a different Δδ¹³C response to biogeochemical change than the rest of the ocean.

Interglacial periods are generally thought to be associated with a decrease in the efficiency of the biological pump and increased deep-ocean ventilation via southern-sourced water masses (Gottschalk et al., 2016). Increased deep-ocean ventilation might be driven by increased winds (Tschumi et al., 2011), which would (apart from changing the SO circulation pattern) also increase gas exchange rates. Each of these processes indeed reduces mean Δδ¹³C in our experiments (Fig. 5), although this is less pronounced in the SO (Fig. 4). However, the interglacial reduction of Δδ¹³C seems to originate from a deep ocean δ¹³C increase compared to the glacial deep ocean δ¹³C (Broecker, 1982; Charles et al., 2010; Oliver et al., 2010). Our results show that neither an inefficient biological pump nor fast gas exchange can be associated with a pronounced deep sea δ¹³C increase relative to our control, because their effects are restricted to the surface ocean. On the other hand, the interglacial decrease in Δδ¹³C is a decrease compared to the glacial state: if glacial SO nutrient uptake was higher (V_max), a return to the “normal” state (i.e. the model control run) would result in a major decrease in Δδ¹³C (Figs. 4 and 5).

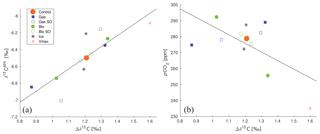
Figure 10 Relationships between global mean Δδ¹³C, δ¹³C^atm, and $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. (a) Global mean Δδ¹³C versus δ¹³C^atm of the different sensitivity experiments. R² of the best-fit line is 0.71, and the line is described by $y=\mathrm{1.3}x-\mathrm{8.1}$. (b) Global mean Δδ¹³C versus $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of the different sensitivity experiments. R² of the best-fit line is 0.39, and the line is described by $y=-\mathrm{54}x+\mathrm{341}$.

3.5 The relationship between Δδ¹³C, δ¹³C^atm, and $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$

One would expect variations in δ¹³C^atm as well as Δδ¹³C to correlate with variations in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$, because similar processes (biology and air–sea gas exchange) steer their distribution and concentrations (Shackleton and Pisias, 1985; this article). Δδ¹³C is considered a promising proxy for reconstructions of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ for times predating ice-core records (Lisiecki, 2010). Here we show that a positive linear relationship between δ¹³C^atm and global mean Δδ¹³C (Fig. 10a) holds over a wide range of biogeochemical states, as simulated in the sensitivity experiments. However, the negative linear relationship between $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and global mean Δδ¹³C (Fig. 10b) is weak (R²=0.39). Yet, previous studies do show the existence of a correlation between local Δδ¹³C and $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (such as found by for example Dickson et al., 2008), and correlation of modified Δδ¹³C between ocean basins with $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (Lisiecki, 2010). The effects of ocean circulation on glacial–interglacial δ¹³C^atm changes, not studied here, are most pronounced in response to Antarctic Bottom Water formation rate variations and are of the order of 0 ‰–0.15 ‰ (Menviel et al., 2015). Our results show that δ¹³C^atm varies by up to about ±0.5 ‰ in response to biogeochemical changes (Table 2). Changes in the POC sinking rate lie approximately along a line in δ¹³C^atm : Δδ¹³C space (Fig. 10a), suggesting that changes in the biological pump efficiency are important for the δ¹³C^atm : Δδ¹³C relationship. Likewise, both the gas exchange rate and biological pump experiments lie along an approximate lines in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ : Δδ¹³C space (Fig. 10b, albeit a different one – leading to a low total correlation). Changes in air–sea gas exchange (as simulated in the gas exchange and sea ice cover experiments) affect δ¹³C^atm more than Δδ¹³C. This confirms the idea that Δδ¹³C is governed by biological processes and will also set δ¹³C^atm, unless air–sea gas exchange gets the chance to dominate δ¹³C^atm. The high potential of SO air–sea gas exchange to change δ¹³C^atm (Table 2: sea ice and gas exchange rate experiments) complements recent studies showing that increased SO ventilation of deep ocean carbon is a likely candidate for glacial–interglacial δ¹³C^atm excursions – which are of the order of 0.5 ‰ (Lourantou et al., 2010; Menviel et al., 2015; Bauska et al., 2016; Eggleston et al., 2016).

4 Summary and conclusions

This study addresses the sensitivity of modelled marine and atmospheric δ¹³C and Δδ¹³C to changes in biogeochemical parameters under constant ocean circulation, focusing on the contribution of the SO (the ocean south of 45^∘ S, 22 % of the global ice-free ocean area). Variations in Δδ¹³C recorded in sediment records are sensitive to ocean circulation changes as shown in previous studies, but here we show that the biogeochemical state of the (Southern) Ocean can also have large effects on Δδ¹³C across all ocean basins. Using the ocean biogeochemistry general circulation model HAMOCC2s, a set of sensitivity experiments was carried out, which focuses on the biogeochemical aspects known to be important for δ¹³C and Δδ¹³C. Specifically, the experiments explore changes in air–sea gas exchange rate, sea ice extent (influencing both biological production and the air–sea gas exchange of carbon), and the efficiency of the biological pump through the POC sinking rate and nutrient uptake rate.

The results show the important role of the SO in determining global δ¹³C and Δδ¹³C sensitivities, as well as the strong spatial differences in these. A new quasi-equilibrium state developed mostly within the first 100–800 years of the sensitivity experiments, except for the POC sinking experiment, where an imbalance between weathering and burial causes a long-term drift. The δ¹³C signature is governed by different processes depending on location: air–sea gas exchange sets surface ocean δ¹³C in all ocean basins, contributing 60 %–100 % to the δ¹³C signature. At depth and with increasing water mass age, the influence of biology increases to 50 % in the oldest water masses (North Pacific) due to POC remineralisation. This spatial pattern behind the δ¹³C signature of a water parcel results in a non-uniform sensitivity of δ¹³C to biogeochemical change. Global mean Δδ¹³C varies by up to about ±0.35 ‰ due to biogeochemical state changes in our experiments (at a constant ocean circulation) (Fig. 5). This amplitude is almost half of the reconstructed variation in Δδ¹³C on glacial–interglacial timescales (1 ‰), and could thus contribute to variations in Δδ¹³C together with ocean circulation changes. However, Δδ¹³C can have a different response on a basin scale: the ocean's oldest water (North Pacific) responds most to biological changes, the young deep water (North Atlantic) responds strongly to air–sea gas exchange changes, and the vertically well-mixed water (SO) has a low or even reversed Δδ¹³C sensitivity compared to the other basins. The amplitude of the Δδ¹³C sensitivity can be higher at decreasing scale, as seen from a maximum sensitivity of about −0.6 ‰ on ocean basin scale (Fig. 4). Interestingly, the direction of both glacial (intensification of Δδ¹³C) and interglacial (weakening of Δδ¹³C) Δδ¹³C change matches changes in biogeochemical processes thought to be associated with these periods. This supports the idea that biogeochemistry explains part of the reconstructed variations in Δδ¹³C, in addition to changes in ocean circulation.

An increased gas exchange rate has the potential to reduce the biologically induced Δδ¹³C through the reduction of surface ocean and atmospheric δ¹³C. Increased gas exchange, however, only reduces Δδ¹³C in the low latitudes: in high latitudes, increased gas exchange will increase Δδ¹³C (by increasing δ¹³C_surface) because of the negative disequilibrium δ¹³C_diseq (i.e. δ¹³C < δ¹³C_eq) in this region, and thus potentially increase δ¹³C_surface (Sect. 3.3.1). Notably, $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$, δ¹³C^atm, and marine δ¹³C are shown to be disproportionally sensitive to SO gas exchange rate changes.

Changes in the efficiency of the biological pump also have a major potential to alter Δδ¹³C as well as $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and δ¹³C^atm. The globally increased POC sinking rate experiment shows that Δδ¹³C strengthens in low latitudes (and more so in older waters) by deepening the low-δ¹³C signature of remineralised POC, while SO Δδ¹³C is not very sensitive to POC sinking rates. The SO effects are comparably small because the vertical mixing in the SO of the low-δ¹³C deep water only causes shifts in the entire δ¹³C profile, not a change in the gradient (Fig. 4). Increased POC sinking causes a long-term imbalance between weathering and sediment burial which leads to an increase in mean δ¹³C and δ¹³C^atm (of about 0.15 ‰) after 2000 years. Increased nutrient uptake in the SO (V_max experiment) results in 13 % lower non-SO POC export production up to ∼35^∘ N, in agreement with previous studies on the role of the SO biological pump in lower-latitude productivity. Interestingly, the increase in Δδ¹³C in all ocean basins occurs without significantly changing mean (deep) ocean ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$, which advocates for increased SO nutrient uptake to explain (part of) glacial–interglacial Δδ¹³C variations. Furthermore, our results show that improved goodness of fit of the model data to the δ¹³C : ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship can be driven by reduced gas exchange as well as biological uptake efficiency in the SO, since both increase the importance of biology relative to air–sea gas exchange for δ¹³C. Caution should thus be exercised when interpreting changes in the fit of observations to the δ¹³C : ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ relationship as changes in ocean ventilation or air–sea gas exchange alone.

A significant linear relationship was found across the sensitivity experiments between δ¹³C^atm and Δδ¹³C (R²=0.71), and a weaker one (R²=0.39) for $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and Δδ¹³C. This result shows that paleo-reconstructions of δ¹³C^atm based on Δδ¹³C could be valid for a wide range of biogeochemical states. Previous studies have shown good correlation between $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and local Δδ¹³C, but our results suggest that the relationship may not be valid if both biological and gas exchange rate changes occur. The maximum response of δ¹³C^atm to the biogeochemical changes imposed in our experiments (up to 0.5 ‰) is larger than the idealised maximum effect of ocean circulation changes on δ¹³C^atm (0 ‰–0.15 ‰; Menviel et al., 2015), which underlines the potential importance of biogeochemical processes for variations in δ¹³C^atm. The high potential of SO air–sea gas exchange to steer δ¹³C^atm (Table 2: sea ice and gas exchange rate experiments) complements recent studies showing that increased SO ventilation of deep ocean carbon is a likely candidate for glacial–interglacial δ¹³C^atm excursions.

As an outlook, the use of a more complex model with a higher horizontal and vertical resolution and a shorter time step (resolving seasonal variations) could provide valuable additional information. For example, the role of different regions within the SO on the global δ¹³C distribution could be better studied with a more complex model. Sediment core-based reconstructions of the global carbon cycle could possibly be aided by a more complex model with a finer grid and higher time resolution, by providing more detailed information on the contribution of biogeochemical processes to local ocean tracers. Next to that, exploring the effect on Δδ¹³C of a glacial model circulation field could provide a way to quantify the maximum combined effect of circulation and biogeochemical change on Δδ¹³C.