What drives the latitudinal gradient in open-ocean surface dissolved inorganic carbon concentration?

Previous work has not led to a clear understanding of the causes of spatial pattern in global surface ocean dissolved inorganic carbon (DIC), which generally increases polewards. Here, we revisit this question by investigating the drivers of observed latitudinal gradients in surface salinity-normalized DIC (nDIC) using the Global Ocean Data Analysis Project version 2 (GLODAPv2) database. We used the database to test three different hypotheses for the driver producing the observed increase in surface nDIC from low to high latitudes. These are (1) sea surface temperature, through its effect on the CO₂ system equilibrium constants, (2) salinity-related total alkalinity (TA), and (3) high-latitude upwelling of DIC- and TA-rich deep waters. We find that temperature and upwelling are the two major drivers. TA effects generally oppose the observed gradient, except where higher values are introduced in upwelled waters. Temperature-driven effects explain the majority of the surface nDIC latitudinal gradient (182 of the 223 µmol kg⁻¹ increase from the tropics to the high-latitude Southern Ocean). Upwelling, which has not previously been considered as a major driver, additionally drives a substantial latitudinal gradient. Its immediate impact, prior to any induced air–sea CO₂ exchange, is to raise Southern Ocean nDIC by 220 µmol kg⁻¹ above the average low-latitude value. However, this immediate effect is transitory. The long-term impact of upwelling (brought about by increasing TA), which would persist even if gas exchange were to return the surface ocean to the same CO₂ as without upwelling, is to increase nDIC by 74 µmol kg⁻¹ above the low-latitude average.

1 Introduction

The ocean absorbs about one-quarter of the anthropogenic CO₂ emitted every year (Le Quéré et al., 2018). It is the largest non-geological carbon reservoir (∼38 000 Gt C; Falkowski et al., 2000), containing 50 times as much carbon as the pre-industrial atmosphere, and thereby modulates the Earth's climate system. Approximately 97 % of the carbon in the ocean is in the form of dissolved inorganic carbon (DIC), which is the total concentration of aqueous CO₂ and bicarbonate and carbonate ions:

$$\begin{array}{}\text{(1)}& \mathrm{DIC}=\left[{\mathrm{CO}}_{\mathrm{2}}^{\ast }\right]+\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]+\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right],\end{array}$$

where [${\mathrm{CO}}_{\mathrm{2}}^{\ast }$] refers to the sum of aqueous CO₂ and undissociated carbonic acid (H₂CO₃), with the latter being negligible (Zeebe and Wolf-Gladrow, 2001).

Understanding what controls the distribution of oceanic DIC is essential for quantifying anthropogenic CO₂ invasion (e.g., Gruber, 1998; Humphreys et al., 2016; Lee et al., 2003; Sabine et al., 1999, 2002; Vázquez-Rodríguez et al., 2009) and consequent ocean acidification (e.g., Doney et al., 2009; Orr et al., 2005). As most marine organisms live in the sunlit surface ocean, where CO₂ exchange with the atmosphere happens, the controls on surface ocean DIC in particular merit investigation.

Many previous studies focused on the vertical, rather than latitudinal, distribution of DIC. They investigated the contributions of the different “carbon pumps” – solubility pump, soft tissue pump, and carbonate pump (Cameron et al., 2005; Gruber and Sarmiento, 2002; Toggweiler et al., 2003a, b) – to the pattern of DIC with depth. The solubility pump is based on the assumption that, at high latitudes where deep waters form, DIC is high because the low water temperature increases CO₂ solubility. Lee et al. (2000) used this principle to predict salinity-normalized DIC (nDIC) from empirical functions of sea surface temperature and nitrate that varied seasonally and geographically.

Key et al. (2004) depicted the global distribution of surface DIC using an earlier version (GLODAPv1) of the dataset than we used in this study, noting that the surface DIC pattern is more similar to nutrients (including in the Southern Ocean, where both DIC and nutrients are enriched) than to salinity – unlike total alkalinity (TA), whose pattern more closely resembles that of salinity (Fry et al., 2015). Using the data from the new GLODAPv2 database (Key et al., 2015; Olsen et al., 2016), surface DIC is confirmed here to have its highest values at high latitudes, like nutrients, and to reach its lowest values at low latitudes in each basin (Fig. 1a; more details in Sect. 3.1). Earlier studies (Lee et al., 2000; Toggweiler et al., 2003a; Williams and Follows, 2011, Sect. 6.3 “What controls DIC in the surface ocean?”) suggested that temperature is of primary importance in regulating surface DIC (e.g., Lee et al., 2000; Toggweiler et al., 2003a; Williams and Follows, 2011; Humphreys, 2017). Under this assumption, surface waters in cool regions at high latitudes should hold more DIC than surface waters in the warm regions at low latitudes.

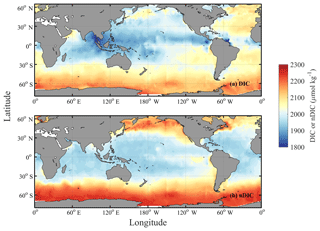
Figure 1 Spatial distributions of DIC and nDIC. (a) DIC (normalized to year 2005); (b) salinity-normalized DIC (nDIC, DIC normalized to reference year of 2005 and salinity of 35) in the surface global ocean. The latitudinal trends are clear, particularly for nDIC.

Williams and Follows (2011) argued that another variable also exerts control on the surface DIC distribution: TA sets the equilibrium capacity for seawater to hold DIC in solution (Omta et al., 2011; Humphreys et al., 2018), so higher surface TA values may lead to higher DIC. Takahashi et al. (2014) explored the seasonal distribution of climatological surface DIC using seawater pCO₂ from the Lamont Doherty Earth Observatory (LDEO) database and TA estimated from salinity, qualitatively attributing seasonal differences (on a regional scale) to the greater upward mixing of high-CO₂ deep waters in winter and summer biological carbon drawdown. They noted the potential for upwelling to alter surface DIC, but focused on DIC seasonality rather than its spatial variability. In recent years, the global surface DIC database has greatly expanded (e.g., Bates et al., 2006; Sasse et al., 2013), culminating in GLODAPv2 (Key et al., 2015; Olsen et al., 2016; Lauvset et al., 2016), but the drivers of the global surface DIC distribution have not yet been reassessed.

The processes that influence the distribution of surface DIC at the local scale can be divided into those which change DIC by direct addition or removal, and those which affect DIC indirectly. The direct processes include (1) biological carbon assimilation during primary production and release during remineralization (Bozec et al., 2006; Clargo et al., 2015; Toggweiler et al., 2003b; Yasunaka et al., 2013); (2) transport of DIC-rich deep waters into the surface layer (Jiang et al., 2013; Lee et al., 2000); and (3) production and export of CaCO₃. Indirect processes include (4) seawater dilution or concentration due to precipitation or evaporation (Friis et al., 2003); (5) warming and cooling, which alter CO₂ solubility and induce air–sea gas exchange that acts to reduce air–sea CO₂ disequilibrium (Bozec et al., 2006; Toggweiler et al., 2003a; Williams and Follows, 2011); and (6) the above processes (1–4) through their impact on TA – if high/low TA values are not matched by high/low DIC values then the resulting low/high seawater pCO₂ stimulates CO₂ ingassing/outgassing until DIC matches TA (Humphreys et al., 2018). The effects of equilibrium processes (the effects through temperature and upwelled TA) change the surface ocean DIC at which air–sea CO₂ equilibrium occurs, so these effects can persist beyond the air–sea CO₂ equilibrium timescale (months to a year; Jones et al., 2014). The effects of disequilibrium processes, such as direct DIC supply from upwelling, and biological uptake of DIC in response to upwelled nutrients (principally iron; Moore et al., 2016) can persist no longer than the CO₂ equilibrium timescale.

Our study builds on previous work in several ways. First, whereas many previous studies looked to understand the vertical DIC distribution, our target is to understand the latitudinal surface DIC distribution. Second, we identify the most important processes, not just the variables, driving the surface DIC distribution (Fig. 2). Third, we use a much larger observational global dataset – GLODAPv2.

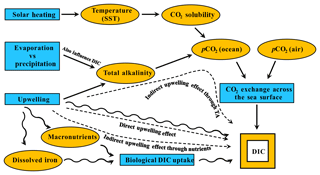
Figure 2 Major controls on surface DIC. Schematic showing the main processes exerting an influence over the concentration of DIC in the global surface ocean (producing variation with latitude). Blue shapes are processes and orange shapes are variables. Straight solid arrows represent equilibrium processes regulating DIC in the long term and wavy solid arrows represent disequilibrium processes regulating DIC in the short term. In the paper, we evaluate the upwelling effect on surface DIC in the Southern Ocean. Dashed arrows with text denote the three different ways that upwelling affects DIC: the direct effect through upwelled DIC, the indirect effect through upwelled nutrients which stimulate biological removal of DIC, and the indirect effect through upwelled TA changing the equilibrium DIC with the atmosphere.

We evaluate three main hypotheses as to which processes cause the increase in surface DIC and nDIC from low to high latitude (Fig. 1):

1. latitudinal variation in solar heating via its effect on sea surface temperature, and hence CO₂ solubility;

2. evaporation and precipitation, through their effects on TA; and

3. upwelling and winter entrainment through the introduction of DIC- and TA-rich deep waters to the (sub)polar surface oceans, when coupled with iron limitation of biological uptake of DIC.

It is easier to constrain the dynamics of upwelling and quantify their impact on surface DIC in the Southern Ocean (where upwelling has been more comprehensively studied; e.g., Marshall and Speer, 2012; Morrison et al., 2015) than in the subarctic North Atlantic and North Pacific oceans (where upward transport occurs via deep mixing in the winter, combined with upwelling in the North Pacific). The Southern Ocean also plays a crucial role in the global overturning circulation (e.g., Marshall and Speer, 2012), and the global carbon cycle (Landschützer et al., 2015; Mikaloff-Fletcher, 2015). Therefore, we focused on the Southern Ocean for the evaluation of the third hypothesis. A novel conclusion of this study is that upwelling, whose global significance has previously been overlooked, is very important in shaping the spatial distribution of surface ocean DIC, in part because upwelling of TA changes equilibrium DIC.

2 Methods

We used data from GLODAPv2 (Key et al., 2015; Olsen et al., 2016). This compilation contains data from over 700 cruises conducted from 1972 to 2013, with about a third collected since 2003. The data have undergone secondary quality control and have been adjusted for consistency (Key et al., 2015; Lauvset and Tanhua, 2015; Olsen et al., 2016).

2.1 Data processing

We define the “surface” ocean as the uppermost 30 m at latitudes greater than 30^∘, and shallower than 20 m at latitudes less than 30^∘ (following e.g., Fry et al., 2015; Lee et al., 2006). Only open-ocean data (water depth > 200 m) were included in this study (Fig. 3).

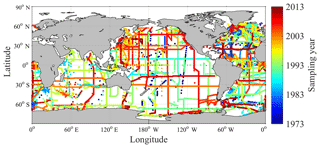
Figure 3 Spatial and temporal distribution of GLODAPv2 sampling stations (with Arctic and Mediterranean Sea data removed).

We excluded regions perturbed by river inputs in order to remove confounding factors affecting the latitudinal distributions of DIC and nDIC on smaller length scales than investigated here. We excluded the Arctic Ocean (> 65^∘ N) (Fig. 3) because it is heavily influenced by river inputs (Fry et al., 2015; Jiang et al., 2014), all data from the Mediterranean Sea and the Red Sea because of their very high salinity (Jiang et al., 2014), and some data (those where S is less than 34) from other ocean areas: the Amazon River plume in the North Atlantic (5–10^∘ N, > 45^∘ W), the Ganges–Brahmaputra plume in the Bay of Bengal (> 5^∘ N, 80–94^∘ E) (both Fry et al., 2015) and the western North Atlantic margins (Cai et al., 2010). We also excluded low-latitude ocean areas affected by upwelling (i.e., the eastern equatorial Pacific and northern Californian upwelling regions).

Because atmospheric CO₂ increased during the period when the GLODAPv2 data were collected (1972–2013), DIC has also increased in surface waters (Bates et al., 2014). To prevent temporal DIC trends from generating artificial spatial variability, we normalized surface DIC to a reference year of 2005, by assuming that surface seawater pCO₂ tracks atmospheric pCO₂ (Feely, 2008; see also CO₂ time series in the North Pacific at https://pmel.noaa.gov/co2/file/CO2+time+series, last access: 30 January 2019). We first calculated the change in atmospheric mole fraction of CO₂ (xCO_2,air) from the reference year 2005:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }x{\mathrm{CO}}_{\mathrm{2},\mathrm{air}}=x{\mathrm{CO}}_{\mathrm{2},\mathrm{air}}^t-x{\mathrm{CO}}_{\mathrm{2},\mathrm{air}}^{\mathrm{2005}},\end{array}$$

where the superscript “t” and “2005” refer to year, and the globally averaged atmospheric xCO₂ data can be found at https://www.esrl.noaa.gov/gmd/ccgg/trends/, last access: 30 January 2019 (neither spatial nor seasonal variability in atmospheric CO₂ is taken into account; the associated error in surface DIC is less than 2 µmol kg⁻¹).

Then we converted ΔxCO_2,air into ΔpCO_2,air (Takahashi et al., 2009) just above the sea surface, using calculated humidity data. It is then assumed that ΔpCO_2,sw, representing the change in sea surface pCO₂ relative to the year 2005, is equal to ΔpCO_2,air.

Therefore the sea surface pCO₂ normalized to year 2005 was calculated as

$$\begin{array}{}\text{(3)}& p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}^{\mathrm{2005}}=p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}^t-\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}},\end{array}$$

where ${p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}}^t$ was calculated from in situ DIC, TA, temperature, and salinity using CO₂SYS v1.1 (van Heuven et al., 2011; dissociation constants used are described in Sect. 2.3).

Since the anthropogenic CO₂ perturbation does not change TA, DIC normalized to the year 2005 was calculated with inputs of in situ TA and $p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}^{\mathrm{2005}}$ using CO₂ SYS (van Heuven et al., 2011):

$$\begin{array}{}\text{(4)}& {\mathrm{DIC}}^{\mathrm{2005}}=f\left(T_{\text{in situ}},S_{\text{in situ}},{\mathrm{TA}}_{\text{in situ}},p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}^{\mathrm{2005}}\right).\end{array}$$

The concentration of DIC hereinafter refers to DIC normalized to the year 2005.

2.2 Salinity normalization

Salinity normalization was used to correct for the influence of precipitation and evaporation in the open ocean (Postma, 1964). Data were normalized to a reference salinity of 35 using a standard procedure:

$$\begin{array}{}\text{(5)}& nX=X_{\mathrm{obs}}\times \mathrm{35}/S_{\mathrm{obs}},\end{array}$$

where nX refers to the normalized variable, X_obs is the observed value of the variable, and S_obs is the observed salinity.

We acknowledge that this approach (Eq. 5) can create artificial variance in DIC distribution (Friis et al., 2003) because it ignores the influences of riverine input and upwelling from below the thermocline. We avoided the riverine problem by excluding affected regions (Sect. 2.1). We found that correcting for the “non-zero intercept” of DIC–salinity plots (Friis et al., 2003) in different ocean basins has negligible influence on salinity normalization of DIC, accounting for at most 7 µmol kg⁻¹ change in DIC; upwelling from below the thermocline also has negligible influence, accounting for at most 4 µmol kg⁻¹ change in DIC. These changes are small compared to the DIC latitudinal gradient of about 200 µmol kg⁻¹ that we investigate here.

2.3 Carbonate chemistry

Carbonate system variables were calculated from DIC and TA using version 1.1 of CO₂SYS for MATLAB (van Heuven et al., 2011). The dissociation constants for carbonic acid and bisulfate were taken from Lueker et al. (2000) and Dickson (1990), respectively, and the total borate–salinity relationship was taken from Lee et al. (2010).

2.4 Calculation of DIC and nDIC latitudinal gradients

The magnitude of the latitudinal gradient depends on the time of year because it is calculated from DIC values that are higher in winter at high altitudes. The seasonal amplitude of surface nDIC varies over the global open ocean. It is generally small at low latitudes: ∼20 µmol kg⁻¹ in the subtropical Pacific Ocean (Keeling et al., 2004) and ∼40 µmol kg⁻¹ in the subtropical Atlantic Ocean (Bates et al., 1996). It is much larger at some (but not all) high-latitude locations: ∼113 µmol kg⁻¹ in the northwestern Pacific Ocean (Kawakami et al., 2007) and ∼60 µmol kg⁻¹ in the subarctic northeast Pacific Ocean (Wong et al., 2002), but only ∼25 µmol kg⁻¹ at the KERFIX site in the Southern Ocean (Louanchi et al., 1999). Because most ship-collected data (as contained in GLODAPv2) are collected in spring or summer months, the latitudinal gradients averaged across the whole year will be larger in some locations than presented here, and the magnitudes of the latitudinal gradients presented here should be considered lower estimates. For instance, the observed nDIC difference (ΔnDIC) between the North Pacific (40–60^∘ N) and low latitudes (30^∘ S–30^∘ N) is 171 µmol kg⁻¹ when calculated from summer data only and 224 µmol kg⁻¹ when calculated from winter data only. For the Southern Ocean, ΔnDIC is 214 µmol kg⁻¹ in summer and 240 µmol kg⁻¹ in winter. This sensitivity to time of year should be noted but is not considered further here because it is relatively small compared to the overall magnitude of ΔnDIC.

2.5 Calculations of the effects of various processes on DIC

The second hypothesis (evaporation and precipitation through their effects on TA) was evaluated by salinity normalization (Eq. 5). The methods for calculating the impacts of the other two processes on the surface DIC concentration are now explained. The effect of upwelling is evaluated in the Southern Ocean, from both short- and long-term perspectives. In addition, we also quantify the effect of iron limitation, which would potentially affect the observed (n)DIC distribution.

2.5.1 SST-driven effect

The temperature effect on the carbonate system has two aspects. First, when water temperature increases, the equilibria between carbonate species (Eq. 6) shift towards increasing the aqueous CO₂ and carbonate ion concentrations (Dickson and Millero, 1987):

$$\begin{array}{}\text{(6)}& {\mathrm{CO}}_{\mathrm{2}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\rightleftharpoons \mathrm{2}{\mathrm{HCO}}_{\mathrm{3}}^{-}.\end{array}$$

Second, CO₂ solubility is lower at higher temperatures and vice versa (Weiss, 1974). Neither effect alters DIC directly, but both change the seawater pCO₂. A larger proportion of DIC exists as aqueous CO₂ at higher temperatures and the ratio of pCO₂ to [CO₂] also increases as solubility decreases (Eq. 7, Henry's law):

$$\begin{array}{}\text{(7)}& p{\mathrm{CO}}_{\mathrm{2}}=\left[{\mathrm{CO}}_{\mathrm{2}}\right]/K_{\mathrm{H}},\end{array}$$

where K_H is the Henry's constant (solubility) for CO₂.

Both effects tend to increase sea surface pCO₂ as seawater warms, potentially increasing the net sea-to-air CO₂ flux; the induced outgassing of CO₂ reduces sea surface pCO₂ and DIC as it shifts the system towards CO₂ equilibrium. Therefore, for an open-ocean system in contact with the atmosphere, sea surface temperature (SST) can control the DIC distribution, and this can by itself produce DIC latitudinal variations.

To examine the magnitude of the expected temperature-induced DIC changes, we chose the low-latitude area as the reference, then removed the latitudinal SST variation and recalculated the open-ocean surface DIC everywhere for a constant SST of 27 ^∘C (the mean sea surface temperature in the subtropics from 30^∘ S to 30^∘ N). We first calculated the in situ pCO₂ from observed SST, SSS (sea surface salinity), TA, and DIC using CO₂SYS. The calculated pCO₂ from TA and DIC has been found to agree well with the measured pCO₂ by Takahashi et al. (2014) (root-mean-square deviation of ±6.8 µatm). We then altered the sea surface temperature from its in situ value to 27 ^∘C, which would change the solubility of CO₂ and induce air–sea CO₂ gas exchange. Then air–sea CO₂ gas exchange (which does not change TA) was assumed to proceed until pCO₂ was back to the same level as before resetting the temperature. Next, we used CO₂SYS to calculate DIC_SST=27 (Table 1) based on an input temperature of 27 ^∘C, observed salinity and TA, and the in situ pCO₂ calculated as above. DIC_SST=27 thus represents temperature-normalized DIC, and should exhibit the same spatial variability as DIC except that the temperature-induced component of the variability has been removed. Finally, the difference between observed DIC and DIC_SST=27 gives the DIC variation attributed to temperature variation (see Table 1 for definitions of each term):

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }{\mathrm{DIC}}_{\mathrm{temp}}={\mathrm{DIC}}_{\mathrm{obs}}-{\mathrm{DIC}}_{\mathrm{SST}=\mathrm{27}}.\end{array}$$

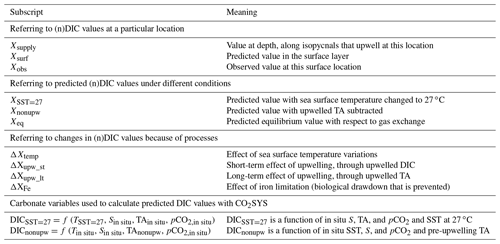
Table 1 Definitions of subscripts and main terms used in the text. X represents any variable involved in the calculations. The program CO₂SYS was used to calculate values under different conditions.

The same procedure was followed for calculating ΔnDIC_temp:

$$\begin{array}{}\text{(9)}& \mathrm{\Delta }{\mathrm{nDIC}}_{\mathrm{temp}}={\mathrm{nDIC}}_{\mathrm{obs}}-{\mathrm{nDIC}}_{\mathrm{SST}=\mathrm{27}}.\end{array}$$

2.5.2 Upwelled DIC-driven effect (short-term effect of upwelling)

Upwelling of DIC-rich subsurface waters can increase the surface DIC. The largest upwelling flux anywhere in the world takes place in the Southern Ocean (Talley, 2013). Subsurface waters in the Southern Ocean upwell along the neutral density isopycnals of 27.6, 27.9, and 27.9 kg m⁻³ in the southern Atlantic, Indian, and Pacific oceans, respectively (Ferrari et al., 2014; Lumpkin and Speer, 2007; Marshall and Speer, 2012; Talley, 2013).

Upwelling occurs within the Antarctic Circumpolar Current (ACC) where the wind stress is greatest (Morrison et al., 2015). As the upwelled water subsequently advects away, the effects of upwelling on DIC are transported to nearby locations. Therefore, instead of a direct supply from deep to surface locations such as L3 (Fig. 4), DIC is brought to the subsurface primarily along isopycnals (shown in Fig. 4 as the black curve to L1), finally reaching the surface at L2. Then, the upwelled waters with enriched DIC, TA, and nutrients feed both branches of the Southern Ocean overturning circulation. One branch is transported northwards via Ekman transport from L2 to L3, as shown by the black arrow towards the Equator, and the other is recycled to form Antarctic Bottom Water (AABW) (Talley, 2013). The effect of upwelling on sea surface temperature is negligible and not considered here because both deep water and high-latitude surface waters have similarly low temperatures.

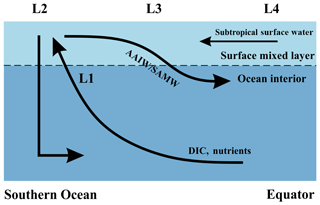
Figure 4 A schematic illustrating locations of interest and assumed major flow paths in the Southern Ocean. Black arrows represent the flow directions of water masses. The lower curved arrow denotes upwelling of deep water along isopycnal surfaces, and the upper curved arrow denotes subduction to form Subantarctic Mode Water (SAMW) and Antarctic Intermediate Water (AAIW). L1: upwelling water below the mixed layer, prior to any influence of surface processes; L2: sea surface within the core of the Southern Ocean upwelling south of 50^∘ S (Morrison et al., 2015); L3: sea surface from 30 to 50^∘ S; L4: sea surface north of 30^∘ S, which experiences no direct effects from upwelling in the Southern Ocean.

We first consider the increase in DIC induced by the upwelling of deep water with high DIC concentrations. While some of the initial increase is usually removed shortly afterwards by biological export fueled by the nutrients brought up at the same time, excess DIC remains if the subsequent biological removal of DIC does not match the initial increase. Phosphorus has the simplest nutrient behavior in the ocean with only one significant source to the ocean as a whole (river input) and one major sink (organic matter burial) (Ruttenberg, 2003; Tyrrell, 1999). In this study, the salinity-normalized phosphate (nPhos) concentration was used as a proxy for calculating how much salinity-normalized DIC (nDIC) was upwelled along with it and not yet removed again by biological uptake of phosphate and DIC. We used salinity-normalized concentrations to correct for the influence of precipitation (rainfall) that dilutes DIC and phosphate concentrations in proportion to the effects on salinity (Eq. 5). In this calculation, it was assumed that the only external source of phosphate to surface waters is from upwelling and the only subsequent loss is through export of organic matter, leading to the equation:

$$\begin{array}{}\text{(10)}& {\mathrm{nPhos}}_{\mathrm{surf}}={\mathrm{nPhos}}_{\mathrm{supply}}-\mathrm{NCP}/R_{\mathrm{C}:\mathrm{P}},\end{array}$$

where the subscript “supply” indicates the end-member concentration of deep water supplied along the upwelling isopycnals (i.e., the value at L1 in Fig. 4), and the subscript “surf” indicates the surface water concentration at some later time. NCP refers to the total time-integrated net community production (uptake and export by biology) in carbon units, and R_C:P is the Redfield ratio of carbon to phosphorus. R_C:P is given the standard value of 106:1 (Redfield, 1963), except for the cold nutrient-rich high-latitude region in the Southern Ocean (south of 45^∘ S), where R_C:P is given a lower value of 78:1 (Martiny et al., 2013). We only considered the spatial variation in R_C:P in this study. R_C:P has seasonal variation as well (e.g., Frigstad et al., 2011), but this is much smaller than its latitudinal variation. nPhos_surf refers to the observed surface value of nPhos at some location distant from where upwelling occurs.

Another possible process involved in the change of DIC during its upwelling and subsequent advection is calcium carbonate (CaCO₃) precipitation and dissolution (Balch et al., 2016), which alters DIC and TA with a ratio of 1:2. In order to quantify the magnitude of this process, we used Alk^∗ (Fry et al., 2015) as an indicator, which is capable of diagnosing CaCO₃ cycling in the context of the large-scale ocean circulation (see more details on Alk^∗ distribution in Fig. 10). The change in Alk^∗ concentrations between its supplied and surface end-members is attributed to CaCO₃ precipitation–dissolution and assimilation of inorganic nutrients by primary production (Brewer and Goldman, 1976):

$$\begin{array}{}\text{(11)}& {\displaystyle }{\mathrm{Alk}}_{\mathrm{surf}}^{\ast }={\mathrm{Alk}}_{\mathrm{supply}}^{\ast }-\mathrm{\Delta }{\mathrm{Alk}}_{\mathrm{CaCO}\mathrm{3}}^{\ast }-\mathrm{NCP}/R_{\mathrm{DIC}:\mathrm{TA}},\text{(12)}& {\displaystyle }\begin{array}{r}{\mathrm{Alk}}^{\ast }={\displaystyle \frac{{\mathrm{Alk}}_{\mathrm{m}}-{\mathrm{Alk}}_{\mathrm{r}}+\mathrm{1.36}\times {\mathrm{NO}}_{\mathrm{3}}^{-}}{S_{\mathrm{obs}}}}\times \mathrm{35}\\ +{\mathrm{Alk}}_{\mathrm{r}}-\mathrm{2300}\mathrm{\mu }\mathrm{mol}{\mathrm{kg}}^{-\mathrm{1}}\end{array},\end{array}$$

where R_DIC:TA is the relative ratio of $-\mathrm{106}/\mathrm{17}$ between changes in DIC and TA during primary production (Wolf-Gladrow et al., 2007). Alk_m is the measured TA, Alk_r is the riverine TA end-member (zero in the Southern Ocean), and 2300 µmol kg⁻¹ is the average TA in the low-latitude surface oceans. ${\mathrm{Alk}}_{\mathrm{surf}}^{\ast }$ is calculated by Eq. (12); the substitution into Eq. (11) allows the calculation of ΔAlk${}_{{\mathrm{CaCO}}_{\mathrm{3}}}^{\ast }$.

Assuming the carbon source is from upwelled CO₂-rich deep waters and carbon sinks are from organic matter export (NCP) and CaCO₃ cycling, then

$$\begin{array}{}\text{(13)}& {\mathrm{nDIC}}_{\mathrm{surf}}={\mathrm{nDIC}}_{\mathrm{supply}}-\mathrm{NCP}-\mathrm{0.5}\times \mathrm{\Delta }{\mathrm{Alk}}_{\mathrm{CaCO}\mathrm{3}}^{\ast }.\end{array}$$

Three hydrographic sections, one in each of the Indian (I95E), Pacific (P150W), and Atlantic (A25W) oceans, were used to determine the different supply concentrations (nPhos_supply, Alk${}_{\mathrm{supply}}^{\ast }$, and nDIC_supply) for each basin (see Fig. 5c inset). In the Indian Ocean, nPhos_supply, Alk${}_{\mathrm{supply}}^{\ast }$, and nDIC_supply along the 27.9 kg m⁻³ isopycnal are 2.29±0.01, 109.4±1.0, and 2273.1±1.1 µ mol kg⁻¹, respectively (values here are expressed as mean ± standard error of the mean), as it approaches the surface. In the Pacific Ocean, nPhos_supply, Alk${}_{\mathrm{supply}}^{\ast }$, and nDIC_supply along the 27.9 kg m⁻³ isopycnal are 2.32±0.01, 108.1±1.9, and 2277.2±1.8 µmol kg⁻¹, respectively. In the Atlantic Ocean, nPhos_supply, Alk${}_{\mathrm{supply}}^{\ast }$, and nDIC_supply along the 27.6 kg m⁻³ isopycnal are 2.28±0.01, 103.5±1.1, and 2254.6±1.3 µmol kg⁻¹, respectively (Fig. 5).

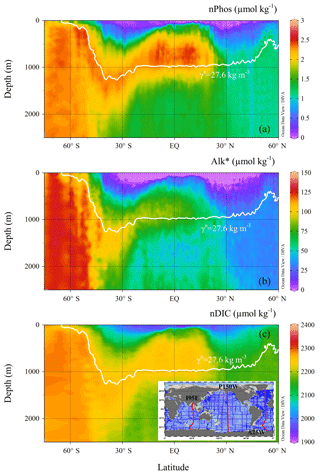
Figure 5 Vertical distributions of (a) nPhos, (b) Alk^∗, and (c) nDIC along the Atlantic Ocean section. The Indian and Pacific sections are not shown. The selected Atlantic section (A25W) is shown as the red line on the right-hand side of the inset. The neutral density isopycnal along which upwelling occurs is indicated by the white contour, which is characterized by neutral density of 27.6 kg m⁻³ in the Atlantic sector of the Southern Ocean.

Since nPhos_surf tends to decrease to zero upon moving northwards, due to biological uptake, nDIC_surf has a relatively constant value in the subtropical regions (data not shown), where it is not influenced by upwelling in the Southern Ocean. Because of this, the potential effect of upwelling on surface nDIC is calculated as the excess in nDIC_surf compared to the subtropical average value (30^∘ S–30^∘ N):

$$\begin{array}{}\text{(14)}& \mathrm{\Delta }{\mathrm{nDIC}}_{\mathrm{upw}\mathrm{\_}\mathrm{st}}={\mathrm{nDIC}}_{\mathrm{surf}}-\stackrel{\mathrm{‾}}{{\mathrm{nDIC}}_{\mathrm{surf}}(\mathrm{30}{}^{\circ }\mathrm{S}-\mathrm{30}{}^{\circ }\mathrm{N})}.\end{array}$$

2.5.3 Upwelled TA-driven effect (long-term effect of upwelling)

Some effects of upwelling on DIC are temporary, becoming overridden later by gas exchange. In contrast, the effect of upwelled TA persists because it changes the equilibrium DIC with respect to gas exchange (DIC_eq) (discussed also in Sect. 4.1.3). Upwelling of high-TA water has a long-lasting effect on DIC because, if all else remains constant, an increase in TA decreases the fraction of DIC that exists as CO₂ molecules. The resulting decrease in CO₂ concentration lowers seawater partial pressure of CO₂ (pCO₂), having the potential to lower seawater pCO₂ to below atmospheric values which in turn drives an influx of CO₂ from the atmosphere, raising DIC (Humphreys et al., 2017). The effects of upwelling are complex because they consist of both direct and indirect effects on DIC (Fig. 2), lasting over both short (when DIC is altered but DIC_eq is not) and long (when DIC_eq is altered) timescales. The different effects and the meanings of the terms used here are illustrated in Fig. 6.

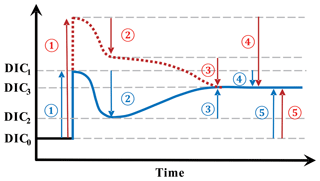
Figure 6 A schematic illustrating the various effects of upwelling on surface DIC. Numbers represent processes changing surface DIC, and arrows point in the direction of change. (1) The direct effect of upwelling which elevates surface DIC from DIC₀ to DIC₁; (2) the DIC uptake by biology supported by upwelled nutrients, dropping DIC from DIC₁ to DIC₂. The processes of (1) and (2) make up the short-term effect of upwelling (i.e., difference between DIC₂ and DIC₀); (3) the change brought about by air–sea CO₂ gas exchange which continues towards the equilibrium with the atmosphere (DIC₃, whose level is determined by the amount of upwelled TA as well as by temperature); (4) the combination of both (2) and (3) makes up the total indirect effect of upwelling (the difference between DIC₃ and DIC₁); (5) the long-term impact of upwelling on the level of surface DIC is the difference between DIC₃ and DIC₀. Blue and red indicate two scenarios with different amounts of upwelled DIC relative to upwelled TA, but the same amounts of upwelled TA. Blue is for upwelled water with a deficit in additional DIC relative to additional TA whereas red is for an excess in DIC relative to TA.

The calculation of the long-term effect of upwelling through upwelled TA in the Southern Ocean (i.e., the difference between DIC₃ and DIC₀ in Fig. 6) was achieved through five steps.

1. Calculate TA in the Southern Ocean with the upwelling effect subtracted, TA_nonupw:

   $$\begin{array}{}\text{(15)}& {\mathrm{TA}}_{\mathrm{nonupw}}={\mathrm{TA}}_{\mathrm{obs}}-\left({\mathrm{Alk}}^{\ast }\times S_{\mathrm{obs}}/\mathrm{35}\right),\end{array}$$

   where TA_obs is the observed in situ TA, and Alk^∗ is the TA tracer (Fry et al., 2015) revealing excess TA supplied by the large-scale ocean circulation (upwelling in the Southern Ocean), as well as removal by calcification and export (Eq. 12). Since Alk^∗ is a salinity-normalized concept, it is necessary to restore it to the in situ salinity before subtracting it from the in situ TA.

2. Calculate in situ sea surface pCO₂, following the same method as described in Sect. 2.5.1.

3. Calculate DIC with the effect of upwelled TA subtracted. We calculated DIC_nonupw using CO₂SYS with inputs of TA_nonupw and in situ pCO₂, SST, and salinity.

4. Normalize salinity for consistency with other calculated effects.

5. Finally, the long-term effect of upwelling through the upwelled TA and the subsequent air–sea gas exchange is calculated as

   $$\begin{array}{}\text{(16)}& \mathrm{\Delta }{\mathrm{nDIC}}_{\mathrm{upw}\mathrm{\_}\mathrm{lt}}={\mathrm{nDIC}}_{\mathrm{obs}}-{\mathrm{nDIC}}_{\mathrm{nonupw}},\end{array}$$

   where ΔnDIC_{upw_lt} corresponds to the magnitude of (5) in Fig. 6.

2.5.4 Iron-driven effect

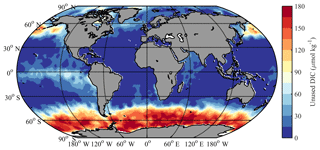
The iron-limitation-driven DIC differences (ΔDIC_Fe) relate to the concepts of “unused nutrient”, which can be thought of as the amounts of macronutrients and DIC that are left behind after iron limitation brings an end to biological uptake, in those regions where iron is the limiting nutrient. Iron limitation alters the impact of upwelling. In locations experiencing upwelling but where nitrate is the proximate limiting nutrient, the quantity of upwelled DIC might more or less be balanced by the quantity of subsequently exported DIC (fueled by the upwelled nutrients). In the Southern Ocean, however, the two appear not to be close to balance, even before considering iron limitation. According to the calculations in Sect. 2.5.2, the ratio of the excess upwelled nDIC against nPhos is around $\mathrm{250}:\mathrm{2.3}\approx \mathrm{109}:\mathrm{1}$ for the Southern Ocean, considerably exceeding the low C:P (average $\approx \mathrm{80}:\mathrm{1}$) of organic matter in the region (Martiny et al., 2013). So even if all upwelled phosphate were to be used up and then exported in biomass in conjunction with carbon, a considerable surplus of DIC would be left behind. A lack of iron in surface waters, however, leads to even more upwelled DIC being left behind after the end of blooms induced by the upwelled nutrients.

We used phosphate as the unused nutrient from which to calculate ΔDIC_Fe. For each $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid in the surface open ocean, the unused phosphate was taken from its annual minimum concentration based on the monthly data in World Ocean Atlas 2013 version 2 (WOA, 2013: https://www.nodc.noaa.gov/OC5/woa13/, last access: 30 January 2019, Boyer et al., 2013; Garcia et al., 2014). The unused phosphate was then converted into unused DIC based on a standard R_C:P of 106:1 (Redfield, 1963) for most of the global ocean, with the exceptions described in Sect. 2.5.2.

The amount of ΔDIC_Fe was therefore calculated as

$$\begin{array}{}\text{(17)}& \mathrm{\Delta }{\mathrm{DIC}}_{\mathrm{Fe}}=\text{unused\hspace{0.17em} phosphate}\times R_{\mathrm{C}:\mathrm{P}}.\end{array}$$

2.6 Uncertainty estimation

Uncertainties in the effects of different drivers were determined by a Monte Carlo approach (following, e.g., Juranek et al., 2009; Ribas-Ribas et al., 2014). For example, the uncertainty of ΔnDIC_temp was calculated as follows: (1) given that ΔnDIC_temp is the difference between nDIC_obs and nDIC_SST=27 (Eq. 9), its uncertainty is propagated from the uncertainties of both nDIC_obs and nDIC_SST=27, where the uncertainty of nDIC_obs is 5 µmol kg⁻¹ (Table 2), and the uncertainty of nDIC_SST=27 was determined by a Monte Carlo approach; (2) for calculation of the uncertainty of nDIC_SST=27 (see its function in Table 1), we first calculated artificial random errors (normally distributed according to the central limit theorem, with a mean of zero and a standard deviation equal to the accuracy/uncertainty of measurement) using a random number generator. Then, new carbonate system variable values (the original ones plus the randomly generated errors) were input into the CO₂SYS program (van Heuven et al., 2011) to calculate new nDIC_SST=27 values. By doing this 1000 times, we obtained a set of 1000 different values for every single data point in the dataset. We used the standard deviations of these sets to characterize their individual uncertainties. The overall uncertainty of nDIC_SST=27 was 6.4 µmol kg⁻¹; (3) by applying the same Monte Carlo method, but to calculate the uncertainty propagated through Eq. (9), we then calculated the uncertainty of ΔnDIC_temp to be 8.0 µmol kg⁻¹ (see Table 2 for other variables).

Table 2 Uncertainties for variables in this study.

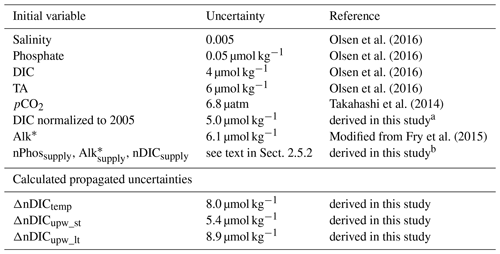
^a The uncertainty of DIC normalized to 2005 was primarily propagated from TA and $p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}^{\mathrm{2005}}$. The uncertainty of $p{\mathrm{CO}}_{\mathrm{2},\mathrm{sw}}^{\mathrm{2005}}$ was calculated from error propagation (Fornasini, 2008) to be 0.17 µatm. ^b The uncertainties for variables with the subscript “supply” were from their standard error of the mean.

3 Results

3.1 Spatial distributions of observed DIC and nDIC

Surface observations reveal values of DIC across the global ocean ranging from less than 1850 µmol kg⁻¹ in the tropics to more than 2200 µmol kg⁻¹ in the high latitudes (Fig. 1a). To first order, surface DIC increases polewards, being positively correlated with absolute latitude (Spearman's rank correlation coefficient ρ=0.71 for the global oceans, Table 3). Spatially, it is monotonically inversely related to sea surface temperature ($\mathit{\rho }=-\mathrm{0.78}$, Table 3), with DIC being highest where the surface ocean is coolest. Another conspicuous feature of surface DIC is the higher values (by ∼100 µmol kg⁻¹) in the tropical and subtropical Atlantic Ocean relative to the same latitudes in the Pacific and Indian oceans (Fig. 1a), as attributed to the transport of water vapor from the Atlantic to the Pacific (Broecker, 1989). This is not considered further here because our main purpose is to explain the sizable observed latitudinal gradients in DIC (on average 153 µmol kg⁻¹ higher in the Southern Ocean than at low latitudes, for instance) and nDIC (on average 223 µmol kg⁻¹ higher in the Southern Ocean than at low latitudes).

Table 3 Global and regional correlations between DIC and nDIC and SST and latitude.

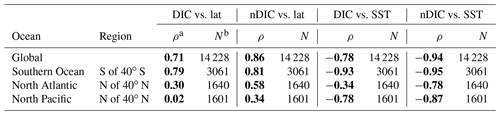
^a The Spearman's rank correlation coefficient, for assessing monotonic relationships (there is a nonlinear relationship between SST and CO₂ solubility). Statistically significant correlations are shown in bold. ^b The number of data points from that area that were used in calculating the correlations.

Salinity-normalized DIC (nDIC) increases towards the poles in all three ocean basins (Fig. 1b), although less strongly in the North Atlantic. The surface nDIC correlates more tightly with latitude and SST than does DIC, yielding a positive correlation with absolute latitude and a negative correlation with SST (ρ=0.86 and −0.94, respectively, for the global ocean, Table 3).

The distributions of surface DIC and particularly nDIC also show modest regional maxima in the eastern equatorial Pacific, the Arabian Sea, and the eastern boundaries of the Pacific and Atlantic ocean basins, presumably as a result of upwelling (Capone and Hutchins, 2013; Chavez and Messié, 2009; Millero et al., 1998; Murray et al., 1994).

3.2 SST-driven effect in the global surface ocean

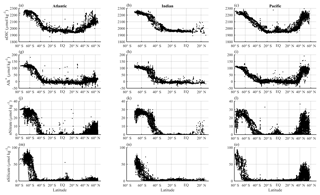
The differences between the latitudinal patterns of DIC_obs and DIC_SST=27 are shown in Fig. 7. As expected, DIC_SST=27 agrees well with DIC_obs in the subtropics where SST is close to 27 ^∘C; the differences become larger with increasing latitude and decreasing SST (Fig. 7a–c). Correcting for salinity variations (Fig. 7d–f) greatly reduces the variability in DIC at low latitudes: nDIC_obs is fairly constant at ∼1970 µmol kg⁻¹ in the subtropics. ΔnDIC_temp (Eq. 8 but for nDIC), the temperature-driven CO₂ gas exchange effect on surface nDIC, increases sharply with latitude (Fig. 7g–i), reaching ∼200 µmol kg⁻¹ at 60^∘ N in the northern part of the Atlantic and Pacific oceans and ∼220 µmol kg⁻¹ at 70^∘ S in the Southern Ocean. The average ΔnDIC_temp in the Southern Ocean is 182 µmol kg⁻¹, which is large enough to account by itself for most – but not all – of the nDIC latitudinal gradient of 223 µmol kg⁻¹ (2193–1970 µmol kg⁻¹).

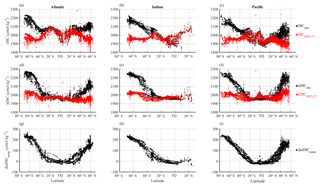
Figure 7 Latitudinal distributions of calculated temperature effect on surface DIC. Different columns show different basins (Atlantic, Indian, and Pacific) and different rows show different calculated DIC variables. Panels (a), (b), and (c) show the observed surface DIC (black) and predicted DIC at SST of 27 ^∘C (red). Panels (d), (e), and (f) show the observed surface nDIC (black) and predicted nDIC at SST of 27 ^∘C (red). Panels (g), (h), and (i) show ΔnDIC_temp, where nDIC_SST=27 is subtracted from nDIC_obs to obtain the calculated temperature effect.

ΔDIC_temp and ΔnDIC_temp are very similar in magnitude, with the largest deviations (at high latitudes) being less than 10 µmol kg⁻¹. Uncertainties associated with the salinity normalization process must therefore be small and are not considered further.

The estimated overall uncertainty of the SST-driven effect on surface nDIC (Table 2) ranges from 5 to 8 µmol kg⁻¹, which is of comparable magnitude to the uncertainty of DIC normalized to 2005 and much smaller than the large latitudinal variations in ΔnDIC_temp.

3.3 Upwelling-driven effects in the Southern Ocean

The upwelling-driven effects in the Southern Ocean calculated from both short- and long-term perspectives are shown in Fig. 8. The values were calculated from data collected along selected transects in each of the Atlantic, Indian, and Pacific sectors.

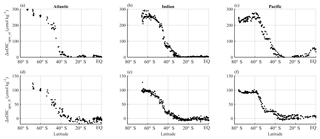
Figure 8 Latitudinal distributions of calculated upwelling effects on surface nDIC. Different columns show different sectors in ocean basins (Atlantic, Indian, and Pacific) and different rows show different calculated effects on surface DIC. Panels (a), (b), and (c) show the short-term effect of upwelling (ΔnDIC_{upw_st}), which is driven by the direct supply of DIC from deep water and subsequent change by biology in the Southern Ocean. Panels (d), (e), and (f) show the long-term effect of upwelling (ΔnDIC_{upw_lt}), which is the difference between the observed nDIC value (determined mainly by the amount of upwelled TA, as well as by SST) and pre-upwelling nDIC value. The results were calculated from the three selected transects defined in Sect. 2.5.2.

ΔnDIC_{upw_st} increases polewards (Fig. 8a–c), with the same trends as surface phosphate (not shown), because it is calculated from phosphate. It can be seen that surface nDIC is potentially elevated dramatically by the Southern Ocean upwelling. The effect is of larger magnitude (average of 220 µmol kg⁻¹ in the Southern Ocean) than that calculated for ΔnDIC_temp (Fig. 7g–i).

Figure 8d–f show the long-term effect of upwelling, which is controlled by the concentration of TA in the upwelled water (how much upwelling increases surface TA values by). The average magnitude of ΔnDIC_{upw_lt} is around 74 µmol kg⁻¹ for the Southern Ocean.

The estimated overall uncertainty of upwelling-driven effects on surface nDIC (Table 2) ranges from 5 to 9 µmol kg⁻¹, close to the uncertainty of DIC normalized to 2005, and much smaller than the large latitudinal variations in ΔnDIC_{upw_st} and ΔnDIC_{upw_lt}.

Figure 9 Calculated potential impact of iron limitation on surface DIC. Different colors correspond to different amounts of “unused DIC”, calculated with the Redfield ratio from observed residual phosphate.

3.4 Iron-driven effect in the global surface ocean

As shown in Fig. 9, ΔDIC_Fe is close to zero except in the classic HNLC regions (i.e., the North Pacific, the equatorial Pacific, and the Southern Ocean; Moore et al., 2013). There is also some residual nitrate during most summers in the Iceland and Irminger basins of the North Atlantic due to the seasonal iron limitation there (Nielsdóttir et al., 2009). The surface Southern Ocean south of 40^∘ S has the largest unused DIC (ΔDIC_Fe of up to 180 µmol kg⁻¹, average of 120 µmol kg⁻¹), followed by the North Pacific 40–65^∘ N (ΔDIC_Fe of up to 120 µmol kg⁻¹, average of 75 µmol kg⁻¹) and the equatorial Pacific (average of 35 µmol kg⁻¹). It is negligible elsewhere in the tropics and subtropics.

4 Discussion

4.1 Factors controlling the surface nDIC latitudinal variation

All effects discussed in this section are effects on nDIC rather than on DIC.

4.1.1 Effect of SST variation in the global surface ocean

The previously accepted explanation for higher DIC at high latitudes is that cooler SSTs there increase CO₂ solubility, resulting in a higher equilibrium DIC (Toggweiler et al., 2003a; Williams and Follows, 2011). Our results support an important role for SST, but also that other processes contribute significantly.

Our analysis concludes that the latitudinal gradient in temperature is capable of raising nDIC by about 180 µmol kg⁻¹ in the Southern Ocean, or in other words, explaining about four-fifths of the observed gradient of 223 µmol kg⁻¹. SST variation is thus able to explain most of the observed pattern.

4.1.2 Effect of TA distribution in the global surface ocean

A second factor that has been proposed as influential in driving spatial variations in the concentration of DIC in the surface ocean is TA (Williams and Follows, 2011). Our analysis supports this conclusion, although we note that the effect of TA is most prominent at low latitudes. Large differences in DIC are observed between the subtropical gyres, where values are relatively high, and the vicinity of the Equator, where values are relatively low (Fig. 1a). These differences in DIC are driven initially by the direct effects of evaporation and precipitation on DIC. However, direct effects of evaporation and precipitation on TA also lead to indirect effects on DIC because of the influence of TA on the value of DIC required for gas exchange equilibrium with a given atmospheric CO₂ level. The indirect effects will dominate over longer timescales (see Sect. 4.2 and Fig. 6). The role of TA explains the much clearer relationship between latitude and nDIC than between latitude and DIC (Fig. 1, Table 3); normalizing DIC to salinity is almost the same as normalizing DIC to TA because salinity and TA are highly correlated in the surface open ocean. As a result, the effect of TA on DIC is counteracted by salinity normalization, with the pattern in nDIC (Fig. 1b) then revealing more clearly how other factors impact DIC.

The latitudinal pattern in TA is not the dominant driver of the DIC trend because TA values are generally lower at high latitudes (where precipitation often exceeds evaporation) than they are at low latitudes (where evaporation often exceeds precipitation). However, TA is also biologically cycled and thus not perfectly correlated to salinity (Fry et al., 2015) and the presence of excess TA in deep water upwelled at high latitudes does contribute to the DIC trend.

4.1.3 Effect of upwelling in the Southern Ocean

Although not traditionally considered a factor, our analyses show that upwelling is important in driving the latitudinal gradient in DIC. Upwelling of DIC by itself is capable of producing an nDIC latitudinal gradient of 220 µmol kg⁻¹ in the Southern Ocean, even higher than the effect of temperature (Fig. 8a–c, Table 4). However, the contribution of upwelling is reduced by about two-thirds if only the long-term effect through upwelled TA is considered (see Fig. 6 for definitions of terms).

Table 4 Summary of nDIC differences between low and high latitudes. Each ΔnDIC value is the amount by which the annual average nDIC value for the high-latitude region exceeds the annual average value for the low latitudes (30^∘ S to 30^∘ N). Percentages in brackets represent the proportion of the observed nDIC difference in the second column; n.c.: not calculated.

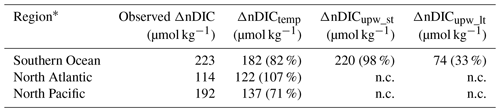
^* The regions are defined as follows: North Atlantic: 40–60^∘ N; North Pacific: 40–60^∘ N; Southern Ocean: south of 40^∘ S.

Deep water usually has higher concentrations of nutrients, nDIC and nTA, than surface water does. Introduction of deep water into the surface mixed layer therefore usually stimulates increases in these concentrations, with three main consequences for DIC (Fig. 6) as follows. (a) If the upwelled water has higher DIC than the surface, the upwelling causes an immediate initial increase in DIC; (b) additional nutrients stimulate phytoplankton blooms until the proximate limiting nutrient runs out, leading to a reduction in DIC over timescales of days to weeks (or months if, for instance, the upwelling occurs at high latitudes during winter when phytoplankton cannot bloom); (c) finally, air–sea gas exchange tends to remove any upwelling-induced air–sea CO₂ disequilibrium over a period of months to a year (Jones et al., 2014), although full equilibrium is seldom achieved across the global surface ocean (Takahashi et al., 2014).

The upwelling effects in Fig. 8 are calculations based on phosphate and TA concentrations, taking into account both the amount upwelled and the amount subsequently removed by biology. They therefore correspond to the sum of the direct upwelling effect (1 in Fig. 6) and the indirect upwelling effect through supplied nutrients (2 in Fig. 6). There are two reasons why the initial amount of upwelled DIC considerably exceeds the amount of DIC subsequently taken up by phytoplankton growth fueled by the upwelled nutrients (why 1 > 2) in the Southern Ocean.

Firstly, iron is typically much scarcer in deep waters than macronutrients are, relative to phytoplankton need (Moore, 2016). Regions like the Southern Ocean that are strongly influenced by upwelling are for this reason often iron-limited (Moore, 2016), leading to large amounts of “unused DIC” (order of 120 µmol kg⁻¹ in the Southern Ocean – Fig. 9) accompanying unused macronutrients. This scarcity of iron also leads to muted seasonal cycles of DIC (Merlivat et al., 2015) and thus year-round persistence of unused DIC. Secondly, as described in Sect. 2.5.2, the higher C:P ratio of supply ($\sim \mathrm{109}:\mathrm{1}$) compared to removal ($\sim \mathrm{80}:\mathrm{1}$) implies a considerable surplus of DIC even without iron limitation.

The upwelling effects shown in Fig. 8a–c are however relatively short term, and are expected to be overridden by air–sea gas exchange within months (Jones et al., 2014). They are thus likely to be most significant in the vicinity of where upwelling takes place (Morrison et al., 2015). For effects that may persist further away from locations of upwelling, it is important to also consider the long-term effect (5 in Fig. 6), the magnitude of which is dictated mainly by the change in TA brought about by upwelling. The level of TA in upwelled water (∼2315, 2340, and 2337 µmol kg⁻¹ in the Atlantic, Indian, and Pacific sectors of the Southern Ocean, respectively, calculated according to the same method as in Sect. 2.5.2) are higher than the typical levels of TA in the surface waters of the high-latitude Southern Ocean (∼2300, 2289, and 2288 µmol kg⁻¹ in the Atlantic, Indian, and Pacific sectors, respectively). The increase in TA brought about by upwelling corresponds to a long-term upwelling effect on nDIC of about 74 µmol kg⁻¹ (Fig. 8d–f) in the Southern Ocean.

Our results show that upwelling in the Southern Ocean can, by itself, generate high-latitude nDIC values that are around 220 µmol kg⁻¹ greater than subtropical values. We emphasize that there is also a sizable long-term effect of upwelling (forcing nDIC values to be around 74 µmol kg⁻¹ higher than they would be otherwise) after the operation of short-term effect. Contrary to what might typically be assumed, the long-term effects of upwelling are dictated by the amounts of TA upwelled, and not by the amounts of DIC or nutrients.

4.2 A new understanding of the controls on the surface DIC distribution

Our analysis revises the prevailing paradigm of the causes of the latitudinal gradient in surface DIC. Previously, the gradient was thought to be completely explained by the effect of sea surface temperature on CO₂ solubility, but we have shown that upwelling is also an important contributor. DIC and nDIC would still be elevated at high latitudes even without any temperature effect.

Neither temperature patterns nor upwelling are responsible for all of the observed large latitudinal gradients in DIC and nDIC (for instance, the ∼220 µmol kg⁻¹ difference in nDIC between low latitudes and the Southern Ocean), but rather they are jointly responsible. There is an apparent contradiction because both ΔnDIC_temp and ΔnDIC_{upw_st} appear to account for more than 80 % of the nDIC latitudinal gradient. While both processes are capable individually of raising nDIC by 182 and 220 µmol kg⁻¹ in the Southern Ocean, acting together they raise it by only 223 µmol kg⁻¹ instead of 400 µmol kg⁻¹. An obvious explanation of this apparent paradox is that when we consider upwelling effects, we should consider not only its short-term effect through supplying DIC and nutrients (1+2 in Fig. 6), but also its long-term effect with gas exchange with the atmosphere ($\mathrm{5}=\mathrm{1}+\mathrm{2}+\mathrm{3}$ in Fig. 6), the amount of which is a function of the amount of upwelled TA (which, together with temperature, controls the equilibrium DIC). The sum of the SST-driven effect and the long-term effect of upwelling approximately equals the nDIC latitudinal gradient (Table 4).

On the global scale, therefore, the ultimate controls on the surface DIC and nDIC latitudinal gradients are the spatial patterns of SST and upwelling, and the chemical composition of the upwelled water.

4.3 Importance of upwelling confirmed by the North Atlantic

From inspection of the global nDIC distribution (Fig. 1b), it can be seen that nDIC increases with latitude in all basins, but, as shown in Table 4, does so less strongly in the North Atlantic (difference between high latitudes and low latitudes of 114 µmol kg⁻¹) than in the North Pacific (difference of 192 µmol kg⁻¹). Although the latitudinal temperature gradient is less pronounced in the North Atlantic, this is not enough to explain the variation in gradients between the two basins: the average temperature of the high-latitude North Atlantic is 12.4 ^∘C and of the high-latitude North Pacific is 9.5 ^∘C, which can explain about 20 µmol kg⁻¹ of variation between the two nDIC gradients but cannot explain the observed 78 µmol kg⁻¹ variation (Table 4).

The reason for the discrepancy is that the Southern Ocean and the North Pacific experience elevations in values due to inputs of deep water whereas the North Atlantic does not. Upwelling occurs in the Southern Ocean and entrainment due to deep winter mixing occurs in the subarctic North Pacific (Mecking et al., 2008; Ohno et al., 2009) where it entrains waters high in both TA (Fry et al., 2016) and DIC. While deep winter mixing also occurs in the high-latitude North Atlantic (de Boyer Montégut et al., 2004), the entrained waters left the surface relatively recently and hence there is little accumulated remineralized DIC and TA in the deep water that is reintroduced to the surface. For this reason, winter entrainment produces little increase in surface nDIC in the North Atlantic. This makes the North Atlantic useful in discriminating between the two effects because, uniquely out of the three regions, only the SST effect operates there. As expected, the SST effect is able to completely account for the observed nDIC gradient in the North Atlantic, whereas it cannot in the other two regions (second and third columns in Table 4). The North Atlantic confirms the important contribution of upwelling to latitudinal gradients, while also showing that latitudinal gradients occur in the absence of upwelling.

Figure 10 Latitudinal distributions of sea surface nDIC, Alk^∗ (Fry et al., 2015), salinity-normalized nitrate, and silicate in each ocean basin.

4.4 Comparison of nDIC distribution to Alk^∗ and nutrients

Figure 10 shows a comparison between the patterns of nDIC, the TA tracer Alk^∗ (Eq. 11; Fry et al., 2015), and salinity-normalized nutrients. The similarities and differences in distributions of Alk^∗ and nutrients have previously been discussed by Fry et al. (2015). Here we extend the comparison to also include nDIC. All exhibit low and fairly constant values at low latitudes. This is primarily due to biological uptake and restricted supply from subsurface waters, for most variables, but is also due to fairly uniform high temperatures for nDIC. All increase polewards due to upwelling/entrainment (and also declining SST for nDIC), and all exhibit maxima at high latitudes in the Southern Ocean and North Pacific. All exhibit a more modest increase in the North Atlantic than in the North Pacific because the deep water formed relatively recently. There are differences in the latitudes at which the different parameters start to increase when moving from the Equator towards Antarctica, reflecting the different processes involved. Surface nDIC is the first to start increasing, under the influence of SST (third row in Fig. 7), at 20–25^∘ S. Alk^∗ and nutrients, however, influenced by upwelling/entrainment, do not start to increase until somewhere between 30 and 50^∘ S.

4.5 Implications for the future CO₂ sink under climate change

It is widely understood that global warming may alter the spatial distribution and intensity of upwelling in the ocean (Bakun, 1990; McGregor et al., 2007; Wang et al., 2015). It could either increase it on average, due to higher average wind speeds in a warmer, more energetic atmosphere (Bakun, 1990; Wang et al., 2015), or decrease it on average, due to enhanced stratification as the temperature differential between surface and deep waters is increased (Barton et al., 2013; Sarmiento et al., 2004). Furthermore, it is widely understood that an increase in upwelling would lead to an increase in the amount of CO₂ outgassed from the ocean, as larger quantities of CO₂-rich deep water are brought up to the surface and their CO₂ vented to the atmosphere (Evans et al., 2015; Marinov et al., 2006; Morrison et al., 2015). However, we have identified an additional effect here. Changes in upwelling would alter the distribution of carbon in the surface ocean not only through the supply of CO₂, but also through the supply of TA, which determines the eventual surface carbonate system equilibrium with the same atmospheric pCO₂ (Humphreys et al., 2018). That is to say, the impact of changes in upwelling on the ocean's carbon source–sink strength depends not only on the DIC content of the upwelled water but also on its TA content. Ocean carbon cycle models should include these additional consequences if they are to make accurate predictions about the impacts of global warming on future carbon cycling. They should include the several routes identified here by which upwelling affects surface DIC: through upwelling of DIC, through upwelling of nutrients, and through upwelling of TA.

5 Conclusions

We investigated the global surface DIC and nDIC distributions in order to explain the large differences between high-latitude (especially Southern Ocean) and low-latitude regions. This issue has been addressed in previous studies and here we revisited it using new analytical approaches that lead to new findings. We considered three drivers for how the phenomenon could be explained: (1) sea surface temperature variations through their effect on CO₂ system equilibrium constants, (2) salinity-related TA variations through their effect on pCO₂, and (3) upwelling in the subpolar oceans. Our analyses confirmed that temperature plays a dominant role through its effect on solubility, and is able to explain a large fraction of the surface nDIC latitudinal gradient (182 µmol kg⁻¹ out of 223 µmol kg⁻¹ in the high-latitude Southern Ocean). Variations in TA associated with evaporation and precipitation are unable to explain higher DIC concentrations at higher latitudes because alone they would drive the opposite DIC pattern. Their role is therefore to reduce the magnitude of the polewards gradient in DIC. Upwelling, whose role in driving the large-scale spatial patterns has not previously been appreciated, accounts for a sizable component of the surface nDIC latitudinal gradient (on average 220 µmol kg⁻¹ in the Southern Ocean). Its importance is magnified by the iron limitation that frequently occurs in upwelling areas, leaving behind residual upwelled excess DIC and macronutrients that cannot be utilized by biology. We emphasize that the upwelling of TA alongside DIC generates a prolonged effect that persists beyond CO₂ gas exchange re-equilibration timescales. The long-term effect of upwelling (74 µmol kg⁻¹ in the Southern Ocean) helps explain the shortfall between the observed nDIC latitudinal gradient (223 µmol kg⁻¹) and the magnitude of the temperature-driven effect (182 µmol kg⁻¹). On the global scale, we conclude that no single mechanism accounts for the full amplitude of surface DIC latitudinal variations but that temperature and the long-term effect of upwelling, in that order, are the two major drivers.