Changes in gross oxygen production, net oxygen production, and air-water gas exchange during seasonal ice melt in Whycocomagh Bay, a Canadian estuary in the Bras d'Or Lake system

Sea ice is an important control on gas exchange and primary production in polar regions. We measured net oxygen production (NOP) and gross oxygen production (GOP) using near-continuous measurements of the O₂∕Ar gas ratio and discrete measurements of the triple isotopic composition of O₂, during the transition from ice-covered to ice-free conditions, in Whycocomagh Bay, an estuary in the Bras d'Or Lake system in Nova Scotia, Canada. The volumetric gross oxygen production was $\mathrm{5.4}\begin{array}{c}+\mathrm{2.8}\\ -\mathrm{1.6}\end{array}$ mmol O₂ m⁻³ d⁻¹, similar at the beginning and end of the time series, and likely peaked at the end of the ice melt period. Net oxygen production displayed more temporal variability and the system was on average net autotrophic during ice melt and net heterotrophic following the ice melt. We performed the first field-based dual tracer release experiment in ice-covered water to quantify air–water gas exchange. The gas transfer velocity at >90 % ice cover was 6 % of the rate for nearly ice-free conditions. Published studies have shown a wide range of results for gas transfer velocity in the presence of ice, and this study indicates that gas transfer through ice is much slower than the rate of gas transfer through open water. The results also indicate that both primary producers and heterotrophs are active in Whycocomagh Bay during spring while it is covered in ice.

1 Introduction

The annual cycle of sea ice formation and melt regulates primary production and CO₂ uptake and ventilation in polar regions. Ice alters the rate of air–water gas exchange, reduces the penetration of light into surface water, changes stratification and mixing processes, and harbors microbes and biogenic gases including CO₂ (Cota, 1985; Loose et al., 2011a; Loose and Schlosser, 2011).

The question of whether climate change will increase or decrease Arctic Ocean carbon uptake is a topic of considerable debate (Bates et al., 2006; Bates and Mathis, 2009; Cai, 2011). Global warming is causing dramatic reductions in sea ice cover and increases in freshwater inflow and organic carbon supply to the Arctic Ocean, which impacts ecosystems (ACIA, 2004; Vaughan et al., 2013; Macdonald et al., 2015). Because conducting field work in the Arctic is challenging, measurements of productivity and gas exchange are limited. Biogeochemical time-series observations resolving seasonal changes in productivity are particularly scarce in the Arctic (MacGilchrist et al., 2014; Stanley et al., 2015). Measurements at Palmer Station in Antarctica show a strong seasonality in biological productivity and carbon uptake associated with changes in light, physical mixing, and grazing, and demonstrate the benefits of high-frequency sampling for quantifying CO₂ uptake in seasonally ice-covered waters (Ducklow et al., 2013; Tortell et al., 2014; Goldman et al., 2015).

The parameterization of gas exchange in the presence of ice also remains highly uncertain. Many investigators have assumed that there is negligible gas transfer through ice, and therefore the gas transfer velocity can be linearly scaled as a function of the fraction of open water, multiplied by the open water gas transfer velocity (Takahashi et al., 2009; Legge et al., 2015; Evans et al., 2015; Stanley et al., 2015). A recent field study by Butterworth and Miller (2016) in the Southern Ocean at 0 %–100 % ice cover verified this approach. However, other studies report that gas exchange is reduced or enhanced in the presence of sea ice relative to a linear scaling based on the fraction of open water, including some studies measuring higher transfer velocities in ice-covered waters than in open water (Fanning and Torres, 1991; Else et al., 2011; Papakyriakou and Miller, 2011; Rutgers van der Loeff et al., 2014). Additional studies show that gas exchange in ice-covered waters cannot be predicted from wind speed alone, which may be a cause of the wide range of results (Loose et al., 2009, 2016; Lovely et al., 2015). An additional factor reducing air–water exchange in ice-covered waters is that ice significantly reduces fetch for wave generation, and therefore wind-driven near-surface turbulence (Squire et al., 1995; Overeem et al., 2011). However, other processes may enhance near-surface turbulence in the presence of sea ice including convection associated with heat loss and brine rejection (Morison et al., 1992; Smith and Morison, 1993), boundary layer shear between ice and water (McPhee, 1992; Saucier et al., 2004), and wave interactions with drifting ice (Kohout and Meylan, 2008).

In this study, we measured productivity and gas exchange over a 1-month period during and following ice melt in Whycocomagh Bay, an estuary in the Bras d'Or Lake system on Cape Breton Island in Nova Scotia, Canada (see Sect. 1.1 for a full site description and map). We performed two dual tracer release experiments at different fractions of ice cover to quantify air–water gas exchange by adding ³He and SF₆ to the mixed layer. We measured net oxygen production (NOP) and gross oxygen production (GOP) at Little Narrows, while Whycocomagh Bay transitioned from completely ice-covered to ice-free conditions. GOP is the total amount of O₂ generated by autotrophic microbes as a result of photosynthesis. NOP is GOP minus respiratory consumption of O₂ by autotrophs and heterotrophs. The NOP∕GOP ratio provides an estimate of the export efficiency, i.e., the fraction of autotrophic production available for export to waters below the mixed layer. The time-series approach allowed us to quantify non-steady-state O₂ fluxes, which can be a significant fraction of the total O₂ flux in many regions (Hamme et al., 2012; Tortell et al., 2014; Manning et al., 2017b). We quantify GOP with discrete measurements of the triple oxygen isotopic composition of O₂ (Luz et al., 1999; Luz and Barkan, 2000; Juranek and Quay, 2013) and NOP with near-continuous measurements of the O₂∕Ar saturation anomaly (Cassar et al., 2009).

To our knowledge, there are no other published field-based experiments where the dual tracer technique was used in the presence of ice, and this study adds to a limited number of in situ measurements of NOP and GOP during ice melt (Goldman et al., 2015; Stanley et al., 2015; Eveleth et al., 2017).

1.1 Site description

The Bras d'Or Lake system consists of several interconnected channels and basins and has a total surface area of 1070 km² and an average depth of ∼30 m (maximum 280 m) (Petrie and Raymond, 2002; Petrie and Bugden, 2002). The Bras d'Or Lake system exchanges water with the Atlantic Ocean primarily through the Great Bras d'Or Channel at the northeastern region of the estuary; this channel has a shallow (16 m deep) and narrow (0.3 km wide) sill at the mouth (Petrie and Raymond, 2002). We conducted the work for this study in Whycocomagh Bay, an enclosed embayment approximately 13 km long and 3 km wide, at the northwestern end of the estuary, approximately 60 km from the open ocean (Fig. 1). Whycocomagh Bay is separated from the rest of the Bras d'Or Lake system by Little Narrows, a channel which is approximately 0.2 km wide and 0.5 km long. In Whycocomagh Bay, there are two basins (western and eastern basin) that are up to 40 m deep. Little Narrows channel is ∼15–20 m deep (Gurbutt and Petrie, 1995). The annual maximum ice cover is typically reached in early March. Ice disappears rapidly during April until its total melt by the first week of May (Petrie and Bugden, 2002).

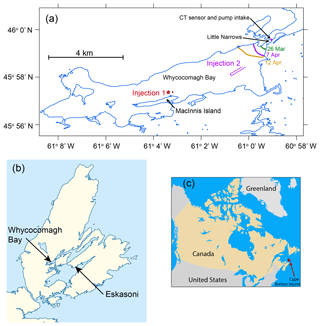
Figure 1 Map of Whycocomagh Bay and surrounding region. (a) Map of Whycocomagh Bay showing the locations of Injections 1 and 2 and the sampling equipment at Little Narrows. For Injection 1, the injection location is shown with a red star and the location where initial samples were collected is shown with a red circle. The colored lines labeled 26 March, 7 and 12 April show the location of the ice edge on these days. (b) Map of Cape Breton Island, showing the location of Whycocomagh Bay and Eskasoni (where wind speeds were obtained). (c) Map of Canada showing location of Cape Breton Island.

The Bras d'Or Lakes system exhibits standard estuarine circulation with freshwater flowing outward at the surface and denser saltwater flowing inward in the deeper layers (Gurbutt et al., 1995; Gurbutt and Petrie, 1995). The deep water in western Whycocomagh Bay is strongly isolated due to the presence of a sill at the bottom of Little Narrows channel, and very little mixing occurs between the surface and sub-surface waters (Petrie and Bugden, 2002). Whycocomagh Bay receives a relatively large amount of freshwater compared to other regions of the bay. This freshwater forms ice in winter and the stratification remains very stable, preventing vertical mixing (Krauel, 1975). In general, excluding the narrow channels in direct contact with the ocean, the Bras d'Or Lakes system does not exhibit significant tidally driven variability in temperature, salinity, and sea surface level (Krauel, 1975; Petrie, 1999; Petrie and Bugden, 2002; Dupont et al., 2003). A 21 d time series in western Whycocomagh Bay showed no detectable diurnal or semidiurnal tides (Dupont et al., 2003).

To our knowledge, there are no previously published measurements of water-column chemistry in Whycocomagh Bay in ice-covered conditions. Measurements from July 1974 showed that the western portion of Whycocomagh Bay became anoxic in the isolated deep waters below 25 m depth, whereas measurements in the eastern portion of the basin (closer to Little Narrows) showed the water column had an O₂ saturation of 61 % at the bottom depth of 30 m (Krauel, 1975; Gurbutt and Petrie, 1995). Measurements collected from 1995 to 1997 (from late April to late September) showed O₂ concentrations in Whycocomagh Bay from 1 to 5 m depth were near equilibrium (94 % to 112 % saturation) throughout the bay. In the deeper waters, O₂ concentrations in eastern Whycocomagh Bay ranged from 69 % at 25 m depth on 28 April 1996 to 54 % at 13 m depth on 26 September 1995 and 30 % at 30 m depth on 23 September 1996, and the western basin was persistently anoxic (Strain et al., 2001).

2 Field and analytical methods

2.1 Sampling setup at Little Narrows

Table 1 presents key events that occurred during the experiment. We continuously sampled water at Little Narrows channel (Fig. 1) during a 33 d time series (25 March–28 April 2013). We moored a Goulds SB Bruiser 5–18 GPM submersible pump with intake at ∼0.5 m depth (within the mixed layer), placed inside a mesh filter bag to prevent large particles from clogging the pump, and a conductivity and temperature (CT) sensor (Sea-Bird Electronics SBE37) at ∼0.5 m depth. From the submersible pump, water flowed through flexible high-pressure PVC tubing submerged underwater to a 3-port pressure-relief valve (on shore) and was then pumped along shore (∼50 m) to our sampling apparatus. The water passed through three 10^′′ canister filters (100, 20, and 5 µm nominal pore size) and then into a sampling manifold containing valves for distributing water for measurement of O₂∕Ar (continuously, by mass spectrometry) and for discrete sampling. As discussed below, we sampled discretely for SF₆, ³He, and O₂∕Ar and the triple oxygen isotopic composition of O₂, and near-continuously for O₂∕Ar. Excess water flowed through tubing back into the bay. We covered the tubing on shore and the filter canisters in foam insulation to minimize temperature changes in the water.

Table 1 Key events during experiment

We deployed a Nortek acoustic Doppler current profiler (ADCP) at ∼4 m depth in the middle of the channel from 7 to 28 April. The mean current speed at 0.5 m depth was 3.4 km d⁻¹ (3.9 cm s⁻¹) with an orientation toward 31^∘ (approximately along the channel axis), indicating the transit time through Little Narrows is relatively short. The ADCP data are shown in Supplement Fig. S1. Our measurements (salinity, O₂∕Ar, etc.) did not display any correlation with tidal cycles, consistent with previous studies of the Bras d'Or Lakes system indicating tides have a negligible influence on water properties within Whycocomagh Bay (Krauel, 1975; Petrie, 1999; Petrie and Bugden, 2002; Dupont et al., 2003).

The CT sensor was initially placed closer to shore than the water pump because the cable was not long enough to reach the pump, but after obtaining a longer cable, we were able to co-locate the CT sensor with the water pump (beginning 12 April). For the discrete samples, we used the CT sensor temperature and salinity measurements beginning on 12 April (when we moved the CT to the same location as the pump) to calculate the equilibrium concentration of each gas. Prior to 12 April, we collected measurements with a YSI temperature and salinity probe from the water on shore and used these measurements as the temperature and salinity for the discrete samples. We determined the average warming through the underway line to be 0.37±0.22 ^∘C based on comparisons between the temperatures from the CT sensor (in situ) and the YSI probe (on shore) after 12 April and applied this offset to all YSI temperature measurements. For the continuous O₂∕Ar data we used a temperature record from a thermocouple located in the sampling bucket because it had fewer gaps in time. We calibrated the thermocouple using an Aanderaa 4330 optode sensor which contains a temperature sensor (accuracy ±0.03 ^∘C) and then decreased the temperature by 0.37 ^∘C to correct for warming effects.

We installed the gas chromatograph (for measurement of SF₆) and mass spectrometer (for measurement of O₂∕Ar) inside a garage connected to the Little Narrows Ferry building. The majority of the wet equipment was set up outside the garage adjacent to a window on the garage, which was used for connecting equipment and power cables between the outdoors and indoors.

We deployed the water pump and in situ CT sensor to the east (oceanward) of the Little Narrows cable ferry which periodically crosses the channel and operates 24 h per day. We found no correlations between our temperature, salinity, and geochemical measurements and the position of the ferry within the channel. We collected conductivity, temperature, and depth (CTD) profiles with a SBE 19Plus sensor at Little Narrows, usually by boat using a winch, but occasionally by lowering the CTD by hand on a rope from the Little Narrows cable ferry. This CTD package was also equipped with an O₂ sensor, but unfortunately the O₂ sensor malfunctioned throughout the experiment. Therefore, we can characterize vertical structure of salinity and temperature but not O₂.

The GPS-equipped boat enabled us to map out the location of the ice edge nearest to Little Narrows, to perform the second tracer injection, and to sample after the tracer injection.

2.2 Tracer injections

The approach in this study was to dissolve the tracer mixture (³He∕SF₆) in Whycocomagh Bay, and sample continuously at Little Narrows, a constriction at the mouth of the bay. The net surface flow within Whycocomagh Bay, Little Narrows, and St. Patrick's Channel is toward the ocean due to the substantial freshwater inputs to the bay from surface runoff and precipitation (Gurbutt and Petrie, 1995; Yang et al., 2007), and therefore tracer dissolved within the bay at the surface will eventually pass through Little Narrows, or be ventilated to the atmosphere. Two tracer injections occurred during the time series, resulting in estimates of the gas transfer velocity for two extremes: near-complete ice cover and essentially ice-free conditions.

Injection 1 occurred through a hole in the ice from 30 to 31 March, near MacInnis Island (Fig. 1a). Approximately 0.11 mol SF₆ and $\mathrm{4.0}\times {\mathrm{10}}^{-\mathrm{4}}$ mol ³He were diluted by a factor of 50 with N₂ and then bubbled using a manifold within the mixed layer, over a 21 h period. The ice thickness was ∼0.3 m and the injection occurred in the upper 0.5 m of the water column. Because the tracer was added at a fixed location, it was added very slowly to increase the fraction of the gas that dissolved. We sampled for initial ³He and SF₆ concentrations at the injection site, immediately before starting the injection, and after terminating the tracer addition, by drilling several holes >10 m away from the injection site (because the bubbling action would have perturbed gas concentrations at the injection site). Subsequently, we sampled the tracer as it flowed through Little Narrows from 7 to 11 April. From 31 March to 11 April, the bay was nearly completely full of ice, with a small opening near Little Narrows (Fig. 1a). We also collected under-ice samples for O₂∕Ar and O₂ triple oxygen isotope (TOI) composition immediately before and after the injection but they displayed a wide range in values for O₂∕Ar, from −14 % to 2 %. Therefore, we were unable to define any initial under-ice values for these parameters.

Injection 2 occurred by boat on the morning of 19 April. By this time, the bay was nearly ice-free and all tracer from the previous experiment had passed through and/or been ventilated to the atmosphere such that the tracer concentrations at Little Narrows were below detection. While the boat was moving, we used the same manifold as for Injection 1 to bubble approximately 4.4 mol SF₆ and 0.021 mol ³He, diluted by a factor of four with N₂ into the mixed layer (Fig. 1a). The injection lasted 40 min. We detected the tracers at Little Narrows beginning on 20 April 23:30 UTC and measured the change in the ratio between 20 and 23 April as the tracer patch flowed through Little Narrows. We used a higher quantity and concentration of SF₆ and ³He during this injection because we expected the tracer would be ventilated more rapidly due to higher gas exchange rates given the open water conditions. We were able to inject the tracer more rapidly because it was distributed over a large area instead of through a small hole in the ice.

2.3 Measurement of O₂∕Ar and the triple oxygen isotopic composition of O₂

We set up an equilibrator inlet mass spectrometer (EIMS) for measurement of O₂∕Ar similarly to the system described in Cassar et al. (2009). However, we used a larger membrane contactor cartridge (Liqui-Cel MiniModule 1.7×5.5) because the design is more robust than the Liqui-Cel MicroModule 0.75×1 used by Cassar et al. (2009). The water flow rate through the cartridge was ∼1.5 L min⁻¹. We attached a custom female Luer-Lok fitting paired to a capillary adapter to the upper headspace sampling port and the lower sampling port was left closed.

For O₂∕Ar and the triple oxygen isotopic composition of O₂, we collected samples in pre-evacuated, pre-poisoned glass flasks from a spigot in the water pumped to shore, or for shipboard sampling, using a small submersible water pump. Analysis occurred within ∼6 months of flask evacuation and 4 months of sample collection at the Woods Hole Oceanographic Institution with a Thermo Fisher Scientific MAT 253 isotope ratio mass spectrometer, following the method of Barkan and Luz (2003) with modifications as described in Stanley et al. (2010, 2015).

The precision of the discrete samples, calculated based on the standard deviation of equilibrated water samples run daily along with the environmental samples was 0.011 and 0.020 ‰ for δ¹⁷O and δ¹⁸O, respectively, 5.6 per meg for ¹⁷Δ, and 0.07 % for O₂∕Ar. The mean difference between the EIMS and discrete samples was 0.05 %, and the mean magnitude of the difference was 0.35 %; given the small mean offset, the EIMS data were not calibrated using discrete samples.

2.4 Measurement of SF₆

For SF₆, we collected ∼20 mL of water in 50 mL glass gas-tight syringes, then added ∼20 mL of nitrogen and allowed the samples to be shaken for 10 min to achieve equilibration between the headspace and water (Wanninkhof et al., 1987). After the water equilibrated to room temperature, we injected 1 mL of the headspace into an SRI-8610C gas chromatograph with an electron capture detector, heated to 300 ^∘C (Lovely et al., 2015). We calibrated the detector response using a 150 parts per trillion SF₆ standard (balance N₂).

We also operated an automated gas extraction system at Little Narrows which sampled nearly every hour. The system recirculated a 118 mL loop of water through a membrane contactor, and the headspace of the membrane contactor was under vacuum, causing the dissolved gas to be extracted from the water into the headspace. When the automated system showed measurable SF₆ in the water, we began collecting discrete samples for SF₆ and ³He.

SF₆ equilibrium solubility concentrations are calculated following Bullister et al. (2002) and diffusivity is from King and Saltzman (1995). Precision of the system, based on the standard deviation of measurements of the 150 ppt standard, was 7 %. We assume a dry atmospheric mole fraction of 8 ppt for SF₆ (Bullister, 2015).

2.5 Measurement of ³He

For ³He analysis, we collected samples in copper tubes, mounted in aluminum channels and sealed the samples at each end using clamps. Sample analysis occurred at the Lamont Doherty Earth Observatory, using a VG5400 mass spectrometer for ³He and ⁴He concentration (Ludin et al., 1998). Error for ³He sample analysis (combined precision and accuracy) was ≤2 % of the measured ³He-excess concentration above equilibrium. We used He solubility from Dempsey E. Lott III and William J. Jenkins (personal communication, 2015) and diffusivity from Jähne et al. (1987a). The Lott and Jenkins solubility values are ∼2 % higher than published data from Weiss (1971). The He solubility is for bulk He and we calculate the ³He solubility using an atmospheric mole ratio $M\left({}^{\mathrm{3}}\mathrm{He}\right)/M\left({}^{\mathrm{4}}\mathrm{He}\right)=\mathrm{1.399}\times {\mathrm{10}}^{-\mathrm{6}}$ (Mamyrin et al., 1970; Porcelli et al., 2002), although some more recent results indicate the current ratio may be slightly lower, $\simeq \mathrm{1.390}\times {\mathrm{10}}^{-\mathrm{6}}$ (Brennwald et al., 2013). We use the He equilibrium isotopic fractionation as described in Benson and Krause (1980b).

3 Calculations, results, and discussion

The three goals of the experiment were to (1) quantify gas transfer velocity by dual tracer release, (2) quantify gross oxygen production from the triple isotopic composition of O₂, and (3) quantify net oxygen production from O₂∕Ar. We begin by discussing the hydrographic characteristics of the study area and then describe the calculations, results, and interpretation for each of the three goals, in sequence.

3.1 Hydrography

We began sampling O₂ at Little Narrows on 25 March, when Whycocomagh Bay was nearly (>95 %) fully covered by ice, and completed sampling on 28 April, when the bay was completely ice-free (Fig. 2). The surface ice cover retreated most rapidly between 16 and 18 April and was completely gone by 22 April or perhaps even earlier. Figure 2 shows 18 April and 23 April; MODIS satellite images on 22 April were also ice-free (but more blurry, and so are not shown in the figure) and we estimated ice cover to be <10 % in the bay during surveys by boat during daytime on 20 April. The ice was likely melting even at the beginning of the time series since the surface water temperature was always above the freezing temperature of water (Fig. 3). Changes in surface ice cover and total ice volume are both important factors during the study; changes in ice volume/thickness will affect stratification and convection in the mixed layer as well as light penetration through the ice, and the surface ice cover affects the rate of gas exchange (Smith and Morison, 1993; Butterworth and Miller, 2016; Loose et al., 2016).

CTD profiles at Little Narrows channel near the water pump intake showed substantial changes in stratification during the time series (Fig. 3). From 25 March through 8 April the water column was strongly stratified and we estimated the mixed layer depth to average 0.8(0.3) m. During this period, it was often difficult to determine the exact mixed layer depth because the mixed layer depth was similar to the length of the CTD instrument and obtaining a stable CTD response so close to the surface was challenging. Following 8 April, the mixed layer deepened and warmed and its salinity increased, likely due to convection and heating following sea ice melt. For this period, we defined the mixed layer depth as the first depth where the density is 1 kg m⁻³ greater than the value at 1 m. The mixed layer reached a maximum of 3.0 m on 23 April and then shoaled by the end of the time series on 28 April. On most days, the density profile and mixed layer depth were driven by stratification in salinity, but for the final profile on 28 April the mixed layer depth was determined by a combination of temperature and salinity stratification due to heat uptake by the surface water following the ice melt. These changes in mixed layer depth must be considered in order to interpret the O₂ measurements and to quantify the gas transfer velocity.

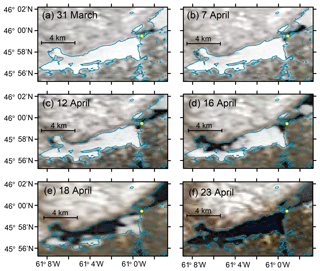
Figure 2 Satellite images showing changes in ice cover in Whycocomagh Bay. MODIS Terra true color images showing changes ice cover during the time series between 31 March and 23 April. Little Narrows is indicated with a yellow circle in all images. Ice cover retreated most rapidly between 12 and 20 April. Shoreline data (blue lines) are from GeoGratis/Natural Resources Canada (http://geogratis.gc.ca, last access: 27 August 2019) and satellite data are from NASA Worldview (http://worldview.earthdata.nasa.gov, last access: 27 August 2019).

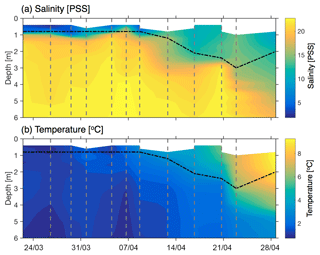
Figure 3 Temperature and salinity profiles at Little Narrows. (a) Salinity and (b) temperature profiles measured at Little Narrows. The vertical grey dashed lines indicate the timing of CTD casts (22, 26, 29, and 31 March, and 4, 6, 8, 12, 16, 20, 23, and 28 April). The black dot-dashed line shows the estimated mixed layer depth. The data in this plot were binned into 0.2 m depth bins from 0.4 to 3.0 and 0.3 m depth bins from 3.3 to 9.9 m. The shallowest depth varies between casts due to challenges in getting stable CTD data in the upper 1 m.

3.2 Gas transfer velocity

3.2.1 Calculation

We calculate the gas transfer velocity using the dual tracer approach (Watson et al., 1991; Wanninkhof et al., 1993). For each experiment, we dissolved a mixture of ³He and SF₆ in the water, both of which are normally present at very low ambient concentrations, and then measured the change in the ratio of the two gases as a function of time. Measuring two tracers enables correction for dilution and mixing, which reduces the excess concentrations of both gases (relative to air–water equilibrium) but does not change their ratio. Over time, the concentrations of both gases decay toward air–water equilibrium as gas is ventilated to the atmosphere through gas exchange. Because the molecular diffusivity of ³He is 8–9 times higher than SF₆, ³He is lost to the atmosphere more rapidly than SF₆, and therefore the ³He:SF₆ ratio decreases with time. The ratio of the gas transfer velocity for the two gases is expressed as

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{k_{{}^{\mathrm{3}}\mathrm{He}}}{k_{{\mathrm{SF}}_{\mathrm{6}}}}}={\left({\displaystyle \frac{{\mathit{\text{Sc}}}_{{}^{\mathrm{3}}\mathrm{He}}}{{\mathit{\text{Sc}}}_{{\mathrm{SF}}_{\mathrm{6}}}}}\right)}^{-n},\end{array}$$

where k is the gas transfer velocity (m d⁻¹) and Sc is the Schmidt number (unitless), defined as the kinematic viscosity of water divided by the molecular diffusivity of the gas in water, and n is an empirical exponent, typically between 0.5 and 0.67 (Jähne et al., 1984; Liss and Merlivat, 1986). Using a time series of measurements of the two gases, the gas transfer velocity for ³He is calculated as

$$\begin{array}{}\text{(2)}& k_{{}^{\mathrm{3}}\mathrm{He}}=h{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\ln \left({\left[{}^{\mathrm{3}}\mathrm{He}\right]}_{\mathrm{exc}}/{\left[{\mathrm{SF}}_{\mathrm{6}}\right]}_{\mathrm{exc}}\right)}{\mathrm{1}-{\left({\mathit{\text{Sc}}}_{{\mathrm{SF}}_{\mathrm{6}}}/{\mathit{\text{Sc}}}_{{}^{\mathrm{3}}\mathrm{He}}\right)}^{-n}}}\right).\end{array}$$

Here h is the mixed layer depth, [³He]${}_{\mathrm{exc}}=[{}^{\mathrm{3}}\mathrm{He}{]}_{\mathrm{meas}}-[{}^{\mathrm{3}}\mathrm{He}{]}_{\mathrm{eq}}$ where [³He]_exc is the ³He-excess concentration, [³He]_meas is the measured concentration, and [³He]_eq is the equilibrium concentration (calculated as a function of temperature and salinity). [SF₆]_exc is defined analogously.

We can write the analytical solution to Eq. (2) as (Ho et al., 2011b)

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& {\left({\displaystyle \frac{[{}^{\mathrm{3}}\mathrm{He}{]}_{\mathrm{exc}}}{[{\mathrm{SF}}_{\mathrm{6}}{]}_{\mathrm{exc}}}}\right)}_t={\left({\displaystyle \frac{[{}^{\mathrm{3}}\mathrm{He}{]}_{\mathrm{exc}}}{[{\mathrm{SF}}_{\mathrm{6}}{]}_{\mathrm{exc}}}}\right)}_{t-\mathrm{1}}\\ & \exp \left(-{\displaystyle \frac{k_{{}^{\mathrm{3}}\mathrm{He}}\mathrm{\Delta }t}{h}}\left[\mathrm{1}-{\left({\displaystyle \frac{{\mathit{\text{Sc}}}_{{\mathrm{SF}}_{\mathrm{6}}}}{{\mathit{\text{Sc}}}_{{}^{\mathrm{3}}\mathrm{He}}}}\right)}^{-n}\right]\right).\end{array}\end{array}$$

Using this equation and a cost function, we can find the value of $k_{{}^{\mathrm{3}}\mathrm{He}}$ that minimizes the error between the measured and modeled [³He]_exc / [SF₆]_exc. Once $k_{{}^{\mathrm{3}}\mathrm{He}}$ is known, we can calculate k for any other gas using Eq. (1) by substituting ${\mathit{\text{Sc}}}_{{\mathrm{SF}}_{\mathrm{6}}}$ for the Schmidt number of the gas of interest. For example, for Sc=600 (the Schmidt number for CO₂ at 20 ^∘C in freshwater),

$$\begin{array}{}\text{(4)}& k_{\mathrm{600}}=k_{{}^{\mathrm{3}}\mathrm{He}}{\left({\displaystyle \frac{\mathrm{600}}{{\mathit{\text{Sc}}}_{{}^{\mathrm{3}}\mathrm{He}}}}\right)}^{-n}.\end{array}$$

For this study, we use a Schmidt number dependence of n=0.5 which is appropriate for wavy, unbroken water surfaces (no bubble entrainment) (Jähne et al., 1984, 1987a; Liss and Merlivat, 1986; Ho et al., 2011b). At Little Narrows, we observed that tidal currents generated surface waves, even at low wind speeds. These waves produce near-surface water turbulence which is the ultimate driver of air–water gas exchange (Jähne et al., 1987b; Wanninkhof et al., 2009).

The Schmidt number at a salinity of 4 PSS and temperature of 2 ^∘C is 305 for ³He and 2684 for SF₆. The initial ${\mathit{\text{Sc}}}_{{\mathrm{SF}}_{\mathrm{6}}}/{\mathit{\text{Sc}}}_{{}^{\mathrm{3}}\mathrm{He}}$ ratio was 8.7 for Injection 1 and 8.2 for Injection 2.

3.2.2 Results

The gas transfer velocity was much lower for Injection 1, which was sampled while the basin was essentially full of ice (31 March–10 April), compared to Injection 2, which was sampled when the basin was nearly ice-free (20–23 April). We used Eq. (3) to model the measurements. We started the model at the time of the first measurement, initialized it with an initial excess concentration ratio and ran it through time for the duration of the injection. We selected the value of $k_{{}^{\mathrm{3}}\mathrm{He}}$ yielding the smallest root mean square deviation (RMSD) between the measured ratio and modeled ratio for each injection. The model ran 1000 times using a Monte Carlo simulation where the measured excess concentration ratios, including the initial condition, are varied with a Gaussian distribution, with the standard deviation being the estimated measurement error in the ratio (7.3 %).

We assume a constant $S{c}_{{}^{\mathrm{3}}\mathrm{He}}/{\mathit{\text{Sc}}}_{{\mathrm{SF}}_{\mathrm{6}}}$ and mixed layer depth (h) for each injection. In actuality, during each injection ${\mathit{\text{Sc}}}_{{}^{\mathrm{3}}\mathrm{He}}$ varies by ∼1 % and the ratio of the Schmidt numbers varies by less than 0.2 %, so this is a small source of error. For Injection 1, we assume a mixed layer depth (h) of 0.8(0.3) m. This depth is consistent with the salinity profiles at Little Narrows (Fig. 3a) between 31 March and 8 April (between 0.6 and 1.0 m depth), as well as measurements with a hand-held temperature probe at the site of Injection 1 which indicated that the mixed layer depth was between 0.75 and 1 m. The mixed layer depth may have increased slightly between 8 and 10 April, but was likely 1.3 m or less (Fig. 3).

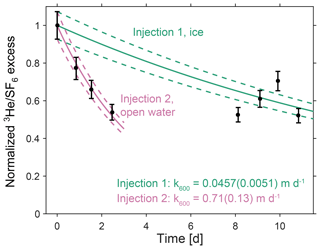
Figure 4 Measured and modeled excess tracer ratios. Measured and modeled ratio of excess ³He∕SF₆, normalized to the initial measured ratio for each injection. The modeled excess ratio is calculated using the $k_{{}^{\mathrm{3}}\mathrm{He}}$ that minimizes error between the model and measurements. Model results are shown for the model initialized with the initial measured concentration (solid lines), and starting 1 standard deviation above or below the measured initial concentration (based on an error of 7.3 % in the tracer ratio, dashed lines).

Table 2 Data for determination of the gas transfer velocity.

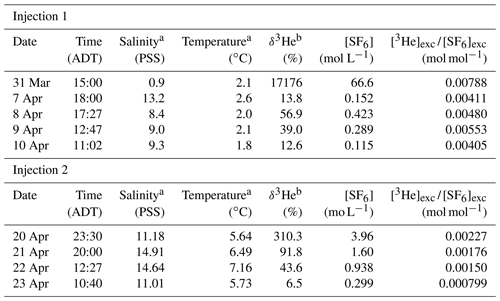
^a During Injection 1, we measured temperature and salinity with a YSI probe to a precision of one decimal place. During Injection 2, we measured temperature with a calibrated thermocouple and salinity with the in situ CTD, to a precision of two decimal places. ^b δ³He = ((³He∕⁴He)_meas/(³He∕⁴He)_eq).

For Injection 1, the excess SF₆ and ³He concentrations were reduced by 2 orders of magnitude by the time the tracer reached Little Narrows (7–11 d after injection). The tracer ratio did not display a consistent decrease over the 3 days we sampled it at Little Narrows, which may be due to the substantially lower gas transfer velocity, as well as the very low tracer concentrations potentially increasing measurement uncertainty. The best fit to all the measurements was k₆₀₀=0.0457(0.0051) m d⁻¹, in the presence of ice and a shallow mixed layer, with the uncertainty the standard deviation of the distribution of k₆₀₀ from the Monte Carlo simulation (Fig. 4).

The mixed layer appeared to deepen between the CTD profiles on 8 April 16:08 UTC and 12 April 19:13 UTC (Fig. 3), and it is possible that the mixed layer depth on 9–10 April may have been slightly deeper than the estimate of 0.8(0.3) m. However, if mixed layer deepening had a significant influence on our gas transfer velocity estimate, we would expect k₆₀₀ (calculated assuming a constant mixed layer depth) to be lowest when calculated over the longest time period, using the sample collected on 10 April. Instead, the gas transfer velocity was actually the lowest when integrated to 9 April (the excess tracer ratio appears above the best-fit line) and second lowest on 8 April. Since the gas transfer velocities for Injection 1 integrate over 7–10 d, any change in mixed layer depth during the last 1–2 d will have a small effect on the calculated k.

For Injection 2, we use a mixed layer depth of 2.7(0.3) m based on CTD profiles at Little Narrows on 20 and 23 April, which had mixed layer depths of 2.4 and 3.0 m, respectively (Fig. 3a). Calculation of the gas transfer velocity for Injection 2 was relatively straightforward as the ratio of excess ³He∕SF₆ steadily decreased over the five measurements (Table 2). The best fit to all four measurements was k₆₀₀=0.71(0.13) m d⁻¹ for open water (Fig. 4).

Using the published He solubility from Weiss (1971) instead of the unpublished data of Dempsey E. Lott III and William J. Jenkins (personal communication, 2015) results in a gas transfer velocity that is 8 % lower in the presence of ice (for Injection 1) and 0.4 % lower in open water (for Injection 2).

3.2.3 Discussion

The gas transfer velocity calculated for Injection 1 is the effective gas transfer velocity (k_eff); it averages the gas transfer velocity through ice (k_ice), weighted by the time the tracer spent under ice, and the gas transfer velocity for open water (k), weighted by the time the tracer spent in open water (Loose et al., 2014). In partially ice-covered waters, the effective gas transfer velocity is sometimes calculated as

$$\begin{array}{}\text{(5)}& k_{\mathrm{eff}}=\left(f\right)k+(\mathrm{1}-f)k_{\mathrm{ice}},\end{array}$$

where f is the fraction of open water (Loose et al., 2014; Lovely et al., 2015). If k_ice is negligible, then k_eff=(f)k (Loose and Jenkins, 2014; Crabeck et al., 2014; Butterworth and Miller, 2016). For Injection 2, we determined k, the value for open water. We expect k_ice to be lower than k because the ice acts as a physical barrier to gas exchange. The rate of gas molecular diffusion in water (Jähne et al., 1987a; King and Saltzman, 1995) is higher than gas diffusion through ice (Gosink et al., 1976; Ahn et al., 2008; Loose et al., 2011b; Lovely et al., 2015). However, the exact rate of gas diffusion through saltwater ice (and by extension the value of k_ice) is not well constrained and likely varies based on the physical properties of the ice such as brine volume and temperature (Golden et al., 2007; Loose et al., 2011b; Zhou et al., 2013; Moreau et al., 2014; Lovely et al., 2015).

To evaluate these results within the framework of Eq. (5), we must estimate the fractional ice cover during Injection 1. Visual surveys along the shoreline of Whycocomagh Bay and satellite data indicated that the bay was nearly fully covered with a continuous sheet of ice from 31 March to 10 April, except for an opening close to Little Narrows (Fig. 2a–b). Beginning between 7 and 12 April, a small region of water appeared to open up along the shoreline northwest of the site of Injection 1; however, by this time the tracer patch had moved eastward close to Little Narrows and likely was not significantly affected by this open water (Fig. 2c). We mapped out the location of the ice edge closest to Little Narrows by boat on 26 March and 7 and 12 April (Fig. 1a). Using these surveys and shoreline data, we calculate that for the surface area of the bay between the injection site and Little Narrows, f=0.01 on 26 March, 0.05 on 7 April, and 0.08 on 12 April. The f experienced by the tracer patch during Injection 1 is likely between 0.02 and 0.08 because the tracer was injected on 30–31 March and flowed through the open water near Little Narrows between 6 and 11 April. If k for open water is the same for both injections (k=0.71 m d⁻¹), then the results yield k_eff=(f)k with f=0.064, which is consistent with the fraction of open water we estimate for Injection 1. Thus we conclude that k_ice was negligible, compared to k. For example, if k_ice was even 10 % of k for open water, then k_eff for Injection 1 would have been ∼0.11 m d⁻¹, more than double the observed value of 0.0457(0.0051) m d⁻¹. One source of uncertainty in estimating the correct value of f is that the transit speed between the injection site and Little Narrows was non-constant. The mean current velocity at Little Narrows channel was 3.4 km d⁻¹, but the tracer took approximately 8 d to flow 7 km from the injection site to Little Narrows.

In calculating GOP and NOP by oxygen mass balance, we apply the tracer-based gas transfer velocities estimated by dual tracer release throughout the time series, since there is no consensus on the best treatment of gas transfer in lakes and estuaries (Clark et al., 1995; Cole and Caraco, 1998; Crusius and Wanninkhof, 2003; Ho et al., 2011a), nor on the parameterization of gas transfer in the presence of ice (Else et al., 2011; Lovely et al., 2015; Butterworth and Miller, 2016). Additionally, if bottom-derived turbulence (e.g., from tidal flow) is a significant contributor to air–water gas exchange, a parameterization based on wind speed alone may not be appropriate. This method of calculating one average k₆₀₀ for each injection does not enable the development of a wind speed-dependent parameterization for the gas transfer velocity.

Because the k₆₀₀ values for Injection 1 and Injection 2 are very different, the treatment of the gas transfer velocity in between the two injections strongly affects the productivity estimates for this period. We use k₆₀₀=0.0457(0.0051) m d⁻¹ from the beginning of the time series until the end of 15 April. Figure 2d, collected on 16 April, is the first satellite image showing substantial open water within Whycocomagh Bay, but the open water is primarily in the western half of the bay, far from Little Narrows. We use k₆₀₀=0.71(0.13) m d⁻¹ from 21 April until the end of the time series on 28 April. Surveys by boat on 19 and 20 April indicated <10 % ice cover on these days, and we collected the first tracer measurements following Injection 2 on 20 April 23:30 UTC. Between 16 and 20 April, we apply a linear interpolation of the k₆₀₀ for Injection 1 and Injection 2 as a function of time. The gas transfer velocity is most uncertain during the period when the ice cover rapidly decreased because we do not have any measurements of gas transfer at intermediate ice cover. However, because the ice cover retreated rapidly, only 4 days of the productivity estimates (out of a 33 d time series) are affected by the uncertainties in gas transfer at intermediate ice cover.

3.2.4 Comparison with other estimates

To compare the gas exchange estimates with other published studies, we use wind speed data measured at 10 m height (u₁₀) at Eskasoni Reserve, 27 km northeast of Little Narrows (Fig. 1b) and archived by the Government of Canada (http://climate.weather.gc.ca, last access: 27 August 2019). The archived data are 2 min averages measured once per hour. During the period that samples with tracer from Injection 2 were collected (between 20 April 23:00 and 23 April 11:00), the average wind speed was 2.6(1.4) m s⁻¹ and the median was 2.2 m s⁻¹. The calculated k₆₀₀ over this time period from dual tracer data is 0.71(0.13) m d⁻¹. Cole and Caraco (1998) found k₆₀₀=0.636(0.029) m d⁻¹ (95 % confidence interval) and their estimate is independent of wind speed in a lake with daily wind speeds of 1.39(0.06) m s⁻¹ (95 % confidence interval); this k₆₀₀ is consistent within uncertainty with the Injection 2 result. Standard open ocean parameterizations that use a quadratic dependence on wind speed predict k₆₀₀ ≃ 0.5–0.6 m d⁻¹ with uncertainties of ∼20 % or ∼0.10 m d⁻¹ (Ho et al., 2006; Sweeney et al., 2007; Wanninkhof, 2014).

Crusius and Wanninkhof (2003) found that in a lake gas exchange can be estimated nearly equally well using three different parameterizations. Using their parameterizations with the wind speed record during our time series, we calculate transfer velocities of 0.32–0.66 m d⁻¹, and the velocity is most similar to our result when we use a constant gas transfer velocity k₆₀₀=0.24 m d⁻¹ for u₁₀<3.7 m s⁻¹ and $k_{\mathrm{600}}=\mathrm{1.23}{u}_{\mathrm{10}}-\mathrm{4.30}$ for u₁₀≥3.7 m s⁻¹. However, Crusius and Wanninkhof (2003) parameterized the gas transfer using instantaneous (e.g., 1 min averaged) winds measured throughout the time series, not once per hour, and emphasize the importance of including the variability in short-term winds when quantifying gas exchange at low wind speeds. If gas transfer velocity has a nonlinear dependence on wind speed, then short-term wind speed measurements will more accurately represent the gas transfer than wind speed values averaged over longer periods (Livingstone and Imboden, 1993; Crusius and Wanninkhof, 2003). Since we only have 2 min averages measured once per hour (for a total of 60 measurements during Injection 2), the wind record we use may not fully represent the variability in winds during the Injection 2 measurement period.

A source of error in comparisons with published results is that the wind speed data come from a different location than the study area. Although Eskasoni Reserve is adjacent to the Bras d'Or Lake, the local topography and bathymetry are different near the reserve and in Whycocomagh Bay. Thus, it is likely that the wind speed and momentum stress at the air–water interface differ at Whycocomagh Bay compared to Eskasoni Reserve (Ortiz-Suslow et al., 2015).

The measurements are in agreement with other studies showing that gas transfer velocity is significantly reduced under near-complete ice cover (Lovely et al., 2015; Butterworth and Miller, 2016) and contrast with studies showing enhanced gas transfer under >85 % ice cover (Fanning and Torres, 1991; Else et al., 2011). We find that k_eff=(f)k for >90 % ice cover, but we cannot evaluate whether the same equation holds at intermediate ice cover because there was no injection at a lower fractional ice cover. In this study, the ice cover was near-continuous across the entire bay during Injection 1 and likely did not contain the ice leads that are common in Arctic and Antarctic sea ice; differences in gas transfer behaviour are expected based on the nature of the ice pack.

3.3 Gross oxygen production

3.3.1 Calculation

The triple oxygen isotopic composition of O₂ is an effective tracer of gross photosynthetic O₂ production (Juranek and Quay, 2013). Due to reactions in the upper atmosphere that impart a small mass-independent isotopic signature on atmospheric oxygen, dissolved O₂ derived from air–water exchange has a unique triple isotopic signature compared to O₂ generated by photosynthesis and O₂ consumed by respiration. We characterize the oxygen isotopic composition using

$$\begin{array}{}\text{(6)}& {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=X^{\mathrm{18}}/X_{\mathrm{std}}^{\mathrm{18}}-\mathrm{1},\end{array}$$

and express the δ¹⁸O in ‰ by multiplying by 1000. Here $X^{\mathrm{18}}=r({}^{\mathrm{18}}\mathrm{O}/{}^{\mathrm{16}}\mathrm{O})$ is the measured ratio and $X_{\mathrm{std}}^{\mathrm{18}}=r({}^{\mathrm{18}}\mathrm{O}/{}^{\mathrm{16}}\mathrm{O}{)}_{\mathrm{std}}$ is the ratio of the isotopes in the standard. We calculate δ¹⁷O analogously. For GOP studies, O₂ in air is the standard for isotopic measurements of O₂ and isotopes of H₂O are referenced to the VSMOW-SLAP scale. For clarity, we distinguish between the isotopic composition of the two substrates (O₂ and H₂O) as δ¹⁸O-O₂ and δ¹⁸O-H₂O.

The term ¹⁷Δ quantifies the triple isotopic composition of dissolved O₂:

$$\begin{array}{}\text{(7)}& {}^{\mathrm{17}}\mathrm{\Delta }=\ln ({\mathit{\delta }}^{\mathrm{17}}\mathrm{O}\text{-}{\mathrm{O}}_{\mathrm{2}}+\mathrm{1})-\mathit{\lambda }\ln (\mathit{\delta }{}^{\mathrm{18}}\mathrm{O}\text{-}{\mathrm{O}}_{\mathrm{2}}+\mathrm{1}).\end{array}$$

We report ¹⁷Δ with λ=0.5179, the ratio of the fractionation factors for respiratory O₂ consumption in ¹⁷O relative to ¹⁸O (i.e., $\mathit{\lambda }{=}^{\mathrm{17}}\mathit{ϵ}{/}^{\mathrm{18}}\mathit{ϵ}$, where ϵ is the isotopic fractionation of O₂ due to respiratory consumption) (Luz and Barkan, 2005). This value for λ is selected so that ¹⁷Δ is nearly unaffected by respiratory O₂ consumption and reflects the proportion of O₂ that is derived from photosynthesis relative to air–water gas exchange (Hendricks et al., 2005; Juranek and Quay, 2013; Nicholson et al., 2014). We report ¹⁷Δ in per meg (1 per meg = 0.001 ‰) due to the small range of values in natural waters, typically 8–242 per meg (Juranek and Quay, 2013; Manning et al., 2017a).

Two key constraints in the calculation of GOP from measurements of the triple isotopic composition of O₂ are the isotopic composition of O₂ derived from air–water exchange and the isotopic composition of photosynthetic O₂. The composition of photosynthetic O₂ is dependent on the triple oxygen isotopic composition of H₂O, the substrate for photosynthetic O₂, and the isotopic fractionation associated with photosynthetic O₂ production. In oceanic studies, a common assumption is that the H₂O isotopic composition is equivalent to VSMOW (standard mean ocean water), but in brackish systems it is necessary to estimate the isotopic composition of water and incorporate this into the GOP calculation (Manning et al., 2017a).

Because we did not measure the triple oxygen isotopic composition of H₂O, we use previously published measurements of δ¹⁸O-H₂O and published relationships between δ¹⁷O-H₂O and δ¹⁸O-H₂O (Luz and Barkan, 2010; Li and Cassar, 2016) to estimate the values of δ¹⁸O-H₂O and δ¹⁷O-H₂O during the time series, as described in Manning et al. (2017a). We assume that the waters in the estuary represent a mixture of two endmembers: seawater and meteoric (precipitation-derived). We define the salinity and δ¹⁸O-H₂O for the two endmembers and then calculate δ¹⁸O-H₂O for each water sample collected during the time series as a linear function of salinity. A similar approach is applied for δ¹⁷O-H₂O.

For the seawater endmember, we use compilations of δ¹⁸O-H₂O and salinity (Schmidt, 1999; Bigg and Rohling, 2000) available from an online database (Schmidt et al., 1999). We included all 19 near-surface samples (<5 m depth) between 44–48^∘ N and 58–64^∘ W in the database. For these samples, the average δ¹⁸O-H₂O = −1.68(0.26) ‰ and salinity = 31.25(0.30) PSS.

For the meteoric water endmember, we use an 8-year time series of δ¹⁸O-H₂O measured in Truro, Nova Scotia (200 km southwest of our study area and at 40 m elevation), and archived in the Global Network of Isotopes in Precipitation (GNIP) database (IAEA/WMO, 2016). The amount-weighted value of δ¹⁸O-H₂O over the time series was −9.3(3.1) ‰ versus VSMOW, using precipitation measurements from Truro, NS, over the same time period from the Government of Canada historical weather database (http://climate.weather.gc.ca, last access: 27 August 2019). Also, Timsic and Patterson (2014) measured δ¹⁸O-H₂O = −8.8(0.1) ‰ on a water sample collected in July 2009 from the Skye River, within the Whycocomagh Bay watershed (Parker et al., 2007), consistent with the average Truro, NS, value.

Using the two endmembers, S=0 PSS, δ¹⁸O-H₂O = −9.3 ‰ (local meteoric water) and S=31.25 PSS, δ¹⁸O-H₂O = −1.68 ‰ (local seawater), we derive the equation δ¹⁸O-H₂O = 0.2439S−9.30 (Fig. 5). This equation is consistent with published δ¹⁸O-H₂O measurements from within the estuary (Fig. 5). Mucci and Page (1987) collected water samples from the Bras d'Or Lake in November 1985 and found a salinity of S = 26.42 (1.12) PSS and δ¹⁸O = −2.99 (0.32) ‰ for samples at 17 different stations (albeit none within Whycocomagh Bay). Notably, VSMOW (S=34.5 PSS) plots 0.9 ‰ above the local mixing line, which demonstrates the importance of accurately defining both the freshwater and seawater endmembers.

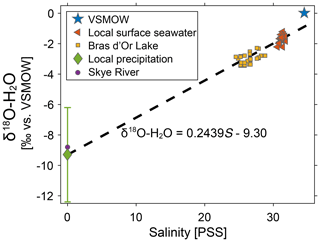
Figure 5 δ¹⁸O-H₂O regression versus salinity. Measurements of δ¹⁸O-H₂O in local surface seawater, the Bras d'Or Lake, local precipitation, and the Skye River (within the Whycocomagh Bay watershed). The regression is calculated using the local precipitation and seawater values. The local precipitation value is plotted as 9.3(3.1) ‰, with the error bar the standard deviation of the amount-weighted annual average.

Then, for the two endmember values of δ¹⁸O-H₂O, we estimate δ¹⁷O-H₂O using the following equation:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& {}^{\mathrm{17}}\mathrm{O}\text{-}\mathrm{excess}=\ln \left({\mathit{\delta }}^{\mathrm{17}}\mathrm{O}\text{-}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{1}\right)\\ & -{\mathit{\lambda }}_{\mathrm{w}}\ln \left(\mathit{\delta }{}^{\mathrm{18}}\mathrm{O}\text{-}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{1}\right),\end{array}\end{array}$$

with λ_w=0.528 and all isotopic compositions referenced to VSMOW-SLAP. Equations (7) and (8) have a similar form; however, researchers in the H₂O isotope community have traditionally used the ¹⁷O-excess terminology, whereas researchers in the O₂ isotope community have used the ¹⁷Δ notation (Luz and Barkan, 2010). The value of λ_w=0.528 is well established for meteoric waters and seawater (Meijer and Li, 1998; Landais et al., 2008; Luz and Barkan, 2010). Spatial variability in the ¹⁷O-excess of natural waters is less well understood due to the currently limited observations at sufficient accuracy to resolve the small excess (Luz and Barkan, 2010; Li et al., 2015). To calculate the freshwater and seawater endmembers for δ¹⁷O-H₂O, we use the average values of ¹⁷O-excess of 33 per meg for meteoric water and −5 per meg for seawater (Luz and Barkan, 2010). The endmembers are δ¹⁷O-H₂O = −4.888 ‰ and −0.908 ‰ for meteoric water and seawater, respectively, and the linear regression is δ¹⁷O-H₂O = 0.1274S−4.89. These δ values for H₂O, referenced to VSMOW, are subsequently referenced to atmospheric O₂ using results from Barkan and Luz (2011). In this study, the choice of δ¹⁸O-H₂O is more important than the ¹⁷O-excess because ¹⁷O-excess varies by less than 0.1 ‰ between samples, whereas the freshwater δ¹⁸O-H₂O differs from VSMOW by 9.1 ‰. We discuss the sensitivity of the GOP calculations to the assumed ¹⁷O-excess and δ¹⁸O-H₂O below, and the effect of other processes on the isotopic composition of H₂O in Sect. 3.6.

We calculate GOP using Eq. (7) from Manning et al. (2017a), which is equivalent to Eq. (S8) from Prokopenko et al. (2011),

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& \mathrm{GOP}=k_{{\mathrm{O}}_{\mathrm{2}}}[{\mathrm{O}}_{\mathrm{2}}{]}_{\mathrm{eq}}{\displaystyle \frac{\left[\frac{X^{\mathrm{17}}-X_{\mathrm{eq}}^{\mathrm{17}}}{X^{\mathrm{17}}}-\mathit{\lambda }\frac{X^{\mathrm{18}}-X_{\mathrm{eq}}^{\mathrm{18}}}{X^{\mathrm{18}}}\right]}{\left[\frac{X_p^{\mathrm{17}}-X^{\mathrm{17}}}{X^{\mathrm{17}}}-\mathit{\lambda }\frac{X_p^{\mathrm{18}}-X^{\mathrm{18}}}{X^{\mathrm{18}}}\right]}}\\ & +{\displaystyle \frac{h\left[{\mathrm{O}}_{\mathrm{2}}\right]\frac{{\partial }^{\mathrm{17}}\mathrm{\Delta }}{\partial t}}{\left[\frac{X_p^{\mathrm{17}}-X^{\mathrm{17}}}{X^{\mathrm{17}}}-\mathit{\lambda }\frac{X_p^{\mathrm{18}}-X^{\mathrm{18}}}{X^{\mathrm{18}}}\right]}}.\end{array}\end{array}$$

In this equation, $k_{{\mathrm{O}}_{\mathrm{2}}}$ is the gas transfer velocity for O₂ (m d⁻¹), [O₂] is the O₂ concentration (mol m⁻³), h is the mixed layer depth (m), $X^{\mathrm{17}}=r({}^{\mathrm{17}}\mathrm{O}/{}^{\mathrm{16}}\mathrm{O})$, and λ=0.5179 (Eq. 7). The subscripts eq and p refer to O₂ at air–water equilibrium and produced by photosynthesis and terms without a subscript ([O₂], X¹⁷, and ¹⁷Δ) are the measured mixed layer values. The first term on the right-hand side of Eq. (9) is the steady-state GOP term, and the second term is the non-steady-state GOP term. If the system is at steady state with respect to ¹⁷Δ (i.e., there is no change in ¹⁷Δ with time), then the second term on the right-hand side of Eq. (9) equals zero and can be eliminated.

This non-steady-state equation for GOP incorporates temporal variability in both O₂ concentration and isotopic composition (see Eq. 5 in Prokopenko et al., 2011). It does not account for time variability in mixed layer depth (e.g., entrainment of deeper waters into the mixed layer), nor does it account for vertical diffusion of O₂ across the mixed layer. In order to account for vertical processes in the O₂ mass balance, we would need to have triple oxygen isotope measurements below the mixed layer (Castro Morales et al., 2013; Munro et al., 2013; Wurgaft et al., 2013; Nicholson et al., 2014). Since we do not have these data, we cannot correct for vertical processes affecting the O₂ budget.

We calculate $X_{\mathrm{eq}}^{\mathrm{18}}$ based on Benson and Krause (1980a, 1984) and $X_{\mathrm{eq}}^{\mathrm{17}}$ using ¹⁷Δ_eq=8 per meg (Reuer et al., 2007; Stanley et al., 2010), which is consistent with the daily measurements of distilled water equilibrated at room temperature that were analyzed along with the environmental samples (8.1 per meg with a standard error of 1.6 per meg, n=12), as well as prior measurements of distilled water equilibrated at <5 ^∘C (Rachel H. R. Stanley, unpublished data). We calculate $X_p^{\mathrm{18}}$ and $X_p^{\mathrm{17}}$ using the salinity-dependent isotopic composition of H₂O defined above and isotopic fractionation factors for photosynthetic O₂ with respect to H₂O based on data in Luz and Barkan (2011) for average phytoplankton (${\mathit{\alpha }}_p^{\mathrm{18}}=\mathrm{1.0033890}$ and ${\mathit{\alpha }}_p^{\mathrm{17}}=\mathrm{1.0017781}$). The Matlab code used to calculate GOP and the triple oxygen isotopic composition of water (from two-endmember mixing of δ¹⁸O-H₂O and salinity) is available online (Manning and Howard, 2017).

We calculate gross oxygen production using samples collected at Little Narrows from 25 March to 27 April (Fig. 6). Visual inspection of the ¹⁷Δ data indicated that ¹⁷Δ changed during the time series, and therefore the calculation includes a non-steady-state GOP term. The non-steady-state term in Eq. 9 is h[O₂]${\partial }^{\mathrm{17}}\mathrm{\Delta }/\partial t$. To calculate the rate of change in ¹⁷Δ with time, we first averaged the data into 24 h bins (beginning and ending at 19:30, local sunset) to avoid over-weighting times when samples were collected at higher frequency. We calculated the average ¹⁷Δ and sampling time for all samples collected each day. Next, we separated the data into two periods: one period began on 25 March and ended 19 April 07:30, and the second period covered the remainder of the time series (ending 27 April). A linear regression of ¹⁷Δ versus time for the two time periods yielded a slope of 0.67 per meg d⁻¹ (r²=0.47) for the first period and −2.99 per meg d⁻¹ (r² = 0.94) for the second period. The approximate timing for the change between periods was determined by visual inspection and then adjusted to maximize the r² and so that the equations of the two lines gave very similar ¹⁷Δ values at 19 April 00:00 (within 1 per meg). Splitting the period from 25 March to 19 April into two separate regressions (or one period where ¹⁷Δ increased and one period where it was constant) yielded much lower r² values and a discontinuous ¹⁷Δ record (different ¹⁷Δ values at the end of one period and the start of another), so a single regression was used for this period.

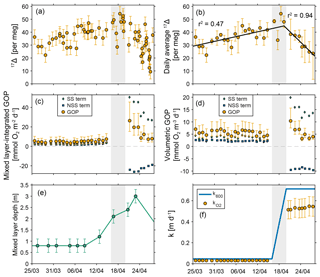
Figure 6 Gross oxygen production at Little Narrows. Gross oxygen production at Little Narrows and data used in the calculation. ¹⁷Δ measurements from (a) all samples and (b) daily averaged values with the two linear regressions shown. Gross oxygen production in (c) mixed layer-integrated and (d) volumetric units. The green diamonds and blue squares show the values of the two terms in the GOP calculation (steady state, SS, and non-steady state, NSS), and the yellow circles show the total GOP (the sum of the two terms). Error bars are only shown on the total GOP for clarity. The SS and NSS terms are slightly offset in time to make it easier to see both terms at the start of the time series. (e) Mixed layer depth. (f) Gas transfer velocity for a gas with a Schmidt number of 600 (blue line) and for O₂ (yellow circles), which has a variable Schmidt number based on temperature and salinity. The shaded grey area is the period where we do not calculate GOP due to uncertainties related to the rapidly melting ice cover and non-steady-state term.

The other two variables in the non-steady-state GOP term are the mixed layer depth (h) and [O₂]. We estimate [O₂] as

$$\begin{array}{}\text{(10)}& \left[{\mathrm{O}}_{\mathrm{2}}\right]\simeq [{\mathrm{O}}_{\mathrm{2}}{]}_{\mathrm{eq}}{\displaystyle \frac{{\mathrm{O}}_{\mathrm{2}}/\mathrm{Ar}}{{\left({\mathrm{O}}_{\mathrm{2}}/\mathrm{Ar}\right)}_{\mathrm{eq}}}}.\end{array}$$

This estimate assumes that [Ar] = [Ar]_eq. If [Ar] is, for example, 2 % supersaturated, then the estimated [O₂] and non-steady-state GOP term will be 2 % too high (Cassar et al., 2011).

Using Eq. (9), GOP is estimated for each sample, using an isotopic composition for H₂O based on the salinity of the sample, and a mixed layer depth, rate of change in ¹⁷Δ with time, and gas transfer velocity based on the sampling time (values shown in Fig. 6), and then calculate the daily average GOP from all samples on a given day (beginning and ending at 19:30, local sunset). The mean number of samples per day was two, the maximum was four, and a few days had no measurements. The uncertainty in GOP on each day is calculated by propagating uncertainty in $k_{{\mathrm{O}}_{\mathrm{2}}}$ (11 % for Injection 1, 18 % for Injection 2), uncertainty in the mixed layer depth (from 10 % to 38 %, 0.3 m), uncertainty in the rate of change in ¹⁷Δ with time (22 % and 9 % where ¹⁷Δ is increasing and decreasing, respectively), and uncertainty in the photosynthetic endmember (discussed below). Measurement uncertainty in the isotopic composition of O₂ is excluded from the error calculation because it is a random error, rather than a systematic error (meaning that by taking many measurements of ¹⁷Δ over several days, the measurements with high and low ¹⁷Δ will average out) and because the measurement error is smaller than most other sources of error. All uncertainties are expressed as the standard deviation.

The isotopic composition of H₂O is one of the largest sources of error: if the ¹⁸O-H₂O endmembers for meteoric water and local seawater are changed to the minimum values of −12.4 ‰ and −1.94 ‰ (1 standard deviation below the mean value) and then δ¹⁸O-H₂O and δ¹⁷O-H₂O are re-calculated for each sample, GOP is on average 48 % higher. If we shift the δ¹⁸O-H₂O endmembers for meteoric water and local seawater to the maximum values of −6.2 ‰ and 1.42 ‰, respectively, GOP is on average 23 % lower. The calculated GOP increases nonlinearly as the isotopic composition of photosynthetic O₂ becomes more different from the isotopic composition of equilibrated O₂ (Manning et al., 2017a). If the ¹⁷O-excess of H₂O is increased or decreased by 20 per meg, GOP changes by an average of 10 %.

GOP calculated with the local isotopic composition of H₂O is 46 %–97 % higher (mean 74 % higher) than GOP calculated assuming the water's isotopic composition is equivalent to VSMOW. Using the local isotopic composition of water instead of VSMOW is particularly important in this study because the system is not pure seawater. However, even in some oceanic regions such as the Arctic, the isotopic composition of H₂O can be substantially different from VSMOW (LeGrande and Schmidt, 2006). The definition and importance of the photosynthetic endmember for GOP calculations in different environments warrant further review (Manning et al., 2017a).

We calculate the mixed layer-integrated GOP (mmol O₂ m⁻² d⁻¹) and the volumetric GOP (mmol O₂ m⁻³ d⁻¹), which is the mixed layer-integrated GOP divided by the mixed layer depth. For this time series GOP is only calculated for the mixed layer because there are no O₂ measurements below the mixed layer. The average errors in the daily GOP are $\begin{array}{c}+\mathrm{77}\\ -\mathrm{49}\end{array}$ % and $\begin{array}{c}+\mathrm{52}\\ -\mathrm{31}\end{array}$ % for the volumetric and mixed layer-integrated GOP, respectively.

3.3.2 Results and discussion

We do not present GOP estimates during the period where ice cover decreased most rapidly (16–19 April, grey shaded area in Fig. 6) due to the large uncertainties in GOP at this time. We do not have an estimate of $k_{{\mathrm{O}}_{\mathrm{2}}}$ at intermediate or varying ice cover, nor do we have estimates of ice cover on 17 April or 19 April, because clouds obscured the satellite images on those days. Additionally, the exact timing of the change in the sign of the non-steady-state term is unclear. For example, on 18 April the calculated GOP assuming ¹⁷Δ is increasing at 0.67 per meg d⁻¹ (the slope of the first best-fit line in Fig. 6b) is 58 mmol O₂ m⁻² d⁻¹ and the calculated GOP assuming ¹⁷Δ is decreasing at 2.99 per meg d⁻¹ (the slope of the second best-fit line in Fig. 6b)) is 27 mmol O₂ m⁻² d⁻¹ on 18 April. The concentration of photosynthetic O₂ is highest during this time (¹⁷Δ=48–54 per meg on 16, 18, and 19 April), despite the increasing gas transfer velocity. It is likely that GOP peaked during or soon after the end of the ice melt period and then declined to values similar to the beginning of the time series, but the uncertainties in GOP from 16 to 19 April are large.

Before interpreting the GOP results, we emphasize that the impact of changing mixed layer depth on the O₂ mass balance is not accounted for in our calculations. The mixed layer deepened from 8 to 23 April and then appeared to shoal from 23 to 28 April. If the ¹⁷Δ value below the mixed layer were higher (lower) than ¹⁷Δ in the mixed layer, this would cause us to overestimate (underestimate) GOP as the mixed layer deepened.

Overall, the rate of volumetric mixed layer GOP was relatively constant throughout the time series at 5.7$\begin{array}{c}+\mathrm{3.1}\\ -\mathrm{1.9}\end{array}$ mmol O₂ m⁻³ d⁻¹. The mixed layer-integrated GOP showed larger changes with time that are related to the influence of changes in the mixed layer depth on the non-steady-state term. From 25 March through 8 April, mixed layer-integrated GOP was 4.6$\begin{array}{c}+\mathrm{3.7}\\ -\mathrm{2.6}\end{array}$ mmol O₂ m⁻² d⁻¹. Beginning after 8 April, the mixed layer depth began to increase and the non-steady-state calculation showed a substantial increase in mixed layer-integrated GOP to 7.2$\begin{array}{c}+\mathrm{5.4}\\ -\mathrm{3.3}\end{array}$ mmol O₂ m⁻³ d⁻¹ on 14 April, a 56 % increase. The non-steady-state GOP term is multiplied by the mixed layer depth, and therefore it increases linearly as the mixed layer deepens, causing the total mixed layer-integrated GOP to decrease. However, the non-steady-state GOP term is constant in volumetric units because the mixed layer depth cancels out of the equation. After the ice was gone, ¹⁷Δ began to decrease, and so did the mixed layer-integrated GOP. On the last 4 days of the time series, the mixed layer-integrated GOP was 8.7$\begin{array}{c}+\mathrm{3.6}\\ -\mathrm{6.3}\end{array}$ mmol O₂ m⁻² d⁻¹, 89 % higher than the average value prior to 9 April, but the mixed layer was also more than twice as deep at the end of the time series compared to the beginning.

The result that volumetric GOP was similar at the beginning and end of the time series indicates that ice-free conditions are not a pre-requisite for phytoplankton growth in this system. Currently, ecosystem dynamics within and below ice formed from fresh and brackish waters are not well understood (Salonen et al., 2009; Bertilsson et al., 2013; Hampton et al., 2015). Other investigators have shown that photosynthetic microbes can inhabit the interior, upper surface, and lower surface of ice, and tend to be most concentrated on the bottom surface (Welch et al., 1988; Cota et al., 1991; Frenette et al., 2008; Boetius et al., 2013). Traditionally, investigators have argued that ice-associated communities are most prevalent in ice formed from seawater; as salinity increases, the volume of unfrozen brines within the ice that the microbes can inhabit increases, and the bottom surface of the ice becomes more uneven, increasing bottom algal settlement efficiency (Legendre et al., 1981; Gosselin et al., 1986). However, more recently, investigators have also found algae growing within and on the bottom of freshwater ice in lakes and rivers, including locations in Canada such as the Great Lakes and the St. Lawrence River (Bondarenko et al., 2006; Frenette et al., 2008; Twiss et al., 2012; D'souza et al., 2013).

Phytoplankton can also grow in the water column beneath ice, especially under thin first-year ice (Legendre et al., 1981; Mundy et al., 2009; Arrigo et al., 2012). Bare ice transmits more light to surface waters than snow-covered ice, and melt pond-covered ice transmits 4 times as much light as bare ice (Light et al., 2008; Arrigo et al., 2012; Light et al., 2015). First-year ice in the Arctic (0.5–1.5 m thick) transmits ∼47 %–75 % of incident light through melt pond-covered ice and ∼13 %–25 % of incident light through snow-free ice (Arrigo et al., 2012; Light et al., 2015). The ice in the Bras d'Or Lake near the site of Injection 1 was ∼0.3 m thick on 29 March, and therefore likely similar or greater fractions of light were transmitted through the ice. Ice transmitting just 2 % of surface irradiance may support high rates of photosynthetic activity if the phytoplankton are acclimated to lower light levels (Cota, 1985). We observed melt ponds in Whycocomagh Bay during tracer injections on 31 March and frequently during visual surveys in April. The shallow mixed layer prior to ice melt (∼0.8 m from the beginning of the time series until 8 April) would have kept phytoplankton in the mixed layer close to the surface and therefore receiving light that penetrated through the ice.

Our O₂ mass balance techniques will record GOP by free-floating phytoplankton in the water column below the ice, as well as GOP by ice-associated phytoplankton if the O₂ they produce diffuses into the water rather than into the ice surface or atmosphere. Bottom-associated algae likely release much of their O₂ into the water column, especially for filamentous forms such as the diatoms frequently observed in Lake Erie and the Arctic (D'souza et al., 2013; Boetius et al., 2013).

We believe that the O₂ measurements at Little Narrows from the beginning of the time series through 16 April (the date when the fraction of open water in Whycocomagh Bay began to increase rapidly) are generally representative of the under-ice rates due to the rapid transport of water through Little Narrows channel. The mean current speed at Little Narrows channel at 0.5 m depth was 3.4 km d⁻¹. The distance between the ice edge and the sampling intake ranged from ∼0.4 to 1 km between the beginning of the time series and 12 April. Assuming a gas transfer velocity for O₂ of 0.5 m d⁻¹ once the water mass encountered open water and a mixed layer depth between 0.8 and 2 m, the residence time of O₂ in the mixed layer was 1.6–4 d. Assuming a current speed of 3.4 km in open water, the water mass would have only been exposed to open water for between 0.1 and 0.3 d (20 % or less of the residence time of O₂). However, we recognize that the current speed near the ice edge may have been somewhat slower than the speed at the constriction at Little Narrows; therefore, the transit time in open water may have been somewhat longer than 0.1–0.3 d.

3.4 Net oxygen production and export efficiency

3.4.1 Calculation

We quantify non-steady-state NOP, incorporating the observed changes in O₂∕Ar during the time series. We estimate NOP as

$$\begin{array}{}\text{(11)}& \mathrm{NOP}=k_{{\mathrm{O}}_{\mathrm{2}}}\mathrm{\Delta }({\mathrm{O}}_{\mathrm{2}}/\mathrm{Ar})[{\mathrm{O}}_{\mathrm{2}}{]}_{\mathrm{eq}}+h{\displaystyle \frac{\partial \mathrm{\Delta }({\mathrm{O}}_{\mathrm{2}}/\mathrm{Ar})}{\partial t}}[{\mathrm{O}}_{\mathrm{2}}{]}_{\mathrm{eq}},\end{array}$$

where $k_{{\mathrm{O}}_{\mathrm{2}}}$ is the real-time gas transfer velocity (m d⁻¹), [O₂]_eq is the equilibrium O₂ concentration (mol m⁻³), and h is the mixed layer depth (m) (Hamme et al., 2012). The first term on the right-hand side of Eq. (11) is the steady-state NOP term, and the second term is the non-steady-state NOP term, which is dependent on the rate of change in Δ(O₂∕Ar) with time. To calculate the rate of change in Δ(O₂∕Ar) with time, we resampled the data to a fixed 5 s interval (each scan of all masses took 5–6 s) and filled in gaps with a linear interpolation. Then we applied a third-order lowpass Butterworth filter with a cutoff frequency of 0.3 d⁻¹ to generate a smooth O₂∕Ar record (Roberts and Roberts, 1978) (Fig. 7). We selected the cutoff frequency to remove the short-term variability from tides and diel changes in photosynthesis and respiration, and to minimize the number of times the inflection of the curve changed while capturing the overall trends in O₂∕Ar. Below we discuss the sensitivity of the calculated NOP to the choice of cutoff frequency. Finally, we calculated the derivative of Δ(O₂∕Ar) with respect to time using the filtered record. We applied the same filtering method to the in situ salinity and thermocouple temperature data and used the filtered data to calculate the [O₂]_eq and $k_{{\mathrm{O}}_{\mathrm{2}}}$, to prevent short-term fluctuations in salinity and temperature from producing apparent changes in NOP. We calculate the daily NOP (from 19:30 to 19:29 local time) using the average ∂Δ (O₂∕Ar)/∂t based on the filtered record and the average Δ(O₂∕Ar) (using the raw, unfiltered data).

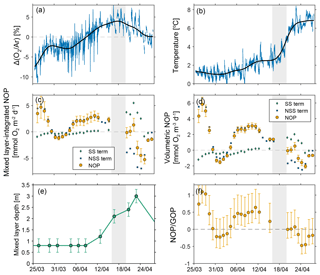
Figure 7 Net oxygen production at Little Narrows. Net oxygen production at Little Narrows and data used in the calculation. (a) Δ(O₂∕Ar) and (b) temperature measurements. The blue lines are the raw data and the black line is the filtered data. NOP in (c) mixed layer-integrated and (d) volumetric units. The green diamonds and blue squares show the values of the two terms in the GOP calculation (steady state, SS, and non-steady state, NSS). (e) Mixed layer depth. (f) Export efficiency ratio (NOP∕GOP). The shaded grey area is the period where we do not calculate NOP due to uncertainties related to the rapidly melting ice cover.

As for the GOP calculations, our NOP calculations do not account for the impact of changing mixed layer depth, nor the impact of vertical diffusion, on the O₂ mass balance because we do not have any measurements of O₂ below the mixed layer (Munro et al., 2013; Castro Morales et al., 2013). We expect that the O₂ concentration below the mixed layer was lower than the concentration within the mixed layer, based on past measurements showing undersaturated O₂ in the subsurface waters of Whycocomagh Bay (Krauel, 1975; Gurbutt and Petrie, 1995; Strain et al., 2001). Therefore, vertical processes would likely cause us to underestimate NOP. For example, a deepening of the mixed layer between 8 and 23 April may have entrained waters with a lower O₂ concentration into the mixed layer, causing a decrease in O₂ (and O₂∕Ar). Using Eq. (11), we would interpret this decrease in O₂ as a decrease in NOP.

To calculate the uncertainty in NOP, uncertainty in $k_{{\mathrm{O}}_{\mathrm{2}}}$ (11 % for Injection 1, 18 % for Injection 2), mixed layer depth (0.3 m, 10 %–38 %), and the non-steady-state term are propagated. Uncertainty in the non-steady-state term is based on the results using different filtering methods. A conservative 13 % error associated with the cutoff frequency choice is included in the estimates of daily NOP. Uncertainty in Δ(O₂∕Ar) (<0.1 %, based on the mean offset between the EIMS and the discrete samples) has a negligible impact on NOP, relative to the other sources of error. The average errors in the daily NOP are ±0.8 mmol O₂ m⁻² d⁻¹ (34 %) and ±0.3 mmol O₂ m⁻³ d⁻¹ (23 %) for the mixed layer-integrated and volumetric NOP, respectively. All uncertainties are the standard deviation.

Finally, we calculate the ratio of NOP to GOP for each daily estimate (the export efficiency). This ratio is similar to an f-ratio or an e-ratio (Dugdale and Goering, 1967; Laws et al., 2000) and provides information on the fraction of GOP that is available for export out of the mixed layer (Fig. 7f). The uncertainties in the NOP∕GOP ratio on each day are quite large. In a steady-state NOP and GOP calculation, the gas transfer velocity $k_{{\mathrm{O}}_{\mathrm{2}}}$ cancels out of the equation for the NOP∕GOP ratio, and therefore it is not a source of uncertainty; however, in the non-steady-state term the $k_{{\mathrm{O}}_{\mathrm{2}}}$ does not cancel out.

3.4.2 NOP results and comparison of NOP and GOP

As for GOP, we do not present NOP estimates during 16–19 April due to the uncertainties associated with the rapid decrease in ice cover. There are additional uncertainties in NOP from 12 to 23 April due to the increasing mixed layer depth, which may have entrained lower-O₂ waters into the mixed layer. Historical O₂ data from Whycocomagh Bay showed that there is a strong decrease in O₂ with depth below the mixed layer; however, to our knowledge, no prior measurements during ice melt have been published (Krauel, 1975; Gurbutt and Petrie, 1995; Strain et al., 2001).

Based on the non-steady-state NOP estimates, the ecosystem was on average net autotrophic as the ice was melting, from the beginning of the time series through 15 April (mean volumetric NOP of 1.9(2.1) mmol O₂ m⁻³ d⁻¹, median 2.5 mmol O₂ m⁻³ d⁻¹). During the (nearly) ice-free period from 20 April through the end of the time series, the community was on average net heterotrophic but with a smaller magnitude than during the start of the time series (mean volumetric NOP of −0.7(0.9) mmol O₂ m⁻³ d⁻¹, median −0.7 mmol O₂ m⁻³ d⁻¹). When the bay was nearly full of ice cover (from the beginning of the time series until ∼16 April), NOP was dominated by the non-steady-state term, and this term was positive except for between 31 March and 3 April when it was negative but small in magnitude. As the ice cover retreated, the non-steady-state term decreased and became negative on 18 April. From 18 to 22 April the steady-state term was roughly equal in magnitude but opposite in sign to the non-steady-state NOP term. The NOP is more strongly negative from 23 to 25 April (volumetric NOP of −1.6(0.5) mmol O₂ m⁻³ d⁻¹) and then on the last 2 days of the time series Δ(O₂∕Ar) was close to 0, and so was the rate of change in Δ(O₂∕Ar) with time (volumetric NOP of −0.7 mmol O₂ m⁻³ d⁻¹). If the time series had continued for longer, it would have been possible to observe whether the NOP value eventually stabilized near 0 following the dynamic ice melt period or whether it continued to oscillate between periods of net autotrophy and net heterotrophy.

The ratio of NOP∕GOP has large uncertainties but qualitatively follows the trends of NOP, since the mixed layer-integrated GOP was relatively constant throughout the time series, whereas the mixed layer-integrated NOP was far more variable. At the start of the time series, there are two dates where NOP∕GOP > 1, which by definition is not possible. The high NOP∕GOP values could be due to uncertainty in the isotopic composition of water, which enters into the GOP calculation but not the NOP calculation, and/or the non-steady-state terms for GOP and NOP. Vertical diffusion across the mixed layer is another possible cause of the estimated NOP∕GOP ratios exceeding 1; because we do not have measurements below the mixed layer, we cannot compute a correction for vertical mixing. The gradients in ¹⁷Δ and Δ(O₂∕Ar) are likely different with depth, leading to different magnitudes of the vertical mixing correction for NOP and GOP, which could potentially lead to errors in the estimated NOP∕GOP ratio (Sect. 3.6). We recommend that researchers planning future studies using O₂-based tracers include depth profiles of O₂∕Ar and ¹⁷Δ in their experimental design (Castro Morales et al., 2013; Munro et al., 2013; Wurgaft et al., 2013).

The GOP results demonstrate that GOP was similar when Whycocomagh Bay was full of ice and when it was ice-free (on a volumetric basis). On the other hand, the calculated volumetric NOP was generally positive when the bay was full of ice, but began to decrease toward negative values around 12 April. The mixed layer depth was ∼0.8 m from the beginning of the time series until 12 April, deepened from 12 to 23 April and then increased until the end of the time series. The apparent decrease in volumetric NOP beginning around 12 April could be due to a number of factors, including an increase in respiration and recycling of organic carbon by autotrophs and/or heterotrophs, and/or vertical processes that are not taken into account in our calculations. We note that the mixed layer NOP was actually lowest and ΔO₂∕Ar was decreasing between 23 and 27 April, a period where the mixed layer actually appeared to shoal. Therefore a deepening mixed layer cannot be the only driver of the decrease in NOP following ice melt.

3.5 Comparison to other productivity estimates

To our knowledge, our data are the only published estimates of NOP and GOP in the Bras d'Or Lake system. Geen (1965) measured primary production by ¹⁴C uptake in the Bras d'Or Lake during summer 1962–1964 and found an average uptake rate at 5 m depth, the depth of maximum photosynthesis, of ∼4 mmol C m⁻³ d⁻¹ (50 mg C m⁻³ d⁻¹) (Geen and Hargrave, 1966). These rates are based on 6 h daytime incubations and ignore nighttime respiratory loss of ¹⁴C, and therefore approximate net primary production (NPP, gross primary production minus autotrophic respiration) or something between NPP and gross primary production (GPP) (Bender et al., 1999; Marra, 2002, 2009; Quay et al., 2010). Assuming a C:O₂ ratio of 1.1–1.4 (Laws, 1991), the equivalent O₂ production based on the ¹⁴C incubations is 4.4–5.6 mmol O₂ m⁻³ d⁻¹. Thus, the ¹⁴C-PP is between the average NOP and GOP values, as expected.

In the Bras d'Or Lake, Hargrave and Geen (1970) found, based on summertime incubations, that zooplankton grazing was sufficient to consume all of the daily primary production, indicating the estuary ecosystem metabolism may be close to balanced (NOP ∼0) on a daily basis. We obtained a more dynamic record of NOP, with an average volumetric rate of 1.1±2.0 mmol O₂ m⁻³ d⁻¹ over the entire time series.

Comparisons with in situ gas tracer-based productivity estimates in other environments are challenging because mixed layer-integrated rates are most commonly calculated, and the mixed layer in many other systems is much deeper than 0.8–3 m. In the Beaufort Gyre (Arctic Ocean) Stanley et al. (2015) estimate a steady-state GOP of 16(5) and 38(3) mmol O₂ m⁻² d⁻¹ in summer 2011 (higher ice cover) and 2012 (lower ice cover), respectively, and NOP of 3 mmol O₂ m⁻² d⁻¹ in both summers. Mixed layer depths were ∼10 m. Mixed layer-integrated GOP increases as the mixed layer depth increases, but trends in NOP are less clear.

3.6 Effect of physical processes on productivity estimates

There are a number of additional environmental processes that may affect the O₂ isotope and O₂∕Ar mass balance in the mixed layer but cannot be directly quantified from the time series. However, in some cases we can determine whether these processes would tend to increase or decrease our NOP and GOP estimates.

The isotopic composition of freshwater within the bay may have varied during our time series, which would impact the GOP estimates. Using model results from Gurbutt and Petrie (1995), we calculate that the residence time of water in Whycocomagh Bay is ∼0.7 years for surface waters (0–10 m) with respect to freshwater input and ∼2 year for deep waters (10 m to bottom) with respect to exchange with the surface waters. Thus we expect the isotopic composition of the water in the mixed layer of Whycocomagh Bay to reflect some average over multiple months. For example, if a substantial portion of the meltwater entering the estuary is derived from snow rather than from ice that freezes from water within the bay, its isotopic composition will be more reflective of seasonal precipitation. If we calculate an amount-weighted δ¹⁸O-H₂O for meteoric water at Truro, NS, using only the months when ice was present in Whycocomagh Bay in 2013 (January–April), δ¹⁸O-H₂O = −11.0(3.6) ‰ versus VSMOW, which is within the uncertainty of our annually averaged value (−9.3(3.1) ‰). In general, a lower value of δ¹⁸O-H₂O will increase GOP estimates.

The freezing and melting of ice in saline waters will generate a nonlinear salinity–δ¹⁸O-H₂O relationship because the δ¹⁸O-H₂O value of sea ice is similar to the water from which it formed (within ∼2–3 ‰) (Tan and Strain, 1980; Macdonald et al., 1995, 1999), but the salinity in sea ice is substantially lower due to brine rejection (O'Neil, 1968; Weeks and Ackley, 1986). We are not able to accurately quantify the triple oxygen isotopic composition of H₂O in the ice and in water, nor can we quantify the timing and volume of ice freezing and melt within Whycocomagh Bay (although we know when the ice cover decreased most rapidly, the ice volume was decreasing throughout our time series). The volume contribution and isotopic composition of other sources of water inputs (e.g., riverine input and melting snow) are another source of uncertainty in the calculations.

In addition to affecting the isotopic composition of H₂O, ice melt and riverine inflow may affect the NOP and GOP calculations in other ways. If the ice melted at the upper surface (in contact with the atmosphere) and then drained through brine channels in the ice, it likely had an isotopic composition and gas ratio similar to air-equilibrated water (¹⁷Δ ≃ 8 per meg and Δ(O₂∕Ar) ≃ 0 %). Thus, water in melt ponds that was added to the water column would tend to decrease GOP, as ¹⁷Δ always exceeded 8 per meg in the mixed layer (Fig. 6a) and either increase or decrease NOP, since Δ(O₂∕Ar) transitioned from negative to positive as the ice was melting. If the ice melted at the bottom (in contact with the water), its effect on NOP and GOP estimates is less clear. During sea ice formation, approximately 40 %–55 % of the O₂ and Ar originally dissolved in the water is retained in the ice matrix (i.e., within the ice itself, in gas bubbles, or in brine pockets) and the remainder is excluded, generating supersaturations of the gases in the water below the ice (Top et al., 1988; Hood et al., 1998; Loose et al., 2009). Photosynthesis and respiration both occur in sea ice (Loose et al., 2011a; Zhou et al., 2014) and will change the O₂∕Ar and ¹⁷Δ signatures within the ice, and it is difficult to predict what proportions of the O₂ within brine pockets in the ice remained within the brines, migrated into the water column, or migrated into the atmosphere prior to the complete melting of the ice. We measured an ice thickness of ∼0.3 m near the injection site on 29 March, and thus if the mixed layer depth after ice melt was 2.5 m deep, the ice could contribute ∼11 % of the mixed layer volume, or ∼5 % of the mixed layer O₂ (assuming [O₂] in ice is ∼45 % of the equilibrium [O₂] in water). Thus bottom-ice melt would likely be a minor influence on the oxygen mass balance. We observed bare ice and melt ponds at the surface of the ice (Figs. 2–4) and the water temperature throughout our time series was above freezing, which would stimulate bottom melt. Therefore, both surface and bottom melt likely occurred during the time series. The volume, O₂ concentration and isotopic composition of runoff and river water during our time series are also poorly constrained, and thus these water sources are another uncertainty in our NOP and GOP calculations.

It is likely that GOP occurred below the mixed layer but was not quantified by our methods because we only had measurements within the mixed layer. In open water, the Secchi depth at the ice edge on 26 March (just west of Little Narrows) was 1.9 m, yielding a euphotic zone depth of ∼5 m (defined as the depth where 1 % of surface photosynthetically active radiation penetrates) and the Secchi depth at Little Narrows on 7 April was ∼4.5 m, giving an approximate euphotic zone depth of 12 m (Idso and Gilbert, 1974). Mixed layer depths during our time series ranged from 0.8 to 3.0 m. Even in field studies where O₂ measurements below the euphotic zone are available, it is challenging to quantify this subsurface productivity because the biological O₂ fluxes below the mixed layer are small and the physical fluxes are large and highly uncertain, as they are driven by lateral and vertical mixing rather than air–water gas exchange (Giesbrecht et al., 2012; Munro et al., 2013; Manning et al., 2017b).

We also cannot correct our results for the effect of entrainment of deeper waters into the mixed layer (Hendricks et al., 2004; Munro et al., 2013; Wurgaft et al., 2013). We were not able to sample below the mixed layer, but we hypothesize that ¹⁷Δ and O₂∕Ar both likely decreased below the mixed layer when the ice was melting and the mixed layer was deepening. Therefore, entrainment of these waters into the mixed layer would tend to decrease NOP and GOP estimates. Respiration increases with depth, causing [O₂] and Δ(O₂∕Ar) to decrease with depth in oceanic systems (Spitzer and Jenkins, 1989; Emerson et al., 1991). In some oceanic regions, photosynthesis below the mixed layer generates excess ¹⁷Δ (because there is no process decreasing ¹⁷Δ below the mixed layer), which can then be entrained into the euphotic zone, where ¹⁷Δ is lower because some of the photosynthetic O₂ is ventilated to the atmosphere (Hendricks et al., 2004; Sarma et al., 2005; Juranek and Quay, 2013). In this study, the gas transfer velocity out of the mixed layer was extremely low up until 16 April, and therefore photosynthetic O₂ (i.e., ¹⁷Δ) would also accumulate in the mixed layer, likely at a greater rate than below the mixed layer due to photosynthesis rates being higher closer to the surface. Once the gas transfer velocity increased to the open water value (20 April), it is not clear whether we would expect to observe an excess of ¹⁷Δ below the mixed layer, and therefore whether entrainment would increase or decrease GOP.

Another source of error in our interpretation of the O₂ data is that we must assume that spatial variability in O₂ has a negligible effect on our calculations. We interpret all changes in O₂ assuming that we are measuring the same water mass; this is an oversimplification because the bay is within an estuary that experiences tidal flows. However, spatial surveys of O₂∕Ar during a pilot experiment in 2011 indicated that spatial variability in O₂ within the Bras d'Or Lake is relatively low.

4 Conclusions

Using the dual tracer (³He∕SF₆) technique in the Bras d'Or Lake, we found that at >90 % ice cover, the gas transfer velocity was 6 % of the open water gas transfer velocity. This result indicates that k_ice is negligible.

The volumetric GOP was similar at the beginning and end of the time series, when the basin was full of ice and when it was ice-free. Volumetric NOP was more variable with time; Whycocomagh Bay was on average net autotrophic (NOP > 0) while the bay was ice-covered, and net heterotrophic (NOP < 0) but with a smaller magnitude after the bay was ice-free. These results indicate that an algal bloom (increasing NOP) can occur in an ice-covered estuary, similar to observations of net autotrophy under ice in the Great Lakes, Arctic, and Antarctic (Tortell and Long, 2009; Twiss et al., 2012; D'souza et al., 2013). The apparent decrease in NOP may be due to a number of factors, such as an increase in heterotrophic respiration of organic carbon and/or the entrainment of waters with a lower O₂ concentration into the mixed layer (Wurgaft et al., 2013; Castro Morales et al., 2013; Nicholson et al., 2014).

Obtaining a time series of O₂ data and obtaining simultaneous gas transfer velocity measurements were both critical for quantifying productivity. The non-steady-state term was a significant contributor to NOP and GOP throughout the time series, and time-series measurements are needed to quantify the non-steady-state O₂ flux. Additionally, because the gas transfer velocity was ∼16 times higher at the end of the time series than at the beginning and the values of ¹⁷Δ and Δ(O₂∕Ar) changed with time, the relative importance of the steady-state term versus the non-steady-state term changed substantially during our time series.

In future studies in similar settings, we recommend authors collect measurements of O₂∕Ar and triple oxygen isotopes below the mixed layer in order to better correct for the impact of vertical processes on the O₂ mass balance. For tidally influenced regions, surveys of lateral variability in O₂∕Ar and ¹⁷Δ could also help to constrain the influence of horizontal advection on the O₂ mass balance (Munro et al., 2013; Howard et al., 2017). Measurements of nutrients and dissolved organic carbon could be useful for inferring the causes of changes in GOP and NOP. We also encourage measurement of the triple isotopic composition of H₂O (Manning et al., 2017a).