the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Physical constraints for respiration in microbial hotspots in soil and their importance for denitrification
Steffen Schlüter
Jan Zawallich
Hans-Jörg Vogel
Peter Dörsch
Soil denitrification is the most important terrestrial process returning reactive nitrogen to the atmosphere, but remains poorly understood. In upland soils, denitrification occurs in hotspots of enhanced microbial activity, even under well-aerated conditions, and causes harmful emissions of nitric (NO) and nitrous oxide (N2O). The timing and magnitude of such emissions are difficult to predict due to the delicate balance of oxygen (O2) consumption and diffusion in soil. To study how spatial distribution of hotspots affects O2 exchange and denitrification, we embedded microbial hotspots composed of porous glass beads saturated with growing cultures of either Agrobacterium tumefaciens (a denitrifier lacking N2O reductase) or Paracoccus denitrificans (a “complete” denitrifier) in different architectures (random vs. layered) in sterile sand that was adjusted to different water saturations (30 %, 60 %, 90 %). Gas kinetics (O2, CO2, NO, N2O and N2) were measured at high temporal resolution in batch mode. Air connectivity, air distance and air tortuosity were determined by X-ray tomography after the experiment. The hotspot architecture exerted strong control on microbial growth and timing of denitrification at low and intermediate saturations, because the separation distance between the microbial hotspots governed local oxygen supply. Electron flow diverted to denitrification in anoxic hotspot centers was low (2 %–7 %) but increased markedly (17 %–27 %) at high water saturation. X-ray analysis revealed that the air phase around most of the hotspots remained connected to the headspace even at 90 % saturation, suggesting that the threshold response of denitrification to soil moisture could be ascribed to increasing tortuosity of air-filled pores and the distance from the saturated hotspots to these air-filled pores. Our findings suggest that denitrification and its gaseous product stoichiometry depend not only on the amount of microbial hotspots in aerated soil, but also on their spatial distribution. We demonstrate that combining measurements of microbial activity with quantitative analysis of diffusion lengths using X-ray tomography provides unprecedented insights into physical constraints regulating soil microbial respiration in general and denitrification in particular. This paves the way to using observable soil structural attributes to predict denitrification and to parameterize models. Further experiments with natural soil structure, carbon substrates and microbial communities are required to devise and parametrize denitrification models explicit for microbial hotspots.
- Article
(6686 KB) - Full-text XML
-
Supplement
(1092 KB) - BibTeX
- EndNote
Soil carbon and nitrogen turnover is governed by soil heterogeneity at the microscale. Much of the turnover is concentrated in microsites, providing favorable conditions (pO2, temperature, pH) and substrates (carbon, nutrients) for soil microbial activity. The partitioning of aerobic and anaerobic respiration in microsites is largely controlled by the water content in the soil matrix which defines the scale across which O2 diffuses towards microsites of high O2-consuming activity. Aqueous diffusion lengths range from distances across thin water films in well-aerated soils, to individual soil aggregates of different radii at field capacity, up to the distance to the soil surface when the soil is saturated (Smith et al., 2003; Elberling et al., 2011; Ball, 2013; Parkin, 1987). Aerobic respiration is less affected by soil moisture than anaerobic respiration and typically peaks around water saturations of 20 %–60 % (Schaufler et al., 2010; Ruser et al., 2006; Moyano et al., 2012). Bulk soil respiration starts to decline at higher saturations due to the development of anoxic microsites with lower redox potential, supporting carbon mineralization at typically only 1∕10 of the rates observed under oxic conditions (Keiluweit et al., 2017). Denitrification, i.e., the dissimilatory respiration of N oxyanions instead of oxygen, is commonly observed at water saturations above 60 %–70 % and peaks beyond 90 % (Ruser et al., 2006; Linn and Doran, 1984). The occurrence of anaerobic microsites is governed by the balance between saturation-dependent diffusion and microbial consumption of O2, which in turn depends on the quantity, quality and distribution of soil organic matter in the soil matrix and environmental factors like temperature and pH, which control microbial activity (Tecon and Or, 2017; Nunan, 2017; Smith et al., 2003). In fact, water films around decaying plant material may suffice to induce anaerobic respiration, if microbial respiration exceeds O2 diffusion through that minute barrier (Parkin, 1987; Kravchenko et al., 2017).
The interplay between physical constraints and biological activity in soil controls microbial respiration at microscopic scales and complicates the prediction of denitrification and N-gas fluxes at larger scales. For instance, nitrous oxide (N2O) emissions are notoriously variable in space, which has been attributed to heterogeneous distribution of anoxic microsites in the soil (Mathieu et al., 2006; Röver et al., 1999; Parkin, 1987; Parry et al., 1999). Together with the often-observed high temporal variability of microbial respiration and its fluctuations under transient conditions, this has led to the notion of “hotspots” and “hot moments” for microbial activity and emissions (Groffman et al., 2009; Kuzyakov and Blagodatskaya, 2015). “Hotspots” of denitrification have traditionally been linked to diffusion constraints in soil aggregates (Smith, 1980; Arah and Vinten, 1995). Cell numbers and O2 concentration have been shown to decline exponentially towards aggregate centers (Sexstone et al., 1985; Horn et al., 1994; Zausig et al., 1993; Højberg et al., 1994) and the critical aggregate radius for the development of anoxic centers and is variable but typically > 1 mm (Sierra and Renault, 1996; Højberg et al., 1994; Schlüter et al., 2018). However, anoxic microsites have also been reported for smaller aggregates (equivalent diameter of 0.03–0.13 mm) in well-aerated, repacked soils (Keiluweit et al., 2018).
An important but often neglected aspect of physical diffusion constraints on microbial respiration is the spatial distribution of microbial hotspots within the soil matrix. Incubation experiments were either designed to control the aggregate size in repacked soil (Mangalassery et al., 2013; Miller et al., 2009) or the volume fraction of sieved soil mixed evenly into sterile quartz sand (Keiluweit et al., 2018). Some incubation studies were carried out with undisturbed soil and investigated diffusion constraints within the pore network (Rabot et al., 2015). However, these studies did not address the spatial distribution of hotspots nor the diffusion lengths towards air-filled pores. The vast majority of incubation studies merely reports bulk soil properties like carbon and nitrogen content, bulk density and water saturation. Notable exceptions are Kravchenko et al. (2017), who controlled the position of microbial hotspots by placing decaying plant leaf material into repacked soils with different aggregate sizes and water saturations, and Ebrahimi and Or (2018), who placed several layers of remolded aggregates as artificial hotspots into a sand matrix and controlled the volume fraction of anaerobic and aerobic respiration by adjusting the water table in the sand column. Such systematic studies with simplified soil aggregate analogues, yet fully accounting for transport processes from and towards hotspots, including interactions between hotspots, are needed to improve our understanding about how physical constraints on microbial respiration control the anaerobic soil volume and hence denitrification activity.
The objective of the present study was to study the interplay between microbial activity and physical diffusion in controlling aerobic and anaerobic respiration for different spatial distributions of hotspots. We embedded uniform artificial hotspots saturated with oxically growing denitrifier pure cultures (Schlüter et al., 2018) in sterile sand in two different architectures: either densely packed in two layers with minimal distance between hotspots within a layer or distributed randomly with maximum spacing between individual hotspots (Fig. 1b–c). We presumed that the competition for oxygen would depend on this separation distance between the hotspots, which in turn would control microbial cell growth and O2 consumption and thus affect the timing and velocity of the aerobe–anaerobe transition in respiration with consequences for the onset of denitrification and its gaseous product stoichiometry. Further, by placing hotspots with complete (P. denitrificans) and truncated (A. tumefaciens) denitrifiers in distinct horizontal layers, we expected to see interactions between hotspots acting as mere N2O sources and hotspots potentially being N2O sinks (by reducing N2O to N2). To create contrasting velocities of oxygen transfer between headspace and hotspots, we incubated the different hotspot architectures at three water saturations, thereby addressing the question of how overall oxygen supply (regulated by saturation) and local oxygen availability (regulated by hotspot distribution) interact in regulating denitrification activity. The overall goal of our reductionist approach with artificial hotspots, pure bacterial strains and a closed incubation system was to reduce the inherent complexity of soil in order to (i) identify processes that governed denitrification at the pore scale and (ii) create an experimental dataset for validation of pore-scale denitrification models.
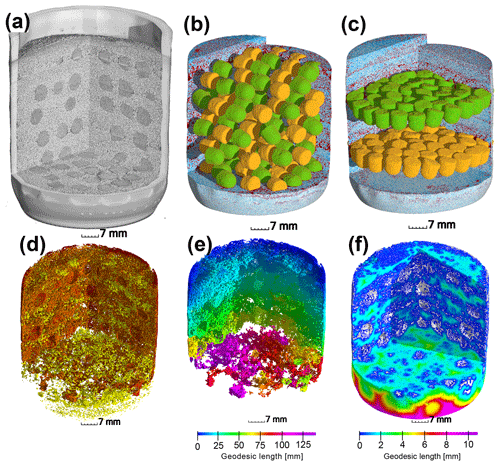
Figure 1Upper row: (a) X-ray CT scan of an incubation jar with random hotspot architecture and medium saturation (60 % WFPS). (b) Image segmentation of the same jar into air (red), water (blue), sand (transparent), A. tumefaciens hotspots (orange) and P. denitrificans hotspots (green). (c) A different jar at medium saturation (60 % WFPS) with layered Pd–At hotspot architecture. Lower row: a jar with random distribution at high saturation (90 % WFPS). (d) Air connectivity, determined as the volume fraction of air connected to the headspace (red, disconnected air shown in yellow). (e) Air tortuosity as derived from the geodesic length to the headspace within the connected air cluster. (f) Diffusion lengths determined as the geodesic length to the closest connected air cluster (white) within water-filled pores.
For this, we monitored O2, CO2, NO, N2O and N2 at high temporal resolution and determined the morphology of the air-filled pore space in terms of air connectivity, air tortuosity and air distance by X-ray computed tomography after the experiment.
2.1 Microbial hotspots
Two denitrifier strains were used in this study: Paracoccus denitrificans expresses all denitrification enzymes necessary to reduce to N2, whereas Agrobacterium tumefaciens lacks the gene nosZ encoding nitrous oxide reductase (N2OR), which makes N2O the final denitrification product. Moreover, the two strains differ in their regulatory phenotypes with respect to inducing denitrification in response to oxygen depletion, which leads to characteristic patterns of product accumulation (Bergaust et al., 2011). P. denitrificans induces NO and N2O reductase early during O2 depletion (Bergaust et al., 2010), thus releasing little N2O. By contrast, A. tumefaciens is known to be less stringent in controlling intermediates, which may result in the release of large amounts of NO, up to cell-toxic, millimolar concentrations (Bergaust et al., 2008). Both strains were grown oxically in Sistrom's medium (Sistrom, 1960) as described in a previous study (Schlüter et al., 2018), but at double strength to provide enough substrate for depleting O2 during aerobic growth once transferred to the porous glass beads. The medium was amended with 10 mm NH4NO3 and 5 mM KNO3 for anaerobic growth. To produce microbial hotspots, porous borosilicate glass beads (VitraPOR P100, ROBU Glasfilter Geräte GmbH) with a diameter of 7 mm, a porosity of 32 % and a medium pore diameter of 60 µm were saturated with a freshly inoculated growth medium (≈108 cells mL−1) by submersion into one of the two cultures. In the following, the inoculated porous glass beads are referred to as At (A. tumefaciens) and Pd (P. denitrificans) hotspots. Detailed information about the culture conditions and the inoculation procedure can be found in Schlüter et al. (2018).
2.2 Repacked sand
A total of 50 At and Pd hotspots each were placed into 120 mL of washed, sterile quartz sand (0.2–0.5 mm grain size), yielding a volume fraction of 14 % (20 mL; Fig. S1a in the Supplement). The sand was packed into 240 mL glass jars (Ball Corporation, Bloomfield, CA) in portions of 10 mL layers and adjusted to target saturation by adding sterile water with a spray can. The packing procedure resulted in some minor changes in porosity between layers and some larger gaps around the hotspots (Fig. S3) which affected air distribution in the sand (Fig. S2a). Three saturations were used, corresponding to water-filled pore spaces (WFPSs) of 30 %, 60 % and 90 %. The fully saturated hotspots were placed into the sand at three different architectures (Fig. 1). For the “random” distribution, the hotspots were placed in five equidistant (∼9.8 mm, center to center) horizontal layers with a random distribution of 10 At and 10 Pd hotspots per layer. The average spacing between neighboring hotspots (surface to surface) was approx. 6 mm in this architecture, which was the maximum possible spacing for this amount of hotspot volume (Fig. 1b). For the “layered At–Pd” and “layered Pd–At” distributions, all 50 hotspots of each strain were placed into one of two horizontal layers spaced 21 mm from each other (center to center) at an average headspace distance of 18.2 and 39.2 mm, respectively, where the order represents top–bottom. The average spacing between neighboring hotspots (surface to surface) was approx. 1 mm in these densely packed layers (Fig. 1c). Care was taken to keep the hotspots cool (on crushed ice) during the packing procedure. The pore size distribution of the porous hotspots and the sand in the bulk soil and in hotspot vicinity are reported in Fig. S3.
2.3 Incubation
To establish aerobic and anaerobic growth patterns and denitrification kinetics for both bacterial strains when growing inside the porous glass beads, a pre-experiment was conducted without sand. A total of 50 Pd or At hotspots were placed in septum-sealed 120 mL serum bottles (Fig. S1b) and incubated at 15 ∘C under either oxic (He∕O2 80∕20 %) or anoxic (He 100 %) conditions in two replicates per treatment. Headspace concentrations of O2, CO2, NO, N2O and N2 were measured every 4 h by piercing the septum with a hypodermic needle mounted to the robotic arm of an autosampler (GC-PAL, CTC Analytics, Switzerland). The autosampler was connected to a gas chromatograph (Agilent Model 7890A, Santa Clara, CA, USA) and a NO analyzer (Teledyne 200, San Diego, CA, USA) via a peristaltic pump. Detailed information about the robotized incubation system and the experimental setup can be retrieved elsewhere (Molstad et al., 2007; Schlüter et al., 2018).
In the main experiment, freshly inoculated glass beads were packed into incubation vessels as described above, three replicates for each of the nine combinations of saturation and hotspot distribution. Jars with 30 % and 60 % WFPS were flushed with He∕O2 for 40 min, using 10 cycles of vacuum (3 min) and purging (1 min). Jars with 90 % WFPS were flushed using 180 cycles of mild vacuum (∼600 mbar) and O2∕He purging to avoid structural changes of the packed columns due to bubbling of trapped gas. The jars were then placed into a water bath kept at 15 ∘C and after temperature equilibration O2∕He overpressure was released. Gas concentrations in the headspace were analyzed as described above. Gas production and consumption kinetics were used to calculate the fraction of electrons diverted to O2 or N oxyanions and thus to estimate the contribution of denitrification to total respiration () (Schlüter et al., 2018; Bergaust et al., 2011). The and product ratios were estimated from the cumulative release of gaseous denitrification products (NO, N2O, N2), after subtracting precursors from products (NO from N2O+N2 and NO+N2O from N2). The rationale behind the latter was to mimic an open system, in which N gases released to the atmosphere are not available any longer as electron acceptors for denitrification. This approach cannot make up for the general shortcoming of closed systems that accumulate gaseous and dissolved intermediates to high concentrations, but N2O concentrations in soil air reaching > 100 ppm are reported occasionally (Risk et al., 2014; Russenes et al., 2019). Details about the calculation of denitrification product ratios can be found in the Supplement (S1.2).
2.4 X-ray tomography and image analysis
After the incubation experiment, the glass jars were scanned with X-ray micro-tomography (X-tek XCT 225, Nikon Metrology) with a beam energy of 145 kV, a beam current of 280 µA, an exposure time of 708 ms per frame, a 0.5 mm copper filter for reducing beam hardening artefacts and a total of 3000 projections for a full scan. Individual hotspots were also scanned (100 kV, 90 µA, 1000 ms per frame, no filter) to analyze the internal pore morphology. The 2-D projections were reconstructed into a 3-D image with a resolution of 35 µm using a filtered-back projection algorithm in the X-tek CT Pro 3-D software. Image processing from raw gray-scale data (Fig. 1a) to segmented data including sand grains, air and water (Fig. 1b–c) was carried out according to well-established protocols for multi-phase segmentation (Schlüter et al., 2014). The porous glass beads were assigned to At or Pd hotspots according to the orientation of the flat end in the random architecture or by the vertical position in the layered architecture (Fig. 1b–c). The segmented images were analyzed with respect to three different spatial attributes of the air-filled pore spaces deemed important for oxygen supply:
-
Air connectivity by distinguishing isolated air-filled pores and air-filled pores with a continuous path to the headspace (yellow and red in Fig. 1d). Air connectivity is then defined as the ratio of connected air-filled pore space and total air-filled pore space.
-
Air tortuosity as derived from the geodesic length of connected air-filled pores. The geodesic length is the distance of any connected air voxel to the headspace along curved paths around obstacles like solid particles and water-blocked pores (Fig. 1e). Air tortuosity is the ratio between geodesic and vertical Euclidean distance to the headspace averaged over all connected, air-filled voxels. It is a proxy for the diffusive transport of gaseous oxygen in air-filled pores.
-
Air distances of water-filled pores as defined by the average geodesic distance from any water voxel to the closest air-filled pore with headspace connection (white in Fig. 1f). Air distance is a proxy for the slow diffusive transport of dissolved oxygen.
All image processing steps were carried out with Fiji ImageJ (Schindelin et al., 2012) and associated plugins (Legland et al., 2016; Doube et al., 2010) or with VGSTUDIO MAX 2.1 (Volume Graphics). Each image processing and analysis step is explained in detail in the Supplement (S1.3).
3.1 Aerobic respiration and denitrification in unconstrained hotspots without sand
At grew faster than Pd at 15 ∘C in the experiment with loosely placed porous glass beads, as indicated by faster O2 consumption and CO2 accumulation in the oxic treatment (Fig. 2a, b). Also under fully anoxic conditions, At accumulated CO2 faster than Pd (Fig. 2b). N-gas kinetics clearly reflected the disparate regulatory phenotypes of the two bacterial denitrifiers. Anoxic At instantly accumulated large amounts of NO (Fig. 2c) which persisted until all was reduced to N2O (as judged from the stable plateau in N2O, Fig. 2d). Due to slower growth and O2 consumption, Pd induced denitrification much later than At, but accumulated fewer intermediates (NO, N2O) than At. Oxically incubated Pd accumulated no detectable NO, indicating efficient regulation of denitrification when switched slowly to anaerobic conditions in hotspots. Also, NO may have been reduced to N2O when diffusing from the anoxic center to the boundary of the hotspots. In the initially oxic treatments, denitrification contributed 7 % to the total electron flow in At hotspots and 13 % in Pd hotspots measured over the entire period, reflecting the fact that (i) Pd has one more reduction step in the denitrification sequence and that (ii) At used less nitrate for anaerobic respiration in anoxic hotspots centers and more oxygen for aerobic respiration in oxic hotspots margins than Pd.
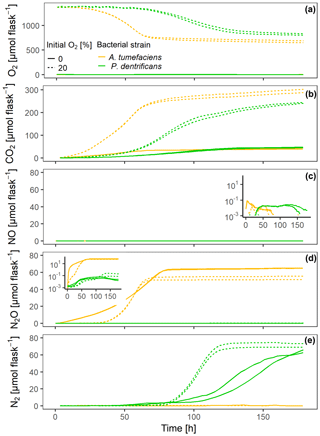
Figure 2Gas kinetics of individual sets of hotspots that were loosely placed in empty flasks (50 each), saturated with a growth medium and inoculated with two different bacterial strains – either a full denitrifier (P. denitrificans) or a truncated denitrifier lacking N2O reductase (A. tumefaciens) – under oxic and anoxic conditions: (a) O2, (b) CO2, (c) NO, (d) N2O, (e) N2.
3.2 Effects of hotspot distribution in sand
The distribution of microbial hotspots within the sand strongly impacted bulk respiration. This is evident for treatments with medium saturation (60 % WFPS) for the first 210 h of incubation (Fig. 3) and with other saturations for the entire incubation period (300 h; Figs. S4–6). The random distribution of hotspots allowed for much faster aerobic growth than the layered architectures, leading to complete consumption of O2 from the jars within 70 h (Fig. 3a). Given the slow growth of Pd (Fig. 2a), initial O2 consumption was dominated by the activity of At hotspots, turning them partly anoxic. Hence, the pronounced NO peak in the random treatment, coinciding with complete O2 exhaustion from the headspace (Fig. 3c), was due to At denitrification, similar to what was seen in the unconstrained At hotspots under anoxic conditions (Fig. 2c). N2O production was observed long before O2 was depleted from the headspace (Fig. 3d) and is attributed entirely to At denitrification. Pd denitrification did not start before all O2 was depleted and manifested itself in a transient increase in N2O production at ∼70 h together with an exponential increase in N2 production (Fig. 3e) which was also observed with unconstrained Pd hotspots (Fig. 2e). Note that the apparent net consumption of CO2 (Fig. 3b) upon O2 depletion was due to internal alkalization driven by accelerating denitrification, once all hotspots turned anoxic.
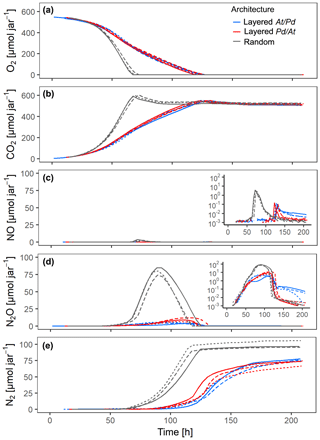
Figure 3Gas kinetics in all treatments at medium saturation in the sand (60 % WFPS) and an initial O2 concentration of 20 % in the headspace for three different hotspot architectures containing a total of 100 hotspots, in which the hotspots either had maximum separation distance (random) or were densely packed in layers either with all At hotspots (layered At–Pd) or all Pd hotspots (layered Pd–At) in the upper layer: (a) O2, (b) CO2, (c) NO, (d) N2O, (e) N2. Data are only shown for the first 210 h of the incubation period (300 h total). Different line styles represent replicates.
In the layered architectures, O2 consumption was slower and complete anoxia was not reached before 120 h into the incubation. In contrast to the random architecture, less O2 was available for each individual hotspot in the densely packed hotspot layers, allowing for less aerobic growth per unit time. As a consequence, there was more time for fully denitrifying At hotspots to interact with Pd hotspots, which induced denitrification gradually between 80 and 120 h. Indeed, less N2O accumulated in the headspace than in the random treatment (Figs. 3d, S6d) and the onset of N2 accumulation appeared long before complete O2 depletion in the headspace (Fig. 3a, e). In other words, Pd hotspots consumed N2O produced in At hotspots. Upon O2 depletion in the headspace, a burst of NO production occurred (Fig. 3c), as seen previously with At hotspots (Fig. 2c). However, since Pd denitrification was now fully developed, the NO peak was much more short-lived than with the random distribution, because Pd hotspots reduced NO produced by At hotspots all the way to N2.
The effect of vertical order in the layered hotspot architecture was small, but consistent among all denitrification products. The distribution with Pd hotspots on top (layered Pd–At) consumed the NO and N2O produced in At hotspots much quicker than the At–Pd architecture (Fig. 3c–d) and accumulated N2 faster after complete O2 depletion (Fig. 3e). Both observations highlight the effect of shorter diffusion distances between the headspace and the Pd hotspot layer in the layered Pd–At architecture.
3.3 Effects of matrix saturation
Differences in water saturation resulted in different absolute amounts of oxygen initially present in the jars (Fig. 4a) but did not affect the O2 concentration in the sand matrix. Oxygen was depleted slightly faster at 60 % than at 90 % saturation even though there was absolutely more O2 initially present at 60 % WFPS. This illustrates the paramount role of oxic growth for the oxic–anoxic transition in the hotspots: the more O2 available initially, the stronger the aerobic growth and the faster the oxic–anoxic transition.
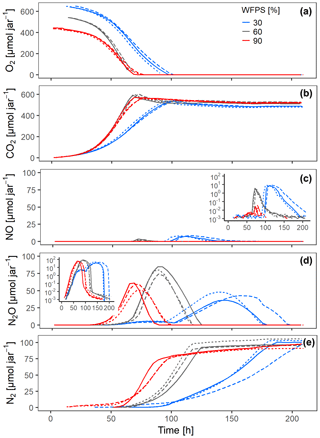
Figure 4Gas kinetics of randomly placed hotspots at three different saturations in the sand and an initial O2 concentration of 20 % in the headspace: (a) O2, (b) CO2, (c) NO, (d) N2O, (e) N2. Different lines styles represent replicates.
Increasing saturation from 60 % to 90 % in the randomly distributed hotspots had a strong effect on the timing and accumulation of denitrification products. The expected NO burst upon O2 depletion was damped by 2 orders of magnitude (Fig. 4c), because the oxic–anoxic transition proceeded more smoothly in the 90 % treatment and NO was reduced further to N2O before it could escape to the headspace. On the other hand, N2O and N2 production commenced earlier in the 90 % than in the 60 % treatment (Fig. 4d–e), indicating that O2 availability was a priori smaller irrespective of metabolic activity (which was larger in the 60 % treatment). The switch from net N2O production to net N2O consumption indicates the moment when microbial activity in Pd hotspots caught up with At hotspots.
Surprisingly, O2 consumption in the 30 % treatments was slow despite having the largest amount of O2 in the jar. This was caused by unintended substrate limitation. Due to overlapping pore size distribution between porous hotspots and sand (Fig. S3c), the medium was sucked by capillary force from the hotspot into the surrounding sand, as could be seen in a parallel experiment with brilliant blue dye (Fig. S7). This separated bacterial cells, which were likely immobilized in the pore space of the hotspots, temporarily from a considerable fraction of the carbon and supplied with the medium, before the dissolved substrate would diffuse back into the hotspots due to the evolving gradient induced by consumption in the hotspots. Decreasing the saturation from 60 % to 30 % also resulted in different timing and accumulation of denitrification products. The slow oxic growth of both At and Pd hotspots due to the substrate diffusion limitation at 30 % WFPS provided more time for Pd hotspots to interact with At hotspots than in the 60 % WFPS treatment. Indeed, the NO burst from At hotspots after complete O2 exhaustion in the random architecture was 50 % higher at 30 % WFPS, indicating higher At cell numbers due to prolonged oxic growth (Fig. 4c), whereas the N2O peak was 50 % lower, due to concomitant N2O reduction in Pt hotspots (Fig. 4d).
3.4 Mass balances
By the end of the incubation, oxygen was exhausted in all treatments. Likewise, was consumed by all treatments, except for the layered hotspots at 30 % and 60 % WFPS. This means that respiration was electron acceptor limited and that the cumulated recovery of denitrification products can be compared with the amount of initially present (Fig. S8). The balance between aerobic and anaerobic respiration, (Bergaust et al., 2011), is given by the electron flow to nitrogenous electron acceptors relative to the total electron flow, including O2 respiration (Fig. 5). When seen over all three water saturations, early-stage denitrification under oxic headspace conditions (Fig. 5a) showed a threshold response to increasing moisture with disproportionally higher ratios at 90 % WFPS (17 %–27 %) than at 60 % or 30 %. The proportions of electrons diverted to denitrification at low and medium saturations were small (2 %–7 %) and even smaller than those observed in unconstrained hotspots (7 %–13 %). Differences between saturations were less pronounced when the entire incubation period was considered (Fig. 5b), since fully anoxic conditions during late stage incubation overrode saturation effects. Overall, the effect of hotspot architecture on ratios was smaller than the effect of saturation.
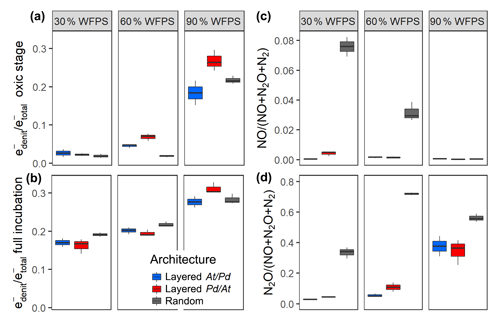
Figure 5The proportion of denitrification in total respiration expressed as relative electron flow for all architectures and saturations. Values are reported for (a) the initial, oxic to hypoxic stage (O2 present in headspace) and (b) for the full incubation period of 300 h. The product ratios for NO (c) and N2O (d) consider the full incubation period and are corrected for the release of precursor gases. Data shown as box–whisker plots: whiskers – min and max; middle lines – median.
This stands in stark contrast to the pronounced effect of hotspot architecture on denitrification product ratios (Fig. 5c, d). Hotspot architecture governed growth rates through local competition for O2 and therewith the number of active cells involved in net production sites (At hotspots) and net consumption sites (Pd hotspots) of NO once O2 was exhausted. In layered hotspot architectures there was hardly any net release of NO to the headspace irrespective of saturation (Fig. 5c). With random hotspot architecture, there was substantial NO release, the magnitude of which, however, decreased linearly with saturation. This pattern in NO stoichiometry clearly reflects the number of At cells at the moment of complete O2 depletion, as affected by oxic growth, which lasted longer with lower saturation. The N2O product ratio (Fig. 5d) was influenced by both saturation and hotspot architecture. In layered architectures, the N2O product ratio increased exponentially with increasing saturation similar to what was observed for relative electron flow to denitrification (Fig. 5a). In random architectures, the N2O product ratio was consistently higher than in layered architectures irrespective of saturation, yet the highest ratio was reached at 60 % WFPS, due to the most vigorous growth, and hence fastest oxic–anoxic transition at intermediate saturation.
3.5 Pore space properties
At the lowest saturation (30 % WFPS), the entire air-filled pore space was connected to the headspace (Fig. 6a) and tortuosity was close to unity, i.e., the diffusion lengths in air only depended on the vertical distance to the headspace (Fig. 6b). The diffusion distances in water-filled pores (Fig. 6c) corresponded to the size of small, evenly distributed water clusters. At medium saturation (60 % WFPS), the amount of disconnected air was still negligible and tortuosity increased only slightly. The increase in air distance was due to a few large water pockets, which were caused by the step-wise addition of water to the repacked sand. Only at 90 % saturation did a considerable air volume of 5 %–20 % became disconnected from the headspace. The path along which the remaining air was connected to the headspace became more tortuous with increasing saturation, and average diffusion distances in water to the connected air cluster increased to 1 mm. This is still surprisingly short as compared to the size of the hotspots (7 mm). Independent tests showed that the high air connectivity at this low air content was facilitated by vacuum application during He∕O2 purging prior to the incubation. Directly after packing, the continuous air cluster only reached 10–15 mm into the sand (data not shown), whereas bubbling due to vacuum application formed continuous air channels that reached deep into the sand matrix, connecting even the deepest hotspots with the headspace. Moreover, some larger gaps remained around hotspots during packing, which tended to be air-filled after wetting. This is reflected in the consistently higher air connectivity, lower air tortuosity and lower air distance, when only pores in the direct vicinity of hotspots are analyzed (Fig. 6a–c). More than 90 % of hotspot surfaces still had a direct air-filled connection with the headspace at 90 % WFPS (Fig. 6a). Depth profiles of these pore space attributes are reported in Fig. S2.
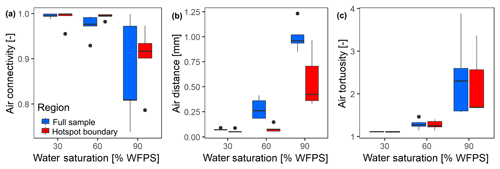
Figure 6Morphological properties of air-filled pores at different saturations averaged over different hotspot architectures (n=5). These properties are reported separately for the entire pore space within the region of interest (full sample) and for the pore space in direct vicinity to the porous glass beads (hotspot boundary): (a) air connectivity represents the volume fraction of air with direct connection to the headspace. (b) Air tortuosity represents the ratio between geodesic length to the headspace and Euclidean distance for any voxel within the connected air-cluster. (c) Air distance represents the geodesic distance to the connected air cluster within the water-filled pores. Data shown as box–whisker plots: whiskers – min and max; middle lines – median; dots – outliers.
4.1 Physical constraints on denitrification kinetics
The experimental setup in this incubation study was designed to investigate physical constraints on microbial respiration in hotspots as affected by the interplay between gaseous diffusion through a sterile matrix and local competition for oxygen. For this, we compared different combinations of water saturation in the matrix and spatial distributions of hotspots, which led to different physical constraints for the supply of hotspots with oxygen. As a consequence, oxic growth rates differed among treatments which had various implications on denitrification, as summarized in a conceptual scheme (Fig. 7).
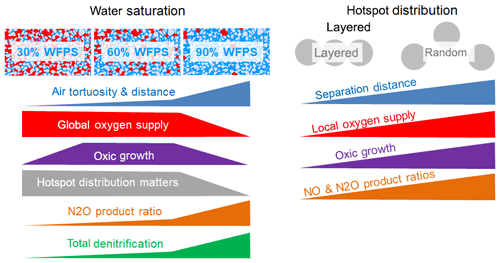
Figure 7Summary of the experimental findings about the impact of water saturation and spatial hotspot distribution on the physical constraints on the supply of hotspots with oxygen, the resulting growth rates and the implication of various aspects of denitrification.
Our setup is a coarse simplification of soil in which metabolic activity in hotspots not only depends on oxygen supply, but also on diffusion of substrates from the matrix to the hotspots. As such, our experiment does not allows to draw direct conclusions about the functioning of hotspots in real soils. However, by placing denitrifiers and their substrates into hotspots, we considerably reduced the level of complexity and created a system that is amenable to studying the dynamic interrelations between denitrifier growth, oxygen consumption and induction of denitrification by gas kinetics.
Soil N2O emissions are known to be highly variable in time, and a unifying concept incorporating dynamic changes in denitrification activity and product stoichiometry in response to changing environmental conditions is still missing. Our model system provides the first dataset for validating mathematical process models that are explicitly accounting for structural distribution of hotspots and dynamic changes in boundary conditions (here mimicked by different hotspot architectures and declining oxygen concentrations in the headspace during batch incubation, respectively). The development of such models is a core activity of the DASIM project (http://www.dasim.net/, last access: 26 September 2019). By combining metabolic measurements with advanced structural imaging and computation, we also provide a link to parameterizing such models with real soil data in future research.
Inoculating growing denitrifiers into porous glass beads and embedding them in sterile sand resulted in a highly dynamic system with respect to oxygen consumption and induction of denitrification. This was intended for the sake of experimental depth, but it must be noted that oxic–anoxic transitions are likely slower, i.e., less dynamic in real-soil hotspots. In real soils, even highly organic hotspots contain a fair amount of recalcitrant organic C that limits microbial growth and oxygen consumption. Also with respect to denitrification stoichiometry, real soils may be expected to be less dynamic as multiple denitrifying phenotypes contained in the natural soil microbiome (Roco et al., 2017) utilize denitrification intermediates mutually. Notwithstanding, soil NO and N2O emissions are known to be episodic in nature. Large, denitrification-driven emission pulses occur upon abrupt changes in O2 availability, caused by external factors like heavy rainfalls or soil freezing (Flessa et al., 1995), O2 consumption by nitrification after ammoniacal fertilization (Huang et al., 2014), or incorporation of easily degradable organic matter (Flessa et al., 1995) which cannot be captured satisfactorily by common steady-state models for soil respiration and N2O emission (Parton et al., 2001; Li et al., 1992). Even though the concept of hotspots is central in the understanding of denitrification dynamics in upland soils, common soil denitrification models do not account for the dynamics of spatially explicit hotspots in the soil matrix but rather scale bulk denitrification with a generic anoxic volume fraction (Li et al., 2000; Blagodatsky et al., 2011). To advance soil denitrification models, it is obvious that microbial respiration dynamics in hotspots have to be targeted, both conceptually (Wang et al., 2019) and experimentally (Kravchenko et al., 2017; Ebrahimi and Or, 2018). Our study is a first step in this direction.
One of the main findings of this study is that soil microbial respiration and the propensity to develop denitrifying anoxic hotspots does depend on their distribution in space. The onset of denitrification and its kinetics were linked to the spatial and temporal extent of anoxia developing in hotspot centers, which was governed by the interplay between denitrifier growth, diffusional constraints and hotspot architecture. When distributed randomly, microbial activity was most disperse relative to available oxygen, resulting in more growth, faster O2 drawdown and earlier anoxia than when packed densely in layers (Fig. 3). Rapid oxic–anoxic transitions led to higher release rates of denitrification intermediates and increased NO and N2O product ratios (Fig. 5c–d). This effect was most pronounced at low and intermediate saturations but was dampened at 90 % WPFS because oxygen supply was impeded by bulk diffusion irrespective of hotspot placement. Thus, our results highlight the significance of hotspot distribution at low soil moisture levels and exemplifies why N2O emissions are notoriously difficult to predict under these conditions.
Even though we failed to fully synchronize At and Pd growth in time, our experiment demonstrates that contrasting denitrification phenotypes may interact in modulating N2O flux to the atmosphere. Pd hotspots reduced N2O released from At hotspots irrespective of the layers' orientation (Fig. 3d), which can be attributed to the high degree of air connectivity in the sand column (Fig. 1d). We had expected more N2O reduction with Pd on top (layered Pd–At), but since At grew faster than Pd, partial anoxia and NO and N2O formation was induced in At, long before N2O consuming activity was induced in Pd hotspots. Future experiments with artificial hotspots should therefore carefully consider potential growth rates and air connectivity in packed soil.
4.2 Physical constraints on cumulative denitrification
The cumulative release of gaseous denitrification products, as described by electron flow ratios, depended less on hotspot architecture than on soil moisture. Electron flows to denitrification ranged from < 5 % of total respiratory flow at low to medium saturations (30 %, 60 % WFPS) to almost 23 % at 90 % WFPS (Fig. 5a). We attribute the generally low denitrification electron flow in our experiments to the small active volume relative to the sterile sand matrix (the total volume fraction of hotspots was 14 %, less of which was actually anoxic) and the large amount of oxygen initially present in the incubation jars. Yet, we found a typical, nonlinear denitrification response to soil moisture (Fig. 5a). This threshold behavior is well known (Weier et al., 1993) and has been attributed to a disproportional contribution of small pores to the anoxic volume at higher saturation (Schurgers et al., 2006). In our system, consisting of coarse sand with a relatively homogenous pore size distribution, we attribute the nonlinear response to an increase in tortuosity of air-filled pores and an increase in distance to the next continuous air-filled pore that were pronounced enough to impair the oxygen supply to hotspots. Air connectivity also increased nonlinearly but did not reach a critical value (Fig. 6), ruling out the possibility that differences in NO and N2O release at different saturations were due to gas entrapment but rather due to elongated diffusion pathways in air-filled and water-filled pores, leading to longer residence times of denitrification intermediates and a stronger reduction of intermediates in hotspots along the way to the headspace.
We cannot rule out bacterial spread out of the hotspots and that some denitrification might have occurred in the sand matrix. Nitrate and dissolved carbon diffused out of the hotspots, and in addition at the lowest saturation (30 % WFPS) those substrates were transported convectively by capillary forces. This was demonstrated with a separate dye experiment (Fig. S7). The fact that oxygen consumption was slow at 30 % WFPS is indirect evidence that most bacteria remained in the hotspots. In other words, under well-aerated conditions only substrate limitation can explain a reduction in microbial growth as compared to the 60 % WFPS and this can only occur if the substrates left the hotspots, but the cells did not follow to the same degree. For the 60 % and 90 % WFPS cases it is unclear as to how bacterial dispersal is really relevant. A. tumefaciens is known to possess flagella (Merritt et al., 2007), but P. denitrificans is not motile. Experimental data on bacterial dispersal rates in soil are scarce. In a recent study with Bacillus subtilis and Pseudomonas fluorescens inoculated to repacked soils at similar bulk density (1.5 g cm−1) and saturation (60 %), the first cells appeared in a distance of 15 mm after 9 d (Juyal et al., 2018). In our experiment, with the highest substrate concentration and the largest internal surface area in the hotspots, denitrification occurred after 3–6 d. Hence, some cells may have colonized the immediate vicinity of hotspots, but cell densities outside the hotspots were likely low.
Saturation-dependent threshold behavior for denitrification is a well-studied phenomenon in soils (Linn and Doran, 1984; Ruser et al., 2006; Paul et al., 2003), but due a lack of pore-scale measurements it is often attributed to reduced bulk soil diffusivity. In undisturbed soil, the relative importance of air connectivity and distances between air-filled and water-filled pores might be more relevant for impairing oxygen supply and inducing denitrification. Air connectivity to the headspace was shown to affect N2O emissions in terms of magnitude and responsiveness in repeated wetting–drying cycles in an intact soil column (Rabot et al., 2015). In agricultural soil with different crop rotations, N2O emissions were shown to correlate positively with the volume fraction of soil with macropore distances larger than 180 µm, which was used as an ad hoc definition for poorly aerated soil (Kravchenko et al., 2018). In a mesocosm study on microstructural drivers for local redox conditions, none of the investigated soil pore metrics derived from X-ray CT data (excluding those examined here) correlated with redox kinetics during a wetting–drying cycle (Wanzek et al., 2018). Hence, combining metabolic monitoring by high-resolution gas kinetics with direct assessment of diffusion lengths of gaseous and dissolved oxygen and denitrification products via X-ray microtomography emerges as a promising tool to study physical constraints for aerobic and anaerobic respiration in soil. However, meaningful metrics derived from X-ray data relevant for denitrification are yet to be developed and will require additional experiments with both artificial and real soils. Improved understanding of factors and mechanisms controlling denitrification and N-gas emission on a three-dimensional micro-scale may help to design and test soil management strategies that mediate the return of excess nitrogen to the atmosphere in a controlled way, i.e., with as little as possible NO and N2O release, be it by crop residue (Kravchenko et al., 2017), pH (Russenes et al., 2016) or irrigation (Bergstermann et al., 2011) management. At the same time, our experiments call for the implementation of spatially explicit reaction–diffusion algorithms (Hron et al., 2015; Ebrahimi and Or, 2016) in soil process models. For instance, diffusion lengths between hotspots and air-filled pores connected to the headspace may serve as a useful metric to be implemented on model concepts like the anaerobic soil volume fraction in larger-scale continuum models (Li et al., 2000; Schurgers et al., 2006; Blagodatsky et al., 2011).
Using a highly simplified model system, we demonstrate that the denitrification in heterogeneous media like soil critically depends on water saturation as well as on the spatial distribution of microbial hotspots. Hotspot architecture effects were particularly pronounced with respect to denitrification stoichiometry, resulting in vastly different NO and N2O release rates. Even though our experiment was conducted in a closed system, with growing denitrifier strains and a limited amount of substrate, the results are relevant for real soils in that they represent a benchmark scenario of hotspot-driven denitrification. More importantly, our reductionist approach resulted in an experimental dataset that is amenable to process-based, pore-scale denitrification models, which will be the subject of a future study.
Hotspot architecture played a more pronounced role for denitrification kinetics at lower soil moisture (30 % WFPS and 60 % WFPS). Hence, denitrification and its gaseous product stoichiometry do not only depend on the amount of microbial hotspots in aerated soil, but also on their spatial distribution. The total amount of denitrification measured as cumulative electron flow, in turn, depended more on water saturation, which is in line with the well-known saturation-dependent threshold behavior in denitrification also found in natural soil. For the case of artificial soil used in our study, we found that this threshold behavior was best explained by increased air tortuosity and air distance at high saturations. Future experiments with artificial and natural soils are needed to fully capture the regulation of denitrification at the micro-scale.
All segmented X-ray µCT files and the GC data are permanently available through the UFZ archive with data description using a standardized metadata catalogue (Dublin Core) and with access via URL: http://www.ufz.de/record/dmp/archive/7291 (Schlüter, 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-3665-2019-supplement.
SS, HJV and PD designed the experiments. SS, JZ and PD carried them out. SS, JZ and PD processed the data. SS prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We thank Ali Ebrahimi and two anonymous reviewers for the constructive comments. We thank Linda Bergaust for providing the bacterial strains, Jing Zhu for laboratory support, and Olaf Ippisch and Marcus Horn for helpful discussions during the planning of the experiment.
This research has been supported by the Deutsche Forschungsgemeinschaft through the research unit
DFG-FOR 2337: Denitrification in Agricultural Soils: Integrated
Control and Modelling at Various Scales (DASIM) (grant no. 270261188). Peter Dörsch
received funding from the FACCE-ERA-GAS project MAGGE-pH
under the grant agreement no. 696356
The article processing charges for this open-access
publication were covered by a Research
Centre of the Helmholtz Association.
This paper was edited by Jianming Xu and reviewed by Ali Ebrahimi and two anonymous referees.
Arah, J. R. M. and Vinten, A. J. A.: Simplified models of anoxia and denitrification in aggregated and simple-structured soils, Eur. J. Soil Sci., 46, 507–517, https://doi.org/10.1111/j.1365-2389.1995.tb01347.x, 1995.
Ball, B. C.: Soil structure and greenhouse gas emissions: a synthesis of 20 years of experimentation, Eur. J. Soil Sci., 64, 357–373, https://doi.org/10.1111/ejss.12013, 2013.
Bergaust, L., Shapleigh, J., Frostegard, A., and Bakken, L.: Transcription and activities of NOx reductases in Agrobacterium tumefaciens : The influence of nitrate, nitrite and oxygen availability, Environ. Microbiol., 10, 3070–3081, 2008.
Bergaust, L., Mao, Y., Bakken, L., and Frostegard, A.: Denitrification response patterns during the transition to anoxic respiration and posttranscriptional effects of suboptimal pH on nitrogen oxide reductase in Paracoccus denitrificans, Appl. Environ. Microbiol., 76, 6387–6396, 2010.
Bergaust, L., Bakken, Lars, R., and Frostegård, Å.: Denitrification regulatory phenotype, a new term for the characterization of denitrifying bacteria, Biochem. Soc. T., 39, 207–212, https://doi.org/10.1042/bst0390207, 2011.
Bergstermann, A., Cárdenas, L., Bol, R., Gilliam, L., Goulding, K., Meijide, A., Scholefield, D., Vallejo, A., and Well, R.: Effect of antecedent soil moisture conditions on emissions and isotopologue distribution of N2O during denitrification, Soil Biol. Biochem., 43, 240–250, https://doi.org/10.1016/j.soilbio.2010.10.003, 2011.
Blagodatsky, S., Grote, R., Kiese, R., Werner, C., and Butterbach-Bahl, K.: Modelling of microbial carbon and nitrogen turnover in soil with special emphasis on N-trace gases emission, Plant Soil, 346, 297–330, https://doi.org/10.1007/s11104-011-0821-z, 2011.
Doube, M., Kłosowski, M. M., Arganda-Carreras, I., Cordelières, F. P., Dougherty, R. P., Jackson, J. S., Schmid, B., Hutchinson, J. R., and Shefelbine, S. J.: BoneJ: Free and extensible bone image analysis in ImageJ, Bone, 47, 1076–1079, 2010.
Ebrahimi, A. and Or, D.: Microbial community dynamics in soil aggregates shape biogeochemical gas fluxes from soil profiles – upscaling an aggregate biophysical model, Glob. Change Biol., 22, 3141–3156, 2016.
Ebrahimi, A. and Or, D.: Dynamics of soil biogeochemical gas emissions shaped by remolded aggregate sizes and carbon configurations under hydration cycles, Glob. Change Biol., 24, e378–e392, https://doi.org/10.1111/gcb.13938, 2018.
Elberling, B., Askaer, L., Jørgensen, C. J., Joensen, H. P., Kühl, M., Glud, R. N., and Lauritsen, F. R.: Linking Soil O2, CO2, and CH4 Concentrations in a Wetland Soil: Implications for CO2 and CH4 Fluxes, Environ. Sci. Technol., 45, 3393–3399, https://doi.org/10.1021/es103540k, 2011.
Flessa, H., Dörsch, P., and Beese, F.: Seasonal variation of N2O and CH4 fluxes in differently managed arable soils in southern Germany, J. Geophys. Res.-Atmos., 100, 23115–23124, https://doi.org/10.1029/95JD02270, 1995.
Groffman, P. M., Butterbach-Bahl, K., Fulweiler, R. W., Gold, A. J., Morse, J. L., Stander, E. K., Tague, C., Tonitto, C., and Vidon, P.: Challenges to incorporating spatially and temporally explicit phenomena (hotspots and hot moments) in denitrification models, Biogeochemistry, 93, 49–77, 2009.
Højberg, O., Revsbech, N. P., and Tiedje, J. M.: Denitrification in soil aggregates analyzed with microsensors for nitrous oxide and oxygen, Soil Sci. Soc. Am. J., 58, 1691–1698, 1994.
Horn, R., Stepniewski, W., Wlodarczyk, T., Walenzik, G., and Eckhardt, F.: Denitrification rate and microbial distribution within homogeneous model soil aggregates, Int. Agrophys., 8, 65–74, 1994.
Hron, P., Jost, D., Bastian, P., Gallert, C., Winter, J., and Ippisch, O.: Application of Reactive Transport Modeling to Growth and Transport of Microorganisms in the Capillary Fringe, Vadose Zone J., 14, 1–17, https://doi.org/10.2136/vzj2014.07.0092, 2015.
Huang, T., Gao, B., Hu, X.-K., Lu, X., Well, R., Christie, P., Bakken, L. R., and Ju, X.-T.: Ammonia-oxidation as an engine to generate nitrous oxide in an intensively managed calcareous Fluvo-aquic soil, Sci. Rep., 4, 3950, https://doi.org/10.1038/srep03950, 2014.
Juyal, A., Eickhorst, T., Falconer, R., Baveye, P. C., Spiers, A., and Otten, W.: Control of Pore Geometry in Soil Microcosms and Its Effect on the Growth and Spread of Pseudomonas and Bacillus sp, Front. Environ. Sci., 6, 1–12, https://doi.org/10.3389/fenvs.2018.00073, 2018.
Keiluweit, M., Wanzek, T., Kleber, M., Nico, P., and Fendorf, S.: Anaerobic microsites have an unaccounted role in soil carbon stabilization, Nat. Commun., 8, 1771, https://doi.org/10.1038/s41467-017-01406-6, 2017.
Keiluweit, M., Gee, K., Denney, A., and Fendorf, S.: Anoxic microsites in upland soils dominantly controlled by clay content, Soil Biol. Biochem., 118, 42–50, https://doi.org/10.1016/j.soilbio.2017.12.002, 2018.
Kravchenko, A. N., Toosi, E. R., Guber, A. K., Ostrom, N. E., Yu, J., Azeem, K., Rivers, M. L., and Robertson, G. P.: Hotspots of soil N2O emission enhanced through water absorption by plant residue, Nat. Geosci., 10, 496–500, https://doi.org/10.1038/ngeo2963, 2017.
Kravchenko, A. N., Guber, A. K., Quigley, M. Y., Koestel, J., Gandhi, H., and Ostrom, N. E.: X-ray computed tomography to predict soil N2O production via bacterial denitrification and N2O emission in contrasting bioenergy cropping systems, GCB Bioenergy, 10, 894–909, https://doi.org/10.1111/gcbb.12552, 2018.
Kuzyakov, Y. and Blagodatskaya, E.: Microbial hotspots and hot moments in soil: Concept & review, Soil Biol. Biochem., 83, 184–199, 2015.
Legland, D., Arganda-Carreras, I., and Andrey, P.: MorphoLibJ: integrated library and plugins for mathematical morphology with ImageJ, Bioinformatics, 32, 3532–3534, 2016.
Li, C., Frolking, S., and Frolking, T. A.: A model of nitrous oxide evolution from soil driven by rainfall events: 1. Model structure and sensitivity, J. Geophys. Res.-Atmos., 97, 9759–9776, https://doi.org/10.1029/92JD00509, 1992.
Li, C., Aber, J., Stange, F., Butterbach-Bahl, K., and Papen, H.: A process-oriented model of N2O and NO emissions from forest soils: 1. Model development, J. Geophys. Res.-Atmos., 105, 4369–4384, 2000.
Linn, D. and Doran, J.: Effect of water-filled pore space on carbon dioxide and nitrous oxide production in tilled and nontilled soils, Soil Sci. Soc. Am. J., 48, 1267–1272, 1984.
Mangalassery, S., Sjögersten, S., Sparkes, D. L., Sturrock, C. J., and Mooney, S. J.: The effect of soil aggregate size on pore structure and its consequence on emission of greenhouse gases, Soil Till. Res., 132, 39–46, https://doi.org/10.1016/j.still.2013.05.003, 2013.
Mathieu, O., Lévêque, J., Hénault, C., Milloux, M.-J., Bizouard, F., and Andreux, F.: Emissions and spatial variability of N2O, N2 and nitrous oxide mole fraction at the field scale, revealed with 15N isotopic techniques, Soil Biol. Biochem., 38, 941–951, 2006.
Merritt, P. M., Danhorn, T., and Fuqua, C.: Motility and chemotaxis in Agrobacterium tumefaciens surface attachment and biofilm formation, J. Bacteriol., 189, 8005–8014, https://doi.org/10.1128/JB.00566-07, 2007.
Miller, M. N., Zebarth, B. J., Dandie, C. E., Burton, D. L., Goyer, C., and Trevors, J. T.: Denitrifier Community Dynamics in Soil Aggregates under Permanent Grassland and Arable Cropping Systems, Soil Sci. Soc.f Am. J., 73, 1843–1851, https://doi.org/10.2136/sssaj2008.0357, 2009.
Molstad, L., Dörsch, P., and Bakken, L. R.: Robotized incubation system for monitoring gases (O2, NO, N2O, N2) in denitrifying cultures, J. Microbiological Meth., 71, 202–211, 2007.
Moyano, F. E., Vasilyeva, N., Bouckaert, L., Cook, F., Craine, J., Curiel Yuste, J., Don, A., Epron, D., Formanek, P., Franzluebbers, A., Ilstedt, U., Kätterer, T., Orchard, V., Reichstein, M., Rey, A., Ruamps, L., Subke, J. A., Thomsen, I. K., and Chenu, C.: The moisture response of soil heterotrophic respiration: interaction with soil properties, Biogeosciences, 9, 1173–1182, https://doi.org/10.5194/bg-9-1173-2012, 2012.
Nunan, N.: The microbial habitat in soil: Scale, heterogeneity and functional consequences, J. Plant Nutr. Soil Sc., 180, 425–429, https://doi.org/10.1002/jpln.201700184, 2017.
Parkin, T. B.: Soil microsites as a source of denitrification variability, Soil Sci. Soc. Am. J., 51, 1194–1199, 1987.
Parry, S., Renault, P., Chenu, C., and Lensi, R.: Denitrification in pasture and cropped soil clods as affected by pore space structure, Soil Biol. Biochem., 31, 493–501, https://doi.org/10.1016/S0038-0717(98)00101-1, 1999.
Parton, W. J., Holland, E. A., Del Grosso, S. J., Hartman, M. D., Martin, R. E., Mosier, A. R., Ojima, D. S., and Schimel, D. S.: Generalized model for NOx and N2O emissions from soils, J. Geophys. Res.-Atmos., 106, 17403–17419, https://doi.org/10.1029/2001JD900101, 2001.
Paul, K. I., Polglase, P. J., O'Connell, A. M., Carlyle, J. C., Smethurst, P. J., and Khanna, P. K.: Defining the relation between soil water content and net nitrogen mineralization, Eur. J. Soil Sci., 54, 39–48, https://doi.org/10.1046/j.1365-2389.2003.00502.x, 2003.
Rabot, E., Lacoste, M., Hénault, C., and Cousin, I.: Using X-ray Computed Tomography to Describe the Dynamics of Nitrous Oxide Emissions during Soil Drying, Vadose Zone J., 14, 1–10, https://doi.org/10.2136/vzj2014.12.0177, 2015.
Risk, N., Wagner-Riddle, C., Furon, A., Warland, J., and Blodau, C.: Comparison of Simultaneous Soil Profile N2O Concentration and Surface N2O Flux Measurements Overwinter and at Spring Thaw in an Agricultural Soil, Soil Sci. Soc. Am. J., 78, 180–193, https://doi.org/10.2136/sssaj2013.06.0221, 2014.
Roco, C. A., Bergaust, L. L., Bakken, L. R., Yavitt, J. B., and Shapleigh, J. P.: Modularity of nitrogen-oxide reducing soil bacteria: linking phenotype to genotype, Environ. Microbiol., 19, 2507–2519, https://doi.org/10.1111/1462-2920.13250, 2017.
Röver, M., Heinemeyer, O., Munch, J. C., and Kaiser, E.-A.: Spatial heterogeneity within the plough layer: high variability of N2O emission rates, Soil Biol. Biochem., 31, 167–173, 1999.
Ruser, R., Flessa, H., Russow, R., Schmidt, G., Buegger, F., and Munch, J. C.: Emission of N2O, N2 and CO2 from soil fertilized with nitrate: effect of compaction, soil moisture and rewetting, Soil Biol. Biochem., 38, 263–274, https://doi.org/10.1016/j.soilbio.2005.05.005, 2006.
Russenes, A. L., Korsaeth, A., Bakken, L. R., and Dörsch, P.: Spatial variation in soil pH controls off-season N2O emission in an agricultural soil, Soil Biol. Biochem., 99, 36–46, https://doi.org/10.1016/j.soilbio.2016.04.019, 2016.
Russenes, A. L., Korsaeth, A., Bakken, L. R., and Dörsch, P.: Effects of nitrogen split application on seasonal N2O emissions in southeast Norway, Nutr. Cycl. Agroecosys., 115, 41–56, https://doi.org/10.1007/s10705-019-10009-0, 2019.
Schaufler, G., Kitzler, B., Schindlbacher, A., Skiba, U., Sutton, M. A., and Zechmeister-Boltenstern, S.: Greenhouse gas emissions from European soils under different land use: effects of soil moisture and temperature, Eur. J. Soil Sci., 61, 683–696, https://doi.org/10.1111/j.1365-2389.2010.01277.x, 2010.
Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., Preibisch, S., Rueden, C., Saalfeld, S., and Schmid, B.: Fiji: an open-source platform for biological-image analysis, Nat. Methods, 9, 676–682, 2012.
Schlüter, S.: Dataset – Schlueter_et_al_2019_Biogeosciences, http://www.ufz.de/record/dmp/archive/7291, last access: 26 September 2019.
Schlüter, S., Sheppard, A., Brown, K., and Wildenschild, D.: Image processing of multiphase images obtained via X-ray microtomography: A review, Water Resour. Res., 50, 3615–3639, 2014.
Schlüter, S., Henjes, S., Zawallich, J., Bergaust, L., Horn, M., Ippisch, O., Vogel, H.-J., and Dörsch, P.: Denitrification in Soil Aggregate Analogues-Effect of Aggregate Size and Oxygen Diffusion, Front. Environ. Sci., 6, 1–10, https://doi.org/10.3389/fenvs.2018.00017, 2018.
Schurgers, G., Dorsch, P., Bakken, L., Leffelaar, P., and Haugen, L. E.: Modelling soil anaerobiosis from water retention characteristics and soil respiration, Soil Biol. Biochem., 38, 2637–2644, https://doi.org/10.1016/j.soilbio.2006.04.016, 2006.
Sexstone, A. J., Revsbech, N. P., Parkin, T. B., and Tiedje, J. M.: Direct measurement of oxygen profiles and denitrification rates in soil aggregates, Soil Sci. Soc. Am. J., 49, 645–651, 1985.
Sierra, J. and Renault, P.: Respiratory Activity and Oxygen Distribution in Natural Aggregates in Relation to Anaerobiosis, Soil Sci. Soc. Am. J., 60, 1428–1438, https://doi.org/10.2136/sssaj1996.03615995006000050020x, 1996.
Sistrom, W. R.: A Requirement for Sodium in the Growth of Rhodopseudomonas spheroides, Microbiology, 22, 778–785, 1960.
Smith, K. A.: A model of the extent of anaerobic zones in aggregated soils, and its potential application to estimates of denitrification, J. Soil Sci., 31, 263–277, https://doi.org/10.1111/j.1365-2389.1980.tb02080.x, 1980.
Smith, K. A., Ball, T., Conen, F., Dobbie, K. E., Massheder, J., and Rey, A.: Exchange of greenhouse gases between soil and atmosphere: interactions of soil physical factors and biological processes, Eur. J. Soil Sci., 54, 779–791, https://doi.org/10.1046/j.1351-0754.2003.0567.x, 2003.
Tecon, R. and Or, D.: Biophysical processes supporting the diversity of microbial life in soil, FEMS Microbiol. Rev., 41, 599–623, https://doi.org/10.1093/femsre/fux039, 2017.
Wang, B., Brewer, P. E., Shugart, H. H., Lerdau, M. T., and Allison, S. D.: Soil aggregates as biogeochemical reactors and implications for soil–atmosphere exchange of greenhouse gases – A concept, Glob. Change Biol., 25, 373–385, https://doi.org/10.1111/gcb.14515, 2019.
Wanzek, T., Keiluweit, M., Varga, T., Lindsley, A., Nico, P. S., Fendorf, S., and Kleber, M.: The Ability of Soil Pore Network Metrics to Predict Redox Dynamics is Scale Dependent, Soil Systems, 2, 66–91, 2018.
Weier, K. L., Doran, J. W., Power, J. F., and Walters, D. T.: Denitrification and the Dinitrogen/Nitrous Oxide Ratio as Affected by Soil Water, Available Carbon, and Nitrate, Soil Sci. Soc. Am. J., 57, 66–72, https://doi.org/10.2136/sssaj1993.03615995005700010013x, 1993.
Zausig, J., Stepniewski, W., and Horn, R.: Oxygen Concentration and Redox Potential Gradients in Unsaturated Model Soil Aggregates, Soil Sci. Soc. Am. J., 57, 908–916, https://doi.org/10.2136/sssaj1993.03615995005700040005x, 1993.





