Evaluating the simulated mean soil carbon transit times by Earth system models using observations

One known bias in current Earth system models (ESMs) is the underestimation of global mean soil carbon (C) transit time (τ_soil), which quantifies the age of the C atoms at the time they leave the soil. However, it remains unclear where such underestimations are located globally. Here, we constructed a global database of measured τ_soil across 187 sites to evaluate results from 12 ESMs. The observations showed that the estimated τ_soil was dramatically shorter from the soil incubation studies in the laboratory environment (median = 4 years; interquartile range = 1 to 25 years) than that derived from field in situ measurements (31; 5 to 84 years) with shifts in stable isotopic C (¹³C) or the stock-over-flux approach. In comparison with the field observations, the multi-model ensemble simulated a shorter median (19 years) and a smaller spatial variation (6 to 29 years) of τ_soil across the same site locations. We then found a significant and negative linear correlation between the in situ measured τ_soil and mean annual air temperature. The underestimations of modeled τ_soil are mainly located in cold and dry biomes, especially tundra and desert. Furthermore, we showed that one ESM (i.e., CESM) has improved its τ_soil estimate by incorporation of the soil vertical profile. These findings indicate that the spatial variation of τ_soil is a useful benchmark for ESMs, and we recommend more observations and modeling efforts on soil C dynamics in regions limited by temperature and moisture.

1 Introduction

Carbon (C) cycle feedback to climate change is highly uncertain in current Earth system models (ESMs) (Friedlingstein et al., 2006; Bernstein et al., 2008; Ciais et al., 2013; Bradford et al., 2016), which largely stems from their diverse simulations of C exchanges among the atmosphere, vegetation, and soil (Luo et al., 2016; Smith et al., 2016; Mishra et al., 2017). Soil organic carbon (SOC) represents the largest terrestrial carbon pool, which stores at least 3 times as much as the atmospheric and vegetation C reservoirs (Parry et al., 2007; Bloom et al., 2016). However, a 5- to 6-fold difference in soil C stocks among ESMs or offline global land surface models has been found (Todd-Brown et al., 2013; Luo et al., 2016). It is difficult to reduce or even diagnose this uncertainty, as many processes collectively affect the time of C atoms' transit in the soil system (i.e., transit time, τ_soil) (Sierra et al., 2017; Spohn and Sierra, 2018). Some recent attempts at evaluating and diagnosing the modeled SOC in ESMs have shown significant simulation uncertainties in the τ_soil (Todd-Brown et al., 2013; Carvalhais et al., 2014; He et al., 2016; Koven et al., 2017). For example, there is a 4-fold difference in the simulated τ_soil among the ESMs from the Coupled Model Intercomparison Project Phase 5 (CMIP5) (Todd-Brown et al., 2013). A recent data-driven analysis has suggested that the current ESMs have substantially underestimated the τ_soil by 16–17 times at the global scale (He et al., 2016). Therefore, identifying the locations of such underestimations is critical to improve the predictive ability of ESMs for the terrestrial C cycle, and the construction of a benchmarking database of available observations is urgently needed (Koven et al., 2017).

The terms of transit time, turnover time, and age of soil C have been muddled in diagnosing the models (Sierra et al., 2017). The diagnostic times derived from observational data are based on the different assumptions and mainly derived from four approaches. The first approach is commonly defined as “turnover time”, calculated by the division of SOC stock by C fluxes such as net primary productivity (NPP) or heterotrophic respiration (R_h). It assumes the soil system is a time-invariant linear system in a steady state (Bolin et al., 1973; Sanderman et al., 2003; Six and Jastrow, 2012). The second approach is based on the shifts in stable isotopic C (¹³C) after successive changes in C₃–C₄ vegetation, together with additional information from the disturbed and undisturbed soils (Balesdent et al., 1987; Zhang et al., 2015). The third approach is based on simulating soil C dynamics with linear models by assimilating the observational data from laboratory incubations of soil samples (Xu et al., 2016). The last approach derives the weighted inverse of the first-order cycling rate by fitting a one- or multiple-pool linear model to field observations of radiocarbon (¹⁴C) (Trumbore et al., 1993; Fröberg et al., 2011). The diagnostic times derived from the first three approaches indicate the transit times, which are the mean ages of C atoms leaving the carbon pools during a certain time (Rasmussen et al., 2016). Lu et al. (2018) has evaluated the deviation between C transit and turnover times with the CABLE model. Their results have shown that the global latitudinal pattern of C transit and turnover times is consistent under a steady-state assumption and autonomous conditions except for 8 % of divergence in the northern high latitudes (>60^∘ N). However, the diagnostic time calculated by the radiocarbon signal indicates the average age of C atoms stored in the C pools. Although radiocarbon has been widely used to quantify the age or transit time of soil C, its validity has been challenged by some recent theoretical analyses (Sierra et al., 2017; Metzler et al., 2018). Rasmussen et al. (2016) has marked off the transit time and mean system age in a mathematic way and further applied it in the Carnegie–Ames–Stanford approach (CASA) model. Also, the methodological uncertainty is large, especially when these approaches are applied to estimate the τ_soil of different soil fractions (Feng et al., 2016). Thus, this study mainly collects the τ_soil values from the approaches of stock over flux, ¹³C changes, and lab incubations in further analyses.

In this study, we first construct a database from the literatures which reported τ_soil (Fig. 1a, Supplement on Text S1). Then, the database is used to evaluate the simulated τ_soil by the ESMs in CMIP5. The SOC τ_soil values were calculated under a homogenous one-pool assumption at steady state for all studies. Data from observations and the CMIP5 ensemble were then used to calculate the τ_soil based on both one-pool and three-pool models. Many ESMs, e.g., CESM, have released new versions in recent years, so we also evaluate whether the simulated τ_soil has been improved. In the case of CESM, one of its major developments in soil C cycling is the vertically resolved soil biogeochemical scheme (Koven et al., 2013). Thus, we employ a matrix approach developed by Huang et al. (2017) to examine the impact of the vertically resolved soil biogeochemical scheme on the τ_soil simulated by CESM.

2 Materials and methods

2.1 A global database of site-level τ_soil

We collected the literatures that reported the τ_soil based on measurements (Text S1 in the Supplement): (1) δ¹³C shifts after successive changes in C₃-C₄ vegetation, (2) measurements of CO₂ production in laboratory SOC incubation over at least 7 months, and (3) simultaneous measurements of SOC stock and heterotrophic respiration (stock over flux). We constructed a database containing the measured τ_soil from 187 sites across the globe (Fig. 1). Based on the homogenous assumption, the soil system is a time-invariant linear system at the steady state. The τ_soil derived from this database is under a one-pool assumption. The information of climate (e.g., mean annual temperature and precipitation) was also collected from the literature or extracted from the WorldClim database version 1.4 (http://worldclim.org/, last access: 1 June 2019, Hijmans et al., 2005) if literature was not available. The WorldClim dataset provided a set of free global climate data for ecological modeling and Geographic Information System analysis with a spatial resolution of 0.86 km² (Hutchinson et al., 2004). We extracted the mean temperature and precipitation by averaging the monthly climate data over 1990–2000 for those observational sites with missing climate information. The classes of biomes were processed to match the seven biome classifications adopted by the MODIS land cover product MCD12C1 (NASA LP DAAC, 2008; Friedl et al., 2010) and Todd-Brown et al. (2013) (Fig. S1): (1) tropical forest including evergreen broadleaf forest between 25^∘ N and 25^∘ S; (2) temperate forest including deciduous broadleaf, evergreen broadleaf outside of 25^∘ N and 25^∘ S, and mixed forest south of 50^∘ N; (3) boreal forest including evergreen needleleaf forest, deciduous needleleaf forest, and mixed forest north of 50^∘ N; (4) grassland and shrubland including woody savanna south of 50^∘ N and savanna and grasslands south of 55^∘ N; (5) deserts and savanna including barren or sparsely vegetated open shrubland south of 55^∘ N and closed shrubland south of 50^∘ N; (6) tundra; and (7) croplands. Other land cover types like permanent wetland, urban, and bare land were not included in this study.

2.2 Outputs of Earth system models from CMIP5

The historical simulation outputs of 12 ESMs participating in CMIP5 from 1850 to 1860 (https://esgf-data.dkrz.de/search/cmip5-dkrz/, last access: 11 January 2016) were analyzed in this study (Table S1). For each model, the SOC, litter C, NPP, and heterotrophic respiration (R_h) were extracted from the outputs in historical simulations (cSoil, cLitter, npp, and rh, respectively, from the CMIP5 variable list). The litter and soil carbon were summed as the bulk soil carbon stock. Among the 12 models, only the inmcm4 model did not output NPP, so we calculated it as gross primary production minus autotrophic respiration. Due to the diverse spatial resolutions among the models, we aggregated the results of different models to $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ with the nearest interpolation method (Fig. S2). The τ_soil of SOC was calculated as the ratio of carbon stock over flux (NPP or R_h):

$$\begin{array}{}\text{(1)}& {\mathit{\tau }}_{\mathrm{soil}}={\displaystyle \frac{\mathrm{SOC}}{\mathrm{flux}}}.\end{array}$$

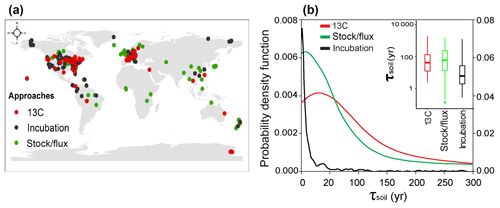
Figure 1 Spatial distributions of observational sites for estimates of SOC transit time (τ_soil, year). (a) The site locations of measurements with different approaches. (b) Probability density functions of τ_soil measured with different approaches. Note that the left axis is for the ¹³C and stock-over-flux approaches, and the right axis is for laboratory incubation studies.

2.3 Estimating the SOC τ_soil with a three-pool model

To examine whether the major findings of this data–model comparison are affected by the one-pool homogenous assumption, we fitted a three-pool model with observational data and model ensemble outputs at the biome level. In this study, a three-pool C model consisted of fast, slow, and passive pools and carbon transfers among three pools (Fig. S3a). This model shares the same framework with the CENTURY and the terrestrial ecosystem models (Bolker et al., 1998; Liang et al., 2015). The dynamics of soil carbon pools follow first-order differential kinetics. The total C stocks and CO₂ efflux from observations and the CMIP5 ensemble were separated into pool-specific decomposition rates by the deconvolution analysis (Fig. S3a, Liang et al., 2015). We assumed the total soil carbon input equals total soil respiration at the steady state.

Based on the theoretical analysis, the dynamics of the three-pool model can be mathematically described by the matrix equation (Luo et al., 2003; Xia et al., 2013) as

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}C\left(t\right)}{\mathrm{d}t}}=I\left(t\right)-\mathbf{AKC}\left(t\right),\end{array}$$

where the matrix C(t)=(C₁(t), C₂(t), C₃(t))^T is used to describe soil carbon pool sizes. A is a matrix given by

$$\begin{array}{}\text{(3)}& \mathbf{A}=\left(\begin{array}{rrr}-\mathrm{1}& f_{\mathrm{12}}& f_{\mathrm{13}}\\ f_{\mathrm{21}}& -\mathrm{1}& \mathrm{0}\\ f_{\mathrm{31}}& f_{\mathrm{32}}& -\mathrm{1}\end{array}\right).\end{array}$$

The elements f_ij are carbon transfer coefficients, indicating the fractions of the carbon entering the ith (row) pool from the jth (column) pool. K is a 3×3 diagonal matrix indicating the decomposition rates (the amounts of carbon per unit mass leaving each of the pools per year). The matrix of K is given by K=diag (k₁, k₂, k₃).

The parameters in the three-pool model were estimated based on Bayesian probabilistic inversion (Eq. 4). The posterior probability density function P(θ|Z) of model parameters (θ) can be represented by the prior probability density function (P(θ)) and a likelihood function (P(Zlθ)) (Liang et al., 2015; Xu et al., 2016). The likelihood function was calculated by the minimum error between observed and modeled values with Eq. (5). In this study, we adopted the prior ranges of model parameters from Liang et al. (2015).

$$\begin{array}{}\text{(4)}& P\left(\mathit{\theta }\mathrm{|}Z\right)\propto P\left(Z\mathrm{|}\mathit{\theta }\right)\cdot P\left(\mathit{\theta }\right)\end{array}$$

$$\begin{array}{}\text{(5)}& P\left(Z\mathrm{|}\mathit{\theta }\right)\propto \exp \left\{-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\sigma }}_i^{\mathrm{2}}\left(t\right)}}\sum _{i=\mathrm{1}}^n\sum _{t\in \mathrm{obs}\left(Z\right)}[Z_i\left(t\right)-X_i\left(t\right){]}^{\mathrm{2}}\right\}\end{array}$$

Here Z_i(t) and X_i(t) are the observed and modeled transit times, and ${\mathit{\sigma }}_i^{\mathrm{2}}\left(t\right)$ is the standard deviation of measurements. The posterior probability density function of the parameters was constructed with two steps: a proposing step and a moving step. In the first step, the dataset was generated based on the previously accepted data with a proposal distribution:

$$\begin{array}{}\text{(6)}& {\mathit{\theta }}^{\mathrm{new}}={\mathit{\theta }}^{\mathrm{new}}+{\displaystyle \frac{d({\mathit{\theta }}_{\max }-{\mathit{\theta }}_{\min })}{D}},\end{array}$$

where θ_max and θ_min are the maximum and minimum values of the given parameters, d is the random variable between −0.5 and 0.5 with uniform distribution, and D is used to control the proposing step size in this study. In the moving step, the new data θ^new is tested against the Metropolis criteria to quantify whether it should be accepted or rejected. The parameters of posterior probability density function were constructed with the Metropolis–Hastings algorithm. The Metropolis–Hastings algorithm was run 50 000 times for observed data. Accepted parameter values were used in further analysis.

Based on the concepts of mean age and mean transit time published by Rasmussen et al. (2016) and Lu et al. (2018), the mean carbon age defined as the whole time carbon atoms are stored in the carbon pools and then the mean age of carbon ${\stackrel{\mathrm{‾}}{a}}_i\left(t\right)$ in a certain carbon pool i could be calculated with Eq. (7):

$$\begin{array}{}\text{(7)}& {\stackrel{\mathrm{‾}}{a}}_i\left(t\right)=\mathrm{1}+{\displaystyle \frac{\sum _{i=\mathrm{1}}^{\mathrm{3}}({\stackrel{\mathrm{‾}}{a}}_j\left(t\right)-{\stackrel{\mathrm{‾}}{a}}_i\left(t\right))\cdot f_{ij}\left(t\right)\cdot C_i-{\stackrel{\mathrm{‾}}{a}}_j\left(t\right)\cdot I_i\left(t\right)}{C_i}},\end{array}$$

where the f_ij(t) values are the carbon fraction transfer coefficients from jth to ith pools, and I_i(t) is the external input into the ith carbon pool. The transit time τ_i(t) was defined as the mean age of carbon atoms leaving the carbon pool at a specific time:

$$\begin{array}{}\text{(8)}& {\mathit{\tau }}_i\left(t\right)=\sum _{i=\mathrm{1}}^d{f}_i\left(t\right)\cdot a_i\left(t\right),\end{array}$$

where the f_i(t) is the fraction of carbon with mean age a_i(t).

2.4 Matrix approach through CLM4.5 and CLM4.5_noV

The Community Land Model version 4.5 (CLM4.5) is the terrestrial component of the Community Earth System Model (CESM). This version mainly consists of exchanges among different carbon and nitrogen pools and other biogeochemical cycles and includes a vertical dimension of soil carbon and nitrogen transformations (Koven et al., 2013). The matrix approach was applied to extract the soil module from the original CLM4.5, which could evaluate which processes influence τ_soil in the model (Huang et al., 2017). Once we obtain the total carbon pool and R_h in each pool, we can calculate the τ_soil with Eq. (1). We represented the structure of SOC as seven carbon pools as (i) one coarse woody debris (CWD) pool, (ii) three litter pools (litter1, litter2, and litter3), and (iii) three soil carbon pools (soil1, soil2, and soil3). In this matrix, carbon is transferred from three litter pools and CWD to three soil pools with different transfer rates. In each layer, these transfer rates are regulated by the transfer coefficients and fractions. C inputs from litterfall were allocated into different C compartments by modifications by soil environmental factors (temperature, moisture, nitrogen, and soil oxygen) and vertical transfer process. To understand whether the incorporation of soil vertical profile affects the simulation of τ_soil, we compared the results based on the matrix approach with (i.e., CLM4.5) or without (i.e., CLM4.5_noV) the soil vertical transfer process.

In CLM4.5, soil C dynamics was simulated with 10 soil layers, and the same organic matter pools among different vertical soil layers are allowed to mix mainly through diffusion and advection. The matrix approach determines the soil dynamic of each SOC pool by simulating the first-order kinetics as Eq. (9):

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}C\left(t\right)}{\mathrm{d}t}}=\mathbf{B}\left(t\right)I\left(t\right)-\mathbf{A}\mathit{\xi }\left(t\right)\mathbf{KC}\left(t\right)\mathbf{V}\left(t\right)\mathbf{C}\left(t\right),\end{array}$$

where the C_(t) is the organic carbon pool size at time t. I_(t) is the total organic carbon inputs while B_(t) is the vector of partitioning coefficients. K is a diagonal matrix that represents the intrinsic decomposition rate of each carbon pool. The decomposition rate in the matrix approach is modified by the transfer matrix A and environmental scalars ξ. The scalar matrix ξ shown in Eq. (10) is the environmental factor to modify the SOC intrinsic decomposition rate. Each scalar matrix combines temperature (ξ_T), water (ξ_W), oxygen (ξ_O), depth (ξ_D), and nitrogen (ξ_N) controlled scalars for SOC decay.

$$\begin{array}{}\text{(10)}& {\mathit{\xi }}^{\prime }={\mathit{\xi }}_{\mathrm{T}}{\mathit{\xi }}_{\mathrm{W}}{\mathit{\xi }}_{\mathrm{O}}{\mathit{\xi }}_{\mathrm{D}}{\mathit{\xi }}_{\mathrm{N}}\end{array}$$

A is the horizontal carbon transfer matrix, which quantifies C movement among different carbon pools shown as matrix (10). The non-diagonal entries A_ij shown in matrix (10) represent the fraction of carbon that moves from the jth to the ith pools. In CLM4.5 and CLM4.5_noV, transfer coefficients are the same in each soil layer.

$$\begin{array}{}\text{(11)}& \mathbf{A}=\left(\begin{array}{ccccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& f_{\mathrm{44}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& f_{\mathrm{52}}& f_{\mathrm{53}}& \mathrm{0}& f_{\mathrm{55}}& f_{\mathrm{56}}& f_{\mathrm{57}}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& f_{\mathrm{64}}& f_{\mathrm{65}}& f_{\mathrm{66}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& f_{\mathrm{75}}& f_{\mathrm{76}}& f_{\mathrm{77}}\end{array}\right)\end{array}$$

V(t) is the vertical carbon transfer coefficient matrix among different soil layers, and each of the diagonal blocks is a tridiagonal matrix that describes transfer coefficients with V_ij(t). In this section, CLM4.5_noV assumes no vertical transfers in all pools. Therefore, V(t) for CLM4.5_noV is a blank matrix in the simulation. In contrast, CLM4.5 was assigned by a matrix with vertical transfers in each C pool. The vertical transfer rates among different C pool categories in CLM4.5 are matrix (12).

$$\begin{array}{ll}\text{(12)}& {\displaystyle }& {\displaystyle }\mathbf{V}\left(t\right)={\displaystyle }& {\displaystyle }\left(\begin{array}{ccccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& V_{\mathrm{22}}\left(t\right)& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& V_{\mathrm{33}}\left(t\right)& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& V_{\mathrm{44}}\left(t\right)& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& V_{\mathrm{55}}\left(t\right)& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& V_{\mathrm{66}}\left(t\right)& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& V_{\mathrm{77}}\left(t\right)\end{array}\right)\end{array}$$

2.5 Statistical analyses

The median and interquartile were used for the quantification of both observational and modeling results due to the fact that the probability distribution of τ_soil is not normal. To test the difference in τ_soil among three approaches, we first normalized the data with the log-transformation and then applied the one-way ANOVA with a multi-comparison technique (Fig. 1b insert). The linear regression and correlation analyses were performed in R (3.2.1; R development Core team, 2015).

The Gaussian kernel density estimation was used to obtain the distributions of observed transit times (Sheather and Marron, 1990; Saoudi et al., 1997). The Gaussian kernel density estimation is a nonparametric approach to estimate the probability density function of a random variable. Let (x₁x₂⋯, x_n) denote the observed SOC τ_soil with density function f as below:

$$\begin{array}{}\text{(13)}& {\widehat{f}}_{\mathrm{h}}\left(x\right)={\displaystyle \frac{\mathrm{1}}{nh}}\sum _{i=\mathrm{1}}^{n}K\left({\displaystyle \frac{x-x_i}{h}}\right),\end{array}$$

where K is the nonnegative function than integrates to one and has a mean of zero, and h>0 is a smoothing parameter called the bandwidth. The bandwidth for approaches of stable isotope ¹³C, stock over flux, and incubation are 48.61, 35.13, and 2.62, respectively.

3 Results and discussion

3.1 τ_soil and its spatial variation using different approaches

The one-way ANOVA with multi-comparison analysis showed no significant difference in the log-transformed τ_soil between the methods of ¹³C (median = 60 years; interquartile range = 8 to 29 years) and stock over flux (16; 3 to 156 years, Fig. 1b). The range of these field in situ measurements (31; 5 to 84 years) is comparable to a former estimate of mean SOC turnover time (48 with 24 to 107 years) across 20 long-term experiments in temperate ecosystems using the ¹³C labeling approach (Schmidt et al., 2011). However, the estimates of τ_soil from laboratory studies (4; 1 to 15 year) were significantly shorter than those from the other two methods (Fig. 1b). It suggests that the τ_soil could be underestimated by the measurements from the laboratory incubation studies. Thus, the τ_soil values from the laboratory incubation studies were excluded in the following analyses.

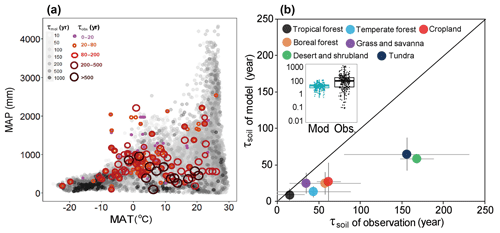
Figure 2 Global spatial variation of SOC transit time (τ_soil) with climate and the difference of τ_soil estimation between observations and models. (a) Spatial variation of τ_soil with mean annual temperature (MAT) and mean annual precipitation (MAP). (b) Comparisons of modeled against observed τ_soil. Details for the classification of biomes are provided in the method section.

We then integrated the estimates of τ_soil based on the ¹³C and stock-over-flux approaches to examine the inter-biome difference. As shown by Fig. 2b, the longest τ_soil was found in desert and shrubland (170; 58 to 508) and tundra (159; 39 to 649 years). Boreal forest (58; 25 to 170 years) has a longer τ_soil than the temperate (44; 13 to 89 years) and tropical forests (15; 9 to 130 years). Grassland and savanna had short τ_soil (35; 21 to 57 years) and croplands had moderate (62; 21 to 120 years) τ_soil in comparison with other biomes (Fig. 2).

3.2 Modeled τ_soil in the CMIP5 ensemble and its estimation biases

The longest ensemble mean τ_soil values of multiple models were found in dry and cold regions (Fig. 2). In comparison with the integrated observations from ¹³C and stock over flux, the modeled τ_soil values were significantly shorter across all biomes (Fig. 2b insert). The negative bias was larger in dry (desert, grassland, and savanna) and cold (tundra and boreal forest) regions than tropical and temperate forests. The longest modeled τ_soil appeared in the tundra ecosystem with a median of 64 years. The modeled median τ_soil values were also shorter than observations in tropical forest (9 years), temperate forests (13 years), boreal forest (24 years), grassland/savanna (25 years), desert and shrubland (58 years), and croplands (27 years) (Fig. 2). In comparison with the observations, the models obviously underestimated the τ_soil in the cold and dry biomes (Fig. 2b). A recent global data–model comparison study at $\mathrm{0.5}{}^{\circ }\times \mathrm{0.5}{}^{\circ }$ resolution also detected a similar spatial pattern of underestimation bias in ecosystem C turnover time (Carvalhais et al., 2014), but its magnitudes of bias in the cold regions are much smaller than those found in this study.

By grouping the τ_soil into different climatic categories, we found that the observed τ_soil significantly covaried with MAT ($y=-\mathrm{5.28}x+\mathrm{156.04}$, r²=0.48, P<0.01) and MAP ($y=-\mathrm{68.19}x+\mathrm{1222.6}$, r²=0.60, P<0.01) (Fig. 3). These results support the previous findings of negative covariations between τ_soil and temperature at both the site and global levels (Trumbore et al., 1996). Although there is no significant correlation between τ_soil and MAP in the observations, the models produced negative correlations of τ_soil with MAT (r²=0.24, P<0.05) and MAP (r²=0.44, P<0.05) (Fig. 3).

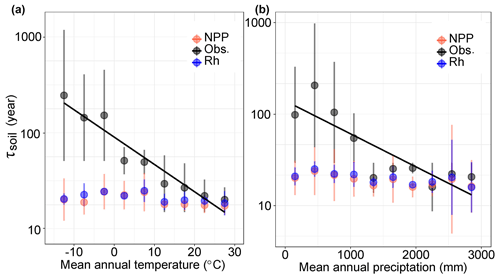
Figure 3 Relationships between SOC transit time (τ_soil) and climate factors in both observations and CIMP5 models. The black solid lines show the negative correlation between τ_soil and (a) mean annual temperature and (b) mean annual precipitation. The black dots indicate the aggregated τ_soil over each category of MAT ($y=-\mathrm{5.47}x+\mathrm{1971.5}$, r²=0.49, P<0.01) or MAP ($y=-\mathrm{68.19}x+\mathrm{1222.6}$, r²=0.60, P<0.01). The red and blue dots present the mean value of multiple models based on the ratios of carbon stock over NPP and R_h, respectively.

3.3 Estimation of the τ_soil with a three-pool model

With the three-pool model, the total C stocks and CO₂ efflux from observations and the CMIP5 ensemble were separated into pool-specific decomposition rates by the deconvolution analysis (Fig. S3a; Liang et al., 2015). Seven out of 11 parameters were constrained for tropical forest and cropland (Fig. S4, Fig. S9). Eight out of 11 parameters were constrained for temperate, boreal forest, and desert and shrubland (Figs. S5, S6, S8). Five out of 11 parameters were constrained for the tundra ecosystem (Fig. S7). For grassland and savanna, seven out of 11 parameters were constrained (Fig. S10).

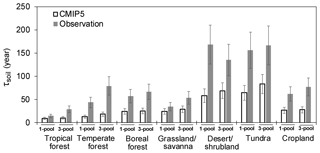
Figure 4 The SOC transit time (τ_soil) calculated from the one- and three-pool models under the steady-state assumption.

The longest simulated τ_soil appeared in tundra (167 years) and desert (135 years) (Fig. 4, Table S3). Temperate forest (79 years) has a longer τ_soil than the boreal (66 years) and tropical forests (29 years). Grassland and savanna had short τ_soil (53.8 years) and croplands had moderate (77 years) τ_soil in comparison with other biomes. The τ_soil calculated from the one- and three-pool models did not show a large difference across all biomes. Also, estimates based on these two model structures showed the largest underestimation of τ_soil in the tundra and desert (Fig. 4).

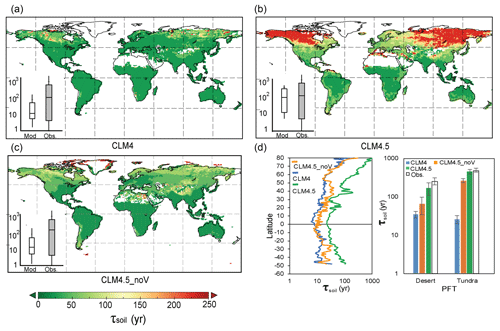
Figure 5 Simulated SOC transit time (τ_soil) by CLM4 (a, median global τ_soil=20.56 years), CLM4.5 (b, median global τ_soil=127.50 years), and CLM4.5_noV (c, median global τ_soil=22.24 years). Panel (d) shows the latitudinal spatial distribution of the mean τ_soil of different models in desert and tundra. The inserts in (a)–(c) compare the τ_soil between models and observations. The bottom and top of the box represent the first and third quartiles.

3.4 Improved modeling of τ_soil with vertically resolved SOC dynamics

Given that many ESMs have further developed their representations of the soil biogeochemistry in recent years, we also examined whether the τ_soil estimates have been improved by one of the CMIP5 models (i.e., CESM). It is encouraging that the biases of τ_soil in dry and cold regions have been substantially reduced in the new land version of CESM (i.e., version 4.5 of the Community Land Model, CLM4.5). One major improvement in CLM4.5 is the vertically resolved SOC dynamics (Koven et al., 2013). The soil organic carbon is allowed to transfer through diffusion and advection up to 3.8 m within 10 layers. In each layer, the transfer rates are regulated by the environmental scalars (i.e., temperature, soil moisture, and available oxygen). The τ_soil values simulated by CLM4.5 are longer than those in CLM4 (with median value 137 years and 21 years), especially in northern high-latitudinal regions. By turning off the vertical C movements with a matrix approach (i.e., there is no vertical C transfer; thus, the vertical matrix is a zero matrix in Eq. 12), we showed a similar pattern of underestimation on τ_soil by CLM4.5 (i.e., CLM4.5_noV in Fig. 5). Huang et al. (2017) also reported the longer τ_soil and high carbon storage capacity in northern high latitudes. These results suggest that the vertically resolved soil biogeochemistry is promising in improving the τ_soil estimates by ESMs. However, it should be noted that the spatial variation of τ_soil is still largely underestimated by the CLM4.5 (Fig. 5b insert).

Higher NPP values simulated by ESMs in the cold and dry regions have been reported by previous studies (Shao et al., 2013; Smith et al., 2016; Xia et al., 2017). The models produce high NPP in cold regions largely because they overestimate the efficiency of plants transferring assimilated C to growth (Xia et al., 2017). The CMIP5 models overestimate the precipitation and underestimate the dryland expansion 4-fold during 1996–2005 (Ji et al., 2015), which could lead to high NPP and fast SOC turnover rates. These results suggest that once the NPP simulation is improved without the correction of the τ_soil underestimation, the models will produce smaller SOC stock in the cold and dry ecosystems.

This study shows that adding the vertical resolved biogeochemistry is a promising approach to correct the bias of τ_soil in current models. However, other processes such as microbial dynamics, SOC stabilization, and nutrient cycles could affect the estimation of τ_soil but are so far fully considered by the CMIP5 models (Luo et al., 2016). For example, adding soil microbial dynamics could increase τ_soil in cold regions by lowering the transfer proportion of decomposed SOC to the atmosphere (Wieder et al., 2013). By contrast, the incorporation of nitrogen cycles might shorten τ_soil by increasing plant C transfers to short-lived litter pools (e.g., O-CN and CABLE models) (Gerber et al., 2010) or reducing litter C transfers to the slow soil C pools (e.g., LM3V model) (Xia et al., 2013).

Large challenges still exist in using observations derived from different methods to constrain the modeled τ_soil. Laboratory incubation studies report much shorter τ_soil than other methods, mainly due to the optimized soil moisture and/or temperature during the soil incubation (Stewart et al., 2008; Feng et al., 2016). This suggests that the ESM models will largely underestimate τ_soil if its turnover parameters are derived from laboratory incubation studies. It should be noted that the observations from the ¹³C and the stock-over-flux approaches in this study are derived for the bulk soil. However, SOC is commonly represented as multiple pools with different cycling rates in most of the CMIP5 models (Luo et al., 2016; Sierra et al., 2017, 2018; Metzler and Sierra, 2018). As synthesized by Sierra et al. (2017), the observations of τ_soil are useful for a specific model once its pool structure is identified. This study also detects a difference in the estimated τ_soil between the one- and three-pool models (Fig. 4). Thus, model databases, such as bgc-md (https://github.com/MPIBGC-TEE/bgc-md, last access: 2 February 2019), are a useful tool to improve the integration of observations and soil C models. An enhanced transparency of C-cycle model structure in ESMs is highly recommended, especially when they participate in the future model intercomparison projects such as CMIP6 (Jones et al., 2016).

4 Conclusions

This study detected large underestimation biases of τ_soil in ESMs in cold and dry biomes, especially the tundra and desert. Improving the modeling of SOC dynamics in these regions is important because the cold ecosystems (e.g., the permafrost regions) are critical for global C feedback to future climate change (Schuur et al., 2015) and the dry regions strongly regulate the interannual variability of land CO₂ sink (Poulter et al., 2014; Ahlström et al., 2015). The current generation of ESMs represents the soil C processes with a similar model formulation as first-order C transfers among multiple pools (Sierra and Markus, 2015; Luo et al., 2016; Metzler and Sierra, 2018). Thus, tremendous research efforts are still required to attribute the underestimation biases of τ_soil in current ESMs to their sources, such as model structure, parameterization, and climate forcing. Reducing these biases would largely improve the accuracy of ESMs in the projection of the future terrestrial C cycle and its feedback to climate change. Recent modeling activities aiming to increase the soil heterogeneity, for example, soil vertical profile (Koven et al., 2013, 2017) and microbial dynamics (Allison et al., 2010; Wieder et al., 2013), are promising. Overall, this study shows the great spatial variation of τ_soil in natural ecosystems, and we recommend more research efforts to improve its representation by ESMs in the future.