the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Biological and biogeochemical methods for estimating bioirrigation: a case study in the Oosterschelde estuary
Emil De Borger
Justin Tiano
Ulrike Braeckman
Tom Ysebaert
Karline Soetaert
Bioirrigation, the exchange of solutes between overlying water and sediment by benthic organisms, plays an important role in sediment biogeochemistry. Bioirrigation either is quantified based on tracer data or a community (bio)irrigation potential (IPc) can be derived based on biological traits. Both these techniques were applied in a seasonal study of bioirrigation in subtidal and intertidal habitats in a temperate estuary. The combination of a tracer time series with a high temporal resolution and a mechanistic model allowed for us to simultaneously estimate the pumping rate and the sediment attenuation, a parameter that determines irrigation depth. We show that, although the total pumping rate is similar in both intertidal and subtidal areas, there is deeper bioirrigation in intertidal areas. This is explained by higher densities of bioirrigators such as Corophium sp., Heteromastus filiformis and Arenicola marina in the intertidal, as opposed to the subtidal, areas. The IPc correlated more strongly with the attenuation coefficient than the pumping rate, which highlights that the IPc index reflects more the bioirrigation depth than the rate.
- Article
(1299 KB) - Full-text XML
-
Supplement
(993 KB) - BibTeX
- EndNote
Bioirrigation is the process in which benthic organisms actively or passively exchange sediment porewater solutes with the overlying water column as a result of burrowing, pumping (ventilation) and feeding activities (Kristensen et al., 2012). This exchange plays an important role in marine- and lacustrine-sediment biogeochemistry, as oxygen-rich water is brought into an otherwise subsediment or anoxic-sediment matrix. This allows for aerobic degradation processes to take place, as well as the reoxidation of reduced substances (Aller and Aller, 1998; Kristensen, 2001), and enables sediment-dwelling organisms to forage and live in the otherwise anoxic deeper sediment layers (Olaffson, 2003; Braeckman et al., 2011). By extending the sediment–water interface in the vertical dimension, burrowing organisms increase the exchange surface, especially when burrow water is refreshed by ventilation activities. This enhances nutrient exchange (Quintana et al., 2007) and increases degradation rates (Na et al., 2008). Sedimentary bioirrigation is the result of the combined actions of a multitude of organisms sharing the same habitat. Some organisms such as the smaller meiofauna, located close to the sediment–water interface, exchange only small amounts of solute, but due to their high densities their activities affect the sediment porosity and as such exert a significant effect on sediment–water exchanges in the top layers of the sediment (Aller and Aller, 1992; Rysgaard et al., 2000). On the opposite end of the spectrum are larger infaunal species such as the burrowing shrimp Upogebia pugettensis (Dana) which constructs burrows that extend up to 1 m into the sediment and actively ventilates these burrows using its pleopods (D'Andrea and DeWitt, 2009). These deep burrows substantially extend the oxic sediment–water interface into the sediment, influencing the associated microbial respiration through various pathways (Nielsen et al., 2004). The effect of bioirrigation also depends on the sediment matrix. In muddy sediments, where permeability is low, bioirrigation impacts are localized close to the burrow wall, as the transport of solutes radiating from the burrows is governed by diffusion (Aller, 1980). In sandy, more permeable sediments the pressure gradients caused by ventilation activities induce water flows through the surrounding sediments, thus affecting the sediment matrix further away from the burrow walls (Meysman et al., 2005; Timmermann et al., 2007). Therefore, the effects of bioirrigation depend on a combination of the species community, species' individual behavior including ventilation activity, the depths at which these activities occur, and the sediment matrix the species inhabit.
Bioirrigation can be quantified with biogeochemical methods, or a qualitative estimate can be calculated by an index of bioirrigation based on biological information. The biogeochemical methods estimate the exchange rates of a tracer substance (usually inert) between the overlying water and the sediment, by fitting a linear model (De Smet et al., 2016; Mestdagh et al., 2018; Wrede et al., 2018) or a quasi-mechanistic model (Berelson et al., 1998; Andersson et al., 2006) through measured concentration time series. A linear decrease returns the rate of disappearance of the tracer from the water column over a given time period, but it gives little information on the bioirrigation process itself, e.g., what is the actual pumping rate, and where in the sediment are solutes exchanged? While sometimes the depth distribution of the tracer in the sediment is characterized postexperiment to obtain this information (Martin and Banta, 1992; Berg et al., 2001; Hedman et al., 2011), this step is often overlooked. By increasing the temporal resolution of the tracer concentration measurements, an exponential decrease can be fitted through the data, from which a bioirrigation rate can be derived which is independent of the length of the experiment (Meysman et al., 2006; Na et al., 2008). For these applications fluorescent tracers are used, as they can be monitored in situ, and the measurement is instantaneous. So far, this method has been applied in controlled settings but not yet in field applications.
The index approach starts with the quantification of the abundance and biomass of organisms inhabiting the sediment and an assessment of how these organisms bioirrigate. The latter is performed based on a set of life history traits which are assumed to contribute to bioirrigation: the type of burrow they inhabit, their feeding type and their burrowing depth. Species are assigned one trait score for each trait, independent of the biological context in which they occur (but see Renz et al., 2018). The species biomass and abundance, combined with their trait scores, are then used to derive an index that represents the community (bio)irrigation potential (BIPc and IPc in Renz et al., 2018, and Wrede et al., 2018, respectively), a similar practice to that carried out for bioturbation with the community bioturbation potential (BPc; Queirós et al., 2013). The inherent assumptions of this approach are that bioirrigation activity increases linearly with the number of organisms and scales with their mean weight through a metabolic scaling factor. The advantage of biologically based indices is that large datasets of benthic communities are currently available (e.g., Craeymeersch et al., 1986; Degraer et al., 2006; Northeast Fisheries Science Center, 2018), so these data have great potential to derive information on the temporal and spatial variability in bioirrigation. However, in contrast to the related bioturbation potential (Solan et al., 2004), the classification of sediments according to their bioirrigation potential is a very recent endeavor, and the underlying mechanistic basis of these indices, i.e., what they actually describe, should be explored further. As a first step in this direction, the IPc index of Wrede et al. (2018) has been calibrated against bromide uptake rates for selected individual species and communities in the German Bight of the North Sea.
The aim of the current study was to compare bioirrigation rate measurements with an index of bioirrigation in natural sediments of a temperate estuarine system, the Oosterschelde. Samples were collected across different seasons at three subtidal and three intertidal sites with different benthic communities and sediments varying from muddy to sandy. Bioirrigation rates were derived by fitting a novel mechanistic model through a quasi-continuous time series of a fluorescent tracer, while biological information was used to calculate the IPc index.
2.1 Sampling
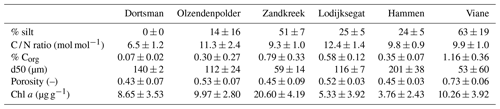
Field samples were collected in the Oosterschelde (SW Netherlands) from August 2016 to December 2017 (Fig. 1). Six sites (three subtidal, three intertidal) were selected based on results from previous sampling efforts to reflect the variability in inundation time and sediment composition present in this area (Table 1). The intertidal sites Zandkreek (51.55354∘ N, 3.87278∘ E), Dortsman (51.56804∘ N, 4.01425∘ E) and Olzendenpolder (51.46694∘ N, 4.072694∘ E) were sampled by pressing two cylindrical PVC cores (14.5 cm Ø, 30 cm height) in the sediment at low tide up to a depth of 20 cm at most and extracting them from the sediment. The subtidal sites Hammen (51.65607∘ N, 3.858717∘ E), Viane (51.60675∘ N, 3.98501∘ E) and Lodijksegat (51.48463∘ N, 4.166001∘ E) were sampled in the same way, but sediment was retrieved from duplicate deployments of an NIOZ box corer aboard the research vessel Delta. In total 70 individual cores in the intertidal and 47 in the subtidal areas were retrieved. Sediment permeability has a strong influence on bioirrigation rates (Aller, 1983; Meysman et al., 2006). Sediment permeability was not directly measured, but additional samples for sediment characteristics relating to this property (grain size distribution and porosity) were taken from the top 2 cm of sediment at each site, using a cut-off syringe. From the same samples, a subsample was collected for determining the chlorophyll a content and C / N ratios in the sediment, as measures of food availability and quality, respectively.
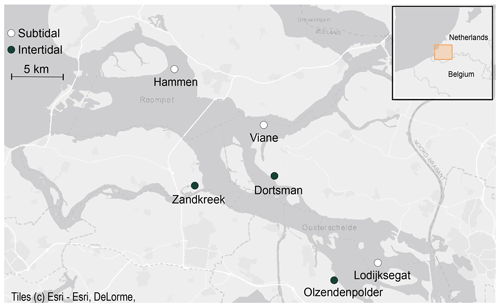
Figure 1Subtidal (white dots) and intertidal (black dots) sampling stations in the Oosterschelde estuary (© Esri).
Table 1Sampling frequency of the different research sites and average seasonal temperature of the water in the incubation cores during the measurements.
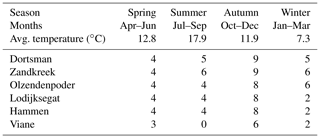
After transportation to the laboratory, the cores were placed into seawater tanks in a climate room set to the average water temperature of the month in which the samples were taken (Table 1, seasonal averages). By adding 0.45 µm filtered Oosterschelde water, the overlying water height was brought to at least 10 cm, and air stones and a stirring lid (central Teflon-coated magnet stirrer) with sampling ports were used to keep the water oxygenated. The sediment cores were left to acclimatize for 24 to 48 h before starting the irrigation experiment. For the irrigation measurements, a stock solution of 1 mg L−1 uranine (sodium fluoresceine – ) was prepared by dissolving 1 mg of uranine salts into 1 L of 0.45 µm filtered Oosterschelde water. Short experiments were performed to assess possible interactions between the tracer and the incubation cores and stirring devices (Supplement). To start the experiment, 30 to 40 mL of the stock solution was added to the overlying water to achieve a starting concentration of uranine of about 10 µg L−1. The concentration of the fluorescent tracer was subsequently measured every 30 s for a period of at least 12 h with a fluorometer (Turner Designs Cyclops-6) placed in the water column through a sampling port in the stirring lid of the core, ±6 cm below the water surface. After the measurement, the sediment was sieved over a 1 mm sieve and the macrofauna was collected and stored in 4 % buffered formalin for species identification and abundance and biomass determination.
Sediment grain size was determined by laser diffraction on freeze-dried and sieved (<1 mm) sediment samples in a Malvern Mastersizer 2000 (McCave et al., 1986). Water content was determined as the volume of water removed by freeze-drying wet sediment samples. Sediment porosity was determined from water content and solid-phase density measurements, accounting for the salt content of the pore water. Chl a was extracted from the freeze-dried sediment sample using acetone and quantified through UV spectrophotometry (Ritchie, 2006). The C / N ratio was calculated from total C and N concentrations, determined using an Interscience Flash 2000 organic element analyzer.
2.2 Model
The exchange of a tracer (T) between the sediment and the overlying water is described in a (vertical) one-dimensional mechanistic model that includes molecular diffusion, adsorption to sediment particles and bioirrigation. The bioirrigation is implemented as a nonlocal exchange in which a pumping rate (r) exponentially decays with distance from the sediment surface (z). This exponential decay mimics the depth-dependent distribution of faunal biomass often found in sediments (Morys et al., 2017) and the associated decreasing number of burrow cross sections with depth (Martin and Banta, 1992; Furukawa et al., 2001).
The mass balance for a dissolved tracer (T; Eq. 1) and the adsorbed tracer (A; Eq. 2) in an incubated sediment with height hS, at a given depth (z; cm) and time (t; hours) in the sediment is
In this equation, φz is sediment porosity (–) and ρ is sediment density (g cm−3).
In the equation for T (Eq. 1), the first term represents transport due to molecular diffusion, where Ds is the sediment diffusion coefficient (cm2 h−1). The second term represents the exchange of tracer between the water column (TOW) and any sediment depth z due to irrigation, where the exchange rate decreases exponentially as modulated by the attenuation coefficient a (cm−1). The exponential term is scaled with the integrated value, so the exchange rate r reflects the total rate of bioirrigation, expressed in centimeters per hour.
The loss term for the tracer by adsorption (third term) depends on the deviation from the local equilibrium of the tracer with the actual adsorbed fraction on the sediment and with parameters k (h−1); the rate of adsorption; and EqA, the adsorption equilibrium (mL g−1).
The dissolved tracer concentration in the water column (TOW; Eq. 3) decreases by the diffusive flux into the sediment and the integrated irrigation flux, corrected for the thickness of the overlying water (hOW; cm):
The concentration of A in the overlying water equals 0.
The model was implemented in Fortran and integrated using the ode.1D solver from the R package deSolve (Soetaert et al., 2010; R Core Team, 2013). The sediment was subdivided into 50 layers; the thickness of the first layer was set equal to 0.5 mm and then exponentially increased until the total sediment modeled was equal to the sediment height in each laboratory experiment.
2.3 Model fitting
Most of the input parameters of the model were constrained by physical measurements. Sediment porosity ϕ and specific density ρ (g cm−3) were derived from sediment samples taken alongside the cores in the field. The adsorption equilibrium EqA (in mL g−1) was determined from batch adsorption experiments (see Supplement). The modeled sediment height (hS) and water column height (hOW) were set equal to the experimental conditions. This left two parameters governing the bioirrigation rate to be estimated by model fitting: r, the integrated pumping rate, and a, the attenuation coefficient. Fitting of the model to the experimental data was carried out with the R package FME (Soetaert and Petzoldt, 2010). First an identifiability analysis was performed to investigate the certainty with which these parameters could be derived from model fitting given the experimental data. This entails a local sensitivity analysis to quantify the relative effects of said parameters on model output and a collinearity analysis to test whether parameters were critically correlated, and thus not separately identifiable or the opposite. Then both parameters were estimated by fitting the model to each individual tracer time series through minimization of the model cost (the weighted sum of squares) using the pseudorandom search algorithm (Price, 1977) followed by the Levenberg–Marquardt algorithm. Lastly, a sensitivity analysis was performed to calculate confidence bands around the model output, based on the parameter covariance matrix derived from the fitting procedure (Soetaert and Petzoldt, 2010).
2.4 Calculation of IPc and BPc
The retrieved benthic macrofauna were identified down to the lowest-possible taxonomic level and counted, and their ash-free dry weight (gAFDW m−2) was converted from blotted wet weight according to Sistermans et al. (2006). Based on the species abundance and biomass, the irrigation potential of the benthic community in a sediment core (IPc; Eq. 4) was calculated as described in Wrede et al. (2018):
in which Bi represents the biomass (gAFDW m−2); Ai the abundance (ind. m−2) of species i in the core; and BTi, FTi and IDi are descriptive numerical scores for the species burrowing type, feeding type and injection pocket depth, respectively. The values for FTi, BTi and IDi were the same as those applied by Wrede et al. (2018). If not available, values were assigned based on the closest taxonomic relative, with possible adjustments to correct for size differences and feeding type as taxonomic relation is not always a measure of similarity in traits.
The community bioturbation potential (BPc; Eq. 5) was calculated as described in Solan et al. (2004):
with Mi the mobility score and Ri the reworking score for species i from Queirós et al. (2013). Note that the biomass B in this case is the blotted wet weight of the organisms.
2.5 Data analysis
Differences in model-derived pumping rates r and attenuation coefficient a between subtidal and intertidal areas were tested using a two-sided t test (using a significance level of 0.05). For further multivariate analysis, species densities, biomass and estimated irrigation parameters were averaged per station and per season (Fig. 2) since not all six stations were sampled on the same date. The patterns in abiotic conditions, species composition and bioirrigation rates were analyzed using ordination techniques for multivariate datasets, as described in Thioulouse et al. (2018), and implemented in the ade4 R package (Dray and Dufour, 2007). In this procedure, a coinertia analysis and permutation first tests the null hypothesis that there is no significant relationship between environmental variables and species densities, and then the correlation of the bioirrigation rates to the environment–species data is assessed. In a first step, the species data matrix was processed by centered principle component analysis (PCA). For this the species' relative densities were used to emphasize the specific functional role of some species within the communities (Beauchard et al., 2017) and to reduce the effects of heavy outliers. Secondly the environmental-variable matrix was processed by multiple correspondence analysis (MCA; Tenenhaus and Young, 1985). This technique can account for nonlinear relationships between variables but requires all variables to be categorical. Sediments were categorized based on grain size according to the Udden–Wentworth scale (Wentworth, 1922) of silt (<63 µm), very fine sand (>63, <125 µm) and fine sand (>125, <250 µm); the Chl a content was categorized to distinguish between sites with low (<8 µg g−1), intermediate (8–16 µg g−1) and high (> 16 µg g−1) chlorophyll content. Two abiotic variables were already categorical: habitat type (intertidal versus subtidal) and season. Sediment porosity and the C / N ratio were not used in the analysis given the small range within these data (Table 2). In a third step, the two ordinations were combined in a coinertia analysis (CoIA; Dray et al., 2003) to explore the costructure between the species and the environmental variables. The significance of the overall relationship (the costructure of species and environment) between the two matrices was tested by a Monte Carlo procedure based on 999 random permutations of the row matrices (Heo and Gabriel, 1998). Finally, the correlations between the response variables relating to irrigation (estimated irrigation parameters, calculated IPc, BPc) and the two axes of the coinertia analysis were assessed using the Pearson correlation coefficient assuming a significance level of 0.05. Results are expressed as mean ±SD.
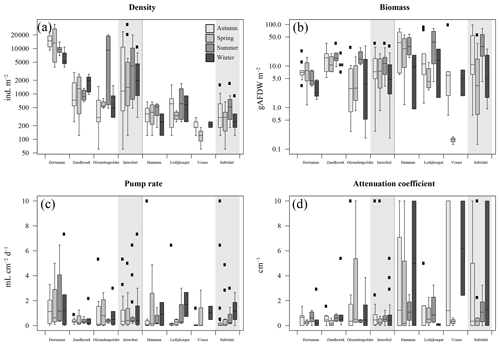
Figure 2(a) Organism densities (ind. m−2); (b) organism biomass as ash-free dry weight (gAFDW m−2); (c) model-derived pumping rate (mL cm−2 d−1); (d) model-derived attenuation coefficient (cm−1). Data arranged per station (white areas) and per habitat type, intertidal and subtidal (grey shaded areas). Black squares are outliers.
3.1 Environmental variables
Sediment descriptors are summarized in Table 2. Chlorophyll a concentrations in the upper 2 cm of the sediment varied from 3.76±2.43 µg g−1 in Hammen to 20.60±4.19 µg g−1 in Zandkreek and were higher in the intertidal (13.34±6.53 µg g−1) than in the subtidal (5.88±4.20 µg g−1) areas. In the intertidal areas, the median grain size (d50) and silt content ranged from 59 µm with 52 % silt to 140 µm with 0 % silt. In the subtidal the range in grain size was broader, from 53 µm with 63 % silt to 201 µm with 24 % silt. The C / N ratio (mol mol−1) was similar for all sites (9.3±1.0–12.3±1.4) with the exception of Dortsman, where values were lower (6.5±1.2). Dortsman was also the site where the organic carbon content was lowest (0.07±0.02 %). The organic carbon content increased with silt content to the highest values in the most silty station, Viane (1.16±0.36 %).
3.2 Macrofauna
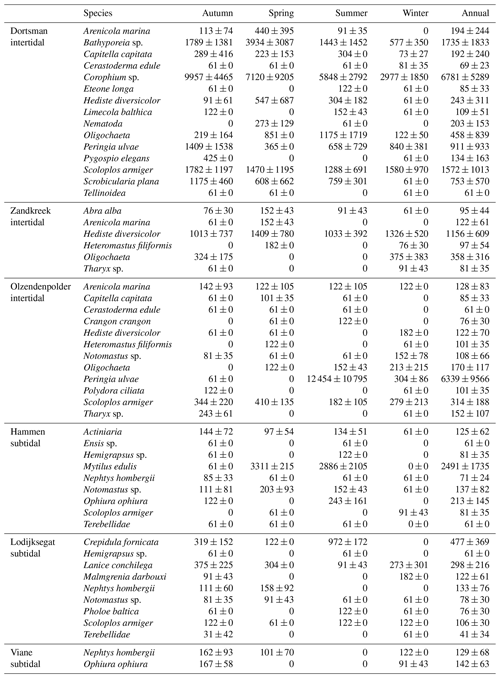
In total, 60 species were identified in the six different stations (Table 3). Species abundances in the intertidal areas were generally 1, sometimes 2, orders of magnitude higher than in the subtidal areas (see Fig. 2a and b for seasonal species density and biomass data). In the intertidal areas, maximum abundances were observed in Dortsman in autumn and spring, with peak values of 15 202 ± 4863 and 16 054 ± 13 939 ind. m−2, respectively, mainly due to high abundances of the amphipods Corophium sp. and Bathyporeia sp. (respective peak values of 9957±4465 and 3934±3087 ind. m−2). Subtidal densities varied less and were highest in Lodijksegat in autumn and summer (peak values of 661±502 and 790±678 ind. m−2, respectively). Faunal biomass was larger in the subtidal areas (22.31±26.42 gAFDW m−2), as opposed to the intertidal areas (10.51±8.59 gAFDW m−2), with peak summer values at the subtidal Lodijksegat station (39.90±34.87 gAFDW m−2) coinciding with high abundances (972±172 ind. m−2) of the common slipper limpet Crepidula fornicata (Linnaeus, 1758).
3.3 Bioirrigation rates
A typical time series of uranine concentrations shows the tracer to exponentially decrease towards a steady value (Fig. 3a). The pumping rate and irrigation attenuation (parameters r and a) have an opposite effect on tracer concentrations in the overlying water, but a collinearity analysis (Soetaert and Petzoldt, 2010) showed that these two parameters could be fitted simultaneously. The attenuation coefficient a affects the depth of the sediment which is irrigated, with larger values of a resulting in shallower bioirrigation. Higher pumping rates, r, entail a faster removal of the tracer from the water. Compared to the parameters r and a, the rate of adsorption, k, had a 1000-fold weaker effect on the outcome. Its value was set to 1 (h−1) implying that it takes about 1 h for the sediment-adsorbed tracer fraction to be in equilibrium with the porewater tracer fraction.
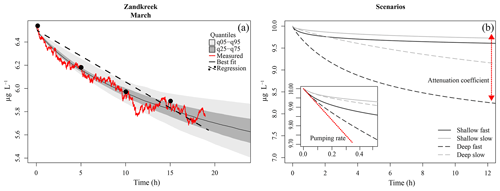
Figure 3(a) Model fit to data (red line) from a core at Zandkreek in March 2017. The best-fit tracer profile (solid black line) is shown, along with the range of model outputs as quantiles (light and dark grey). An example of a linear fit (dashed line) through (fictitious) samples taken every 5 h (dots) is also shown. (b) Example model output for different combinations of pumping rate (slow = 0.15 mL cm−2 h−1; fast = 0.8 mL cm−2 h−1), and attenuation coefficients (shallow = 5 cm−1; deep = 0.5 cm−1). The inset shows a close-up of the first half hour of the simulation. The red line illustrates the effect of the pumping rate, which has the strongest initial effect; the red arrow illustrates the effect of the attenuation coefficient, which determines the depth of the irrigation.
In 11 out of 117 cases the fitting procedure yielded fits for which both the attenuation coefficient a and the pumping rate r were not significantly different from 0 and for which bioirrigation was thus assumed to be absent. These were predominantly observed in November and December (7 out of 11 nonsignificant fits), and in these cases the tracer concentration did not notably change but rather fluctuated around a constant value.
The fitted irrigation rates and attenuation coefficients did not show clear seasonal trends in the intertidal stations (Fig. 2). In the subtidal stations, irrigation rates were lowest in autumn and highest in winter (Fig. 2c). There was no significant difference in irrigation rates between the subtidal (0.547±1.002 mL cm−2 h−1) and intertidal (0.850±1.157 mL cm−2 h−1) stations (Welch two-sample t test; p=0.708). Seasonally averaged irrigation rates were highest at Lodijksegat in winter (1.693±1.375 mL cm−2 h−1), whereas in autumn at that same station they were lowest (0.091±0.078 mL cm−2 h−1). The model-derived attenuation coefficients were significantly higher in the subtidal (2.387±3.552 cm−1) than in the intertidal (0.929±1.793 cm−1) stations (Welch two-sample t test; p=0.041).
3.4 Coinertia analysis
The first and second axes of the coinertia analysis (CoiA) explained 57 % and 19 % of the variance in the dataset, respectively (histogram inset Fig. 4a). The Monte Carlo permutation test resulted in a significant RV coefficient (the multivariate generalization of the squared Pearson correlation coefficient) of 0.62 (p<0.001), showing that the species data and the environmental data are significantly correlated. Both the first and second axes of the MCA performed on the environmental parameters and of the PCA performed on the species community were correlated, indicated by high Pearson correlation coefficients (see Fig. 4 for a summary of the CoIA). Figure 4a shows the costructure between abiotic samples (circles) and species samples (arrow tips); grey circles D, O and Z are for intertidal sites Dortsman, Olzendenpolder and Zandkreek, respectively; white circles H, L and V are for subtidal sites Hammen, Lodijksegat and Viane, respectively. Arrow length corresponds to the dissimilarity between the abiotic data and the species data (the larger the arrow, the larger the dissimilarity). Pearson's correlation on the second axis explains 19 % of the variation in the dataset. Figure 4b shows MCA based on environmental variables. Figure 4c shows species projections (dark arrows) and projected response variables (bioirrigation parameters and bioturbation and bioirrigation index) onto the coinertia axes (grey arrows). The directions of arrows in Fig. 4b and c correspond to the directions in which stations are grouped in terms of abiotic data (circles) and species composition (arrow tips) in Fig. 4a (r=0.92; p<0.001). In the MCA of the environmental variables, the first axis reflected mainly a grain size gradient from very fine sandy to silty (Fig. 4b), with subtidal sites Lodijksegat (L) and Hammen (H) on the very fine sandy end and the intertidal site Zandkreek (Z) on the high-silt end (Fig. 4a). The Chl a content and the immersion type (intertidal vs. subtidal) were the main factors associated with axis 2. This axis separated the subtidal station Viane (V) from the intertidal stations Dortsman (D) and Olzendenpolder (O; Fig. 4a). Of the different seasons, only summer correlated to the second axis. The PCA of the relative species abundances showed that in more fine sandy subtidal stations species such as the reef-forming Mytilus edulis (Linnaeus) and Lanice conchilega (Pallas) were found (Fig. 4c). The species Corophium sp. and Peringia ulvae (Pennant) dominated in the intertidal areas, while Ophiura ophiura (Linnaeus) and Nephtys hombergii (Lamarck) were mainly found in the subtidal areas.
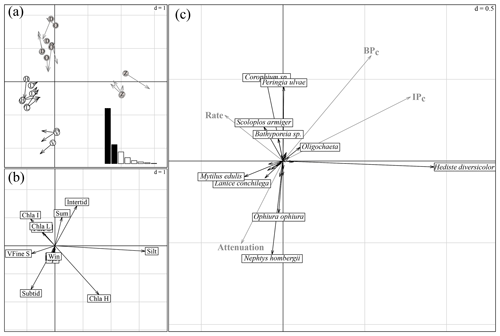
Figure 4Summary of the coinertia analysis (CoIA). (a) Costructure between abiotic samples (circles) and species samples (arrow tips); grey circles D, O and Z for intertidal sites Dortsman, Olzendenpolder and Zandkreek, respectively; white circles H, L and V for subtidal sites Hammen, Lodijksegat and Viane, respectively. Arrow length corresponds to the dissimilarity between the abiotic data and the species data (the larger the arrow, the larger the dissimilarity). Pearson's correlation between the circle and arrow tip coordinates on the first axis, r=0.95 and p<0.001, and on the second axis, r=0.92 and p<0.001. Sites are more similar in terms of environmental conditions (circles) or species (arrow tips) when they group more closely together. Inset: eigenvalue diagram of the costructure; first axis explains 57 %, second axis explains 19 % of the variation in the dataset. (b) MCA based on environmental variables. (c) Species projections (dark arrows) and projected response variables (bioirrigation parameters and bioturbation and bioirrigation index) onto the coinertia axes (grey arrows). The directions of arrows in (b) and (c) correspond to the directions in which stations are grouped in terms of abiotic data (circles) and species composition (arrow tips) in (a).
The correlation tests resulted in significant correlations between the first and the second axes of the coinertia analysis (CoiA) with the BPc (axis 1 – r=0.54, p=0.008; axis 2 – r=0.65, ) and between the first CoiA axis and the IPc (axis 1 – r= 0.78, ; Fig. 4c; see Table 5 for full correlation statistics). Values for these indices are highest in the intertidal samples (Dortsman) and lowest in the subtidal, high Chl a samples (Viane), where also, respectively, the highest and lowest species densities were recorded. The attenuation coefficient a was significantly and negatively correlated with the second axis (; p=0.005). The attenuation coefficient increased in the opposite direction of the BPc and IPc indices (Fig. 4c). No significant correlations were found for the model-derived pumping rate r (axis 1 – , p=0.107; axis 2 – r=0.263, ). The pumping rate increased towards the intermediate and low Chl a samples, almost perpendicular to both the IPc and BPc arrows and the attenuation coefficient (Fig. 4c).
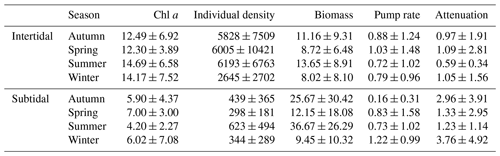
Table 4Seasonally averaged values for Chl a in the upper 2 cm of the sediment (µg Chl a g−1), species density (ind. m−2), biomass (gAFDW m−2), pumping rate (mL cm−2 h−1) and the attenuation coefficient (cm−1) for the intertidal and the subtidal areas.
4.1 Advantages of mechanistic modeling
Bioirrigation is a complex process with profound effects on sediment biogeochemistry (Aller and Aller, 1998; Kristensen, 2001). For a better understanding of how bioirrigation affects the sediment matrix and to construct indices of irrigation based on species composition and life history traits, it is crucial to understand the mechanistic bases of the process. This is the first study in which continuous measurements of a tracer substance and a mechanistic model have been combined to study the bioirrigation behavior of species assemblages across a range of estuarine habitats. In bioirrigation experiments, the tracer concentration in the overlying water decreases as it is diluted through mixing with porewater from the sediment. Initially, the sediment porewater is devoid of tracer, so the dilution of the overlying water concentration is maximal. As the sediment itself becomes charged with tracer, the effect of sediment–water exchange on the bottom-water concentration will decrease until the tracer concentration in the bioirrigated part of the sediment and bottom-water concentration are equal and a quasi-steady state is achieved in which only molecular diffusion further slowly redistributes the tracer in the sediment. This verbal description of a bioirrigation experiment shows that there are two important aspects to the data: the rate of bioirrigation determines the initial decrease of tracer and how quickly the steady state will be reached, while the sediment volume over which bioirrigation occurs determines the difference between initial and ultimate water column tracer concentrations at a steady state.
The 1-D mechanistic model applied to our data comprises both these aspects, which are encompassed in two parameters: the integrated rate of bioirrigation (r) and the attenuation coefficient (a) that determines the irrigation depth. In model simulations, the differences between fast and slow pumping rates mainly manifest themselves in the first part of the time series, while differences in irrigation depths are mainly discernable after several hours (Fig. 3b). This adds nuance to the interpretation of bioirrigation rates, as similar irrigation rates may have divergent effects on sediment biogeochemistry when the depth over which solutes are exchanged differs. We have shown here that this nuance is at play in the Oosterschelde, where model-derived pumping rates are very similar in subtidal and intertidal sediments, but the attenuation coefficient was higher for subtidal sites than for intertidal sites, implying a shallower bioirrigation pattern in the former. It should be noted that, as the incubation chambers contained at most 20 cm of sediment, the effects of individuals living at greater depths (e.g., larger A. marina, or N. latericeus) were not included in the incubations, and thus these were not accounted for in our estimates of bioirrigation. This means that the bioirrigation patterns described are only applicable to the upper 20 cm of the sediment.
Our tracer time series were measured at sufficiently high resolution (0.033 Hz) and for a sufficiently long time so that both the initial decrease and the concentration to which the tracer converges were recorded. Indeed, identifiability analysis, a procedure to discover which model parameters can be estimated from data (Soetaert and Petzoldt, 2010), showed that the information in our data was sufficient to estimate these two parameters (r and a) with high confidence. This represents a significant improvement over discrete tracer measurements, from which deriving information on the depth distribution of irrigation is problematic (Andersson et al., 2006). Other data and/or models may not be able to derive these two quantities. Often bioirrigation is estimated from linear fits through scarce (≤5 measurements) tracer concentration measurements (De Smet et al., 2016; Mestdagh et al., 2018; Wrede et al., 2018). This procedure is mainly applied when bromide is used as a tracer, as concentrations of this substance need to be measured in an elemental analyzer, a procedure which, for practical reasons, does not allow quasi-continuous measurements from the same sample. This has a major drawback, as the linearization of the exponential decrease will clearly underestimate the pumping rates, and it will be influenced by the (unknown) tracer depth (Fig. 3). Indeed, these linear-fit methods are sensitive to the chosen duration of the experiment, and results based on a time series of 6 h will not give the same results as those based on a 12 h measurement.
4.2 Spatiotemporal variability in bioirrigation
Our data show that, although total pumping rates are similar in the subtidal and intertidal sediments of the Oosterschelde, irrigation is shallower in the subtidal sediments, as indicated by the higher attenuation coefficient (Fig. 2c, d). The species community in the subtidal sediments that is responsible for pumping is less dense, but (on average) the biomass is higher than in the intertidal sediments (Table 4). In Viane, the site where bioirrigation is lowest, only two species occur, Ophiura ophiura (Linneaus) and Nephtys hombergii, and neither is typically associated with bioirrigation, although O. ophiura can significantly disturb the sediment surface, inducing shallow irrigation (Fig. 4c). The other two subtidal stations harbor two polychaete species that have been found to be prominent bioirrigators: Lanice conchilega (Lodijksegat) and Notomastus latericeus (Sars; both Lodijksegat and Hammen). The sand mason worm L. conchilega lives in tubes constructed from shell fragments and sand particles which extend down to 10–15 cm (in the study area) and significantly affects the surrounding biogeochemistry (Forster and Graf, 1995; Braeckman et al., 2010). The highest densities of this species were observed in autumn at Lodijksegat, but interestingly this coincided with the lowest bioirrigation values for this station (Table 2; densities are 375±22 ind. m−2; Fig. 2c; bioirrigation is 0.091±0.176 mL cm−2 h−1). High densities of C. fornicata, an epibenthic gastropod, in the same samples may possibly compete with the infauna, suppressing the bioirrigation behavior through constant agitation of the feeding apparatus, similar to what happens in nonlethal predator–prey interactions (Maire et al., 2010; De Smet et al., 2016). C. fornicata is also known to cause significant biodeposition of fine particles on the sediment surface (Ehrhold et al., 1998; Ragueneau et al., 2005). This could decrease the permeability of the surface layers and as such decrease the extent of possible bioirrigation. Burrows of N. latericeus extend down to 40 cm, and they have no lining, which – in theory – would facilitate irrigation. However, the burrows are considered semipermanent, which in turn limits the depth up to which bioirrigation plays a role (Kikuchi, 1987; Holtmann et al., 1996). The presence of these polychaetes is thus not per se translated into high irrigation rates, though there does appear to be a link to the depth over which bioirrigation occurs, with this being deepest in Lodijksegat (lowest a) where the species are present and shallowest in Viane (highest a) which lacks these species.
In the intertidal stations the main species described as bioirrigators are the mud shrimp Corophium sp., the lugworm Arenicola marina (Linnaeus) and the capitellid polychaete Heteromastus filiformis (Claparède). Corophium sp. is an active bioirrigator that lives in lined U-shaped burrows 5 to 10 cm in depth (McCurdy et al., 2000; De Backer et al., 2010). A. marina is often noted as the main bioirrigator and bioturbator in marine intertidal areas (Huettel, 1990; Volkenborn et al., 2007). This species constructs U-shaped burrows of 20 to 40 cm deep and typically injects water to this depth in irrigation bouts of 15 min (Timmermann et al., 2007). H. filiformis creates mucus-lined permanent burrows in sediments up to 30 cm deep (Aller and Yingst, 1985). These species are present in all intertidal sites presented here. High densities of Corophium sp. are found in these where high irrigation rates are measured (Table 2 and Fig. 2; Dortsman, 6781±5289 ind. m−2, bioirrigation rates between 0.942 and 1.149 mL cm−2 h−1).
The higher abundance of previously mentioned bioirrigators in the intertidal, as opposed to the subtidal areas, explains the lower attenuation coefficient values in the intertidal areas. Intertidal areas also experience stronger variations in physical stressors such as waves, temperature, light, salinity and precipitation than subtidal areas do (Herman et al., 2001) and are more subject to biological stressors such as predation by birds (Fleischer, 1983; Granadeiro et al., 2006; Ponsero et al., 2016). Burrowing more deeply or simply residing in deeper sediment layers for a longer time are valid strategies for species in the intertidal areas to combat these pressures (Koo et al., 2007; MacDonald et al., 2014).
4.3 The bioirrigation potential
The community irrigation potential (Eq. 4; Wrede et al., 2018) subsumes both the depth of bioirrigation and the rate. The former is represented by the injection depth (ID), while the latter relates to the burrowing type (BT) and feeding type (FT) of the species' traits scaled with their size and abundance. Interestingly, in the Oosterschelde data, only one of the irrigation parameters correlates to the IPc: the attenuation coefficient (Fig. 4c). This is most likely a consequence of the fact that the IPc index was calibrated using the Br− linear-regression method (Wrede et al., 2018), which may mainly quantify the irrigation depth. Nevertheless, the lack of a relation between the pumping rate and the IPc is surprising, since this index does include traits that are expected to affect the pumping rate and it is scaled for metabolic activity. This suggests that bioirrigation is a process which not only depends on the species characteristics but also includes context-dependent trait modalities that need to be considered.
Functional roles of species may differ depending on the context in which they are evaluated, and the a priori assignment of a species to a functional effect group may therefore be too simplistic (Hale et al., 2014; Murray et al., 2014). Christensen et al. (2000) for instance reported irrigation rates of sediments in Kertinge Nor, Denmark, with high abundances of Hediste diversicolor (O.F. Müller, 1776; 600 ind. m−2 at 15 ∘C) that varied with a factor of 4 depending on whether the organism was suspension feeding (2704±185 L m−2 d−1) or deposit feeding (754±80 L m−2 d−1). In our study, the intertidal station Zandkreek also had very high abundances of H. diversicolor (peak at 2550 ind. m−2 in April) but much lower irrigation rates (128.6±160.6 L m−2 d−1). Possibly, the higher Chl a concentrations in Zandkreek (20.2 µg gDW−1) compared to the sediment in Christensen et al. (2000; ±7 µg gDW−1, converted from µg gWW−1) caused the species to shift even more to deposit feeding. Similarly, previously reported irrigation rates of Lanice conchilega in late summer were quantified to range between 26.45 and 33.55 L m−2 d−1 (3243±1094 ind. m−2), in an intertidal area in Boulogne-sur-Mer, France (De Smet et al., 2016), whereas we measured rates that were more than an order of magnitude higher in the same season (229.3±327.8 L m−2 d−1; Fig. 2c), although densities were an order of magnitude lower (298±216 ind. m−2). Lanice conchilega is also known to switch from suspension feeding to deposit feeding when densities are lower (Buhr, 1976; Buhr and Winter, 1977). This suggests that bioirrigation activity is higher when the L. conchilega is deposit feeding, although there could be of course additional context-dependent factors at play.
The species community in which an organism occurs can also affect the bioirrigation behavior. Species regularly compete for the same source of food (e.g., filter feeders), with species changing their feeding mode to escape competitive pressure (Miron et al., 1992). Species also compete in the form of predator–prey interactions that have also been shown to alter behavior. For example, the presence of Crangon crangon has been shown to reduce the food uptake of L. conchilega (De Smet et al., 2016) and alter the sediment-reworking mode of L. balthica (Maire et al., 2010), in both cases because C. crangon preys on the feeding apparatus of these species protruding from the sediment. If bioirrigation is to provide oxygen or to reduce the buildup of metabolites, then, given sufficient densities of other bioirrigating organisms, oxygen halos may overlap (Dornhoffer et al., 2012), reducing the need for individuals to pump. In Zandkreek for instance, Arenicola marina (Linnaeus, 1758) was present in many samples, except during summer and autumn (Fig. 2b), while Hediste diversicolor was present in constant densities throughout the year. Although A. marina is a very vigorous bioirrigator, its presence did not lead to a doubled pumping rate, suggesting an adaptation of the ventilation behavior to the activity of H. diversicolor, or vice versa. This implies that simply summing individual species' irrigation scores to obtain a bioirrigation rate may be too simplistic.
With these considerations in mind it appears that a comprehensive understanding of the ecology of species at the appropriate spatial scale and within the appropriate environmental context is a prerequisite for the application of an index to predict bioirrigation rates (and by extension other functional traits). The current index (Eq. 4) contains burrow type, feeding mode, burrow depth and an exponent to scale the metabolic rate, but from our analysis it appears that introducing more context dependency could improve results. In Renz et al. (2018) for example, a distinction was made between an organism's activity based on the sediment type in which it occurred (cohesive or permeable sediment) in the calculation of their index, the community bioirrigation potential (BIPc), although no comparison with measured irrigation rates has taken place. Furthermore, Wrede et al. (2018) suggested including a temperature correction factor (Q10) in the calculations to account for the expected metabolic response of macrofauna to increasing water temperatures (Brey, 2010). This temperature effect on benthic activity has indeed been noticed in similar works (Magni and Montani, 2006; Rao et al., 2014), but in our study and others the highest temperatures were not clearly associated with the highest functional process rates (Schlüter et al., 2000; Braeckman et al., 2010; Queirios et al., 2015). The reasons for this ranged from a noncoincidence of the annual food pulse and the temperature peak to the presence of confounding factors in the analysis such as faunal abundances and behavior (Forster et al., 2003).
Based on the above, we stress the importance of measuring bioirrigation rates in field settings, as it is through repeated measurements that the complex interactions of species communities and their environment will be best understood.
By fitting fluorescent tracer measurements using a mechanistic model we were able to infer more detailed information on the bioirrigation process in species communities than we would by an exchange rate alone, thereby improving on linear-regression techniques. Benthic organisms differ strongly in the magnitude and mode in which they express functional traits. With this study we aimed to determine whether bioirrigation can be predicted by an index of bioirrigation, calculated based on functional traits. This index was correlated to the attenuation coefficient but not the bioirrigation rate. Our findings also highlight the importance of the context in which indices for functional processes should be evaluated, because of the confounding roles of environmental conditions and behavior. Different species assemblages can have the same bioirrigation rates but differ in the sediment depth over which they exchange solutes. This is important to consider when implementing bioirrigation in models of sediment biogeochemistry.
Model code will be made available on request to the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-1701-2020-supplement.
EDB developed the model, performed model simulations and statistical analysis, and prepared the manuscript with contributions from all coauthors. JT collected field data, performed measurements and analyzed macrofauna. UB and TY contributed to the manuscript. KS developed and implemented the model and contributed to the manuscript.
The authors declare that they have no conflict of interest.
Emil De Borger is a doctoral research fellow funded by the Belgian Federal Science Policy Office (BELSPO), contract BR/154/A1/FaCE-It. Justin Tiano is a doctoral research fellow funded by the European Maritime and Fisheries Fund (EMFF) and the Netherlands Ministry of Agriculture, Nature and Food Quality (LNV; grant no. 1300021172). Ulrike Braeckman is a postdoctoral research fellow at Research Foundation – Flanders (FWO; grant no. 1201716N). We thank the field technicians and laboratory staff, Pieter Van Rijswijk, Peter van Breugel and Yvonne van der Maas, as well as students that assisted with the processing of samples, Paula Neijenhuis, Jolien Buyse and Vera Baerends. For help with the ordination methods we thank Olivier Beauchard. Lastly we thank the crew of the research vessel Delta.
This research has been supported by BELSPO (contract BR/154/A1/FaCE-It), the EMFF and the Netherlands LNV (grant no. 1300021172), and the FWO (grant no. 1201716N).
This paper was edited by Perran Cook and reviewed by two anonymous referees.
Aller, R. C.: Quantifying solute distributions in the bioturbated zone of marine sediments by defining an average microenvironment, Geochim. Cosmochim. Ac., 44, 1955–1965, https://doi.org/10.1016/0016-7037(80)90195-7, 1980.
Aller, R. C.: The importance of the diffusive permeability of animal burrow linings in determining marine sediment chemistry, J. Mar. Res., 41, 299–322, https://doi.org/10.1357/002224083788520225, 1983.
Aller, R. C. and Aller, J. Y.: Meiofauna and solute transport in marine muds, Limnol. Oceanogr., 37, 1018–1033, https://doi.org/10.4319/lo.1992.37.5.1018, 1992.
Aller, R. C. and Aller, J. Y.: The effect of biogenic irrigation intensity and solute exchange on diagenetic reaction rates in marine sediments, J. Mar. Res., 56, 905–936, https://doi.org/10.1357/002224098321667413, 1998.
Aller, R. C. and Yingst, J. Y.: Effects of the marine deposit-feeders Heteromastus filiformis (Polychaeta), Macoma balthica (Bivalvia), and Tellina texana (Bivalvia) on averaged sedimentary solute transport, reaction rates, and microbial distributions, J. Mar. Res., 43, 615–645, https://doi.org/10.1357/002224085788440349, 1985.
Andersson, J. H., Middelburg, J. J., and Soetaert, K.: Identifiability and uncertainty analysis of bio-irrigation rates, J. Mar. Res., 64, 407–429, https://doi.org/10.1357/002224006778189590, 2006.
Beauchard, O., Veríssimo, H., Queirós, A. M., and Herman, P. M. J.: The use of multiple biological traits in marine community ecology and its potential in ecological indicator development, Ecol. Indic., 76, 81–96, https://doi.org/10.1016/j.ecolind.2017.01.011, 2017.
Berelson, W. M., Heggie, D., Longmore, A., Kilgore, T., Nicholson, G., and Skyring, G.: Benthic Nutrient Recycling in Port Phillip Bay, Australia, Estuar. Coast. Shelf S., 46, 917–934, https://doi.org/10.1006/ecss.1998.0328, 1998.
Berg, P., Rysgaard, S., Funch, P., and Sejr, M. K.: Effects of bioturbation on solutes and solids in marine sediments, Aquat. Microb. Ecol., 26, 81–94, https://doi.org/10.3354/ame026081, 2001.
Braeckman, U., Provoost, P., Gribsholt, B., Van Gansbeke, D., Middelburg, J. J., Soetaert, K., Vincx, M., and Vanaverbeke, J.: Role of macrofauna functional traits and density in biogeochemical fluxes and bioturbation, Mar. Ecol.-Prog. Ser., 399, 173–186, https://doi.org/10.3354/meps08336, 2010.
Braeckman, U., Van Colen, C., Soetaert, K., Vincx, M., and Vanaverbeke, J.: Contrasting macrobenthic activities differentially affect nematode density and diversity in a shallow subtidal marine sediment, Mar. Ecol.-Prog. Ser., 422, 179–191, https://doi.org/10.3354/meps08910, 2011.
Brey, T.: An empirical model for estimating aquatic invertebrate respiration, Methods Ecol. Evol., 1, 92–101, https://doi.org/10.1111/j.2041-210x.2009.00008.x, 2010.
Buhr, K.-J.: Suspension-feeding and assimilation efficiency in Lanice conchilega (Polychaeta), Mar. Biol., 38, 373–383, https://doi.org/10.1007/BF00391377, 1976.
Buhr, K.-J. and Winter, J. E.: Distribution and Maintenance of a Lanice Conchilega Association in the Weser Estuary (Frg), With Special Reference To the Suspension – Feeding Behaviour of Lanice Conchilega, Pergamon Press Ltd., Oxford, 1977.
Christensen, B., Vedel, A., and Kristensen, E.: Carbon and nitrogen fluxes in sediment inhabited by suspension-feeding (Nereis diversicolor) and non-suspension-feeding (N. virens) polychaetes, Mar. Ecol.-Prog. Ser., 192, 203–217, https://doi.org/10.3354/meps192203, 2000.
Craeymeersch, J., Kingston, P., Rachor, E., Duineveld, G., Heip, C., and Vanden Berghe, E.: North Sea Benthos Survey, available at: http://ipt.vliz.be/eurobis/resource?r=nsbs (last access: 27 March 2020), 1986.
D'Andrea, A. F. and DeWitt, T. H.: Geochemical ecosystem engineering by the mud shrimp Upogebia pugettensis (Crustacea: Thalassinidae) in Yaquina Bay, Oregon: Density-dependent effects on organic matter remineralization and nutrient cycling, Limnol. Oceanogr., 54, 1911–1932, https://doi.org/10.4319/lo.2009.54.6.1911, 2009.
De Backer, A., van Ael, E., Vincx, M., and Degraer, S.: Behaviour and time allocation of the mud shrimp, Corophium volutator, during the tidal cycle: A laboratory study, Helgoland Mar. Res., 64, 63–67, https://doi.org/10.1007/s10152-009-0167-6, 2010.
Degraer, S., Wittoeck, J., Appeltans, W., Cooreman, K., Deprez, T., Hillewaert, H., Hostens, K., Mees, J., Vanden Berghe, E., and Vincx, M.: Macrobel: Long term trends in the macrobenthos of the Belgian Continental Shelf. Oostende, Belgium, available at: http://www.vliz.be/vmdcdata/macrobel/ (last access: 21 July 2019), 2006.
De Smet, B., Braeckman, U., Soetaert, K., Vincx, M., and Vanaverbeke, J.: Predator effects on the feeding and bioirrigation activity of ecosystem-engineered Lanice conchilega reefs, J. Exp. Mar. Biol. Ecol., 475, 31–37, https://doi.org/10.1016/j.jembe.2015.11.005, 2016.
Dornhoffer, T., Waldbusser, G. G., and Meile, C.: Burrow patchiness and oxygen fluxes in bioirrigated sediments, J. Exp. Mar. Bio. Ecol., 412, 81–86, https://doi.org/10.1016/j.jembe.2011.11.004, 2012.
Dray, S. and Dufour, A.-B.: The ade4 Package: Implementing the Duality Diagram for Ecologists, J. Stat. Softw., 22, 1–20, https://doi.org/10.18637/jss.v022.i04, 2007.
Dray, S., Chessel, D., and Thioulouse, J.: Co-inertia analysis and the linking of ecological data tables, Ecology, 84, 3078–3089, https://doi.org/10.1890/03-0178, 2003.
Ehrhold, A., Blanchard, M., Auffret, J.-P., and Garlan, T.: Conséquences de la prolifération de la crépidule (Crepidula fornicata) sur l'évolution sédimentaire de la baie du Mont-Saint-Michel (Manche, France), Comptes Rendus l'Académie des Sci. – Ser. IIA – Earth Planet. Sci., 327, 583–588, https://doi.org/10.1016/S1251-8050(99)80111-6, 1998.
Fleischer, R. C.: Relationships between Tidal Oscillations and Ruddy Turnstone Flocking, Foraging, and Vigilance Behavior, Condor, 85, 22–29, https://doi.org/10.2307/1367881, 1983.
Forster, S. and Graf, G.: Impact of irrigation on oxygen flux into the sediment: intermittent pumping by Callianassa subterranea and “piston-pumping” by Lanice conchilega, Mar. Biol., 123, 335–346, https://doi.org/10.1007/BF00353625, 1995.
Forster, S., Khalili, A., and Kitlar, J.: Variation of nonlocal irrigation in a subtidal benthic community, J. Mar. Res., 61, 335–357, https://doi.org/10.1357/002224003322201223, 2003.
Furukawa, Y., Bentley, S. J., and Lavoie, D. L.: Bioirrigation modeling in experimental benthic mesocosms, J. Mar. Res., 59, 417–452, https://doi.org/10.1357/002224001762842262, 2001.
Granadeiro, J. P., Dias, M. P., Martins, R. C., and Palmeirim, J. M.: Variation in numbers and behaviour of waders during the tidal cycle: implications for the use of estuarine sediment flats, Acta Oecol., 29, 293–300, https://doi.org/10.1016/j.actao.2005.11.008, 2006.
Hale, R., Mavrogordato, M. N., Tolhurst, T. J., and Solan, M.: Characterizations of how species mediate ecosystem properties require more comprehensive functional effect descriptors, Sci. Rep., 4, 6463, https://doi.org/10.1038/srep06463, 2014.
Hedman, J. E., Gunnarsson, J. S., Samuelsson, G., and Gilbert, F.: Particle reworking and solute transport by the sediment-living polychaetes Marenzelleria neglecta and Hediste diversicolor, J. Exp. Mar. Bio. Ecol., 407, 294–301, https://doi.org/10.1016/j.jembe.2011.06.026, 2011.
Heo, M. and Gabriel, K. R.: A permutation test of association between configurations by means of the RV coefficient, Commun. Stat. B-Simul., 27, 843–856, https://doi.org/10.1080/03610919808813512, 1998.
Herman, P. M. J., Middelburg, J. J., and Heip, C. H. R.: Benthic community structure and sediment processes on an intertidal flat: Results from the ECOFLAT project, Cont. Shelf Res., 21, 2055–2071, https://doi.org/10.1016/S0278-4343(01)00042-5, 2001.
Holtmann, S. E., Groenewold, A., Schrader, K. H. M., Asjes, J., Craeymeersch, J. A., Duineveld, G. C. A., van Bostelen, A. J., and van der Meer, J.: Atlas of the zoobenthos of the Dutch continental shelf, Ministry of Transport, Public Works and Water Management, Rijswijk, available at: http://www.marinespecies.org/aphia.php?p=taxdetails&id=130644 (last access: 19 July 2019), 1996.
Huettel, M.: Influence of the lugworm Arenicola marina on porewater nutrient profiles of sand flat sediments, Mar. Ecol.-Prog. Ser., 62, 241–248, https://doi.org/10.3354/meps062241, 1990.
Kikuchi, E.: Effects of the brackish deposit-feeding polychaetes Notomastus sp. (Capitellidae) and Neanthes japonica (Izuka) (Nereidae) on sedimentary O2 consumption and CO2 production rates, J. Exp. Mar. Bio. Ecol., 114, 15–25, https://doi.org/10.1016/0022-0981(87)90136-5, 1987.
Koo, B. J., Kwon, K. K., and Hyun, J. H.: Effect of environmental conditions on variation in the sediment-water interface created by complex macrofaunal burrows on a tidal flat, J. Sea Res., 58, 302–312, https://doi.org/10.1016/j.seares.2007.07.002, 2007.
Kristensen, E.: Impact of polychaetes (Nereis spp. and Arenicola marina) on carbon biogeochemistry in coastal marine sediments, Geochem. T., 2, 92–103, https://doi.org/10.1039/b108114d, 2001.
Kristensen, E., Penha-Lopes, G., Delefosse, M., Valdemarsen, T., Quintana, C. O., and Banta, G. T.: What is bioturbation? the need for a precise definition for fauna in aquatic sciences, Mar. Ecol.-Prog. Ser., 446, 285–302, https://doi.org/10.3354/meps09506, 2012.
MacDonald, E. C., Frost, E. H., MacNeil, S. M., Hamilton, D. J., and Barbeau, M. A.: Behavioral response of Corophium volutator to shorebird predation in the upper bay of Fundy, Canada, PLoS One, 9, e110633, https://doi.org/10.1371/journal.pone.0110633, 2014.
Magni, P. and Montani, S.: Seasonal patterns of pore-water nutrients, benthic chlorophyll a and sedimentary AVS in a macrobenthos-rich tidal flat, Hydrobiologia, 571, 297–311, https://doi.org/10.1007/s10750-006-0242-9, 2006.
Maire, O., Merchant, J. N., Bulling, M., Teal, L. R., Grémare, A., Duchêne, J. C., and Solan, M.: Indirect effects of non-lethal predation on bivalve activity and sediment reworking, J. Exp. Mar. Bio. Ecol., 395, 30–36, https://doi.org/10.1016/j.jembe.2010.08.004, 2010.
Martin, W. R. and Banta, G. T.: The measurement of sediment irrigation rates: A comparison of the Br-tracer and 222Rn∕226Ra disequilibrum techniques, J. Mar. Res., 50, 125–154, https://doi.org/10.1357/002224092784797737, 1992.
McCave, I. N., Bryant, R. J., Cook, H. F., and Coughanowr, C. A.: Evaluation of a laser-diffraction-size analyzer for use with natural sediments, J. Sediment. Res., 56, 561–564, https://doi.org/10.1306/212f89cc-2b24-11d7-8648000102c1865d, 1986.
McCurdy, D. G., Boates, J. S., and Forbes, M. R.: Reproductive synchrony in the intertidal amphipod Corophium volutator, Oikos, 88, 301–308, https://doi.org/10.1034/j.1600-0706.2000.880208.x, 2000.
Mestdagh, S., Bagaço, L., Braeckman, U., Ysebaert, T., De Smet, B., Moens, T., and Van Colen, C.: Functional trait responses to sediment deposition reduce macrofauna-mediated ecosystem functioning in an estuarine mudflat, Biogeosciences, 15, 2587–2599, https://doi.org/10.5194/bg-15-2587-2018, 2018.
Meysman, F. J. R., Galaktionov, O. S., and Middelburg, J. J.: Irrigation patterns in permeable sediments induced by burrow ventilation: A case study of Arenicola marina, Mar. Ecol.-Prog. Ser., 303, 195–212, https://doi.org/10.3354/meps303195, 2005.
Meysman, F. J. R., Galaktionov, O. S., Gribsholt, B., and Middelburg, J. J.: Bio-irrigation in permeable sediments: An assessment of model complexity, J. Mar. Res., 64, 589–627, https://doi.org/10.1357/002224006778715757, 2006.
Miron, G., Desrosiers, G., Retière, C., and Masson, S.: Variations in time budget of the polychaete Nereis virens as a function of density and acclimation after introduction to a new burrow, Mar. Biol., 114, 41–48, 1992.
Morys, C., Powilleit, M., and Forster, S.: Bioturbation in relation to the depth distribution of macrozoobenthos in the southwestern Baltic Sea, Mar. Ecol.-Prog. Ser., 579, 19–36, https://doi.org/10.3354/meps12236, 2017.
Murray, F., Douglas, A., and Solan, M.: Species that share traits do not necessarily form distinct and universally applicable functional effect groups, Mar. Ecol.-Prog. Ser., 516, 23–34, https://doi.org/10.3354/meps11020, 2014.
Na, T., Gribsholt, B., Galaktionov, O. S., Lee, T., and Meysman, F. J. R.: Influence of advective bio-irrigation on carbon and nitrogen cycling in sandy sediments, J. Mar. Res., 66, 691–722, https://doi.org/10.1357/002224008787536826, 2008.
Nielsen, O. I., Gribsholt, B., Kristensen, E., and Revsbech, N. P.: Microscale distribution of oxygen and nitrate in sediment inhabited by Nereis diversicolor: Spatial patterns and estimated reaction rates, Aquat. Microb. Ecol., 34, 23–32, https://doi.org/10.3354/ame034023, 2004.
Northeast Fisheries Science Center: Benthic Habitat Database, available at: https://catalog.data.gov/dataset/benthic-habitat-database (last access: 19 July 2019), 2018.
Olaffson, E.: Do Macrofauna Structure Meiofauna Assemblages in Marine Soft-Bottoms? A review of Experimental Studies, Vie Milieu, 53, 249–265, 2003.
Ponsero, A., Sturbois, A., Desroy, N., Le Mao, P., Jones, A. and Fournier, J.: How do macrobenthic resources concentrate foraging waders in large megatidal sandflats?, Estuar. Coast. Shelf S., 178, 120–128, https://doi.org/10.1016/j.ecss.2016.05.023, 2016.
Price, W. L.: A controlled random search procedure for global optimisation, Comput, J., 20, 367–370, https://doi.org/10.1093/comjnl/20.4.367, 1977.
Queirós, A. M., Birchenough, S. N. R., Bremner, J., Godbold, J. A., Parker, R. E., Romero-Ramirez, A., Reiss, H., Solan, M., Somerfield, P. J., Van Colen, C., Van Hoey, G., and Widdicombe, S.: A bioturbation classification of European marine infaunal invertebrates, Ecol. Evol., 3, 3958–3985, https://doi.org/10.1002/ece3.769, 2013.
Queirios, A. M., Stephens, N., Cook, R., Ravaglioli, C., Nunes, J., Dashfield, S., Harris, C., Tilstone, G. H., Fishwick, J., Braeckman, U., Somerfield, P. J., and Widdicombe, S.: Can benthic community structure be used to predict the process of bioturbation in real ecosystems?, Prog. Oceanogr., 137, 559–569, https://doi.org/10.1016/j.pocean.2015.04.027, 2015.
Quintana, C. O., Tang, M., and Kristensen, E.: Simultaneous study of particle reworking, irrigation transport and reaction rates in sediment bioturbated by the polychaetes Heteromastus and Marenzelleria, J. Exp. Mar. Biol. Ecol., 352, 392–406, https://doi.org/10.1016/j.jembe.2007.08.015, 2007.
Ragueneau, O., Chauvaud, L., Moriceau, B., Leynaert, A., Thouzeau, G., Donval, A., Le Loc'h, F., and Jean, F.: Biodeposition by an invasive suspension feeder impacts the biogeochemical cycle of Si in a coastal ecosystem (Bay of Brest, France), Biogeochemistry, 75, 19–41, https://doi.org/10.1007/s10533-004-5677-3, 2005.
Rao, A. M. F., Malkin, S. Y., Montserrat, F., and Meysman, F. J. R.: Alkalinity production in intertidal sands intensified by lugworm bioirrigation, Estuar. Coast. Shelf S., 148, 36–47, https://doi.org/10.1016/j.ecss.2014.06.006, 2014.
R Core Team: R: A language and environment for statistical computing, available at: http://www.r-project.org/ (last access: 27 March 2020), 2013.
Renz, J. R., Powilleit, M., Gogina, M., Zettler, M. L., Morys, C., and Forster, S.: Community bioirrigation potential (BIPc), an index to quantify the potential for solute exchange at the sediment-water interface, Mar. Environ. Res., 141, 214–224, https://doi.org/10.1016/j.marenvres.2018.09.013, 2018.
Ritchie, R. J.: Consistent sets of spectrophotometric chlorophyll equations for acetone, methanol and ethanol solvents, Photosynth. Res., 89, 27–41, https://doi.org/10.1007/s11120-006-9065-9, 2006.
Rysgaard, S., Christensen, P. B., Sørensen, M. V., Funch, P., and Berg, P.: Marine meiofauna, carbon and nitrogen mineralization in sandy and soft sediments of Disko Bay, West Greenland, Aquat. Microb. Ecol., 21, 59–71, https://doi.org/10.3354/ame021059, 2000.
Schlüter, M., Sauter, E., Hansen, H. P., and Suess, E.: Seasonal variations of bioirrigation in coastal sediments: Modelling of field data, Geochim. Cosmochim. Ac., 64, 821–834, https://doi.org/10.1016/S0016-7037(99)00375-0, 2000.
Sistermans, W. C. H., Hummel, H., Dekker, A., and Dek, L. A.: Inventarisatie macrofauna Westerschelde Najaar 2005, Centrum voor Estuariene en Mariene Ecologie (NIOO-CEME), Yerseke, 2006.
Soetaert, K. and Petzoldt, T.: Inverse Modelling, Sensitivity and Monte Carlo analysis in R Using PAckage FME, J. Stat. Softw., 33, 1–28, https://doi.org/10.18637/jss.v033.i03, 2010.
Soetaert, K., Petzoldt, T., and Setzer, R. W.: Solving Differential Equations in R : Package deSolve, J. Stat. Softw., 33, 1–25, https://doi.org/10.18637/jss.v033.i09, 2010.
Solan, M., Cardinale, B. J., Downing, A. L., Engelhardt, K. A. M., Ruesink, J. L., and Srivastava, D. S.: Extinction and Ecosystem Funciton in the Marine Benthos, Science, 306, 1177–1180, https://doi.org/10.1126/science.1103960, 2004.
Tenenhaus, M. and Young, F. W.: An analysis and synthesis of multiple correspondence analysis, optimal scaling, dual scaling, homogeneity analysis and other methods for quantifying categorical multivariate data, Psychometrika, 50, 91–119, https://doi.org/10.1007/BF02294151, 1985.
Thioulouse, J., Dray, S., Dufour, A.-B., Siberchicot, A., Jombart, T., and Pavoine, S.: Multivariate Analysis of Ecological Data, 1st Edn., Springer-Verlag New York, New York, 2018.
Timmermann, K., Banta, G. T., and Glud, R. N.: Linking Arenicola marina irrigation behavior to oxygen transport and dynamics in sandy sediments, J. Mar. Res., 64, 915–938, https://doi.org/10.1357/002224006779698378, 2007.
Volkenborn, N., Hedtkamp, S. I. C., van Beusekom, J. E. E., and Reise, K.: Effects of bioturbation and bioirrigation by lugworms (Arenicola marina) on physical and chemical sediment properties and implications for intertidal habitat succession, Estuar. Coast. Shelf S., 74, 331–343, https://doi.org/10.1016/j.ecss.2007.05.001, 2007.
Wentworth, C. K.: A Scale of Grade and Class Terms for Clastic Sediments, J. Geol., 30, 377–392, https://doi.org/10.1086/622910, 1922.
Wrede, A., Beermann, J., Dannheim, J., Gutow, L., and Brey, T.: Organism functional traits and ecosystem supporting services – A novel approach to predict bioirrigation, Ecol. Indic., 91, 737–743, https://doi.org/10.1016/j.ecolind.2018.04.026, 2018.