The pH dependency of the boron isotopic composition of diatom opal (Thalassiosira weissflogii)

The high-latitude oceans are key areas of carbon and heat exchange between the atmosphere and the ocean. As such, they are a focus of both modern oceanographic and palaeoclimate research. However, most palaeoclimate proxies that could provide a long-term perspective are based on calcareous organisms, such as foraminifera, that are scarce or entirely absent in deep-sea sediments south of 50^∘ S in the Southern Ocean and north of 40^∘ N in the North Pacific. As a result, proxies need to be developed for the opal-based organisms (e.g. diatoms) found at these high latitudes, which dominate the biogenic sediments recovered from these regions. Here we present a method for the analysis of the boron (B) content and isotopic composition (δ¹¹B) of diatom opal. We apply it for the first time to evaluate the relationship between seawater pH, δ¹¹B and B concentration ([B]) in the frustules of the diatom Thalassiosira weissflogii, cultured across a range of carbon dioxide partial pressure (pCO₂) and pH values. In agreement with existing data, we find that the [B] of the cultured diatom frustules increases with increasing pH (Mejía et al., 2013). δ¹¹B shows a relatively well defined negative trend with increasing pH, completely distinct from any other biomineral previously measured. This relationship not only has implications for the magnitude of the isotopic fractionation that occurs during boron incorporation into opal, but also allows us to explore the potential of the boron-based proxies for palaeo-pH and palaeo-CO₂ reconstruction in high-latitude marine sediments that have, up until now, eluded study due to the lack of suitable carbonate material.

1 Introduction

The high-latitude regions, such as the Southern Ocean and the subarctic North Pacific Ocean, exert key controls on atmospheric carbon dioxide (CO₂) content. Both areas are where upwelling of deep carbon- and nutrient-rich water occurs, which promotes outgassing of previously stored carbon to the atmosphere and nutrient fertilisation of primary productivity, in turn drawing down CO₂. The balance of processes involved in determining whether these oceanic regions are a source or sink of CO₂ is poorly understood, to the extent that the oceanic controls on glacial–interglacial pH and pCO₂ changes remain a subject of vigorous debate (e.g. Martin, 1990; Sigman and Boyle, 2000). Recently, several studies have shown how the boron isotope pH proxy applied to calcitic foraminifera successfully tracks surface water CO₂ content, thus documenting changes in air–sea CO₂ flux along the margins of these regions (e.g. Martínez-Botí et al., 2015; Gray et al. 2018). However, the lack of preserved marine carbonates in areas that are thought to be key in terms of glacial–interglacial CO₂ change (e.g. the polar Antarctic zone; Sigman et al., 2010) represents a currently insurmountable problem, preventing the determination of air–sea CO₂ flux using boron-based proxies in regions that are likely to play the most important role in glacial–interglacial CO₂ change. There is therefore a clear need for the boron isotope palaeo-pH proxy to be developed in biogenic silica (diatom frustules, radiolarian shells), which is preserved in high-latitude settings, to better understand these key regions and their role in natural climate change.

The boron isotopic system has been used extensively in marine carbonates for the reconstruction of past ocean pH and past atmospheric pCO₂ (e.g. Hemming and Hanson, 1992; Pearson and Palmer, 2000; Hönisch and Hemming, 2005; Foster, 2008; Henehan et al., 2013; Chalk et al., 2017; Sosdian et al., 2018). Comprehensive calibration work has been completed for numerous species of foraminifera that are currently used in palaeoceanographic reconstruction (e.g. Henehan et al., 2016; Rae et al., 2011). From this it has been shown that while δ¹¹B compositions are fairly similar among carbonates, species-specific differences exist in the relationship between the δ¹¹B of dissolved borate and that of foraminifera. Once this relationship is known, this δ¹¹B–pH calibration can be applied to fossils found in deep-sea sediment cores, reliably reconstructing past ocean pH and pCO₂ (e.g. Hönisch and Hemming, 2005; Foster, 2008; Hönisch et al., 2009; Chalk et al., 2017). However, thus far the boron isotopic composition (expressed as δ¹¹B) and B concentration ([B]) of the siliceous fraction of deep-sea sediments remain poorly studied.

Early exploratory work by Ishikawa and Nakamura (1993) showed that biogenic silica and diatom ooze collected from modern deep-sea sediments in the North Pacific and equatorial Pacific had relatively high boron contents (70–80 ppm) but a very light isotope ratio. For example, a diatom ooze was shown to have a δ¹¹B of −1.1 ‰ whilst radiolarian shells had a δ¹¹B of +4.5 ‰. While some of this light δ¹¹B may have partly arisen due to clay contamination (reducing the diatom ooze sample by up to 3 ‰; Ishikawa and Nakamura, 1993), it also likely reflects an opal : seawater isotopic fractionation arising from the substitution of borate for silicate in tetrahedral sites in the opal (Ishikawa and Nakamura, 1993). A similarly light δ¹¹B was also observed in marine cherts from deep-sea sediments by Kolodny and Chaussidon (2004; −9.3 to +8 ‰), but these are likely diagenetic and therefore unlikely to be primary seawater precipitates. A recent culture study of the diatoms Thalassiosira weissflogii and T. pseudonana showed that the boron content of cultured opal was significantly lower than suggested by the bulk sampling of Ishikawa and Nakamura (1993) at around 5–10 ppm, increasing as pH increased from 7.6 to 8.7 (Mejía et al., 2013). This suggests the seawater tetrahydroxyborate anion (borate; $\mathrm{B}(\mathrm{OH}{)}_{\mathrm{4}}^{-}$) is predominantly incorporated into the diatom frustule rather than boric acid (B(OH)₃), and it implies there is potential for the boron content of diatom opal to trace pH in the past (Mejía et al., 2013).

Here, the relationship between δ¹¹B of the frustules of the diatom T. weissflogii and seawater pH is investigated for the first time using a batch culturing technique and different air–CO₂ mixtures to explore a range of pH (8.53±0.73 to 7.48±0.08). The aim of this study was also to develop a methodology for measuring the boron isotopic composition of biogenic silica by MC-ICP-MS (multicollector inductively coupled plasma mass spectrometry) and apply this method to explore the response of the boron-based proxies ([B] and δ¹¹B) in diatom frustules to changing pH. Ultimately, we show how boron isotopes measured in diatom frustules may provide further insight into boron uptake and physiological activity within diatoms and test the potential of δ¹¹B and boron content in diatoms as proxies for the ocean carbonate system.

2 Methods

2.1 Experimental setup

The centric diatom T. weissflogii (Grunow in van Heurck, PCC 541, CCAP 1085/1; Hasle and Fryxell, 1977) was grown in triplicate in enriched sterile and filtered seawater (K/1; 0.2 µm; seawater sourced from Labrador Sea; Keller et al., 1987) in 3 L glass Erlenmeyer flasks for a maximum of 1 week for each experiment. Initial nutrient concentrations within the seawater before enrichment were assessed on a SEAL Analytical QuAAtro analyser with a UV–Vis spectrometer and ranged from 23.3 to 27.5 µM for nitrate (+ nitrite), 4.3 to 5.4 µM for silicic acid and 1.4 to 1.6 µM for phosphate. The culture experiments were bubbled with air–CO₂ mixtures in different concentrations (sourced from BOC; https://www.boconline.co.uk, last access: 24 March 2020) to provide a pH range at constant bubble rates, and every flask was agitated by hand twice daily to limit algal settling and aggregation. The monocultures were grown in nutrient-replete conditions at constant temperature (20 ^∘C) and on a 12 h : 12 h light–dark cycle (with 192 µE m⁻² s⁻¹, or 8.3 E m⁻² d⁻¹ during the photoperiod). The diatoms were acclimated to each pCO₂ treatment for at least 10 generations before inoculating the culture experiment flasks. All culture handling was completed within a laminar flow hood to ensure sterility. The flow hood surfaces were cleaned with 90 % ethanol before and after handling, as well as the outer surface of all autoclaved labware entering the laminar flow hood such as bottles and pipettes.

The cultured diatom samples were collected by centrifugation at 96 h, during the exponential growth phase. Each flask was simultaneously disconnected from the gas supply with the culture immediately centrifuged at 3700 rpm for 30 min into a pellet, rinsed with Milli-Q and frozen at −20 ^∘C in sterile plastic 50 mL centrifuge tubes. Around 10 mg of diatom biomass was harvested in each experiment.

2.2 Growth rate and cell size

A 5 mL subsample was taken from each culture flask through sterilised Nalgene tubing into sterile syringes and sealed in sterile 15 mL centrifuge tubes. Triplicate cell counts using a Coulter Multisizer™ 3 (Beckman Coulter) were performed daily on each experimental flask. Growth rates were calculated using Eq. (1):

$$\begin{array}{}\text{(1)}& \mathit{\mu }=(\ln N_t-\ln N_i)/(t-t_i),\end{array}$$

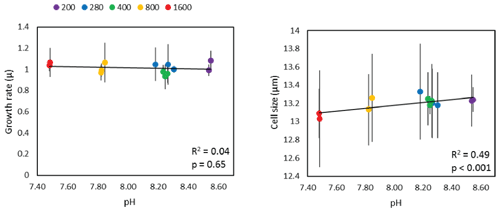
where N_i is the initial cell density at the start of the experiment (t_i) and N_t is the cell density at time t. Triplicate estimates of cell size were also determined using the Coulter Multisizer™ 3 to determine the mean cell size over time in each flask. Figure 1 shows that although there is no statistically significant relationship between pH and diatom growth rate, cell size does show a small, but statistically significant, positive slope.

Figure 1 Diatom growth rate and cell size as a function of pH labelled according to CO₂ treatment. Linear-least-squares regressions, including R² and p values are also shown.

2.3 pH, DIC and δ¹¹B of the culture media

A pH meter (Orion 410A) calibrated using standard National Bureau of Standards (NBS) buffers prior to sample extraction was used to monitor the evolution of pH through the experiment on a daily basis. For fully quantitative constraints on the carbonate system of the culture media, dissolved inorganic carbon (DIC) was measured in triplicate, every other day, for each pH treatment (i.e. once per experiment flask). The 100 mL sample bottles were filled to overflowing and immediately closed with ground glass stoppers, then uncapped to be poisoned with 20 µL saturated mercuric chloride solution (HgCl₂) to prevent any further biologically induced changes in DIC, before being sealed with a 1 mL air headspace and Apiezon L grease, and stored in complete darkness until analysis (Dickson et al., 2007). Analysis of DIC was performed by acidification with excess 10 % phosphoric acid and CO₂ transfer in a nitrogen gas stream to an infrared detector using a DIC analyser AS-C3 (Apollo SciTech, DE, USA) at the University of Southampton. The DIC results were calibrated using measurements of batch 151 certified reference material obtained from A. G. Dickson (Scripps Institution of Oceanography, CA, USA). The accuracy of the DIC analysis was ca. 3 µmol kg⁻¹. Carbonate system parameters, including seawater pCO₂, were calculated using measured pH_NBS and DIC values, temperature, salinity, and nutrients with the CO₂SYS v1.1 program (van Heuven et al., 2011; using constants from Dickson, 1990; Lueker et al., 2000; Lee et al., 2010), which was also used to convert pH meter readings from the NBS to the total scale (used throughout).

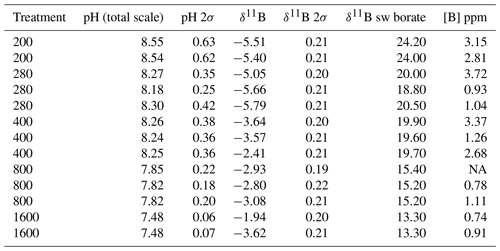
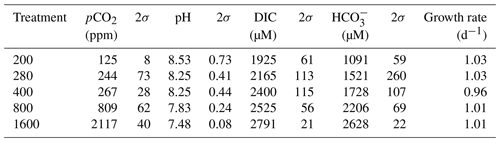
All flasks were initially filled with media from the same large batch, and all culture treatments therefore started with the same initial pH. The pH for all treatments was then altered by bubbling through the different air–CO₂ mixtures, ranging from low pH (target = 1600 ppm, high pCO₂) to high pH (target = 200 ppm, low pCO₂). Almost all treatments held relatively constant DIC and pH until the final 24 h of the experiment, when marked changes in DIC and pH in all culture treatments were observed (Fig. 2), which in most cases was likely due to the growth of diatoms and an associated net removal of DIC, despite the constant addition of pCO₂. In order to account for these non-steady-state conditions of the carbonate system, the mean pH and pCO₂ of each treatment were calculated based on the number of cells grown per 24 h along with the pH/pCO₂ measured in that 24 h, thus adjusting for the observed exponential growth rate of T. weissflogii (Table 1).

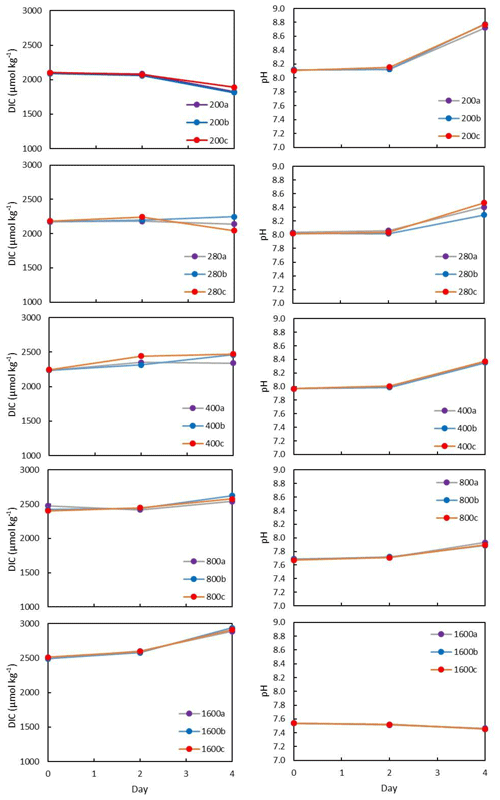
Figure 2 Each culture treatment labelled according to target pCO₂ and showing the evolution in the culture media through the experiment. All treatments exhibit changes in DIC due to diatom growth balanced with the input of CO₂. The higher pCO₂, the more DIC increases towards the end of the experiment.

Table 1 Mean carbonate system parameters experienced under the average growth conditions as calculated for each culture treatment on the basis of the number of cells grown in each 24 h period of the batch experiment.

The boron concentration of the culture media was not determined but is assumed to be the same as Labrador seawater (∼4.5 ppm; Lee et al., 2010). The boron isotopic composition of the culture media was determined using standard approaches (Foster et al., 2010) to be 38.8±0.19 ‰ (2 SD).

2.4 Preparing cultured diatoms for δ¹¹B and B∕Si analysis

In order to examine reproducibility and accuracy of our boron measurements, an in-house diatom reference material was used to develop a method for measuring boron isotopes and boron concentration in biogenic silica. A British Antarctic Survey core catcher sample (TC460) from core TC460 in the Southern Ocean (−60.81534^∘ N, −50.9851^∘ E; water depth 2594 m) was used for this purpose (supplied by Claus-Dieter Hillenbrand, British Antarctic Survey). Although the diatom assemblage was not characterised in the core catcher, the nearest sediment sample in the core is dominated by Hyalochaete Chaetoceros resting spores, representing circa 70 % of the total diatom content, with sea ice and cool open water species making up the bulk of the remaining 30 % (e.g. Actinocyclus actinochilus, Fragilariopsis curta, F. cylindrus, F. obliquecostata, Odontella weissflogii and Thalassiosira antarctica). A pure diatom sample of mixed species was separated from this bulk sediment and cleaned of clay contamination at the University of Nottingham following an established diatom separation technique (Swann et al., 2013). Briefly, the bulk sample underwent organic removal and carbonate dissolution (using 30 % H₂O₂ and 5 % HCl), heavy liquid separation in several steps at different specific gravities using sodium polytungstate (SPT) and visual monitoring throughout the process to ensure the sample was free from non-diatom material, such as clay particulates. After the final SPT separation, samples were rinsed thoroughly with Milli-Q and sieved at 10 µm to remove all SPT traces.

The culture samples and the diatom fraction from TC460 were first acidified (H₂SO₄), and organics were oxidised using potassium permanganate and oxalic acid (following Horn et al., 2011, and Mejía et al., 2013). The samples were rinsed thoroughly using Milli-Q water via centrifugation and transferred to acid-cleaned Teflon beakers. A secondary oxidation was completed under heat using perchloric acid. Finally, the organic-free samples were rinsed thoroughly with Milli-Q via filtration.

In the boron-free HEPA-filtered clean laboratory at the University of Southampton, each sample was dissolved completely in a gravimetrically known amount of NaOH (0.5 M from 10 M concentrated stock supplied by Fluka) at 140 ^∘C for 6 to 12 h and briefly centrifuged prior to boron separation to ensure no insoluble particles were loaded onto the boron column. Anion exchange columns containing Amberlite IRA 743 resin were then used to separate the matrix from the boron fraction of each sample following Foster (2008). Briefly, the dissolved opal was loaded directly onto the column without buffering and the matrix removed with 9×200 µL washes of Milli-Q. This was collected for subsequent analysis, and the pure boron fraction was then eluted and collected in 550 µL of 0.5 M HNO₃ acid. The level of potential contamination was frequently monitored using total procedural blanks (TPBs) measured in every batch of columns. The TPBs comprised an equivalent volume of sodium hydroxide (NaOH, 0.5 M) as used in the samples of each batch (ca. 0.2–4 mL). This was analysed following the sample analysis protocols detailed below; typically the TPBs for this work contained less than 40 pg of boron. This equates to a typical blank contribution of ca. 0.015 %, which results in a negligible correction and is therefore ignored here.

Prior to isotope analysis, all boron fractions were collected in pre-weighed acid-cleaned Teflon beakers, and their mass was recorded using a Precisa balance. A 10 µL aliquot was taken and diluted with 490 µL 0.5 M HNO₃ in acid-cleaned plastic centrifuge tubes (2 mL). This was then analysed using a Thermo Fisher Scientific Element 2XR ICP-MS at the University of Southampton, with boron concentration determined using standard approaches and a gravimetric standard containing boron, silicon, sodium and aluminium. In order to determine the B∕Si ratio and hence the B concentration of the opal, the Si concentration must also be quantitatively measured. This is achieved here by using a known concentration and mass of NaOH to dissolve each sample; by measuring the Si∕Na ratio the Si concentration of each opal sample can be determined. From this, assuming a chemical formula of SiO₂•H₂O and a H₂O content of 8 % (Hendry and Anderson, 2013), the B content of the opal in parts per million can be estimated. As detailed above, during the purification procedure, sample matrix was washed off the column using Milli-Q and collected in pre-weighed acid-cleaned Teflon beakers. These samples were then diluted with 3 % HNO₃ enriched with Be, In and Re for the internal standardisation and measured on the Thermo Scientific XSeries ICP-MS. The standards run on the XSeries consisted of varied concentrations of the gravimetric standard also used on the Element 2XR ICP-MS, containing B, Si, Na and Al.

The boron isotopic composition of the biogenic silica samples was determined on a Thermo Scientific Neptune MC-ICP-MS, also situated in a boron-free HEPA-filtered laboratory at the University of Southampton, following Foster (2008). Instrument-induced fractionation of the ¹¹B∕¹⁰B ratio was corrected using a sample-standard bracketing routine with NIST SRM 951, following Foster (2008). This allows a direct determination of δ¹¹B without recourse to an absolute value for NIST SRM 951 (Foster, 2008) using the following equation, where ¹¹B∕¹⁰B_standard is the mean ¹¹B∕¹⁰B ratio of the standards bracketing the sample of interest.

$$\begin{array}{}\text{(2)}& \mathit{\delta }{}^{\mathrm{11}}\mathrm{B}=\left[\left({\displaystyle \frac{{}^{\mathrm{11}}\mathrm{B}/{}^{\mathrm{10}}{\mathrm{B}}_{\mathrm{sample}}}{{}^{\mathrm{11}}\mathrm{B}/{}^{\mathrm{10}}{\mathrm{B}}_{\mathrm{standard}}}}\right)-\mathrm{1}\right]\times \mathrm{1000}\end{array}$$

The reported δ¹¹B is an average of the two analyses, with each representing a fully independent measurement (i.e. the two measurements did not share blanks or bracketing standards). Machine stability and accuracy was monitored throughout the analytical session using repeats of NIST SRM 951, as well as boric acid reference materials AE120, AE121 and AE122 that gave δ¹¹B (±2 SD) of $-\mathrm{20.19}\pm \mathrm{0.20}$ ‰, 19.60±0.28 ‰ and 39.31±0.28 ‰, which are within the error of the gravimetric values from Vogl and Rosner (2012).

The reproducibilities of the δ¹¹B and [B] measurements were assessed by repeat measurements of TC460 of different total B concentration (11 to 34 ng of B). In order to assess the accuracy of this method, we follow Tipper et al. (2008) and Ni et al. (2010) and use standard addition. To this end, known amounts of NIST SRM 951 standard were mixed with known quantities of TC460. All mixtures were passed through the entire separation and analytical procedure, including aliquots of pure standard and sample. A sodium acetate–acetic acid buffer was added to all 951 boric acid used prior to mixing, to ensure the pH was sufficiently elevated for the column separation procedure (following Foster, 2008). The amount of biogenic silica matrix added to the columns for each mixture was kept constant, so the volume added to the column was altered for each mixture accordingly. Uncertainty in the δ¹¹B calculated for each mixture was determined using a Monte Carlo procedure (n=1000) in R (R Core Team, 2019) propagating uncertainties, at 95 % confidence, in known isotopes ratios (±0.2 ‰), sample concentration (±6 %) and measured masses (±0.5 %).

3 Results and discussion

3.1 Analytical technique

3.1.1 Purification

The Na, Si and Al concentrations of the matrix fraction of several replicates of the diatom fraction of TC460 are shown in Fig. 3a–d. Prior to purification, Na and Si concentrations were consistently around 265 and 114 ppm respectively, whereas Al was more variable at 5–25 ppb. The boron content of these matrix samples in all cases was at the blank level. The concentration of these elements in the boron fraction is shown in Fig. 3e–g, highlighting that the column procedure was sufficient to concentrate boron and remove Na and Si, which are both present at the sub-5 ppb level (i.e. at less than 0.002 % of matrix concentration). The Al is likely present in the diatom frustule (e.g. Koning et al., 2007) and is elevated in the boron fraction compared to the matrix fraction (Fig. 3). Diatom-bound Al is likely present as the anion $\mathrm{Al}(\mathrm{OH}{)}_{\mathrm{4}}^{-}$, hence its elevation in the boron fraction. Although this is a detectable level of Al, it is unlikely that this level of contamination will influence the mass fractionation of these samples when measured by MC-ICP-MS (Foster et al., 2008; Guerrot et al., 2010).

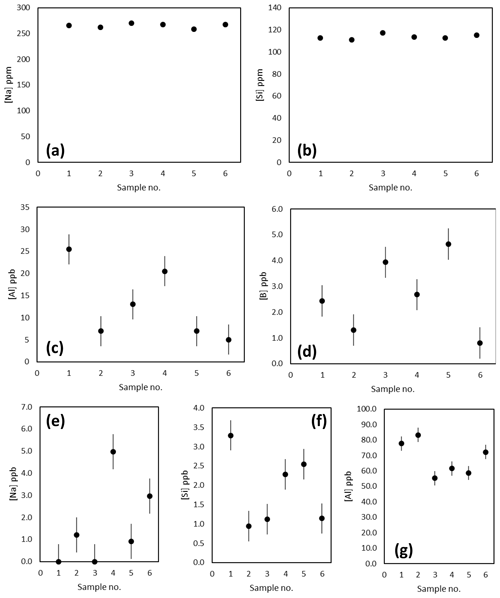
Figure 3 (a–d) Concentration of Na, Si, Al and B in the matrix fraction by ICP-MS. These analyses suggest blank levels of B are present in the matrix washed off the Amberlite IRA 743 resin-based column. (e–f) Concentration of the Na, Si and Al in the boron fraction indicating blank levels of Na (ca. 1.7 ppb) and Si (ca. 1.9 ppb) and a higher concentration of Al (ca. 68 ppb) are present.

3.1.2 Accuracy and reproducibility

Throughout the duration of this study, a single dissolution of the diatom fraction of TC460 was measured 18 times in separate analyses at various concentrations, in order to assess external reproducibility of this method. Carbonates generally have a reproducibility of ±0.20 ‰ (2σ) at an analyte concentration of 50 ppb boron using the MC-ICP-MS methods at the University of Southampton (e.g. Chalk et al., 2017). The repeated measurements of TC460 gave a reproducibility of ±0.28 ‰ (2σ) over 18 samples, ranging from 19 to 61 ppb (11 to 34 ng) boron (Fig. 4). The insensitivity of δ¹¹B to the boron concentration analysed confirms that blank contamination during purification is not significant. Figure 4 shows that there is also no correlation between Al content of the boron fraction and measured δ¹¹B, confirming that Al contamination does not influence mass fractionation.

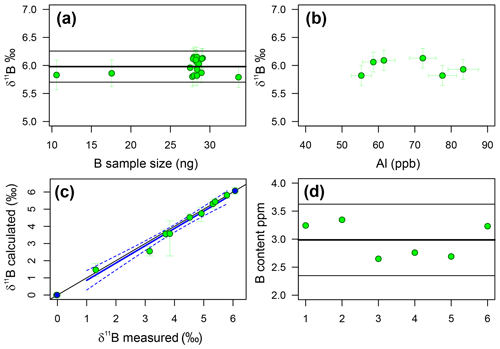
Figure 4 (a) The reproducibility of the TC460 diatom core catcher in-house standard. Samples of different concentration (∼10 to ∼ 30 ng B) lie within error of the mean (5.98 ‰ ± 0.28 ‰, 2σ). This compares well to carbonates (2σ=0.20 ‰). (b) Aluminium concentration of the B fraction from TC460 (as ppb of the solution analysed for δ¹¹B) shows no correlation with δ¹¹B, likely suggesting there is no significant effect on mass fractionation for this level of Al. (c) The results of the standard addition experiment. The blue line is a least-squares regression between the measured δ¹¹B of each mixture (green circles) and the calculated δ¹¹B of that mixture given known endmember values (endmembers shown as blue circles). R²=0.97, p<0.0001, slope = 1.01±0.07 and intercept = $-\mathrm{0.15}\pm \mathrm{0.29}$. The 1 : 1 line is shown as a black line, and dotted blue lines show the 95 % confidence limit of the regression. Note that the endmembers were not used in the regression. (d) B content in parts per million of six repeat samples of the diatom fraction of TC460. The black line indicates the mean value, and the grey lines show 2σ of 2.99±0.64 ppm.

Figure 4 shows the results of the standard addition experiment, and when the uncertainty in the δ¹¹B of the mixture is considered, it is clear that nearly all the mixtures lie within error of the 1 : 1 line, indicating that there is a lack of a significant matrix effect when analysing the δ¹¹B of biogenic silica as described herein. A linear-least-squares regression of the mixtures has a slope of 1.01±0.07 and an intercept of $-\mathrm{0.15}\pm \mathrm{0.29}$ ‰, implying the approach is accurate to ±0.29 ‰, which is remarkably similar to the stated reproducibility of TC460 (±0.28 ‰ at 2σ).

B and Si content were determined separately and combined post-analysis in order to estimate the B∕Si ratio for each sample and hence the B concentration. The reproducibility of this method was tested using six repeats of the diatom fraction of TC460. The mean of all six measurements is 2.99±0.64 ppm; (2σ; Fig. 4), implying this multistage method of determining the B content of diatoms is precise to ±20 % at 95 % confidence.

3.2 Diatom cultures

3.2.1 Boron content of the frustule of T. weissflogii

The boron content of T. weissflogii increases as a function of pH from around ∼1 to ∼4 ppm over a range of average culture pH from 7.5 to 8.6 (Fig. 5; Table 2). While this is lower by an order of magnitude than the limited previous studies of boron in sedimentary diatoms (Ishikawa and Nakamura, 1993), it is similar to boron concentration in the bulk diatom fraction of TC460 (Fig. 4d) and to that observed in previous culturing studies of this diatom species (Fig. 5; Mejía et al., 2013). In detail, however, our concentrations are around 2–3 times lower than Mejía et al. (2013), perhaps due to (i) the different analytical methods used (laser ablation ICP-MS vs. solution here), (ii) differences in cleaning methods and/or (iii) differences in culturing methodology. Despite the scatter between our treatments (also seen in Mejía et al., 2013; Fig. 5), a least-squares regression through the treatments is significant at the 95 % confidence level ($y=\mathrm{2.15}x-\mathrm{15.56}$, R²=0.46, p=0.015; Fig. 5). The cause of this scatter between treatments is not known but a likely contributor is the relatively high variability in the carbonate system which was observed in each treatment due to the growth of the diatoms in our batch culture setup (Fig. 2).

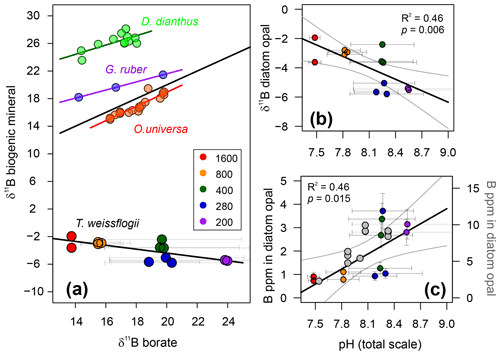
Figure 5 (a) δ¹¹B of T. weissflogii diatom opal plotted against aqueous borate, labelled according to pCO₂ treatment. Also shown are published deep-sea coral Desmophyllum dianthus (Anagnostou et al., 2012) and foraminifera δ¹¹B (Globigerinoides ruber and Orbulina universa; Henehan et al., 2013, 2016, respectively). Least-squares regression lines are also shown. Error bars on δ¹¹B borate are shown at the 95 % confidence level and relate to the drift in experimental conditions. (b) T. weissflogii opal δ¹¹B against pH of each treatment demonstrating a statistically significant negative relationship. Diatom data are labelled according to pCO₂ treatment. (c) Boron content of cultured T. weissflogii diatom opal as a function of pH (using the left y axis), labelled according to pCO₂. A least-squares regression with a 95 % confidence interval is also shown. In grey (and using the right y axis) are data for T. weissflogii from Mejía et al. (2013). Note how both studies show an increase in boron content with increasing pH, but absolute values differ by a factor of 2–3. Uncertainty in all points is shown at the 95 % confidence level. In some cases, the error bars are smaller than the symbols.

Table 2 Treatment name and pH with δ¹¹B and [B] for cultured T. weissflogii.

NA – not available.

Boron is an essential nutrient for diatoms (Lewin, 1966), and it is likely that boric acid passively diffuses across the cell wall to ensure the diatom cell has sufficient boron to meet its biological needs. However, if boric acid were the sole source of boron for the diatoms measured here, we might expect a decrease in boron content as pH increases and external dissolved boric acid concentration declines (Fig. 6).

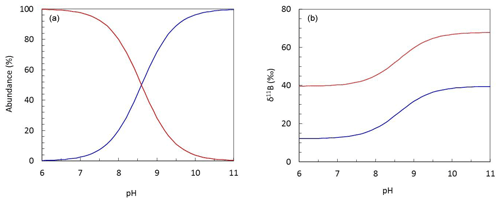
Figure 6 Plots describing (a) the pH-dependent relationship between the abundance of aqueous boron species and (b) the isotopic fractionation observed between boric acid (B(OH)₃; red) and borate ($\mathrm{B}(\mathrm{OH}{)}_{\mathrm{4}}^{-}$; blue) at T=25 ^∘C and S=35.

Several studies note that a number of higher plants have mechanisms for also actively taking up boron, leading to large variations in internal boron concentrations (Pfeffer et al., 2001; Dordas and Brown, 2000; Brown et al., 2002). Indeed, on the basis of a similar dataset to that collected here, Mejía et al. (2013) suggested that borate is likely transported across the cell wall of T. weissflogii as some function of external borate concentration, which shows a positive relationship with external pH (Fig. 6). This hypothesis is developed and discussed further in the next section.

3.2.2 Frustule δ¹¹B of T. weissflogii

The δ¹¹B of T. weissflogii is isotopically light compared to seawater (39.6 ‰; Foster et al., 2010), with an average value across all treatments of −3.95 ‰ (Table 2). Despite the scatter between treatments, similar to the [B] data, Fig. 5 shows that there is a clear relationship between the δ¹¹B of the diatom frustule and pH (R²=0.46, p<0.01), albeit with a negative and relatively shallow slope ($y=-\mathrm{2.61}x+\mathrm{17.12}$).

These results confirm that biogenic silica, free from clay contamination, has a very light boron isotopic composition (Ishikawa and Nakamura, 1993). However, the observed relationship between δ¹¹B in T. weissflogii and pH is radically different to that which is observed in carbonates (Fig. 5), implying a distinctive incorporation mechanism for boron into diatom opal. Much work has been carried out in recent years to show that boron is incorporated in carbonates predominantly as the borate ion with minor, if any, isotopic fractionation (e.g. see Branson, 2018 for a review). It is similarly thought that the borate ion is incorporated into opal in an analogous fashion to its incorporation into clays (Ishikawa and Nakamura, 1993; Kolodny and Chaussidon, 2004). However, such a mechanism in isolation would only be able to generate δ¹¹B in opal of ∼13 ‰ (at the lowest pH). Given the preponderance of isotopically light diatoms, radiolaria and chert δ¹¹B in the literature (including this study; Kolodny and Chaussidon, 2004; Ishikawa and Nakamura, 1993), it is therefore likely that there is an additional light isotopic fractionation of boron on its incorporation into opal, although its absolute magnitude is currently unknown (Kolodny and Chaussidon, 2004).

To make their frustules out of biogenic silica, aqueous Si(OH)₄ is taken up by the diatom cell via active transport by silicon transporter proteins (Amo and Brzezinski, 1999). Once Si(OH)₄ has entered the cell, it accumulates in vacuoles that tend to have a high pH in order to prevent polycondensation of Si(OH)₄ at its higher concentration in the vacuole (Vrieling et al., 1999). The accumulated Si(OH)₄ is then transported to the silicon deposition vesicle (SDV), which is an acidic compartment where the formation of biogenic silica and the construction of the frustule occurs. Without knowledge of the isotopic fractionation of boron on incorporation into biogenic silica, the interpretation of our new δ¹¹B data is challenging. This difficulty is further increased given that the fluid in the SDV is unlikely to have the same δ¹¹B as external seawater, and its relatively acidic pH (∼5.5; Mejía et al., 2013; Vrieling et al., 1999) is likely to promote polymerisation of Si(OH)₄. Nonetheless, the broad similarity between the δ¹¹B of our cultured T. weissflogii with the bulk diatom fraction measured here from sample TC460 and the bulk diatom fraction and radiolarian skeleton measured by Ishikawa and Nakamura (1993; ∼3 ‰) suggests that a large part of the light isotopic composition of biogenic silica is driven by the isotopic fractionation on incorporation rather than “vital effects” relating to the δ¹¹B and pH of the SDV in the different species and organisms. That being said, the >3 ‰ range between different pH treatments in T. weissflogii and the >10 ‰ difference between our Chaetoceros-dominated bulk diatom fraction from TC460 and the cultured T. weissflogii, as well as the negative relationship between pH and diatom δ¹¹B (Fig. 5), argue against a simple two-step model involving borate ion incorporation from seawater with a fixed isotopic fractionation.

The δ¹¹B of the fluid from which our T. weissflogii precipitated their frustules can be calculated if we assume the pH in the SDV of our T. weissflogii is 5.5 across all our treatments (Mejía et al., 2013). Given that at this pH the δ¹¹B of borate is ∼13 ‰, the isotopic composition of this fluid is lighter than seawater, even if we assume an arbitrary −10 ‰ isotopic fractionation on incorporation (blue circles in Fig. 7a). Furthermore, the δ¹¹B of the SDV fluid is inversely correlated with the δ¹¹B of either dissolved borate or dissolved boric acid (Fig. 7a).

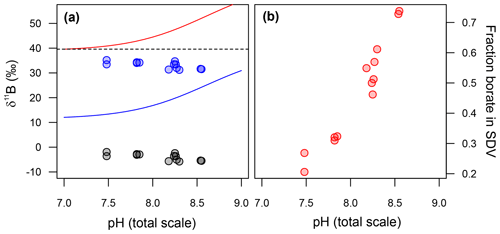
Figure 7 (a) Back-calculated δ¹¹B of the silica deposition vesicle (SDV), and (b) the fraction of boron in the SDV that is derived from external borate. In (a) the diatom δ¹¹B data are shown as grey circles and the calculated δ¹¹B of the SDV as blue circles. Included in this model is an arbitrary −10 ‰ fractionation between the δ¹¹B of the SDV and the opal precipitated. The fraction of borate in the SDV in (b) is a function of this assumption, so these absolute values should be taken as illustrative only.

As discussed above and illustrated schematically in Fig. 8, Mejía et al. (2013) suggested that there are two sources of boron in a diatom cell: (i) passively diffused and isotopically heavy boric acid and (ii) actively transported isotopically light borate ion (see Fig. 8). Assuming that (a) no additional fractionation occurs during uptake and diffusion and (b) only the borate ion is incorporated into the frustule, we can calculate the relative contribution of these two sources of boron as a function of external pH (Fig. 7b). This treatment shows that the relative concentration of borate-derived boron in the SDV fluid increases as external pH increases, though the absolute values here are a function of the magnitude of the isotopic fractionation on incorporation, so we only have confidence in the trends shown in Fig. 7b. Nonetheless, given that the dissolved boric acid concentration decreases and dissolved borate increases as pH is increased (Fig. 6), this is perhaps not surprising.

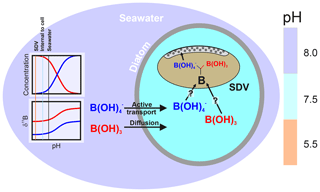
Figure 8 Schematic of the model described herein for boron uptake by T. weissflogii. The speciation behaviour and isotopic composition of boron is also shown in the insert, with the aqueous species colour coded (red represents boric acid, and blue represents borate ion). Seawater boric acid diffuses into the diatom cell, and the borate ion is actively transported, with ${\mathrm{HCO}}_{\mathrm{3}}^{-}$. While it remains unclear how boron enters the silica deposition vesicle, once inside it respeciates into borate ion and boric acid, with the borate ion being incorporated into the frustule. The isotopic composition of internal boron is a function of external pH, which sets the isotopic composition of the incoming species, as well as the balance between active borate ion transport and passive boric acid diffusion. The compartments are colour coded according to approximate pH (scale on the right).

While this finding is entirely compatible with the trend of increasing boron content of T. weissflogii observed as pH increases (Fig. 5), an added complication is that at pH ∼ 5.5 the concentration of borate ion in the SDV is likely to be relatively low (Fig. 6). However, the timescales required to reach equilibrium in the boron system are short (e.g. around 95 µs; Zeebe et al., 2001), meaning that any aqueous borate incorporated into the frustule would be immediately replenished to its equilibrium value by conversion from the more abundant boric acid. Although relevant partition coefficients are likely to be different, a similar process ensures the quantitative removal of boron from pH < 7 solutions by the Amberlite 743 anion exchange resin used for boron purification prior to analysis by MC-ICP-MS (see above; Lemarchand et al., 2002).

Active bicarbonate ion uptake accounts for a substantial amount of the carbon fixed by phytoplankton (e.g. Tortell et al., 2006). As a result, Mejía et al. (2013) proposed that the enrichment of borate ion into the SDV of T. weissflogii and T. pseudonana was the result of the active co-transport of borate ion with bicarbonate ion by bicarbonate transporter proteins. Borate is transported because of its similar charge and size to ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and the phylogenetic similarity between bicarbonate and borate transporters (Mejía et al., 2013). In our model, as external borate ion concentration increases, the borate leak into the diatom cell is also increased. An additional factor is ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ transport, which may be proportionally upregulated as external CO₂ content decreases (and external pH increases) in order to provide the diatom cell with sufficient carbon (Mejía et al., 2013). This may therefore offer a way of driving an elevation of the borate content of the SDV as pH increases (Mejía et al., 2013). Regardless of the exact mechanism, an SDV fluid with an inverse relationship between δ¹¹B and pH is required to explain the δ¹¹B of the T. weissflogii frustule measured here. A simple model whereby external borate ion is an increasingly important contributor to the boron in the SDV as pH increases is able to explain the observed dependency of boron content and δ¹¹B on pH. However, a more complete model of the boron systematics in diatom opal requires a better understanding of isotopic fractionation on incorporation of boron into biogenic silica, the environmental controls on this fractionation, and the nature of the partitioning of boron within the diatom cell and into biogenic silica.

3.2.3 Boron-based pH proxies in diatom opal

The δ¹¹B–pH and B–pH relationships derived here for T. weissflogii potentially offer two independent means to reconstruct the past pH of seawater, particularly in those regions key for CO₂ and heat exchange where foraminifera are largely absent (e.g. at high latitudes). However, the current calibrations (Fig. 5) are relatively uncertain, which may preclude their application to some situations. For instance, recasting the δ¹¹B–pH relationship in terms of δ¹¹B as the dependent variable and using a regression method that accounts for uncertainty in X and Y variables (SIMEX; Carroll et al., 1996) gives the calculated residual pH of the regression as ±0.28 pH units. For the [B] vs. pH relationship, this uncertainty is ±0.36 pH units. At typical surface ocean conditions, such a variability in pH would translate to seawater pCO₂ variability of up to ca. ±250 ppm. Although encouraging, this treatment suggests that additional work is needed before the relationship between δ¹¹B and boron content of diatom opal and seawater pH is a sufficiently precise proxy for a fully quantitative past ocean pH. In particular, future culturing efforts should aim to more carefully control the pH of the culture media. This could be achieved by either using larger volume dilute batch cultures, by harvesting the diatoms earlier in the experiment prior to any significant drift in the carbonate system and/or by using a more robust steady-state chemostat method (e.g. Leonardos and Geider, 2005).

4 Conclusions

In the first study of its kind, we use a modified version of the carbonate boron purification technique of Foster (2008) to show that the δ¹¹B of T. weissflogii opal is pH sensitive but isotopically light (−3.95 ‰ on average) and has an inverse relationship with external seawater pH. Using a novel ICP-MS method we also show that the boron content of T. weissflogii opal increases with increasing pH, supporting the only other study investigating boron in diatoms (Mejía et al., 2013). This suggests that more borate is incorporated into the diatom frustule as the dissolved borate abundance increases with external pH. A simple model is presented, based on Mejía et al. (2013), which implies both of these findings could be due to there being two distinct sources of the boron in the SDV: external boric acid and external borate ion, with the balance of each source changing with external pH. While these results are encouraging, suggesting that the boron proxies in diatom opal may hold considerable promise as a tracer of past ocean pH, more work is needed to fully understand the boron systematics of diatom opal. In particular, there is an urgent need to place boron in opal on firmer ground with precipitation experiments in the laboratory at controlled pH to determine the magnitude of boron isotopic fractionation on boron incorporation into opal as well as the dependence of this fractionation on other environmental factors.