Benchmarking and parameter sensitivity of physiological and vegetation dynamics using the Functionally Assembled Terrestrial Ecosystem Simulator (FATES) at Barro Colorado Island, Panama

Plant functional traits determine vegetation responses to environmental variation, but variation in trait values is large, even within a single site. Likewise, uncertainty in how these traits map to Earth system feedbacks is large. We use a vegetation demographic model (VDM), the Functionally Assembled Terrestrial Ecosystem Simulator (FATES), to explore parameter sensitivity of model predictions, and comparison to observations, at a tropical forest site: Barro Colorado Island in Panama. We define a single 12-dimensional distribution of plant trait variation, derived primarily from observations in Panama, and define plant functional types (PFTs) as random draws from this distribution. We compare several model ensembles, where individual ensemble members vary only in the plant traits that define PFTs, and separate ensembles differ from each other based on either model structural assumptions or non-trait, ecosystem-level parameters, which include (a) the number of competing PFTs present in any simulation and (b) parameters that govern disturbance and height-based light competition. While single-PFT simulations are roughly consistent with observations of productivity at Barro Colorado Island, increasing the number of competing PFTs strongly shifts model predictions towards higher productivity and biomass forests. Different ecosystem variables show greater sensitivity than others to the number of competing PFTs, with the predictions that are most dominated by large trees, such as biomass, being the most sensitive. Changing disturbance and height-sorting parameters, i.e., the rules of competitive trait filtering, shifts regimes of dominance or coexistence between early- and late-successional PFTs in the model. Increases to the extent or severity of disturbance, or to the degree of determinism in height-based light competition, all act to shift the community towards early-successional PFTs. In turn, these shifts in competitive outcomes alter predictions of ecosystem states and fluxes, with more early-successional-dominated forests having lower biomass. It is thus crucial to differentiate between plant traits, which are under competitive pressure in VDMs, from those model parameters that are not and to better understand the relationships between these two types of model parameters to quantify sources of uncertainty in VDMs.

1 Introduction

Climate-change-related feedbacks from the terrestrial biosphere are an important and highly uncertain component of global change (Friedlingstein et al., 2013; Gregory et al., 2009). Tropical forests may contribute substantially to these feedbacks, as vegetation dynamics within these ecosystems may lead to biome shifts and resulting changes to carbon stocks (Cox et al., 2000; Huntingford et al., 2013; Malhi et al., 2009). The majority of Earth system models (ESMs) represent vegetation through conceptual structures that are likely to inhibit realistic or accurate ecosystem responses to global change. In particular, most ESMs use prescribed vegetation distributions, and/or do not represent the functional diversity that exists within tropical forests, and/or impose static vegetation turnover times. Each of these assumptions may substantially bias model results. Prescribed biogeography does not allow models to project either the abrupt changes (Cox et al., 2000) or the long-term committed ecosystem changes (Jones et al., 2009) that may result from vegetation shifts. Conversely, assuming all tropical forests are comprised of a single set of plant traits may lead to overly abrupt changes in response to an imposed forcing, as compared to approaches that allow community-wide shifts in the trait composition of forests (Levine et al., 2016; Powell et al., 2018; Sakschewski et al., 2016). Lastly, assuming fixed turnover times for vegetation may bias the responses to both elevated CO₂ and climate change, as doing so does not permit changes to mortality rates that may result from changes to climate and resource competition (Friend et al., 2014; Koven et al., 2015; McDowell et al., 2018; Powell et al., 2013; Walker et al., 2015), which may be already underway in tropical forests (Brienen et al., 2015).

In addition to the above structural problems in existing ESM vegetation representations, there are enormous uncertainties due to the representation of parameters in such models (Booth et al., 2012). Typically, ESMs are run with a single set of parameters that are chosen through processes that range from formal (but limited-scope) optimization approaches to ad hoc selection of values that give acceptable results. These parameters may or may not be measurable, and if they are measurable, the values used in a given model may need to be scaled up and may or may not agree with observed ranges (Bonan et al., 2012; Rogers, 2014). It is crucial to benchmark ecosystem models against a wide range of observations (Collier et al., 2018; Luo et al., 2012), and at the same time to understand how sensitive model predictions are to uncertainty in the model parameters (Dietze et al., 2014; Raczka et al., 2018), so that we may better assess how much to trust a given model prediction.

Land surface models (LSMs), by virtue of their enormous scope – which typically includes aspects of boundary layer turbulence, radiative transfer, soil hydrology, soil biogeochemistry, plant physiology, land management, and community ecology – have many parameters, all of which are uncertain. In this paper, which focuses on vegetation processes, we broadly separate these model parameters as belonging to two sets: the parameters that comprise a plant functional type (PFT), which we refer to as plant traits, and the parameters that govern the environment in which PFTs exist, which we refer to as ecosystem-level parameters. The importance of this distinction is that, in a dynamic vegetation model with more than one competing PFT, while we can specify the values of the traits of each PFT, the overall trait distributions are controlled by both the trait values of the PFTs and the relative abundance of each PFT. Because the PFT abundances are themselves emergent outcomes that result from the trait values (Fisher et al., 2015), complex feedbacks exist that amplify or attenuate the influence of any given trait value on model predictions as well as trade-offs or other interactions between traits. These feedbacks greatly complicate the assessment of parameter sensitivity in the models. It is thus important to distinguish between the parameter uncertainty associated with plant traits and that associated with ecosystem-level parameters to better understand how they relate to each other and contribute in different ways to model dynamics.

This paper has three goals. The first is to describe a vegetation demographic model (VDM; Fisher et al., 2018) for use in ESMs, which we call the Functionally Assembled Terrestrial Ecosystem Simulator (FATES). A VDM is a size- and age-structured representation of vegetation dynamics within an LSM and may also be coupled within an ESM. The second is to describe FATES behavior at a test bed site at Barro Colorado Island (BCI), Panama. The third goal is to explore the sensitivity of mean-state model predictions by FATES to parameter uncertainty. Because this parameter uncertainty can show up in a number of different ways in a VDM like FATES, we are interested in trying to separate three distinct types of parametric uncertainty: (1) the direct effects of traits on physiological predictions by the model, (2) the indirect effects of trait control on competitive outcomes, which further affect ecosystem-level processes, and (3) how non-trait parameters interact with each of these trait uncertainties to further affect model dynamics.

To do this, we first describe the model and the data that comprise the test bed used to drive the model. This test bed includes distributions of plant traits, most of which are based directly on observations across research sites in Panama. We then describe a series of numerical experiments aimed at exploring the structural and parametric uncertainty in the model. These include (1) assessing direct control of trait uncertainty on model predictions using an ensemble of model runs with only one PFT per ensemble member, (2) separating ensembles where we embed FATES within two related but divergent land surface models, the Energy Exascale Earth System Model (E3SM) Land Model (ELM) and the Community Land Model (CLM), (3) ensembles where we add greater numbers of competing PFTs (from 1 to 2 to 10) into each ensemble member, and (4) a set of ensembles where we compete two PFTs against each other in each ensemble member while also varying a set of ecosystem-level parameters that govern competition and disturbance in the model.

2 Methods

2.1 Description of the FATES model

FATES is a size- and age-structured vegetation model whose foundations are based on a representation of ecosystem biophysics from CLM4.5 (Oleson et al., 2013), a discretization of individual plant and forest disturbance dynamics based on the ecosystem demography (ED) approach (Moorcroft et al., 2001), and an approach to scale from individual plants to a forest canopy based on the perfect plasticity approximation (PPA; Purves et al., 2008), all of which were first brought together in the CLM ED model (Fisher et al., 2015). Following the development of CLM4.5, FATES was created by separating the demographic components of the CLM ED model from CLM itself to facilitate a more modular structure, to combat the “shanty-town syndrome” prevalent in land surface models (Clark et al., 2017), whereby new model features are added without a clear infrastructure for supporting the additional complexity that they bring, and to enable FATES to be used within multiple ESMs, initially both the CLM and ELM.

The two key structural components that FATES adds to a traditional land surface model, the ED and PPA approaches, are described elsewhere in greater detail (e.g., Fisher et al., 2018), so we only briefly summarize them here. ED (Moorcroft et al., 2001) describes an approach to represent a spatially heterogeneous forest canopy comprised of individual trees existing on a complex disturbance history by approximating the forest as a set of partial differential equations in a two-dimensional space comprised of plant size and the age of a given location since its last disturbance event. These continuous equations are then solved numerically by discretizing the ecosystem along each of these two dimensions: plant growth and mortality are discretized by tracking cohorts of individual trees that have a similar size, and disturbance history is tracked as a set of patches with shared disturbance histories, such that each patch may have several cohorts growing on it. The number of patches and cohorts varies in time. New cohorts are generated by recruitment, existing cohort number densities are reduced by mortality, cohorts are merged if they grow to be sufficiently similar, and cohorts are split by any process – such as light competition – that leads to divergence in outcomes across plants at a similar stage. New patches are generated during disturbance events by reducing the area of existing patches, and patches may be merged if their disturbance history or composition is sufficiently similar.

The PPA (Purves et al., 2008) describes an approach of organizing trees (or, equivalently, cohorts) into discrete canopy strata by rank-ordering the trees from tallest to shortest and defining canopy trees as those whose cumulative crown area equals that of the ground (or, when combined with ED, patch area) that they occupy. Fisher et al. (2010) added a modified form of the PPA, whereby the cohorts, rather than being strictly rank-ordered in their separation between canopy and understory, were probabilistically sorted into the canopy and understory based on a function of their height.

Since the original version of CLM ED described in Fisher et al. (2015), there have been numerous developments in the FATES model, which we briefly summarize here. These relate to five main areas: (1) the overall structure of the model and its modularization from the CLM, (2) changes to canopy biophysics, (3) changes to allocation and allometry, (4) changes to the representation of disturbance, and (5) changes to the canopy sorting approach. For a complete reference of the FATES model, see https://fates-docs.readthedocs.io/en/latest/index.html (last access: 1 October 2019), and for a schematic of key processes and their linkages in FATES, see Fig. 1.

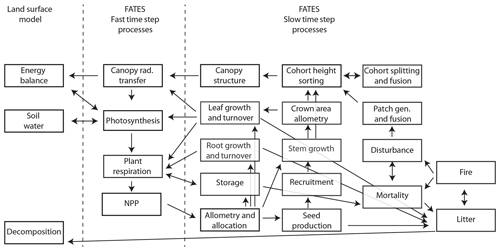
Figure 1 Overall process schematic of FATES. Boxes represent major processes, and arrows represent linkages in the form of material flows or other dependencies. Fast time step processes are resolved every 30 min, and slow time step processes are resolved daily.

A key distinction between CLM ED and FATES is the modularization of the code into a separate repository, with clearly identified boundary conditions between the demography code and the rest of the LSM into which FATES is embedded. Information is passed between FATES and the LSM at two different frequencies: a biophysics frequency, with a default time step of 30 min, and a vegetation dynamics frequency, with a default time step of 1 d. Within each biophysics time step, the LSM provides FATES with information about the current state of the soil moisture, atmospheric radiation inputs, atmospheric thermodynamic state, and some time-averaged functions of the environment. FATES solves the photosynthesis equations for sunlit and shaded leaves, separately for each PFT, along vertical gradients both within each cohort's canopy and between cohorts residing in different canopy layers, to calculate water and carbon fluxes at the level of individual leaves. FATES then provides the LSM with transpiration, integrated canopy conductance, and albedo terms, which the LSM then uses to calculate the energy fluxes at the whole-canopy level. FATES also calculates autotrophic respiration at the biophysics time steps and integrates the resulting net primary productivity (NPP) over the day to end up with an increment of carbon per cohort at the end of each day. Heterotrophic respiration is handled outside of FATES by the LSM it is embedded within.

At the daily time step, FATES sequentially allocates the daily carbon increment per cohort. If this carbon increment is negative, the amount is subtracted from the cohort's storage pool. If the increment is positive, then the cohort allocates it, first to replenish storage and then to compensate for tissue turnover. If the remaining carbon increment is still positive, the cohort will then allocate to any organ pools that are below their allometric targets, which are intrinsic functions for a given PFT that are defined relative to the cohort's stem diameter. If, after this, carbon still remains to be allocated, the cohort will grow its stem diameter, allocating to each pool proportionally to that pool's derivative with respect to stem diameter.

A key development since Fisher et al. (2015) has been modularizing all allometry functions so that PFTs of different allometric functional forms and parameters can exist and compete against each other. FATES requires four distinct types of allometric models to be defined for each PFT: height, crown area, sapwood cross-sectional area, and target biomass pools. All of these are prescribed as functions of a cohort's stem diameter, which thus serves as the basic index for all allometry. FATES currently has six separate allometric target biomass pools: leaf, stem, coarse root, fine root, seed, and storage. Of these, FATES also assumes that the target values of fine-root and storage pools are both linearly proportional to the target leaf biomass pool and that the target coarse-root pool is linearly proportional to the target stem biomass pool. Thus only three index target pools exist: leaf, stem, and seed. As a further simplification, FATES currently assumes that sapwood cross-sectional area at breast height is a constant fraction of a cohort's target leaf area, and thus the sapwood allometry follows the leaf area allometry.

FATES currently allows several allometric models for determining tree height. These include a generic power law relationship as well as the models described in O'Brien et al. (1995), Poorter et al. (2006), Chave et al. (2014), and Martínez Cano et al. (2019). For the simulations described here, we use the Martínez Cano et al. (2019) allometry for all cases, which uses a Michaelis–Menten form to calculate height (H) from stem diameter (D):

$$\begin{array}{}\text{(1)}& H={\displaystyle \frac{a{D}^b}{k+D^b}}.\end{array}$$

We use a single mean set of height allometry parameters for all PFTs in this model, with the mean based on the results from Martínez Cano et al. (2019): a=57.6, b=0.74, and k=21.6.

Crown allometry (C) in FATES is set as a two-parameter power law of diameter, subject to a maximum stem diameter for crown allometry:

$$\begin{array}{}\text{(2)}& C=\left\{\begin{array}{cc}f{D}^g& D<D_{max}\\ f{D}_{max}^g& D\ge D_{max}\end{array}\right.,\end{array}$$

We treat the crown area allometry coefficient (f) and exponent (g) in the above equation as plant traits that we vary based on species-level values, as described below, and we use a single maximum size for crown allometry (D_max), for all model runs, of 200 cm. Plants can continue to grow past D_max, but they do so at a progressively slower rate because the gross primary productivity (GPP) per individual becomes capped by the crown allometry, while the carbon cost of growth continues to increase with increasing stem size.

For the target stem biomass allometric model, FATES includes several options, including a power law of diameter, as well as the functional forms of Saldarriaga et al. (1988) and Chave et al. (2014), which both relate target aboveground biomass to both the stem diameter and height. For all of the experiments described below, we use the Chave et al. (2014) aboveground biomass allometry, expressed in units of kilograms of carbon per individual tree:

$$\begin{array}{}\text{(3)}& \mathrm{AGB}=cj({\mathit{\rho }}_{\mathrm{w}}{D}^{\mathrm{2}}h{)}^p,\end{array}$$

where the parameters j and p have values of 0.0673 and 0.976, respectively, ρ_w is the plant trait wood density, and c is the carbon-to-biomass ratio in wood, which we set as 0.5 for all cases. We did not yet fully explore the sensitivity of model dynamics to the alternate aboveground biomass allometries; this remains future work.

For target leaf biomass, we use a power law allometric model:

$$\begin{array}{}\text{(4)}& L=m{D}^g,\end{array}$$

where the leaf allometric coefficient m is a plant trait that we allow to vary, as described below, and the target leaf allometric exponent g has the same value as the crown area allometric exponent above. As with the crown area, we set a maximum stem diameter above which target leaf biomass remains constant and use the same maximum diameter for both allometries. Setting the exponent on leaf biomass to be the same as that of crown area is equivalent to asserting that a tree's (target) crown depth and leaf area index (LAI) within the footprint of its crown does not vary over the course of its growth trajectory. This holds true – within a given canopy strata – even though FATES does allow specific leaf area (SLA) to vary vertically through the canopy. However, the canopy trimming logic described in Fisher et al. (2015), as well as the relative ability of a plant to actually achieve its target leaf biomass, can lead to large differences in crown depth between the canopy and understory strata, and thus differences in crown depth can occur along growth trajectories.

For seed production, FATES uses as its target a constant fraction of NPP once tissue turnover and storage demands have been met. This represents a biomass flux from the individual cohorts to the site-level seed pool, which then serves as a basis for recruitment flux from the seed pool to new cohorts. This fraction is a plant trait that varies among PFTs. This approach represents an extremely simplified view of reproduction, which we plan to develop further, but does at least allow us to test baseline sensitivity of the current configuration.

In early versions of FATES, the presence of understory trees that persist for long periods of time but only grow very slowly – as is observed in real forests – was difficult to achieve because of the lack of any stabilizing term on an individual cohort's carbon dynamics. If a given cohort's NPP was even slightly negative for sufficiently long, then its storage pool would eventually be reduced to below zero, at which point the entire cohort would die. In order to prevent this and allow the model to produce multiple canopy strata, we added a stabilizing term to the carbon budgets of trees, whereby when their storage pools become depleted, we simultaneously increase the rate of carbon starvation mortality and decrease the rate of maintenance respiration. This reduction of maintenance respiration during carbon starvation is consistent with observations of trees under acute carbon stress (Sevanto et al., 2014). Because the physiologic basis and form of this process is poorly constrained, we use heuristic functions here to define these processes. First, we define a target carbon storage pool (S_t):

$$\begin{array}{}\text{(5)}& S_{\mathrm{t}}=nL,\end{array}$$

where n is a parameter that linearly relates the target storage pool to the target leaf biomass L. If a given plant is unable to achieve its target carbon storage because of having a negative NPP at any given time, then its actual storage pool S will drop below the target storage pool S_t. Then we set both the carbon starvation mortality rate (M_cs) and the fractional rate of maintenance respiration (R) on the ratio of S to L:

$$\begin{array}{}\text{(6)}& {\displaystyle }{M}_{\mathrm{cs}}=\left\{\begin{array}{cc}{M}_{\mathrm{cs},\max }(\mathrm{1}-S/L)& S<L\\ \mathrm{0}& S\ge L\end{array}\right.,\text{(7)}& {\displaystyle }R=\left\{\begin{array}{cc}\left(\mathrm{1}-q^{S/L}\right)/(\mathrm{1}-q)& S<L\\ \mathrm{1}& S\ge L\end{array}\right.,\end{array}$$

where M_cs,max is a trait that defines the maximum rate of carbon starvation mortality, and q is a parameter that governs the curvature of the respiration reduction function. Thus we implicitly assume that there is a critical storage pool S_c=L that sets the total-plant storage level where mortality begins; the implied parameter $S_{\mathrm{c}}/L=\mathrm{1}$ could be made explicit, but we left this as an implicit parameter here due to the generally weak data constraints on it at present. For the experiments described here, we use a single value, 0.01, of the q parameter and allow the maximum rate of carbon starvation mortality M_cs,max to be a PFT trait. Because both the increase in mortality and the decrease in respiration begin when S drops below L, the parameter (n−1) thus sets the size of the carbon storage buffer that determines how much cumulative negative NPP a plant can experience before it begins to suffer from carbon starvation.

In FATES, we separate as distinct traits the top-of-canopy values of maximum carboxylation at reference temperature ($V_{\mathrm{c},\max ,\mathrm{25},\mathrm{top}}$), leaf carbon-to-nitrogen ratios (C : N), and leaf mass per area (LMA). Though these traits are highly coordinated in plants (Wright et al., 2004), we allow this coordination to occur in FATES at the point of defining a PFT that has a specific set of trait values rather than by imposing the trait coordination within the model itself. Exceptions to this rule include that we do define the maximum rate of electron transport at reference temperature (J_max,25) as a direct function of $V_{\mathrm{c},\max ,\mathrm{25}}$. Also, FATES scales leaf traits vertically through the canopy so that $V_{\mathrm{c},\max ,\mathrm{25}}$, leaf N per unit area, and LMA decrease exponentially with overlying leaf area, following Lloyd et al. (2010) and Kovenock (2019). This allows shaded leaves, which are deeper in the canopy, to be thinner and have lower maximum photosynthetic rates ($V_{\mathrm{c},\max ,\mathrm{25}}$, J_max) than sun-exposed, top-of-canopy leaves and maintains a fixed leaf C : N throughout the canopy, following observations (Lloyd et al., 2010).

We generalized some aspects of canopy sorting and disturbance in FATES, as compared to their CLM ED representations, where some strong assumptions were implicit in the model structure. For example, gap-phase disturbance in FATES occurs when canopy trees die. When a given canopy tree dies, or more precisely, when the rate of mortality in a canopy cohort, m_c (as measured by the total crown area of trees that died; in m² ha⁻¹ yr⁻¹), is greater than zero, the patch that previously contained the canopy trees may or may not split off newly disturbed patch area. A pair of ecosystem-level parameters, the fraction of newly dead crown area that becomes a new patch (a new parameter, f_d, a unitless ratio), and the fractional understory mortality during a transition to a new patch due to disturbance, m_u,d, control the outcomes of disturbance, as described below and in Fig. 2a. The rate of new patch area formation, r_d (m² ha⁻¹ yr⁻¹), equals

$$\begin{array}{}\text{(8)}& r_{\mathrm{d}}=m_{\mathrm{c}}\cdot f_{\mathrm{d}}.\end{array}$$

When new patch area is created from an existing (“donor”) patch, the new patch is initialized with a fraction of the understory plants and litter from the donor patch. The pools from the donor patch are thus split in proportion to the fraction of the old patch area transferred to the new patch. Thus when new patch area is created, all understory cohorts in the existing patch are split, with resulting number densities in the corresponding cohorts in the new and old patches proportional to the fraction of patch area disturbed. Formerly understory trees in this newly disturbed patch may, however, be killed in the disturbance event itself; thus the m_u,d term is applied during the disturbance event.

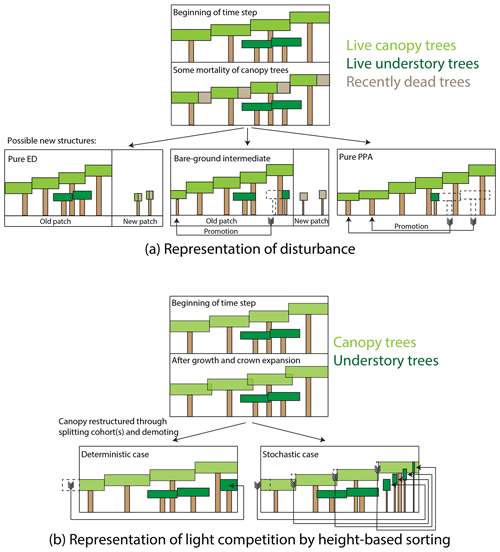
Figure 2 Schematic of how disturbance and height sorting are represented in the FATES model. (a) Representation of disturbance. When canopy trees die, some fraction of the crown area of the dead trees is transferred to a newly disturbed patch, while the remainder remains in the old patch. Trees can be promoted from the understory to the canopy either in the old patch or if they are transferred to the new patch area as survivors of the disturbance event. Endmembers of this case are the “pure-ED” case, in which all crown area becomes new patch area, and the “pure-PPA” case, in which no newly disturbed patch area is created. We also consider an intermediate case, in which half of the dead tree canopy becomes disturbed, but with no survivorship of trees in the newly disturbed patch. (b) Representation of height sorting. When canopy tree crown area exceeds the patch area that the trees are on due to crown growth, canopy trees are “demoted” to the understory. In the deterministic case, trees are rank-ordered by height and the shortest cohort is split at the point where total tree crown area equals patch area, and the remaining cohort is demoted. In the probabilistic case, all canopy trees are demoted, with the fraction of each cohort demoted based on the cohorts' relative heights.

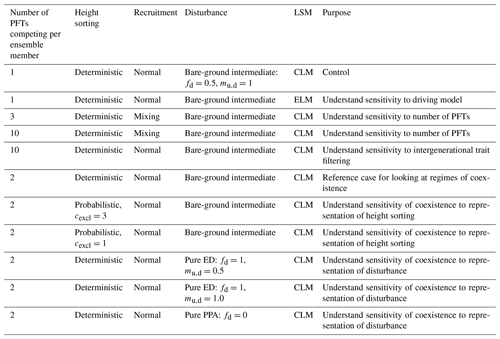
The f_d parameter thus allows FATES to scale continuously between two endmembers in how the simulated ecosystem responds to gap-phase disturbance dynamics (Fig. 2a). If f_d equals 1, then the existing patch area shrinks in tandem with the reduction in tree crown area within the patch's canopy. What this means is that it is effectively not possible for trees in the understory to be “promoted” to the canopy while remaining in a patch – their only route to the canopy is to survive that disturbance event, whereupon they are promoted into the canopy of the new patch. We refer here to this endmember as a “pure-ED” representation of disturbance (on account of its similarity to the original ecosystem demography approach). At the other extreme, if f_d equals 0, then no new patch area is created and there is no horizontal heterogeneity in the system (i.e., there is only ever one patch). In this case, when canopy trees die, the entire void in the canopy created by the loss of their crown area is filled through promotion of trees from the understory within the patch. We refer to this endmember as the “pure-PPA” endmember of disturbance. Intermediate cases exist between these endmembers, where a fraction of understory trees may be promoted from within a patch while a fraction of new patch area is generated. A special intermediate case considered here is a “bare-ground intermediate”, where m_u,d equals 1 – i.e., all cohorts in the understory that are transferred to a new patch are killed during the disturbance event, and thus the new patch area starts from bare ground. This bare-ground intermediate, with $m_{\mathrm{u},\mathrm{d}}=\mathrm{1}$ and f_d=0.5, is equivalent to the equations and PPA-type model described in Farrior et al. (2016). We will consider each of these three special cases – the two endmembers and the bare-ground intermediate – below.

A last set of modifications since Fisher et al. (2015) are in regards to the canopy sorting via the PPA. As described above, the original PPA (Purves et al., 2008) used a deterministic ranking of trees based on their heights and separated them in each time step based on whether their height was above or below the height, z^*, equal to the tree whose cumulative crown area equaled the area of the ground that trees occupied. Fisher et al. (2010) modified this to create a probabilistic PPA whereby the relative probability of trees in a cohort (or, equivalently, the fractional number density of trees of a given cohort) being assigned to the canopy was proportional to their size raised to a parameter called the competitive exclusion parameter c_excl. In FATES, we generalized the height sorting so that it can use either the deterministic- or probabilistic-sorting approach to the PPA and discuss both versions below.

2.2 Site description and driving data

All model experiments here are conducted at Barro Colorado Island (BCI), Panama (9.151^∘ N, 79.855^∘ W). The environment at BCI has a mean precipitation of 2600±480 mm yr⁻¹, with a 4-month dry season during which precipitation drops below 100 mm yr⁻¹. The ecosystem at BCI is a primary forest, with a disturbance regime characterized by primarily small-scale disturbance and subject to elevated mortality rates during ENSO-driven droughts. The site includes a 50 ha census plot, in which every stem ≥1 cm diameter has been measured every 5 years since 1982, with 321 species identified (Condit et al., 2017), as well as eddy covariance and other observations.

We force the model with drivers measured at the BCI meteorological station for the period 1986–2017; these data are available at https://biogeodb.stri.si.edu/physical_monitoring/research/barrocolorado (last access: November 2017). All site-level data were scanned for quality assurance and quality control (QA/QC) as described by Faybishenko et al. (2018). The QA/QC procedure of time-series data was performed using the R (https://www.r-project.org/, RStudio v1.1, last access: 9 October 2017) software, with the application of libraries “zoo” (Zeileis et al., 2019), “xts” (Ryan et al., 2018), “tsoutliers” (López-de-Lacalle, 2019), and “Rssa” (Korobeynikov et al., 2017). The procedure includes the following major steps – the identification of problems in the datasets (QA) and then data cleaning, flagging, and gap filling of missing data (QC). Step 1 (QA) includes an initial visual inspection and cataloging data, determining the temporal frequency of sampling to assess data availability and preliminary assessing data quality. Step 2 (QC) includes processing and cleaning raw datasets; formatting timestamps; detecting and removing duplicates, bad data, and outliers; gap filling of missing data; and flagging quality-controlled data. For each simulation, we recycled meteorology over the 1986–2017 period.

2.3 Plant trait data and application to FATES PFT definition

A key conceptual point in this study is that we define a PFT only as a vector of plant traits; we do not make any further a priori assumptions about the ecological role that a given PFT plays. In some of these experiments, we do diagnose properties of a PFT that allow us to – in certain cases – make post hoc distinctions such as “early-successional” or “late-successional” PFTs, and in this paper all PFTs may be thought of as belonging to tropical forest tree communities, but we essentially take a probabilistic view of PFTs here as being random draws from some continuous trait covariance matrix. To define this matrix, we assemble several datasets and cross-reference them based on mean values per plant species, with Latin binomials used as the reference index.

We start with two datasets describing plant traits at BCI, and at two other sites across a precipitation gradient in Panama, Parque Nacional Metropolitano (PNM) and Fort San Lorenzo (SLZ), which are originally described in Osnas et al. (2018) and Wright et al. (2010). Data from these sets used here include leaf lifespan, leaf mass per unit area (LMA), wood density, mortality of 10 cm and larger trees, and leaf N content. For these datasets, we only use values for trees in the canopy stratum. Where a given species occurs in more than one site, we use mean values across the sites. Because these are the only datasets that include leaf lifespan estimates, where other datasets also include an estimate of LMA for a given species, we only use the estimates in these datasets, as they will correspond to the specific individuals with which leaf lifespan is also measured.

We add two further datasets on leaf traits, both based on canopy crane measurements at PNM and SLZ sites: Gu et al. (2016) and Rogers et al. (2017) and Wu et al. (2019). Each of these contain estimates of V_c,max, LMA, wood density, and leaf N content. We use FATES temperature scaling functions to calculate V_c,max at the reference temperature (25 ^∘C) based on the temperature at which specific V_c,max observations were made. Together these sets of traits describe plant variation along the leaf and wood economic spectra, two critical axes of functional diversity (Baraloto et al., 2010; Wright et al., 2004).

Lastly, we add a dataset on crown area allometry from trees at BCI (Martínez Cano et al., 2019). The crown area allometry in FATES is defined with crown area, C, set as a power law relationship with diameter, D, as described above, so for each species we use the crown area coefficient g and exponent d as reported in Martínez Cano et al. (2019). These crown area traits control the overall light interception ability of plants, and how it changes over plant size, and thus are important determinants of both baseline growth rates (for coefficient g) and the derivative of growth rates with respect to plant size (for exponent d).

In total, we thus use eight traits from the observational datasets: $V_{\mathrm{c},\max ,\mathrm{25},\mathrm{top}}$ (µmol CO₂ m⁻² s⁻¹), wood density (g cm⁻³), LMA (m² g⁻¹), leaf N per unit area (Leaf N/area; g m⁻²), leaf lifespan (year), background tree mortality (yr⁻¹), crown area coefficient (m² cm⁻¹), and crown area intercept (unitless). We assume lognormal distributions for $V_{\mathrm{c},\max ,\mathrm{25},\mathrm{top}}$, LMA, Leaf N/area, leaf lifespan, and background tree mortality and normal distributions for wood density, crown area coefficient, and crown area intercept, with correlations between these traits as determined from the data. The full matrix of observed traits is shown in Fig. 3, where each dot represents a pair of mean trait values for a given species, and the histograms across the diagonal show the full distribution of species-mean values for each trait.

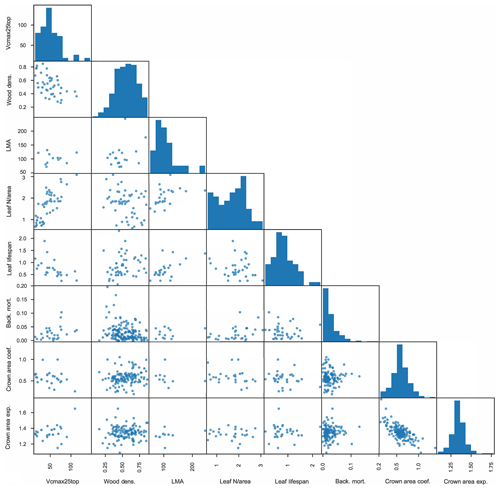
Figure 3 Matrix of plant trait data used to inform FATES ensembles. Measured traits are as follows: leaf $V_{\mathrm{c},\max ,\mathrm{25},\mathrm{top}}$ (µmol CO₂ m⁻² s⁻¹), wood density (g cm⁻³), leaf mass per unit area (m² g⁻¹), leaf N per unit area (g m⁻²), leaf lifespan (year), plant mortality rate (yr⁻¹), coefficient of relationship of crown area to stem diameter (m² cm⁻¹), and exponent of relationship of crown area to stem diameter (unitless). Each dot represents one pair of species-level trait values where both traits are measured for a given species; histograms show the distributions of all species-level values for a given trait.

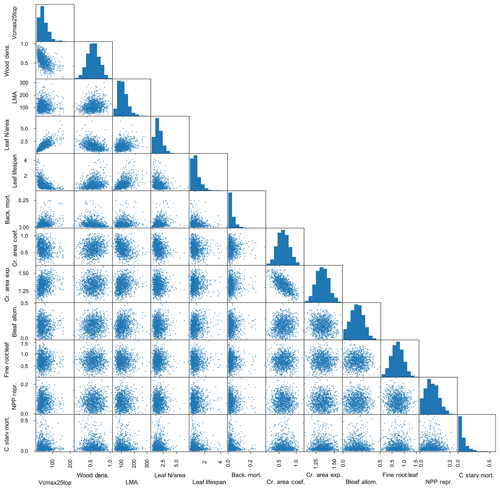
Figure 4 Resampled trait matrix, including eight observed and four unobserved traits, as used to define PFTs in FATES simulations. Eight observed traits are as in Fig. 3 (with background mortality set to be the observed plant mortality). Four additional unobserved traits are as follows: allometric coefficient of relationship of leaf biomass to stem diameter (kg cm⁻¹), allometric ratio of fine-root biomass to leaf biomass (unitless), fractional NPP allocated to reproduction (unitless), and maximum rate of carbon starvation mortality (yr⁻¹). Bleaf is leaf biomass.

In addition to the observed traits that allow us to generate prior distributions on values based on data, we also want to include parameter variation in a small set of traits that are poorly observed but that we expect to be important in model dynamics. We thus add four more unobserved trait values: the allometric coefficient of relationship of leaf biomass to stem diameter (kg cm⁻¹), the allometric ratio of fine-root biomass to leaf biomass (unitless), the fractional allocation to reproduction (unitless), and the maximum rate of carbon starvation mortality (yr⁻¹). For each of these, we assume no correlations with other observed traits, and we assume the first three of these to be normally distributed and that the last (maximum rate of carbon starvation mortality) is lognormally distributed as we do for the background mortality trait. The choice of these additional traits are to extend the possible range of dynamics to include crown thickness, plant carbon use efficiency, understory mortality rates and thus shade tolerance, and reproductive fecundity as possible determinants in the competitiveness of a given PFT. Table 1 lists each of the parameters varied, and the most closely associated process box is shown in Fig. 1.

Table 1 Traits varied within each ensemble in order to define plant functional types, their units, and the process or processes (as diagrammed in Fig. 1) most closely associated with each trait.

We thus define a single 12×12 trait covariance matrix as the basis of all experiments described below, representing the data-constrained hypervolume from which we sample plant functional types. In all experiments, the vector of trait values that defines a PFT is sampled as a single random draw from this 12×12 trait covariance matrix. An example of resampled trait matrix from a single model ensemble is shown in Fig. 4. The traits considered in this study are not meant to be comprehensive but are meant to cover a range of processes in the model, including (a) physiology and the leaf economic spectrum; (b) allocation of biomass within a whole plant to leaves, roots, and reproduction; (c) patterns of acquisition of the primary resource, light, through crown area allometry; and (d) mortality rates in both the canopy and understory.

2.4 Model testing data

We make use of the long-term forest dynamics plot census data at BCI (Hubbell et al., 1999). We use a total of five censuses here, beginning with the 1985 census. We use the census data in three ways in this paper. (1) To more rapidly equilibrate the model, we initialize the forest with observed size distributions (from the 2005 census); in simulations with more than one PFT present, we use the same initial size distribution for each PFT. In order to remove the initial imprint of these initial size distributions on the model output, we integrate FATES for 200 or 300 years (depending on the experiment); after this spin-up time the model dynamics have diverged from the initialization (e.g., Fig. 5b). (2) We compare model predictions of size distributions to the census data of the forest as a whole. (3) We compare model predictions of aboveground biomass against observations, which are also derived from the BCI census data, that are reported in Meakem et al. (2018), which are approximately 13.6 kg C m⁻²; we assign ±10 % uncertainty to these biomass observations to account for allometric uncertainty (Chave et al., 2003).

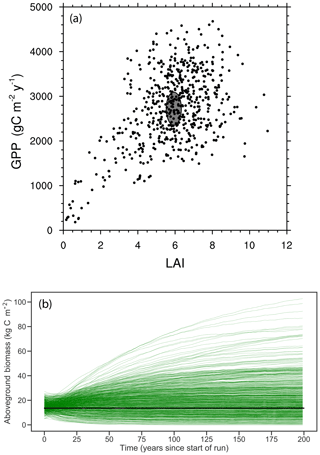
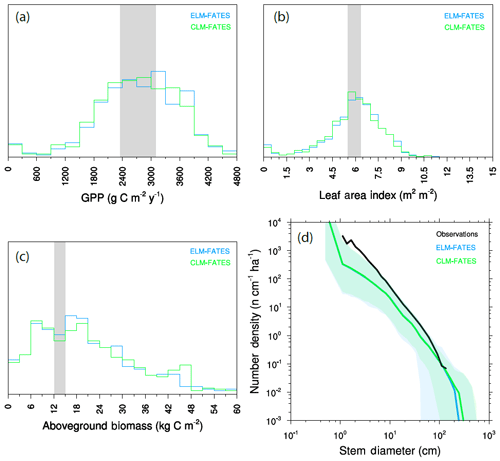
Figure 5 Joint distribution of modeled GPP and LAI (a) and modeled time series of biomass trajectories (b) for a 576-member ensemble of site-scale FATES simulations, where each ensemble member, represented here as an individual dot, has a single PFT defined as a random draw from the 12-trait covariance matrix shown in Fig. 3. Site-level observations of LAI and GPP (mean ± 1 SD) are shown in (a) as a grey ellipse, and observed mean biomass is shown in (b) as black line.

We compare fluxes of GPP as well as the sensible and latent heat fluxes to observations made with an eddy-covariance system. The tower used for these measurements is 41 m a.g.l. (meters above ground level) on a plateau on BCI. The eddy-covariance system includes a sonic anemometer (CSAT3, Campbell Scientific, Logan, UT) and an open-path infrared CO₂–H₂O gas analyzer (LI-7500, LI-COR, Lincoln, NE). High-frequency (10 Hz) measurements were acquired by a data logger (CR1000, Campbell Scientific) and stored on a local PC. Data were processed with a custom program using a standard routine described in Detto et al. (2010). GPP was derived from daytime values of net ecosystem exchange (NEE) by adding the corresponding mean daily ecosystem respiration obtained as the intercept of the light response curve (Lasslop et al., 2010). The light curve was fitted on a 15 d moving window using a rectangular hyperbolic function (runs with friction velocity less than 0.4 m s⁻¹ were excluded). Lastly, we compare LAI as predicted by FATES to observations of LAI reported in Detto et al. (2018).

2.5 Model experiment descriptions

We define a series of model experiments here to explore parametric and structural uncertainty in the model and how trait uncertainty can combine with vegetation dynamics to feed back on model predictions (Table 2). We first begin with single-PFT experiments, randomly drawing a set of PFTs and running each of them as a separate FATES simulation. We refer to the set of such simulations, which differ only in their PFT specification, as an ensemble of simulations and each separate FATES run as an ensemble member. The size of each of the ensembles here is 576 members, chosen as a somewhat arbitrary number but one which balances computational costs against statistical sampling depth while allowing one simulation per CPU on the 36-core computing nodes used for most simulations. We compare outputs from these ensembles against a set of observations (of biomass, LAI, and eddy covariance) at BCI to assess patterns of variability in the model and comparisons to observations. We perform these single-PFT ensembles, with an identical set of ensemble members each for two different model configurations, CLM-FATES and ELM-FATES, in order to further test the structural uncertainty of embedding FATES within two closely related, yet divergent, land models.

Table 2 Experimental matrix used in this study. Each ensemble above consists of 576 ensemble members, with one or more PFTs per ensemble member chosen as a random draw from the 12×12 trait covariance matrix.

We assess parameter sensitivity via direct trait control of model predictions in the one-PFT simulations by fitting splines of each of the model predictions that we analyze as a function of each of the traits that we vary across the ensemble. We calculate the maximum potential variance explained as the fraction of variance in the predictions across the ensemble that is predicted by the fitted spline. Because some of the traits are correlated, we also assess the minimum variance explained, which we calculate by first subtracting the variance explained by all other traits and then assessing how much of the remaining variance is explained by the trait of interest (Xu, 2013; Xu and Gertner, 2008).

As a next experiment, we add increasing numbers of competing PFTs to the model. The premise of this is that a model can represent plant trait diversity either through multiple realizations of the model where plants with each set of traits only interact with plants of the same type or alternately through allowing plants with different traits to interact with each other through competition for resources. In a PFT-based model such as FATES, these options exist on a continuum: as we add further PFTs to a given simulation, we increase the diversity that is resolved within each simulation and thus, in principle, should reduce the variability across simulations. The goal here is to ask how increasing the diversity that is resolved within any specific simulation changes the distribution of model predictions, as compared to an ensemble approach, where we only account for diversity by non-interacting PFTs. Again, we construct each experiment as a perturbed-parameter ensemble – where we use the random draws of parameter values to construct new parameter vectors for each model run – but instead of including a single PFT in each ensemble member, we do 576 model runs with three PFTs and 576 runs with 10 PFTs, in each case drawing all PFTs at random from the multivariate trait distributions. We refer to these as the three-PFT ensemble and the 10-PFT ensemble, respectively.

We conduct the last (10-PFT) experiment twice. In the first instance, we force the model to maintain functional diversity by evenly recruiting from a mixed-PFT seed pool into each PFT, thus preventing competitive exclusion and intergenerational trait filtering. This approach still allows trait filtering to occur within the lifespan of an individual plant but prevents any PFT from completely excluding the others, thus acting as a discrete-PFT analog to the continuous generation of the trait diversity approach used in the model of Sakschewski et al. (2016). In the second instance, we allow the normal intergenerational trait filtering to occur; i.e., each PFT reproduces only recruits of its own PFT with no supplement so that PFTs may go extinct.

Lastly we perform a series of two-PFT ensembles aimed at asking whether we can identify regimes where trade-offs in general, and in particular early–late-successional trade-offs, lead to a degree of coexistence, after 300 years, in the model. To do this, we again conduct 576-member ensembles, where each ensemble member is comprised of PFTs that are randomly drawn from the same trait covariance matrix. In this case, we also explore different values of the ecosystem structural parameters that govern light competition and gap-phase disturbance dynamics, as described above and shown in Fig. 2. The control for this set of ensembles uses the “deterministic-PPA” mode for height sorting and a bare-ground intermediate representation of disturbance (which we also use in all preceding experiments). Two additional ensembles vary light competition parameters to use probabilistic PPA height sorting with c_excl=3 and probabilistic PPA height sorting with c_excl=1. In three further ensembles, we vary the disturbance parameters f_d and m_u,d to explore the two extreme representations of disturbance to the pure-ED and pure-PPA endmembers, and in the pure-ED case, we explore the sensitivity of the model to m_u,d, or how many understory plants are killed during a disturbance event. This parameter m_u,d has no effect in the pure-PPA case, since there is no disturbance when f_d=0.

3 Results and discussion

3.1 Single-PFT simulations and comparison to observations

A first question is how the distributions of ecosystem-level properties – such as biomass; size distributions; LAI; and carbon, water, and energy fluxes – from a set of single-PFT simulations compare with observations at the site. To answer this, we conduct an ensemble of single-PFT simulations to generate a set of possible forests, each of which is comprised of trees sharing a single set of traits. Results from this single-PFT ensemble are shown in Figs. 5–7. There is a broad range of model predictions, ranging from some ensemble members that fail to establish to others which grow to highly productive forests.

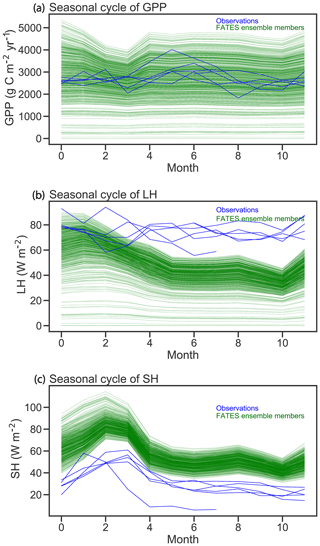
Figure 6 Comparison of FATES simulations of mean annual cycles in gross primary productivity, latent heat (LH), and sensible heat (SH) with eddy-covariance observations from Barro Colorado Island flux tower. Green lines correspond to the mean annual cycle from each FATES ensemble member. Blue lines show individual years of eddy-covariance data.

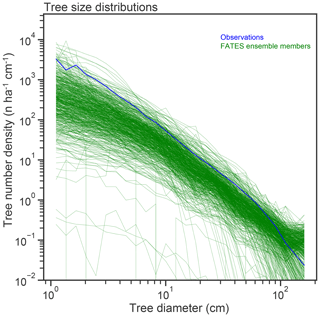
Figure 7 Stem size distributions (in number – n – of trees per hectare per centimeter width of size class bin), of single-PFT ensemble members, as compared to census data from the BCI forest dynamics plot.

The joint distribution of GPP and LAI (Fig. 5a) shows that the overall ensemble spread is roughly centered around the observed values (shown as ellipse in Fig. 5a), though with wide spread and a tail that extends to low-productivity, low-LAI simulations. Likewise, trajectories of biomass in these simulations (Fig. 5b), where each simulation is initialized with observed size distributions and is then integrated for 200 years to come into a quasi-steady state that is determined by the ensemble parameters, converge towards a distribution in biomass that spans the observed estimates (black line in Fig. 5b). While the ensemble distributions in LAI and GPP are roughly symmetric, albeit with a tail extending to the low-GPP, low-LAI zone in Fig. 5a, the distribution of biomass shows a tail in the other direction towards extremely high biomass forests, with some ensemble members converging towards values that are several times those observed.

Seasonal cycles of ecosystem fluxes, as compared to observations from the eddy-covariance tower at BCI (Fig. 6), show both the wide spread of ensemble members, as discussed above, and two systematic model–data mismatches. The first of these is in the shape and amplitude of the seasonal cycles: FATES simulations systematically predict a decrease in GPP during the dry season (February–April) as compared to the eddy-covariance data that do not show a systematic decrease in productivity during the dry season. The second bias is that the FATES simulations here systematically predict a lower latent heat flux and a higher sensible heat flux than the observations. Similar biases are also documented in Huang et al. (2019). In this paper, we do not try to correct these biases, which likely arise from a combination of (a) not including a broader set of plant traits that govern ecohydrological processes, such as those traits that govern stomatal conductance, canopy turbulence, or rooting depth distributions; (b) not using a full plant hydraulics model (Christoffersen et al., 2016; Xu et al., 2016); (c) not including processes known to increase GPP during the dry seasons of tropical forests, such as replacement of old leaves with leaves with greater photosynthetic capacity (Wu et al., 2017); and/or (d) biases in the soil hydrologic modules in which hillslope hydrologic processes are largely ignored (Fan et al., 2019). A fuller analysis of plant hydrologic traits, as well as the structural changes to represent plant hydrodynamics and photosynthetic seasonality, is underway in FATES but beyond the scope of this paper.

Observed tree size distributions are an emergent outcome resulting from the growth rates, death rates, and light competition parameters in a forest. In principle, the accurate prediction of diameter distributions, which follows a Weibull distribution (approximately power function at small diameters, dropping off at larger sizes), is possible in a vegetation demographic model using the combined hypotheses of ED and PPA (Farrior et al., 2016) or through the combined ED and plant hydrodynamic hypotheses (Powell et al., 2018). The ensemble of FATES simulations shown here roughly capture the shape of the curve (Fig. 7) though, again, with considerable spread and some systematic biases. The wide spread in simulations shows that some trait combinations lead to outcomes with either too many or two few trees at the larger end of the tree size distribution. The more systematic bias is that most of the ensemble members show too many very large trees, and too few small trees, as compared to observations, suggesting an overall bias in the rates of establishment, growth, and death. The degree of this ensemble-level bias – close to an order of magnitude – shows some sensitivity to ecosystem-level parameters, as discussed further below, which suggests modest control by representation of gap-phase disturbance dynamics and light competition parameters.

Parametric control by plant traits on several ecosystem-level model predictions is shown via variance decomposition in Fig. 8. While the analysis here is not meant to be as comprehensive as that of Massoud et al. (2019), Fig. 8 nonetheless shows that each of these model predictions shows sensitivity to a different set of traits, thus highlighting the complex mapping of trait variation onto model predictions. Further, many of these model predictions show a high degree of sensitivity across several variables. To some degree, this arises because of the correlations between trait values, such as through the leaf economic spectrum, which can be seen by the large spread between the maximum potential variance explained by a given trait (closed circles) and the minimum variance explained by that trait (open circles). However, in other instances, such as for tree growth rates in the canopy, sets of relatively uncorrelated parameters, such as wood density and the set of leaf-economic-spectrum traits, jointly control the rates. And in other cases, individual traits directly affect the rates predicted; an example of this is the canopy mortality rates, which in this mean-state configuration effectively show only the background mortality rates. Understory mortality rates are slightly more complex, with joint control of both the background mortality rates and the maximum rate of carbon starvation as well as small contributions from the leaf and stem physiological traits. Trait control over LAI shows that, because of the combined effects of within-cohort leaf optimization, and the potential for multiple canopy strata to exist, there is a relatively weak direct control on ecosystem-level LAI by the direct leaf-to-stem allometric-coefficient trait; LAI is equally constrained by the leaf-economic-spectrum traits that control the marginal costs and benefits of additional leaves at the bottom of the canopy, as well as a small contribution from the reproductive allocation trait, which sets how the recruitment rate and thus many small plants are contributing to the understory LAI.

Figure 8 Variance decomposition of trait control on ecosystem states and vital rates. Shown are the fractions of variance explained by each of the 12 traits for seven ecosystem variables. Filled circles and associated lines show the maximum potential fraction of variance explained by each trait, without considering trait-trait correlations. Open circles show the minimum fraction of variance explained by each trait after first subtracting out the variance explained by all other traits.

3.2 Sensitivity of results to land surface model

FATES is designed to work as a modular representation of plant biophysical and community assembly processes within a host land surface model rather than being a land surface model on its own. It has been developed out of the CLM ED framework described by Fisher et al. (2015) and currently works within two related but distinct LSMs: CLM5 (Lawrence et al., 2019; Wieder et al., 2019) and ELMv1 (Golaz et al., 2019). This modularity of FATES and its ability to work within alternate LSMs represents an important capability. As LSMs have grown ever more complex, the infrastructure for managing model complexity and attributing model behavioral differences to structural and parametric assumptions has not grown equivalently; a potential strategy for addressing this complexity problem is to separate the representation of processes in such a way that they can be explored as conditional on alternate boundary conditions, following the “modular complexity” approach described in Fisher and Koven (2020). Such an approach can allow, for example, one to ask how the representation of soil physics of biogeochemistry feeds back onto an identical representation of plant physiology in order to better separate the contributions of each to total model prediction uncertainty. Here we begin to test this approach by testing the exact same representation of FATES within the alternate LSMs it can be run in.

We repeated the ensemble described above using FATES embedded within ELMv1 and compare the ensemble predictions between the two models in Fig. 9. The ensembles used identical plant traits, forcing data, and other FATES parameters; however, many aspects of the LSMs differ, particularly including soil depth and the number of soil layers. Thus the two ensembles can be considered an experiment to the sensitivity of the structural representation of the physical soil environment that the vegetation is growing in. Distributions between mean GPP (Fig. 9a), LAI (Fig. 9b), and biomass (Fig. 9c) are all similar, as are the final size distributions of the plant community (Fig. 9d). This demonstrates that the diversity of plant traits used here, at least in this generally well-watered site, has a stronger control on model predictions than whatever structural divergences have accumulated in the representation of the soil environment between these models.

Figure 9 Comparison of FATES simulations as embedded within two land surface models: ELM-FATES and CLM-FATES. (a) GPP, (b) LAI, and (c) aboveground biomass. Observational range shown as grey band in (a)–(c).

3.3 Sensitivity of results to the number of competing PFTs

The above experiments each contained a single PFT in each ensemble member, and so the ensemble spread of the predictions demonstrates the global trait sensitivity of monocultural forests, in the absence of competition effects. In real tropical forest ecosystems, the enormous trait diversity exists as a mosaic of plants of different species, each competing for resources and contributing to ecosystem-level dynamics. A key goal of models such as FATES is to explore how this heterogeneity in traits at the scale of individual cohorts of plants interacts with atmospheric and soil processes to govern ecosystem fluxes and structure. Thus we want to move away from the monocultural representation to ask how trait diversity affects model predictions in the presence of competitive interactions. To do this, we conduct experiments to add greater amounts of trait diversity into each ensemble by increasing the number of PFTs in each run. We first hold disturbance and light competition parameters constant; in Sect. 3.4 below, we vary these parameters to explore their role in governing competitive outcomes.

We calculate further ensembles, drawing plant traits from the same distribution as before, but with either three or 10 PFTs per ensemble member. To separate competition during the recruitment process from competition by larger-statured plants, we first “force” some degree of coexistence between functional types by recruiting equally into the smallest-size cohorts of all PFTs, as described above. Figure 10a–d show a key set of model predictions for each of these simulations. For all outputs (GPP, LAI, aboveground biomass, size distributions), adding additional PFTs to each ensemble member both narrows the ensemble distribution and induces a shift towards values indicative of a higher-productivity forest comprised of larger trees.

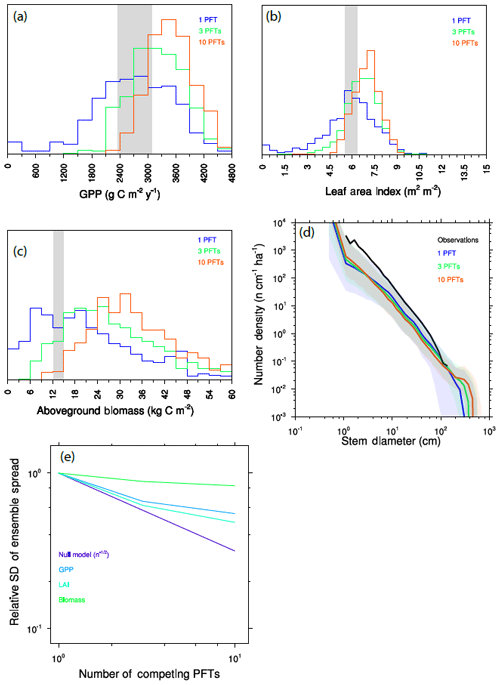
Figure 10 Variation between ensemble members as a function of the number of competing PFTs in each ensemble member. (a–c) Histograms of mean GPP (a), LAI (b), and aboveground biomass (c). Observational range shown as grey band in (a)–(c). (d) Size distributions of ensembles. (e) Standard deviation across ensemble members as a function of the number of competing PFTs, as compared to a null model, which considers the distribution changes purely to be a sampling problem, for expected reduction in variation between ensemble members in the absence of competition effects.

This narrowing and shifting of the ensemble distributions are separate but related outcomes of resolving trait diversity and competitive interactions. In the single-PFT case, functional diversity is only resolved across ensemble members, which are each comprised of monoculture forests. As we add PFTs, each ensemble member better samples the observed functional diversity, so we expect that the differences between ensemble members should decrease as a result. But at the same time, competitive dynamics mean that some traits will be more competitive and therefore more strongly represented in each ensemble member. Thus the single-PFT ensemble will most evenly sample throughout the possible trait distribution, while ensembles comprised of greater numbers of interacting PFTs will unevenly sample the parts of the distribution that are more competitive.

We can quantify these competitive effects on ensemble spread by looking at how the standard deviation of the ensemble shrinks as we add more PFTs (Fig. 10e). We can formulate a null model: if competition did not matter for a given trait, then we would expect that the narrowing of the distribution upon adding further PFTs would follow a statistical sampling relationship for independent variables and therefore decrease as proportional to $n^{-\mathrm{1}/\mathrm{2}}$, where n is the number of PFTs. This null model thus represents the “selection effect” of Tilman et al. (1997). In practice, what is observed here is a rate of narrowing with additional PFTs that is much smaller than this null model – i.e., the null model narrows much faster than the realized model outcomes. This shows that competition is an important component of the higher PFT cases, both in maintaining variability within an ensemble and in increasing the ensemble mean productivity by weighting the overall ecosystem function towards the part of the trait distribution that is more productive.

Different variables are more strongly affected by competitive dynamics than others: of the three we show here, and comparing the one-PFT and 10-PFT cases, the competitive effects on LAI are smaller than those for GPP, which are in turn smaller than for biomass, where an increasing PFT number has very little effect on the ensemble spread. An explanation for why the competitive effects have stronger effects on some variables than others may be the relative control of a given prediction by very competitive – and thus very large – trees. Leaf area is provided by trees of both canopy strata and so is represented most evenly across the spectrum of the competitiveness. The relative contribution by a given PFT to GPP at the ecosystem level is roughly proportional to the fraction of the canopy that the given PFT crown occupies. Because crown area scales with diameter to the power of ∼1.3 (Fig. 3 and Martínez Cano et al., 2019), and the relative proportion of trees in the canopy to the understory will further be dominated by larger trees, GPP will be more dominated by larger trees than their relative contribution to LAI. Biomass is even further dominated by large trees: combining allometry Eqs. (1) and (3) above implies that a given plant's contribution will scale with its diameter to the power of roughly 2.1, which would imply that trees that are extremely large should more seriously impact biomass than either GPP or LAI.

The convergence of the model with increasing numbers of PFTs towards higher-productivity forests than are observed demonstrates that, even with the strong assertion of neutral filtering between generations that we use in these ensembles, either the competitive filtering within each generation is still too strong or other biases in the model which are compensated for in single-PFT simulations become evident in the more diverse simulations. This is most apparent in the tree size distributions (Fig. 10d), where the 10-PFT ensembles generate many more large-statured trees than either the lower-PFT-number simulations or the sizes that are observed. Possible causes for this bias include the following: (a) that the marginal competitiveness associated with a given trait advantage in the model is too strong, as compared to more neutral dynamics that may occur in real forests (Hubbell, 2011); (b) that additional, unmeasured trade-offs associated with the set of possible strategies – which might constrain the set of possible trait combinations to remove superspecies or loser species – are insufficiently represented (Clark et al., 2018); (c) that processes which govern tree vital rates at the large end of the size distribution are poorly represented, such as senescence strategies that are observed in forest demography (Johnson et al., 2018; Needham et al., 2020); or (d) that other density-dependent effects such as herbivory or pathogen load act to reduce the competitive success of any given species in real forests (Connell, 1971; Janzen, 1970), though such effects should be weaker for functional types than species.

We further investigate the degree of competitive filtering within and between generations by re-running the 10-PFT ensemble, but in this instance, we allow species to go extinct by re-coupling the rate of recruitment of a given PFT to the seed production by that PFT. Comparisons of the resulting predictions (Fig. 11a–d) show only subtle differences in the ecosystem-level rates investigated here: biomass and GPP are barely shifted, while the distribution of LAI is slightly expanded towards higher values, and the number of small trees is slightly decreased when we allow intergenerational competition to play out. Thus the effects of trait filtering during recruitment are much more muted in the model than the trait filtering that happens after recruitment has occurred. This can further be illustrated if we compare ranked abundance curves for the two ensembles of trees greater than 1 cm vs. trees greater than 10 cm (Fig. 11e–f): at 1 cm, the presence or absence of recruitment filtering leads to a marked change in the slope of ranked abundance curves, whereas at 10 cm the slopes of the two cases are roughly similar. Even when we force the model to allow neutral filtering during recruitment, by the time trees grow to 10 cm, the resolved filtering is strongly evident.

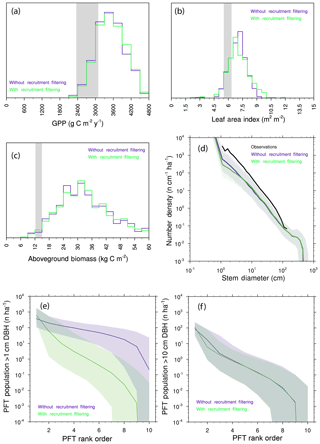
Figure 11 Predictions from 10-PFT ensembles with and without recruitment filtering. (a–c) Histograms of mean GPP (a), LAI (b), and aboveground biomass (c). Observational range shown as grey band in (a)–(c). (d) Size distributions of ensembles. (e–f) Rank abundance curves for PFTs. (e) PFT abundances for all trees greater than 1 cm diameter (DBH – diameter at breast height). (f) PFT abundances for all trees greater than 10 cm diameter. For all cases in (e)–(f), solid line is the median ensemble member, and shaded range is the 5th–95th percentiles across 576 ensembles.

3.4 Regimes of coexistence and their sensitivity to disturbance and light competition parameters

In order to represent shifts in plant trait distributions at a given location under global change pressures, a model like FATES must be capable of maintaining some degree of trait heterogeneity in the first instance. The maintenance of functional diversity in ecosystems is a complex topic (Chave, 2004; Chesson, 2000), and its analysis in the context of Earth-system-type models such as FATES is in its infancy (Fisher et al., 2018). Here we seek to first understand which combinations of traits within FATES allow stable coexistence of PFTs in the mean state and whether there is other ecosystem-level parametric control on these regimes of coexistence. In particular, we expect that a model that resolves heterogeneity in the light environment can accommodate at least two niches, for fast-growing early-successional plants and shade-tolerant, slow-growing plants (Moorcroft et al., 2001). We can represent such a trade-off as a line connecting two points that represent two sets of PFT vital rates in a growth–mortality space (Fig. 12); while we expect that only the combinations that define a trade-off – i.e., a positive slope – between growth and mortality can stably coexist, we do not know what the range of possible stable lines might be. To investigate these questions, we conducted a series of six sets of paired-PFT ensembles (last six rows of Table 2), each using the same 576 pairs of two-PFT, but with different values of ecosystem-level parameters that govern light competition and disturbance.

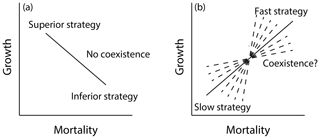
Figure 12 Growth–mortality trade-off and possible regimes of coexistence in a model like FATES along a successional axis. In a growth–mortality space, if a line connecting two PFTs comprising the system is negative as in (a), one PFT should be competitively dominant and exclude the other. If the slope of the line is positive as in (b), coexistence may be possible; however the range of slopes that may permit coexistence in tropical forests is not known a priori.

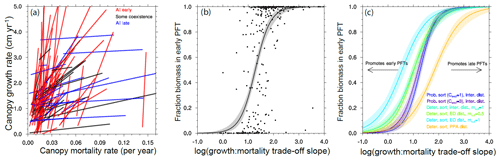
Figure 13 Competitive outcomes between two PFTs as a function of PFT growth and mortality rates along an early–late-successional continuum. Only ensemble members where a successional trade-off, i.e., one of the PFTs both grows and dies faster than the other PFT, are shown. (a) The lines connecting paired PFTs in a growth–mortality trade-off space, for a random subset of ensemble members in the reference case, are colored by the competitive outcome in each member to show the importance of the slope of the trade-off line in determining the outcome. (b–c) The relative fraction of total ecosystem biomass in the faster, early-successional PFT is plotted against the log of the ratios of the slope of the growth–mortality trade-off in each PFT pairing. Curves in (b)–(c) show a continuous logistic regression as applied to the PFT biomass fractions in each experiment. Panel (b) shows the individual ensemble members as well as the logistic regression for the reference case. Panel (c) shows only the logistic regression fit for each of the cases, demonstrating that the parameter uncertainty related to disturbance and height sorting that differentiates each ensemble leads to divergent outcomes in the relative success between early- and late-successional PFTs. See Fig. 1 for qualitative schematics of the different structural cases.

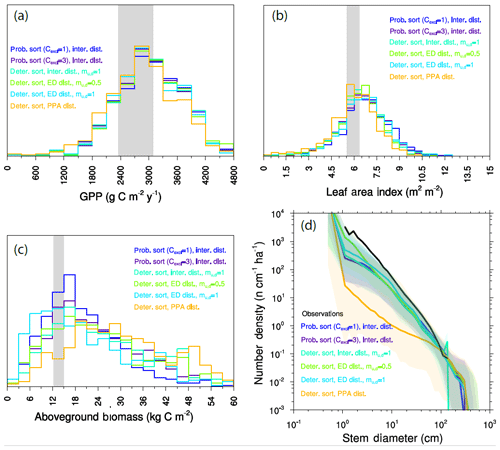
Figure 14 Ecosystem-level model results of paired PFT competition experiments. Ensemble distributions of (a) GPP, (b) LAI, (c) biomass, and (d) size distributions for each of the paired-PFT cases.

There are many different ways that a plant can grow quickly or slowly (Fig. 8). This creates a problem in trying to map sets of plant traits directly onto the potential for a given pair of trait combinations to coexist with each other. To overcome this, we first want to reduce the problem from the high-dimensional set of plant traits that we use to define a PFT to a lower-dimensional set of PFT vital rates that may act to determine the coexistence dynamics. The simplest set of rates to propose are growth and mortality rates of canopy trees. For each set of traits that comprise a PFT, we evaluate the mean growth and mortality rates for a tree of that PFT, conditional on the tree being approximately 20 cm in size and located within the canopy strata of the forest. This permits a mapping between the 12-dimensional trait space and a two-dimensional growth vs. mortality space (Fig. 8). Within this reduced space, we can evaluate the slope of lines connecting pairs of competing PFTs, as in Fig. 12, to identify the range of slopes that permit coexistence between PFT pairs. An example of this is shown in Fig. 13.

In Fig. 13a we show the lines connecting paired PFTs for a subset of ensemble members in the reference (deterministic sorting, intermediate bare ground) case. We first identify the canopy growth and mortality rates (of 20 cm diameter trees) and examine only combinations with a positive slope in a growth–mortality space, i.e., ones where we can classify an early- and late-successional PFT where the early-successional PFT has both higher growth and higher mortality rates than the late-successional PFT. We color the lines based on whether, after 300 years, there is a degree of coexistence (which we define as having less than 95 % of the biomass in either of the PFTs) and, if not, which PFT is dominant. The slope of the lines shows evident control on the competitive outcome, with high slope lines dominated by early-successional PFTs, moderate slopes having some coexistence, and low slopes dominated by late-successional PFTs.

To begin to quantitatively compare the effects of the ecosystem-level parameters on these competitive outcomes, we can first plot the fraction of biomass in each ensemble member existing in an early-successional PFT against the log of the slope of the line connecting the two PFTs in this growth–mortality trade-off space (Fig. 13b). The points follow a roughly sigmoidal shape, again showing that low slopes (i.e., small difference in growth, large difference in mortality) lead to a competitive exclusion by the late-successional PFT, large slopes (large difference in growth, small difference in mortality) lead to competitive exclusion by the early-successional PFT, and intermediate slopes can either lead to coexistence or exclusion by either of the PFTs. Following this pattern, we then fit a logistic function to the ensemble of growth–mortality trade-off slopes and coexistence states.

We can then compare the effects of the different ecosystem structural parameters by comparing the resulting fitted logistic curves for each ensemble (Fig. 13c). The differences between these curves indicate the tendency for a given set of ecosystem parameters to favor PFTs with traits and the resulting set of vital rates that make them either early or late successional: curves with a midpoint that is shifted to the left in Fig. 13c favor early-successional PFTs, and those with a midpoint shifted to the right favor late-successional PFTs. For height-sorting parameters, the more probabilistic the height sorting, the more it favors late-successional PFTs. This makes sense: at the margin, if growing tall more quickly than its neighbors is less likely to make a tree end up in the canopy, then that means that outliving its neighbors becomes relatively more important. The converse is also true in that the rapid growth of early-successional trees becomes more important if even a tiny difference in growth pays off with a position in the canopy.

For disturbance parameters, the story is slightly more complicated: in the case of no gap-generating disturbance (the pure-PPA disturbance case), early-successional strategies are highly unlikely to pay off, as there is no environmental niche for those PFTs to occupy. The converse is also true for the high-disturbance pure-ED case, which is the most conducive to early-successional PFTs as long as the disturbance generates bare ground (i.e, $m_{\mathrm{u},\mathrm{d}}=\mathrm{1}$) for new recruits to exploit. But if we reduce the intensity of disturbance by allowing a fraction of trees in the understory to survive disturbance events (by setting m_u,d to 0.5), doing so effectively counteracts the increased niche area for the fast-growing, fast-dying trees by giving slow-growing understory trees a chance to end up in newly created patches and dominate them. Thus the disturbance cases that are bare-ground intermediate (f_d=0.5, $m_{\mathrm{u},\mathrm{d}}=\mathrm{1}$) and pure ED with fractional understory mortality (f_d=1, $m_{\mathrm{u},\mathrm{d}}=\mathrm{0.5}$) are relatively similar in their relative tendency to promote success between early- and late-successional PFTs.

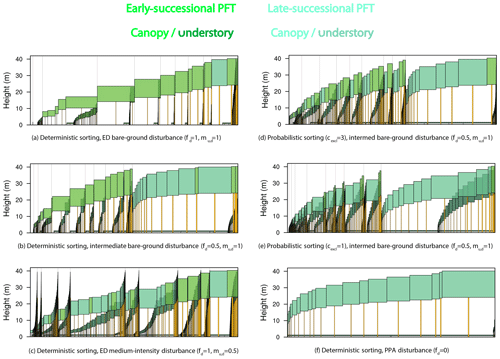
Figure 15 Forest structure and composition at year 600 of one ensemble member for each structural sensitivity experiment. Experiments are as in Figs. 13–14 and ordered from most promoting of early-successional to late-successional PFTs: (a) deterministic sorting, pure-ED, bare-ground (f_d=1, $m_{\mathrm{u},\mathrm{d}}=\mathrm{1}$) disturbance; (b) deterministic sorting, intermediate bare-ground disturbance; (c) deterministic sorting, pure-ED medium-intensity (f_d=1, $m_{\mathrm{u},\mathrm{d}}=\mathrm{0.5}$) disturbance; (d) probabilistic sorting (c_excl=3), intermediate bare-ground disturbance; (e) probabilistic sorting (c_excl=1), intermediate bare-ground disturbance; and (f) deterministic sorting, pure-PPA (f_d=0) disturbance. The same ensemble member was used for each panel so that plant traits are identical across experiments. Each panel depicts individual cohorts, arranged from tallest to shortest within a patch from right to left. The horizontal axis of each panel shows area: both cohort crown area and patch area. Older patches are to the right, with thin vertical lines separating patches. Cohort widths in the figure are proportional to the crown area of each cohort. Within the canopy, different PFTs are given different colors, with an early-successional PFT in light green and a late-successional PFT in blue–green. Understory cohorts are shaded darker than canopy cohorts.

These ecosystem-level parametric differences in the balance between competitive outcomes are large: over an order of magnitude in growth–mortality trade-off slopes separates the midpoint of the logistic regressions between the various cases in Fig. 13c. Because parameters such as f_d and m_u,d are poorly constrained at present, they represent a significant source of uncertainty in model predictions; constraining these parameters with census data thus represents an opportunity for reducing this uncertainty. Furthermore, looking at the sensitivity of the relative success of species with different growth and mortality rates across gradients of disturbance intensity or frequency may provide further benchmarks of models of this type.

Canopy growth and mortality rates are only one possible set of plant vital rates that may determine coexistence. If, instead of using canopy growth and mortality rates as the dependent variables to explain competitive outcomes produced by FATES, we substitute canopy growth rates and understory mortality rates, as may be expected given the importance of shade tolerance in defining successional strategies, we do not see a clear sigmoidal pattern as in Fig. 13. Thus, within the FATES predictions explored here, canopy mortality rates are more determinative of success than understory mortality rates.

Overall distributions of ecosystem-level model predictions (Fig. 14) are relatively similar to the earlier experiments, though some differences can be seen. GPP distributions are similar between the cases. LAI distributions are slightly shifted towards higher values in the probabilistic-height-sorting relative to the deterministic-height-sorting cases and are lower in the pure-PPA disturbance case, likely because of overall suppression of the understory in the absence of disturbance. Biomass distributions are shifted towards lower values in the probabilistic-height-sorting cases, as well as in the pure-ED case with $m_{\mathrm{u},\mathrm{d}}=\mathrm{1}$, and towards higher values in the pure-PPA disturbance case. The height sorting appears to have little effect on size distributions, while the disturbance parameters have a strong effect: the pure-PPA disturbance case has a greater deficit of small trees, while the pure-ED disturbance case has greater number of trees in the smaller size classes (but still not as many as observed). These effects on size distributions make sense from the perspective of small trees in each of these cases. In the pure-PPA disturbance case, no new patches are created, so there are no gaps in which small trees can grow. In the pure-ED disturbance case, when the m_u,d – the parameter that controls the fraction of small understory trees that both survive the death of a canopy tree above them and find themselves in a newly opened patch – is 0.5 (thus representing a medium intensity to disturbance), it provides an additional pathway for plants that are recruited into older patches to make it to the canopy. In the higher-intensity bare-ground ($m_{\mathrm{u},\mathrm{d}}=\mathrm{1}$) and pure-PPA disturbance cases, the only such pathway for plants recruited into older patches is for them to persist in the understory and grow through to the canopy, which fewer of them are able to do.

The difference in forest structure that results from these ecosystem-level parameters can be further seen in Fig. 15, which shows, in a quantitative way, the ecosystem structure as sketched out in Fig. 2 for a single ensemble member of each of the cases in Fig. 13, which maintained some degree of early–late PFT coexistence in each of the different cases. In each panel in Fig. 14a–f, the FATES patches and cohorts are drawn out and rank-ordered by height, with the tallest to the right within each patch, with cohort width proportional to the crown area occupied by each cohort, and with patches similarly arrayed with oldest to the right and the patch width proportional to the patch area. Thus the width of all canopy cohorts in a closed-canopy patch equals the width of the patch that they occupy. Cohorts are colored by PFT (color) and canopy position (shading), with yellow–green representing an early-successional PFT, blue–green representing a late-successional PFT, and darker shading of each for the understory cohorts. Shown is the final year of a 600-year set of simulations, started from bare-ground initial conditions. Differences between the cases are evident in the resulting structure of the forests. The fractional coverage of PFTs roughly follows the pattern in Fig. 13. The relative heterogeneity of patch area follows the f_d parameter, with most heterogeneous patches when f_d=1 and no heterogeneity when f_d=0. Reducing the disturbance intensity parameter m_u,d from 1 to 0.5 causes a small number of large trees, which had been in the understory prior to disturbance, to remain even in newly disturbed patches, thus making the character of patches more similar across ages. Shifting the height sorting to a more probabilistic treatment shifts the relative size distributions of canopy and understory trees within any patch. Animations of annual snapshots of one of these ensemble members are in supplementary Video SV1 (Koven, 2019b), which shows the emergence of heterogeneity in structure and composition over time. Figures 13–15 demonstrate the wide range of outcomes, both in terms of PFT composition and in the size and age structure of the forest, that result from these ecosystem-level height-sorting and disturbance parameters.

4 Conclusions

Land surface and ecosystem carbon models are highly dependent on parameters that are both imperfectly known and that may have highly diverse values within any given ecosystem. We attempt to separate some of these different controls on model dynamics by distinguishing plant trait variation from other ecosystem parameters, to explore how representing diversity in plant traits affects predictions made by a VDM, and to determine how ecosystem-level parameters govern competitive outcomes and other predictions by the model.

In a single-PFT configuration, where competitive pressures on trait values are not present, the model exhibits both some agreement and some biases as compared to a set of observations that span from physiological processes to ecosystem structure. The degree of agreement with observations is not sensitive to the choice of two related land models in which we run FATES, which both behave similarly.

As we add the effects of competitive pressures on parameter uncertainty, by increasing the number of PFTs competing within any given simulation, these shift the distributions of model predictions in a systematic way. Productivity and biomass increase as we add further PFTs to a simulation, in ways that push the model, which agrees roughly with observations of biomass and productivity in a single-PFT configuration, further from the observations as we add more diversity, even though such increased diversity in the model should better represent processes that exist in species-rich tropical forests. This emphasizes the need to better represent trade-offs that equalize competitive performance among species, so as to limit the competitive ability of any given functional type to outcompete other types. These effects of competition are only partially dependent on filtering that may occur from one generation to the next, as they are also strongly present even when we prevent advantages in population numbers to be passed on from one generation to the next.

We further explore the effects of non-trait parameter variability on competitive outcomes in a set of paired-PFT experiments to show how the competitively successful strategy between early- and late-successional traits shifts as a result of ecosystem-level parameters. In particular, the parameters that govern both disturbance and competitiveness for light have strong effects on the balance between early- and late-successional PFTs: increases to either the extent or severity of disturbance, or to the efficiency of height-based light competition, all act to shift the community towards early-successional PFTs. These differences in the PFT composition of the modeled forests feed back onto ecosystem-level predictions of states and fluxes by the model.

In order to understand how global change pressures will affect ecosystems, and in turn how ecosystem response will further feed back on global change, we must consider the role of shifts in community structure. VDMs are a promising tool to resolve these processes; however VDMs bring a high degree of complexity that adds greater uncertainty to model predictions than more simple model frameworks that may be more easily tuned to match observations. The results shown here underscore the need to better understand the roles that uncertainty in model parameters plays – both the direct role as well as the indirect roles that govern how parameter uncertainty changes competitive pressures on trait distributions at the ecosystem level. It is thus crucial to understand and integrate these types of uncertainty into projections of the Earth system.