Mineralization of organic matter in boreal lake sediments: rates, pathways, and nature of the fermenting substrates

The complexity of organic matter (OM) degradation mechanisms represents a significant challenge for developing biogeochemical models to quantify the role of aquatic sediments in the climate system. The common representation of OM by carbohydrates formulated as CH₂O in models comes with the assumption that its degradation by fermentation produces equimolar amounts of methane (CH₄) and dissolved inorganic carbon (DIC). To test the validity of this assumption, we modelled using reaction-transport equation vertical profiles of the concentration and isotopic composition (δ¹³C) of CH₄ and DIC in the top 25 cm of the sediment column from two lake basins, one whose hypolimnion is perennially oxygenated and one with seasonal anoxia. Furthermore, we modelled solute porewater profiles reported in the literature for four other seasonally anoxic lake basins. A total of 17 independent porewater datasets are analyzed. CH₄ and DIC production rates associated with methanogenesis at the five seasonally anoxic sites collectively show that the fermenting OM has a mean (± SD) carbon oxidation state (COS) value of $-\mathrm{1.4}\pm \mathrm{0.3}$. This value is much lower than the value of zero expected from carbohydrate fermentation. We conclude that carbohydrates do not adequately represent the fermenting OM in hypolimnetic sediments and propose to include the COS in the formulation of OM fermentation in models applied to lake sediments to better quantify sediment CH₄ outflux. This study highlights the potential of mass balancing the products of OM mineralization to characterize labile substrates undergoing fermentation in sediments.

1 Introduction

Significant proportions of atmospheric methane (CH₄) and carbon dioxide (CO₂), two powerful greenhouse gases, are thought to originate from freshwater lake sediments (Bastviken et al., 2004; Turner et al., 2015; Wuebbles and Hayhoe, 2002), but large uncertainties remain concerning their contribution to the global CO₂ and CH₄ budgets (Saunois et al., 2016). The role of these waterbodies in the global carbon (C) budget has been acknowledged for more than a decade (Cole et al., 2007). Especially in the lake-rich boreal region, lakes are hotspots of CO₂ and CH₄ release (Hastie et al., 2018; Wallin et al., 2018) and intensive sites of terrestrial C processing (Holgerson and Raymond, 2016; Staehr et al., 2012). Using high-resolution satellite imagery, Verpoorter et al. (2014) estimated the number of lakes on earth larger than 0.01 km² to about 27 million and reported that the highest lake concentration and surface area are found in boreal regions. Boreal lakes, which are typically small and shallow, are known to store large amounts of organic C, to warm up quickly, and to develop anoxic hypolimnia in the warm season (Sabrekov et al., 2017; Schindler et al., 1996). Owing to the great abundance of boreal lakes, their sensitivity to climate change, and their foreseen important role in the global C cycle, there is a need to further develop process-based models to better quantify C processing reactions in these lakes and their alteration under warming (Saunois et al., 2016).

In aquatic environments, CH₄ is mainly produced (methanogenesis) in the sediment along with CO₂ at depths where most electron acceptors (EAs) are depleted (Conrad, 1999; Corbett et al., 2013). During its upward migration to the atmosphere, CH₄ is partly aerobically or anaerobically oxidized to CO₂ (methanotrophy) in the upper strata of the sediments and in the water column (Bastviken et al., 2008; Beal et al., 2009; Egger et al., 2015; Ettwig et al., 2010; Raghoebarsing et al., 2006). The oxidation of organic matter (OM) by EAs such as O₂, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, Fe(III), Mn(IV), ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, and humic substances as well as the partial fermentation of high-molecular-weight organic matter (HMW OM) into lower-molecular-weight organic matter (LMW OM) are also potential sources of CO₂ in the sedimentary environment (Corbett et al., 2015). Predicting fluxes of CH₄ and CO₂ from the aquatic sediments and water column to the atmosphere is challenging considering the various transport processes and chemical and microbially mediated reactions implicated and the complexity of natural OM, which serves as substrate (Natchimuthu et al., 2017).

Process-based geochemical models taking into account both the numerous biogeochemical reactions involving C and transport processes are powerful tools that are able to interpret present-day sediment, porewater, and water-column profiles of C species and offer great potential to forecast changes in cycling of this element under variable environmental scenarios (Arndt et al., 2013; Paraska et al., 2014; Saunois et al., 2016; Wang and Van Cappellen, 1996). Nonetheless, the performance of these models depends on the correct formulation of the complete OM mineralization reactions, e.g., OM decomposition to DIC, phosphate, ammonium, and CH₄ through oxidation and fermentation reactions (Burdige, 1991), particularly in terms of the metabolizable organic compounds involved. Up to now, carbohydrates, represented as the simple chemical formula CH₂O (or C₆H₁₂O₆), whose average carbon oxidation state (COS) is zero, are commonly assumed to be representative of the bulk of metabolizable OM, including the substrates involved in fermentation reactions (e.g., Arndt et al., 2013; Arning et al., 2016; Paraska et al., 2014, and references therein). The capacity of CH₂O to represent adequately the ensemble of labile organic compounds is, nevertheless, becoming increasingly questioned in the literature given the variety and complexity of organic molecules present in the environment (Alperin et al., 1994; Burdige and Komada, 2011; Clayer et al., 2016; Jørgensen and Parkes, 2010). Based on the observation that methanogenesis produced CH₄ 3 times faster than CO₂ in the sediments of a boreal, sporadically anoxic lake basin, Clayer et al. (2018) concluded that the fermenting OM had a markedly negative COS value of −1.9. This COS value corresponds more closely to a mixture of fatty acids and fatty alcohols than to carbohydrates (e.g., CH₂O), which would have yielded equivalent CH₄ and CO₂ production rates. The low COS value of metabolizable OM in the sediment layer where methanogenesis occurred in this lake has been attributed to the nearly complete consumption of the most labile organic components (e.g., carbohydrates, proteins) during its downward transport through the water column and the upper sediment layers, thus leaving only material of lower lability such as fatty acids and fatty alcohols available for methanogenesis. Such interpretation, however, must be validated by investigating other lakes before revising the formulation of the fermenting OM used in diagenetic models in order to improve model predictions of C cycling, including greenhouse gas production and emission from these environments.

In this study, the approach described in Clayer et al. (2018), combining concentration and δ¹³C inverse modelling, is applied to the two newly acquired datasets. These datasets include centimetre-scale vertical porewater profiles of the concentrations and of the stable carbon isotope ratios (δ¹³C) of CH₄ and dissolved inorganic carbon (DIC) as well as those of the concentrations of EAs from hypolimnetic sediments of two boreal lake basins showing contrasted O₂ dynamics: one whose hypolimnion remains perennially oxygenated and the other whose hypolimnion becomes anoxic for several months annually. This procedure enables us to constrain the effective rates of OM mineralization reactions and calculate, using a mass balance equation, the COS of the substrates fermenting in the sediments in these two lake basins. In addition, we modelled solute porewater profiles gathered from the scientific literature or from our data repository for four other seasonally anoxic lake basins to estimate, using the mass balance equation, the COS of the substrates fermenting in these sediments. A total of 17 independent datasets are analyzed to provide additional insight into the COS of the fermenting OM in boreal lakes and the associated mineralization pathways.

2 Materials and methods

2.1 Study sites

This study was carried out in two small, dimictic oligotrophic and headwater lakes located within 50 km from Québec City, eastern Canada, with fully forested and uninhabited watersheds (Fig. 1). Lake Tantaré (47^∘04^′ N, 71^∘32^′ W) is part of the Tantaré Ecological Reserve and has four basins connected by shallow channels and a total surface area of 1.1 km². Lake Bédard (47^∘16^′ N, 71^∘07^′ W), lying in the protected Montmorency Forest, comprises only one small (0.05 km²) basin. The samples for this study were collected at the deepest sites of Lake Bédard (10 m) and of the westernmost basin of Lake Tantaré (15 m), hereafter referred to as Basin A of Lake Tantaré to remain consistent with our previous studies (e.g., Clayer et al., 2016; Couture et al., 2008). These two sampling sites were selected based on their contrasting O₂ regimes (Fig. 1): Lake Bédard develops an anoxic hypolimnion early in the summer (D'Arcy, 1993), whereas the hypolimnion of Lake Tantaré Basin A is perennially oxygenated (Couture et al., 2008). The O₂ diffusion depth in the sediments of Lake Tantaré Basin A, as measured with a microelectrode, does not exceed 4 mm (Couture et al., 2016).

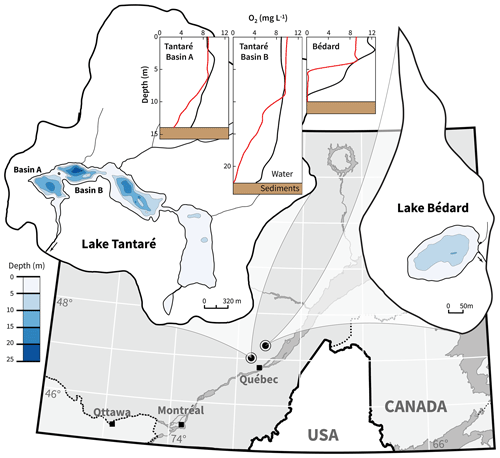
Figure 1 Location map and bathymetry of lakes Tantaré and Bédard. The bathymetric map of Lake Tantaré was reproduced from the map C-9287 of the Service des eaux de surface of the Québec Ministry of Environment. The map of Lake Bédard was reproduced from D'Arcy (1993). Dioxygen concentrations in the water column of Lake Tantaré Basins A and B and of Lake Bédard are given for June (black lines) and October (red lines).

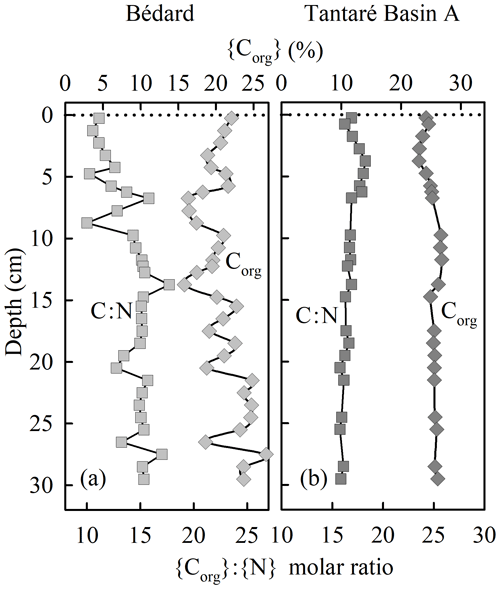
The sediment accumulation rates are 4.0–7.3 and 2.4–46.8 mg cm⁻² yr⁻¹ at the deepest sites of Lake Tantaré Basin A and Lake Bédard, respectively (Couture et al., 2010). The relatively constant organic C (C_org) content (20±2 %; Fig. 2b), the elevated {C_org}:{N} molar ratio (17±2; Fig. 2b), and the δ¹³C (−29 ‰; Joshani, 2015) and δ¹⁵N (+0.5 ‰ to −2.5 ‰; Joshani, 2015) values reported for the sediment OM over the top 30 cm in Lake Tantaré Basin A are typical of terrestrial humic substances (Botrel et al., 2014; Francioso et al., 2005). The C_org content (21±2.7 %; Fig. 2a) and {C_org}:{N} molar ratio (14±1.9; Fig. 2a) reported over the top 30 cm of Lake Bédard sediments show slightly more variation with depth but are also typical of terrestrial OM. In addition, the {C_org}:{S} ratios of both lake basin sediments (50–200) are typical of those reported for soil OM (∼125; Buffle, 1988).

Figure 2 Depth profiles of the organic C concentrations and of the C:N molar ratio in sediment cores collected at the deepest sites of Lake Bédard (a) and Lake Tantaré Basin A (b).

2.2 Sample collection

Sediment porewater samples were acquired by in situ dialysis in October 2015 with peepers (Carignan et al., 1985; Hesslein, 1976) deployed by divers within a 25 m² area at the deepest site of each lake basin. Bottom water O₂ concentrations were ∼2.5 and <0.1 mg L⁻¹ in Lake Tantaré Basin A and in Lake Bédard, respectively. The acrylic peepers comprised two columns of 4 mL cells, filled with ultrapure water and covered by a 0.2 µm Gelman HT-200 polysulfone membrane, which allowed porewater sampling from about 23–25 cm below the sediment–water interface (SWI) to 5 cm above this interface (hereafter referred to as overlying water) at a 1 cm depth resolution. Oxygen was removed from the peepers prior to their deployment, as described by Laforte et al. (2005). Four peepers were left in the sediments of each lake basin for at least 15 d, i.e., a longer time period than that required for solute concentrations in the peeper cells to reach equilibrium with those in the porewater (5–10 d; Carignan et al., 1985; Hesslein, 1976). At least three independent porewater profiles of pH; of the concentrations of CH₄, DIC, acetate, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, Fe, and Mn; and of the δ¹³C of CH₄ and DIC were generated for the two sampling sites. In Lake Bédard, samples were also collected to determine three porewater profiles of sulfide concentrations (ΣS(-II)). After peeper retrieval, samples (0.9–1.9 mL) for CH₄ and DIC concentrations and δ¹³C measurements were collected within 5 min from the peeper cells with He-purged polypropylene syringes. They were injected through rubber septa into He-purged 3.85 mL Exetainers (Labco Limited) after removal of a volume equivalent to that of the collected porewater. The Exetainers were preacidified with 40–80 µL of HCl 1N to reach a final pH ≤2. The protocols used to collect and preserve water samples for the other solutes are given by Laforte et al. (2005).

2.3 Analyses

Concentrations and carbon isotopic composition of CH₄ and DIC were measured as described by Clayer et al. (2018). Briefly, the concentrations were analyzed within 24 h of peeper retrieval by gas chromatography with a precision better than 4 % and detection limits (DLs) of 2 and 10 µM for CH₄ and DIC, respectively. The ¹³C∕¹²C abundance ratios of CH₄ and CO₂ were determined by mass spectrometry with a precision of ±0.2 ‰ when 25 µmol of an equimolar mixture of CH₄ and CO₂ was injected, and results are reported as

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=\mathrm{1000}\left({\displaystyle \frac{{\left(\frac{{{}^{\mathrm{13}}\mathrm{C}}_{\mathrm{solute}}}{{{}^{\mathrm{12}}\mathrm{C}}_{\mathrm{solute}}}\right)}_{\mathrm{sample}}}{{\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\mathrm{standard}}}}-\mathrm{1}\right),\end{array}$$

where the subscript solute stands for CH₄ or DIC, and the reference standard is Vienna Pee Dee Belemnite (VPDB). Acetate concentration was determined by ion chromatography (DL of 1.4 µM) and those of Fe, Mn, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, and ΣS(−II), as given by Laforte et al. (2005).

2.4 Inverse modelling of porewater solutes

The one-dimensional mass-conservation equation (Boudreau, 1997)

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial x}}& \left(\mathit{\phi }{D}_{\mathrm{s}}{\displaystyle \frac{\partial \left[\mathrm{solute}\right]}{\partial x}}\right)+\mathit{\phi }{\mathit{\alpha }}_{\mathrm{Irrigation}}\left(\right[\mathrm{solute}{]}_{\mathrm{tube}}\\ & -\left[\mathrm{solute}\right])+R_{\mathrm{net}}^{\mathrm{solute}}=\mathrm{0}\end{array}\end{array}$$

was used to separately model the porewater profile of each relevant solute, i.e., CH₄, DIC, O₂, Fe, and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, considering steady-state and negligible solute transport by bioturbation and advection. The validity of these assumptions has been previously demonstrated for the study sites (Couture et al., 2008, 2010; Clayer et al., 2016). In this equation, [solute] and [solute]_tube denote a solute concentration in the porewater and in the animal tubes (assumed to be identical to that in the overlying water), respectively; x is depth (positive downward); φ is porosity; D_s is the solute effective diffusion coefficient in sediments; α_Irrigation is the bioirrigation coefficient; and $R_{\mathrm{net}}^{\mathrm{solute}}$ (in moles per cubic centimetre of wet sediment per second) is the solute net production rate (or consumption rate if $R_{\mathrm{net}}^{\mathrm{solute}}$ is negative). D_s was assumed to be φ²D_w (Ullman and Aller, 1982), where D_w is the solute tracer diffusion coefficient in water. The values of D_w, corrected for in situ temperature (Clayer et al., 2018), were 9.5 $\times {\mathrm{10}}^{-\mathrm{6}}$, 6.01 $\times {\mathrm{10}}^{-\mathrm{6}}$, 1.12 $\times {\mathrm{10}}^{-\mathrm{5}}$, 5.81 $\times {\mathrm{10}}^{-\mathrm{6}}$, 3.19 $\times {\mathrm{10}}^{-\mathrm{6}}$, 1.17 $\times {\mathrm{10}}^{-\mathrm{5}}$ cm² s⁻¹ for CH₄, ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, CO₂, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, Fe, and O₂, respectively. The values of α_Irrigation in Lake Tantaré Basin A were calculated as in Clayer et al. (2016), considering that α_Irrigation varies linearly from α_{0_Irrigation} at the SWI (calculated according to Boudreau, 1984, based on an inventory of benthic animals; Hare et al., 1994) to 0 at 10 cm depth (the maximum depth at which chironomids are found in lake sediments; Matisoff and Wang, 1998) and were assumed to be 0 in Lake Bédard since its bottom water was anoxic (Fig. 1).

The $R_{\mathrm{net}}^{\mathrm{solute}}$ values were determined from the average (n=3 or 4) solute concentration profiles by numerically solving Eq. (2) with the computer code PROFILE (Berg et al., 1998). The boundary conditions were the solute concentrations at the top and at the base of the porewater profiles. In situ porewater O₂ profiles were not measured in Lake Tantaré Basin A. For modelling this solute with PROFILE, we assumed that the [O₂] in the overlying water was identical to that measured in the lake bottom water and equal to 0 below 0.5 cm (based on O₂ penetration depth; Couture et al., 2016). This procedure provides a rough estimate of $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$ at the same vertical resolution as for the other solutes. The code PROFILE yields a discontinuous profile of discrete $R_{\mathrm{net}}^{\mathrm{solute}}$ values over depth intervals (zones), which are objectively selected by using the least square criterion and statistical F testing (Berg et al., 1998). In order to estimate the variability in $R_{\mathrm{net}}^{\mathrm{solute}}$ related to heterogeneity within the 25 m² sampling area, additional $R_{\mathrm{net}}^{\mathrm{solute}}$ values were obtained by modelling the average profiles whose values were increased or decreased by 1 standard deviation. This variability generally ranges between 2 and 10 fmol cm⁻³ s⁻¹.

In addition, the computer program WHAM 6 (Tipping, 2002) was used, as described by Clayer et al. (2016), to calculate the speciation of porewater cations and anions. The solute activities thus obtained, together with solubility products (K_s), were used to calculate saturation index values ($\mathrm{SI}=\log \mathrm{IAP}/K_{\mathrm{s}}$, where IAP is the ion activity product).

2.5 Reaction network

The main reactions retained in this study to describe carbon cycling in the sediments of the two lake basins are shown in Table 1. R_i and α_i denote, respectively, the effective (or gross) reaction rate and the carbon isotopic fractionation factor associated with each Reaction (Ri; Table 1). Once oxidants are depleted, fermentation of metabolizable OM of general formula C_xH_yO_z can yield acetate, CO₂, and H₂ (Reaction 1). The coefficient ν₁ in Reaction (R1) constrains the relative contribution of acetoclasty and hydrogenotrophy. The partial degradation of high-molecular-weight OM (HMW OM) into lower-molecular-weight OM (LMW OM) can also produce CO₂ (Reaction R2; Corbett et al., 2013, 2015). Acetoclasty (Reaction R3) and hydrogenotrophy (Reaction R4) yield CH₄. Moreover, CH₄ (Reaction R5) and OM (Reaction R6) can be oxidized to CO₂ when electron acceptors such as O₂, Fe(III), and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ are present. Note that the electron acceptors (EAs) ${\mathrm{NO}}_{\mathrm{3}}^{-}$ and Mn oxyhydroxides were shown to be negligible in these two lake basins (Clayer et al., 2016; Feyte et al., 2012) as well as the precipitation of carbonates whose saturation index values are negative (SI $\le -\mathrm{1.5}$), except for siderite (Reaction R7) in Lake Bédard (SI =0.0 to 0.7 below 10 cm depth).

Table 1 Reactions considered (R1–R7), their reaction rates (R₁–R₇), and carbon isotopic fractionation factors (α₁–α₇).

^a Where ν₁ can have any value between 0 and x, and values for ν₂–ν₄ are unknown. ^b HMW OM and LMW OM designate high- and lower-molecular-weight organic matter, respectively.

2.6 Determining realistic ranges for effective reaction rates

Considering the net reaction rates obtained by inverse modelling, a realistic range of values can be given for each of the effective reaction rates R_i in each depth interval using the general equations described below. The detailed calculations for each R_i at both study sites are described in Sect. S2.

From Table 1, the net rate of CH₄ production, $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$, in the sediments is

$$\begin{array}{}\text{(3)}& R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}=R_{\mathrm{3}}+R_{\mathrm{4}}-R_{\mathrm{5}},\end{array}$$

where R₃ and R₄ are the rates of acetoclastic (Reaction R3) and hydrogenotrophic (Reaction R4) production of CH₄, respectively, and R₅ is the rate of DIC production due to CH₄ oxidation (Reaction R5). The net rate of DIC production, $R_{\mathrm{net}}^{\mathrm{DIC}}$, can be expressed as

$$\begin{array}{}\text{(4)}& R_{\mathrm{net}}^{\mathrm{DIC}}=R_{\mathrm{1}}+R_{\mathrm{2}}+R_{\mathrm{3}}-R_{\mathrm{4}}+R_{\mathrm{5}}+R_{\mathrm{6}}-R_{\mathrm{7}},\end{array}$$

where R₁, R₂, and R₆ are the rates of DIC production due to complete fermentation of labile OM (Reaction R1), partial fermentation of HMW OM (Reaction R2), and OM oxidation (Reaction R6), respectively, and R₇ is the rate of DIC removal by siderite precipitation (Reaction R7). It can also be written that

$$\begin{array}{}\text{(5)}& R_{\mathrm{net}}^{\mathrm{Ox}}=-\mathrm{2}{R}_{\mathrm{5}}-R_{\mathrm{6}},\end{array}$$

where $R_{\mathrm{net}}^{\mathrm{Ox}}$ is the net reaction rate of all relevant oxidant consumption, i.e., O₂, Fe(III), and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ only because ${\mathrm{NO}}_{\mathrm{3}}^{-}$ and Mn(IV) are negligible (see above). For simplicity, $R_{\mathrm{net}}^{\mathrm{Ox}}$ is expressed in equivalent moles of O₂ consumption rate, taking into account that ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and Fe(III) have twice and one quarter the oxidizing capacity of O₂, respectively. In practice, the value of $R_{\mathrm{net}}^{\mathrm{Ox}}$ was calculated by adding those of $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$, $\frac{\mathrm{1}}{\mathrm{4}}{R}_{\mathrm{net}}^{\mathrm{Fe}\left(\mathrm{III}\right)}$, and $\mathrm{2}{R}_{\mathrm{net}}^{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$, where $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$, $R_{\mathrm{net}}^{\mathrm{Fe}\left(\mathrm{III}\right)}$, and $R_{\mathrm{net}}^{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$ were estimated with PROFILE. In this calculation, we assumed that all dissolved Fe is in the form of Fe(II), and that the rate of Fe(II) consumption through Reaction (R7) is negligible compared to those associated with Reactions (R5) and (R6). Under these conditions, $R_{\mathrm{net}}^{\mathrm{Fe}\left(\mathrm{III}\right)}$ equals $-R_{\mathrm{net}}^{\mathrm{Fe}}$. It should be noted that using $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$, $-R_{\mathrm{net}}^{\mathrm{Fe}}$, and $R_{\mathrm{net}}^{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$ to calculate $R_{\mathrm{net}}^{\mathrm{Ox}}$, we indirectly take into account the reoxidation of reduced S and Fe(II), respectively, to ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and Fe(III) by O₂. Indeed, with this procedure, we underestimate the terms $\frac{\mathrm{1}}{\mathrm{4}}{R}_{\mathrm{net}}^{\mathrm{Fe}\left(\mathrm{III}\right)}$ and $\mathrm{2}{R}_{\mathrm{net}}^{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$ because reoxidation reactions are ignored, but we overestimate by the same amount the term $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$. In other words, omission of these reoxidation reactions affects only the relative consumption rates of individual oxidants and not the value of $R_{\mathrm{net}}^{\mathrm{Ox}}$, which is of interest here.

2.7 Constraining effective reaction rates with δ¹³C modelling

Once the range of values has been determined for each of the effective rates R_i (see Table S2), they can be used in another reaction-transport equation to model the δ¹³C profiles of CH₄ and DIC. Only sets of R_i values that yield acceptable modelled δ¹³C profiles, i.e., which fall within 1 standard deviation of the measured δ¹³C profiles (grey area fills in Fig. 4), were kept for COS calculation below (Sect. 2.8). The δ¹³C modelling procedure is summarized below and described in detail in Section S2. This procedure takes into account the effect of diffusion and bioirrigation (in Lake Tantaré Basin A) and the isotopic fractionation effect of each Reaction (Ri).

Briefly, the δ¹³C profiles of CH₄ (δ¹³C–CH₄) and DIC (δ¹³C–DIC) were simulated with a modified version of Eq. (1) (Clayer et al., 2018):

$$\begin{array}{}\text{(6)}& {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=\mathrm{1000}\left({\displaystyle \frac{{\left(\frac{\left[{}^{\mathrm{13}}\mathrm{C}\right]}{\left[C\right]}\right)}_{\mathrm{sample}}}{{\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\mathrm{standard}}}}-\mathrm{1}\right),\end{array}$$

where [C] is the total CH₄ or DIC concentration ([¹²C] can be replaced by [C] since ∼99 % of C is ¹²C), and [¹³C] is the isotopically heavy CH₄ or DIC concentration. Equation (6) allows for calculating a δ¹³C profile once the depth distributions of [¹³C] and [C] are known. This information is obtained by solving the mass-conservation equations of C and ¹³C for CH₄ and DIC. The one-dimensional mass conservation of [C] is given by Eq. (2), where [solute] is replaced by [C], whereas that for [¹³C] is the following modified version of Eq. (2) (Clayer et al., 2018):

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial x}}& \left(\mathit{\phi }{\displaystyle \frac{D_{\mathrm{s}}}{f}}{\displaystyle \frac{\partial \left[{}^{\mathrm{13}}\mathrm{C}\right]}{\partial x}}\right)+\mathit{\phi }{\mathit{\alpha }}_{\mathrm{Irrigation}}\left({\left[{}^{\mathrm{13}}\mathrm{C}\right]}_{\mathrm{tube}}-\left[{}^{\mathrm{13}}\mathrm{C}\right]\right)\\ & +\sum _{i=\mathrm{1}}^{\mathrm{5}}{\displaystyle \frac{R_i}{{\mathit{\alpha }}_i}}\left({\displaystyle \frac{{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_i^{\mathrm{reactant}}}{\mathrm{1000}}}+\mathrm{1}\right){\left({\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}\right)}_{\mathrm{standard}}=\mathrm{0},\end{array}\end{array}$$

where f, the molecular diffusivity ratio, is the diffusion coefficient of the regular solute divided by that of the isotopically heavy solute; α_i is the isotope fractionation factor in Reaction (Ri); and ${{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_i^{\mathrm{reactant}}$ is the δ¹³C of the reactant leading to the formation of the solute (CH₄ or DIC) in Reaction (Ri). Input and boundary conditions used to numerically solve Eqs. (2) and (7) for [C] and [¹³C], respectively, via the bvp5c function of MATLAB^® are described in Sects. 3.4 and S2 of the Supplement.

The goodness of fit of the model was assessed with the norm of residuals (N_res):

$$\begin{array}{}\text{(8)}& N_{\mathrm{res}}=\sqrt{\sum _{x=\mathrm{0.5}}^{\mathrm{22.5}}{\left({{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{m}}-{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{s}}\right)}^{\mathrm{2}}},\end{array}$$

where ${{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{m}}$ and ${{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{s}}$ are the measured and simulated δ¹³C values, respectively. The norm of residuals (N_res) varies between 0 and infinity, with smaller numbers indicating better fits.

2.8 COS calculation

Considering the complete fermentation of metabolizable OM of general formula C_xH_yO_z and making two assumptions, described below for clarity, the COS of the fermenting molecule is given by combining Eqs. S8 and S15 (see Sect. S2 for details):

$$\begin{array}{}\text{(9)}& \mathrm{COS}=-\mathrm{4}\left({\displaystyle \frac{R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}-R_{\mathrm{net}}^{\mathrm{DIC}}-R_{\mathrm{net}}^{\mathrm{Ox}}+R_{\mathrm{2}}}{R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}+R_{\mathrm{net}}^{\mathrm{DIC}}+\left(\mathrm{1}-{\mathit{\chi }}_{\mathrm{M}}\right)R_{\mathrm{net}}^{\mathrm{Ox}}-R_{\mathrm{2}}}}\right),\end{array}$$

where χ_M is the fraction of oxidants consumed by methanotrophy. Equation (9) is only valid if (i) Reaction (R1) is the only source of substrates for hydrogenotrophy and acetoclasty (this assumption is discussed in Sect. 4.2 below) and if (ii) siderite precipitation (Reaction R7) is negligible (saturation index for siderite is negative except below 10 cm depth in the sediment of Lake Bédard; this case is considered in Sect. S2.1.2.2). With values of $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$ and $R_{\mathrm{net}}^{\mathrm{Ox}}$ obtained from PROFILE (Sect. 2.4) and values of R₂ and χ_M constrained by δ¹³C modelling (Sect. 2.7), Eq. (9) can be used to calculate the COS of the fermenting molecule.

2.9 Data treatment of other datasets

To better assess the COS of the fermenting OM in lakes, relevant sets of porewater concentration profiles (CH₄, DIC, EAs, Ca) available from the literature or from our data repository have been modelled with the code PROFILE, as described in Sect. 2.3, to extract their $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$, $R_{\mathrm{net}}^{\mathrm{DIC}}$, and $R_{\mathrm{net}}^{\mathrm{Ox}}$ profiles. These porewater datasets, described in Sect. S3 of the Supplement, had been generated by sampling porewater in the hypolimnetic sediments of (i) Lake Bédard and Basin A of Lake Tantaré on other dates than for this study (Clayer et al., 2016); (ii) Basin B of Lake Tantaré (adjacent to Basin A; Fig. 1) on four occasions (Clayer et al., 2016; 2018); (iii) Williams Bay of Jacks Lake (44^∘41^′ N, 78^∘02^′ W), located in Ontario, Canada, on the edge of the Canadian Shield (Carignan and Lean, 1991); and (iv) the southern basin of the subalpine Lake Lugano (46^∘00^′ N, 3^∘30^′ E), located in Switzerland, on two occasions (Lazzaretti-Ulmer and Hanselmann, 1999). All lake basins except Basin A of Lake Tantaré develop an anoxic hypolimnion.

3 Results

3.1 Solute concentration profiles

Differences among the replicate profiles of CH₄, DIC, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, ΣS(-II), and Fe (Fig. 3) at the two sampling sites are generally small (except perhaps those of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ in Lake Bédard) and should be mainly ascribed to spatial variability within the 25 m² sampling area. Indeed, the main vertical variations in the profiles are defined by several data points without the sharp discontinuities expected from sampling and handling artifacts. Note that the acetate concentrations, which were consistently low (<2 µM), are not shown.

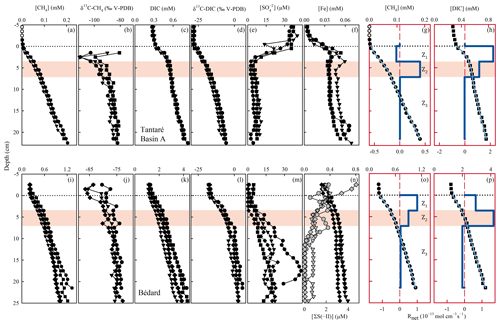
Figure 3 Replicate porewater profiles of CH₄ (a, i), δ¹³C–CH₄ (b, j), DIC (c, k), δ¹³C–DIC (d, l), ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ (e, m), Fe, and ΣS(-II) (f, n), and comparison of the modelled (blue lines) and average (n=3) measured (symbols) concentration profiles of CH₄ (g, o) and DIC (h, p) in Lakes Tantaré Basin A (a–h) and Bédard (i–p). Different symbols indicate data from different peepers and empty symbols are for concentrations below detection limit. The horizontal dotted line indicates the sediment–water interface. The thick and thin blue lines represent the net solute reaction rate ($R_{\mathrm{net}}^{\mathrm{solute}}$) and the modelled concentration profiles, respectively. The red area fills correspond to the sediment zones Z₂.

The low Fe (<5 µM; Fig. 3f) and CH₄ (<2 µM; Fig. 3a) concentrations as well as the relatively high ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations (36 ± 2.1 µM; Fig. 3e) in the sediment-overlying water of Lake Tantaré Basin A are all consistent with the [O₂] (∼2.5 mg L⁻¹) measured in the bottom water and are indicative of oxic conditions at the sediment surface. The sharp Fe gradients near the SWI indicate an intense recycling of Fe oxyhydroxides (Fig. 3f; Clayer et al., 2016), and the concave-down curvatures in the ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ profiles (Fig. 3e) reveal ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ reduction near the SWI. In contrast to Lake Tantaré Basin A, high Fe (>200 µM), measurable CH₄ (>200 µM), low ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ (2.7 ± 1.4 µM), and detectable ΣS(-II) concentrations in the overlying waters of Lake Bédard (Fig. 3i, m and n) are consistent with anoxic conditions at the sediment surface. The absence of a sharp Fe gradient at the SWI in Lake Bédard suggests that Fe oxyhydroxides were not recycled in these sediments when porewater sampling occurred.

In the two lake basins, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations reach a minimum between the SWI and 5 cm depth (Fig. 3e and m) and increase below these depths. While increasing ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations with sediment depth are unusual in lake sediments, the mineralization of sulfur-containing OM in the sediment can be a source of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ in low-${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ environments (Fakhraee et al., 2017). Although unravelling the sediment sulfur cycling is beyond the scope of this study, we note that ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ generation through OM mineralization would be consistent with the fact that the dominant sulfur pool in Lake Tantaré Basin A is bound to sediment OM (Couture et al., 2016).

The concentrations of CH₄ (<1.5 mM; Fig. 3a and i) are well below saturation at 4 ^∘C and in situ pressure (4.4–5.5 mM; Duan and Mao, 2006), implying that CH₄ ebullition is a negligible CH₄ transport process. The CH₄ values increase from <2 µM in the overlying water to 0.18–0.20 mM at the base of the Lake Tantaré Basin A profiles (Fig. 3a) and from 0.2–0.5 to 1.0–1.4 mM in those of Lake Bédard (Fig. 3i). The three CH₄ profiles from Lake Tantaré Basin A (Fig. 3a) show a modest concave-up curvature in their upper part, close to the SWI, indicative of a net CH₄ consumption, and a convex-up curvature in their lower part, typical of a net CH₄ production. Such trends, however, are not observed in Lake Bédard sediments. The CH₄ profiles from this lake exhibit a convex-up curvature over the whole sediment column, although it is more pronounced in its upper part (Fig. 3i).

The DIC concentrations consistently increase from 0.27–0.32 and 1.2–1.5 mM in the sediment-overlying water to 0.76–0.83 and 3.5–4.3 mM at the bottom of the profiles in Lake Tantaré Basin A and Lake Bédard, respectively (Fig. 3c and k). All DIC profiles show a similar shape with a slight concave-up curvature in their lower segment and a convex-up curvature in their upper portions.

3.2 Modelled CH₄ and DIC concentration profiles

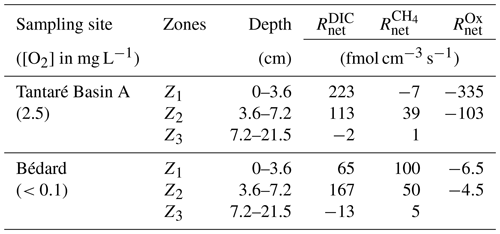
The modelled [CH₄] and DIC profiles accurately fit the average (n=3 or 4) data points (r²>0.996 and r²>0.998 for CH₄ and DIC, respectively; Fig. 3g, h, o, and p). The $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$ profiles reveal three zones in each lake basin, numbered Z₁, Z₂, and Z₃, from the sediment surface whose boundaries match those defined by the $R_{\mathrm{net}}^{\mathrm{DIC}}$ profiles. For Lake Tantaré Basin A, Z₁ corresponds to a net CH₄ consumption and Z₂ and Z₃ to net CH₄ production, with the highest rate in Z₂ (Fig. 3g). In contrast, the three zones in Lake Bédard show net CH₄ production, with the highest rate in Z₁ and the lowest in Z₃ (Fig. 3o). The $R_{\mathrm{net}}^{\mathrm{DIC}}$ profiles in both lake basins show a zone of net DIC consumption below two zones of net DIC production, with the highest rate values in the Z₁ and Z₂ for Lake Tantaré Basin A and Lake Bédard, respectively.

The $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$ and $R_{\mathrm{net}}^{\mathrm{DIC}}$ profiles displayed in Fig. 3 are, among all the possible solutions, the ones that give the simplest rate profile while providing a satisfying explanation of the averaged solute concentration profile as determined by statistical F testing implemented in the code PROFILE (P value ≤0.001 except for the $R_{\mathrm{net}}^{\mathrm{DIC}}$ profile in Lake Bédard, whose P value is ≤0.005). As an additional check of the robustness of the depth distribution of $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$ and $R_{\mathrm{net}}^{\mathrm{DIC}}$ provided by PROFILE, we used another inverse model, i.e., Rate Estimation from Concentrations (REC; Lettmann et al., 2012), to model the average CH₄ and DIC profiles. Note that the statistical method, implemented in REC to objectively select the depth distribution of the net reaction rates, i.e., the Tikhonov regularization technique, differs from that of PROFILE. Figure S1 (Supplement) shows that the two codes predicted mutually consistent $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$ and $R_{\mathrm{net}}^{\mathrm{DIC}}$ profiles, with rate values of similar magnitude. PROFILE was also used to estimate $R_{\mathrm{net}}^{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$, $R_{\mathrm{net}}^{\mathrm{Fe}}$, and $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$ in order to calculate the value of $R_{\mathrm{net}}^{\mathrm{Ox}}$ in each zone at both sampling sites (see Sect. 2.3 for details). The modelled [${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$] and [Fe] profiles accurately fit the data points (r²>0.983; Fig. S3). As expected from the contrasting O₂ regimes of the two lake basins, $R_{\mathrm{net}}^{\mathrm{Ox}}$ values for Lake Tantaré Basin A were 1 to 2 orders of magnitude higher than those for Lake Bédard. The values of $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$, $R_{\mathrm{net}}^{\mathrm{DIC}}$, and $R_{\mathrm{net}}^{\mathrm{Ox}}$ estimated in each zone of each lake basin are reported in Table 2.

Table 2 Net production rates ($R_{\mathrm{net}}^{\mathrm{solute}}$) of CH₄, DIC, and oxidants obtained with the code PROFILE in the three CH₄ consumption and production zones (Z₁, Z₂, and Z₃) for both sampling sites.

3.3 Measured δ¹³C profiles

The δ¹³C–DIC values increase from $-\mathrm{28.2}\pm \mathrm{0.4}$ ‰ and $-\mathrm{17.2}\pm \mathrm{0.7}$ ‰ in the overlying water to $-\mathrm{5.1}\pm \mathrm{1.0}$ ‰ and 3.6 ± 1.7 ‰ at the base of the profiles in Lake Tantaré Basin A and Lake Bédard, respectively (Figs. 3d and l). Similarly, the δ¹³C–CH₄ values in Lake Bédard increase steadily from $-\mathrm{82.5}\pm \mathrm{3.3}$ ‰ in the overlying water to $-\mathrm{74.0}\pm \mathrm{1.5}$ ‰ at 24.5 cm depth (Fig. 3j). Regarding Lake Tantaré Basin A, the CH₄ concentrations above 1.5 cm depth were too low for their ¹³C∕¹²C ratio to be determined. Starting at 1.5 cm depth, the δ¹³C–CH₄ values first decrease from $-\mathrm{91.1}\pm \mathrm{11.1}$ ‰ to $-\mathrm{107.0}\pm \mathrm{6.8}$ ‰ at 2.5 cm depth and then increase progressively to $-\mathrm{83.5}\pm \mathrm{1.6}$ ‰ at the base of the profiles (Fig. 3b). Note that a shift toward more positive δ¹³C–CH₄ values upward, generally attributed to the oxidation of CH₄ (Chanton et al., 1997; Norði et al., 2013), is only observed in the profiles of Lake Tantaré Basin A (Fig. 3b).

As shown in Fig. S2 (Supplement), the isotopic signatures of nearly all samples from the two lake basins fall within the ranges reported for hydrogenotrophic methanogenesis, i.e., CO₂ reduction, in a δ¹³C–CO₂ vs. δ¹³C–CH₄ graph similar to that proposed by Whiticar (1999). Indeed, the values of δ¹³C–CH₄, all of which are lower than −70 ‰ over the whole profiles in the two lake basins, and the large difference (67 ‰ to 92 ‰) between the δ¹³C of gaseous CO₂ (δ¹³C–CO₂) and δ¹³C–CH₄ strongly contrast with the typical δ¹³C–CH₄ values (−68 ‰ to −50 ‰) and with the difference between δ¹³C–CO₂ and δ¹³C–CH₄ (39 ‰ to 58 ‰) reported for acetoclasty (Whiticar, 1999). The δ¹³C results reported previously for another basin of Lake Tantaré (Basin B; Clayer et al., 2018) also show in the hydrogenotrophy domain in Fig. S2.

3.4 Modelled δ¹³C profiles

In order to model the δ¹³C profiles with Eq. (6), accurate profiles of [C] and [¹³C] first need to be determined by numerically solving Eqs. (2) and (7), respectively. The modelled profiles of [CH₄] and DIC obtained with Eq. (2) perfectly replicated the measured profiles of these two solutes. Getting a truthful profile of [¹³C] with Eq. (7) requires accurate values of ${{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_i^{\mathrm{reactant}}$, α_i, and R_i for each of the reactions given in Table 1 and of f for both CH₄ (f−CH₄) and DIC (f−DIC). The multistep procedure to obtain the best [¹³C] profiles for CH₄ and DIC is described in Sect. S2 (Supplement) and allowed us to constrain the f, χ_Mα_i, and R_i values.

Table 3 Molecular diffusivity ratio of CH₄ (f−CH₄) as well as the isotopic fractionation factors (α₁, α₂, α₄–α₇), the fraction of oxidant used by methanotrophy (χ_M), and rates (R₁, R₂, R₄–R₇; fmol cm⁻³ s⁻¹) of each reaction involved in OM mineralization in each zone and for the whole sediment column (ΣR_i; fmol cm⁻² s⁻¹) corresponding to the lowest values of N_res. At both study sites, R₃ was shown to be negligible. See Sect. S2 of the Supplement for details.

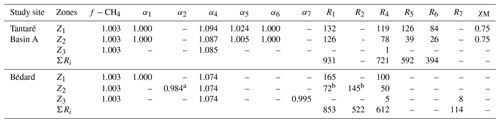
^a The optimal value of α₂, given here for a COS value of −1.5, varies slightly with the COS value (see Sect. S2.2.2.3 of the Supplement). ^b The values of R₁ and R₂, given here
for a COS value of −1.5, vary with the COS value (see Sect. S2.2.2.3 of the Supplement).

The best fits between the simulated and measured δ¹³C profiles of CH₄ and DIC for Lake Tantaré Basin A and Lake Bédard (red lines in Fig. 4) were obtained with the f, α_i, and R_i values displayed in Table 3. The optimal α_i and f values were within the ranges reported in the literature for both lake basins and similar to those reported in our previous study on Lake Tantaré Basin B (Clayer et al., 2018), except for the lower-than-expected value of α₂ (0.984) in the Z₂ of Lake Bédard. Modelled δ¹³C profiles were considered acceptable only when they fell within 1 standard deviation of the measured δ¹³C profiles (grey area fills in Fig. 4). Acceptable modelled δ¹³C profiles were obtained only when methanogenesis was 100 % hydrogenotrophic, i.e., when R₃=0 (see Sect. S2.2.2.1).

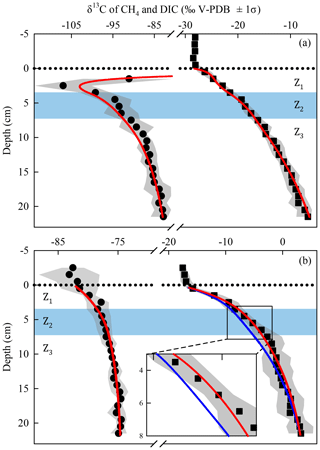
Figure 4 Comparison of the simulated (lines) and measured average (n=3) δ¹³C profiles of CH₄ (circles) and DIC (squares) in the porewater of Lake Tantaré Basin A (a) and Lake Bédard (b). The dotted horizontal line indicates the sediment–water interface. The variability in δ¹³C values (±1 standard deviation – σ) related to the spatial heterogeneity within the sampling area is shown by the grey area fills. The zone Z₂ is delimited by the blue area fill. In panel (b), the blue lines are the profiles simulated with the default rate values and optimal α_i and f values as described in Sect. S2.2.1. The red lines in panel (b) are the profiles simulated with α₂ values of 0.980–0.984 (see Sect. 4.1 for details).

The sharp upward depletion in ¹³C–CH₄ leading to a minimum δ¹³C–CH₄ value at 2.5 cm depth in Lake Tantaré Basin A sediments (Fig. 4a) was unanticipated since it occurs in the methanotrophic zone, i.e., where the remaining CH₄ is expected to be ¹³C-enriched as a result of CH₄ oxidation. Marked ¹³C–CH₄ depletions at the base of the sulfate–methane transition zone, where CH₄ is consumed via ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ reduction, have often been observed in marine sediments (Burdige et al., 2017, and references therein). Such features are generally attributed to the production of CH₄ by hydrogenotrophy from the ¹³C-depleted DIC resulting from the anaerobic CH₄ oxidation, a process referred to as intertwined methanotrophy and hydrogenotrophy (e.g., Borowski et al., 1997; Burdige et al., 2017; Pohlman et al., 2008). Here the modelled δ¹³C–CH₄ profile captured the minimum in δ¹³C–CH₄ in the Z₁ by simply assuming concomitant hydrogenotrophy and methanotrophy in this zone and an upward-increasing α₄ value from 1.085 in the Z₃ to 1.094 in the Z₁ (Sect. S2.2.1 of the Supplement). A small variation with sediment depth in the fractionation factor α₄ is arguably possible since its value depends on the types of microorganisms producing CH₄ (Conrad, 2005).

4 Discussion

4.1 Organic matter mineralization pathways at the sampling sites

The porewater data as well as the combined modelling of carbon isotopes and concentration profiles allow us to highlight key OM mineralization mechanisms and to quantify the relative contribution of methanogenesis and fermentation to OM degradation at both sampling sites. The ¹³C isotopic signatures, i.e., highly negative values of δ¹³C–CH₄ and large differences between δ¹³C–CO₂ and δ¹³C–CH₄ (Sect. 3.3 and Fig. S2 in the Supplement), as well as the modelling of the δ¹³C–CO₂ and δ¹³C–CH₄ profiles (Sect. S2.2.2.1 and Fig. S4a and b in the Supplement) all point to hydrogenotrophy as being the only pathway for methanogenesis in the two lake basins. The dominance of hydrogenotrophy is also consistent with the finding that acetate concentrations were close to or below DL in the porewater samples. Under the condition that acetoclasty is negligible (i.e., x=ν₁), Reaction (R1) from Table 1 becomes

$$\begin{array}{}\text{(10)}& {\mathrm{C}}_x{\mathrm{H}}_y{\mathrm{O}}_z+\left(\mathrm{2}x-z\right){\mathrm{H}}_{\mathrm{2}}\mathrm{O}\stackrel{R_{\mathrm{1}}}{⟶}x{\mathrm{CO}}_{\mathrm{2}}+\left(\mathrm{2}x+{\displaystyle \frac{y}{\mathrm{2}}}-z\right){\mathrm{H}}_{\mathrm{2}}.\end{array}$$

Methanogenesis was also reported to be essentially hydrogenotrophic in the sediments of Basin B of Lake Tantaré (Clayer et al., 2018). The absence of acetoclasty in the sediments of the oligotrophic lakes Bédard and Tantaré is consistent with the consensus that hydrogenotrophy becomes an increasingly important CH₄ production pathway (i) when labile OM is depleted (Chasar et al., 2000; Hornibrook et al., 2000; Whiticar et al., 1986), (ii) with increasing sediment or soil depth (Conrad et al., 2009; Hornibrook et al., 1997), or (iii) with decreasing rates of primary production in aquatic environments (Galand et al., 2010; Wand et al., 2006).

The modelling of concentrations and δ¹³C profiles revealed that oxidative processes occurred essentially in the upper 7 cm of the sediments of the perennially oxygenated Lake Tantaré Basin A, i.e., mainly in the Z₁ and, to a lesser extent, in the Z₂ (Table 3 and Sects. S2.1.2.1 and S2.1.2.2 of the Supplement). Moreover, it showed that methanotrophy was the dominant oxidative reaction in these sediment layers since 75 % of the oxidants were consumed through Reaction (R5) (Sect. S2.2.2.2 of the Supplement). This outcome is consistent with several studies showing that methanotrophy occurs at higher rates than OM oxidation at low EA concentrations (Kankaala et al., 2013; Pohlman et al., 2013; Sivan et al., 2007; Thottathil et al., 2019). Methanotrophy is also evidenced in the Z₁ of this lake basin by the negative $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$ value and by a shift of the δ¹³C–CH₄ profiles to more positive values in their upper part (Fig. 3b and g). Use of Eq. (2) to model the EA profiles with the code PROFILE predicts that O₂ was by far the main EA involved either directly or indirectly via the coupling with the Fe or S cycles in the oxidative processes. Indeed, comparing the values of $R_{\mathrm{net}}^{{\mathrm{O}}_{\mathrm{2}}}$ and $R_{\mathrm{net}}^{\mathrm{Ox}}$ (see Sect. 3.2 and Table 2) shows that O₂ accounts for 87 % and 70 % of the oxidants consumed in the Z₁ and Z₂ of Lake Tantaré Basin A, respectively. Since O₂ penetration in the sediment by molecular diffusion is limited to ∼4 mm, a significant amount of O₂ is predicted by Eq. (2) to be transported deeper in the sediment through bioirrigation. The predominance of O₂ among the EAs consumed in the sediments is consistent with our previous study in this basin of Lake Tantaré (Clayer et al., 2016). Given that methanotrophy is the dominant oxidative process and that O₂ is the main oxidant consumed, it is probable that aerobic oxidation of methane prevails over its anaerobic counterpart in this lake basin. This is in line with the common thinking that CH₄ oxidation in freshwater lake sediments is carried out by methanotrophs essentially in the uppermost oxic sediment layer (Bastviken et al., 2008, and references therein).

In the Z₂ of Lake Bédard, the net rate of DIC production (i.e., 167 fmol cm⁻³ s⁻¹) was more than 3 times that of CH₄ production (50 fmol cm⁻³ s⁻¹; Table 2). Given that the $R_{\mathrm{net}}^{\mathrm{Ox}}$ was negligible in this zone (i.e., $R_{\mathrm{5}}=R_{\mathrm{6}}=\mathrm{0}$), we obtain from Eqs. (3) and (4) and Table 2 $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}=R_{\mathrm{4}}=\mathrm{50}$ fmol cm⁻³ s⁻¹ and $R_{\mathrm{net}}^{\mathrm{DIC}}=R_{\mathrm{1}}+R_{\mathrm{2}}-R_{\mathrm{4}}=\mathrm{167}$ fmol cm⁻³ s⁻¹ (see Sect. S2.1.2.2 of the Supplement). Should we assume that DIC production by Reaction (R2) is negligible, i.e., R₂=0, an R₁∕R₄ ratio of 4.3 would be obtained. This high ratio indicates that DIC was not produced by fermentation (Reaction R1) alone in the Z₂ of this lake. Indeed, methanogenesis through the coupling of Reactions (R1) and (R4) yields an R₁∕R₄ ratio of 2 if the fermenting substrate is carbohydrates (COS of 0) and lower than 2 if the fermenting substrate has a negative COS value. We thus attributed the production of the additional DIC to the partial fermentation of HMW OM, an assumed nonfractionating process reported to occur in wetlands (Corbett et al., 2015). The better fitting of the δ¹³C–DIC profile when α₂ is set to 0.980–0.984 rather than to 1.000 in the Z₂ (compare the blue and red lines in Fig. 4b) suggests that C fractionates during this partial fermentation process.

Table 3 displays the depth-integrated reaction rates (ΣR_i) over the top 21 cm of the sediment column, which are given by

$$\begin{array}{}\text{(11)}& \mathrm{\Sigma }{R}_i=\sum _{j=\mathrm{1}}^{\mathrm{3}}\mathrm{\Delta }{x}_j{R}_i,\end{array}$$

where Δx_j (cm) is the thickness of the zone Z_j. In this calculation, we assume that other zones of CH₄ or DIC production are absent below 21 cm. Values of ΣR_i clearly show that anaerobic carbon mineralization reactions (fermentation and methanogenesis) are important contributors to the overall OM mineralization in the two studied lake basins. Indeed, the sum of the rates of CH₄ production (ΣR₄) and DIC production due to fermentation associated with CH₄ formation (ΣR₁−ΣR₄) and HMW OM partial fermentation (ΣR₂) represents 54 % and 100 % of the total OM degradation rate ($\mathrm{\Sigma }{R}_{\mathrm{1}}+\mathrm{\Sigma }{R}_{\mathrm{2}}+\mathrm{\Sigma }{R}_{\mathrm{6}}$) in the sediment of lakes Tantaré (Basin A) and Bédard, respectively. Considering the sediment accumulation rate and sediment C_org content given in Sect. 2.1, we calculate an average accumulation rate of C_org of $\mathrm{4.7}\times {\mathrm{10}}^{-\mathrm{11}}$ to $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{10}}$ and $\mathrm{2.9}\times {\mathrm{10}}^{-\mathrm{11}}$ to $\mathrm{7.6}\times {\mathrm{10}}^{-\mathrm{10}}$ mol C cm⁻² s ⁻¹ for lakes Tantaré (Basin A) and Bédard, respectively. Hence, the total sediment OM degradation rate ($\mathrm{\Sigma }{R}_{\mathrm{1}}+\mathrm{\Sigma }{R}_{\mathrm{2}}+\mathrm{\Sigma }{R}_{\mathrm{6}}$) of $\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{12}}$ and $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{12}}$ reported in this study for lakes Tantaré Basin A and Bédard, respectively, would involve only 1.2 %–2.8 % and 0.2 %–4.8 % of the total C_org deposited. Given that the remaining 95.2 %–99.8 % of the deposited C_org is preserved in the sediment, it is not surprising that the sediment C_org concentration is constant with depth (Fig. 2).

The contribution of anaerobic mineralization for Lake Tantaré Basin A is about 1.8 times higher than the average of 30 % reported for this lake basin in a previous study (Clayer et al., 2016). This significant discrepancy arises because these authors, in the absence of isotopic data to adequately constrain the R_i values, assumed that R₄=0 in the net methanotrophic zone Z₁. Should we make the same assumption in the present study, we would also estimate that fermentation and methanogenesis represent only 30 % of the total rate of OM degradation in the oxygenated Lake Tantaré Basin A, and we would thus underestimate the importance of methanogenesis. The inclusion of δ¹³C data in the present modelling study thus allowed us to better constrain the effective rates of CH₄ production (R₄). Indeed, a value of R₄=119 fmol cm⁻³ s⁻¹ was required in Eq. (7) to produce an acceptable δ¹³C–CH₄ profile (Table 3 and Fig. S3).

4.2 Organic substrates for methanogenesis at the sampling sites

Table 3 indicates that hydrogenotrophy (Reaction R4) coupled to the complete fermentation of OM (Reaction R1) produces CH₄ at higher rates (R₄) than DIC (R₁−R₄) in the Z₁ and Z₂ of both lake basins. This outcome is inconsistent with the equimolar production of CH₄ and DIC expected from the fermentation of glucose (C₆H₁₂O₆), the model molecule used to represent labile OM in diagenetic models (Paraska et al., 2014), thus suggesting that the fermentation of this compound is not the exclusive source of the H₂ required for hydrogenotrophy. Had OM been represented by C₆H₁₂O₆ in Reaction (R1), the rate of H₂ production by this reaction would have been twice that of CO₂, i.e., 2R₁. For its part, the rate of H₂ consumption through hydrogenotrophy is 4 times that of the CH₄ production, i.e., 4R₄. Hence, an additional H₂ production at rates of up to 212 and 70 fmol cm⁻³ s⁻¹, i.e., 4R₄−2R₁, is needed to balance the H₂ production rate expected from the fermentation of C₆H₁₂O₆ and the H₂ consumption rate by hydrogenotrophy observed in the sediments of Lake Tantaré Basin A and Lake Bédard, respectively. As discussed by Clayer et al. (2018), this additional production rate of H₂ is likely provided by the fermentation of organic substrates that are more reduced than glucose.

Introducing the values of $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$, $R_{\mathrm{net}}^{\mathrm{DIC}}$, $R_{\mathrm{net}}^{\mathrm{Ox}}$, χ_M, and R₂ (Tables 2 and 3) into Eq. (9), we calculate COS values of −3.2 and −0.9 for the Z₁ and Z₂ of Lake Tantaré Basin A, respectively, and of −1.0 to −1.1 for the Z₁ of Lake Bédard, respectively. Note that we were unable to constrain with Eq. (9) the COS for the Z₂ of Lake Bédard since we had to assume a COS value to estimate the R_i, and the COS has no influence on the modelled δ¹³C profiles (Sect. S2.2.2.3 of the Supplement). Negative COS values between −0.9 and −1.1 suggest that fermenting OM in the sediments of the two lake basins would be better represented by a mixture of fatty acids and fatty alcohols than by carbohydrates, as suggested by Clayer et al. (2018) for the sporadically anoxic Lake Tantaré Basin B. For its part, the highly negative COS value of −3.2 calculated for the Z₁ of Lake Tantaré Basin A is unreasonable, and the inaccuracy of the COS determination in this lake basin is discussed in Sect. 4.3.

4.3 Reduced organic compounds as methanogenic substrates in lake sediments

In order to better appraise the COS of the fermenting OM in lakes, relevant datasets of porewater solute concentration profiles were gathered from our data repository and from a thorough literature search. To be able to obtain by reactive-transport modelling the $R_{\mathrm{net}}^{\mathrm{solute}}$ required to calculate the COS with Eq. (9), the datasets had to (i) comprise porewater concentration profiles of CH₄ and DIC and, ideally, those of the EAs; (ii) reveal a net methanogenesis zone; and (iii) enable the estimation of the carbonate precipitation and dissolution contribution to $R_{\mathrm{net}}^{\mathrm{DIC}}$. Detailed information on the origin and processing of the 17 selected datasets, acquired in six different lake basins from one subalpine and three boreal lakes sampled at various dates and/or depths, is given in Sect. S3 of the Supplement. The CH₄ and DIC porewater profiles determined at hypolimnetic sites of these lake basins and their modelling with the code PROFILE are shown in Fig. 5, whereas the $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$, $R_{\mathrm{net}}^{\mathrm{DIC}}$, and $R_{\mathrm{net}}^{\mathrm{Ox}}$ values determined from this modelling are regrouped in Table 4. The COS values displayed in Table 4 for all lake basins and dates were calculated by substituting the appropriate $R_{\mathrm{net}}^{{\mathrm{CH}}_{\mathrm{4}}}$, $R_{\mathrm{net}}^{\mathrm{DIC}}$, $R_{\mathrm{net}}^{\mathrm{Ox}}$, and R₂ values in Eq. 9 and varying χ_M between 0 and 1, except for Lake Tantaré Basin A, for which χ_M equals 0.75 (Table 3). When the value for R₂ was not available, we assumed R₂=0. Equation (9) indicates that R₂>0 would yield lower COS values than those reported in Table 4.

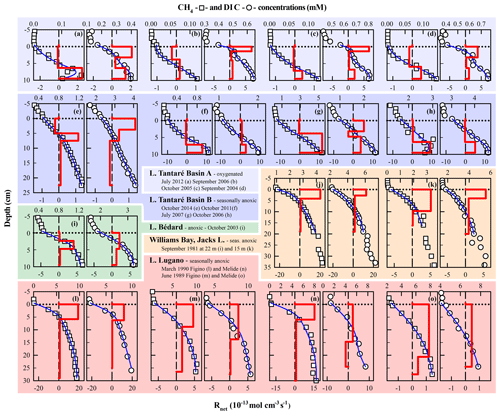
Figure 5 Comparison of the modelled (blue lines) and average (n=3) measured concentration profiles of CH₄ (squares) and DIC (circles) in Lake Tantaré Basin A (a–d) and Basin B (e–h), Lake Bédard (i), Jacks Lake (j–k), and Lake Lugano (l–o) on various sampling dates. The thick red lines represent the net solute reaction rate ($R_{\mathrm{net}}^{\mathrm{solute}}$).

Table 4 Net reaction rates ($R_{\mathrm{net}}^{\mathrm{solute}}$; fmol cm⁻³ s⁻¹) of CH₄, DIC, and oxidants in the zone with the highest production rate of CH₄ as well as the O₂ concentration in the bottom water ([O₂] in mg L⁻¹), the R₂ rates (fmol cm⁻³ s⁻¹), and the average carbon oxidation state (COS) of the fermenting OM at the origin of CH₄ calculated with Eq. (9) at both study sites, Lake Tantaré Basin B (Fig. 1), Jacks Lake (Carignan and Lean, 1991), and Lake Lugano (Lazzaretti-Ulmer and Hanselmann, 1999) for various sampling dates.

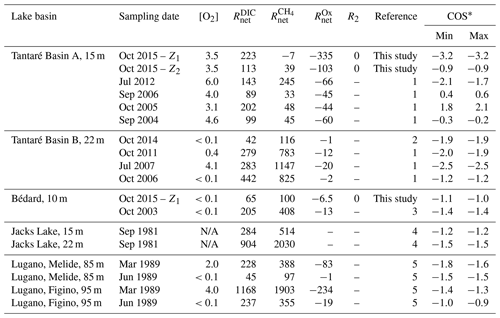
^∗ Minimum and maximum COS values were obtained by setting χ_M to 0 and 1 in Eq. (9), except for Tantaré Basin A in October 2015, for which χ_M is known to be 0.75. References: (1) Clayer et al. (2016), (2) Clayer et al. (2018), (3) see Supplement, (4) Carignan and Lean (1991), (5) Lazzaretti-Ulmer and Hanselmann (1999). N/A: not available.

According to Table 4 the COS values are systematically negative at all dates for Lake Tantaré Basin B, Lake Bédard, Jacks Lake, and the two sites of Lake Lugano, and they vary generally between −0.9 and −1.9, with the exception of a value of −2.5 obtained for Lake Tantaré Basin B in July 2007. This latter value is likely too low to be representative of fermenting material and should be rejected. The mean (± SD) COS values are $-\mathrm{1.7}\pm \mathrm{0.4}$ for Lake Tantaré Basin B, $-\mathrm{1.4}\pm \mathrm{0.4}$ for Lake Bédard, $-\mathrm{1.4}\pm \mathrm{0.2}$ for Jacks Lake, and $-\mathrm{1.4}\pm \mathrm{0.3}$ for Lake Lugano. These COS values, representative of a mixture of fatty acids (COS of −1.0 for C4 fatty acids to about −1.87 for C32 fatty acids) and of fatty alcohols (COS $=-\mathrm{2.00}$), strongly support the idea that methanogenesis in oligotrophic boreal lake sediments and possibly other lake types is fuelled by more reduced organic compounds than glucose. Lipids such as fatty acids and fatty alcohols with similar COS are naturally abundant in sediments to sustain the estimated rates of CH₄ and DIC production during fermentation (Burdige, 2007; Cranwell, 1981; Hedges and Oades, 1997; Matsumoto, 1989). As discussed by Clayer et al. (2018) the most labile organic compounds (i.e., proteins and carbohydrates) can be rapidly degraded during their transport through the water column and in the uppermost sediment layer, leaving mainly lipids as metabolizable substrates at depths where fermentation and methanogenesis occur. This interpretation is consistent with thermodynamic and kinetic evidence that proteins and carbohydrates are more labile and are degraded faster than lipids (LaRowe and Van Cappellen, 2011).

The COS values determined for the perennially oxygenated Basin A of Lake Tantaré (mean of $-\mathrm{0.6}\pm \mathrm{1.1}$; range of −3.2 to 2.1; Table 4) are much more variable than for the five other seasonally anoxic lake basins, including unrealistic values for October 2015 in the Z₁ (−3.2), September 2016 (0.4–0.6), and October 2005 (1.8–2.1). Indeed, the very negative value of −3.2 does not correspond to any degradable compound under anoxic conditions, whereas the positive values of 0.4–0.6 and 1.8–2.1 would involve either amino acids and nucleotides, which are very labile (LaRowe and Van Cappellen, 2011) and tend to be degraded in the water column (Burdige, 2007), or oxidized compounds, such as ketones, aldehydes, and esters, known to be quickly reduced to alcohols. Possible sources of uncertainty in the COS estimation include misquantification of bioirrigation and DIC production through HMW OM fermentation (Reaction R2; Corbett et al., 2013). Clayer et al. (2016) provided evidence that sediment irrigation by benthic animals is effective in Lake Tantaré Basin A and that reaction rates are sensitive to the bioirrigation coefficient. Nevertheless, additional simulations show that changing the bioirrigation coefficient by a factor of 2 (increased and decreased) did not result in significant changes in COS values (<0.2). Bioirrigation might also be misrepresented. Indeed, the term used in Eq. (2) to calculate this contribution, i.e., φα_irrigation([solute]_tube−[solute]), is indeed an approximation of intricate 3-D processes variable in space and time (Meile et al., 2005; Boudreau and Marinelli, 1994; Forster and Graf, 1995; Gallon et al., 2008; Riisgård and Larsen, 2005). On the other hand, DIC production through HMW OM fermentation (Reaction R2; Corbett et al., 2013) was constrained by default in Lake Tantaré Basin A (Table 4). Indeed, fitting with Eq. (7) the experimental δ¹³C data do not allow partitioning of the production of DIC between Reactions (R1) and (R2) given that both processes share the same fractionation factor (${\mathit{\alpha }}_{\mathrm{1}}={\mathit{\alpha }}_{\mathrm{2}}=\mathrm{1.000}$). Equation 9 indicates that, to obtain negative COS values for Lake Tantaré Basin A in September 2006 and October 2005, R₂ should be >11 and >110 fmol cm⁻² s⁻¹, respectively. These R₂ values correspond to transferring >9 % and >44 % of the rate of DIC production from R₁ to R₂ for September 2006 and October 2005, respectively. Hence, owing to the imperfection in the COS estimations for Lake Tantaré Basin A, COS values estimated for this site should be treated with caution. Note that the sediment surface was also oxic at the sites Melide and Figino of Lake Lugano in March 1989 (Table 4), as revealed by detectable bottom water [O₂] (Table 4) and by low [Fe], undetectable ΣS(-II) and [CH₄], and relatively high [${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$] in overlying water (Lazzaretti et al., 1992; Lazzaretti-Ulmer and Hanselmann, 1999). Despite this, the COS values determined for the two sites of Lake Lugano appear realistic and consistent with those calculated for Lake Tantaré Basin B, Lake Bédard, and Jacks Lake. This disparity between Lake Tantaré Basin A and Lake Lugano could be explained by the presence of benthic organisms in the former (Hare et al., 1994), but their absence in the latter, as shown by the presence of varves (Lazzaretti et al., 1992) and the absence of benthos, remains in the recent sediments of Lake Lugano (Niessen et al., 1992).

5 Conclusions

Our results show that fermentation and methanogenesis represent about 50 % and 100 % of OM mineralization in the top 25 cm of the sediments at the hypolimnetic sites in Lake Tantaré Basin A and Lake Bédard, respectively; that methane is produced only by hydrogenotrophy; and that fermentation substrates have a negative COS at these two sites. The association of hydrogenotrophy with the fermentation of reduced OM (COS $<-\mathrm{0.9}$; implying that labile compounds are depleted) in the studied lake sediments is consistent with the fact that hydrogenotrophy becomes increasingly important when labile OM is depleted (Chasar et al., 2000; Hornibrook et al., 2000; Whiticar et al., 1986).

Reactive-transport modelling of 12 datasets of porewater profiles from three boreal lakes – i.e., Lake Bédard, Lake Tantaré (Basin B), and Jacks Lake – as well as of the subalpine Lake Lugano (Melide and Figino sites) consistently showed that the main substrates for sediment methanogenesis at deep seasonally anoxic hypolimnetic sites have a mean COS value of $-\mathrm{1.4}\pm \mathrm{0.3}$. The OM in the sediment of the three boreal lakes, as well as their O₂ seasonal dynamics, is typical of boreal forest lakes. While Lake Bédard experiences prolonged episodes of extended hypolimnetic anoxia, Lake Tantaré Basin B and Jacks Lake show more moderate seasonal anoxia, where some years the hypolimnion of Lake Tantaré Basin B is only hypoxic (Clayer et al., 2016; Carignan et al., 1991). Hence, the selective mineralization of OM described by Clayer et al. (2018), involving the mineralization of the most labile compounds during OM downward migration in the water column and at the sediment surface, leaving mainly reduced organic compounds to fuel methanogenesis in the sediments, likely applies to a large portion of boreal lakes.

Hence, the current representation of the fermenting OM, i.e., CH₂O, in process-based biogeochemical models entails a significant risk of underestimating sedimentary CH₄ production and release to the bottom water and, to a certain extent, of its evasion to the atmosphere under transient environmental scenarios. To better constrain CH₄ and CO₂ production within sediments, we suggest taking specifically into account the COS of the fermenting OM in formulating the reactions of methanogenesis associated with fermentation in these models. For example, the rates of CH₄ (${\mathrm{R}}^{{\mathrm{CH}}_{\mathrm{4}}}$) and DIC (R^DIC) production during fermentation coupled to hydrogenotrophy can be expressed as

$$\begin{array}{}\text{(12)}& {\displaystyle }{R}^{{\mathrm{CH}}_{\mathrm{4}}}=R_{\mathrm{4}}={\displaystyle \frac{\mathrm{4}-\mathrm{COS}}{\mathrm{8}}}{R}_{\mathrm{1}}\text{(13)}& {\displaystyle }{R}^{\mathrm{DIC}}=R_{\mathrm{1}}-R_{\mathrm{4}}=R_{\mathrm{1}}\left(\mathrm{1}-{\displaystyle \frac{\mathrm{4}-\mathrm{COS}}{\mathrm{8}}}\right).\end{array}$$

Given these rate expressions, the stoichiometric formulation of a typical fermentation reaction producing CH₄ becomes

$$\begin{array}{}\text{(14)}& {\mathrm{CH}}_a{\mathrm{O}}_b\to {\displaystyle \frac{\mathrm{4}-\mathrm{COS}}{\mathrm{8}}}{\mathrm{CH}}_{\mathrm{4}}+\left({\displaystyle \frac{\mathrm{4}+\mathrm{COS}}{\mathrm{8}}}\right){\mathrm{CO}}_{\mathrm{2}},\end{array}$$

where a equals $\mathrm{2}-\frac{\mathrm{COS}}{\mathrm{2}}$ and b equals $\mathrm{1}+\frac{\mathrm{COS}}{\mathrm{4}}$. Introducing the average COS values reported in this study ($-\mathrm{1.4}\pm \mathrm{0.3}$) into Eq. (14), the coefficients a and b would take values of 2.7±0.15 and 0.65±0.125, respectively, and the CH₄ and CO₂ stoichiometric coefficients would be 0.68±0.04 and 0.32±0.04, respectively. Note that the same stoichiometric formulation would be obtained with any possible combination of acetoclasty and hydrogenotrophy. Under these conditions, fermentation (Reaction R1) coupled to methanogenesis (Reaction R4) yields 2.2±0.4 times more CH₄ than DIC for the studied lake sediments. Ignoring the implications of the present study regarding the COS of the fermenting OM could lead to the underestimation of CH₄ sediment outflux or of the rate of oxidant consumption required to mitigate this efflux by a factor of up to 2.6.

The approach used to estimate the COS of the fermenting OM, although successful for the seasonally anoxic basins, failed to produce reliable COS values when applied to the perennially oxygenated Basin A of Lake Tantaré. We attribute this peculiarity to a misestimation and/or misrepresentation of the benthic irrigation and to the impossibility of partitioning the DIC production between Reactions (R1) and (R2), which share the same fractionation factor value. Similar problems would likely also be encountered in other lake ecosystems such as epilimnetic sediments and wetlands where solute transport processes remain ill-known. Indeed, these shallow aquatic environments are subject to enhanced benthic activity (Hare, 1995), to plant-mediated transport of CH₄ and O₂ (Chanton et al., 1989; Wand et al., 2006), and to turbulence (Poindexter et al., 2016), which complicates the estimation of CH₄ and CO₂ production and consumption rates. Hence, the remaining challenge resides in the robust estimations of the COS of the fermenting OM in epilimnetic sediments and shallow freshwater environments (e.g., ponds, wetlands) since these environments were shown to be the main contributors to freshwater CH₄ release to the atmosphere (Bastviken et al., 2008; DelSontro et al., 2016). One potential solution is to investigate trends in the oxygen isotope signatures in the sedimentary DIC in addition to δ¹³C values since it is also influenced by the source of the OM undergoing degradation (e.g., Sauer et al., 2001).