Barium stable isotopes as a fingerprint of biological cycling in the Amazon River basin

The biological cycle of rock-derived nutrients on the continents is a major component of element transfer between the Earth's surface compartments, but its magnitude currently remains elusive. The use of the stable isotope composition of rock-derived nutrients, which can be fractionated during biological uptake, provides a promising path forward with respect to quantifying biological cycling and its overall contribution to global element cycling. In this paper, we rely on the nutrient-like behaviour of the trace element barium (Ba) and use its elemental and stable isotope compositions in dissolved and sediment load river samples to investigate biological cycling in the Amazon Basin. From these measurements, we show that dissolved Ba mainly derives from silicate rocks, and a correlation between dissolved Ba and K abundances suggests that biological cycling plays a role in the Ba river budget. Furthermore, the isotope composition of Ba (δ¹³⁸Ba) in the dissolved load was found to be significantly different from that of the parent silicate rocks, implying that dissolved Ba isotopic signatures are affected by (i) the precipitation of soil-forming secondary phases as well as (ii) biological uptake and release from dead organic matter.

Results from an isotope mass balance method applied to the river dissolved load data indicate that, after its release to solution by rock weathering, Ba is partitioned between the river dissolved load, secondary weathering products (such as those found in soils and river sediments), and the biota. In most sub-catchments of the Amazon, river Ba abundances and isotope compositions are significantly affected by biological cycling. Relationships between estimates of Ba cycled through biota and independent metrics of ecosystem dynamics (such as gross primary production and terrestrial ecosystem respiration) allow us to discuss the role of environmental parameters such as climate or erosion rates on the biological cycling of Ba and, by extension, the role of major rock-derived nutrients.

In addition, catchment-scale mass and isotope budgets of Ba show that the measured riverine export of Ba is lower than the estimated delivery of Ba to the Earth surface through rock alteration. This indicates the existence of a missing Ba component, which we attribute to the formation of Ba-bearing particulate organics (possibly accumulating as soil organic matter or currently growing biomass within the catchments) and to organic-bound Ba exported as “unsampled” river particulate organic matter.

Given our findings on the trace element Ba, we explore whether the river fluxes of most major rock-derived nutrients (K, Mg, Ca) might also be significantly affected by biological uptake or release. A first-order correction of river-derived silicate weathering fluxes from biological cycling shows that the carbon dioxide (CO₂) consumption by silicate weathering at the mouth of the Amazon could be several times higher than the previously reported value of 13 × 10⁹ mol CO₂ yr⁻¹ (Gaillardet et al., 1997).

Overall, our study clearly shows that the chemical and isotope compositions of rivers in the Amazon – and most likely in other large river basins – bear a biological imprint, thereby challenging common assumptions made in weathering studies.

1 Introduction

A fundamental process on Earth is the chemical weathering of rocks by atmospheric agents such as oxygen, carbon dioxide (CO₂), and water. Over the long-term evolution of our planet, chemical weathering reactions and the subsequent formation of secondary mineral phases in the ocean and on the continents have been the principal drivers in forming and sustaining habitable conditions on the planet's surface (Langmuir and Broecker, 2012). Continental chemical weathering consists of a series of hydrogeochemical processes that transform rocks within the lithosphere into dissolved solutes, secondary minerals such as clays that form soils, and, most importantly, the living organisms that compose our biota (e.g. Porder, 2019). The complex reactions participating in these transformations occur in what is frequently referred to as the “Critical Zone” of the planet: a thin layer, almost invisible at the planetary scale, that is made of soils, surface and underground waters, and dead and living organic matter (Riebe et al., 2017). These weathering products are then mobilised by the water cycle and harvested by rivers before reaching the ocean. Therefore, rivers integrate the diverse processes of the Critical Zone and offer a quantitative window into the fluxes of matter implied in these processes and their controlling factors (Berner and Berner, 2012).

An important question related to the functioning of the Critical Zone is the role played by living organisms in its continuous transformation and long-term evolution. Biological activity has been suggested to significantly impact the Earth surface via a wide range of processes (Brantley et al., 2011) that often tend to have a variety of impacts on the Critical Zone. On the one hand, the decomposition of organic matter and root respiration in soils generates CO₂ and organic acids that acidify the soil solution and, consequently, trigger chemical weathering reactions (such as the dissolution of primary minerals; e.g. Drever and Stillings, 1997; Calmels et al., 2014). On the other hand, vegetation and roots can also act as stabilising agents by preventing physical erosion and, thus, preserving soil (e.g. Marston, 2010). Furthermore, one of the most prominent effects of the presence of biota on Earth follows from the various strategies adopted by living beings to extract nutrients from rock minerals for their growth and the development of ecosystems (Aerts and Chapin, 1999). A major challenge facing ecosystems lies in the acquisition of these nutrients in a manner that is sustainable in the long term. Consequently, many studies documenting ecosystem nutrient acquisition strategies have emphasised that nutrients are strongly “recycled”. This means that the nutrients contained in dead organic matter are efficiently taken up again after their release into solution (e.g. Jobbágy and Jackson, 2004; Cleveland et al., 2013). Nonetheless, nutrient recycling is never total, such that ecosystems eventually lose a small fraction of their nutrient inventory due to incomplete litter remineralisation. Therefore, an alternative pathway has to exist to balance this nutrient loss. In places where Earth surface rejuvenation is relatively inefficient, strong nutrient depletion is compensated for by atmospheric deposition (Chadwick et al., 1999). In areas where erosion is active, the sustained supply of fresh minerals to the Earth surface provides plants with access to “new” rock-derived nutrients (Porder et al., 2007; Cleveland et al., 2011). However, in such actively eroding areas, the loss of nutrients is also thought to be accelerated by litter erosion (Uhlig et al., 2017; Uhlig and von Blanckenburg, 2019).

As a consequence, biological cycling acts as a “traffic officer” for elements and their isotopes through the Critical Zone, directing their circulation across the Earth surface (e.g. Chaudhuri et al., 2007; Cenki-Tok et al., 2009; Schmitt et al., 2012; Baronas et al., 2018). For simplicity, from the geochemical point of view, it has commonly been assumed that element cycling by the biota is at “equilibrium” at the river scale (e.g. Viers et al., 2014) or, in other words, that the flux of nutrient uptake is compensated for by an equivalent flux of release from the biota (e.g. Gaillardet et al., 1999a). However, more and more studies are now showing that higher plants are a significant reservoir of major rock-derived nutrients such as Ca, Mg, K, or Si at the ecosystem scale (Burghelea et al., 2018) and that nutrient cycling is a key mechanism in the Critical Zone with respect to understanding the partitioning of elements at the Earth surface (e.g. Uhlig et al., 2017).

The abundance and isotope signature of elements involved in biological cycling can be used to appraise nutrient uptake and the subsequent fluxes of elements passing through the Critical Zone. Barium (Ba) is an alkali earth element that has seven stable isotopes (¹³⁰Ba, ¹³²Ba, ¹³⁴Ba, ¹³⁵Ba, ¹³⁶Ba, ¹³⁷Ba, and ¹³⁸Ba; although unstable,¹³⁰Ba is considered to be stable given its half-life of 10²¹ yr). Besides the formation of secondary phases, such as clays or oxides (Gong et al., 2019), and adsorption (Gou et al., 2019), which are considered to be major fractionation processes for a variety of weathering stable isotope tracers, previous studies indicate that Ba is sensitive to uptake by plants and bacteria (Bullen and Chadwick, 2016; Cam et al., 2016; Blondeau et al., 2018). Despite the lack of any known benefit of Ba for plants (Marschner, 2011) and the fact that the accumulation of Ba in plants is toxic (Lamb et al., 2013; Myrvang et al., 2016, and reference therein), Ba has similar chemical properties (ionic radius, charge) to major important rock-derived nutrients such as Mg, Ca, and K (Bullen and Bailey, 2005; Kabata-Pendias and Mukherjee, 2007), leading to significant uptake of Ba in plants and a “nutrient-like behaviour”. In addition to the sizable amount of Ba usually found in plants, the isotope composition of Ba has been found to faithfully trace nutrient cycling – to an even better extent than Sr or Ca stable isotopes (Bullen and Chadwick, 2016). This, along with its lack of sensitivity to redox conditions (unlike some of the transition metals or major constituents of the biosphere such as C, N, or S), makes Ba stable isotopes a potentially powerful tool for quantifying biological cycling within the Critical Zone and leads us to consider (in this work) that Ba can be used at first order as a proxy for the cycling of major rock-derived nutrients.

The study of Ba stable isotope fractionation at the Earth surface has only recently begun (Von Allmen et al., 2010), and most contributions to date have principally focused on seawater (Horner et al., 2015; Cao et al., 2016; Hsieh and Henderson, 2017; Bates et al., 2017; Charbonnier et al., 2018), marine sediments (Bridgestock et al., 2018), and sedimentary barite (Crockford et al., 2019). In addition, the isotope composition of Ba dissolved in continental waters has only been reported for a few rivers, such that constraints are still lacking on the global dissolved Ba riverine flux to the ocean as well as on its isotope composition (Cao et al., 2016; Hsieh and Henderson, 2017; Gou et al., 2019).

In this study, we aim to provide estimates of rock-derived nutrient cycling, to reveal its controlling parameters, and to discuss the potential implications thereof through the use of the abundance and isotope signature of Ba in the Amazon, the world largest river basin. We rely on the abundance and isotope composition of river dissolved and sediment Ba for a series of sub-catchments in the Amazon Basin spanning a variety of different parent rock lithologies, reliefs, climates, and vegetation types. We test different hypotheses to identify the principal drivers of the dissolved Ba isotope composition of these rivers and demonstrate the significant role of biological cycling on the river Ba isotope signature. Using a set of river-scale elemental and isotopic mass budgets for Ba in the Amazon River, we further show that biological cycling has a significant impact on the routing of Ba between the different compartments of the Critical Zone. We examine how this routing is dependent on the environmental conditions and, in particular, how it shifts between the mountainous regions of the Andes and the flatter, more expansive areas of the Amazon Basin. Finally, we explore how the export fluxes of major dissolved species from the Amazon Basin might be impacted by biological cycling and how this might bias estimates of chemical weathering rates based on river chemistry. In summary, our study opens up new perspectives for the use of Ba isotope in sedimentary archives to trace past changes in ecosystem dynamics, provides further constraints on the isotope composition of Ba delivered globally to the oceans, emphasises the role of biological cycling on the routing of elements at the Earth surface, and highlights the role played by life in riverine export.

Figure 1 Map of the Amazon Basin and the locations of the sampling sites.

2 Material and methods

2.1 Geographical and geological setting

The Amazon Basin, the world largest river basin with a drainage area of 5 500 000 km² and a discharge of 6300 km³ yr⁻¹ (Milliman and Farnsworth, 2013), can be divided into three regions (Fig. 1):

1. The Andean belt results from the subduction of the Nazca Plate below the South American Plate. The northern part of the Amazon Andes is composed of a mixture of igneous rocks, such as andesites and sedimentary rocks (e.g. shales and carbonates), of Palaeozoic, Tertiary, and Quaternary ages (Stallard and Edmond, 1983; Putzer, 1984; Moquet et al., 2011) and is drained by the Solimões tributaries, such as the Marañon, the Ucayali, the Huallaga, the Morona, the Tigre, or the Pastaza. The southern part of the Amazon Andes is composed almost exclusively of sedimentary rocks deposited during the same geological periods as in the northern part and is drained by the Madeira tributaries, such as the Beni, the Alto Beni, the Chepete, the Quiquibey, the Madre de Dios, the Mamoré, or the Orthon. Most Andean rivers are characterised by high erosion rates (higher than 500 $\mathrm{t}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$; Wittmann et al., 2011) due to steep slopes, making the Andes the quasi-sole source of sediment to the Amazon mainstream (Gibbs, 1972; Allègre et al., 1996). These sediment-laden rivers, called “white waters” (Gibbs, 1967; Stallard and Edmond, 1983) also feature high dissolved loads. Rivers draining the Andean foreland (e.g. the Purus river), where Andean sediments have accumulated, are also considered to be white waters, although they have lower sediment and dissolved loads than the Andean rivers. In the Andes, the precipitation and temperature are around 1650 mm yr⁻¹ and 20 ^∘C on average respectively, with a more arid and colder climate towards the south (e.g. around 1200 mm yr⁻¹ and 17 ^∘C for the Upper Beni).

2. Amazonian Craton underlie the sedimentary layers of the Amazon plains, and consist of a Precambrian craton composed of plutonic and metamorphic rocks, which crops out north (Guiana Shield) and south (Brazilian Shield) of the Amazon main channel. The Amazon tributaries draining the shields, such as the Tapajós and the Trombetas rivers, are dilute (Stallard and Edmond, 1983; Gaillardet et al., 1997) and feature low erosion rates (about a few tens of tonnes per square kilometre per year; Wittmann et al., 2011); they are also typically “clear water” rivers (Gibbs, 1972; Stallard and Edmond, 1983), characterised by high phytoplanktonic photosynthetic activity. In this region, the precipitation rate is higher (around 2300 mm yr⁻¹) and the temperature is warmer (26 ^∘C) than in the Andes.

3. In the Amazon Plain, all of the tributaries of the Solimões and the Madeira join and are underlain by sediments derived from the Andean belt and the craton. Rivers draining only the Amazon Plain, such as the Upper Rio Negro River, are dilute, sediment-poor, and typically “black water” rivers, characterised by a high dissolved organic carbon concentration. In the Amazon Plain, Andean-fed rivers carrying sediments (around 200 $\mathrm{t}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$; Wittmann et al., 2011) have developed floodplains that store river sediments over periods of time of up to several million years (Wittmann et al., 2011), before their release to the Amazon hydrographic system. Precipitation (2130 mm yr⁻¹) and temperature (25 ^∘C) are relatively similar to those encountered in the craton basins.

Throughout the remainder of the text, we will distinguish our set of sampling sites (Fig. 1) as follows: northern Andean rivers (Solimões sub-basin); southern Andean rivers (Madeira sub-basin); “dilute” rivers, comprising rivers draining the craton and the Amazon Plain only; and the “main tributaries”, with sampling sites in the Amazon Plain but resulting from the mixing of waters derived from several regions (the Andes, the craton, and the Amazon Plain).

2.2 Sampling

The samples used in this study (Fig. 1) have been collected during different sampling cruises performed from 2001 to 2008 (Dosseto et al., 2006; Bouchez et al., 2011; Dellinger et al., 2015b). Most analyses were performed at the High-Resolution Analytical Platform (PARI) of the Institut de physique du globe de Paris (IPGP).

River waters were collected in acid-washed polypropylene containers and were filtered on site using Teflon filtration units (0.2 µm porosity). Water samples were acidified at a pH of ≈ 2 with ultra-pure HNO₃ and stored in a cold room at 4 ^∘C after collection. Major anion and cation concentrations were measured using ion chromatography, the dissolved silica concentration was measured using UV–Vis spectrophotometry, and trace elements were measured using by quadrupole inductively coupled plasma mass spectrometry (ICP-MS).

Sampling procedures for river sediments are reported in Dosseto et al. (2006) and Bouchez et al. (2011). Briefly, at several locations, river sediments were sampled at different depths in the river channel and at the river bottom, in order to access the whole range of river sediment grain sizes. Major and trace element concentrations were measured using inductively coupled plasma atomic emission spectroscopy (ICP-AES) and ICP-MS respectively at the SARM (Service d'Analyse des Roches et des Minéraux) INSU facility (Vandoeuvre-lès-Nancy, France; analytical details are available at http://helium.crpg.cnrs-nancy.fr/SARM, last access: 23 November 2020). In order to characterise the chemical and isotope composition of typical Andean bedrock, outcropping rocks were collected in 2001 and 2005. These rocks were crushed to obtain homogeneous powders, digested using a mix of HNO₃ and HF, and repeatedly taken up in HCl 6 N until full dissolution. Concentrations of major and trace elements in rocks were measured using quadrupole ICP-MS at IPGP.

In order to investigate the relative solubility of Ba (i.e. compared to soluble alkali and alkali earth elements), we produced a compilation of existing data on the chemical composition of the dissolved load of rivers draining single rock types that are significantly present in the Amazon Basin (andesites, shales, plutonic igneous rocks such as granites, and carbonates), as well as a data compilation for the composition of the rock types themselves. The river data compilation is made up of a combination of data from the literature (Edmond et al., 1995; Louvat and Allègre, 1997; Louvat et al., 2008) and our own new data, whereas rock data are derived from the GEOROC (Geochemistry of Rocks of the Oceans and Continents) database (http://georoc.mpch-mainz.gwdg.de/georoc/, last access: 23 November 2020; see Fig. S1 in the Supplement and data tables in the repository https://doi.org/10.5281/zenodo.4050339, Charbonnier et al., 2020).

2.3 Barium chemical separation and isotope measurements

For each river water sample, a volume of 5 to 15 mL of water was evaporated at 100 ^∘C in a Teflon beaker, and the residue was taken up in 0.5 mL HCl 2.5 N. For each solid sample (river sediment or rock), aliquots of homogeneous powder (around 50 mg of crushed powder allowing not only for Ba isotope measurements but also other analyses) were digested using a mix of HNO₃ and HF, evaporated to dryness, and repeatedly taken up in HCl 6 N until full dissolution of the residue. A sample aliquot containing a minimum of 250 ng of Ba was evaporated, and the residue was taken up in 0.5 mL HCl 2.5 N.

The chemical separation of Ba was carried out by ion chromatography using AG50W-X8 ion exchange resin; during this process, the matrix elements such as Na, K, Ca, Mg, Fe, and Al were eluted in a volume of 13 mL of HCl 2.5 N, and Ba was eluted in a volume of 15 mL of HCl 6 N (Van Zuilen et al., 2016b). To ensure a proper purification of Ba from the matrix, the separation procedure was carried out twice in a row. Ba purification from river waters and sediments does not require the use of carbonate co-precipitation – a method usually performed for Ba purification in sea water, which can entail a loss of Ba (e.g. Horner et al., 2015). Therefore, the double-spike method (e.g. Van Zuilen et al., 2016b) was not used here, and we rather corrected the mass instrumental fractionation using the sample–standard bracketing method (see below). However, to ensure correct and accurate Ba isotope measurements, yield and eluate purity were checked for all samples by quadrupole ICP-MS (Table S1 in the Supplement). The total procedural blank was checked for each separation session and was found to have a maximum of 0.2 ng of Ba, which was negligible compared with the typical amount of Ba present in samples.

The isotope ratios of Ba were measured using a multicollector ICP-MS (MC-ICP-MS; Thermo Fisher Neptune) with a stable introduction system (SIS) spray chamber. The Faraday cups were placed to collect the following masses: 129 (L4), 130 (L3), 131 (L2), 132 (L3), 134 (C), 135 (H1), 136 (H2), 137 (H3), and 138 (H4). The concentration of samples and standards were adjusted to 100 µg L⁻¹. Over a session, the reproducibility of the isotope measurement of a pure Ba solution was found to be in the same range as the values reported by Nan et al. (2015). The isobaric interference from Xe on mass 134 was corrected by on-peak zeroes. Although the presence of residual Ce and La in the eluate can, in principle, lead to interferences on ¹³⁸Ba, the very low concentration of these two elements in the river water samples did not significantly impact our measurement, as mass-dependent fractionation was shown for all dissolved load samples by plotting ¹³⁷Ba ∕ ¹³⁴Ba vs. ¹³⁸Ba ∕ ¹³⁴Ba (Fig. S2 in the Supplement). For solid samples, the presence of residual yet measurable amounts of Ce and La in the eluate were shown to affect the ¹³⁸Ba signal to some extent. Therefore, for the whole sample set, mass-dependent fractionation was rather checked using the ¹³⁷Ba ∕ ¹³⁵Ba and ¹³⁷Ba ∕ ¹³⁴Ba ratios (Fig. S2). For the sake of consistency, all data were measured as δ¹³⁷Ba and are reported here as δ¹³⁸Ba, using the mass-dependent relation δ¹³⁸Ba ≈ 1.33 ⋅ δ¹³⁷Ba, with the δ^13xBa defined as follows:

$$\begin{array}{}\text{(1)}& \mathit{\delta }{{}^{\mathrm{13}\mathit{\text{x}}}\mathrm{Ba}}_{\text{smp}}=\left({\displaystyle \frac{{}^{\mathrm{13}\mathit{\text{x}}}\mathrm{Ba}/{{}^{\mathrm{134}}\mathrm{Ba}}_{\text{smp}}}{{}^{\mathrm{13}\mathit{\text{x}}}\mathrm{Ba}/{{}^{\mathrm{134}}\mathrm{Ba}}_{\text{std}}}}-\mathrm{1}\right)\cdot \mathrm{1000},\end{array}$$

where x = 7 or 8, the subscript smp indicates the sample isotope ratio, and the subscript std indicates the reference isotope ratio (NIST SRM 3104a).

Uncertainties on sample δ¹³⁸Ba values are reported as the 95 % confidence interval (CI 95 %), which was calculated as follows:

$$\begin{array}{}\text{(2)}& \text{CI}\mathrm{95}\mathit{\%}=t_{n-\mathrm{1}}\cdot {\displaystyle \frac{\text{SD}}{\sqrt{n}}},\end{array}$$

where SD is the standard deviation over n measurements of the sample (from 0.02 ‰ to 0.15 ‰), and t_n−1 is the student's law factor with n−1 degrees of freedom at a 95 % confidence level. The long-term reproducibility (over 1 year) and the accuracy of the measurements were checked using the following reference materials: SRM3104a (0.00 ‰ ± 0.03 ‰ SD; n = 9 from three chemical separations); SRM3104a spiked with two different river water matrices (−0.03 ‰ ± 0.06 ‰ SD; n = 6 with one chemical separation for each matrix); JB-2 (0.05 ‰ ± 0.08 ‰ SD; n = 9 chemical separations from two digestion batches); and BaBe27 (−0.81 ‰ ± 0.08 ‰ SD; n = 33). These values match well with those reported by Miyazaki et al. (2014) and Van Zuilen et al. (2016b) for two of these reference materials (Babe27 = −0.82 ‰ and JB-2 = 0.07 ‰).

3 Results

The concentration and isotope composition of dissolved and particulate Ba in the Amazon river system are available at https://doi.org/10.5281/zenodo.4050339 (Charbonnier et al., 2020).

3.1 Ba abundance

The concentration of river dissolved Ba in the Amazon Basin ranges from 0.049 to 0.490 µmol L⁻¹ with an average of 0.202 µmol L⁻¹. As water flow can exert a strong control on elemental concentrations through dilution, normalisation to a conservative element such as Na helps with the comparison of dissolved Ba abundances among different water samples. The most Ba-enriched river (the highest Ba∕Na ratio) is the Rio Negro River. The Andean tributaries from the Solimões and Madeira basins show homogeneous Ba∕Na ratios, despite the fact that they drain different rock types. The main tributaries of the Amazon (the Solimões and the Madeira) show significant Ba enrichment with respect to their Andean tributaries.

Our compilation of Ba abundance (expressed as Ba∕X ratios) for rocks and rivers draining single rock types (Fig. S1) highlights that Ba is depleted with respect to other alkali (Li, Na) and alkali earth (Mg, Ca, Sr) elements during chemical weathering and, thus, that Ba is affected by processes in the Critical Zone after its release from rocks at least to a larger extent than these elements are.

The concentration of Ba in the suspended sediments of the Amazon River basin is heterogeneous (from 222 to 836 mg kg⁻¹). This is likely due to the variable quartz abundance throughout the water column and a subsequent dilution effect (Bouchez et al., 2011). Once normalised to the thorium (Th) concentration (with Th being an insoluble element with a magmatic compatibility similar to that of Ba), the Ba abundance is even more variable, with Ba∕Th ratios ranging from 13 to 125. Within this range, some Ba∕Th values differ significantly from the reported ratio for the upper continental crust (Ba∕Th ≈ 50; Taylor and McLennan, 1995; Rudnick and Gao, 2003), suggesting that processes can enrich or deplete Ba in river sediment compared with source rocks and/or that Amazon river sediment Ba is at least partially sourced from other rock types.

The fraction of river-borne Ba exported by Amazon rivers as dissolved species is calculated as follows:

$$\begin{array}{}\text{(3)}& w^{\mathrm{Ba}}={\displaystyle \frac{[\mathrm{Ba}{]}_{\text{diss}}}{[\mathrm{Ba}{]}_{\text{diss}}+[\mathrm{Ba}{]}_{\text{spm}}\cdot \left[\text{spm}\right]}},\end{array}$$

where [Ba]_diss is the concentration of dissolved Ba in rivers (in µg L⁻¹), [Ba]_spm is the Ba concentration in sediment (in mg kg⁻¹), and [spm] is the concentration of suspended particulate matter in the river (obtained by long-term sediment gauging; in g L⁻¹). The fraction of river Ba exported as dissolved Ba ranges from 0.01 to 0.87. The lowest values are found for Andean tributaries, the highest values are found for dilute tributaries, and the main tributaries show intermediate values. Excluding the dilute tributaries, it appears that Ba is mainly transported as solids in rivers. At the mouth of the Amazon, 16 % of Ba is transported in dissolved forms.

3.2 Ba isotope composition

The isotope composition of river dissolved Ba shows a wide range of δ¹³⁸Ba_diss values from 0.29 ‰ to −0.10 ‰ without any clear difference between the various types of rivers. We acknowledge that, at this stage, we lack time series of δ¹³⁸Ba_diss values. This could be problematic as it has been shown, for example, that δ¹³⁸Ba_diss displays temporal variations in the monsoonal Yellow River basin (Gou et al., 2019). However, this variability was attributed to variable degrees of Ba sorption onto particles, enabled by the very high concentration of suspended particulate matter in the Yellow River (several grams per litre; Gou et al., 2019). As the rivers of the Amazon Basin display much lower sediment concentration than that of the Yellow River (of the order of 100 mg L⁻¹ for the largest tributaries; Bouchez et al., 2011), we contend that temporal variability in δ¹³⁸Ba_diss is much less significant.

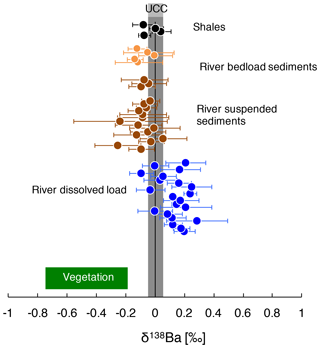
Figure 2 δ¹³⁸Ba of the river dissolved load, river sediments, and shale rocks from the Amazon Basin. The composition of vegetation collected over a soil profile in Hawaii (Bullen and Chadwick, 2016) and the composition of the UCC (upper continental crust; Van Zuilen et al., 2016b; Charbonnier et al., 2018; Nan et al., 2018) reported in the literature are also shown.

The Ba isotope composition of river sediments, δ¹³⁸Ba_sed ranges from 0.06 ‰ to −0.25 ‰, with no significant difference between the isotope composition of Ba in the river suspended load and in bed sediments. The reported average values for plutonic rocks and andesites are 0.00 ‰ ± 0.17 ‰ (SD) and 0.07 ‰ ± 0.02 ‰ (SD) respectively (Charbonnier et al., 2018; Nan et al., 2018). Our own measurements of shale rocks collected in the Andes yield an average value for δ¹³⁸Ba_rock of −0.02 ‰ ± 0.04 ‰ (SD) (Fig. 2). Thus, Ba in secondary weathering products is depleted in the “heavy” Ba isotopes with respect to the parent bedrock, whereas Ba in the dissolved load is enriched in the heavy Ba isotopes (i.e. has higher isotope ratios). This observation is consistent with the premise that the dissolved and suspended loads are complementary phases formed during the partitioning of Ba isotopes by chemical weathering (Fig. 2; Gong et al., 2019).

The Ba isotope composition of river sediments does not show any systematic variation with respect to the Al∕Si ratio (a tracer for sediment grain size), with Al-rich samples (typically suspended matter sampled near the river channel surface) enriched in fine clays and Si-rich samples (typically bedload samples) enriched in coarse quartz (Bouchez et al., 2011, Fig. S3 in the Supplement). This observation contrasts with what has been previously reported for other isotope systems such as ⁸⁷Sr ∕ ⁸⁶Sr or ⁷Li ∕ ⁶Li (Bouchez et al., 2011; Dellinger et al., 2014) and highlights that Ba isotopes in solid-phase weathering products are poorly sensitive to grain size, as shown previously for Ge isotopes (Baronas et al., 2018).

4 Discussion

Significant Ba isotope fractionation is observed in the Amazon Basin between the dissolved and particulate loads of rivers (Fig. 2). In the following sections, we discuss the potential causes for this observation and show the influence of biological cycling on Ba isotope signatures.

4.1 Influence of processes in the Critical Zone on dissolved Ba

Variations in the dissolved Ba abundance and the associated isotope composition could be controlled by variations in the sources of Ba and/or of processes in the Critical Zone affecting Ba after its release from rocks.

Although there are several possible sources of solutes contributing to the overall river chemistry, we show (in Appendix A) that silicate rocks are the main source of dissolved Ba to the river dissolved load in the Amazon Basin, which is consistent with previous observations from other river systems (Gou et al., 2019). This suggests that processes in the Critical Zone act to shift the abundance of river dissolved Ba between different basins. The fact that dissolved Ba is depleted with respect to elements classically considered as soluble (such as Na, Ca, or Mg) compared with rocks further lends support to this inference (Fig. S1).

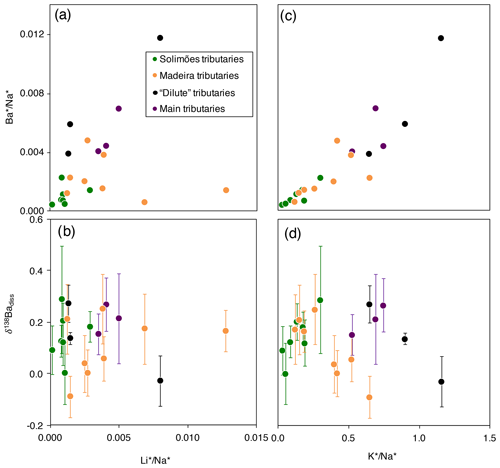
Figure 3 Scatter plots of ${\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}$ and δ¹³⁸Ba_diss vs. ${\mathrm{Li}}^{*}/{\mathrm{Na}}^{*}$ and ${\mathrm{K}}^{*}/{\mathrm{Na}}^{*}$ for the dissolved load of the Amazon rivers (“^*” refers to the dissolved element concentration corrected for non-silicate inputs; see Appendix A for details).

Although still largely unconstrained, it is suspected that Ba incorporation into secondary weathering products (clays or oxyhydroxides) occurs in the Critical Zone (Gong et al., 2019). River dissolved Li abundance and isotope composition can serve as a proxy for the contributions of secondary weathering products to the overall dissolved solute flux (von Strandmann et al., 2012; Dellinger et al., 2015b). When dissolved Ba is compared against dissolved Li, no correlation emerges between ${\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}$ and ${\mathrm{Li}}^{*}/{\mathrm{Na}}^{*}$ (“^*” refers to the dissolved element concentration corrected for non-silicate inputs; see Appendix A for details) nor between ${\mathrm{Li}}^{*}/{\mathrm{Na}}^{*}$ and δ¹³⁸Ba_diss (Fig. 3a, b) even when these elemental ratios are corrected for the source rock composition (these “corrected ratios” actually correspond to the so-called $f_{\text{diss}}^{\mathrm{Ba}}$ and $f_{\text{diss}}^{\mathrm{Li}}$ parameters; see the following text and Fig. S4 in the Supplement). This lack of a correlation implies that at least one other process in the Critical Zone (that is, in addition to the formation of secondary weathering products) scavenges dissolved Ba after its release from rocks. This inference is also supported by the absence of any significant differences in the Ba isotope compositions between shales (which are clay- and oxide-rich sedimentary rocks), unweathered igneous rocks, and river sediments (Fig. 2), which is in contrast to what is observed for Li (Dellinger et al., 2014).

It has been suggested that the isotope composition of Ba in soils is mainly driven by biological uptake and release (Bullen and Chadwick, 2016). This can be tested using the K abundance, which is known to be strongly impacted by biological activity at the Earth surface (Chaudhuri et al., 2007; Tripler et al., 2006; Uhlig et al., 2017; Uhlig and von Blanckenburg, 2019)  in addition to having a magmatic compatibility (Hofmann, 1988) and a high abundance in shales (Taylor and McLennan, 1995; Rudnick and Gao, 2003) similar to those of Ba; these factors suggest similar behaviour of Ba and K at the Earth surface regarding “inorganic” processes (Kabata-Pendias and Mukherjee, 2007). The significant positive relationship between river dissolved ${\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}$ and ${\mathrm{K}}^{*}/{\mathrm{Na}}^{*}$ (Fig. 3c) suggests that the common behaviour of Ba and K extends to the biological realm. However, no correlation is observed between δ¹³⁸Ba_diss and ${\mathrm{K}}^{*}/{\mathrm{Na}}^{*}$ (Fig. 3d).

Overall, the lack of correlation between δ¹³⁸Ba_diss and a range of elemental ratios indicates that a combination of several processes is required to explain the Ba isotope signatures throughout the Amazon. In order to quantify the relative role of each of these processes on the river dissolved Ba budget, we first need to calculate the fraction of weathering-derived Ba that remains in solution after Ba uptake by different processes. This can be done using Na as a reference element, i.e. under the assumption that dissolved Na is released to rivers only by weathering and is not significantly reincorporated in solid secondary weathering products during their formation nor taken up as a nutrient by the biota (Gislason et al., 1996; Georg et al., 2007; Millot et al., 2010; Dellinger et al., 2015b):

$$\begin{array}{}\text{(4)}& f_{\text{diss}}^{\mathrm{Ba}}={\displaystyle \frac{{\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}}{(\mathrm{Ba}/\mathrm{Na}{)}_{\mathrm{0}}}},\end{array}$$

where ${\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}$ is the dissolved Ba∕Na ratio corrected for non-silicate inputs, and (Ba∕Na)₀ is the bedrock ratio (details on the calculation are given in Appendix B). Assuming that Ba and Na are not fractionated with respect to one another during their release from rocks, $f_{\text{diss}}^{\mathrm{Ba}}$ is then a proxy for the reincorporation of Ba into secondary weathering solids (clays, oxides) or into organic matter.

The calculated fraction of initially dissolved Ba left in the dissolved load of rivers, $f_{\text{diss}}^{\mathrm{Ba}}$, ranges from 0.04 in rivers draining only the Andean belt to 1.63 in the Rio Negro River. This latter value for a parameter that, in principle, should be < 1 is somewhat surprising and will be discussed in Sect.  4.5.

$f_{\text{diss}}^{\mathrm{Ba}}$ does not show any correlation with dissolved δ¹³⁸Ba_diss (not shown), supporting the idea that several compartments incorporate Ba in the Critical Zone following its release from rocks and that the various processes responsible for this incorporation are characterised by different isotopic fractionation factors. In the following, in order to quantitatively tease these effects apart, we use a mass balance approach that accounts for the two processes likely to fractionate Ba in the Critical Zone: secondary phase formation and biological uptake.

4.2 Assessing the relative role of biological uptake on the Ba cycle in the Amazon Basin

The element fluxes and isotope composition can be used in tandem to estimate the role of various processes in elemental budgets (e.g. Bouchez et al., 2013; Baronas et al., 2018). To this aim, we consider the behaviour of Ba in the Critical Zone at the catchment scale under a scenario in which dissolved Ba, originally derived from the partial dissolution of rocks, is partitioned into different net uptake and dissolved export fluxes following the framework developed by Bouchez et al. (2013). The partitioning of Ba after its release from rock minerals can be written as follows:

$$\begin{array}{}\text{(5)}& F_{\mathrm{0}}^{\mathrm{Ba}}=F_{\text{diss}}^{\mathrm{Ba}}+F_{\text{bio}}^{\mathrm{Ba}}+F_{\text{sec}}^{\mathrm{Ba}},\end{array}$$

where $F_{\mathrm{0}}^{\mathrm{Ba}}$ is the dissolution flux of Ba from rocks, $F_{\text{diss}}^{\mathrm{Ba}}$ is the flux of river dissolved Ba exported from the system, $F_{\text{bio}}^{\mathrm{Ba}}$ is the net Ba uptake by the biota (“net” meaning Ba uptake minus Ba release during organic matter remineralisation), and $F_{\text{sec}}^{\mathrm{Ba}}$ is the Ba flux associated with the net formation (i.e. precipitation minus redissolution) associated with Ba-bearing secondary weathering products such as clays or oxides.

Then, by dividing both sides of Eq. (5) by $F_{\mathrm{0}}^{\mathrm{Ba}}$, we obtain the relative proportion of all fluxes with respect to the dissolution flux:

$$\begin{array}{}\text{(6)}& \mathrm{1}=f_{\text{diss}}^{\mathrm{Ba}}+f_{\text{bio}}^{\mathrm{Ba}}+f_{\text{sec}}^{\mathrm{Ba}},\end{array}$$

where the $f_i^{\mathrm{Ba}}$ terms reflect the relative role of each process on Ba fluxes within the Critical Zone, with respect to the “initial” release flux of Ba from rocks $F_{\mathrm{0}}^{\mathrm{Ba}}$, and where $f_{\text{diss}}^{\mathrm{Ba}}$ represents the “residual” dissolved Ba flux after each process and is equivalent to that in Eq. (4). In other words, these terms represent the net formation fluxes of different compartments of the Critical Zone: $f_{\text{bio}}^{\mathrm{Ba}}$ is the net uptake of Ba by the biosphere, and $f_{\text{sec}}^{\mathrm{Ba}}$ is the net flux of precipitation of Ba-bearing secondary phases of weathering. It should be emphasised that while these terms reflect the net formation of these pools, in reality the dynamics of these compartments result from the competition between their formation and their destruction. For example, clays formed deep within weathering profiles that are generally in equilibrium with solute-rich waters can be destabilised when exposed to more dilute waters (Dellinger et al., 2015b), and organic matter can be remineralised in reservoirs with long residence times such as soils or floodplains (Bouchez et al., 2014b). Thus, a negative net formation ($f_i^{\mathrm{Ba}}<\mathrm{0}$) indicates that the pool i releases more Ba to the dissolved compartment in the Critical Zone than it incorporates from this dissolved compartment, at least on the timescale over which $f_i^{\mathrm{Ba}}$ is estimated.

Following Bouchez et al. (2013), we can introduce the corresponding isotope mass balance, which, importantly, is only valid at steady state:

$$\begin{array}{}\text{(7)}& {\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}={\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}-f_{\text{bio}}^{\mathrm{Ba}}\cdot {\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}-f_{\text{sec}}^{\mathrm{Ba}}\cdot {\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}},\end{array}$$

where ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$ is the Ba isotope composition of the river, ${\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}$ is the composition of the dissolved load after rock dissolution (assuming congruent dissolution, this parameter equals the isotope composition of the average bedrock), ${\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}$ is the Ba isotope fractionation factor during biological uptake, and ${\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}$ is the Ba isotope fractionation factor associated with the formation of secondary weathering products.

In order to quantify the role of nutrient cycling in the biogeochemical dynamics of Ba at the catchment scale, Eq. (7) can be solved for the term $f_{\text{bio}}^{\mathrm{Ba}}$. Replacing $f_{\text{sec}}^{\mathrm{Ba}}$ by ($\mathrm{1}-f_{\text{bio}}^{\mathrm{Ba}}-f_{\text{diss}}^{\mathrm{Ba}}$) (Eq. 6) in Eq. (7) and rearranging leads to

$$\begin{array}{}\text{(8)}& f_{\text{bio}}^{\mathrm{Ba}}={\displaystyle \frac{{\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}-{\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}+{\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}-\left(f_{\text{diss}}^{\mathrm{Ba}}\cdot {\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}\right)}{\left({\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}-{\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}\right)}}\end{array}$$

Provided that the values of the parameters ${\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}$, ${\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}$, and ${\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}$ can be estimated, $f_{\text{bio}}^{\mathrm{Ba}}$ can be calculated using our measurements of ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$ and $f_{\text{diss}}^{\mathrm{Ba}}$ in Eq. (8). In Appendix B, we discuss how the values of ${\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}$, ${\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}$, and ${\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}$ can be estimated. We also acknowledge that Eq. (8) relies on a steady-state assumption, which is also discussed in Appendix B.

Using these constraints, the calculated $f_{\text{bio}}^{\mathrm{Ba}}$ values over the Amazon Basin range from −0.39${}_{-\mathrm{0.30}}^{+\mathrm{0.25}}$ to 0.57${}_{-\mathrm{0.17}}^{+\mathrm{0.35}}$, and $f_{\text{bio}}^{\mathrm{Ba}}$ at the mouth of the Amazon is 0.28${}_{-\mathrm{0.12}}^{+\mathrm{0.25}}$ (Table S2 in the Supplement). Only a few rivers show a $f_{\text{bio}}^{\mathrm{Ba}}$ close to zero, which challenges the following common assumption that biological cycling operates at steady state from the point of view of the river dissolved load (i.e. that nutrient uptake equals nutrient release) at the catchment scale. Some of the rivers, such as the Mamoré, show a net release from the biosphere ($f_{\text{bio}}^{\mathrm{Ba}}<\mathrm{0}$), emphasising that, locally in time and space, the biota can also act as a source of rock-derived nutrients to the river dissolved load.

The most significant findings of this analysis are the net uptake of Ba ($f_{\text{bio}}^{\mathrm{Ba}}>\mathrm{0}$) by the biota across many regions of the Amazon Basin and the fact that the extent of this net biological uptake (the exact value of $f_{\text{bio}}^{\mathrm{Ba}}$) displays significant spatial variation. Therefore, in the following section, we explore the geomorphological, climatic, and ecological controls on the extent of Ba biological uptake.

4.3 Controls on Ba elemental and isotope partitioning by the weathering regime

The first hypothesis we set out to test regarding the spatial variation in Ba partitioning amongst compartments of the Critical Zone ($f_i^{\mathrm{Ba}}$) across the Amazon Basin is the role of the Earth surface denudation, which varies significantly between the mountainous Andes and the flatter Amazon lowlands. Denudation rates exert a strong control on the so-called “weathering regime”, which in turn influences the behaviour of elements and their isotopes in the Critical Zone (Bouchez et al., 2013; Dellinger et al., 2015b; Frings et al., 2016). The catchment-scale denudation rate (D) is the sum of the chemical weathering (W) and physical erosion (E) rates measured from river material, typically using estimates of weathering-derived solute fluxes (e.g. Gaillardet et al., 1999b) for weathering and sediment gauging for erosion. Alternatively, denudation rates can also be estimated using cosmogenic nuclides such as ¹⁰Be in sediments (e.g. Wittmann et al., 2011). The three rates D, E, and W are typically expressed in units of tonnes per square kilometre per year (or in millimetres per year using a rock-density-based conversion). At one end of the spectrum of D, the “kinetically limited” weathering regime is characterised by high values of D and a short particle residence time in the Critical Zone (West et al., 2005). Under these conditions, the extent of chemical reactions is limited by the kinetics (or how fast the reaction can proceed), leading to a low share of solute export (W for weathering) to total export rates (low values of the W∕D ratios, used as an index for weathering intensity; Bouchez et al., 2014a). On the other end of the spectrum, the “supply-limited” regime, in which D values are low and particles reside for a long time within the weathering reactor, allows for more intense weathering and is characterised by higher W∕D ratios (Riebe et al., 2004). To summarise the relation between these different metrics, the low W∕D ratios of mountainous regions are typically associated with both high W and D fluxes, and high W∕D ratios characteristic of flatter areas are typically associated with both low W and D fluxes.

Weathering intensity, bounded by these kinetically limited and supply-limited weathering regime endmembers, also translates into isotope signatures; for example, denudation exerts a strong control on the behaviour of Li stable isotopes within the Critical Zone by modulating the extent of secondary mineral formation (Dellinger et al., 2015b; Frings et al., 2016). Unlike for Li isotopes, there is no direct relationship between $\mathit{\delta }{{}^{\mathrm{138}}\mathrm{Ba}}_{\text{diss}}$ and D or W∕D in our dataset (Fig. S5 in the Supplement). This is because several processes of the Critical Zone act in conjunction to set the river dissolved Ba isotope signature in the Amazon Basin, as explained in Sect. 4.1, whereas only the formation of secondary products drives dissolved Li isotopes (Lemarchand et al., 2010). However, the individual role of each process in the Critical Zone can be evaluated through the examination of the relationships between the $f_i^{\mathrm{Ba}}$ (Eqs. 4 and 8) fractions estimated above using our mass balance approach as well as the W∕D ratios as markers of the weathering regime.

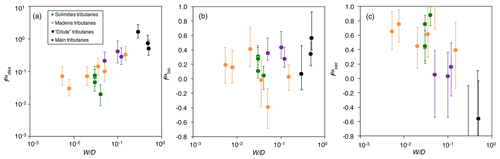
Figure 4 The distribution of Ba amongst different compartments of the Critical Zone ($f_i^{\mathrm{Ba}}$) for (a) dissolved export (diss), (b) biota (bio; Eq. 8), and (c) secondary weathering products such as clays or oxides (sec), once released from rocks vs. W∕D (weathering intensity), in the Amazon Basin. W∕D values are taken from Wittmann et al. (2011) and Dellinger et al. (2015b). In panel (c), $f_{\text{sec}}^{\mathrm{Ba}}$ is calculated as $\mathrm{1}-f_{\text{diss}}^{\mathrm{Ba}}-f_{\text{bio}}^{\mathrm{Ba}}$ (Eq. 6). Uncertainties on $f_i^{\mathrm{Ba}}$ have been evaluated using Monte Carlo error propagation based on the uncertainties on individual parameters (Appendix B; Table S2). Note the logarithmic scale used for $f_{\text{diss}}^{\mathrm{Ba}}$ in panel (a).

The relative role of dissolved export in the total Ba input into the Critical Zone ($f_{\text{diss}}^{\mathrm{Ba}}$) displays a positive relation with W∕D (Fig. 4a). This observation is in contrast to what has been reported for Li, which shows a lesser extent of Li scavenging from the solution (higher $f_{\text{diss}}^{\mathrm{Li}}$) when W∕D is high or low, resulting in a so-called “boomerang” relationship (Dellinger et al., 2015b). Thus, it is likely that even if Ba scavenging during formation of secondary weathering products is hampered at low W∕D because of a kinetic limitation (as it is for Li), another process scavenging dissolved Ba is being enhanced at low W∕D, the nature of which is discussed below. $f_{\text{bio}}^{\mathrm{Ba}}$ does not show any trend with W∕D (Fig. 4b), whereas $f_{\text{sec}}^{\mathrm{Ba}}$ shows a negative relation with W∕D (Fig. 4c).

As the sum of the three $f_i^{\mathrm{Ba}}$ values for each river is equal to one by construction, some of the observed co-variation between $f_i^{\mathrm{Ba}}$ is spurious, as this closure constraint induces a negative covariance between the different f terms. In order to independently examine the role of each process, we translate these Ba fractions (equivalent to non-dimensional Ba fluxes) into area-specific, dimensional fluxes $F_i^{\mathrm{Ba}}$ (expressed in $\mathrm{kg}\mathrm{Ba}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) using the fact that

$$\begin{array}{}\text{(9)}& F_i^{\mathrm{Ba}}=F_{\text{diss}}^{\mathrm{Ba}}\cdot {\displaystyle \frac{f_i^{\mathrm{Ba}}}{f_{\text{diss}}^{\mathrm{Ba}}}}\end{array}$$

by definition from Eq. (6), where i=bio, sec, or diss. In Eq. (10) we can calculate $F_{\text{diss}}^{\mathrm{Ba}}$ using the river discharge, Q (in m³ yr⁻¹); the concentration of silicate-derived river dissolved Ba, [Ba]^* (µg L⁻¹); and the drainage area of the catchment, S (in km²), yielding a flux in milligrams per square kilometre per year ($\mathrm{mg}\mathrm{Ba}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$; Table S2):

$$\begin{array}{}\text{(10)}& F_{\text{diss}}^{\mathrm{Ba}}={\displaystyle \frac{[\mathrm{Ba}{]}^{*}\cdot Q}{S}}\end{array}$$

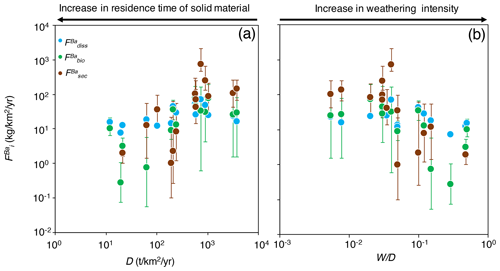
Figure 5 Fluxes of Ba in the Critical Zone ($F_i^{\mathrm{Ba}}$) for dissolved export (diss), the formation of secondary weathering products such as clays or oxides (sec), and biological uptake (bio), from Eq. (9), vs. (a) D (denudation) and (b) W∕D (weathering intensity) in the Amazon Basin. D and W∕D values are taken from Wittmann et al. (2011) and Dellinger et al. (2015b). Uncertainties on $F_i^{\mathrm{Ba}}$ have been evaluated using Monte Carlo error propagation based on the uncertainties on individual parameters (Appendix B; Table S2). Negative median values of $F_i^{\mathrm{Ba}}$ are not plotted here because of the logarithmic scale.

The area-specific flux of dissolved Ba remains constant across the range of denudation rates (Fig. 5a) or weathering regimes, indexed as the W∕D ratio (Fig. 5b). Barium fluxes associated with both biological uptake and the formation of secondary weathering products is high where denudation is high. The flux of Ba associated with secondary phase formation is positively related to the denudation rate and, hence, to the flux of Ba linked to biological uptake. In settings with the highest denudation rates, the formation of secondary weathering products is thought to become kinetically limited (Bouchez et al., 2013; Pogge von Strandmann and Henderson, 2015; Dellinger et al., 2015b). However, such limitation is not apparent for the corresponding Ba flux. This indicates again that the relevant processes for scavenging dissolved elements in the Critical Zone are distinct between Ba and Li.

The absolute flux of dissolved Ba ($F_{\text{diss}}^{\mathrm{Ba}}$) exported by rivers being relatively constant across the Amazon Basin, combined with the fact that the fluxes of Ba associated with biological uptake and secondary phase formation are the highest where D is high, explains why $f_{\text{diss}}^{\mathrm{Ba}}$ (the relative dissolved Ba flux) increases with W∕D (Fig. 4a). Regardless of the explanation for this relatively invariant $F_{\text{diss}}^{\mathrm{Ba}}$, it is critical to note that this behaviour (observed here for Ba across the whole Amazon Basin) is in stark contrast to what has been reported for Li in the Andean part of the Amazon Basin (Dellinger et al., 2015b). In addition, it should be emphasised that the relationships shown in Figs. 4 and 5 include pure Andean rivers (e.g. the Alto Beni), pure dilute rivers (e.g. the Tapajós), and mixed rivers with active floodplains (e.g. the Amazon at Óbidos). Dellinger et al. (2015b) showed a specific behaviour of Li isotopes in floodplains, expressed as a strong enrichment of heavy Li isotopes in rivers featuring active floodplains and as a loss of dissolved Li between the upstream reaches and the downstream reaches of these rivers. Although we cannot fully exclude a role of processes specific to floodplains in the Ba cycle and isotope fractionation in the Amazon Basin, we note that no such loss of dissolved Ba is observed across the few floodplain reaches where such a calculation can be made (see supporting text for details and Table S3 in the Supplement for data; Bouchez et al., 2012; Dellinger et al., 2015b). In most floodplain reaches, the river dissolved Ba flux actually increases downstream, which can be explained by the relative Ba enrichment of pure dilute tributaries (as shown by their relatively high dissolved Ba∕Na ratios; Sect. 4.1) that also contribute water to large rivers featuring active floodplains.

The most interesting and novel observation of Fig. 5 remains the increase in the Ba biological uptake flux with denudation rates. Although this finding relies on isotope mass balance equations that inherently bear some uncertainties – in particular related to the steady-state assumption itself or to parameter estimates (Appendix B) – such a result is consistent with what has been observed at the much smaller soil scale, reporting that biological cycling can be influenced by rock supply rate or age (e.g. Vitousek et al., 2003; Porder et al., 2007). In the following section, we explore potential reasons why such a relationship might exist at the large catchment scale in the Amazon Basin, in particular using independent estimates of parameters relevant to ecosystem dynamics.

4.4 Relationships between biological uptake, weathering regime, and ecosystem dynamics

In the previous section, variations in catchment-scale Ba biological uptake fluxes across the Amazon Basin were examined as a function of D and W∕D as metrics of the weathering regime. In particular, this analysis shows how the partitioning of the nutrient-like element Ba in the Critical Zone differs from that of the non-nutrient Li. Thus, the prominent role of ecosystem dynamics (especially in terms of ecosystem nutrition) in setting Ba partitioning in the Critical Zone is further explored in the present section.

Here, the fluxes of Ba associated with biological uptake are compared to the following two sets of metrics:

1. two catchment-scale carbon fluxes that we believe capture the first-order mass balance dynamics of ecosystems – the gross primary production (GPP; in $\mathrm{t}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) and the terrestrial ecosystem respiration (TER; in $\mathrm{t}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) – which are both retrieved from remote sensing data (Table S4 in the Supplement; Tramontana et al., 2016; Jung et al., 2019, see the supporting text for details);

2. two major climatic factors affecting ecosystems – the mean annual temperature (MAT; in ^∘C) and the mean annual precipitation (MAP; in mm yr⁻¹) (Table S4; https://www.worldclim.org, last access: 23 November 2020, see the supporting text for details).

GPP can be envisaged as a measure of the biomass, as most catchment-scale biomass estimates are derived from GPP estimates anyway (Tramontana et al., 2016; Jung et al., 2019). Respiration of organic matter leads to the release of nutrients to the ecosystem, such that catchment-scale TER can rather be used as a proxy for the recycling of rock-derived nutrients (and of elements characterised by a nutrient-like behaviour such as Ba) through litter remineralisation. Such constraints (GPP, TER, MAP, and MAT) do not rely on any geochemical tool; thus, they offer fully independent information on biological activity across the Amazon Basin compared with the Ba isotope approach used in this study until now.

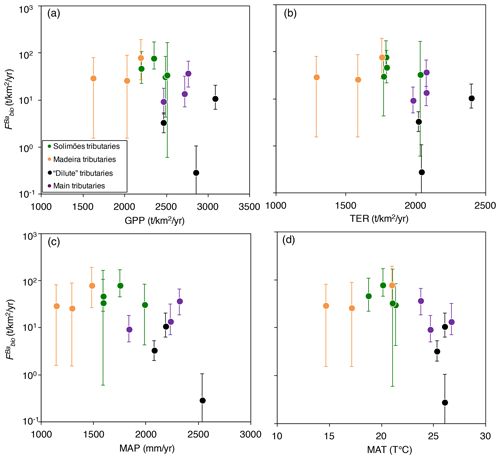
Figure 6 Flux of Ba biological uptake ($F_{\text{bio}}^{\mathrm{Ba}}$; Eq. 9) vs. (a) gross primary production (GPP; in $\mathrm{t}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$), (b) terrestrial ecosystem respiration (TER; in $\mathrm{t}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$), (c) mean annual precipitation (MAP; in mm yr⁻¹), and (d) mean annual temperature (MAT; in T ^∘C). GPP and TER were retrieved from remote sensing data (Tramontana et al., 2016; Jung et al., 2019), and MAP and MAT were derived from https://www.worldclim.org, last access: 23 November 2020.

Ecosystem dynamics, in particular as probed by GPP, are also related to rock-derived nutrient cycling as calculated for Ba isotopes (Fig. 6a, b); this is shown by the broad difference between Andean and Plain tributaries, lending further confidence to the validity of our determination of $F_i^{\mathrm{Ba}}$. In addition, $F_{\text{bio}}^{\mathrm{Ba}}$ is broadly negatively related to both MAP and MAT (Fig. 6c, d), suggesting an impact of climatic factors on Ba biological cycling.

The relationships in Fig. 6 indicate that in the poorly erosive, tectonically quiescent, warm and humid areas of the Amazon Basin such as the craton and the Amazon Plain, the elevated GPP (Fig. 6a) suggests that the size of the biota reservoir is large (as, in particular, allowed by high MAP and MAT), while high TER (Fig. 6b) is indicative of efficient recycling of rock-derived nutrients from litter, resulting, on average, in smaller net fluxes associated with Ba biological uptake ($F_{\text{bio}}^{\mathrm{Ba}}$). On the contrary, in the highly erosive, colder and drier areas of the Andes, the relatively low GPP (Fig. 6a) suggests a smaller size of the biota reservoir. TER is also relatively low in these regions (Fig. 6b), indicating lower efficiency with respect to the nutrient recycling of rock-derived from litter, thereby leading to a higher net flux of Ba biological uptake by the biosphere. This comparison between independent sets of constraints further strengthens our inference that some catchment-scale relationship exists between weathering regime, climate, and nutrient cycling across the Amazon Basin.

To summarise, biological uptake as indexed by $F_{\text{bio}}^{\mathrm{Ba}}$ is higher in the Andes than in the lowland regions of the Amazon Basin. Based on existing knowledge on ecosystem nutrition, a set of mechanistic interpretations can be proposed to explain this finding. First, enhanced nutrient supply to the ecosystem through rejuvenation of the Earth surface by denudation and subsequent weathering (high W and D in the Andes) might simply allow for more vigorous uptake of rock-derived nutrients (e.g. Vitousek et al., 2003; Porder et al., 2007; Hahm et al., 2014; Uhlig and von Blanckenburg, 2019), although we note that no relation exists between W and $F_{\text{bio}}^{\mathrm{Ba}}$ in our dataset (not shown). Second, in mountainous regions, lower temperature and precipitation combined with the short residence time of solid material in the Critical Zone might lead to inefficient release of nutrients from litter (Trumbore et al., 1996). In the plains, higher temperature and precipitation increase the energy available for efficient nutrient recycling, with slow denudation and the subsequent longer residence time of solid material allowing for a nearly closed “recycling loop”. Other factors influencing biological uptake and litter remineralisation that might differ between the Amazon plains and the Andes include the role of soil humidity (Grubb, 1971) and the residence time of water in the subsurface (Torres et al., 2015).

Altogether, a change in nutrient recycling efficiency is a likely explanation for the shift in rock-derived nutrient uptake fluxes between the Andes and the plain, as suggested by Ba isotopes. As a matter of fact, in most ecosystems, the major nutrition acquisition pathway relies on the rapid recycling of litter (e.g. Cleveland et al., 2013; Wilcke et al., 2017; Uhlig and von Blanckenburg, 2019). Nonetheless, recycling is never complete, as a small fraction of litter is exported from soils by erosion before remineralisation (Selva et al., 2007; Scalley et al., 2012), as shown by the presence of particulate organic carbon of biogenic origin in river material (Selva et al., 2007; Bouchez et al., 2014b). Therefore, a slow but sustained supply from rock dissolution is needed to balance the loss from un-recycled nutrients by litter erosion, defined as the “geogenic” pathway (Uhlig and von Blanckenburg, 2019). Our results from the Amazon Basin suggest that a shift occurs in the relative role of these two pathways with respect to the acquisition of rock derived-nutrients, from the predominance of the organic pathway in the hot and humid environment of the plains to an increased importance of the geogenic pathway in the colder, drier, and more erosive Andes (Fig. 6).

The above interpretation can further be tested using a so-called “river-scale mass budget”, which allows an examination of the form under which rock-derived nutrients are exported. Such a test is performed for Ba in the next section.

4.5 The fate of Ba following its biological uptake in the Amazon Basin: clues from Ba elemental and isotope river-scale mass budgets

River-scale mass budgets, based on a hypothesised chemical complementarity between the weathered (chemical export) and eroded (physical export) material exported by rivers, have been used to test whether the chemical composition of the material exported by rivers can be explained by the composition of the rock undergoing erosion and weathering at the scale of large catchments (Stallard, 1995; Gaillardet et al., 1995, 1999a). A failure in such a test can be indicative of issues in estimating the composition of the source rock (Gaillardet et al., 1999a) or in the determination of the composition of the riverine export (Bouchez et al., 2011), of timescale issues related to the typical integration time of the values used for the parameters of the river mass budget (Stallard, 1995; Lemarchand and Gaillardet, 2006), or of any combination thereof.

In the scope of the present study on Ba isotopes, such a river mass budget can be used to test whether all Ba released from rock dissolution is found in the total (that is, dissolved plus particulate) riverine export, in which case the mass budget can be considered to be “equilibrated”. A lack of Ba in the riverine export would then mean that Ba is either currently accumulating in the catchment, and/or that the adopted sampling techniques do not capture the entirety of the riverine Ba export, or at least does not integrate the full river Ba export over the timescale that is relevant to establish the Ba river mass budget. As shown below, the form under which Ba is accumulated in, or exported from the catchment, can also be discussed based on the results of such a river-scale mass budget.

In addition, it is important to note that whereas strong uncertainties affect the different parameters used to compute $f_{\text{bio}}^{\mathrm{Ba}}$ above (in particular on the isotope fractionation factors ${\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}$ and ${\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}$), river-scale mass budgets as performed in the following are only based on the relative partitioning of Ba and its isotopes between the dissolved and solid phases of rivers (Bouchez et al., 2013).

4.5.1 Testing the equilibrium of the Ba river mass budget in the Amazon Basin

To assess whether the Ba river budget is “at equilibrium” in the Amazon, we can compare the fraction of Ba transported as a dissolved species (w^Ba; Eq. 3) against the relative loss of Ba in river sediments compared with the source rocks. To quantify this loss, we normalise the Ba∕Th ratio of river sediments to the Ba∕Th ratio of the source rocks (the full derivation of the following equation is presented in Appendix C).

$$\begin{array}{}\text{(11)}& (\mathrm{Ba}/\mathrm{Th}{)}_n+w_{\text{fluxes}}^{\mathrm{Ba}}=\mathrm{1}\end{array}$$

The two parameters (Ba∕Th)_n and $w_{\text{fluxes}}^{\mathrm{Ba}}$ (as determined from Eq. 3) represent the fraction of dissolved and solid Ba transported in rivers relative to the denudation fluxes respectively. Equation (11) means that when the Ba river mass budget is at equilibrium, the sum of (Ba∕Th)_n and $w_{\text{fluxes}}^{\mathrm{Ba}}$ is equal to one; in other words, data points should lie on the down-sloping diagonal in a $w_{\text{fluxes}}^{\mathrm{Ba}}$ vs. (Ba∕Th)_n diagram (Figs. S6 in the Supplement and 7a). Rivers plotting below this line are characterised by an export of Ba lower than that expected from the basin-scale denudation rate and the Ba concentration in the source rock.

Such a test for an equilibrated river mass budget can also be performed using isotope ratios (Bouchez et al., 2013; Uhlig et al., 2017):

$$\begin{array}{}\text{(12)}& w_{\text{iso}}^{\mathrm{Ba}}={\displaystyle \frac{{\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}-{\mathit{\delta }}_{\text{sed}}^{\mathrm{Ba}}}{{\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}-{\mathit{\delta }}_{\text{sed}}^{\mathrm{Ba}}}}\end{array}$$

In a $w_{\text{iso}}^{\mathrm{Ba}}$ vs. $w_{\text{fluxes}}^{\mathrm{Ba}}$ diagram, if the river mass budget is at equilibrium, the data points should lie along the 1:1 line, whereas in a $w_{\text{iso}}^{\mathrm{Ba}}$ vs. (Ba∕Th)_n diagram, they should lie along the down-sloping diagonal. Note that the $w_{\text{iso}}^{\mathrm{Ba}}$ vs. (Ba∕Th)_n evaluation, unlike the $w_{\text{fluxes}}^{\mathrm{Ba}}$ vs. (Ba∕Th)_n comparison explained above, does not depend on fluxes. In order to provide an example of an equilibrated river mass budget, in Fig. S6 we revisit the data provided by Dellinger et al. (2015a), who showed that the sum of the solid and dissolved Li fluxes exported by rivers in the Amazon, as well as their combined isotope composition, can be accounted for by an independent estimate of the flux and isotope composition of Li eroded and weathered from rocks. The river mass budget of Li shows that at the scale of the Amazon Basin, timescale issues stemming from the comparison of various parameters integrating Earth surface processes over different timescales (e.g. dissolved fluxes or particulate fluxes) are negligible, at least regarding the “inorganic” part of element cycles in the Critical Zone. This observation, combined with the fact that estimates of the Ba abundance and isotope composition of source rocks can be considered fairly reliable (Appendix B), suggests that any disequilibrium that might arise in the Ba river mass budget should find its origin in the nutrient-like behaviour of Ba.

The comparison between $w_{\text{fluxes}}^{\mathrm{Ba}}$ and (Ba∕Th)_n (Eq. C5; Fig. 7a) shows that there is less Ba exported by rivers than expected from denudation rates for most of the Amazon rivers. Notable exceptions are the dilute tributaries (the Rio Negro, the Trombetas, and the Tapajós). It is possible that the export of Th as a dissolved species induced by organic colloids in such rivers compromises the use of the river mass budget (in particular Eqs. C2 and C3; Appendix C). We also note that the input from dust in these lowland areas (Abouchami et al., 2013; Moran-Zuloaga et al., 2018) can be significant, which could bias river-scale mass budgets. In the following, we focus our interpretations on the other river systems, which all display a negative offset from the equilibrium line in Fig. 7a. For these rivers, we note that if a dust component was included on the left-hand side of Eqs. (C1) or (C2), the observed disequilibrium would go in the same direction and would even be larger, thereby leaving this inference unchanged.

The observed disequilibrium in the Ba river mass budget also remains when comparing $w_{\text{iso}}^{\mathrm{Ba}}$ (Eq. 12) to (Ba∕Th)_n (Eq. C5, Fig. 7b) or $w_{\text{fluxes}}^{\mathrm{Ba}}$ to $w_{\text{iso}}^{\mathrm{Ba}}$ (Fig. 7c), despite significant uncertainty on the values of $w_{\text{iso}}^{\mathrm{Ba}}$ due to both analytical uncertainties and error propagation (for example, when ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$ and ${\mathit{\delta }}_{\text{sed}}^{\mathrm{Ba}}$ are close; see Eq. 12 and the discussion in Bouchez et al., 2013).

From here, in order to identify the potential causes of the lack of equilibrium in the river-scale mass budgets observed for most tributaries of the Amazon Basin, we can test the different scenarios that could reconcile the isotopic and elemental exports of Ba by Amazon rivers with denudation rates. As there is less Ba exported by rivers than expected from denudation (Fig. 7a), these different scenarios will all consider that in order to reconcile the two measures, the addition of a “missing Ba component”, associated with a specific isotopic signature referred to as ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ hereafter, is needed. To illustrate these scenarios, the arrows in the panels of Fig. 7 indicate the directions in which the values on the three diagram axes will change upon the addition of the missing Ba component:

1. the missing Ba is in a dissolved form, and its isotopic signature (${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$) is lower than ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$;

2. the missing Ba is in a dissolved form, and ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ is higher than ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$;

3. the missing Ba is in a particulate form, and ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ is lower than ${\mathit{\delta }}_{\text{sed}}^{\mathrm{Ba}}$;

4. the missing Ba is in a particulate form, and ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ is higher than ${\mathit{\delta }}_{\text{sed}}^{\mathrm{Ba}}$.

For scenarios 1 and 2, adding the missing (dissolved) Ba would increase $w_{\text{fluxes}}^{\mathrm{Ba}}$ (Eq. 3) but leave (Ba∕Th)_n unchanged. Scenarios 3 and 4 would result in a decrease in $w_{\text{fluxes}}^{\mathrm{Ba}}$, while the shift they would induce on (Ba∕Th)_n would depend on the Ba∕Th ratio of the missing Ba component. As discussed below in Sect. 4.5.2, we expect that this missing Ba component is of biological nature. In this case, the Ba∕Th ratio of the missing component would likely be relatively high, as Th is not a nutrient. Thus, scenarios 3 and 4 would result in the addition of Ba-rich material to the river solid load and, thus, to an increase in (Ba∕Th)_n, leading to non-vertical vectors in Fig. 7b and c. Finally, following Eq. (12), $w_{\text{iso}}^{\mathrm{Ba}}$ would increase if ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ was higher than ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$ (scenario 1) or than ${\mathit{\delta }}_{\text{sed}}^{\mathrm{Ba}}$ (scenario 3); and it would decrease if ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ was lower (scenarios 2 and 4).

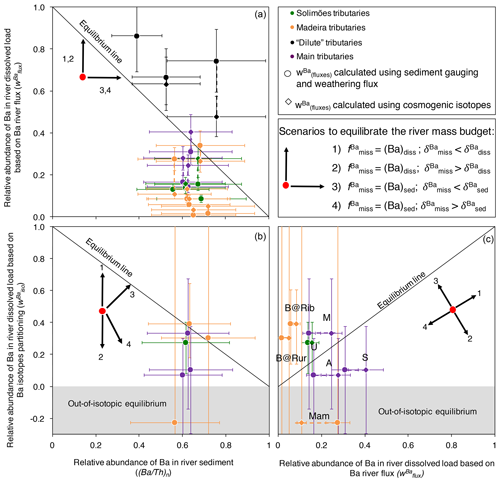
Figure 7 Test for the equilibrium of the river mass budget of Ba in the Amazon Basin using elemental (Eqs. 3 and C4) and isotopic (Eq. 12) ratios. Uncertainties on $w_{\text{fluxes}}^{\mathrm{Ba}}$ and (Ba∕Th)_n have been calculated using Gaussian error propagation. Values of $w_{\text{fluxes}}^{\mathrm{Ba}}$ have been calculated following two methods (river gauging, shown using circles, and cosmogenic nuclides, shown using diamonds; for a given river both estimates are linked by a stippled line), allowing us to partially account for potential timescale issues in the estimation of sediment export (see Appendix C). Uncertainties on $w_{\text{iso}}^{\mathrm{Ba}}$ have been evaluated using Monte Carlo error propagation based on the uncertainties on individual parameters in Eq. (12), and they are shown here as 68 %CI. In panel (c), “B@Rur”, “B@Rib”, “Mam”, “U”, “M”, “A”, and “S” reflect the following respective sampling sites: Beni at Rurrenabaque, Beni at Riberalta, Mamoré, Ucayali, Madeira, Amazon, and Solimões.

While all these scenarios bring the data points closer to the equilibrium line in Fig. 7a by construction, it appears that scenario 2 can be immediately excluded because adding dissolved Ba with a high ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ would shift the river mass budget toward stronger disequilibrium (Fig. 7b, c). In addition, the direction given by the vector of scenario 4 is unlikely to reconcile $w_{\text{iso}}^{\mathrm{Ba}}$ and (Ba∕Th)_n for any river in Fig. 7b and $w_{\text{iso}}^{\mathrm{Ba}}$ and $w_{\text{fluxes}}^{\mathrm{Ba}}$ for most rivers in Fig. 7c. Indeed, some rivers (the Beni at Riberalta and at Rurrenabaque, the Ucayali, and the Madeira) are above the equilibrium line in Fig. 7c, and their Ba river mass budget could be reconciled if vector 1 had a sub-horizontal direction, which could be the case if the difference between ${\mathit{\delta }}_{\text{diss}}^{\mathrm{Ba}}$ and ${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$ was small. However, we first note that the uncertainty on $w_{\text{iso}}^{\mathrm{Ba}}$ for these rivers is large. Second, the most important finding regarding this comparison between $w_{\text{iso}}^{\mathrm{Ba}}$ and $w_{\text{fluxes}}^{\mathrm{Ba}}$ in Fig. 7c is still that the observed disequilibrium cannot be explained by scenario 2 and is unlikely to be explained by scenario 4.

To summarise, ruling out scenarios 2 and 4 allows us to infer that the isotope composition of the missing Ba (${\mathit{\delta }}_{\text{miss}}^{\mathrm{Ba}}$) is lower than that of Ba exported by rivers. Therefore, the remaining valid scenarios are 1 (the missing Ba is dissolved) and 3 (the missing Ba is solid). However, the nature of (and the uncertainties encountered in) the analysis performed above prevents a full assessment of the exact nature of this missing Ba (dissolved or solid) or of its isotope composition.

Nevertheless, the difference between the Li (Fig. S6) and Ba (Fig. 7) river mass budgets as well as the fact that the Ba isotope composition of the missing reservoir is low (which is consistent with the Ba isotope composition of a biological component; Bullen and Chadwick, 2016, and Fig. 2) are strong arguments for a role of biological cycling in forming this Ba component that is missing from the river-scale mass budget. In the following, we further explore this hypothesis by comparing estimates of the amount of missing Ba to other independent estimates of Ba fluxes across the Amazon Basin.

4.5.2 What is the nature of the missing Ba component in the Amazon riverine export?

Given the role of biological uptake on the Ba abundance and isotope ratio in the rivers of the Amazon Basin, here we test for the influence of biological uptake on the missing Ba inferred from the river mass budget above.

First, we quantify the missing Ba as a relative flux ($f_{\text{miss}}^{\mathrm{Ba}}$) as the difference between the Ba flux actually exported by rivers and the Ba export that should result from denudation and the concentration of Ba in rocks. This actually corresponds to the graphical offset (vertical or horizontal) between (Ba∕Th)_n (or equivalently $w_{\text{fluxes}}^{\mathrm{Ba}}$) and the down-sloping diagonal line in Fig. 7:

$$\begin{array}{}\text{(13)}& f_{\text{miss}}^{\mathrm{Ba}}=\mathrm{1}-w_{\text{fluxes}}^{\mathrm{Ba}}-(\mathrm{Ba}/\mathrm{Th}{)}_n\end{array}$$

It is important to note that $f_{\text{miss}}^{\mathrm{Ba}}$ can be interpreted as an actual relative flux of Ba exported from the catchment but missed by our sampling scheme, as a relative rate of Ba build-up in a reservoir within the catchment, or as a combination thereof. We return to this distinction later when discussing the interpretation of $f_{\text{miss}}^{\mathrm{Ba}}$, but we refer to this metric as a relative “flux” for the moment for the sake of simplicity. To compare the flux of missing Ba ($f_{\text{miss}}^{\mathrm{Ba}}$) with the amount of Ba cycled by the biota in the Amazon ($f_{\text{bio}}^{\mathrm{Ba}}$), we first convert $f_{\text{miss}}^{\mathrm{Ba}}$ into a dimensional flux:

$$\begin{array}{}\text{(14)}& F_{\text{miss}}^{\mathrm{Ba}}=D\cdot f_{\text{miss}}^{\mathrm{Ba}}\cdot [\mathrm{Ba}{]}_{\text{rock}},\end{array}$$

where $F_{\text{miss}}^{\mathrm{Ba}}$ is the area-specific flux of missing Ba in rivers (expressed in units such as $\mathrm{kg}\mathrm{Ba}{\mathrm{km}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$). We note that the denudation rates derived from the sum of sediment gauging (E integrating over decades) and silicate weathering flux (W) vs. cosmogenic nuclides which already represents the total denudation flux (D integrating over thousands of years; Wittmann et al., 2011; Dellinger et al., 2015a) can differ (especially in the Beni River system). Therefore, for rivers where both constraints are available, we calculate two values of $F_{\text{miss}}^{\mathrm{Ba}}$: one based on D calculated as E from sediment gauging, in addition to the silicate weathering flux; and the other based on D determined from cosmogenic nuclides.

Figure 8 Flux of Ba biological uptake ($F_{\text{bio}}^{\mathrm{Ba}}$; Eq. 9) vs. the missing Ba flux as quantified from the river-scale mass budget ($F_{\text{miss}}^{\mathrm{Ba}}$; Eq. 14) in the Amazon Basin. Uncertainties have been propagated using a combination of Monte Carlo simulation and Gaussian error propagation.

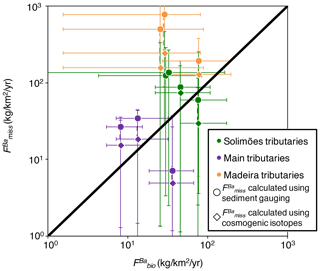
Despite significant uncertainty, it is clear that the missing flux $F_{\text{miss}}^{\mathrm{Ba}}$ (Eq. 14) is of the same order of magnitude as $F_{\text{bio}}^{\mathrm{Ba}}$ (Table S6 in the Supplement; Fig. 8) across the Amazon Basin. This observation further supports that biological uptake is a viable explanation for the disequilibrium in the river mass budget of the Amazon Basin. Interestingly, the relationship between $F_{\text{miss}}^{\mathrm{Ba}}$ and $F_{\text{bio}}^{\mathrm{Ba}}$ is stronger when $F_{\text{miss}}^{\mathrm{Ba}}$ is calculated using cosmogenic isotopes in Eq. (14) (Table S6; Fig. 8). The cosmogenic-derived denudation rates integrate over longer timescales compared with that of sediment gauging (von Blanckenburg, 2005), suggesting that the link between Ba biological uptake and the Ba river mass budget is a long-term feature of the Ba cycle in the Amazon Basin. Altogether, these observations further support that the existence of the missing Ba flux in the Amazon Basin, inferred from the river-scale mass budget performed in Sect. 4.5.1, is indeed linked to biological cycling.

A first possibility to account for such a missing Ba flux could derive from groundwater contributions that can export a significant amount of dissolved Ba. Thus, sampling schemes focusing only on river export might miss this potentially large dissolved Ba flux from the groundwater. However, with the magnitude of the river Ba dissolved flux and that of $F_{\text{miss}}^{\mathrm{Ba}}$ in the Amazon Basin being similar (Tables S.2, S.6) coupled with the fact that the observed Ba concentration in groundwater is similar to those measured in the rivers, this explanation would require that the groundwater discharge of the Amazon River is similar to that of the river discharge. Although seasonal groundwater storage in the Amazon Basin appears to be a significant component of the regional hydrological budget, especially in the central part of the Amazon Basin (Frappart et al., 2019), such a high contribution of groundwater to the overall water export of the whole Amazon Basin seems unlikely. In addition, we do not see any particular reason why such groundwater export would affect Ba and not Li (Figs. 7 and S6). It also appears unlikely that $F_{\text{miss}}^{\mathrm{Ba}}$ could be interpreted as a dissolved pool of Ba accumulating in the catchments given the typical residence times of groundwater even in large catchments and the fact that the observed disequilibrium in the Ba river mass budget seems to hold over long timescales (see above).

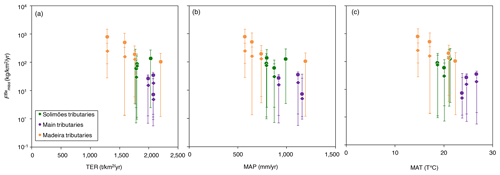
Figure 9 Missing Ba flux ($F_{\text{miss}}^{\mathrm{Ba}}$; Eq. 14) vs. (a) terrestrial ecosystem respiration (TER), (b) mean annual precipitation (MAP), and (c) mean annual temperature (MAT). Uncertainties have been propagated using Monte Carlo simulation and Gaussian propagation error.

Therefore, the most likely interpretation for the existence of a significant missing Ba is the export (if interpreted as an actual flux) or accumulation (if interpreted as a pool building up) of Ba-bearing solids. Given the relationship observed between $F_{\text{bio}}^{\mathrm{Ba}}$ and $F_{\text{miss}}^{\mathrm{Ba}}$ (Fig. 8), it is plausible that these particulates are of organic nature, i.e. living beings or dead organic matter (litter and/or river particulate organic carbon). In support of this interpretation, we note that a relationship exists between TER, MAP, and MAT vs. $F_{\text{miss}}^{\mathrm{Ba}}$ (Fig. 9a–c), showing a more pronounced missing Ba flux, in basins for which precipitation, temperatures, and the efficiency of the remineralisation are lower and, thus, where the formation (and possibly export) of litter and dead particulate organic matter is stronger (Sect. 4.4).

The accumulation of organic-bound Ba within catchments could explain the existence of the missing Ba. For example, a pool of solid, organic-bound Ba could be forming through the accumulation of litter in soils or through an increase in the biomass – this can be the case in areas where forests regrow following deforestation in the Amazon Basin. Although this hypothesis needs to be tested further, the current growth of biomass in some regions of the Andes would support this scenario (e.g. Feeley and Silman, 2010).

Alternatively, the missing Ba could also reflect the existence of a particulate, organic debris flux. Uhlig et al. (2017) suggested that the export of Mg and other rock-derived nutrients as particulate organic matter in mountain belts could represent a crucial missing riverine elemental flux; however, this is traditionally challenging to sample, notably because this export is mostly episodic, and, thus, difficult to constrain, resulting in a typical timescale issue in the river mass budget, where the sampling frequency of river material does not allow one to capture the entirety of the long-term riverine export. In large river systems such as the Amazon, the effect of episodic export on the total organic matter flux is likely to be smeared out, as suggested by the relative regularity of particulate organic carbon fluxes throughout the hydrological cycle (Bouchez et al., 2014b). However, large woody debris (e.g. trunks) or river macrophytes could, in principle, represent a significant fraction of the particulate export of large rivers and be essentially unaccounted for due to the limited amount of water that can be withdrawn with the sampling scheme commonly used (only a few litres with river point samplers) (Bouchez et al., 2011).

To test for the validity of this scenario, we can predict the flux of particulate organic carbon that would be needed to account for the computed $F_{\text{miss}}^{\mathrm{Ba}}$:

$$\begin{array}{}\text{(15)}& F_{\text{miss}}^{\mathrm{C}}={\displaystyle \frac{F_{\text{miss}}^{\mathrm{Ba}}}{(\mathrm{Ba}/\mathrm{C}{)}_{\text{org}}}},\end{array}$$

where $F_{\text{miss}}^{\mathrm{C}}$ is the missing flux of organic carbon, and (Ba∕C)_org is the Ba∕C ratio of the organic matter exported by rivers. $F_{\text{miss}}^{\mathrm{C}}$ can then be compared with $E_{\text{org}}^{\mathrm{C}}$, which is the flux of particulate organic carbon exported by the river:

$$\begin{array}{}\text{(16)}& E_{\text{org}}^{\mathrm{C}}=E\cdot \text{POC},\end{array}$$

where POC represents the relative content of particulate organic carbon in the river sediments (Bouchez et al., 2014b), and E represents the erosion rate (from sediment gauging) (Table S6).

Two estimates can be proposed for the value of (Ba∕C)_org to calculate $F_{\text{miss}}^{\mathrm{C}}$ (Eq. 15). In the first estimate, we take the average concentration of Ba in organic matter of 15 mg kg⁻¹ based on our own compilation (Li, 2000; Chiarenzelli et al., 2001; Bullen and Bailey, 2005; Vaganov et al., 2013, Table S7 in the Supplement), and a concentration of carbon (C) in organic matter of around 50 %. In the second estimate, we use the ratio between the fluxes of Ba and C escaping litter decay, quantified as follows:

$$\begin{array}{}\text{(17)}& (\mathrm{Ba}/\mathrm{C}{)}_{\text{org}}={\displaystyle \frac{F_{\text{bio}}^{\mathrm{Ba}}}{\text{NPP}}},\end{array}$$

where NPP is the net primary productivity calculated as GPP − TER and corresponding to the net accumulation of carbon by the ecosystem. The values of (Ba∕C)_org calculated this way differ significantly between the Andes and the plains. In the Andes, the Ba abundance in organic matter estimated using Eq. (17) is much lower than that derived from our compilation (around 0.60 mg kg⁻¹; Table S6). In the plains, the calculated Ba concentration in organic matter is even lower (around 0.01 mg kg⁻¹; Table S6). At face value, the difference between the values obtained for the Andes and the plains using Eq. (17) suggests that the more efficient nutrient recycling is, the more weakly Ba is retained in the organic material exported by the river.

However, regardless of the value used for (Ba∕C)_org, the comparison between $E_{\text{org}}^{\mathrm{C}}$ (Eq. 16) and $F_{\text{miss}}^{\mathrm{C}}$ (Eq. 15) suggests that more than 99 % of the particulate organic carbon would be missed when estimating the POC flux using a “classical” sampling scheme. We believe that it is unlikely that such a high proportion of the POC flux can be unaccounted for.

Thus, it remains challenging to identify the exact form of the missing Ba (i.e. flux vs. pool or a combination thereof) inferred from the river-scale mass budget. However, the most likely interpretation for the existence of this missing component is the partitioning of Ba into biological material after uptake. As a consequence, our analysis emphasises the role of biological cycling on the routing and transport of rock-derived nutrients at the large catchment scale.

To summarise the above discussion, this examination of the Ba elemental and isotope budgets for a range of different river catchments throughout the Amazon Basin shows how stable isotope signatures can be used to explore nutrient cycling in the Critical Zone and, further, opens the possibility for an application to other isotope systems and other locations. Additionally, applying this approach to Ba provides novel information on the dynamics of the rock-derived nutrients, and possibly of organic matter, at the scale of large catchments.

4.6 A conceptual model for the influence of biological cycling and weathering regime on the fate of Ba as a nutrient-like element in the Amazon Basin

To summarise our analysis, we propose the following interpretation for the behaviour of Ba as a nutrient-like, broadly reflecting the behaviour of major rock-derived nutrients in the Amazon Basin:

• Except for some rivers draining the lowlands (see below), litter remineralisation outpaces litter erosion in the plain regions, allowing the biosphere to efficiently recycle Ba – and, thus, possibly rock-derived nutrients – from the litter; therefore a significant uptake of “new” Ba deriving from rock dissolution is not required (Cleveland et al., 2013). Under such conditions, primary production is strong, as promoted by high MAP and MAT, and soil stability which is promoted by low erosion rates leads to a weak export of particulate organic carbon from the catchment.

• In mountainous regions of the Amazon, nutrient recycling by vegetation from litter is slower than litter erosion. As a consequence, the biota continuously extracts Ba and possibly major rock-derived nutrients from the surrounding rocks, which compensates for the loss of litter by erosion. Primary production is lower because the growth of biota is limited by the low MAP and MAT, strong denudation rates, and the short residence times of material, whereas the export of rock-derived nutrients by particulate organic matter from the catchment (or accumulation within the catchment) is high.

• Some dilute rivers draining the lowlands are enriched in Ba with respect to the source rocks, which implies a net export of dissolved Ba from the biomass and organic matter component of the Critical Zone and, thus, suggests that these pools are currently not at steady state.

4.7 Using Ba stable isotopes to refine the river mass budget of major elements

The above analysis shows that the cycling of Ba (and that of other rock-derived nutrients) by land biota is a significant component of terrestrial biogeochemical cycles. As a consequence, biological cycling within a catchment and the routing, or exchange, of rock-derived elements amongst the different compartments of the Critical Zone could have consequences on the dissolved riverine export of major nutrients (Ca, Mg, K) that are traditionally used to estimate alkalinity fluxes and CO₂ consumption by chemical weathering at the catchment scale. In other words, nutrients that are taken up by the biota to a significant extent simply “go missing” in the river dissolved export fluxes. In the following, we add to existing inventories of river-borne cation concentrations deriving strictly from silicate weathering a component taken up by the biota, in order to update estimates of CO₂ consumption fluxes by silicate weathering reaction at the basin scale in the light of our findings (see Appendix D for details).

First noting that the biological uptake flux of any nutrient X is

$$\begin{array}{}\text{(18)}& [X{]}_{\text{bio}}=[\mathrm{Ba}{]}_{\text{diss}}\cdot {\displaystyle \frac{f_{\text{bio}}^{\mathrm{Ba}}}{f_{\text{diss}}^{\mathrm{Ba}}}}\cdot {\left({\displaystyle \frac{X}{\mathrm{Ba}}}\right)}_{\text{bio}},\end{array}$$

where [X]_bio is the concentration of a major soluble element X (Ca, K, or Mg, [Na]_bio is negligible as Na is not a nutrient) retained by the biosphere, and (X∕Ba)_bio is the X∕Ba ratio of the organic component. The (X∕Ba)_bio ratio is obtained from our own compilation of the chemical composition of the vegetation (Li, 2000; Chiarenzelli et al., 2001; Bullen and Bailey, 2005; Vaganov et al., 2013, ; Table S7). [X]_bio can then be added to the silicate-derived dissolved river concentration of X in the calculation of “corrected” silicate weathering fluxes ($R_{(\text{sil}+\text{bio})/\text{sil}}$). To this end, we express the impact of biological cycling on silicate weathering fluxes as the ratio between cations deriving from silicate weathering added to those deriving from biological cycling (W_silcorr) and uncorrected cations (W_sil):

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& R_{(\text{sil}+\text{bio})/\text{sil}}={\displaystyle \frac{W_{\text{silcorr}}}{W_{\text{sil}}}}\\ & ={\displaystyle \frac{\begin{array}{c}\mathrm{2}\cdot \left([\mathrm{Ca}{]}_{\text{sil}}^{\mathrm{2}+}+[\mathrm{Ca}{]}_{\text{bio}}^{\mathrm{2}+}\right)\\ +\mathrm{2}\cdot \left([\mathrm{Mg}{]}_{\text{sil}}^{\mathrm{2}+}+[\mathrm{Mg}{]}_{\text{bio}}^{\mathrm{2}+}\right)\\ +\left([\mathrm{K}{]}_{\text{sil}}^{+}+[\mathrm{K}{]}_{\text{bio}}^{+}\right)+[\mathrm{Na}{]}_{\text{sil}}^{+}\end{array}}{\mathrm{2}\cdot [\mathrm{Ca}{]}_{\text{sil}}^{\mathrm{2}+}+\mathrm{2}\cdot [\mathrm{Mg}{]}_{\text{sil}}^{\mathrm{2}+}+[\mathrm{K}{]}_{\text{sil}}^{+}+[\mathrm{Na}{]}_{\text{sil}}^{+}}}\end{array}\end{array}$$

W_sil is calculated using the sum of the concentration of each X element from silicate weathering (expressed in meq L⁻¹), with W_sil = 2 ⋅ [Ca]${}_{\text{sil}}^{\mathrm{2}+}$ + 2 ⋅ [Mg]${}_{\text{sil}}^{\mathrm{2}+}$ + $[\mathrm{K}{]}_{\text{sil}}^{+}$ + $[\mathrm{Na}{]}_{\text{sil}}^{+}$ (data from Dellinger et al., 2015b). As our primary interest is to quantify the effect of biological cycling on CO₂ consumption, we do not consider the SiO₂ component of the weathering flux in our analysis.

$R_{(\text{sil}+\text{bio})/\text{sil}}$ values range from ${\mathrm{1.1}}_{-\mathrm{0.1}}^{+\mathrm{1.7}}$ (the Huallaga River) to ${\mathrm{4.8}}_{-\mathrm{1.6}}^{+\mathrm{3.0}}$ (Trombetas River; Table S8 in the Supplement), whereas the value for the mouth of the Amazon is ${\mathrm{2.1}}_{-\mathrm{0.5}}^{+\mathrm{1.1}}$. These numbers show that the CO₂ consumption by silicate weathering, once corrected for biological uptake, could be higher by a factor of around 2 across the Amazon Basin compared with previous estimates. Despite significant uncertainties, this analysis shows that river-derived weathering fluxes warrant re-evaluation regarding the potential role played by the biota as a storage of rock-derived nutrients.

5 Conclusions

In the Amazon, the abundance and isotope composition of Ba – which we show to be sourced mainly from silicate rocks – is controlled by a combination of the formation of secondary weathering products and biological uptake, with a stronger isotope effect from the latter. This nutrient-like behaviour enables the use of Ba as a surrogate for major rock-derived nutrients and allows us to examine the relationships between rock-derived nutrient cycling, weathering, and ecosystem dynamics.

Using isotope mass balance and estimates of isotope fractionation factors, we are able to propose a quantitative pattern for the partitioning of Ba liberated in the Critical Zone through rock weathering amongst secondary phases of weathering, the dissolved load, and the biota. The comparison of this partitioning to catchment-scale mass and isotope budgets of Ba (showing that the riverine export of Ba does not match the flux of Ba release from rocks) suggests that biological cycling of Ba leads to the formation of a missing Ba component in the Critical Zone of the Amazon Basin. Although the exact nature of this missing Ba component remains elusive (in particular regarding the fact that it could be accumulated within the catchment and/or exported by rivers), our favoured interpretation is that it is locked into dead particulate organic matter (i.e. litter or river particulate organic carbon).

The proportion of Ba remaining in solution compared with that “initially” released by mineral dissolution is negatively correlated with denudation rates and positively correlated with weathering intensity, reflecting the combined effects of scavenging by secondary mineral precipitation and biological uptake. Biological uptake of Ba is found to be stronger in the Andes, possibly reflecting the need for the biota to compensate for the depletion of organic components lost by erosion. In the plains, where the denudation rate is low and the energy available for litter remineralisation is high, organic-bound Ba can be released from litter such that additional biological uptake from rock weathering is not required to replace the loss or nutrients bound to solid organic material by the ecosystem.

Finally, using the estimated uptake of Ba by the biosphere, we reassess silicate weathering fluxes calculated from the cation loads of rivers with the effect of biological uptake now corrected for. We show that the cation dissolved load at the mouth of the Amazon is significantly underestimated, shifting the best estimates of CO₂ consumption deduced from the cation dissolved load. This observation should be confirmed by using other rock-derived nutrients to reduce the uncertainties. Furthermore, we believe that the method developed in this study to account for contributions from biological cycling should be extended to other large rivers in order to reassess the CO₂ consumption at a global scale.

To conclude, our work shows that barium and its isotopes can be used to track the cycling of rock-derived nutrients in large river basins and reveal its impact on the routing of nutrients throughout the Critical Zone. Such an informative approach warrants extension to other settings and other isotope systems in order to further reveal the role of life in the chemical weathering process.

Appendix A: Identification of dissolved Ba sources in the Amazon Basin rivers

Spatial variation in the dissolved Ba abundance and isotope composition throughout the Amazon Basin could be due to source effects. For this reason, it is necessary to assess the relative contribution of atmospheric deposition and of release from different rock sources to the Ba river dissolved load (Gou et al., 2019).

Rain water is most likely not a significant source of Ba given the low concentration of dissolved Ba in surface seawater (a common source of solutes to rainwater) compared with that of dissolved Ba in rivers (Gaillardet et al., 2003). It is possible to further quantify the contribution of rain-derived Ba as follows:

$$\begin{array}{}\text{(A1)}& [\mathrm{Ba}{]}_{\text{riv}}^{*}=[\mathrm{Ba}{]}_{\text{riv}}-[\mathrm{Cl}{]}_{\text{atm}}\cdot {\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Cl}}}\right)}_{\text{atm}},\end{array}$$

where $[\mathrm{Ba}{]}_{\text{riv}}^{*}$ is the concentration of dissolved Ba in the river corrected for rain inputs, [Ba]_riv is the measured concentration of Ba of the river, [Cl]_atm is the concentration of dissolved Cl derived from the atmosphere following Gaillardet et al. (1997), and (Ba∕Cl)_atm is the seawater Ba∕Cl ratio of ≈ 2 × 10⁻⁷ assuming that sea salts are the sole Ba contributor to rain. Following this calculation, Ba derived from rain inputs is less than 1 % of the total dissolved Ba for all rivers analysed here.

Carbonate rocks formed in ancient marine environments are one of the most important sources of dissolved alkali earth elements to rivers. However, the abundance of Ba in modern oceans is controlled by barite formation, rather than by carbonate precipitation (Dehairs et al., 1980). None of the ${\mathrm{Ca}}^{*}/{\mathrm{Na}}^{*}$ vs. ${\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}$ and δ¹³⁸Ba vs. ${\mathrm{Ca}}^{*}/{\mathrm{Na}}^{*}$ plots (Fig. S7a and b in the Supplement) show a correlation that could indicate mixing between a silicate and a carbonate weathering endmember as a control on dissolved Ba abundance. We can assess the proportion of river dissolved Ba derived from carbonate weathering using the ${\mathit{\alpha }}_{\mathrm{Ca}}^{\text{carbonate}}$ (proportion of riverine dissolved Ca derived from carbonate weathering) from Dellinger et al. (2015b) using

$$\begin{array}{}\text{(A2)}& [\mathrm{Ba}{]}_{\text{riv}}^{**}=[\mathrm{Ba}{]}_{\text{riv}}^{*}-[\mathrm{Ca}{]}_{\text{riv}}^{*}\cdot {\mathit{\alpha }}_{\mathrm{Ca}}^{\text{carb}}\cdot {\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Ca}}}\right)}_{\text{carb}},\end{array}$$

where $[\mathrm{Ba}{]}_{\text{riv}}^{**}$ is the dissolved concentration of Ba corrected for both rain and carbonate inputs; [Ca]_riv is the measured concentration of dissolved Ca in the river; and (Ba∕Ca)_carb is the ${\mathrm{Ba}}^{*}/{\mathrm{Ca}}^{*}$ ratio of rivers draining only carbonate rocks, corrected for rain inputs, equal to 5 × 10⁻⁵ (median of n=12 measurements; Fig. S1). The highest proportion of dissolved Ba derived from carbonate rocks was found for the Madre de Dios River (about 10 %), whereas carbonate weathering inputs to the Ba dissolved load for other tributaries did not exceed 5 %.

In aqueous solutions, Ba shows a high affinity for sulfate ions, which leads to the formation of barite (BaSO₄) in oceans and marine sediments. In particular, the pre-concentration of Ba and SO₄ induced by organic matter decay in micro-environments leads to the precipitation of BaSO₄ (Griffith and Paytan, 2012). It has been also shown that the weathering of organic-rich sedimentary rocks such as black shales can be an important input of dissolved Ba to rivers (Dalai et al., 2002) which could be due to presence of barite in these rocks (Arndt et al., 2009). In addition, as an alkali earth element, Ba could be contained in trace but significant amounts in gypsum, which could also contribute to the river dissolved Ba budget. To test for both the influence of gypsum and barite dissolution, ${\mathrm{SO}}_{\mathrm{4}}^{*}/{\mathrm{Na}}^{*}$ vs. ${\mathrm{Ba}}^{*}/{\mathrm{Na}}^{*}$ and δ¹³⁸Ba vs. ${\mathrm{SO}}_{\mathrm{4}}^{*}/{\mathrm{Na}}^{*}$ are plotted in Fig. S7c and d. No correlation can be observed between these parameters, implying that neither gypsum nor barite represent significant sources of river dissolved Ba in the Amazon Basin. To conclude, dissolved Ba in the Amazon Basin is almost exclusively derived from silicate rocks, and in our analysis, we consider our estimates of [Ba]^* from Eq. (A1) to reflect silicate-derived inputs.

Appendix B: Parameters and assumptions of the Ba isotope mass balance

The estimation of $f_{\text{bio}}^{\mathrm{Ba}}$ from Eq. (8) requires the estimation of several parameters, which we review hereafter.

Source rock Ba abundance ((Ba∕Na)₀)

In order to compute the values of $f_{\text{diss}}^{\mathrm{Ba}}$, the source ratio (Ba∕Na)₀ first needs to be constrained. In the case of lithologically mixed basins, it can be calculated as follows:

$$\begin{array}{}\text{(B1)}& (\mathrm{Ba}/\mathrm{Na}{)}_{\mathrm{0}}=\sum _{i=\mathrm{1}}\cdot {\mathit{\alpha }}_{\text{rock}i}^{\mathrm{Na}}\cdot {\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Na}}}\right)}_{\mathrm{0}}^i\end{array}$$

Here, ${\mathit{\alpha }}_{\text{rock}i}^{\mathrm{Na}}$ is the proportion of Na, and ${\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Na}}}\right)}_{\mathrm{0}}^i$ is the Ba∕Na ratio of the rock i, where i = shales, andesites, and plutonic rocks, as carbonate and evaporite rocks do not significantly influence the dissolved Ba and Na budgets, as shown in Appendix A. The sources of dissolved Na within the Amazon catchment have been identified by Dellinger et al. (2015b). We used ${\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Na}}}\right)}_{\mathrm{0}}^i$ values of 0.004, 0.013, and 0.006 for andesites, shales, and plutonic rocks respectively. These values derive from our data compilation (see Fig. S1).

Source rock Ba isotope composition (δ¹³⁸Ba_rock)

The value of ${\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}$ used in Eq. (8) depends on the relative contribution of each source rock type with the Ba dissolved flux. Three main silicate rocks have to be considered as potential sources of Ba for the Amazon Basin: shales, andesites, and plutonic rocks. First, using the relative contribution of Na (${\mathit{\alpha }}_i^{\mathrm{Na}}$) calculated by Dellinger et al. (2015b), we can estimate the relative Ba contribution from each rock as follows:

$$\begin{array}{}\text{(B2)}& {\mathit{\alpha }}_{\text{rock}i}^{\mathrm{Ba}}={\displaystyle \frac{(\mathrm{Ba}/\mathrm{Na}{)}_i}{(\mathrm{Ba}/\mathrm{Na}{)}_{\mathrm{0}}}}\cdot {\mathit{\alpha }}_{\text{rock}i}^{\mathrm{Na}}\end{array}$$

Then, the average ${\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}$ value can be calculated as

$$\begin{array}{}\text{(B3)}& {\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}=\sum _{i=\mathrm{1}}{\mathit{\alpha }}_{\text{rock}i}^{\mathrm{Ba}}\cdot {\mathit{\delta }}_{\text{rock}i}^{\mathrm{Ba}},\end{array}$$

where ${\mathit{\delta }}_{\text{rock}}^{\mathrm{Ba}}$ is the Ba isotope composition of each source rock  i. We use our own measurements for shales (${\mathit{\delta }}_{\text{rockshales}}^{\mathrm{Ba}}$ = −0.02 ‰ ± 0.04 ‰; n=4) and data from the literature (Van Zuilen et al., 2016b; Nan et al., 2018) for andesites (${\mathit{\delta }}_{\text{rockandesite}}^{\mathrm{Ba}}$ = 0.07 ‰ ± 0.02 ‰; n=7) and plutonic rocks (${\mathit{\delta }}_{\text{rockplutonic}}^{\mathrm{Ba}}$ = 0.00 ‰ ± 0.04 ‰; n=71).

Ba isotope fractionation factor associated with the formation of secondary weathering products (${\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}$)

As discussed above in Sect. 4.1, secondary phases, e.g. clays or oxyhydroxides, can at least partially drive the isotope composition of dissolved Ba in rivers (Gong et al., 2019). No experimental study on Ba isotope fractionation during the precipitation of secondary weathering phases has been carried out to date, except for sorption on silica hydrogel which did not result in a strong Ba isotope fractionation (Van Zuilen et al., 2016a). Nevertheless, we can try to assess a Ba isotope fractionation factor during the formation of clays and oxides using our own measurements and previously published data. Marine clays do not show large variations in δ¹³⁸Ba, with an isotope composition that is slightly depleted (by ∼ −0.05 ‰) in heavy isotopes with respect to igneous and sedimentary rocks (Bridgestock et al., 2018). Barium isotope fractionation during the formation of secondary weathering products can also be estimated from data on soils. The difference between the soil water and the bulk solid soil Ba isotope composition over a latosol profile in China ranges from −0.01 ‰ to −0.18 ‰ (average value of −0.09 ‰), which is likely induced by the difference in mineralogical composition and by the varying respective role of sorption and precipitation over the profile (Gong et al., 2019). The large river approach undertaken here likely mitigates such mineralogical heterogeneity effects, allowing for the consideration of one “lumped” isotope fractionation factor (Bouchez et al., 2013). Our own measurement of Ba isotopes in sediments from the Amazon rivers show the same slight depletion in heavy isotopes as shales from the Amazon Basin (this study) or as published data on andesites (Van Zuilen et al., 2016b), with δ¹³⁸Ba values ranging from −0.05 ‰ to −0.10 ‰, which is consistent with the estimates reached above. Therefore, taking the above constraints and the associated uncertainty into account, we estimate that ${\mathrm{\Delta }}_{\text{sec-diss}}^{\mathrm{Ba}}$ = −0.09 ‰ ± 0.05 ‰.

Ba isotope fractionation factor associated with biological uptake (${\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}$)

Bullen and Chadwick (2016) showed that the isotope composition of dissolved Ba in the Critical Zone is strongly impacted by biological processes. However, no proper estimate of the Ba isotope fractionation factor associated with biological uptake is currently available. In order to represent the poor constraints on this parameter, we consider ${\mathrm{\Delta }}_{\text{bio-diss}}^{\mathrm{Ba}}$ = −0.25 ‰ to −0.75 ‰ using three δ¹³⁸Ba values reported by Bullen and Chadwick (2016) for vegetation samples as well as the propagated uncertainty on this parameter in the following calculations assuming a uniform distribution between these values.

Discussing the steady-state assumption

Equation (7) assumes that the Ba-bearing materials exported by rivers (excluding primary minerals, i.e. dissolved Ba, organics, and secondary weathering phases) correspond to all Ba derived from rock dissolution, thereby achieving Ba steady state for all compartments of the Critical Zone. In such a case, the net formation of each secondary phase can be envisaged to be compensated for by an erosion flux, as proposed in Bouchez et al. (2013).

In the first “non-steady-state scenario”, the organic reservoir (biota and soil solid organics) grows simply because litter fall and erosion of organic matter are outpaced by biological uptake. In such a scenario, the isotope composition of the dissolved Ba exported by rivers would not change. Therefore, in this case, the strict steady-state assumption can be relaxed for the organic (biota and soil organic matter) reservoir without undermining the validity of the steady-state isotope mass balance of Eq. (7).

Another possibility for non-steady-state dynamics is the scenario where litter remineralisation releases Ba to waters faster than Ba is taken up by vegetation (implying that the organic reservoir decreases in size), in which case the steady-state assumption of the dissolved Ba reservoir is not met, jeopardising the use of Eq. (7) which derives from a steady-state framework (Bouchez et al., 2013). We first note that negative $f_{\text{bio}}^{\mathrm{Ba}}$ values, which should result from cases where remineralisation is outpaced by uptake, are only observed for three rivers from our dataset. Second, if $f_{\text{bio}}^{\mathrm{Ba}}<\mathrm{0}$, over sufficiently short timescales, the isotope composition of dissolved Ba can then rather be interpreted as a mixture between (i) a “rock-derived” endmember, possibly affected by the formation of secondary phases of weathering and (ii) an organic-derived endmember.

Appendix C: River mass budget assumption and derivation

Here, we present a detailed description of the different assumption and derivation required to performed river mass budget in Sect. 4.5.

Quantitatively speaking, for an equilibrated mass budget, the amount of Ba delivered to the Earth surface by rock uplift and conversion into material in the Critical Zone should be equal to the sum of Ba dissolved ($F_{\text{diss}}^{\mathrm{Ba}}$) and solid ($F_{\text{sed}}^{\mathrm{Ba}}$) exports by rivers:

$$\begin{array}{}\text{(C1)}& F_{\text{diss}}^{\mathrm{Ba}}+F_{\text{sed}}^{\mathrm{Ba}}=D\cdot [\mathrm{Ba}{]}_{\text{rock}}\end{array}$$

Using the term D⋅[Ba]_rock (with [Ba]_rock the abundance of Ba in the source rock) in Eq. (C1) is equivalent to assuming that the denudation rate D is a proxy for the supply of rock material to the Earth surface. We acknowledge that D can be seen as an imperfect proxy for the supply of rock material to the Earth surface, as its validity requires that the export of material by the river is equal to the supply of rock at depth and, hence, that some form of steady state exists for the regolith covering the Earth surface. However, we take the fact that the Li river mass budget in the Amazon (using Eq. C1) is at equilibrium (Dellinger et al., 2015a) as a good indicator that this approach is reliable. We also note that this estimate of Ba supply to the Earth surface neglects inputs from rock-derived nutrients from global dust (Abouchami et al., 2013; Moran-Zuloaga et al., 2018), which can be important in the Amazon lowlands (see discussion in Sect. 4.5).

The same equation can be written for Th, which is an insoluble element with a magmatic compatibility close to that of Ba (Gaillardet et al., 1999a), thereby minimising the influence of the crustal composition when using rock Ba∕Th ratios (see below):

$$\begin{array}{}\text{(C2)}& F_{\text{sed}}^{\mathrm{Th}}=D\cdot [\mathrm{Th}{]}_{\text{rock}},\end{array}$$

where [Th]_rock is the abundance of Th in the source rock, and $F_{\text{sed}}^{\mathrm{Th}}$ is the flux of Th transported as solids (i.e. as sediments) by the river. Then dividing each side of Eq. (C1) by Eq. (C2) gives

$$\begin{array}{}\text{(C3)}& {\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Th}}}\right)}_{\text{rock}}={\displaystyle \frac{F_{\text{diss}}^{\mathrm{Ba}}+F_{\text{sed}}^{\mathrm{Ba}}}{F_{\text{sed}}^{\mathrm{Th}}}}\end{array}$$

Moreover, dividing the Ba∕Th ratio of river sediments (Ba∕Th)_sed (Table S5 in the Supplement) by the two sides of Eq. (C3), and noting that ${\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Th}}}\right)}_{\text{sed}}={\displaystyle \frac{F_{\text{sed}}^{\mathrm{Ba}}}{F_{\text{sed}}^{\mathrm{Th}}}}$, gives

$$\begin{array}{}\text{(C4)}& {\displaystyle \frac{{\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Th}}}\right)}_{\text{sed}}}{{\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Th}}}\right)}_{\text{rock}}}}={\left({\displaystyle \frac{\mathrm{Ba}}{\mathrm{Th}}}\right)}_n={\displaystyle \frac{F_{\text{sed}}^{\mathrm{Ba}}}{F_{\text{sed}}^{\mathrm{Ba}}+F_{\text{diss}}^{\mathrm{Ba}}}}\end{array}$$

The term (Ba∕Th)_n in Eq. (C4) corresponds to the inverse of the α-depletion factor of soluble elements in river sediments, introduced by Gaillardet et al. (1999a), and it is conceptually equivalent to $\mathrm{1}+{\mathit{\tau }}_{\mathrm{Ba},\mathrm{Th}}$, where τ_Ba,Th is the mass transfer coefficient developed to quantify the depletion in soluble elements in soils (Brimhall and Dietrich, 1987). Finally, given the definition of w^Ba (Eq. 3), referred to hereafter as “$w_{\text{fluxes}}^{\mathrm{Ba}}$” (for better distinction from “$w_{\text{iso}}^{\mathrm{Ba}}$” calculated below), an equilibrated river mass budget should consequently result in the following equation:

$$\begin{array}{}\text{(C5)}& {\displaystyle \frac{F_{\text{sed}}^{\mathrm{Ba}}}{F_{\text{sed}}^{\mathrm{Ba}}+F_{\text{diss}}^{\mathrm{Ba}}}}+{\displaystyle \frac{F_{\text{diss}}^{\mathrm{Ba}}}{F_{\text{sed}}^{\mathrm{Ba}}+F_{\text{diss}}^{\mathrm{Ba}}}}=(\mathrm{Ba}/\mathrm{Th}{)}_n+w_{\text{fluxes}}^{\mathrm{Ba}}=\mathrm{1}\end{array}$$

Both parameters should, in principle, take values between zero and one, and we note that as Ba is always depleted over Th in the measured river sediment material compared to rocks in our dataset, (Ba∕Th)_n is between zero and one. Regarding $w_{\text{fluxes}}^{\mathrm{Ba}}$, it is important to note that Eq. (3) can be used based on river sediment gauging (yielding the averaged [spm]) as in Eq. (3), or via

$$\begin{array}{}\text{(C6)}& w_{\text{fluxes}}^{\mathrm{Ba}}={\displaystyle \frac{Q\cdot [\mathrm{Ba}{]}_{\text{diss}}}{D\cdot [\mathrm{Ba}{]}_{\text{rock}}}}\end{array}$$

Using Eq. (3), $w_{\text{fluxes}}^{\mathrm{Ba}}$ is between zero and one by construction, whereas if Eq. (C6) is used, it is possible that $w_{\text{fluxes}}^{\mathrm{Ba}}$ takes values higher than one because the numerator and the denominator on the right-hand side of Eq. (C6) are evaluated in independent ways as well as using metrics reflecting different timescales of dynamics in the Critical Zone. However, regardless of the way $w_{\text{fluxes}}^{\mathrm{Ba}}$ is calculated, all values calculated for $w_{\text{fluxes}}^{\mathrm{Ba}}$ in the Amazon Basin are between zero and one in our dataset.

(Ba∕Th)_rock in (Ba∕Th)_n is estimated for each river using the rock contributions given by Dellinger et al. (2017) as well as the Ba∕Th ratios of individual rock types (equal to 48 for igneous plutonic and shale rocks – which have a similar Ba∕Th ratio – and to 140 for andesites; Table S6).

Appendix D: Calculation of dimensional, catchment-scale Ba biological uptake fluxes

The isotope mass balance model presented in Sect. 4.3 allows for the estimation of $f_{\text{bio}}^{\mathrm{Ba}}$, which is a relative, non-dimensional flux of Ba biological uptake with respect to the flux of Ba release from rock partial dissolution. In Sect. 4.7, our analysis requires a dimensional value equivalent for $f_{\text{bio}}^{\mathrm{Ba}}$. Below, we show how to calculate the net biological uptake flux for major rock-derived nutrients based on $f_{\text{bio}}^{\mathrm{Ba}}$ computations.

Recalling the definition of $f_{\text{bio}}^{\mathrm{Ba}}$,

$$\begin{array}{}\text{(D1)}& f_{\text{bio}}^{\mathrm{Ba}}={\displaystyle \frac{F_{\text{bio}}^{\mathrm{Ba}}}{F_{\mathrm{0}}^{\mathrm{Ba}}}},\end{array}$$

and applying the same definition for another element X gives

$$\begin{array}{}\text{(D2)}& f_{\text{bio}}^X={\displaystyle \frac{F_{\text{bio}}^X}{F_{\mathrm{0}}^X}}\end{array}$$

Now recalling the definition of $f_{\text{diss}}^{\mathrm{Ba}}$,

$$\begin{array}{}\text{(D3)}& f_{\text{diss}}^{\mathrm{Ba}}={\displaystyle \frac{F_{\text{diss}}^{\mathrm{Ba}}}{F_{\mathrm{0}}^{\mathrm{Ba}}}},\end{array}$$

and applying the same definition for another element X

$$\begin{array}{}\text{(D4)}& f_{\text{diss}}^X={\displaystyle \frac{F_{\text{diss}}^X}{F_{\mathrm{0}}^X}},\end{array}$$

we can rearrange these equations and obtain the following expression:

$$\begin{array}{}\text{(D5)}& {\displaystyle \frac{f_{\text{bio}}^{\mathrm{Ba}}}{f_{\text{diss}}^{\mathrm{Ba}}}}={\displaystyle \frac{F_{\text{bio}}^{\mathrm{Ba}}}{F_{\text{diss}}^{\mathrm{Ba}}}},\end{array}$$

such that the net, dimensional flux of X biological uptake is

$$\begin{array}{}\text{(D6)}& \begin{array}{rl}{F}_{\text{bio}}^X& =Q\cdot [\mathrm{Ba}{]}_{\text{diss}}\cdot {\displaystyle \frac{f_{\text{bio}}^{\mathrm{Ba}}}{f_{\text{diss}}^{\mathrm{Ba}}}}\cdot {\left({\displaystyle \frac{X}{\mathrm{Ba}}}\right)}_{\text{bio}}\\ & =F_{\text{diss}}^{\mathrm{Ba}}\cdot {\displaystyle \frac{F_{\text{bio}}^{\mathrm{Ba}}}{F_{\text{diss}}^{\mathrm{Ba}}}}\cdot {\left({\displaystyle \frac{X}{\mathrm{Ba}}}\right)}_{\text{bio}}\end{array}\end{array}$$