Southern Ocean Biogeochemical Argo detect under-ice phytoplankton growth before sea ice retreat

The seasonality of sea ice in the Southern Ocean has profound effects on the life cycle (phenology) of phytoplankton residing under the ice. The current literature investigating this relationship is primarily based on remote sensing, which often lacks data for half of the year or more. One prominent hypothesis holds that, following ice retreat in spring, buoyant meltwaters enhance available irradiance, triggering a bloom which follows the ice edge. However, an analysis of Biogeochemical Argo (BGC-Argo) data sampling under Antarctic sea ice suggests that this is not necessarily the case. Rather than precipitating rapid accumulation, we show that meltwaters enhance growth in an already highly active phytoplankton population. Blooms observed in the wake of the receding ice edge can then be understood as the emergence of a growth process that started earlier under sea ice. Indeed, we estimate that growth initiation occurs, on average, 4–5 weeks before ice retreat, typically starting in August and September. Novel techniques using on-board data to detect the timing of ice melt were used. Furthermore, such growth is shown to occur under conditions of substantial ice cover (>90 % satellite ice concentration) and deep mixed layers (>100 m), conditions previously thought to be inimical to growth. This led to the development of several box model experiments (with varying vertical depth) in which we sought to investigate the mechanisms responsible for such early growth. The results of these experiments suggest that a combination of higher light transfer (penetration) through sea ice cover and extreme low light adaptation by phytoplankton can account for the observed phenology.

1 Introduction

The annual advance and retreat of Antarctic sea ice is the largest seasonal event on Earth, covering some 15 million km² (Massom and Stammerjohn, 2010). Such considerable seasonal changes have profound effects on the life cycle (phenology) of phytoplankton residing under the ice (Sallée et al., 2015; Ardyna et al., 2017; Hague and Vichi, 2018). However, the exact character of such effects is currently unknown, primarily because studies investigating phenology in these regions have relied on satellite data, which can contain missing data for half of the year or more (Cole et al., 2012; Racault et al., 2012). In particular, the winter and early spring periods are not taken into account, despite the important role they play in both the overall phenology and subsequent summer production (Llort et al., 2015; Ardyna et al., 2017; Boyce et al., 2017).

Here we present the first-ever comprehensive characterization of under-ice phenology for this period. This is achieved by leveraging under-ice data collected by Argo profiling floats equipped with a suite of biogeochemical sensors, deployed as part of the Southern Ocean Carbon and Climate Observations and Modeling (SOCCOM) project (https://soccom.princeton.edu/, last access: 1 February 2019). Of primary interest to us here is the mechanisms controlling the timing of phytoplankton growth initiation in the unique environment of the seasonal sea ice zone (SSIZ, defined as the ocean region seasonally covered by sea ice). A dominant idea in the literature with regards to such mechanisms holds that, following ice retreat in spring, buoyant meltwaters tend to enhance irradiance levels by rapidly shoaling the mixed layer. This alleviation of light limitation (coupled perhaps with nutrient input) is then used to explain why blooms are often observed in the wake of the receding ice edge (Smith and Nelson, 1985; Smith and Comiso, 2008; Briggs et al., 2017; Sokolov, 2008). The implication here is then that, prior to the release of meltwaters, growth rates remain low, only increasing substantially in response to melting. Hence, a prediction of the hypothesis (which we may term the meltwater hypothesis) is that the timing of melting should precede the timing of rapid growth. This is a somewhat subtle point, since the relevance of meltwaters is usually brought up to explain the presence of blooms, and so is often not explicitly linked to phenology (e.g. Taylor et al., 2013; Uchida et al., 2019). Nevertheless, the hypothesis implicitly assumes that phenology is strongly affected by the release of meltwater.

However, there is increasing evidence that this is not necessarily the case. In an early study, Smetacek et al. (1992) documented an intense bloom under pack ice conditions in early spring (before melting) in the Weddell Sea ice shelf region. More recently, in the Arctic, a similarly intense phytoplankton bloom was observed in the Chukchi Sea under complete ice cover ranging from 0.8 to 1.3 m thick Arrigo et al. (2012). Although this bloom was observed in summer, Assmy et al. (2017) have recently shown that under-ice blooms may develop even earlier in the Arctic due to the presence of leads in spring. In the Southern Ocean, evidence is emerging of earlier-than-expected growth in the deep mixed layers within the SSIZ (Uchida et al., 2019; Prend et al., 2019). The important feature of these studies for the present discussion is that high growth rates have been observed prior to melting and under complete (or near-complete) ice cover. However, the present literature has left several issues related to under-ice phenology unresolved.

First, studies focus almost exclusively on spring and summer and, hence, miss any potential growth occurring in winter. Indeed, it is assumed that such growth is negligible even though this has not been explicitly shown. Second, much attention is paid to regions of high biomass (i.e. blooms) and their associated environmental conditions. Although these regions are no doubt of great interest, their study does not necessarily contribute to an understanding of the mechanisms controlling phenology in general. This is especially true in the Southern Ocean, where large spatial variability is common (Thomalla et al., 2011). Third, the bulk of the present literature is based on studies of Arctic under-ice phenology. Antarctic sea ice is distinct in that it is generally thinner and more dynamic and has much more snow year round that does not form melt ponds (Vancoppenolle et al., 2013). Consequently, the presence of marginal ice zone (MIZ) conditions is also much more prevalent in the Southern Ocean. Note that we would define the MIZ here by dynamical considerations such as wave propagation (i.e. the MIZ may be defined as the region where wave attenuation is below a given threshold) and not a satellite ice concentration threshold (for example, see Squire, 2007; Meylan et al., 2014). This means that seasonal variations in light and nutrients are likely very different, motivating special attention to this unique environment.

2 Methods

The work presented here employs several novel techniques for detecting the timing of phenological events in the seasonally ice-covered Southern Ocean. In particular, the use of profiling float data to detect both the timing of melt and growth initiation avoids several of the shortcomings inherent to satellite and ship-based studies which characterize the present literature on under-ice phenology. First, if in situ data are used, they are limited in space and time and are usually compared to satellite products as a consequence. However, direct comparisons of this kind are often associated with large uncertainties stemming from the coarse spatial resolution of satellite products and differences in the measurement techniques used to produce in situ and satellite data. By using a consistent observing platform, we largely overcome these issues, while still achieving good spatial and temporal coverage at seasonal timescales (see Sect. 3.1). Another clear advantage of the SOCCOM data set is the availability of depth information, allowing us to simultaneously compare the seasonal evolution of temperature, salinity and chlorophyll a (Chl a) in the water column and also compare this to diagnostics such as the mixed layer depth (MLD). Unfortunately, floats analysed in this study are not equipped to measure photosynthetically active radiation (PAR) under ice.

We now move on to a more detailed discussion of the methodology used to detect meltwater release and growth initiation. Following this, we will describe the biogeochemical model experiments used to investigate the drivers of under-ice growth.

2.1 Data sources

Float data used in this study are made available by the SOCCOM project and can be downloaded through their website (https://soccompu.princeton.edu/www/index.html, last access: 1 February 2019). Analysis was done on data from 2014–2019, making use of Chl a, pressure, temperature, salinity and position data available at a 10 d frequency. Satellite sea ice concentration for the period January 2015 to April 2019 is taken from the NOAA and National Snow and Ice Data Center (NSIDC) Climate Data Record (version 3), which makes use of two passive microwave radiometers, namely the Special Sensor Microwave Imager (SSM/I) and the Special Sensor Microwave Imager/Sounder (SSMIS). The data are downloaded at a daily resolution on the NSIDC polar stereographic grid with 25×25 km grid cells. Finally, incident solar radiation at sea level, used to force the model simulations, is taken from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-Interim reanalysis data set. The data resolution is daily (the mean of the day–night cycle) on a $\mathrm{0.75}{}^{\circ }\times \mathrm{0.75}{}^{\circ }$ regular grid.

2.2 Detection of phenological events

Under-ice detection

The first step in our investigation of under-ice phenology was to determine which profiles could be classified as sampling under ice. Since many of the floats deployed in the SOCCOM project are intended to sample under ice, an ice avoidance algorithm is utilized on board. The ice-sensing algorithm simply compares the median temperature between ∼ 50 and 20 m during ascent to a threshold temperature of −1.78 ^∘C. If the observed value is lower than the threshold, it is assumed that sea ice is present overhead. The float then terminates its ascent, stores the profile data and returns to its parking depth (Riser et al., 2018).

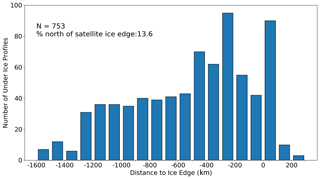
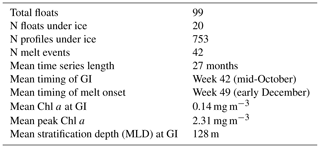
Figure 1 Distribution of great circle distances of under-ice profiles to the estimated satellite sea ice edge (latitude of 15 % sea ice concentration contour). Negative values indicate that the profile is poleward of the ice edge.

Since the freezing point of sea water depends both on temperature and salinity, we chose to include near-surface salinity measurements in our revised under-ice detection algorithm. That is, for each profile, the freezing temperature, based on the salinity closest to the surface, is computed and compared to the temperature measured at the same depth. It is important to note that the depth of these near-surface measurements will vary from ∼ 20–25 m in winter to ∼ 0–5 m in summer. This is because of the on-board ice avoidance algorithm described above; in winter the temperature threshold is generally exceeded, so sampling ceases ∼ 20 m from the surface, while in other months this condition is generally not met, so floats are able to sample much closer to the surface. Therefore, since the on-board ice avoidance algorithm is intentionally conservative, it may assume there is ice present when in fact melting has already occurred (or when the float has moved out of an ice-covered region). Conversely, the ice avoidance algorithm may also incorrectly determine that melting has occurred and attempt to surface when ice is still present overhead.

While the fact that winter profiles generally only sample up to ∼ 20 m may seem unimportant, it actually has significant bearing on the under-ice detection algorithm used in this study. This is because, within the upper 20 m in winter, water is generally above its freezing point (if salinity is taken into account). Therefore, in order to delineate under ice from open ocean profiles, one has to assume some degree of cooling from the last measurement in the profile to the surface. Since the realized degree of cooling over this winter surface layer cannot be observed, we tested several values (the corresponding effect they had on a key result of the paper is shown in Fig. 5). The orange and green curves in Fig. 5 depict the change in the probability density function when increasing and decreasing the cooling threshold (rc) by 20 %, respectively (the details of what is depicted in the figure is discussed below in the “Growth initiation” subsection). The blue curve and associated histogram depicts the chosen value of 0.1 ^∘C used in this study (i.e. we assume a decrease of 0.1 ^∘C from ∼ 20 m to the surface). We would note that the essential features of the distribution remain unchanged in this sensitivity test.

In addition to the above testing, two further checks were performed to assess the validity of using an assumed rate of cooling to detect under-ice profiles. The first approach is shown in Fig. 1, which plots the distribution of distances of the under-ice profiles to the satellite ice edge. Here the ice edge is defined by the 15 % sea ice concentration contour, following previous satellite-based studies (e.g. Stroeve et al., 2016) We found that the vast majority of profiles were located 100 km or more south of the ice edge, with 13.6 % being north of the edge. It is important to point out here that, while sampling under ice, floats do not communicate their location since they are prevented from surfacing. A simple linear interpolation is used to estimate the location of the under-ice profiles (based on the relative time stamp difference), with an approximate maximum error of 100 km, as reported by Riser et al. (2018). It is precisely because of this uncertainty that we chose to use on-board data to detect under-ice profiles (and to detect melting) as opposed to flagging profiles as being under ice based on their relative position to the satellite ice edge. The distribution shown in Fig. 1 is included to illustrate that there is a broad agreement between the two methods, although the use of on-board data should be more accurate given the uncertainty of the float location.

The second approach used to assess the under-ice detection method involved visual inspection of the time series of the mean mixed layer temperature and salinity, like those shown in Fig. 2a (a discussion of how MLD is defined is given below under the “Melt onset detection” subsection). This consisted of comparing the timing of the transition from under ice to open ocean (depicted by the black vertical line in Fig. 2a) with the associated changes in temperature and salinity. Both raw (dashed) and filtered (solid) time series are shown, with a first-order, low-pass Butterworth digital filter employed with a cut-off frequency of 0.1 Hz. By inspecting a subset of float sampling under ice, we found a good visual agreement between the computed timing of the transition (black vertical line) and the corresponding tendency of the curves toward freshening and warming of the surface ocean. The best agreement is achieved by assuming a relative temperature difference (between the last winter measurement and the surface) 0.1 ^∘C as described above, which is why this value was chosen over other candidates. A sample of time series for floats other than those shown in Fig. 2a is provided in the Supplement (Figs. S1–S4).

Melt onset detection

Once a transition from ice cover to open ocean has been established, our algorithm then verifies that these changes are associated with melting. This is done by computing the time derivatives of the surface temperature and salinity at the time of transition (data are taken from measurements closest to the surface). In order to be classified as a melt event, the temperature derivative must be positive (i.e. increasing temperature) with a negative salinity derivative that is persistent for 1 month following transition. An example of a such a melt event is shown in Fig. 2a, where salinity (blue lines) decreases gradually for ∼ 1 month prior to transition, while temperature (red lines) begins to steadily increase after remaining consistently below freezing. At least three consecutive under-ice profiles (equivalent to ∼ 1 month since profiles are at a 10 d frequency) are needed to detect a melt event. In cases where multiple transitions occur in one season, the transition with the strongest signal (i.e. steepest time derivative) of warming and freshening is chosen. This enables us to filter out transitions which occur as a result of advection or high-frequency warming associated with synoptic variability.

Apart from the three criteria discussed above (transition from under ice to open ocean, positive temperature derivative and negative salinity derivative), an additional inspection of the time series of stratification depth (our chosen metric for assessing vertical mixing, termed N_d) was performed. This depth is defined as the point at which the Brunt–Väisälä frequency reaches its maximum value in the upper water column, implying a region of maximum resistance to mixing (Gill, 1982). Furthermore, this measure of the depth of the mixed layer has been shown to be more ecologically relevant in the Southern Ocean than other more traditional methods involving density/temperature thresholds (Carvalho et al., 2017).

Figure 2 Time series of key properties illustrating the methodology used for melt and growth detection. (a) Near-surface temperature (dark red) and salinity (grey) from May to December 2016 in the Ross Sea sector (65^∘ S). Red stars indicate profiles flagged as under ice. Solid lines with markers are filtered time series (higher frequencies have been removed), and dashed lines are raw data. (b) Mean mixed layer Chlorophyll a (dark green) and mixed layer depth plotted for the same period as in (a). For more information, refer to Sect. 2.2.

As is discussed in Sect. 1, the release of meltwater tends to stratify the surface ocean, so N_d should rapidly decrease following the detected melt event. In Fig. 2b, we show an example of such a time series of N_d (in blue), with profiles flagged as under ice shown with red stars. One can clearly see that N_d shoals rapidly at the point of transition from under ice to open ocean, providing further confidence in the melt detection algorithm. Additional figures, which were used to verify the algorithm, are provided in the Supplement (Figs. S1–S4) and show similar results.

Growth initiation (GI)

Our main metric for assessing the relationship between melting and phenology is termed growth initiation (GI). It is defined here as the point at which the time derivative of mean mixed-layer Chl a exceeds the median time derivative computed for the growth period in question. These time derivatives, here taken as a proxy for growth rates, are only computed over the period of positive growth. This period is determined from a filtered time series of mean mixed layer Chlorophyll a (Chl a) used to remove variability at the 10 d sampling frequency (the actual value of the median is computed from the raw signal). A first-order, low-pass Butterworth digital filter is employed with a cut-off frequency of 0.1 Hz. An example of the resulting filtered time series is shown in Fig. 2b and compared to the original raw signal. Also shown in the figure, by the black vertical line, is the timing of GI for this particular season. The distance between the  two black vertical lines in Fig. 2a and b then denotes the timing difference between melting and GI, as shown in Fig. 5 for all float data.

Following Racault et al. (2012), early stages of growth are usually quantified using a metric termed bloom initiation, which is defined as the time at which Chl a concentration first exceeds the long-term median plus 5 %. However, this method is unsuitable in this study for several reasons. First, our time series are, at most, 4 years long, and on average only 2 years long, precluding an estimation of any long-term threshold value. Second, our focus is on the conditions which trigger growth, not necessarily a bloom, which again implies that a comparison to some longer term value must be made. Finally, we believe a metric based on growth rates (as opposed to an absolute threshold value) to be more appropriate, since it avoids any biases in the median which may be created by long periods of close-to-zero Chl a concentration under ice (followed by a rapid increase).

2.3 Model experiments

2.3.1 Model set-up

A biogeochemical box model is employed in this study to investigate the drivers of under-ice growth. The model is based on the biogeochemical flux model (BFM) framework, for which documentation can be found in Vichi et al. (2015). Our particular configuration is a 0.5D box model in which all the major components of the marine biogeochemical system are simulated, namely, phytoplankton, zooplankton, organic and inorganic matter, nutrients and bacterioplankton. The model is termed 0.5D due to the fact that the depth of the box is able to vary, allowing for the simulation of the effect of vertical mixing. In this case, the only effect taken into account is the attenuation of light with increasing mixed layer depth.

Since our study is process-oriented, we chose to simplify the model as much as possible while still retaining the major features of interest. Accordingly, only one phytoplankton (diatoms) and two zooplankton groups (omnivorous mesozooplankton and heterotrophic nanoflagellates) are simulated. In terms of nutrients, phosphate, nitrate and ammonium are included, as well as silicate and iron. Initial nutrient conditions were chosen to be representative of the Southern Ocean south of ∼ 60^∘ S, with non-limiting concentrations of nitrate (31.8 mmol m⁻³), phosphate (2 mmol m⁻³) and silicate (40 mmol m⁻³; Sarmiento and Gruber, 2006). An initial dissolved iron concentration of 0.3 µmol m⁻³ (Tagliabue et al., 2014) was applied to all experiments, which gave the most realistic magnitude of summer growth when compared to float data.

The model is forced daily with solar radiation, satellite sea ice concentration, float temperature and salinity, as well as mixed layer depth derived from float data (refer to Sect. 2.1 for data sources). Time series of incident PAR and mixed layer depth (as estimated by the stratification depth, N_d) for each study region is provided in Fig. S5. Light available at the surface is scaled by the sea ice concentration by simply multiplying the incident radiation by the percentage of open ocean derived from remote sensing data. Note that the Weddell Sea study regions (W60 and W65) use an analytical light forcing described in Vichi et al. (2015).

2.3.2 Experimental design

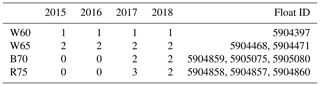
Three core experiments were conducted in four study regions, with each run having a spin-up time of 10 years to allow for adjustment to a repeating annual cycle (although in most cases the adjustment took only a few years). In Table 1, we provide an overview of the available float data in each study region. For every complete time series of float observations, we performed the set of three core experiments. First, two sets of experiments were run to test the effect of sea ice cover on phytoplankton phenology; this included a run with no ice (OPEN) and a run with imposed satellite sea ice concentration (ICE). A third experiment sought to test the combined effect that sea ice cover and increased low light adaptation (LLA) phytoplankton had on phenology. This was achieved by increasing the initial slope of the photosynthesis–irradiance curve by a factor of 10, thus enhancing the photosynthetic efficiency at light levels close to zero. This value is equivalent to what is commonly used for sea ice algae (Tedesco et al., 2010).

Table 1 Number of floats sampled in each year for the four study regions. This number then corresponds to the number of model runs done in each region for each of the three core experiments discussed in the text. Note: W60 – Weddell Sea region at ∼ 60^∘ S; W65 = Weddell Sea ∼ 65^∘ S; B70 – Bellingshausen/Amundsen Sea ∼ 70^∘ S; R75 – Ross Sea south of 75^∘ S.

3 Results

The results presented here fall under two general themes. In the first section, we will test the meltwater hypothesis outlined in Sect. 1, by comparing the timing of the growth initiation (GI) with that of sea ice retreat. Following this, we will present results from a set of simple model experiments in an attempt to explain the observed phenology. In these experiments, we investigate the role sea ice cover and phytoplankton low light adaptation play in controlling winter/spring growth. By placing the experiments in four distinct study regions with different physical conditions, we also utilize the spatial and temporal variability available in the float data set to derive results of wider regional applicability.

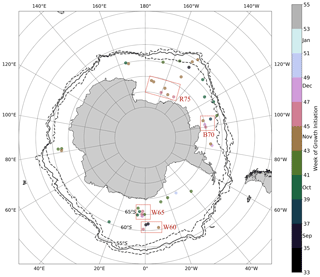
Figure 3 Approximate locations of melt events identified in the under-ice Biogeochemical Argo (BGC-Argo) data set. The solid black line represents the mean maximum extent of the 15 % sea ice concentration contour for the period 2015–2018, while dashed lines represent the interannual variability. The colour of each point represents the timing of the growth initiation (GI) in weeks of the year. Red boxes refer to study regions discussed in the text.

3.1 Observed under-ice growth

Figure 3 plots the approximate mean location of the 42 melt events captured in the Biogeochemical Argo (BGC-Argo) data set. From this map it is clear that a fairly broad spatial distribution is achieved, with all the major ocean basins sampled. However, the Atlantic and Pacific oceans are better represented, with the Weddell, Bellingshausen and Ross seas having the highest concentration of sampling. Meridional floats sample between approximately 60 and 70^∘ S and cover the period 2015–2018. Based on this spatial and temporal distribution, we can expect a large variability in oceanographic conditions. This in turn leads to the large spread observed in the timing of GI (from September to January), represented by the colours of the points in Fig. 3. While there is some indication of the expected progression towards later GI as one moves south (lighter colours), large interannual variability is observed where points are clustered together in space but nevertheless have very different GI values (this difference is as large as 8 weeks in the Weddell Sea at ∼ 65^∘ S).

In Fig. 4a we show more explicitly the relationship between growth initiation timing and latitude. Here we find a statistically significant correlation (p=0.001) of −0.47, implying that 22 % of the variance in GI may be explained by variability in latitude alone. Conversely, the relationship between GI and the timing of meltwater release is insignificant at the 5 % level (p=0.07), with a lower correlation of 0.27 (Fig. 4b). Furthermore, almost all events fall below the 1:1 line in Fig. 4b, revealing that GI tends to precede the release of meltwaters.

Consequently, in Fig. 5 we plot the distribution of the difference in timing between GI and melting. For the majority of the observed events, GI occurs well before the release of meltwaters (the mean timing difference is 4.5 weeks). Furthermore, for 35 % of the events, GI is observed more than 35 d before melting, with a further 25 % preceding melting by 25–35 d. Only 10 %, or four events, occur either at the same time as or after the sea ice retreat. In a complementary analysis, we included Chl a data from ∼ 50 m below the estimated mixed layer depth in the calculation of GI. Overall, this tended to shift GI even earlier in the year by diluting the summer concentration, although in four cases significant Chl a below the mixed layer enhanced the spring growth rate and thus delayed GI.

We would note that our definition of GI (detailed in Sect. 2.2) is likely to be more conservative than the methods employing a threshold value (i.e. likely to delay growth initiation). In addition, GI was also computed using the mean mixed layer particulate organic carbon as opposed to Chl a, which resulted in a timing difference distribution similar to that shown in Fig. 5 (albeit with a smaller time difference; see Supplement Fig. S8). In terms of vertical mixing, average stratification depth (N_d) at GI is ∼ 128 m, with a standard deviation of 51 m. In Fig. S6, we show the value of N_d at GI for all 42 events and the relationship between N_d and GI. We found that N_d generally ranged between ∼ 75 and ∼ 160 m at the timing of growth initiation, with no correlation between N_d and GI. Table 2 highlights some of the salient properties of the data set investigated in this study and summarizes the major findings discussed above.

Table 2 Summary of properties of the under-ice BGC-Argo data set. Note: GI – growth initiation.

While the results discussed up to this point incorporate data from all available under-ice floats, in Fig. 6 we focus on three floats which sampled in close proximity to each other in the Ross Sea. In the figure, each bold line plots the mean value of five time series which correspond to different melt events. Events are separated in space and time; in this particular case, 2017 and 2018 were sampled by three floats, which resulted in five time series (two each, with one of the floats only sampling in 2017). This allows for a clear comparison of the seasonality of Chl a and sea ice, serving as a good example of how phytoplankton are able to sustain growth under near-complete (according to satellite information) ice cover. Indeed, in this particular case, the average satellite sea ice concentrations were consistently above 90 % until late November, by which point Chl a has already been steadily increasing for 2–3 months. Examples of other regions can be found in Fig. S7.

3.2 Regional modelling of under-ice growth

In order to further investigate which factors may drive early growth under ice, we conducted several simplified model experiments in 4 study regions. The objective here is to determine which experiments most closely resemble the observed seasonality of mixed layer Chl a, thereby inferring which factors may be important in promoting under-ice growth. Each region was chosen based on the spatial distribution of melt events shown in Fig. 3. In the Weddell Sea close to 0^∘, two distinct clusters of melt events are seen in Fig. 3 – one centred just south of 60^∘ S and the other around 65^∘ S. For ease of identification, we call these regions W60 and W65, respectively. In the Ross Sea, we selected three floats which sampled in relative proximity north of 75^∘ S (region R75). Finally, we selected three additional floats which sampled in the Amundsen/Bellingshausen Sea (just north of Pine Island Bay) around 70^∘ S (region B70). This allowed us to compare experiments run under different forcing conditions (in particular, sea ice concentration, light and mixed layer depth).

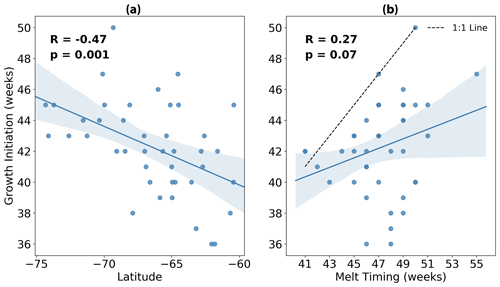
Figure 4 Timing of growth initiation (GI) plotted against (a) average latitude and (b) timing of sea ice melt for each of the 42 melt events shown in Fig. 3. Overlain in blue is the linear regression, with the 95 % confidence intervals for 1000 bootstrapped resamples shaded in light blue. In panel (b), the dashed black line represents the 1:1 line.

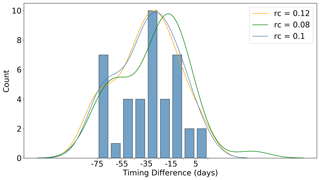
Figure 5 Distribution of the difference in timing (in days) between growth initiation (GI) and melt onset (for all floats sampling under ice). GI is defined as the point at which the time derivative of the mean mixed layer Chl a exceeds the median time derivative (computed for the growth period). Negative values in the distribution indicate that GI has occurred prior to the detected melt onset. Curved lines represent the probability density functions for several values of the assumed cooling threshold (rc) in the upper ∼ 20 m of the water column. This value represents an assumed decrease in temperature over the upper ∼ 20 m, which is required to delineate under ice from open ocean profiles (since floats do not sample the upper ∼ 20 m in winter, they do not sample water below the freezing point). Refer to Sect. 2.2 for a discussion of the methodology used to produce the figure.

Three core experiments were conducted for each region, consisting of first running with no sea ice forcing (OPEN), then with satellite-derived ice concentration (ICE) and, finally, with the low light efficiency of phytoplankton enhanced by a factor of 10 (LLA; sea ice forcing is also kept for these runs). Within each of the four study regions, this set of experiments is conducted for each year available in the float data (and in some cases multiple times for the same year if more than one float sampled the region; see Table 1). Refer to Sect. 2.3.1 for more information on the model setup and forcing and to Sect. 2.3.2 for the experiment design.

The results of all experiments are shown in Fig. 7 and are compared to the phenology obtained from float data. This is done by averaging each of the three core experiments across each study region to give the mean time series of mixed layer Chl a shown by the red (OPEN), blue (ICE) and green (LLA) bold curves (the same is done for the corresponding float observations shown in black). The shading around each of these curves in Fig. 7 represents variability across the set of model runs (or float time series), as was discussed above for Fig. 6. For example, in the case of the B70 region (Fig. 7c), a total of four runs were conducted for each experiment (corresponding to the four float time series available; see Table 1), and so the shaded regions show the variability present across four time series.

By comparing the key phenological features of the time series shown in Fig. 7, we can examine which of the three model configurations most closely matches the float time series. The primary features of interest to us here are timing of the initial growth (i.e. a switch declining to increasing Chl a concentrations) and the subsequent rate of growth in spring. Other features, such as the timing of peak concentration and the intensity of seasonality (i.e. summer–winter Chl a concentration), are not discussed in detail here.

The key finding of the figure is that winter and spring phenology are most closely captured by LLA experiments in the Ross and Bellingshausen/Amundsen seas (regions R75 and B70, respectively), while in the Weddell Sea (regions W65 and W60) a combination of OPEN and LLA experiments can account for the phenology of this period. That is, in the Weddell Sea the timing of the transition from negative to positive derivative in Chl a is better represented by OPEN experiments, while the subsequent rate of growth in spring is more closely simulated by LLA experiments (Fig. 7a, b). Indeed, across all regions the OPEN experiments seem to capture the timing of the minimum Chl a concentration in winter well but then greatly over estimate the spring growth rate. In almost all cases, the ICE experiments overly dampened growth in winter and spring, with the switch from the negative to positive mixed layer Chl a derivative occurring significantly later than observations. However, in the Weddell Sea (W60 and W65), this model configuration suffers least from the compressed seasonality particularly evident in the winter months of other experiments.

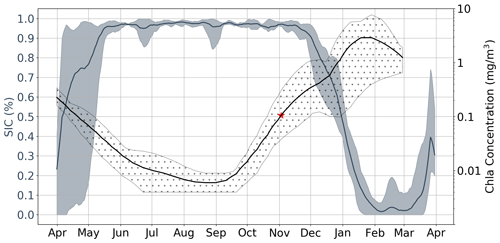
Figure 6 Satellite sea ice concentration (SIC) versus Argo float Chl a for region R75. Shaded regions around each line represent both the spatial and temporal variability present in each data set. That is, each bold line plots the mean value of five time series which are each associated with a specific melt event. Events are separated in space and time; in this particular case, 2017 and 2018 were sampled by three floats (see Table 1), which resulted in five time series (two each, with one of the floats only sampling in 2017). The red star represents the mean value of GI.

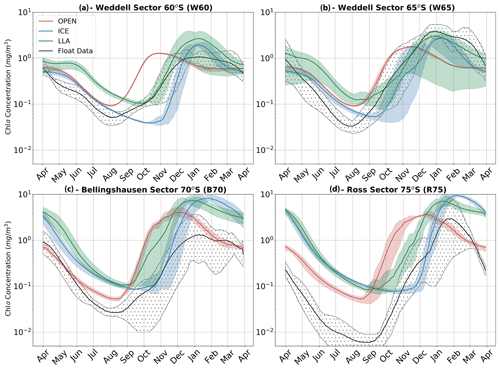
Figure 7 Time series of mean mixed layer Chl a for each of the four regions discussed in the text. In each panel, the observed values (black) are compared to three model experiments; runs with no sea ice are shown in red (OPEN), runs with ice are shown in blue (ICE) and runs with both ice and enhanced low light efficiency by phytoplankton are plotted in green (LLA). The shaded regions for each curve represent the spatial and temporal variability present in each data set as in Fig. 6. Note that the time series run from April to April.

In Fig. 8 we show the timing of GI for each region and experiment, providing a more quantitative view of the relative changes in phenology (each point in the figure represents a separate year or location). GI for the model time series is computed in the same manner as in the float data (see Sect. 2.2), although there was no need for filtering. While the LLA set of experiments generally performs best at reproducing GI, there are notable exceptions in each of the four study regions. In the W60 region, the observed GI occurs between early September and mid-October, with OPEN experiments having growth too early and LLA experiments too late. Moving further south to W65, we see that only LLA is able to capture the observed variability in GI, but that, in some cases, OPEN provides the best fit to the data. Continuing south and west, both B70 and R75 contain cases where GI is best described by ICE simulations. In the following section, we will bring together both the observational and modelling results discussed thus far, thereby shedding light on the possible mechanisms leading to under-ice growth in the Antarctic winter and spring.

4 Discussion

4.1 Relationship between melting and growth

The central question of the present study relates to which conditions are necessary to trigger phytoplankton growth in the Antarctic SSIZ. As has been outlined in Sect. 1, a popular hypothesis holds that the release of buoyant meltwaters following sea ice retreat shoals the mixed layer, relieving light limitation and triggering rapid growth. In contrast to previous studies (e.g. Smith and Nelson, 1985; Smith and Comiso, 2008; Sokolov, 2008; Taylor et al., 2013) relying on satellite data or models, we were able to thoroughly test this hypothesis by utilizing a unique in situ data set of under-ice profiles from BGC-Argo floats. In particular, we were able to test two predictions of the hypothesis; first, that at least part of the variability in the timing of growth initiation (GI) may be explained by the timing of sea ice melt, and second, that GI should either be synchronous with or occur after the release of meltwaters.

Based on the data analysed here, we do not find evidence which convincingly supports either claim. In Figs. 5 and 6, we clearly demonstrate that phytoplankton are able to sustain growth long before significant freshening of the surface ocean. It is important to reiterate here that GI is based on the rate of growth exceeding the median rate, and so the tendency of GI to precede melting (as illustrated by the timing differences between these events shown in Fig. 5) suggests that the rate of growth is already well above average prior to ice retreat. This explains why GI and melting are not correlated in time (Fig. 4b); the release of meltwaters does not appear to relieve light and/or nutrient limitation, and so variability in melt timing cannot account for variability in GI. GI is instead correlated more strongly with latitude (Fig. 4a), suggesting that phytoplankton are responding to changing incident light conditions rather than fresh water fluxes. To be clear, the latitudes plotted in Fig. 4a are computed based on the approximate location of the float at GI, which in almost all cases corresponds to an under-ice condition. Therefore, the correlation found in Fig. 4 implies that light may be non-limiting under Antarctic sea ice (at least in the conditions sampled by the floats), provided it is late enough in the season for there to be sufficient light available at the surface.

Also noteworthy is the extent to which growth occurs prior to melting, with ∼ 60 % of events preceding melting by a month or more. As is discussed in Sect. 3.1, our float data set samples in a wide variety of environmental conditions which exhibit very different sea ice and vertical mixing regimes. This suggests that the results presented here are fairly representative of the SSIZ as a whole, rather than being biased by a particular region or time period. In summary, we have shown that prolonged under-ice phytoplankton growth prior to retreat is typical of the Southern Ocean SSIZ.

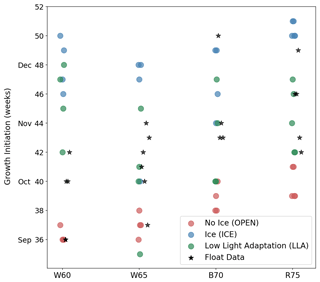
Figure 8 Timing of GI for each study region (horizontal axis) and model experiments (coloured points). Corresponding values from float data are indicated by black stars.

These findings are broadly in agreement with those presented by Uchida et al. (2019), who analysed the same data set and found that early growth initiated in August/September in the region south of ∼ 60^∘ S. However, the authors do not explicitly investigate growth in relation to the release of meltwaters in the SSIZ and appear to conclude that melting generally initiates growth through the release of iron trapped in sea ice and the relief of light limitation.

Our findings are also complementary to those of Briggs et al. (2017), who analysed nine under-ice floats deployed in 2014 and 2015 in the Ross and Weddell seas. Although the authors concluded that respiration dominated during the ice-covered period, their Figs. 4 and 6 show that production begins before the end of the ice-covered period. Indeed, our interest has been the period of initial growth when overall biomass is still generally very low, but growth rates are significant compared to the rest of the growth phase. Briggs et al. (2017) note that nitrate, oxygen and dissolved inorganic carbon (DIC) change during the ice-covered period are consistent with net respiration; however, the modest phytoplankton standing stock present at GI (which occurs at the end of the ice-covered period) may not be sufficient to appreciably reduce nitrate and DIC concentrations and increase oxygen values (see mean Chl a concentration at GI in Table 2). Thus, the seemingly contradictory conclusions of our results are due to differences in which period of the season the analysis is focussed on, with Briggs et al. (2017) focussing on earlier periods in the year when the respiration signal is dominant and the work presented here focussing on the early growth period when respiration switches to production. In the end, higher frequency sampling is needed to more precisely determine the timing of net production.

It is also interesting to note that these results can be interpreted as supporting the disturbance-recovery hypothesis laid out by Behrenfeld and Boss (2014). Using this framework, Behrenfeld and Boss (2014) and Behrenfeld et al. (2017) have argued that growth/bloom initiation occurs much earlier in the year in winter at high latitudes than previously thought, a very similar conclusion to that is arrived at here. However, as will be discussed below, the winter growth shown here does not necessarily require that ecological interactions be invoked to explain it. Indeed, in our regional box model experiments (discussed below), we found that zooplankton have a lagged response to diatom growth in early spring (see Fig. S9), suggesting that other factors are responsible for the timing of the initial growth. Furthermore, altering the zooplankton model parameters (such as lowering the diatom availability) did not lead to a phenology resembling the float data. We therefore note that, while the role played by ecological interactions is not ruled out here, it can be argued that the observed growth can be accounted for by a revision of our understanding of the under-ice light environment and the physiological response by phytoplankton.

4.2 Growth under extreme light limitation

We now move on to the question of how phytoplankton are able to sustain growth under such poor ambient light conditions. Recall that the average stratification depth at the time of GI is around 130 m and that satellite data suggest near-complete ice cover. Although the timing of GI in October would allow for ample light in open ocean conditions, previous studies suggest that light transmittance through typical consolidated ice would be just 1 %–5 % of that incident at the surface (even with a thin snow layer; Fritsen et al., 2011). Two possible explanations for growth under these conditions are then apparent; one, light is more readily available in ice-covered environments than previously thought, and two, phytoplankton are more adapted to extreme low light than previously thought. Hence, the phenomenon can be accounted for by both physical factors (such as sea ice and vertical mixing conditions which alter light availability) and biological ones (such as phytoplankton physiology). Both factors are likely operating simultaneously. Indeed, the very presence of growth indicates light levels above zero, suggesting a revision of our current understanding of under-ice environments.

In our regional box model experiments, we explore both physical and biological factors. The fact that winter and spring phenology is brought closer to observations when low light efficiency is enhanced by an order of magnitude (to a value typical of sea ice algae) certainly suggests a role for phytoplankton adaptation (Fig. 7 – LLA experiments). However, the interpretation is complicated somewhat by the fact that, under certain conditions, phenology may be best described by simulations with no ice (OPEN) or with ice but standard physiology (ICE).

For example, in the Weddell Sea (Fig. 7a, b) early growth in August is best captured by OPEN experiments, but subsequent spring growth rates (October–November) more closely align with LLA simulations. The inference here would be that, in this region, sea ice is unconsolidated and highly permeable to light, allowing growth to initiate as soon as incident radiation is sufficient. This corresponds well with the correlation between GI and latitude shown in Fig. 4a. This is despite the apparently near 100 % sea ice concentration suggested by satellite data (see Figs. 6 and S7). Indeed, at these latitudes, we may actually be in the MIZ, which would explain the higher light permeability. Yet, this is not to say that sea ice has no effect; later in the season growth rates are slowed by its presence, explaining why LLA experiments perform better here. These findings generally agree with previous studies which point to light (as opposed to dissolved iron) being the primary driver of early spring growth in the high latitude Southern Ocean (e.g. see Joy-Warren et al., 2019 and citations therein). We would also note that both silicate and iron are close to their seasonal maximum concentration during late winter/early spring in all our model experiments (see Fig. S10), thus ruling out nutrient limitation in all regions.

Further south in the Bellingshausen and Ross seas, sea ice is expected to be more consolidated in winter and spring, and so phenology is better captured by LLA simulations (note that the offset in winter time Chl a concentrations seen in these regions in Fig. 7c and d is likely due to the need to adjust the metabolic loss terms for phytoplankton in full darkness). However, in two cases the timing of GI most closely matches ICE experiments (see Fig. 8; regions B70 and R75). This may be accounted for by especially thick snow and ice layers in those cases, which led to delayed growth. This highlights the importance of the particularities of ice morphological features and their effect on the light environment, something which does not seem to be captured by satellite sea ice concentration.

Thus, it is both the character of ice and snow overhead and the physiological response to severe light limitation that may address the question raised at the start of this section. A crucial point here is that 100 % sea ice cover (in the winter Antarctic sea ice) as seen from satellite does not necessarily imply a completely consolidated ice surface (Vichi et al., 2019). While the ocean may indeed be completely covered, the ice itself may be unconsolidated, being primarily composed of pancakes loosely connected by frazil or brash ice. Such a condition is common in the Southern Ocean and is maintained by wind and wave action far from the ice edge. Waves are known to propagate several 100 km into the ice, effectively preventing the formation of pack-ice-like conditions (Kohout et al., 2014; Meylan et al., 2014). Wind forcing is also known to be highly effective in causing ice break-up and motion, with intense synoptic events in the Weddell and eastern Indian oceans occurring frequently (Vichi et al., 2019; Uotila et al., 2000). Such events, along with interactions with the westerly wind belt, drive the formation of gaps within the MIZ and within pack ice. Therefore, the highly dynamic nature of Antarctic sea ice may lead to a general enhancement of light availability in the underlying ocean. The presence of even a tiny amount of light may be expected to induce acclimation in primary producers (that are adapted to low light), thereby explaining why model configurations which take this into account produce a more realistic phenology.

5 Conclusions

This study has characterized under-ice phytoplankton phenology using a unique data set of BGC-Argo profiles, complemented by a set of process-oriented biogeochemical model experiments. We have shown that, rather than acting as a trigger as postulated in previous studies, the release of meltwaters enhances growth in an already highly active phytoplankton population. This may explain the decline in phytoplankton stocks observed by Veth et al. (1992) in meltwater lenses of the northwestern Weddell Sea. That is, the decline (in a still highly stratified surface ocean) may be accounted for by the natural reduction occurring in a bloom that already started prior to the melting. Such unexpected early growth (under presumed severe light limitation) may be accounted for by a combination of low light adaptation by phytoplankton and sea ice permeability with respect to light. We argue that such permeability is related to wind and wave forcing, which together preserve an unconsolidated ice morphology that is not captured by current satellite sea ice concentration algorithms.

However, our investigation has not been exhaustive of all possible mechanisms leading to under-ice growth. Future research directions could include an examination of potential discrepancies between the timing of shoaling of the mixed layer and that of active turbulent mixing (e.g. Carranza et al., 2018; Sutherland et al., 2014). An earlier reduction in mixing would increase ambient light and help explain the observed under-ice growth. Other ecological factors could also be explored, such as potential interactions between pelagic and sympagic communities, which are known to be highly efficient at low light intensities (Tedesco and Vichi, 2014 and citations therein). Nevertheless, the findings presented here have important implications for our understanding of how the biogeochemistry of the region may change in the future. With possible earlier sea ice retreat, and a generally thinner and more dynamic ice in some regions (including the Arctic), we may expect even earlier growth than reported here, which would likely alter the seasonal air–sea carbon flux and thus the biological carbon pump.