Implementation and initial calibration of carbon-13 soil organic matter decomposition in the Yasso model

Soils account for the largest share of carbon found in terrestrial ecosystems, and their status is of considerable interest for the global carbon cycle budget and atmospheric carbon concentration. The decomposition of soil organic matter depends on environmental conditions and human activities, which raises the question of how permanent are these carbon storages under changing climate. One way to get insight into carbon decomposition processes is to analyse different carbon isotope concentrations in soil organic matter. In this paper we introduce a carbon-13-isotope-specific soil organic matter decomposition add-on into the Yasso soil carbon model and assess its functionality. The new ¹³C-dedicated decomposition is straightforward to implement and depends linearly on the default Yasso model parameters and the relative carbon isotope (¹³C${/}^{\mathrm{12}}$C) concentration. The model modifications are based on the assumption that the heavier ¹³C atoms are not as reactive as ¹²C. The new formulations were calibrated using fractionated C, ¹³C and δ¹³ measurements from litterbags containing pine needles and woody material, which were left to decompose in natural environment for 4 years. The introduced model modifications considerably improve the model behaviour in a 100-year-long simulation, where modelled δ¹³ is compared against fractionated peat column carbon content. The work presented here is a proof of concept and enables ¹³C to be used as a natural tracer to detect changes in the underlying soil organic matter decomposition.

1 Introduction

Earth system models (ESMs) are essential in our need to understand and examine the global carbon (C) cycle, investigate the influence of environmental and human activities on it, and simulate possible future changes. One part of these complex models is the land-surface components that, for example, describe the C stored in soils as well as the various interactions in soils and between vegetation and the atmospheric boundary layer (Ontl and Schulte, 2012). Total C residing in soils has been estimated to be roughly 3000 Pg (Köchy et al., 2015), but this estimate has large uncertainties as exact quantities are difficult to measure globally. Nevertheless, soils are the second-largest global carbon pool, after oceans. The changing climate conditions are expected to influence the processes controlling C allocation into soils and the permanence of these storage pools (Lugato et al., 2021). A simple approach to track changes in these processes and pools is to examine the ratio of carbon isotopes in, for example, soil litter input and respiration. In order to fully utilise this approach, the underlying model must be capable of reliably simulating carbon-13 isotope (¹³C)-related processes in the soil.

The soil C pool can be divided into different fractions based on their chemical composition, physical characteristics, or assumed turnover or residence times (Poeplau et al., 2018). Soil processes in general are complex as biological, chemical and physical drivers act simultaneously. For modelling purposes, the fate of ¹³C can be used to test alternative model formulations and to give valuable additional information of the optimal parameter values as the ¹³C signatures are sensitive indicators of changes in processes. Soil organic matter (SOM) consists of molecules with different carbon isotopes. In theory, molecules with lighter ¹²C atoms have lower activation (kinetic) energy requirements than those with ¹³C. This leads to easier decomposition of ¹²C-bearing compounds and enrichment of ¹³C in residual organic molecules (Fry, 2006). Estimating ¹³C in different fractions of SOM or varying residence times and adding ¹²C${/}^{\mathrm{13}}$C reaction kinetics into the models would allow verification of the model functioning and improve model predictions. ¹³C-CO₂ measurements associated with gas flux measurements provide a promising way to link soil models to ecosystem models and allow further integration to ESMs, where ¹³C isotopes are used to detect large-scale C-cycling patterns (Flanagan et al., 2005). Furthermore, the use of ¹³C as a natural tracer enables more detailed examination of underlying C-cycling processes (Drake et al., 2019; Blaser and Conrad, 2016; Steinmann et al., 2004).

Additionally, soil carbon sequestration has been a serious topic of interest for several decades as a promising method to mitigate the rising atmospheric carbon dioxide (CO₂) concentrations. These types of methods aim to increase the soil carbon sink by, for example, different soil tilling (Wilman, 2011), crop rotation (Acharya et al., 2012) or fertilisation practises (Triberti et al., 2016). The fundamental problem related to C sequestration is how to demonstrate that the proposed management practice and land use change increase soil C stock size, as well as under what conditions and for how long the C will remain in the soil. The quantification of small changes in soil C stocks is challenging due to large natural variability in soils and the large standing C stock. It has been estimated that the detection of 0.1 kg C m⁻² change (≈1 %) in an agricultural field in Finland where C stock size ranges between 8.4 and 9.8 kg m⁻² in the top 30 cm requires hundreds of soil samples to be analysed (Heikkinen et al., 2020). For this reason, an efficient verification system based on a combination of measurements (C stock size, CO₂ exchange, remote sensing, etc.) and modelling is required, and a new global vision of MRV (monitoring, reporting, verification) platform was proposed by Smith et al. (2020). An overlooked approach to improve MRV is to examine the C isotope compositions in the soil and in heterotrophic respiration. The reason behind the lack of these examinations is simple – such approaches require a model that can reliably represent the soil organic carbon (SOC) dynamics for different carbon isotopes while still retaining relatively straightforward structure. The latter is especially important when we take into account the lack of good-quality calibration and validation data.

In this paper we introduce a simple ¹³C isotopic circulation into the recently re-calibrated SOC model Yasso (Viskari et al., 2022, 2020; Tuomi et al., 2011). In our approach, the decomposition of ¹³C-specific soil organic matter (¹³C-SOM) is linearly dependent on the default Yasso model parameters, the carbon isotope fraction ¹³C${/}^{\mathrm{12}}$C and a new scaling factor θ, which represents the change to the decomposition rate between the carbon isotopes. The underlying hypothesis behind this design is that since ¹³C has a larger atomic weight, it is therefore not as reactive as ¹²C, but environmental factors should still affect the decomposition of SOM, containing either isotope, similarly. We calibrate the new ¹³C-related decomposition parameters (θ) and assess the model functionality both on a short- and long-term (100-year simulation) basis.

Our aim is to improve the Yasso20 model parameterisation (Viskari et al., 2022) to include ¹³C${/}^{\mathrm{12}}$C reaction kinetics in the model by using empirically measured SOM and ¹³C data. The purpose of this paper is to provide a proof of concept, and we hypothesise that measuring ¹³C in soil organic matter fractions (1) detects differences in the pool ¹³C content supporting the ¹³C-fractionation and enrichment theory and (2) allows model development for future improvements in SOM decomposition predictions as ¹³C can be used as a tracer to detect changes in the underlying C decomposition processes.

2 Materials and methods

2.1 Measurements

The SOC measurements were derived from experiments described in Straková et al. (2012), Straková et al. (2011) and Straková et al. (2010), where different types of plant litter were left to decompose inside litterbags in a natural environment at Lakkasuo, a raised bog complex located at the Hyytiälä forestry field station of the University of Helsinki (61.8^∘ N, 24.3^∘ E; 150 m a.s.l.). We utilised data detailing the conditions for pine-branch- and pine-needle-specific litterbags. In addition to determining the initial states for both litter types, 14 litterbags describe the soil conditions for pine branches and 7 for pine needles at later stages of decomposition during the 4-year-long experiment.

The litter was characterised by dividing it into carbon fractions by sequential extractions and hydrolysis according to Hilasvuori et al. (2013, and references therein), also called AWEN extraction (acid, water, ethanol, non-soluble). In short, this included analysing the amounts of nonpolar extracts (corresponds to E), polar extracts (W), acid hydrolysable substances (A) and non-soluble Klason type substances (N). Air-dried litter material was ground in a mill (Fritsch) to pass the 0.5 mm sieve and weighted into a centrifuge tube (35 mL). The amount of extractables was determined through the remaining mass after shaking (2 or 18 h; 250 rpm) with the different solvents followed by filtering through glass crucibles (Robu, borosilicate 3.3, porosity 4). At the start of the extraction procedure, 0.5 g litter mass was used. Dichloromethane (CH₂Cl₂; 15 mL; repeated twice) was first used to remove the nonpolar extractives. A total of 0.35 g of the remaining dried (105 ^∘C) solid sample was weighted again into a centrifuge tube, and hot water (80 ^∘C; 15 mL) was added and kept in a water bath (80 ^∘C; 18 h). After centrifugation (1500×g) the pellet was washed with 30 mL hot water to finish the extraction for polar extractives. In all cases the respective extractives were combined and dried. Evaporation was used for the nonpolar fraction, and warming (50 ^∘C) followed by freeze-drying was the polar fraction. A total of 0.1 g oven-dried (105 ^∘C) material from the residue left after the hot water extraction was weighted into a centrifugation tube, and 1.25 mL 72 % sulfuric acid (H₂SO₄) was added and shaken in room temperature (1 h; 250 rpm). Thereafter 35 mL water was added and incubated in a water bath (95 ^∘C; 18 h) followed by filtration. The remaining mass (Klason lignin) was washed once with hot water (95 ^∘C; 30–40 mL), and the mass was dried overnight in 105 ^∘C. The subsamples for each fraction – i.e. the original litter; the solid remains after dichloromethane, water and acid extraction; and those from the evaporated nonpolar and polar extractants – were analysed for their relative ¹³C${/}^{\mathrm{12}}$C ratios as δ¹³C values. The definition of δ¹³C is given below, where ${\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\mathrm{standard}}=\mathrm{0.01123720}$ is the Vienna Pee Dee Belemnite (Craig, 1957, VPDB).

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=\left({\displaystyle \frac{{\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\mathrm{sample}}}{{\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}_{\mathrm{standard}}}}-\mathrm{1}\right)\cdot \mathrm{1000}\mathrm{‰}\end{array}$$

The isotopic composition of carbon was measured on a NC2500 elemental analyser coupled to a Thermo Scientific Delta V Plus isotope ratio mass spectrometer at the Laboratory of Chronology, Finnish Museum of Natural History. The raw isotope data were normalised with a multi-point calibration using certified isotopic reference materials (USGS-40, USGS-41, IAEA-CH3 and IAEA-CH7). The mean measured (pre-normalisation) δ¹³C values for calibration references were −26.52 for USGS-40, +36.19 for USGS-41, −24.88 for IAEA-CH3 and −32.27 for IAEA-CH7, with an r² of >0.999 between measured and expected values. Replicate analyses of quality control reference materials analysed alongside the unknowns indicate a 1σ internal precision of ≤0.20. For the purpose of model calibration, all samples were scaled to represent the same amount of original matter (we use 1000 mass units of original matter – the given C and ¹³C values are in relation to this value).

In addition to litterbag measurements, we have utilised peat profile measurements, detailed in Hilasvuori et al. (2013), to examine long-term carbon decomposition with the Yasso model. The corresponding profile is given in Table 1, and the age of the three topmost layers is based on radiocarbon signatures (Hilasvuori et al., 2013), which could not be used to accurately estimate the other two layers. We have naively set their age to 20 years each. The fractionated δ¹³C content of these layers is taken directly from Table 2 in (Hilasvuori et al., 2013), and their relation to the Yasso fractions will be given in the results.

Table 1 Peat profile used to examine long-term carbon decomposition.

The meteorological variables required to run the Yasso model were extracted from a nearby weather station measurements (Kolari et al., 2009), located at Hyytiälä (61.85^∘ N, 24.29^∘ E; 180 m a.s.l.). We gathered monthly temperature and annual precipitation from the beginning of year 2005 to the end of 2008. Additionally we calculated averaged monthly temperature and averaged annual precipitation from years 2000–2014 to be used in simulating the long-term carbon decomposition.

2.2 Yasso model

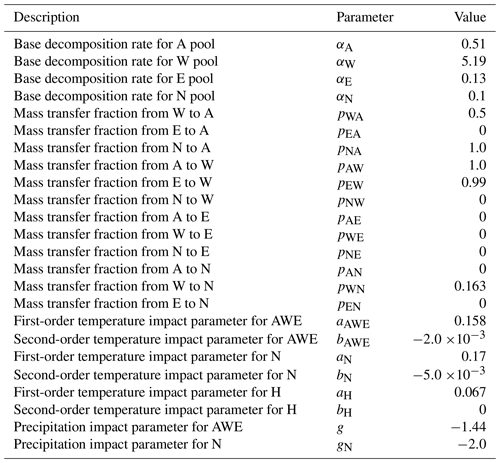
The soil carbon model Yasso was originally built to simulate the soil carbon stock and changes in this stock for forest soils (Liski et al., 2005). Previous versions of the Yasso model have also been incorporated into land-surface models; see e.g. Goll et al. (2017) for Yasso implementation to JSBACH – the land-surface component of the Max Planck Institutes Earth System Model (MPI-ESM). We generate the soil carbon pools utilising a recently re-calibrated version of the model called Yasso20 (Viskari et al., 2022). This calibration utilised multiple global datasets, and we present relevant model parameter values in Appendix Table A1. We introduce a new ¹³C-specific decomposition into this model, which utilises new parameters (θ, explained below). When all θ≡0, both ¹²C and ¹³C use the same standard decomposition parameters; hence, we call this model the default Yasso model and the new version, with optimised θ parameters, as Yasso-C13 or optimised Yasso (Mäkelä, 2021b), when we need to make a distinction. Otherwise, both models are simply referred to as the Yasso model.

Yasso decomposes litter into different pools that represent acid, water and ethanol (A, W and E) soluble matter and a lignin-like pool (N), with all the pools having different decomposition rates. The decomposed C is released back to the atmosphere as heterotrophic respiration, shifted between the AWEN pools or transferred to inactive humus (H) pool. The model is driven with monthly temperature and annual precipitation. The SOC pool decomposition in the Yasso model can be represented by the following equation.

$$\begin{array}{}\text{(2)}& {\mathit{x}}_t=\mathbf{M}{\mathit{x}}_{t-\mathrm{1}}+b_t\end{array}$$

The state vector (x_t), representing the C content in AWEN pools at time t, is calculated by operating the state transition matrix (M) on the state vector of the previous time step (x_t−1) and adding litter input (b_t), which in our simulations is set to zero (as we assume no litter is added into the litterbags after the beginning). The model initial state (in our simulations) is set to match the first measurements. The matrix M=FK is a product of fluxes (F) between the pools and decomposition (K). Pool-specific decomposition rates $\left(k_i,i\in \mathit{\left\{}\text{A,W,E,N}\mathit{\right\}}\right)$, presented in Eq. (3), are dependent on certain parameters ($\mathit{\theta },\mathit{\gamma },\mathit{\beta }$), base decomposition rates (α_i), and functions depicting the effect of woody litter diameter (h(d)), precipitation (P) and temperature (T). See Viskari et al. (2022) for details.

$$\begin{array}{}\text{(3)}& k_i\left(\mathit{\theta }\right)={\displaystyle \frac{{\mathit{\alpha }}_i}{J}}h\left(d\right)\left(\mathrm{1}-e^{{\mathit{\gamma }}_{i}P}\right)\sum _{j=\mathrm{1}}^J{e}^{{\mathit{\beta }}_{i,\mathrm{1}}{T}_j+\mathit{\beta }i,\mathrm{2}{T}_j^{\mathrm{2}}}\end{array}$$

We introduce ¹³C-SOM decomposition into the Yasso model by adding separate ¹³C-specific storages for each AWEN pool and including an additional ¹³C-specific SOM decomposition step. The input data (essentially carbon content) is first separated into ¹³C-specific content and the rest of the carbon. The Yasso model is first run normally as in Eq. (2), which is followed by ¹³C decomposition using a modified version of the pool-specific base decomposition rate:

$$\begin{array}{}\text{(4)}& {\mathit{\alpha }}_i^{*}=(\mathrm{1}+{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}\mathit{\theta }){\mathit{\alpha }}_i.\end{array}$$

The new coefficients ${\mathit{\alpha }}_i^{*}$ replace α_i in Eq. (3), which essentially introduces a dependency for the mass ratio of the carbon isotopes (¹³C${/}^{\mathrm{12}}$C) as well as a free parameter θ to the Yasso model for each ¹³C-AWEN pool separately. We did not include a parameter for the humus pool (H) as we did not have measurements to calibrate the related parameter. Additionally, we do not include the humus pool in the bulk carbon examinations for the same reason – bulk carbon refers to the total sum of carbon in AWEN pools.

2.3 Model calibration

We calibrated the four θ parameters related to the decomposition of each AWEN pool ¹³C-SOM. The objective function (f) of the calibration is the cumulative squared error of the observed and modelled δ¹³C values:

$$\begin{array}{}\text{(5)}& f=\sum _i({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{i,\mathrm{modelled}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{i,\mathrm{observed}}{)}^{\mathrm{2}}.\end{array}$$

Here the summation is taken over all AWEN pools and available litterbag measurements (with measurements indicating zero concentration for total carbon content removed from the calculations). The unnormalised (pointwise) parameter likelihood is calculated as $\mathcal{L}=e^{-f}$.

Since we had only four parameters to calibrate, we produced a parameter grid by fixing an increment and giving each parameter a initial value of zero. Then we added multiple new values symmetrically around the initial value with the given increment. We ran the model with every member of the parameter grid to get an estimate of the overall shape of the parameter likelihood. This process was repeated several times with grid re-centred to the point with maximum likelihood and with readjusted (smaller) increment. The results were also verified with independent runs using different initial values. All experiments were run on a eight-core laptop utilising RStudio version 1.4.1103. We used the R interface of Yasso (see code and data availability) in addition to R.utils version 2.10.1 (no other libraries were needed).

Figure 1 Presented are the pointwise parameter likelihoods (when setting the other parameters at their optimal values), divided by the maximum likelihood value. The vertical lines indicate the parameter value with the highest likelihood.

3 Results

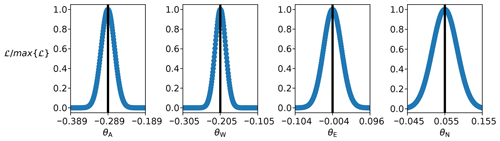
The Yasso model calibration resulted in strictly unimodal parameter probability distributions (Fig. 1). This was not unexpected as each calibrated parameter could only directly affect a single AWEN pool. The optimised parameter values are ${\mathit{\theta }}_{\mathrm{A}}=-\mathrm{0.289}$, ${\mathit{\theta }}_{\mathrm{W}}=-\mathrm{0.205}$, ${\mathit{\theta }}_{\mathrm{E}}=-\mathrm{0.004}$ and θ_N=0.055 (we also note that the precision of the calibration was left at the third decimal as likelihood values started to plateau). When we examine the parameter combinations with highest likelihoods (top 250 values), the strongest correlations (≈0.77) are present between θ_A and θ_W, θ_A, and θ_N, as well as θ_W and θ_N.

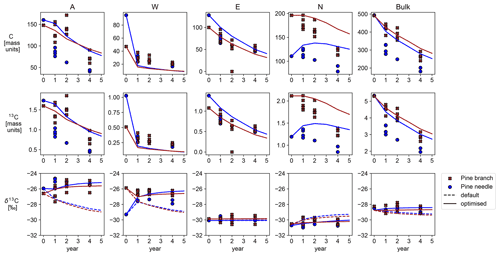
Figure 2 Shown are time series produced by the default and optimised Yasso model versions for the different AWEN pools together with assimilated observations. The model results for C and ¹³C concentrations are on top of each other.

The default and optimised parameter values were used to generate SOM decomposition and related C, ¹³C and δ¹³C time series from the given initial states (Fig. 2). The differences between the simulated ¹³C concentrations are too small to be evident (C concentrations are identical), but we get a clear signal from the δ¹³C values. The default model depicts changing δ¹³C, which is driven by differences in the initial isotopic fractions between the pools and the rate of the flow of carbon between the pools.

Both model versions tend to underestimate the speed of SOM decomposition (the C and ¹³C concentrations) at Lakkasuo (Fig. 2) for the A and N pools and overestimate for the W pool. The bulk carbon content behaves similarly to A and N pools as these contain the most carbon. The default Yasso model is reducing the relative ¹³C content (reducing the δ¹³C values) for the A and W pools and deviating from the observations, whereas the optimised model version seems to be increasing the relative ¹³C content and following the observations more closely. There is no apparent difference for the E pool, but the calibration has lowered the rate of ¹³C enrichment for the N pool. We have calculated and gathered the mean and standard deviation of the corresponding pointwise δ¹³C model bias values (model − observations) for the individual AWEN pools to Table 2.

Table 2 Calculated default and optimised model bias (model − observations) mean and standard deviation for the different AWEN pools.

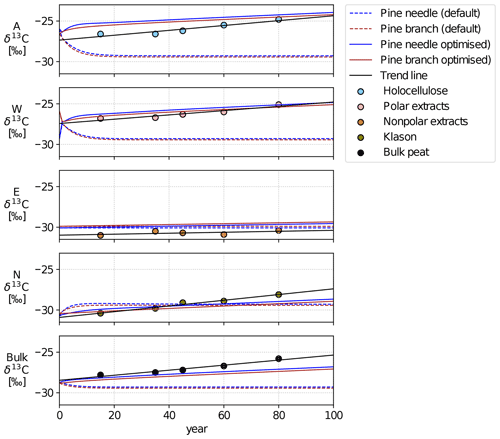
Figure 3 Time series of simulated δ¹³C values of the different AWEN pools for the default and optimised Yasso model versions. Scatterplot shows the peat column δ¹³C values at different depths, positioned at the midpoint of assumed age, along with corresponding trend lines.

The Lakkasuo initial states and generated average year (averaged monthly temperature and annual precipitation) from years 2000–2014 were used to simulate a 100-year-long carbon decomposition (Fig. 3). This simulation can be compared to Lakkasuo peat column δ¹³C values at different depths given in Table 1 and in Hilasvuori et al. (2013). The holocellulose values are comparable to the A pool, Klason to the N pool, nonpolar extracts to the E pool and polar extracts to the W pool. A noteworthy detail is that in the short term (Fig. 2) the default model increased the relative ¹³C content (δ¹³C values) of E and N more than the optimised version, but on longer timescale this situation is reversed (Fig. 3). The difference in δ¹³C values for bulk C, between the default and optimised model versions at the end of the 100-year-long simulation, translates to approximately 0.3 ‰ difference in C mass percentage.

4 Discussion

We have introduced simple modifications to the Yasso model in order to account for ¹³C-SOM decomposition. Incorporation of δ¹³C on SOM decomposition models is a necessary step towards integration of Earth system and dynamic land ecosystem models. The δ¹³C values of different organic compounds or chemical fractions of mixed organic material can be used as natural tracers which provide a unique tool to investigate and uncover complex decomposition processes in the soil. Examples of such approaches include, for example, examination of tree carbon use by chasing ¹³C-CO₂ pulse in the respiration of leaves, whole crowns, roots, and soil (Drake et al., 2019); an analysis of how stable isotope fractionation might be used to identify microbial function without incubation in soil samples (Blaser and Conrad, 2016); and assessment of carbon uptake and respiration fluxes via the use of ¹3C depleted CO₂ (Steinmann et al., 2004).

In the current study, we introduced new θ parameters to account for ¹³C-SOM decomposition in the Yasso model. The calibration of these parameters only depends on the δ¹³C values, i.e. the relative carbon isotope concentrations, and revealed unimodal distributions for all four AWEN pool related parameters. Considering the acquired optima and taking into account that generally the ratio ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}\approx \mathrm{0.01}$, then the new ¹³C-SOM decomposition utilises values that differ at maximum 3 ‰ (for θ_A) from the default decomposition parameter values. Therefore, it is not surprising that both default and optimised model versions generate nearly identical SOM decomposition both on a short- (Fig. 2) and long-term basis. Moreover, the 0.3 ‰ relative difference in bulk C between the model versions at the end of the 100-year simulation is too small to be used directly to improve bulk C estimates. The benefits come in the various ways ¹³C can be used as a natural tracer.

The acquired optima for θ_A,θ_E and θ_W are all negative, which is consistent with the initial hypothesis and ¹³C-fractionation and enrichment theory. In the model, this translates to reduced ¹³C-SOM decomposition rate (Fig. 2). Likewise, the positive value for θ_N implies increased ¹³C-SOM decomposition when compared to the default model. However, the reduction in δ¹³C values, when compared to the default model version, is only true on shorter timescales (Fig. 2) as each pool has a trend to increase relative ¹³C content during the 100-year-long simulation (Fig. 3). This is due to the reduced ¹³C-SOM decomposition in other pools – as there is more ¹³C present in these pools, there is more ¹³C available to be transported into the N pool, which compensates for the increased decomposition. The positive θ_N goes against the initial hypothesis but is a direct result of model structure. It could be worthwhile to investigate how modifications to the model, such as adding multiple soil layers with differences in the effects of temperature, precipitation or Q10 (see e.g. Fig. 1 in Hilasvuori et al., 2013), would improve the model capabilities.

The straightforward changes to the Yasso model have improved the model capabilities in reproducing observed δ¹³C values in short (Fig. 2) and longer timescales (Fig. 3). Results from the 100-year-long simulation seem to corroborate the initial hypothesis for A, W and N pools that the relative ¹³C content in soil (larger δ¹³C values) increases with time. The optimised model even yields a positive trend for E pool δ¹³C, whereas the default model tends to converge the δ¹³C values of all pools to roughly −30. The optimised model behaviour follows the trend of these measurements, and the results are highly encouraging, even though the model is driven with a single averaged year representing the meteorological conditions from the beginning of the 21st century.

Estimation and modelling of soil organic matter decomposition, but also C sequestration, are current scientific challenges. We have demonstrated how ¹³C can be implemented into a soil carbon model, so that carbon isotope signals could then be used to analyse carbon cycles in more detail and to improve model capabilities, accuracy and predictability. The required model modifications were straightforward and resulted in drastic improvement of modelled δ¹³C values of SOM extracts. Although we emphasise the preliminary nature of our results due to limited calibration dataset, we foresee the model to act as a truly important tool to understand the role of isotopic fingerprints within soil carbon decomposition. The experiments demonstrated here should be viewed as a proof of concept, but further research is needed to verify the model capabilities on other sites, ecosystems and larger areas. Future research is expected to also include different management practices and croplands. Since the production of AWEN extractions with δ¹³C measurements is labour-intensive, future research will likely rely on inverse calibration on larger δ¹³C datasets that are rather straightforward to produce, or meta-analysis using literature-based values could be also used for further evaluation across varying scales (local, regional, global).

5 Conclusions

We have demonstrated how to incorporate ¹³C-SOM decomposition into the Yasso model and calibrate it. The model modifications were simple and straightforward and resulted in significantly improved simulated δ¹³C values. The results support the initial hypothesis of ¹³C-fractionation and enrichment theory. The capability of a model to simulate soil ¹³C content and isotope-specific SOM decomposition improves the applicability of the Yasso-C13 model to scale processes from the ecosystem level to the regional and global scale using δ¹³C as a tracer. Conceptually the presented work is on solid ground, but the lack of suitable calibration and validation data urges further studies with new, precise experimental δ¹³C data suitable for Yasso-C13 model calibration and validation.

Appendix A: Yasso model parameters

Table A1 Utilised Yasso model parameter values.