the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Integration of tree hydraulic processes and functional impairment to capture the drought resilience of a semiarid pine forest
Daniel Nadal-Sala
David Kraus
Uri Hochberg
Tamir Klein
Yael Wagner
Fedor Tatarinov
Dan Yakir
Nadine K. Ruehr
Drought stress causes multiple feedback responses in plants. These responses span from stomata closure and enzymatic downregulation of photosynthetic activity to structural adjustments of xylem biomass and leaf area. Some of these processes are not easily reversible and may persist long after the stress has ended. Despite a multitude of hydraulic model approaches, simulation models still widely lack an integrative mechanistic description of how this sequence of physiological to structural tree responses may be realized that is also simple enough to be generally applicable.
Here, we suggest an integrative, sequential approach to simulate drought stress responses. First, decreasing plant water potential triggers stomatal closure alongside a downregulation of photosynthetic performance, thereby effectively slowing down further desiccation. A second protective mechanism is introduced by increasing the soil–root resistance, represented by a disconnection of fine roots after a threshold soil water potential has been reached. Further decreases in plant water potential due to residual transpiration and loss of internal stem water storage consistently lead to a loss of hydraulic functioning, which is reflected in sapwood loss and foliage senescence. This new model functionality has been used to investigate the responses of tree hydraulics, carbon uptake, and transpiration to soil and atmospheric drought in an extremely dry Aleppo pine (Pinus halepensis Mill.) plantation.
Using the hypothesis of a sequential triggering of stress-mitigating responses, the model was able to reflect carbon uptake and transpiration patterns under varying soil water supply and atmospheric demand conditions – especially during summer – and respond realistically regarding medium-term responses, such as leaf and sapwood senescence. We could show that the observed avoidance strategy was only achieved when the model accounted for very early photosynthesis downregulation, and the relatively high measured plant water potentials were well reproduced with a root–soil disconnection strategy that started before major xylem conductance losses occurred. Residual canopy conductance was found to be pivotal in explaining dehydration and transpiration patterns during summer, but it also disclosed the fact that explaining the water balance in the driest periods requires water supply from stem water and deep soil layers. In agreement with the high drought resistance observed at the site, our model indicated little loss of hydraulic functioning in Aleppo pine, despite the intensive seasonal summer drought.
- Article
(2138 KB) - Full-text XML
-
Supplement
(1150 KB) - BibTeX
- EndNote
Reduced tree growth and increased tree mortality following hot and dry spells have been widely observed (e.g., Thom et al., 2023; Ryan, 2011; Hammond et al., 2021). This trend is expected to extend into the future, as a rising vapor pressure deficit (VPD) and more irregular precipitation patterns are predicted, leading to increases in drought severity (Huber et al., 2021; Tschumi et al., 2022). The extent of tree decline, however, also depends on the ability of tree species to withstand or respond to stress. This includes responses that are not easily reversible after rewetting and will, therefore, impact the tree carbon and water balance in the period following the cessation of stress, introducing so-called legacy effects (Ruehr et al., 2019).
To evaluate tree and forest responses to environmental changes, physiologically oriented simulation models are essential tools. These models describe various physiological processes and their dependence on environmental driving forces, and this information is then used to derive changes in biomass and dimensional growth (Fontes et al., 2010; Trugman et al., 2019). However, the various known internal feedback responses to primary damage (López et al., 2021; Blackman et al., 2023) are still lacking a unified mechanistic formulation. A main reason for this deficit is that several tree processes that occur at various temporal scales are involved. For example, stomatal closure may occur immediately and is easily reversible, but less-reversible responses, such as loss of xylem, roots, or foliage, are usually only observed after prolonged and/or severe drought stress (Barbeta and Peñuelas, 2016; Nadal-Sala et al., 2021a; Nardini et al., 2016). Immediate and intermediate responses during drought are stomatal closure, photosynthetic enzyme degradation, and a decrease in mesophyll conductance (all regarded as non-stomatal limitations to photosynthesis) (Salmon et al., 2020; Dewar et al., 2018). This is followed by fine-root retraction from the soil, which prevents potential water loss into the soil and restricts further water uptake (Yang et al., 2023), and xylem embolism, which reduces conductance further but can lead to tree mortality (Brodribb and Cochard, 2009; Ruffault et al., 2022). Before death, however, the remaining evaporative demand can be further reduced by decreasing the evaporative surface itself, i.e., by shedding foliage (Blackman et al., 2023; Cardoso et al., 2020). These responses might be consistently considered using a hierarchical triggering effect, in which responses depend on one another, or by sequential initiation at decreasing levels of plant hydration, represented by parameters such as the plant water potential (Walthert et al., 2021) or plant water storage (Paschalis et al., 2024).
Current developments in physiologically oriented stand-level simulation models propose the calculation of hydraulic and stomatal conductance as a function of leaf water potential (Kennedy et al., 2019; Christoffersen et al., 2016; Eller et al., 2018); these processes then drive losses in xylem conductance and leaf shedding (Xu et al., 2016), triggering tree mortality when drought stress intensifies (Yao et al., 2022; Torres-Ruiz et al., 2024). Including non-stomatal limitations on photosynthesis based on the leaf water potential was first introduced by Tuzet et al. (2003). Since then, it has been identified as a key explanatory process for leaf exchange dynamics under sustained drought stress conditions (Keenan et al., 2010; Yang et al., 2019; Gourlez de la Motte et al., 2020). In connection with a plant hydraulic model, it has been shown to result in more realistic water potential developments (Sabot et al., 2022). Nevertheless, it is difficult to realistically reproduce plant water potential developments without sacrificing parsimony (Drake et al., 2017; Cochard et al., 2021). Based on this struggle to establish a simple but consistent and generally applicable solution, the need for a representation of hydraulic processes that also accounts for non-stomatal impacts is becoming increasingly recognized. For example, drought stress can trigger the adjustment of allometric relations, such as larger root-to-shoot and root-to-leaf ratios, that favor water uptake and reduce water losses (Brunner et al., 2015; Lemaire et al., 2021) or competition processes at the stand level that lead to density-dependent tree mortality (Trugman, 2022; Pretzsch and Grote, 2024).
The full effect of such secondary responses can only be evaluated when both the mitigating impact on tree water loss and the trade-off with respect to carbon acquisition and allocation change are considered (Ruehr et al., 2019; Müller and Bahn, 2022). For example, degraded enzymes require a number of days to recover, during which their full photosynthetic capacity is not available, and foliage that is lost during a drought event will slow down desiccation, allowing trees to survive longer under hydric stress (Blackman et al., 2023, 2019), but will not be available for carbon assimilation after stress release, hindering recovery (Galiano et al., 2011). Moreover, damage to conductive tissue that is inherently related to potentially reduced carbon uptake is not reversed quickly via the refilling of the embolism (which is also an energy-consuming process); rather, the reversal of damage mostly depends on the regrowth of new xylem tissue (Hammond et al., 2019; Rehschuh et al., 2020; Gauthey et al., 2022). Such secondary effects do not need a new functionality in ecosystem models; rather, they can be considered in existing integrated modeling frameworks, allowing for the simulation of stress legacies in ecosystem-process-based models. Moreover, the simulation of mechanistic stress-driven tree mortality might be facilitated if the tissue function has been damaged beyond critical levels (McDowell et al., 2022; Breshears et al., 2018) or if regrowth and repair decrease resources for the growth of assimilating tissues, with detrimental impacts on the acquisition of new carbon and nutrients (Bigler et al., 2007; McDowell et al., 2008; Rukh et al., 2023).
Previous attempts to incorporate explicit definitions of plant hydraulics in process-based models have been proven to capture instantaneous responses of leaf gas exchange to drought stress (e.g., De Kauwe et al., 2015a; Sperry et al., 2017; Tuzet et al., 2017; Cochard, 2021; Sabot et al., 2022). Similarly, plant hydraulics has also been used to investigate tree structural adjustments in response to drought stress, e.g., loss of xylem conductance due to cavitation (Whitehead et al., 1984; Tyree and Sperry, 1989), leaf shedding (Nadal-Sala et al., 2021a), and fine-root biomass adjustments (Sperry et al., 1998). Overall, applying hydrological model schemes has been found to be promising to investigate plant strategies to minimize drought stress that are based on different trait expressions (Mirfenderesgi et al., 2019). However, modeling tree hydraulic processes at the stand level is still challenging due to the complex interaction of environmental boundary conditions, such as evaporative demand and soil properties, plant morphology (root distribution and individual size), anatomy (xylem conductivity and its vulnerability to embolism), physiology (photosynthetic capacity and stomatal responsiveness) (Trugman et al., 2019; Mencuccini et al., 2019), and the representation of competition when shifting from a single tree to the stand level (Trugman, 2022). Specific problems include the consideration of tree capacitance (Blackman et al., 2019; Preisler et al., 2022), water loss after full stomatal closure (Barnard and Bauerle, 2013; Duursma et al., 2019), seasonal acclimation of xylem properties to low water potentials (Feng et al., 2023), or the issue of embolism recovery (Arend et al., 2022).
The importance of considering first-level responses for drought stress mitigation as well as their trade-offs have been theoretically highlighted (Li et al., 2022; Trugman et al., 2019) and empirically demonstrated (e.g., Arend et al., 2022), but consistent model implementations are still scarce. Current approaches either concentrate on instantaneous stomatal responses alone (Eller et al., 2020) or responses directly affecting tree mortality (Yao et al., 2022). The few physiologically based approaches are computationally demanding and difficult to combine with established stand-level forest models (Ruffault et al., 2022), while the parameters required for an in-depth representation of the whole-plant hydraulic pathway are manifold and difficult to calibrate against measurements. Thus, in order to investigate the implications of sequential hydraulic stress responses, we integrated tree hydraulic and stress impairment processes into an existing modeling framework, LandscapeDNDC (Haas et al., 2013). The approach was inspired by recent model innovations (e.g., De Kauwe et al., 2020; De Cáceres et al., 2021; Ruffault et al., 2022) but is not aimed at simulating precise soil and plant water potentials, as these depend on very specific soil and plant properties that are spatially heterogenous and highly dynamic. Instead, we propose a relatively simple but robust model scheme in which soil water potentials are derived from generally available soil texture information and one average canopy water potential is assumed to impact responses of all leaves as well as the xylem (see Fig. 1). The approach presented here, which is based on two simple but well-established hydraulic principles and allometric relationships, also represents the major legacy mechanisms and medium-term feedbacks currently discussed (Trugman, 2022).
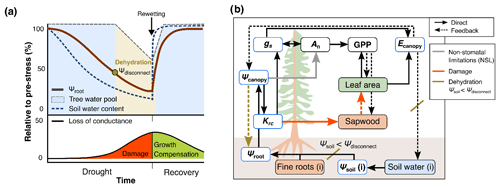
Figure 1Conceptual scheme of the hydraulic approach implemented into the model framework. (a) Theoretical progression of drought and recovery alongside the soil water content (SWC) dynamics and the relative impacts of SWC on the root water potential and tree water pool. Once the root water potential (Ψroot) falls below a threshold, roots disconnect from the soil (Ψdisconnect) and trees begin to dehydrate, emptying an internal tree water pool. During this stage, the functional damage to the trees causes a loss of hydraulic conductance. Following rewetting, functional impairment is slowly reversed via the regrowth of foliage and sapwood area. (b) Schematic overview of hydraulic processes, including the decrease in the photosynthetic capacity (An) (non-stomatal limitation, NSL) and, thus, gross primary productivity (GPP), which in turn affects stomatal conductance (gs) and transpiration (Ecanopy). The root–soil disconnect (Ψsoil<Ψdisconnect) is highlighted, triggering tree dehydration and biomass loss induced by declining root-to-canopy hydraulic conductance (Krc).
To evaluate this new model approach, we required a site that exhibited a full range of water availability, from no drought to very severe drought, and at which long-term measurements existed, in order to be able to constrain and evaluate the model processes. Therefore, we focused on a seasonal, dry forest site dominated by Aleppo pine trees (Pinus halepensis Mill.) in Yatir Forest, Israel. The site is characterized by a semiarid climate and has a short wet season in winter and a prolonged dry summer period with no rain and a high VPD (Wang et al., 2020). Considering the fact that the forest might already be at its limits with respect to survival and that climate projections suggest an additional precipitation decrease of up to 20 % (IPCC, 2019; D'Andrea et al., 2020), investigations that target the resilience of the trees in this region might be of particular interest.
Our central physiological hypothesis states that a cascade of mechanisms in plants are triggered in response to declining water potential to prevent further dehydration (Novick et al., 2022). The intensity of such responses increases with decreasing water potential (Walthert et al., 2021), and the sensitivity of these responses is inversely related to the carbon cost of their reversal. The suggested model scheme (Fig. 1) represents a consistent implementation of this hypothesis, which will be tested by investigating the transition from wet to extreme dry conditions. In particular, the following objectives are targeted:
- i.
First, we aim to evaluate the newly developed plant hydraulics module at an extreme, seasonal, dry forest site. In particular, the module is challenged to represent the two main seasonal stomatal behaviorial trends in Yatir Forest – VPD-driven stomatal limitation during times of ample soil moisture and soil-moisture-driven limitations under dry environmental conditions.
- ii.
Second, we wish to determine the potential importance of hydraulically driven non-stomatal limitations on photosynthetic assimilation.
- iii.
Third, we focus on assessing the impact of considering a root–soil disconnection process under realistic, prolonged drought stress conditions.
Furthermore, we depict and discuss how the proposed hydraulic modeling scheme could be used to alter simulated leaf and sapwood area dynamics.
2.1 Site description
Yatir Forest (31.34° N, 35.05° E) in Israel is an Aleppo pine plantation established during the 1960s. The site conditions are characterized by an exceptionally dry climate: annual precipitation totals 285 mm, while potential evaporation is >5-fold higher (Schiller, 2010; Ungar et al., 2013). Typically, the forest experiences a 6- to 8-month-long rain-free period during summer.
The soil at the site is a Rendzic Leptozol with an extremely clay-enriched layer at ca. 1 m depth, a permanent wilting point of 10.7 % volumetric soil water content (SWC), and a high stone content (Klein et al., 2014; Preisler et al., 2019). Van Genuchten parameters have been directly derived from soil water retention curves, measured at four different depths at the investigation site (Klein et al., 2014). The threshold for water uptake has been set by a threshold parameter (Ψdisconnect) which is calibrated to gas exchange (see Sect. 2.3.3). This is, however, close to the water potential that develops at wilting point according to the initialized van Genuchten parameters and the measured clay and sand content. The soil water potential at wilting point decreased with depth and was slightly below −2 MPa in the upper 20 cm. During the study period, stand density was determined to be 357 trees ha−1, the average diameter at breast height of all trees was about 18.5 cm, and the average tree height was 9.3 m (based on Rohatyn, 2017, and Fedor Tatrinov, personal communication, 2019). Natural regeneration is negligible (Pozner et al., 2022). Specific initializations for model simulations are given in Table S1 in the Supplement.
2.2 Observational data
Carbon and water fluxes and supplementary meteorological data are measured at a 19 m high flux tower at the site, in the geographical center of Yatir Forest. Weather variables include the incoming photosynthetic active radiation, air temperature, vapor pressure deficit, wind speed, and precipitation; these parameters have been continuously recorded since the year 2000 (Grünzweig et al., 2003). Measurements are carried out according EUROFLUX standards, and data are included in the CARBOEUROFLUX network (Aubinet et al., 1999). We selected the period between 2012 and 2015 for our study, as it provides ample high-quality eddy-covariance (EC) data as well as sap flux measurements and is freely available from the Integrated Carbon Observation System (ICOS) data portal (Warm Winter 2020 Team and ICOS Ecosystem Thematic Centre, 2022, https://www.icos-cp.eu/data-products/2G60-ZHAK, last access: 25 August 2023). We purposefully concentrated on a couple of years in order to omit any potential impact of stand structural changes or increasing atmospheric CO2 concentration (e.g., Norby et al., 2005).
EC measurements of net ecosystem production (NEP) and calculations of gross primary production (GPP) and ecosystem respiration (ER) using site-specific relations to temperature, as described in Tatarinov et al. (2016), are provided on the ICOS data portal (Warm Winter 2020 Team and ICOS Ecosystem Thematic Centre, 2022, https://www.icos-cp.eu/data-products/2G60-ZHAK, last access: 25 August 2023). Daily values were only calculated with good and very good NEP data quality, according to the EUROFLUX methodology. All other data were considered to be missing values. Days with more than two 30 min daytime values missing were excluded from the model evaluation (ca. 35 %).
Sap flow measurements are based on up to 16 trees and were collected using lab-manufactured thermal dissipation sensors (Granier and Loustau, 1994) at 30 min intervals. Sap flow was calculated following Granier and Loustau (1994), implementing corrections (Kanety et al., 2014). Sap flow was transformed to tree transpiration using individual tree sapwood basal area. Transpiration at the stand level was obtained by multiplying the average tree sap flux density per unit sapwood area by the mean tree sapwood cross-sectional area and the stand density. All data used for the evaluation are presented in Fig. 2. For further details regarding sap flow measurements, the reader is referred to Klein et al. (2014).
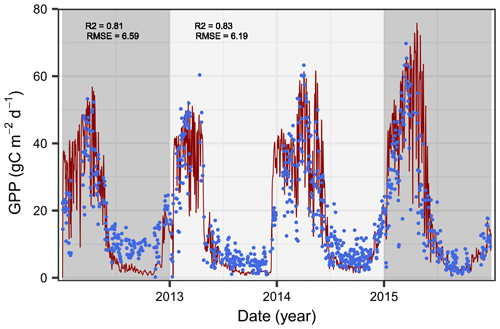
Figure 2Comparison of simulated (red lines) and observed (blue dots) gross primary production (GPP) in Yatir Forest. The periods used for the Bayesian calibration (2013–2014, light gray) and model evaluation (2012 and 2015, dark gray) are highlighted, and the goodness of fit between the model and observations is indicated using the Pearson correlation (R2) and the root-mean-square error (RMSE).
Litterfall was collected in 25 litter traps of 0.5 m2 each for 10 consecutive years (2003–2012). Litter was removed from the traps every 1–2 months; sorted into needle, reproductive, woody, and residual fractions; and oven-dried at 65 °C for 2 d (Maseyk et al., 2008). For the purpose of this analysis, only needle litter was considered. To be able to compare simulated and observed dynamics, total leaf biomass was bootstrapped for the 2003–2012 period to derive the annual median (see Fig. S1) and then multiplied by an average needle longevity of 3 years (Maseyk et al., 2008).
SWC was monitored continuously at the site throughout the 2013–2015 period, using TRIME-PICO 64 sensors (IMKO Micromodultechnik GmbH, Ettlingen, Germany) installed at depths of 5, 15, 30, 50, 70, and 100 cm in five soil pits, and averaged over the whole profile. Air temperature and relative humidity were monitored continuously above the canopy at the flux tower (Tatarinov et al., 2016). The measured soil water content and its representation by the model are given in the Supplement (Fig. S2).
2.3 Model description
2.3.1 LandscapeDNDC and the physiological simulation model
LandscapeDNDC (https://ldndc.imk-ifu.kit.edu, last access: 25 August 2023) is a simulation platform for terrestrial ecosystem models (Grote et al., 2011; Haas et al., 2013). It has been designed to reproduce atmosphere–biosphere exchange process of carbon, water, and nitrogen, including trace gas exchanges. For this purpose, detailed soil process modules are provided to be coupled with ecosystem modules that are parameterized at the species level and cover grasslands, crops, and forests. The LandscapeDNDC model framework uses daily maximum and minimum temperature, radiation, VPD, and precipitation as meteorological inputs, which are downscaled to hourly values. The canopy is divided into multiple layers, the height and extension of which depend on the initialized ecosystem structure, and microclimate is calculated for each layer (using an empirical canopy model; Grote et al., 2009). Similarly, soil is divided into a user-defined number of layers, each holding chemical and texture information (Holst et al., 2010). Foliage and fine roots are distributed across the canopy and rooting space, respectively, according to a distribution function described in Grote and Pretzsch (2002).
The water balance is derived by considering all major ecosystem fluxes (evaporation from interception, transpiration, ground surface, and soil; runoff; and percolation) and pools (water storage at the leaf surface, at the ground, and in each soil layer) and is based on the original model for denitrification and decomposition (Li et al., 1992). The soil water content and soil water distribution are basically represented with a bucket approach, and soil water potentials are calculated based on soil properties using the equations suggested by van Genuchten (1980). Forest carbon gain and loss due to growth and maintenance respiration as well as phenology, allocation, and senescence processes are considered within the physiological simulation model (PSIM), which uses the Farquhar model to estimate hourly carbon assimilation (Farquhar et al., 1980). The modeling of assimilation in PSIM is then linked to a stomatal conductance module to optimize gas exchange. For standard simulations, the procedure suggested by Leuning (1995) is applied, but it is possible to select or to introduce alternative approaches (see below). Maintenance respiration is calculated based on temperature and nitrogen concentrations in the different tissues (Cannell and Thornley, 2000). The remaining photosynthates are allocated into different tree compartments (reserves, foliage, fine roots, and living wood) according to their respective sink strength, which is based on allometric relations (define demand originating from foliage development), tissue loss rates (increase demand), and environmental limitations (prevent allocation to inactive tissues) (Grote, 1998). In case none of the compartments have any demands, the carbon is distributed according to allometric ratios between leaves, fine roots, and sapwood (in case of undetermined growth) or between fine roots and sapwood (otherwise). Senescence of tree compartments is generally derived from a specific longevity for each tissue. Currently, enhanced senescence of tissue under stressful environmental conditions is not considered.
In this configuration, LandscapeDNDC has been used to investigate gas exchange and biomass growth in forested ecosystems (Rahimi et al., 2021; Cade et al., 2021; Dirnböck et al., 2020). It has also been evaluated at different European forest sites (Mahnken et al., 2022; Nadal-Sala et al., 2021b); one result of these evaluations is that the sensitivity of carbon and water fluxes to the vapor pressure deficit is generally not sufficiently well represented. Thus, we implemented a new hydraulic conductance scheme as well a mechanism for stress-induced senescence of sapwood and foliage into this framework, the latter of which is described in more detail below.
2.3.2 Representation of hydraulic conductance
Stomatal closure
The newly implemented hydraulic approach into LandscapeDNDC allows for the calculation of the canopy water potential based on the soil water potential and fine-root vertical distribution (see also Fig. 1a). On the one hand, stomatal conductance (gs) is regulated in order to optimize net photosynthesis (An, µmol m−2 LA s−1, where LA denotes leaf area), which is calculated here according to Farquhar et al. (1980); on the other hand, gs is regulated considering a peaked Arrhenius response of photosynthetic parameters with leaf temperature (Medlyn et al., 2002) and hydraulic safety, calculated from hourly mean canopy water potential following Eller et al. (2020):
Here is the increase in net photosynthesis per unit of internal carbon dioxide (Ci) increase (i.e., the gain function for stomata opening on net assimilation), while ξ is the cost function, which represents the loss of hydraulic conductance with increasing stomatal opening. The function ensures that increases in An increase the stomatal conductance and vice versa, while gs decreases with increasing plant resistance and vapor pressure (VPDm, mmol mol−1). The single terms are the whole-plant resistance to water flow (rp, m2 s MPa mmol−1), which is calculated from whole-plant minimum hydraulic resistance as defined in Eller et al. (2020) (RPMIN, m2 s MPa mmol−1); the relative root-to-canopy hydraulic conductance (, unitless); and the partial derivatives of and mean canopy water potential (Ψcan_mean). These are computed at hourly time steps as the linear gradient between (Ψcan_mean) and (0.5(Ψcan_mean+ΨREF)), respectively. , in turn, depends on species-specific parameters (ACOEF and ΨREF). Ψcan_mean is assumed to be represented simply by the average of the predawn canopy water potential (Ψcan_PD) and the hourly calculated canopy water potential (Ψcanopy; see Eq. 3) from the previous time step, to avoid abrupt drops in water potential along the plant hydraulic pathway (Eller et al., 2018). Ψcan_PD is the value of Ψcanopy obtained directly before sunrise. Finally, stomatal conductance cannot decrease below a given minimum conductance (gMIN), which represents canopy leakiness.
In order to enhance the impact of hydraulic constraints, we additionally consider a non-stomatal downregulation of photosynthesis – hereafter referred to as NSL – that has been suggested by various authors (e.g., De Kauwe et al., 2015a; Drake et al., 2017). Here, we assume a direct dependency on declining Ψcan_PD using an equation suggested by Tuzet et al. (2003) and tested in Nadal-Sala et al. (2021a):
where ΨNSL and ANSL are species-specific parameters (see Table 1). The function results in decreases in the photosynthetic potential and, thus, further reductions in stomatal conductance (according to Eq. 1a). The importance of this mechanism has been tested by running the model with and without the additional impact on photosynthesis.
Plant water potential and hydraulic conductance
The relevant water potential for the canopy conductance control is Ψcanopy, which is calculated from the xylem water potential following Darcy's law (Ψxylem, MPa) and canopy transpiration of the previous time step (Tcanopy, mmol m−2 LA s−1) divided by root/canopy hydraulic conductance (Krc, in mmol m−2 LA s−1 MPa−1), also considering the gravitational effect of canopy height. The conductance term Krc is obtained from the previous hour Ψcan_mean and the species-specific xylem hydraulic vulnerability curve, which is assumed to follow a Weibull function (Neufeld et al., 1992):
Here, KSPEC, ΨREF, and ACOEF are empirically determined coefficients (see Table 1) describing the shape of the vulnerability curve, as obtained from field measurements (Wagner et al., 2022). The decline in Ψcanopy considers the gravitational impact of canopy height h (m), where ρ is water density at 25 °C (997 kg m−3) and g represents gravitational acceleration (9.8 m s−2). Multiplication by 10−6 converts the term to megapascals. In order to determine Ψxylem, the root water potential (Ψroot, MPa) has to be defined first from the soil water potential (Ψsoil, MPa) and fine-root vertical distribution. Ψsoil is defined for each soil layer based on its water content, specific texture properties, and water holding capacity according van Genuchten et al. (1991), with parameters determined according to Klein et al. (2014). Assuming that Ψroot equilibrates with Ψsoil overnight, it is generally calculated as the average Ψsoil of all (n) layers weighted by the respective fine-root biomass fraction (De Kauwe et al., 2015b). The fine-root distribution is described using an empirical function (Grote and Pretzsch, 2002) parameterized with in situ data (Preisler et al., 2019). We also consider that roots decouple from the soil under extremely low water potential conditions in order to prevent root-to-soil water flow (North and Nobel, 1991; Carminati et al., 2009; Carminati and Javaux, 2020):
Here, “i” indicates any given soil layer, frfi is the relative root fraction per layer, and Ψdisconnect (MPa) is the species-specific water potential threshold at which the roots are decoupled from the soil. As long as Ψsoil is larger than Ψdisconnect, transpiration demand is determining the soil water uptake (UPTsw, mm); thus, water demand and supply are assumed to be in equilibrium, and Ψxylem is equal to the water potential in the roots (Ψroot, MPa). As long as Ψsoil allows, water uptake is distributed throughout the soil layers according to the fine-root distribution and relative soil water availability. However, if the water reservoir within the core rooting zone is empty (Ψsoil≤Ψdisconnect), remaining transpiration needs to be supplied by other sources, such as the stem water storage. Accordingly, a tree water deficit (WD) develops cumulatively during the time without soil water uptake and then recovers as soon as UPTsw is larger than Tcanopy. Note that the implemented hydraulic processes do not principally limit WD. Therefore, a conceptual decision needs to be made by the model user to either consider trees dead once a critical plant water potential has been crossed (e.g., at 88 % percent loss of conductance – PLC; Liang et al., 2021), which would indicate that capacitance is depleted to a certain level (e.g., estimated to be about 30 % of the living biomass dry weight; Ziemińska et al., 2020), or allow for water uptake from deep soil. In our case, trees never reached such critical water potentials, likely due to water supply from undefined deeper soil layers in accordance with earlier investigations at the site (Raz-Yaseef et al., 2010; Helman et al., 2017). However, this continued water uptake in the model does not refill the depleted water sources in the trees; rather, it solely supports residual transpiration as long as Ψsoil≤Ψdisconnect. Hence, the trees continue to dehydrate, and the water potential during this period (Ψdehydration, MPa) is calculated from the difference between Ψcan_mean and Ψroot as follows:
Note that Ψdehydration is an integrated term that increases throughout the period of “k” days as long as Ψsoil≤Ψdisconnect. As canopy water potential also includes a reduction by gravitational force (see Eq. 3) but Ψdehydration only expresses the dehydration effect, this term needs to be re-added to avoid double-accounting in the calculation of Ψcanopy. The difference between corrected canopy water potential and Ψroot is then averaged over all daylight hours “j” per day. Additionally, a reduction term is required (Eq. 5b) that accounts for the fact that not all transpired water is drawn from the foliage but also from other living tree compartments (Tyree and Yang, 1990). Therefore, we further assume that water capacitance is linearly related to biomass and that water deficits immediately equilibrate over all tissues (with BF, BS, and BR representing foliage, sapwood, and fine-root biomass, respectively, all in kilograms per square meter of ground).
Xylem inactivation and leaf senescence
A new feature of the hydraulic module is the representation of the progressive loss of xylem functionality presented as sapwood area decline as Ψxylem decreases (see Fig. 1; e.g., Choat et al., 2018; Rehschuh et al., 2020). The loss is calculated based on a hydraulic vulnerability curve represented with a Weibull function as follows:
Here, BAxylem is the basal area of xylem per tree (m−2 per tree), Δxylem,t is the daily reduction in xylem basal area (m−2 per tree), and Ψcan_PD,t and are the canopy predawn Ψ for the present day and the previous day, respectively (both in MPa). ACOEF and ΨREF are species-specific parameters (see Table 1). This process is not directly reversible, with xylem functionality being regained only via the regrowth of new tissue (see Fig. 1b; Hammond et al., 2019). Finally, in this model version, leaf area is reduced proportionally to , according to the pipe model (Shinozaki and Yoda, 1964).
2.3.3 Model initialization and parameterization
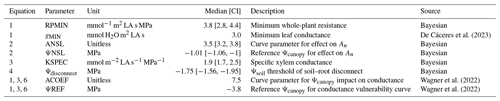
Parameters for the LandscapeDNDC core processes, such as the species-specific temperature sum that determines leaf flushing, the electron transport rate under standard conditions that defines photosynthesis, allometric relations and tissue longevities that drive allocation, and senescence, were obtained from the literature (Bernacchi et al., 2001; Infante et al., 1999; Kattge and Knorr, 2007; Medlyn et al., 2002; Navas et al., 2003) (see Table S2 in the Supplement for P. halepensis parameters). Note that some of these parameters are derived directly at the investigation site, including those describing photosynthesis (Maseyk et al., 2008), foliage biomass and development (Zinsser, 2017), and fine-root distributions (Klein et al., 2014). Therefore, absorption properties of canopy and rooting space, the dimensions of which are defined by the respective stand and soil inventory information (see Sect. 2.1), are actually based on measurements. Moreover, some parameters that were used for the new hydraulic scheme, such as those related to xylem vulnerability (Wagner et al., 2022), were available from observations at Yatir Forest (Table 1).
With the exception of the loss of conductance parameters (ACOEF and ΨREF) and the residual conductance term (gMIN), which were taken from the literature, the hydraulic parameters for the new module were calibrated using an inverse Bayesian calibration (Hartig et al., 2014; Dormann et al., 2018) based on GPP measurements for the 2013–2014 period (Table 1). We implemented a Gaussian likelihood function, with a “differential evolution with snooker update” algorithm as a sampler (DEzs; ter Braak and Vrugt, 2008). A total of 50 000 simulations were run for the calibration, with a burn-in of 30 000 simulations. The three chains of the calibration had converged at this point, i.e., Gelman–Rubin score for all marginal posteriors <1.1 (Gelman et al., 2013). The LandscapeDNDC simulations were then run with the median values for each calibrated parameter. Adjusting parameters using only the GPP resulted in the advantage that we could use sap flow and water potential measurements for evaluation. On the other hand, the procedure bears considerable uncertainty with respect to the system behavior throughout the whole range of environmental conditions observed. In order to ensure that all parameters can be varied within reasonable boundaries without getting unrealistic impacts, we investigate the sensitivity of transpiration and plant water potential to gMIN and all calibrated parameters with standard values used for all other parameters (see Figs. S3 and S4). Priors and credible intervals for each parameter were selected within literature boundaries broad enough to allow the model to capture the responses, but the values were sufficiently constricted to constrain them to biologically meaningful limits. For example, the median of gMIN for woody species was reported as 3.0 mmol m−2 LA s−1 for P. halepensis, but the range for semiarid plants is given as 1.1–6.3 mmol m−2 LA s−1 by Machado et al. (2021) (see Table S3 for the prior distribution).
2.3.4 Statistical analysis
All analyses were performed using the R software, version 4.1.2 (R Core Team, 2021). The parameter calibration of LandscapeDNDC was done using the “BayesianTools” package (Hartig et al., 2019). When a type-I linear relationship was applied, the simulated vs. observed evaluation was given as Spearman's R2 and the root-mean-square error (RMSE). To assess the relationship between measured sap flow – as a proxy for transpiration – and modeled daily plant Ψ gradient (ΔΨplant, in MPa), calculated as ), a type-II linear regression was implemented according to Muggeo (2017). To derive the threshold at which the modeled daily Ψcanopy became uncoupled from VPD but driven by SWC, we performed a truncated linear analysis with the BayesianTools package.
3.1 Model evaluation
The simulated GPP dynamics after model calibration captured the observed GPP pattern with a Pearson correlation coefficient of R2∼0.8 (Fig. 2). The impact of the summer drought on tree water relations was reflected in the GPP dynamics, with lowest uptake rates during the driest period (April–October). This clearly represents a huge improvement over previous versions of the LandscapeDNDC model (see Fig. S5) and indicates the suitability of the newly implemented hydraulic processes to capture GPP dynamics, particularly during extreme drought. The agreement was only slightly higher during the period used for the Bayesian parameter calibration than when strictly undertaking a comparison with the evaluation period, indicating a low bias in the calibrated parameters. Despite the good overall fit, particularly covering the steep decline after the rainy season, GPP seems to be underestimated in the dry period, particularly during the first year. However, as the deviation is considerably stronger in the first year, temporally restricted impacts deriving from the model initialization, such as available surplus water from the previous year, actual leaf biomass, or the spatial redistribution of water originating from rainfall events not covered in the data set, are likely influences (Shachnovich et al., 2008).
3.2 Sensitivity of tree water relations to seasonal drought and VPD
The model simulations captured the strong seasonality in water availability at Yatir Forest, with mild and relatively wet winter conditions and dry summer periods. This was reflected in the modeled predawn plant water potential (Ψcan_PD) that ranged between −0.7 MPa during the wet winter season and −2.3 MPa during the dry summer period (black line in Fig. 3a). For evaluation, we compared occasional plant water potential measurements during the years 2012–2014 with Ψcan_mean, which varies during the day (gray area in Fig. 3a). Except for one event at the onset of the dry period in 2013, which showed particularly low values, simulations covered all measured potentials within the uncertainty ranges. It should be noted that the daily variability in Ψplant decreases considerably when approaching a plant water potential of −1.75 MPa (=Ψdisconnect), after which no additional water is taken up and the daily cycle is only driven by the redistribution of water within the plant. During this time, further tree dehydration depends strongly on gMIN, VPD, and leaf area (see also Figs. S3 and S6). The modeled daily gradient in water potential () over the three simulation years was in high agreement with the observed transpiration rates (Fig. 3b). Furthermore, we found good agreement between the simulated and observed transpiration rates (Fig. 3c) while also properly reproducing soil water content (SWC) dynamics (see Fig. S2).
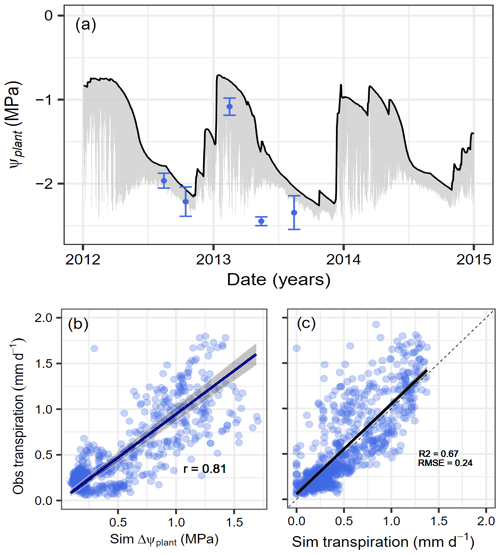
Figure 3Simulated and observed water potential and transpiration responses to seasonal drought at Yatir Forest. Dynamics of simulated plant water potentials (Ψcan_PD, Ψcan_mean, and Ψmeasured) and transpiration rates with observations at Yatir Forest from 2012 to 2014. (a) Seasonal dynamics in predawn plant water potential (black line) and the daily water potential gradient (gray area). Observations represent midday leaf water potentials (blue circles) with uncertainty ranges given (± SD) as reported by Preisler et al. (2019). (b) Relationship between simulated ΔΨplant (see text for explanation) and observed transpiration rates are given with the Pearson correlation coefficient for a type-II linear regression. (c) Comparison of observed against simulated daily transpiration rates.
The simulations indicate that internal tree hydraulic dynamics are generally limited by soil water availability and that the decrease is steeper after a threshold at about 15.8 % SWC (95 % CI [15.4, 16.5]) has been reached, which is well before Ψdisconnect (Fig. 4a). As long as the availability of soil water is above the threshold, transpiration is more sensitive to changes in VPD; below this threshold, the sensitivity to SWC is more strongly expressed (Fig. 4b). Hence, during the wet season, stomatal conductance depends mostly on evapotranspiration demand, whereas conductance is mostly limited by soil water availability in the period of soil drying.
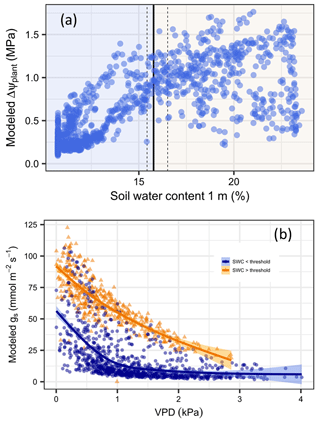
Figure 4Identification of dominant drivers for the daily drop in plant water potential and stomatal conductance in Aleppo pines at Yatir Forest. (a) ΔΨplant in relation to water content within the rooted soil (SWC, in %). Vertical lines indicate the SWC at which a shift in the driver dominance occurs (a solid line denotes the median; dashed lines are 95 % confidence intervals). (b) Relationships between daytime daily averaged stomatal conductance and daytime daily averaged VPD for SWC above (orange triangles) and below (blue dots) the SWC threshold.
3.3 Sensitivity of tree water relations to non-stomatal limitations
The sensitivity of simulated water fluxes to specific processes has been investigated by testing the responses of transpiration and plant water potential to variations in hydraulic parameters (Fig. S3). As the sensitivity to the process of non-stomatal limitation depends on various parameters and model assumptions, we tested the impact of early, moderate, and late onset of the NSL impact (Fig. S4). The respective simulations demonstrate that an early onset of photosynthesis decline decreases gs and transpiration considerably faster than a late onset and is able to prevent plant water potentials from reaching damaging levels (Fig. 5). Without considering the direct limitation on photosynthesis, gs responses to Ψcan_PD are delayed; consequently, stomatal closure is reached at an unrealistic low water potential for an isohydric species such as Aleppo pine.
3.4 Hydraulic impairment and leaf shedding
Based on the evaluated plant water potentials, the additional stress-induced loss of xylem area according to Eq. (6) accumulates to 3.4 % yr−1–6.3 % yr−1 of total sapwood area. The net loss of sapwood, which is composed of tissue loss by age as well as by low plant water potentials, occurs solely during the dry season when allocation to sapwood is zero or close to zero (brown areas in Fig. 6). It starts at Ψcan_PD values of approximately −1.25 MPa, far away from both P12 (−2.9 MPa) and P50 (−3.6 MPa) – i.e., the plant water potentials at which a 12 % and 50 % of xylem conductance has been lost, respectively (see Fig. S4). The additional stress-induced loss of conductance, albeit relatively small, is responsible for the differences in functional sapwood area during the dry seasons of the different years. During the wet season, sapwood growth generally copes with – or even exceeds – the demands for foliage supply (determined by the sapwood area foliage area ratio; Table S2) and is thus positive (green areas in Fig. 6).
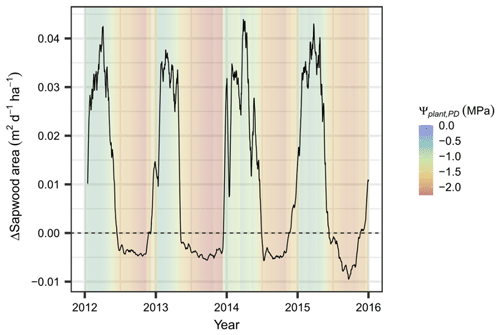
Figure 6Simulated sapwood area dynamics at Yatir Forest. Simulated net gains and losses of active sapwood area (ΔSapwood area) are presented as a 7 d moving average during 2012–2015. The corresponding daily predawn plant water potential is given as a shaded background.
The overall pattern of foliage litterfall reproduced the observed seasonal dynamics reasonably well (Fig. 7). In our model, flushing and phenological leaf senescence are determined to start by the onset of the wet period in January and end by mid-September, closely after the onset of the dry period. According to our model concept, functional xylem losses translate into additional foliage losses during the dry season, resulting in stress-induced litterfall between September and December. However, similar to the relatively small amount of drought-induced loss in sapwood area, stress-induced foliage senescence was only small.
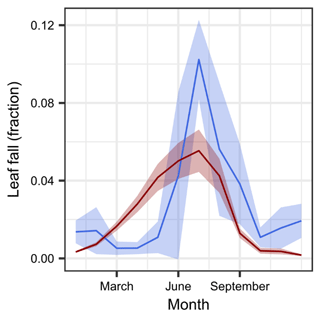
Figure 7Seasonality in leaf litterfall from observations in Yatir Forest and respective simulation results. Simulated (red) and observed (blue) monthly median litterfall values are shown as a fraction of the average leaf biomass. Note that simulations are from 2012 to 2015, whereas observations were integrated from 2003 to 2012. The shaded areas represent the 95 % CI.
3.5 Sensitivities of drought-induced tissue senescence to gMIN and root–soil disconnection
Hydraulic damage in the model is mostly restricted to the period after the roots become disconnected from the soil, and dehydration during this period depends largely on residual evaporation (gMIN). Therefore, we have tested the sensitivity of the model to variations in the gMIN and Ψdisconnect parameters. The selected range was determined based on published values for conductance under dry conditions (Klein et al., 2011; Llusia et al., 2016) and observed ranges of predawn water potentials in P. halepensis at different sites (Atzmon et al., 2004). Over the observed range, an increase in both gMIN and Ψdisconnect results in linearly increased sapwood area damage and percent loss of conductivity (Fig. 8). The selected parameter combination does fall in the lower range of conductivity loss that has been observed at the site (gray area in Fig. 8); at the same time, the analysis shows that the tissue damage is particularly sensitive to Ψdisconnect and can easily be under- or overestimated.
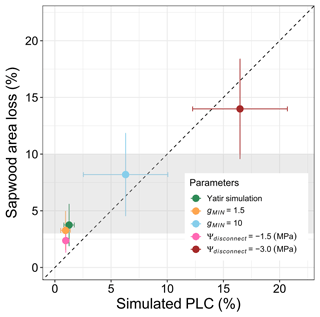
Figure 8Impacts of changes in the hydraulic key parameters gMIN and Ψdisconnect on sapwood area loss. Simulated sapwood area loss is shown as annual averages obtained during the 2012–2015 period in relation to simulated maximum percent loss of conductance during summer (PLC, in %). For comparison, sapwood area losses of about 3 %–10 %, as reported in Wagner et al. (2022) and Feng et al. (2023) for the 2020–2021 period, are indicated using the gray shaded area.
Our simulations indicate a tight coordination of drought-induced physiological responses in a seasonal, summer-dry forest that are triggered by decreasing plant water potential, affecting stomatal closure, soil–root disconnection, and tissue senescence. In the selected case study, P. halepensis shows an expressed isohydric behavior, which is in close agreement with previous observations (Fotelli et al., 2019; Klein et al., 2011). Accordingly, a seasonal differentiation in the importance of environmental drivers with respect to stomatal conductance was clearly apparent, with fully open stomata during the rainy season and gradually declining conductance down to a very small minimum towards the end of the dry period (see also Fig. S7). We could show that VPD was the main influence on stomatal behavior during the period with sufficient soil water supply, whereas SWC limited gas exchange during the rest of the year. When the soil water content was close to its minimum, gMIN was the most important parameter affecting the dehydration processes and, hence, tissue damage under prolonged drought stress. Our simulations, which are in close agreement with sap flow measurements, indicate that transpiration could not be supported solely by soil water within the assumed rooting zone during the peak of the dry season. The water additionally required was in the range of approximated capacitance (a few millimeters) during 3 of the 4 investigated years, but it increased cumulatively up to 25 mm in 1 of the investigated years. We suppose that the supply from deeper soil layers is the most likely explanation for this, which is in line with earlier investigations (Raz-Yaseef et al., 2010). Even assuming that the damage to xylem and needles is linearly related to the PLC curve development, the model indicates only minor damage to the Aleppo pines in Yatir Forest, which demonstrates the effectiveness of physiological countermeasures such as the early onset of the NSL impact, which slows down the decrease in the internal water potential, or the high resistance to xylem damage, as indicated by the PLC curve.
The simulations capture all water fluxes within a reasonable range. Water losses by transpiration are about 66 % of precipitation: interception and soil evaporation cover about 11 % of this amount each, while the remaining water is lost to percolation during high-rainfall events (see Table S4). This means that model estimates are similar with respect to interception and transpiration but smaller regarding total evaporation, compared with eddy-flux measurements documented by earlier studies at this site (Raz-Yaseef et al., 2010; Ungar et al., 2013). One reason for this may be that soil evaporation has been underestimated by the model, possibly originating from a faster water transport away from the soil surface than what is actually happening at the site. Furthermore, water adsorption from the air might play a role under semiarid conditions with temperatures below condensation point during nighttime (Qubaja et al., 2020). The latter leads to water condensing on plant surfaces during the night and then evaporating in the morning; thus, this water adds to evaporation but is not considered in the model. Overall, percolation is simulated to be considerably higher (36 mm on average over the 4 years simulated) than the additional water needed to supply transpiration when the upper soil water is depleted (maximum of approximately 20 mm in 2013), supporting the model assumption that the trees are able to take up water from deeper soil layers – a mechanism that has already been assumed a this site (Preisler et al., 2019).
4.1 Drought stress mitigation due to enhanced stomatal sensitivity
Within the hydraulic scheme, the stomatal conductance mechanism not only needs to account for various drivers but also has to consider each of them appropriately during any specific phase of stress. For example, stomatal regulation under humid to moderately dry conditions is most sensitive to VPD (Novick et al., 2016; Tatarinov et al., 2016). This sensitivity is captured well with the introduced hydraulic approach which decreases gs with an increasing VPD to avoid excessively low water potentials (objective i in Sect. 1). The enhanced sensitivity of stomata is particularly triggered by the consideration of photosynthesis downregulation under drought stress. This is a mechanism that is very suitable for representing isohydric behavior, which is supported by the finding that the NSL effects are indeed particularly observed in isohydric species such as birch, poplar, and pine (Uddling et al., 2005; Salmon et al., 2020). Under the selected extremely dry conditions, the sensitivity to the NSL is combined with a rather insensitive (or resistant) conductance loss curve, which ensures the survival of the species. However, it is not yet clear if this relationship between the NSL and vulnerability could be scaled with the drought sensitivity in general.
The observed shift in Aleppo pines' water management from demand-driven (VPD-driven) to supply-limited (SWC-limited) driving factors is best represented by accounting for a very sensitive direct impact of drought stress on assimilation. Such a consideration has been demonstrated to be particularly suitable under conditions of a steep decline in water availability (objective ii in Sect. 1). The integration of the NSL effect considerably enhances stomatal sensitivity to drought via a feedback mechanism from limited photosynthetic carbon uptake (Flexas and Medrano, 2002; Tissue et al., 2005; Gallé et al., 2007; Zhou et al., 2013). Hence, it enables a very steep response and avoids the necessity for a rather unrealistically low water potential under drought stress (Sabot et al., 2022). Hoshika et al. (2022) found an important role of photosynthesis downregulation for deciduous as well as evergreen oaks, and Wilson et al. (2000) estimated that this mechanism is responsible for approximately 75 % of the stomatal regulation in several deciduous trees. Nevertheless, the sensitivity of this mechanism is certainly species-specific (Lobo-do-Vale et al., 2023) and may strongly vary with foliage age (see, e.g., Wilson et al., 2000). Consequently, accounting for this NSL effect has been considered recently in various models (Dewar et al., 2022; Nadal-Sala et al., 2021a; Salmon et al., 2020) and might be essential to represent fast stomatal (particularly isohydric) responses to high evaporation demand (e.g., Yang et al., 2019; Gourlez de la Motte et al., 2020).
The vulnerability curves previously established for P. halepensis all indicate a medium sensitivity to declining plant water potential, with 50 % of the conductance lost at about −3.5 to −5 MPa (Gattmann et al., 2023; Oliveras et al., 2003; Wagner et al., 2022). However, soil water potentials in Yatir Forest can easily drop below −10 MPa in the upper layers (Klein et al., 2014). To avoid plant dehydration but still use the measured vulnerability curves, we defined that the roots disconnect from the soil (calibrated at about −1.75 MPa), leading to a slowdown of the water potential decrease and conductance loss as well as a slowdown of soil water depletion. The threshold obtained by Bayesian calibration is very close to the value of approximately −2 MPa reported by Klein et al. (2014), which is also indicated as the wilting point of the upper soil. This strengthens our notion that changes in root–soil resistance are very important to constrain the hydraulic damage of a drought-stressed plant (objective iii in Sect. 1). The importance of root detachment from the soil when calculating the increase in resistance with decreasing soil water has been found to account for more than 95 % of total plant hydraulic resistance (Rodriguez-Dominguez and Brodribb, 2020), supporting our assumptions. The process is being increasingly recognized and implemented in hydraulic models (e.g., Lei et al., 2023). This is based on experimental evidence that roots lose contact with the soil under dry conditions (Carminati et al., 2009; Rodriguez-Dominguez and Brodribb, 2020), which has been suggested as a determining factor for soil water depletion, slowing down soil drying (Carminati and Javaux, 2020). In fact, considering soil–root decoupling using a Ψsoil threshold can be seen as a simplification of more complex models, which explicitly simulate a steep root–soil conductance decline (Cochard et al., 2021; Sperry et al., 2017; De Cáceres et al., 2023). In the current approach, actual water compartments within the tree are only very coarsely considered to achieve plant water potentials less negative than soil water potentials. We have used a further simplification by assuming a nonspecific water supply from internal tree water storages or deeper soil; this is necessary to sustain transpiration during summer without a further depletion of soil water reserves, which is in agreement with in situ observations (Preisler et al., 2019). Complex plant hydraulic models avoid these simplifications by explicitly calculating more water pools and using a higher tissue-level resolution, thereby providing a high degree of realism but introducing more uncertainties related to the parameterization of the soil layer composition, tree compartment conductivity and hydraulic segmentation, fine-root distribution, and fine-root size and density (e.g., Cochard et al., 2021; Haverd et al., 2016).
Overall, the simulations clearly demonstrate the importance of residual water loss via leaf leakiness and bark transpiration in tree dehydration processes (Márquez et al., 2021; Machado et al., 2021). This is in agreement with previous work highlighting the importance of stem internal water reserves for the survivorship of Aleppo pine in Yatir Forest during the summer dry season (Preisler et al., 2022).
4.2 Consideration of structural hydraulic constraints
Although we were not able to refer simulated loss of sapwood area directly to measurements, independent observations at the same site indicate that the projected sapwood area reduction of up to 6 % is close to the in situ branch embolism values observed for Aleppo pine trees during summer, which were indicated to be 8 %–10 % (Wagner et al., 2022). Other reported values for the P. halepensis embolism that have been measured near Tel Aviv, Israel, indicate less than 5 % functional loss at the end of summer (Feng et al., 2023). Although Aleppo pines have been shown to be well adapted to extreme drought conditions, an increase in critical stress damage can still be expected under future hotter and drier conditions that will increase residual water loss and may amplify hydraulic damage, particularly under high-VPD conditions (e.g., Wagner et al., 2022). Similarly, leaf area loss was within the observed limits of litterfall, although this could not be evaluated directly with the available data. This is partly based on the small difference between litterfall due to needle longevity and stress-induced senescence and partly owing to the time lag between the death of needles and actual litterfall. To better evaluate the approach, model applications at other long-term observations sites in dry regions (e.g., in France or Italy; Reichstein et al., 2002) will be required.
Based on the results at the quite extreme site in Israel, we think that the model makes it possible to address the prime legacy impacts of drought stress by linking tree hydraulics to stress-induced leaf senescence and sapwood inactivation. Stress-induced structural adjustments have been identified as a stress response signal, resulting in a reduction in drought vulnerability, for instance, by decreasing the leaf area available for evaporation through hydraulic segmentation (Hochberg et al., 2017; Wolfe et al., 2016). On the other hand, tissue losses are costly and, if not replaced by reserves as soon as conditions are favorable again, can lead to a lower carbon “income”. Thus, the introduction of a mechanistic representation of sapwood and foliage mortality makes it possible to integrate hydraulic failure and carbon starvation into a unified model framework. On the one hand, the loss of hydraulic conductivity provides a means to trigger tree death directly based on a xylem damage threshold beyond which regrowth is impossible (Hammond et al., 2019; Trugman et al., 2018); on the other hand, an increasing carbon demand to regenerate conductive woody tissue leads to a supply shortfall for building new leaves (and roots), thereby reducing tree C uptake and potentially inducing a long-term decline process under recurrent drought stress. Whether (1) a tree is able to survive and recover or (2) the additional carbon demand results in its delayed death depends on the balance between resource supply and demand, which are both strongly influenced by stand structure, competition, and climatic boundary conditions (Camarero, 2021).
4.3 Further model developments
In order to better capture forest responses to increases in extreme events, process-based models, such as LandscapeDNDC, that integrate microenvironmental, physiological, and tree growth processes are important tools – not only to project carbon and water fluxes but also to implement mitigation efforts such as irrigation schemes into forest management. Here, we consider two main avenues for further model developments that include a better description of tree capacitance and an explicit characterization of tissue senescence responses to drought. Both are not only limited by modeling capabilities but also by limitations of our current understanding.
Our modified model allows for residual transpiration after full stomatal closure that originates from undefined water sources (as described above), such as tree capacitance or deep soil water access. While the importance of the presence such water reserves is generally undisputed (e.g., Gleason et al., 2014; Ripullone et al., 2020) and has recently been found to be a major determinant for survival or decline (Schmied et al., 2023), the supply of water from the plant tissue is nevertheless limited and, thus, needs to be constrained. The limitation of water storage depends on structural variables, namely stem dimension (Zweifel et al., 2020) and wood traits (Christoffersen et al., 2016), but its availability may also be described dynamically, e.g., as a function of xylem activity (e.g., water is released only after cavitation has occurred; Hölttä et al., 2009). In turn, the dehydration rate is determined by leaf leakiness, incomplete stomatal closure, and bark transpiration, among others (Duursma et al., 2019). Hence, the residual conductance gMIN and the stem water capacitance are key for tree survivorship as drought progresses (Blackman et al., 2019). As gMIN is not directly affected by the increase in water potential, the logical next step is to link the depletion of stem water to the process of hydraulic failure (Scholz et al., 2011). Alternatively, residual conductance and capacitance impacts may be implemented dynamically, for example, as a function of air temperature (Schuster et al., 2016), which has recently been realized in the SurEau model available within the medfate model package (De Cáceres et al., 2023). Besides this, to our knowledge, none of the processes mentioned above are considered in ecosystem or forest models yet.
Drought-induced defoliation has been addressed with the suggested model approach, but it is questionable if foliage dynamics should respond to sapwood dynamics following the pipe model theory (Yoda et al., 1963). The reasons for this are twofold. First, it is unlikely that irreversible xylem damage occurs at low water potentials, although the representation of PLC indicates damage, albeit very little. Thus, it would be logical to introduce some species-specific thresholds accounting for xylem structure and stability (Gauthey et al., 2022). Second, the current event chain does not allow for preventive leaf shedding. An alternative has been proposed with the “hydraulic fuse” hypothesis of Hochberg et al. (2017) that postulates a direct dependence of leaf shedding on plant water potential in order to capture the protective acclimation processes to drought (Wolfe et al., 2016; Li et al., 2020), with hydraulic segmentation among different tree compartments at its core. However, the benefit of losing leaves depends on the costs of rebuilding new ones as well as on the xylem hydraulic failure risk at faster declining water potentials. Thus the tendency to shed leaves protectively may be less expressed in trees with higher leaf longevity (Mediavilla et al., 2022) or in the exceptional case of trees being able to refill the embolized vessels (Choat et al., 2018). Moreover, we still lack empirical evidence of a mechanistic description that is general enough to link leaf senescence to xylem water potential decline. Deriving such relationships in a range of tree species would provide exciting possibilities for further model development. Aleppo pine, although considered to be a relatively drought-resistant species, has been shown to die due to hydraulic failure once a specific xylem disfunction threshold is reached (Morcillo et al., 2022).
The implementation of a hydraulic strategy into a process-based model allows for feedback responses and enables one to represent the individual responses of different species or evaluate the suitability of different leaf shedding strategies under future environmental conditions. Such an approach could be used to investigate, for example, the benefit of a high-resistance strategy with costly tissues (e.g., evergreen species and high wood density) compared with a highly vulnerable species with tissues that are less costly to reproduce (Saunders and Drew, 2022).
In order to capture drought impacts on forest functioning, models need to address both the quickly reversible physiological responses and the slowly reversible impacts from drought-induced functional impairment and structural damage. This is highly challenging since they need to be addressed in good agreement with the available observations while adhering to the maximum parsimony principia. Example simulations based on the presented hydraulic approach could demonstrate that early non-stomatal impacts are able to effectively reduce the desiccation process and delay the onset of more severe damage. Furthermore, increased resistance at the root–soil interface seems to support the principle of reducing the water uptake capacities to prevent more severe damage. Following this principle, we propose that the suggested simple representation of plant water potential is also able to drive long-term responses leading to structural adjustment and, thus, represent legacy impacts of drought on plant function. We consider it a prerequisite for a mechanistical representation of a progressive decline in tree functioning and consequent mortality following recurrent and intense droughts. The mechanistic link between stress-induced damage from hydraulic impairment and carbon allocation processes may be suitable to shed new light on the hydraulic failure and carbon starvation continuum resulting in tree mortality.
The LandscapeDNDC model source code for released versions of the model is permanently available online at the Radar4KIT database (https://doi.org/10.35097/438; Butterbach-Bahl et al., 2021). The published model version that has been used as the basis for the integration of the new hydraulic scheme is “win64 ldndc-1.30.4”, which can also be freely downloaded upon request from the following website: https://ldndc.imk-ifu.kit.edu/download/download-model.php (last access: 25 August 2023). The new model options described in this paper are documented in the online model description (https://ldndc.imk-ifu.kit.edu/doc/ldndc-doxy.php, last access: 25 August 2023). All input data to run the model are either freely available on the internet (see Sect. 2.2) or are provided in the Supplement (soil properties, initial stand properties, and species-specific parameters).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-21-2973-2024-supplement.
DNS, RG, and NKR designed the conceptual approach, determined the modeling setup, and led the manuscript writing. RG, DNS, and DK coded the hydraulic module into LandscapeDNDC. DNS performed the data analysis. DY, FT, UH, YW, and TK contributed to the field measurements at Yatir Forest and provided the observational data. All co-authors contributed to writing and revising the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors are grateful to Yakir Preisler, Eyal Rotenberg, and Josef Gruenzweig for field support.
This research has been supported by the German Research Foundation through the Emmy Noether Programme (grant nos. RU 1657/2-1 and RU 1657/2-2) and the German Israeli Foundation for Scientific Research and Development (grant nos. SCHM 2736/2-1 and YA 274/1-1). Nadine K. Ruehr has also been financially supported by the Helmholtz Initiative and Networking fund (grant no. W2/W3-156).
The article processing charges for this open-access publication were covered by the Karlsruhe Institute of Technology (KIT).
This paper was edited by David Medvigy and reviewed by Miquel de Cáceres and one anonymous referee.
Arend, M., Link, R. M., Zahnd, C., Hoch, G., Schuldt, B., and Kahmen, A.: Lack of hydraulic recovery as cause of post-drought foliage reduction and canopy decline in European beech, New Phytol., 234, 1195–1205, https://doi.org/10.1111/nph.18065, 2022.
Atzmon, N., Moshe, Y., and Schiller, G.: Ecophysiological response to severe drought in Pinus halepensis Mill. trees of two provenances, Plant Ecol., 171, 15–22, https://doi.org/10.1023/b:vege.0000029371.44518.38, 2004.
Aubinet, M., Grelle, A., Ibrom, A., Rannik, Ü., Moncrieff, J., Foken, T., Kowalski, A. S., Martin, P. H., Bernhofer, C., Clement, R., Elbers, J., Granier, A., Grünwald, T., Morgenstern, K., Pilegaard, K., Rebmann, C., Snijders, W., Valentini, R., and Vesala, T.: Estimates of the annual net carbon and water exchange of forests: the EUROFLUX methodology, Adv. Ecol. Res., 30, 113–175, https://doi.org/10.1016/S0065-2504(08)60018-5, 1999.
Barbeta, A. and Peñuelas, J.: Sequence of plant responses to droughts of different timescales: lessons from holm oak (Quercus ilex) forests, Plant Ecol. Divers., 9, 321–338, https://doi.org/10.1080/17550874.2016.1212288, 2016.
Barnard, D. M. and Bauerle, W. L.: The implications of minimum stomatal conductance on modeling water flux in forest canopies, J. Geophys. Res.-Biogeo., 118, 1322–1333, https://doi.org/10.1002/jgrg.20112, 2013.
Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, A. R., and Long, S. P.: Improved temperature response functions for models of Rubisco-limited photosynthesis, Plant Cell Environ., 24, 253–259, https://doi.org/10.1111/j.1365-3040.2001.00668.x, 2001.
Bigler, C., Gavin, D. G., Gunning, C., and Veblen, T. T.: Drought induces lagged tree mortality in a subalpine forest in the Rocky Mountains, Oikos, 116, 1983–1994, https://doi.org/10.1111/j.2007.0030-1299.16034.x, 2007.
Blackman, C. J., Li, X., Choat, B., Rymer, P. D., De Kauwe, M. G., Duursma, R. A., Tissue, D. T., and Medlyn, B. E.: Desiccation time during drought is highly predictable across species of Eucalyptus from contrasting climates, New Phytol., 224, 632–643, https://doi.org/10.1111/nph.16042, 2019.
Blackman, C. J., Billon, L.-M., Cartailler, J., Torres-Ruiz, J. M., and Cochard, H.: Key hydraulic traits control the dynamics of plant dehydration in four contrasting tree species during drought, Tree Physiol., 43, 1772–1783, https://doi.org/10.1093/treephys/tpad075, 2023.
Breshears, D. D., Carroll, C. J. W., Redmond, M. D., Wion, A. P., Allen, C. D., Cobb, N. S., Meneses, N., Field, J. P., Wilson, L. A., Law, D. J., McCabe, L. M., and Newell-Bauer, O.: A Dirty Dozen Ways to Die: Metrics and Modifiers of Mortality Driven by Drought and Warming for a Tree Species, Frontiers in Forests and Global Change, 1, 4, https://doi.org/10.3389/ffgc.2018.00004, 2018.
Brodribb, T. J. and Cochard, H.: Hydraulic failure defines the recovery and point of death in water-stressed conifers, Plant Physiol., 149, 575–584, https://doi.org/10.1104/pp.108.129783, 2009.
Brunner, I., Herzog, C., Dawes, M., Arend, M., and Sperisen, C.: How tree roots respond to drought, Front. Plant Sci., 6, 547, https://doi.org/10.3389/fpls.2015.00547, 2015.
Butterbach-Bahl, K., Grote, R., Haas, E., Kiese, R., Klatt, S., and Kraus, D.: LandscapeDNDC (v1.30.4), Karlsruhe Institute of Technology (KIT) [code], https://doi.org/10.35097/438, 2021.
Cade, S. M., Clemitshaw, K. C., Molina-Herrera, S., Grote, R., Haas, E., Wilkinson, M., Morison, J. I. L., and Yamulki, S.: Evaluation of LandscapeDNDC Model Predictions of CO2 and N2O Fluxes from an Oak Forest in SE England, Forests, 12, 1517, https://doi.org/10.3390/f12111517, 2021.
Camarero, J. J.: The drought-dieback-death conundrum in trees and forests, Plant Ecol. Divers., 14, 1–12, https://doi.org/10.1080/17550874.2021.1961172, 2021.
Cannell, M. G. R. and Thornley, J. H. M.: Modelling the components of plant respiration: Some guiding principles, Ann. Bot., 85, 45–54, https://doi.org/10.1006/anbo.1999.0996, 2000.
Cardoso, A. A., Batz, T. A., and McAdam, S. A. M.: Xylem Embolism Resistance Determines Leaf Mortality during Drought in Persea americana, Plant Physiol., 182, 547–554, https://doi.org/10.1104/pp.19.00585, 2020.
Carminati, A. and Javaux, M.: Soil Rather Than Xylem Vulnerability Controls Stomatal Response to Drought, Trends Plant Sci., 25, 868–880, https://doi.org/10.1016/j.tplants.2020.04.003, 2020.
Carminati, A., Vetterlein, D., Weller, U., Vogel, H.-J., and Oswald, S. E.: When Roots Lose Contact, Vadose Zone J., 8, 805–809, https://doi.org/10.2136/vzj2008.0147, 2009.
Choat, B., Brodribb, T. J., Brodersen, C. R., Duursma, R. A., López, R., and Medlyn, B. E.: Triggers of tree mortality under drought, Nature, 558, 531–539, https://doi.org/10.1038/s41586-018-0240-x, 2018.
Christoffersen, B. O., Gloor, M., Fauset, S., Fyllas, N. M., Galbraith, D. R., Baker, T. R., Kruijt, B., Rowland, L., Fisher, R. A., Binks, O. J., Sevanto, S., Xu, C., Jansen, S., Choat, B., Mencuccini, M., McDowell, N. G., and Meir, P.: Linking hydraulic traits to tropical forest function in a size-structured and trait-driven model (TFS v.1-Hydro), Geosci. Model Dev., 9, 4227–4255, https://doi.org/10.5194/gmd-9-4227-2016, 2016.
Cochard, H.: A new mechanism for tree mortality due to drought and heatwaves, Peer Community Journal, 1, e36, https://doi.org/10.24072/pcjournal.45, 2021.
Cochard, H., Pimont, F., Ruffault, J., and Martin-StPaul, N.: SurEau: a mechanistic model of plant water relations under extreme drought, Ann. Forest Sci., 78, 55, https://doi.org/10.1007/s13595-021-01067-y, 2021.
D'Andrea, E., Rezaie, N., Prislan, P., Gričar, J., Collalti, A., Muhr, J., and Matteucci, G.: Frost and drought: Effects of extreme weather events on stem carbon dynamics in a Mediterranean beech forest, Plant Cell Environ., 43, 2365–2379, https://doi.org/10.1111/pce.13858, 2020.
De Cáceres, M., Mencuccini, M., Martin-StPaul, N., Limousin, J.-M., Coll, L., Poyatos, R., Cabon, A., Granda, V., Forner, A., Valladares, F., and Martínez-Vilalta, J.: Unravelling the effect of species mixing on water use and drought stress in Mediterranean forests: A modelling approach, Agr. Forest Meteorol., 296, 108233, https://doi.org/10.1016/j.agrformet.2020.108233, 2021.
De Cáceres, M., Molowny-Horas, R., Cabon, A., Martínez-Vilalta, J., Mencuccini, M., García-Valdés, R., Nadal-Sala, D., Sabaté, S., Martin-StPaul, N., Morin, X., D'Adamo, F., Batllori, E., and Améztegui, A.: MEDFATE 2.9.3: a trait-enabled model to simulate Mediterranean forest function and dynamics at regional scales, Geosci. Model Dev., 16, 3165–3201, https://doi.org/10.5194/gmd-16-3165-2023, 2023.
De Kauwe, M. G., Kala, J., Lin, Y.-S., Pitman, A. J., Medlyn, B. E., Duursma, R. A., Abramowitz, G., Wang, Y.-P., and Miralles, D. G.: A test of an optimal stomatal conductance scheme within the CABLE land surface model, Geosci. Model Dev., 8, 431–452, https://doi.org/10.5194/gmd-8-431-2015, 2015a.
De Kauwe, M. G., Zhou, S.-X., Medlyn, B. E., Pitman, A. J., Wang, Y.-P., Duursma, R. A., and Prentice, I. C.: Do land surface models need to include differential plant species responses to drought? Examining model predictions across a mesic-xeric gradient in Europe, Biogeosciences, 12, 7503–7518, https://doi.org/10.5194/bg-12-7503-2015, 2015b.
De Kauwe, M. G., Medlyn, B. E., Ukkola, A. M., Mu, M., Sabot, M. E. B., Pitman, A. J., Meir, P., Cernusak, L., Rifai, S. W., Choat, B., Tissue, D. T., Blackman, C. J., Li, X., Roderick, M., and Briggs, P. R.: Identifying areas at risk of drought-induced tree mortality across South-Eastern Australia, Glob. Change Biol., 26, 5716–5733, https://doi.org/10.1111/gcb.15215, 2020.
Dewar, R., Mauranen, A., Mäkelä, A., Hölttä, T., Medlyn, B., and Vesala, T.: New insights into the covariation of stomatal, mesophyll and hydraulic conductances from optimization models incorporating nonstomatal limitations to photosynthesis, New Phytol., 217, 571–585, https://doi.org/10.1111/nph.14848, 2018.
Dewar, R., Hölttä, T., and Salmon, Y.: Exploring optimal stomatal control under alternative hypotheses for the regulation of plant sources and sinks, New Phytol., 233, 639–654, https://doi.org/10.1111/nph.17795, 2022.
Dirnböck, T., Kraus, D., Grote, R., Klatt, S., Kobler, J., Schindlbacher, A., Seidl, R., Thom, D., and Kiese, R.: Substantial understory contribution to the C sink of a European temperate mountain forest landscape, Landscape Ecol., 35, 483–499, https://doi.org/10.1007/s10980-019-00960-2, 2020.
Dormann, C. F., Calabrese, J. M., Guillera-Arroita, G., Matechou, E., Bahn, V., Bartoń, K., Beale, C. M., Ciuti, S., Elith, J., Gerstner, K., Guelat, J., Keil, P., Lahoz-Monfort, J. J., Pollock, L. J., Reineking, B., Roberts, D. R., Schröder, B., Thuiller, W., Warton, D. I., Wintle, B. A., Wood, S. N., Wüest, R. O., and Hartig, F.: Model averaging in ecology: a review of Bayesian, information-theoretic, and tactical approaches for predictive inference, Ecol. Monogr., 88, 485–504, https://doi.org/10.1002/ecm.1309, 2018.
Drake, J. E., Power, S. A., Duursma, R. A., Medlyn, B. E., Aspinwall, M. J., Choat, B., Creek, D., Eamus, D., Maier, C., Pfautsch, S., Smith, R. A., Tjoelker, M. G., and Tissue, D. T.: Stomatal and non-stomatal limitations of photosynthesis for four tree species under drought: A comparison of model formulations, Agr. Forest Meteorol., 247, 454–466, https://doi.org/10.1016/j.agrformet.2017.08.026, 2017.
Duursma, R. A., Blackman, C. J., Lopéz, R., Martin-StPaul, N. K., Cochard, H., and Medlyn, B. E.: On the minimum leaf conductance: its role in models of plant water use, and ecological and environmental controls, New Phytol., 221, 693–705, https://doi.org/10.1111/nph.15395, 2019.
Eller, C. B., Rowland, L., Oliveira, R. S., Bittencourt, P. R. L., Barros, F. V., da Costa, A. C. L., Meir, P., Friend, A. D., Mencuccini, M., Sitch, S., and Cox, P.: Modelling tropical forest responses to drought and El Niño with a stomatal optimization model based on xylem hydraulics, Philos. T. R. Soc. B, 373, 20170315, https://doi.org/10.1098/rstb.2017.0315, 2018.
Eller, C. B., Rowland, L., Mencuccini, M., Rosas, T., Williams, K., Harper, A., Medlyn, B. E., Wagner, Y., Klein, T., Teodoro, G. S., Oliveira, R. S., Matos, I. S., Rosado, B. H. P., Fuchs, K., Wohlfahrt, G., Montagnani, L., Meir, P., Sitch, S., and Cox, P. M.: Stomatal optimization based on xylem hydraulics (SOX) improves land surface model simulation of vegetation responses to climate, New Phytol., 226, 1622–1637, https://doi.org/10.1111/nph.16419, 2020.
Farquhar, G. D., Von Caemmerer, S., and Berry, J. A.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, https://doi.org/10.1007/BF00386231, 1980.
Feng, F., Wagner, Y., Klein, T., and Hochberg, U.: Xylem resistance to cavitation increases during summer in Pinus halepensis, Plant Cell Environ., 46, 1849–1859, https://doi.org/10.1111/pce.14573, 2023.
Flexas, J. and Medrano, H.: Drought-inhibition of photosynthesis in C3 plants: stomatal and non-stomatal limitations revisited, Ann. Bot., 89, 183–189, https://doi.org/10.1093/aob/mcf027, 2002.
Fontes, L., Bontemps, J.-D., Bugmann, H., Van Oijen, M., Gracia, C., Kramer, K., Lindner, M., Rötzer, T., and Skovsgaard, J. P.: Models for supporting forest management in a changing environment, For. Syst., 19, 8–29, https://doi.org/10.5424/fs/201019S-9315, 2010.
Fotelli, N. M., Korakaki, E., Paparrizos, A. S., Radoglou, K., Awada, T., and Matzarakis, A.: Environmental Controls on the Seasonal Variation in Gas Exchange and Water Balance in a Near-Coastal Mediterranean Pinus halepensis Forest, Forests, 10, 313, https://doi.org/10.3390/f10040313, 2019.
Galiano, L., Martínez-Vilalta, J., and Lloret, F.: Carbon reserves and canopy defoliation determine the recovery of Scots pine 4 yr after a drought episode, New Phytol., 190, 750–759, https://doi.org/10.1111/j.1469-8137.2010.03628.x, 2011.
Gallé, A., Haldimann, P., and Feller, U.: Photosynthetic performance and water relations in young pubescent oak (Quercus pubescens) trees during drought stress and recovery, New Phytol., 174, 799–810, https://doi.org/10.1111/j.1469-8137.2007.02047.x, 2007.
Gattmann, M., McAdam, S. A. M., Birami, B., Link, R., Nadal-Sala, D., Schuldt, B., Yakir, D., and Ruehr, N. K.: Anatomical adjustments of the tree hydraulic pathway decrease canopy conductance under long-term elevated CO2, Plant Physiol., 191, 252–264, https://doi.org/10.1093/plphys/kiac482, 2023.
Gauthey, A., Peters, J. M. R., Lòpez, R., Carins-Murphy, M. R., Rodriguez-Dominguez, C. M., Tissue, D. T., Medlyn, B. E., Brodribb, T. J., and Choat, B.: Mechanisms of xylem hydraulic recovery after drought in Eucalyptus saligna, Plant Cell Environ., 45, 1216–1228, https://doi.org/10.1111/pce.14265, 2022.
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B.: Bayesian Data Analysis, 3rd Edn., Chapman and Hall/CRC, New York, 675 pp., https://doi.org/10.1201/b16018, 2013.
Gleason, S. M., Blackman, C. J., Cook, A. M., Laws, C. A., and Westoby, M.: Whole-plant capacitance, embolism resistance and slow transpiration rates all contribute to longer desiccation times in woody angiosperms from arid and wet habitats, Tree Physiol., 34, 275–284, https://doi.org/10.1093/treephys/tpu001, 2014.
Gourlez de la Motte, L., Beauclaire, Q., Heinesch, B., Cuntz, M., Foltýnová, L., Sigut, L., Manca, G., Ballarin, I., Vincke, C., Roland, M., Ibrom, A., Lousteau, D., and Bernard, L.: Non-stomatal processes reduce gross primary productivity in temperate forest ecosystems during severe edaphic drought, Philos. T. R. Soc. B, 375, 20190527, https://doi.org/10.1098/rstb.2019.0527, 2020.
Granier, A. and Loustau, D.: Measuring and modelling the transpiration of a maritime pine canopy from sap-flow data, Agr. Forest Meteorol., 71, 61–81, https://doi.org/10.1016/0168-1923(94)90100-7, 1994.
Grote, R.: Integrating dynamic morphological properties into forest growth modeling. II. Allocation and mortality, Forest Ecol. Manage., 111, 193–210, https://doi.org/10.1016/S0378-1127(98)00328-4, 1998.
Grote, R. and Pretzsch, H.: A model for individual tree development based on physiological processes, Plant Biol., 4, 167–180, https://doi.org/10.1055/s-2002-25743, 2002.
Grote, R., Lavoir, A. V., Rambal, S., Staudt, M., Zimmer, I., and Schnitzler, J.-P.: Modelling the drought impact on monoterpene fluxes from an evergreen Mediterranean forest canopy, Oecologia, 160, 213–223, https://doi.org/10.1007/s00442-009-1298-9, 2009.
Grote, R., Korhonen, J., and Mammarella, I.: Challenges for evaluating process-based models of gas exchange at forest sites with fetches of various species, For. Syst., 20, 389–406, https://doi.org/10.5424/fs/20112003-11084, 2011.
Grünzweig, J. M., Lin, T., Rotenberg, E., Schwartz, A., and Yakir, D.: Carbon sequestration in arid-land forest, Glob. Change Biol., 9, 791–799, https://doi.org/10.1046/j.1365-2486.2003.00612.x, 2003.
Haas, E., Klatt, S., Fröhlich, A., Werner, C., Kiese, R., Grote, R., and Butterbach-Bahl, K.: LandscapeDNDC: A process model for simulation of biosphere-atmosphere-hydrosphere exchange processes at site and regional scale, Landscape Ecol., 28, 615–636, https://doi.org/10.1007/s10980-012-9772-x, 2013.
Hammond, W. M., Yu, K. L., Wilson, L. A., Will, R. E., Anderegg, W. R. L., and Adams, H. D.: Dead or dying? Quantifying the point of no return from hydraulic failure in drought-induced tree mortality, New Phytol., 223, 1834–1843, https://doi.org/10.1111/nph.15922, 2019.
Hammond, W. M., Johnson, D. M., and Meinzer, F. C.: A thin line between life and death: radial sap flux failure signals trajectory to tree mortality, Plant Cell Environ., 44, 1311–1314, https://doi.org/10.1111/pce.14033, 2021.
Hartig, F., Dislich, C., Wiegand, T., and Huth, A.: Technical Note: Approximate Bayesian parameterization of a process-based tropical forest model, Biogeosciences, 11, 1261–1272, https://doi.org/10.5194/bg-11-1261-2014, 2014.
Hartig, F., Minunno, F., Paul, S., Cameron, D., and Ott, T.: BayesianTools: General-purpose MCMC and SMC samplers and tools for Bayesian statistics, R package version 0.1.6, GitHub [code], https://github.com/florianhartig/BayesianTools (last access: 17 June 2024), 2019.
Haverd, V., Cuntz, M., Nieradzik, L. P., and Harman, I. N.: Improved representations of coupled soil–canopy processes in the CABLE land surface model (Subversion revision 3432), Geosci. Model Dev., 9, 3111–3122, https://doi.org/10.5194/gmd-9-3111-2016, 2016.
Helman, D., Lensky, I. M., Osem, Y., Rohatyn, S., Rotenberg, E., and Yakir, D.: A biophysical approach using water deficit factor for daily estimations of evapotranspiration and CO2 uptake in Mediterranean environments, Biogeosciences, 14, 3909–3926, https://doi.org/10.5194/bg-14-3909-2017, 2017.
Hochberg, U., Windt, C. W., Ponomarenko, A., Zhang, Y.-J., Gersony, J., Rockwell, F. E., and Holbrook, N. M.: Stomatal Closure, Basal Leaf Embolism, and Shedding Protect the Hydraulic Integrity of Grape Stems, Plant Physiol., 174, 764–775, https://doi.org/10.1104/pp.16.01816, 2017.
Holst, J., Grote, R., Offermann, C., Ferrio, J. P., Gessler, A., Mayer, H., and Rennenberg, H.: Water fluxes within beech stands in complex terrain, Int. J. Biometeorol., 54, 23–36, https://doi.org/10.1007/s00484-009-0248-x, 2010.
Hölttä, T., Cochard, H., Nikinmaa, E., and Mencuccini, M.: Capacitive effect of cavitation in xylem conduits: results from a dynamic model, Plant Cell Environ., 32, 10–21, https://doi.org/10.1111/j.1365-3040.2008.01894.x, 2009.
Hoshika, Y., Paoletti, E., Centritto, M., Gomes, M. T. G., Puértolas, J., and Haworth, M.: Species-specific variation of photosynthesis and mesophyll conductance to ozone and drought in three Mediterranean oaks, Physiol. Plantarum, 174, e13639, https://doi.org/10.1111/ppl.13639, 2022.
Huber, N., Bugmann, H., Cailleret, M., Bircher, N., and Lafond, V.: Stand-scale climate change impacts on forests over large areas: transient responses and projection uncertainties, Ecol. Appl., 31, e02313, https://doi.org/10.1002/eap.2313, 2021.
Infante, J. M., Damesin, C., Rambal, S., and Fernandez-Ales, R.: Modelling leaf gas exchange in holm-oak trees in southern Spain, Agr. Forest Meteorol., 95, 203–223, https://doi.org/10.1016/S0168-1923(99)00033-7, 1999.
IPCC: Climate Change and Land: an IPCC special report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems, edited by: Shukla, P. R., Skeg, J., Calvo Buendia, E., Masson‐Delmotte, V., Pörtner, H.-O., Roberts, D. C., Zhai, P., Slade, R., Connors, S. C., Van Diemen, S., Ferrat, M., Haughey, E., Luz, S., Pathak, M., Petzold, J., Portugal Pereira, J., Vyas, P., Huntley, E. J., Kissick, K., Belkacemi, M., and Malley, J. O., Intergovernmental Panel on Climate Change (IPCC), https://doi.org/10.25561/76618, 2019.
Kanety, T., Naor, A., Gips, A., Dicken, U., Lemcoff, J. H., and Cohen, S.: Irrigation influences on growth, yield, and water use of persimmon trees, Irrigation Sci., 32, 1–13, https://doi.org/10.1007/s00271-013-0408-y, 2014.
Kattge, J. and Knorr, W.: Temperature acclimation in a biochemical model of photosynthesis: a reanalysis of data from 36 species, Plant Cell Environ., 30, 1176–1190, https://doi.org/10.1111/j.1365-3040.2007.01690.x, 2007.
Keenan, T., Sabaté, S., and Gracia, C.: Soil water stress and coupled photosynthesis-conductance models: Bridging the gap between conflicting reports on the relative roles of stomatal, mesophyll conductance and biochemical limitations to photosynthesis, Agr. Forest Meteorol., 150, 443–453, 2010.
Kennedy, D., Swenson, S., Oleson, K. W., Lawrence, D. M., Fisher, R., Lola da Costa, A. C., and Gentine, P.: Implementing Plant Hydraulics in the Community Land Model, Version 5, J. Adv. Model. Earth Sy., 11, 485–513, https://doi.org/10.1029/2018MS001500, 2019.
Klein, T., Cohen, S., and Yakir, D.: Hydraulic adjustments underlying drought resistance of Pinus halepensis, Tree Physiol., 31, 637–648, https://doi.org/10.1093/treephys/tpr047, 2011.
Klein, T., Rotenberg, E., Cohen-Hilaleh, E., Raz-Yaseef, N., Tatarinov, F., Preisler, Y., Ogée, J., Cohen, S., and Yakir, D.: Quantifying transpirable soil water and its relations to tree water use dynamics in a water-limited pine forest, Ecohydrology, 7, 409–419, https://doi.org/10.1002/eco.1360, 2014.
Lei, G., Zeng, W., Huu Nguyen, T., Zeng, J., Chen, H., Kumar Srivastava, A., Gaiser, T., Wu, J., and Huang, J.: Relating soil-root hydraulic resistance variation to stomatal regulation in soil-plant water transport modeling, J. Hydrol., 617, 128879, https://doi.org/10.1016/j.jhydrol.2022.128879, 2023.
Lemaire, C., Blackman, C. J., Cochard, H., Menezes-Silva, P. E., Torres-Ruiz, J. M., and Herbette, S.: Acclimation of hydraulic and morphological traits to water deficit delays hydraulic failure during simulated drought in poplar, Tree Physiol., 41, 2008–2021, https://doi.org/10.1093/treephys/tpab086, 2021.
Leuning, R.: A critical appraisal of a combined stomatal-photosynthesis model for C3 plants, Plant Cell Environ., 18, 339–355, https://doi.org/10.1111/j.1365-3040.1995.tb00370.x, 1995.
Li, C., Frolking, S., and Frolking, T. A.: A model of nitrous oxide evolution from soil driven by rainfall events: 1. Model structure and Sensitivity, J. Geophys. Res., 97, 9759–9776, https://doi.org/10.1029/92JD00509, 1992.
Li, X., Smith, R., Choat, B., and Tissue, D. T.: Drought resistance of cotton (Gossypium hirsutum) is promoted by early stomatal closure and leaf shedding, Funct. Plant Biol., 47, 91–98, https://doi.org/10.1071/FP19093, 2020.
Li, X., Xi, B., Wu, X., Choat, B., Feng, J., Jiang, M., and Tissue, D.: Unlocking Drought-Induced Tree Mortality: Physiological Mechanisms to Modeling, Front. Plant Sci., 13, 835921, https://doi.org/10.3389/fpls.2022.835921, 2022.
Liang, X., Ye, Q., Liu, H., and Brodribb, T. J.: Wood density predicts mortality threshold for diverse trees, New Phytol., 229, 3053–3057, https://doi.org/10.1111/nph.17117, 2021.
Llusia, J., Roahtyn, S., Yakir, D., Rotenberg, E., Seco, R., Guenther, A., and Peñuelas, J.: Photosynthesis, stomatal conductance and terpene emission response to water availability in dry and mesic Mediterranean forests, Trees-Struct. Funct., 30, 749–759, https://doi.org/10.1007/s00468-015-1317-x, 2016.
Lobo-do-Vale, R., Rafael, T., Haberstroh, S., Werner, C., and Caldeira, M. C.: Shrub Invasion Overrides the Effect of Imposed Drought on the Photosynthetic Capacity and Physiological Responses of Mediterranean Cork Oak Trees, Plants, 12, 1636, https://doi.org/10.3390/plants12081636, 2023.
López, R., Cano, F. J., Martin-StPaul, N. K., Cochard, H., and Choat, B.: Coordination of stem and leaf traits define different strategies to regulate water loss and tolerance ranges to aridity, New Phytol., 230, 497–509, https://doi.org/10.1111/nph.17185, 2021.
Machado, R., Loram-Lourenço, L., Farnese, F. S., Alves, R. D. F. B., de Sousa, L. F., Silva, F. G., Filho, S. C. V., Torres-Ruiz, J. M., Cochard, H., and Menezes-Silva, P. E.: Where do leaf water leaks come from? Trade-offs underlying the variability in minimum conductance across tropical savanna species with contrasting growth strategies, New Phytol., 229, 1415–1430, https://doi.org/10.1111/nph.16941, 2021.
Mahnken, M., Cailleret, M., Collalti, A., Trotta, C., Biondo, C., D'Andrea, E., Dalmonech, D., Gina, M., Makela, A., Minunno, F., Peltoniemi, M., Trotsiuk, V., Nadal-Sala, D., Sabate, S., Vallet, P., Aussenac, R., Cameron, D., Bohn, F., Grote, R., and Augustynczik, A.: Accuracy, realism and general applicability of European forest models, Glob. Change Biol., 28, 6921–6943, https://doi.org/10.1111/gcb.16384, 2022.
Márquez, D. A., Stuart-Williams, H., and Farquhar, G. D.: An improved theory for calculating leaf gas exchange more precisely accounting for small fluxes, Nat. Plants, 7, 317–326, https://doi.org/10.1038/s41477-021-00861-w, 2021.
Maseyk, K. S., Lin, T., Rotenberg, E., Grünzweig, J. M., Schwartz, A., and Yakir, D.: Physiology-phenology interactions in a productive semi-arid pine forest, New Phytol., 178, 603–616, https://doi.org/10.1111/j.1469-8137.2008.02391.x, 2008.
McDowell, N., Pockman, W. T., Allen, C. D., Breshears, D. D., Cobb, N., Kolb, T., Plaut, J., Sperry, J., West, A., Williams, D. G., and Yepez, E. A.: Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought?, New Phytol., 178, 719–739, https://doi.org/10.1111/j.1469-8137.2008.02436.x, 2008.
McDowell, N. G., Sapes, G., Pivovaroff, A., Adams, H. D., Allen, C. D., Anderegg, W. R. L., Arend, M., Breshears, D. D., Brodribb, T., Choat, B., Cochard, H., De Cáceres, M., De Kauwe, M. G., Grossiord, C., Hammond, W. M., Hartmann, H., Hoch, G., Kahmen, A., Klein, T., Mackay, D. S., Mantova, M., Martínez-Vilalta, J., Medlyn, B. E., Mencuccini, M., Nardini, A., Oliveira, R. S., Sala, A., Tissue, D. T., Torres-Ruiz, J. M., Trowbridge, A. M., Trugman, A. T., Wiley, E., and Xu, C.: Mechanisms of woody-plant mortality under rising drought, CO2 and vapour pressure deficit, Nat. Rev. Earth Environ., 3, 294–308, https://doi.org/10.1038/s43017-022-00272-1, 2022.
Mediavilla, S., Martínez-Ortega, M., Andrés, S., Bobo, J., and Escudero, A.: Premature losses of leaf area in response to drought and insect herbivory through a leaf lifespan gradient, J. Forest. Res., 33, 39–50, https://doi.org/10.1007/s11676-021-01351-7, 2022.
Medlyn, B. E., Dreyer, E., Ellsworth, D., Forstreuter, M., Harley, P. C., Kirschbaum, M. U. F., Le Roux, X., Montpied, P., Strassmeyer, J., Walcroft, A., Wang, K., and Loustau, D.: Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data, Plant Cell Environ., 25, 1167–1179, https://doi.org/10.1046/j.1365-3040.2002.00891.x, 2002.
Mencuccini, M., Manzoni, S., and Christoffersen, B.: Modelling water fluxes in plants: from tissues to biosphere, New Phytol., 222, 1207–1222, https://doi.org/10.1111/nph.15681, 2019.
Mirfenderesgi, G., Matheny, A. M., and Bohrer, G.: Hydrodynamic trait coordination and cost–benefit trade-offs throughout the isohydric–anisohydric continuum in trees, Ecohydrology, 12, e2041, https://doi.org/10.1002/eco.2041, 2019.
Morcillo, L., Muñoz-Rengifo, J. C., Torres-Ruiz, J. M., Delzon, S., Moutahir, H., and Vilagrosa, A.: Post-drought conditions and hydraulic dysfunction determine tree resilience and mortality across Mediterranean Aleppo pine (Pinus halepensis) populations after an extreme drought event, Tree Physiol., 42, 1364–1376, 10.1093/treephys/tpac001, 2022.
Muggeo, V. M. R.: Interval estimation for the breakpoint in segmented regression: a smoothed score-based approach, Aust. NZ J. Stat., 59, 311–322, https://doi.org/10.1111/anzs.12200, 2017.
Müller, L. M. and Bahn, M.: Drought legacies and ecosystem responses to subsequent drought, Glob. Change Biol., 28, 5086–5103, https://doi.org/10.1111/gcb.16270, 2022.
Nadal-Sala, D., Grote, R., Birami, B., Knüver, T., Schwarz, S., and Ruehr, N.: Leaf shedding and non-stomatal limitations of photosynthesis improve hydraulic resistance of Scots pine saplings during severe drought stress, Front. Plant Sci., 12, 715127, https://doi.org/10.3389/fpls.2021.715127 2021a.
Nadal-Sala, D., Grote, R., Birami, B., Lintunen, A., Mammarella, I., Preisler, Y., Rotenberg, E., Salmon, Y., Tatrinov, F., Yakir, D., and Ruehr, N.: Assessing model performance via the most limiting environmental driver (MLED) in two differently stressed pine stands, Ecol. Appl., 31, e02312, https://doi.org/10.1002/eap.2312, 2021b.
Nardini, A., Casolo, V., Dal Borgo, A., Savi, T., Stenni, B., Bertoncin, P., Zini, L., and McDowell, N. G.: Rooting depth, water relations and non-structural carbohydrate dynamics in three woody angiosperms differentially affected by an extreme summer drought, Plant Cell Environ., 39, 618–627, https://doi.org/10.1111/pce.12646, 2016.
Navas, M.-L., Ducout, B., Roumet, C., Richarte, J., Garnier, J., and Garnier, E.: Leaf life span, dynamics and construction cost of species from Mediterranean old-fields differing in successional status, New Phytol., 159, 213–228, https://doi.org/10.1046/j.1469-8137.2003.00790.x, 2003.
Neufeld, H. S., Grantz, D. A., Meinzer, F. C., Goldstein, G., Crisosto, G. M., and Crisosto, C.: Genotypic Variability in Vulnerability of Leaf Xylem to Cavitation in Water-Stressed and Well-Irrigated Sugarcane, Plant Physiol., 100, 1020–1028, https://doi.org/10.1104/pp.100.2.1020, 1992.
Norby, R. J., DeLucia, E. H., Gielen, B., Calfapietra, C., Giardina, C. P., King, J. S., Ledford, J., McCarthy, H. R., Moore, D. J. P., Ceulemans, R., De Angelis, P., Finzi, A. C., Karnosky, D. F., Kubiske, M. E., Lukac, M., Pregitzer, K. S., Scarascia-Mugnozza, G. E., Schlesinger, W. H., and Oren, R.: Forest response to elevated CO2 is conserved across a broad range of productivity, P. Natl. Acad. Sci. USA, 102, 18052–18056, https://doi.org/10.1073/pnas.0509478102, 2005.
North, G. B. and Nobel, P. S.: Changes in Hydraulic Conductivity and Anatomy Caused by Drying and Rewetting Roots of Agave deserti (Agavaceae), Am. J. Bot., 78, 906–915, https://doi.org/10.2307/2445169, 1991.
Novick, K. A., Ficklin, D. L., Stoy, P. C., Williams, C. A., Bohrer, G., Oishi, A. C., Papuga, S. A., Blanken, P. D., Noormets, A., Sulman, B. N., Scott, R. L., Wang, L., and Phillips, R. P.: The increasing importance of atmospheric demand for ecosystem water and carbon fluxes, Nat. Clim. Change, 6, 1023–1027, https://doi.org/10.1038/nclimate3114, 2016.
Novick, K. A., Ficklin, D. L., Baldocchi, D., Davis, K. J., Ghezzehei, T. A., Konings, A. G., MacBean, N., Raoult, N., Scott, R. L., Shi, Y., Sulman, B. N., and Wood, J. D.: Confronting the water potential information gap, Nat. Geosci., 15, 158–164, https://doi.org/10.1038/s41561-022-00909-2, 2022.
Oliveras, I., Martínez-Vilalta, J., Jimenez-Ortiz, T., José Lledó, M., Escarré, A., and Piñol, J.: Hydraulic properties of Pinus halepensis, Pinus pinea and Tetraclinis articulata in a dune ecosystem of Eastern Spain, Plant Ecol., 169, 131–141, https://doi.org/10.1023/A:1026223516580, 2003.
Paschalis, A., De Kauwe, M. G., Sabot, M., and Fatichi, S.: When do plant hydraulics matter in terrestrial biosphere modelling?, Glob. Change Biol., 30, e17022, https://doi.org/10.1111/gcb.17022, 2024.
Pozner, E., Bar-On, P., Livne-Luzon, S., Moran, U., Tsamir-Rimon, M., Dener, E., Schwartz, E., Rotenberg, E., Tatarinov, F., Preisler, Y., Zecharia, N., Osem, Y., Yakir, D., and Klein, T.: A hidden mechanism of forest loss under climate change: The role of drought in eliminating forest regeneration at the edge of its distribution, Forest Ecol. Manage., 506, 119966, https://doi.org/10.1016/j.foreco.2021.119966, 2022.
Preisler, Y., Tatarinov, F., Grünzweig, J. M., Bert, D., Ogée, J., Wingate, L., Rotenberg, E., Rohatyn, S., Her, N., Moshe, I., Klein, T., and Yakir, D.: Mortality versus survival in drought-affected Aleppo pine forest depends on the extent of rock cover and soil stoniness, Funct. Ecol., 33, 901–912, https://doi.org/10.1111/1365-2435.13302, 2019.
Preisler, Y., Hölttä, T., Grünzweig, J. M., Oz, I., Tatarinov, F., Ruehr, N. K., Rotenberg, E., and Yakir, D.: The importance of tree internal water storage under drought conditions, Tree Physiol., 42, 771–783, https://doi.org/10.1093/treephys/tpab144, 2022.
Pretzsch, H. and Grote, R.: Tree mortality. Revisited under changed climatic and silvicultural conditions, in: Progress in Botany, edited by: Cánovas, F. M., Lüttge, U., Risueño, M. C., and Pretzsch, H., Springer, Cham, 351–393, https://doi.org/10.1007/124_2023_69, 2024.
Qubaja, R., Amer, M., Tatarinov, F., Rotenberg, E., Preisler, Y., Sprintsin, M., and Yakir, D.: Partitioning evapotranspiration and its long-term evolution in a dry pine forest using measurement-based estimates of soil evaporation, Agr. Forest Meteorol., 281, 107831, https://doi.org/10.1016/j.agrformet.2019.107831, 2020.
Rahimi, J., Ago, E. E., Ayantunde, A., Berger, S., Bogaert, J., Butterbach-Bahl, K., Cappelaere, B., Cohard, J.-M., Demarty, J., Diouf, A. A., Falk, U., Haas, E., Hiernaux, P., Kraus, D., Roupsard, O., Scheer, C., Srivastava, A. K., Tagesson, T., and Grote, R.: Modeling gas exchange and biomass production in West African Sahelian and Sudanian ecological zones, Geosci. Model Dev., 14, 3789–3812, https://doi.org/10.5194/gmd-14-3789-2021, 2021.
Raz-Yaseef, N., Yakir, D., Rotenberg, E., Schiller, G., and Cohen, S.: Ecohydrology of a semi-arid forest: partitioning among water balance components and its implications for predicted precipitation changes, Ecohydrology, 3, 143–154, https://doi.org/10.1002/eco.65, 2010.
R Core Team: R: A language and environment for statistical computing. R Foundation for Statistical Computing, R Foundation for Statistical Computing [code], Vienna, Austria, https://www.R-project.org (last access: 17 June 2024), 2021.
Rehschuh, R., Cecilia, A., Zuber, M., Faragó, T., Baumbach, T., Hartmann, H., Jansen, S., Mayr, S., and Ruehr, N. K.: Drought-induced xylem embolism limits the recovery of leaf gas exchange in Scots pine, Plant Physiol., 184, 852–864, https://doi.org/10.1104/pp.20.00407, 2020.
Reichstein, M., Tenhunen, J. D., Roupsard, O., Ourcival, J.-M., Rambal, S., Dore, S., and Valentini, R.: Ecosystem respiration in two Mediterranean evergreen Holm Oak forests: drought effects and decomposition dynamics, Funct. Ecol., 16, 27–39, https://doi.org/10.1046/j.0269-8463.2001.00597.x, 2002.
Ripullone, F., Camarero, J. J., Colangelo, M., and Voltas, J.: Variation in the access to deep soil water pools explains tree-to-tree differences in drought-triggered dieback of Mediterranean oaks, Tree Physiol., 40, 591–604, https://doi.org/10.1093/treephys/tpaa026, 2020.
Rodriguez-Dominguez, C. M., and Brodribb, T. J.: Declining root water transport drives stomatal closure in olive under moderate water stress, New Phytol., 225, 126–134, https://doi.org/10.1111/nph.16177, 2020.
Rohatyn, S.: Alterations in ecosystem water cycle associated with land-use changes under different precipitation regimes, M.Sc., Faculty of Agriculture, Food and Environment, The Hebrew University of Jerusalem, Rehovot, 70 pp., 2017.
Ruehr, N., Grote, R., Mayr, S., and Arneth, A.: Beyond the extreme: recovery of carbon and water relations in woody plants following heat and drought stress, Tree Physiol., 39, 1285–1299, https://doi.org/10.1093/treephys/tpz032, 2019.
Ruffault, J., Pimont, F., Cochard, H., Dupuy, J.-L., and Martin-StPaul, N.: SurEau-Ecos v2.0: a trait-based plant hydraulics model for simulations of plant water status and drought-induced mortality at the ecosystem level, Geosci. Model Dev., 15, 5593–5626, https://doi.org/10.5194/gmd-15-5593-2022, 2022.
Rukh, S., Sanders, T. G. M., Krüger, I., Schad, T., and Bolte, A.: Distinct Responses of European Beech (Fagus sylvatica L.) to Drought Intensity and Length – A Review of the Impacts of the 2003 and 2018–2019 Drought Events in Central Europe, Forests, 14, 248, https://doi.org/10.3390/f14020248, 2023.
Ryan, M. G.: Tree responses to drought, Tree Physiol., 31, 237–239, https://doi.org/10.1093/treephys/tpr022, 2011.
Sabot, M. E. B., De Kauwe, M. G., Pitman, A. J., Medlyn, B. E., Ellsworth, D. S., Martin-StPaul, N. K., Wu, J., Choat, B., Limousin, J.-M., Mitchell, P. J., Rogers, A., and Serbin, S. P.: One Stomatal Model to Rule Them All? Toward Improved Representation of Carbon and Water Exchange in Global Models, J. Adv. Model. Earth Sy., 14, e2021MS002761, https://doi.org/10.1029/2021MS002761, 2022.
Salmon, Y., Lintunen, A., Dayet, A., Chan, T., Dewar, R., Vesala, T., and Hölttä, T.: Leaf carbon and water status control stomatal and nonstomatal limitations of photosynthesis in trees, New Phytol., 226, 690–703, https://doi.org/10.1111/nph.16436, 2020.
Saunders, A. and Drew, D. M.: Measurements done on excised stems indicate that hydraulic recovery can be an important strategy used by Eucalyptus hybrids in response to drought, Trees-Struct. Funct., 36, 139–151, doi10.1007/s00468-021-02188-7, 2022.
Schiller, G.: The case of Yatir Forest, in: Forest Management and the Water Cycle, edited by: Bredemeier, M., Cohen, S., Godbold, D. L., Lode, E., Pichler, V., and Schleppi, P., Ecological Studies, Springer Netherlands, 163–186, https://doi.org/10.1007/978-90-481-9834-4_9, 2010.
Schmied, G., Pretzsch, H., Ambs, D., Uhl, E., Schmucker, J., Fäth, J., Biber, P., Hoffmann, Y.-D., Šeho, M., Mellert, K. H., and Hilmers, T.: Rapid beech decline under recurrent drought stress: Individual neighborhood structure and soil properties matter, Forest Ecol. Manage., 545, 121305, https://doi.org/10.1016/j.foreco.2023.121305, 2023.
Scholz, F. G., Phillips, N. G., Bucci, S. J., Meinzer, F. C., and Goldstein, G.: Hydraulic Capacitance: Biophysics and Functional Significance of Internal Water Sources in Relation to Tree Size, in: Size- and Age-Related Changes in Tree Structure and Function, edited by: Meinzer, F. C., Lachenbruch, B., and Dawson, T. E., Springer Netherlands, Dordrecht, 341–361, 2011.
Schuster, A.-C., Burghardt, M., Alfarhan, A., Bueno, A., Hedrich, R., Leide, J., Thomas, J., and Riederer, M.: Effectiveness of cuticular transpiration barriers in a desert plant at controlling water loss at high temperatures, AoB PLANTS, 8, plw027, https://doi.org/10.1093/aobpla/plw027, 2016.
Shachnovich, Y., Berliner, P. R., and Bar, P.: Rainfall interception and spatial distribution of throughfall in a pine forest planted in an arid zone, J. Hydrol., 349, 168–177, https://doi.org/10.1016/j.jhydrol.2007.10.051, 2008.
Shinozaki, K. and Yoda, K.: A quantitative analysis of plant form – the pipe model theory. I. Basic analyses, Japanese Journal of Ecology, 14, 97–105, https://doi.org/10.18960/SEITAI.14.3_97, 1964.
Sperry, J. S., Adler, F. R., Campbell, G. S., and Comstock, J. P.: Limitation of plant water use by rhizosphere and xylem conductance: results from a model, Plant Cell Environ., 21, 347–359, https://doi.org/10.1046/j.1365-3040.1998.00287.x, 1998.
Sperry, J. S., Venturas, M. D., Anderegg, W. R. L., Mencuccini, M., Mackay, D. S., Wang, Y., and Love, D. M.: Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost, Plant Cell Environ., 40, 816–830, https://doi.org/10.1111/pce.12852, 2017.
Tatarinov, F., Rotenberg, E., Maseyk, K., Ogée, J., Klein, T., and Yakir, D.: Resilience to seasonal heat wave episodes in a Mediterranean pine forest, New Phytol., 210, 485–496, https://doi.org/10.1111/nph.13791, 2016.
ter Braak, C. J. F. and Vrugt, J. A.: Differential Evolution Markov Chain with snooker updater and fewer chains, Stat. Comput., 18, 435–446, https://doi.org/10.1007/s11222-008-9104-9, 2008.
Thom, D., Buras, A., Heym, M., Klemmt, H.-J., and Wauer, A.: Varying growth response of Central European tree species to the extraordinary drought period of 2018–2020, Agr. Forest Meteorol., 338, 109506, https://doi.org/10.1016/j.agrformet.2023.109506, 2023.
Tissue, D. T., Griffin, K. L., Turnbull, M. H., and Whitehead, D.: Stomatal and non-stomatal limitations to photosynthesis in four tree species in a temperate rainforest dominated by Dacrydium cupressinum in New Zealand, Tree Physiol., 25, 447–456, https://doi.org/10.1093/treephys/25.4.447, 2005.
Torres-Ruiz, J. M., Cochard, H., Delzon, S., Boivin, T., Burlett, R., Cailleret, M., Corso, D., Delmas, C. E. L., De Caceres, M., Diaz-Espejo, A., Fernández-Conradi, P., Guillemot, J., Lamarque, L. J., Limousin, J.-M., Mantova, M., Mencuccini, M., Morin, X., Pimont, F., De Dios, V. R., Ruffault, J., Trueba, S., and Martin-StPaul, N. K.: Plant hydraulics at the heart of plant, crops and ecosystem functions in the face of climate change, New Phytol., 241, 984–999, https://doi.org/10.1111/nph.19463, 2024.
Trugman, A. T.: Integrating plant physiology and community ecology across scales through trait-based models to predict drought mortality, New Phytol., 234, 21–27, https://doi.org/10.1111/nph.17821, 2022.
Trugman, A. T., Detto, M., Bartlett, M. K., Medvigy, D., Anderegg, W. R. L., Schwalm, C., Schaffer, B., and Pacala, S. W.: Tree carbon allocation explains forest drought-kill and recovery patterns, Ecol. Lett., 21, 1552–1560, https://doi.org/10.1111/ele.13136, 2018.
Trugman, A. T., Anderegg, L. D. L., Sperry, J. S., Wang, Y., Venturas, M., and Anderegg, W. R. L.: Leveraging plant hydraulics to yield predictive and dynamic plant leaf allocation in vegetation models with climate change, Glob. Change Biol., 25, 4008–4021, https://doi.org/10.1111/gcb.14814, 2019.
Tschumi, E., Lienert, S., van der Wiel, K., Joos, F., and Zscheischler, J.: The effects of varying drought-heat signatures on terrestrial carbon dynamics and vegetation composition, Biogeosciences, 19, 1979–1993, https://doi.org/10.5194/bg-19-1979-2022, 2022.
Tuzet, A., Perrier, A., and Leuning, R.: A coupled model of stomatal conductance, photosynthesis and transpiration, Plant Cell Environ., 26, 1097–1116, https://doi.org/10.1046/j.1365-3040.2003.01035.x, 2003.
Tuzet, A., Granier, A., Betsch, P., Peiffer, M., and Perrier, A.: Modelling hydraulic functioning of an adult beech stand under non-limiting soil water and severe drought condition, Ecol. Model., 348, 56–77, https://doi.org/10.1016/j.ecolmodel.2017.01.007, 2017.
Tyree, M. T. and Sperry, J. S.: Vulnerability of Xylem to Cavitation and Embolism, Annu. Rev. Plant Physiol., 40, 19–36, https://doi.org/10.1146/annurev.pp.40.060189.000315, 1989.
Tyree, M. T. and Yang, S.: Water-storage capacity of Thuja, Tsuga and Acer stems measured by dehydration isotherms, Planta, 182, 420–426, https://doi.org/10.1007/BF02411394, 1990.
Uddling, J., Hall, M., Wallin, G., and Karlsson, P. E.: Measuring and modelling stomatal conductance and photosynthesis in mature birch in Sweden, Agr. Forest Meteorol., 132, 115–131, https://doi.org/10.1016/j.agrformet.2005.07.004, 2005.
Ungar, E. D., Rotenberg, E., Raz-Yaseef, N., Cohen, S., Yakir, D., and Schiller, G.: Transpiration and annual water balance of Aleppo pine in a semiarid region: Implications for forest management, Forest Ecol. Manage., 298, 39–51, https://doi.org/10.1016/j.foreco.2013.03.003, 2013.
Van Genuchten, M. T.: A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., 44, 892–898, https://doi.org/10.2136/sssaj1980.03615995004400050002x, 1980.
Van Genuchten, M. T., Leij, F. J., and Yates, S. R.: The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils, U.S. Salinity Laboratory, U.S. Department of Agriculture, Riverside, California, Research Report, 93, 1991.
Wagner, Y., Feng, F., Yakir, D., Klein, T., and Hochberg, U.: In situ, direct observation of seasonal embolism dynamics in Aleppo pine trees growing on the dry edge of their distribution, New Phytol., 235, 1344–1350, https://doi.org/10.1111/nph.18208, 2022.
Walthert, L., Ganthaler, A., Mayr, S., Saurer, M., Waldner, P., Walser, M., Zweifel, R., and von Arx, G.: From the comfort zone to crown dieback: Sequence of physiological stress thresholds in mature European beech trees across progressive drought, Sci. Total Environ., 753, 141792, https://doi.org/10.1016/j.scitotenv.2020.141792, 2021.
Wang, H., Gitelson, A., Sprintsin, M., Rotenberg, E., and Yakir, D.: Ecophysiological adjustments of a pine forest to enhance early spring activity in hot and dry climate, Environ. Res. Lett., 15, 114054, https://doi.org/10.1088/1748-9326/abc2f9, 2020.
Warm Winter 2020 Team and ICOS Ecosystem Thematic Centre: Warm Winter 2020 ecosystem eddy covariance flux product for 73 stations in FLUXNET-Archive format – release 2022-1 (Version 1.0), ICOS Carbon Portal [data set], https://doi.org/10.18160/2G60-ZHAK, 2022.
Whitehead, D., Edwards, W. R. N., and Jarvis, P. G.: Conducting sapwood area, foliage area, and permeability in mature trees of Picea sitchensis and Pinus contorta, Can. J. Forest Res., 14, 940–947, https://doi.org/10.1139/x84-166, 1984.
Wilson, K. B., Baldocchi, D. D., and Hanson, P. J.: Quantifying stomatal and non-stomatal limitations to carbon assimilation resulting from leaf aging and drought in mature deciduous tree species, Tree Physiol., 20, 787–797, https://doi.org/10.1093/treephys/20.12.787, 2000.
Wolfe, B. T., Sperry, J. S., and Kursar, T. A.: Does leaf shedding protect stems from cavitation during seasonal droughts? A test of the hydraulic fuse hypothesis, New Phytol., 212, 1007–1018, https://doi.org/10.1111/nph.14087, 2016.
Xu, X., Medvigy, D., Powers, J. S., Becknell, J. M., and Guan, K.: Diversity in plant hydraulic traits explains seasonal and inter-annual variations of vegetation dynamics in seasonally dry tropical forests, New Phytol., 212, 80–95, https://doi.org/10.1111/nph.14009, 2016.
Yang, J., Duursma, R. A., De Kauwe, M. G., Kumarathunge, D., Jiang, M., Mahmud, K., Gimeno, T. E., Crous, K. Y., Ellsworth, D. S., Peters, J., Choat, B., Eamus, D., and Medlyn, B. E.: Incorporating non-stomatal limitation improves the performance of leaf and canopy models at high vapour pressure deficit, Tree Physiol., 39, 1961–1974, https://doi.org/10.1093/treephys/tpz103, 2019.
Yang, Y., Ma, X., Yan, L., Li, Y., Wei, S., Teng, Z., Zhang, H., Tang, W., Peng, S., and Li, Y.: Soil–root interface hydraulic conductance determines responses of photosynthesis to drought in rice and wheat, Plant Physiol., 194, 376–390, https://doi.org/10.1093/plphys/kiad498, 2023.
Yao, Y., Joetzjer, E., Ciais, P., Viovy, N., Cresto Aleina, F., Chave, J., Sack, L., Bartlett, M., Meir, P., Fisher, R., and Luyssaert, S.: Forest fluxes and mortality response to drought: model description (ORCHIDEE-CAN-NHA r7236) and evaluation at the Caxiuanã drought experiment, Geosci. Model Dev., 15, 7809–7833, https://doi.org/10.5194/gmd-15-7809-2022, 2022.
Yoda, K., Kira, T., Ogawa, H., and Hozumi, K.: Self-thinning in overcrowded pure stands under cultivated and natural conditions, J. Mol. Biol., 14, 107–129, 1963.
Zhou, S., Duursma, R. A., Medlyn, B. E., Kelly, J. W. G., and Prentice, I. C.: How should we model plant responses to drought? An analysis of stomatal and non-stomatal responses to water stress, Agr. Forest Meteorol., 182–183, 204–214, https://doi.org/10.1016/j.agrformet.2013.05.009, 2013.
Ziemińska, K., Rosa, E., Gleason, S. M., and Holbrook, N. M.: Wood day capacitance is related to water content, wood density, and anatomy across 30 temperate tree species, Plant Cell Environ., 43, 3048–3067, https://doi.org/10.1111/pce.13891, 2020.
Zinsser, J.: Vertical distribution of plant area density and canopy surface temperature of a semi-arid forest, Yatir Israel, Master, Institute of Meteorology and Climate Research – Atmospheric Environmental Research Karlsruhe Institute for Technology, Karlsruhe, 94 pp., 2017.
Zweifel, R., Etzold, S., Haeni, M., Feichtinger, L., Meusburger, K., Knuesel, S., von Arx, G., Hug, C., De Girardi, N., and Giuggiola, A.: Dendrometer, sap flow, meteorology and soil volumetric water content measurements during a long-term irrigation experiment in a Scots pine forest at Pfynwald, Swiss Rhone valley (2011–2017), PANGAEA, https://doi.org/10.1594/PANGAEA.918631, 2020.