the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Position-specific kinetic isotope effects for nitrous oxide: a new expansion of the Rayleigh model
Wenjuan Ma
Nathaniel E. Ostrom
Nitrous oxide (N2O) is a potent greenhouse gas and the most significant anthropogenic ozone-depleting substance currently being emitted. A major source of anthropogenic N2O emissions is the microbial conversion of fixed nitrogen species from fertilizers in agricultural soils. Thus, understanding the enzymatic mechanisms by which microbes produce N2O has environmental significance. Measurement of the 15N 14N isotope ratios of N2O produced by purified enzymes or axenic microbial cultures is a promising technique for studying N2O biosynthesis. Typically, N2O-producing enzymes combine nitrogen atoms from two identical substrate molecules (NO or NH2OH). Position-specific isotope analysis of the central (Nα) and outer (Nβ) nitrogen atoms in N2O enables the determination of the individual kinetic isotope effects (KIEs) for Nα and Nβ, providing mechanistic insight into the incorporation of each nitrogen atom. Previously, position-specific KIEs (and fractionation factors) were quantified using the Rayleigh distillation equation, i.e., via linear regression of δ15Nα or δ15Nβ against [], where f is the fraction of substrate remaining in a closed system. This approach, however, is inaccurate for Nα and Nβ because it does not account for fractionation at Nα affecting the isotopic composition of substrate available for incorporation into the β position (and vice versa). Therefore, we developed a new expansion of the Rayleigh model that includes specific terms for fractionation at the individual N2O nitrogen atoms. By applying this Expanded Rayleigh model to a variety of simulated N2O synthesis reactions with different combinations of normal, inverse, and/or no KIEs at Nα and Nβ, we demonstrate that our new model is both accurate and robust. We also applied this new model to two previously published datasets describing N2O production from NH2OH oxidation in a methanotroph culture (Methylosinus trichosporium) and N2O production from NO by a purified Histoplasma capsulatum (fungal) P450 NOR, demonstrating that the Expanded Rayleigh model is a useful tool in calculating position-specific fractionation for N2O synthesis.
- Article
(1029 KB) - Full-text XML
-
Supplement
(1808 KB) - BibTeX
- EndNote
Nitrous oxide (N2O) is a greenhouse gas with a global warming potential approximately 300 times greater than that of CO2 (100-year time horizon) (Stocker et al., 2013). In addition, N2O is the primary source of stratospheric NOx and is therefore a significant ozone-depleting substance (Ravishankara et al., 2009). Levels of atmospheric N2O are increasing by an average of ∼ 0.29 % annually (Lan et al., 2022), primarily due to rising anthropogenic N2O emissions, which comprise approximately 40 % of annual global N2O emissions (Tian et al., 2020). In the US, at least 70 % of annual anthropogenic N2O emissions result from agricultural practices, such as the application of nitrogen-containing fertilizer (e.g., ammonium and nitrate) to the field. Soil microbes can metabolize these nitrogen-containing compounds through processes such as nitrification and denitrification, producing N2O either as a side product (nitrification), intermediate (complete denitrification), or end product (incomplete denitrification) (Kuypers et al., 2018). Understanding the underlying mechanisms of N2O production for each metabolic pathway is critical for tracing and ultimately mitigating environmental N2O emissions.
Many different types of enzymes catalyze N2O formation in microbes. Examples of N2O-producing enzyme families include cytochrome P460 (Caranto et al., 2016) and hydroxylamine oxidoreductase (Yamazaki et al., 2014) in nitrifiers, “bacterial” nitric oxide reductases (cNOR, qNOR, etc.) found in bacterial and archaeal denitrifiers, and fungal nitric oxide reductase (P450 NOR) from fungal denitrifiers (Yamazaki et al., 2014; Yang et al., 2014; Lehnert et al., 2018) as well as detoxifying enzymes such as flavodiiron nitric oxide reductases (Romão et al., 2016). Distinguishing among different sources of N2O in the environment and identifying the relative contribution of each source are challenging and require a combination of analytical methods. One useful technique for N2O source apportionment is stable isotope analysis. This method takes advantage of the fact that many physical and chemical processes, such as enzyme-catalyzed reactions, generally have slightly different rate constants for different isotopes of the same element (e.g., 14N and 15N). In an isotopically sensitive process, the isotope that reacts faster will be more prevalent (enriched) in the product relative to the substrate. Different processes generally have distinct patterns of isotopic enrichment and thus have unique isotopic signatures.
Stable isotope analysis is particularly useful for studying N2O synthesis because the central (Nα) and outer (Nβ) nitrogen atoms in N2O are non-equivalent and non-exchangeable, and the isotope ratios of these two nitrogen atoms can be determined individually (Toyoda and Yoshida, 1999). These position-specific isotope ratios can aid in identifying which enzyme produces or which enzymes produce N2O in microbial cultures under varying growth conditions (Sutka et al., 2003, 2004, 2006, 2008; Toyoda et al., 2005; Frame and Casciotti, 2010; Yamazaki et al., 2014; Haslun et al., 2018). Additionally, because isotopic enrichment is typically dependent on the rate-limiting step(s) of the enzyme-catalyzed reaction, analyzing the isotopic signatures of individual enzymes can provide valuable insights into each enzyme's catalytic mechanism.
Isotopic enrichment for a specific process can be quantified by determining a parameter known as the fractionation factor (). For reactions with first-order kinetics, is equal to the rate constant of the heavy isotope (kH) divided by the rate constant for the light isotope (kL). Because values are typically close to 1, is often converted to its per mil equivalent, the enrichment factor () (Mariotti et al., 1981).
Notably, is also equal to the inverse of the kinetic isotope effect (KIE =kL/kH). The KIE and fractionation factor values for a specific reaction describe the isotopic preference of that reaction. Most commonly, the light isotope reacts faster than the heavy isotope (i.e., KIE >1), which is designated as a normal KIE. Conversely, when the heavy isotope reacts faster (KIE <1), the reaction is said to have an inverse KIE. If the heavy and light isotopes react at the same rate (KIE = 1), the reaction has no kinetic isotope effect.
Mariotti et al. (1981) derived an approximation of the Rayleigh distillation equation (hereafter referred to as the (standard) Rayleigh equation) that is frequently used to determine enrichment factors in closed systems (Eq. 2) (Mariotti et al., 1981).
Here, δ15Np is the δ value of accumulated product (p) at time t, δ15Ns0 is the δ value of the substrate at t= 0, and f is the fraction of substrate remaining at time t (f = Ns Ns0). (The δ values are directly related to isotope ratios; see the “Isotope nomenclature” section below.) Notably, the Rayleigh equation is based on the assumption that the element of interest is transferred from the substrate to a single position (or equivalent positions) in the product.
The Rayleigh equation (Eq. 2) holds true for δ15Nbulk (the average of δ15Nα and δ15Nβ) because the overall reaction can be thought of as the unidirectional conversion of two identical substrate molecules (e.g., two NO or two NH2OH molecules) to one product molecule with two nitrogen atoms (2S→P2). In the absence of side reactions, this means that δ15Nbulk can be calculated at any point during the reaction (i.e., for any value of f) as long as the δ value of the initial substrate (δ15Ns0) and the enrichment factor (εN-bulk) are known. In practice, the εN-bulk value for a specific enzymatic reaction is found by plotting δ15Nbulk versus []. Because it is assumed that changes in δ15Nbulk are due solely to the bulk kinetic isotope effect of the reaction in question, the slope of this plot (determined by linear regression) is the bulk enrichment factor (εN-bulk), and the y intercept corresponds to δ15Ns0.
Unfortunately, the relationship between δ15Nα, δ15Nβ, and their corresponding enrichment factors is more complex because the two N atoms are non-exchangeable and both steps that incorporate NO (or NH2OH) are potentially isotopically sensitive. In other words, fractionation at the α position alters the isotopic ratio of the remaining substrate (δ15Ns) that is available for incorporation into the β position, and vice versa. Thus, simply determining the change in δ15Nα (or δ15Nβ) as a function of [] over the course of the reaction (i.e., finding the slope of a Rayleigh plot via linear regression of δ15Nα or δ15Nβ against [) is not an accurate method for calculating the enrichment factor for Nα (or Nβ).
The complexity of calculating enrichment factors for a branched N2O biosynthesis reaction can be demonstrated mathematically by substituting (δ15Nα+δ15Nβ) for δ15Np and () for in the Rayleigh equation (Eq. 2), yielding Eq. (3).
Here, εN−α and εN−β stand for the isotopic enrichment factors for the α and β nitrogen atoms, respectively. Equation (3) can then be rearranged to solve for δ15Nα (Eq. 4).
The underlying difficulty in using Eq. (4) is that for a given value of f, δ15Nα depends not only on δ15Ns0 and εN−α, but also on εN−β and the current δ15Nβ value. Put another way, we have one equation and two unknowns (εN−α and εN−β).
To address this issue, we developed an expanded version of the Rayleigh model that includes specific terms for the individual nitrogen atoms in N2O. To test the robustness of this new Expanded Rayleigh model, we generated simulated isotopic data for each of five different potential catalytic mechanisms for N2O formation. For each N2O synthesis scenario, the size and skewness of the simulated measurement error were varied, and 1000 simulated datasets were generated for each combination of error level and skewness type. We then applied the standard Rayleigh model and Expanded Rayleigh model to each dataset to determine εN-bulk, εN−α, and εN−β and compared the precision and accuracy of the two models. Finally, we compared the results of applying the standard Rayleigh model and Expanded Rayleigh model to previously published isotopic data.
2.1 Isotope nomenclature
The isotopic ratio, R, is defined as the abundance of the heavy isotope (15N) divided by the abundance of the light isotope (14N).
In the case of nitrogen, 14N is naturally much more abundant than 15N (the atom percent of 15N in atmospheric N2 (air) is 0.3663 ± 0.0004 %, so R = 0.0036765) (Junk and Svec, 1958; Mariotti et al., 1981; Skrzypek and Dunn, 2020). The R value of a sample is usually measured relative to that of a standard (). For nitrogen, the standard is atmospheric N2. Because there is naturally little variation in 15N, values are typically close to 1, and isotopic ratios are usually converted to the δ notation, which is commonly expressed in the per mil form (‰) by multiplying the unitless form of δ by 1000:
where Rsample is the isotopic ratio of the sample, and Rstandard is the isotopic ratio of the analytical standard (Mariotti et al., 1981). The per mil form of δ is used throughout this paper.
Nbulk is defined as the total number of “equivalents” of nitrogen atoms in N2O, or 2⋅ (mol of N2O). Nα and Nβ are defined as the number of moles of N at the α (central) and β (outer) positions of N2O, respectively.
Thus, 15Nbulk is defined as the total number of moles of 15N at both the α and β positions.
Similarly, 14Nbulk is defined as the total number of moles of 14N at the α and β positions of N2O.
2.2 α, ε, and KIE
As discussed above, the isotopic fractionation factor () is equal to the inverse of the kinetic isotope effect (KIE) for first-order reactions and for higher-order reactions when the rare (heavy) isotope is dilute (i.e., 15N or 13C at natural abundance) (Eq. 10) (Bigeleisen and Wolfsberg, 1958). KIE is defined as the rate constant of the light isotope, kL, divided by the rate constant of the heavy isotope, kH (Eq. 11).
Formally, is defined as the isotopic ratio of instantaneously produced product (Rpi) divided by the isotopic ratio of residual substrate at the same instant (Rs) (Eq. 12) (Mariotti et al., 1981).
As noted above, the fractionation factor can also be expressed in per mil (‰) terms by using Eq. (1) to convert α to the per mil enrichment factor, ε.
2.3 Assumptions
We used the Rayleigh equation (Eq. 2) to determine αN-bulk, the fractionation factor for Nbulk. The Rayleigh model depends on five key assumptions, as outlined below.
2.3.1 Assumption 1
The reaction is irreversible and occurs in a closed system in the absence of side reactions (Mariotti et al., 1981).
This means that the final δ15Nbulk value is equal to the initial δ15Ns value (δ15Ns0).
2.3.2 Assumption 2
The bulk fractionation factor ( or αN-bulk) is constant.
This means that the isotopic ratio of bulk N produced in an infinitely short time period (Rbulk,i) divided by the isotopic ratio of the remaining substrate (Rs) is constant (Eq. 14) (Mariotti et al., 1981).
This assumption should be valid as long as the rate-limiting step of the chemical transformation in question remains the same.
2.3.3 Assumption 3
The light isotope (14N) is much more abundant than the heavy isotope (15N), which is true for all experiments performed with 15N at or near natural abundance.
This assumption was employed by Mariotti and colleagues to approximate total N abundance (14N +15N) as 14N in their definition of f (Mariotti et al., 1981). For N2O isotopocules, the assumption that 14N ≫ 15N also means that variations in the apportionment of 15N between the α and β positions will not significantly affect the abundance of 14N at the α or β position. Thus, at or near the natural abundance of 15N, both 14Nα and 14Nβ may be approximated as 0.5⋅14Nbulk. This approximation underlies the assumption that δ15Nbulk is approximately equal to the average of δ15Nα and δ15Nβ (Eq. 15).
Equation (15) is routinely used in isotopic studies of N2O to calculate δ15Nβ values using experimentally determined δ15Nbulk and δ15Nα values (Toyoda and Yoshida, 1999).
2.3.4 Assumption 4
The values of δs0 and δs are relatively close to 0 ‰.
Mariotti's approximation of the Rayleigh equation uses a simplification that is only valid if and are small relative to 1 (Mariotti et al., 1981). In practice, for an N2O synthesis reaction where εN-bulk is −20 ‰, a δ15Ns0 value of ± 100 ‰ will introduce an error of ∼ 2 ‰ when εN-bulk is determined using this approximation (Table S1).
2.3.5 Assumption 5
The absolute value of ε (e.g., εN-bulk) is relatively small.
The magnitude of δ15Ns values depends on both δ15Ns0 and εN-bulk. Thus, similar to the previous assumption, this assumption was introduced to facilitate the approximation that δ15N is small relative to 1 (Mariotti et al., 1981). As with Assumption 4, the error introduced by this approximation increases as the absolute value of ε increases. For a reaction where δ15Ns0 is equal to 0 ‰ and εN-bulk is equal to ± 50 ‰, this approximation introduces an error of ∼ 1 ‰ to ε values (εN-bulk, εN−α, and εN−β), while a reaction where εN-bulk is equal to ± 100 ‰ introduces an error of 5 ‰–6 ‰ (Table S2).
2.3.6 Assumption 6
For the purposes of modeling N2O synthesis, we will use all of the well-established assumptions listed above. Additionally, to account for fractionation at Nα and Nβ individually, we introduce one more assumption: the individual fractionation factors for the α and β nitrogen atoms in N2O (αN−α and αN−β) are essentially constant.
We define αN−α and αN−β in a manner analogous to that of αN-bulk (Eq. 14). Thus, αN−α is defined as the isotopic ratio of Nα from instantaneously produced N2O (Rα,i) divided by Rs (Eq. 16).
Similarly, αN−β is defined as the instantaneous isotopic ratio of Nβ (Rβ,i) divided by Rs (Eq. 17).
Put another way, we assume a priori that the processes that govern preferential incorporation of one isotope over another remain unchanged at both the α and β positions of N2O during the course of the reaction. We expect this assumption to be valid throughout the reaction, as long as the rate-limiting steps of N2O biosynthesis are unchanged.
2.4 The standard Rayleigh model and simulation of error-free δ15Nbulk and δ15Ns values
To compare the standard Rayleigh approach and our nonlinear expansion of the Rayleigh model, we simulated isotopic data for a number of different combinations of kinetic isotope effects for Nα and Nβ (see Table 1 and Fig. 1). Each idealized, error-free dataset had three groups of equally spaced values of f (0.7–0.3), similar to a typical experiment with three replicates (Tables S4–8). For each dataset, δ15Ns0 was set at 0 ‰, and εN-bulk was set at either −20 ‰ (normal KIE, KIE = 1.0204) or +20 ‰ (inverse KIE, KIE = 0.9804). Equation (2), Mariotti's approximation of the Rayleigh model for accumulated product (Mariotti et al., 1981), was used to calculate δ15Nbulk values of N2O for each value of f (δ15Nbulk=δ15Np). Similarly, δ values for remaining substrate (δ15Ns) were calculated using Eq. (18), Mariotti's approximation of the Rayleigh model written in terms of substrate (Mariotti et al., 1981).
The δ15Nbulk and δ15Ns values simulated using the standard Rayleigh equation are shown in Fig. 1 in gray and orange, respectively.
Table 1Parameters for idealized, error-free datasets describing N2O synthesis for five simulated scenarios (Datasets 1–5) with varying combinations of εN-bulk and ρ.
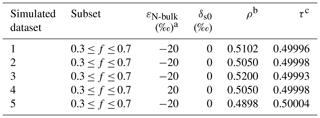
a Note that an ε value of −20 ‰ corresponds to a KIE of 1.0204 and an ε value of +20 ‰ corresponds to a KIE of 0.9804. b Parameter introduced in the Expanded Rayleigh model (Eq. 23): ρ = 15NNbulk. c Parameter introduced in the Expanded Rayleigh model (Eq. 24): τ = 14NNbulk. τ was calculated for each value of f; the average value of τ is listed.
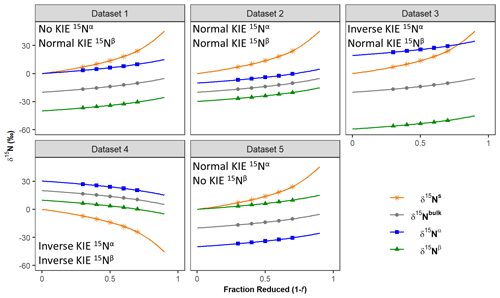
Figure 1Simulated δ15N values for N2O synthesis in a closed system with different combinations of KIE 15Nα and KIE 15Nβ. δ15N values of remaining substrate (δ15Ns) and accumulated product (N2O) (δ15Nbulk, δ15Nα, and δ15Nβ) are plotted as a function of the fraction of substrate reduced (1−f) with reactions progressing from left to right. Values of δ15Nbulk and δ15Ns were calculated using Eq. (2) or Eq. (18) (Mariotti's approximation of the Rayleigh equation; Mariotti et al., 1981), where ε15Nbulk is set to −20 ‰ (Datasets 1–3 and 5) or +20 ‰ (Dataset 4) and the initial δ15Ns value (δ15Ns0) is set to 0 ‰. Values of δ15Nα and δ15Nβ were calculated using Eqs. (27) and (28). For Datasets 1 and 5, either ε15Nα or ε15Nβ was set to 0 ‰ (no isotope effect, KIE = 1), and the corresponding value of ρ was back-calculated (see the Supplement for details). For Datasets 2–4, values of δ15Nα and δ15Nβ were calculated using pre-determined values of ρ that were less than (Datasets 2 and 4) or greater than (Dataset 3) the value of ρ from Dataset 1. See Table 3 for the KIE values for each simulation.
2.5 Nonlinear expansion of the Rayleigh model
Simulated δ15Nα and δ15Nβ values were calculated based on the assumption that, like the fractionation factor for bulk N, the fractionation factors for the individual Nα and Nβ atoms are constant (see Assumption 6 above). To relate αN−α and αN−β to αN-bulk, we define the fraction of instantaneously converted 15Nbulk (15Nbulk,i) that is incorporated into the α position as ρ (Eq. 19).
Similarly, we define the fraction of instantaneously converted 14N (14Nbulk,i) that goes to the α position as τ (Eq. 20).
In keeping with the premise that αN−α and αN−β are constant, we assume a priori that ρ and τ are constant. Thus, the equation for αN−α may be written in terms of ρ, τ, and αN-bulk.
In the absence of side reactions, 15Nbulk,i must be equal to the sum of 15Nα,i and 15Nβ,i. Similarly, 14Nbulk,i must be equal to the sum of 14Nα,i and 14Nβ,i. Thus, the equation for αN−β may also be written in terms of ρ, τ, and αN-bulk.
Equations (21) and (22) form the basis for the Expanded Rayleigh model.
To simulate δ15Nα and δ15Nβ values and determine the corresponding fractionation factors, ρ and τ must be related to accumulated isotope ratios, Rα and Rβ. Although ρ is formally defined in Eq. (19) as the fraction of instantaneously converted 15N apportioned to the α position, ρ can also be written in terms of accumulated 15N values as long as ρ is constant.
Similarly, as long as τ is constant, τ may be written in terms of accumulated 14N values.
Using the definition of ρ from Eq. (23), Rα can be written in terms of ρ by substituting 15Nα with ρ⋅15Nbulk and replacing 14Nα with 0.5 ⋅ (Nbulk) - 15Nα (Eq. 25).
The same approach can be used to define Rβ in terms of ρ (Eq. 26).
The term 0.5 ⋅ Nbulk is equal to moles of N2O (Eq. 7), and 15Nbulk can be calculated for any value of f using Nbulk and δ15Nbulk (see the Supplement). Equations (25) and (26) can be converted to δ notation as follows (see Eq. 6).
Equations (27) and (28) can be used to determine δ15Nα and δ15Nβ based on δ15Nbulk as long as ρ is constant and δ15Nbulk can be approximated as the average of δ15Nα and δ15Nβ (see Eq. 15 and Table S3).
2.6 Simulation of error-free δ15Nα and δ15Nβ values
Idealized, error-free δ15Nα and δ15Nβ values (shown in Fig. 1) were simulated for the values of ρ listed in Table 1 by calculating δ15Nα and δ15Nβ using Eqs. (27) and (28) (Tables S4–8). As outlined in Table 1, five different scenarios with different combinations of isotope effects (none, normal, or inverse) for the α and β nitrogen atoms of N2O were simulated. For Datasets 1 and 5, either ε15Nα or ε15Nβ was set to 0 ‰ (no isotope effect, KIE = 1), and the corresponding values of ρ and τ were back-calculated (see the Supplement for details). The remaining values of ρ were chosen to produce datasets with the different combinations of normal and/or inverse isotope effects (Datasets 2–4). The ρ values tested (0.4898–0.5200) are all close enough to 0.5 such that the average of δ15Nα and δ15Nβ is approximately equal to δ15Nbulk (Table S3). In all cases, discrepancies between δ15Nbulk values calculated using Eq. (2) and δ15Nbulk values calculated by averaging δ15Nα and δ15Nβ (Eq. 15) are well below the typical analytical error of 0.5 ‰–0.7 ‰ (Yang et al., 2014).
2.7 Determination of ρ and τ for the Expanded Rayleigh model
To determine αN−α and αN−β using Eqs. (21) and (22), ρ and τ must be calculated using values that can be measured experimentally (see Fig. 2 for the general workflow for using the Expanded Rayleigh model to determine αN−α and αN−β). Because the abundance of 14N is so much greater than that of 15N, variations in 15N apportionment between Nα and Nβ are negligible when determining the fraction of 14Nbulk at the α position (i.e., τ). For enzyme-catalyzed N2O synthesis with substrate at or near the natural abundance of 15N, we have found that τ is always 0.5000 (see the analysis of data from Sutka et al., 2006, and Yang et al., 2014, below). For the purposes of testing our new Expanded Rayleigh model, we calculated more precise values of τ. To do this, τ was calculated for each value of f using Eq. (24), and the average τ value for each dataset was used to calculate fractionation factors.
To determine ρ using values that can be measured experimentally, Eq. (15) is rewritten so that ρ is the only unknown parameter. This can be accomplished by replacing δ15Nα with the equivalent term from Eq. (27), producing Eq. (29), a nonlinear equation we have named nonlinear model 1.
Alternatively, δ15Nβ could be replaced with a term that includes ρ (Eq. 28), producing Eq. (30) (nonlinear model 2).
Both nonlinear models were used to find the optimal value of ρ via nonlinear least-squares regression for each of our simulated datasets.
2.8 Generation of datasets with simulated error
To mimic experimental error, 1000 simulated datasets were generated from each error-free dataset by adding random error to Ns, δ15Nbulk, and δ15Nα using a modified version of the procedure outlined by Scott and colleagues (Scott et al., 2004). Error was propagated to f by recalculating f using the Ns values with error added (f = Ns / Ns0). Similarly, error was propagated to δ15Nβ by recalculating δ15Nβ using δ15Nbulk and δ15Nα values with error added (Eq. 15). For each simulation, fractionation factors and KIE values were calculated using the standard Rayleigh model and the Expanded Rayleigh model (versions 1 and 2), and the KIE values from each set of 1000 simulations were averaged. Three “levels” of error (low, medium, and high) and three types of skewness (none, left-skewed, and right-skewed; see below) were used for a total of nine conditions (Table 2; Figs. 3 and S1–4). For simulations with low error, the standard deviation of each randomly generated error term was set to the level of error expected in a typical experiment (Table 2). The standard deviation of Ns values was set to 1.5 % of Ns0 (the maximum value of Ns), which corresponds to the estimated level of error in gas volume measurements (see the Supplement). The standard deviations of δ15Nbulk and δ15Nα were set to 0.5 ‰ and 0.7 ‰, respectively, which correspond to standard deviations typical for isotopic analysis of N2O via isotope ratio mass spectrometry (IRMS) (Yang et al., 2014). To further test the robustness of the linear and nonlinear models, medium- and high-level error terms were generated by multiplying the low-level error terms for Ns, δ15Nbulk, and δ15Nα by the appropriate factor (Table 2). The multiplication factors for medium- and high-level error were chosen so that the average R2 values produced by linear regression of δ15Nbulk against [] were approximately 0.7 and 0.4, respectively. Similar R2 values have been observed for standard Rayleigh linear regression plots for N2O biosynthesis (e.g., Yang et al., 2014; Figs. S2–4).
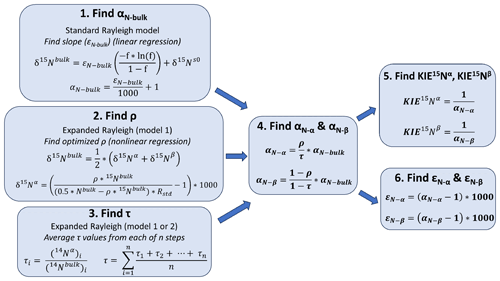
Figure 2General workflow for using the Expanded Rayleigh model to determine fractionation factors (α) and kinetic isotope effects (KIEs) for the individual N atoms (Nα and Nβ) in N2O. To determine the fractionation factors for the α and β atoms in N2O (αN−α and αN−β), three separate values must be calculated. (1) The fractionation factor for bulk N (αN-bulk) is determined by finding the slope (εN-bulk) of a standard Rayleigh plot where y = [] and x=δ15Nbulk and converting εN-bulk to αN-bulk as has been previously described (Mariotti et al., 1981). (2) Nonlinear modeling is used to determine the optimal value of ρ (the fraction of 15Nbulk at the α position). For Expanded Rayleigh model 1 (shown here), δ15Nα is replaced in the top equation with an equivalent expression that includes ρ (bottom equation) to generate the model used for nonlinear least-squares regression (Eq. 29). For Expanded Rayleigh model 2, δ15Nβ is substituted, producing Eq. (30) (not shown). (3) The value of τ (the fraction of 14Nbulk at the α position) is determined by dividing 14Nα by 14Nbulk for each step of the reaction and averaging the results. (4) Finally, αN-bulk, ρ, and τ are used to calculate αN−α and αN−β. (5–6) These individual fractionation factors can be converted to the corresponding KIE values (Eq. 10) or ε values (Eq. 1).
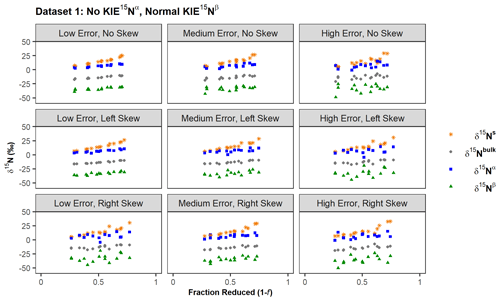
Figure 3Example simulations derived from Dataset 1 with varying levels of error and types of skewness. Each panel shows a single dataset (representative of 1000 simulated datasets) consisting of three replicates with five time points each. All simulations were derived from Dataset 1 (δ15Ns0= 0 ‰, εN-bulk= −20 ‰ (KIE 15Nbulk= 1.0204), KIE 15Nα= 1.0000, and KIE 15Nβ= 1.0417). Each level of error and type of skewness is described in Table 2. Example graphs derived from Datasets 2–4 are shown in Figs. S1–4.
For each level of error, three sets of 1000 simulations with different types of skewness (no skew, left-skewed, or right-skewed) were performed to mimic types of skewness that might be observed in experimental data. For example, if N2O leaks from a sample bottle prior to analysis, the quantity of N2O produced will be underestimated, and the corresponding values of Ns and f will be overestimated. Additionally, since light isotopes have a higher rate of both diffusion and effusion, values of δ15Nbulk, δ15Nα, and δ15Nβ will be overestimated. This scenario is represented by simulations where the random error values added to Ns, δ15Nbulk, and δ15Nα were derived from left-skewed distributions. Skewness classifications were then assigned based on the skewness of the residuals for the standard Rayleigh model where the dependent variable (y) is δ15Nbulk (Table 2). Simulations with residuals between −0.5 and 0.5 (inclusive) were designated “no skew,” meaning the distribution of these residuals did not differ significantly from the normal distribution. Simulations where standard Rayleigh residuals had a skewness value less than −0.5 were designated “left-skewed” (i.e., left-tailed distribution), and simulations where skewness was greater than 0.5 were designated “right-skewed” (i.e., right-tailed distribution).
Table 2Standard deviation and skewness of random error added to simulated Ns, δ15Nbulk, and δ15Nα values.
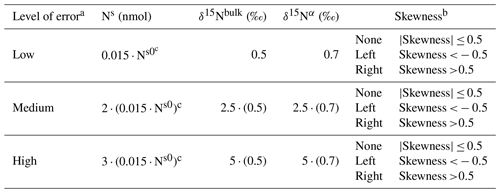
a “Level of error” refers to the standard deviations of Ns (nmol of remaining substrate), δ15Nbulk, and δ15Na. b Skewness of the residuals for the standard Rayleigh model (linear regression of δ15Nbulk against []). c Ns0 refers to nanomoles (nmol) of substrate at time 0 (i.e., the maximum amount of substrate). Ns0 was set to 10 000 nmol in all simulations.
Table 3KIE values for Nbulk, Nα, and Nβ calculated directly from simulation input values (Actual) or from the standard Rayleigh model or Expanded Rayleigh model applied to error-free simulated datasets.
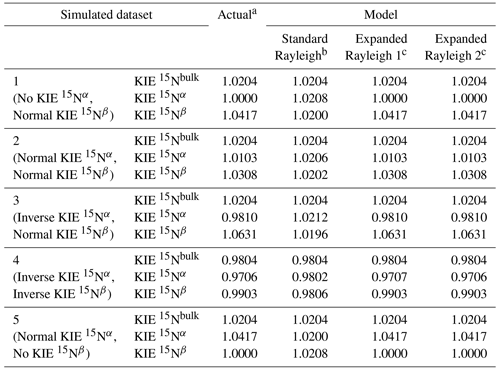
a Actual values were calculated directly from the input values used to generate the dataset. b KIE values were calculated from εN-bulk, εN−α, or εN−β values obtained via linear regression of δ15Nbulk, δ15Nα, or δ15Nβ against [] (see Eq. 2). c For the Expanded Rayleigh model, αN-bulk was determined with the standard Rayleigh approach, ρ was determined via nonlinear regression (nonlinear model 1 or 2, Eq. 29 or Eq. 30), and τ was determined by averaging 14NNbulk for every step of the reaction.
To assess the accuracy of each model under different circumstances, average KIE values and standard deviations were calculated for each set of 1000 simulations with error. The absolute relative difference of each average KIE was calculated using Eq. (31):
where the estimate is the average KIE and actual values were calculated directly from the input values for simulations without error (see Table 3). Lower absolute relative difference values indicate higher accuracy. Goodness of fit was assessed for the (linear) standard Rayleigh model and nonlinear models 1 and 2 by calculating the average root mean square error (RMSE) for each set of 1000 simulations. For each simulation, p values for εN-bulk and ρ (coefficients extracted from the (linear) standard Rayleigh model and nonlinear model 1 or 2, respectively) were determined using the one-sample t test (two-sided) (Baty et al., 2015; Ritz and Streibig, 2008; Kalpiæ et al., 2011). The null hypothesis used to calculate these p values is that there is no kinetic isotope effect. For the linear model, this means that the null hypothesis is εN-bulk= 0 (KIE 15Nbulk= 1). For the nonlinear models, the null hypothesis is that ρ= 0.5 (KIE 15Nα= 1 and KIE 15Nβ= 1).
2.9 Analysis of previously published experimental data
The standard and Expanded Rayleigh models were applied to published data on N2O produced from NH2OH by Methylosinus trichosporium (ATCC 49243) (Sutka et al., 2006). We calculated values of f, δ15Nα, and δ15Nβ using the N2O concentrations, δ15Nbulk values, and site preference (SP) values from replicate B measured by Sutka et al. (see Table S14 for original data and our calculated values and Fig. 4 for a graphical representation of these data). SP is defined as the difference between δ15Nα and δ15Nβ.
The data for replicate B were chosen because these data had a range of f values large enough for εN-bulk to be determined via the standard Rayleigh method (linear regression of δ15Nbulk against []). See the Supplement for details.
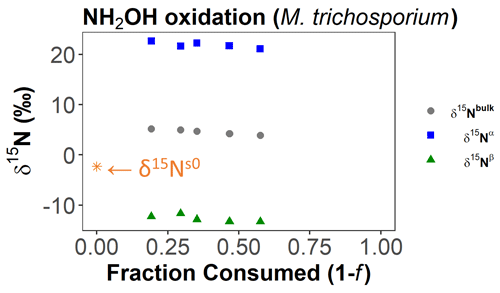
Figure 4Experimentally measured δ15N values for N2O synthesis from NH2OH in a pure culture of Methylosinus trichosporium (data modified from Sutka et al., 2006). Data previously reported for M. trichosporium (Methylocystis sp.) replicate B (Sutka et al., 2006). δ15N values of accumulated product (N2O) (δ15Nbulk, δ15Nα, and δ15Nβ) are plotted as a function of the fraction of substrate consumed (1−f) with the reaction progressing from left to right. We back-calculated values of f, δ15Nα, and δ15Nβ using the reported N2O concentrations, δ15Nbulk values, and SP values. The initial measured δ15N value of NH2OH (δ15Ns0), −2.3 ‰, is shown at f = 1.
We also applied the standard and Expanded Rayleigh models to previously published isotopic data on N2O production from purified Histoplasma capsulatum (fungal) P450 NOR (Fig. 5 and Table S16) (Yang et al., 2014). Because this dataset covered a wide range of f values (f = 0.42-0.87) and δ15Nbulk varied linearly with [], we used the standard Rayleigh model (Eq. 2) to determine εN-bulk via linear regression of δ15Nbulk against []. εN-bulk was determined for each of three independent biological replicates (13 observations per replicate), and the results were averaged. Similarly, to determine standard Rayleigh values of εN−α and εN−β, we performed linear regression of δ15Nα or δ15Nβ against [] for each independent replicate and averaged the results.
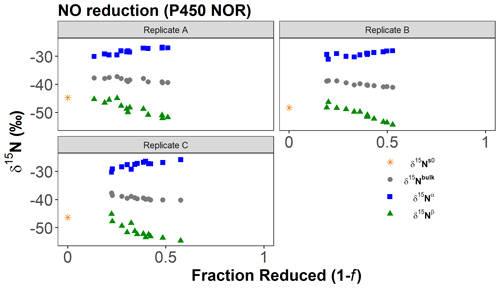
Figure 5Experimentally measured product δ15N values and calculated δ15Ns0 values for N2O synthesis from NO by purified H. capsulatum P450 NOR. Adapted with permission from Yang et al. (2014). Copyright 2014 American Chemical Society. Data previously reported for H. capsulatum (fungal) P450 NOR replicates A–C (Yang et al., 2014). δ15N values of accumulated product (N2O) (δ15Nbulk, δ15Nα, and δ15Nβ) are plotted as a function of the fraction of substrate reduced (1−f) with the reaction progressing from left to right. We back-calculated δ15Ns0 for each replicate by finding the intercept of the corresponding standard Rayleigh plot (Eq. 2) where x = [] and y=δ15Nbulk.
To apply the Expanded Rayleigh model to the isotopic data on N2O production by P450 NOR, we used a modified procedure because, in this case, ρ and τ vary linearly with []. Using nonlinear regression to determine ρ yields a value of ρ in between the more extreme values of ρ observed at the start and end of the reaction and does not represent the data from the overall reaction very well. Therefore, instead of using nonlinear model 1 (Eq. 29) or model 2 (Eq. 30) to determine ρ using data from the entire reaction, we calculated ρ for each individual time point (i.e., each individual value of f) using Eq. (23). Similarly, τ was calculated for each individual observation using Eq. (24). These individual ρ and τ values were then used to calculate αN−α (Eq. 21) and αN−β (Eq. 22) values for each value of f, which were then converted to KIE values using Eq. (10). This approach yielded KIE values that increased (KIE 15Nα) or decreased (KIE 15Nβ) as the reaction progressed. To estimate the range of position-specific KIEs produced by the Expanded Rayleigh model, individual KIE 15Nα and KIE 15Nβ values representing the early part of the reaction (f = 0.8 ± 0.03) or the latter part of the reaction (late reaction, f = 0.5 ± 0.03) were averaged (Tables 6 and S17).
2.10 Modeling, statistical analysis, and figures
Modeling and statistical analyses of simulated and experimental δ values were performed with R statistical software (R Core Team, 2022), and figures were produced with ggplot2 (Wickham, 2016). To determine ρ for the Expanded Rayleigh model, nonlinear least-squares regression was performed as previously described (Baty et al., 2015) using a starting ρ value of 0.5.
For datasets with simulated error, random numbers representing simulated error were generated using the rsn function from the skew-normal distribution package (Azzalini, 2023), and skewness was calculated with the moments package (Komsta and Novomestky, 2022). In the moments package, skewness is defined as , where n is the sample size, is the sample mean, and s is the sample standard deviation (Hippel, 2011).
For previously published experimental data, a linear model was used to determine if SP, ρ, or τ varied as a function of [].
3.1 Error-free simulations
To demonstrate that the standard Rayleigh model produces inaccurate results for the individual nitrogen atoms in N2O, idealized, error-free datasets were simulated representing different scenarios with varying combinations of KIEs for Nα and Nβ (Fig. 1 and Table 1). Because these data were simulated assuming that the fractions of 15N and 14N apportioned to each position remain constant (i.e., constant ρ and τ), the distance between δ15Nα and δ15Nβ over the course of each reaction is constant, and the rates of change in δ15Nα, δ15Nβ, and δ15Nbulk with respect to reaction progress (1−f) are essentially equal (Fig. 1). Thus, when the standard Rayleigh model (Eq. 2) is applied to each dataset, the slopes (ε) of δ15Nα, δ15Nβ, and δ15Nbulk against [] for each dataset are all approximately equal, as are the corresponding KIE 15Nbulk, KIE 15Nα, and KIE 15Nβ values (Table 3). While the standard Rayleigh KIE 15Nbulk values match the actual KIE 15Nbulk values, the KIE 15Nα and KIE 15Nβ values determined using the standard Rayleigh approach differ significantly from the actual KIEs calculated from simulation input values (Table 3). In each of the five simulated reactions (Datasets 1–5), the isotopic preference for Nα differs from that of Nβ, which can be verified visually by noting that the δ15Nα values are significantly different than the δ15Nβ values throughout each reaction (Fig. 1). However, in all five cases, the standard Rayleigh model produces KIE values for Nα and Nβ that are approximately equal, highlighting the fact that the standard Rayleigh model inaccurately quantifies 15N apportionment between Nα and Nβ. (If KIE 15Nα were equal to KIE 15Nβ, the curves for δ15Nα, δ15Nβ, and δ15Nbulk shown in Fig. 1 would all be on top of each other.)
The inadequacies of the standard Rayleigh model are most evident when Nα and Nβ have opposing kinetic isotope effects, i.e., scenarios where there is an inverse isotope effect at one position and a normal isotope effect at the other position (Dataset 3), or when only one position has a nonzero fractionation factor (Datasets 1 and 5). In these cases, the standard Rayleigh model fails to predict the correct type of isotope effect for one of the nitrogen atoms. For example, Dataset 1 represents a scenario where there is no isotopic preference at the α position, meaning instantaneous δ15Nα (δ15Nαi) is always equal to δ15Ns, which can be verified visually by noting that accumulated δ15Nα≈δ15Ns at the start of the reaction (Fig. 1). Under these circumstances, KIE 15Nα is equal to 1.0000. However, the standard Rayleigh model predicts a much higher KIE 15Nα value (1.0208), incorrectly indicating that there is a reasonably strong, normal KIE at the α position. The standard Rayleigh KIE 15Nβ value calculated for Dataset 1 is also too low (1.0200 instead of 1.0417), underestimating the preference for 14N at the β position. Similarly misleading results are produced for Dataset 5, where there is no isotope effect for Nβ, but the standard Rayleigh model predicts a normal isotope effect at this position. Along the same lines, the standard Rayleigh KIE values for Dataset 3 incorrectly indicate that both Nα and Nβ have normal isotope effects when, in this case, Nα actually has an inverse isotope effect. Thus, even for a simulated dataset with no experimental error, the standard Rayleigh model produces results that are quantitatively – and sometimes qualitatively – incorrect.
The standard Rayleigh model produces inaccurate results for the individual N atoms in N2O because the changes in δ15Nα depend on both KIE 15Nα and KIE 15Nβ, as do changes in δ15Nβ. Linear regression of standard Rayleigh plots for δ15Nα or δ15Nβ fails to capture this nuance. To address this issue, we developed the Expanded Rayleigh model that introduces two new parameters, ρ and τ, to define how 15Nbulk and 14Nbulk, respectively, are apportioned between Nα and Nβ. Fractionation factors for Nα and Nβ are determined by combining αN-bulk, ρ, and τ (Eqs. 21 and 22). For experiments conducted at the natural abundance of 15N, the value of τ, which is equal to 14Nα/14Nbulk, should always be quite close to 0.5, as discussed above. Indeed, each simulated reaction step has a mean value of τ equal to 0.500 for Datasets 1–5 (Tables S9–13), so the average value of 14NNbulk was used to calculate αN−α and αN−β. To determine the value of ρ that fits the entire dataset as accurately as possible, we performed nonlinear least-squares regression using the formula shown in Eq. (29) (nonlinear model 1) or Eq. (30) (nonlinear model 2). For error-free Datasets 1–5, nonlinear least-squares regression with either nonlinear model correctly predicted ρ. Combining these ρ and τ values with αN-bulk values derived from the standard Rayleigh equation yields KIE 15Nα and KIE 15Nβ values that are identical to the expected values out to three or four decimal places (Table 3). Thus, unlike the standard Rayleigh approach, the Expanded Rayleigh model successfully recapitulates the kinetic isotope effects for Nα and Nβ in an error-free dataset.
Table 4Precision and accuracy of values calculated with Expanded Rayleigh model 1 using simulated datasets derived from Dataset 1 (no isotope effect for Nα, normal isotope effect for Nβ). n/a – not applicable.
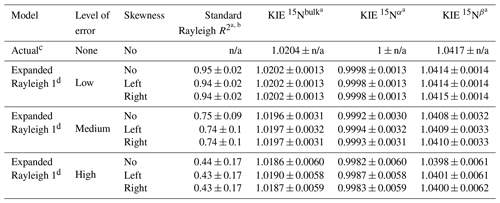
a Average value ± standard deviation calculated from 1000 values generated from 1000 simulated datasets. b Average R2 value for linear regression of δ15Nbulk against [] (using Eq. 2, the standard Rayleigh equation). c Actual values were calculated directly from the input values used to generate the dataset. d For Expanded Rayleigh model 1, αN-bulk was determined with the standard Rayleigh approach, ρ was determined via nonlinear regression (nonlinear model 1, Eq. 29), and τ was determined by averaging 14NNbulk for every step of the reaction (Eq. 24). The results for Expanded Rayleigh model 2 (Table S9) are very similar.
3.2 Application of the Expanded Rayleigh model to simulations with error
To test the robustness of the Expanded Rayleigh model, we applied this model to simulated data with error at varying levels of size and skewness (Table 2; Figs. 3 and S1–4) and averaged the results from 1000 simulations for each error category (Tables 4 and S9–13). These results indicate that at a low level of error (the level of error expected for a typical experiment), the KIE values produced by the Expanded Rayleigh model are quite accurate (absolute difference relative to true values is 0.001, or 0.1 %, see Eq. 31), regardless of the skewness of the standard Rayleigh model residuals (Figs. 6 and S5–8). The standard deviations for each average KIE 15Nbulk, KIE 15Nα, or KIE 15Nβ value (0.0013–0.0014) are also similar to standard error values from typical experiments (∼ 0.0004–0.0021) (Tables 5 and 6) (Sutka et al., 2006; Yang et al., 2014). As the absolute value of the simulated error increases, the average KIE values become less accurate, and the corresponding standard deviations increase. Nonetheless, even at the highest level of error, the maximum absolute relative difference of average KIE values is 0.005 (0.5 % difference), and the range of values covered by average KIE ± standard deviation includes the actual KIE value. Thus, the Expanded Rayleigh model provides a robust method for determining KIE values even when the datasets have a high level of error or skewness.
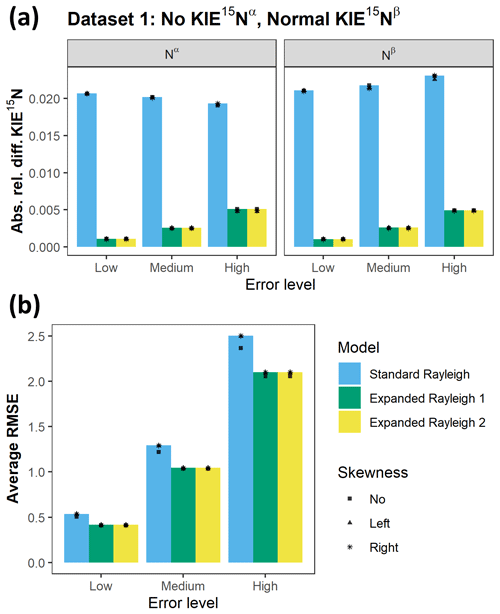
Figure 6Comparison of the accuracy and goodness of fit of the standard Rayleigh model and Expanded Rayleigh models 1 and 2. (a) Comparison of the accuracy of KIE 15Nα and KIE 15Nβ values. For each model, the absolute relative difference for KIE 15Nα and KIE 15Nβ values (average for 1000 simulated datasets derived from Dataset 1) is shown. Actual values for Dataset 1: δ15Ns0= 0 ‰, εN-bulk= −20 ‰ (KIE 15Nbulk= 1.0204), KIE 15Nα= 1.0000, and KIE 15Nβ= 1.0417. Absolute relative difference (Eq. 31) is the absolute value of the difference between the estimated value and actual value divided by the actual value (|(estimate – actual)/actual|). (b) Comparison of the average RMSE values for each set of 1000 simulated datasets derived from Dataset 1. Both the standard Rayleigh model and the Expanded Rayleigh model (1 and 2) use δ15Nbulk as the dependent variable, so average RMSE values can be compared directly. Lower RMSE values indicate a better goodness of fit. At each error level (low, medium, and high), the absolute relative difference value (a) or average RMSE (b) is depicted with a symbol that represents skewness type as shown in the legend. Note that in most cases these symbols overlap.
In contrast to the Expanded Rayleigh model, the KIE 15Nα and KIE 15Nβ values determined for simulations with error using the standard Rayleigh model alone are much less accurate (Figs. 6 and S5–8). For all simulations derived from Datasets 1–5 at all levels of error and types of skewness, the absolute relative differences of average standard Rayleigh KIE 15Nα and KIE 15Nβ values ranged from 0.01–0.04 (1 %–4 % difference). These absolute relative differences are 2–40 times higher than the corresponding differences of Expanded Rayleigh model estimates (Figs. 6 and S5–8). Differences of this magnitude are large enough that the true KIE 15Nα and KIE 15Nβ values typically do not fall within the range covered by average KIE ± standard deviation calculated using the standard Rayleigh model (data not shown). Thus, as discussed for the no-error simulations, standard Rayleigh KIE 15Nα and KIE 15Nβ values do not accurately quantify isotopic fractionation at the α and β positions of N2O and can even lead to inaccurate designation of the type of KIE (i.e., no KIE, normal KIE, or inverse KIE) at either Nα or Nβ. In short, for all levels of error and types of skewness tested, the standard Rayleigh model is only accurate for bulk N. To obtain KIE 15Nα and KIE 15Nβ values with the same level of accuracy as KIE 15Nbulk, the KIE 15Nbulk value obtained via the standard Rayleigh model must be combined with ρ and τ parameters from the Expanded Rayleigh model.
The error for KIE 15Nα and KIE 15Nβ values is derived from three sources: error in αN-bulk, error in ρ, and error in τ. In all of our simulations with added error, the most significant source of error is the error associated with αN-bulk, which is derived from linear regression of δ15Nbulk against []. As the level of error increases, the accuracy of εN-bulk (and thus the accuracy of αN-bulk and KIE 15Nbulk) decreases more significantly than the accuracy of ρ and τ estimates (Tables S9–13). The same trend is apparent for other assessments of model fit. The RMSE values for the nonlinear regression portion of the Expanded Rayleigh model (1 or 2) are always slightly lower than the RMSE values for the standard Rayleigh linear model (Figs. 6 and S5–8), indicating that the linear and nonlinear models produce similar “goodness of fit” values. Similarly, the p values for εN-bulk, the slope of the linear regression model, are always greater than the p values for ρ, the coefficient extracted from the nonlinear portion of the Expanded Rayleigh model (in both cases, the null hypothesis is that KIE = 1; see the Methods section). Out of each set of 1000 simulations at high-level error, a small number of simulated datasets (14 %–19 %) produce linear regression plots where confidence in the slope is low (i.e., εN-bulk p value >0.05) (data not shown). In contrast, all of the simulations derived from all five datasets with varying types of KIEs produce ρ values that are likely to be significant (p value <0.001). Overall, application of the Expanded Rayleigh model to simulated datasets with varying types of error indicates that this method of determining individual fractionation factors for Nα and Nβ is robust even at high levels of error.
3.3 Application of the Expanded Rayleigh model to previously published isotopic data
As a proof-of-concept example, we applied the standard Rayleigh model and the Expanded Rayleigh model to previously published experimental data and compared the results. We chose data collected for N2O biosynthesis by a culture of M. trichosporium (Methylocystis sp.) grown aerobically in the presence of NH2OH (Sutka et al., 2006). Methylocystis species encode the gene for hydroxylamine oxidoreductase (HAO), an enzyme that not only converts NH2OH to NO during nitrification, but also produces N2O under certain conditions (Yamazaki et al., 2014). As Methylocystis species lack the gene for cytochrome P460 (which has also been shown to convert NH2OH to N2O) (Caranto et al., 2016), the isotopic fractionation observed in this experiment is assumed to be due to only one process: HAO-catalyzed conversion of NH2OH to N2O. Indeed, the εN-bulk value for N2O produced in this experiment (5.3 ± 0.4 ‰ for replicate B, KIE 15Nbulk= 0.9947 ± 0.0004; see Table S15; Sutka et al., 2006) is similar to the εN-bulk value of 2.0 ‰ (KIE 15Nbulk= 0.9980) reported for purified HAO from Nitrosomonas europaea (Yamazaki et al., 2014). The differences between δ15Nα and δ15Nβ (SP) are also very similar for the two experiments, indicating that HAO was the primary source of N2O production in the cultures of M. trichosporium, meaning the Rayleigh model could be applied to this system.
Application of the standard Rayleigh model (Eq. 2) to δ15Nbulk via linear regression of δ15Nbulk against [] indicated that εN-bulk was 5.3 ± 0.4 ‰ and KIE 15Nbulk was 0.9947 ± 0.0004 (inverse isotope effect) (Table 5) for N2O production by M. trichosporium. Similarly, application of the standard Rayleigh model to δ15Nα and δ15Nβ produced a KIE 15Nα value of 0.9952 ± 0.0015 and a KIE 15Nβ value of 0.9942 ± 0.0021. Thus, the standard Rayleigh model predicts an inverse isotope effect for both Nα and Nβ, which theoretically means that both positions are enriched in 15N relative to the substrate. However, all of the δ15Nβ values (−11.7 ‰ to −13.3 ‰) are more negative than the measured δ15Ns0 value of −2.3 ‰ (Fig. 4 and Table S14), indicating that 15N is depleted at the β position and that 14N is preferred (normal isotope effect). The δ15Nα values (21.1 ‰ to 22.7 ‰), in contrast, are more positive than δ15Ns0, indicating that there is an inverse isotope effect at this position. The Expanded Rayleigh model produces position-specific KIEs that match this qualitative assessment: KIE 15Nα= 0.9779 ± 0.0004 (inverse), and KIE 15Nβ= 1.0121–1.0122 ± 0.0004 (normal) (Table 5). Additionally, the values of ρ and τ do not vary significantly with f (Table S15), indicating that fractionation at the α and β positions appears to be constant. Comparison of the RMSE values for the standard (linear) Rayleigh model and the nonlinear portion of the Expanded Rayleigh model also indicates that both models have a similar goodness of fit. Thus, the Expanded Rayleigh model can be applied to experimental data to accurately assess position-specific KIEs.
Table 5Comparison of standard Rayleigh and Expanded Rayleigh KIE values ± standard error for N2O produced from NH2OH by an axenic culture of M. trichosporium (Methylocystis sp.). Values were calculated using isotopic data previously published for M. trichosporium replicate B (Sutka et al., 2006). n/a – not applicable.

a RMSE (root mean square error) for the standard Rayleigh model (Eq. 2) with linear regression of δ15Nbulk against []. b RMSE for nonlinear model 1 or 2 (Eq. 29 or Eq. 30). c Average value ± standard error. d KIE values were calculated from εN-bulk, εN−α, or εN−β values obtained via linear regression of δ15Nbulk, δ15Nα, or δ15Nβ against []. e For the Expanded Rayleigh model, bulk values (αN-bulk, εN-bulk, and KIE 15Nbulk) were determined with the standard Rayleigh approach, ρ was determined via nonlinear regression, and τ was determined by averaging 14NNbulk for every step of the reaction. Then αN−α and αN−β were calculated with Eq. (21) or Eq. (22) and converted to KIE values using Eq. (10). The only difference between Expanded Rayleigh models 1 (Eq. 29) and 2 (Eq. 30) is which δ value (δ15Nα or δ15Nβ) is substituted with a ρ-containing expression in the nonlinear model.
We also compared the results of applying the standard and Expanded Rayleigh models to previously published isotopic data on NO reduction to N2O by purified H. capsulatum P450 NOR (Yang et al., 2014). In this experiment, δ15Nbulk varied linearly with [] (R2= 0.68–0.94), and averaging the slopes of the standard Rayleigh plots for each individual replicate indicated that εN-bulk was equal to 9.10 ‰ ± 1.42 and KIE 15Nbulk was equal to 0.9910 ± 0.0014 (Tables 6 and S17). In other words, on average, N2O became depleted in 15N (i.e., δ15Nbulk decreased) as the reaction proceeded (Fig. 5 and Table S16). However, the Nα position became more enriched in 15N as the reaction progressed (i.e., δ15Nα increased as f decreased). Consequently, ρ increased (and τ decreased) over the course of the reaction (Table S17), and the observed values of αN−α and αN−β also varied with f, in contrast to Assumption 6 (above). Thus, the Expanded Rayleigh model, which is based on the assumption that αN−α and αN−β remain constant over the course of the reaction, does not fit these data optimally. Therefore, using nonlinear regression (Eq. 29 or Eq. 30) to determine ρ is not appropriate in this case. Using a modified version of the Expanded Rayleigh model, however, we calculated ρ for each individual time point and estimated apparent KIE 15Nα and KIE 15Nβ values for the beginning and end of the observed range of f values (see the Methods section). Our estimated KIE 15Nα values ranged from 0.9823 ± 0.0016 (earlier in the reaction) to 0.9781 ± 0.0016 (later in the reaction), indicating that the Nα position is subject to an inverse isotope effect throughout the reaction. On the other hand, the KIE 15Nβ estimates ranged from 0.9998 ± 0.0015 to 1.0041 ± 0.0013, suggesting that there is essentially no apparent isotope effect at the β position, especially early in the reaction. These results are consistent with a qualitative assessment of the δ values. For example, the δ15Nα values (−25.8 ‰ to −31.0 ‰) are more positive than the calculated δ15Ns0 values (i.e., the intercept of the standard Rayleigh plots for δ15Nbulk), which range from −44.7 ‰ to −48.3 ‰. This indicates that the α position is enriched in 15N relative to the substrate. On the other hand, the δ15Nβ values near the start of the reaction (−45.2 ‰ to −48.3 ‰) are similar to the calculated δ15Ns0 values, suggesting that there is very little isotopic fractionation at the β position.
In contrast to the Expanded Rayleigh model estimates, the standard Rayleigh calculations yield a normal isotope effect for Nα (KIE 15Nα= 1.0127 ± 0.0030) and an inverse isotope effect for Nβ (KIE 15Nβ= 0.9694 ± 0.0022). (Note that applying the standard Rayleigh model to individual observations and averaging KIEs for the early and later parts of the reaction yields similar results to applying the standard Rayleigh model to the entire reaction (Tables 6 and S17; see the Supplement for details). While it is possible that Nβ exhibits an apparent inverse isotope effect near the beginning of the reaction, the magnitude of this effect is likely much smaller (i.e., early KIE 15Nβ is much closer to 1) than the standard Rayleigh calculations suggest. More strikingly, the standard Rayleigh prediction that Nα is subject to a normal isotope effect (14N preferred) is clearly incorrect, as the α position is enriched in 15N relative to the initial substrate. Moreover, as 15N is depleted from the substrate pool, the fraction of 15N incorporated into the α position increases, indicating that the preference for 15N at Nα increases (becomes more inverse) as the reaction proceeds. Overall, analysis of the P450 NOR data demonstrates that even for reactions where the apparent position-specific KIEs vary, the Expanded Rayleigh model produces considerably more accurate KIE estimates than the standard Rayleigh model.
4.1 Proper application of the Expanded Rayleigh model
The Rayleigh model has been used to study kinetic isotope effects for decades and has been adapted many different times for use in specific scenarios. However, to our knowledge, this is the first examination of how the Rayleigh model applies to a process where two heavy atoms from the same substrate pool (e.g., NO or NH2OH) are incorporated into non-equivalent positions in the product (e.g., N2O). Our simulations of different N2O-producing scenarios demonstrate that the original Rayleigh model should not be applied to the individual atoms in such cases as this produces inaccurate results. However, the new Expanded Rayleigh model presented here can be used to accurately determine individual kinetic isotope effects. This expanded model allows for a more granular analysis than would be possible from determining only bulk kinetic isotope effects and SP.
In practice, when can the Expanded Rayleigh model be used? To develop the Expanded Rayleigh model, we employed the same assumptions that the original model is founded on. Therefore, any situations where the original Rayleigh model applies will also likely be suitable for the Expanded Rayleigh model. More specifically, the Expanded Rayleigh model will likely produce accurate results for any closed system where N2O is produced from a substrate pool with 15N at or near natural abundance, as long as the rate-determining step for each atom remains constant. Thus, the Expanded Rayleigh model is ideally suited for studies of isolated N2O-synthesizing enzymes, as this experimental setup provides a closed system where N2O is produced by a single catalytic process.
One method for confirming that the rate-determining steps of N2O synthesis are constant is to determine if εN-bulk and SP are constant for a particular dataset. If enzymatic catalysis is rate-limiting throughout a time course experiment, εN-bulk will be constant, and the slope of a standard Rayleigh plot should be linear. In contrast, if substrate diffusion (or some other process) becomes rate-limiting, curvilinear behavior may be exhibited in a standard Rayleigh plot, as has been observed for multi-step N2O production in microbial cultures (Sutka et al., 2008; Haslun et al., 2018). Of course, to use the Expanded Rayleigh model, εN−α and εN−β must be constant as well. To verify that the individual fractionation factors are constant, one could plot δ15Nα and δ15Nβ against [] (i.e., create standard Rayleigh plots for δ15Nα and δ15Nβ) and confirm that these plots are linear and roughly parallel. Alternatively, SP (the difference of δ15Nα and δ15Nβ; Eq. 32) can be monitored over time. The lack of a significant trend in SP values is a reasonably good indication that εN−α and εN−β are constant. In studies of microbial cultures where N2O is predominantly produced by a single type of enzyme (e.g., bacterial NOR, fungal NOR, or HAO), SP generally remains constant as substrate is consumed (Toyoda et al., 2005; Sutka et al., 2006; Sutka et al., 2008; Haslun et al., 2018). The fact that SP is constant for a variety of N2O production pathways in a microbial cell suggests that enzyme-specific fractionation at Nα and Nβ typically remains constant, meaning the Expanded Rayleigh model can likely be accurately applied to a variety of N2O-producing enzymes.
Table 6Comparison of standard Rayleigh and Expanded Rayleigh KIE values ± standard error for N2O production from NO by purified Histoplasma capsulatum (fungal) P450 NOR (calculated using previously published isotopic data; Yang et al., 2014).
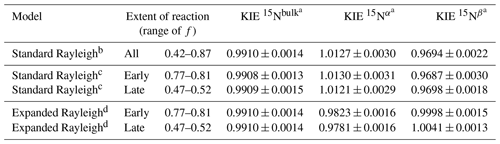
a Average value ± standard deviation. b KIE values were calculated from εN-bulk, εN−α, or εN−β values obtained via linear regression of δ15Nbulk, δ15Nα, or δ15Nβ against []. The standard Rayleigh model values presented here differ slightly from the previously published values (Yang et al., 2014) due to our exclusion of the earliest observation(s) from each replicate (i.e., observations with the highest values of f were excluded). c For the standard Rayleigh model applied to individual observations, εN-bulk, εN−α, or εN−β values were determined using Eq. (S24); the y intercept listed in that equation corresponds to the y intercept of δ15Nbulk, δ15Nα, or δ15Nβ against [] (determined by linear regression of the data from each replicate). KIE values for six (early) or seven (late) individual observations were pooled and averaged. d For the Expanded Rayleigh model applied to individual observations, bulk values (αN-bulk, εN-bulk, and KIE 15Nbulk) were determined with the standard Rayleigh approach. ρ was calculated for each observation using Eq. (23) (ρ= 15NNbulk), and τ was determined for every step of the reaction using Eq. (24) (τ=14NNbulk). Then αN−α and αN−β were calculated for each individual observation with Eq. (21) or Eq. (22) and converted to KIE values using Eq. (10). KIE 15Nα and KIE 15Nβ values for six (early) or seven (late) individual observations were pooled and averaged.
At present, there is a scarcity of studies reporting N2O fractionation by purified enzymes for multiple values of f, limiting our ability to test the Expanded Rayleigh model with published experimentally derived datasets. We were, however, able to apply the Expanded Rayleigh model to previously published data on M. trichosporium cultures (Sutka et al., 2006), whose HAO-catalyzed oxidation of NH2OH was the primary source of N2O and displayed constant values of εN-bulk and SP. Thus, we were able to calculate observed values of KIE 15Nα and KIE 15Nβ that serve as reasonable estimates of HAO-specific isotope effects (Table 5). Additionally, we have used the Expanded Rayleigh model to re-evaluate isotopic data our group has collected for purified fungal P450 NOR (Table 6) (Yang et al., 2014). The value of εN-bulk for P450 NOR appears to be constant, but SP increased by 14 ‰ as the fraction of NO reduced changed from 10 % to 50 % (Yang et al., 2014). Given the proposed P450 NOR reaction mechanism, the observed isotope effect for the first NO molecule is influenced by both an equilibrium isotope effect related to NO binding and an intrinsic KIE associated with catalysis (Yang et al., 2014). Conversely, the rate-determining steps for the second NO molecule are likely only associated with catalysis. Thus, the isotopic fractionation for the first nitrogen atom to be incorporated will be more sensitive to changes in NO concentration as the reaction progresses than the second N atom, leading to SP values that are not constant. Even in these circumstances, however, the Expanded Rayleigh model estimates for KIE 15Nα and KIE 15Nβ are a significant improvement on the previously published standard Rayleigh estimates, which incorrectly predict a normal isotope effect at the α position. Overall, the Expanded Rayleigh model fits the available data on isotopic fractionation during N2O biosynthesis reasonably well, although we recommend collecting isotopic data across a range of f values to confirm that SP (and therefore KIE 15Nα and KIE 15Nβ) remains constant when using this model.
As outlined above (in the Assumptions section), the Expanded Rayleigh model is most accurate for reactions where the isotopic fractionation factors (εN-bulk, εN−α, and εN−β) and δ15Ns0 values are not too extreme. This stipulation, which also applies to the standard Rayleigh equation, is necessary in part because an approximation introduced by Mariotti and colleagues (Mariotti et al., 1981) decreases in accuracy the farther δ15Ns0 and δ15Ns are from 0 ‰. Additionally, extremely high positive values of δ15Ns0 or εN-bulk would result in large positive product δ values, corresponding to an increased abundance of 15N in the product. As both the nonlinear Rayleigh model and the underlying calculation of δ15Nβ values depend on the assumption that the amount of 15N in N2O is close to the natural abundance, the accuracy of the Expanded Rayleigh model would decrease in such circumstances. Thus, applying the Expanded Rayleigh model to experiments with spiked 15N is not advised. Simulations of δ values calculated without using Mariotti's approximation indicate that for absolute values of εN-bulk or δ15Ns0 less than or equal to 50 ‰, the level of error introduced by Mariotti's approximation is similar to the expected level of experimental error (i.e., absolute relative difference in KIE values of ∼ 0.001) (Tables S1–2).
The magnitude of εN−α and εN−β must also be considered when applying the Expanded Rayleigh model. In theory, if isotopic enrichment at Nα or Nβ is very large, the assumption that essentially equal amounts of 14N are apportioned to each position (i.e., that τ≈0.5) would be violated, and Eq. (15) would no longer hold. However, violating this assumption would require unusually large heavy-atom kinetic isotope effects or a spiked sample. As outlined in Table S3, for a simulated reaction where εN-bulk is set at −20 ‰ (KIE 15Nbulk= 1.0204) and δ15Ns0 is 0 ‰, individual KIE values would have to be significantly lower than 0.96 or greater than 1.08 to introduce error greater than analytical error. These KIE 15Nα or KIE 15Nβ values correspond to ρ values less than 0.47 or greater than 0.53. In practice, our group has found that for two different types of N2O-producing enzymes, ρ is nowhere near these extremes. For example, for purified P450 NOR (Yang et al., 2014) and for HAO-catalyzed NH2OH oxidation in an axenic culture (Sutka et al., 2006), ρ does not exceed 0.509 (Tables S15 and S17). Overall, we anticipate that the Expanded Rayleigh model will be applicable to a wide variety of N2O biosynthesis reactions.
4.2 Other practical considerations
The Expanded Rayleigh model presented here does not require measurement of δ15Ns0. This is advantageous for N2O synthesis reactions where NO is the substrate because directly measuring an accurate δ15N value for NO is quite challenging due to the reactivity of NO, the lack of isotopic standards for NO, and the fact that 14N16O has the same molecular weight as 15N15N. However, δ15Ns0 can be directly measured when NH2OH is used as the substrate for N2O production. Determining δ15Ns0 experimentally may be useful in validating application of the standard Rayleigh model, as the intercept of the standard Rayleigh model is expected to be equal to δ15Ns0. For example, we determined that the intercept of the standard Rayleigh plot for N2O produced by NH2OH oxidation by M. trichosporium is 0.5 ± 0.3 ‰, which is similar to the measured δ15Ns0 value of −2.3 ‰ (Sutka et al., 2006), confirming that the standard Rayleigh model is applicable for this dataset. Thus, when feasible, measuring δ15Ns0 would complement the expanded Rayleigh approach.
The nonlinear portion of the Expanded Rayleigh model (used to determine ρ) can be written in two forms, nonlinear model 1 (Eq. 29) and nonlinear model 2 (Eq. 30). Both models are based on the assumption that δ15Nbulk is equal to the average of δ15Nα and δ15Nβ (Eq. 15). Therefore, both models are expected to produce very similar results as long as that assumption holds. Indeed, as we have demonstrated here, both models yield nearly identical values of ρ, KIE 15Nα, and KIE 15Nβ for simulated datasets (Figs. 6 and S5–8; Tables S9–13), and we have obtained similar results for the available experimental data on N2O production from NH2OH (Table 5). Thus, either version of the Expanded Rayleigh model may be used. If there is any doubt about which version to use, we recommend selecting the model that has a lower RMSE value (and thus fits the data better).
In this paper, we presented the Expanded Rayleigh model, a novel adaptation of the Rayleigh distillation equation that describes the position-specific isotopic enrichment that occurs at Nα and Nβ during N2O synthesis. Using simulated datasets representing multiple different combinations of KIEs, we demonstrated that the Expanded Rayleigh model accurately recapitulates KIE 15Nα and KIE 15Nβ for a wide variety of scenarios. Our simulations also demonstrate that this new model is robust even when applied to skewed data and/or data with a high level of error. Additionally, we have shown the Expanded Rayleigh model fits the experimentally measured isotopic data for N2O production from NH2OH quite well (Sutka et al., 2006) and provides significantly improved estimates for the position-specific KIEs for P450 NOR-catalyzed N2O synthesis. Thus, the Expanded Rayleigh model provides a reliable method for quantifying isotopic fractionation at Nα and Nβ, and it promises to be a valuable tool for experimentally probing the catalytic mechanisms of N2O-synthesizing enzymes. Finally, we note that the Expanded Rayleigh model will also likely be appropriate for the analysis of other reactions where two atoms from the same substrate pool are incorporated into distinct, non-exchangeable positions in the product.
All code used in this manuscript is available at https://doi.org/10.5281/zenodo.13931602 (Rivett, 2024a). The results for each of the 1000 simulations with error (derived from Datasets 1–5) can be found at https://doi.org/10.5281/zenodo.13323399 (Rivett, 2024b).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-21-4549-2024-supplement.
EDR, NEO, and ELH conceived this study. EDR developed the model and analyzed the data with contributions from WM, NEO, and ELH. WM provided critical input for statistical analysis and coding. EDR prepared the original draft of the manuscript and figures, and all authors participated in editing and revision of the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We thank Julius Campeciño and Helen Kreuzer for a careful reading of a draft of this manuscript and for their insightful comments and questions. We also thank Julius Campeciño for helpful discussions during initial development of the Expanded Rayleigh model. We also acknowledge an anonymous reviewer whose comments first alerted us to the complications associated with position-specific application of the Rayleigh model.
This material is based upon work supported by the Great Lakes Bioenergy Research Center, US Department of Energy, Office of Science, Biological and Environmental Research Program under award number DE-SC0018409.
This paper was edited by Perran Cook and reviewed by one anonymous referee.
Azzalini, A.: The R package 'sn': The Skew-Normal and Related Distributions such as the Skew-t and the SUN (version 2.1.1), CRAN [code], http://azzalini.stat.unipd.it/SN/ (last access: 10 October 2024), 2023.
Baty, F., Ritz, C., Charles, S., Brutsche, M., Flandrois, J.-P., and Delignette-Muller, M.-L.: A Toolbox for Nonlinear Regression in R: The Package nlstools, J. Stat. Softw., 66, 1–21, https://doi.org/10.18637/jss.v066.i05, 2015.
Bigeleisen, J. and Wolfsberg, M.: Theoretical and experimental aspects of isotope effects in chemical kinetics, Adv. Chem. Phys., 1, 15–76, 1958.
Caranto, J. D., Vilbert, A. C., and Lancaster, K. M.: Nitrosomonas europaea cytochrome P460 is a direct link between nitrification and nitrous oxide emission, P. Natl. Acad. Sci. USA, 113, 14704–14709, https://doi.org/10.1073/pnas.1611051113, 2016.
Frame, C. H. and Casciotti, K. L.: Biogeochemical controls and isotopic signatures of nitrous oxide production by a marine ammonia-oxidizing bacterium, Biogeosciences, 7, 2695–2709, https://doi.org/10.5194/bg-7-2695-2010, 2010.
Haslun, J. A., Ostrom, N. E., Hegg, E. L., and Ostrom, P. H.: Estimation of isotope variation of N2O during denitrification by Pseudomonas aureofaciens and Pseudomonas chlororaphis: implications for N2O source apportionment, Biogeosciences, 15, 3873–3882, https://doi.org/10.5194/bg-15-3873-2018, 2018.
Hippel, P. V.: Skewness, in: International Encyclopedia of Statistical Science, edited by: Lovric, M., Springer Berlin Heidelberg, Berlin, Heidelberg, 1340–1342, https://doi.org/10.1007/978-3-642-04898-2_525, 2011.
IPCC: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK, and New York, NY, USA, ISBN 978-1-107-05799-1, 2013.
Junk, G. A. and Svec, H. J.: Nitrogen isotope abundance measurements, US atomic energy commission, Office of technical information, Office of Technical Services, Department of Commerce, Washington, D. C., ISC 1138, 1958.
Kalpiæ, D., Hlupiæ, N., and Lovriæ, M.: Student's t-Tests, in: International Encyclopedia of Statistical Science, edited by: Lovric, M., Springer Berlin Heidelberg, Berlin, Heidelberg, 1559–1563, https://doi.org/10.1007/978-3-642-04898-2_641, 2011.
Komsta, L. and Novomestky, F.: moments: Moments, Cumulants, Skewness, Kurtosis and Related Tests, R package version 0.14.1 [code], https://CRAN.R-project.org/package=moments (last access: 10 October 2024), 2022.
Kuypers, M. M. M., Marchant, H. K., and Kartal, B.: The microbial nitrogen-cycling network, Nat. Rev. Microbiol., 16, 263–276, https://doi.org/10.1038/nrmicro.2018.9, 2018.
Lan, X., Thoning, K. W., and Dlugokencky, E. J.: Trends in globally-averaged CH4, N2O, and SF6 determined from NOAA Global Monitoring Laboratory measurements, Version 2023-11, https://doi.org/10.15138/P8XG-AA10, 2022.
Lehnert, N., Dong, H. T., Harland, J. B., Hunt, A. P., and White, C. J.: Reversing nitrogen fixation, Nat. Rev. Chem., 2, 278–289, https://doi.org/10.1038/s41570-018-0041-7, 2018.
Mariotti, A., Germon, J. C., Hubert, P., Kaiser, P., Letolle, R., Tardieux, A., and Tardieux, P.: Experimental determination of nitrogen kinetic isotope fractionation: Some principles; illustration for the denitrification and nitrification processes, Plant Soil, 62, 413–430, https://doi.org/10.1007/BF02374138, 1981.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, CRAN [code], https://www.R-project.org/ (last access: 10 October 2024), 2022.
Ravishankara, A. R., Daniel, J. S., and Portmann, R. W.: Nitrous oxide (N2O): The dominant ozone-depleting substance emitted in the 21st century, Science, 326, 123–125, https://doi.org/10.1126/science.1176985, 2009.
Ritz, C. and Streibig, J. C.: Nonlinear Regression with R, 1st Edn., Use R!, Springer, New York, ISBN 9780387096162, 2008.
Rivett, E.: position-specific-kie (v1.0.0), Zenodo [code], https://doi.org/10.5281/zenodo.13931602, 2024a.
Rivett, E.: Results for datasets with simulated error (derived from Datasets 1–5) (Version 2), Zenodo [data set], https://doi.org/10.5281/zenodo.13323399, 2024b.
Romão, C. V., Vicente, J. B., Borges, P. T., Frazão, C., and Teixeira, M.: The dual function of flavodiiron proteins: oxygen and/or nitric oxide reductases, J. Biol. Inorg. Chem., 21, 39–52, https://doi.org/10.1007/s00775-015-1329-4, 2016.
Scott, K. M., Lu, X., Cavanaugh, C. M., and Liu, J. S.: Optimal methods for estimating kinetic isotope effects from different forms of the Rayleigh distillation equation, Geochim. Cosmochim. Ac., 68, 433–442, https://doi.org/10.1016/s0016-7037(03)00459-9, 2004.
Skrzypek, G. and Dunn, P. J. H.: Absolute isotope ratios defining isotope scales used in isotope ratio mass spectrometers and optical isotope instruments, Rapid Commun. Mass. Sp., 34, e8890, https://doi.org/10.1002/rcm.8890, 2020.
Sutka, R. L., Ostrom, N. E., Ostrom, P. H., Gandhi, H., and Breznak, J. A.: Nitrogen isotopomer site preference of N2O produced by Nitrosomonas europaea and Methylococcus capsulatus Bath, Rapid Commun. Mass. Sp., 17, 738–745, https://doi.org/10.1002/rcm.968, 2003.
Sutka, R. L., Ostrom, N. E., Ostrom, P. H., Gandhi, H., and Breznak, J. A.: Nitrogen isotopomer site preference of N2O produced by Nitrosomonas europaea and Methylococcus capsulatus Bath, Rapid Commun. Mass. Sp., 18, 1411–1412, https://doi.org/10.1002/rcm.1482, 2004.
Sutka, R. L., Ostrom, N. E., Ostrom, P. H., Breznak, J. A., Gandhi, H., Pitt, A. J., and Li, F.: Distinguishing nitrous oxide production from nitrification and denitrification on the basis of isotopomer abundances, Appl. Environ. Microb., 72, 638–644, https://doi.org/10.1128/aem.72.1.638-644.2006, 2006.
Sutka, R. L., Adams, G. C., Ostrom, N. E., and Ostrom, P. H.: Isotopologue fractionation during N2O production by fungal denitrification, Rapid Commun. Mass. Sp., 22, 3989–3996, https://doi.org/10.1002/rcm.3820, 2008.
Tian, H., Xu, R., Canadell, J. G., Thompson, R. L., Winiwarter, W., Suntharalingam, P., Davidson, E. A., Ciais, P., Jackson, R. B., Janssens-Maenhout, G., Prather, M. J., Regnier, P., Pan, N., Pan, S., Peters, G. P., Shi, H., Tubiello, F. N., Zaehle, S., Zhou, F., Arneth, A., Battaglia, G., Berthet, S., Bopp, L., Bouwman, A. F., Buitenhuis, E. T., Chang, J., Chipperfield, M. P., Dangal, S. R. S., Dlugokencky, E., Elkins, J. W., Eyre, B. D., Fu, B., Hall, B., Ito, A., Joos, F., Krummel, P. B., Landolfi, A., Laruelle, G. G., Lauerwald, R., Li, W., Lienert, S., Maavara, T., MacLeod, M., Millet, D. B., Olin, S., Patra, P. K., Prinn, R. G., Raymond, P. A., Ruiz, D. J., van der Werf, G. R., Vuichard, N., Wang, J., Weiss, R. F., Wells, K. C., Wilson, C., Yang, J., and Yao, Y.: A comprehensive quantification of global nitrous oxide sources and sinks, Nature, 586, 248–256, https://doi.org/10.1038/s41586-020-2780-0, 2020.
Toyoda, S. and Yoshida, N.: Determination of nitrogen isotopomers of nitrous oxide on a modified isotope ratio mass spectrometer, Anal. Chem., 71, 4711–4718, https://doi.org/10.1021/ac9904563, 1999.
Toyoda, S., Mutobe, H., Yamagishi, H., Yoshida, N., and Tanji, Y.: Fractionation of N2O isotopomers during production by denitrifier, Soil Biol. Biochem., 37, 1535–1545, https://doi.org/10.1016/j.soilbio.2005.01.009, 2005.
Wickham, H.: ggplot2: Elegant Graphics for Data Analysis [code], Springer, New York, https://doi.org/10.1007/978-3-319-24277-4, 2016.
Yamazaki, T., Hozuki, T., Arai, K., Toyoda, S., Koba, K., Fujiwara, T., and Yoshida, N.: Isotopomeric characterization of nitrous oxide produced by reaction of enzymes extracted from nitrifying and denitrifying bacteria, Biogeosciences, 11, 2679–2689, https://doi.org/10.5194/bg-11-2679-2014, 2014.
Yang, H., Gandhi, H., Ostrom, N. E., and Hegg, E. L.: Isotopic fractionation by a fungal P450 nitric oxide reductase during the production of N2O, Environ. Sci. Technol., 48, 10707–10715, https://doi.org/10.1021/es501912d, 2014.





