the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the predictability of turbulent fluxes from land: PLUMBER2 MIP experimental description and preliminary results
Anna Ukkola
Sanaa Hobeichi
Jon Cranko Page
Mathew Lipson
Martin G. De Kauwe
Samuel Green
Claire Brenner
Jonathan Frame
Grey Nearing
Martyn Clark
Martin Best
Peter Anthoni
Gabriele Arduini
Souhail Boussetta
Silvia Caldararu
Kyeungwoo Cho
Matthias Cuntz
David Fairbairn
Craig R. Ferguson
Hyungjun Kim
Yeonjoo Kim
Jürgen Knauer
David Lawrence
Xiangzhong Luo
Sergey Malyshev
Tomoko Nitta
Jerome Ogee
Keith Oleson
Catherine Ottlé
Phillipe Peylin
Patricia de Rosnay
Heather Rumbold
Bob Su
Nicolas Vuichard
Anthony P. Walker
Xiaoni Wang-Faivre
Yunfei Wang
Yijian Zeng
Accurate representation of the turbulent exchange of carbon, water, and heat between the land surface and the atmosphere is critical for modelling global energy, water, and carbon cycles in both future climate projections and weather forecasts. Evaluation of models' ability to do this is performed in a wide range of simulation environments, often without explicit consideration of the degree of observational constraint or uncertainty and typically without quantification of benchmark performance expectations. We describe a Model Intercomparison Project (MIP) that attempts to resolve these shortcomings, comparing the surface turbulent heat flux predictions of around 20 different land models provided with in situ meteorological forcing evaluated with measured surface fluxes using quality-controlled data from 170 eddy-covariance-based flux tower sites.
Predictions from seven out-of-sample empirical models are used to quantify the information available to land models in their forcing data and so the potential for land model performance improvement. Sites with unusual behaviour, complicated processes, poor data quality, or uncommon flux magnitude are more difficult to predict for both mechanistic and empirical models, providing a means of fairer assessment of land model performance. When examining observational uncertainty, model performance does not appear to improve in low-turbulence periods or with energy-balance-corrected flux tower data, and indeed some results raise questions about whether the energy balance correction process itself is appropriate. In all cases the results are broadly consistent, with simple out-of-sample empirical models, including linear regression, comfortably outperforming mechanistic land models.
In all but two cases, latent heat flux and net ecosystem exchange of CO2 are better predicted by land models than sensible heat flux, despite it seeming to have fewer physical controlling processes. Land models that are implemented in Earth system models also appear to perform notably better than stand-alone ecosystem (including demographic) models, at least in terms of the fluxes examined here. The approach we outline enables isolation of the locations and conditions under which model developers can know that a land model can improve, allowing information pathways and discrete parameterisations in models to be identified and targeted for future model development.
- Article
(4135 KB) - Full-text XML
-
Supplement
(16540 KB) - BibTeX
- EndNote
Land models (LMs) simulate terrestrial water, energy, and biogeochemical cycles. They simulate the exchange of heat and moisture between the land and atmosphere inside weather forecast models (e.g. Boussetta et al., 2013; Bush et al., 2023), soil moisture and streamflow in hydrological and agricultural applications (e.g. Clark et al., 2015a, b; Buechel, 2021), ecological dynamics and carbon exchange in ecosystem modelling (e.g. Knauer et al., 2023; Bennet et al., 2024), and most of these processes combined inside climate models (e.g. Lawrence et al., 2019; Vuichard et al., 2019; Bi et al., 2020). The fidelity of LM simulations is therefore consequential economically, socially, and environmentally.
This paper focuses on a relatively simple question: how should we fairly assess the fidelity of land models? We aim to develop an evaluation framework that gives us confidence that LM evaluation is not partial – not dependent upon a particular metric, observational data choice, over-calibration or overfitting, a particular location or time, or a subset of processes – and so it is the closest we can reasonably expect to a summative understanding of the shortcomings or strengths of a particular model. This aim is the basis of a LM comparison experiment, PLUMBER2, and we use results from PLUMBER2 to illustrate the framework. It follows the first Protocol for the Analysis of Land Surface Models (PALS) Land Surface Model Benchmarking Evaluation Project (PLUMBER; Best et al., 2015; Haughton et al., 2016) and addresses many of the shortcomings in its first iteration.
Our question is intentionally methodological, since the consequence of getting the answer wrong is very real – we rely on LMs for a great deal of scientific inference and societally relevant predictions. We consider our aim in two parts. First, what kind of simulation environment allows for the best observational constraint of LMs, so that poor model performance might fairly be attributed to a LM? Second, how do we best structure an evaluation framework to give us confidence in this kind of attribution? We discuss these two questions in turn and highlight how the experimental framework of PLUMBER2 addresses them in a way that the original PLUMBER experiment could not.
While most LMs are applied on regional or global grids, diagnostic evaluation of LMs (that is, understanding why they might be wrong) at these scales is difficult (Wartenburger et al., 2018; Seiler et al., 2022). First, at this scale LMs need to be driven by reanalysis-based meteorology with unquantified uncertainty (Arora et al., 2023), making the attribution of model–observation mismatch inconclusive. Next, observationally based flux evaluation products at these scales, typically also without quantified uncertainty, usually have a low time resolution (e.g. monthly; Pan et al., 2020), so an assessment of process representation in LMs can only be made using emergent outcomes rather than directly.
Site-based LM simulations using observational data collected at flux towers offer a solution to some of these issues, but they come with their own challenges. On the positive side, meteorological variables that drive LMs are directly measured at tower sites at a time resolution appropriate for LM simulation (typically 30 min), and uncertainties are relatively small and quantifiable (Schmidt et al., 2012). Vegetation properties are often documented at site locations, reducing parameter uncertainty in LM simulations (Falge et al., 2017). The fluxes into the atmosphere that LMs are evaluated against are also measured and aggregated to the same time step size as the meteorological driving data. For these reasons, both PLUMBER and PLUMBER2 involve the evaluation of LMs at flux tower sites, but PLUMBER2 examines a much broader range of environments (170 sites instead of 20).
There are however several complicating factors that also make LM constraint using tower data incomplete. The spatial scale represented by a flux tower's fetch – typically not larger than 1 km2 – is at the very highest resolution of application scales for most LMs (Chu et al., 2021). However, all LMs are designed using leaf-scale or canopy-scale theories (Bonan et al., 2021) and do not contain an explicit length scale that modifies simulation characteristics for the size of a grid cell, so it is unclear whether this represents a problem. Next, not all LM parameters are measured at sites, and indeed at some sites little information is available beyond a broad indication of vegetation type (Falge et al., 2017). The available information is, however, likely closer to being representative than parameter values prescribed at the grid scale that cannot be observed directly. Finally, and most importantly, the measurement of turbulent fluxes comes with significant uncertainty. Site measurements regularly do not close the energy balance (Stoy et al., 2013; Mauder et al., 2020) in a way that LMs are structurally required to do, and measurements are likely to have much greater uncertainty in periods of low turbulence (Goulden et al., 1996; Aubinet et al., 2012). These issues were both ignored in the first PLUMBER experiment but are directly addressed in PLUMBER2, with evaluation involving both raw and energy-balance-corrected site data as well as filtering to remove periods of low turbulence.
To address our second question, we outline three key aspects of an evaluation framework that will allow attribution of poor model–observation agreement to poor model performance. They are (a) an appropriate suite of metrics, (b) a mechanism to establish threshold values in those metrics that reasonably define “good” or “poor” performance, and (c) a summative indicator that can fairly synthesise information using (a) and (b) to provide a representative overall picture.
For a given variable time series, there are of course many metrics one might use to assess model performance, and it is well recognised that using a single metric will generally not allow for holistic assessment of model performance (Collier et al., 2018; Abramowitz et al., 2019). Both PLUMBER and PLUMBER2 focused on a broad collection of metrics that (i) assessed a wide range of aspects of model performance and (ii) were independent in the sense that a change to a model prediction might affect any one of these metrics without affecting others (Gupta et al., 2009).
Next, establishing a priori performance expectations in the form of thresholds in these metrics is key to defining good model performance. Models will never agree with observations exactly, but if we can understand how well a perfect model could simulate a given environment given the information provided in its driving variables and observational uncertainty, it would tell us exactly which aspects of observed site behaviour were predictable and which were not. This idea can be approximated by using out-of-sample empirical models to predict site fluxes using the same meteorological driving variables as the LMs as predictors (e.g. Abramowitz, 2005; Best et al., 2015; Whitley et al., 2017). While the PLUMBER experiment conducted investigations using simple out-of-sample empirical models to do this, here we offer a much more comprehensive range of empirical approaches. By varying the complexity of empirical models and the number and types of predictors we provide them with, we create a hierarchy of benchmark levels of performance in any given metric that reflects different structural assumptions. For example, a LM should provide a more sophisticated prediction of evapotranspiration than a simple empirical model based on incoming shortwave radiation alone, since it contains information about soil moisture availability, soil temperature, vegetation, and evaporative demand. By providing some empirical models with lagged variables or using machine learning structures that allow internal states, we can begin to quantify how much predictive ability model states like soil moisture should provide.
Finally, with many variables, metrics, sites, empirical benchmarks, and LMs, the importance of a summative indicator that appropriately synthesises information and reduces the dimensionality of results should be clear. In PLUMBER, each LM was ranked against benchmark models from best- to worst-performing, and the ranks were averaged over sites and metrics. However, it has since become clear that this can create misleading results. Consider the following example. A LM and three benchmarks have biases in latent heat flux at three sites of (32, 30, 31, 29), (48, 47, 45, 46), and (12, 52, 29, 85) W m−2, respectively, translating into ranks of (4, 2, 3, 1), (4, 3, 1, 2), and (1, 3, 2, 4) and an average rank of (3.3, 2.6, 2.3, 2.3). This summative indicator misleadingly suggests that the LM is comfortably the worst model of the four, when the actual site biases suggest that models were nearly indistinguishable at the first two sites and the LM notably superior at the third. Using results from PLUMBER2, we examine two alternative summative indicators that resolve this issue. A summary of the main differences between PLUMBER and PLUMBER2 is shown in Table 1.
Before detailing our methodology below, we emphasise that this experimental description paper does not investigate process representations or flaws of any particular model – given the number of models, sites, and benchmarks, doing so would necessarily present an incomplete picture. We instead focus on developing a fair, holistic framework for LM evaluation, comparison, and quantification of performance expectations and present a high-level overview of PLUMBER2 results that will serve as a basis for future detailed process-level analyses that are already underway.
2.1 Flux tower data
LMs completed simulations at 170 flux tower sites for PLUMBER2, forced with in situ half-hourly or hourly meteorological variables. The aim was to maximise the number of sites that met variable availability and quality control requirements and had open-access data. FLUXNET2015, FLUXNET La Thuile Free-Fair-Use, and OzFlux collections were used as the starting point, and after processing with the FluxnetLSM package (Ukkola et al., 2017) we ensured that the sites had a reference (measurement) height, canopy height, and IGBP (International Geosphere–Biosphere Programme) vegetation type; had whole years of data; and were not missing significant periods of key forcing variables (where gap-filling counted as missing), specifically incoming solar radiation (SWdown), air temperature (Tair), specific humidity (Qair), or precipitation (Rainf). Discerning thresholds in these variables was clearly subjective but involved consideration of the proportion of time series with measured data, length of gaps, coincidence between variables, and ubiquity of site type – see Ukkola et al. (2022) for details. Gap-filling (including allowing 100 % synthesised data) of downwelling longwave radiation (LWdown) used the approach of Abramowitz et al. (2012). Surface air pressure (PSurf) was based on elevation and temperature, and ambient CO2 was based on global values (Ukkola et al., 2022).
Since most sites had no publicly available leaf area index (LAI) data and none had time-evolving LAI data, we specified a remotely sensed LAI time series for each site to try to minimise differences between LMs. LMs that predict LAI would clearly not utilise this (Table S3 in the Supplement). The LAI time series were derived from either MODIS (8-daily MCD15A2H product, 2002–2019) or the Copernicus Global Land Service (monthly, 1999–2017), with one of these chosen for each site based on a site-by-site analysis considering plausibility and some in situ data provided for each time step of meteorological forcing. Time-varying LAI was provided for the time period covered by the remotely sensed products, and otherwise a climatology was constructed from all the available years. Some LMs utilised this LAI estimate for a single vegetation type simulation and others partitioned it into a mixed vegetation type representation. LAI estimates remain a key issue for observational constraint of LMs at the site and global scales.
Energy balance closure in flux tower data is particularly relevant in the context of this experiment. At a range of timescales, most sites do not obey the assumed equality of net radiation with the sum of latent heat flux, sensible heat flux, and ground heat flux (Wilson et al., 2002; Stoy et al., 2013; Mauder et al., 2020; Moderow et al., 2021). We therefore need to be careful when attributing model–observation mismatch to model error, since LMs are fundamentally constrained to conserve energy. Energy balance closure correction was part of the FLUXNET2015 release (the bulk of the sites here), and we replicated this approach for sites from the other sources. The analyses below consider both uncorrected and corrected latent and sensible heat fluxes, were only conducted on flux time steps that were not gap-filled, and were also run separately filtered by time steps with wind speeds above 2 m s−1 so that potential concerns about measurement fidelity in low-turbulence periods (typically nighttime) could be investigated.
Forcing and evaluation files were produced in an updated version of ALMA NetCDF (Polcher et al., 1998, 2000), with CF-NetCDF standard name attributes and Coupled Model Intercomparison Project (CMIP)-equivalent names included where possible. A complete list of these variables, as well as those requested in LM output, is shown in Table S1. Table S2 shows a complete site and site property list. Each site has a page at https://modelevaluation.org (last access: 9 December 2024) with more details, including additional references, metadata, photographs, and time series plots. The site locations are shown by Ukkola et al. (2022). The site vegetation types and distribution in the mean precipitation–temperature space are shown in Fig. S1 in the Supplement. Their location in a Budyko-style dryness index versus (water) evaporative fraction plot (Budyko, 1974; Chen and Sivapalan, 2020) is shown in Fig. S2a. It is typically assumed that all sites will lie below 1 on the horizontal axis (i.e. evapotranspiration will be less than precipitation) and to the right of the 1–1 line (potential evapotranspiration > evapotranspiration), with drier, water-limited sites close to 1 on the horizontal axis on the right-hand side and wetter, energy-limited sites towards the bottom left-hand side close to the 1–1 line.
This is however clearly not true for these site data. To understand why, we first examined the cumulative precipitation at each site compared to an in situ based gridded precipitation product – REGEN (Contractor et al., 2020) – and identified those sites that appeared anomalous. Clearly there are many good reasons why site-based precipitation might disagree with a gridded product, even if it were perfect. A subset of the sites was nevertheless identified as having precipitation data that were a priori not realistic, either because missing data had not been gap-filled (and were not flagged as missing so that precipitation flat-lined), units were reported incorrectly (e.g. US-SP1 appears to use inches rather than millimetres), or winter snowfall was apparently not included in the precipitation totals (Fig. S3). Sixteen sites were removed from the analysis as a result. These issues were unfortunately only identified after all the modelling groups had completed their 170 site simulations, so the LM analyses below are conducted on the remaining 154 sites.
While removing these sites did lessen the extent of the problem, it did not by any means solve it (Fig. S2b – the same as Fig. S2a but with 154 instead of 170 sites). Next, we examined whether using the entire time series for each site instead of filtering out gap-filled time steps (Fig. S2a has gap-filled data removed) resulted in any qualitative change – it did not (Fig. S2c). Finally, we investigated whether using energy-balance-corrected fluxes had an impact. Figure S2d shows that it did indeed have a marked effect – but the proportion of sites where evapotranspiration exceeded precipitation increased.
Figure S2a–d reinforce how complicated the simulation task is for LMs, with around 30 % of the sites showing an average evapotranspiration exceeding the average precipitation. Despite posing this as a data quality problem above, there are many sound, physically plausible reasons for this, such as hillslope or preferential flow, irrigation, or groundwater access by vegetation. Needless to say, most LMs will simply be unable to reproduce this behaviour since these inputs and processes are usually not included. We discuss this issue, its influence on results, and implications for LM evaluation in the “Results” and “Discussion and conclusions” sections.
2.2 Land model simulations
Mechanistic LMs ran offline in single-site mode (as opposed to gridded simulations), forced by observed meteorology from the 170 sites. Simulations were requested as “out-of-the-box”, using default (usually vegetation-type-based) parameters for each site, as if the LMs were running a global simulation. Models used the IGBP vegetation type prescribed in each forcing file where possible, mapped to the plant functional type (PFT) schemes used by each model. In addition, site canopy height and reference height (measurement height, assumed to be the lowest atmospheric model layer height) were provided. No additional parameter information for the sites was prescribed.
The rationale behind this setup was to understand the fidelity in flux prediction that LMs provide in a well-constructed global simulation, noting that different LMs had to adapt their representation approaches in slightly different ways to achieve this (e.g. some use mixed vegetation types to describe a single location). While we might ideally additionally like to ensure that LMs use an appropriate soil type for each site, these are not universally measured or available for all sites, so LMs used their default global soil type grid.
Models were not allowed to calibrate to site fluxes, as we are primarily interested in the insights LMs provide into the system rather than their fitting ability, which might leave little to distinguish them from machine learning approaches that we already know will perform better (Abramowitz, 2012; Beaudry and Renner, 2012; Best et al., 2015; Nearing et al., 2018). Out-of-sample testing for any model, even if only partly empirical, is key to understanding its predictive ability (Abramowitz et al., 2019), especially when it needs to be applied globally.
Different LMs require different periods of spin-up until model states reach an equilibrium, depending on whether they include a dynamic carbon (C) and/or nitrogen (N)/phosphorus (P) cycle(s), vegetation, or stand dynamics. For models where soil temperature and moisture spin-up is sufficient (e.g. if LAI is prescribed rather than predicted), we suggested that model spin-up use the site forcing file and repeatedly simulate the entire period, for at least 10 years of simulation, before beginning a simulation of the first year of the site data.
For LMs with prognostic LAI and/or soil C, N, and P pools, the process was more complicated. LM simulations were initialised with a spin-up routine resulting in equilibrium conditions of C stocks (and N and P if available) representing the year 1850. Climatic forcing for the spin-up came from the site's eddy covariance forcing file, which was continuously repeated. Atmospheric CO2 and N deposition levels representing the year 1850 were set to 285 ppm and 0.79 kg N ha−1 yr−1, respectively. The transient phase covered the period 1851 to the year prior to the first year in the site data. LMs were forced with historical changes in atmospheric CO2 and N deposition, continually recycling the meteorological inputs. The meteorological time series was repeated intact rather than in a randomised way to avoid splitting of the observed meteorological years at the end of each calendar year. This of course does not accurately replicate the land use history of different sites, but in most cases detailed site-level histories were not available.
All models participating in PLUMBER2 are shown in Table S3. While some simulation setup information is included in the “Notes” column, more detailed information is available on the “Model Outputs” profile page for each set of simulations submitted to https://modelevaluation.org. While the modelling groups were asked to report as many variables as possible from Table S1, the breadth of the contributions was highly variable, so in an attempt to include all the participants, the analyses here focus on latent heat flux (Qle), sensible heat flux (Qh), and net ecosystem exchange (NEE) of CO2 only.
In addition to the LMs, two “physical benchmarks” were also included as per Best et al. (2015) – an implementation of a Manabe bucket model (Manabe, 1969) and a Penman–Monteith model (Monteith and Unsworth, 1990) with a reference stomatal resistance and unrestricted water availability.
2.3 Empirical machine-learning-based benchmarks
As suggested above, empirical models are key to quantifying site predictability and so setting benchmark levels of performance for LMs that reflect the varying difficulty or complexity of prediction at different sites, unknown issues with data quality at some sites, and, more broadly, understanding the amount of information that LM inputs provide about fluxes. To do this meaningfully, all empirical models need to provide out-of-sample predictions. That is, every site simulation made here by an empirical model has not used that site's data to build or train the empirical model and so cannot be overfitted to the characteristics or noise of the site. If the site is unusual or its data are poor, the empirical models will provide a poor simulation, thus setting a lower benchmark of performance for the LMs.
A hierarchy of different empirical models was used. From the simplest, with the lowest performance expectations, to the most complicated with highest expectations, these are the following:
-
1lin. A linear regression of each flux against downward shortwave radiation (SWdown) using half-hourly data, training on 169 sites and predicting on 1, repeated 170 times as per Abramowitz (2012) and Best et al. (2015). Two versions were created – one trained to predict raw fluxes (1lin_raw) and one trained to predict energy-balance-corrected fluxes (1lin_eb).
-
2lin. A multiple linear regression of each flux using SWdown and air temperature (Tair) as predictors, using half-hourly data, and training on 169 sites and predicting on 1 site, as per Abramowitz (2012) and Best et al. (2015).
-
3km27. All site time steps of three predictors – SWdown, Tair, and relative humidity (RH) – from 169 training sites are sorted into 27 clusters using k means, and all site time steps in each cluster are used to establish multiple linear regression parameters against each flux for that cluster. Time steps at the prediction site are sorted into clusters based on their proximity to cluster centres, and regression parameters for each cluster are then used to make predictions at the test site, as per Abramowitz (2012) and Best et al. (2015); 27 clusters were chosen to approximately allow each predictor high, medium, and low clusters: 33 = 27. Two versions were created – one to predict raw fluxes (3km27_raw) and one to predict energy-balance-corrected fluxes (3km27_eb).
-
6km729. As per 3km27 but uses six predictors – SWdown, Tair, RH, Wind, Precip, and LWdown (see Table S1 for the variable definitions) – and 729 k-means clusters, training on 169 sites and predicting on 1 site, similar to Haughton et al. (2018). The 729 clusters were chosen to approximately allow each predictor high, medium, and low clusters: 36 = 729.
-
6km729lag. As per 6km729 but with lagged Precip and Tair as additional predictors. These took the form of six additional predictors: mean Precip and Tair from the previous 1–7, 8–30, and 31–90 d. Training on 169 sites and predicting on 1 site took place similarly to Haughton et al. (2018).
-
RF. A random forest model with Tair, SWdown, LWdown, Qair, Psurf, Wind, RH, CO2air, vapour pressure deficit (VPD), and LAI as predictors. These predictor variables are listed in order of variable importance. While Precip was originally included, it actually offered negative variable importance – suggesting that including Precip reliably degraded the empirical prediction out-of-sample. Training was on 169 sites and predicting on 1 out-of-sample site, repeated 170 times. As a nominally more sophisticated empirical model than the cluster + regression approaches above, RF offers a lower-bound estimate of the predictability of fluxes from instantaneous conditions (no lags). Two versions were created – one to predict raw fluxes (RF_raw) and one to predict energy-balance-corrected fluxes (RF_eb).
-
LSTM. A long short-term memory model given as much information as the LMs. Two types of input features were used for training: dynamic features – CO2air, LWdown, Precip, Psurf, Qair, RH, SWdown, Tair, VPD, Wind, and LAI – and static site attributes that are constant per site (mean annual temperature MAT, range of annual MAT, mean annual precipitation MAP, mean LAI, range of annual LAI, elevation, canopy height, reference height, latitude, mean SWdown, PET, and IGBP vegetation type). Training was on 167 sites and prediction was on the 3 remaining sites (randomly chosen), repeated to make out-of-sample predictions at all the sites. A single LSTM was used to predict Qle, Qh, and NEE simultaneously to account for the fact that the three fluxes are all components of a highly coupled system. The LSTM provides a lower-bound estimate of the predictability of fluxes using both instantaneous and meteorological conditions as well as internal states based on them – a proxy for LM states. Two versions were created – one to predict raw fluxes (LSTM_raw) and one to predict energy-balance-corrected fluxes (LSTM_eb).
2.4 Analyses
The dimensionality and complexity of the PLUMBER2 data obviously present many options for interrogating the performance of LMs. Our analysis focuses on a relatively high-level overview without any intention of being comprehensive – we anticipate that analysis of PLUMBER2 simulations will extend well beyond the scope of this paper and will take some time. The results below consider mean fluxes, variable ratios such as the evaporative fraction, and water use efficiency before examining the two summative indicators that are detailed.
The set of metrics we use, shown in Table S4, is independent in the sense that, for a given observational time series, a change can be made to the model time series that will affect any one of these metrics without affecting the others. This is not true, for example, of RMSE and correlation. Metrics are calculated separately for each model at each site.
Next, we examine our two summative indicators. To do this, we first set a reference group of benchmark empirical models and compare all the LMs to this reference group. Suppose we wish to compare a given LM against 1lin, 3km27, and LSTM, for example. Then, for each metric (m), at each site, and for each variable, we have metric values for the LM, 1lin, 3km27, and LSTM. We then define the normalised metric value (NMV) for this LM at this site and for this variable and metric in one of two ways.
First, as with PLUMBER, we define LM performance relative to a range of metric values that includes the LM and empirical benchmarks. Instead of using ranks though, we normalise this range to define the dependent normalised metric value (dNMV) as
So, a dependent NMV simply denotes where in the metric range of these four models the LM was, scaled to be between 0 and 1, with lower values representing better performance. This allows us to average the NMV over metrics, sites, variables, vegetation types, or other groupings to get an aggregate indication of the performance.
The second approach, independent NMV (iNMV), defines the normalised metric range using only the reference benchmark models:
An iNMV allows us to define lower and upper performance expectations to be independent of the LM being assessed. We might expect that 1lin as the simplest model will typically have a value of 1 and LSTM 0, and the LM, if its performance lies between these two, will have a value somewhere in this interval. It also allows the LM to score a much lower value than 0 if it performs much better than the empirical models and, conversely, a value much larger than 1 if it is much worse.
To illustrate why such a detailed approach to analysis is necessary, we now briefly show why some common heuristic measures of performance are inadequate. Figures S4, S5, and S6 show the performance results of the 1lin model at the US-Me2 site, examining latent heat flux, sensible heat flux, and NEE in three different common graphical performance measures. These are the average diurnal cycle of NEE, shown for different seasons (Fig. S4); a smoothed time series of Qh (Fig. S5); and the average monthly values of Qle showing the evaporative seasonal cycle (Fig. S6). In most contexts, if these blue curves were plots of a LM's performance, the reader would accept this as qualitative or even quantitative evidence of excellent LM performance. However, these represent perhaps the simplest possible model – a simple linear regression against shortwave, out-of-sample (trained on other sites only). They illustrate just how much site variability can simply be driven by instantaneous shortwave radiation and that visual closeness of curves and an ability to capture seasonal variability, diurnal variability, and even interannual variability should not a priori be accepted as evidence of good model performance.
As noted above, all the analyses were filtered to exclude time steps at each site where observational flux data were flagged as missing or gap-filled. Analyses were half-hourly or hourly, depending on the reported time step size at each site, except for models that only reported monthly outputs, which were then analysed with monthly averages. All data management and analyses were conducted at https://modelevaluation.org (Abramowitz, 2012) and can be repeated there. The analysis codebase used for PLUMBER2 at https://modelevaluation.org is available from modelevaluation.org (2024).
In examining the results from the PLUMBER2 experiment, we emphasise that our aim here is to demonstrate that we have created a holistic environment and methodology that allow us to fairly attribute model–observation mismatch to LMs where appropriate. We do provide a broad overview of the many dimensions of the PLUMBER2 results, but we do not investigate process representations or flaws of any model – doing so would necessarily present an incomplete picture, since these kinds of findings are specific to particular models, environments, and circumstances.
Figure 1 shows Qle versus Qh, averaged across all the sites for participating models that reported both variables. The dashed lines show a proxy for the observed available energy (around 69 W m−2, defined as Qle + Qh assuming that the mean ground heat flux on longer timescales is 0) and the observed Bowen ratio (around 0.7). Perhaps unsurprisingly, the models differ most in their partitioning of surface energy (spread along the available energy axis) rather than the amount of available energy (spread along the Bowen ratio axis), supporting previous findings (Haughton et al., 2016). Those LMs that do not operate in a coupled modelling system (i.e. not coupled to an atmospheric model; EntTBM, LPJ-GUESS, MuSICA, QUINCY, and STEMMUS-SCOPE) also appear to have a much broader spread of estimates than those used in coupled models (they are furthest from the observed Bowen ratio in Fig. 1), and the unrestricted moisture store of the Penman–Monteith model makes it a clear outlier.
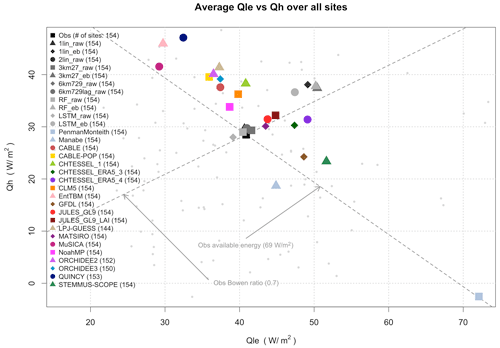
Figure 1Latent heat flux (Qle) versus sensible heat flux (Qh) averaged over 154 sites, shown for models that submitted both quantities. The dashed lines show observed values of the average available energy (Qle + Qh) and the average Bowen ratio (Qh Qle) across the sites, using raw (as opposed to energy-balance-corrected) flux data. The smaller light-grey dots in the background represent the individual site averages.
When averaged across all the sites, the LMs do not appear to show any clear systematic bias in energy partitioning relative to observations across the ensemble. Note that in Fig. 1 the observations do not have the FLUXNET2015 energy balance correction applied (the equivalent figure using energy-balance-corrected fluxes is shown in Fig. S7a). Aside from showing a little more available energy (their mean is slightly offset from the observed available energy line by less than 10 %), the LMs are relatively evenly spread around the observational Bowen ratio. This lends little support to an argument of systematic observational bias in the partitioning of available energy leading to apparent poor LM performance.
The empirical models trained to predict raw fluxes (those labelled *_raw) are tightly clustered around the observational crosshairs. While it is not surprising that regression-based models perform well on the mean, these models are entirely out-of-sample, demonstrating that forcing meteorology alone provides enough information to predict mean fluxes accurately out-of-sample. The energy-balance-corrected observations lie amongst the empirical models trained to predict energy-balance-corrected fluxes (labelled *_eb; the cluster of grey points with higher available energy in Fig. 1 – see Fig. S7a). The average Bowen ratio increases slightly to 0.73 instead of 0.7 with energy balance correction. Perhaps more interesting is that the corrected version of the flux observations contains an average of 16 W m−2 additional energy across these sites, an increase of about 23 %, and that this value sits much further outside the spread of the mechanistically modelled estimates of available energy than the observed value in Fig. 1. So, in this simple metric at least (and indeed in more below), the LMs' performance is not improved with energy-balance-corrected flux data. While we present results from comparisons with raw fluxes in the main part of this paper, comparisons against energy-balance-corrected data, where they qualitatively differ, are discussed and shown in the Supplement. Similarly, when we filter analyses to only include time steps with a wind speed above 2 m s−1 (Fig. S7b), the scatter of the models in Fig. 1 changes surprisingly little.
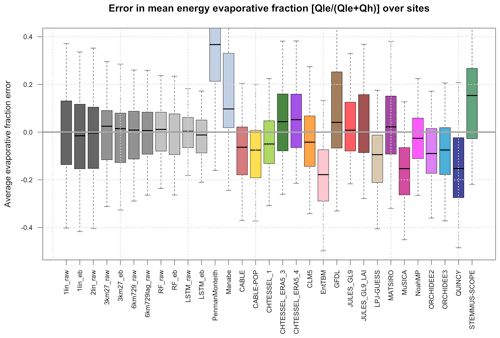
Figure 2Boxplots of errors in the site mean energy evaporative fraction Qle (Qle + Qh) over all the sites, shown separately for each model using raw flux data across 154 sites.
Figure 2 shows boxplots of errors in the average energy evaporative fraction (EF) across the same sites, shown separately for each participating model. The energy evaporative fraction is defined using average flux values at each site: Qle (Qle + Qh). The equivalent plots using energy-balance-corrected data and data filtered for wind speed are almost indistinguishable from Fig. 2 and so have not been included. Consistent with what we saw in Fig. 1, the mechanistic benchmarks and ecosystem models show the largest deviation from the site observations, and empirical approaches are reliably zero-centred despite having no explicit mechanism to constrain the ratio between Qle and Qh. The more sophisticated empirical models (6km*, RF, and LSTM), as well as being zero-error-centred, show less spread, meaning that they have fewer large errors in the energy evaporative fraction. Once again, there does not appear to be any obvious reason to suspect a bias in partitioning in observations – some LMs (6) show a high EF bias and others (11) a low bias.
An equivalent version of this figure showing the water evaporative fraction, Qle Rainf, is shown in Fig. S8a and b using raw and energy-balance-corrected fluxes, respectively. Once again, the models are scattered well about the zero error line when raw fluxes are used, and almost all of them appear strongly negatively biased when compared to the energy-balance-corrected fluxes. The equivalent plots using wind-speed-filtered data are qualitatively the same as Fig. S8a and b and so are not included here.
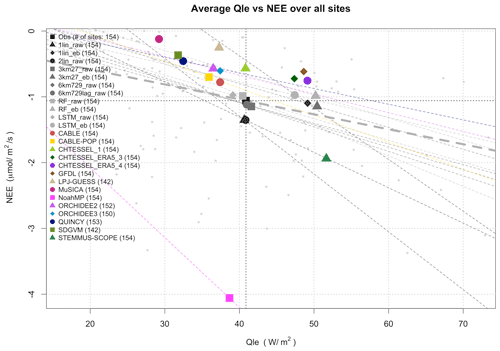
Figure 3Qle versus the NEE of CO2 averaged over 154 sites, shown for models that submitted both quantities. The observed value is shown in black with crosshairs. The light-grey dots in the background represent individual observed site averages, with the linear fit between them shown in bold dashed grey. Regression lines are also shown for LMs that have a stronger fit than in the observed case (R2=0.19).
Figure 3 is similar to Fig. 1 but shows the average Qle versus the NEE of CO2 for LMs that reported both variables. Given the expectation that NEE is likely to be strongly dependent on site history and that we could not reliably include this information in the modelling protocol or account for it in this plot, there is no a priori reason to expect a clear relationship across all the sites here, beyond both fluxes being dependent on stomatal function. While we might broadly expect increasing carbon uptake with increasing Qle, as shown by the observed regression line in Fig. 3, the fit is relatively weak (R2 is 0.19). LM regressions are shown where their fit has a higher R2 than the observed one, although we note that, aside from ORCHIDEE2, CABLE-POP, and Noah-MP, only empirical models meet this criterion (which is unsurprising, since they effectively act as data smoothers).
With the exception of Noah-MP, STEMMUS-SCOPE, and some empirical models, all LMs predict less net carbon uptake than is observed. This may well be because the models were run without any site history. That is, the simulated ecosystems were closer to equilibrium than those in the real world. In equilibrium, vegetation and soil carbon stocks are high and thus respiration is also higher, as it is generally simulated as a function of carbon stocks. Ecosystem models predict the lowest carbon uptake but a large range of Qle values (MuSICA, LPJ-GUESS, QUINCY, and SDGVM). The equivalent plot with energy-balance-corrected Qle values (not shown) simply moves the “observed” black square to the right, once again sitting amongst 1lin_eb, 3km27_eb, RF_eb, and LSTM_eb. Once again, the energy-balance-corrected data do not appear to match LM simulations better than raw flux data.
We also note that, while LMs' spread might well be because of a lack of site history information, the empirical models show that missing this information does not actually reduce NEE predictability to a large degree (all the empirical models are within 0.35 µmol m−2 s−1 of the observations). The empirical models also do not have any site history and indeed in most cases do not even use any estimate of LAI. They are trained only at other sites, so they cannot infer any site history information from the meteorology–flux relationship. Despite this, they cluster quite tightly around the observations in Fig. 3, whether predicting raw Qle (cluster of grey points in the crosshairs) or energy-balance-corrected Qle (cluster of grey points to the right of this). They all suggest a net uptake of C across these sites within a narrow range spread around the observations.
Figure 4 is similar to Fig. 2 but shows error in water use efficiency (NEE Qle), expressed in micro-mol of carbon gained per gram of water (left vertical axis), and error as a percentage of observed water use efficiency (WUE) (right vertical axis), with the heavy pink dashed lines representing ±100 %. This shows that almost all LMs underestimate WUE, typically by about 50 %, which is presumably related to the broad underprediction of NEE by LMs that is evident in Fig. 3. At the other end of the spectrum, Noah-MP shows a very high WUE bias, which is consistent with its overprediction of C uptake in Fig. 3 (due to a high dynamically predicted LAI). The empirical models, without any explicit constraint on the ratios of predicted variables (they are predicted independently), are better spread around the observed values. Note that this statement applies equally to those empirical models trained on raw flux tower data and those trained on energy-balance-corrected data. Only the simplest empirical model – 1lin – shows 25th or 75th percentiles (across the sites) outside the 100 % error in WUE, whereas most (8 out of 14) of the LMs do. The equivalent plot using energy-balance-corrected Qle data is shown in Fig. S9 and looks qualitatively similar to Fig. 4. For this metric, there are no discernible differences in performance across the types of LMs.
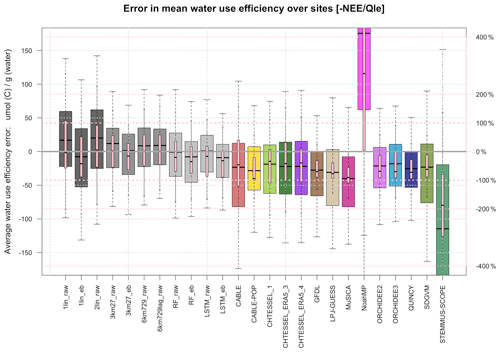
Figure 4Boxplots of errors in the site mean ecosystem water use efficiency (−NEE Qle) over all the sites, shown separately for each model. WUE error is expressed in both micro-mol of carbon gained per gram of water lost (left vertical axis, grey and multi-coloured boxplots) and error percentage of the observed WUE (right vertical axis, pink boxplots), with the heavy pink lines representing ± 100 %.
As noted above, a range of alternative versions of the plots above is available in the Supplement, examining sensitivity to energy-balance-corrected data and low-turbulence periods. Additional analyses, such as water evaporative fraction boxplots (Fig. 8a and b) and variable density estimates for each model (Fig. S10a and b), are also in the Supplement.
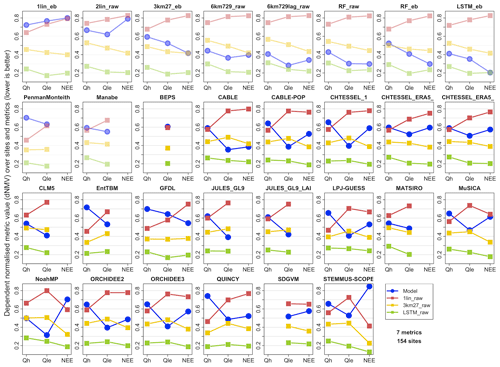
Figure 5The average performance across all 154 sites and seven metrics for Qh, Qle, and NEE (lower is better). The average performance is the mean of the dependent normalised metric values (dNMVs) within the range of metric values across the models being compared in each panel (four in total: the LM in blue – shown in the plot title – and three reference benchmarks 1lin_raw in red, 3km27_raw in yellow, and LSTM_raw in green). The first 10 panels (faded) show empirical or physical benchmark models.
We now investigate a more direct comparison between LMs and empirical benchmarks by exploring results using our two summative indicators. Figure 5 shows modified “PLUMBER plots”, similar to Best et al. (2015), but here using the average of the dNMVs in the range of metric values across the four models being compared in each panel (one LM, 1lin_raw, 3km27_raw, and LSTM_raw). This is as opposed to the average rank of metric values used in Best et al. (2015), which can distort results when metric values are clustered, as noted in Sect. 1. Each panel in Fig. 5 shows the model in the panel title in blue, with benchmark empirical models in red (1lin_raw), yellow (3km27_raw), and green (LSTM_raw). Lower values represent better performance. The LMs are shown alphabetically, with the first 10 panels, faded, showing the remaining empirical models and physical benchmarks against these three benchmark models.
The out-of-sample LSTM_raw on average performs best across all the fluxes for these sites and metrics. The performance of the LMs is highly variable, with half of them being better than the 3km27_raw model for Qle, 15 of 18 worse than the out-of-sample simple linear regression (1lin_raw) for Qh, and NEE typically being between the 1lin_raw and 3km27_raw performance levels (12 of 14 LM variants). Overall, it is clear that LMs tend to perform better against the benchmarks for Qle and NEE than Qh, typically falling within the range of these three benchmarks for Qle and NEE. CLM5, MATSIRO, and Noah-MP are the only LMs with Qh metrics within this range. The LMs falling outside the benchmark dNMV ranges for Qle and NEE are a mixture of LSMs and ecosystem models. The equivalent plot using energy-balance-corrected Qle and Qh observations is shown in Fig. S11a. The performance of the LMs against the benchmarks remains remarkably similar, with some LMs slightly better and others slightly worse against corrected data. Filtering for higher wind speed time steps (Fig. S11b, using raw flux data) also appears to make no qualitative difference, if anything making the LM performance worse relative to these empirical benchmarks. While this may appear to be a marked improvement in LM performance relative to the results in Best et al. (2015), these results are not directly comparable, something we explore further in the “Discussion and conclusions” section.
When we look at the same set of figures using an iNMV instead of a dNMV, the picture is very different (Fig. 6). Recall that an iNMV sets the normalised metric range (0, 1) based on the three reference out-of-sample empirical models (1lin, 3km27, and LSTM) only rather than these three and the LM, and it then compares the LM to this range. For example, if the three reference empirical models have mean biases in Qle of 35, 28, and 25 W m−2 (a range of 10 W m−2) and the LM has a bias of only 10 W m−2, the iNMVs of the reference models are 1, 0.3, and 0, respectively, and the LM has an iNMV of −1.5 (remembering that lower is better). Alternatively, if the LM has a bias of 50 W m−2, its iNMV will be 2.5. So, iNMVs are not constrained to be in the unit interval, as they are for dNMVs.
Figure 6 shows the same data as Fig. 5 but uses iNMVs instead of dNMVs. The iNMVs for the three reference models are now identical across all the LM panels, so the iNMVs for each LM are directly comparable. Note however that the vertical axis scale is different in each panel, so we can see the range for each LM. The LM performance in iNMVs clearly looks a lot worse. This tells us that when LMs perform worse than the out-of-sample linear response to shortwave 1lin, they often perform a lot worse (at least a lot worse relative to the range between 1lin and LSTM_raw). While some LMs (CABLE, CABLE-POP, CHTESSEL, CLM, JULES, Noah-MP, and ORCHIDEE) perform within the range of the three empirical models for some variables, averaged over all the variables, no LM outperforms the out-of-sample linear regression against SWdown. This is a sobering result. LM performance is particularly poor relative to the benchmarks for Qh, with no models within the range of the benchmarks (compared to 40 % of them for Qle and 29 % for NEE).
Equivalent plots to Fig. 6 using energy-balance-corrected fluxes (Fig. S11c) and time steps with wind speed >2 m s−2 (Fig. S11d) are shown in the Supplement. Again, the LM performance appears remarkably similar despite the significant changes made with the target energy-balance-corrected data (Fig. 1). It remains true that no LMs outperform the 1lin averaged over all the fluxes. Note that, in this comparison, where energy-balance-corrected data are the reference target, the versions of the empirical models trained for this target are used for comparison (i.e. 1lin_eb, 3km27_eb, and LSTM_eb).
We also note that, despite this result, some LMs do perform better than the empirical benchmarks for a subset of the metrics in Table S4, for some variables. Figure S11e–k are versions of Fig. 6 constructed with only one metric at a time. LMs tend to perform better in the 5th percentile and probability density function (PDF) overlap metrics and worst in temporal correlation and normalised mean error (NME). It is also apparent that RF, 6km729, and 6km729lag all outperform the LSTM in quite a few of these metrics. Despite this, we did not investigate alternatives to the LSTM as the high-level empirical benchmark.
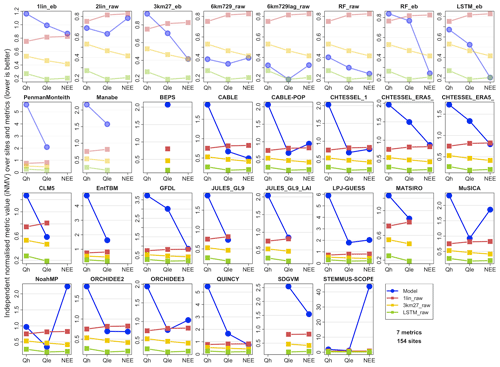
Figure 6Like Fig. 5 but using the average of independent normalised metric values (iNMVs) defined by the range of metric values across the three reference models (1lin_raw, 3km27_raw, and LSTM_raw). Note that the different panels have different y axes.
We now examine the discrepancy between our best-performing out-of-sample empirical model and a given mechanistic model in more detail. This defines an amount which we know the mechanistic model can improve by. This also allows us to define model performance in a way that accounts for site complexity, peculiarity, and predictability, together with the observational errors particular to each site, and it avoids some misleading statistics like large RMSE values at sites that simply have larger fluxes. For this purpose, we use one of the best-performing empirical models as the reference model, LSTM_raw. While it is the best-performing model in this collection, it provides a lower-bound estimate of the predictability of fluxes at each site, since we can almost certainly produce better empirical models.
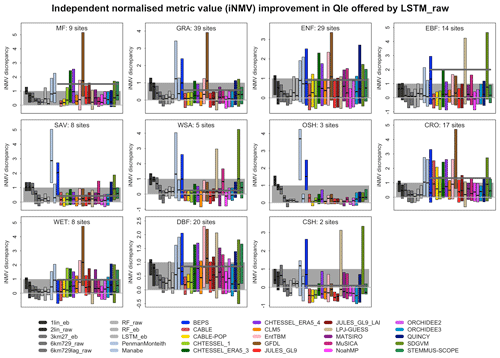
Figure 7Independent normalised metric discrepancy between each model and LSTM_raw for Qle, sorted by vegetation type. The average of all the LMs for each vegetation type is shown by the bold dark-grey line, and the zero line is in light grey. Lower scores are better.
In Fig. 7, we look at the discrepancy in iNMVs between each mechanistic model and LSTM_raw for latent heat flux predictions. The results are shown in a separate panel for each IGBP vegetation type and each model as a boxplot within each panel. Only the interquartile range and median estimates are shown for each boxplot. The observed vegetation types are used for each site, noting that some LMs with dynamic vegetation might represent these sites differently. Values below 0 show that the LM performed better than the three benchmark empirical models (1lin, 3km27, and LSTM). Values between 0 and 1 mean that the LM performed within the range of the benchmark models (shaded grey background), and values above 1 mean that the LM was worse than 1lin. The average of all mechanistic LMs for each vegetation type is shown by the dark-grey horizontal line, with the zero line in light grey. Each boxplot represents the difference in independent normalised metric values across all the metrics in Table S4.
There are clearly variations in performance across the vegetation types, and while the mean LM performance is worst for open shrubland (OSH), evergreen broadleaf forest (EBF), and mixed forest (MF), the results across the different LMs vary significantly. Overall, the LM performance appears better for grass-dominated vegetation types (grassland and savannas) than tree ecosystems. The equivalent plots for Qh (Fig. S12b), using energy-balance-corrected data (Fig. S12a for Qle, Fig. S12c for Qh) and NEE (Fig. S12d), suggest that there is no clear differentiation of performance by vegetation type – no particular vegetation type is consistently anomalous. While some of the LM means (dark-grey line) appear to change markedly for Qle after energy balance correction (most notably for grassland sites), this seems to be at least partially because of significant changes to outlier LMs rather than a change in the aggregate behaviour. Some LMs show improved performance using energy-balance-corrected data, others show degradation, although more appear to improve. There is definitely less of a change for Qh as a result of energy balance correction. Also note that, in all of these figures, the LM mean is often well above most of the 25th–75th percentile boxplots. This simply reinforces the point made above that, when LMs are worse than the reference benchmarks, they are often much worse (the smallest and largest 25 % of the values obviously do not contribute to these boxplots). Figure 13a–e show the same information but sorted by model rather than vegetation type.
Finally, we examine LM performance in the context of the issue we raised in Sect. 2.2. A significant proportion of the sites had Qle fluxes larger than incident rainfall, and since this is something that most LMs will be structurally prohibited from replicating (with the possible exception of wetlands), we explore why this might be the case and whether the issue has biased our overall conclusions about LM performance. Figure 8 once again shows the iNMV improvement offered by the LSTM over LMs on a per-site basis, with the median difference for all of the LMs plotted (shown in colours). Each site's location is shown on axes of observed water evaporative fraction versus dryness index, as in Fig. S2a–d. Note that the location of the 1–1 line relative to the sites is very much dependent on our estimate of potential evapotranspiration (PET), which is given here by the Penman–Monteith model described above, so it is entirely plausible that a different estimate would see all the sites (with the exception of US-Bkg) lying to the right of the 1–1 line. We might also wish to plot a curve in this figure illustrating the Budyko hypothesis (Budyko, 1974), although there is no single accepted derivation of an equation that describes the asymptotic behaviour it suggests (Sposito, 2017; Mianabadi et al., 2019), but the spread of the sites should make it clear why this is not particularly useful. Many sites have a water evaporative fraction above 1. This emphasises that the conceptual idealisation of the Budyko hypothesis only applies at very large spatial scales and/or under idealised circumstances of water availability. Irrigation or landscape features like topography or hillslope, sub-surface bedrock bathymetry, or groundwater can mean that it is entirely physically reasonable for a location to exhibit a water evaporative fraction above 1, as around 30 % of these sites do. These factors are likely to still be relevant at scales of tens of kilometres, so it seems unreasonable to suggest that these effects are not also relevant for gridded simulations.
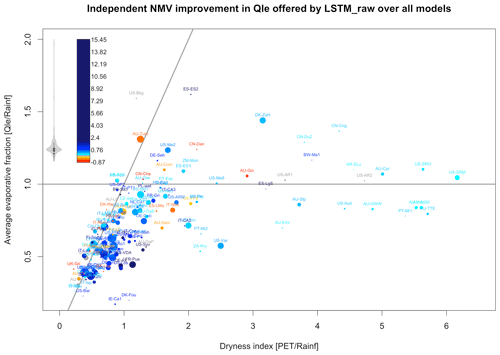
Figure 8The iNMV improvement offered by LSTM over the median iNMV of all the LMs (excluding empirical and physical benchmarks), shown in colour for Qle. Each site's location is shown on the axes of the observed water evaporative fraction versus the dryness index. The prevalence of particular colour values is shown by the violin plot to the left of the colour legend. Values within [−0.1, 0.1] are shown in grey, and values above 2 have a constant, dark-blue colour. The dot sizes indicate the length of the site data, ranging from 1 year (smallest) to 21 years (largest) – see Table S2 for the site details.
Of the sites in Fig. 8 with a water evaporative fraction greater than 1, only one is irrigated (ES-ES2) and none are wetland sites. Hillslope factors are quite plausibly important in four others (CN-Dan, DK-ZaH, US-SRG, and US-SRM). One is affected by fire prior to the measurement period, which might mean that accumulated water was available (US-Me6). The others are sites from the La Thuile release not included in FLUXNET2015, which raises the possibility of data quality concerns (BW-Ma1, ES-ES1, RU-Zot, US-Bkg, and US-SP3). However, for the majority there is no immediately obvious explanation (AR-SLu, AU-Cpr, AU-Cum, AU-Gin, AU-Otw, AU-Tum, CN-Cha, CN-Cng, CN-Du2, DE-Seh, FR-Fon, US-AR1, US-AR2, US-Me2, and ZM-Mon). While the data used in Fig. 8 are filtered for gap-filled and other quality control flags, we can confirm that using the entire time series for each site does not result in any qualitative change to the site locations in this figure (Fig. S2c).
The equivalent plots of Fig. 8 for corrected Qle, Qh, corrected Qh, and NEE are shown in Fig. S14a–d. None of these show a markedly higher density of poor LM performance (green-blue dots) above the 1.0 line, where Qle exceeds precipitation on average. So, despite there being a structural impediment to LMs simulating these sites, that impediment is clearly not the major cause of the LMs' poor performance. These figures also do not appear to support the community's heuristic expectation that LM performance will decrease with dryness. While there is a cluster of energy-limited sites where LMs consistently outperform LSTM_raw (red–orange–yellow dots), there are also several water-limited sites where LMs do well, and the sites worst simulated by LMs, shown in blue, seem evenly spread throughout the figures.
While it is clear that LSTM_raw broadly outperforms LMs at most sites, there are clearly some sites (red–orange–yellow) where LMs on aggregate outperform LSTM. This does not appear to be the case consistently across all three fluxes for any particular site, however, nor indeed is there any clear signal about the types of sites (in terms of vegetation type, dryness, or available energy) that are better simulated. This probably suggests that these outcomes may be more stochastic than the result of any structural advantage the LMs might have.
In addressing our overall goal of fairly assessing the fidelity of land models, we aimed to create an evaluation framework that met two criteria: (1) a simulation environment that offered enough observational constraint to attribute model–observation mismatch to a model, where appropriate, and (2) a benchmarking approach within that environment that could ensure this attribution was fair by quantifying reasonable performance expectations. Below we discuss the extent to which this was achieved, what we learned from applying the framework to the PLUMBER2 experimental results, caveats, and implications for future research.
4.1 Simulation environment, observational constraint, and data quality
There are several important findings in terms of observational constraint. The first is that we can conclusively say that this simulation environment does offer enough observational constraint to diagnose model performance. The fact that a broad range of empirical models, trained at sites other than where they are tested, can reliably outperform LMs tells us that enough information is available to LMs to do better. What is less clear is whether the lack of constraint on LM parameter specification causes poor LM performance – something we discuss in more detail below.
In terms of observational data quality, despite raw and energy-balance-corrected fluxes clearly being very different, our conclusions about model performance are relatively similar with or without the correction. This qualitative similarity is only clear because of the ability to define performance expectations using empirical benchmarks separately in each case. Similarly, restricting analyses to low-turbulence periods does not result in a qualitative change to the performance assessment of LMs, so it is clear that, while there may well be issues with nighttime flux tower data, they are not the primary cause of the poor agreement between LMs and tower fluxes.
Next, the use of empirical benchmarks trained separately to predict raw and energy-balance-corrected fluxes also gives us some insight into how appropriate the FLUXNET2015 energy balance correction process might be. Figure 1 and its equivalents in the Supplement show that, in general, available energy in LMs is indeed higher than in raw observations (noting that a priori this is not evidence that the observations are wrong). However, the energy-balance-corrected versions of this plot show an even larger discrepancy. Similarly, the differences between corrected and uncorrected water evaporative fractions (Fig. S8a and b) show that corrected Qle fluxes look markedly different to almost all models. The plots based on iNMVs do seem to show that the correction process helps improve the overall performance for several LMs. There is, however, more subtle evidence in the performance of the empirical models that gives us other, contradictory information. LSTM_raw is the best-performing reference model in Fig. 6 and, as expected, LSTM_eb, trained to match qualitatively different (energy-balance-corrected) target data, does not perform as well against raw flux data as LSTM_raw. This is what we would expect. However, when we look at the reverse situation, using LSTM_eb as the reference model and energy-balance-corrected fluxes as the target data (shown in Fig. S11c), the situation is quite different. LSTM_raw performs worse for Qh, as expected, but it performs better than LSTM_eb for Qle. This tells us that, unlike for Qh, a sophisticated machine learning (ML) model trained on the corrected Qle flux has no advantage in predicting corrected Qle than the same ML model trained on raw fluxes – in fact, it has a disadvantage. A similar result can be seen for 6km729lag. It is less sophisticated than LSTM_eb and is trained to predict raw fluxes, yet it outperforms LSTM_eb. This suggests that the correction to Qle makes these fluxes less predictable and that the correction to Qle is categorically incorrect, whereas the correction to Qh may well add some value. This may suggest that the missing energy in uncorrected fluxes might be more likely to be in Qh fluxes (agreeing with other proposed correction approaches – see Charuchittipan et al., 2014).
Finally, we discuss the structural assumption in most LMs that horizontal transport of water between grid cells is negligible. A significant number of sites show a water evaporative fraction greater than 1, which, despite being entirely physically plausible, is simply not possible for most current LM process representations to replicate. This tells us that either (a) access to groundwater beyond gravity drainage is common, (b) below-surface bedrock structure has a significant local hydrological effect, and/or (c) horizontal advection of moisture in soil (and locally on the surface) plays a significant role in moisture availability at the ∼ 1 km2 spatial scale (i.e. flux tower fetch). Very few global coupled models include any of these effects. It is very likely that almost all sites and indeed much larger spatial scales are affected by this same issue to varying degrees, even if their water evaporative fractions do not appear to be anomalously high. This may well include all spatial scales below river and groundwater basin scales. Despite this revelation, it is remarkable that LM performance is apparently not any worse for sites where evapotranspiration exceeds precipitation (Figs. 8 and S14a–d). This suggests that, despite the structural assumption being violated in the LMs here, other aspects of process representation are more detrimental to overall LM performance.
4.2 Benchmarking methodology
It should be clear that choices made in how we assess model performance can result in markedly different conclusions. The difference in apparent LM performance between dNMVs and iNMVs as a summative indicator is stark. By excluding the LM we are evaluating from the criteria that define good or bad performance (the set of the three empirical models), we define benchmark levels of performance that are independent of the LM being evaluated. This means that when the LM is much better or much worse than a priori expectations, it will get a score that is proportionally much better or much worse. Using metric ranks or dNMVs instead limits the cost of poor performance in the cumulative metrics shown in PLUMBER-style plots (Best et al., 2015) and so gives an artificially positive indication of LM performance relative to the reference benchmark models.
We suggest that the framework we present provides a way of assessing the significance of proposed improvements to LM performance that is relatively insensitive to metric choice and critically is based on a demonstrated capacity for improvement. That is, when a LM is worse than an out-of-sample empirical model given the same predictors, we know that there is enough information provided to the LM to do better. We suggest that the summative analysis we present here using iNMVs is a fairer, more comprehensive representation of LM performance than either the original PLUMBER paper or the dNMV versions of the same analyses.
Beyond a lower-bound estimate of potential improvement, the hierarchy of empirical models we examined also provides more nuanced information about performance expectations. The difference in performance between 6km729 and 6km729lag, for example, quantifies the improvements in flux simulation we should expect from adding model states such as soil moisture and temperature rather than simply having an instantaneous response to meteorology (Fig. S13a–e). The same is also true of the RF and LSTM, although they had slightly different predictor sets and architectures. The simplest model, 1lin, also makes it clear that much of what we might heuristically regard as high model fidelity is a simple linear response to shortwave forcing (Figs. S4, S5, and S6 and, perhaps most importantly, Fig. 6). It should be abundantly clear that simple diagnostics can be very misleading and that defining good model performance is inherently complicated. Without the empirical model hierarchy detailed here, judgements about LM performance would almost certainly be susceptible to confirmation bias.
4.3 PLUMBER, PLUMBER2, and implications for LMs
It might appear from Fig. 5 that many LMs (CABLE, CHTESSEL, CLM, JULES, MATSIRO, MuSICA, ORCHIDEE, and Noah-MP) perform better here than the 3km27 model for Qle, something that could represent progress since the original PLUMBER experiment (where no models outperformed the 3km27 model for standard metrics – see Best et al., 2015). There are however some differences here that mean the PLUMBER and PLUMBER2 results are not directly comparable. First, the single set of metrics we use here is a combination of the “standard”, “distribution”, and “extremes” metrics used in PLUMBER, and the worst LM performance in PLUMBER was for the standard metrics alone. Next, Fig. 5 uses a (dependent) normalised metric range rather than ranks. We also have fewer models, and different models, in each panel that is used to calculate the metric range, and the results are calculated over 154 instead of 20 sites. It nevertheless remains true that Qh is much more poorly predicted than Qle.
While of a similar performance standard to Qle prediction overall, NEE was notably underpredicted by LMs in a way that Qle was not. While it seems obvious that a lack of site history in the LM setup (noting that this information was not available) is the cause of this, it is intriguing to see that empirical models (also not given this information) were able to predict NEE without this bias, in most cases without any LAI information at all (Figs. 3 and 4). These empirical models were out-of-sample (they did not use any data from the sites they predicted in their training). This is an indication that the importance of site history and leaf area is overstated in our LMs and is not as important as we may believe for flux prediction.
These results raise the question of whether LMs are too complex for the level of fidelity they provide. It is at least theoretically possible, for example, that a LM is perfect, but because we are unable to precisely prescribe its parameters for these site simulations (and global simulations), we actively hinder its ability to get the right result. What the out-of-sample empirical models show is that the information available in LM meteorological variables alone – without any description of what type of vegetation or soil might be at a given site, or indeed what the reference height of the measurements might be – is enough to outperform all of the LMs. This is not to say that LMs could not perform better if more detailed site-specific information were available, but the way that they were run here was designed to mimic their application at global scales, and for that job they are considerably more complicated than is justified by their performance. A more detailed examination of how well LMs perform when given detailed site information would not simply require us to show that metric scores for LMs improved when given this information: it would require that LMs come closer to outperforming ML approaches also provided with similar site-specific information.
There are of course other reasons why we might want complexity in a LM beyond improved performance, like the ability to infer the impacts of particular decisions on a broader range of processes within the land system. However, it is important to know the degree of predictability that is possible with the increasing amount of information that our models are provided with – what we are missing out on that is categorically achievable. The fact that increasing model complexity has been found to show little relationship with performance under some circumstances, even when additional site information is provided, should be concerning (Lipson et al., 2023). We also need to recognise that the many increases in sophistication that we might want to include to improve the representativeness of LMs (Fisher and Koven, 2020) may come at a significant cost. The more degrees of freedom we have in a model, the broader the range of observational data we need to effectively constrain it, the less able we are to pinpoint model shortcomings, and the more susceptible we become to getting the right answer for the wrong reasons (Lenhard and Winsberg, 2010). A very crude statistical analogy might be that, if we have a model with one process that is right 90 % of the time, the model is 90 % accurate. However, if we have a model with 10 serial processes that are right 90 % of the time, the model is 0.910 = 35 % accurate (although only if the errors are independent).
This of course does not mean that LMs will always appear to perform badly in global-scale studies, especially if performance expectations are not quantified in the way we have done here. Figures S4, S5, and S6 show that we can explain a considerable amount of observed variability with very simple models, and examining results on longer timescales, as is typically the case in global studies, will not change this. We are only able to draw the conclusions we have here because we have clearly defined performance expectations in terms of the amount of information available to LMs about surface flux prediction, and we have examined this close to the process scale rather than averaging over longer periods and spatial scales.
4.4 Next steps
As with most model comparisons, the summary statistics presented in this paper do not give us any categorical indications about how to start improving models. They nevertheless allow us, perhaps for the first time, to fairly account for some of the inevitable difficulties and eccentricities associated with using observed data. By evaluating performance relative to out-of-sample empirical estimates, we can quantify expectations of achievable LM improvement and isolate the circumstances under which this potential for improvement is most apparent. We did not actively explore these circumstances in detail here, since they are particular to each LM, but we have nevertheless provided an approach to achieve this. Some clear indications are already evident from the sites shown in green and particularly blue in Figs. 8 and S14a, b, c, d. These are sites where we know that LM prediction can be substantially improved, since an out-of-sample empirical model offers substantial performance improvements using the same predictors as LMs. These of course form the average discrepancy across all the LMs, so the capacity for improvement at a particular site is likely to vary for different models. Equivalent figures for each individual model and variable can be found at https://modelevaluation.org in the PLUMBER2 workspace on the profile page for each submitted model output. The data and analysis code from this experiment are also available, and we openly invite further analyses and contributions from the community.
The next steps for the community towards building LMs that better utilise the information available to them seem reasonably clear. Understanding the shortcomings of a LM is not a simple process, so moving away from in-house, ad hoc model evaluation towards more comprehensive, community-built evaluation tools where the efforts of those invested in model evaluation are available to everyone will be key. This will allow results to be comparable across institutions and routine automated testing to become part of the model development cycle. This will need to cover both global scales (e.g. ILAMB; Hoffman et al., 2017; Collier et al, 2018) and site-based process evaluation (e.g. https://modelevaluation.org; Abramowitz, 2012). In both cases, inclusion of empirical performance estimates, such as those shown here, will be key to distinguishing incremental improvements from qualitative improvements in LM performance.
Finally, there is obviously much, much more to explore in the PLUMBER2 dataset. Most participants submitted many more variables than were examined in this paper (and several came close to the list in Table S2). The vast majority of submissions to PLUMBER2, as well the forcing and evaluation data, are publicly available at https://modelevaluation.org as a community resource for further analyses, and we actively invite further collaborations to utilise the dataset that this experiment has produced. This paper nevertheless provides the community with a benchmarking framework that is relatively insensitive to observational errors and choices in evaluation metrics, and it defines model performance in terms of demonstrated capacity for improvement rather than model–observation mismatch alone.
The flux tower data used here are available at https://doi.org/10.25914/5fdb0902607e1 as per Ukkola et al. (2021, 2022) and use data acquired and shared by the FLUXNET community, including these networks: AmeriFlux, AfriFlux, AsiaFlux, CarboAfrica, CarboEuropeIP, CarboItaly, CarboMont, ChinaFlux, Fluxnet-Canada, GreenGrass, ICOS, KoFlux, LBA, NECC, OzFlux-TERN, TCOS-Siberia, and USCCC. The ERA-Interim reanalysis data are provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) and are processed by LSCE. The FLUXNET eddy covariance data processing and harmonisation was carried out by the European Fluxes Database Cluster, AmeriFlux Management Project, and Fluxdata project of FLUXNET, with the support of CDIAC, the ICOS Ecosystem Thematic Center, and the OzFlux, ChinaFlux, and AsiaFlux offices. All the land model simulations in this experiment are hosted at https://modelevaluation.org and, to the extent that participants have no legal barriers to sharing them, are available after registration at https://modelevaluation.org. The analyses shown here were also performed on modelevaluation.org, using the codebase publicly available at modelevaluation.org (2024).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-21-5517-2024-supplement.
The experimental design was conceived by GAb with assistance from ML, MGDK, AU, MC, and wider community feedback. The data processing and analysis were developed and completed by GAb, with input from ML, MGDK, AU, and JCP. The empirical model simulations were completed by JCP, SH, SG, GA, CB, JF, and GN. The physical benchmark models were built and run by MB and HR. The mechanistic land model simulations were completed by MGDK, AU, JK, XL, DF, SB, KO, DL, XWF, CO, PP, PdR, NV, HR, MB, SM, TN, HK, YZ, YW, BS, YK, KC, APW, PA, GAr, MC, JO, SC, and CRF. The manuscript was written by GAb, with feedback and iterations between all the co-authors.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Gab Abramowitz, Sanaa Hobeichi, Jon Cranko Page, Anna Ukkola, and Martin G. De Kauwe acknowledge the support of the Australian Research Council (ARC) Centre of Excellence for Climate Extremes (grant no. CE170100023). Anna Ukkola acknowledges the support of the ARC Discovery Early Career Researcher Award (no. DE200100086). This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (NCI), which is supported by the Australian government. Bob Su, Yunfei Wang, and Yijian Zeng acknowledge the support of the Netherlands Organisation for Scientific Research (NWO) (WUNDER project, grant no. KICH1.LWV02.20.004) and the Netherlands eScience Center (EcoExtreML project, grant no. 27020G07). Jonathan Frame acknowledges the support of a NOAA Cooperative Agreement (no. NA19NES4320002). The contributions by Keith Oleson and David Lawrence are supported by the National Center for Atmospheric Research (NCAR), sponsored by the National Science Foundation (NSF) under grant no. 1852977. Computing and data storage resources for CLM5, including the Cheyenne supercomputer (https://doi.org/10.5065/D6RX99HX), were provided by the Computational and Information Systems Laboratory (CISL) at NCAR. Hyungjun Kim was supported by a National Research Foundation of Korea (NRF) grant funded by the South Korean government (MSIT) (no. 2021H1D3A2A03097768). Anthony P. Walker acknowledges that ORNL is managed by UT-Battelle, LLC, for the DOE under contract no. DE-AC05-100800OR22725. The LSTM models were run with computing resources provided by the NASA Terrestrial Hydrology programme (grant no. 80NSSC18K0982). The Noah-MP simulations were funded by NASA (grant no. 80NSSC21K1731).
This paper was edited by Paul Stoy and reviewed by three anonymous referees.
Abramowitz, G.: Towards a benchmark for land surface models, Geophys. Res. Lett., 32, L22702, https://doi.org/10.1029/2005GL024419, 2005.
Abramowitz, G.: Towards a public, standardized, diagnostic benchmarking system for land surface models, Geosci. Model Dev., 5, 819–827, https://doi.org/10.5194/gmd-5-819-2012, 2012.
Abramowitz, G., Pouyanné, L., and Ajami, H.: On the information content of surface meteorology for downward atmospheric long-wave radiation synthesis, Geophys. Res. Lett., 39, L04808, https://doi.org/10.1029/2011GL050726, 2012.
Abramowitz, G., Herger, N., Gutmann, E., Hammerling, D., Knutti, R., Leduc, M., Lorenz, R., Pincus, R., and Schmidt, G. A.: ESD Reviews: Model dependence in multi-model climate ensembles: weighting, sub-selection and out-of-sample testing, Earth Syst. Dynam., 10, 91–105, https://doi.org/10.5194/esd-10-91-2019, 2019.
Arora, V. K., Seiler, C., Wang, L., and Kou-Giesbrecht, S.: Towards an ensemble-based evaluation of land surface models in light of uncertain forcings and observations, Biogeosciences, 20, 1313–1355, https://doi.org/10.5194/bg-20-1313-2023, 2023.
Aubinet, M., Feigenwinter, C., Heinesch, B., Laffineur, Q., Papale, D., Reichstein, M., Rinne, J., and Van Gorsel, E.: Nighttime Flux Correction, in: Eddy Covariance: A Practical Guide to Measurement and Data Analysis, edited by: Aubinet, M., Vesala, T., and Papale, D., Springer Netherlands, Dordrecht, 1st edn., 438 pp., https://doi.org/10.1007/978-94-007-2351-1, 2012.
Beaudry, N. and Renner, R.: An intuitive proof of the data processing inequality, Quantum Inf. Comput., 12, 432–441, https://doi.org/10.48550/arXiv.1107.0740, 2012.
Bennett, A. C., Knauer, J., Bennett, L. T., Haverd, V., and Arndt, S. K.: Variable influence of photosynthetic thermal acclimation on future carbon uptake in Australian wooded ecosystems under climate change, Glob. Change Biol., 30, e17021, https://doi.org/10.1111/gcb.17021, 2024.
Best, M. J., Abramowitz, G., Johnson, H. R., Pitman, A. J., Balsamo, G., Boone, A., Cuntz, M., Decharme, B., Dirmeyer, P., Dong, J., Ek, M., Guo, Z., Haverd, V., van den Hurk, B. J., Nearing, G. S., Pak, B., Peters-Lidard, C., Santanello, J., Stevens, L., and Vuichard, N.: The plumbing of land surface models: benchmarking model performance, J. Hydrometeorol., 16, 1425–1442, https://doi.org/10.1175/JHM-D-14-0158.1, 2015.
Bi, D., Dix, M., Marsland, S., O'Farrell, S., Sullivan, A., Bodman, R., Law, R., Harman, I., Srbinovsky, J., Rashid, H. A., Dobrohotoff, P., Mackallah, C., Yan, H., Hirst, A., Savita, A., Dias, F. B., Woodhouse, M., Fiedler, R., and Heerdegen, A.: Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model, J. South. Hemisph. Earth Syst. Sci., 70, 225–251, https://doi.org/10.1071/ES19040, 2020.
Bonan, G. B., Patton, E. G., Finnigan, J. J., Baldocchi, D. D., and Harman, I. N.: Moving beyond the incorrect but useful paradigm: reevaluating big-leaf and multilayer plant canopies to model biosphere-atmosphere fluxes – a review, Agr. Forest Meteorol., 306, 108435, https://doi.org/10.1016/j.agrformet.2021.108435, 2021.
Boussetta, S., Balsamo, G., Beljaars, A., Panareda, A.-A., Calvet, J.-C., Jacobs, C., van den Hurk, B., Viterbo, P., Lafont, S., Dutra, E., Jarlan, L., Balzarolo, M., Papale, D., and van der Werf, G.: Natural land carbon dioxide exchanges in the ECMWF Integrated Forecasting System: Implementation and Offline validation, J. Geophys. Res., 118, 1–24, https://doi.org/10.1002/jgrd.50488, 2013.
Budyko, M. I.: Climate and life, p. 508, 1st Edn., Academic Press, New York, ISBN 0121394506, 1974.
Buechel, M.: Understanding hydrological change with land surface models, Nat. Rev. Earth. Environ., 2, 824, https://doi.org/10.1038/s43017-021-00241-0, 2021.
Bush, M., Boutle, I., Edwards, J., Finnenkoetter, A., Franklin, C., Hanley, K., Jayakumar, A., Lewis, H., Lock, A., Mittermaier, M., Mohandas, S., North, R., Porson, A., Roux, B., Webster, S., and Weeks, M.: The second Met Office Unified Model–JULES Regional Atmosphere and Land configuration, RAL2, Geosci. Model Dev., 16, 1713–1734, https://doi.org/10.5194/gmd-16-1713-2023, 2023.
Charuchittipan, D., Babel, W., Mauder, M., Leps, J.-P., and Foken, T.: Extension of the averaging time in Eddy-covariance measurements and its effect on the energy balance closure, Bound.-Lay. Meteorol., 152, 303–327, https://doi.org/10.1007/s10546-014-9922-6, 2014.
Chen, X. and Sivapalan, M.: Hydrological basis of the Budyko curve: Data-guided exploration of the mediating role of soil moisture, Water Resour. Res., 56, e2020WR028221, https://doi.org/10.1029/2020WR028221, 2020.
Chu, H., Luo, X., Ouyang, Z., Chan, W. S., Dengel, S., Biraud, S. C., Torn, M. S., Metzger, S., Kumar, J., Arain, M. A., Arkebauer, T. J., Baldocchi, D., Bernacchi, C., Billesbach, D., Black, T. A., Blanken, P. D., Bohrer, G., Bracho, R., Brown, S., Brunsell, N. A., Chen, J., Chen, X., Clark, K., Desai, A. R., Duman, T., Durden, D., Fares, S., Forbrich, I., Gamon, J. A., Gough, C. M., Griffis, T., Helbig, M., Hollinger, D., Humphreys, E., Ikawa, H., Iwata, H., Ju, Y., Knowles, J. F., Knox, S. H., Kobayashi, H., Kolb, T., Law, B., Lee, X., Litvak, M., Liu, H., Munger, J. M., Noormets, A., Novick, K., Oberbauer, S. F., Oechel, W., Oikawa, P., Papuga, S. A., Pendall, E., Prajapati, P., Prueger, J., Quinton, W. L., Richardson, A. D., Russell, E. S., Scott, R. L., Starr, G., Staebler, R., Stoy, P. C., Stuart-Haëntjens, E., Sonnentag, O., Sullivan, R. C., Suyker, A., Ueyama, M., Vargas, R., Wood, J. D., and Zona, D.: Representativeness of eddy-covariance flux footprints for areas surrounding AmeriFlux sites, Agr. Forest Meteorol., 301–302, 108350, https://doi.org/10.1016/j.agrformet.2021.108350, 2021.
Clark, M. P., Nijssen, B., Lundquist, J., Kavetski, D., Rupp, D., Woods, R., Gutmann, E., Wood, A., Brekke, L., Arnold, J., Gochis, D., and Rasmussen, R.: A unified approach to process-based hydrologic modeling. Part 1: Modeling concept, Water Resour. Res., 51, 2498–2514, https://doi.org/10.1002/2015WR017198, 2015a.
Clark, M. P., Nijssen, B., Lundquist, J., Kavetski, D., Rupp, D., Woods, R., Gutmann, E., Wood, A., Gochis, D., Rasmussen, R., Tarboton, D., Mahat, V., Flerchinger, G., and Marks, D.: A unified approach for process-based hydrologic modeling: Part 2. Model implementation and example applications. Water Resour. Res., 51, 2515–2542, https://doi.org/10.1002/2015WR017200, 2015b.
Collier, N., Hoffman, F. M., Lawrence, D. M., Keppel-Aleks, G., Koven, C. D., Riley, W. J., Mu, M., and Randerson, J. T.: The International Land Model Benchmarking (ILAMB) system: Design, theory, and implementation, J. Adv. Model. Earth Sy., 10, 2731–2754, https://doi.org/10.1029/2018MS001354, 2018.
Contractor, S., Donat, M. G., Alexander, L. V., Ziese, M., Meyer-Christoffer, A., Schneider, U., Rustemeier, E., Becker, A., Durre, I., and Vose, R. S.: Rainfall Estimates on a Gridded Network (REGEN) – a global land-based gridded dataset of daily precipitation from 1950 to 2016, Hydrol. Earth Syst. Sci., 24, 919–943, https://doi.org/10.5194/hess-24-919-2020, 2020.
Falge, E., Aubinet, M., Bakwin, P. S., Baldocchi, D., Berbigier, P., Bernhofer, C., Black, T. A., Ceulemans, R., Davis, K. J., Dolman, A. J., Goldstein, A., Goulden, M. L., Granier, A., Hollinger, D. Y., Jarvis, P. G., Jensen, N., Pilegaard, K., Katul, G., Kyaw Tha Paw, P., Law, B. E., Lindroth, A., Loustau, D., Mahli, Y., Monson, R., Moncrieff, P., Moors, E., Munger, J. W., Meyers, T., Oechel, W., Schulze, E.-D., Thorgeirsson, H., Tenhunen, J., Valentini, R., Verma, S. B., Vesala, T., and Wofsy, S. C.: FLUXNET Research Network Site Characteristics, Investigators, and Bibliography, 2016, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/1530, 2017.
Fisher, R. A. and Koven, C. D.: Perspectives on the future of land surface models and the challenges of representing complex terrestrial systems, J. Adv. Model. Earth Sy., 12, e2018MS001453, https://doi.org/10.1029/2018MS001453, 2020.
Goulden, M. L., Munger, J. W., Fan, S.-M., Daube, B. C., and Wofsy, S. C.: Measurements of carbon sequestration by long-term eddy covariance: methods and a critical evaluation of accuracy, Glob. Change Biol., 2, 169–182, https://doi.org/10.1111/j.1365-2486.1996.tb00070.x, 1996.
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009.
Haughton, N., Abramowitz, G., Pitman, A. J., Or, D., Best, M. J., Johnson, H. R., Balsamo, G., Boone, A., Cuntz, M., Decharme, B., Dirmeyer, P. A., Dong, J., Ek, M., Guo, Z., Haverd, V., van den Hurk, B. J. J., Nearing, G. S., Pak, B., Santanello, J. A., Stevens, L. E., and Vuichard, N.: The plumbing of land surface models: is poor performance a result of methodology or data quality?, J. Hydrometeorol., 17, 1705–1723, https://doi.org/10.1175/JHM-D-15-0171.1, 2016.
Haughton, N., Abramowitz, G., and Pitman, A. J.: On the predictability of land surface fluxes from meteorological variables, Geosci. Model Dev., 11, 195–212, https://doi.org/10.5194/gmd-11-195-2018, 2018.
Hoffman, F. M., Koven, C. D., Keppel-Aleks, G., Lawrence, D. M., Riley, W. J., Randerson, J. T., Ahlström, A., Abramowitz, G., Baldocchi, D. D., Best, M. J., Bond-Lamberty, B., De Kauwe, M. G., Denning, A. S., Desai, A., Eyring, V., Fisher, J. B., Fisher, R. A., Gleckler, P. J., Huang, M., Hugelius, G., Jain, A. K., Kiang, N. Y., Kim, H., Koster, R. D., Kumar, S. V., Li, H., Luo, Y., Mao, J., McDowell, N. G., Mishra, U., Moorcroft, P. R., Pau, G. S. H., Ricciuto, D. M., Schaefer, K., Schwalm, C. R., Serbin, S. P., Shevliakova, E., Slater, A. G., Tang, J., Williams, M., Xia, J., Xu, C., Joseph, R., and Koch, D.: International Land Model Benchmarking (ILAMB) 2016 Workshop Report, DOE/SC-0186, U.S. Department of Energy, Office of Science, Germantown, Maryland, USA, https://doi.org/10.2172/1330803, 2017.
Knauer, J., Cuntz, M., Smith, B., Canadell, J. G., Medlyn, B. E., Bennett, A. C., Caldararu, S., and Haverd, V.: Higher global gross primary productivity under future climate with more advanced representations of photosynthesis, Sci. Adv., 9, eadh9444, https://doi.org/10.1126/SCIADV.ADH9444, 2023
Lawrence, D. M., Fisher, R. A., Koven, C. D., Oleson, K. W., Swenson, S. C., Bonan, G., Collier, N., Ghimire, B., Kampenhout, L., Kennedy, D., Kluzek, E., Lawrence, P. J., Li, F., Li, H., Lombardozzi, D., Riley, W. J., Sacks, W. J., Shi, M., Vertenstein, M., Wieder, W. R., Xu, C., Ali, A. A., Badger, A. M., Bisht, G., Broeke, M., Brunke, M. A., Burns, S. P., Buzan, J., Clark, M., Craig, A., Dahlin, K., Drewniak, B., Fisher, J. B., Flanner, M., Fox, A. M., Gentine, P., Hoffman, F., Keppel-aleks, G., Knox, R., Kumar, S., Lenaerts, J., Leung, L. R., Lipscomb, W. H., Lu, Y., Pandey, A., Pelletier, J. D.,Perket, J., Randerson, J. T., Ricciuto, D. M., Sanderson, B. M., Slater, A., Subin, Z. M., Tang, J., Thomas, R. Q., Val Martin, M., and Zeng, X.: The Community Land Model Version 5: Description of New Features, Benchmarking, and Impact of Forcing Uncertainty, J. Adv. Model. Earth Sy., 11, 4245–4287, https://doi.org/10.1029/2018MS001583, 2019.
Lenhard, J. and Winsberg, E.: Holism, entrenchment, and the future of climate model pluralism, Stud. Hist. Philos. M. P., 41, 253–262, https://doi.org/10.1016/j.shpsb.2010.07.001, 2010.
Lipson, M., Grimmond, S., Best, M., Abramowitz, G., Coutts, A., Tapper, N., Baik, J.-J., Beyers, M., Blunn, L., Boussetta, S., Bou-Zeid, E., De Kauwe, M. G., de Munck, C., Demuzere, M., Fatichi, S., Fortuniak, K., Han, B.-S., Hendry, M., Kikegawa, Y., Kondo, H., Lee, D.-I., Lee, S.-H., Lemonsu, A., Machado, T., Manoli, G., Martilli, A., Masson, V., McNorton, J., Meili, N., Meyer, D., Nice, K. A., Oleson, K. W., Park, S.-B., Roth, M., Schoetter, R., Simon, A., Steeneveld, G.-J., Sun, T., Takane, Y., Thatcher, M., Tsiringakis, A., Varentsov, M., Wang, C., Wang, Z.-H., and Pitman, A.: Evaluation of 30 urban land surface models in the Urban-PLUMBER project: Phase 1 results, Q. J. Roy. Meteor. Soc., 150, 126–169, https://doi.org/10.1002/qj.4589, 2023.
Manabe, S.: Climate and the ocean circulation: I. The atmospheric circulation and the hydrology of the earth's surface, Mon. Weather Rev., 97, 739–805, https://doi.org/10.1175/1520-0493(1969)097<0739:CATOC>2.3.CO;2, 1969.
Mauder, M., Foken, T., and Cuxart, J.: Surface-Energy-Balance Closure over Land: A Review, Bound.-Lay. Meteorol., 177, 395–426, https://doi.org/10.1007/s10546-020-00529-6, 2020.
Mianabadi, A., Coenders-Gerrits, M., Shirazi, P., Ghahraman, B., and Alizadeh, A.: A global Budyko model to partition evaporation into interception and transpiration, Hydrol. Earth Syst. Sci., 23, 4983–5000, https://doi.org/10.5194/hess-23-4983-2019, 2019.
modelevaluation.org: ME.org R library, GitLab, https://gitlab.com/modelevaluation/me.org-r-library, last access: 2 November 2024.
Moderow, U., Grünwald, T., Queck, R., Spank, U., and Bernhofer, C.: Energy balance closure and advective fluxes at ADVEX sites, Theor. Appl. Climatol., 143, 761–779, https://doi.org/10.1007/s00704-020-03412-z, 2021.
Monteith, J. L. and Unsworth, M. H.: Principals of Environmental Physics, 2nd edn., Edward Arnold, 241 pp., ISBN 071312931X, 1990.
Nearing, G. S., Ruddell, B. L., Clark, M. P., Nijssen, B., and Peters-Lidard, C.: Benchmarking and process diagnostics of land models, J. Hydrometeorol., 19, 1835–1852, https://doi.org/10.1175/JHM-D-17-0209.1, 2018.
Pan, S., Pan, N., Tian, H., Friedlingstein, P., Sitch, S., Shi, H., Arora, V. K., Haverd, V., Jain, A. K., Kato, E., Lienert, S., Lombardozzi, D., Nabel, J. E. M. S., Ottlé, C., Poulter, B., Zaehle, S., and Running, S. W.: Evaluation of global terrestrial evapotranspiration using state-of-the-art approaches in remote sensing, machine learning and land surface modeling, Hydrol. Earth Syst. Sci., 24, 1485–1509, https://doi.org/10.5194/hess-24-1485-2020, 2020.
Polcher, J., McAvaney, B., Viterbo, P., Gaertner, M.-A., Hahmann, A., Mahfouf, J.-F., Noilhan, J., Phillips, T., Pitman, A. J., Schlosser, C. A., Schulz, J.-P., Timbal, B., Verseghy D., and Xue, Y.: A proposal for a general interface between land-surface schemes and general circulation models, Global Planet. Change, 19, 263–278, https://doi.org/10.1016/S0921-8181(98)00052-6, 1998.
Polcher, J., Cox, P., Dirmeyer, P., Dolman, H., Gupta, H., Henderson-Sellers, A., Houser, P., Koster, R., Oki, T., Pitman, A., and Viterbo, P.: GLASS: Global Land- Atmosphere System Study, GEWEX News, Vol. 10, No. 2, International GEWEX Project Office, Silver Spring, MD, 3–5, 2000.
Schmidt, A., Hanson, C., Chan, W. S., and Law, B. E.: Empirical assessment of uncertainties of meteorological parameters and turbulent fluxes in the AmeriFlux network, J. Geophys. Res., 117, G04014, https://doi.org/10.1029/2012JG002100, 2012.
Seiler, C., Melton, J. R., Arora, V. K., Sitch, S., Friedlingstein, P., Anthoni, P., Goll, D., Jain, A. K., Joetzjer, E., Lienert, S., Lombardozzi, D., Luyssaert, S., Nabel, J. E. M. S., Tian, H., Vuichard, N., Walker, A. P., Yuan, W., and Zaehle S.: Are terrestrial biosphere models fit for simulating the global land carbon sink?, J. Adv. Model. Earth Sy., 14, e2021MS002946, https://doi.org/10.1029/2021MS002946, 2022.
Shevliakova, E., Malyshev, S., Martinez-Cano, I., Milly, P. C. D., Pacala, S. W., Ginoux, P. Dunne, K. A., Dunne, J. P., Dupuis, C., Findell, K. L., Ghannam, K., Horowitz, L. W., Knutson, T. R., Krasting, J. P., Naik, V., Phillipps, P., Zadeh, N., Yan Yu, Zeng, F., and Zeng, Y.: The land component LM4.1 of the GFDL Earth System Model ESM4.1: Model description and characteristics of land surface climate and carbon cycling in the historical simulation, J. Adv. Model. Earth Sy., 16, e2023MS003922, https://doi.org/10.1029/2023MS003922, 2023,
Sposito, G.: Understanding the Budyko Equation, Water, 9, 236, https://doi.org/10.3390/w9040236, 2017.
Stoy, P. C., Mauder, M., Foken, T., Marcolla, B., Boegh, E., Ibrom, A., Arain, M. A., Arneth, A., Aurela, M., Bernhofer, C., Cescatti, A., Dellwik, E., Duce, P., Gianelle, D., van Gorsel, E., Kiely, G., Knohl, A., Margolis, H., McCaughey, H., Merbold, L., Montagnani, L., Papale, D., Reichstein, M., Saunders, M., Serrano-Ortiz, P., Sottocornola, M., Spano, D., Vaccari, F., and Varlagin, A.: A data-driven analysis of energy balance closure across FLUXNET research sites: the role of landscape scale heterogeneity, Agr. Forest Meteorol., 171–172, 137–152, https://doi.org/10.1016/j.agrformet.2012.11.004, 2013.
Ukkola, A. M., Haughton, N., De Kauwe, M. G., Abramowitz, G., and Pitman, A. J.: FluxnetLSM R package (v1.0): a community tool for processing FLUXNET data for use in land surface modelling, Geosci. Model Dev., 10, 3379–3390, https://doi.org/10.5194/gmd-10-3379-2017, 2017.
Ukkola, A. M., Abramowitz, G., and De Kauwe, M. G.: PLUMBER2: forcing and evaluation datasets for a model inter-comparison project for land surface models v1.0, Geonetwork [data set], https://doi.org/10.25914/5fdb0902607e1, 2021.
Ukkola, A. M., Abramowitz, G., and De Kauwe, M. G.: A flux tower dataset tailored for land model evaluation, Earth Syst. Sci. Data, 14, 449–461, https://doi.org/10.5194/essd-14-449-2022, 2022.
Vuichard, N., Messina, P., Luyssaert, S., Guenet, B., Zaehle, S., Ghattas, J., Bastrikov, V., and Peylin, P.: Accounting for carbon and nitrogen interactions in the global terrestrial ecosystem model ORCHIDEE (trunk version, rev 4999): multi-scale evaluation of gross primary production, Geosci. Model Dev., 12, 4751–4779, https://doi.org/10.5194/gmd-12-4751-2019, 2019.
Wartenburger, R., Seneviratne, S. I., Hirschi, M., Chang, J., Ciais, P., Deryng, D., Elliott, J., Folberth, C., Gosling, S. N., Gudmundsson, L., Henrot, A.-J., Hickler, T., Ito, A., Khabarov, N., Kim, H., Leng, G., Liu, J., Liu, X., Masaki, Y., Morfopoulos, C., Müller, C., Schmied, H. M., Nishina, K., Orth, R., Pokhrel, Y., Pugh, T. A. M., Satoh, Y., Schaphoff, S., Schmid, E., Sheffield, J., Stacke, T., Steinkamp, J., Tang, Q., Thiery, W., Wada, Y., Wang, X., Weedon, G. P., Yang, H., and Zhou, T.: Evapotranspiration simulations in ISIMIP2a-Evaluation of spatio-temporal characteristics with a comprehensive ensemble of independent datasets, Environ. Res. Lett., 13, 075001, https://doi.org/10.1088/1748-9326/aac4bb, 2018.
Whitley, R., Beringer, J., Hutley, L. B., Abramowitz, G., De Kauwe, M. G., Evans, B., Haverd, V., Li, L., Moore, C., Ryu, Y., Scheiter, S., Schymanski, S. J., Smith, B., Wang, Y.-P., Williams, M., and Yu, Q.: Challenges and opportunities in land surface modelling of savanna ecosystems, Biogeosciences, 14, 4711–4732, https://doi.org/10.5194/bg-14-4711-2017, 2017.
Wilson, K., Goldstein, A., Falge, E., Aubinet, M., Baldocchi, D., Berbigier, P., Bernhofer, C., Ceulemans, R., Dolman, H., Field, C., Grelle, A., Ibrom, A., Law, B. E., Kowalski, A., Meyers, T., Moncrieff, J., Monson, R., Oechel, W., Tenhunen, J., Valentini, R., and Verma, S.: Energy balance closure at FLUXNET sites, Agr. Forest Meteorol., 113, 223–243, https://doi.org/10.1016/S0168-1923(02)00109-0, 2002.





