Spatial biases reduce the ability of Earth system models to simulate soil heterotrophic respiration fluxes

Heterotrophic respiration (R_h) is, at a global scale, one of the largest CO₂ fluxes between the Earth's surface and atmosphere and may increase in the future. The previous generation of Earth system models (ESMs) was able to reproduce global fluxes relatively well, but at that, time no gridded products were available to perform an in-depth evaluation. The capacity of the new generation of ESMs used within the Coupled Model Intercomparison Project Phase 6 (CMIP6) to reproduce this flux has not been evaluated, meaning that the realism of resulting CO₂ flux estimates is unclear. In this study, we combine recently released observational data on R_h and ESM simulations to evaluate the ability of 13 ESMs from CMIP6 to reproduce R_h. Only 4 of the 13 tested ESMs were able to reproduce the total R_h flux, but spatial analysis underlined important bias compensation for most of the ESMs, which generally showed an overestimation in tropical regions and an underestimation in arid regions. To identify the main drivers of the bias, we performed an analysis of the residuals and found that mean annual precipitation was the most important driver explaining the difference between ESM simulations and observation-derived products of R_h, with a higher bias between ESM simulations and R_h products where precipitation was high. Based on our results, next-generation ESMs should focus on improving the response of R_h to soil moisture.

1 Introduction

Soil organic carbon stocks represent around 3 times the amount of carbon in the atmosphere (Scharlemann et al., 2014). This soil carbon is used as a substrate by soil microorganisms to obtain their energy and feed their metabolism, which accounts for the majority of heterotrophic soil organism biomass. Annual fluxes that result from the respiration of these heterotrophic organisms (hereafter referred to as heterotrophic respiration) are estimated (Warner et al., 2019; Hashimoto et al., 2015; Konings et al., 2019; Ciais et al., 2021) to be 5 times higher than annual anthropogenic emissions (Friedlingstein et al., 2022) and roughly similar to annual terrestrial net primary production (Zhao et al., 2005). Thus, due to the size of fluxes relating to heterotrophic respiration, even minor changes in soil organic carbon dynamics can lead to significant impacts on carbon feedbacks and, ultimately, on climatic changes. As a result, modification of soil organic carbon stocks due to human activities is considered to be an important driver of future climate trajectories (Chabbi et al., 2017).

Although heterotrophic respiration fluxes are important, the way this flux is represented in Earth system models (ESMs), which aim to simulate the most important drivers of the Earth's climate system, is currently challenged. This is because important drivers are missing, and while new approaches have been proposed (Huang et al., 2021; Wieder et al., 2015), these lack sufficient evaluation of long-term time series (Le Noë et al., 2023). Thus, identifying the accuracy of predictions of heterotrophic respiration fluxes by ESMs is key in helping constrain carbon–climate feedbacks in ESMs. The ability of ESMs to reproduce this flux was previously studied by Shao et al. (2013), but this was done using the previous generation of ESMs using the simulations done during the Coupled Model Intercomparison Project Phase 5 (CMIP5). Moreover, at that time, no gridded products were available. Since then, the models have been greatly improved, and assessing how accurately current ESMs reproduce the fluxes associated with heterotrophic respiration is therefore of major importance. Until now, it has not been possible to undertake a robust spatial assessment because of the lack of observation-derived gridded products of R_h. In recent years, new gridded products have been derived from either (i) upscaling of local observations or (ii) calculations using atmospheric inversions and satellite observations. These products provide the opportunity to evaluate the simulations of ESMs used within the Coupled Model Intercomparison Project Phase 6 (CMIP6) against observation-derived products for heterotrophic respiration. CMIP is a key initiative which aims to compare current ESMs and is a central element of national and international assessments of climate change (Masson-Delmotte et al., 2021).

In this study, we have two major aims:

1. to compare predictions of the total flux of heterotrophic respiration from 13 Earth system models with three recent gridded products of heterotrophic respiration derived from observations and to identify the spatial biases of heterotrophic respiration in the models

2. to identify the major drivers of the heterotrophic respiration bias in Earth system models to propose new developments for the next generation of Earth system models using a model residual approach to disentangle the main effect.

2 Materials and methods

2.1 Earth system model simulations

In this study, we used the model outputs from the sixth Couple Model Intercomparison Project (CMIP6) (Eyring et al., 2016), which coordinates global climate model simulations of the past, current, and future climate. CMIP6 proposes historical simulations spanning from 1850 to 2014. Historical simulations are driven from an initial point chosen in control integration (piControl). We chose to use the latest CMIP6 results for the basic initial state (r1i1p1f1). We chose outputs from 13 ESMs that provide heterotrophic respiration fluxes (BCC-CSM2-MR, BCC-ESM1, CanESM5, CESM2, CNRM-ESM2-1, E3SM-1-1-ECA, IPSL-CM6A-LR, MIROC-ES2L, MPI-ESM1-2-LR, NorCPM1, NorESM2-LM, SAM0-UNICON, and UKESM1-0-LL). The variable used is R_h, corresponding to the total heterotrophic respiration on land. We computed annual averages over the 1990–2010 period, which corresponds to the period in which most of the observations in the global Soil Respiration Database (Bond-Lamberty and Thomson, 2010) v3.0 were made. Two of the observation products we used were obtained using those data.

2.2 Observation-derived products

In this study, we used three observation-derived products (Warner et al., 2019; Konings et al., 2019; Hashimoto et al., 2015). In Warner et al. (2019), the authors predicted annual soil respiration and associated uncertainty across terrestrial areas at a resolution of 1 km using a quantile regression forest algorithm trained with observations from the global Soil Respiration Database (Bond-Lamberty and Thomson, 2010) v3.0 (commit no. 651770 in GitHub, https://github.com/bpbond/srdb, last access: 26 January 2024) spanning from 1961 to 2011 but mostly after 1990. Then they deduced R_h from the soil respiration using two different methods (Bond-Lamberty et al., 2004; Subke et al., 2006). They therefore proposed two R_h maps derived from a unique mean map of R_s from the quantile regression forest model. Here, we decided to use the mean of two approaches as a reference for Warner et al.'s (2019) R_h results. The second product we used – that from Hashimoto et al. (2015) – is also based on the Soil Respiration Database (Bond-Lamberty and Thomson, 2010) v3.0, but in this case, the R_h flux was derived using a climate-driven model of soil respiration derived from the Raich's model (Raich et al., 2002). Hashimoto et al. provided a 0.5^∘ resolution product at a monthly step time between 1965 and 2012. In our case, we used the yearly average over the period. The third product used – that of Konings et al. (2019) – estimated R_h as a residual remote sensing data point, exploiting recent advances in carbon flux estimations. In contrast with the two other products, which are bottom-up, the Konings et al. (2019) product proposes a top-down approach combining net ecosystem productivity estimates from atmospheric inversions with an optimally scaled gross primary productivity dataset derived from satellite observations. R_h is then derived using the CARbon DAta MOdel fraMework (CARDAMOM). Their result is a monthly evaluation of R_h between January 2010 and December 2012 at a resolution of $\mathrm{4}{}^{\circ }\times \mathrm{5}{}^{\circ }$.

2.3 Data treatment and regridding

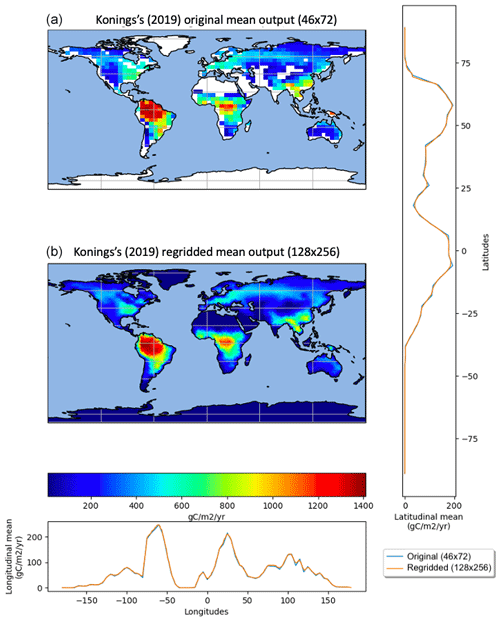
Since the ESM outputs and products were not at the same resolution, we chose a reference for map grid resolution. The coarsest resolution was from Konings et al.'s (2019) product, with a $\mathrm{4}{}^{\circ }\times \mathrm{5}{}^{\circ }$ resolution grid. Reducing the resolution of every R_h map to match this would cause a substantial loss of information. Thus, we increased the resolution of those datasets and decreased the very-fine-scale maps to an arbitrary reference corresponding to the CNRM-ESM2-1 model, which runs at a 0.7^∘ resolution. We chose to set the reference as the maximum resolution available among CMIP6's ESMs predicting R_h. We used the common regridding routine Climate Data Operators (CDO) remapdis (NCO module), which performs regridding by distance-weighted average remapping and conserves latitudinal and longitudinal means. The CDO software is a collection of multiple operators for standard processing of climate and forecast model data. The operators include simple functions (statistical and arithmetic) to be used for data selection, subsampling, and spatial interpolation. To avoid coastal pixels encroaching into oceans, we weighted each pixel by the proportion of its area covered by land. The sum of R_h over the land was compared before and after regridding to ensure that it was conservative. When comparing the original and the regridded version of the Konings et al. (2019) product, we observed a very similar pattern (Fig. 1).

Figure 1 Mean R_h spatial distribution over 2010–2012 from the Konings et al. (2019) product – original (46×72, a) vs. regridded (128×256, b).

2.4 Comparison between models' outputs and heterotrophic respiration products

To estimate the ability of the CMIP6 models to reproduce soil heterotrophic respiration, we first compared the global flux summed over all the grid cells and averaged over the 1990–2010 period (in Pg C yr⁻¹). We also compared the R_h maps after regridding, averaged over the 1990–2010 period. We also performed latitudinal and longitudinal mean calculus, including oceanic zero values. Secondly, we wanted to assess spatial bias distribution. Therefore, we (i) compared CMIP6 model averages with observation products and (ii) compared each CMIP6 model with observation products. Thus, we first represented the model average (over the period 1990–2010) and all the observation-derived products in the same figure with their associated latitudinal and longitudinal means. We also calculated the 25th and 75th quantiles of latitudinal and longitudinal CMIP6 model means. Then, we computed the difference for each individual CMIP6 model with the median of the three observation products. To compare the ESMs with the observation products, we calculated the root mean square error (RMSE) and the R² using the median of the observation products. Finally, we also calculated the median absolute deviation (MAD) for each grid cell, and we calculated the number of pixels for each model that fit within the median ± MAD.

2.5 ESM residual analysis

We defined the ESM residuals as the median of the differences between each individual CMIP6 model outputs and the observation-based products' medians calculated for each grid cell. The ESM residuals were calculated in three steps:

1. We first calculated the median for each cell (i), which we called R_h_obs_i, using the three observation-derived products together with Eq. (1), with R_h_Hashimoto et al. (2015)_i, R_h_Warner et al. (2019)_i, and R_h_Konings et al. (2019)_i being the heterotrophic respirations given for the grid cell I by Hashimoto et al. (2015), Warner et al. (2019), and Konings et al. (2019), respectively. We consider this median to be our best estimate.

   $$\begin{array}{}\text{(1)}& \begin{array}{rl}{R}_{\mathrm{h}}\mathit{\_}{\mathrm{obs}}_i=& \mathrm{Med}(R_{\mathrm{h}}\mathit{\_}\mathrm{Hashimoto}\mathrm{et}\mathrm{al}.(\mathrm{2015}{)}_i,\\ & R_{\mathrm{h}}\mathit{\_}\mathrm{Warner}\mathrm{et}\mathrm{al}.(\mathrm{2019}{)}_i,\\ & R_{\mathrm{h}}\mathit{\_}\mathrm{Konings}\mathrm{et}\mathrm{al}.\left(\mathrm{2019}{)}_i\right)\end{array}\end{array}$$

2. Next, we calculated the residual between each CMIP6 model output and our best estimate, which we called Res_X_i (X being the model's name), for each grid cell i using Eq. (2).

   $$\begin{array}{}\text{(2)}& \mathrm{Res}\mathit{\_}{X}_i=R_{\mathrm{h}}\mathit{\_}{X}_i-R_{\mathrm{h}}\mathit{\_}{\mathrm{obs}}_i\end{array}$$

3. Finally, we calculated the ESM residuals (Res_i) as the median of these model-specific residuals (Res_X_i) using Eq. (3).

   $$\begin{array}{}\text{(3)}& R_{\mathrm{h}}\mathit{\_}{X}_i-R_{\mathrm{h}}\mathit{\_}{\mathrm{obs}}_i\end{array}$$

Using the ESM residuals, we performed a statistical analysis to identify the main drivers of disagreement between predictions and observations. Following this we undertook a two-step methodology. First, we compared several linear generalized least-square models with different spatial structures (Gaussian, exponential, spherical, linear, or rational) (gls package, Venables and Ripley, 2002) and without spatial structures to estimate the effect of spatial correlation. Based on Akaike information criterion (AIC) values, we selected the rational quadratic spatial correlation structure that had the smallest AIC values for the second step of the analysis. Then, we used generalized additive mixed models with ESM residuals as variables to explain the mean annual temperature (MAT), mean annual precipitation (MAP), observation-derived SOC, and ESM residuals on net primary production (NPP) and lithology as predictor variables. MAT and MAP are derived from the Global Soil Wetness Project Phase 3 (GSWP3) reanalysis (http://hydro.iis.u-tokyo.ac.jp/GSWP3/ last access: 5 April 2022). SOC was taken from the Soilgrid250m product (Hengl et al., 2017). ESM residuals on NPP are calculated as the median of the difference between ESM NPP and NPP from the Global Inventory Monitoring And Modeling Studies group (GIMMS). Lithology maps from the global lithological map (GLiM) (Hartmann and Moosdorf, 2012) were used, but since lithology was not significant (p>0.05) and since the model had a lower AIC without this variable, it was not included in the final generalized additive mixed model presented here. All statistical analyses were carried out using R v3.5 (R Core Team, 2018).

3 Results

3.1 Global heterotrophic respiration flux and spatial biases

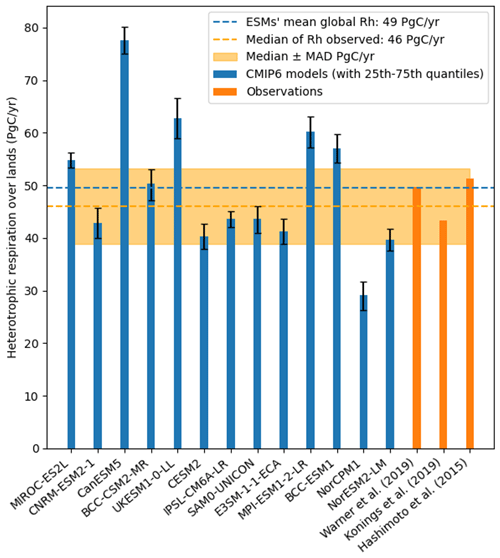
Global heterotrophic respiration flux simulated by the 13 ESMs ranges from 29 to 78 Pg C yr⁻¹ (Fig. 2), whereas the equivalent estimates for observationally derived products estimates range from 43 to 51 Pg C yr⁻¹. The multi-model mean of the ESMs (49 Pg C yr⁻¹) falls within the range of the observation-derived products. However, only 4 out of 13 ESMs (BCC-CSM2-MR, CNRM-ESM2-1, IPSL-CM6A-LR, and SAM0-UNICOM) simulate an overall heterotrophic respiration flux that is within the range of the observation-derived products (Fig. 2). When comparing the model observation products with the median ± MAD from the observation products (46±7 Pg C yr⁻¹), 7 out of the 13 ESMs predicted a heterotrophic respiration within this range (Fig. 2). The R² between the model outputs and the median of the observation products range between 0.57 for E3SM-1-1-ECA and 0.82 for MIROC-ES2L (Table 1). When using RMSE to compare the model outputs and the median of the observation products, we obtained values of 170.9 gC m⁻² yr⁻¹ for IPSL-CM6A-LR and 345.1 gC m⁻² yr⁻¹ for CanESM5 (Table 1). Finally, we also estimated the number of pixels that fell within the median ± MAD, and, using this metric, BCC-ESM1 was the best-performing model followed by BCC-CSM2-MR and CNRM-ESM2-1.

Table 1 Evaluation metrics for the different Earth system models.

Figure 2 Global estimations of soil heterotrophic respiration mean over 1990–2010 period.

Despite similar global-scale values, regional-scale differences between the observation-derived products are much larger (Fig. 3). The Konings et al. (2019) product estimates large heterotrophic fluxes in the tropics and lower fluxes in other regions such as the west coast of Northern America or central Asia as compared to the Warner et al. (2019) and Hashimoto et al. (2015) products that share similar spatial patterns (Fig. 4). The mean of the 13 ESM simulations also gives a much larger heterotrophic respiration flux over the tropics, in particular over southeast Asia compared to any of the three observation-derived products. In general, the heterotrophic respiration fluxes from the mean of the 13 ESMs is closer to that of the Konings et al. (2019) product over the tropics but closer to the Warner et al. (2019) and Hashimoto et al. (2015) products over temperate regions. For boreal regions, the three observation-derived products and the 13 ESMs means are very close.

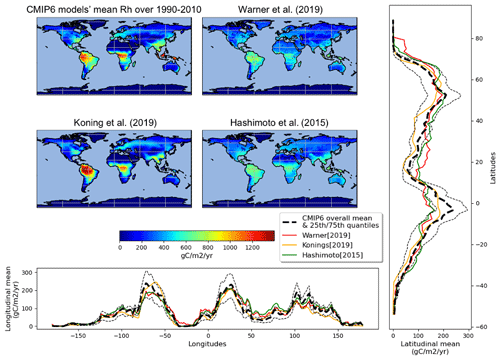
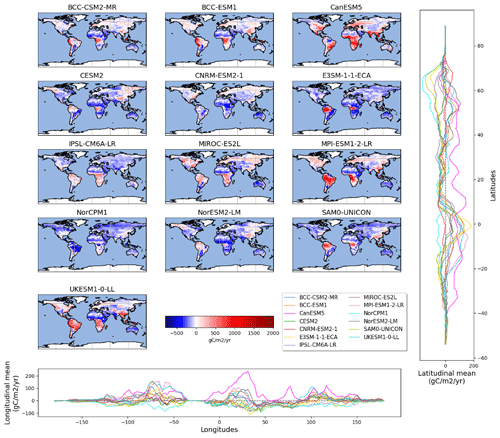
Figure 3 Comparison of mean soil heterotrophic respiration spatial distribution among mean CMIP6 outputs and observation data.

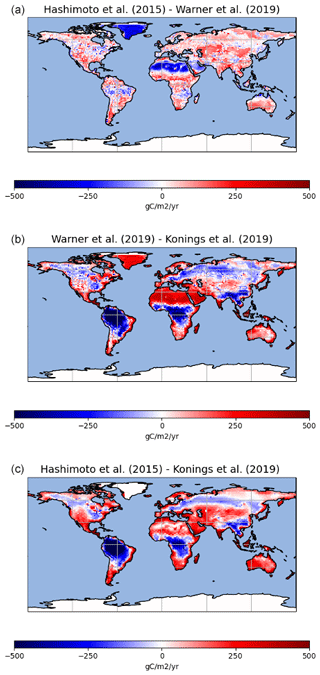
Figure 4 Maps of differences between the observation-based products used in this study (Hashimoto et al., 2015, and Warner et al., 2019, in a; Warner et al., 2019, and Konings et al., 2019, in b; and Hashimoto et al., 2015, and Konings et al., 2019, in c).

To generate our best estimate of heterotrophic respiration fluxes from the three observation-derived products, we calculated the median for each cell. Thus, we obtained the spatially distributed best estimate. At each grid cell, we then compared each ESM with the observation-derived products' median (Fig. 5). This evaluation indicates that, compared to observation-based products, ESMs (apart from the ESM NorCPM1) tend to overestimate heterotrophic respiration fluxes in tropical regions (approx. 1000 gC m⁻² yr⁻¹ for MPI-ESM1-2-LR over the Amazon or 1500 gC m⁻² yr⁻¹ for UKESM1-0-LL over southeast Asia, for instance). Models perform relatively well in temperate regions, with a bias close to 0 gC m⁻² yr⁻¹ for BCC-ESM-1 over North America and Europe. Important discrepancies were observed for boreal regions, with some models underestimating the heterotrophic respiration fluxes to a large degree (e.g., NorCPM1 or SAM0-UNICON) and one overestimating the fluxes (MPI-ESM1-2-LR). The BCC models (BCC-CSM2-MR and BCC-ESM1) performed quite well over this region. Importantly, the four models that predict a global heterotrophic respiration flux within the range given by the observation-derived products (BCC-CSM2-MR, CNRM-ESM2-1, IPSL-CM6A-LR, and SAM0-UNICOM) do not perform well at finer scales – with overestimation of the flux in some regions and underestimation in others. Therefore, this good global-scale performance masks spatial bias compensation.

Figure 5 Spatially distributed residuals of CMIP6 ESM predictions over the period 1990–2010 with respect to median observation products.

3.2 Identification of the major drivers of the heterotrophic respiration bias in Earth system models

In order to improve predictions of heterotrophic respiration fluxes in future ESMs, we need to understand the spatial biases we observed and determine their causes. To explore these biases, we performed a statistical analysis based on a generalized additive mixed model of the ESM residuals, defined as the median of the differences between each CMIP6 model's output and the median of the observation-based products calculated in each grid cell. ESMs share a very common approach based on first-order kinetics with soil organic decomposition driven by soil moisture and temperature (Varney et al., 2022; Todd-Brown et al., 2014). This approach is derived from the very first attempts to describe soil organic decomposition with mathematical equations (Henin and Dupuis, 1945) and is still the most used to describe this process (Manzoni and Porporato, 2009; Wutzler et al., 2008). Since soil organic matter (SOM) decomposition schemes in ESMs are very similar, comparing each model individually can be redundant and not very informative and less generalizable. To allow broader conclusions and suggestions to improve ESM performances, we decided to perform the residual analysis on the ESM median rather on each individual model.

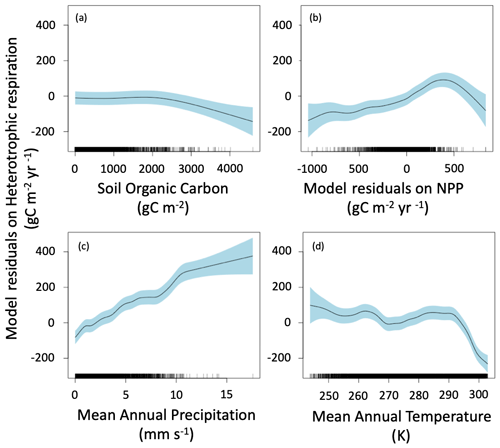
The main drivers of heterotrophic respiration are soil carbon availability, soil moisture and temperature, carbon inputs, and mineralogy (Doetterl et al., 2015). To explain our model residuals, we used soil organic carbon, net primary production residuals calculated using similar methods to heterotrophic respiration flux residuals, mean annual precipitation, mean annual temperature, and lithology. Our method identified the main drivers of ESM residuals as soil organic carbon, net primary production residuals, mean annual precipitation, and mean annual temperature (Fig. 6). The effect of lithology was not statistically significant (p>0.05), and the model had a lower AIC without this variable; thus, we did not include lithology in the final model presented here. The residuals due to soil organic carbon stock are close to zero for soil with a low carbon stock, but heterotrophic respiration is under estimated by ESMs for soils rich in organic carbon (> 3000 g C m⁻²) (Fig. 6a). The model residuals for heterotrophic respiration flux are partially explained by the model residuals on net primary production, with a slight increase from model underestimation to model overestimation when model residuals on net primary production increase from −1000 to 400 g C m⁻² yr⁻¹. We noted that, when net primary production fits well with satellite products (i.e., model residuals close to 0 g C m⁻² yr⁻¹), the ESM residuals on the heterotrophic respiration flux are also close to 0 g C m⁻² yr⁻¹. For a few grid cells where ESMs largely overestimate net primary production (i.e., model residuals higher than 400 g C m⁻² yr⁻¹), the ESM residuals on heterotrophic respiration flux tend to be negative, suggesting that ESMs underestimate heterotrophic respiration flux. The clearest tendency we obtained was with mean annual precipitation: the more it increases, the more the models overestimate the heterotrophic respiration flux (Fig. 6c). The median ESM residual was also partially controlled by mean annual temperature (Fig. 6d), with a relatively low overestimation by the models for cold temperatures, such as those recorded in polar climate zones and in some continental climate zones (e.g., subarctic climate); a relatively good fit for temperatures between 0 and 20 ^∘C, corresponding to temperate and some continental climate zones (e.g., hot summer continental climates); and then a sudden underestimation for warm temperatures above 20 ^∘C, corresponding to tropical and dry climate zones. This sudden underestimation might be explained by an arbitrary maximum respiration level observed in this dataset and identified as the result of the temperature dependence of soil respiration used by Hashimoto et al. (2015) (Varney et al., 2020). Such a bias may therefore be a consequence of the observation-based products used here rather than being a real bias in ESMs. Similar results were obtained when performing the same analysis with means rather than medians (Fig. 7).

Figure 6 Median of ESM residuals on soil heterotrophic respiration. The residuals are explained by soil organic carbon (a), median of NPP residuals (b), mean annual precipitation (c), and mean annual temperature (d). Negative values mean model underestimation.

4 Discussion

In this study we evaluated, for the first time, the ability of the ESMs to reproduce heterotrophic respiration fluxes. Indeed, previous datasets were not gridded, and, so far, spatial patterns of heterotrophic respiration in ESMs could only be constrained indirectly by constraining other C fluxes including heterotrophic respiration, such as net ecosystem exchange fluxes, or through ecosystem respiration in which heterotrophic respiration is just one component, the other being the autotrophic respiration (Stoy et al., 2013). We showed that only 4 out of 13 of the CMIP models produce global-scale estimates that are consistent with observation-derived products. However, we also showed that this consistency was due to spatial bias compensations driven by different environmental variables. Heterotrophic respiration represents a carbon flux that is roughly 5 times that of anthropogenic emissions (Friedlingstein et al., 2022), and, as such, it is vital that work is done to improve the ability of ESMs to reproduce this flux. Nevertheless, we also observed large discrepancies between observation-based products, showing that our ability to provide heterotrophic flux based on observations is not optimal. To better constrain ESM projections, some efforts are needed to reduce residuals between observation-based products.

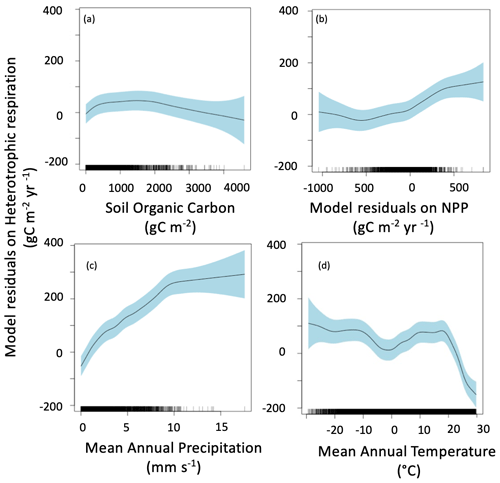
Figure 7 Mean of ESM residuals on soil heterotrophic respiration. The residuals are explained by soil organic carbon (a), mean of NPP residuals (b), mean annual precipitation (c), and mean annual temperature (d). Negative values mean model underestimation.

However, working only on heterotrophic respiration may not be sufficient to improve the entire soil organic carbon module of the ESMs (Table 2). ESM capacities to reproduce observed soil organic carbon stocks also need to be improved (Ito et al., 2020; Varney et al., 2022). To improve both soil organic carbon stocks and heterotrophic respiration fluxes, soil organic carbon decomposition rates must be better constrained. The ESM residual analysis we performed here suggests some new research avenues relating to the response of the major drivers. First, most of the boundary conditions of the soil organic carbon modules of an ESM are calculated by the ESM itself. Thus, if soil moisture, soil temperature, or litter production are incorrect, the soil organic carbon dynamic cannot be correct. We observed that, when the residual of NPP was close to zero, the residual on heterotrophic respiration is also close to zero. Thus, improving the plant functioning scheme may ultimately improve the capacities of the ESMs to reproduce the heterotrophic respiration flux. Our study also showed that mean annual temperature is an important driver of the ESM residuals, in particular for hot regions with large underestimations of the flux. These regions probably correspond to very arid regions since, for most of the ESMs, heterotrophic respiration fluxes from regions like Australia, the Middle East, or northern Africa tend to be underestimated. Nevertheless, the underestimation observed in these regions may be also due to reduced C inputs and low SOC stocks, reducing the heterotrophic respiration fluxes.

Table 2 Summary of the main features proposed in this study to improve the heterotrophic respiration fluxes in Earth system models.

The response of soil organic decomposition by microorganisms is likely to be temperature dependent, with lower rates of decomposition in cold regions and higher rates in hot regions (Wang et al., 2010; Zhou et al., 2009). In contrast, the response of soil organic decomposition to temperature in ESMs is generally controlled by Q₁₀ equations (Davidson and Janssens, 2006), with fixed parameters that are not dynamic and not spatially distributed (Ito et al., 2020). Previous studies suggested that a spatially distributed Q₁₀ constrained by observations is an important step to improve ESMs (Koven et al., 2017; Varney et al., 2020). Our results support this and hint that having more flexible Q₁₀ parameters may help to improve ESM capacities to reproduce observation-derived products of heterotrophic respiration fluxes. Moreover, land surface schemes of ESMs are known to be very sensitive to Q₁₀ values (Jones et al., 2003; Todd-Brown et al., 2018).

Finally, we observed a relatively linear, positive relationship between mean annual precipitation and the ESMs' residuals (Fig. 6c). This response is probably driven by soil moisture because it is a key driver of microbial activity and therefore of heterotrophic respiration fluxes (Moyano et al., 2012). ESMs use three main groups of soil moisture response function (Falloon et al., 2011): (i) some models do not represent soil moisture effect; (ii) some models increase soil organic decomposition when soil moisture increases, assuming less water limitation for microbial activity; and (iii) some models assume a humped relationship between soil moisture and soil organic decomposition, with high decomposition at intermediate soil moisture and low decomposition in very wet soils, where microbial activity is reduced because of limitations in relation to oxygen availability, and in dry soils, where microbial activity is reduced because of limitations in relation to water. As with Q₁₀, the land surface models are highly sensitive to which soil moisture response function is chosen, and most of the ESMs use option (ii) (Varney et al., 2022). Soil incubations have repeatedly shown that the response of heterotrophic respiration fluxes to soil moisture is approximated by a bell-shaped function, with parameters depending on soil organic carbon, soil clay content, and soil bulk density (Moyano et al., 2012). Thus, for wet soils, heterotrophic respiration fluxes are probably reduced because of oxygen limitation. Implementing this bell-shaped function approach is necessary to accurately represent the soil organic carbon stock of peatland in some land surface schemes used by ESMs (Qiu et al., 2019). The approach proposed by Moyano et al. (2012) seems to be well adapted to constraining ESMs since the author proposed several versions of the bell-shaped function and defined a function using drivers that are included in ESMs (model 2 in Moyano et al., 2012). The model including bulk density might perform better, but bulk density is not calculated by ESMs, and, consequently, such an approach is hardly implementable in ESMs. Other approaches have been proposed in the literature (Davidson et al., 2014; Sierra et al., 2015), but the solutions proposed are mostly based on O₂ diffusion, which is more mechanistic but more difficult to implement in an ESM compared to a more empirical solution, such as that proposed by Moyano et al. (2012). Gas diffusion implementation at the spatial resolution of ESMs is quite challenging because it depends on drivers that are highly variable at small scales. Not considering the possible oxygen limitation effect on wet soils may explain why ESMs tends to overestimate the heterotrophic respiration flux when mean annual precipitation is high. Changing the soil moisture function to better represent this effect should be relatively easy and may substantially improve the capacities of ESMs to reproduce the heterotrophic respiration flux.

Another important parameter controlling heterotrophic respiration flux is carbon use efficiency, defined as the ratio between the carbon remaining in a system and the carbon entering that system (Manzoni et al., 2018). In our context. this is the ratio between the carbon mineralized through microbial heterotrophic respiration and the carbon incorporated into the microbial biomass. The heterotrophic respiration flux therefore results from two processes in ESMs, namely the soil organic carbon decomposition and its allocation to other soil carbon pools or to heterotrophic respiration. Carbon use efficiency is highly variable and depends on several biotic and abiotic factors (Sinsabaugh et al., 2013; Manzoni, 2017; Manzoni et al., 2012). In ESMs, carbon use efficiency is neither dynamic nor spatially distributed, and, thus, having flexible carbon use efficiency control may help to reproduce observations (Zhang et al., 2018). A simple approach that may aid in a better representation of heterotrophic respiration fluxes is optimizing the carbon use efficiency parameters of the ESMs using a Bayesian approach, as is done for other land fluxes (Kuppel et al., 2012). This would result in a spatially distributed set of parameters for carbon use efficiency, but this approach would not be dynamic. Another option that might benefit the current large carbon use efficiency measures existing in the literature (Manzoni et al., 2012) is defining statistical functions predicting carbon use efficiency based on explanatory variables that could themselves be dynamic (soil temperature, pH, soil C:N ratio, etc.). Thus, carbon use efficiency might be spatialized and dynamic.

A better representation of the heterotrophic respiration flux is also important for other biogeochemical variables, particularly in ESMs with explicit nitrogen cycle representation in their land surface scheme. Indeed, heterotrophic respiration fluxes are indicators of soil organic carbon decomposition, but when nitrogen is explicitly represented, it also becomes an indicator of soil N mineralization (Vuichard et al., 2019). In the field, the soil organic matter is composed by complex molecules made of carbon and nitrogen, among others (Cleveland and Liptzin, 2007). Microorganisms decompose soil organic matter, releasing CO₂ to the atmosphere and mineral nitrogen to the soil solution. Microbial activity is therefore a major driver of mineral nitrogen availability and partially controls nitrogen limitations on primary production and therefore on land carbon sink (Bragazza et al., 2013). Since more and more ESMs explicitly represent the nitrogen cycle in their land surface models (Varney et al., 2022; Davies-Barnard et al., 2020), this results in well-constrained heterotrophic respiration fluxes that may help to constrain the nitrogen mineralization flux as they both come from the soil organic matter decomposition by extracellular enzymes. A better representation of the mineral N release flux would probably, in turn, improve the simulation of NPP.

5 Conclusions

Our study showed that, despite previous ESM evaluations of heterotrophic respiration (Shao et al., 2013), few current ESMs represented total heterotrophic respiration flux well, and all failed at representing its spatial distribution. Since heterotrophic fluxes are large and are a major determinant of whether land surfaces represent a carbon sink or source, it is of major importance to better constrain these fluxes and to determine how they will be impacted by climate and land use changes. We showed that current ESMs failed to reproduce heterotrophic respiration fluxes where precipitation is important, probably because heterotrophic respiration responses to soil moisture are poor representations of reality. Nevertheless, it is important to note that soil moisture is not only driven by precipitation. Other water fluxes like runoff, drainage, and evapotranspiration affect the water balance in soils. In this study we did not directly consider soil moisture because it was not available for all the ESMs. Another limitation of our study is that we did not account for other important drivers of heterotrophic respiration in our model residual analysis like pH, microbial biomass, nitrogen availability, etc. We decided to focus on explanatory variables calculated by all the models because we aimed to identify biases due to feedbacks between ESM variables rather than to identify missing mechanisms. We propose several options to improve the ESM without extensive modifications of the current schemes. We believe that our proposals would be relatively easy to implement in the next generation of ESMs, resulting in a possible reduction of the observed spatial bias and a better response to climate change.