Enhancing environmental models with a new downscaling method for global radiation in complex terrain

Global radiation is a key climate input in process-based models (PBMs) for forests, as it determines photosynthesis, transpiration and the canopy energy balance. While radiation is highly variable at a fine spatial resolution in complex terrain due to shadowing effects, the data required for PBMs that are currently available over large extents are generally at a spatial resolution coarser than ∼9 km. Downscaling large-scale radiation data to the high resolution available from digital elevation models (DEMs) is therefore of potential importance to refine global radiation estimates and improve PBM estimations. In this study, we introduced a new downscaling model that aims to refine sub-daily global radiation data obtained from climate reanalysis data or projections at large scales to the resolution of a given DEM. First, downscaling involves splitting radiation into a direct and diffuse fraction. The influences of surrounding mountains' shade on direct radiation and the “bowl” (deep valley) effect (or sky-view factor) on diffuse radiation are then considered. The model was evaluated by comparing simulated and observed radiation at the Mont Ventoux study site (southeast of France) using the recent ERA5-Land hourly data available at a 9 km resolution as input and downscaled to different spatial resolutions (from 1 km to 30 m resolution) using a DEM. The downscaling algorithm improved the reliability of radiation at the study site, in particular at scales below 150 m. Finally, by using two different PBMs (CASTANEA, a PBM simulating tree growth, and SurEau, a plant hydraulic model simulating hydraulic failure risk), we showed that accounting for fine-resolution radiation can have a great impact on predictions of forest functions.

1 Introduction

Studies assessing the impacts of climate change on forest ecosystem functions increasingly rely on high-resolution spatial and temporal climate data. For example, process-based models (PBMs) that aim to evaluate the effect of climate on forest functions and services require daily or sub-daily temporal resolution meteorology as input (e.g. Davi et al., 2006; De Cáceres et al., 2023; Granier et al., 2007; Ruffault et al., 2013, 2022, 2023) to simulate key ecophysiological processes (transpiration, photosynthesis or water potential). However, even relatively fine-grained (i.e. 1 km) historical or projected climate products (Hijmans et al., 2005; Brun et al., 2022) do not correspond to the “topographic scale” and cannot reproduce the fine-scale patterns observed in heterogeneous landscapes. Moreover, employing spatially coarse climatic projections can lead to biased and irrelevant inferences of local ecological patterns (Bedia et al., 2013) or to substantial errors in impact studies (e.g. Patsiou et al., 2014; Randin et al., 2009). Therefore, improving methodologies to provide climatic data variables at a high spatiotemporal resolution is crucial to better understand and predict the spatial heterogeneity in forest structure and function.

Among climate variables, radiation is a key driver of plant functions and productivity globally (Churkina and Running, 1998), acting through two main mechanisms. On the one hand, global radiation determines the photosynthetically active radiation (PAR), i.e. the available energy for photosynthesis and thus plant productivity. Numerous studies have shown the relationship between the amount of solar radiation and the distribution of plant species or communities worldwide (Dirnbock et al., 2003; Franklin, 1998; Meentemeyer et al., 2001; Tappeiner et al., 1998; Zimmermann and Kienast, 1999). On the other hand, the radiation reaching a vegetation surface is an important component of the canopy energy balance, driving the surface temperature and vapour pressure deficit (Monteith, 1981). Thus, radiation is a key driver of evapotranspiration and is involved in most potential evapotranspiration formulations (Fisher et al., 2011) and water balance models (Granier et al., 1999; Ruffault et al., 2013; De Cáceres et al., 2015). Through its effect on the leaf temperature and vapour pressure deficit, radiation also influences the water status of the leaves which, in turn, drives many plant functions, including growth, stomatal aperture and desiccation (Martin-StPaul et al., 2017, 2025).

In regions with complex orography, climatic variations can occur over distances ranging from a few metres to a few kilometres. This phenomenon, referred to as the topoclimate (Bramer et al., 2018), can play a crucial role in shaping the flora and fauna habitat as well as a multitude of ecosystem processes related to climatic variability (Austin, 2002; Piedallu and Gégout, 2008; Randin et al., 2009). Accounting for topographic effects on spatial radiation patterns has been well studied with the purpose, for instance, of improving niche models (that predict the distribution of plants as a function of environmental variables) in mountainous areas (Piedallu and Gégout, 2008; Randin et al., 2009). Thus far, such radiation data have been measured or computed from local meteorological stations, from coarse-scale global meteorological products (such as reanalysis data) or from geostationary satellite data products at a resolution of a few kilometres (e.g. De Cáceres et al., 2018; Roerink et al., 2012).

Direct radiation is a primary driver of topoclimate variation, as it can undergo changes at a very local scale due to several processes. At the massif scale, the surrounding topography can cast shadows on a given point, as sunrays can be physically interrupted. In other words, the presence of nearby high peaks will impact the rays directly coming from the Sun. At the (spatial) point scale, the slope and aspect (azimuth) will additionally modify the direct radiation intensity received. In the Northern Hemisphere, a south face will receive more radiation than a north face, and this will be modulated by the angle between the sunrays and the slope at the point. Similarly, the surrounding topography will affect diffuse radiation (e.g. on cloudy days) isotropically (at 360°), leading to lower radiation in valley bottoms (i.e. the sky-view factor or the “bowl effect”).

Historically, the primary method for accounting for the effects of topography on radiation has been to rely on slope or aspect. Indeed, these parameters are relatively simple to measure (e.g. through GIS), and the global radiation flux at the surface can be easily derived from them (Austin et al., 1990; Carroll et al., 1999; Clark et al., 1999; Pierce et al., 2005). However, this downscaling approach overlooks a significant portion of the processes involved in radiation attenuation due to sky obstruction by surrounding topography. Shading and the sky view were taken into account at a later stage, in particular in the radiation parameterisation scheme (Müller and Scherer, 2005) and in several of its applications (e.g. Senkova et al., 2007; Buzzi, 2008). Regional climate models (RCMs), on the other hand, calculate radiation by accounting for atmospheric processes in relation to land-surface processes (e.g. the energy balance). Nevertheless, they typically operate on fixed grids, usually at scales of several kilometres (Bailey et al., 2023), which are not precise enough for operational use at the point level. More recently, another method that has been employed is statistical downscaling, which is empirical and based on regressions (Davy and Kusch, 2021; Fealy and Sweeney, 2008) or machine learning techniques (Hernanz et al., 2023). However, this requires a lot of field data in different contexts to elaborate an empirical model.

Piedallu and Gégout (2008) proposed a method using the slope and the aspect of the point to calculate the Sun intensity and considered the surrounding topography to compute radiation accounting for direct shadowing. They produced a fine-scale (50 m×50 m) map of France that is dedicated to statistical niche modelling or mortality risk assessment (Piedallu and Gégout, 2008). However, in the case of process-based vegetation models, this has several limitations. Firstly, their approach relies on interpolated meteorological station data to compute the radiation correction at a monthly time step and is, thus, limited in terms of temporal and spatial accuracy, leading to significant biases in vegetation growth or the smoothing of climatic extremes. Secondly, they do not separate diffuse and direct radiation using clouds; rather, they only employ an empirical correction of the total radiation using cloud cover. Finally, the sky-view factor on diffuse radiation is not taken into account. This method based on measurements is, thus, limited for projection purposes and requires a large network of equipped stations, resulting in uncertainty. Moreover, it has only been applied to France and has not been generalised to other regions or periods.

In this study, we present a process-based method to downscale coarse resolution (generally 0.1° at best for reanalysis or meteorological models) or geostationary product (2 km resolution at best) global radiation data (such as global reanalysis or climate projections) made on flat surfaces down to the level of a 1 km to 30 m resolution digital elevation model (DEM) by accounting for slope, aspect, the shadowing effect on direct radiation and the sky-view factor on diffuse radiation. The method can be applied at any resolution, depending on the choice of DEM. Moreover, it can be applied to any type of radiation data, making it applicable to any region in the world and to historical periods as well as future projections. The possibility to use reanalysis-derived radiation data further ensures physical consistency between the different climate variables used in PBMs. The algorithm was tested on Mont Ventoux and compared with PAR measurements recorded during 2 years at seven sites in this complex topographic area. Finally, we evaluated how this new radiation product can impact ecological predictions by simulating the gross primary productivity (GPP) and the risk of drought-induced mortality for the European beech (Fagus sylvatica) using two PBMs.

2 Methods

2.1 Radiation downscaling model

The proposed radiation downscaling model aims to refine sub-daily global radiation data obtained from reanalysis data at large scales to the resolution of a given DEM. This process-based method can be adapted depending on the input dataset and accounts for the shadowing effect on direct radiation and the sky-view factor on diffuse radiation. In order to ensure its versatility and applicability, we reduced the need for external data that can be challenging to obtain at the local scale, such as cloudiness (Dubayah and Loechel, 1997; Piedallu and Gégout, 2007). The only required input is a DEM whose resolution will determine the final spatial resolution of the radiation data.

Our methodology involves four distinct steps, outlined as follows (see Fig. 1 for visualisation):

• i.

  splitting direct and diffuse radiation from a large-scale global radiation dataset (optional if the data already contain direct and diffuse radiation);

• ii.

  downscaling direct radiation by considering local topography and shadowing effects;

• iii.

  downscaling diffuse radiation by estimating the proportion of diffuse radiation that reaches the target point relative to the surrounding topography;

• iv.

  summing the downscaled direct and diffuse radiation components.

These steps are described in detail in the subsequent sections.

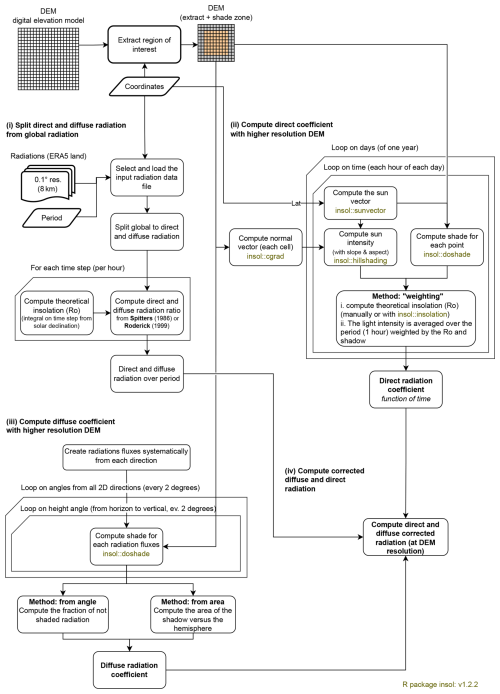
Figure 1 Simplified workflow of radiation downscaling, showing the four different steps of the procedure. The bold boxes in the top left show the input data required (DEM, coordinates, period and large-scale radiation), the green boxes show the functions of the external R package used (insol), the truncated boxes show the loops and the rounded boxes show the various stages.

2.1.1 Splitting direct and diffuse radiation

In cases where only global radiation is available from the input dataset, as in products like ERA5-Land (Muñoz-Sabater et al., 2021), a first step involves extracting hourly direct and diffuse radiation (Fig. 1i). Various methods exist for this purpose (Oliphant and Stoy, 2018). In this study, we adopted the approach proposed by Spitters et al. (1986). This choice was driven by the relative simplicity of this approach and the fact that it was originally developed for European landscapes. Additionally, we explored other methods, such as that proposed by Roderick (1999) and that proposed by Bird and Hulstrom (1981). Results obtained using the Roderick (1999) method align consistently with those presented herein (results not displayed). Unlike the method by Spitters et al. (1986), the method by Bird and Hulstrom (1981) does not rely on global radiation values; instead, the latter method aims to derive the values of direct and diffuse radiation from theoretical radiation, temperature and humidity, among other factors. However, the outcomes generated by this model significantly deviated from those obtained using the Spitters et al. (1986) method and exhibited inconsistency with available measurements (not shown).

The method of Spitters et al. (1986) that was used in this study is an empirical computation technique based on the ratio between theoretical extraterrestrial irradiance (R₀) and the observed value of global radiation (R_g). Specifically, it operates on the assumption that as the ratio of R_g to R₀ decreases, the proportion of diffuse radiation (R_diff) relative to direct radiation (R_dir) increases – an effect attributed to cloud cover.

To compute R₀ (in W m⁻²), a common physically based approach involves using the radiation incident on a plane parallel to the Earth's surface and the sine of solar elevation (which is dependent on latitude and solar time), as follows (Spitters et al., 1986; Widén and Munkhammar, 2019):

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{R}_{\mathrm{0}}=R_{\text{sc}}[\mathrm{1}+\mathrm{0.033}\times \cos (\text{doy}\times \mathrm{360}/\mathrm{365}\left)\right]\times \sin \left(\mathit{\beta }\right),\\ {\displaystyle }& {\displaystyle }\begin{array}{rl}{\displaystyle }\sin \left(\mathit{\beta }\right)=& {\displaystyle }\sin \left(\mathit{\lambda }\right)\times \sin \left(\mathit{\delta }\right)+\cos \left(\mathit{\lambda }\right)\times \cos \left(\mathit{\delta }\right)\\ {\displaystyle }& {\displaystyle }\times \cos (\mathrm{15}\times (t_{\mathrm{h}}-\mathrm{12}\left)\right),\end{array}\\ {\displaystyle }& {\displaystyle }\mathit{\delta }={\displaystyle \frac{\mathit{\pi }\times \mathrm{23.45}}{\mathrm{180}}}\times \sin \left(\mathrm{2}\times \mathit{\pi }\times {\displaystyle \frac{\text{doy}+\mathrm{284}}{\mathrm{365}}}\right).\end{array}\end{array}$$

Here, R_sc represents the solar constant (1361 W m⁻²; Coddington et al., 2016), doy is the day of the year, sin (β) is the sine of the solar elevation angle, λ is the latitude of the site (in radians), δ is the solar declination angle (in degrees) and t_h is the hour (in solar time).

It is important to note that, in this study, global radiation is not treated as a singular value but rather as an average over a short period of time (e.g. between h_t and h_t+1, using an hourly time step with ERA5-Land). Thus, sin (β) needs to be integrated:

$$\begin{array}{}\text{(2)}& {\displaystyle }\begin{array}{rl}{\displaystyle }{\int }_{h_t}^{h_{t+\mathrm{1}}}\sin \left(\mathit{\beta }\right)=& {\displaystyle }\sin \left(\mathit{\lambda }\right)\times \sin \left(\mathit{\delta }\right)+\cos \left(\mathit{\lambda }\right)\times \cos \left(\mathit{\delta }\right)\times {\displaystyle \frac{\mathrm{15}\times \mathit{\pi }}{\mathrm{180}}}\\ {\displaystyle }& {\displaystyle }\times \left[\sin \left({\displaystyle \frac{\mathit{\pi }}{\mathrm{180}}}\times \mathrm{15}\times (h_{t+\mathrm{1}}-\mathrm{12})\right)\right.\\ {\displaystyle }& {\displaystyle }\left.-\sin \left({\displaystyle \frac{\mathit{\pi }}{\mathrm{180}}}\times \mathrm{15}\times (h_t-\mathrm{12})\right)\right].\end{array}\end{array}$$

We then use the relationship between the fraction of diffuse radiation (R_diff) compared to global radiation data (R_g) and the fraction of global radiation data (R_g) compared to theoretical radiation (R₀), as recommended by De Jon (1980) for hourly radiation (described in Spitters et al., 1986, including values for daily radiation).

$$\begin{array}{}\text{(3)}& {\displaystyle }\begin{array}{rlrl}{\displaystyle }& {\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}=\mathrm{1}& {\displaystyle }& {\displaystyle }\text{for }{\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{0}}}}\le \mathrm{0.22}\\ {\displaystyle }& {\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}=\mathrm{1}-\mathrm{6.4}\times {\left({\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{0}}}}-\mathrm{0.22}\right)}^{\mathrm{2}}& {\displaystyle }& {\displaystyle }\text{for }\mathrm{0.22}<{\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{0}}}}\le \mathrm{0.35}\\ {\displaystyle }& {\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}=\mathrm{1.47}-\mathrm{1.66}\times {\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{0}}}}& {\displaystyle }& {\displaystyle }\text{for }\mathrm{0.35}<{\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{0}}}}\le K\\ {\displaystyle }& {\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}=L& {\displaystyle }& {\displaystyle }\text{for }K<{\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{0}}}}\end{array}\end{array}$$

Here, $L=\mathrm{0.847}-\mathrm{1.61}\times \sin \left(\mathit{\beta }\right)+\mathrm{1.04}\times {\sin }^{\mathrm{2}}\left(\mathit{\beta }\right)$ and $K=\frac{\mathrm{1.47}-L}{\mathrm{1.66}}$.

Following Spitters et al. (1986), the final step involves subtracting the circumsolar component (R_circum) of diffuse radiation from the direct flux: under clear skies, diffuse irradiance is anisotropic, due to the presence of aerosols in the atmosphere, and the intensity is therefore higher in the direction of the Sun. It is thus necessary to attribute the excess diffuse irradiance observed near the direction of global radiation to direct radiation.

$$\begin{array}{}\text{(4)}& R_{\text{circum}}={\cos }^{\mathrm{2}}\left({\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}-\mathit{\beta }\right)\times {\cos }^{\mathrm{3}}\left(\mathit{\beta }\right)\end{array}$$

To determine the corresponding fraction of diffuse radiation under intermediate-sky conditions (clear to cloudy skies), we adopt the interpolation method introduced by Klucher (1978):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}={\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}÷\left[\mathrm{1}+\left(\mathrm{1}-{\left({\displaystyle \frac{R_{\text{diff}}}{R_{\mathrm{g}}}}\right)}^{\mathrm{2}}\right)\times R_{\text{circum}}\right].\end{array}$$

Finally, considering that global radiation (R_g) comprises the sum of diffuse (R_diff) and direct (R_dir) radiation components, the value of R_dir can be directly inferred from the other two components.

2.1.2 Downscaling direct radiation

To downscale direct radiation (Fig. 1ii), two distinct processes were considered. Firstly, the path of sunrays was examined to determine if any obstruction in the topography may block them. Secondly, if unobstructed, the slope and aspect of the pixel are used to compute the radiation intensity relative to a horizontal surface.

For both processes, the initial step involved computing the Sun vector in 3D. This was achieved using the “insol” R package (version 1.2.2, Corripio, 2020), specifically the “sunvector” function, which defines the vector based on longitude, latitude and time (day, hour and minute). To assess whether radiation is obstructed by a summit, the close topography derived from a DEM is computed using the “doshade” function within the insol package. To determine Sun intensity, the “hillshading” function from the same package is utilised, requiring both the Sun vector and the topography (previously normalised into unit vectors with the “cgrad” function). Note that the same package is now available for Python (at https://pypi.org/project/insolation/, last access: 19 December 2024, and https://www.meteoexploration.com/insol/, last access: 19 December 2024).

Considering that the input radiation is accumulated over a specific period (e.g. 1 h in ERA5-Land) as well as to account for spatial variations in radiation intensity (primarily due to the angle of the sunrays) and shadow projections, several time steps are employed for downscaling the direct radiation. In this study, the default value of three time steps per hour (n=3) was adopted. Additionally, to aggregate the values while also considering temporal variations in radiation intensity, each value is weighted by the theoretical extraterrestrial irradiance (R₀ in Eq. 1). This yields a corrected direct radiation ($R_{{\text{dir}}_{\text{cor}}}$):

$$\begin{array}{}\text{(6)}& R_{{\text{dir}}_{\text{cor}}}=R_{\text{dir}}\times {\displaystyle \frac{{\sum }_{t_{\mathrm{1}}}^{t_n}\left(R_{\mathrm{0}}\times S\times \frac{I_{\text{slope}}}{I_{\text{vert}}}\right)}{{\sum }_{t_{\mathrm{1}}}^{t_n}{R}_{\mathrm{0}}}}.\end{array}$$

Here, S represents the shadow parameter (with a value of 0 indicating shadow and 1 indicating no shadow), and I_slope and I_vert denote the illumination intensity over the slope and a vertical surface, respectively, to derive the relative intensity of sunlight over the slope.

2.1.3 Downscaling diffuse radiation

Diffuse radiation is independent of the Sun's inclination. It emanates uniformly from all directions within the sky dome, limited in this study to the top half-sphere. Therefore, its downscaling (Fig. 1iii) relies on the surrounding topography in all 360° horizontal directions, particularly the proportion of diffuse radiation from all directions that can reach the point under study.

Various methods exist to compute this fraction, including employing numerous random rays or determining (for regular 3D-distributed vectors) the level of shadow. In this study, a specific method was devised. It involves computing, for each azimuth angle (with fixed steps of 2°), the minimum unshaded radiation using the doshade R function described previously and a DEM.

Subsequently, these values are utilised to calculate the shaded area of the top half-sphere and, thus, the proportion of diffuse radiation reaching the focal point. Finally, this proportion is applied to the diffuse radiation computed in Sect. 2.1.1 to derive the corrected diffuse radiation ($R_{{\text{diff}}_{\text{cor}}}$).

The corrected diffuse and direct radiation can then be directly employed or recombined into corrected global radiation ($R_{{\mathrm{g}}_{\text{corr}}}$), e.g. to serve as input to a model of forest function or dynamics.

2.1.4 DEM data

In various steps of the radiation downscaling, the utilisation of a DEM is imperative (Sect. 2.1.2 and 2.1.3). In this study, we evaluated radiation downscaling using different DEMs characterised by varying resolutions.

The first dataset is the DEM provided by the Shuttle Radar Topography Mission (SRTM, 2013), offering a resolution of 1 arcsec (approximately 30 m). In order to clarify the impact of using different resolutions, the resolution of the SRTM product was downgraded to obtain products with respective resolutions of 60, 90, 125, 185, 250 and 500 m using the aggregate function (R, terra 1.7.23 library).

An additional series of DEMs was employed: the Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010, Danielson and Gesch, 2011), which encompasses spatial resolutions of 30, 15 and 7.5 arcsec, corresponding approximately to resolutions of 1 km, 500 m and 250 m, respectively. These datasets were compiled from diverse sources. However, for the metropolitan France region, the primary source of the dataset was the 1 arcsec SRTM DEM.

The interest in these DEMs lies in their applicability beyond the geographic scope covered in this study. Their availability at a global terrestrial scale renders them suitable for use in various locations worldwide (with the exception of SRTM, which is limited to latitudes between 60° N and 56° S).

2.2 Study area

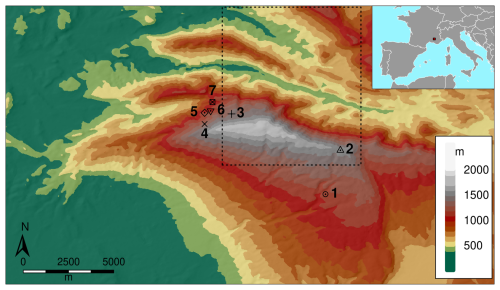
The study area was Mont Ventoux, a mountain located in southeastern France, with its highest point reaching an elevation of 1912 m (44.174° N, 5.27794° E; Fig. 2). While Mont Ventoux is predominantly oriented in an east–west direction, it exhibits notable variations with respect to slopes and aspects. The southern flank is characterised by gradual inclines, whereas steeper slopes are evident on its northern side. Mont Ventoux presents a predominantly wooded landscape, featuring a mixed beech–fir forest on its northern side and a mixed European beech–black pine forest on its southern side, particularly above an elevation of 800 m (Jean et al., 2023). Below this elevation, the dominant species are more typical of the Mediterranean biome and include coppices of downy oak (Quercus pubescens), evergreen oak (Quercus ilex), Aleppo pine (Pinus halepensis) and a natural regeneration of Atlas cedar (Cedrus atlantica) from old plantation trials in the early 20th century.

Figure 2 Map of the study area (Mont Ventoux). Mont Ventoux is located in southeastern France (see the inset). Observation points (symbols with associated numbers) and the ERA5-Land tile (dotted outline) used in this study are indicated.

2.3 Global radiation measurements

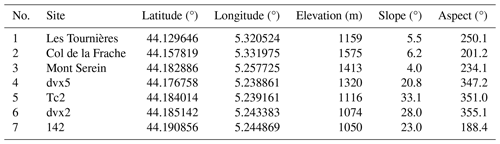
On 27 June 2016, we installed seven mini weather stations at different strategic elevations and locations on Mont Ventoux (Table 1), each equipped with loggers (YBdesign) and sensors for photosynthetically active radiation (PAR, 400–700 nm), temperature and relative humidity. The sensors were installed on a vertical pole and positioned horizontally (levelled with a spirit level). The PAR sensors (CBE80, SOLEMS) and the thermo-hydrometers (EE07-PFT, E+E) were calibrated using a reference weather station at the National Research Institute for Agriculture, Food and Environment (INRAE) campus of Avignon before the beginning of the experiment. The mini weather stations were positioned in clearings with forest edges a minimum distance of 30 m from the station. The data were recorded at a 1 h time step. The photosynthetic flux density values delivered by the sensors were converted into watts per square metre (W m⁻²) of global radiation using an empirical relationship calibrated on the Integrated Carbon Observing System (ICOS) Font-Blanche experimental site (Moreno et al., 2021).

Table 1 List and main characteristics of the Mont Ventoux observation sites at which radiation measurements were performed. Slope and aspect (azimuth) were computed from a 30 m resolution SRTM DEM.

The observed radiation was compared with the radiation from ERA5-Land before and after downscaling using DEMs at different resolutions. In order to facilitate the comparison between the ERA5-Land reanalysis dataset and observations, which may contain some gaps due to power failure, we aggregated radiation data over various periods (annually or seasonally). This approach involved excluding time steps with missing data, separately for each site. Moreover, for comparison with the observations, the correction of the light intensity due to the angle of the direct light rays in relation to the slope and aspect (the hillshading function; Sect. 2.1.2) was deactivated (Sect. 3.1), as the measurements were carried out on a device that was placed horizontally.

2.4 Modelling the effect of radiation downscaling on plant functions

To quantify the influence of downscaled radiation on specific applications, we assessed the impact of radiation downscaling on beech (Fagus sylvatica) forest functions using process-based vegetation modelling in a mountainous area of the Mont Ventoux massif (where radiation measurements were located).

We employed two complementary forest vegetation models to quantify how radiation downscaling affects the spatial patterns of the GPP and drought-induced risk of hydraulic failure; these models were the forest growth model CASTANEA (Dufrêne et al., 2005) and the plant hydraulic model SurEau (Cochard et al., 2021; Ruffault et al., 2022), respectively.

CASTANEA is a comprehensive forest soil–vegetation–atmosphere model coupled with a growth module. It simulates carbon (photosynthesis and respiration) and water fluxes (transpiration, soil water content and soil water potential) at a 30 min to daily time step for an average tree in a homogeneous forest stand. A carbon allocation module assigns a proportion of the daily net primary productivity (NPP) toward various plant compartments (stem, roots, fine roots, flowers, acorn, leaves and storage) using empirical coefficients. Carbon and water fluxes, including gross and net ecosystem photosynthesis, respiration, transpiration, latent heat fluxes, soil water content, and plant water potential, have been validated on different species and sites, including beech on Mont Ventoux (Davi et al., 2005; Cailleret and Davi, 2011; Delpierre et al., 2012). In this study, the canopy GPP was used to demonstrate the effects of radiation downscaling on potential productivity.

SurEau is a plant hydraulic model that is dedicated to simulating the risk of drought-induced hydraulic failure due to xylem embolism, a leading mechanism of plant mortality under drought conditions (Cochard et al., 2021; Ruffault et al., 2022). The model simulates water fluxes and water potential along the soil–plant hydraulic continuum at a 30 min time step and considers leaf stomata and their regulation as well as cuticular transpiration and plant organ capacitance. The model is parameterised with various measurable plant traits previously collected for the target species (Ruffault et al., 2022). In this study, the drought-induced risk of hydraulic failure (or the percentage loss of hydraulic conductance) in the vascular system was used as a proxy for hydraulic risk during a given summer.

We conducted spatial simulations for one pixel at a 0.1° resolution ($\sim \mathrm{11}\mathrm{km}\times \mathrm{8}\mathrm{km}$ at these coordinates), covering a large part of the Mont Ventoux northern face where the measurements were conducted. The simulations covered the years 2016 and 2017, encompassing the same geographical area as outlined in Sect. 2.3, spanning a segment of Mont Ventoux ranging from 5.25 to 5.35° W and from 44.15 to 44.25° N.

Climate data were directly sourced from the ERA5-Land hourly dataset (Muñoz-Sabater et al., 2021), including temperature, precipitation, wind speed, relative humidity and global radiation. The latter was downscaled using the method presented in Sect. 2.1, employing one of the DEMs discussed in Sect. 2.1.4.

To maintain consistency and avoid introducing uncertainty from disparate datasets, all other non-climatic inputs were set constant across the study area, as described hereafter. The species selected, Fagus sylvatica (European beech), is one of the most common species present on Mont Ventoux (Lander et al., 2021), and its traits are already available for the two models (Cailleret and Davi, 2011; Cailleret et al., 2013; Davi and Cailleret, 2017; Ruffault et al., 2022), with the leaf area index set at 3.5. The soil characteristics corresponded to the median value extracted from the SoilGrids database for the whole study area (Poggio et al., 2021).

3 Results

3.1 Comparison between simulated and observed global radiation

The comparison of ERA5-Land global radiation, both uncorrected and corrected, with observed global radiation across the seven studied sites showed the benefit of our downscaling method with respect to accurately estimating local global radiation (Figs. 3, 4; Table 2).

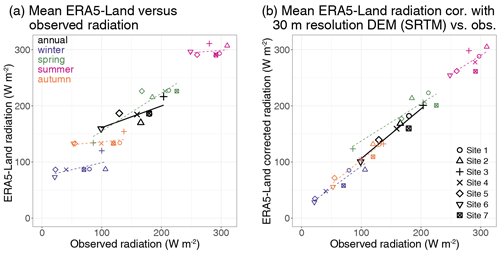
Figure 3 Comparison of the observed radiation (a) with the ERA5-Land product and (b) with corrected radiation from ERA5-Land using a 30 m resolution DEM. For each of the seven points studied, the annual (in black) and seasonal (in colours) mean radiation values (W m⁻²) are shown, along with the linear regression line (equation, r² and RMSE; see Table 2).

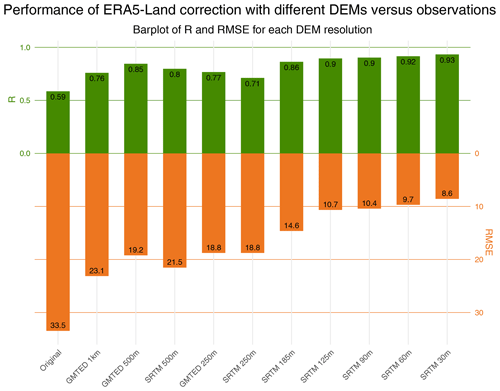
Figure 4 Comparison of the performance of the ERA5-Land product and corrected radiation from ERA5-Land using different DEMs with observed radiation. The annual correlation r² is represented in green, while the RMSE (W m⁻²) is given in orange.

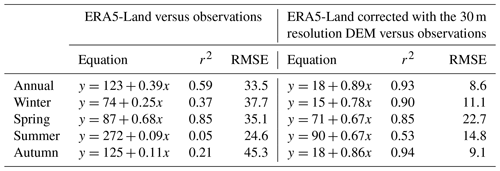
Table 2 Linear regression parameters and statistics (r² and RMSE, in W m⁻²) for comparison of the observed radiation with the ERA5-Land product and with corrected radiation from ERA5-Land using the 30 m DEM (see Fig. 3).

Specifically, the correlation between the observed and simulated yearly mean global radiation increased from r²=0.59 to r²=0.93, while the RMSE decreased from 33.5 to 8.6 W m⁻², for the raw ERA5-Land radiation and ERA5-Land radiation corrected with a 30 m resolution DEM, respectively (Fig. 3, Table 2). However, this increase in the performance of estimating global radiation did not progress consistently as the resolution of our downscaling approach increased. We observed a slight and heterogeneous improvement in the corrected radiation from 1 km to 250 m resolution compared with the raw ERA5-Land resolution (around 9 km). It was not until the resolution reached around 200 m that a significant and continuous improvement was observed (decrease in RMSE, increase in r²) until 30 m resolution (Fig. 4).

Our results further showed that the absolute performance of radiation models (in terms of the r²) and their relative differences remained consistent across the different studied seasons (Table 2), despite some particularities. During winter, ERA5-Land raw data showed a weak correlation with observations (r²=0.37, RMSE = 38 W m⁻²), which substantially improved with correction (r²=0.90, $\text{RMSE}=\mathrm{11}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}$). Similarly, but more pronounced, correlations and RMSE values were considerably enhanced in autumn (r²=0.21–0.94, RMSE=9–45 W m⁻²). In summer, the correlation with the ERA5-Land data was almost zero, whereas it exceeded 0.5 with the corrected radiation data. In contrast, the correlation was stable and high (r²=0.85) in spring but did not improve with downscaling, while the RMSE improved with correction (RMSE=23–35 W m⁻²). Further analysis also revealed that the uncorrected (Fig. 3a) and corrected (Fig. 3b) seasonal data showed different behaviour; thus, the equations of the seasonal curves for corrected ERA5-Land radiation closely aligned with the 1 : 1 line, in accordance with an important decrease in the RMSE. It is noteworthy that most of the improvement came from points located on northern slopes (points 4, 5 and 6; Fig. 3). Accordingly, the daily bias from those points was reduced compared with the uncorrected data, while points located on flat surfaces or southern slopes showed low and non-significant bias (not shown).

Figure 5 depicts the global radiation values for two distinct sites during two different periods. Site 1 (see Table 1) represents a slightly south-facing location with little shade from topographical features, particularly evident in winter. Site 5, on the other hand, is situated on a north-facing (and slightly west-facing) slope; this aspect affects sunlight exposure, especially during winter months. Two 3 d periods were selected for analysis: one period in summer (19–21 August 2016), to observe the impact during peak Sun exposure (21 August), a cloudy day (20 August) and an intermediate day (19 August), and another period in winter (12–14 January 2017), which comprised cloudless days and aimed to assess the effect of the downscaling on low-inclination radiation in a mountainous region. Three types of radiation values are presented: observed values (Sect. 2.3), original ERA5-Land values (the 9 km resolution tile indicated in Fig. 2) and values following the application of the radiation downscaling with the SRTM DEM (∼30 m resolution; as described in Sect. 2.1 but without the hillshading function so as to be comparable with measurements that are made with horizontally set sensors). The presence of clouds was assessed with data combining high-resolution cloud information directly inferred from satellite observations, such as the Copernicus Atmosphere Monitoring Service (CAMS) solar radiation time-series data (available on https://ads.atmosphere.copernicus.eu/stac-browser/collections/cams-solar-radiation-timeseries, last access: 22 October 2024), as represented in Fig. S1 in the Supplement. The difference between sky-view and all-sky radiation indicates the presence of clouds.

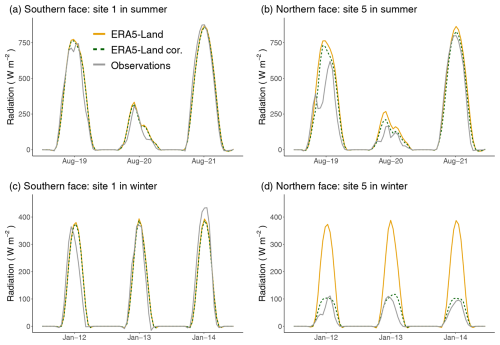
Figure 5 Radiation for the original ERA5-Land data (orange line), after downscaling with the SRTM DEM (30 m resolution; dotted dark-green line) and for the observations (grey line) for site 1 (a, b) and site 5 (c, d) for two different dates: one in summer (19–21 August 2016; a, c) and one in winter (12–14 January 2017; b, d).

At site 1 (Fig. 5a, b, c), where surrounding topographical features have minimal impact on radiation, the values from ERA5-Land were close to the observations and there was no significant change after radiation downscaling. These trends held for both clear and cloudy days and for both winter and summer periods. At site 5, disparities between original and corrected ERA5-Land values were more significant due to topographical influences compared with site 1. In summer (Fig. 5b), discrepancies existed between original and corrected ERA5-Land values. Corrected values accurately depict the evolution measured, especially the 21 August, and constantly more closely represented measured values, although they still struggled to replicate sub-daily variations. Particularly, a dip in the curve around 10:00 LT appeared to be present on 19 August, possibly indicating a shadow or the presence of localised clouds or fog, but was not represented in the original or corrected radiations. In winter (Fig. 5d), downscaling markedly impacted radiation values, with corrected values nearly 4 times lower than ERA5-Land values at the northern site, closely aligning with observed values.

Note that, if the effect of the slope and aspect on radiation intensity were activated in the script, the effect of the light intensity could increase in the corrected radiation on the southern faces, mainly on clear days and in winter (e.g. +10 % for point 1). In contrast, it could reduce the corrected radiation on cloud-free days (e.g. by a factor of 2 for 21 August at point 5).

3.2 Application on the Mont Ventoux massif

3.2.1 Heterogeneity in global radiation

Applying our approach across a heterogeneous geographical area illustrates the spatial and temporal variability in global radiation introduced by downscaling (Fig. 6).

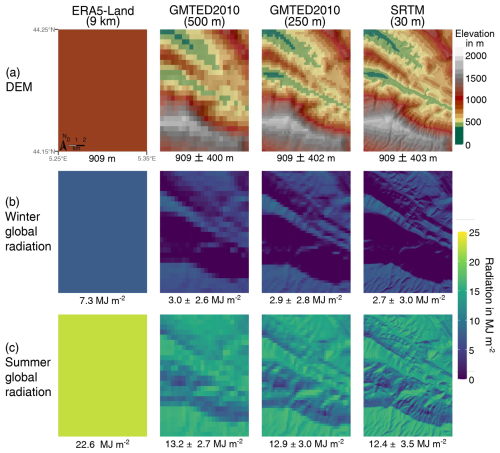
Figure 6 Global radiation from ERA5-Land and resulting from downscaling obtained from DEMs with different resolutions. Row (a) shows the ERA5-Land tile (left) and DEMs with different resolutions (500, 250 and 30 m, from left to right). The remaining rows present the daily global radiation for two distinct dates (b) in winter (13 January 2017) and (c) in summer (19 August 2016). Regional mean values and standard deviations are indicated at the bottom of each map.

Radiation downscaling exerted a clear impact in the mountainous region under study, halving the original ERA5-Land global radiation. An evident differentiation emerged between south-facing slopes, which received more radiation, and north-facing slopes, which exhibited minimal radiation levels in winter (approaching zero). Mean radiation values decreased with an increasing resolution of the three DEMs used, indicating an average decrease of 10.7 % on 13 January 2017 and of 5.9 % on 19 August 2016 when transitioning from the GMTED DEM at approximately 500 m to the SRTM DEM at an approximate 30 m resolution. Conversely, the standard deviation increased with resolution, rising by 13.5 % and 30.0 %, respectively. During winter, the standard deviation was similar in magnitude to the mean due to low radiation values, whereas in summer, it accounted for 20 %–25 % of the mean.

These differences in the standard deviation due to topography implied significant differences between the different DEMs, as well as with the original ERA5-Land values. For instance, the daily accumulation of radiation value recorded on 13 January was 7.3 MJ m⁻² in the reanalysis, whereas the maximum daily radiation reached 9.3 MJ m⁻² in the ERA5-Land tile with downscaling conducted using the 250 m DEM. Similarly, on 13 January (Fig. 6b), the spatial pattern representing a denser “line” denoting stronger radiation values around 44.19° N, 5.3° E was relatively narrow with the 30 m DEM (approximately 200 m wide), whereas it doubled in width with the 500 m DEM.

3.2.2 Modelling the influence of radiation downscaling on vegetation function

Modifying radiation across the entire area according to each DEM had a tangible impact on the predictions of vegetation processes, as seen in the model output shown in Fig. 7. In general, the simulations remained consistent across the study area, despite potential variations introduced by the different topographies used during downscaling. With the three different downscaling methods (from 8 km to 500, 250 and 30 m, respectively), there is a discernible reduction in the GPP, ranging between 5 % and 8 %, as well as in the risk of hydraulic failure, which showed decreases of between 14 % and 23 %. Moreover, the standard deviation introduced between the values was quite significant, varying between 8 % and 13 % for the two outputs studied.

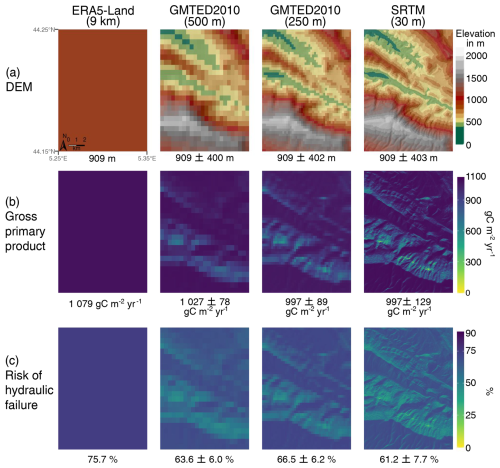
Figure 7 Row (a) shows the ERA5-Land tile (left) and the DEMs with different resolutions (500, 250 and 30 m, from left to right). Rows (b) and (c) present the gross primary productivity and risk of hydraulic failure simulated with CASTANEA and SurEau, respectively, from ERA5-Land and resulting from global radiation downscaling obtained from DEMs with different resolutions. Regional mean values and standard deviations are indicated at the bottom of each map.

Upon comparing the patterns obtained with the corresponding DEMs, we observed that south-facing slopes tended to exhibit higher annual productivity (Fig. 7b) but were susceptible to greater hydraulic stress (as indicated by the darker colours in Fig. 7c). Conversely, north-facing slopes generally manifested lower GPP values, as simulated by the CASTANEA model, but exhibited a reduced risk of hydraulic failure.

To evaluate the potential impact of these discrepancies on drought-induced mortality, we computed the risk of hydraulic failure from the SurEau simulations. The relationship between mortality due to water stress and the risk of hydraulic failure is often conceptualised as a threshold effect (Choat et al., 2018), although this notion is occasionally questioned (Hammond et al., 2019). Setting the risk of hydraulic failure threshold at which trees die to 50 %, we obtained drought-induced mortality percentages in terms of the surface of 100 %, 97 %, 98 % and 89 % for the original ERA5-Land tile and the data downscaled to 500, 250 and 30 m, respectively. Note that, as the total soil-available water accessible to the trees used in this study came from a single value taken from the median over the area of the SoilGrids database (Poggio et al., 2021), which is subject to uncertainty, the results are consistent with each other.

4 Discussion

4.1 Performance of the downscaling method

The radiation downscaling method that we present in this study significantly improved radiation predictions in mountainous regions compared with those provided by reanalysis products. More specifically, we demonstrated that accounting for the impact of topography and distinguishing between direct and diffuse radiation allowed us to better capture seasonal radiation patterns. On the north-facing side of our study area, where global radiation is reduced due to the obstruction of direct sunlight by surrounding mountains, our downscaling method significantly lowered radiation levels, particularly during winter when the Sun is at its lowest position on the sky. Conversely, on the south-facing slopes, the steepness of the terrain and the more direct alignment with the Sun resulted in increased radiation levels. This effect was also particularly pronounced in winter, when the Sun was lower in the sky but more favourably oriented towards these slopes. Consequently, our method represented the spatial heterogeneity in radiation that can be observed in complex terrain, significantly improving radiation estimations from larger-scale reanalysis products when a fine downscaling scale is chosen. This corroborates the results reported by other studies based on slope, aspect ratio and sky view, which indicate improved results after downscaling (Müller and Scherer, 2005; Senkova et al., 2007; Buzzi, 2008). Nevertheless, none of these studies combined both high spatial (here ∼30 m) and temporal (hourly) resolution. Furthermore, via comparison with precisely resolved data combining high-resolution cloud information and information directly inferred from satellite observations (CAMS data; Fig. S1), the quality of our results is confirmed. In summer, the CAMS data are consistent with both our results and the observations. In winter, the results presented in Fig. 5 are much closer to the observations at the south-facing site, while the topographical correction allows us to be very close to the observations at the north-facing site, whereas the CAMS data are very far from observed values at the latter site.

Our analysis showed a clear but non-uniform improvement in radiation estimates as the resolution of our downscaling method increased. While no continuous improvement was observed at resolutions coarser than 250 m, a gradual improvement emerged for finer resolutions, down to 30 m. This suggests that topoclimatic processes, such as the effects of topography on local radiation patterns, operate at these finer spatial scales, highlighting the importance of high-resolution estimations for accurately representing the influence of terrain on local climate. On the other hand, our results for resolutions coarser than 250 m, suggest that insufficient improvement in resolution during the downscaling introduces some variance (due to the inherent uncertainty in the method and additional processing of the variable) which can mitigate improvements in the representation of radiation at the site level.

As we clearly observed in our study area, the impact of radiation downscaling was primarily observed in regions with significant shadow casting, the effect of which becomes more pronounced as the Sun's zenithal angle decreases. Due to energy equilibrium and conservation at the large scale, this implies that an increase in radiation was observed on south-facing slopes or on mountaintops. This effect was particularly pronounced when the angle between the incoming direct radiation and the aspect of the relief (slope and azimuth) approached an angle that was perpendicularity relative to a flat surface. However, it is worth noting that our study area is not characterised by extremely steep mountains, so these effects were primarily observed on moderate slopes. In regions with much steeper terrain, we would expect the impact of topography on radiation to be even more pronounced, especially at valley bottoms, where shading effects could remain significant even on south-facing slopes.

An important source of uncertainty in our radiation downscaling method likely stems from the way in which global radiation is split into direct and diffuse components using the ratio of R_g to R₀ as a proxy for cloud cover. This approach cannot capture the spatial and temporal heterogeneity in cloud cover, which can be especially significant in mountainous regions (Buzzi, 2008). This explains why, while daily patterns were effectively estimated, sub-daily variations were more difficult to capture. For instance, in Fig. 5b, the dip at around 10:00 LT on 19 August may suggest the presence of microclimatic conditions, such as clouds or fog, the effect of which is not considered in our downscaling method. Actually, the original ERA5-Land data cannot depict the presence of isolated clouds as they occur on the day presented for summer in Fig. 5, as they provide averaged values of incoming radiation over the whole mesh area. Such occurrences could be tracked using higher-resolution solar radiation products such as those obtained from satellite imagery and, in particular, geostationary satellites with a spatial resolution in the order of 2 to 3 km and a time resolution of between 5 and 15 min (e.g. Roerink et al., 2012; Bojanowski et al., 2014). Indeed, this dip may be associated with the presence of small clouds or fog capping Mont Ventoux during the morning, signalled by the drop-out between the CAMS clear-sky and all-sky data (Fig. S1). Similarly, the small dip observed in Fig. 5a, shortly after the one present in Fig. 5b and studied earlier, is actually related to the presence of small clouds or fog capping Mont Ventoux during the morning, moving from one site to another. Further analyses using such data could help quantify the extent to which this effect contributes to overall uncertainty in our methodology.

4.2 Implications of radiation downscaling for modelling studies and perspectives for improvement

Using downscaled radiation estimations as input in two process-based forest models provides an overview of the impact that radiation downscaling can have on different forest processes, namely GPP or drought-induced mortality. Overall, our results revealed that the effects of topography on local radiation patterns can have important implications for these key forest processes. For instance, when considering processes that are based on thresholds, such as the drought-induced mortality associated with the risk of hydraulic failure, the mortality rate was reduced from 100 % to 89 %. As could be deduced from the results on radiation alone, the impact of downscaling on the GPP and drought-induced mortality was most pronounced in areas with significant topographic features, such as north-facing slopes due to shading or south-facing slopes due to increased radiation levels.

While the effect of topography on forest ecological processes is often assessed through its impact on temperature or precipitation patterns (Randin et al., 2009), these results suggest that spatial heterogeneity in radiation, via its interaction with topography, also seems crucial for accurately assessing ecological responses and potential threshold effects in complex terrain. Future studies could benefit from integrating our radiation downscaling method to improve predictions of forest functions at a very local scale.

However, these findings should be interpreted with caution, as only solar radiation was downscaled in our study, leading to potential decoupling with the other forcing variables (temperature, humidity, precipitation and wind). Downscaling methods exist for these variables, for example, the use of a simple adiabatic gradient for temperature or kriging methods/high-resolution radar data for rainfall (Liston and Elder, 2006; Davy and Kusch, 2021) or dynamic models (Maraun et al., 2010), but they are not consistent with the one proposed here. Therefore, we need to check the consistency of each of the downscaling methods or evaluate if it is possible to integrate this method or its outputs to downscale other variables with other methods. Indeed, it is important to start from physically consistent data – in this case, ERA5-Land – that can be adapted, as the method can be adapted to any global (or direct and indirect) radiation input. Finally, the method developed here is only applicable to shortwave radiation, which is the only radiation currently required by the models used. Nevertheless, the principle of the method presented here could be used as a starting point for downscaling longwave radiation. Following the principle presented in Senkova et al. (2007), the method used for diffuse radiation (based on the sky view) could be partially applicable to longwave radiation. If it is considered to be isotropic, incoming atmospheric radiation could be downscaled directly on the basis of the methodology used to downscale diffuse incoming solar radiation. However, it would be necessary to account for the radiation emitted by land surfaces in view, as emitted radiation from the surface is usually significantly higher than atmospheric radiation (and this would be particularly true for cloudless skies). This would require the knowledge of the surface temperatures of the surrounding areas, but it is also important to recall that the net longwave radiation has a significantly lower impact on the surface energy balance than the net shortwave radiation (e.g. Mira et al., 2016).

5 Conclusion

In this study, we developed a process-based method to downscale global radiation data from flat surfaces, such as coarse-spatial-resolution global reanalysis data. The method builds upon existing research, but it goes further than traditional process-based radiation downscaling methods by accounting for the shadowing effect on direct radiation and for the sky-view factor on diffuse radiation (Piedallu and Gégout, 2008). The recent ERA5-Land hourly data available at 9 km resolution for Mont Ventoux were used to compare the impact of radiation downscaling computed from different DEMs.

The radiation downscaling method effectively captured the overall trend in the radiation distribution across mountainous regions. Agreement with observations was improved for downscaled radiation compared with original ERA5-Land data, especially during the winter months due to the higher zenithal angle. This improvement was particularly significant and increased gradually after a certain spatial resolution (∼150 m). The implications of downscaling for modelling studies was further investigated using two different PBMs representing GPP and the risk of hydraulic failure. The impact of downscaling on those variables was most pronounced in areas with significant topographic features, such as mountainous regions or canyons. Assessing the spatial heterogeneity in radiation, via its interaction with topography, is crucial to accurately address ecological responses and potential threshold effects in complex terrain.

The method can be applied at any resolution, depending on the choice of DEM. Moreover, it can be applied to any type of radiation data, making it applicable to any region in the world and to historical periods as well as future projections. Finally, the method could involve other types of climatic data from the same input dataset, such as temperature or precipitation, thereby ensuring physical consistency between the variables. In the future, such methods could be included in more generic climate downscaling tools (e.g. meteoland; De Cáceres et al., 2018) to facilitate the application of PBMs at fine resolution.