Efficiency metrics for ocean alkalinity enhancements under responsive and prescribed atmospheric pCO₂ conditions

Ocean alkalinity enhancement (OAE) and direct ocean removal (DOR) are emerging as promising technologies for enacting negative emissions. The long equilibration timescales, potential for premature subduction of surface water parcels, and extensive horizontal transport and dilution of added alkalinity make direct experimental measurement of induced CO₂ uptake challenging. Therefore, the challenge of measurement, reporting, and verification (MRV) will rely to a great extent on general circulation models, parameterized and constrained by experimental measurements. A number of recent studies have assessed the efficiency of OAE using different model setups and different metrics. Some models use prescribed atmospheric CO₂ levels, while others use fully coupled Earth system models. The former ignores atmospheric feedback effects, while the latter explicitly models them. In this paper it is shown that, even for very small OAE deployments, which do not substantially change atmospheric pCO₂, the change in oceanic CO₂ inventories differs significantly between these methods due to atmospheric feedback causing some ocean CO₂ off-gassing. An analogous off-gassing occurs during direct air capture (DAC). Due to these feedback effects, care must be taken to compute the correct metrics when assessing OAE efficiency with respect to determining negative emissions credits, as opposed to determining the effect on global temperatures. This paper examines the commonly used metrics of OAE efficiency, their exact physical meanings, the assumptions inherent in their use, and the relationship between them. It is shown that the efficiency metric η(t), used in prescribed pCO${}_{\mathrm{2}}^{\mathrm{atm}}$ simulations, equals the equivalent schedule of a gradual DAC removal and storage in a fully coupled system.

1 Introduction

In recent years, the search for technologies capable of removing CO₂ from the atmosphere has intensified. Among other approaches, there has been a rise in interest in marine carbon dioxide removal (mCDR) (National Academies Press, 2022), in particular ocean alkalinity enhancement (OAE) (Eisaman et al., 2023; Renforth and Henderson, 2017) and cultivation of algae (Ritschard, 1992). Unlike terrestrial CDR approaches, which remove CO₂ directly from the atmosphere, mCDR approaches either remove CO₂ from the surface ocean or increase the capacity of surface ocean water to hold CO₂ by adding alkalinity. Either way, the partial pressure of CO₂ (pCO₂) is reduced in surface waters, which causes a subsequent transfer of CO₂ from the atmosphere to the ocean. This uptake does not happen instantly but instead occurs gradually (Jones et al., 2014; Broecker and Peng, 1982), with the potential for the CO₂-deficient water parcel to be subducted and removed from contact with the atmosphere (He and Tyka, 2023; Bach et al., 2023). In the latter case, the mCDR potential can be delayed for centuries to millennia if the water parcel does not remix with the surface layers on timescales relevant for the CDR effort. Several studies that aim to quantify the equilibration dynamics and the equilibration e-folding times have been published (Wang et al., 2023; Tyka et al., 2022; He and Tyka, 2023; Zhou et al., 2024; Suselj et al., 2024). It has been shown that the equilibration kinetics and completeness vary significantly depending on the induction location and season. These studies have focused on the immediate effects of increased surface alkalinity, which occurs on short to medium timescales. Likewise, this work here focuses only on the gas-exchange questions and ignores longer-term physical or biological effects, such as induced changes in carbonate precipitation or dissolution.

How much CO₂ is drawn into the ocean upon addition of some quantity of alkalinity? Changing the alkalinity of seawater by a small amount ΔAlk reduces the pCO₂ by $\frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{Alk}}\mathrm{\Delta }\mathrm{Alk}$, while increasing DIC (dissolved inorganic carbon) by a small amount ΔDIC increases the pCO₂ by $\frac{\partial p{\mathrm{CO}}_{\mathrm{2}}}{\partial \mathrm{DIC}}\mathrm{\Delta }\mathrm{DIC}$. Therefore, the relative quantity of DIC that exactly counterbalances the pCO₂ for a particular increase in alkalinity is

$$\begin{array}{}\text{(1)}& {\mathit{\eta }}_{{\mathrm{CO}}_{\mathrm{2}}}={\left.{\displaystyle \frac{\partial \left[\mathrm{DIC}\right]}{\partial \left[\mathrm{Alk}\right]}}\right|}_{p{\mathrm{CO}}_{\mathrm{2}}},\end{array}$$

depending on the local state of the carbonate system ${\mathit{\eta }}_{{\mathrm{CO}}_{\mathrm{2}}}\approx \mathrm{0.83}$ (Renforth and Henderson, 2017), varying from 0.9 closer at the poles to 0.79 at the Equator (${\mathit{\eta }}_{{\mathrm{CO}}_{\mathrm{2}}}$ is the inverse of the isocapnic quotient, as introduced by Humphreys et al., 2018). Given that equilibration is not instantaneous, it makes sense to define a time-dependent OAE efficiency factor, which tracks the equilibration from the moment the alkalinity is altered:

$$\begin{array}{}\text{(2)}& \mathit{\eta }\left(t\right)=\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk},\end{array}$$

where ΔAlk is the quantity of alkalinity added, and $\mathrm{\Delta }\mathrm{DIC}=\sum {\mathrm{DIC}}^{\mathrm{OAE}}-\sum {\mathrm{DIC}}^{\mathrm{Ref}}$ is the difference in the total inventory of DIC between a perturbed and a reference simulation. In other words, η(t) tracks the progress of the equilibration (He and Tyka, 2023; Zhou et al., 2024; Suselj et al., 2024) by quantifying the excess CO₂ taken up by the ocean relative to the unperturbed reference simulation. These simulations have typically been carried out with the partial CO₂ pressure in the atmosphere ($p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$) held constant or prescribed (Wang et al., 2023; Tyka et al., 2022; He and Tyka, 2023; Zhou et al., 2024; Suselj et al., 2024; Köhler et al., 2013; Burt et al., 2021), meaning that the $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in the perturbed simulation equals that in the reference.

However, in reality, the uptake of CO₂ by the ocean would be accompanied by an equal reduction in atmospheric CO₂, which in turn affects the pCO₂ gradient across the sea–air interface (Jin et al., 2008; Oschlies, 2009; Schwinger et al., 2024). This feedback acts to reduce the total transfer of CO₂ from the atmosphere to the ocean. Additional couplings of this sort also exist as the atmosphere is further coupled with the terrestrial carbon sink (Oschlies, 2009). Of course, the system relaxation observed when considering coupled reservoirs is not unique to OAE. It also applies to direct air capture and fossil fuel emissions (Zarakas et al., 2024; Stocker et al., 2014; Jeltsch-Thömmes et al., 2024), with coupled reservoirs acting to buffer the perturbation and reduce its magnitude over time.

OAE simulations have also been conducted in models which include full atmosphere treatment and terrestrial feedbacks and account for future emission scenarios and ocean dynamics in an integrated fashion (Keller et al., 2014; González and Ilyina, 2016; Lenton et al., 2018; Köhler, 2020; Jeltsch-Thömmes et al., 2024; Schwinger et al., 2024; Yamamoto et al., 2024). In such environments, the metric $\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ tracks a fundamentally different quantity, as it measures the combined effect of intervention-driven CO₂ uptake and subsequent reservoir feedbacks (where ΔDIC(t) is computed over the whole reservoir). These studies generally simulated the addition of large quantities of alkalinity over long periods, perhaps leading to the impression that system feedback effects can be ignored for small, short, and/or local additions such as done when calculating OAE impulse response functions (Zhou et al., 2024).

Given the central importance of models in addressing the measurement, reporting, and verification (MRV) challenge in OAE, it is worth carefully examining the physical meaning of the above metrics in the two kinds of atmosphere treatments in order to avoid confusion. Given that a prescribed atmosphere is not an accurate representation of reality, what is the physical meaning of $\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ obtained under prescribed pCO₂ conditions? Is the assumption of an unresponsive atmosphere justified when only very small quantities of alkalinity are considered, as encountered during pulse injection studies (He and Tyka, 2023; Zhou et al., 2024; Suselj et al., 2024), given that it would cause only an infinitesimally small change in global atmospheric pCO₂?

This paper seeks to clarify these questions with the help of a simple numerical general circulation model and an analytical box model, with the hope to give a more precise definition of η(t) and establish equivalent metrics to use in the case of fully coupled Earth system models.

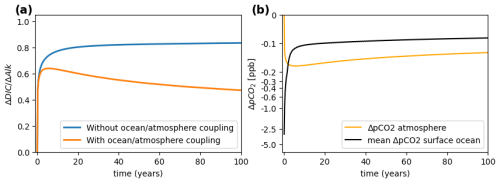
Figure 1 (a) Comparison of the increase in total ocean DIC following an ocean-wide 1-month pulse of alkalinity of a total of 0.5 Tmol applied to the surface layer under a prescribed (non-responsive) atmosphere (blue) and a coupled (responsive) atmosphere (orange). Note that the total quantity of CO₂ in the atmosphere is ≈73.5 Pmol in the case of the orange curve; i.e., the perturbation of 0.5 Tmol is tiny in comparison. (b) Concurrent pCO₂ changes in the atmosphere and surface ocean (under coupled simulation). The atmosphere ΔpCO₂ decreases below that of the surface ocean after about 2 years, after which the ocean off-gases until eventual equilibrium is reached (well beyond 100 years).

2 Methods

To compare the effect of different atmosphere treatments, a simple numerical general circulation model was run using MITgcm (Marshall et al., 1997). The purpose here is not to simulate detailed realism as would be obtained from a fully coupled Earth system model but to interrogate and compare the basic principles and behavior of OAE under coupled and prescribed atmospheres. The simulation had a resolution of 2.8°×2.8° (a 128×64 worldwide spherical polar grid) and 20 exponentially spaced depth levels, from 10 m thick at the surface to 690 m thick at the seafloor. The simulation was initialized and forced as detailed in Dutkiewicz et al. (2005). The MITgcm GEOM and DIC modules were used to simulate the soft tissue and carbonate pumps, as well as ocean–atmosphere gas exchange. In the case of a prescribed atmosphere, the pCO₂ of the atmosphere was initialized to 415 µatm and kept constant throughout. In the case of a responsive, coupled atmosphere, it was initialized in the same way, but the pCO₂ was continuously recalculated based on the integrated total flux through the air–sea interface at each step. For this calculation, the total dry mass of the atmosphere was assumed to be 5.1352×10¹⁸ kg (Trenberth and Smith, 2005) with a mean molecular mass of 28.97 g mol⁻¹. The total moles of dry gas in the atmosphere was thus 1.77×10²⁰ moles, and the total amount of atmospheric CO₂ was 7.35×10¹⁶ moles. In all simulations the atmosphere was assumed to be instantaneously mixed. This is obviously an oversimplification; however, it is a very reasonable one, as atmospheric mixing is fast relative to the timescale of OAE equilibration.

For the pulsed OAE injections, 0.5 Tmol of alkalinity was released into the surface simulation cell (10 m depth) in a 1-month pulse (starting 1 January), similar to Zhou et al. (2024), and the total volume-integrated DIC and Alk of the ocean were monitored for the rest of the simulation (100 years). A reference run without alkalinity addition was also conducted. Each run was repeated with both a prescribed and a responsive atmosphere. Note that in this simplified model setup, all simulations have precisely the same ocean circulation and climate forcing and do not explicitly model any interacting terrestrial carbon cycle.

Injections were conducted as a global uniform addition and in local patches in three different locations. The uniform alkalinity additions were also conducted with different amounts (50 Tmol, 500 Gmol, 5 Gmol), equivalent to negative emissions of the order of 170 Mt, 1.7 MtCO₂, and 170 kt of CO₂. The three different point-injection locations were off the coast of Brazil (2.50° S, 37.50° W), near Iceland (61.50° N, 19.50° W), and in Hawai'i (19.02° N, 155.49° E). The patches were 2.8°×2.8° in size.

3 Results

3.1 Numerical circulation model

Figure 1a compares the time evolution of $\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ for a 1-month pulse release of alkalinity, simulated with a prescribed (non-responsive) and a coupled (responsive) atmosphere. It can be seen that the curve of the former approaches 0.85, as expected. In contrast, the curve obtained from the same alkalinity addition under responsive conditions deviates after a few years and begins to decline again; i.e., the ocean is outgassing CO₂ relative to the reference simulation. Note that the quantity of alkalinity released in these simulations was very small, just 0.5 Tmol, and the changes occurring in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ are of the order of 10⁻¹⁰ atm (Fig. 1b).

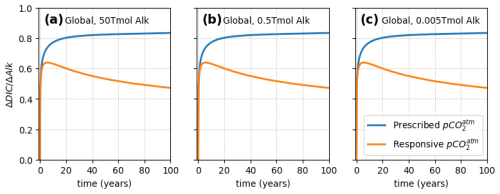
Figure 2 Increase in total ocean DIC following a worldwide 1-month pulse of alkalinity (ΔAlk) applied to the surface layer, under a prescribed (non-responsive) atmosphere (blue) and a coupled (responsive) atmosphere. Three different amounts were added, between 50 and 0.005 Tmol. It can be seen that atmosphere feedbacks occur proportionally to the OAE perturbation size and affect $\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ at all scales.

Figure 2 shows further simulation results but with different injection amounts. The effect of modeling a responsive atmosphere on $\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ is observed to be the same in all cases and independent of the quantity of alkalinity released. This result confirms that under responsive atmosphere conditions, outgassing is expected (Oschlies, 2009) irrespective of the size of the alkalinity injection. This outgassing can seem counterintuitive, since the addition of alkalinity to seawater simply increases its capacity for CO₂, as calculated from the carbonate system, and begs the question of why the CO₂ uptake would overshoot and then off gas, even when alkalinity is added uniformly, reducing $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{ocn}}$ everywhere.

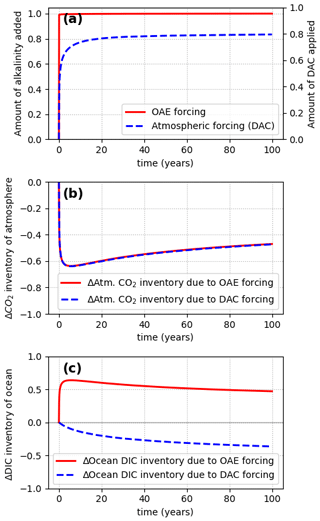
Figure 3 All simulations shown here were conducted under responsive atmosphere conditions. (a) Forcing – instantaneous addition of alkalinity to the ocean (OAE pulse) in red and gradual direct air capture (DAC) and removal from the atmosphere in dashed blue. In the case of DAC, CO₂ was removed on a schedule given by the η(t) curve corresponding to the alkalinity release done with OAE. Panel (b) shows the respective changes in the total atmospheric CO₂ inventory under responsive atmosphere conditions. It can be seen that both kinds of perturbations lead to identical atmospheric inventory changes. Therefore, interventions shown in (a) can be considered equivalent negative emissions interventions from an atmospheric pCO₂ perspective. Note that the changes in the ocean inventory are not equal, shown in panel (c). This is because in the case of OAE, the capacity of the ocean for CO₂ is increased, and CO₂ is thus absorbed from the atmosphere, whereas in the case of DAC and storage, CO₂ is removed from the system entirely, resulting in decreasing inventories in the atmosphere and the ocean.

This can be further illuminated when looking at the time evolution of ΔpCO₂ at the ocean surface and in the atmosphere (Fig. 1b). The ΔpCO₂ of the surface ocean (black line) is maximally negative right at the moment of alkalinity addition and increases thereafter due to both the uptake of CO₂ by the surface ocean and, critically, the dilution of alkalinized and partially equilibrated waters by mixing and subduction into depth. Or, put another way, deep-water parcels, which did not receive the OAE-induced pCO₂ reduction, are now reaching the surface and outgassing to the now slightly CO₂-reduced atmosphere. The change in atmospheric ΔpCO₂ begins at zero and decreases with CO₂ transfer to the ocean. At some point during the equilibration the $\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ becomes more negative than the surface ocean, at which point a phase of outgassing occurs. As is demonstrated later with the help of a box model, the overshoot and outgassing occur due to continuing mixing and dilution of surface water with deep-water parcels, which increases surface ΔpCO₂.

Such outgassing effects caused by coupled reservoirs are of course not limited to OAE. Indeed, direct removal of CO₂ from the atmosphere (DAC) induces a similar outgassing from the ocean, similarly reducing the removal effect on the atmosphere. Likewise, fossil fuel emissions of CO₂ fall under the same reservoir re-equilibration, with only an estimated 30 % of anthropogenic emissions remaining in the atmosphere (Stocker et al., 2014).

The results above demonstrate that the metric $\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ does not reflect the true amount of CO₂ transferred from the atmosphere to the ocean once the feedback and coupling between the ocean and other reservoirs, such as the atmosphere, are taken into account. Do previous OAE simulations therefore overestimate the effectiveness of OAE (Oschlies, 2009), or should the effectiveness of OAE be considered relative to an equivalent direct air capture (DAC) removal and storage method (i.e., relative to emissions of fossil fuels), which is subject to the same feedback effects? For the purposes of assigning carbon credits, it makes sense for the effectiveness of OAE to be measured relative to direct atmosphere removal (i.e., DAC with subsequent permanent storage) or relative to fossil fuel emissions (Zarakas et al., 2024). In other words, 1 t of CO₂ removal is equivalent to 1 t of negative CO₂ emissions. When it comes to the slow and incomplete equilibration of surface water following an OAE deployment, the question therefore becomes the following: what is the equivalent CO₂ removal directly from the atmosphere compared to the removal of atmospheric CO₂ due to an alkalinity addition?

3.2 Physical meaning of the quantity η(t)

Given the prevalence of prior studies conducted under constant pCO₂ (Wang et al., 2023; Tyka et al., 2022; He and Tyka, 2023; Zhou et al., 2024; Suselj et al., 2024; Köhler et al., 2013; Burt et al., 2021), it is important to establish the physical meaning of the quantity η(t) when obtained under such prescribed atmospheric conditions. Since OAE removes CO₂ gradually from the atmosphere, it is a reasonable hypothesis that the η(t) curve obtained under prescribed atmospheres gives the equivalent DAC removal. If true, one would expect that under responsive atmosphere conditions the OAE deployment and a DAC removal at a rate given by $\mathrm{d}\mathit{\eta }\left(t\right)/\mathrm{d}t$ should also yield the same reduction in atmospheric CO₂. To verify this hypothesis, a simulation was conducted (under responsive atmosphere conditions) in which CO₂ was removed directly from the atmosphere, at the rate of $\mathrm{d}\mathit{\eta }\left(t\right)/\mathrm{d}t\times \mathrm{0.5}$ Tmol. No other perturbation was made in this simulation. Note that throughout this paper the term DAC is taken to mean direct air capture with permanent storage; i.e., CO₂ is directly and permanently removed from the atmosphere. The results are shown in Fig. 3, with the solid red curves showing the OAE deployment and the dashed blue curves showing the equivalent (gradual) direct atmospheric CO₂ removal simulation. It can be seen that the total change in atmospheric CO₂ inventory is the same, caused either by an instantaneous release of alkalinity or by a gradual direct CO₂ removal from the atmosphere at a schedule given by η(t) (Fig. 3b).

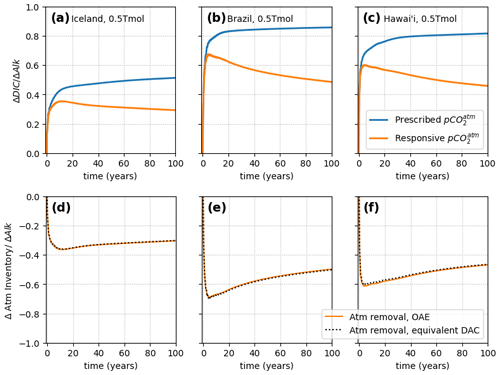
Figure 4 Increase in total ocean DIC following a 1-month pulse of alkalinity (ΔAlk) applied to the surface layer at a specific location, under a prescribed (non-reactive) atmosphere (blue) and a coupled (reactive) atmosphere. The three different point-injection locations were off the coast of Brazil (2.50° S, 37.50° W), near Iceland (61.50° N, 19.50° W), and in Hawai'i (19.02° N, 155.49° E).

3.3 Point injections

So far, only globally uniform alkalinity injections have been considered. To investigate the effect of localized OAE deployments, which are much more realistic from an implementation perspective, three simulations were carried out where alkalinity was pulse added at a single location, under both responsive and non-responsive coupling to the atmosphere, with results shown in Fig. 4. As can be seen, the effect of including a responsive atmosphere is significant and qualitatively the same as in the global OAE additions. The locality of the CO₂ uptake does not affect the relative magnitude of the atmosphere feedback, which acts over the entire ocean, owing to the rapid atmosphere mixing. Explicit modeling of atmospheric mixing, which in reality is not instantaneous, potentially alters this picture, but the true mixing is still very fast compared to the mixing and CO₂ uptake timescales of the OAE plume. Thus, the atmospheric approximation used here should capture the first-order behavior correctly. Because the ocean dynamics of the OAE plume depend strongly on the local ocean circulation and carbonate system state (Zhou et al., 2024; He and Tyka, 2023; Suselj et al., 2024), the η(t) curves are different for each location, as expected. Consequently, the amount of atmosphere feedback is also different in each case, as it is proportional to the amount of CO₂ removed from the atmosphere. Figure 4d–f show that in each case, under responsive atmosphere conditions, the CO₂ uptake caused by an instantaneous, local OAE deployment equals that of the equivalent, gradual DAC removal at a rate of $\mathrm{d}\mathit{\eta }\left(t\right)/\mathrm{d}t$. This is exactly analogous to the global OAE case and shows that the feedback behavior is independent of the locality of the OAE deployment.

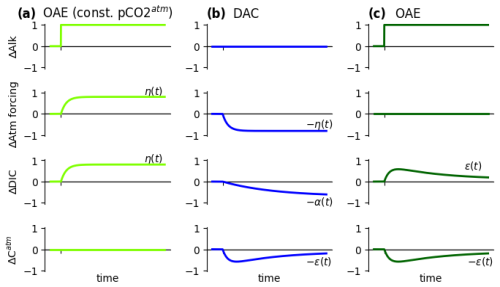
Figure 5 The relationship between OAE under prescribed $p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{atm}}$ and responsive $p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{atm}}$ can be illustrated considering the following scenarios and their superposition: (a) in the first scenario, an instantaneous OAE pulse (ΔAlk) is initiated under prescribed $p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{atm}}$ conditions. In order to keep ΔC^atm at zero, additional CO₂ is added to the atmosphere at the same rate at which it is absorbed by the ocean due to the added alkalinity. (This produces the same scenario as if the atmosphere volume was simply simulated as infinite.) The ocean absorbs CO₂, and the intrinsic OAE efficiency curve is obtained as $\mathit{\eta }\left(t\right)=\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ and is determined solely by the ocean dynamics, gas exchange, and surface carbonate chemistry. (b) The second scenario represents a gradual atmospheric removal of CO₂, i.e., DAC, on a schedule proportional to η(t) (obtained from the first scenario). Removal of CO₂ from the atmosphere induces off-gassing from the atmosphere ($\mathrm{\Delta }\mathrm{DIC}=-\mathit{\alpha }\left(t\right)$) such that the resultant atmospheric inventory drops rapidly at first due to DAC forcing but then returns somewhat over time due to off-gassing ($\mathrm{\Delta }{C}^{\mathrm{atm}}=-\mathit{\epsilon }\left(t\right)=-\mathit{\eta }\left(t\right)+\mathit{\alpha }\left(t\right)$). (c) Finally, consider the superposition of both scenarios at once, where the functions of (a) and (b) are added. The atmospheric forcing from (a) and (b) is canceled, leaving only the OAE forcing (ΔAlk). Since there is no direct atmospheric forcing, this scenario represents a normal instantaneous OAE addition under responsive atmosphere conditions. The atmospheric inventory must then follow the same trajectory as in the second scenario, namely $\mathrm{\Delta }{C}^{\mathrm{atm}}\left(t\right)=-\mathit{\epsilon }\left(t\right)$. Consequently, the ocean inventory must increase by the same amount, ΔDIC(t)=ε(t), as the total CO₂ in the system remains constant. Under a responsive atmosphere, the quantity $\mathit{\epsilon }\left(t\right)=\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ therefore does not represent the intrinsic OAE efficiency η(t) because it also contains the effect of the atmospheric feedback: $\mathit{\epsilon }\left(t\right)=\mathit{\eta }\left(t\right)-\mathit{\alpha }\left(t\right)$.

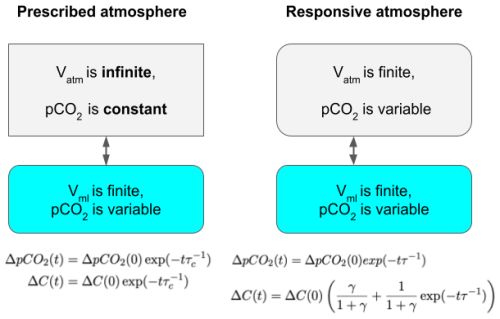
Figure 6 Two simple box models, one with a static, prescribed atmosphere and one with a responsive finite-volume atmosphere. The resulting decay laws for the partial pressure difference, ΔpCO₂, and the CO₂ inventory difference, ΔC(0), are given at the bottom. Note that ΔpCO₂ decays to zero in both cases, but the total inventory of CO₂ returns to its original value only in the case of a prescribed atmosphere.

3.4 Analytical box model

The equivalence of the η(t) curve and the gradual removal of CO₂ from the atmosphere can also be shown to be analytically exact in a simple box model, as shown in Fig. 6. A full derivation of the following results is given in the Supplement, with the following section summarizing the key results and conclusions. The model describes two coupled reservoirs, atmosphere (atm) and ocean (ocn). Each has a partial pressure of CO₂ ($p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ and $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{ocn}}$), a total (integrated) amount of CO₂ (denoted by C^atm and C^ocn), and a given volume (V_atm and V_ml).

The atmospheric partial pressure $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is directly proportional to the total amount of CO₂ in the atmosphere C^atm (in mol):

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{d}p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}}{\mathrm{d}{C}^{\mathrm{atm}}}}={\displaystyle \frac{V_{\mathrm{m}}p}{V_{\mathrm{atm}}}},\end{array}$$

where V_m is the molar volume of gas (0.024 m³ mol⁻¹), and p is the atmospheric pressure. In the ocean reservoir, which is in active contact with the atmosphere, specifically the mixed layer, the differential relationship between pCO₂ and C, for small changes, is

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{d}p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{ocn}}}{\mathrm{d}{C}^{\mathrm{ocn}}}}={\displaystyle \frac{\mathrm{1}}{\mathit{\alpha }{V}_{\mathrm{ml}}}}{\displaystyle \frac{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}{\partial \left[\mathrm{DIC}\right]}},\end{array}$$

where [DIC] is the concentration of total dissolved carbon, α is the solubility of CO₂ in seawater (≈34 mol m³ atm⁻¹), and the term $\frac{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}{\partial \left[\mathrm{DIC}\right]}$ accounts for the vastly increased capacity of ocean water for CO₂ due to the carbonate system, with a typical value of $\approx \mathrm{1}/\mathrm{20}$ (Zeebe and Wolf-Gladrow, 2001).

These two reservoirs can exchange CO₂, and the flux of CO₂ across the air–water interface, $F_{{\mathrm{CO}}_{\mathrm{2}}}$, is typically modeled as proportional to the partial pressure difference,

$$\begin{array}{}\text{(5)}& F_{{\mathrm{CO}}_{\mathrm{2}}}=k_w\mathit{\alpha }(p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}-p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{ocn}})=k_w\mathit{\alpha }\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}},\end{array}$$

where k_w is the gas transfer velocity (m s⁻¹). Given this simple box model setup, one can show that the total transfer rate of CO₂, following an initial ocean DIC deficit of ΔC(0), is given by

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{d}C}{\mathrm{d}t}}=\mathrm{\Delta }C\left(\mathrm{0}\right)\left({\displaystyle \frac{k_{w}A}{V_{\mathrm{ml}}}}{\displaystyle \frac{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}{\partial \left[\mathrm{DIC}\right]}}\right)\exp (-t{\mathit{\tau }}^{-\mathrm{1}}),\end{array}$$

where the characteristic timescale of equilibration (e-folding time) is given by τ:

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathit{\tau }={\left[k_{w}A\mathit{\alpha }\left({\displaystyle \frac{V_{\mathrm{m}}p}{V_{\mathrm{atm}}}}+{\displaystyle \frac{\mathrm{1}}{\mathit{\alpha }{V}_{\mathrm{ml}}}}{\displaystyle \frac{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}{\partial \left[\mathrm{DIC}\right]}}\right)\right]}^{-\mathrm{1}},\end{array}$$

and A is the area over which gas exchange occurs. Integrating this rate with respect to time gives the time evolution ΔC(t) of a starting DIC deficit ΔC(0) in the ocean reservoir of such a box model (details of the derivation are found in the Supplement).

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }C\left(t\right)=\mathrm{\Delta }C\left(\mathrm{0}\right)\left({\displaystyle \frac{\mathit{\gamma }}{\mathrm{1}+\mathit{\gamma }}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\mathit{\gamma }}}\exp (-t{\mathit{\tau }}^{-\mathrm{1}})\right)\end{array}$$

Here, γ expresses the ratio of the capacities of the two interacting reservoirs.

$$\begin{array}{}\text{(9)}& \mathit{\gamma }={\displaystyle \frac{V_{\mathrm{m}}p\mathit{\alpha }{V}_{\mathrm{ml}}}{V_{\mathrm{atm}}}}{\displaystyle \frac{\partial \left[\mathrm{DIC}\right]}{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}}\end{array}$$

Note that under finite, responsive atmosphere conditions, some fraction of the initial pulse will always remain in the reservoir it was induced in, even once the pCO₂ values have reached equilibrium, because as the pCO₂ of the reservoir increases, that of the atmosphere decreases, until they are equal. Equation (8) shows that the fraction that will move to the other reservoir is $\frac{\mathrm{1}}{\mathrm{1}+\mathit{\gamma }}$, while the fraction that will remain in the ocean is $\frac{\mathit{\gamma }}{\mathrm{1}+\mathit{\gamma }}$.

3.4.1 Simulations with prescribed pCO₂

The frequently taken assumption that atmospheric pCO₂ is prescribed corresponds to the assumption that V_atm=∞; i.e., it assumes an atmosphere which can accommodate arbitrary movement of CO₂ in or out of it, without a change in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. In this case, the ODE for the pCO₂ difference simplifies to the often-used gas-exchange expression (Zeebe and Wolf-Gladrow, 2001)

$$\begin{array}{}\text{(10)}& {\displaystyle }\mathrm{\Delta }C\left(t\right)=\mathrm{\Delta }C\left(\mathrm{0}\right)\exp (-t{\mathit{\tau }}_{\mathrm{c}}^{-\mathrm{1}}),\end{array}$$

where the depth of the mixed layer $z_{\mathrm{ml}}=V_{\mathrm{ml}}/A$, and the e-folding time, denoted here as τ_c for constant atmosphere, is

$$\begin{array}{}\text{(11)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{c}}={\left[{\displaystyle \frac{k_{w}A}{V_{\mathrm{ml}}}}{\displaystyle \frac{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}{\partial \left[\mathrm{DIC}\right]}}\right]}^{-\mathrm{1}}.\end{array}$$

This law results in a simple equilibration in which the initial deficit ΔC(0) is completely replenished by the atmosphere and goes to zero, consistent with the fact that the atmosphere is modeled as having an infinite capacity.

This simpler equilibration law has been the basis of the η(t) curve obtained in OAE efficiency simulations (Tyka et al., 2022; He and Tyka, 2023; Zhou et al., 2024; Suselj et al., 2024).

$$\begin{array}{}\text{(12)}& {\displaystyle }\mathit{\eta }\left(t\right)=\mathrm{1}-{\displaystyle \frac{\mathrm{\Delta }C\left(t\right)}{\mathrm{\Delta }C\left(\mathrm{0}\right)}}=\mathrm{1}-\exp (-t{\mathit{\tau }}_{\mathrm{c}}^{-\mathrm{1}})\end{array}$$

How significant is the difference between Eqs. (8) and (10)? Considering some reasonable values ($V_{\mathrm{atm}}=\mathrm{3.96}\times {\mathrm{10}}^{\mathrm{18}}$ m³, α=34 mol m⁻³ atm⁻¹, $\frac{\partial \left[\mathrm{DIC}\right]}{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}=\mathrm{20}$ (from Zeebe and Wolf-Gladrow, 2001), and a mixed-layer depth of 100 m), one obtains γ≈0.15, meaning the fraction of an induced ocean CO₂ deficit which will remain in the ocean is $\frac{\mathit{\gamma }}{\mathrm{1}+\mathit{\gamma }}\approx \mathrm{13}\mathit{\%}$. For example, in the case of an alkalinity addition, assume 1 mol of alkalinity addition creates a DIC deficit (Renforth and Henderson, 2017) of 0.83 mol. At full equilibration this deficit will cause $\mathrm{0.83}\times \mathrm{87}\mathit{\%}=\mathrm{0.72}$ mol of CO₂ to be absorbed by the ocean. At that point the pCO₂ of the atmosphere will have changed sufficiently to be in a new equilibrium with the surface ocean. Note that this quantity decreases when the depth (i.e., the volume) of the equilibrating ocean reservoir increases. For example, assuming a depth of 400 m, the ocean would absorb only 0.52 mol CO₂.

Figure 7a compares the evolution of η(t) over time for a 100 m deep ocean reservoir for a prescribed (infinite) and a responsive (finite) atmosphere. Figure 7b shows the same but for a deeper, 400 m reservoir. It is notable that (under a responsive atmosphere) the bigger the ocean reservoir is, the less CO₂ needs to transfer to the ocean in order to match the pCO₂ across the boundary. For example, for the 400 m deep ocean reservoir, for every 1 mol of DIC deficit induced, the ocean would take up only 0.63 mol of CO₂ before the pCO₂ values are in equilibrium.

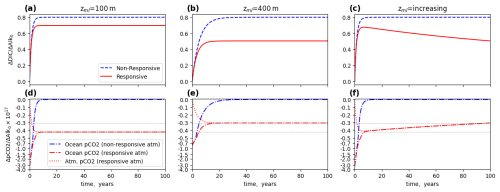
Figure 7 Box model comparison of η(t) over 100 years, under different mixed-layer assumptions. For simplicity, $\partial \left[\mathrm{DIC}\right]/\partial \left[\mathrm{Alk}\right]$ is assumed to be 0.8. The ocean carbon uptake is calculated with Eq. (10) (non-responsive atmosphere) or Eq. (8) (responsive atmosphere). (a) Mixed-layer depth z_ml=100 m, (b) mixed-layer depth z_ml=400 m, (c) linear interpolation of z_ml= from 100 to 400 m over 100 years. (d–f) Corresponding changes in pCO₂ in the ocean and atmosphere respectively. It should be noted that the simple interpolation in (f) does not account for the lag in ocean re-equilibration following the deepening of the mixed layer observed in Fig. 1b.

Now, consider what happens when the ocean reservoir slowly increases in depth. A DIC deficit induced at the surface will initially equilibrate just from the relatively thin mixed layer, which experiences rapid mixing. Over time, however, slower mixing processes exchange water parcels between the mixed layer and deeper layers. If one considers this, crudely, as a gradual deepening of the reservoir which is exchanging with the atmosphere on longer timescales, one can express the effective exchanging ocean volume V_ml as a function which increases over time. Figure 7c shows how η(t) evolves over time when V_ml increases linearly from 100 to 400 m in a span of 100 years. Initially the equilibration occurs from a shallow reservoir, and η(t) rises quickly and reaches relatively high values as in Fig. 7a. Over time, however, as the equilibration slowly proceeds to deeper layers, the equilibrium situation begins to resemble Fig. 7b. Because the carbon uptake initially overshoots relative to the eventual equilibrium point, a process of net out-gassing occurs. This sort of out-gassing has previously been described by other authors (Oschlies, 2009). Despite our crude assumptions here about the linear subduction of the excess alkalinity, the behavior of the curve qualitatively matches that observed in the numerical simulation (Figs. 1 and 2).

3.4.2 Equivalent removal from the atmosphere

We have shown earlier that the function $\mathit{\eta }\left(t\right)=\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$, determined under constant-$p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ conditions, does not properly describe the actual movement of CO₂ from the atmosphere into the ocean under realistic conditions (where feedback of the atmosphere is taken into account). This raises the following question: what physical quantity does η(t) represent, if anything? To illuminate this question, consider the following scenario. How would the total inventory of CO₂ in the atmosphere evolve, under realistic responsive atmosphere conditions, if CO₂ was directly removed from the atmosphere at a rate proportional to $\mathrm{d}\mathit{\eta }\left(t\right)/\mathrm{d}t$, using a terrestrial technology like DAC, instead of indirectly, by applying an alkalinity pulse to the ocean? Specifically, the rate of carbon removal out of the atmosphere would be

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\mathrm{d}\mathrm{\Delta }{C}^{\mathrm{atm}}}{\mathrm{d}t}}=\mathrm{\Delta }C\left(\mathrm{0}\right){\displaystyle \frac{\mathrm{d}\mathit{\eta }\left(t\right)}{\mathrm{d}t}}=\mathrm{\Delta }C\left(\mathrm{0}\right){\mathit{\tau }}_{\mathrm{c}}^{-\mathrm{1}}\exp (-t{\mathit{\tau }}_{\mathrm{c}}^{-\mathrm{1}}),\end{array}$$

where ΔC(0) is a scaling factor that sets the total, eventual amount of CO₂ removed.

This steady removal of CO₂ from the atmosphere lowers the pCO₂ of the atmosphere. Since the atmosphere now develops a ΔpCO₂ deficit, relative to the ocean, the ocean reacts and degasses into the atmosphere (remember all Δ values are differences between a reference and a perturbed simulation). What is the combined effect on the total atmospheric CO₂ inventory, i.e., the sum of direct removal and ocean reactance? The total rate of change is the sum of the direct CO₂ removal rate (Eq. 13) and the rate due to gas exchange between the ocean and atmosphere (due to the imbalance of ΔpCO₂):

$$\begin{array}{}\text{(14)}& {\displaystyle \frac{\mathrm{d}\mathrm{\Delta }{C}^{\mathrm{atm}}}{\mathrm{d}t}}=\mathrm{\Delta }C\left(\mathrm{0}\right){\mathit{\tau }}_{\mathrm{c}}^{-\mathrm{1}}\exp (-t{\mathit{\tau }}_{\mathrm{c}}^{-\mathrm{1}})-k_{w}A\mathit{\alpha }\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}\left(t\right).\end{array}$$

Through substitution of $\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}\left(t\right)$ the above equation can be shown to equal the following expression (for a full derivation, see the Supplement).

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\mathrm{d}\mathrm{\Delta }{C}^{\mathrm{atm}}}{\mathrm{d}t}}=\mathrm{\Delta }C\left(\mathrm{0}\right)\left[{\displaystyle \frac{k_{w}A}{V_{\mathrm{ml}}}}{\displaystyle \frac{\partial \left[{\mathrm{CO}}_{\mathrm{2}}\right]}{\partial \left[\mathrm{DIC}\right]}}\right]\exp (-t{\mathit{\tau }}^{-\mathrm{1}})\end{array}$$

This equation for the net rate of change in the atmospheric carbon inventory equals precisely that obtained earlier when considering a pulsed DIC deficit in the ocean (Eq. 6). This result reveals the exact meaning of the η(t) OAE efficiency curve: the OAE curve of an instantaneously induced ocean-based DIC deficit (obtained under artificial, non-responsive conditions) gives the progression of the equivalent gradual removal of CO₂ directly from the atmosphere (under real, responsive conditions); both result in the same reduction in net atmospheric carbon inventory.

3.5 Measuring η(t) in coupled models

Practical OAE deployments will rely on modeling to estimate the amount of carbon removal credits they generate over time, especially in the far field, where the induced changes in pCO₂ are diluted far below experimental detection thresholds (Ho et al., 2023) but where the majority of the excess CO₂ uptake will take place (Zhou et al., 2024; He and Tyka, 2023). While one way to calculate the amount of credits is to keep $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ prescribed, future modeling efforts will likely want to employ more accurate fully coupled Earth system models, with forward-looking ocean state prediction, which will require the inclusion of atmosphere coupling and consideration of different emission scenarios, which have the potential to change ocean circulation and therefore affect η(t). How can the quantity η(t) be calculated in such a model?

Fundamentally, η(t) expresses the efficiency of OAE relative to direct air removal and storage. Therefore, the reference state should not be an unperturbed model run but one that reflects an equivalent DAC removal. The simplest approach would be to run a simulation in which an amount of atmospheric CO₂ is removed at the start of the reference simulation, equimolar to the amount of alkalinity added during OAE (Yamamoto et al., 2024). The difference in atmospheric CO₂ inventory, $\mathit{\eta }\approx \mathrm{1}-\frac{\sum {\mathrm{CO}}_{\mathrm{2}}^{\mathrm{OAE}}-\sum {\mathrm{CO}}_{\mathrm{2}}^{\mathrm{DAC}}}{\mathrm{\Delta }\mathrm{Alk}}$, would then capture the efficiency of an OAE deployment relative to a straightforward direct removal of CO₂ from the atmosphere. However, this comparison is not quite exact because the true equivalent DAC removal is a gradual one, not a sudden DAC pulse, as shown earlier. Therefore, the atmospheric feedback would differ between the simulation and the reference. Thus, this does not yield exactly the same quantity as η(t) but only an approximation (Yamamoto et al., 2024). The approximation will be reasonable for OAE locations where uptake is fast and worse for locations where it is slow or incomplete. Instead, a simple and elegant way to create a suitable reference state was suggested by Schwinger et al. (2024). First, the OAE-perturbed simulation is carried out with a fully coupled model. Then, one conducts an additional reference simulation (Ref^*) in which the atmosphere pCO₂ is prescribed at the exact trajectory obtained in the earlier fully coupled simulation with the OAE intervention. However, in the new reference simulation no OAE is performed – only the atmospheric pCO₂ is prescribed. The difference in the ocean inventories between these two simulations is then equivalent to the η(t) obtained in a prescribed simulation:

$$\begin{array}{}\text{(16)}& \mathit{\eta }\left(t\right)={\displaystyle \frac{\sum {\mathrm{DIC}}^{\mathrm{OAE}}-\sum {\mathrm{DIC}}^{{\mathrm{Ref}}^{*}}}{\mathrm{\Delta }\mathrm{Alk}}}.\end{array}$$

In the case of the two-box model used earlier, it can be shown that this equivalence is mathematically exact (see Supplement for proof). The disadvantage is that for every OAE simulation, a separate reference simulation must be run, since the CO₂ feedback depends on the trajectory of the OAE perturbation.

3.6 Limitations

3.6.1 Coupling to other reservoirs

So far, only the ocean and atmospheric reservoirs and their interaction have been considered. The third major reservoir for CO₂ is the terrestrial biosphere, which absorbs up to 30 % of anthropogenic emissions (Crisp et al., 2022) and has a finite capacity, responds to changes in $p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{atm}}$, and has considerable inter-annual variability (Carroll et al., 2020; Crisp et al., 2022). The terrestrial reservoir does not directly interact with the ocean; rather, it interacts via the atmosphere. Therefore, from the ocean's point of view it acts as an extension of the atmosphere reservoir's capacity and is therefore implicitly included in the theoretical considerations presented earlier. The approach described above (Schwinger et al., 2024), of creating a reference state by prescribing the pCO₂ changes observed during a perturbed simulation, will also work in the case where a terrestrial sink is included in the Earth system model, as the prescribed pCO₂ in the reference run includes any indirect ocean–land coupling via the atmosphere.

However, including the terrestrial reservoir does alter the effective capacity of the atmosphere sink (from the ocean's perspective) and will reduce the atmosphere–ocean feedback effect in magnitude and time evolution. That is because the removal of a quantity of atmospheric CO₂ will cause a reduction in the terrestrial uptake rate and therefore buffer the atmospheric change. This additional buffering then somewhat reduces the induced ocean outgassing. Simulations intending to accurately model the changes in ocean DIC due to OAE should therefore include a terrestrial model. However, simulations intending to merely assess the efficiency (η(t)) of OAE deployments can reasonably assume a prescribed $p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{atm}}$ trajectory, since the inclusion of an additional atmosphere-coupled reservoir will not affect η(t).

However, other reservoirs which couple directly to ocean pCO₂ would not be accurately covered by this approach. For example, if the model includes biological productivity which removes DIC and if this productivity is dependent on ocean DIC concentration, then this essentially constitutes a coupled reservoir with its own feedback effects (which may be linear or non-linear). In that case, the altered productivity rates would also need to be prescribed in the reference state because the change in ocean DIC differs between OAE and direct air removal methods. Similarly, ocean carbonate precipitation and dissolution depend on ocean pCO₂ and are influenced by all OAE methods and should be factored out when calculating relative efficiencies. Of course, in the case that the total capacity of such additional reservoirs is small, they may not make a significant difference to the OAE efficiency, but this would need to be confirmed in future studies.

3.6.2 Model resolution

The work presented here aims to investigate the important first-order effects of coupling to a responsive atmosphere reservoir on the commonly used metrics of OAE efficiency; however several simplifying assumptions were made.

The analytical model is of course highly simplified, modeling the ocean and atmosphere as simple zero-dimensional coupled reservoirs, and is intended to merely demonstrate the fundamental effects of reservoir coupling on the efficiency metrics and its dependence on mixed-layer depth and dilution in general. Broadly, however, it captures the essence of the behavior, as confirmed by the numerical model. The latter, while more realistic than the box model, is still quite coarse and unable to resolve any fine circulation features or eddy currents. As is typical for non-eddy-resolving models, medium- to fine-scale transport features are accounted for in the form of implicit diffusion terms, which do not capture the dilution of point-source alkalinity additions accurately and are unable to resolve eddy-scale behaviors. Filamentation (Munk et al., 2000; McWilliams et al., 2015), for example, could create areas of high alkalinity interspersed with areas of low excess alkalinity and affect vertical mixing in complex ways, until proper mixing and dilution are achieved. Such fine details can only be resolved in high-resolution models and exceed the scope of the present work. The timescale of CO₂ equilibration is typically of the order of 1–10 years (or even longer in some locations), with the majority of CO₂ uptake occurring when the alkalinity is already widely dispersed (Zhou et al., 2024). Detailed modeling of the subduction and transport of the alkalinity plume affects the η(t) curves considerably (as can also be seen by the differences in the three locations shown here). However, the relationship between prescribed vs. responsive atmospheres is the same, meaning that the metric η(t) under prescribed conditions equals the equivalent gradual, atmospheric CO₂ removal under responsive conditions, no matter how complex the ocean dynamics are.

3.6.3 Atmospheric mixing

The modeling done here assumes that the atmosphere acts as an instantly mixed reservoir. In reality, mixing of atmospheric air parcels occurs on a timescale of weeks to months (Lal and Rama, 1966). For individual OAE deployments, where the area of counterfactual gas exchange is small and localized, this could in principle slightly change the uptake curve η(t). Stagnant, locally CO₂-depleted air parcels in contact with DIC-deficient surface water parcels would slow down the equilibration process and exacerbate the effect of atmospheric feedback temporarily by reducing the local pCO₂ gradient. However, compared to the timescale of OAE equilibration, which occurs over many years, this is unlikely to significantly change the overall equilibration time. Inter-hemisphere mixing is slower than longitudinal mixing and has a mixing time of ∼ 1.3 years (Geller et al., 1997). This could potentially increase the amount of atmospheric feedback in the medium term, since the effective volume of the exchanging atmosphere is halved. In the long run, however, the system would be expected to return to the same equilibration state obtained when assuming a well-mixed atmosphere, since any deviations due to localized effects would equilibrate out over time.

3.7 Non-linear effects

The considerations presented here all assume linearity of the response of reservoirs to marginal additions of CO₂ as a first-order approximation. Non-linear effects or extreme tipping points are beyond the scope of the analysis presented here.

4 Conclusions

Emissions of CO₂ into the atmosphere and removals of CO₂ from the atmosphere (via DAC) both induce a rebalancing of CO₂ from or to the atmosphere into other coupled reservoirs. However, as these feedback effects are approximately symmetrical, the impact on atmospheric pCO₂ is the same for emissions and removals, except for the sign. Therefore, when accounting for negative emissions, such CO₂ removals are always counted relative to tailpipe emission of CO₂; in other words, the removal of 1 kg of CO₂ using direct air removal (DAC) offsets the emission of 1 kg of CO₂ elsewhere. When applying metrics to evaluate negative emission technologies (NETs) which do not remove CO₂ directly from the atmosphere but indirectly and with a time delay, the desired metric should thus represent the equivalent DAC removal over time due to some initial NET perturbation.

To obtain this metric, which should exclude the effects of reservoir feedbacks common to DAC and OAE, one needs to be careful in using the correct counterfactual reference depending on whether reservoir feedbacks are accounted for in the simulation or not.

We have shown that in simulations which use a prescribed atmospheric pCO₂, the quantity $\mathit{\eta }\left(t\right)=\mathrm{\Delta }\mathrm{DIC}\left(t\right)/\mathrm{\Delta }\mathrm{Alk}$ yields the desired metric; i.e., η(t) is the equivalent, gradual removal of CO₂ from the atmosphere if it were conducted using the direct air capture method, under responsive atmosphere conditions and other couplings. In other words, η captures the efficiency of OAE relative to direct atmosphere removal and ignores reservoir feedbacks common to all negative emission technologies. It should be noted that there exists no instantaneous DAC removal pulse that would cause the same evolution of atmospheric pCO₂ as an instantaneous release of alkalinity to the ocean.

For OAE, η(t) is expected to equilibrate over a period of a few years to decades following an alkalinity addition and ultimately asymptote around 0.85 mol C (mol Alk)⁻¹, unless significant quantities of alkalinity were subducted into the deep ocean before air–sea gas exchange was completed (Zhou et al., 2024).

It is important to realize that η(t) does not quantify the excess amount of CO₂ taken up by the ocean due to an OAE deployment, since that includes reservoir feedbacks. Consequently, to avoid confusion, it is most precise to say that 1 mol of alkalinity can offset up to 0.85 mol of emissions, rather than stating that it can cause the uptake of up to 0.85 mol of CO₂.

Conversely, we propose following the nomenclature of Jeltsch-Thömmes et al. (2024) to denote the efficiency of OAE with respect to its ability to reduce atmospheric carbon inventories under fully coupled Earth system models, which includes all the reservoir feedbacks, as ε(t). This quantity is relevant for the calculation of the reduction in future radiative forcing and global temperatures due to OAE deployments. Prior work has shown that ε can reach values almost as high as η(t) in the short term but is expected to eventually decrease to around 0.35 mol C (mol Alk)⁻¹ on longer timescales (Jeltsch-Thömmes et al., 2024).

However, ε is less useful for assigning or comparing carbon credits because its value is dependent on future emission scenarios, changes to land sink capacities, etc., which are independent of the OAE intervention and common among all CDR efforts.

Ocean variables (such as ΔpH or ΔΩ) are affected by OAE deployments (e.g., pH is increased), and the subsequent influx of CO₂ tends to neutralize some of these changes (e.g., pH returns to near the starting value). When studying these changes close to the OAE deployment and while the plume has not yet dispersed and diluted, the use of prescribed atmospheres yields reasonable approximations, since the buffering effect of coupled reservoirs is comparatively slow and non-local.

On the other hand, if one wishes to calculate the long-term counterfactual effects of an OAE deployment on these ocean variables, the use of a fully coupled model is necessary because the feedback effects influence the behavior of such variables. For example, the OAE effect on pH is greater in a fully coupled model because less CO₂ enters the ocean to neutralize the excess alkalinity than would be calculated under a prescribed CO₂ atmosphere.

An alternative way to compare negative emissions technologies (NETs) and to measure credits would be to focus on the expected global warming potential (GWP) of a given intervention. GWP is commonly used to compare the radiative forcing effect of different greenhouse gases (GWP, 2023), integrated over some period of time, typically 50 years (GWP-50) or 100 years (GWP-100). Similarly, an NET intervention could be quantified by its negative GWP over some period of time, where DAC with storage would have a GWP of −1.0, analogous to the way CO₂ emissions are assigned a GWP of 1.0. NETs with delayed CO₂ effects would then have a GWP of a slightly lower magnitude, which accounts for the missed radiative cooling during the delay period. The advantage of such an accounting system is that NET interventions that remove CO₂ immediately at the time of the intervention (e.g., DAC) and those that remove it gradually (e.g., OAE, enhanced weathering, reforestation), as well as other interventions such as those which instead affect albedo, could all be compared more directly on the same scale.