Characterisation of uncertainties in an ocean radiative transfer model for the Black Sea through ensemble simulations

In this paper, we investigate the influence of uncertainties in inherent optical properties on the modelling of radiometric quantities by an ocean radiative transfer (RT) model, particularly irradiance and reflectance. The radiative transfer model is coupled to a 3D physical–biogeochemical model of the Black Sea. It describes the vertical propagation of incident irradiance within the water column along three streams in downward (direct and diffuse) and upward directions, with a spectral resolution of 25 nm in the visible range. The propagation of irradiance streams is governed by the inherent optical properties of four major optically active constituents found in seawater and provided by the biogeochemical model: pure water, phytoplankton, non-algal particles, and coloured dissolved organic matter (CDOM). Sea surface reflectance is then derived as the ratio between the simulated upward and downward irradiance streams, directly connecting the model with remote-sensed data. In this configuration, the coupling is one-way: the radiative transfer model is projecting model variables into the space of satellite observations, working as an observation operator. In the stochastic version of the model, uncertainties are injected in the form of random perturbations of the inherent optical properties of the water constituents. Different ensemble configurations are derived, and their quality is assessed by comparison with in situ and remote-sensed observations.

We find that the modelling of the uncertainties in the radiative transfer model parameterisation allows us to simulate distributions of radiative fields that are partially consistent with observations. The ensemble is consistent with remote-sensed reflectance data in summer and autumn, especially in the central parts of the basin. The quality of the ensemble is lower in winter and early spring, suggesting the existence of another major source of uncertainty or that the quality of the deterministic solution is insufficient. CDOM dominates absorption in short wavebands with a relatively high uncertainty that influences irradiance and reflectance outputs. This dominant role calls for better representation of CDOM to improve model calibration. Contributions from phytoplankton and non-algal particles are more significant for (back)scattering. The results of this paper suggest that the integration of a radiative transfer model into a physical–biogeochemical model would be beneficial for calibration, validation, and data assimilation purposes, offering a better link between model variables and radiometric observations.

1 Introduction

The spectral distribution of light in the ocean is closely linked to biological activity, biogeochemical cycles, and upper-ocean physics (Mobley et al., 2015). The biological productivity of the ocean is directly controlled by the amount of light available to phytoplankton for photosynthesis (Kettle and Merchant, 2008; Gregg and Rousseaux, 2016). The spectral range for photosynthetically active radiation (PAR) corresponds mainly to the visible range and represents about 45 % of the total incident radiation at sea surface. Upon reaching the ocean surface, a small part of the incoming radiation is directly reflected depending on the surface albedo. The rest of the solar irradiance is transmitted to the ocean, and its vertical spectral distribution is determined by the optical properties of seawater components such as water molecules, dissolved and particulate materials of various sizes, and living material (Mobley et al., 2015). The characterisation of those properties is therefore essential. Marine optics also influences temperature, as most of the absorbed irradiance is converted into energy to heat up the water column (Baird et al., 2020). Those processes participate in modifying the upper-ocean stratification and turbulence, thus influencing the distribution of optically active components close to the ocean surface. As such, a bio-optical feedback exists between phytoplankton, upper-ocean physics, and surface circulation (Fujii et al., 2007; Cahill et al., 2008, 2023; Skákala et al., 2022).

Optically active constituents are defined by their ability to absorb and scatter radiation, called inherent optical properties (IOPs). IOPs depend on the medium and are independent of the ambient light field. They can be described by the absorption and (back)scattering spectra of each water constituent. The determination and parameterisation of IOPs are a major challenge in modelling coupled physical and bio-optical processes (Manizza et al., 2005; Werdell et al., 2018). Most of the vertically resolved biogeochemical models solve only the direct downward component of light in a one-stream model, with a single equation describing the decrease in irradiance with depth following Beer's law (e.g. Lengaigne et al., 2007), in a limited number of spectral bands, usually two or three. They differentiate the red part from the rest of the visible range, which is further separated in some cases between the blue and green wavebands (Aumont et al., 2015; Butenschön et al., 2016). The absorption and (back)scattering processes are then not distinguished and are merged within a more general attenuation coefficient to represent the attenuation of light over the water column. Over the years, models were developed with different approaches to refine the representation of light (Ackleson et al., 1994; Bissett et al., 1999; Gregg and Casey, 2009; Mobley, 2011).

Remote-sensed optical observations rely on passive radiometers to measure top-of-atmosphere radiance in the visible and near-infrared bands. Then, the use of atmospheric corrections allows us to estimate water-leaving irradiance to compute remote-sensed reflectance (R_RS) in several wavebands. In units of sr⁻¹, R_RS is a measure of the water-leaving irradiance normalised by the above water downwelling irradiance. To compare these data with biogeochemical variables, inversion ocean colour algorithms compute intermediate products such as surface chlorophyll from reflectances in selected wavebands. These algorithms remain rather uncertain, and a more straightforward use of reflectance would mitigate the influence of imperfect inversion algorithms. However, a one-stream optical model does not simulate the upward irradiance and thus cannot provide estimates of sea surface reflectance. So far, limited use of optical properties has been made in data assimilation (Ciavatta et al., 2014; Jones et al., 2016), which could change with recent hyperspectral sensors such as those of the PRISMA and PACE missions. In recent years, new optical models have emerged to fill this gap and resolve sea surface reflectance (Dutkiewicz et al., 2015). Some of these models resolve three streams of irradiance by considering scattered irradiance in both downward and upward directions, with higher spectral resolution matching the measured wavebands. As a three-stream optical model adds complexity to coupled modelling frameworks, it also becomes necessary to assess the relative uncertainties in the information produced by the model and by satellite sensors.

In this paper, we couple a 3D ocean physical–biogeochemical model implemented in the Black Sea with a radiative transfer (RT) model as previously used in a global setup as in Dutkiewicz et al. (2015). The RT model describes the in-water irradiance along the vertical and in three streams: direct downward, diffuse downward, and diffuse upward. Its spectral range includes the wavebands corresponding to those typically used in remote sensing (e.g. 412, 490, or 555 nm). The penetration of spectral irradiance is determined in 33 wavelengths by the absorption and scattering properties of the medium that are derived from concentrations of optically active components. According to the literature, four main optically active elements are considered: water molecules, phytoplankton, non-algal particles, and coloured dissolved organic matter (CDOM). Based on the simulated irradiance streams, the RT model is used to estimate sea surface reflectance. Then, we combine the model-derived reflectances in selected wavebands to obtain an estimation of surface chlorophyll, as it is done in satellite inversion algorithms. With this approach using reflectance-derived chlorophyll, the difference between model- and satellite-estimated chlorophyll is reduced thanks to the common use of empirical inversion algorithms. Dutkiewicz et al. (2018) presented a proof of concept for the use of a new estimate of chlorophyll (they introduced a proxy for chlorophyll called “derived chlorophyll a”), enquiring on the opportunities provided by the use of RT within a coupled biogeochemical framework. They found that this proxy compared better to measurements than the “actual” chlorophyll from their biogeochemical model, with better performances using region-specific methods rather than a global method. In this paper, we use a similar proxy in the Black Sea to evaluate its potential use in this region. We also aim at building up from their work by analysing more thoroughly the inner operation of the RT model with regard to the propagation of uncertainties in such a framework. Here, we focus on the deep sea, where BGC-Argo data are available to estimate the contribution of CDOM. Due to a lack of information on CDOM in the shelf region, the results presented in this paper are mainly valid for the deeper parts of the Black Sea (Grégoire et al., 2023).

By perturbing the optical properties of the four selected water constituents, we also aim to use this implementation to assess the intrinsic uncertainty of the RT model. An ensemble simulation strategy is set up to inject perturbations in the IOPs and evaluate their influence on the outputs of the RT model: irradiance and sea surface reflectance. This analysis comes in three steps:

1. Assessment of the effect of uncertainties in the parameterisation of absorption and (back)scattering for each constituent separately.

2. Estimation of the combined effect of uncertainties for all uncertain constituents on irradiance and reflectance fields.

3. Evaluation of our ability to provide distributions of sea surface reflectance that are consistent with observations by modelling these uncertainties.

To focus the analysis on the RT model, we use it as an observation operator. The RT model takes information from the biogeochemical model without feeding back to the hydrodynamics and biogeochemistry models and therefore does not influence temperature and primary production.

The following section presents the deterministic coupled modelling framework and the parameterisation of the optically active components available in the RT model. Section 3 describes the stochastic modelling approach and the introduction of uncertainties within the RT equation. In Sect. 4, we describe the ensemble simulations and results, investigating the impact of uncertainties and the ability of the model to produce relevant surface reflectance distributions. Finally, in Sect. 5, we discuss the assumptions and limitations of the study and provide an outlook for future work.

2 Deterministic modelling framework

In this section, we describe the modelling framework and the observations used for system validation. A schematic description of the modelling framework, the diagnostics provided by the RT model, and the relevant observations (detailed in Sect. 4) are presented in Fig. 1. The deterministic model couples a physical–biogeochemical model for the Black Sea with a three-stream RT model. Gathering information from the biogeochemical and hydrodynamics models (Sect. 2.1), the three-stream RT model (Sect. 2.2) computes fields of irradiance and sea surface reflectance. These can be compared to both in situ and remote-sensed data (Sect. 2.3). The required inputs to perform this operation are provided by the NEMO–BAMHBI system for IOPs (Sect. 2.4) and forced from simulation outputs from a regional atmospheric model (MAR) configuration (Sect. 2.5) for above-water irradiance.

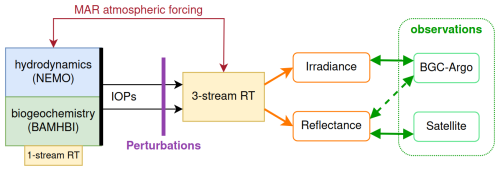
Figure 1 Coupled NEMO–BAMHBI modelling framework with the three-stream RT model functioning in one-way coupling. The RT model is used as an observation operator, projecting model variables into the space of observations. Since it does not feed back to NEMO–BAMHBI, a simple one-stream RT model is kept to compute temperature. Among the outputs of the RT model, irradiance is compared to BGC-Argo data and reflectance is compared to remote-sensed data and BGC-Argo data, through inversion algorithms used to retrieve surface chlorophyll.

2.1 Physical–biogeochemical coupled system NEMO–BAMHBI

The physical–biogeochemical coupled system NEMO–BAMHBI is implemented within the Black Sea Monitoring and Forecasting system of the Copernicus Marine Service. The hydrodynamics are solved with NEMO 4.2, which is online coupled to the biogeochemical model. The Biogeochemical Model for Hypoxic and Benthic Influenced areas (BAMHBI) is a biogeochemical model that describes the biogeochemical cycles of carbon and nitrogen through the food web, from bacteria up to mesozooplankton (Grégoire et al., 2008; Grégoire and Soetart, 2010; Capet, 2014). It explicitly represents processes in the anoxic layer, with a 28-variable pelagic component (including the carbonate system) and a 6-variable benthic component.

The default light penetration scheme used in BAMHBI is a one-stream (i.e. direct downward) RT scheme in three wavebands: two in the visible range and one in the infrared. The sea surface radiation is computed using astronomical forcing to estimate the radiance at the top of the atmosphere and is propagated to the sea surface using the cloud cover data from a regional atmospheric model (MAR) run for the Black Sea. The sea surface radiation is then attenuated with depth following Beer's law with attenuation derived from concentrations of biogeochemical variables: pure water, phytoplankton, suspended minerals, and CDOM. This simple RT model is then used to derive PAR, and the amount of irradiance absorbed is a source term in the equation of conservation of thermic energy in NEMO.

In operational and reanalysis mode, the coupled model works with a horizontal resolution of 2.5 km and 59 unevenly distributed vertical levels, with thinner layers close to the surface and the pycnocline. However, in this study, we use a horizontal resolution of 15 km with the same vertical levels. The reduced horizontal resolution is chosen here to minimise computational costs for ensemble runs. In the configuration used in this study, we use a velocity forcing as a boundary condition at the Bosphorus Strait for exchanges with the Mediterranean Sea, as described in Stanev and Beckers (1999). It is assumed that there are no exchanges with the Azov Sea. River runoffs and atmospheric deposition of nutrients (phosphorus, nitrate, and ammonium) are based on climatology. The initial conditions for the simulations performed in this study are taken from a longer stable run in a similar model configuration.

2.2 The radiative transfer observation operator

The 1D three-stream RT model is directly inspired by the model described in Dutkiewicz et al. (2015) within the framework of the global MITgcm. Three streams of irradiance are computed based on the absorption and (back)scattering properties of the medium: a downward direct irradiance (E_d) that accounts for transmitted light, a downward scattered irradiance (E_s) that accounts for light that has been scattered in the forward direction, and an upward irradiance (E_u) that accounts for light that has been backscattered towards the ocean surface. Resolving the three irradiance streams allows comparison with remote-sensed data thanks to the computation of the upward E_u stream at the surface, while the downward E_d and E_s streams are a decomposition of the single stream found in one-stream RT models.

The RT model simulates irradiance streams in 33 wavebands ranging between 250 and 4000 nm, with a finer 25 nm resolution in the visible range. This operator is 1D and therefore processes each water column individually. On the vertical, we consider that all scattering happens only either forwards or backwards. We only represent elastic scattering, assuming that inelastic scattering processes are of lower magnitude. The attenuation coefficients are derived from absorption (a), scattering (b), and backscattering (b_b) coefficients, all in units of m⁻¹. The propagation of light in the water column is then described by the following system of equations:

$$\begin{array}{ll}\text{(1)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{E}_{\mathrm{d}}\left(\mathit{\lambda }\right)}{\mathrm{d}z}}=-{\displaystyle \frac{a\left(\mathit{\lambda }\right)+b\left(\mathit{\lambda }\right)+b_{\mathrm{b}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{d}}}}}{E}_{\mathrm{d}}\left(\mathit{\lambda }\right),{\displaystyle }& {\displaystyle \frac{\mathrm{d}{E}_{\mathrm{s}}\left(\mathit{\lambda }\right)}{\mathrm{d}z}}=-{\displaystyle \frac{a\left(\mathit{\lambda }\right)+r_{\mathrm{s}}{b}_{\mathrm{b}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{s}}}}}{E}_{\mathrm{s}}\left(\mathit{\lambda }\right)+{\displaystyle \frac{r_{\mathrm{u}}{b}_{\mathrm{b}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{u}}}}}{E}_{\mathrm{u}}\left(\mathit{\lambda }\right)\\ \text{(2)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{b\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{d}}}}}{E}_{\mathrm{d}}\left(\mathit{\lambda }\right),{\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{d}{E}_{\mathrm{u}}\left(\mathit{\lambda }\right)}{\mathrm{d}z}}=-{\displaystyle \frac{a\left(\mathit{\lambda }\right)+r_{\mathrm{u}}{b}_{\mathrm{b}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{u}}}}}{E}_{\mathrm{u}}\left(\mathit{\lambda }\right)+{\displaystyle \frac{r_{\mathrm{s}}{b}_{\mathrm{b}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{s}}}}}{E}_{\mathrm{s}}\left(\mathit{\lambda }\right)\\ \text{(3)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{b_{\mathrm{b}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{d}}}}}{E}_{\mathrm{d}}\left(\mathit{\lambda }\right),\end{array}$$

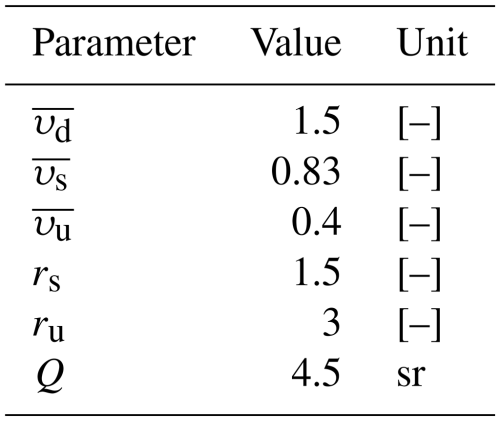
where r_s and r_u are dimensionless normalised effective scattering coefficients and $\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{d}}}$, $\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{s}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{u}}}$ are average cosines accounting for the angle of incidence of light, also dimensionless (Aas, 1987). These coefficients are approximated with constant values and are detailed in Table 1. This system is closed for each water column, with two surface conditions provided by the radiative forcing on E_d and E_s and one bottom condition imposing E_u to 0.

We define PAR as the total irradiance in the visible range, scaled by the angular coefficients $\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{d}}}$, $\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{s}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{u}}}$. Although the PAR simulated by the RT model is not used in the coupled framework in a one-way configuration, it is a useful quantity that can be used for comparison with in situ data. In units of W m⁻², it is derived with

$$\begin{array}{}\text{(4)}& \mathrm{PAR}=\underset{\mathrm{400}\mathrm{nm}}{\overset{\mathrm{700}\mathrm{nm}}{\int }}\left[{\displaystyle \frac{E_{\mathrm{d}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{d}}}}}+{\displaystyle \frac{E_{\mathrm{s}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{s}}}}}+{\displaystyle \frac{E_{\mathrm{u}}\left(\mathit{\lambda }\right)}{\stackrel{\mathrm{‾}}{{\mathit{\upsilon }}_{\mathrm{u}}}}}\right]\mathrm{d}\mathit{\lambda }.\end{array}$$

We then define the sea surface reflectance R in the upper layer z=0 (below surface) based on the three streams of irradiance as follows:

$$\begin{array}{}\text{(5)}& R\left(\mathit{\lambda }\right)={\displaystyle \frac{E_u^{z=\mathrm{0}}\left(\mathit{\lambda }\right)}{E_d^{z=\mathrm{0}}\left(\mathit{\lambda }\right)+E_s^{z=\mathrm{0}}\left(\mathit{\lambda }\right)}}.\end{array}$$

The simulated reflectance is not strictly the same quantity as the remote-sensed reflectance R_RS, which is estimated above the sea surface. Following Dutkiewicz et al. (2018), two corrections are made to make the modelled reflectance comparable to R_RS satellite measurements. The subsurface reflectance is first adjusted so that the upwelling irradiance stream E_u is transformed into upwelling radiance as seen by satellite instruments. This transformation is performed according to the bidirectional reflectance distribution function (BRDF) of the ocean surface. The BRDF depends on many variables, such as the wave state at the surface, the solar zenith angle, and the optical properties at the air–sea interface (Morel et al., 2002). It is simplified here in a constant coefficient Q. Q is generally estimated between 3 and 6 sr. In this study, we set Q to 4.5 sr.

$$\begin{array}{}\text{(6)}& R_{\mathrm{RS}}^{\mathrm{below}}\left(\mathit{\lambda }\right)={\displaystyle \frac{R\left(\mathit{\lambda }\right)}{Q}}\end{array}$$

An additional correction is performed to account for interface effects. It aims to translate subsurface remote-sensed reflectance to above-surface remote-sensed reflectance following Lee et al. (2002).

$$\begin{array}{}\text{(7)}& R_{\mathrm{RS}}\left(\mathit{\lambda }\right)={\displaystyle \frac{\mathrm{0.52}{R}_{\mathrm{RS}}^{\mathrm{below}}\left(\mathit{\lambda }\right)}{\mathrm{1}-\mathrm{1.7}{R}_{\mathrm{RS}}^{\mathrm{below}}\left(\mathit{\lambda }\right)}}\end{array}$$

R_RS(λ) is now directly comparable to remote-sensed reflectance data. Among the available satellite products, we will be using the multi-satellite product provided by the Copernicus Marine Service for the Black Sea for validation and comparison. It combines measurements from the Sentinel-3A, Sentinel-3B, Aqua, Suomi NPP, and JPSS-1 satellites. This L3 product is available from 1997 and provides daily measurements of sea surface reflectance with a horizontal resolution of 1 km in six wavebands centred on 412, 443, 490, 510, 555, and 670 nm.

Table 1 Average cosines and normalised effective scattering coefficients used in RT equations.

2.3 Ocean colour algorithms

Ocean colour algorithms are used to estimate surface chlorophyll from sea surface reflectance. In the Black Sea, the Copernicus Marine Service uses a merged product between two algorithms: a band-ratio algorithm and a neural-network-based method (Zibordi et al., 2015). The neural network is used primarily for complex waters, such as coastal areas of the northwestern continental shelf of the Black Sea. The blue/green band-ratio algorithm is based on reflectances in the 490 and 555 nm wavebands and is used to derive an estimate of surface chlorophyll (Kajiyama et al., 2018). We choose to reproduce the band-ratio algorithm to derive an estimate of surface chlorophyll based on the reflectances simulated in the RT model (Dutkiewicz et al., 2018). This choice over the neural network approach is motivated by our focus on the deep parts of the basin, where the band-ratio algorithm is predominantly used. In the following, we call this the reflectance-derived chlorophyll estimate (rCHL):

$$\begin{array}{}\text{(8)}& \log \left(\mathrm{rCHL}\right)=\sum _{k=\mathrm{0}}^{\mathrm{3}}{c}_k\times {\left[\log \left({\displaystyle \frac{R_{\mathrm{RS}}\left(\mathrm{490}\right)}{R_{\mathrm{RS}}\left(\mathrm{555}\right)}}\right)\right]}^k.\end{array}$$

The algorithm described in Kajiyama et al. (2018) provides the c_k coefficients for the western Black Sea. We choose here to expand this formulation to the entire basin. This new estimate is not independent of the chlorophyll simulated in BAMHBI, since outputs of BAMHBI intervene in the simulation of reflectances, but it provides a quantity that corresponds more closely to satellite chlorophyll products. From the perspective of modelling, using a reflectance ratio is also interesting, as it removes the uncertainty that arises from the simplification of BRDF.

2.4 Optically active components

The absorption and scattering of light by seawater are modelled as the linear combination of individual contributions from pure water, phytoplankton, non-algal particles, and CDOM. Sources from the literature for specific coefficients used to derive each contribution are summarised in Table 2. In the following, the subscripts “w”, “phy”, “prt”, and “cdom” denote their respective contributions. We assume here that CDOM only participates in absorption and not in scattering as in Dutkiewicz et al. (2015) and Álvarez et al. (2023).

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }a\left(\mathit{\lambda }\right)=a_{\mathrm{w}}\left(\mathit{\lambda }\right)+a_{\mathrm{phy}}\left(\mathit{\lambda }\right)+a_{\mathrm{prt}}\left(\mathit{\lambda }\right)+a_{\mathrm{cdom}}\left(\mathit{\lambda }\right)\text{(10)}& {\displaystyle }& {\displaystyle }b\left(\mathit{\lambda }\right)=b_{\mathrm{w}}\left(\mathit{\lambda }\right)+b_{\mathrm{phy}}\left(\mathit{\lambda }\right)+b_{\mathrm{prt}}\left(\mathit{\lambda }\right)\text{(11)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{b}}\left(\mathit{\lambda }\right)=b_{\mathrm{b},\mathrm{w}}\left(\mathit{\lambda }\right)+b_{\mathrm{b},\mathrm{phy}}\left(\mathit{\lambda }\right)+b_{\mathrm{b},\mathrm{prt}}\left(\mathit{\lambda }\right)\end{array}$$

2.4.1 Water

The absorption and scattering properties of water (a_w, b_w, and b_b,w) have been well documented by laboratory experiments (Pope and Fry, 1997; Morel et al., 2007; Mason et al., 2016). Water is an important constituent with a very high absorbing power in the infrared and ultraviolet and a lower absorbing power in the visible range. Scattering by water is considered isotropic, meaning that, in 1D, $b_{\mathrm{w}}=b_{\mathrm{b},\mathrm{w}}$. Absorption and scattering spectra for water in the visible range are provided in Fig. 2, with higher absorption and lower scattering for longer wavelengths.

2.4.2 Phytoplankton and non-algal particles

Absorption and (back)scattering by phytoplankton (a_phy, b_phy, and b_b,phy) are modelled as the sum of individual IOPs for each phytoplankton functional type (PFT) solved in BAMHBI: these are large flagellates (representative of dinoflagellates), small flagellates (representative of coccolithophores), and diatoms, all of which are the dominant species in the Black Sea (Silkin et al., 2021). The specific absorption and (back)scattering coefficients associated with phytoplankton are adapted from Álvarez et al. (2022) to the PFTs modelled in BAMHBI. Specific coefficients for absorption ($a_{\mathrm{phy}}^i$) have units of m² mgChl⁻¹, while specific coefficients for scattering ($b_{\mathrm{phy}}^i$ and $b_{\mathrm{b},\mathrm{phy}}^i$) have units of m² mmolC⁻¹:

$$\begin{array}{}\text{(12)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{phy}}\left(\mathit{\lambda }\right)=\sum _i{a}_{\mathrm{phy}}^i\left(\mathit{\lambda }\right){\mathrm{CHL}}^i,\text{(13)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{phy}}\left(\mathit{\lambda }\right)=\sum _i{b}_{\mathrm{phy}}^i\left(\mathit{\lambda }\right)C_{\mathrm{chl}}^i,\text{(14)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{b},\mathrm{phy}}\left(\mathit{\lambda }\right)=\sum _i{b}_{\mathrm{b},\mathrm{phy}}^i\left(\mathit{\lambda }\right)C_{\mathrm{chl}}^i,\end{array}$$

where CHLⁱ is the chlorophyll concentration for each PFT in units of mgChl m⁻³ and $C_{\mathrm{chl}}^i$ is the carbon content in each PFT in units of mmolC m⁻³. Specific absorption and scattering spectra for phytoplankton are provided in Fig. 2.

Similarly, the optical properties of non-algal particles (a_prt, b_prt, and b_b,prt) are derived from specific coefficients ($a_{\mathrm{prt}}^{\mathrm{0}}$, $b_{\mathrm{prt}}^{\mathrm{0}}$, and $b_{\mathrm{b},\mathrm{prt}}^{\mathrm{0}}$, respectively) from Gallegos et al. (2011) and Álvarez et al. (2022). The computation of these coefficients relies on the use of particulate organic carbon (POC; computed dynamically in BAMHBI) as a proxy for particle concentration, assuming uniformity in the size and distribution of particles as in Dutkiewicz et al. (2015). Specific absorption and scattering spectra for particles are provided in Fig. 2.

$$\begin{array}{}\text{(15)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{prt}}\left(\mathit{\lambda }\right)=a_{\mathrm{prt}}^{\mathrm{0}}\left(\mathit{\lambda }\right)\mathrm{POC}\text{(16)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{prt}}\left(\mathit{\lambda }\right)=b_{\mathrm{prt}}^{\mathrm{0}}\left(\mathit{\lambda }\right)\mathrm{POC}\text{(17)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{b},\mathrm{prt}}\left(\mathit{\lambda }\right)=b_{\mathrm{b},\mathrm{prt}}^{\mathrm{0}}\left(\mathit{\lambda }\right)\mathrm{POC}\end{array}$$

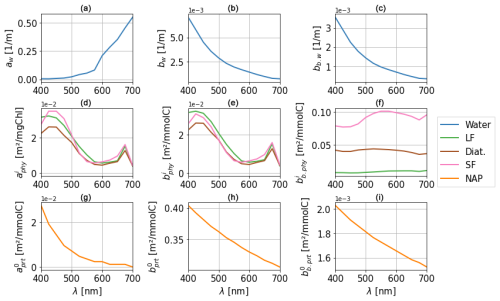
Figure 2 Optical properties for water (a_w, b_w, and b_b,w) (a–c), phytoplankton ($a_{\mathrm{phy}}^i$, $b_{\mathrm{phy}}^i$, and $b_{\mathrm{b},\mathrm{phy}}^i$) (d–f), and non-algal particles (NAP) ($a_{\mathrm{prt}}^{\mathrm{0}}$, $b_{\mathrm{prt}}^{\mathrm{0}}$, and $b_{\mathrm{b},\mathrm{prt}}^{\mathrm{0}}$) (g–i). The three PFTs represented here are large flagellates (LF), diatoms (Diat.), and small flagellates (SF). Spectral resolution in the model is 25 nm in the visible range (400–700 nm).

2.4.3 CDOM

Although CDOM is a major contributor to irradiance absorption within the water column, it is not explicitly simulated in the NEMO–BAMHBI framework. We choose here to derive a forcing for a_cdom from a collection of BGC-Argo profiles. The RT model is run by deriving IOPs from BGC-Argo data to reproduce irradiance profiles at a reference wavelength λ_ref=412 nm by optimising a_cdom to fit the measured profiles. The description of data and the setup and detail of the method of this experiment are presented in Appendix A.

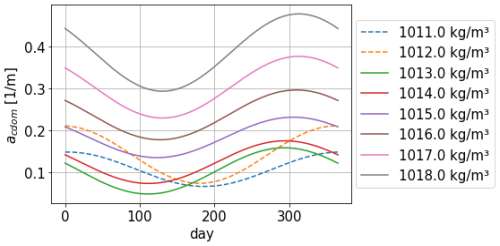
The forcing for a_cdom(λ_ref) depends on time and seawater density ρ as a way to account for ocean physics and spatial and seasonal variability. It also accounts for the increase in CDOM, and therefore in a_cdom, with depth. This approach is not valid in coastal areas and on the continental shelf, where we observe low densities due to large freshwater discharges from rivers. With this method, low-density areas are associated with low CDOM, which goes against the high biological activity observed around river estuaries. Since this forcing is generated using data from the central parts of the basin, we acknowledge that it will not be representative of shallow areas. We interpolate this dataset to generate annual cycles for each density scale.

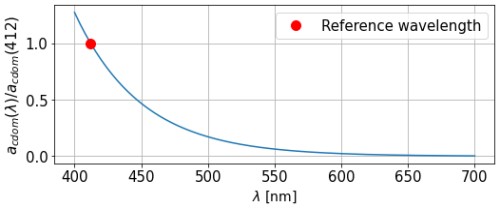
Figure 3 Absorption spectrum for CDOM as the ratio with absorption at the reference wavelength λ_ref=412 nm.

Pope and Fry (1997); Morel (1974)Álvarez et al. (2022)Álvarez et al. (2022)Gallegos et al. (2011)

Table 2 Specific IOPs for the main water constituents and their references.

CDOM is dominant in the blue and decreases for longer wavelengths, parameterised with an exponential law for the absorption coefficient of parameter S_cdom (Twardowski et al., 2004; Kitidis et al., 2006; Dutkiewicz et al., 2015). A range of values for this slope is prescribed in Álvarez et al. (2022), and we fit it using BGC-Argo irradiance profiles at 380 and 490 nm in a benchmark 1D RT model. We use S_cdom=0.02  nm⁻¹ for our model, leading to the spectrum in Fig. 3. The uncertainty associated with this extrapolation coefficient will be studied in the next section of the paper. Our forcing for a_cdom is finally written as

$$\begin{array}{}\text{(18)}& a_{\mathrm{cdom}}(\mathit{\rho },\mathit{\lambda })=a_{\mathrm{cdom}}(\mathit{\rho },{\mathit{\lambda }}_{\mathrm{ref}})e^{-S_{\mathrm{cdom}}(\mathit{\lambda }-{\mathit{\lambda }}_{\mathrm{ref}})}.\end{array}$$

2.5 Atmospheric forcing

The ocean model is forced with the outputs of an MAR regional atmospheric model configuration (Gallée et al., 2013). When run over the Black Sea, MAR provides the boundary conditions for ocean physics: wind velocity, humidity, precipitation, 2 m temperature, mean sea level pressure. The spectral RT model also requires a boundary condition for spectral irradiance. MAR has been extended with a spectral radiative scheme, ecRad, developed by Hogan and Bozzo (2018) to represent the radiative effect of clouds and aerosols in the ECMWF integrated forecasting system. An accurate description of gas optics is also included in the ecCKD tool used in ecRad (Hogan and Matricardi, 2022). Using this extension, MAR provides direct and scattered downward irradiance just above the sea surface in the 33 wavebands selected for the ocean RT model. The irradiance below sea surface is then derived considering surface albedo. The MAR configuration extended with the ecRad scheme is described and validated in Grailet et al. (2025).

In this study, we consider the surface radiative forcing to be accurate and therefore ignore its uncertainty. Although an error in the surface irradiance propagated within the water column, the IOPs would not be altered. Irradiance fields in the water column would be biased due to surface error, but reflectance would not be significantly influenced as it is a variable that is normalised by the incident light. We would therefore obtain very similar results regardless of the surface forcing. This change also would not influence the rest of the NEMO–BAMHBI system in the one-way configuration of the coupled model. The scope of this paper is thus focused on the parameterisation of IOPs in the RT model used as an observation operator.

3 Modelling of uncertainties

In this section, we describe the method we applied to transform the deterministic RT model into a probabilistic model, explicitly simulating the internal sources of uncertainties of the model. Within the RT operator, the optical properties of phytoplankton, non-algal particles, and CDOM are uncertain. We aim at quantifying the influence of these uncertainties on the computation of irradiance and reflectance fields. A generic method is presented in this section to perturb IOPs in a similar way for the three constituents.

3.1 Stochastic fields

All stochastic perturbations introduced in the model are produced using the generic approach implemented in the NEMO framework by Brankart et al. (2015) and subsequently used in the context of coupled physical–biogeochemical modelling by Garnier (2016) and Popov et al. (2024). We start by generating Gaussian processes, characterised by their mean and time–space covariance. The stochastic processes are updated at each time step of the model to simulate the evolution of uncertainties and are correlated in time with a time correlation parameter representative of biogeochemical processes. In our application, we use first-order autoregressive processes (AR1), which means that the value of the process η at time step t_k only depends on η at the previous time step t_k−1:

$$\begin{array}{}\text{(19)}& \mathit{\eta }\left(t_k\right)=\mathit{\phi }\mathit{\eta }\left(t_{k-\mathrm{1}}\right)+\sqrt{\mathrm{1}-{\mathit{\phi }}^{\mathrm{2}}}w,\end{array}$$

where w is a random Gaussian noise of mean μ₀ and standard deviation σ₀, and

$$\begin{array}{}\text{(20)}& \mathit{\phi }=e^{-\mathrm{1}/\mathit{\tau }},\end{array}$$

where w is a normalised white noise (with zero mean and unit standard deviation). With Eq. (19), we can produce AR1 processes with a correlation function given by

$$\begin{array}{}\text{(21)}& \mathrm{corr}\left(\mathrm{\Delta }t\right)=\exp (-\mathrm{\Delta }t/\mathit{\tau }),\end{array}$$

where Δt is the time difference and τ is the decorrelation length scale (both in number of time steps). It represents a decorrelation time at which the influence of a perturbation is $\mathrm{1}/e$, after which it tends to 0. With Eq. (19), we obtain processes with zero mean and unit standard deviation, which can then be rescaled to obtain processes with the required mean (μ₀) and standard deviation (σ₀).

By applying this method independently at each model grid point, we obtain maps of independent stochastic processes that are uncorrelated in space. The space correlation is obtained by applying a filtering operator to the uncorrelated noise. Here, we use a Laplacian filter to generate a perturbation field η^′ from the above time-correlated point-wise time series of perturbations of the four neighbouring grid points.

$$\begin{array}{}\text{(22)}& \begin{array}{rl}{\mathit{\eta }}_{i,j}^{\prime }\left(t_k\right)& =\mathrm{0.5}{\mathit{\eta }}_{i,j}\left(t_k\right)+\mathrm{0.125}\left({\mathit{\eta }}_{i-\mathrm{1},j}\right(t_k)+{\mathit{\eta }}_{i+\mathrm{1},j}(t_k)\\ & +{\mathit{\eta }}_{i,j-\mathrm{1}}\left(t_k\right)+{\mathit{\eta }}_{i,j+\mathrm{1}}\left(t_k\right)),\end{array}\end{array}$$

where (i,j) is the index of any grid point. This filtering process can be repeated several times to widen the spatial correlation. In this study, this filtering is repeated five times, thus generating a spatial correlation length scale of 75 km (i.e. 5 times the spatial resolution of 15 km). The resulting field is normalised again to maintain the required standard deviation.

This transformation produces stochastic fields with space and time correlation structures that remain Gaussian. As we want to simulate fields of multiplicative noise, we need random positive numbers. Gaussian processes are thus inappropriate, and we apply an exponential transform to convert the distribution towards a log-normal distribution, noted η^′′.

$$\begin{array}{}\text{(23)}& {\mathit{\eta }}_{i,j}^{\prime \prime }\left(t_k\right)=e^{{\mathit{\eta }}_{i,j}^{\prime }\left(t_k\right)}\end{array}$$

The exponential transform of a Gaussian law transforms the mean and standard deviation of the initial Gaussian distribution. We want the resulting log-normal distribution to have a unit mean and a standard deviation σ to generate a spread without introducing bias. This constrains the choice for μ₀ and σ₀ in the initial Gaussian distribution that are obtained with

$$\begin{array}{}\text{(24)}& {\displaystyle }& {\displaystyle }{\mathit{\mu }}_{\mathrm{0}}=-{\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{2}}}{\mathrm{2}}},\text{(25)}& {\displaystyle }& {\displaystyle }{\mathit{\sigma }}_{\mathrm{0}}^{\mathrm{2}}=\ln (\mathrm{1}+{\mathit{\sigma }}^{\mathrm{2}}).\end{array}$$

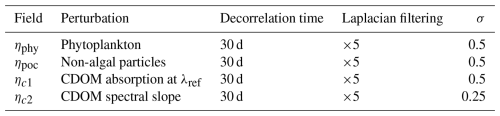
The resulting 2D maps of stochastic fields follow a log-normal distribution of unit mean and standard deviation σ. The time–space correlation structure of these AR1 processes can be tuned with the correlation timescale τ and the number of passes of the horizontal Laplacian filter. In the following, we call this field of perturbation η. These stochastic processes are used as multiplicative noises applied to IOPs in the RT model, with parameters as described in Table 3.

Table 3 Time and spatial correlation properties of the stochastic fields generated to perturb IOPs, with standard deviations of each perturbation.

3.2 Uncertainties on phytoplankton and non-algal particles

Uncertainties in IOPs are the joint effect of uncertainties in both the concentrations simulated by BAMHBI and the parameterisation of the optical properties (i.e. specific absorption and scattering coefficients) of active components (Eqs. 12 to 17). Since the modelling of the effect of these two sources of uncertainty on the IOPs can be done in a similar way, we consider that perturbing the abundance of the optically active component mimics the effect of uncertainty in both the abundance and the parameterisation. It should be noted that BAMHBI may miss a phytoplankton group that is important in the Black Sea, besides the three PFTs it solves, but this uncertainty is not considered here.

Similarly for non-algal particles, we find uncertainties in both the parameterisation of their optical properties and the concentrations. We assume that particles are uniform in size and therefore all share the same specific optical properties. In reality, non-algal particles come in a larger range of sizes, and this assumption of uniformity injects uncertainty into the model. Furthermore, the derivation of the particle concentration from POC may also be inaccurate. For both chlorophyll and non-algal particles, the perturbations that are applied are in the form of 2D horizontal fields as described in Sect. 3.1. As such, the perturbation does not modify the vertical structure of the chlorophyll and POC fields and cannot account for inaccuracy on the depth of chlorophyll or POC maxima.

We choose to model the uncertainties associated with the abundance of optically active components in the model by introducing multiplicative coefficients η_phy and η_poc into the computation of absorption and scattering coefficients. The η_phy and η_poc fields are generated following the method described in Sect. 3.1. As such, chlorophyll and POC concentrations are perturbed only at the interface between BAMHBI and the RT model, without influencing the biogeochemical processes described in BAMHBI. Absorption and scattering coefficients thus become

$$\begin{array}{}\text{(26)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{phy}}^{\mathrm{sto}}\left(\mathit{\lambda }\right)={\mathit{\eta }}_{\mathrm{phy}}{a}_{\mathrm{phy}}\left(\mathit{\lambda }\right),\text{(27)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{phy}}^{\mathrm{sto}}\left(\mathit{\lambda }\right)={\mathit{\eta }}_{\mathrm{phy}}{b}_{\mathrm{phy}}\left(\mathit{\lambda }\right),\text{(28)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{b},\mathrm{phy}}^{\mathrm{sto}}\left(\mathit{\lambda }\right)={\mathit{\eta }}_{\mathrm{phy}}{b}_{\mathrm{b},\mathrm{phy}}\left(\mathit{\lambda }\right),\text{(29)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{prt}}^{\mathrm{sto}}\left(\mathit{\lambda }\right)={\mathit{\eta }}_{\mathrm{poc}}{a}_{\mathrm{prt}}\left(\mathit{\lambda }\right),\text{(30)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{prt}}^{\mathrm{sto}}\left(\mathit{\lambda }\right)={\mathit{\eta }}_{\mathrm{poc}}{b}_{\mathrm{prt}}\left(\mathit{\lambda }\right),\text{(31)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{b},\mathrm{prt}}^{\mathrm{sto}}\left(\mathit{\lambda }\right)={\mathit{\eta }}_{\mathrm{poc}}{b}_{\mathrm{b},\mathrm{prt}}\left(\mathit{\lambda }\right).\end{array}$$

The decorrelation time is set to 30 d, consistent with the scale of biogeochemical changes in the Black Sea. Laplacian filtering generates a spatial correlation length scale of approximately 75 km. Finally, the standard deviation is set here to 0.5, based on the ranges of inherent optical properties found in the literature (Gallegos et al., 2011; Dutkiewicz et al., 2015; Álvarez et al., 2022). An example of the resulting field is shown in Fig. 4. The same perturbation field is used for all 59 vertical layers of the model.

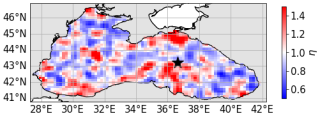
Figure 4 Perturbation field generated according to the method described in Sect. 3.1, following a log-normal distribution with unit mean and standard deviation 0.5, with five passes of Laplacian filtering for space correlation. The black star indicates the location of coordinates 43.22° N, 36.63° E used in later sections to describe the results in this paper.

3.3 Uncertainty on CDOM

Since CDOM is not explicitly simulated in BAMHBI, its absorption is parameterised from BGC-Argo data. However, the data do not cover the entire basin at all seasons, and we rely on extrapolations to cover the remaining areas and times. This likely introduces uncertainties in the model, in addition to potential observation errors. The approximation of the CDOM absorption spectrum by a decreasing exponential law may also lead to uncertainties in the representation of CDOM in the RT model, as indicated by the numerous ranges that can be found in the literature for S_cdom (Terzić et al., 2021). Uncertainty in CDOM absorption is modelled in two steps, perturbing separately the reference absorption profile at 412 nm and the exponential slope of the absorption spectrum, both described in Sect. 2.4.2.

We therefore introduce uncertainty on CDOM absorption in two ways. Firstly, a multiplicative factor field η_c1 is used to perturb the reference absorption coefficient from the reference profile. Then, an η_c2 field is used to perturb the exponential slope. Both fields are generated according to the method presented in Sect. 3.1.

$$\begin{array}{}\text{(32)}& a_{\mathrm{cdom}}^{\mathrm{sto}}(\mathit{\rho },\mathit{\lambda })={\mathit{\eta }}_{c\mathrm{1}}{a}_{\mathrm{cdom}}(\mathit{\rho },{\mathit{\lambda }}_{\mathrm{ref}})\times e^{-{\mathit{\eta }}_{c\mathrm{2}}{S}_{\mathrm{cdom}}(\mathit{\lambda }-{\mathit{\lambda }}_{\mathrm{ref}})}\end{array}$$

As for chlorophyll and non-algal particles, the decorrelation time is set to 30 d and the spatial correlation length scale is set to 75 km. The standard deviation for the perturbation of the reference profile is set to 0.5, based on the ranges of CDOM profiles found in the BGC-Argo observations. This standard deviation accounts for the rather simplified representation of spatial and temporal variability in the CDOM concentration and absorption power. The standard deviation for the exponential slope is set to 0.25 based on the range of possible values found in the literature (Terzić et al., 2021). The same perturbation field is used for all 59 vertical layers of the model.

4 Ensemble simulations

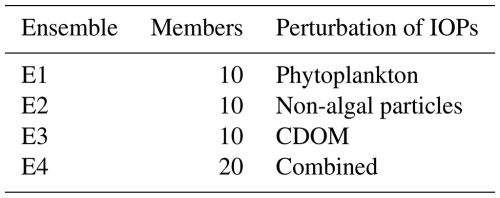
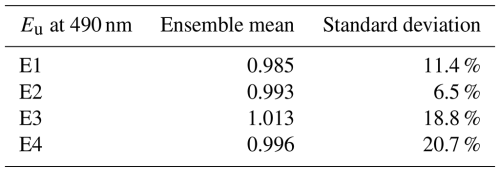
In this section, we explore the impact of simulating uncertainties as described in Sect. 3 in the modelling framework complemented by the RT model described in Sect. 2. A deterministic reference simulation and four distinct ensembles are simulated. E1 and E2 are 10-member ensembles each with perturbations on the optical properties of phytoplankton only and non-algal particles only, respectively, as described in Sect. 3.2. E3 is a 10-member ensemble with perturbations on the optical properties of CDOM only, as described in Sect. 3.3. In this ensemble, both the reference profile for CDOM absorption at λ_ref and the spectral dependence of CDOM absorption are perturbed. E4 is a 20-member ensemble combining the perturbations used in E1, E2, and E3 (i.e. on chlorophyll, non-algal particles, and CDOM).

Table 4 Overview of ensembles E1, E2, E3, and E4.

All ensemble simulations are performed over 15 months: a spin-up time of 3 months between October and December 2016 followed by the simulation of 2017. The whole Black Sea domain is simulated. A total of 10 members are simulated for ensembles E1, E2, and E3, as few members are deemed enough to evaluate the influence of each perturbation. The most important results described in this section come from ensemble E4, which combines perturbations. As such, 20 members were simulated to allow a more reliable statistical analysis of the ensemble. However, when E4 is directly compared to E1, E2, or E3, it is limited to its first 10 members for consistency.

We begin by studying the individual influence of perturbations on spectral irradiance profiles and surface reflectance. Then, we assess the impact of the combination of uncertainties in E4. Finally, we compare the ensemble results to the observation data to evaluate the ability of the different ensembles to produce distributions that are consistent with the observations.

4.1 Influence of perturbations on radiative transfer

The perturbation of IOPs influences the vertical propagation of irradiance in the water column by modifying the absorption and (back)scattering properties of the medium. In the case of CDOM, the perturbation only modifies absorption (see Eqs. 1, 2, and 3). Modifying the absorption affects the total amount of irradiance propagating in the water column, while a modification of the (back)scattering coefficients affects the direction of light (downward or upward). The three irradiance streams, E_d, E_s, and E_u, are affected by absorption and backscattering. The perturbation of scattering coefficients changes the amount of direct irradiance that is scattered but does not influence the backscattered stream or reflectance. It also has no influence on the total downwelling irradiance defined as the sum of direct and scattered streams.

The dominant optical constituent for absorption and (back)scattering varies during the season, region, and waveband. In the following, we focus on the spectral bands used in satellite inversion algorithms in the Black Sea to compute surface chlorophyll: 490 and 555 nm. Appendix B provides an overview of the model performance in other wavebands in the visible range. Figure 5 presents a time series of perturbed IOPs at 490 nm in ensembles with individual perturbations throughout 2017, in the eastern part of the basin and at shallow depth (10.6 m). For absorption, we note that the spread around CDOM is the largest, in agreement with the high uncertainty set for CDOM absorption that is not explicitly modelled in BAMHBI. Scattering coefficients are 10 to 100 times larger than absorption coefficients, while backscattering is about 10 times lower. Figure 7 below illustrates how the perturbation of these coefficients influences the irradiance streams in E4, highlighting that most of the light is converted into the downward diffuse part E_s.

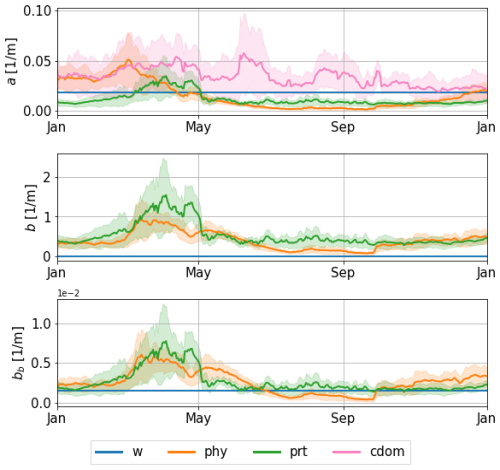
Figure 5 Time series of absorption, scattering, and backscattering coefficients at 490 nm from the perturbed runs at 43.22° N, 36.63° E (see location in Fig. 4) in 2017, at 10.6 m depth. The solid lines represent the ensemble mean, and the shaded areas cover 1 standard deviation around the ensemble mean.

In the eastern gyre, CDOM has no clear seasonality. It dominates absorption throughout the year, with lower values at the end of summer and autumn. (Back)scattering is mainly dominated by non-algal particles, except at the end of the year, when phytoplankton reaches a similar and even larger contribution. Overall, we identify three different regimes throughout the year. In spring, we observe high biological activity associated with a phytoplankton bloom. Absorption is mostly dominated by CDOM, with high phytoplankton contribution, while scattering is dominated by non-algal particles, as their concentration increases after the phytoplankton bloom. During summer, we observe a regime of low biological activity once the high concentrations of phytoplankton and particles start to decrease after the bloom. At this stage, CDOM dominates absorption, whereas backscattering is dominated by non-algal particles. During the autumn, the contribution of phytoplankton increases again until it reaches a level similar to that of CDOM and water for absorption. For scattering, both contributions from phytoplankton and particles gradually increase in autumn. It is worth noting that the introduction of perturbations in this setup allows a change in the constituent dominating absorption or (back)scattering. For instance, during blooms, perturbing the model may create a switch from a domination of absorption by CDOM to a domination by phytoplankton or, conversely, when contributions are of similar magnitude in the deterministic simulation. These three regimes are valid for the deep sea. In coastal and shallow areas, such as the northwestern shelf, biological activity follows different patterns. There, the contributions of phytoplankton and particles remain high throughout the year, with a lower contribution of CDOM to absorption. On the shelf, scattering and backscattering are mostly dominated by non-algal particles. However, in this paper, we focus on the deep central areas of the basin, as it is where the CDOM forcing is the most reliable.

Figure 6 presents the seasonal cycle of the surface reflectance R_RS(490) and rCHL (as defined in Eq. 8) generated by the ensembles. Perturbations in backscattering and absorption influence the upward diffuse irradiance (see Fig. 7), which in turn modifies surface reflectance. Although backscattering directly influences the fractions of light scattered upward in the E_u stream, absorption is also of significant importance, as it drives the ability of the water column to propagate irradiance streams. For instance, with low absorption, the thickness of the surface layer in which backscattered light eventually reaches back to the surface increases. In spring, perturbations of chlorophyll and CDOM generate the largest dispersion (Fig. 6). Low biological activity in summer leads to reduced dispersion in ensembles E1, E2, and E3, until it increases again in autumn and triggers the dispersion of members. Perturbing the optical properties of non-algal particles seems to only have a limited influence on rCHL, and the perturbations remain significant in their influence on surface reflectance.

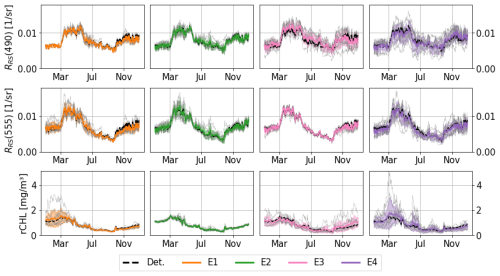
Figure 6 Time series of sea surface reflectance at 490 nm (R_RS(490)) and reflectance-derived chlorophyll (rCHL) in 2017 at the location 43.22° N, 36.63° E. For each ensemble, the standard deviation is represented with a shaded area. Phytoplankton, non-algal particles, and CDOM optical properties are perturbed in E1 (in orange), E2 (in green), and E3 (in red), respectively. All optical properties except pure water are perturbed in E4 (in purple). Each thinner grey line represents an individual member of the ensemble.

Although CDOM shows a large spread at 490 nm, it has little influence on reflectance at 555 nm, as its contribution to absorption is lower at longer wavelengths. On the other hand, the perturbation of contributions from phytoplankton and non-algal particles has a greater influence on reflectance at 555 nm. We also notice that some members drift from the deterministic run or from the ensemble mean. For instance, in the E1 ensemble (perturbation of phytoplankton optical properties), one member (in grey) reaches high values for rCHL during the diatom bloom, while reflectance values at 490 nm remain rather close to those of the other members. In this case, it is associated with higher absorption at 555 nm that lowers the backscattered signal. In all of the experiments, the ensemble means remain rather close to the deterministic run, showing that no significant bias is introduced with the ensemble.

4.2 Combined vs. individual perturbations

The different regimes evidenced with individual perturbations are also highlighted in the E4 ensemble with combined perturbations. The evolution of reflectance and rCHL (Fig. 6) simulated by the E4 ensemble exhibits patterns similar to those observed in the E1, E2, and E3 ensembles. For surface reflectance, early in the year, the spread of the E4 ensemble is only slightly larger than that of the E3 ensemble at 490 nm in which only the optical properties of CDOM are perturbed. During spring bloom, the spread in E4 becomes larger as the result of a combined effect of CDOM (E3), phytoplankton (E1), and non-algal particles (E2). Similarly, in summer, and despite the low dispersion observed in E1 and E2, the spread in E4 is greater than with individual perturbations, suggesting the influence of non-linearities. CDOM contributes the most to the uncertainty of R_RS at 490 nm, which is consistent with its higher absorption power in shorter wavelengths. At 555 nm, CDOM contributes less to absorption with a greater influence of phytoplankton and non-algal particles. The seasonal evolution of rCHL (right-hand panels of Fig. 6) simulated by E4 suggests a dominance of phytoplankton early in the year with a lower contribution of CDOM in the ensemble spread. The extent of the spread is much higher in E4 during the spring bloom than in E1 or E3, again exhibiting the non-linear character of the perturbations and amplification by the model non-linear dynamics. In both E1 and E4, one member of each ensemble presents much higher values of rCHL compared to the ensemble mean, thus largely increasing the spread of the ensemble. In summer, perturbations in CDOM and phytoplankton dominate the E4 spread with a lower influence of non-algal particles. In autumn, CDOM perturbations again dominate the spread of rCHL.

Figure 7 shows the effect of combined perturbations of absorption and (back)scattering coefficients on the three streams of irradiance in the eastern gyre of the Black Sea in early summer. The influence of perturbations is represented with both the ensemble mean (dotted lines) and the standard deviation of the ensemble. This figure shows that CDOM dominates absorption at depth at 490 nm, consistent with the results presented in Fig. 5. (Back)scattering gradually increases with depth and is dominated by phytoplankton and particles that result from a former bloom, also with a significant contribution of water to backscattering at surface. Below 2–3 m, the downward diffusion stream largely dominates the other two streams and penetrates waters below 40 m. The direct downward stream E_d at 490 nm is fully absorbed after 5 to 7 m, mostly by CDOM, and is (back)scattered by phytoplankton and non-algal particles. The upward backscattered stream E_u, which contributes to the reflectance, is the smallest one and is present up to around 30 m.

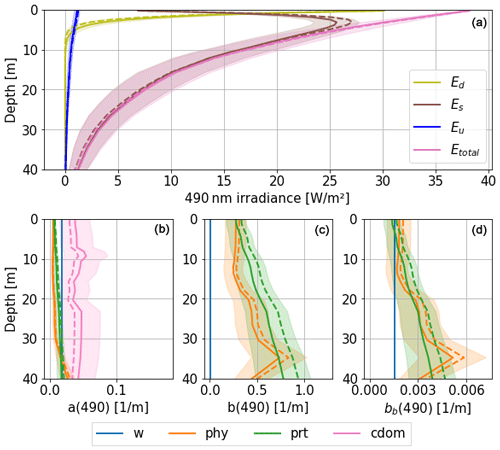
Figure 7 Irradiance (a) and IOP (b–d) profiles at 490 nm. Profiles are taken here at 43.22° N, 36.63° E on 23 June 2017, at solar zenith. Solid lines represent the ensemble mean with shaded areas representing standard deviation of the ensemble. Dotted lines represent the deterministic run.

Most of the simulated variability in the total stream E_total occurs at low depths and is mainly due to the variability in the scattered stream E_s. The impact of the uncertainty in IOPs on direct and backscattered irradiances (E_d and E_u) is lower in magnitude due to lower absorption and backscattering coefficients. In this example, the combined effect of perturbations results in an increase in the total absorption (i.e. the ensemble mean is larger than the deterministic solution over the whole column), while for (back)scattering it is opposite. This results in a lower ensemble mean irradiance compared to the deterministic simulation close to the surface, while the backscattered E_u stream is also lower (Fig. 7a). The uncertainty in total light increases with depth and below 20 m has a spread comparable to the average light. At depth, this range is consistent with higher chlorophyll-a dynamics. For comparison, the standard deviation of E_total is 21 % at 10 m depth and 53 % at 30 m depth.

Figure 8 presents the spread of the upward diffuse irradiance E_u at 490 nm at the surface simulated over the whole Black Sea in summer in the four ensemble experiments. Since the incident irradiance is the same in all ensembles, the difference in E_u results only from the perturbation of IOPs. It shows that the perturbation of CDOM has the largest influence on E_u, which subsequently influences sea surface reflectance. Although CDOM does not backscatter light, it absorbs the three streams including E_u (Eq. 3). The perturbation of phytoplankton IOPs has the second-largest influence, with non-algal particles having the least influence. Their contribution is 2-fold: directly on backscattering and through absorption. The standard deviations and ensemble means are summarised in Table 5. It is worth noting that the ensemble means are kept close to 1, again showing that no bias is introduced with the perturbations.

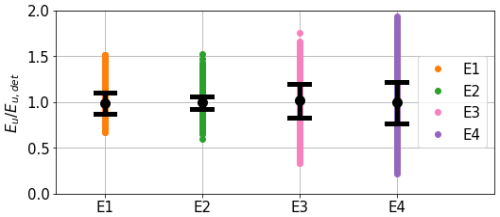
Figure 8 Distributions of E_u(490) at sea surface normalised by its deterministic value for the whole basin on 23 June 2017 and for each experiment. Circles and black lines represent the ensemble mean and standard deviation.

In Fig. 8, E4 shows greater extrema in the ensemble than E1, E2, and E3, but the standard deviation of E_u remains rather close to that of E3, where only the CDOM was perturbed, with 20.7 % for E4. The amplitude of the combined perturbation is therefore lower than the sum of amplitudes of individual perturbations, exhibiting the non-linearity of this relationship. The increase in spread still shows that perturbations are amplified when combined and do not cancel each other out. It should also be noted that the standard deviation for each ensemble is lower than the 50 % standard deviation used to generate perturbations.

Table 5 Ensemble statistics for normalised upward irradiance fields $E_{\mathrm{u}}/E_u^{\text{ref}}$.

4.3 Comparison to observations

In this subsection, we assess the quality of the E4 ensemble by comparing the distribution of simulated irradiance and reflectance fields with observations.

4.3.1 BGC-Argo profiles

A collection of 108 BGC-Argo profiles from floats 6901866 and 7900591, collected during 2017 in the eastern gyre of the Black Sea, is used to compare the ensemble E4 with in situ observations. As we want to assess the representation of marine optics within the water column regardless of the surface forcing, we normalise the irradiance profiles by their surface values. PAR data from BGC-Argo floats are given in units of µmol s⁻¹ m⁻². The conversion to W m⁻², the unit used in the model outputs, is performed using 1 W m⁻² = 4.6 µmol s⁻¹ m⁻² to obtain comparable quantities. This approximation is given for daylight conditions in Thimijan and Heins (1983). In sunny conditions, this coefficient would normally have to be lower. Figure 9 shows the average normalised profiles of the simulated and measured downwelling irradiance at 490 nm and PAR. The downwelling irradiance E_down is defined here as the sum of the direct and scattered irradiance streams E_d and E_s. It shows that, while there is good agreement close to the surface for both variables, divergences appear at depths greater than 15 m. This result, while expected, since the calibration of CDOM optics was performed on the same type of data, illustrates that the RT model is able to represent the total amount of light in a way that is consistent with in situ data at shallow depths. Below 15 m, when the signals begin to diverge, about 70 % of the irradiance has already been absorbed.

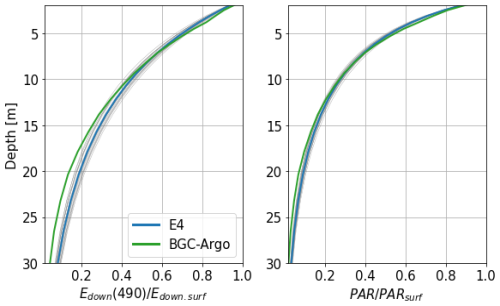
Figure 9 Profiles of downwelling irradiance E_down at 490 nm and PAR from BGC-Argo data and the E4 ensemble normalised by their surface values. Each thinner grey line represents an individual member of the ensemble.

The comparison to BGC-Argo measurements reveals a rather strong agreement between observed irradiance profiles and their equivalent computed by the RT model, although not all of the observed profiles fall within the ensemble spread throughout the year. Figure 10 shows the time series of E_down(490) and PAR at 10.6 m depth, both directly and normalised by their surface values. Although the observations remain contained within the ensemble spread during winter and spring, the ensemble then overestimates the irradiance and PAR (i.e. does not absorb enough) during early summer. For PAR data, some of the discrepancies in summer could be explained by inconsistent unit conversion in sunny conditions. Some residual error can likely be attributed to the BGC-Argo measurements (e.g. sensor drift, sensitivity to temperature), in particular, close to the surface. The agreement is then better during the early autumn, still with an overestimation in the final months of the year. This appears more clearly in the normalised profiles, where the biases appear distinctly in summer and at the end of the year. We also notice some outliers in the observations that seem to indicate isolated events of underestimated irradiance, but those data points may indicate local fine-scale variations that are not captured or observation error.

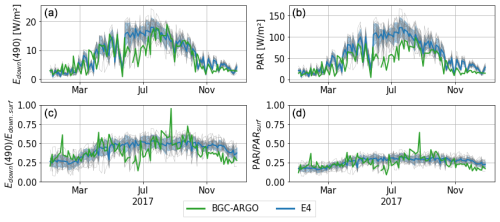
Figure 10 Time series in 2017 of downwelling irradiance (i.e. E_d+E_s) at 490 nm (a) and PAR at 10.6 m depth (b) for the E4 ensemble and BGC-Argo data from floats 6901866 and 7900591. They are also shown normalised with their surface value (c, d). Floats here both drift in the eastern part of the basin during this period. Each thin grey line represents an ensemble member. The standard deviation of the ensemble is represented with the shaded blue area.

Although some of the data remain outside the ensemble spread, it seems that the ensemble is able to capture most of the measurements from BGC-Argo data. Figure 11 shows a rank histogram that gathers the normalised data from the time series in Fig. 10 illustrating the dispersion of the observation data within the ensemble members. A rank histogram (Candille and Talagrand, 2004) aims at assessing the reliability of an ensemble. A rank is attributed to each observation that is equal to its relative position among the realisations of the ensemble for this observation. The entire set of observations is ranked within the sorted ensemble of corresponding simulated data. A flat histogram evidences perfect reliability, i.e. an ensemble distribution that matches the distribution of observations. A convex rank histogram suggests that the ensemble is over-dispersive (all observations tend to be within the ensemble), while a concave rank histogram suggests that the ensemble is under-dispersive (observations tend to be outside of the ensemble). The extreme ranks correspond to observations that are lower or higher than all realisations of the ensemble. To compute this histogram, we consider an observation error of 6 % on the normalised irradiance measured by the BGC-Argo floats. This value is the one prescribed for the satellite products (information from manufacturer – https://biogeochemical-Argo.org/measured-variables-general-context.php, last access: 13 May 2025).

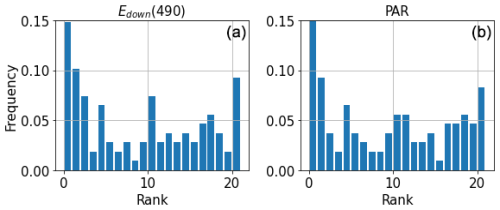
Figure 11 Rank histograms using BGC-Argo data in 2017 for E_down(490) (a) and PAR (b), at 10.6 m depth. Observations are sorted within the E4 ensemble.

Some observations are not captured by the ensemble (Fig. 11), suggesting that the ensemble is under-dispersed. Figure 9 shows that, despite excellent agreement close to the surface (also evidenced in Fig. 10), irradiance tends to be slightly overestimated deeper in the water column, regardless of the perturbation. Nonetheless, the ensemble is close to representing the distribution of measured irradiance streams. It is worth mentioning that the number of observations may not be sufficient here to provide a full picture of the reliability of the ensemble. Although it provides an overview of the ability of the model to reproduce the distribution of downwelling irradiance, the greater number of observations provided by satellite data offers a larger dataset to assess the ensemble skill.

4.3.2 Remote-sensed data

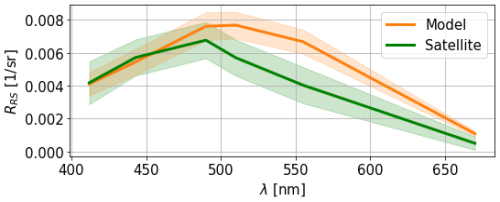
Comparison with remote-sensed data allows better coverage of the basin both spatially and temporally. We start by studying the temporal signature of the ensemble by comparing time series of reflectance in the eastern gyre at 490 and 555 nm and rCHL. Figure 12 shows that the simulated reflectances are higher than observations for most of the year, with the exception of the summer period, where higher reflectances are sensed by satellite instruments. These likely correspond to a coccolithophore bloom (Kubryakov et al., 2021), of which the magnitude is largely underestimated in the model. This underestimation of reflectance by the model is observed for both the 490 and 555 nm wavebands. Interestingly, the chlorophyll from remote-sensed reflectance does not peak during the coccolithophore bloom event. The bias is greatly reduced in the estimation of rCHL. Indeed, as this quantity is a ratio between reflectances in two wavebands that are rather close, uncertainties on measurement and corrections such as the BRDF coefficient partly cancel out. However, we still observe a clear overestimation in the model during winter and early spring. From June and until the end of the year, observations are captured by the ensemble at this location of the eastern gyre.

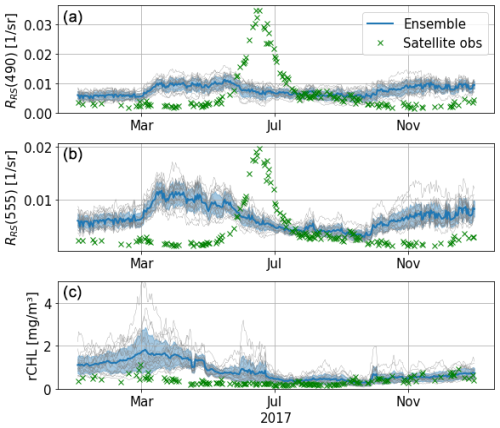
Figure 12 Time series in 2017 of R_RS at 490 (a) and 555 nm (b) and of reflectance-derived chlorophyll (c). Series are taken in the eastern gyre (43.22° N, 36.63° E). The standard deviation of the ensemble is represented by shaded blue areas, and each thin grey line corresponds to a member of the ensemble.

To better characterise the quality of the ensemble of rCHL outputs, we compute the rank histograms over the whole basin at three dates selected in winter (5 March), at the end of spring (8 June), and at the end of summer (13 September) during days with limited cloud cover for better satellite coverage over the whole basin. The observation error used to generate these rank histograms is set to 30 %, as in Popov et al. (2024). Figure 13 presents the resulting rank histograms and the associated maps. Rank maps show the spatial distribution of observation ranks. In this representation, we discard coastal and shallow areas, as these are more complex waters where the ocean colour algorithm described in Sect. 2.5 shows weak performances. Therefore, only areas of the basin with a depth greater than 150 m are considered.

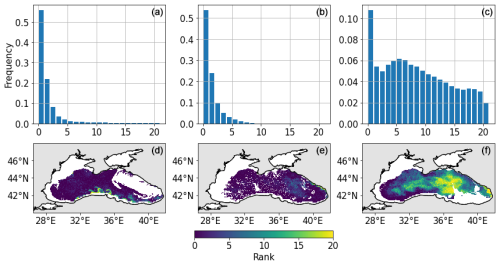
Figure 13 Rank histograms and maps for rCHL on 5 March (a, d), 8 June (b, e), and 13 September (c, f).

Figure 13 shows the spatial and temporal location of the bias in rCHL. It confirms the presence of the bias at the beginning of the year, such as on the 5 March, with few observations that are captured by the ensemble in the south of the Black Sea. In June, the bias seems to decrease with a greater number of observations that are captured by the ensemble in the eastern part of the basin. This is confirmed by the rank histogram that presents a lower peak and better-distributed data. However, data remain gathered on the left side of the rank histogram, exhibiting an overestimation of rCHL by the ensemble. The bias there seems to be mainly located at the periphery of the gyres, whereas observations close to the centre of both gyres appear to be better captured. In September, the flatter rank histogram shows that the model captures the observations in a more consistent way. We may still observe a positive bias in the southwestern parts of the basin, but central areas are consistently represented.

Finally, we proceed to a more complete comparison between the chlorophyll estimated by the satellite and the BGC-Argo with that predicted by the BAMHBI model and estimated from the reflectance rCHL. We subsample model and satellite surface chlorophyll data at the times and locations of BGC-Argo measurements. For the BGC-Argo and BAMHBI deterministic run, surface chlorophyll is defined as the average concentration over the top 10 m, which corresponds to the average water optical depth in the Black Sea (Peneva and Stips, 2005). The resulting time series are presented in Fig. 14.

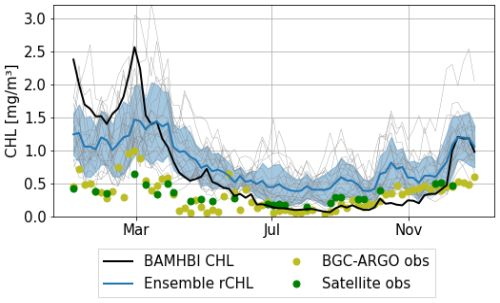
Figure 14 Surface chlorophyll estimated by BGC-Argo, satellite, the biogeochemical model (dynamically simulated by BAMHBI) and estimated from reflectance (rCHL). Comparisons are shown at times and locations of BGC-Argo measurements in 2017, along BGC-Argo float 6901866.

Despite the bias observed in rCHL in the first months of the year, surface chlorophyll derived from reflectance appears to be closer to observations than the chlorophyll computed by the biogeochemical model. In winter, both estimates of chlorophyll overestimate its concentration, but the deviation is lower with rCHL. Then, both methods provide similar estimates in spring before exhibiting contrasting results in summer and autumn with a slight overestimation for rCHL and an underestimation for BAMHBI chlorophyll. In the last months of the year, both estimates remain close to observations. Despite the use of BAMHBI chlorophyll as an optical component that governs the propagation of light and then the surface reflectance from which rCHL is derived, both signals do not seem to always follow similar patterns throughout the year, even during blooms. This highlights the role of the other constituents when biological activity is high. We also note that the in situ BGC-Argo data are rather consistent with the remote-sensed data.

5 Discussion

In this section, we first analyse the quality of the generated ensemble to represent the variability in the observations before summarising the main impacts of IOP uncertainties on the simulated radiative fields. Limitations of the approach are discussed, and the potential of using radiometric data to better constrain biogeochemical models is discussed based on our results.

5.1 Quality of the ensemble

Taking uncertainties into account in the formulation of the RT model, we produce ensemble distributions of irradiance and rCHL that provide enriched information compared to a single deterministic simulation. To test the quality of the ensemble, we assess the consistency of the simulated distribution of irradiance and reflectance-derived chlorophyll (rCHL) with remote-sensed and in situ observations. The ensemble E4 that combines all the perturbations under-disperses the distribution of the downwelling irradiance at 490 nm and PAR when compared to BGC-Argo data, with an increasing bias observed with depth.

From the analysis of surface reflectance distributions, we notice that the consistency of the ensemble-generated rCHL with satellite data varies throughout the year. The ensemble shows good agreement from the end of spring until late autumn in most parts of the basin (excluding shallow areas such as the continental shelf). The rank histograms (Fig. 13) show that the distribution of rCHL is closer to that of observations in the second half of the year. In winter and early spring, the consistency of the ensemble data with observations is lower and observations are not captured. In fact, this is the time period during which the deterministic biogeochemical model strongly overestimates chlorophyll as measured by satellites. Further calibration of the biogeochemical model or better parameterisation of its uncertainties, including from other sources that were not accounted for, is needed under those conditions to first improve the deterministic solution.

It should be noted that this analysis is essentially valid in the surface layer and the visible spectral range. Comparison to BGC-Argo profiles shows a mismatch at depth over 15 m (Fig. 9), where about 30 % of the incident irradiance is still propagating downward. There, the current parameterisation of absorption may be lacking to accurately represent irradiance profiles. The uniformity of perturbations applied on the vertical also does not allow us to account for an inaccurate depth of phytoplankton maximum, for instance, that has a significant influence on the propagation of irradiance in lower depths. The results obtained at the surface remain close to the observations and confirm the benefits of using ensemble methods to describe uncertain processes and parameters such as IOPs.

5.2 Influence of uncertainties in IOPs on radiative fields

As shown in the time series in Fig. 5, CDOM has the greatest influence on absorption in the blue end of the visible spectrum and less so at 555 nm. Phytoplankton and non-algal particles dominate scattering and backscattering with seasonal variations in their relative dominance imprinted by the bloom dynamics. With depth, all contributions increase as concentrations of phytoplankton, non-algal particles, and CDOM gradually increase. The direct irradiance stream E_d only penetrates a few metres due to the high scattering properties of the water components, as seen in Fig. 7. Below, the light field is strongly dominated by the downward diffuse stream E_s. The upward stream E_u is always of smaller magnitude and almost null below 25 m. The spread in the vertical light field is mostly due to the downward diffuse stream. As a consequence of uncertainties in absorption and (back)scattering, its spread increases with depth and below 10 m has a magnitude that can impact photosynthesis and then the amplitude of the deep chlorophyll maximum. This effect is not tested here, since the light generated by the RT model is not used to force the biogeochemical model.

As presented in Fig. 7, with a_cdom, for instance, we sometimes observe a mean effect that deviates the ensemble mean from the deterministic results. This is likely caused by model non-linearities such as the S_cdom coefficient in the formulation of a_cdom and despite the introduction of perturbations that do not create bias in the perturbed IOPs. It could also be noted that this effect could be mitigated by increasing the ensemble size, which could explain deviations in (back)scattering coefficients. In general, combining perturbations increases the spread of the ensemble compared to single perturbations as shown in Fig. 8. The non-linear character of the model, however, leads to lower spreads in E4 than the simple sum of spreads with individual perturbations. In all four ensembles, the spreads in irradiance and reflectance remain lower than the 50 % standard deviations used to perturb the IOPs.

5.3 Importance of CDOM

CDOM largely dominates the absorption at short wavelengths (lower than 500 nm) and strongly influences the propagation of the three light streams. Since CDOM is not explicitly simulated by the biogeochemical model, we assume its uncertainty to be the largest. The comparison of ensembles shows that the ensemble that combines the different sources of perturbations has similar patterns to that obtained with CDOM perturbations, only with a wider spread. The high influence of CDOM perturbation on the outputs of the RT model shows how important this component is and what variations its inaccurate estimation can generate. Perturbing CDOM has a strong influence on E_u and therefore on R_RS. Unfortunately, most biogeochemical models either strongly oversimplify or do not explicitly solve CDOM dynamics. The reasons are the lack of knowledge and data to parameterise CDOM, although its inclusion in models was proven relevant (Terzić et al., 2019). In our study, CDOM is represented as a forcing derived from BGC-Argo data. This approach has limitations, since BGC-Argo floats do not cover the shallow areas of the basin. In order to link CDOM seasonal and spatial variability to ocean physics, the CDOM forcing is scaled by seawater density, with CDOM being parameterised as an increasing function of density as described in Sect. 2.4.3. However, this procedure results in low CDOM values in low density areas that do not match the reality of coastal areas largely influenced by river discharges. Although the perturbation of CDOM absorption accounts for the uncertainty that arises from the method used to derive its forcing, the large variations that could be observed in coastal areas are likely not captured by the ensemble due to the different biogeochemical mechanisms at play. These results highlight the need for better representation of CDOM in biogeochemical models to successfully model RT in shorter wavelengths and provide a more complete assessment of the spatial and temporal variability in CDOM absorption.

5.4 Limitations of the approach

The optically active components considered here are the three phytoplankton functional groups simulated in BAMHBI, non-algal particles, and CDOM. The results of this study are influenced by the way these components are modelled in the biogeochemical model. Firstly, as described above, the forcing used to represent CDOM absorption has its limitations, especially near shallow areas. We also ignore suspended minerals that can also be optically important, limiting the accuracy of our study on the continental shelf (Stramski et al., 2016). Moreover, as in Dutkiewicz et al. (2015), the size of particles is assumed to be uniform, which is an oversimplification. The modelling of phytoplankton optics is also largely influenced by the PFTs simulated in the model, which are representative of diatoms, dinoflagellates, and small flagellates. This last group mainly integrates coccolithophores, although BAMHBI does not consider calcification. The analysis of reflectance fields clearly shows that the model misses the reflectance peaks in June associated with the coccolithophore bloom. During this period, BAMHBI simulates a bloom of small flagellates, but its optical signature is underestimated. This arises both from a flawed parameterisation of IOPs and from an underestimation of the bloom in BAMHBI. We could also investigate the inclusion of more PFTs that are relevant for the Black Sea, such as diazotrophs (Dechenne, 2023) or Synechococcus (Uysal, 2001).

There are still improvements to be made in the current formulation of the stochastic RT model based on the current variables provided by BAMHBI. Several challenges remain in calibrating the deterministic RT model properly due to the rather limited amount of optical in situ data in the Black Sea and the composition of phytoplankton. The addition of stochastic processes as described in this paper only allows us to account for model uncertainty up to a certain extent. For instance, the perturbations applied here do not influence the depth of optically active constituents. This would likely need to be perturbed, too, if we seek to explain discrepancies with observations. With the current method, a phytoplankton bloom that is too deep in the model will not see its depth perturbed. In this study, we also chose to only perturb the RT model with no feedback towards the hydrodynamical and biogeochemical models (i.e. the modified light field is not the one used in the coupled model). By considering it and other sources of uncertainty, such as surface radiation, that affect biological processes, we may be able to capture some of the observations that remain outside of the ensemble E4 spread and provide a more complete description of the sensitivity of the RT model.

5.5 Radiometric observations to constrain coupled physical–biogeochemical models

The analysis performed with this RT model also paves the way to use radiometric quantities for calibration, validation, and assimilation in a physical–biogeochemical model in the Black Sea. Comparison to reflectance data still shows high biases that would require prior corrections, but the definition of reflectance ratios, or associated variables such as reflectance-derived chlorophyll (rCHL), shows promising results. Band ratios remove some of the uncertainties associated with corrections.

This study also provides a better understanding of the strengths and limitations of ocean colour algorithms. While those algorithms aim at estimating surface chlorophyll concentrations, the ocean colour products fundamentally remain optical quantities that are compared to biogeochemical variables in models. Based on colour, the use of the blue/green band ratio algorithm does not only “see” chlorophyll, but also other types of in-water material. As such, reflectance-derived chlorophyll proves itself to be closer to the satellite-retrieved chlorophyll than the chlorophyll computed in BAMHBI. Currently, ocean colour products are being assimilated in biogeochemical models that rarely resolve reflectance. This study hints at the opportunities provided by working directly with ocean colour derived from reflectances, which accounts for more than just chlorophyll and therefore may be closer to the true meaning of such estimates. It also suggests that the assimilation of satellite surface reflectances has the potential to correct the IOPs and ultimately improve the simulation of irradiance streams and reflectances.

6 Conclusion and perspectives

The modelling of light in the coupled physical–biogeochemical NEMO–BAMHBI framework for the Black Sea is enriched by adding a spectral radiative transfer model that explicitly solves the upward and downward light field at high spectral resolution. This offers a direct connection between model variables and remote-sensed reflectance data, without relying on inversion algorithms. Four optically important water constituents are considered: pure water, phytoplankton, non-algal particles, and CDOM. We aim at assessing the relative contribution of each constituent while accounting for the uncertainties in their IOPs using ensemble simulations. CDOM clearly dominates absorption at short wavelengths throughout the year, while phytoplankton and non-algal particles dominate the (back)scattering, having the largest influence during and following algal blooms.

As it is not explicitly simulated in BAMHBI, we assume higher uncertainty on CDOM absorption than phytoplankton and non-algal particles. The ensembles show that the perturbation of CDOM has a dominant influence on the radiative fields. Its major role highlights the need for a better representation of this component in our biogeochemical model, which will require high-quality data in the Black Sea. Such data are currently practically non-existent in the central areas and shelf zone, thus hampering modelling capabilities.

The quality of the generated ensembles is assessed by comparing the ensemble distributions of irradiances, reflectances, and reflectance-derived chlorophyll (rCHL) with observations. We find that the distributions generated by the ensemble do not capture all the spatial and temporal variability in the measurements performed in the Black Sea. This is particularly the case in coastal areas and during winter and important blooms. This suggests that the introduction of uncertainties in IOPs is not enough to fully account for uncertainties in the RT model. Firstly, vertical perturbations that could influence the position of the deep chlorophyll maximum are missing and could be added to simulate uncertainties more realistically. Other sources need to be considered, such as forcings or parameterisation of the hydrodynamics and biogeochemistry. Their influence has been studied in other frameworks, such as in Garnier et al. (2016).

Comparison to remote-sensed data shows promising agreement on reflectance ratios, even though the reflectances themselves are less accurately modelled. Uncertainties on the atmospheric correction or interface effects (e.g. BRDF) are indeed removed using reflectance ratios between close wavebands. We also show that rCHL provides estimates of chlorophyll that are closer to remote-sensed data than the chlorophyll modelled in BAMHBI based on biological mechanisms. Using reflectances could then allow us to better characterise errors in the model.

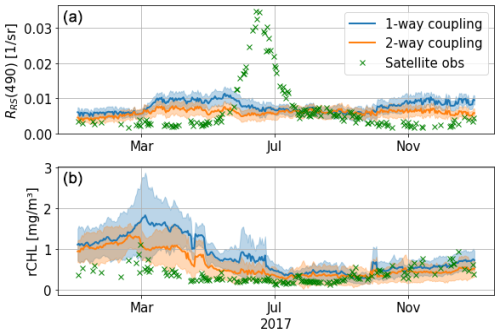
Figure 15 Time series of R_RS(490) (a) and rCHL (b) at 43.22° N, 36.63° E with the one-way (E4, in blue) and two-way (in orange) configurations.

Finally, in this paper, the coupling between the physical–biogeochemical model and the RT model is one-way. This means that the chlorophyll and non-algal particles simulated by BAMHBI are used to compute the IOPs in the RT model, but the light field produced by the RT model is not used to compute temperature and photosynthetic active radiation. Rather, a simple one-stream optical model differentiating three wavelengths is used to force the physical–biogeochemical model. We test a two-way configuration that, despite biases in the simulated radiative fields, shows promising results. The simulated time series of R_RS(490) and rCHL agree better with satellite data (Fig. 15). We find that, in this two-way configuration, the irradiance feedback towards the coupled framework does not disrupt the simulation of reflectance, although it decreases R_RS(490) to bring it closer to satellite observations. For rCHL, however, this first outlook shows that we are able to better compare remote-sensed data with this two-way configuration, especially in the first months of the year. A two-way configuration for the coupled framework NEMO–BAMHBI RT model will possibly pave the way towards the explicit assimilation of multispectral satellite reflectance in coupled physical–biogeochemical ocean models.

Appendix A: Generation of a_cdom forcing

CDOM is a major contributor to absorption in seawater, but it is not explicitly simulated in the NEMO–BAMHBI framework. Therefore, we cannot use the same approach as for phytoplankton and non-algal particles. We choose here to derive a forcing for a_cdom from the in situ BGC-Argo data. A collection of 625 profiles from floats 6901866 and 6903240 provides measurements of irradiance in three wavebands (E_Argo at 380, 412, and 490 nm), chlorophyll concentration (chl_Argo), backscattering coefficient at 700 nm (bbp_700,Argo), and CDOM (cdom_Argo). Some profiles are discarded depending on the quality control flag for variables of interest. Float 6901866 has measurements between June 2015 and June 2019 in the entire basin with limited coverage of the central parts. Float 6903240 has measurements between April 2018 and July 2022, mostly around the western gyre. Both floats do not cover the continental shelf, where the dynamics of CDOM are more complex.

In the RT model, we parameterise the optical properties of phytoplankton and non-algal particles from biogeochemical variables of BAMHBI. We use the same parameterisation to derive a_cdom. We choose a reference wavelength λ_ref=412 nm in the range of high CDOM absorption and with irradiance profiles measured by BGC-Argo floats to derive a reference a_cdom profile. We use the RT model to simulate the same profiles that are measured. Optical properties of water are known in the same way as described in Sect. 2.4.1. Optical properties of phytoplankton are derived using chlorophyll profiles from BGC-Argo data instead of BAMHBI variables. However, we cannot discriminate between PFTs and therefore assume that chlorophyll is equally distributed between the three PFTs solved in BAMHBI. The optical properties of non-algal particles are derived from profiles of particulate backscattering coefficient at 700 nm bbp_700,Argo. We assume this coefficient to be the sum of contributions from phytoplankton and non-algal particles to derive a POC concentration that is used to apply our parameterisation:

$$\begin{array}{}\text{(A1)}& {\mathrm{POC}}_{\mathrm{Argo}}={\displaystyle \frac{{\mathrm{bbp}}_{\mathrm{700},\mathrm{Argo}}-b_{\mathrm{b},\mathrm{phy}}\left(\mathrm{700}\right)}{b_{\mathrm{b},\mathrm{prt}}^{\mathrm{0}}\left(\mathrm{700}\right)}}.\end{array}$$

We assume that the optical properties of CDOM on a water column are a linear function of CDOM concentration; i.e. on a water column, all CDOM has the same absorbing power. We want a_cdom profiles to have the same shape as CDOM profiles measured by BGC-Argo float. We therefore assume

$$\begin{array}{}\text{(A2)}& a_{\mathrm{cdom}}=k_{\mathrm{cdom}}{\mathrm{cdom}}_{\mathrm{Argo}},\end{array}$$

where k_cdom is unknown. Starting with an initial value of k=1 m⁻¹, we then compute the downwelling irradiance stream E_loop(λ_ref) for all profiles and compare them with the BGC-Argo irradiance profiles. For each profile, the parameter k is then updated to minimise the difference between the E_loop(λ_ref) and E_Argo(λ_ref) profiles in the top 30 m of the ocean (21 model layers), normalised by their surface value for consistency in assessing the influence of IOPs. This simple optimisation problem is written as follows:

$$\begin{array}{}\text{(A3)}& min\sum _{k=\mathrm{1}}^{\mathrm{21}}({\displaystyle \frac{E_{\mathrm{loop}}\left({\mathit{\lambda }}_{\mathrm{ref}}\right)}{E_{\mathrm{loop}}({\mathit{\lambda }}_{\mathrm{ref}}{)}^{\mathrm{surf}}}}-{\displaystyle \frac{E_{\mathrm{Argo}}\left({\mathit{\lambda }}_{\mathrm{ref}}\right)}{E_{\mathrm{Argo}}({\mathit{\lambda }}_{\mathrm{ref}}{)}^{\mathrm{surf}}}}).\end{array}$$

We use a deviation threshold of 2 % to accept a value of k for a given profile. Using this method for each profile of our collection, we get a new collection of k_Argo and then of a_cdom(λ_ref) profiles. We now store values of a_cdom(λ_ref) according to time and seawater density to link each time and location of the basin to a value of a_cdom(412). We interpolate this dataset to generate annual cycles for each density scale to smooth out the forcing. Figure A1 shows the resulting forcing for a_cdom(λ_ref) for selected seawater densities.

Figure A1 a_cdom forcing scaled in density for λ_ref=412 nm. This forcing was generated using a collection of BGC-Argo profiles in the deeper areas of the Black Sea.

Appendix B: Model performance in the visible spectral range

In this paper, we focus on the wavebands that are used to derive rCHL, centred on 490 and 555 nm, respectively, in the blue and the green. More generally, we computed irradiance and sea surface reflectance in the six wavebands that are found in the multi-satellite reflectance product for the Black Sea made available by the Copernicus Marine Service, centred on 412, 443, 490, 510, 555, and 670 nm. Figure B1 shows the average spectral sea surface reflectance in the eastern gyre of the Black Sea over 2017. As seen previously in the 490 and 555 nm centred wavebands, the model tends to overestimate sea surface reflectance. The model reflectance is consistent with remote-sensed data up to around 475 nm, after which the bias gradually increases for longer wavelengths. The deviation then decreases at the near-infrared end of the spectral range.

Figure B1 R_RS average spectra in the eastern gyre over 2017. Uncertainties in model and remote-sensed data are represented in shaded areas.