Field heterogeneity of soil texture controls leaf water potential spatial distribution predicted from UAS-based vegetation indices in non-irrigated vineyards

Grapevine water status exhibits substantial variability even within a single vineyard. Understanding how edaphic, topographic, and climatic conditions impact grapevine water status heterogeneity at the field scale, in non-irrigated vineyards, is essential for winemakers as it significantly influences wine quality. This study aimed to quantify the spatial distribution of grapevine leaf water potential (Ψ_leaf) within vineyards and to assess the influence of soil property heterogeneity, topography, and climatic conditions on intra-field variability in two non-irrigated vineyards during two viticultural seasons. By combining multilinear vegetation indices from very-high-spatial-resolution multispectral, thermal, and lidar imageries collected with uncrewed aerial systems (UASs), we efficiently and robustly captured the spatial distribution of Ψ_leaf across both vineyards on different dates. Our results demonstrated that in non-irrigated vineyards, the spatial distribution of Ψ_leaf was mainly governed by the within-vineyard soil hydraulic conductivity heterogeneity (R² up to 0.81) and was particularly marked when the evaporative demand and the soil water deficit increased, since the range of Ψ_leaf was greater, up to 0.73 MPa, in these conditions. However, topographic attributes (elevation and slope) were less related to grapevine Ψ_leaf variability. These findings show that the soil property within-field spatial distribution and climatic conditions are the primary factors governing Ψ_leaf heterogeneity observed in non-irrigated vineyards, and their effects are concomitant.

1 Introduction

Accurately quantifying grapevine water status is crucial for winemakers as it significantly impacts wine quality (Dry and Loveys, 1999; van Leeuwen et al., 2009). Detailed spatial information on grapevine water status can be particularly useful for providing guidelines on viticultural management to optimize grape production. This is especially important in the context of climate change, which poses crucial challenges for freshwater use in viticulture (Gambetta et al., 2020). Many authors have demonstrated that grapevine water status exhibits substantial variability even within a single field, particularly when significant water restriction is found (Acevedo-Opazo et al., 2010; Brillante et al., 2017a; Tisseyre et al., 2005). Measuring leaf and/or stem water potential is an effective method to assess grapevine water status (Choné et al., 2001) but accurate measurements of leaf and stem water potentials are usually achieved on single plants using a Scholander pressure bomb (Scholander et al., 1965) or with psychrometers. Several authors have reported a high magnitude of variation in leaf water potential over the viticultural season (e.g., 1.6 MPa in Ojeda et al., 2005) and at the within-field level (e.g., 1.2 MPa in Ojeda et al., 2005; 0.7 MPa in Brillante et al., 2017a). Yet, these methods are time-consuming and labor-intensive and are therefore not effective at instantaneously capturing the within-field heterogeneity of grapevine water status (Romero et al., 2018), particularly under heterogeneous soil and microclimatic conditions generally observed in a vineyard.

Remote sensing technological advances give good opportunities for time- and cost-efficient detection of the spatial and temporal variability of plant water status (Acevedo-Opazo et al., 2008). Particularly, uncrewed aerial systems (UASs) are useful tools to assist precision viticulture thanks to high-spatial-resolution imagery, allowing differentiation of row and inter-row information. UASs can transport different sensors to measure and estimate plant traits, e.g., canopy area, biomass, leaf pigment concentration, or grapevine water status, through vegetation indices (VIs) (Baluja et al., 2012; Poblete et al., 2017; Romero et al., 2018; Serrano et al., 2010; Zarco-Tejada et al., 2013). Most of the sensors used in precision viticulture are multispectral sensors, allowing the calculation of VIs based on the visible (red, green, blue), red-edge, and near-infrared (NIR) reflectance of plants (Ferro and Catania, 2023). Several studies found low to moderate correlations between multispectral VIs and grapevine leaf water potential, with maximum R² ranging between 0.4 and 0.5 (Baluja et al., 2012; Espinoza et al., 2017; Romero et al., 2018; Tang et al., 2022). VIs based on NIR and red-edge bands are better correlated with grapevine water potential as they are greatly affected by leaf structure and chlorophyll content, both being considered indicators of grapevine water status (Penuelas et al., 1997; Rapaport et al., 2015). Recently, machine learning models (i.e., random forest) have been applied to combine multispectral information from grapevines and predict grapevine water potential. These models performed better (R² around 0.85) than using single multispectral VIs (Poblete et al., 2017; Romero et al., 2018); however, there was a significant loss of predictive power between calibration and validation (R² decreased and RMSE increased significantly) (Tang et al., 2022). Nevertheless, the combination of several VIs to predict grapevine water status is more efficient since each VI can bring complementary information (Xue and Su, 2017).

In dry conditions, grapevines close stomata, limiting transpiration but preventing them from reaching excessively negative water potentials that could lead to xylem cavitation and death (Gambetta et al., 2020). Once stomata are closed and transpiration is restrained, leaf temperature increases (Costa et al., 2010). Canopy temperature can therefore potentially be used to develop an index giving information on stomatal conductance and leaf water potential (Jones et al., 2002). Thermal VIs such as the crop water stress index (Idso et al., 1981) have shown moderate (but better than multispectral VIs) correlations with grapevine water potential, with R² of 0.55 (Romero et al., 2018). Some studies even showed a significant correlation, with R² around 0.80, between leaf water potential and the crop water stress index in Mediterranean vineyards (Bellvert et al., 2014; Möller et al., 2007). Thermal sensors are not as used as multispectral sensors in precision viticulture (Ferro and Catania, 2023). These sensors are generally more expensive and subjected to less straightforward calibration (Berni et al., 2009). Thermal data processing is less simple than multispectral data but complementary information obtained by multispectral and thermal sensors could improve the ability to remotely monitor grapevine leaf water potential (Tang et al., 2022).

The use of laser scanning sensors (light detection and ranging – lidar) for estimating biophysical parameters of vineyard canopy is still relatively uncommon compared to other available sensors (Ferro and Catania, 2023). Point clouds obtained from lidar sensors are suitable for detecting structural features of grapevine such as canopy height, canopy width, or even leaf area index (Bates et al., 2021; Comba et al., 2018). These structural features reflect the result of cumulative water potential of grapevine and could therefore contain information on grapevine water status (Baluja et al., 2012). As a result, the combination of multispectral, thermal, and lidar (structural) data obtained from different sensors on board uncrewed aerial vehicles could potentially be used to improve the mapping of grapevine leaf water potential within a vineyard.

In addition to the value of remotely monitoring grapevine leaf water potential in an accurate way through UASs, it is also interesting to study which factors spatially determine leaf water potential at the vineyard scale. Several studies have tried to assess the influence of irrigation management on grapevine water status with UAS platforms (De Bei et al., 2011; Bellvert et al., 2012, 2015; Espinoza et al., 2017; Möller et al., 2007). However, most of these studies were conducted on vineyards with homogeneous edaphic conditions but different irrigation treatments. It remains unclear how robust these water status mapping approaches are when applied across vineyards with varying edaphic and meteorological conditions (Helman et al., 2018). Few studies have evaluated how spatialized information on grapevine water status gives us information about how environmental heterogeneity within a vineyard affects the distribution of grapevine water potential (Brillante et al., 2017a). It is known that the soil and the climate mainly affect grapevine water potential, and their effects are concomitant (Van Leeuwen et al., 2004). The soil, through its texture and its ability to retain and conduct water, determines the water supply to the root system. Soil depth, texture, structure, and percentage of coarse elements also affect the growth of the root system and therefore the available water for the plant (Van Leeuwen et al., 2018). Grapevine water status is also affected by the vapor pressure deficit (VPD, corresponding to the atmospheric evaporative demand), which depends on temperature and air humidity (Soar et al., 2006). Grapevines should therefore find an equilibrium between water supply in the soil and water demand in the atmosphere by regulating their water potential and stomatal conductance to maintain gas exchanges for photosynthesis, while preventing excessive negative water potential leading to xylem cavitation (Gambetta et al., 2020). Topographic attributes, such as slope and elevation, can also impact grapevine performance (Bramley et al., 2011; Karn et al., 2024). On the one hand, this influence is indirect since topography controls the redistribution of soil particles within the vineyard and therefore creates soil texture spatial heterogeneity (Fraga et al., 2014). On the other hand, topography can directly influence grapevine water status through its impact on water drainage and runoff, sunlight exposure, and temperature variations within the vineyard (Brillante et al., 2017a; Karn et al., 2024). These effects foster microenvironments within a vineyard that could affect grapevine water status (Rabia et al., 2022).

In this study, we aimed to quantify the spatial distribution of grapevine leaf water potential within a vineyard and to assess the impact of edaphic, topographic, and climatic conditions on intra-field heterogeneity. We evaluated the capabilities of UASs equipped with multispectral, thermal, and lidar sensors to monitor grapevine leaf water potential on two non-irrigated vineyards during two viticultural seasons.

2 Methodology

2.1 Site descriptions

This study was conducted on two non-irrigated Belgian vineyards, grassed in the inter-rows, namely the Château de Bousval vineyard and the Domaine W vineyard (Fig. 1a). At the Château de Bousval vineyard (Genappe, Belgium; 50°36^′45.0^′′ N, 4°31^′19.6^′′ E), we focused on an east-facing plot of Chardonnay grafted on 3309C rootstock, planted in 2014 with vertical shoot positioning, 1.6 m inter-row, and 0.8 m inter-cep. The field rises between 110 and 125 m above sea level (Fig. 1b), and the average slope is 6 %. At the Domaine W vineyard (Tubize, Belgium; 50°41^′19.4^′′ N, 4°09^′36.9^′′ E), two Chardonnay plain fields grafted on 101-14Mgt rootstock were selected for this study, rising between 52 and 54 m above sea level (Fig. 1g), with rows oriented north–south. The grapevines were planted in 2016 with vertical shoot positioning, 2.2 m inter-row, and 1 m inter-cep. These vineyards were selected due to their similar pedogenesis but contrasting layering. In the Château de Bousval vineyard, the soil is made of a loamy top layer overlying a sandy subsoil, but the depth of the interface between these two layers changes within the plot, reaching more than 3 m at the lowermost side (east side) of the field, due to an accumulation of loamy colluviums. At the upper part (west side) of the field, the loamy layer is around 0.4 m depth. We know, on the whole field, the depth of the interface between the loam and the sand (Fig. 1c). Moreover, in this vineyard, we also know that grapevine roots reach a depth of at least 2.5 m on the whole field (Delval et al., 2024a). In the Domaine W vineyard, the soil heterogeneity is less marked in terms of soil texture. The northwestern part of the field is defined by a silty loam soil on the first horizons of the profile and silty clay loam soil thereafter. The southeastern part is defined by a silty loam soil on the whole profile (Fig. 1h). These differences in terms of soil texture have only been observed in a single location in each subplot. Therefore, unlike Bousval, the depth of the interface between silty loam soil and silty clay loam soil is not accurately known on the whole field. A stream runs adjacent to the southeast parcel, raising the water table in this area within the reach of the roots. Root depth on this vineyard is at least 2 m everywhere in the field (Delval et al., 2024b).

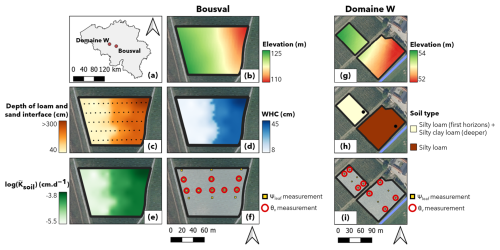
Figure 1 (a) Location of the vineyards in Belgium. (b–f) Topographic attributes, edaphic properties, and location of measurements in the Château de Bousval vineyard: (b) elevation, (c) kriged map of the depth of the interface between the loamy soil and the sandy subsoil (the black points are locations of soil samples used to determine the depth of the interface in situ and used for kriging), (d) water-holding capacity (WHC) on 2.5 m depth (Eq. 6), (e) averaged soil hydraulic conductivity (${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}})$ at 2.5 m depth (Eq. 7), and (f) locations of the leaf water potential (Ψ_{leaf_meas}) and volumetric water content (θ_v) profile measurements. (g–i) Topographic attributes, edaphic properties, and location of measurements in the Domaine W vineyard: (g) elevation, (h) soil type (the black points are locations of soil samples to determine soil type in situ), and (i) locations of the leaf water potential (Ψ_{leaf_meas}) and volumetric water content (θ_v) profile measurements. In (g), (h), and (i), the blue line is a stream adjacent to the southeastern plot.

2.2 Meteorological conditions

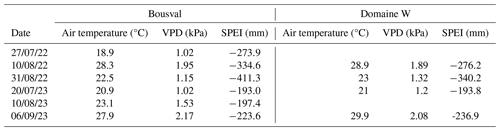
Both vineyards are equipped with weather stations providing hourly meteorological data. The meteorological conditions during each flight are provided in Table 1. The atmospheric conditions and the evaporative demand are characterized with the vapor pressure deficit (VPD). The daily water deficit, which refers to the standardized precipitation evapotranspiration index (SPEI – Vicente-Serrano et al., 2010), is calculated as follows:

$$\begin{array}{}\text{(1)}& \mathrm{SPEI}=\sum _i\left(P_i-{\mathrm{ET}}_{{\mathrm{0}}_i}\right),\end{array}$$

with i=1 corresponding to 1 April of the respective year (budburst of grapevines), P_i the daily precipitation, and ET_0i the daily reference evapotranspiration. The more negative the SPEI, the greater the water deficit. ET₀ is calculated from the Food and Agriculture Organization (FAO) Penman–Monteith method (Allen et al., 1998).

Table 1 Meteorological conditions during each flight campaign.

Despite relatively similar air temperatures and VPDs during the 2022 and 2023 flights, 2022 was a drier year than 2023. The SPEI for any date in 2022 is significantly more negative than that for any date in 2023 in both vineyards (Table 1), indicating drier conditions in 2022 than in 2023.

2.3 Data acquisition and processing

Uncrewed aircraft system (UAS) data acquisition took place during the vine growth period in 2022 and 2023. Three flight campaigns were carried out in 2022 and three in 2023, for a total of six flight campaigns. Data were acquired before the veraison (27 July 2022 and 20 July 2023), at the start of the veraison (10 August 2022 and 10 August 2023), and just before harvest (31 August 2022 and 6 September 2023). Flights started around 12:00 (UTC +2) at Bousval and around 13:30 (UTC +2) at Domaine W. Three sensors were used in this study, a Micasense RedEdge-M multispectral sensor (Micasense Inc., Seattle, WA, USA), an FLIR Vue Pro R thermal camera (FLIR Systems, Wilsonville, OR, USA), and a YellowScan Surveyor lidar (YellowScan, Saint-Clément-De-Rivière, France), mounted on a DJI Matrice 600 (SZ DJI Technology Co Ltd., Shenzen, China). The Micasense RedEdge-M is a five-narrowband multispectral camera, capturing blue (465–485 nm), green (550–570 nm), red (663–673 nm), red-edge (712–722 nm), and NIR (820–860 nm) wavelengths of the electromagnetic spectrum. Just before and after each flight, the Micasense RedEdge-M sensor was calibrated thanks to a reflectance panel to ensure accurate and consistent reflectance measurements, enabling reliable comparisons of data captured under varying light conditions and at different times. Images were acquired to ensure approximately 90 % forward and lateral overlap. To process the multispectral imagery, orthomosaics were first created for each band of the sensor using Pix4D (Pix4D, Lausanne, Switzerland). Ground control points (GCPs) were used for georeferencing.

The FLIR Vue Pro R is a radiometric thermal sensor that captured longwave infrared radiation in the 7.5–13.5 µm range. This sensor needs radiometric calibration parameters such as emissivity of the canopy, air temperature, and humidity to capture accurately the surface temperature. Thermal imagery was also processed using Pix4D. The same GCPs as for multispectral imagery were used, enabling georeferencing consistent with multispectral data.

The lidar system, operating with a wavelength of 903 nm, is composed of a Velodyne lidar puck, onboard computer, inertial measuring units (IMU), and Global Navigation Satellite System (GNSS) receiver. Ranging data are provided by the lidar puck. The IMU measured the variations in attitude and orientation, and the GNSS provided positioning. To process the lidar data, YellowScan's CloudStation software was used to align the flight strips for georeferencing and to apply corrections through GNSS offset (lever arms), sensor angle (boresight), and GNSS post-processing with precise position techniques (Bates et al., 2021).

Multispectral and thermal sensors were mounted on the same DJI Matrice 600 and data were collected at the exact same time. The lidar data were collected directly after the multispectral and thermal data. Multispectral and thermal flights were conducted at an altitude of 100 m above ground level and at a flight speed of 6 m s⁻¹, yielding flight durations of approximately 7 min and resulting in a native pixel resolution of 7 cm for multispectral and thermal data. For the lidar flight, the UAS maintained an altitude of 50 m above the ground, with a ground speed of 5 m s⁻¹, giving a spatial resolution of 16 cm for lidar data. Due to technical issues, there are no thermal data at Bousval on 27 July and 31 August 2022, no multispectral data at Domaine W on 10 August 2022, and no multispectral, thermal, and lidar data at Domaine W on 27 July 2022 and 10 August 2023 (Table 2).

Table 2 Availability of the UAS data during the six flight campaigns in the two vineyards.

At the same time as collecting UAS data, we measured grapevine leaf water potential (Ψ_{leaf_meas}) on various 2×2 m² zones homogeneously distributed across the fields using a Scholander pressure bomb (670 Pressure Chamber, PMS Instrument Company). The Ψ_{leaf_meas} was measured on 14 2×2 m² zones at Bousval (Fig. 1f) and on 12 2×2 m² zones at Domaine W (Fig. 1i). For each sampled grapevine, Ψ_{leaf_meas} values were recorded for three to five mature leaves, covered by an aluminum zip bag 45 min before the measurement. In addition, the soil water content profile to a depth of 105 cm (every 15 cm) was also measured in eight measurement zones in each vineyard (Fig. 1f and i) before each flight with a TRIME-FM3 time domain reflectometry combined with an access T3 tube (IMKO GmbH, Ettlingen, Germany).

2.4 Pure grapevine pixel extraction

The fine spatial resolution of the UAS data makes it possible to distinguish rows and inter-rows. We used the k-means algorithm to generate a binary mask that distinguishes pure grapevine canopy pixels from inter-row soil and grass pixels. The k-means algorithm determined the optimal thresholding value to maximize the between-class variance and minimize the within-class variance (MacQueen, 1967). The k-means algorithm has already shown good ability to extract pure vine pixels based on multispectral vegetation indices (Cinat et al., 2019). This segmentation enables the computation of vegetation indices on grapevines only and facilitates the derivation of a Ψ_leaf prediction model specifically focused on the grapevine itself. The workflow of the segmentation method used in this study is illustrated in Fig. 2. The algorithm was performed using RStudio (RStudio Team, 2022). The method consists of six steps and was performed for each date, generating a mask per date.

1. The initial step was to use the canopy height, derived from the lidar data, to get a first raw distinction between rows and inter-rows. We derived the height of the canopy (canopy height model, CHM) thanks to the difference between the digital surface model (DSM) and the digital terrain model (DTM): CHM = DSM − DTM. We considered grapevine rows to be represented by every pixel greater than 1 m. This step allowed for the removal of a large part of pixels representing inter-rows.

2. Due to a coarser spatial resolution of lidar data, we used multispectral data to get a finer separation and be sure that we extracted only pure grapevine pixels. We identified the most relevant spectral bands capable of distinguishing between vineyard rows and inter-row vegetation to choose a proper vegetation index for the mask creation. The modified soil adjusted vegetation index (MSAVI), suggested by Qi et al. (1994), was selected due to its incorporation of the red and NIR bands known for their sensitivity to vegetation density, as well as its ability to minimize soil brightness influences in sparse crops (Binte Mostafiz et al., 2021). We applied the mask obtained in step 1 to the MSAVI raster.

3. We subdivided the new MSAVI raster into smaller areas (rectangles of 10 m ×1.5 m). By reducing the area in which the k-means algorithm was applied, the non-vine pixels in that area exhibited greater similarity, allowing the algorithm to better discriminate between grapevine and grass pixels.

4. The k-means algorithm was then applied in each rectangle. The number of clusters was set to three to distinguish among the three classes identifiable within the rectangles: pure grapevine pixels, mixed pixels, and pure grass pixels.

5. Following the algorithm execution, only the class with the highest mean value of MSAVI was retained, aiming to automatically extract grapevine class. This class was expected to have the highest MSAVI value since it represents the class with the highest biomass density.

6. Finally, the outputs of the algorithm were combined to create a unified shapefile, representing a binary mask that isolates pure grapevine canopy pixels across the field. This mask was subsequently utilized to filter out non-vine or mixed pixels (spatial resolution of 7 cm ×7 cm) from UAS data, and only the remaining grapevine pixels were used for further analysis.

Figure 2 Process of segmenting grapevine pixels from inter-row pixels to generate a pure grapevine mask. (1) First raw distinction between rows (>1 m) and inter-rows (<1 m) using the canopy height derived from the lidar data. (2) Application of the raw grapevine mask obtained in (1) to the modified soil adjusted vegetation index (MSAVI) raster. (3) Subdivision of the new MSAVI raster obtained in (2) into smaller areas (rectangles of 10 m ×1.5 m). (4) Application of k-means algorithm in each rectangle. The number of clusters was set to three (pure grapevine, mixed, pure grass). (5) Selection of pure grapevine pixels based on the clustering obtained with the k-means algorithm. (6) Creation of a unique mask to extract pure grapevine pixels (spatial resolution of 7 cm ×7 cm) from each raster of vegetation indices.

2.5 Generation and extraction of UAS-based variables

We calculated multiple widely used multispectral vegetation indices (VIs), exploiting different band combinations. The multispectral VIs used in this study were obtained from the review of Giovos et al. (2021). A total of 43 multispectral VIs were retained in this study, as they constitute those most frequently used to monitor and estimate vine water stress and delineate management zones in viticulture. We also exploited the specific red, blue, green, NIR, and red-edge bands alone. The complete list of all the indices and how they are calculated can be found in Table S1 in the Supplement.

In addition, we calculated thermal VIs, namely the canopy surface temperature (CST, °C) and the difference between CST and air temperature (d$T=\mathrm{CST}-T_{\mathrm{a}}$, °C). The crop water stress index (CWSI) was also computed using the simplified formula suggested by Jones (2013):

$$\begin{array}{}\text{(2)}& \mathrm{CWSI}={\displaystyle \frac{\mathrm{CST}-T_{\mathrm{wet}}}{T_{\mathrm{dry}}-T_{\mathrm{wet}}}}.\end{array}$$

Two different CWSIs were derived.

• a.

  CSWIa: T_dry and T_wet were measured during the UAS surveys by a meteorological station.

• b.

  CWSIb: T_dry and T_wet were derived from the pure canopy pixels and were respectively considered to be CST_max and CST_min.

Structural features of the grapevines were derived from the lidar data. We derived the height of the canopy (CH) thanks to the difference between the DSM and the DTM as explained before. We also derived the leaf area index (LAI) with the lidar method developed by Bates et al. (2021). From the lidar data, we also derived the elevation and the slopes of the different vineyards, but these parameters were not used to predict Ψ_leaf since they do not vary over time. However, they were used to interpret the spatial distribution of Ψ_leaf.

After applying the binary mask to isolate pure vine pixels on each index map described above, we extracted the averages of the index values within the 2×2 m² zones defined before for the grapevine leaf water potential measurements (Fig. 1f and i) in order to predict leaf water potential.

2.6 Leaf water potential prediction

As a preliminary step, we examined the univariable relationships between in situ Ψ_{leaf_meas} and the different VIs, based on Pearson's coefficient (Pearson's ρ), to account for linear relations, and based on Spearman's coefficient (Spearman's ρ), to account for monotonic relations. Person's ρ quantifies the strength and direction of a linear relationship, while Spearman's ρ is valuable for detecting and quantifying associations when nonlinear relationships are assumed. We therefore compared Pearson's ρ and Spearman's ρ to evaluate if the relation between Ψ_{leaf_meas} and a VI was linear or not. These analyses enable us to assess the capability of simple remotely sensed VIs to evaluate Ψ_leaf. All in situ measurement data points (n=132; 6×14 at Bousval and 4×12 at Domaine W) across all vineyards and days were used for a comprehensive analysis.

We then used the stepwise regression method to develop a multiple linear regression model to predict leaf water potentials (Ψ_{leaf_pred}) based on a multiple linear combination of the VIs presented previously (Eq. 3). We also predicted an uncertainty, quantified by the confidence interval of 95 % on Ψ_{leaf_pred} (IC${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}}$). Stepwise regression is a step-by-step iterative construction of a linear regression model that involves the selection of independent variables to be used in a final model (Wilkinson, 1979). Stepwise regression can be achieved either by trying out one independent variable at a time and including it in the regression model if it is statistically significant (forward selection) or by including all independent variables in the model and eliminating those that are not statistically significant (backward elimination). A combination of both methods is also possible and was used in this study (bidirectional elimination). This method used the Akaike information criterion to add or remove VIs from the multiple linear regression model, minimizing the number of predictor variables but keeping a high predictive power (Akaike, 1974). Stepwise regression models were implemented in RStudio (RStudio Team, 2022) using the stats package.

$$\begin{array}{}\text{(3)}& {\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}}={\mathit{\beta }}_{\mathrm{1}}\times {\mathrm{VI}}_{\mathrm{1}}+{\mathit{\beta }}_{\mathrm{2}}\times {\mathrm{VI}}_{\mathrm{2}}+\mathrm{\cdots }+{\mathit{\beta }}_n\times {\mathrm{VI}}_n+\mathit{\alpha },\end{array}$$

with β_i the regression weights (or beta coefficients) and α the intercept. β_i can be interpreted as the average effect on the predicted variable (Ψ_{leaf_pred}) of a one unit increase in VI_i, holding all other predictors fixed. We applied this method to different combinations of VIs and single bands to predict Ψ_leaf. We tested a total of seven data combinations: (1) multispectral only (M), (2) thermal only (T), (3) lidar only (L), (4) multispectral and thermal (M+T), (5) multispectral and lidar (M+L), (6) thermal and lidar (T+L), and (7) multispectral, thermal, and lidar (M+T+L).

For each date, we randomly selected 70 % of the data to train the different models and 30 % to validate them. The data used for calibration and validation were the same for each model. We evaluated the performance of the models thanks to the coefficient of determination (R²) and the root mean squared error (RMSE). The model with the best performance was then employed to predict the Ψ_leaf over the fields for each flight.

We then verified the reliability of the model. To determine that there is no redundancy and similar information in the multiple linear regression model, we used the variance inflation factor (VIF). The VIF assesses if a predictor variable is collinear with the other predictor variables (multicollinearity) in the multiple linear regression model, which could degrade the precision of an estimate and reduce the reliability and the robustness of the model (Allen, 1997). VIF less than 5 indicates a low correlation between a predictor variable and the other ones, VIF between 5 and 10 indicates a moderate correlation, and VIF greater than 10 indicates a high correlation (James et al., 2021). VIF was computed using the car package in RStudio. We also used partial regression plots to show the effect of a predictor variable on the prediction of Ψ_leaf, after considering the effects of the other predictor variables. If the slope of the linear regression in a partial regression plot is significantly different from 0 (p value <0.001), then it justifies the presence of a predictor variable in the multiple linear model (Moya-Laraño and Corcobado, 2008). The correlation (R²) of the linear model in a partial regression plot allows quantifying the unique relationship between the predicted variable (Ψ_leaf) and a predictor variable (VI) while controlling the effects of the other variables. The higher the R², the greater the influence of the predictive factor (VI) on the predicted variable (Ψ_leaf) (Zhou et al., 2008).

We carried out unpaired Wilcoxon tests to statistically compare if the medians of the Ψ_{leaf_pred} are significantly different (p value <0.05) or not (p value >0.05) between dates and vineyards. We performed the Wilcoxon test using the stats package (v4.1.1) of the R Statistical Software (v4.0.4) (RStudio Team, 2022).

2.7 Relations between leaf water potential and environmental factors

To understand how environmental conditions influence the spatial distribution of Ψ_{leaf_pred}, we analyzed the relations between the linear combination of VPD and SPEI (Table 1) and the median Ψ_{leaf_pred} (Ψ_{leaf_pred_median}) (Eq. 4) and between the linear combination of VPD and SPEI and the distribution of Ψ_{leaf_pred} (Ψ_{leaf_pred_max}−Ψ_{leaf_pred_min}) (Eq. 5).

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=a\times \mathrm{SPEI}+b\times \mathrm{VPD}+c,\text{(5)}& {\displaystyle }\begin{array}{rl}({\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\max }& -{\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\min })=a\times \mathrm{SPEI}\\ & +b\times \mathrm{VPD}+c,\end{array}\end{array}$$

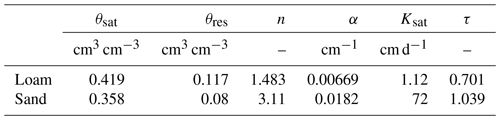
with a and b the regression coefficients and c the intercept. We applied analysis of covariance (ANCOVA) to assess if these relations are vineyard-specific or not. Relations were considered statistically different for p values less than 0.05. For each date, we also quantified the correlation between Ψ_{leaf_pred} and the elevation and between Ψ_{leaf_pred} and the slope. At Bousval, since we accurately know the depth of the interface between the loamy soil and the sandy subsoil (Fig. 1c), we also quantified the correlation between Ψ_leaf and the water-holding capacity (WHC) and between Ψ_leaf and an averaged soil hydraulic conductivity (${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$). We used the coefficient of determination R² as we assumed that these relations are linear. For these relations, we assumed that grapevines have a uniform root depth of 2.5 m throughout the vineyard. We also assumed, in this study, that the soil unsaturated hydraulic properties of the loamy and sandy soils are the same everywhere in the field. The soil hydraulic properties were measured by the Hyprop (METER Group Inc., Pullman, WA, USA) evaporation method (Bezerra-Coelho et al., 2018). The soil water content at the permanent wilting point (pF 4.2) was measured by a pressure plate (Ridley and Burland, 1993). Hyprop-fit software was used to optimize the unsaturated hydraulic parameters of van Genuchten (1980) for each soil texture (Table 3). Everywhere in the Bousval vineyard, we calculated the WHC [cm] (Fig. 1d) and K_soil [cm d⁻¹] (Fig. 1e) for a depth of 2.5 m thanks to the following equations.

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\mathrm{WHC}& ={\left[z_{\mathrm{LS}}\times \left(\mathit{\theta }\left(h_{\mathrm{FC}}\right)-\mathit{\theta }\left(h_{\mathrm{PWP}}\right)\right)\right]}_{\mathrm{loam}}\\ & +[\left(\mathrm{250}-z_{\mathrm{LS}}\right)\times \left(\mathit{\theta }\left(h_{\mathrm{FC}}\right)-\mathit{\theta }\left(h_{\mathrm{PWP}}\right)\right){]}_{\mathrm{sand}},\end{array}\end{array}$$

with z_LS [cm] the depth of the interface between the loamy soil and the sandy subsoil, θ(h) the water content [cm³ cm⁻³] at the suction h [cm] of the respective soil texture, h_FC the suction at the field capacity (in this study we assumed that $h_{\mathrm{FC}}=-\mathrm{300}$ cm), and h_FC the suction at the permanent wilting point (in this study we assumed that $h_{\mathrm{PWP}}=-\mathrm{15}\mathrm{000}$ cm).

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}& ={\left[{\displaystyle \frac{z_{\mathrm{LS}}}{\mathrm{250}}}\times {\displaystyle \frac{{\int }_{h_{\mathrm{FC}}}^{h_{\mathrm{PWP}}}K\left(h\right)\mathrm{d}h}{h_{\mathrm{FC}}-h_{\mathrm{PWP}}}}\right]}_{\mathrm{loam}}\\ & +{\left[{\displaystyle \frac{(\mathrm{250}-z_{\mathrm{LS}})}{\mathrm{250}}}\times {\displaystyle \frac{{\int }_{h_{\mathrm{FC}}}^{h_{\mathrm{PWP}}}K\left(h\right)\mathrm{d}h}{h_{\mathrm{FC}}-h_{\mathrm{PWP}}}}\right]}_{\mathrm{sand}},\end{array}\end{array}$$

with K (h) the soil hydraulic conductivity [cm d⁻¹] at the suction h [cm].

Table 3 Unimodal van Genuchten hydraulic parameters of the loamy soil and the sandy subsoil at the Château de Bousval vineyard.

3 Results

3.1 In situ measurements of leaf water potential and relations with UAS-based VIs

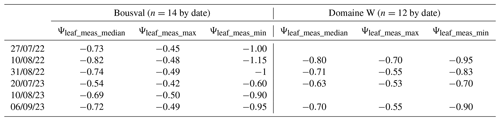
Ψ_leaf was measured (Ψ_{leaf_meas}) at the same time as the collection of UAS data, at different dates in 2022 and 2023, with a Scholander pressure bomb (Fig. 3). We measured a more negative median leaf water potential (Ψ_{leaf_meas_median}) in 2022 than in 2023 in both vineyards, linked to warmer and drier conditions (Table 1). Moreover, in each vineyard, the soil was significantly drier in 2022 than in 2023 (Fig. S1 in the Supplement). For the same date, we also measured a slightly lower Ψ_{leaf_meas_median} at Bousval compared to Domaine W (e.g., on 31 August 2022 ${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{meas}\mathrm{\_}\mathrm{median}}=-\mathrm{0.74}$ MPa at Bousval and ${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{meas}\mathrm{\_}\mathrm{median}}=-\mathrm{0.7}$1 MPa at Domaine W), except on 20 July 2023 (Table 4). We observed a greater Ψ_{leaf_meas} heterogeneity (Ψ_{leaf_meas_max}−Ψ_{leaf_meas_min}) at Bousval compared to Domaine W. This heterogeneity is even more marked in 2022, when conditions were hot and dry. At Bousval, on each date, the minimum Ψ_{leaf_meas} was measured at the upper part (west side) of the parcel, where the loamy soil is shallower, while the maximum Ψ_{leaf_meas} values were measured at the lowermost side (east side) (Fig. 3a), where the loamy soil is deeper. At Domaine W, there is less Ψ_{leaf_meas} heterogeneity, but we generally measured a lower Ψ_{leaf_meas} in the northwestern plot than in the southeastern plot (Fig. 3b).

Figure 3 Leaf water potential measured (Ψ_{leaf_meas}) with a Scholander pressure bomb in (a) 14 zones at the Château de Bousval vineyard and (b) 12 zones at the Domaine W vineyard at the same time of UAS flights. Points circled in blue were used for the calibration of the multiple linear regression models.

Table 4 Median leaf water potential (Ψ_{leaf_meas_median}) as well as the maximum (Ψ_{leaf_meas_max}) and minimum (Ψ_{leaf_meas_min}) leaf water potentials (all in MPa) measured in the two vineyards during each UAS flight.

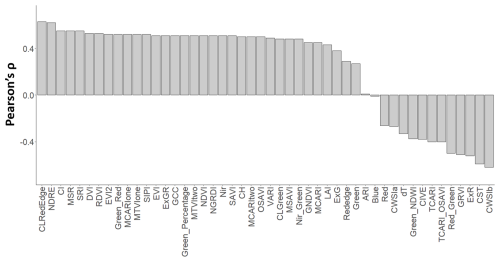
By examining the univariable relationships between Ψ_{leaf_meas} and the different VIs, including both vineyards and all dates (Fig. S2), we found that the correlations (Pearson's ρ) between Ψ_{leaf_meas} and VIs are low to moderate, ranging from $\mathit{\rho }=-\mathrm{0.61}$ to ρ=0.63 (Fig. 4). We found a maximum ρ of 0.63 between Ψ_{leaf_meas} and chlorophyll red edge (CLRededge). The second-best ρ was found with the normalized difference red-edge (NDRE) index (ρ=0.62). These two VIs are the only ones considered in this study to contain both NIR and red-edge bands, which have been shown to be strongly correlated with the chlorophyll content of grapevines and therefore influenced by the water status (Laroche-Pinel et al., 2021a; Tang et al., 2022). However, in our case, these ρ values indicate a moderate correlation of these VIs with Ψ_{leaf_meas}. The third-best correlation was found with the thermal index CWSIb, with a Pearson's ρ of −0.61. All other VIs have a lower correlation with Ψ_{leaf_meas}, with ρ ranging between 0.55 and $-\mathrm{0.59}.$ This suggests that single VIs cannot accurately predict Ψ_leaf in the investigated vineyards, and more complex approaches, such as multiple linear regression models, are needed to better estimate Ψ_leaf. For all indices, Pearson's ρ (linear relation – Fig. 4) is larger than Spearman's ρ (nonlinear relation – Fig. S3). Linear relations between Ψ_{leaf_meas} and VI therefore have a higher predictive power than nonlinear relations (Rebekić et al., 2015), justifying the use of partial linear regression (and not nonlinear) to construct a multiple linear regression and predict Ψ_leaf.

Figure 4 Pearson's coefficient (Pearson's ρ) quantifying the linear correlation between measured Ψ_leaf (Ψ_{leaf_meas}) and each vegetation index (VI) by taking all the measurements in both vineyards and at all dates.

3.2 Predicting leaf water potential based on multiple linear regression models

In response to the limited correlations obtained from simple linear regressions between Ψ_{leaf_meas} and VIs, we explored multiple linear regression models to better predict Ψ_leaf (Fig. S4). We used the stepwise regression method to minimize the number of VIs in the multiple regression and to keep the most significative to predict Ψ_leaf. Figure 5a and b respectively show the R² and RMSE obtained by comparing measured Ψ_leaf (Ψ_{leaf_meas}) and predicted Ψ_leaf (Ψ_{leaf_pred}) for the datasets used for calibration (70 % of the data) and validation (30 % of the data) and for the seven data combinations (see Methodology section). The models showed a high consistency between the calibration and validation datasets, with small differences in terms of R² and RMSE. This showed a great robustness of these models. For example, the model using multispectral, thermal, and lidar data to predict Ψ_{leaf_pred} (Fig. 5c) has R²=0.80 and R²=0.78 for the calibration and validation, respectively, and an RMSE of 0.07 MPa and =0.08 MPa for the same respective datasets. It is interesting to note that R² and RMSE respectively increase and decrease by adding information from different sensors to the model. For example, the predictive power of the model containing multispectral and thermal data is greater than the predictive power of the model constructed with multispectral data only. The best multiple linear model was the one containing information from all sensors, i.e., multispectral, thermal, and lidar data. We therefore used this model (model 1 in Table 5; Fig. 5c) to predict Ψ_{leaf_pred} at Bousval on 10 August 2022, 20 July2023, 10 August 2023, and 6 September 2023 and at Domaine W on 31 August 2022, 20 July 2023, and 6 September 2023. Due to technical problems with not being able to obtain data from all sensors for certain dates (Table 2), we predicted Ψ_{leaf_pred} at Bousval on 27 July and 31 August 2022 by using the multiple linear model combining multispectral and lidar data (model 2 in Table 5; Fig. 5d); we used the multiple linear model combining thermal and lidar (model 3 in Table 5; Fig. 5e) to predict Ψ_{leaf_pred} at Domaine W on 10 August 2022. Models 2 and 3 in Table 5 are the most robust and have the best R² and RMSE for the data available for the respective dates and vineyards (Fig. 5a, b). In each model, the confidence interval on Ψ_{leaf_pred} increases with decreasing Ψ_{leaf_pred} (more negative Ψ_{leaf_pred}). Model 1, combining multispectral, thermal, and lidar data (Fig. 5c), has the lowest uncertainty in the prediction of Ψ_{leaf_pred}, with a 95 % confidence interval (CI_0.95) varying between 0.14 MPa (when Ψ_{leaf_pred} is high) and 0.28 MPa (when Ψ_{leaf_pred} is low). This is not surprising since this model has the highest predictive power (R²). Model 2 (Fig. 5d), combining multispectral and thermal data, shows a lower uncertainty (0.18 MPa < CI_0.95<0.36 MPa) than model 3 (Fig. 5e), combining thermal and lidar data (0.20< CI_0.95<0.40).

Table 5 Vegetation index (VI), spectral bands or structural features, and regression weights (β_i) and intercept (α) used in the different multiple linear regression models (Eq. 3) to predict Ψ_leaf (Ψ_{leaf_pred}). CI_0.95 indicates the 95 % confidence interval on the β_i and α of each model; the p value shows the significance of the variable (β_i or α) in the model assuming that all other variables exist in the model (significance: p value $<{\mathrm{0.001}}^{***}$; p value $<{\mathrm{0.01}}^{**}$; p value $<{\mathrm{0.05}}^{*}$). Model 1 was constructed based on a combination of multispectral (M), thermal (T), and lidar (L) data; model 2 was constructed based on a combination of multispectral (M) and lidar (L) data; and model 3 was constructed based on thermal (T) and lidar (L) data. The equations for calculating the VIs contained in each model are given in Table S1.

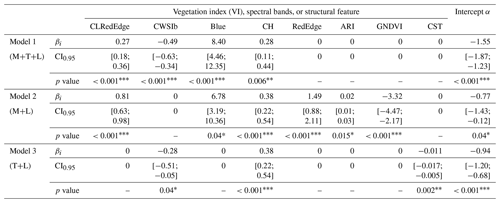
In models 2 and 3 (Table 5), we retrieved the same VIs (CLRedEdge, CWSIb), spectral bands (blue), and structural features (canopy height, CH) used to predict Ψ_{leaf_pred} in model 1, showing consistency in the parameters used to estimate grapevine Ψ_{leaf_pred}. Multicollinearity between the predictors was controlled by calculating the variance inflation factor (VIF). For each model, the VIFs were lower than 5 for each VI (Tables S2 to S4), suggesting low multicollinearity between them and enforcing the reliability of each model (James et al., 2021). This absence of multicollinearity between VIs shows that each predictor variable provides significant additional information in the prediction of Ψ_{leaf_pred}. This is confirmed by the partial regression plots (Figs. S6 to S8), showing that each VI used in each model has a significant influence on the prediction of Ψ_{leaf_pred} (p value <0.05). In model 1, accounting for multispectral, thermal, and lidar data, the partial correlations (R²) showed that CLRedEdge and CWSIb have the most significant influence on the prediction of Ψ_leaf (R²=0.49 and R²=0.56, respectively), while the blue band (R²=0.21) and the canopy height (R²=0.13) have less impact (Fig. S5). For model 2, accounting for multispectral and lidar data, CLRedEdge is also the VI influencing the prediction of Ψ_{leaf_pred} (R²=0.47) the most, while the other VIs have less impact (R²<0.30) (Fig. S6). CWSIb influenced Ψ_{leaf_pred} (R²=0.37) the most for model 3, accounting for thermal and lidar data (Fig. S7). Regardless of the model, the VIs with the greatest influence on Ψ_{leaf_pred} are therefore the same (CLRedEdge and/or CWSIb). There is therefore a high consistency in the VIs, and in the explanatory power of each VI, for the prediction of Ψ_{leaf_pred}.

3.3 Leaf water potential mapping

Ψ_{leaf_pred} maps (Fig. 6a), predicted with multiple regression model obtained with the stepwise regression method, showed a relatively constant pattern over time in both vineyards. At the Bousval vineyard, we observed more negative Ψ_{leaf_pred} in the western part of the plot. In the Domaine W vineyard, Ψ_{leaf_pred} was lower in the northwestern plot than in the southeastern plot. The spatial heterogeneity of Ψ_{leaf_pred} is much larger at Bousval than at Domaine W, particularly during the drought conditions in 2022 (Fig. 7a). For example, on 10 August 2022, which was the driest day (Table 1), Ψ_{leaf_pred} was distributed between −0.52 and −1.25 MPa at Bousval but between −0.70 and −0.97 MPa at Domaine W. Although the ranges of Ψ_{leaf_pred} are different, for the same date, the median Ψ_{leaf_pred} values (Ψ_{leaf_pred_median}) are similar (p value <0.05) in both vineyards, except for on 20 July 2023 for which Ψ_{leaf_pred_median} was slightly greater at Bousval (${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.50}$ MPa at Bousval; ${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.54}$ MPa at Domaine W). Regarding the temporal dynamics, at Bousval Ψ_{leaf_pred} decreased between 27 July 2022 (${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.74}$ MPa) and 10 August 2022 (${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.84}$ MPa), then re-increased on 31 August 22 (${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.76}$ MPa). We observed similar temporal dynamics at Domaine W, with a re-increase in Ψ_{leaf_pred} between 10 August 2022 (${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.8}$3 MPa) and 31 August 2022 (${\mathrm{\Psi }}_{\mathrm{leaf}\mathrm{\_}\mathrm{pred}\mathrm{\_}\mathrm{median}}=-\mathrm{0.75}$ MPa). At Bousval, Ψ_{leaf_pred_median} values are similar (p value <0.05) on 27 July and 10 August 22. In 2023, Ψ_{leaf_pred} decreased over the season, with Ψ_{leaf_pred_median} of −0.50 and −0.54 MPa on 20 July 2023 at Bousval and Domaine W, respectively, and −0.74 and −0.73 MPa on 6 September 2023 in the same respective vineyards. In both vineyards we observed similar Ψ_{leaf_pred_median} for the last date of 2022 and the last date of 2023 (Fig. 7a).

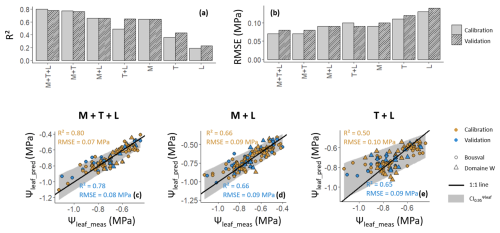
Figure 5 (a) R² and (b) RMSE obtained by comparing measured Ψ_leaf (Ψ_{leaf_meas}) and predicted Ψ_leaf (Ψ_{leaf_pred}) from multiple linear models for the different data combinations. (c, d, e) Relations between Ψ_{leaf_meas} and Ψ_{leaf_pred} for the three multiple linear models used in this study. The relationships were fitted with 95 % confidence intervals (CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}}$ – shaded area). The relation in (c) was used to predict Ψ_leaf at Bousval on 10 August 2022, 20 July 2023, 10 August 2023, and 6 September 2023 and at Domaine W on 31 August 2022, 20 July 2023, and 6 September 2023 by using multispectral (M), thermal (T), and lidar (L) data. The relation in (d) was used to predict Ψ_leaf at Bousval on 27 July and 31 August 2022 by using multispectral (M) and lidar (L) data. The relation in (e) was used to predict Ψ_leaf at Domaine W on 10 August 2022 by using thermal (T) and lidar (L) data.

The uncertainty in Ψ_{leaf_pred} (CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}$), quantified by the 95 % confidence interval on the prediction (Fig. 6b), follows the same spatial pattern as predicted Ψ_{leaf_pred} (Fig. 6a), with greater uncertainty when Ψ_{leaf_pred} is more negative. The median value of the uncertainty (median CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}$) also seems particularly affected by the model used (Table 5) to estimate Ψ_{leaf_pred} (Fig. 6c). Ψ_{leaf_pred} at Domaine W on 10 August 2022 shows the greatest uncertainty, with a median value of 0.28 MPa. This is not surprising since the model used to predict Ψ_{leaf_pred} on this date (model 3 in Table 5) only considers thermal and lidar data and is the one showing the lowest predictive power (R²) and the greatest uncertainty (Fig. 5e). For the same date at Bousval and for the same Ψ_{leaf_pred_median} (Fig. 7a), the uncertainty is significantly lower (median CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}=\mathrm{0.22}$ MPa – Fig. 6c), since we used the model involving multispectral, thermal, and lidar data to estimate Ψ_{leaf_pred} (model 1 in Table 5), which is the one showing the highest predictive power (R²) and the lowest uncertainty (Fig. 5c). Ψ_{leaf_pred} predicted with the model involving multispectral and lidar data (model 2 in Table 5) shows greater uncertainty, with a median value of 0.26 MPa at Bousval on 27 July and 31 August 2022. In both vineyards, the lowest uncertainty was on 20 July 2023 (median CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}=\mathrm{0.17}$ MPa), for which we also predicted the highest Ψ_leaf.

There is a high correlation between Ψ_{leaf_pred_median} and the range of Ψ_{leaf_pred} (Ψ_{leaf_pred_max}−Ψ_{leaf_pred_min}), with R²=0.97 at Bousval and R²=0.94 at Domaine W (Fig. 7b). The range of Ψ_{leaf_pred} increased when Ψ_{leaf_pred_median} decreased. These relations are vineyard-specific (p value of ANCOVA test is lower than 0.05). The slope of the linear relation between Ψ_{leaf_pred_median} and the distribution of Ψ_{leaf_pred} is significantly greater at Bousval (slope $=-\mathrm{1.38}$) than at Domaine W (slope $=-\mathrm{0.31}$).

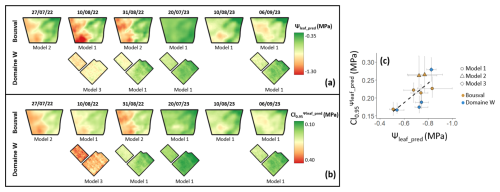
Figure 6 (a) Maps of Ψ_leaf predicted (Ψ_{leaf_pred}) with the multiple linear regression model in both vineyards. (b) Maps of uncertainty in Ψ_{leaf_pred}, quantified by the 95 % confidence interval on the prediction (CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}$). Ψ_{leaf_pred} at Bousval on 10 August 2022, 20 July 2023, 10 August 2023, and 6 September 2023 and at Domaine W on 31 August 2022, 20 July 2023, and 6 September 2023 was predicted with the model involving multispectral, thermal, and lidar data (model 1 in Table 5). Ψ_{leaf_pred} at Bousval on 27 July and 31 August 2022 was predicted with the model involving multispectral and lidar data (model 2 in Table 5). Ψ_{leaf_pred} at Domaine W on 10 August 2022 was predicted with the model involving thermal and lidar data (model 3 in Table 5). (c) The relation between Ψ_{leaf_pred} and CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}$. The points correspond to the median, and the horizontal and vertical bars respectively show the quartiles around Ψ_{leaf_pred} and CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}$. The dashed black line is the linear regression; the slope of this regression is different from 0 (p value <0.001).

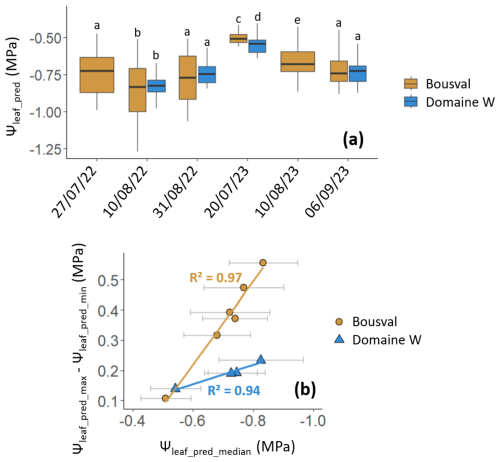
Figure 7 (a) Box plots indicating the median and quartiles, as well as the minimum and maximum of the spatial distribution of the predicted Ψ_leaf (Ψ_{leaf_pred}). The letters above each box plot are the results of the Wilcoxon tests; the same letter indicates a statistically similar (p value >0.05) median. (b) Relation between the median Ψ_{leaf_pred} (Ψ_{leaf_pred_median}) and the distribution of Ψ_{leaf_pred} (Ψ_{leaf_pred_max}−Ψ_{leaf_pred_min}). The horizontal bars are the median CI${}_{\mathrm{0.95}}^{\mathrm{\Psi }\mathrm{leaf}\mathrm{\_}\mathrm{pred}}$ (median uncertainty) on Ψ_{leaf_pred_median}.

3.4 Environmental factors influencing the spatial distribution of leaf water potential

At Bousval, Ψ_{leaf_pred} was the most correlated with the averaged soil hydraulic conductivity at 2.5 m depth ${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$ (Fig. 8). The correlation was better in 2022 than in 2023, with the best correlation on 10 August 2022 (R²=0.81), the driest day (Table 1). The water-holding capacity at 2.5 m depth (WHC) is less correlated with Ψ_{leaf_pred}; however, we also find the best correlation on 10 August 2022 (R²=0.67). At Bousval, the elevation was moderately correlated with Ψ_{leaf_pred}, particularly in 2022 (e.g., R²=0.42 on 10 August 2022). This is not surprising since the interface between the loamy and sandy soil horizons is shallower in the upper part of the parcel (western part) and deeper in the lower part due to an accumulation of loamy colluviums (Fig. 1c). However, the correlation between Ψ_{leaf_pred} and elevation is lower than the correlation between Ψ_{leaf_pred} and ${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$ and between Ψ_{leaf_pred} and WHC, showing that soil properties have a greater influence on the spatial distribution of Ψ_{leaf_pred} than the elevation. The slope showed the lowest correlation with Ψ_{leaf_pred} (maximum R²=0.15 on 31 August 2022). It is interesting to note that on 20 July 2023, the correlation between Ψ_{leaf_pred} and all topographic and soil properties is low (e.g., R²=0.24 between Ψ_{leaf_pred} and ${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$). At Domaine W, the slope and elevation showed a low correlation with Ψ_{leaf_pred}. The maximum R² between Ψ_{leaf_pred} and slope was 0.09 and was 0.24 between Ψ_{leaf_pred} and elevation on 20 July 2023. These low correlations are not surprising since this vineyard is almost flat (Fig. 1g).

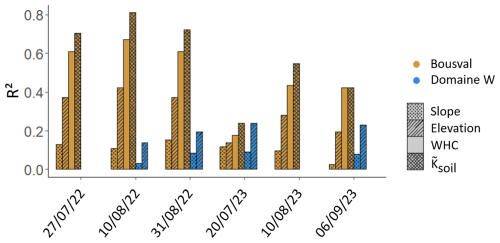
Figure 8 Coefficient of determination (R²) of the linear relation between predicted Ψ_leaf (Ψ_{leaf_pred}) and elevation, between Ψ_{leaf_pred} and slope, between Ψ_{leaf_pred} and the water-holding capacity at 2.5 m (WHC – only at the Château de Bousval vineyard), and between the averaged soil hydraulic conductivity values (${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$ – only at the Château de Bousval vineyard).

As shown in Fig. 7b, the slope of the linear relation between Ψ_{leaf_pred_median} and the distribution of Ψ_{leaf_pred} is significantly greater at Bousval than at Domaine W, showing that environmental conditions at Bousval are much more heterogeneous (i.e., heterogeneity of soil properties), which is reflected in a larger range of the distribution of Ψ_leaf, particularly when conditions are drier. In this study, we quantified the water deficit thanks to the standardized precipitation evapotranspiration index (SPEI – Eq. 1). More negative SPEI indicates a greater water deficit. We also used VPD to characterize the atmospheric conditions and quantify the evaporative demand. Ψ_{leaf_pred_median} is highly correlated (R²=0.82) with the linear combination of SPEI and VPD (Fig. 9a). Interestingly, this relation is not vineyard-specific (p value of ANCOVA test is greater than 0.05). Ψ_{leaf_pred_median} is positively correlated with SPEI (regression coefficient a in Eq. 4 is 0.001) and negatively correlated with VPD (regression coefficient b in Eq. 4 is −0.13). This means that Ψ_{leaf_pred_median} decreases when SPEI decreases and when VPD increases. In other words, the median Ψ_leaf in a vineyard is more negative for greater water deficit (SPEI) and evaporative demand (VPD). The distribution of Ψ_{leaf_pred} (Ψ_{leaf_pred_max}−Ψ_{leaf_pred_min}) is also correlated (R²=0.54) with the linear combination of SPEI and VPD (Fig. 9b). This relation, unlike the one with Ψ_{leaf_pred_median}, is vineyard-specific (p value of ANCOVA test is lower than 0.05). The distribution of Ψ_{leaf_pred} is negatively correlated with SPEI (regression coefficient a in Eq. 5 is −0.001) and positively correlated with VPD (regression coefficient b in Eq. 5 is 0.08). This means that the range of the distribution of Ψ_{leaf_pred} increases when SPEI decreases and VPD increases. In other words, in a vineyard, the spatial heterogeneity of Ψ_leaf is more important for greater water deficit (SPEI) and evaporative demand (VPD).

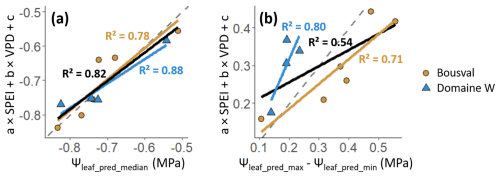
Figure 9 (a) Relation between median Ψ_{leaf_pred} (Ψ_{leaf_pred_median}) and the linear combination of SPEI and VPD (Eq. 4 – a=0.001; $b=-\mathrm{0.13}$; $c=-\mathrm{0.26}$). (b) Relation between the distribution of Ψ_{leaf_pred} (Ψ_{leaf_pred_max}−Ψ_{leaf_pred_min}) and the linear combination of SPEI and VPD (Eq. 5 – $a=-\mathrm{0.001}$; b=0.08; $c=-\mathrm{0.17}$). In each panel, the brown lines are the linear regressions on the brown circles, the blue lines are the linear regressions on the blue triangles, the black lines are the linear regressions on all points, and the dashed gray lines are the 1:1 lines.

4 Discussion

In this study, we attempted to map grapevine leaf water potential (Ψ_leaf) intra-field heterogeneity to assess the impact of topographic, edaphic, and climatic conditions on the spatial distribution of Ψ_leaf. Our study demonstrated that a multilinear combination of multispectral VIs, thermal VIs, and structural features from lidar data, with UASs collecting high-spatial-resolution imagery, is efficient (R²=0.80 and RMSE =0.07 MPa for the calibration; R²=0.78 and RMSE =0.08 MPa for the validation) at capturing the spatial distribution of grapevine Ψ_leaf across different vineyards during two viticultural seasons. We showed that the heterogeneity of edaphic conditions has the greatest influence on the spatial heterogeneity of Ψ_leaf, particularly when the water deficit and evaporative demand increase.

4.1 Discrimination between grapevine canopy and inter-row pixels

The k-means algorithm, which is a standard and well-known unsupervised method for classification, is regularly and efficiently applied to multispectral UAS data to discriminate between the grapevine (or other row-crop cultivations) rows and bare-soil inter-rows of a vineyard (Calvario et al., 2017; Cinat et al., 2019; Gavrilović et al., 2024). In vineyards with inter-row vegetation (i.e., grass), segmentation tasks become more challenging. This complexity arises because the spectral signature of such vegetation often closely resembles that of grapevine canopy, making differentiation difficult and leading to overestimation or underestimation of grapevine pixels (Nolan et al., 2015). Relying solely on multispectral data is insufficient for distinguishing between grapevine and grass pixels when using the k-means algorithm (Poblete-Echeverría et al., 2017). In this study, we discriminated between the grapevine canopy and inter-row soil and grass pixels using the k-means algorithm by first applying the algorithm on the canopy height, derived from the lidar data, to get a first raw distinction between rows (grapevine) and inter-rows (grass and soil). We then applied it a second time to the multispectral data to get a finer discrimination and to extract only pure grapevine canopy pixels, with a spatial resolution of 7 cm ×7 cm, which is almost similar to other recent studies (Berry et al., 2024; Laroche-Pinel et al., 2024). Integrating additional data sources, such as structural (lidar), likely improved classification accuracy with the k-means algorithm. Other studies highlighted the best performance in the detection of grapevine canopy when using complemented unsupervised methods and/or data sources (Poblete-Echeverría et al., 2017). Other methods to discriminate between rows and inter-rows, such as artificial neural networks or random forest, could deliver satisfactory results, but their accuracy depends on proper training. This requires creating a manually labeled dataset to calibrate the models effectively. Additionally, both of these supervised methods involve numerous parameters that must be carefully tuned to optimize performance and demand more computational resources (Nolan et al., 2015; Poblete-Echeverría et al., 2017).

4.2 Leaf water potential prediction with a combination of multispectral, thermal, and lidar UAS data

We used the stepwise regression method to find the best multilinear regression to predict Ψ_leaf with several UAS-based multispectral VIs, thermal VIs, and structural features (lidar) measured on grapevines (Wilkinson, 1979). The univariable linear relation between measured Ψ_leaf and VIs (Pearson's ρ> Spearman's ρ – Fig. S3b) justifies the use of this statistical method to better predict Ψ_leaf. Other statistical methods could also be used to predict Ψ_leaf, such as principal component regression (PCR) or random forest. To support our approach (stepwise regression), we also implemented the PCR and random forest methods (Fig. S4). However, while the random forest models gave the highest R² and lowest RMSE for the calibration dataset, there was a great loss of predictive power when we validated the model (R² decreased and RMSE increased). This showed some evidence of model overfitting, affecting the robustness of the model constructed with the random forest. Generally, the R² and RMSE were respectively higher and lower for the stepwise regression model compared to the PCR model. The stepwise regression method therefore showed more robustness than the random forest method when we validated models and a better predictive power compared to PCR (Fig. S8). Other studies using random forest or artificial neural networks to predict Ψ_leaf with UAS-based multispectral VIs lost predictive power when they validated their model, showing that the model structure was overfitted (Poblete et al., 2017; Romero et al., 2018; Tang et al., 2022). Our analysis highlighted the importance of incorporating multispectral, thermal, and lidar data to improve the prediction of Ψ_leaf. The use of data from different sensors also makes it possible to limit the uncertainty in Ψ_leaf (Fig. 5). Tang et al. (2022) already mentioned that data combination from multiple sensors acquiring data in different regions of the electromagnetic spectrum will allow mapping Ψ_leaf with more accuracy. In our model, the multispectral VI CLRedEdge (calculated based on the NIR and red-edge bands), the reflectance in the blue band, the thermal VI CWSIb, and the canopy height (CH) all significantly influence Ψ_leaf and are used in the multilinear regression to predict it (model 1 in Table 5). It is interesting to note that these indices, bands, and features are also used in the models for which only multispectral and lidar data (model 2 in Table 5) or thermal and lidar data (model 3 in Table 5) are used to predict Ψ_leaf. Although they are not significantly correlated with measured Ψ_leaf when taken one by one (Fig. 4), information contained in these indices is complementary and their combination enables Ψ_leaf to be predicted with high predictive power (e.g., R²=0.80 and RMSE =0.07 MPa for calibration and R²=0.78 and RMSE =0.08 MPa for calibration, for model 1). Discarding VIs which are not directly correlated with Ψ_leaf is not required, since multilinear modeling techniques can identify the patterns in the data and assign individual weights to inputs, allowing multilinear models to fit accordingly (Romero et al., 2018). NIR and red-edge spectral regions, used to calculate CLRedEdge, have already been investigated to predict vegetation water potential (Giovos et al., 2021; Pôças et al., 2015; Soubry et al., 2017; Zygielbaum et al., 2009). Although these bands, and derived VIs, are commonly associated with plant structural traits (e.g., biomass, vigor), the red-edge region is often used as a reference to detect chlorophyll content in vegetation (Clevers and Gitelson, 2013; Gamon and Surfus, 1999; Rallo et al., 2014). Plant water status is indicative of and closely related to chlorophyll content, as changes in this pigment content induce changes in leaf spectral properties in the red-edge region (Carter and Knapp, 2001). NIR electromagnetic region has also been shown to be affected by the leaf structure and leaf water content of grapevines (De Bei et al., 2011; Marañón et al., 2023; Tardaguila et al., 2017). VIs calculated based on NIR and red-edge bands, such as CLRedEdge, have good potential to quantify grapevine water potential (Becker et al., 2020; Giovos et al., 2021). Additionally, bands in the visible domain, such as the blue band, can provide valuable information about plant water status, as pigment contents and composition govern reflectance in this domain (Gamon et al., 1992; Moya et al., 2004) and are related to processes associated with grapevine water status (Zarco-Tejada et al., 2013). Blue wavelengths are strongly absorbed by carotenoids (carotenes and xanthophylls). These pigments, and their proportion, also serve as indicators of plant water status (Gitelson et al., 2006). Moreover, the blue reflectance enables atmospheric corrections and allows for a more linear relationship with vegetation status (Gitelson et al., 2002). Thermal VIs also provide information on grapevine water status. Strong relationships have been found between CWSI and the stomatal conductance of grapevines (Pagay and Kidman, 2019; Pou et al., 2014), which is directly linked (nonlinearly) to Ψ_leaf. During drought, grapevines close stomata to prevent the plant from reaching excessively negative water potentials leading to xylem cavitation (Gambetta et al., 2020). Stomatal closure can also induce lower grapevine growth by reducing photosynthesis (Dry and Loveys, 1998). This could explain why canopy height (CH), retrieved with lidar point clouds, is also used to predict Ψ_leaf. García-Tejera et al. (2021) showed that changes in plant canopy structure, including canopy height and width, influence the water flow between the soil and the atmosphere, thereby affecting Ψ_leaf. Thermal remote sensing metrics provide short-term information on grapevine water status, such as Ψ_leaf or stomatal conductance variations (Acevedo-Opazo et al., 2010; Santesteban et al., 2017), while multispectral VIs and structural features (lidar) reveal mid- to long-term water status effects on grapevine structure and traits like leaf pigment content (Baluja et al., 2012; Zarco-Tejada et al., 2013). The three approaches (multispectral, thermal, and lidar) therefore provide complementary information and their multilinear combinations, through VIs and structural features, allow the accurate and robust assessment of intra-field variability of grapevine leaf water potential, thanks to high-spatial-resolution sensors mounted on UASs.

Other sensors could also be tested and used to spatially monitor grapevine Ψ_leaf. Adding information from more and narrower spectral bands, collected with hyperspectral sensors, could improve the capability to remotely monitor grapevine Ψ_leaf (Pôças et al., 2015; Tang et al., 2022). Studies using hyperspectral sensors to measure plant water potential generally get higher correlations than studies using multispectral sensors (Pôças et al., 2015; Rodríguez-Pérez et al., 2007; Zarco-Tejada et al., 2013). For example, the photochemical reflectance index (PRI, calculated with spectral reflectance at 545 and 567 nm) is a good indicator (R² between 0.5 and 0.6) of crop water status (Stagakis et al., 2012; Suárez et al., 2008). Zarco-Tejada et al. (2013) even obtained a better correlation (R²=0.82) in vineyards by combining PRI with other hyperspectral VIs, such as the renormalized difference vegetation index (RDVI, based on reflectance at 700 and 761 nm) and the ratio $R_{\mathrm{700}}/R_{\mathrm{670}}$ (based on reflectance at 670 and 700 nm), highlighting that the combination of several VIs brings complementary information to better estimate the leaf water potential of grapevines. Shortwave infrared (SWIR) data (1000–2200 nm) also have good potential to monitor grapevine water status, since this spectral range contains the water absorption bands (Laroche-Pinel et al., 2021b). VIs calculated with SWIR bands, such as the normalized drought water index (NDWI) (Gao, 1996), showed good correlations (R²=0.58) with grapevine Ψ_leaf (Caruso and Palai, 2023).

4.3 Intra-field variability of grapevine leaf water potential

We observed good stability in the Ψ_leaf pattern for each date in both vineyards (Fig. 6a). At the Domaine W vineyard, the spatial heterogeneity of Ψ_leaf is less marked than at the Bousval vineyard. For example, on 10 August 2022 (driest day), although median Ψ_leaf was similar in both vineyards, the range of the distribution of Ψ_leaf was 0.73 MPa at Bousval but only 0.27 MPa at Domaine W. The magnitude of variation in Ψ_leaf at the within-field level predicted at Bousval is consistent with other studies. Brillante et al. (2017a) also observed a difference of 0.70 MPa between maximum and minimum Ψ_leaf within a vineyard in California. They hypothesized, without directly proving it, that this variability was due to the short distance differences of soil properties in the vineyard. Tang et al. (2022) observed a spatial variability up to 0.67 MPa, but this was due to differences in irrigation treatment in a vineyard with gravelly loam soil. At Bousval, the spatial distribution of Ψ_leaf is highly correlated (Fig.8 – R² up to 0.81), with an averaged soil hydraulic conductivity ${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$. In this vineyard, Ψ_leaf was significantly more negative in the western part of the plot, where the interface between the loamy soil and the sandy subsoil is more superficial, compared to the eastern part where the loamy soil is clearly deeper. Grapevine water potential is significantly influenced by the soil texture. It is well-known that the soil water potential around the roots affects Ψ_leaf, since the difference between the two water potentials is the driving force for transpiration (Tyree and Zimmermann, 2002). The soil water potential in the vicinity of the roots decreases as the plant takes up water, resulting in a significant loss of soil hydraulic conductivity around the roots (Cai et al., 2022). This reduction of hydraulic conductivity generates large gradients in soil water potential in the vicinity of the roots, leading to a significant drop in Ψ_leaf to support a slight increase in transpiration (Carminati and Javaux, 2020). The soil texture determines soil hydraulic properties, thereby influencing grapevine hydraulics (Lavoie-Lamoureux et al., 2017; Tramontini et al., 2013). Therefore, in a sandy soil, the decline in soil hydraulic conductivity around the roots is sharper than in a fine-textured soil, leading to a significantly greater reduction of water potential at the soil–root interface; this directly impacts Ψ_leaf, which also decreases more rapidly (Cai et al., 2022). In soil-water-limited conditions, such as in 2022 (Fig. S1), we can assume that soil hydraulic conductivity drop is larger in the western part of the Bousval vineyard, where most of the grapevine roots are found in the sandy subsoil (Delval et al., 2024b), leading to a greater drop in soil–root interface water potential and consequently to a larger decline in Ψ_leaf. We can therefore affirm that in a non-irrigated vineyard, the edaphic heterogeneity (i.e., in terms of soil hydraulic conductivity) governs the spatial heterogeneity (and patterns) of grapevine Ψ_leaf, particularly during drought. At the Domaine W vineyard, we always predicted lower Ψ_leaf in the northwest parcel than in the southeast plot. We observed, but only in a single location in each subplot, that the northwest parcel is made of a silty loam soil on the first horizons and silty clay loam soil thereafter, while the southeast parcel is composed of a silty loam soil on the whole profile (Fig. 1h). Although the vertical distribution of soil texture is not accurately known in the whole field, we could assume that this spatial difference in soil properties has an influence on the spatial heterogeneity of Ψ_leaf, since other factors such as the elevation (R²=0.24) and the slope (R²=0.09) have low correlation with the spatial distribution of Ψ_leaf (Fig. 8). However, other studies comparing loamy and loamy clay soils showed only a moderate effect on grapevine Ψ_leaf (Brillante et al., 2017b), explaining the lower range of Ψ_leaf observed in this vineyard. Other factors could potentially influence the spatial distribution of Ψ_leaf at Domaine W. For example, in this vineyard, the level of the water table is higher in the southeastern parcel due to the stream running parallel to the plot (Fig. S1c). It has been observed that this water table reaches the roots, and water consumed by the grapevines is therefore certainly replaced by vertical soil water movements (capillary rises) (Van Leeuwen et al., 2018). The presence of a water table within the reach of the roots prevents or mitigates a decrease in Ψ_leaf (Tramontini et al., 2013). Further investigations should be done to better understand the spatial heterogeneity of Ψ_leaf in the Domaine W vineyard.

We showed that the linear combination of SPEI and VPD was correlated with the median (Ψ_{leaf_median} – R²=0.82) and the range (Ψ_{leaf_max}−Ψ_{leaf_min} – R²=0.54) of leaf water potential (Fig. 9). In a vineyard, the Ψ_{leaf_median} is more negative when the water deficit and the evaporative demand are greater (i.e., when SPEI is lower and VPD is higher). Interestingly, we showed that this relation was independent of the vineyard (p value >0.05). The range of Ψ_leaf is more important for greater water deficit and evaporative demand. This relation was vineyard-dependent (p value <0.05). While the edaphic heterogeneity can explain the Ψ_leaf spatial heterogeneity observed within a vineyard, the median and range of Ψ_leaf are particularly affected by the weather conditions (i.e., evaporative demand) and the intensity of water deficit. When evaporative demand and water deficit are greater, the spatial heterogeneity of Ψ_leaf is particularly marked and follows ${\stackrel{\mathrm{̃}}{K}}_{\mathrm{soil}}$ intra-field patterns. Therefore, weather conditions also have a great influence on the temporal variability of Ψ_leaf (Brillante et al., 2017a). The impact of weather conditions on Ψ_leaf can explain why we observed a re-increase in Ψ_{leaf_median} between 10 and 31 August 2022 in both vineyards, since VPD on 10 August 2022 was significantly higher than VPD on 31 August 2022. Plants exposed to a higher evaporative demand experience a greater loss in water potential at the soil–root interface, resulting in more negative Ψ_leaf. Conversely, for grapevines exposed to lower VPD, the drop in Ψ_leaf is more limited since the water potential at the soil–root interface is higher (Cai et al., 2022; Carminati and Javaux, 2020). Spatial soil property distribution, weather conditions, and intensity of water deficit mainly influence grapevine leaf water potential heterogeneity, as well as the median and range of Ψ_leaf observed in a vineyard, and their effects are concomitant (Van Leeuwen et al., 2018).

It is interesting to note that on 20 July 2023, Ψ_leaf is relatively homogeneous within both vineyards and its distribution (Ψ_{leaf_max}−Ψ_{leaf_min}) is therefore low (Fig. 7a). At Bousval, Ψ_leaf was still slightly lower in the western part of the parcel, but the difference was significantly less marked compared to the other dates (Fig. 6). The same observations can be made at Domaine W, with slightly more negative Ψ_leaf in the northwestern plot but less marked variability compared to other dates. On 20 July 2023, the soil was the wettest ever measured for this study (Fig. S1), and the water deficit (SPEI) and the evaporative demand were the lowest among all dates (Table 1). In non-limiting soil conditions, water flow is primarily governed by plant hydraulic conductance instead of soil hydraulic conductivity, even in sandy soils (Draye et al., 2010; Passioura, 1980). Therefore, plant hydraulic conductance mainly affects leaf water potential distribution in these conditions. Although it is well-known that edaphic conditions influence grapevine hydraulic conductance (Tramontini et al., 2013), notably through their impact on xylem (Hochberg et al., 2015), root (Ollat et al., 2015), and canopy (Pereyra et al., 2023) architecture, we can assume that the within-field grapevine hydraulic conductance is significantly less heterogenous than within-field soil hydraulic conductivity. This is not surprising since in this study, for a given vineyard, we only worked on one cultivar–rootstock combination. Although some studies highlighted the predominance of the soil effect on grapevine water potential (Taylor et al., 2010; Tramontini et al., 2013), it would be interesting to carry out research to understand how, within the same vineyard with different cultivar–rootstock combinations, this affects the range of within-field Ψ_leaf.

Other studies showed that topographic attributes, such as slope and elevation, could also impact grapevine performance (Bramley et al., 2011; Karn et al., 2024). In this study, we only observed a maximum R²=0.13 and R²=0.54, respectively, between Ψ_leaf and slope and between Ψ_leaf and elevation. This is consistent with Brillante et al. (2017a), who showed that slope and elevation differences are less significantly related to grapevine water status heterogeneity in vineyards with moderate or no slope, which is the case in the present study. It has been shown that topographic attributes have a real influence on grapevines for vineyards with steep slopes (Brillante et al., 2017b).

5 Conclusions

We aimed to accurately map the grapevine leaf water potential (Ψ_leaf) within non-irrigated vineyards and assess the impact of edaphic, topographic, and climatic conditions on the Ψ_leaf intra-field heterogeneity. We combined UAS-based multispectral, thermal, and lidar data to spatially predict grapevine Ψ_leaf. The data provided by different sensors acquiring data in different regions of the electromagnetic spectrum brought complementary information on grapevine water status and allowed the development of a robust and high-predictive-power model (R²=0.80 and RMSE =0.07 MPa for the calibration; R²=0.78 and RMSE =0.08 MPa for the validation) to estimate grapevine Ψ_leafin two vineyards during two viticultural seasons. While thermal VIs (e.g., CWSI) provide short-term information, such as Ψ_leaf variations, multispectral (e.g., CLRedEdge and blue reflectance band) and lidar (from which we can derive grapevine structural features) data are associated with mid- to long-term water status effect on grapevine structure (e.g., canopy height) and traits like leaf pigment content. Our results provided evidence that in non-irrigated vineyards, grapevine water status is highly variable within a vineyard, up to 0.73 MPa. This spatial distribution of Ψ_leaf is mainly governed by the within-vineyard soil hydraulic conductivity heterogeneity and is particularly marked when the evaporative demand and the water deficit are greater, since the range of Ψ_leaf increases in these conditions. Knowledge of the spatial variability of grapevine water status, through grapevine Ψ_leaf, could help winegrowers to accurately optimize viticultural management during the different phenological stages of the grapevine. Although promising, our results are limited to one grapevine cultivar (cv. Chardonnay) and two vineyards. To further improve the robustness and reliability of the method used in this study, additional UAS observations should be done to represent a broader range of cultivars, rootstocks, management systems, and environmental conditions to examine how other viticultural factors may affect grapevine Ψ_leaf spatial heterogeneity. Moreover, accurate spatialized information on grapevine Ψ_leaf could be used in functional–structural grapevine models (Yang et al., 2023) to predict berry growth and quality (i.e., sugar content) as well as its variation at the field scale.