the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Applicability and consequences of the integration of alternative models for CO2 transfer velocity into a process-based lake model
Anne Ojala
Ivan Mammarella
Jouni Heiskanen
Kukka-Maaria Erkkilä
Heli Miettinen
Timo Vesala
Timo Huttula
Freshwater lakes are important in carbon cycling, especially in the boreal zone where many lakes are supersaturated with the greenhouse gas carbon dioxide (CO2) and emit it to the atmosphere, thus ventilating carbon originally fixed by the terrestrial system. The exchange of CO2 between water and the atmosphere is commonly estimated using simple wind-based parameterizations or models of gas transfer velocity (k). More complex surface renewal models, however, have been shown to yield more correct estimates of k in comparison with direct CO2 flux measurements. We incorporated four gas exchange models with different complexity into a vertical process-based physico-biochemical lake model, MyLake C, and assessed the performance and applicability of the alternative lake model versions to simulate air–water CO2 fluxes over a small boreal lake. None of the incorporated gas exchange models significantly outperformed the other models in the simulations in comparison to the measured near-surface CO2 concentrations or respective air–water CO2 fluxes calculated directly with the gas exchange models using measurement data as input. The use of more complex gas exchange models in the simulation, on the contrary, led to difficulties in obtaining a sufficient gain of CO2 in the water column and thus resulted in lower CO2 fluxes and water column CO2 concentrations compared to the respective measurement-based values. The inclusion of sophisticated and more correct models for air–water CO2 exchange in process-based lake models is crucial in efforts to properly assess lacustrine carbon budgets through model simulations in both single lakes and on a larger scale. However, finding higher estimates for both the internal and external sources of inorganic carbon in boreal lakes is important if improved knowledge of the magnitude of CO2 evasion from lakes is included in future studies on lake carbon budgets.
- Article
(3146 KB) - Full-text XML
-
Supplement
(838 KB) - BibTeX
- EndNote
The majority of inland waters, especially in the boreal zone, are supersaturated with carbon dioxide (CO2), with concentrations that can exceed the equilibrium concentration by several times, and are therefore net sources of carbon to the atmosphere (Cole et al., 1994; Algesten et al., 2014). The contribution of lakes to the global carbon budget is recognized to be substantial in comparison to the role of marine and terrestrial ecosystems as global carbon sinks, but quantitative estimates of the global contribution of lakes and other inland waters show significant variation (Cole et al., 2007; Battin et al., 2009; Tranvik et al., 2009). Atmospheric CO2 exchange between lakes and the atmosphere is one of the key processes needed to be determined in constructing carbon budgets of lakes and in evaluating the role of lakes in global carbon cycling.
The exchange of weakly soluble gases, like CO2 and oxygen, across the air–water interface is often modeled as a boundary-layer process in which the gas flux is proportional to the gas concentration gradient at the interface. The proportionality factor k is known as the gas transfer velocity. In many long-used models for the gas transfer velocity, or gas exchange models, k is parameterized as a function of wind speed alone (Wanninkhof, 1992; Cole and Caraco, 1998). However, direct measurements of air–water CO2 exchange using the eddy covariance (EC) method (Jonsson et al., 2008; MacIntyre et al., 2010; Heiskanen et al., 2014) have resulted in higher estimates of k compared to wind-based gas exchange models. For weakly soluble gases, k depends mainly upon turbulence in near-surface water (Banerjee, 2007), which is not generated merely by wind. Near-surface turbulence is initiated predominantly by wind shear and negative buoyancy flux related to thermal convection induced by surface heat loss (Imberger, 1985). Buoyancy flux is relatively more important in small, wind-sheltered lakes, and parameterizations of the gas transfer velocity that are based solely on wind speed may not be applicable under such conditions (Read et al., 2012). Turbulence-driven gas exchange models have been shown to be well in accordance with in situ measurements of k (e.g., Zappa et al., 2007; Vachon et al., 2010).
In surface renewal models, k is calculated as a function of the turbulent kinetic energy dissipation rate ε, which provides an indication of the intensity of near-surface turbulence (MacIntyre et al., 1995). Kinetic energy dissipation can be due to viscous and thermal processes, and ε is thus dependent on wind shear and convective heat flux (Lombardo and Gregg, 1989). Wind shear is characterized by wind-induced water-side friction velocity. The water-side friction velocity can be estimated from the atmospheric friction velocity, which can be measured directly (Mammarella et al., 2015) or calculated by bulk formulas using meteorological variables (Fairall et al., 1996). Heat-induced turbulence is generated if the surface heat flux is directed out of the lake. If measurements of the components of surface heat flux are not available, they can also be estimated using bulk formulas (Fairall et al., 1996).
Global estimates of carbon emissions from lakes often use conservative estimates of CO2 fluxes or models that yield potentially underestimated values for k, leading to low estimates of CO2 fluxes (e.g., Cole et al., 2007; Raymond et al., 2013). Thus, revised estimates of lacustrine CO2 emissions will require higher net ecosystem production in the land-based ecosystems of the terrestrial biosphere to close the global carbon balance (Battin et al., 2009). Many studies concerning modeling lake carbon balance (e.g., Bade et al., 2004; McDonald et al., 2013) or the determination of lake carbon budgets (e.g., Sobek et al., 2006; Stets et al., 2009; Chmiel et al., 2016) also use simple wind-based models for k. Potential subsequent underestimates in carbon efflux may have consequences for the interpretation of carbon budgets in single lakes (Dugan et al., 2016). A higher efflux may result in a reevaluation of the amount of net ecosystem production in lakes, or it can mean that external carbon sources are inadequately accounted for in lake carbon budgets.
The efflux of CO2 from a lake is sustained mainly by in-lake CO2 production through the bacterial or photochemical degradation of organic matter in the water column or in sediment. Widely across the boreal zone, the importance of the degradation of allochthonous organic matter as an inorganic carbon source in lakes is conspicuous (Jonsson et al., 2001; Sobek et al., 2003). Also, the direct loading of terrestrially produced dissolved inorganic carbon (DIC) through surface water and groundwater inflows may lead to high CO2 concentrations in some lakes (Maberly et al., 2013; Weyhenmeyer et al., 2015; Einarsdóttir et al., 2017).
In this study, we evaluated the performance of different gas exchange models in the simulation of air–water CO2 flux in a boreal lake with a process-based lake model and the adaptability of the lake model application to different CO2 losses via efflux. We also calculated CO2 budgets for the epilimnion of the lake during summer stratification on the basis of the simulation results and assessed the relative importance of different biogeochemical processes for the epilimnetic CO2 conditions. We incorporated four alternative gas exchange models into a vertical process-based physico-biogeochemical lake model for the simulation of year-round profiles of water temperature and CO2 concentrations with a daily time step. We then applied the lake model to a humic boreal lake located in southern Finland for the period 2013–2014, calibrating each of the resultant alternative lake model versions against high-frequency water column CO2 concentration measurements. We compared the simulated gas transfer velocities and air–water CO2 fluxes with those calculated with the gas exchange models on the basis of measurement data. The aims of our study are (i) to assess the applicability of gas exchange models of different complexity to a process-based lake model with a daily time step and (ii) to assess the implications of higher CO2 efflux estimates for the lake carbon budget.
2.1 Modeling approach
In this study, we assessed the applicability of four different models for the gas transfer velocity, referred to as gas exchange models, to a process-based physico-biogeochemical lake model, MyLake C. The four gas exchange models were selected because their performance in estimating air–water CO2 fluxes in a small boreal lake has been extensively assessed in previous studies by Heiskanen et al. (2014), Mammarella et al. (2015), and Erkkilä et al. (2018) by comparing the calculated fluxes with direct CO2 flux measurements. The models include (1) the widely applied experimental wind-based regression formula by Cole and Caraco (1998), (2) a boundary-layer model developed by Heiskanen et al. (2014), (3) a surface renewal model by Tedford et al. (2014), and (4) a regression model by MacIntyre et al. (2010).
2.1.1 Parameterization of air–water gas exchange
The flux of CO2 between water and the atmosphere, , can be parameterized as the product of the CO2 concentration difference between the surface water and the atmosphere with the gas transfer velocity k (Cole and Caraco, 1998):
where Cw is the CO2 concentration in the surface water below the air–water interface, Ceq is the equilibrium concentration of CO2, that is, the water column CO2 concentration in the state of equilibrium with the overlying atmosphere, and α is the chemical enhancement factor applicable for reactive gases, such as CO2. Gas fluxes from water to the atmosphere are thus defined to be positive. If a lake is nonalkaline, α can be assumed to be 1 (Cole and Caraco, 1998). The equilibrium concentration is calculated by Henry's law as
where KH is the temperature-dependent aqueous-phase solubility (also known as the Henry's law constant) of CO2 at surface water temperature, χ is the mole fraction of the gas in the atmosphere, and pa is the atmospheric pressure.
The gas transfer velocity k can be simply parameterized as a function of wind speed alone, or more complex models can be applied to describe the air–water gas exchange process or the near-surface turbulence that governs the gas exchange. In each of the four gas exchange models assessed in this study, the parameterization of k is made using a different combination of parameters. The parameters of each model and their units are listed in Table 1. With the exception of the simple wind-based model by Cole and Caraco (1998), near-surface turbulence is driven in the models by both wind shear and thermal convection promoted by heat loss from the surface.
Cole and Caraco (1998)Heiskanen et al. (2014)MacIntyre et al. (2010)Tedford et al. (2014)Table 1Parameters used in the parameterizations of the gas transfer velocity in the gas exchange models by Cole and Caraco (1998), Heiskanen et al. (2014), MacIntyre et al. (2010), and Tedford et al. (2014).

Convection-driven turbulence occurs when surface heat flux is directed out of the lake, that is, when the buoyancy flux is negative (MacIntyre et al., 2010). The buoyancy flux β is defined as (Imberger, 1985)
where g is the gravitational acceleration, αw is the thermal expansion coefficient of water, Qeff is the effective heat flux, ρw is the density of water, and is the specific heat capacity of water. The effective heat flux is defined as
where is the net surface heat flux, QH is sensible heat flux, QL is latent heat flux, QLW is net longwave radiation, QSW is shortwave radiation, and zAML is the depth of the actively mixing layer (AML) (Imberger, 1985). All heat fluxes from the atmosphere into the lake are defined as positive. The last three terms in the equation represent the fraction of shortwave radiation that is trapped within the AML, denoted as QSW,AML. The attenuation of shortwave radiation at depth z in the water column can be calculated using the Beer–Lambert law:
where KL is the total attenuation coefficient of shortwave radiation. The AML is defined as the near-surface layer in which the water column temperature is within a certain range, usually 0.02 ∘C, of the temperature at the air–water interface (MacIntyre et al., 2001). The buoyancy flux is positive when the near-surface water is heating and negative under cooling conditions.
In the boundary-layer model developed by Heiskanen et al. (2014), near-surface turbulence is parameterized through wind-induced and convection-induced water-side velocity scales, which are characterized by the wind-induced water friction velocity at a reference depth, u*ref, and the penetrative convection velocity w*, respectively. The penetrative convection velocity is calculated as (Imberger, 1985)
The gas transfer velocity can also be parameterized by the total turbulent kinetic energy dissipation rate ε (MacIntyre et al., 1995). The rate can be measured directly or estimated from other measurable quantities with similarity scaling (Tedford et al., 2014). In the parameterization of ε by Tedford et al. (2014), both wind-induced stress and heat-induced convection generate turbulence near the lake surface during cooling, but wind is the only factor responsible for the turbulence during heating. The total turbulent kinetic energy dissipation rate is determined in terms of shear production , where u*w is the wind-induced water-side friction velocity, κ=0.4 is the von Kármán constant, and z′ is a reference depth, and convective turbulence production εc, which equals the buoyancy flux β as
The wind-induced water friction velocity u*w can be calculated from the atmospheric friction velocity , where τ is the wind shear stress and ρa is the density of air, as in MacIntyre et al. (1995):
2.1.2 Gas exchange models
The widely applied experimental wind-based regression formula for k by Cole and Caraco (1998) gives the gas transfer velocity in (cm h−1) as
where U10 (m s−1) is the wind speed at 10 m and Sc is the temperature-dependent Schmidt number of CO2.
In the boundary-layer model by Heiskanen et al. (2014), the wind-induced water friction velocity is approximated to be a linear function of the wind speed at 1.5 m of height, U1.5:
where C1 is an empirical dimensionless constant, and the equation for kHE (m s−1) is
where and C2=0.07 is another experimental dimensionless constant. The model by Heiskanen et al. (2014) is used in the vertical process-based Arctic Lake Biogeochemistry Model (ALBM) (Tan et al., 2017), which simulates inorganic and organic carbon cycling in permafrost lakes. The model by Heiskanen et al. (2014) is also included in the LakeMetabolizer package (Winslow et al., 2016), in which several lake metabolism models can be combined with models for computing the gas transfer velocity.
In the simple wind-based regression model by MacIntyre et al. (2010), the gas transfer velocity kMI (cm h−1) is calculated separately for heating and cooling conditions as
In the surface renewal model of air–water gas exchange, k is parameterized as a function of the total turbulent kinetic energy dissipation rate as , where c is an empirical dimensionless constant and ν is the kinematic viscosity of water (MacIntyre et al., 1995). Tedford et al. (2014) integrated the parameterization of the total turbulent kinetic energy dissipation rate, εTE, into the surface renewal model to yield a model for the gas transfer velocity in units of meters per second:
The models by Cole and Caraco (1998), Heiskanen et al. (2014), and Tedford et al. (2014) are included in a gas exchange model intercomparison study by Dugan et al. (2016).
2.1.3 Lake model MyLake C
We used an application of a one-dimensional process-based lake model, MyLake C (Kiuru et al., 2018), for the simulation of the vertical distributions of water column temperature, CO2 concentration, and air–water CO2 flux in the study lake. In addition, we integrated three alternative models for the gas transfer velocity into the lake model. MyLake C simulates inorganic and organic carbon cycling in a lake, taking into account terrestrial carbon loading, air–water exchange of CO2, and changes in water column pH. However, groundwater exchange and changes in water level due to rainfall or evaporation are excluded. The model operates on a daily time step, and the vertical grid length can be defined by the user. The model is based on a lake model, MyLake v1.2 (Saloranta and Andersen, 2007), which simulates lake thermal structure, seasonal ice and snow cover, and phosphorus–phytoplankton dynamics. In the model, vertical heat and mass diffusion are calculated with a diffusion equation using a vertical turbulent diffusion coefficient derived from the buoyancy frequency and parameterized by lake surface area by default. Settling of particulate substances is also taken into account in the equation. In addition, convective and wind-induced water column mixing processes are included. As an exception to the daily time step, heat exchange between the water column and the atmosphere is calculated separately for daytime and nighttime. MyLake v1.2 and its various extensions have been used in studies on stratification and lake ice cover (e.g., Saloranta et al., 2009; Dibike et al., 2012; Gebre et al., 2014), total phosphorus concentration and phytoplankton biomass (e.g., Romarheim et al., 2015; Couture et al., 2018), dissolved organic carbon (DOC) concentration (Holmberg et al., 2014; de Wit et al., 2018), and dissolved oxygen (DO) conditions (Couture et al., 2015).
MyLake C has been designed to include only the most substantial physical, chemical, and biological processes related to carbon cycling in a well-balanced and robust way. CO2 is produced in the lake through organic carbon degradation both within the water column as well as in the sediment and through phytoplankton respiration. Inorganic carbon production is coupled to DO consumption and vice versa. A division is made between readily degradable, phytoplankton-originated autochthonous particulate organic carbon (POC) and more refractory allochthonous POC. The model also includes the sedimentation, resuspension, and permanent burial of POC. Correspondingly, DOC is classified into three compound classes with different bacterial degradabilities. A separate submodule (Holmberg et al., 2014) calculates the conversion of DOC into DIC via bacterial and photochemical degradation. The meteorological model forcing includes daily global radiation, cloud cover fraction, atmospheric temperature, relative humidity, atmospheric pressure, wind speed at 10 m of height, and precipitation. Hydrological forcing data include daily inflow volumes, inflow temperatures, inflow pH, and the inflow concentrations of modeled substances, including DOC, POC, and DIC. Complete data requirements are presented and model structure and applied equations are described in detail in Kiuru et al. (2018).
MyLake uses the Air–Sea Toolbox (Air-Sea, 1999) based on the parameterizations and algorithms in Fairall et al. (1996) for the calculation of surface wind stress and the components of surface heat flux. The sensible heat flux QH, the latent heat flux QL, and the wind shear stress τ are obtained from aerodynamic bulk formulas of the form
where is the specific heat capacity of air, Ch and Cl are the transfer coefficients of sensible and latent heat, respectively, Cd is the drag coefficient, U is wind speed, Ta is air temperature, Ts is water surface temperature, Le is the latent heat of evaporation of water, qa is the specific humidity, and qs is the saturation specific humidity at the water surface temperature. No wind-sheltering effect on U is applied in the calculation of surface wind stress and surface heat flux components.
The air–water CO2 flux (MyLake C: ) is calculated with Eq. (1) using the model for k by Cole and Caraco (1998) (Eq. 9). The chemical enhancement factor α is set to 1, and the temperature dependence of the aqueous-phase solubility KH is calculated according to Weiss (1974).
In this study, we incorporated the models for k by Heiskanen et al. (2014) (Eq. 11), MacIntyre et al. (2010) (Eq. 12), and Tedford et al. (2014) (Eq. 13) into MyLake C as alternatives to the default model by Cole and Caraco (1998). The constants in the model by Tedford et al. (2014) are defined as c=0.5 and m as in Erkkilä et al. (2018). In MyLake C, the actively mixing layer includes the model grid layers in which the water column temperature is within 0.02 ∘C of the temperature of the topmost grid layer. The temperature dependence of Sc for CO2 is determined for surface water conditions using the polynomial fit in Wanninkhof (1992). The approximation is used for the wind speed at different heights.
2.2 Model application
We used the MyLake C application to Lake Kuivajärvi presented in Kiuru et al. (2018) as the basis of the study. The model setup, including model forcing data and the initial in-lake conditions, is nearly identical to that described in Kiuru et al. (2018). The minor differences are pointed out in Sect. 2.2.2.
2.2.1 Study lake
Lake Kuivajärvi is an oblong, mesotrophic, and humic lake located in southern Finland (61∘ 50′ N, 24∘ 16′ E) at the vicinity of SMEAR II (Station for Measuring Ecosystem–Atmosphere Relations; Hari and Kulmala, 2005). The length of the lake is 2.6 km, the maximum width is 0.3 km, and the surface area is 0.63 km2. The north–south-oriented lake has two distinct basins. The maximum depth of the deeper southern basin is 13.2 m (Heiskanen et al., 2014), which is more than double the mean depth of 6.3 m. A measurement platform (Lake-SMEAR) is situated close to the deepest region of the lake. The approximate retention time of the lake is 0.65 years. Lake Kuivajärvi is surrounded by managed mixed coniferous forest together with small open wetland areas (Miettinen et al., 2015). The majority of the catchment area (9.4 km2) of the lake is flat. The main inlet stream with a mean pH of 6.5 (Dinsmore et al., 2013) drains four upstream lakes, which are smaller in area than Lake Kuivajärvi. The lake is dimictic: the spring turnover usually occurs rapidly right after ice-off in late April or early May, and the summer stratification period lasts until the autumn turnover in September or October. The duration of the ice-covered period and the concomitant inverse stratification is usually 5–6 months (Heiskanen et al., 2015). The turnover periods are hot moments for the release of CO2 accumulated in the hypolimnion of the lake during stratification (Miettinen et al., 2015). Because of high terrestrial inputs of organic matter, the median concentration of DOC in the surface water is 12–14 mg L−1 (Miettinen et al., 2015) and water clarity is rather low, with a median light attenuation coefficient KL being around 0.6 m−1 (Heiskanen et al., 2015).
2.2.2 Model forcing and calibration data
The meteorological forcing data and hydrological loading data used in the model application are described in detail in Kiuru et al. (2018). The daily averages of wind speed at 1.5 m and incoming shortwave radiation together with in-lake temperature and CO2 concentration were obtained from automatic platform measurements (Heiskanen et al., 2014; Mammarella et al., 2015); the remaining meteorological forcing data were obtained from SMEAR II or from weather stations (Finnish Meteorological Institute) in Hyytiälä located less than 1 km from the lake (precipitation) and in Tikkakoski located approximately 95 km to the northeast of the lake (cloud cover fraction). Differing from Kiuru et al. (2018), the CO2 mixing ratio in the atmosphere was assumed to be 395 ppm on the basis of the rather fragmentary time series of high-frequency in situ measurements of the CO2 mixing ratio, the method of which is described in Erkkilä et al. (2018).
The construction of the time series for lake inflow was based on continuous measurements of the discharges at the main inlet and at the outlet of Lake Kuivajärvi in 2013–2014 (Dinsmore et al., 2013). Because the total measured outflow volumes were approximately double the main inlet discharge volumes on an annual scale, the daily inflow volumes were corrected by a factor of 2 in order to include the potential contributions of smaller inlet streams and groundwater to lake inflow. At the main inlet, water temperature was measured approximately two times a month in 2013 and continuously in 2014, and CO2 concentration was measured two times a month in 2013 but mostly at intervals of 2–3 d around the period of ice-off in April and May using the procedure described in Miettinen et al. (2015). Daily time series were generated by linear interpolation.
The model was calibrated against the daily averages of the automatic high-frequency CO2 concentration measurements: an optimal set of selected model parameters was estimated so that the simulated CO2 concentration time series matched the corresponding measured CO2 concentration time series as well as possible. The estimation was performed using a statistical inference algorithm. In addition, the automatic water column temperature measurements were used in model performance validation. The CO2 concentrations were measured at 0.2, 1.5, 2.5, and 7.0 m, and the temperature measurements were performed at 0.2 m, at 0.5 m intervals from 0.5 to 5.0 m, and at 6, 7, 8, 10, and 12 m using the measurement systems described in Heiskanen et al. (2014) and Mammarella et al. (2015).
2.2.3 Model assessment data
We used additional meteorological measurements in assessing the performance of the alternative models for k incorporated into MyLake C during the period May–October 2013. An EC system located on the measurement platform measures the turbulent fluxes of momentum, heat, and water vapor (H2O) over the lake (Mammarella et al., 2015). The EC flux measurement system includes an ultrasonic anemometer (USA-1; Metek GmbH, Elmshorn, Germany) and a closed-path infrared gas analyzer (LI-7200; LI-COR Inc., Nebraska, USA) for measuring CO2 and H2O mixing ratios at 1.8 m of height above the lake surface. Air temperature and relative humidity were measured with a Rotronic MP102H/HC2-S3 (Rotronic Instrument Corp., NY) and radiation components with a CNR1 net radiometer (Kipp & Zonen, Delft, the Netherlands). Automatic platform measurements of net surface longwave radiation and EC measurements of sensible heat flux, H2O flux, and momentum flux were used in the determination of net surface heat flux and atmospheric friction velocity. During EC data post-processing, latent heat flux was calculated from the H2O flux, and the atmospheric friction velocity was derived from the momentum flux. All EC measurement data were given as half-hour block averages. The EC measurements are explained in more detail in Erkkilä et al. (2018), and a description of EC data post-processing is found in Mammarella et al. (2015) and Mammarella et al. (2016). Contrary to the model forcing data, the air temperatures that were used in the measurement-based determination of the gas transfer velocities were obtained from the platform measurements instead of SMEAR II when platform measurements were available. In addition, the rather intermittent platform measurement data on relative humidity were used. In the calculation of the water-side friction velocity, missing relative humidities were replaced by a value of 75 %, which is close to the average of the SMEAR II measurements of relative humidity in May–October 2013: 72 %. The corresponding averages over the period May–August 2013, for which platform measurements were quite applicable, were 66 % and 68 % for the SMEAR II and platform measurements, respectively. Thus, the relative humidity can be assumed to have been slightly higher over the lake than at SMEAR II.
The estimation of the flux footprint distribution functions was made using the model by Kormann and Meixner (2001). The average footprint contributing to 80 % of the fluxes varies from 100 up to about 300 m from the measurement platform depending on atmospheric stability conditions as described in Mammarella et al. (2015). Only wind directions along the lake (130–180 and 320–350∘) were included in the calculations to ensure that heat fluxes from the surrounding land were excluded. Furthermore, possible remaining effects of transversal advection during calm nights were removed through EC quality screening. In addition to the exclusion of some of the EC measurement data through the application of the quality screening criteria presented in Erkkilä et al. (2018), there was a gap in the heat flux data on 14–27 June because of EC system malfunction. The monthly data coverage was 43 %–69 % and 32 %–70 % of the original data for sensible and latent heat fluxes, respectively. We constructed gap-filled half-hour time series for sensible and latent heat fluxes using linear fits between the measured sensible heat flux and wind speed multiplied by the air–surface water temperature difference and between the measured latent heat flux and wind speed multiplied by the vapor pressure difference, according to Mammarella et al. (2015). Only the vapor pressures calculated from the measured relative humidities were used in the latter fit. The fitting was performed independently for each month.
We compared the simulated gas transfer velocities for CO2 and the simulated air–water CO2 fluxes to those determined directly from measurements using the corresponding gas exchange models. The latter are hereinafter referred as to calculated gas transfer velocities and calculated CO2 fluxes. The calculated CO2 transfer velocities for each of the four gas exchange models were obtained using the daily averages of required measured variables. The calculated air–water CO2 fluxes were further obtained as the product of the calculated CO2 transfer velocities and the daily averages of the measured air–water CO2 concentration gradient. The conditions were thus compatible with the daily time step applied in MyLake C. The atmospheric equilibrium concentrations of CO2 were calculated from the measured atmospheric CO2 mixing ratios. The daily averages of the depth of the AML were estimated from the daily averaged temperature profiles as the depth at which water column temperature was within 0.25 ∘C of the temperature at 0.2 m as in Erkkilä et al. (2018). As in MyLake C, the approximation was used in the calculations. Following Mammarella et al. (2015), a value of 2 m−1 was used for the total attenuation coefficient of shortwave radiation KL in the calculation of Qeff.
2.2.4 Model calibration and validation
We estimated the MyLake C parameters utilizing a Markov chain Monte Carlo-based Bayesian inference algorithm following the procedures in the original calibration of the Lake Kuivajärvi application presented in Kiuru et al. (2018). Each of the four new versions of the MyLake C Lake Kuivajärvi application, using the models for k by Cole and Caraco (1998) (both the MyLake C version and the respective gas exchange model being hereinafter referred to as CC), Heiskanen et al. (2014) (HE), MacIntyre et al. (2010) (MI), and Tedford et al. (2014) (TE), was calibrated individually. The simulations with the MyLake C versions using different gas exchange models are hereinafter collectively referred to as GEMs. The model grid length was 0.5 m. The model was run from 8 January 2013 to 31 December 2014. The calibration period extended from 8 January to 31 December 2013, and the measurements in 2014 were used for model validation.
The calibrations were performed against the daily averages of the automatic water column CO2 concentration measurements at the depths of 0.2, 2.5, and 7 m. We chose to apply the automatic measurements instead of the corresponding manual measurements used in the model calibration in Kiuru et al. (2018) because the calculation of daily CO2 fluxes was based on the automatic measurements at 0.2 m in this study, and the simulation results were thus comparable with the calculated CO2 fluxes. Even though the near-surface CO2 concentration was the most significant factor considering air–water CO2 exchange, deeper depths were included so that model behavior would also remain reasonable at deeper levels.
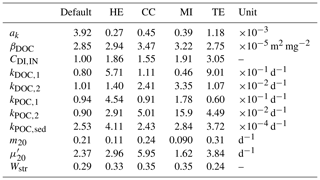
The calibrated model parameters were selected on the basis of the original calibration. However, because the new calibrations were not performed against water column DO concentrations, the parameters related to interactions between DO and CO2, the photosynthetic quotient and the respiratory quotient, were excluded from the parameter set. The DIC inflow concentration scaling factor CDI,IN, applied during open-water seasons, was introduced as a new calibration parameter. The other parameters included in the calibration were the vertical turbulent diffusion parameter ak, the wind-sheltering coefficient Wstr, the DOC-related specific attenuation coefficient of photosynthetically active radiation βDOC, the maximal phytoplankton growth rate at 20 ∘C , the phytoplankton death rate at 20 ∘C m20, the degradation rates of labile DOC kDOC,1 and semilabile DOC kDOC,2, the fragmentation rates of autochthonous POC kPOC,1 and allochthonous POC kPOC,2, and the sedimentary POC degradation rate kPOC,sed. The parameters obtained in the original calibration, or the default parameters, were used as the means of the prior parameter distributions.
One parameter chain with 3000 iterations was produced in each calibration. The starting points were set to 50th percentiles of the prior distributions. The first half of each resultant chain was discarded as a burn-in period, and the final parameters chains included 1500 parameter sets. The medians of the final posterior distributions (Figs. S1–S4 in the Supplement) were chosen as the calibrated parameters. They are presented, together with the default parameters, in Table 2. After the calibrations, additional goodness-of-fit metrics were calculated. The Nash–Sutcliffe (NS) efficiency gives a relative evaluation assessment, determining the relative magnitude of the residual variance compared to the variance of measurement data (Moriasi et al., 2007). The value of the normalized bias (B*) describes a systematic overestimation () or underestimation () of a state variable in the simulation, whereas the normalized unbiased root mean square difference () shows if the standard deviation of the simulated values is higher () or smaller () than that of the measurements (Los and Blaas, 2010).
Table 2Calibrated model parameters for the different versions of MyLake C application to Lake Kuivajärvi with different incorporated gas exchange models (HE: Heiskanen et al., 2014, CC: Cole and Caraco, 1998, MI: MacIntyre et al., 2010, TE: Tedford et al., 2014). The default parameter values were used as the means of the prior parameter distributions.
2.2.5 Calculation of CO2 budgets
After the calibrations, we calculated CO2 budgets for the epilimnion of the lake during periods of continuous summer stratification in 2013 and 2014 for each GEM. The epilimnion was defined as the layer in which water temperature was within 1 ∘C of surface temperature. The stratified period was defined to begin on the day of the formation of the thermocline after ice-off and to finish when the depth of the epilimnion (zepi) reached the value of 7 m in the simulations. The exchange of CO2 between the epilimnion and the atmosphere is balanced in MyLake C by (1) net external loading of CO2, (2) net epilimnetic CO2 production, and (3) the release of CO2 from deeper layers to the epilimnion. The net external loading equals the amount of terrestrially produced CO2 entering the lake via stream inflow subtracted by the amount of CO2 in lake outflow. The release of CO2 from the metalimnion or the hypolimnion occurs through the deepening of the epilimnion due to wind-induced mixing or thermal convection. If the epilimnetic volume becomes smaller, a portion of CO2 is again confined below the epilimnion and the amount of CO2 in the remaining epilimnion is reduced.
3.1 Model calibration
Even though the differences between the formulations of the gas exchange models incorporated into MyLake C are rather notable, the resultant CO2 concentrations did not differ substantially between the GEMs, that is, between the simulations with the MyLake C versions using different gas exchange models (Fig. 1). However, an optimal simulation result can be attained through many different combinations of processes related to in-lake carbon dynamics and fluvial and atmospheric exchange in MyLake C, which is seen in the variation between the parameter values obtained from the different calibrations (Table 2). The calibrations were performed only against CO2 concentrations, and the aim of the calibration was not to try to reproduce the actual in-lake carbon cycling but rather to compare different possible ways to generate an optimal water column CO2 concentration. The performance metrics for CO2 concentration shown in the Supplement (Table S1) indicate that all GEMs yielded CO2 concentrations () that were too low at all depths during the calibration and validation periods with only a few exceptions. However, the CO2 concentration measurements performed during the ice-covered periods were largely not applicable at 0.2 m because of the lake ice cover and sometimes also inapplicable at deeper levels because of incorrect functioning of the measurement system.
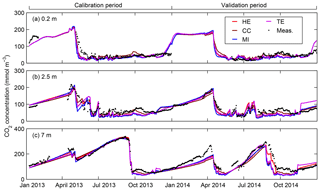
Figure 1Simulation results for CO2 concentration with each GEM (mmol m−3) versus the daily averages of automatic high-frequency CO2 concentration measurements at the depths of (a) 0.2 m, (b) 2.5 m, and (c) 7.0 m in Lake Kuivajärvi during the calibration year 2013 and the validation year 2014.
The average near-surface (0–0.5 m) CO2 concentrations over the open-water seasons were notably higher in CC (44.3 and 40.3 mmol m−3 in the calibration year 2013 and in the validation year 2014, respectively) than in the other GEMs (HE: 34.2 and 31.6 mmol m−3; MI: 31.5 and 29.4 mmol m−3; TE: 36.9 and 34.1 mmol m−3). Only the days with available corresponding water column CO2 concentration measurement data were included in the averaging of the simulated near-surface CO2 concentrations over the open-water seasons. By contrast, the averages of the measured near-surface (0.2 m) CO2 concentrations over the open-water seasons were 45.2 mmol m−3 in 2013 and 37.2 mmol m−3 in 2014. Thus, CC yielded a higher near-surface CO2 concentration compared to the measurements in 2014 when only the ice-free season, the period of air–water CO2 exchange, is considered. The simulated open-water seasons were determined from the simulated ice-off and ice-on dates. Because CO2 flux differs from zero starting from the day after ice-off in MyLake C, the simulated open-water seasons applied in the study were 3 May–25 November 2013 and 16 April–22 November 2014. In 2013, the observed open-water season lasted from 1 May to 27 November. In 2014, the observed ice-off date was 12 April.
The simulated CO2 transfer velocities and air–water CO2 fluxes are presented in Fig. S5. The yearly average values of k were lowest in CC and rather similar between the other GEMs (CC: 2.81 and 2.76 cm s−1 for the calibration period and the validation period, respectively; HE: 5.44 and 5.33 cm s−1; MI: 5.87 and 5.82 cm s−1; TE: 4.73 and 4.66 cm s−1). The differences in the simulated fluxes between GEMs were dissimilar to those in k because of the differences in the simulated near-surface CO2 concentrations. The smallest k values in CC were compensated for by the highest near-surface CO2 concentrations. By contrast, a high daily CO2 efflux due to a high k in MI reduced the simulated near-surface CO2 concentration compared to the other GEMs during the whole simulation period. Overall, the differences in yearly air–water CO2 fluxes between GEMs were smaller than those in the values of k (CC: 0.22 and 0.20 for the calibration period and the validation period, respectively; HE: 0.28 and 0.26 ; MI: 0.25 and 0.24 ; TE: 0.28 and 0.27 ).
The CO2 efflux during the first few days after ice-off was higher in GEMs with a high k, which increased the water column pH in comparison to CC. The differences remained rather constant during most of the open-water seasons. The near-surface pH was on average 0.20–0.26 and 0.18–0.25 units higher in the other GEMs than in CC during the open-water seasons of 2013 and 2014, respectively. As a result, the average fractions of CO2 of DIC in the near-surface layer were respectively 6–8 and 5–6 percentage units higher in CC than in other GEMs, which also contributed to the higher near-surface CO2 concentration in CC than in other GEMs. In addition, the open-water season average near-surface pH was 0.22 units higher in 2014 than in 2013 in all GEMs. Accumulation of bicarbonate in the water column in the course of the simulations may have resulted in an excessively high pH and thus a relatively lower CO2 concentration in 2014 compared to 2013.
The differences in simulated temperatures between GEMs, primarily due to different attenuation of shortwave radiation in the water column, were rather small, especially at 0.2 m and at 2.5 m (Fig. S6). High epilimnetic concentrations of both Chl a and DOC, resulting from a low phytoplankton death rate and a high allochthonous POC fragmentation rate, respectively, in MI resulted in the strongest attenuation of shortwave radiation and thus the highest near-surface temperature because of a thinner and warmer epilimnion than in other GEMs. The open-water season average near-surface temperatures were 0.28–0.47 and 0.65–0.86 ∘C lower than the corresponding measured averages in the calibration and validation periods, respectively, being highest in MI and lowest in TE. The differences were greatest in November before ice-on. The simulated near-surface temperatures tended to be somewhat too low in spring and early summer during both periods and somewhat too high in the late summer and autumn of the calibration year.
Heat transfer to the depth of 7 m right after the onset of the summer stratified period was insufficient in the calibration year in all GEMs, and small values of ak also reduced heat transfer through the epilimnion during summer stratification. As a result, water column temperature remained too low at the depth of 7 m, which was located in the hypolimnion for most of the summer, during the stratified period in the simulations. However, the performance of the simulation of CO2 concentration was also successful at the depth of 7 m. The summertime mixed layer thickness was rather similar between GEMs during the calibration year but more variable during the validation year. Simulated thermocline deepening matched the measurements during the late summer of the calibration year but was too early in the validation year. The deepening was slowest in HE because a somewhat stronger temperature gradient in the metalimnion, which was due to the smallest ak, and resisted wind-induced thermocline erosion during summer.
3.2 Effective heat flux
The effective heat fluxes at the air–water interface simulated with each GEM on 3 May to 31 October 2013 and the corresponding values calculated on the basis of heat flux and radiation measurements are presented in Fig. 2a. The largest differences between the magnitudes and the directions of simulated and measured Qeff were seen in early May. The simulated Qeff was directed out of the lake throughout the study period except for a few occasions in early May and in October, whereas measurement-based calculations yielded more frequent occurrences of a positive daily Qeff. Also, a negative Qeff was often overestimated by the simulations because of overly high negative sensible and latent heat fluxes and net longwave radiation (Fig. S7). The performance of the simulation of the components of surface heat flux was rather poor (Table S2). Overall, the Qeff simulation performance was not very good (R2 = 0.39–0.41, RMSE = 48.2–49.2 W m−2, NS = 0.11–0.14, , n=164). The differences in the simulated Qeff between GEMs, resulting mainly from different surface temperatures, were quite small.
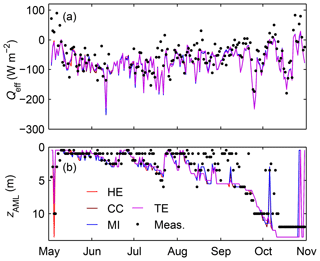
Figure 2(a) Daily effective surface heat fluxes (W m−2) simulated with each GEM and calculated on the basis of heat flux measurements. (b) Simulated and empirically determined depths of the daily actively mixing layer (m) in Lake Kuivajärvi in May–October 2013.
The extent of shortwave radiative heating of the AML, QSW,AML, is dependent on zAML. The simulated zAML was greater than the measured daily average with a few exceptions at the beginning and near the end of the study period (Fig. 2b), which increased the simulated QSW,AML and decreased a negative Qeff. The simulation with a daily time step generated clear temperature variation in the epilimnion only on days with a high amount of surface heating in early summer and midsummer, which resulted in an overly deep AML during most of the period. In addition, the model with a sequential description of thermal processes did not catch simultaneous wind mixing and surface heat exchange processes that resulted in a deeper observational AML in spring and late autumn. However, day-to-day variation in the discrepancy of QSW,AML was high throughout the study period. Also, the simulations highly underestimated the atmospheric friction velocity (R2=0.35, RMSE = 0.11 m s−1, NS = −3.2, , n=166) (Fig. S8), the simulated u*a being on average only 46 % of the measured daily average. The simulated daily drag coefficient Cd at 1.5 m was affected by atmospheric stability conditions. The median Cd varied from to between the GEMs.
3.3 CO2 exchange
The differences between simulated gas transfer velocities for CO2 and the respective calculated values during the study period 3 May–31 October 2013 were rather small in the cases of gas exchange models based solely on wind speed, CC and MI, but the discrepancies were higher in HE and TE, which also include the effect of thermal convection on gas exchange (Fig. 3, Table S3). The simulations with CC and MI often yielded slightly higher values of k than the respective calculations because the simulated surface temperature was higher than the measured daily average (Fig. S6), and thus the temperature-dependent Schmidt number correction of k was different. Also, the occurrences of a simulated negative β in early May in MI yielded higher kMI compared to the respective calculated values obtained from the observed positive β. The simulated kHE was often higher than the calculated counterpart because of a high negative Qeff or a deep AML in the simulations (Fig. 2), which resulted in a high penetrative convection velocity. In HE, the effects of wind-induced shear and thermal convection on k are set to be roughly of the same order of magnitude and the wind-induced shear velocity is calculated from wind speed, whereas CO2 flux is driven principally by wind shear, which is calculated directly from u*a, in TE. Because the simulated u*a was consistently significantly lower than the corresponding daily measured average, the simulated kTE was on average 40 % lower than the calculated value.
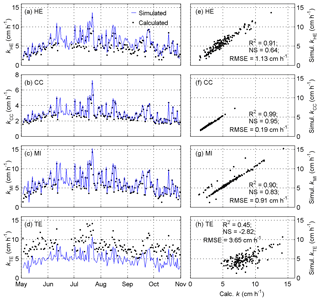
Figure 3Simulated and calculated gas transfer velocities for CO2 (cm h−1) in Lake Kuivajärvi on 3 May–31 October 2013 obtained with the gas exchange models by (a, e) Heiskanen et al. (2014), (b, f) Cole and Caraco (1998), (c, g) MacIntyre et al. (2010), and (d, h) Tedford et al. (2014).
The simulated near-surface CO2 concentrations were significantly too low during most of the study period in all GEMs except for CC, which yielded concentrations in autumn that were too high (Fig. 4, Table S3). The higher the simulated k and daily CO2 efflux, the greater the resulting decrease in near-surface CO2 concentration. The decline of the near-surface CO2 concentration after ice-off was too rapid in all GEMs, especially in MI, the GEM with the highest k. The simulated near-surface CO2 concentration also declined close to the atmospheric equilibrium concentration in all GEMs in late summer because of an insufficient gain of CO2 in a shallow epilimnion developed under warm and calm conditions. The low simulated air–water CO2 concentration gradients in May resulted in an underestimated air–water CO2 flux from the water column compared to the respective calculated fluxes (Fig. 5, Table S3). The simulated flux was notably lower than the calculated flux in TE during the whole study period because of a small kTE. In contrast, CC notably overestimated the corresponding calculated CO2 flux in August and September because of a high simulated near-surface CO2 concentration. Also, the simulated CO2 flux was slightly higher than the calculated flux in HE in August and September because of high epilimnetic net CO2 production. The total simulated CO2 flux during May–October matched the calculated flux in CC but was notably lower in HE and MI and less than half of the calculated flux in TE (Table 3). The underestimated near-surface CO2 concentrations were somewhat compensated for by the higher simulated kHE and kMI compared to the calculated counterparts, which decreased the difference between the simulated and calculated fluxes in HE and MI.
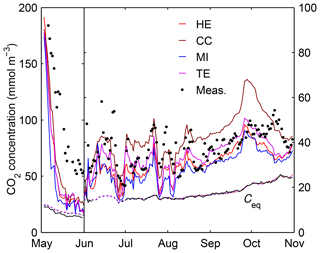
Figure 4Simulated CO2 concentrations (mmol m−3) in the surface layer (0–0.5 m) obtained with each GEM and the daily averages of the automatic measurements at 0.2 m in Lake Kuivajärvi in May–October 2013. Also shown are the atmospheric equilibrium concentrations of CO2 (Ceq) obtained from the simulations (dotted colored lines) and calculated from the measured atmospheric CO2 concentration and surface water temperature (solid black line). Note the different vertical scales in May and in June–October.
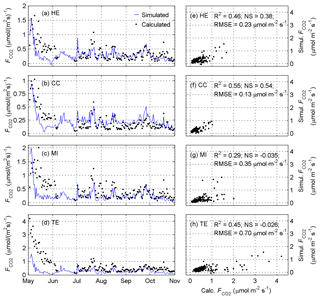
Figure 5Simulated and calculated air–water CO2 fluxes () in Lake Kuivajärvi on 3 May–31 October 2013 obtained with the gas exchange models by (a, e) Heiskanen et al. (2014), (b, f) Cole and Caraco (1998), (c, g) MacIntyre et al. (2010), and (d, h) Tedford et al. (2014).
Table 3Total and monthly averages of simulated and calculated CO2 fluxes () in May–October 2013 obtained with different gas exchange models. Only the days with available measurement data are included in the averaging of the simulated fluxes. Monthly values for June are excluded because measurement data were available only for 7 d.
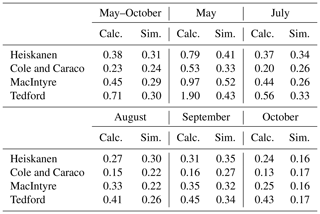
The applied gas exchange models yielded notably different calculated monthly CO2 effluxes (Table 3). The CO2 fluxes were calculated using the measured air–water CO2 concentration gradients, and thus the differences between the calculated fluxes were only due to different values of k. Monthly fluxes calculated with MI were nearly or even more than double those calculated with the other wind-based model CC. Days with a positive β, resulting in a lower kMI, occurred mainly in May and October, and thus the difference between the CO2 fluxes calculated with MI and CC was slightly smaller in those months. The models that include the effect of thermal convection, HE and TE, yielded notably higher CO2 fluxes than the simplest model, CC. Nevertheless, the CO2 fluxes calculated with MI were slightly higher than those calculated with HE. The CO2 fluxes calculated with TE were clearly the highest in all months, which was, however, not the case in the simulations.
The calculated daily values of k and CO2 flux were dependent on the calculation interval. If the daily k had been calculated as the daily average of calculated half-hour values of k instead of using the daily averages of the input variables, the results would have been different. The daily averages of calculated half-hour kMI (RMSE = 0.70 cm h−1, ) and kTE (RMSE = 0.22 cm h−1, ) were lower than the respective values calculated using daily averages of input variables, whereas the opposite was the case for kHE (RMSE = 0.48 cm h−1, ) and kCC (RMSE = 0.16 cm h−1, ). In contrast, the calculation of a daily CO2 flux as the average of half-hour fluxes yielded a slightly higher CO2 flux in all GEMs (HE: RMSE = 0.066 , ; CC: RMSE = 0.034 , ; MI: RMSE = 0.10 ,; TE: RMSE = 0.11 , ).
The differences resulting from the different methods of the calculation of a daily k can partly be explained by the behavior of the driving variables of the models. Using the daily averages of the input variables in the calculation may have smoothened out the effects of the spells of stronger negative buoyancy flux or a deeper AML that increase the half-hour kHE and the effects of the occasions of positive buoyancy flux that decrease the half-hour kMI. Daily averaging of wind speed may have cut out the rapid increase in kCC under stronger wind conditions during the course of day due to the greater-than-linear dependence of kCC on wind speed. By contrast, because the dependence of kTE on u*a is less than linear and the impact of thermal convection on kTE is minor, the effect of the diel variation of u*a and thus the relative difference between the methods of the calculation of kTE was rather small.
3.4 Lake CO2 budgets
The simulated CO2 budgets for the epilimnion of the lake during periods of continuous summer stratification in 2013 and 2014 differed between GEMs as a response to different CO2 effluxes (Table 4). The simulations were not able to reproduce the short-lived episodes of a very shallow epilimnion on days with high solar radiation and low wind speeds in late August and early September 2013, but at other times the simulated zepi matched the depths estimated from the measured daily temperature profiles rather well (Fig. 6). The epilimnion formed 11 d earlier and extended to 7 m 16–22 d later in 2013 than in 2014. The in-lake CO2 concentrations were higher at the onset of stratification in 2013 than in 2014 because of less effective water column ventilation during the shorter spring mixing period. As a result, the amount of CO2 in the epilimnion decreased during the stratified period in 2013, whereas it increased slightly in 2014.
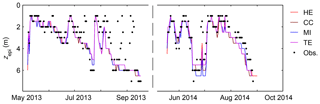
Figure 6Simulated and observed depths of the epilimnion (m) in Lake Kuivajärvi during the continuous summer stratification in 2013 and 2014. The simulations were performed using each of the gas exchange models incorporated into MyLake C.
Table 4Simulated CO2 budgets (kg CO2) for the epilimnion of Lake Kuivajärvi during summer stratification in 2013 and 2014 using different gas exchange models incorporated into MyLake C.
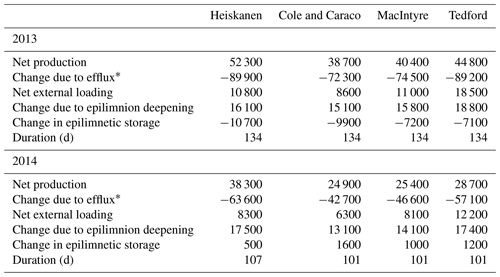
* The change in water column CO2 content due to CO2 efflux was approximately 1 % lower than the amount of CO2 evaded because of consequent equilibrium reactions in the carbonate system.
A higher net in-lake CO2 production or a higher terrestrial CO2 load was required to compensate for the higher CO2 efflux in GEMs that yielded higher values of k (Table 4). Phytoplankton concentration, regulated in MyLake C by growth and death rates μ′ and m, respectively, impacts CO2 dynamics both directly through the amount of carbon fixation and indirectly through changes in epilimnetic thermal structure due to the attenuation of solar radiation. A high μ′ resulted in faster phytoplankton growth in spring and thus in an earlier occurrence of the spring bloom, and a small m resulted in a higher phytoplankton biomass during midsummer and late summer. HE and MI yielded the highest maximum near-surface Chl a concentrations, approximately 15 mg m−3 in 2013 and close to 20 mg m−3 in 2014. In CC and TE, Chl a concentrations were greater than 10 mg m−3 during the growth peaks but less than 5 mg m−3 at other times because of the high values of m. The open-water season average near-surface Chl a concentration was highest in HE (9.6 and 9.3 mg m−3 in 2013 and 2014, respectively), followed by MI (7.5 and 6.1 mg m−3), CC (3.9 and 4.0 mg m−3), and TE (2.3 and 2.1 mg m−3).
However, a high phytoplankton biomass did not imply high CO2 consumption because of phosphorus limitation of phytoplankton growth in the model and the resultant reduction of photosynthetic CO2 consumption under high Chl a and low bioavailable phosphorus concentrations in the simulations. Instead, CO2 fixation occurred at a steady rate and the total CO2 consumption over the whole growing season was relatively higher under a low Chl a concentration due to a high m. The highest average phytoplankton biomass in HE resulted in the highest CO2 fixation; however, total net CO2 production was also highest in HE because of high kPOC,1 and kDOC,1. Small values of kPOC,1 and kDOC,2 resulted in a relatively low net CO2 production despite low CO2 fixation and a high kPOC,sed in TE. Net CO2 production was lowest in CC because of rather high total CO2 fixation during the long growing season and the rather small kPOC,1 and kDOC,1.
A considerable increase in the inflow DIC concentration by way of the scaling factor was essential in order to significantly increase the terrestrial CO2 input to the lake in GEMs with a high CO2 efflux. The measured inflow CO2 concentration was 200–250 mmol m−3 until ice-off, less than 80 mmol m−3 during May, and mainly between 50 and 100 mmol m−3 during the summer and autumn. Thus, the default inflow CO2 concentration was only approximately double the simulated near-surface CO2 concentrations during most of the open-water season, and the effect of external CO2 loading on in-lake CO2 concentration was inevitably rather small, especially during the low-discharge period in late summer and autumn. The values of CDI,IN determined the order of the amounts of the net external CO2 load to the lake in the GEMs (TE: 42 000 and 45 000 kg CO2 over the years 2013 and 2014, respectively; MI: 27 500 and 31 400 kg CO2; HE: 26 500 and 30 600 kg CO2; CC: 22 200 and 25 800 kg CO2).
However, the total net external CO2 loads to the lake over the stratification periods were slightly higher than the net external CO2 loads to the epilimnion in Table 4 because stream inflow was directed into the metalimnion on days when the inflow temperature was lower than the epilimnetic temperature. The epilimnetic loads were 90 %–92 % and 98 %–99 % of the total loads in 2013 and 2014, respectively, the proportions being highest in CC and lowest in MI. The amount of CO2 outflow was relatively large in CC because of the high epilimnetic CO2 concentration; thus, the net external CO2 load was relatively lower in CC than in other GEMs compared to the differences in CDI,IN. In addition, because inflow pH was unaltered in the scaling of inflow DIC concentration, some of the increased CO2 load was eventually evaded to the atmosphere in the simulations, but the bicarbonate fraction of DIC remained in the water column, which resulted in a slight increase in in-lake pH and a decline in the CO2 fraction of DIC, especially in GEMs with a high k. Nevertheless, the impact of different amounts of bicarbonate loading on the in-lake pH was minor compared to the impact of different springtime CO2 effluxes between GEMs.
4.1 Differences between calculated and simulated CO2 fluxes
There was less variation between the air–water CO2 fluxes simulated with different GEMs, that is, simulated with the MyLake C versions using different gas exchange models, than between the CO2 fluxes calculated with the corresponding different gas exchange models on the basis on measured surface heat fluxes and air–water CO2 concentration gradients (Table 3). This was caused both by differences between the simulated and calculated values of k and by insufficient epilimnetic CO2 production in the simulations. An increased terrestrial CO2 loading or an increased in-lake CO2 production was needed to balance the higher CO2 loss from the epilimnion through efflux in GEMs with a higher k compared to the simple wind-based CC (Table 4). Still, the simulations yielded near-surface CO2 concentrations that were too low (Fig. 4, Table S3), which contributed to the underestimation of CO2 fluxes (Fig. 5). Calibrating the model only against the near-surface CO2 concentration and thus using even higher values for organic carbon fractionation and degradation parameters would have improved the performance of the simulation of epilimnetic CO2 concentration; however, it would have resulted in uncontrollable and probably excessively high CO2 concentrations in deeper layers, which is disadvantageous in a year-round, vertically layered lake model.
The day-to-day performance of the simulation of epilimnetic CO2 concentration was also partly determined by the simulated thermal stratification and epilimnetic volume. The simulations generally yielded a near-surface CO2 concentration that was too low when the simulated zepi was in accordance with the observed depth and performed more adequately only during periods when the simulated zepi was too high (Figs. 4 and 6). The measurements showed an increase in the near-surface CO2 concentration when the epilimnion became thicker, and vice versa, during the stratified period in 2013. Thermocline tilting-induced upwelling and convection-induced entrainment transported more CO2-rich water into the epilimnion on windy and cool days (Heiskanen et al., 2014). Conversely, high solar radiation input combined with calm conditions results in the warming of near-surface water and the formation of a thin epilimnion with a lower CO2 concentration. High solar radiation also enhances photosynthesis and thus increases the uptake of CO2 (Provenzale et al., 2018). An overly deep simulated epilimnion resulted in enhanced CO2 release from deeper layers and a higher total net CO2 production in a larger epilimnetic volume, which were able to compensate for the CO2 efflux in the simulations.
The accuracy of the determination of a daily Qeff and the applicability of the concept of a daily AML are issues that may cause uncertainties when gas exchange models are used either to calculate or to simulate daily estimates of k. The calculated half-hour Qeff was generally directed into the lake on some occasions during daytime because of solar heating of the AML and always directed out of the lake at nighttime; zAML often increased during nighttime and decreased under the radiative heating of near-surface water during daytime. Boundary-layer models and surface renewal models have been developed to describe the short-term dynamics of turbulence in a shallow AML, and thus they may not perform equally well in calculations with a daily time step.
The wind-based CC yielded the lowest and the surface renewal model TE the highest calculated air–water CO2 fluxes, which is in line with the comparisons of different gas exchange models using data from Lake Kuivajärvi by Mammarella et al. (2015) and Erkkilä et al. (2018); however, the differences in simulated CO2 fluxes between CC and other GEMs were notably smaller than the corresponding differences in the two experimental studies. The performance of TE is strongly dependent on the magnitude of u*a because wind shear is highly dominant over thermal convection as the generator of turbulence in the model. Because the simulations yielded significantly lower u*a compared to the values obtained through EC measurements (Fig. S8), the CO2 flux obtained with TE was much lower than the corresponding calculated flux. Also, Erkkilä et al. (2018) found that u*a calculated from wind speed was lower than the measured u*a in Lake Kuivajärvi. Bulk models for surface stress may yield low values for u*a over a lake, especially when parameterized for open-sea conditions with low surface roughness (Wang et al., 2015), which is the case in MyLake C. Lake size may also affect the relative differences between gas transfer velocities obtained with different gas exchange models. Dugan et al. (2016) applied different gas exchange models to the calculation of DO exchange in temperate lakes of various sizes. Simple, wind-based models yielded clearly lower values of k than more complex models in lakes similar to Lake Kuivajärvi in size, whereas the differences between the model types were smaller in larger lakes with generally higher wind speeds and a higher relative importance of wind-induced mixing compared to convection. In addition, ecosystem-specific empirical regression models may not be suitable for lakes with dissimilar characteristics (Vachon and Prairie, 2013).
4.2 Comparison to EC CO2 flux measurements
Estimates of air–water CO2 fluxes obtained with the gas exchange models applied in our study have been compared with 30 min block-averaged EC CO2 flux measurements over Lake Kuivajärvi (Heiskanen et al., 2014; Mammarella et al., 2015; Erkkilä et al., 2018). Heiskanen et al. (2014) compared the half-hour k calculated with HE, CC, and MI with those obtained through EC measurements of CO2 flux in August–November 2011. In the study, the average values of kHE and kMI were approximately 70 % of the corresponding measurement-based values, but the average kCC was only about half of the average kHE and kMI. Erkkilä et al. (2018) compared the daily medians of EC CO2 flux during a 2-week period in October 2014 with the daily median CO2 fluxes calculated with CC, HE, and TE. The CO2 fluxes obtained with HE and TE were 60 % of the EC CO2 fluxes and approximately double the CO2 fluxes obtained with CC. Overall, TE yielded the best correspondence with the EC fluxes. TE also outperformed CC in the comparison of half-hour CO2 fluxes during the open-water periods of 2010 and 2011 in Mammarella et al. (2015). In our study, the best agreement with simulated and calculated CO2 fluxes was found in CC, whereas TE yielded the lowest simulated fluxes in comparison to the corresponding calculated fluxes. Thus, none of the GEM outputs can be considered compatible with EC CO2 fluxes, provided that the conclusions from the half-hour comparisons in the abovementioned studies can be extended to a daily scale.
The simulation results for the daily air–water CO2 fluxes cannot be directly compared with EC data because the data coverage of EC flux measurements is often low. For example, the data coverages for CO2 flux were 27 % and 37 % in Erkkilä et al. (2018) and Mammarella et al. (2015), respectively. Quality screening excludes much of the measurement data, and short-time system malfunction may cause significant data loss during long study periods. Daily average or median EC CO2 flux may not be representative for the whole day because of the temporal bias of the measurements. EC flux measurements often tend to be inapplicable, especially at nighttime, because of flux nonstationarity during light winds and cooling (Heiskanen et al., 2014) or the advection of CO2 from the surrounding forest (Erkkilä et al., 2018). EC CO2 fluxes over boreal lakes are often enhanced at night by water-side convection (Podgrajsek et al., 2015) or because of a higher air–water CO2 concentration gradient due to the absence of photosynthesis as a CO2 sink (Erkkilä et al., 2018).
Both the calculated and the simulated values of k were determined by means of the platform data. They were thus suitable for comparison with each other but may not represent the average conditions over the lake and hence may not yield correct estimates of whole-lake CO2 fluxes. Wind speed, u*a, QH, and QL were measured at a single point on the platform, and the source area of the EC measurements of u*a, QH, and QL ranges from 100 to 300 m along the wind direction over the lake (Mammarella et al., 2015). Thus, the values may not be representative for the whole lake. Wind speed and the resulting u*a over lakes surrounded by forests are lower in sheltered nearshore areas than in the central zones of the lakes (Markfort et al., 2010). Sheltering affects the spatial variation of wind speed, especially in small lakes such as Lake Kuivajärvi. Because QH and QL are dependent on wind speed over the lake, they may also be higher at the center of the lake than in nearshore areas. Also, the estimation of u*a, QH, and QL in the simulations was based on wind speed and other forcing data obtained from the single-point measurements, and the simulated values may have been overestimates of the spatial averages. However, despite the same measurement location, some disparities existed between the simulated and measured QH and QL. The differences may be in part attributed to an underestimation of surface heat fluxes by the EC method, which was seen, for example, in a study on energy balance over a small boreal lake by Nordbo et al. (2011) and also in Mammarella et al. (2015). The sum of the measured EC heat fluxes in Lake Kuivajärvi was on average 83 % and 79 % of available energy in 2010 and 2011, respectively, in Mammarella et al. (2015). In addition, the total relative random error of the EC measurements is generally around 10 % for both sensible heat flux and latent heat flux as estimated in Mammarella et al. (2015). Considerable spatial variability may also occur in near-surface water CO2 concentration in small, shallow boreal lakes (Natchimuthu et al., 2017), which may result in further discrepancies in the estimates on whole-lake CO2 flux obtained on the basis of gas exchange models or by using a vertical, horizontally integrated lake model.
4.3 Factors influencing the epilimnetic CO2 budget
The model parameter sets obtained through calibration of the MyLake C applications using different incorporated gas exchange models were notably different from each other, thus emphasizing different processes related to carbon cycling within the water column or to carbon exchange with the surrounding terrestrial ecosystem or the atmosphere. However, considering the main objective of the study, which is the simulation of near-surface CO2 concentration and air–water CO2 flux, the different outcomes of the calibration processes, that is, the different model parameter sets, can be considered equally justified as they give insight on the diversity of biogeochemical processes that impact lacustrine CO2 dynamics.
Phytoplankton is a significant factor in the lake CO2 budget and the main driver of the diurnal variation of CO2 concentration in Lake Kuivajärvi (Provenzale et al., 2018). In MyLake C, inorganic carbon is fixed by phytoplankton and carbon is stored in autochthonous organic matter within the water column or in bottom sediments until it is mineralized by bacteria. A relatively large portion of epilimnetic phytoplankton and dead autochthonous particulate organic matter sank from the epilimnion into deeper layers in MI because of the small values of m and kPOC,1. Production of CO2 via the degradation of phytoplankton-originated organic matter, as well as the release of bioavailable phosphorus in the epilimnion through the mineralization of autochthonous organic matter, was also slow in MI because of a small kDOC,1. As a result, the net production of CO2 in the epilimnion was rather low in MI (Table 4) despite the relatively high simulated phytoplankton biomass. Overall, differences in total net CO2 consumption by phytoplankton during the stratified period between GEMs were rather small despite the large variation in the simulated phytoplankton biomasses because of the phosphorus limitation of photosynthesis in GEMs with a high phytoplankton biomass and because of the variation in the length of the active growing season between GEMs.
The simulated Chl a concentrations were rather constant over the growing season with the exception of the substantial spring growth peaks in CC and TE. There are no data on Chl a concentration in Lake Kuivajärvi in 2013, but the Chl a concentration at 0–3 m was at its highest, 30–50 mg m−3, in mid-July and decreased to a level of less than 2 mg m−3 in late autumn in the years 2011–2012 (Heiskanen et al., 2015). The epilimnetic Chl a concentration is usually 3–5 mg m−3 during the growing season with diatom-induced peaks under cool conditions in spring and autumn (Provenzale et al., 2018). Thus, the GEMs with low near-surface Chl a concentrations, CC and TE, may have yielded better estimates of the overall phytoplankton biomass than HE and MI. However, the net consumption of CO2 by phytoplankton was not only related to the amount of phytoplankton biomass. Nevertheless, none of the GEMs captured the supposed monthly variation of epilimnetic CO2 concentration caused by the seasonal succession of phytoplankton.
A conspicuously high CDI,IN was needed to balance the high CO2 efflux in the GEMs with a high k (Table 2). The restriction of the scaling of the inflow DIC concentration to the open-water season was a rough way to increase the gain of epilimnetic CO2, and the summertime inflow CO2 concentrations may have been unnaturally high, especially in TE. However, the use of CDI,IN can be thought as the inclusion of the input of CO2 through groundwater seepage to the lake. In budget calculations, groundwater DIC load can be generally estimated by applying groundwater DIC flow as a percentage of stream DIC load (Chmiel et al., 2016). The amount of inflowing groundwater and its properties in Lake Kuivajärvi are unknown. However, in addition to inflow through minor inlet streams and surface runoff, especially during snowmelt in spring, groundwater seepage may contribute somewhat to the total lake inflow volume because the measured total outflow volume over the year 2013 was approximately double the inflowing volume via the main inlet stream. The CO2 concentration in groundwater in southern Finland is around 700–900 mmol m−3 (Lahermo et al., 1990), which is about tenfold higher than the estimated average inflow CO2 concentration in Lake Kuivajärvi over the stratified period in 2013, 86 mmol m−3, and well in line with the yearly average groundwater CO2 concentration near a boreal stream determined by Leith et al. (2015). Thus, groundwater-derived CO2 transport to the lake may also affect the water column CO2 concentration.
The effect of CO2 inputs through minor inlets or groundwater may be supported by the fact that the simulated near-surface CO2 concentration decreased too fast in all GEMs after ice-off in May 2013, that is, during a period when the snowmelt-induced flow in minor inlet streams may be substantial and when the groundwater level is generally relatively high (Fig. 4). The simulated epilimnetic CO2 sinks were rather small at that time because net CO2 consumption by phytoplankton was low in cool water and because CO2 efflux was relatively low because of a low air–water CO2 concentration gradient. Labile, autochthonous DOC was absent in the epilimnion in the simulations, and the degradation of allochthonous DOC was slow under the relatively cold conditions in May. Despite the measured inflow CO2 concentration being approximately twice the simulated epilimnetic CO2 concentration and the scaled inflow CO2 concentrations and terrestrial CO2 loads being even higher, the decline of the epilimnetic CO2 concentration was rapid in all GEMs. The high abundance of diatoms in Lake Kuivajärvi in spring may have resulted in a supply of easily degradable organic matter, but net primary production also consumed CO2. Thus, substantial CO2 loadings through surface runoff, minor inlet streams, or groundwater seepage could have been plausible additional sources of epilimnetic CO2 in May, provided that the additional surface inflow was rich in CO2. The impact of groundwater seepage is supported by a study on the carbon budget of a small boreal lake by Chmiel et al. (2016), in which a discrepancy between estimates of the gain and loss of inorganic carbon was explained by a possible underestimation of the impact of groundwater inflow.
4.4 Implications for lake modeling
None of the four MyLake C versions with different gas exchange models surpassed the other ones in the study because of the complex interplay between the near-surface water CO2 concentration and air–water CO2 flux in the simulations. A higher CO2 efflux would have required a higher gain of CO2 in the lake through in-lake CO2 production or external loading of inorganic carbon, but the MyLake C versions with gas exchange models yielding a high k were not capable of increasing the CO2 gain sufficiently. Hence, it is not a trivial task to judge which of the four gas exchange models is most suitable for integration into MyLake C or other coupled physical–biogeochemical lake models. However, several experimental studies (e.g., Jonsson et al., 2008; MacIntyre et al., 2010; Heiskanen et al., 2014) have shown that traditional, wind-based models often yield low CO2 fluxes when compared to estimates based on direct measurements. Thus, it is recommended to strive to use the more sophisticated and probably more correct gas exchange models provided that the biogeochemical lake model can be made adaptable to higher CO2 losses and that the parameters included in the more complex, turbulence-based models can be correctly simulated. This also means that further improvements related to the description of in-lake carbon processes in lake models and to the modeling or other means of estimation of external inorganic and organic carbon loading are still needed. Despite the challenges in using complex process-based models in the assessment of carbon cycling in lakes, modeling is an effective means to quantify underlying processes related to lacustrine CO2 emissions and to study the development of lake ecosystems under changing conditions.
We studied the applicability of four gas exchange models with different complexity incorporated into a vertical physico-biogeochemical lake model, MyLake C, to the simulation of air–water CO2 exchange and water column CO2 concentration in a humic boreal lake. The gas transfer velocities simulated using the simplest, wind-based gas exchange model by Cole and Caraco (1998), or CC, were best in accordance with the corresponding values calculated on the basis of direct in-lake measurements, whereas simulations with the other gas exchange models either overestimated (the models by Heiskanen et al., 2014 and MacIntyre et al., 2010) or underestimated (the model by Tedford et al., 2014) the respective calculated gas transfer velocities because of discrepancies in the simulation of wind stress or daily effective surface heat flux.
None of the applied gas exchange models resulted in a highly improved simulation performance regarding water column CO2 concentration or air–water CO2 flux. On the contrary, the more complex gas exchange models, which include both wind-induced stress and heat-induced convection as the drivers of CO2 exchange, yielded higher gas transfer velocities and thus higher CO2 fluxes in the simulations, which resulted in difficulties in obtaining a sufficient gain of CO2 in the water column to balance the loss to the atmosphere. In addition, the model with a daily time step was not always able to simulate the changes in near-surface CO2 concentration and air–water CO2 flux resulting from short-term physical processes, such as nighttime cooling or simultaneous surface heating and wind mixing. As a result, all the incorporated gas exchange models except for CC yielded summertime epilimnetic CO2 concentrations in the simulations that were notably too low, which was also reflected by a significant underestimation of CO2 fluxes compared to the corresponding fluxes calculated from the calculated gas transfer velocities and measured air–water CO2 concentration gradients. The daily CO2 fluxes simulated with CC were closest to the corresponding calculated fluxes. The long and widely used CC was, however, shown to produce CO2 flux estimates that are too low, and its use was discouraged in an empirical gas exchange model intercomparison study by Erkkilä et al. (2018), whereas the more complex models yielded presumably more correct CO2 fluxes. Nevertheless, it has to be noted that the comparison between the gas exchange models is more complex in our modeling study than in Erkkilä et al. (2018) because of the interplay between the simulated CO2 flux and water column CO2 concentration.
The present model application was not highly adaptable to increased CO2 effluxes. The extent of the in-lake production of CO2 is largely related to model structure, process descriptions, and the estimation of parameter values, whereas the amount of external CO2 input is governed by the quality of hydrological forcing data. Therefore, research on processes contributing to carbon cycling in boreal freshwaters and on the roles of different internal and external sources of CO2, such as groundwater, in lakes is sorely needed in order to enhance the predictive performance of model simulations.
The issues raised in our study concerning lacustrine carbon budgets can also be generalized to a larger scale. The application of advanced gas exchange models has been shown to lead to increased estimates of CO2 emissions from boreal inland waters. Thus, higher estimates of net terrestrial ecosystem production and carbon flux from land to inland waters are required to close the regional carbon budget. Also, the use of advanced, possibly more correct gas exchange models in the assessment of global gas efflux from freshwaters may result in higher estimates of the impact of freshwater ecosystems on global carbon cycling.
The MATLAB model code for the MyLake C application presented in this study is freely available at https://github.com/biogeochemistry/MyLake_C/tree/MyLake_C-gtsv (last access: 29 August 2019). The automatic water column temperature and CO2 concentration data, the SMEAR meteorological data, and the manual measurement data presented in this study are available in the AVAA open research data publishing platform (https://avaa.tdata.fi/web/smart/smear/download/, last access: 29 August 2019). The metadata of these measurements are available via the ETSIN service (https://etsin.avointiede.fi/, last access: 29 August 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-16-3297-2019-supplement.
PK, TV, AO, and TH conceived the idea and designed the modeling study. PK developed the model application, conducted the model simulations, and performed the analyses. IM, JH, and TV designed the field experiments. IM, JH, and HM participated in the field measurements. IM and KME participated in the automatic measurement data post-processing. PK prepared the paper with contributions from all coauthors.
The authors declare that they have no conflict of interest.
The work of Petri Kiuru was funded by grants awarded by the Kone Foundation and Maa- ja vesitekniikan tuki ry. The authors acknowledge the following: the Academy of Finland Centre of Excellence (272041 and 118780), Academy Professor projects (1284701 and 1282842), and ICOS Finland (281255) funded by the Academy of Finland; the European Union Horizon 2020 project RINGO (730944); and the AtMath project funded by the University of Helsinki. We thank Miitta Rantakari for the provision of the inflow data.
This research has been supported by the Academy of Finland (grant nos. 272041, 118780, 1284701, 1282842, and 281255), the European Commission (Horizon 2020 (grant no. 730944)), the Koneen Säätiö, and the Maa- ja vesitekniikan tuki ry.
This paper was edited by Gwenaël Abril and reviewed by two anonymous referees.
Air-Sea: Air-Sea Toolbox by Rich Pawlowicz and Bob Bearsley, available at: https://sea-mat.github.io/sea-mat (last access: 27 February 2019), 1999. a
Algesten, G., Sobek, S., Bergström, A.-K., Ågren, A., Tranvik, L. J., and Jansson, M.: Role of lakes for organic carbon cycling in the boreal zone, Glob. Change Biol., 10, 141–147, https://doi.org/10.1111/j.1365-2486.2003.00721.x, 2014. a
Bade, D. L., Carpenter, S. R., Cole, J. J., Hanson, P. C., and Hesslein, R. H.: Controls of δ13C-DIC in lakes: Geochemistry, lake metabolism, and morphometry, Limnol. Oceanogr., 49, 1160–1172, https://doi.org/10.4319/lo.2004.49.4.1160, 2004. a
Banerjee, S.: The Air-Water Interface: Turbulence and Scalar Exchange, in: Transport at the Air-Sea Interface: Measurements, Models and Parametrizations, edited by: Garbe, C. S., Handler, R. A., and Jähne, B., 87–101, Springer, Berlin, Heidelberg, 2007. a
Battin, T. J., Luyssaert, S., Kaplan, L. A., Aufdenkampe, A. K., Richter, A., and Tranvik, L. J.: The boundless carbon cycle, Nat. Geosci., 2, 598–600, https://doi.org/10.1038/ngeo618, 2009. a, b
Chmiel, H. E., Kokic, J., Denfeld, B. A., Einarsdóttir, K., Wallin, M. B., Koehler, B., Isidorova, A., Bastviken, D., Ferland, M.-È., and Sobek, S.: The role of sediments in the carbon budget of a small boreal lake, Limnol. Oceanogr., 61, 1814–1825, https://doi.org/10.1002/lno.10336, 2016. a, b, c
Cole, J. J. and Caraco, N. F.: Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF6, Limnol. Oceanogr., 43, 647–656, https://doi.org/10.4319/lo.1998.43.4.0647, 1998. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Cole, J. J., Caraco, N. F., Kling, G. W., and Kratz, T. K.: Carbon dioxide supersaturation in the surface waters of lakes, Science, 265, 1568–1570, https://doi.org/10.1126/science.265.5178.1568, 1994. a
Cole, J. J., Prairie, Y. T., Caraco, N. F., McDowell, W. H., Tranvik, L. J., Striegl, R. G., Duarte, C. M., Kortelainen, P., Downing, J. A., Middelburg, J. J., and Melack, J.: Plumbing the global carbon cycle: Integrating inland waters into the terrestrial carbon budget, Ecosystems, 10, 172–185, https://doi.org/10.1007/s10021-006-9013-8, 2007. a, b
Couture, R.-M., Wit, H. A., Tominaga, K., Kiuru, P., and Markelov, I.: Oxygen dynamics in a boreal lake responds to long-term changes in climate, ice phenology, and DOC inputs, J. Geophys. Res.-Biogeo., 120, 2441–2456, https://doi.org/10.1002/2015JG003065, 2015. a
Couture, R.-M., Moe, S. J., Lin, Y., Kaste, Ø., Haande, S., and Solheim, A. L.: Simulating water quality and ecological status of Lake Vansjø, Norway, under land-use and climate change by linking process-oriented models with a Bayesian network, Sci. Total Environ., 621, 713–724, https://doi.org/10.1016/j.scitotenv.2017.11.303, 2018. a
de Wit, H. A., Couture, R.-M., Jackson-Blake, L., Futter, M. N., Valinia, S., Austnes, K., Guerrero, J.-L., and Lin, Y.: Pipes or chimneys? For carbon cycling in small boreal lakes, precipitation matters most, Limnol. Oceanogr. Lett., 3, 275–284, https://doi.org/10.1002/lol2.10077, 2018. a
Dibike, Y., Prowse, T., Bonsal, B., de Rham, L., and Saloranta, T.: Simulation of North American lake-ice cover characteristics under contemporary and future climate conditions, Int. J. Climatol., 32, 695–709, https://doi.org/10.1002/joc.2300, 2012. a
Dinsmore, K. J., Wallin, M. B., Johnson, M. S., Billett, M. F., Bishop, K., Pumpanen, J., and Ojala, A.: Contrasting CO2 concentration discharge dynamics in headwater streams: A multi-catchment comparison, J. Geophys. Res.-Biogeo., 118, 445–461, https://doi.org/10.1002/jgrg.20047, 2013. a, b
Dugan, H. A., Woolway, R. I., Santoso, A. B., Corman, J. R., Jaimes, A., Nodine, E. R., Patil, V. P., Zwart, J. A., Brentrup, J. A., Hetherington, A. L., Oliver, S. K., Read, J. S., Winters, K. M., Hanson, P. C., Read, E. K., Winslow, L. A., and Weathers, K. C.: Consequences of gas flux model choice on the interpretation of metabolic balance across 15 lakes, Inland Waters, 6, 581–592, https://doi.org/10.1080/IW-6.4.836, 2016. a, b, c
Einarsdóttir, K., Wallin, M. B., and Sobek, S.: High terrestrial carbon load via groundwater to a boreal lake dominated by surface water inflow, J. Geophys. Res.-Biogeo., 122, 15–29, https://doi.org/10.1002/2016JG003495, 2017. a
Erkkilä, K.-M., Ojala, A., Bastviken, D., Biermann, T., Heiskanen, J. J., Lindroth, A., Peltola, O., Rantakari, M., Vesala, T., and Mammarella, I.: Methane and carbon dioxide fluxes over a lake: comparison between eddy covariance, floating chambers and boundary layer method, Biogeosciences, 15, 429–445, https://doi.org/10.5194/bg-15-429-2018, 2018. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Fairall, C. W., Bradley, E. F., Rogers, D. P., Edson, J. B., and Young, G. S.: Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Atmosphere Response Experiment, J. Geophys. Res.-Oceans, 101, 3747–3764, https://doi.org/10.1029/95JC03205, 1996. a, b, c
Gebre, S., Boissy, T., and Alfredsen, K.: Sensitivity of lake ice regimes to climate change in the Nordic region, The Cryosphere, 8, 1589–1605, https://doi.org/10.5194/tc-8-1589-2014, 2014. a
Hari, P. and Kulmala, M.: Station for Measuring Ecosystem–Atmosphere Relations (SMEAR II), Boreal Environ. Res., 10, 315–322, 2005. a
Heiskanen, J. J., Mammarella, I., Haapanala, S., Pumpanen, J., Vesala, T., MacIntyre, S., and Ojala, A.: Effects of cooling and internal wave motions on gas transfer coefficients in a boreal lake, Tellus B, 66, 22827, https://doi.org/10.3402/tellusb.v66.22827, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x
Heiskanen, J. J., Mammarella, I., Ojala, A., Stepanenko, V., Erkkilä, K.-M., Miettinen, H., Sandström, H., Eugster, W., Leppäranta, M., Järvinen, H., Vesala, T., and Nordbo, A.: Effects of water clarity on lake stratification and lake-atmosphere heat exchange, J. Geophys. Res.-Atmos., 120, 7412–7428, https://doi.org/10.1002/2014JD022938, 2015. a, b, c
Holmberg, M., Futter, M. N., Kotamäki, N., Fronzek, S., Forsius, M., Kiuru, P., Pirttioja, N., Rasmus, K., Starr, M., and Vuorenmaa, J.: Effects of changing climate on the hydrology of a boreal catchment and lake DOC – Probabilistic assessment of a dynamic model chain, Boreal Environ. Res., 19, 66–82, 2014. a, b
Imberger, J.: The diurnal mixed layer, Limnol. Oceanogr., 30, 737–770, https://doi.org/10.4319/lo.1985.30.4.0737, 1985. a, b, c, d
Jonsson, A., Meili, M., Bergström, A.-K., and Jansson, M.: Whole-lake mineralization of allochthonous and autochthonous organic carbon in a large humic lake (Örträsket, N. Sweden), Limnol. Oceanogr., 46, 1691–1700, https://doi.org/10.4319/lo.2001.46.7.1691, 2001. a
Jonsson, A., Åberg, J., Lindroth, A., and Jansson, M.: Gas transfer rate and CO2 flux between an unproductive lake and the atmosphere in northern Sweden, J. Geophys. Res.-Biogeo., 113, G04006, https://doi.org/10.1029/2008JG000688, 2008. a, b
Kiuru, P., Ojala, A., Mammarella, I., Heiskanen, J., Kämäräinen, M., Vesala, T., and Huttula, T.: Effects of climate change on CO2 concentration and efflux in a humic boreal Lake: A modeling study, J. Geophys. Res.-Biogeo., 123, 2212–2233, https://doi.org/10.1029/2018JG004585, 2018. a, b, c, d, e, f, g, h
Kormann, R. and Meixner, F. X.: An Analytical Footprint Model For Non-Neutral Stratification, Bound.-Lay. Meteorol., 99, 207–224, https://doi.org/10.1023/A:1018991015119, 2001. a
Lahermo, P., Ilmasti, M., Juntunen, R., and Taka, M.: The geochemical atlas of Finland, Part 1: The hydrogeochemical mapping of Finnish groundwater, Geological Survey of Finland, Espoo, 1990. a
Leith, F. I., Dinsmore, K. J., Wallin, M. B., Billett, M. F., Heal, K. V., Laudon, H., Öquist, M. G., and Bishop, K.: Carbon dioxide transport across the hillslope–riparian–stream continuum in a boreal headwater catchment, Biogeosciences, 12, 1881–1892, https://doi.org/10.5194/bg-12-1881-2015, 2015. a
Lombardo, C. P. and Gregg, M. C.: Similarity scaling of viscous and thermal dissipation in a convecting surface boundary layer, J. Geophys. Res.-Ocean., 94, 6273–6284, https://doi.org/10.1029/JC094iC05p06273, 1989. a
Los, F. and Blaas, M.: Complexity, accuracy and practical applicability of different biogeochemical model versions, J. Marine Syst., 81, 44–74, https://doi.org/10.1016/j.jmarsys.2009.12.011, 2010. a
Maberly, S. C., Barker, P. A., Stott, A. W., and De Ville, M. M.: Catchment productivity controls CO2 emissions from lakes, Nat. Clim. Change, 3, 391–394, https://doi.org/10.1038/nclimate1748, 2013. a
MacIntyre, S., Wanninkhof, R., and Chanton, J.: Trace gas exchange across the air–water interface in freshwater and coastal marine environments, in: Biogenic trace gases: Measuring emissions from soil and water, edited by: Matson, P. and Harriss, R., 52–97, Wiley-Blackwell, Cambridge, MA, 1995. a, b, c, d
MacIntyre, S., Eugster, W., and Kling, G. W.: The critical importance of buoyancy flux for gas flux across the air-water interface, in: Gas Transfer at Water Surfaces. Geophysical Monograph 127, edited by: Donelan, M. A., Drennan, W. M., Saltzman, E. S., and Wanninkhof, R., 135–139, American Geophysical Union, https://doi.org/10.1029/GM127p0135, 2001. a
MacIntyre, S., Jonsson, A., Jansson, M., Åberg, J., Turney, D. E., and Miller, S. D.: Buoyancy flux, turbulence, and the gas transfer coefficient in a stratified lake, Geophys. Res. Lett., 37, L24604, https://doi.org/10.1029/2010GL044164, 2010. a, b, c, d, e, f, g, h, i, j, k, l, m
Mammarella, I., Nordbo, A., Rannik, Ü., Haapanala, S., Levula, J., Laakso, H., Ojala, A., Peltola, O., Heiskanen, J., Pumpanen, J., and Vesala, T.: Carbon dioxide and energy fluxes over a small boreal lake in Southern Finland, J. Geophys. Res.-Biogeo., 120, 1296–1314, https://doi.org/10.1002/2014JG002873, 2015. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Mammarella, I., Peltola, O., Nordbo, A., Järvi, L., and Rannik, Ü.: Quantifying the uncertainty of eddy covariance fluxes due to the use of different software packages and combinations of processing steps in two contrasting ecosystems, Atmos. Meas. Tech., 9, 4915–4933, https://doi.org/10.5194/amt-9-4915-2016, 2016. a
Markfort, C. D., Perez, A. L. S., Thill, J. W., Jaster, D. A., Porté-Agel, F., and Stefan, H. G.: Wind sheltering of a lake by a tree canopy or bluff topography, Water Resour. Res., 46, W03530, https://doi.org/10.1029/2009WR007759, 2010. a
McDonald, C. P., Stets, E. G., Striegl, R. G., and Butman, D.: Inorganic carbon loading as a primary driver of dissolved carbon dioxide concentrations in the lakes and reservoirs of the contiguous United States, Global Biogeochem. Cy., 27, 285–295, https://doi.org/10.1002/gbc.20032, 2013. a
Miettinen, H., Pumpanen, J., Heiskanen, J. J., Aaltonen, H., Mammarella, I., Ojala, A., Levula, J., and Rantakari, M.: Towards a more comprehensive understanding of lacustrine greenhouse gas dynamics – Two-year measurements of concentrations and fluxes of CO2, CH4 and N2O in a typical boreal lake surrounded by managed forests, Boreal Environ. Res., 20, 75–89, 2015. a, b, c, d
Moriasi, D. N., Arnold, J. G., Liew, M. W. V., Bingner, R. L., Harmel, R. D., and Veith, T. L.: Model evaluation guidelines for systematic quantification of accuracy in watershed simulations, T. ASABE, 50, 885–900, https://doi.org/10.13031/2013.23153, 2007. a
Natchimuthu, S., Sundgren, I., Gålfalk, M., Klemedtsson, L., and Bastviken, D.: Spatiotemporal variability of lake mathitpCO2 and CO2 fluxes in a hemiboreal catchment, J. Geophys. Res.-Biogeo., 122, 30–49, https://doi.org/10.1002/2016JG003449, 2017. a
Nordbo, A., Launiainen, S., Mammarella, I., Leppäranta, M., Huotari, J., Ojala, A., and Vesala, T.: Long-term energy flux measurements and energy balance over a small boreal lake using eddy covariance technique, J. Geophys. Res.-Atmos., 116, D02119, https://doi.org/10.1029/2010JD014542, 2011. a
Podgrajsek, E., Sahlée, E., and Rutgersson, A.: Diel cycle of lake-air CO2 flux from a shallow lake and the impact of waterside convection on the transfer velocity, J. Geophys. Res.-Biogeo., 120, 29–38, https://doi.org/10.1002/2014JG002781, 2015. a
Provenzale, M., Ojala, A., Heiskanen, J., Erkkilä, K.-M., Mammarella, I., Hari, P., and Vesala, T.: High-frequency productivity estimates for a lake from free-water CO2 concentration measurements, Biogeosciences, 15, 2021–2032, https://doi.org/10.5194/bg-15-2021-2018, 2018. a, b, c
Raymond, P. A., Hartmann, J., Lauerwald, R., Sobek, S., McDonald, C., Hoover, M., Butman, D., Striegl, R., Mayorga, E., Humborg, C., Kortelainen, P., Dürr, H., Meybeck, M., Ciais, P., and Guth, P.: Global carbon dioxide emissions from inland waters, Nature, 503, 355–359, https://doi.org/10.1038/nature12760, 2013. a
Read, J. S., Hamilton, D. P., Desai, A. R., Rose, K. C., MacIntyre, S., Lenters, J. D., Smyth, R. L., Hanson, P. C., Cole, J. J., Staehr, P. A., Rusak, J. A., Pierson, D. C., Brookes, J. D., Laas, A., and Wu, C. H.: Lake-size dependency of wind shear and convection as controls on gas exchange, Geophys. Res. Lett., 39, L09405, https://doi.org/10.1029/2012GL051886, 2012. a
Romarheim, A. T., Tominaga, K., Riise, G., and Andersen, T.: The importance of year-to-year variation in meteorological and runoff forcing for water quality of a temperate, dimictic lake, Hydrol. Earth Syst. Sci., 19, 2649–2662, https://doi.org/10.5194/hess-19-2649-2015, 2015. a
Saloranta, T. M. and Andersen, T.: MyLake – A multi-year lake simulation model code suitable for uncertainty and sensitivity analysis simulations, Ecol. Model., 207, 45–60, https://doi.org/10.1016/j.ecolmodel.2007.03.018, 2007. a
Saloranta, T. M., Forsius, M., Järvinen, M., and Arvola, L.: Impacts of projected climate change on the thermodynamics of a shallow and a deep lake in Finland: Model simulations and Bayesian uncertainty analysis, Hydrol. Res., 40, 234–248, https://doi.org/10.2166/nh.2009.030, 2009. a
Sobek, S., Algesten, G., Bergström, A.-K., Jansson, M., and Tranvik, L. J.: The catchment and climate regulation of pCO2 in boreal lakes, Glob. Change Biol., 9, 630–641, https://doi.org/10.1046/j.1365-2486.2003.00619.x, 2003. a
Sobek, S., Söderbäck, B., Karlsson, S., Andersson, E., and Brunberg, A. K.: A carbon budget of a small humic lake: An example of the importance of lakes for organic matter cycling in boreal catchments, Ambio, 35, 469–475, https://doi.org/10.1579/0044-7447(2006)35[469:ACBOAS]2.0.CO;2, 2006. a
Stets, E. G., Striegl, R. G., Aiken, G. R., Rosenberry, D. O., and Winter, T. C.: Hydrologic support of carbon dioxide flux revealed by whole-lake carbon budgets, J. Geophys. Res., 114, G01008, https://doi.org/10.1029/2008JG000783, 2009. a
Tan, Z., Zhuang, Q., Shurpali, N. J., Marushchak, M. E., Biasi, C., Eugster, W., and Walter Anthony, K.: Modeling CO2 emissions from Arctic lakes: Model development and site-level study, J. Adv. Model. Earth Sy., 9, 2190–2213, https://doi.org/10.1002/2017MS001028, 2017. a
Tedford, E. W., MacIntyre, S., Miller, S. D., and Czikowsky, M. J.: Similarity scaling of turbulence in a temperate lake during fall cooling, J. Geophys. Res.-Ocean., 119, 4689–4713, https://doi.org/10.1002/2014JC010135, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Tranvik, L. J., Downing, J. A., Cotner, J. B., Loiselle, S. A., Striegl, R. G., Ballatore, T. J., Dillon, P., Finlay, K., Fortino, K., Knoll, L. B., Kortelainen, P. L., Kutser, T., Larsen, S., Laurion, I., Leech, D. M., McCallister, S. L., McKnight, D. M., Melack, J. M., Overholt, E., Porter, J. A., Prairie, Y., Renwick, W. H., Roland, F., Sherman, B. S., Schindler, D. W., Sobek, S., Tremblay, A., Vanni, M. J., Verschoor, A. M., von Wachenfeldt, E., and Weyhenmeyer, G. A.: Lakes and reservoirs as regulators of carbon cycling and climate, Limnol. Oceanogr., 54, 2298–2314, https://doi.org/10.4319/lo.2009.54.6_part_2.2298, 2009. a
Vachon, D. and Prairie, Y. T.: The ecosystem size and shape dependence of gas transfer velocity versus wind speed relationships in lakes, Can J. Fish. Aquat. Sci., 70, 1757–1764, https://doi.org/10.1139/cjfas-2013-0241, 2013. a
Vachon, D., Prairie, Y. T., and Cole, J. J.: The relationship between near-surface turbulence and gas transfer velocity in freshwater systems and its implications for floating chamber measurements of gas exchange, Limnol. Oceanogr., 55, 1723–1732, https://doi.org/10.4319/lo.2010.55.4.1723, 2010. a
Wang, B., Ma, Y., Chen, X., Ma, W., Su, Z., and Menenti, M.: Observation and simulation of lake-air heat and water transfer processes in a high-altitude shallow lake on the Tibetan Plateau, J. Geophys. Res.-Atmos., 120, 12327–12344, https://doi.org/10.1002/2015JD023863, 2015. a
Wanninkhof, R.: Relationship between wind speed and gas exchange over the ocean, J. Geophys. Res.-Ocean., 97, 7373–7382, https://doi.org/10.1029/92JC00188, 1992. a
Weiss, R.: Carbon dioxide in water and seawater: the solubility of a non-ideal gas, Mar. Chem., 2, 203–215, https://doi.org/10.1016/0304-4203(74)90015-2, 1974. a
Weyhenmeyer, G. A., Kosten, S., Wallin, M. B., Tranvik, L. J., Jeppesen, E., and Roland, F.: Significant fraction of CO2 emissions from boreal lakes derived from hydrologic inorganic carbon inputs, Nat. Geosci., 8, 933–936, https://doi.org/10.1038/ngeo2582, 2015. a
Winslow, L. A., Zwart, J. A., Batt, R. D., Dugan, H. A., Woolway, R. I., Corman, J. R., Hanson, P. C., and Read, J. S.: LakeMetabolizer: an R package for estimating lake metabolism from free-water oxygen using diverse statistical models, Inland Waters, 6, 622–636, https://doi.org/10.1080/IW-6.4.883, 2016. a
Zappa, C. J., McGillis, W. R., Raymond, P. A., Edson, J. B., Hintsa, E. J., Zemmelink, H. J., Dacey, J. W. H., and Ho, D. T.: Environmental turbulent mixing controls on air-water gas exchange in marine and aquatic systems, Geophys. Res. Lett., 34, L10601, https://doi.org/10.1029/2006GL028790, 2007. a





