Variable C∕P composition of organic production and its effect on ocean carbon storage in glacial-like model simulations

During the four most recent glacial maxima, atmospheric CO₂ has been lowered by about 90–100 ppm with respect to interglacial concentrations. It is likely that most of the atmospheric CO₂ deficit was stored in the ocean. Changes in the biological pump, which are related to the efficiency of the biological carbon uptake in the surface ocean and/or of the export of organic carbon to the deep ocean, have been proposed as a key mechanism for the increased glacial oceanic CO₂ storage. The biological pump is strongly constrained by the amount of available surface nutrients. In models, it is generally assumed that the ratio between elemental nutrients, such as phosphorus, and carbon (C∕P ratio) in organic material is fixed according to the classical Redfield ratio. The constant Redfield ratio appears to approximately hold when averaged over basin scales, but observations document highly variable C∕P ratios on regional scales and between species. If the C∕P ratio increases when phosphate availability is scarce, as observations suggest, this has the potential to further increase glacial oceanic CO₂ storage in response to changes in surface nutrient distributions. In the present study, we perform a sensitivity study to test how a phosphate-concentration-dependent C∕P ratio influences the oceanic CO₂ storage in an Earth system model of intermediate complexity (cGENIE). We carry out simulations of glacial-like changes in albedo, radiative forcing, wind-forced circulation, remineralization depth of organic matter, and mineral dust deposition. Specifically, we compare model versions with the classical constant Redfield ratio and an observationally motivated variable C∕P ratio, in which the carbon uptake increases with decreasing phosphate concentration. While a flexible C∕P ratio does not impact the model's ability to simulate benthic δ¹³C patterns seen in observational data, our results indicate that, in production of organic matter, flexible C∕P can further increase the oceanic storage of CO₂ in glacial model simulations. Past and future changes in the C∕P ratio thus have implications for correctly projecting changes in oceanic carbon storage in glacial-to-interglacial transitions as well as in the present context of increasing atmospheric CO₂ concentrations.

1 Introduction

During the last four glacial maxima, atmospheric CO₂ (henceforth $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$) was lowered by ∼90–100 ppm compared to the interglacials (Petit et al., 1999; Lüthi et al., 2008). Due to the difference in size between the oceanic, terrestrial, and atmospheric carbon reservoirs, where the oceanic reservoir is by far the largest with >90 % of their summed carbon contents (reviewed by Ciais et al., 2013), it is likely that most of the CO₂ that was removed from the atmosphere was stored in the glacial ocean. In addition, studies of paleo-proxy records indicate that carbon storage in the glacial terrestrial biosphere was smaller compared to in interglacial climate (Shackleton, 1977; Duplessy et al., 1988; Curry et al., 1988; Crowley, 1995; Adams and Faure, 1998; Ciais et al., 2012; Peterson et al., 2014). During deglaciation, radiocarbon evidence indicates that CO₂ was rapidly released from the ocean back to the atmosphere (Marchitto et al., 2007; Skinner et al., 2010).

Numerous processes, both physical and biological, have been identified as possible contributors to increased glacial oceanic storage. As glacial climate was substantially colder than interglacial climate, the global averages of surface and ocean temperature at the Last Glacial Maximum (LGM) are estimated to have been 3–8 and 2.0–3.2 ^∘C colder respectively, than the pre-industrial averages (Stocker, 2014; Headly and Severinghaus, 2007; Bereiter et al., 2018). Due to the temperature effect on solubility, a colder ocean can hold more carbon. However, glacial changes in salinity partly offset the temperature effect on solubility (reviewed by Kohfeld and Ridgwell, 2009). A colder climate is also drier, and the dry conditions led to increased glacial dust deposition compared to interglacial climate (Mahowald et al., 2006). It has been hypothesized that the addition of dust contributed to increased iron availability in the surface ocean and that this contributed to a strengthening of the biological sequestration of carbon in the glacial ocean compared to interglacials (Martin, 1990). The addition of iron would allow for more complete usage of other nutrients in regions where iron is limiting for biological production. Such strengthening of the retention of biologically sourced carbon in the deep ocean (or the so-called biological pump), through changes in nutrient availability, light conditions, and/or ocean circulation, has long been considered an important player in the glacial increase in ocean CO₂ storage (Broecker, 1982a; Sarmiento and Toggweiler, 1984; Archer et al., 2000; Sigman and Boyle, 2000). Other studies have pointed to changes in carbonate preservation in coral reefs and deep-sea marine sediments (Berger, 1982; Broecker, 1982a; Archer and Maier-Reimer, 1994). It is likely that reduced ventilation of the deep water, through changes in ocean circulation and expanded sea ice cover acting as a barrier for air–sea gas exchange, contributed to increasing the glacial ocean carbon retention (e.g. Boyle and Keigwin, 1987; Duplessy et al., 1988; Stephens and Keeling, 2000; Marchitto and Broecker, 2006; Adkins, 2013; Menviel et al., 2017; Skinner et al., 2017). Model studies by Menviel et al. (2017) show that reduced Southern Hemisphere westerly winds produce reduced ventilation of Antarctic Bottom Water (AABW) in line with evidence from proxy records of δ¹³C . In addition, it has been shown that strengthening of the winds over the Southern Ocean was a likely contributor to deglacial outgassing of CO₂ from the ocean to the atmosphere (Mayr et al., 2013). Extensive summaries of the processes responsible for high glacial ocean carbon storage, and examples of their interactions, are given by Brovkin et al. (2007), Kohfeld and Ridgwell (2009), Hain et al. (2010), and Sigman et al. (2010). Despite the efforts of identifying the responsible processes, models have been struggling to achieve the full lowering of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ expected for a glacial.

In this paper, we focus on the biological pump and how it responds to glacial-like changes in climate. Our aim is to investigate how the level of simplification of the biological carbon uptake in an Earth system model may affect the glacial drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. Most biogeochemical models used in glacial climate studies have a simple representation of biological production, which assumes that carbon, C, and inorganic nutrients such as phosphorus, P, are taken up in fixed proportion to each other. This is modelled using the average ratio of C∕P of the ocean organic matter originally observed by Redfield (1963) (C∕P = 106∕1) or adjustments to these suggested in follow-up studies (Takahashi et al., 1985; Anderson and Sarmiento, 1994).

We investigate whether allowing for a flexible C∕P stoichiometric ratio increases model ocean CO₂ storage in a glacial-like climate. This possibility was suggested in studies by Broecker (1982b), Archer et al. (2000), and Galbraith and Martiny (2015), but the implications of Redfield versus flexible C∕P for glacial ocean carbon storage have not previously been tested in an Earth system model. This type of non-Redfieldian dynamics was applied in the model used in Eggleston and Galbraith (2018) and Galbraith and de Lavergne (2018), but their results were not analysed in terms of difference from a Redfield model version. In addition, Buchanan et al. (2018) explored the importance of dynamic response of ocean biology, such as flexible stoichiometry, for modelled ocean biogeochemistry in pre-industrial simulations. They found that the dynamic response was fundamental for stabilizing the response of ocean dissolved inorganic carbon (DIC) to changes in the physical circulation state.

We conduct a sensitivity study, where we apply glacial-like changes to an interglacial control state. Changes in radiative forcing, albedo, wind-forced circulation, remineralization depth, and dust are applied separately and in combination. Here, changes in radiative forcing and albedo serve to cool the climate and to mimic glacial temperature and ice conditions. The surface wind stress is reduced in the polar regions, in order to pursue reduced AABW ventilation as suggested by paleo-proxy evidence (Menviel et al., 2017; Skinner et al., 2017). Ocean cooling reduces the degradation rate of sinking particulate organic carbon, which increases the average depth of remineralization of organic carbon (Matsumoto, 2007). Drier glacial climate resulted in increased dust deposition, and thereby iron flux, to the ocean (Martin, 1990). All these changes act to increase ocean carbon storage and thereby reduce $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. The applied changes are not expected to induce a full glacial maximum model state, but they allow us to explore several important effects on the biological and solubility carbon pumps and produce a state with glacial-like climate conditions.

We apply the perturbations in two different versions of the Earth system model cGENIE: an original version using fixed Redfield stoichiometry of C∕P (Ridgwell et al., 2007) plus a co-limitation by iron (Tagliabue et al., 2016) for biological production and a modified version using the non-Redfieldian, nutrient-concentration-dependent C∕P stoichiometry suggested by Galbraith and Martiny (2015) and iron co-limitation.

We show that flexible C∕P stoichiometry allows a larger glacial ocean CO₂ storage, as predicted by the box-model study of Galbraith and Martiny (2015), and that flexible stoichiometry has the largest impact for perturbations in remineralization depth and dust forcing. Additionally, we show that flexible stoichiometry allows for increased ocean carbon storage without decreasing the storage of preformed nutrients in the deep ocean.

2 Methods

2.1 Model description

cGENIE is an Earth system model of intermediate complexity, with a 3D frictional-geostrophic ocean (36×36 equal-area horizontal grid, 16 depth levels), 2D energy–moisture balance atmosphere with prescribed wind fields, and interactive atmospheric chemistry and ocean biogeochemistry. The model code and user handbook can be found in the cGENIE GitHub repository (cGENIE GitHub repository, 2019). We run a version of cGENIE with the same phosphorus-plus-iron (Fe) co-limitation scheme as used in the iron cycle model inter-comparison study of Tagliabue et al. (2016). The model branch enabled for use with flexible C∕P ratios (see Sect. 2.2) is tagged as release v0.9.5, and the model configurations used in this paper are included in this release (cGENIE release v0.9.5, 2019, see Code availability for details).

2.2 Stoichiometry

In the original version of the cGENIE Earth system model (Ridgwell et al., 2007), as well as in the version of Tagliabue et al. (2016), the stoichiometric ratios are based on Redfield (1963). Thus, there is a fixed relationship between the number of moles of the elements that are taken up (positive) or released (negative) during production of organic matter in the ocean. This relationship is $\mathrm{P}/\mathrm{C}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{1}/\mathrm{106}/-\mathrm{138}$, where O₂ is dissolved oxygen (nitrogen is assumed only implicitly for the purpose of accounting for organic matter creation and remineralization-related alkalinity transformations in the ocean; Ridgwell et al., 2007). An exception is iron, where Fe∕C varies as a function of iron availability as described in Watson et al. (2000).

Although the average elemental composition of organic matter in the ocean is close to the Redfield ratios, the stoichiometry of production of new organic material has shown high in situ variability. Variability occurs between species, but also within the same species, and has been shown to depend on environmental factors such as nutrient availability, water temperature, and light (e.g. Le Quéré et al., 2005; Galbraith and Martiny, 2015; Yvon-Durocher et al., 2015; Tanioka and Matsumoto, 2017; Garcia et al., 2018a; Moreno et al., 2018). We test the importance of this variability for glacial ocean CO₂ storage by running the same experiments with the fixed Redfield stoichiometry version of cGENIE and with a model version where we have implemented the linear regression model presented by Galbraith and Martiny (2015) (Eq. 1). These two model versions are henceforth denoted RED and GAM.

The flexible stoichiometry in GAM depends on the ambient concentration of dissolved phosphate ([PO₄]) in the water:

$$\begin{array}{}\text{(1)}& \mathrm{P}/\mathrm{C}=\mathrm{1}/{\left({\displaystyle \frac{\left[{\mathrm{PO}}_{\mathrm{4}}\right]}{\mathrm{144.9}\mathrm{\mu }{\mathrm{molL}}^{-\mathrm{1}}}}+\mathrm{0.0060}\right)}^{-\mathrm{1}}.\end{array}$$

This relation shows that, when [PO₄] is low, organisms bind more C per atom of P than they do under high-[PO₄] conditions (Fig. 1). Equation (1) is applied in cGENIE in the calculations of biological C uptake at the surface ocean based on the surface concentration of PO₄. In Sect. 3.1.2, Eq. (1) is also used to translate model surface PO₄ fields to the corresponding surface C∕P ratios for the organic matter produced in each grid cell. Note that, while we change the ratio of C∕P, the ratio of C∕O₂ remains the same in all experiments. As a result, the P∕O₂ ratio changes between experiments.

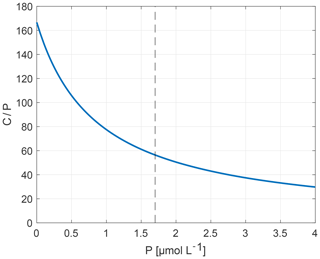
Figure 1 Flexible stoichiometry C∕P (y axis) dependent on the P concentration (µmol L⁻¹) (x axis), as described by Eq. (1). Here, we extend the relationship beyond the observational interval 0–1.7 µmol L⁻¹ (bounded by dashed line) which forms the basis of the relation derived by Galbraith and Martiny (2015).

2.3 Experiments

We start all experiments from an interglacial–modern (IG-M) control state, which has been run for 10 000 years to steady state, using either Redfield (Ctrl_RED) or variable (Ctrl_GAM) stoichiometry. The control states have a prescribed $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of 278 ppm and the same climate (Table 1). However due to the differences in C∕P, they have different ocean carbon inventories (Table S1 in the Supplement). In Ctrl_GAM, the export flux of organic matter (see Ridgwell et al., 2007) has a global average C∕P composition of 121∕1, and thus the global ocean carbon storage is larger than in Ctrl_RED. This also suggests that a perturbation, which increases ocean storage of P through the biological pump, could cause storage of 15 (i.e. 121–106) more carbon atoms in simulations using GAM compared to RED, simply because the average composition of the formed biological material is different. To distinguish between the role of the flexibility of the stoichiometry and the change in the mean composition of organic material, we add a control state with fixed stoichiometry where C∕P = 121∕1 (henceforth denoted Ctrl₁₂₁).

Table 1 List of experiments. Ensemble member acronyms, short descriptions of what the simulation tests, and specifications of parameter settings for each ensemble member. The $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is either prescribed to pre-industrial level (PI) = 278 ppm or freely varying with changes in climate and ocean circulation. The radiative forcing is either coupled to the $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of the atmospheric chemistry module of the model or fixed at a value corresponding to $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}=\mathrm{185}$ ppm. The zonal albedo profile is either representative of IG-M conditions or of the LGM. The wind stress is either IG-M or has an adjusted peak in wind stress at $\pm {\mathrm{50}}^{\circ }$ N. The IG-M remineralization length scale (RLS) is 590 m. If RLS is changed, it is multiplied by a factor (fr). Dust forcing is either IG-M or representative of LGM. Each experiment is conducted using model versions with C∕P fixed at 106∕1 (Redfield, 1963,  denoted RED), C∕P variable with surface ocean PO₄ concentration (Galbraith and Martiny, 2015, denoted GM15), and C∕P fixed at 121∕1 (denoted 121; see Sect. 2.3).

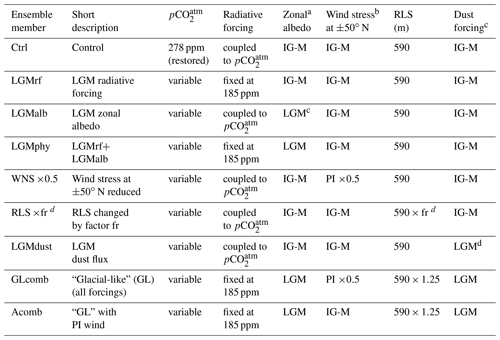
^a Calculated from the HADCM3 LGM (21 ka) simulation of Davies-Barnard et al. (2017). ^bSee Lauderdale et al. (2013) for example of reduced peak wind profile for the Southern Hemisphere. ^c Re-gridded LGM dust flux from Mahowald et al. (2006). ^d fr denotes multiplication factor for remineralization length scale. We test multiplication factors between 0.75 and 1.75, corresponding to a change in RLS between −25 % and +75 %.

In order to explore the effects of variable stoichiometry, we make a sensitivity study where we apply changes to boundary conditions, individually and in combination (see Sect. 2.3.3), that may be representative of changes that occurred during glacial periods. All experiments are listed in Table 1.

The applied changes in boundary conditions are

• physical perturbations (colder climate) of

  • –

    radiative forcing corresponding to LGM CO₂ = 185 ppm and

  • –

    zonal albedo profile representative of LGM (calculated from the LGM climate simulation of Davies-Barnard et al., 2017);

• physical perturbations (weaker overturning) of

  • –

    reduced wind forcing over the Southern Ocean (Lauderdale et al., 2013, e.g.) and north of 35^∘ N (see Sect. 2.3.1); and

• biological perturbations of

  • –

    changed remineralization length scale (e.g. Matsumoto, 2007; Chikamoto et al., 2012; Menviel et al., 2012) and

  • –

    increased dust forcing, as simulated for the LGM (regridded from Mahowald et al., 2006).

By applying the above perturbations, we aim to approach, but not fully resolve, some of the characteristics of the LGM ocean, which appears to have had a global average ocean temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$) 2.57 ±0.24 ^∘C colder than the Holocene (Bereiter et al., 2018), a weakly ventilated deep ocean (e.g. Menviel et al., 2017), and a more efficient biological pump (e.g. Sarmiento and Toggweiler, 1984; Martin, 1990; Sigman and Boyle, 2000). We also aim to increase carbon retention in the deep ocean (Muglia et al., 2018).

The physical perturbations serve to achieve a colder climate ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ cools by 2.1 ^∘C compared to Ctrl, thus 80 % of the observed 2.6 ^∘C; see Sect. 3.2.1) and weaker overturning (see Sect. 3.2.2 and Fig. 2) with a longer residence time of the Antarctic Bottom Water (AABW) cell compared to Ctrl. Colder conditions achieve a stronger solubility pump, thereby strengthening the retention of carbon in the deep ocean. As the physical perturbations affect the ocean circulation and temperature, they also affect the nutrient distribution and the rates of nutrient upwelling and biological growth (slower growth in colder water). They thereby affect the biological productivity (Ridgwell et al., 2007).

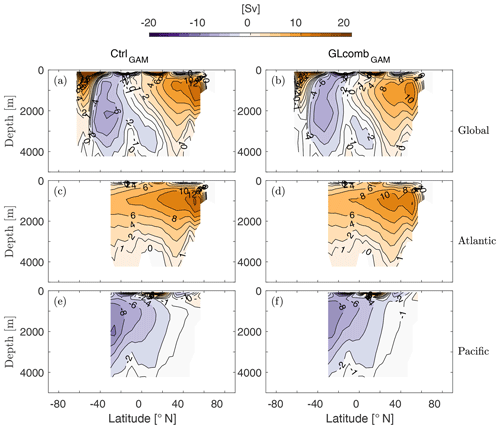
Figure 2 The Eulerian component of the global (a, b), Atlantic (c, d), and Pacific (e, f) ocean meridional overturning stream function (1 Sv = 10⁶ m³ s⁻¹) of Ctrl_GAM (a, c, e) and GLcomb_GAM (b, d, f). Note that the eddy-induced transport of tracers is taken into account through a skew-diffusive flux (Griffies, 1998) that is present in the velocity fields used to compute the Eulerian stream function.

The biological perturbations serve to achieve a more efficient biological pump, which is connected with increased retention of nutrients and carbon in the deep ocean, and lower surface nutrient concentrations in productive regions (see Sect. 3.2.3 and 3.2.4). With flexible stoichiometry, lower surface nutrient concentrations result in higher C∕P ratios, further increasing the export production and thereby the carbon retention in the deep ocean. In our experiments, we show that the flexible stoichiometry amplifies the response of the biological pump to both physical and biological perturbations.

The perturbations and the experiments are described in detail in Sect. 2.3.1–2.3.3.

2.3.1 Physical perturbations

We change the physical conditions for climate by changing radiative forcing and albedo to LGM-like conditions and denote these changes as LGMphy. We set the radiative forcing in the model to correspond to an atmosphere with 185 ppm CO₂ instead of 278. However, we allow the $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ to freely evolve (starting from the value of 278 ppm of the Ctrl-state atmosphere) in response to the cooler climate. For albedo, we apply a zonal LGM albedo profile (calculated from the LGM climate simulation of Davies-Barnard et al., 2017). Assumptions of a simple zonal profile, instead of a 2D field re-gridded from PMIP LGM simulations, allow for a better consistency with the original zonal mean albedo profile developed for the modern configuration of GENIE (Marsh et al., 2011). Together, the changes in radiative forcing and albedo cause the global ocean average temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$) to decrease by 2.1 ^∘C compared to Ctrl (see Sect. 3.2.1).

To achieve a longer residence time of the AABW water mass, and an associated increase in carbon and nutrient retention, we apply weaker winds (denoted WNA ×0.5). We use the Southern Ocean wind profile of Lauderdale et al. (2013), where the peak westerly wind strength at 50°S has been halved compared to the control state (see Sect. 2.3.3). The winds north and south of the peak are reduced accordingly to give a continuous profile (see Fig. 2a of Lauderdale et al., 2013). The result is a weaker overturning (see Table 2) and a longer residence time of the AABW as may be expected for the glacial ocean (Menviel et al., 2017; Skinner et al., 2017) (see also Sect. 4.5). Thus, this approach is justifiable in a model of reduced complexity. However, there are studies suggesting that the Southern Ocean winds may in fact have been stronger during glacial times (Sime et al., 2013, 2016; Kohfeld et al., 2013). To avoid an expansion of the North Atlantic Deep Water (NADW) overturning cell that would be inconsistent with the glacial ocean (Duplessy et al., 1988; Lynch-Stieglitz et al., 1999; Curry and Oppo, 2005; Marchitto and Broecker, 2006; Hesse et al., 2011), winds north of 35^∘ N are also gradually reduced so that the wind strength north of 50^∘ N is reduced by half compared to the control state. In cGENIE, gas transfer velocities are calculated as a function of wind speed (described in Ridgwell et al., 2007), and following Wanninkhof (1992). Consequently, weaker winds also lead to reduced gas exchange with the atmosphere.

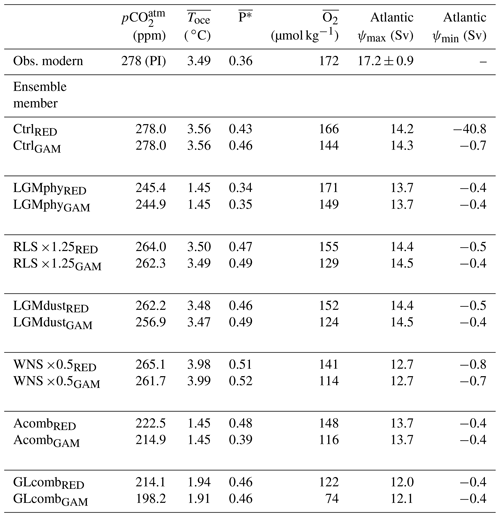
Table 2 Atmospheric CO₂ ($p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$, ppm); global ocean averages of temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$, ^∘C), $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$, and $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$ (µmol kg⁻¹); Atlantic overturning stream function (ψ, sverdrups (Sv)); and maximum and minimum north of −30^∘ N, for observations, and for selected ensemble members in each model version (RED and GAM). Climatological modern-day $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ and $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$ were computed using the World Ocean Atlas 2018 (Locarnini et al., 2018; Garcia et al., 2018c). $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ for the modern-day ocean is estimated by Ito and Follows (2005). Average modern-day AMOC strength is estimated by McCarthy et al. (2015) from the RAPID-MOCHA array at 26^∘ N (corresponding to Atlantic ψ_max in the model). Note that observed $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is given for pre-industrial (PI) climate, as we do not model anthropogenic release of CO₂.

2.3.2 Biological perturbations

In the ocean, phytoplankton growth rates and remineralization of particulate organic carbon are processes that both work more slowly at colder temperatures (Eppley, 1972; Laws et al., 2000). Cooling of the ocean would thus lead to decreased production of particulate organic matter (POC) and simultaneously to a slower degradation of POC, with competing effects on export production (i.e. the amount of C captured by primary production that leaves the surface ocean without being remineralized) (Matsumoto, 2007). However, Matsumoto (2007) shows that the effect of slower remineralization dominates the effect on export production. It has therefore been hypothesized that the cooling of the glacial ocean led to a deepening of the remineralization length scale (henceforth denoted RLS) in the ocean and thereby more efficient retention of organic carbon in the deep ocean (Matsumoto, 2007; Chikamoto et al., 2012), which in turn caused a lowering of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. Menviel et al. (2012) find that such a deepening results in model changes in export production in poor agreement with paleo-proxies, while Chikamoto et al. (2012) find improved model agreement with the glacial proxy records of export production and stable carbon isotopes for temperature-dependent growth rates and remineralization. Deeper remineralization also results in increased nutrient retention in the deep ocean, thus causing changes in surface nutrient fields and in C∕P ratios of GAM. We test the effect of changes in RLS by multiplying the model default RLS by a factor fr (RLS × fr; see Sect. 2.3.3 ).

Increased dust forcing leads to increased iron (Fe) availability. This allows for increased productivity (and hence more efficient usage of other nutrients) in the high-nutrient, low-chlorophyll (HNLC) regions in the North Pacific, equatorial Pacific, and Southern Ocean, where iron (Fe) is the limiting micronutrient (Martin, 1990; Moore et al., 2013). The variable stoichiometry in GAM is expected to be influential if the concentrations of P decrease in such regions as a result of increased Fe availability. This process may hence be of importance in a glacial scenario where dust forcing increases as a result of the drier conditions (Martin, 1990; Moore et al., 2013). We apply the regridded LGM dust fields of Mahowald et al. (2006) and denote this change as LGMdust.

2.3.3 Sensitivity experiments and combined simulations

In the sensitivity study, for each of the three C∕P parameterizations, we first change one forcing at a time (see Table 1). We run simulations where we individually apply the LGM boundary conditions for radiative forcing (LGMrf), albedo (LGMalb), and dust (LGMdust) and one simulation with halved wind stress near the poles (−50 and 50^∘ N) (WNS ×0.5). For the remineralization length scale (RLS), we test a range of values of the multiplication factor RLS ×fr, where $\mathrm{fr}=\mathit{\{}\mathrm{0.75},\mathrm{1.25},\mathrm{1.75}\mathit{\}}$. This allows us to test the sensitivity to deep-ocean retention of organic carbon.

We then run simulations where we combine several changes in forcing. We get a colder climate simulation (LGMphy) by combining LGMrf and LGMalb. In simulation Acomb, we combine LGMrf, LGMalb, LGMdust, and RLS ×1.25 (see Table 1). Kwon et al. (2009) show that small changes in remineralization depth can cause substantial changes in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. With the RLS deepening of 25 %, we keep the corresponding changes in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ from exceeding the ∼20–30 ppm obtained in other studies (Matsumoto, 2007; Menviel et al., 2012). We finally run a glacial-like simulation GLcomb (see Sect. 3.3), which is similar to Acomb but also includes the change in wind stress WSN ×0.5. The achieved GLcomb model state does not represent a full glacial maximum state but is more glacial-like compared to the control state; it has a colder climate (see Table 2), reduced deep-ocean ventilation, and more carbon retention in the deep ocean.

2.4 Observations

For comparison and validation of model results, we use records of ocean-state variables from climatological mean fields of modern observations and proxy observations from the LGM.

Modern data of ocean temperature, oxygen, and nutrients are retrieved from the World Ocean Atlas 2018 (Locarnini et al., 2018; Garcia et al., 2018c, b) and we use the proxy estimates of LGM ocean temperature from Bereiter et al. (2018). Average modern-day strength of the Atlantic meridional overturning circulation (AMOC) is estimated by McCarthy et al. (2015) from the RAPID-MOCHA array at 26^∘ N.

We use model–data comparison of benthic δ¹³C to assess the statistical similarity (correlation) between both the model control state and glacial-like state (see Sect. 2.3) to benthic δ¹³C data representing the late Holocene (0–6 ka, HOL) and Last Glacial Maximum (19–23 ka, LGM) (Peterson et al., 2014). Locations of core sites can be seen in Fig. S1 in the Supplement (see also Fig. 1 in Peterson et al., 2014). Note that LGM benthic δ¹³C is more ¹³C-depleted than that in the Holocene due to the addition of ¹³C-depleted terrestrial carbon to the glacial ocean (Shackleton, 1977; Curry et al., 1988; Duplessy et al., 1988), which is not simulated in our model experiments. Therefore, to compare our glacial-like simulations (GLcomb) to LGM observations, we subtract a Holocene–LGM global average difference of 0.32 ‰ (Gebbie et al., 2015) from the GLcomb experiments. Gebbie et al. (2015) state that the wide range of error for the estimate of glacial-to-modern change in benthic δ¹³C of 0.32±0.20 ‰ suffers from a lack of observations in all ocean basins but the Atlantic. Therefore, we place more emphasis on the results of the model–data comparison in the Atlantic than in the Indo-Pacific sector.

2.5 Nutrient utilization efficiency

The extent to which biology succeeds in using the available nutrients can be determined by calculating the nutrient utilization efficiency $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ (Ito and Follows, 2005; Ödalen et al., 2018),

$$\begin{array}{}\text{(2)}& \stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}={\displaystyle \frac{\stackrel{\mathrm{‾}}{{\mathrm{P}}_{\mathrm{rem}}}}{\stackrel{\mathrm{‾}}{{\mathrm{P}}_{\mathrm{tot}}}}},\end{array}$$

which is the fraction of remineralized (P_reg) to total (P_tot) nutrients (in this case, PO₄) in the ocean. Overlines denote global averages. Remineralized nutrients have been transported from the surface to the interior ocean by the biological pump, and P_rem is given by

$$\begin{array}{}\text{(3)}& {\mathrm{P}}_{\mathrm{rem}}={\mathrm{P}}_{\mathrm{tot}}-{\mathrm{P}}_{\mathrm{pre}}.\end{array}$$

Here, P_pre is preformed PO₄ – the concentration of PO₄ that was present in the water parcel as it sank, and thus the fraction that was not used by biology in the surface ocean. In cGENIE, the concentration of preformed tracers is set in the surface ocean and then passively advected through the ocean interior (Ödalen et al., 2018). The biological pump also captures carbon, and a similar relationship can be used for concentrations of DIC, where

$$\begin{array}{}\text{(4)}& {\mathrm{DIC}}_{\mathrm{rem}}={\mathrm{DIC}}_{\mathrm{tot}}-{\mathrm{DIC}}_{\mathrm{pre}}.\end{array}$$

DIC_rem is used to compute the ocean storage of remineralized acidic carbon (AC_rem; see Appendix A). AC_rem is biological carbon that entered the ocean in the form of CO₂ in soft tissue (as opposed to carbonates in hard tissue), measured independently of oxygen consumption and/or remineralized phosphate.

In cGENIE, P_pre and DIC_pre are modelled as passive tracers (Ödalen et al., 2018). Hence, we can use the model output for P_pre in Eq. (3) to compute $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ (Eq. 2).

In a model with a fixed Redfield ratio, $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ determines the effect of the biological pump on $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. For example, it has been found that a higher $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ in the initial state gives a lower potential for drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in response to similar perturbations (Marinov et al., 2008; Ödalen et al., 2018). However, with variable stoichiometry this is no longer true, since the amount of carbon retained in the deep ocean is not necessarily proportional to $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$.

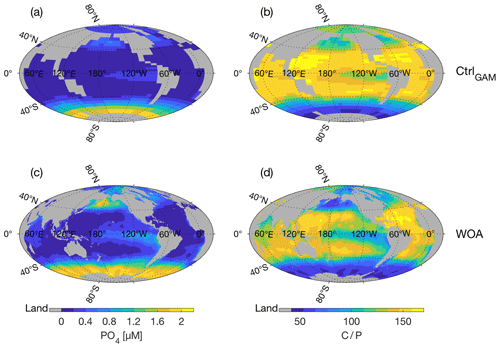
Figure 3 Surface PO₄ concentration (µM) (a, c) and corresponding C∕P as calculated using parametrization of Galbraith and Martiny (2015) (b, d). Panels show Ctrl_GAM (a, b) and climatological mean fields (World Ocean Atlas 2018, Garcia et al., 2018b) (c, d).

3 Results

3.1 Control states

3.1.1 Ocean temperature and circulation

As the three control states Ctrl_RED, Ctrl_GAM, and Ctrl₁₂₁ are driven by the same physical forcings and have the same $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$, they have the same ocean circulation pattern (Fig. 2a, c, e and Tables 2 and S2) and climate (exemplified by global ocean average temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$) in Tables 2 and S2). The surface ocean nutrient fields are fairly similar, with small differences due to the different C∕P parameterizations (compare Figs. 3a and S2). The strength of the Atlantic meridional overturning circulation (AMOC), diagnosed in the model as the maximum of the Atlantic meridional overturning stream function deeper than 1000 m, is 14 Sv (1 Sv $=\mathrm{1}\times {\mathrm{10}}^{\mathrm{6}}$ m³ s⁻¹) in all control states (Tables 2, S2). Results from the RAPID-MOCHA array at 26^∘ N suggest an average AMOC strength of 17.2±0.9 Sv (McCarthy et al., 2015); thus our control-state AMOC is a little bit weaker than in the present-day climate. The observational estimate for $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ according to the World Ocean Atlas 2018 (Locarnini et al., 2018) is 3.49 ^∘C, thus comparable to the 3.56 ^∘C of our Ctrl simulations. The surface nutrient concentrations of our control-state Ctrl_GAM (Fig. 3a) compare reasonably well with observed surface ocean concentrations of PO₄ (Fig. 3c), with some underestimation in the Pacific equatorial region, the North Pacific Ocean, and the Labrador Sea. The agreement with observations is better for Ctrl_GAM than for Ctrl_RED (Fig. S2).

3.1.2 Surface nutrient distribution and C∕P ratios

In Fig. 3 we see that surface PO₄ fields (left-hand column) and the corresponding fields of surface C∕P ratios (as given by Eq. (1), right-hand column) of Ctrl_GAM (Fig. 3a, b) and of climatological mean PO₄ fields (Fig. 3c, d) are similar in their pattern as well as in the magnitudes of values. Note that high concentrations of PO₄ correspond to low C∕P ratios, and vice versa. The highest climatological mean PO₄ concentrations in the northern and equatorial Pacific are not fully reproduced by the model, but the pattern is reproduced well. In the surface C∕P field of Ctrl_GAM (Fig. 3b), we see the signature of very high nutrient concentrations in the Southern Ocean ($>\mathrm{1}\mathrm{\mu }\mathrm{mol}{\mathrm{L}}^{-\mathrm{1}}$, Fig. 3b) as a band of low ratios, with the most extreme values near the Antarctic continent, as seen in the climatological mean fields (Fig. 3d).

The nutrient utilization efficiency $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ (Eq. 2) in the three control states differs by a few percent: 0.43, 0.46, and 0.42 in Ctrl_RED, Ctrl_GAM, and Ctrl₁₂₁ respectively (Table 2). The fraction of DIC_rem in DIC_tot (see Sect. 2.5, Eq. 4, Table S1) is 0.065, 0.077, and 0.072 in Ctrl_RED, Ctrl_GAM, and Ctrl₁₂₁ respectively.

3.1.3 Ocean dissolved O₂

The most apparent difference between Ctrl_RED and Ctrl_GAM is in deep-ocean oxygen concentrations, where the global ocean average dissolved O₂ concentration ($\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$) in Ctrl_GAM (144 µmol kg⁻¹) is lower than in Ctrl_RED and Ctrl₁₂₁ (166 and 152 µmol kg⁻¹ respectively). Compared to climatological mean fields (World Ocean Atlas 2018, Fig. 4a–b), both Ctrl_RED (Fig. 4c–d) and Ctrl_GAM (Fig. 4e–f) agree reasonably well with the real ocean. Ctrl_GAM appears to better capture the equatorial oxygen minimum in the Atlantic basin than Ctrl_RED but is too low in the North Pacific. In Ctrl_GAM (Fig. 4f), the North Pacific is markedly lower in oxygen than in Ctrl_RED (Fig. 4d) and even anoxic in the oxygen minimum zone (OMZ). This should be kept in mind when analysing the oxygen sections of the glacial-like states GLcomb_RED (Fig. 4g–h) and GLcomb_GAM (Fig. 4i–j). Global averages for dissolved O₂ are given in Table 2.

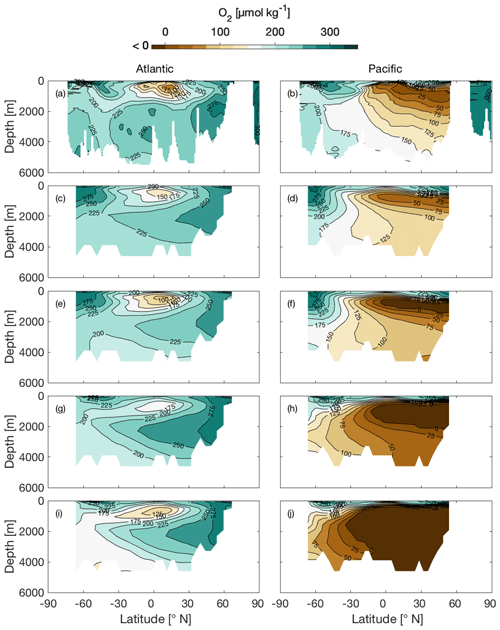
Figure 4 Sections of O₂ concentration (µmol kg⁻¹) along 25^∘ W in the Atlantic basin (left-hand column) and along 135^∘ W in the Pacific basin (right-hand column). Panels show climatological mean fields (World Ocean Atlas 2018, Garcia et al., 2018c) (a, b) and model states Ctrl_RED (c, d), Ctrl_GAM (e, f), GLcomb_RED (g, h), and GLcomb_GAM (i, j).

3.1.4 Ocean δ¹³C

By comparing Ctrl_RED δ¹³C and Holocene (0–6 ka, HOL) benthic δ¹³C values, we estimate a global model–data correlation of 0.78 (Table S3). The modern-day Atlantic Ocean has a distinctive spatial δ¹³C pattern (Figs. 5a, S1) with ¹³C-enriched values in the intermediate-depth (<2 km) North Atlantic and Nordic Seas and ¹³C-depleted values in the deep (>2.5 km) South Atlantic. While the model produces a weaker gradient than the observed HOL Atlantic Ocean (corr. 0.50, Table S3) the model correlates well with eastern Atlantic δ¹³C records (Fig. S1). For the Indo-Pacific, the weaker benthic δ¹³C gradient is well represented by the model (Fig. 5e). This pattern emerges mainly due to ¹³C-depleted, biologically sourced carbon that is accumulated in the weak circulation region of the interior North Pacific (Matsumoto et al., 2002). However, Indo-Pacific δ¹³C values of Ctrl_RED are overall lower than the HOL observations. The overall model–data correlation for the Indo-Pacific is 0.39 (Table S3). Comparing the control states of the RED and GAM model versions, δ¹³C patterns (Figs. 5a, e and S3a, e) and model–data correlations with HOL observations (Table S3) are similar between the model versions, with somewhat lower correlations for GAM.

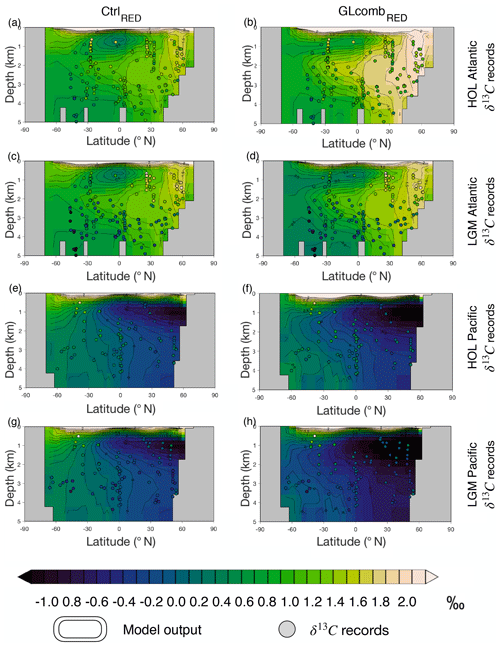
Figure 5 Model ocean δ¹³C (contours) compared to the two proxy record time slices (HOL and LGM) of benthic δ¹³C (circles) of Peterson et al. (2014). The upper half of the figure shows the Atlantic Ocean (a–d), while the lower half shows the Pacific Ocean (e–h). The columns represent the model simulations (Ctrl_RED or Ctrl_GAM), while each row represents one of the proxy record time slices (HOL or LGM). The left-hand column shows Ctrl_RED (a, c, e, g) and the right-hand column shows GLcomb_RED (b, d, f, h). The rows show, from top to bottom, (a, b) HOL Atlantic, (c, d) LGM Atlantic, (e, f) HOL Pacific, and (g, h) LGM Pacific. Note that, before we compare GLcomb_RED to LGM observations (d, h), a constant of 0.32 ‰ is subtracted from the simulated δ¹³C, to account for terrestrial release of δ¹³C-depleted terrestrial carbon which is not modelled. The corresponding comparison for model version GAM is shown in Fig. S3.

3.2 Sensitivity experiments

The applied changes listed in Table 1 cause changes in ocean characteristics such as overturning circulation, temperature, surface nutrient distributions, and biological productivity, which result in changed $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. The resulting steady-state global average values for temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$), dissolved oxygen ($\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$), and nutrient utilization efficiency $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$, as well as the maximum and minimum of the Atlantic meridional overturning stream function, are listed in Table 2.

3.2.1 Radiative forcing and albedo

In the simulations where radiative forcing and albedo are changed to represent LGM conditions (LGMrf + LGMalb = LGMphy), the reductions in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ are similar in the RED and the GAM model versions. In LGMphy, the resulting $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is 245.4 and 244.9 ppm, thus showing a reduction of 33 ppm compared to the Ctrl 278 ppm (Fig. 6). Here, variable C∕P does not impact the results, because changes in the surface nutrient distribution (Fig. 7a), and the associated changes in C∕P (Fig. 8a), are limited to very high latitudes where productivity is already low in the control state, due to low temperatures and a lack of light and iron. The drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ can mainly be attributed to the increase in solubility carbon (C_sat,T), due to ocean cooling, and to an increase in sea ice, which prevents air–sea gas exchange and therefore causes an increase in disequilibrium carbon (C_dis) (Ödalen et al., 2018). Ocean cooling amounts to 2.1 ^∘C in LGMphy compared to Ctrl ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ in Table 2). In cGENIE, the increase in C_sat,T associated with ocean cooling corresponds to $\sim \mathrm{7}\pm \mathrm{1.5}$ ppm ^∘C⁻¹ (Ödalen et al., 2018, Supplement Fig. S1). Thus, in LGMphy C_sat,T and C_dis should contribute roughly 40 % and 60 % respectively of the change in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$. Note that cGENIE underestimates the true effect of ocean cooling on solubility, due to a temperature restriction on the solubility constants (Ödalen et al., 2018). This temperature restriction limits solubility from changing below 2.0 ^∘C. In this case, the solubility effect on $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of reducing $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ by 2.1 ^∘C (from 3.6 to 1.5 ^∘C, ∼15 ppm) is thus comparable to only 1.6 ^∘C of cooling (from 3.6 to 2.0 ^∘C, ∼11 ppm), and the solubility effect is underestimated by ∼4 ppm. As we do not change salinity, we are simultaneously likely to overestimate the increase in solubility between Ctrl and a glacial-like state by ∼6 ppm (Kohfeld and Ridgwell, 2009). This effect is consistent for any choice of C∕P parametrization and is therefore not explored further.

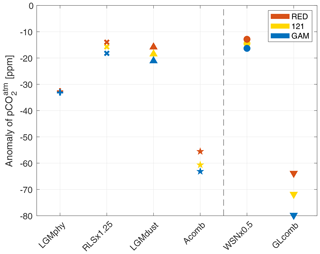
Figure 6 Resulting CO₂ anomaly, with respect to the control-state 278 ppm, of the sensitivity experiments LGMphy (plus symbol), RLS ×1.25 (times symbol), LGMdust (upward arrowheads), and WSN ×0.5 (circles) and of the combined experiments Acomb (stars) and GLcomb (downward arrowheads). Results of the different model versions RED, 121, and GAM are shown in red, yellow, and blue respectively. The vertical dashed line separates simulations without (left) and with (right) wind perturbation.

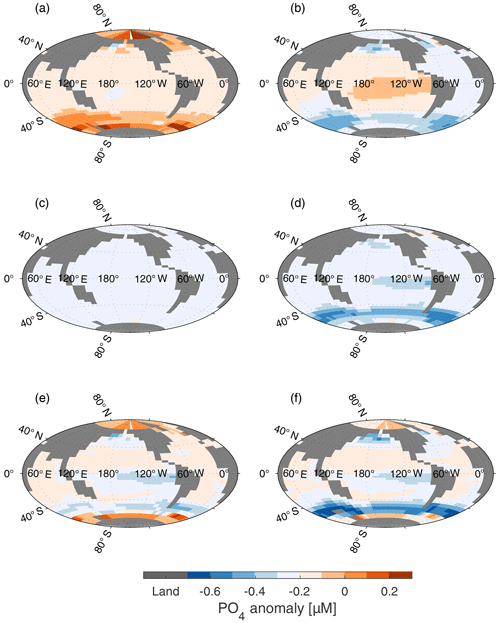
Figure 7 Surface PO₄ anomaly (µM), with respect to surface concentration of PO₄ in Ctrl_GAM (Fig. 3a), for (a) LGMphy_GAM, (b) WSN ×0.5_GAM (c) RLS ×1.25_GAM, (d) LGMdust_GAM, (e) Acomb_GAM, and (f) GLcomb_GAM. Changes in surface nutrient fields are similar for all three model versions (RED, GAM, 121); thus only GAM is shown.

3.2.2 Reduced wind forcing

When the peak of Southern Ocean (henceforth SO) winds is reduced, the strength of the overturning circulation of AABW decreases (see difference in Southern Hemisphere overturning stream function between Fig. 2a and b). Thus, given that the volume of AABW does not change, its residence time increases. This also means that the upwelling nutrient-rich water in the SO stays near the surface for longer and loses more nutrients before being subducted. This decreases the SO concentration of preformed phosphate in WNS ×0.5_RED compared to Ctrl, as seen in Fig. 7b, and increases the nutrient utilization efficiency $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ (Table 2, Fig. 9). This leads to a drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of 12.9 ppm compared to Ctrl_RED (Fig. 6). As the nutrient concentration in the SO decreases (Fig. 7b), the flexible C∕P ratio (Fig. 8b) leads to an increased carbon capture efficiency in GAM compared to RED (see GLcomb-Ctrl of biologically sourced carbon (AC_rem) in Fig. 9), which is partly compensated for by a reverse effect in the Pacific equatorial region. Consequently, in WSN×0.5_GAM, we get a reduction of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of 16.3 ppm compared to Ctrl_GAM (Fig. 6). Hence, for halved peak wind stress at ±50^∘ N, the flexible stoichiometry increases the drawdown by ∼26 %.

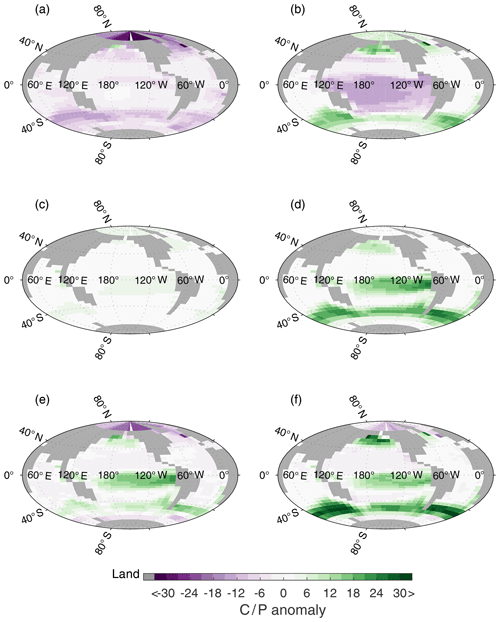
Figure 8 Surface C∕P anomaly, with respect to C∕P of Ctrl_GAM (Fig. 3b), for (a) LGMphy_GAM, (b) WSN ×0.5_GAM (c) RLS ×1.25_GAM, (d) LGMdust_GAM, (e) Acomb_GAM, and (f) GLcomb_GAM.

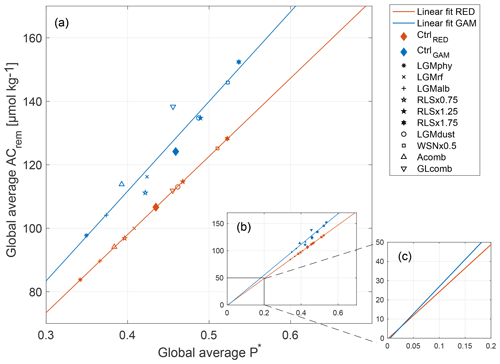
Figure 9 Remineralized acidic carbon (AC${}_{\mathrm{rem}}={\mathrm{DIC}}_{\mathrm{rem}}-(\mathrm{1}/\mathrm{2})\times {\mathrm{ALK}}_{\mathrm{rem}}$; see Appendix A) as a function of $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$. Simulations using model versions RED and GAM are shown in red and blue respectively. Different symbols indicate the sensitivity experiments, listed in the panel on the right-hand side. Red and blue lines show linear least-squares fits to the separate ensembles for RED and GAM. Panels illustrate (a) the deviation from the least-squares fit of the GAM ensemble as opposed to the RED ensemble, (b) the linear fits extrapolated to the origin, and (c) a zoom-in around the origin, where the RED (red) line goes through the origin, while the GAM (blue) does not.

3.2.3 Remineralization length scale

When the remineralization length scale (RLS) increases, the biological material reaches deeper before it is remineralized, and it takes longer for it to be returned to the surface. Therefore, more of the biologically sourced carbon (AC_rem) and nutrients are present in the deep ocean at any given time, leading to an increase in $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ (Table 2, Fig. 9) and a decrease in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (Fig. 6). The deeper we make the RLS, the bigger the drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ – in RLS ×1.25_RED and RLS ×1.75_RED $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ decreases by 14 and 33 ppm respectively compared to Ctrl_RED. In GAM, the drawdown in each experiment is increased by an additional ∼30 %; thus RLS ×1.25_GAM and RLS ×1.75_GAM see a reduction of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of 18 and 44 ppm respectively compared to Ctrl_GAM (Table S2). Our changes in RLS cause very small, but global, changes in PO₄ concentrations (global average anomaly = −0.016 µM, RLS ×1.25 in Fig. 7c), which, through the small resulting changes in C∕P (Fig. 8c), still contribute to the additional drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in GAM.

In a sensitivity test where we make the RLS 25 % shallower (which would be representative of a warmer climate compared with Ctrl), the $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ increases by 18 and 23 ppm in RED and GAM respectively compared to their control states (see RLS ×0.75_RED and RLS ×0.75_GAM in Table S2). Interestingly, the response in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is again ∼30 % larger in GAM. The variable stoichiometry thus amplifies the effect on $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ by any change in RLS. The potential implications of this result for warm climate scenarios are further discussed in Sect. 4.1.

3.2.4 Dust forcing

The simulations with LGM dust forcing (LGMdust, Table 1) show the largest difference in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ between the RED and the GAM. In LGMdust_RED, $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ decreases by 16 ppm compared to Ctrl_RED, whereas LGMdust_GAM sees a reduction of 21 ppm compared to Ctrl_GAM (Fig. 6). The drawdown is thus ∼30 % larger with variable stoichiometry. About a third (∼10 % of ∼30 %) of the increase in drawdown can be explained by a change in average C∕P composition of the organic material that is exported out of the surface ocean (see Sect. 4.4).

As anticipated, the iron added by the dust forcing allows more efficient usage of P in the HNLC regions, which increases the ocean storage of biologically sourced carbon P_rem (thus, P^* increases, Table 2, Fig. 9). This reduces the surface nutrient concentrations in these areas (Fig. 7d). In the GAM model version, this is followed by increased C∕P ratios in these areas (Fig. 8d), resulting in a lower $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in LGMdust_GAM than in LGMdust_RED. The largest anomalies in PO₄ concentrations, and consequently in C∕P, are observed in the subantarctic zone of the Southern Ocean, particularly in the Atlantic and Indian sectors. This subantarctic increase in biological efficiency is consistent with radionuclide proxy data (¹⁰Be, ²³⁰Th, ²³¹Pa) from the LGM (e.g. Kumar et al., 1995; Kohfeld et al., 2005).

3.3 Combined experiments

We show the results of two different combined simulations; Acomb and GLcomb. GLcomb is the “glacial-like” simulation, which combines all the sensitivity experiments (Table 1). Acomb omits the reduction in wind stress.

3.3.1 Ocean temperature and circulation

In the glacial-like simulations, GLcomb_RED and GLcomb_GAM, the global average ocean temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$) is 1.7 ^∘C lower than in the respective control states (Table 2). Headly and Severinghaus (2007) estimate LGM $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ to have been 2.7±0.6 ^∘C colder than the modern ocean, while a more recent estimate by Bereiter et al. (2018) constrains $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ to 2.57±0.24. GLcomb is thus just outside the 1 standard deviation limit of the warm end of the Headly and Severinghaus (2007) estimate for the LGM. In Acomb, $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ is 2.1 ^∘C cooler than Ctrl; thus this simulation falls within the uncertainty of the Headly and Severinghaus (2007) estimate. Compared to the Bereiter et al. (2018) estimate, our combined experiments GLcomb and Acomb achieve 64 % and 82 % of the glacial–interglacial difference in $\stackrel{\mathrm{‾}}{T_{\mathrm{oce}}}$ respectively. As anticipated, our combined forcings do not induce a full glacial maximum state but rather a state with glacial-like climate conditions.

Ocean overturning circulation weakens in GLcomb compared to Ctrl (Fig. 2, Table 2), mainly as a result of the wind stress reduction. For example, the AMOC (here measured as the maximum of the Atlantic overturning stream function) reduces in strength by ∼15 %, from 14 to 12 Sv (Table 2). The global meridional overturning stream function reveals that the SO overturning cell sees a reduction in transport (Fig. 2d), which is associated with weaker upwelling and thus longer residence time for AABW, as hypothesized for the glacial ocean (e.g. Menviel et al., 2017; Skinner et al., 2017). In Acomb, where the wind stress is kept at modern values, the ocean overturning circulation remains similar to the control state (Table 2).

3.3.2 Surface nutrient distribution and C∕P ratios

In the surface nutrient anomalies (GLcomb-Ctrl, shown for GAM in Fig. 7f), we see the strongest response in the Southern Ocean, with different effects south and north of the so-called biogeochemical divide described by Marinov et al. (2006). Marinov et al. (2006) show that the air–sea balance of CO₂ is dominated by processes in the waters close to Antarctica, whereas global export production is instead controlled by the biological pump and circulation in the subantarctic region. The border between these two regimes is referred to as the biogeochemical divide. South of the biogeochemical divide, close to the Antarctic continent, we see an increase in GLcomb nutrient concentrations compared to Ctrl (Fig. 7f), which coincides with an increase in sea ice in this area (Fig. S4). Colder conditions due to changed albedo and radiative forcing, with more sea ice than in the control state, cause a reduction in biological production, leaving more unused P in the surface layer (Fig. 7a). North of the biogeochemical divide, increased aeolian dust flux increases the productivity of the biology, which reduces P in the surface compared to the control (Fig. 7d). In combination with circulation changes, resulting from the reduced SO wind stress (Fig. 7b), and deeper remineralization (Fig. 7c), P concentrations in the subantarctic region are strongly reduced (Fig. 7f). In the equatorial and North Pacific, there is also a reduction of P (Fig. 7f), mainly due to the increased dust flux (Fig. 7d). There is an increase in P seen in the Arctic, again coincident with an increase in sea ice in the same area. As a result of these changes, we see strong positive anomalies in C∕P in the HNLC regions and negative anomalies in the highest latitude bands (Fig. 8f). The organic matter that is exported out of the upper layer (henceforth referred to as export production) in GLcomb_GAM has a global average C∕P ratio of 134∕1.

3.3.3 Ocean dissolved O₂

Despite colder conditions, which allow for more dissolution of O₂, the reduction in $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$ is evident in the GLcomb simulations (Fig. 4). This mirrors the increase in AC_rem (Fig. 9). The $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$ reduction is about 50 % larger in GAM compared to RED. As the initial-state Ctrl_GAM is already lower in oxygen than Ctrl_RED (144 µmol kg⁻¹ compared to 166 µmol kg⁻¹), and variable stoichiometry allows for additional ocean storage of organic carbon, the end-state $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$ is drastically lower in GLcomb_GAM (74 µmol kg⁻¹) compared to GLcomb_RED (122 µmol kg⁻¹).

3.3.4 Ocean δ¹³C

In GLcomb_RED (contours in Fig. 5b, d), the Atlantic north–south gradient in δ¹³C is stronger than in Ctrl_RED (contours in Fig. 5a, c). This strong gradient is not observed in the Holocene Atlantic δ¹³C data (dots in Fig. 5a, b), but it is prominent in the LGM time slice (dots in Fig. 5c, d). The LGM observations are reproduced well in GLcomb_RED (corr. 0.62, Table S3), especially in the east Atlantic (corr. 0.77). When we correct GLcomb_RED for the absence of injected terrestrial carbon, we see clear similarities with LGM observations (Fig. 5d), though the southernmost cores still indicate more ¹³C-depleted conditions than the model. In the Indo-Pacific, GLcomb_RED is too ¹³C-depleted compared to LGM observations, particularly with the correction for the absence of a terrestrial signal (Fig. 5h), and the model–data correlation is poor (0.05). For the Indo-Pacific, the model–data correlation for Holocene data is similar between GLcomb_RED and Ctrl_RED (0.24 and 0.39 respectively, Table S3). This suggests that the poor correlation with LGM benthic records is simply due to our changes in forcings being insufficient to achieve the required rearrangements in Indo-Pacific circulation patterns. In GLcomb, similarly as in Ctrl, there is very little difference between the RED and GAM model versions in terms of δ¹³C patterns (compare Fig. 5d, h to Fig. S3d, h) and model–data correlations (Table S3). However, there are overall lower values of δ¹³C in GAM, reflecting the larger storage of biologically sourced carbon in the deep ocean in this model version.

3.3.5 Atmospheric CO₂

In the combined experiments Acomb and GLcomb, $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ decreases strongly compared to the control state (reduction of between −56 and −80 ppm, Fig. 6). This is partly a result of colder conditions (Table 2), which lead to increased solubility for CO₂ in seawater and an expanded sea-ice cover (Fig. S4) which restricts air–sea gas exchange. The latter slows down the equilibration of the CO₂-rich upwelling water with the atmosphere before it is subducted into the deep ocean and thus causes increased C_dis. In Acomb and GLcomb, changes in biological production (see Sect. 3.3.2) and storage of biologically sourced carbon (Fig. 9) also contribute strongly to the reduced $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$.

The combined experiments show a striking difference in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ between the model versions RED and GAM; in GLcomb_RED and GLcomb_GAM, we achieve drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ of −64 and −80 ppm respectively, from the 278 ppm of the control states (Fig. 6). This corresponds to an increase in ocean carbon storage of 139 and 173 PgC respectively (Table S1). The drawdown is thus 25 % larger in GAM than in RED. In Acomb, where the perturbation in wind stress is omitted, drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is smaller than in GLcomb and the difference between model versions is less pronounced, but there is still a 14 % difference between Acomb_RED and Acomb_GAM (−56 and −63 ppm respectively (Fig. 6).

4 Discussion

4.1 Accounting for variable C∕P in ocean carbon cycle models

The representation of ocean biology in general circulation models (GCMs) tends to be oversimplified (Le Quéré et al., 2005) and the development of the models is often held back by constraints imposed by maintaining the computational efficiency of the model. The Galbraith and Martiny (2015) empirical model is simple and based on nutrient variables that are already present in biogeochemical models (nitrate and phosphate). By implementing the GAM parametrization, or possibly a power law such as that described by Tanioka and Matsumoto (2017), an additional facet of the complexity of ocean biology can be implicitly accounted for at a relatively small computational cost. Previous model ensemble studies have shown that this type of dynamical response of the biology to changes in the modelled ocean state can improve the model's ability to realistically simulate ocean biogeochemistry (Buchanan et al., 2018). In pre-industrial and future simulations respectively, Buchanan et al. (2018) and Tanioka and Matsumoto (2017) find that the flexible stoichiometry acts to stabilize the response of ocean DIC to changes in the physical (circulation) state. In our glacial-like simulations, we find that the response of ocean DIC, and thus $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$, to the combined perturbations is greater in the simulations with flexible stoichiometry. Nonetheless, our study confirms the potential importance of dynamical biological response for the outcome of model studies.

The approach taken by both Galbraith and Martiny (2015) and Tanioka and Matsumoto (2017) is to adapt a function to species-independent C : P observations. This means that they account for the adaptation of plankton to the surrounding conditions, in terms of both species composition and individuals being more frugal in low-nutrient conditions. This is one of the main advantages of such an approach, as it can be applied in a model without different plankton functional types, which is what we use here. Ganopolski and Brovkin (2017) appear to succeed with full glacial–interglacial CO₂ cycles in CLIMBER-2, which does not have flexible stoichiometry for primary producers but which has a temperature limitation on growth and explicit phyto- and zooplankton with different C uptake rates. This combination may perhaps achieve a similar response in carbon export in their simulations, when moving into a colder climate, as the flexible stoichiometry does in our simulations. The next step to approach a more realistic modelling of the biological pump would be to include a representation of preferential remineralization of nutrients (e.g. Kolowith et al., 2001; Letscher and Moore, 2015), but this goes beyond the scope of the present study.

One drawback of the Galbraith and Martiny (2015) approach is that it assumes that the C∕P ratio continues to increase continuously with increasing [PO₄]. As such, in a high-surface-[PO₄] region like the Southern Ocean, GAM does not represent the effects on C∕P of temperature and light and the associated non-linear effects that could be of importance here (e.g. Yvon-Durocher et al., 2015; Tanioka and Matsumoto, 2017; Moreno et al., 2018). Up to [PO₄]=1.7 µM, the GAM parametrization fits the binned observational data well (see Figs. 1 and S2 in Galbraith and Martiny, 2015). To account for the lack of observational data at higher [PO₄] in Galbraith and Martiny (2015), we have tested the effect of saturation of the C∕P ratio at higher [PO₄] in Ctrl and GLcomb simulations where we kept $\mathrm{C}/\mathrm{P}=\mathrm{55}/\mathrm{1}$ at [PO₄]>1.7 µM. The increase in ocean carbon storage and decrease in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ between Ctrl and GLcomb are nearly identical with GAM; thus saturation of the C∕P ratio at very high [PO₄] causes no noticeable impact on our results.

Our sensitivity experiments RLS ×0.75 and RLS ×1.25 reveal that the response in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ to the perturbation is enhanced in GAM compared to RED for both increased and decreased RLS. While increased RLS would be an effect of ocean cooling, and thus of interest for glacial studies, reduced RLS would be a consequence of ocean warming (Matsumoto, 2007). Matsumoto (2007) describes how decreased RLS would have a positive feedback on $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in a future warming climate. Our results imply that flexible C∕P could have a further reinforcing effect on this feedback. It would therefore be of interest to apply a parametrization of flexible C∕P in models used for simulations of future climate feedbacks.

4.2 Decoupling of biologically sourced carbon and nutrient utilization efficiency

Many studies have suggested increased ocean storage of organic carbon as a potentially important contributor to the low glacial $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ (e.g. Sarmiento and Toggweiler, 1984; Martin, 1990; Archer et al., 2000; Sigman and Boyle, 2000). However, biological production depends on water temperature (Eppley, 1972) and decreases in cold conditions. This temperature effect is parameterized in cGENIE as a local temperature-dependent uptake rate modifier proportional to $e^{(T/\mathrm{15.9}{}^{\circ }\mathrm{C})}$, and we see overall reduced productivity in our cold climate simulations (see e.g. LGM_phy, Table S1). As the climate cools, the temperature effect leads to a decrease in biological productivity and a subsequent decrease in $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ (see LGM_phy in Fig. 9). If productivity decreases, other mechanisms are needed to offset this decrease, if the total ocean storage of organic carbon is to increase. Mechanisms that can contribute to increased deep-ocean carbon retention are for example reduced SO overturning circulation (increased residence time of the AABW; Menviel et al., 2017) and deeper remineralization (Matsumoto, 2007; Chikamoto et al., 2012), which we apply through our perturbations in winds (Sect. 3.2.2) and RLS (Sect. 3.2.3). From our results, it is evident that variable stoichiometry can be another contributing factor. In our simulations, global average export production decreases, in terms of both POP (particulate organic phosphorus) and POC (particulate organic carbon), by 15 % between Ctrl_RED and GLcomb_RED because of the colder climate. However, the variable stoichiometry in GAM partly offsets this decrease in biological carbon capture – while the export production in terms of POP decreases by 17 %, the corresponding decrease in POC is only 10 %. Thus, in GLcomb_GAM we achieve an increase in ocean inventory of remineralized carbon, which exceeds the one of GLcomb_RED (Fig. 9).

Due to the competing effects between decreased export production and increased retention that are introduced by the different forcing components, the net change in P_rem, and thus in $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$, is very small when moving from the control state (Ctrl) to the glacial-like state (GLcomb) (Fig. 9). In the fixed stoichiometry case (RED), there is a small net increase in $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ of 0.020 in GLcomb compared to Ctrl, which is linearly related to a small increase in storage of AC_rem in the ocean. In the case with variable stoichiometry (GAM), there is instead a very small decrease in $\stackrel{\mathrm{‾}}{{\mathrm{P}}^{*}}$ of 0.003. With a linear response, we would thus expect a decrease in storage of AC_rem as well. Instead, we see a reasonably large increase in global average AC_rem. In summary, we suggest this is a result of changes in surface P fields (see Fig. 7).

The reduced $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in GLcomb_GAM, compared to GLcomb_RED, can be explained by the non-linearity introduced by the local variability in C∕P. When changes in ocean circulation, remineralization depth, and dust deposition cause the local nutrient availability in the surface waters to change, this affects the elemental composition of the exported organic material (Fig. S5). In GLcomb, there is a reduction of the surface layer P concentration compared to Ctrl in some key (HNLC) regions. In GAM, this decrease in surface P results in an increase in C∕P. This further strengthens the biological pump in these key regions, resulting in a non-linear relationship between storage of remineralized phosphate and biologically sourced carbon (Fig. 9). In Ctrl_GAM, the average elemental C∕P composition is 121∕1. In GLcomb_GAM, this average is 134∕1 (Table S1, Fig. S5). This means that even though the same amount of P is exported to the deep ocean, the organic molecules carry more carbon, which is released in the deep ocean during remineralization. In Ctrl_GAM, the global average concentration of P_rem is 1.16 µmol kg⁻¹ (compared with 1.17 µmol kg⁻¹ in GLcomb_GAM). By increasing the average C∕P composition of 1.16 µmol kg⁻¹ organic molecules from 121 to 134 (i.e. by 13 units), this causes an increase in C_soft by ∼15 µmol kg⁻¹, which corresponds to the observed increase in AC_rem. From this, we conclude that, in a system where stoichiometry is variable on a local scale, ocean storage of biologically sourced CO₂ can change while the amount of remineralized nutrients remains constant.

Note also that Ctrl_GAM has a larger inventory of DIC as well as C_soft compared to Ctrl_RED. Ödalen et al. (2018) found that drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in response to a perturbation is larger when the control state has a smaller inventory of DIC and C_soft. Yet, the effect of applying the same perturbation results in a larger drawdown of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in GAM than in RED. This is opposite of the conclusions of Ödalen et al. (2018). The reason is that the flexible stoichiometry in effect increases the drawdown potential, which more than compensates for the increased carbon inventory in the control state. In GLcomb_GAM, the C∕P in global average export production increases from the control 121∕1 to 134∕1, which reflects the increased storage of organic carbon allowed by the flexible stoichiometry.

4.3 Implications of flexible C∕P for deep-ocean oxygen

Studies have shown that deep-ocean O₂ concentrations were lower during the LGM than in the Holocene (e.g. Bradtmiller et al., 2010; Jaccard and Galbraith, 2012; Galbraith and Jaccard, 2015). Here, we discuss implications of using flexible C∕P for the model's ability to reproduce ocean oxygen patterns and concentrations in the different time periods.

In the Atlantic, Ctrl_GAM (Fig. 4e) reproduces the climatological mean extent of the oxygen minimum zone (OMZ) (Fig. 4a) better than Ctrl_RED (Fig. 4c) does. In the Pacific Ocean, the O₂ gradient in the climatological mean fields (Fig. 4b) is more gradual compared to that of the control states (Fig. 4d, f), but the core of the OMZ is well reproduced by the model. The forcings applied to GLcomb are not sufficient to reproduce a full glacial state. Still, we do get a vertical expansion of the OMZ in GLcomb_RED (Fig. 4h) compared to Ctrl_RED (Fig. 4c), in agreement with the findings of Hoogakker et al. (2018). In GLcomb_GAM, oxygen depletion is too extensive (see below), but the tendency of vertical expansion compared to the control state is present here as well.

In our glacial-like states, we see a significant reduction of O₂ compared to the control state in both RED and GAM (Fig. 4d and e). This response is expected when we apply increased dust deposition and deeper remineralization (Galbraith and Jaccard, 2015), and the direction of the overall response of deep-ocean O₂ to the glacial-like forcings is in line with observations. The reduction in O₂ is stronger in GAM, due to the larger storage of respired carbon in this model version.

Finally, it should be noted that Ctrl_GAM (Fig. 4c) displays deeper oxygen minima in the oxygen minimum zones of both the Atlantic equatorial region and the North Pacific compared to what is seen in Ctrl_RED (Fig. 4b) and in climatological mean fields. In Ctrl_GAM, a large part of the interior North Pacific is anoxic (Fig. 4c), while the climatological mean fields (Fig. 4a) indicate very low oxygen levels, but not anoxia. As illustrated by simulations in Galbraith and de Lavergne (2018), variable stoichiometry in itself is not always sufficient to achieve widespread deep-ocean de-oxygenation in a model under glacial-like climate change. Among other factors, model ocean oxygen conditions are also dependent on deep water formation characteristics of the model (Galbraith and de Lavergne, 2018). The deep water formation characteristics of a model affect the amount of time available for remineralization and, consequently, the oxygen consumption. In addition, due to a lack of resolution deep water formation in climate models generally happens as open water convection, rather than as dense plumes along slopes (Heuzé et al., 2013). This may cause too much oxygen to be entrained into the deep ocean (Galbraith and de Lavergne, 2018). In cGENIE, this effect is small enough not to cancel the increased O₂ consumption caused by the higher average C∕P in Ctrl_GAM compared to Ctrl_RED.

In summary, the GAM version of the model quantitatively reproduces the observed O₂ patterns of both the LGM and the Holocene, but with too low concentrations. If this parametrization of variable stoichiometry is to be used in cGENIE in future studies, we suggest some retuning, for example by reducing the global average concentration of nutrients, to improve the representation of observed modern-day ocean O₂ concentrations in the GAM control state.

4.4 Effect of modified but fixed C∕P

Part of the observed difference in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ between GLcomb_RED and GLcomb_GAM results from a difference in global average C∕P in the control states (Ctrl_RED and Ctrl_GAM). In Ctrl_GAM, the average C∕P in the export production is close to 121∕1, instead of 106∕1 as in Ctrl_RED. We illustrate the consequences of this difference by running parallel simulations with fixed C∕P of 121∕1 (model version 121).

In a simulation with reduced wind stress (WNS ×0.5₁₂₁), $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ is reduced by −14.5 ppm compared to Ctrl_RED (Table S2). The corresponding $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ drawdown in WNS ×0.5_RED and WNS ×0.5_GAM is −12.9 and −16.3 ppm respectively. This indicates that, for the reduced wind stress case, about half of the enhanced drawdown achieved by the flexible stoichiometry can be attributed to a difference in the mean C∕P composition of the organic material between the control states Ctrl_RED and Ctrl_GAM. Similarly, for the enhanced dust deposition experiments, LGMdust₁₂₁ explains about one-third of the difference in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ between LGMdust_RED and LGMdust_GAM (Table S2). In the combined experiment GLcomb, we can attribute about half (−8 ppm of −17 ppm) of the observed difference in drawdown between RED and GAM to the difference in control-state average C∕P. In Acomb, the control-state difference in C∕P accounts for about two-thirds of the difference between model versions (−5 ppm of −8 ppm). Evidently, the individual perturbation simulations and GLcomb have smaller fractions of the change in $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ that are due to changed average C∕P. As shown above, the simulations with 121 indicate that, depending on the change in forcing, between one-third and two-thirds of the difference in drawdown between RED and GAM is due to the difference in average C∕P between the control states (Fig. 6, Table  S2). From this, we conclude that the effects of the perturbations do not add linearly.

As outlined in Sect. 4.3, an increase in C∕P reduces deep-ocean O₂ concentrations, through an increase in regenerated carbon. In this respect, the 121 experiments fall between the corresponding RED and GAM experiments. For example, the global ocean average O₂ concentration, $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$, in Ctrl₁₂₁ is 152 µmol kg⁻¹, which is lower than Ctrl_RED (166 µmol kg⁻¹), but higher than Ctrl_GAM (144 µmol kg⁻¹). Similarly, GLcomb₁₂₁ has a lower $\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{2}}}$ than GLcomb_RED (96 compared to 122 µmol kg⁻¹), but higher than GLcomb_GAM (74 µmol kg⁻¹).

The observed effects of modified average C∕P could have implications for model intercomparison projects, if they compare results from models that use different versions of fixed stoichiometry (for example, Anderson and Sarmiento, 1994 or Takahashi et al., 1985 stoichiometries, compared to Redfield, 1963). The problem with different stoichiometry assumptions in models is extensively discussed by Paulmier et al. (2009). Our study shows a direct consequence of such differences, with a different model response to the same perturbation.

4.5 What can we learn from the model–data comparison of δ¹³C ?

Proxy records of benthic δ¹³C indicate a change in ocean δ¹³C across the deglaciation. The whole ocean deglacial change has been estimated to ∼0.35 ‰ (Peterson et al., 2014; Peterson and Lisiecki, 2018), and the surface-to-deep gradient weakened (shown in numerous studies; see e.g. Curry et al., 1988; Duplessy et al., 1988; Curry and Oppo, 2005; Herguera et al., 2010; Peterson and Lisiecki, 2018, and references therein). Here we compare model ocean δ¹³C of our simulations to the benthic δ¹³C records, to see how well the simulations capture the observed patterns and whether there is a difference in model–data correlation between RED and GAM.

The model–data comparison in δ¹³C (Sect. 3.1.4) suggests that the Ctrl simulations are overall well correlated with Holocene benthic δ¹³C data (HOL in Table S3). For the Atlantic, the correlation of the Ctrl simulations is higher with the LGM benthic δ¹³C (LGM in Table S3) than with HOL. However, the standard deviations (SDs) suggest that the Atlantic north–south gradient is not as strong as in an LGM ocean state and thus more similar to the modern ocean.

When we apply our combined forcings in the GLcomb simulations, we achieve a stronger δ¹³C gradient in the Atlantic, allowing for a closer match with LGM data in terms of SDs. A stronger gradient in δ¹³C and more depleted values suggest weaker ventilation of the deep ocean. The poor correlation in the Indo-Pacific, which may be partly due to sparse mid-ocean observations for almost 70 % of the ocean volume, makes the global statistics for LGM observations difficult to interpret. The forcings applied to GLcomb are factors that are likely to be important for the glacial ocean circulation and biogeochemistry. However, these forcings are not sufficient to reproduce a full glacial state (i.e. the use of the term glacial-like simulations rather than LGM simulation). Other forcings that have shown to be important for modelling of glacial δ¹³C are, for example, brine rejection (Bouttes et al., 2010, 2011), and freshwater forcing (Schmittner et al., 2002; Hewitt et al., 2006; Bouttes et al., 2012). The fact that some important forcings are missing is likely the main cause for the model–data discrepancy, and the reason for why we do not achieve a glacial Pacific Ocean circulation consistent with observed δ¹³C patterns.

Each of the two observational datasets (HOL and LGM) displays similar correlations across the two model simulations. The correlation of the HOL δ¹³C records with Ctrl_RED, Ctrl_GAM, GLcomb_RED, and GLcomb_GAM is in all cases between 0.76 and 0.78. Meanwhile, the correlation of LGM δ¹³C records with the same four simulations is in all cases between 0.55 and 0.58. That our GLcomb simulations still correlate so well with the HOL dataset suggests the applied forcings have not caused these simulations to be clearly different from Ctrl in terms of water mass distribution. For the same reason, the correlation with LGM δ¹³C records does not significantly improve from Ctrl to GLcomb. The water mass distribution in cGENIE is strongly constrained by the resolution of the model, especially in the vertical. Changes in temperature and salinity that should cause changes in water mass volume may not be sufficient to allow a water mass to extend to the next vertical level of the model. As a consequence, while the gradient between water masses may become more or less pronounced, the interface of water masses may still remain at the same depth. The applied changes affect the chemical and biological conditions for ocean carbon storage, such as CO₂ solubility (temperature dependent) and nutrient availability, more than the physical conditions, such as water mass volume and turnover time. To achieve a full glacial state with cGENIE, with a more glacial-like water mass distribution, additional physical forcings (see above) are likely to be required.

How δ¹³C is represented in cGENIE is detailed in Appendix B. The very small differences between RED and GAM suggests that using variable stoichiometry does not impact our ability to represent the δ¹³C patterns seen in observational data. However, we note that some retuning of the modern control state is recommended before cGENIE with variable stoichiometry is used in other studies.

5 Conclusions

In this paper, we examine the potential role of variable stoichiometry in biological production for glacial ocean CO₂ storage. We show that flexible C∕P composition of organic matter allows a stronger response of $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ to glacial-like changes in climate, remineralization length scale, and aeolian dust flux. We conclude that variable stoichiometry may be important for glacial ocean CO₂ storage and for achieving the full extent of drawdown of atmospheric CO₂ in model simulations. In the experiment GLcomb_RED, with glacial-like climate and Redfield stoichiometry (Redfield, 1963), ocean carbon storage increases by 139 PgC and atmospheric CO₂ decreases by 64 ppm. In GLcomb_GAM, with glacial-like climate changes and variable stoichiometry, the corresponding numbers are 173 PgC and 80 ppm. Hence, the drawdown of atmospheric CO₂ increases by 25 % when C∕P is variable.

About half of the increased drawdown of CO₂ results from different global average C∕P in the export production. In addition, flexible stoichiometry allows increased carbon capture through the biological pump, while maintaining or even decreasing the ratio of remineralized to total nutrients in the deep ocean. With fixed stoichiometry, an increase in remineralized carbon is inevitably tied to a corresponding increase in remineralized nutrients.

We apply variable C∕P parameterized as a simple function of the surface water concentration of PO₄, as suggested by Galbraith and Martiny (2015). Tanioka and Matsumoto (2017) suggest that it is unrealistic for C∕P to continue to increase indefinitely with increased [PO₄] and therefore suggest a more complex power-law function, which takes into account saturation of the C∕P ratio at high concentrations of PO₄. However, we found that saturation of the C∕P ratio at concentrations higher than the observational upper bound of 1.7 µM causes no noticeable impact on our results.

The representation of flexible stoichiometry used in this study (Galbraith and Martiny, 2015) can be used without large increases in computational cost. It makes it possible to take into account, to first approximation, the complex biological changes that occur in the ocean during long-timescale climate change scenarios (see e.g. McInerney and Wing, 2011). We show here that, for glacial–interglacial cycles, this complexity contributes to changes in atmospheric CO₂ through flexible C∕P ratios. Flexible C∕P also has the potential to be an additional positive feedback of ocean warming on $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}$ in future climate.

Appendix A: Regenerated acidic carbon

Carbon enters the ocean mainly in the form of CO₂ and dissolved carbonate. Despite this, the major fraction of carbon in the ocean is as bicarbonate ions. The source-related state variables acidic and basic carbon (AC and BC respectively) allow us to separate the ocean DIC inventory into the sources of CO₂ (AC) and dissolved carbonate (BC). The concept of the sourced related state variables was first described by Walin et al. (2014).

AC and BC are defined from DIC and alkalinity (ALK) as

$$\begin{array}{}\text{(A1)}& {\displaystyle }\mathrm{AC}=\mathrm{DIC}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathrm{ALK},\text{(A2)}& {\displaystyle }\mathrm{BC}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathrm{ALK}.\end{array}$$

Total AC and BC include all ocean sources of carbon, including (but not limited to) river runoff, air–sea gas exchange, and the biological pump.

To isolate the CO₂ that was supplied to the ocean via biological soft tissue, we make use of the separation of DIC and ALK into their preformed and remineralized fractions (see Sect. 2.5). Thus, we then compute the remineralized acidic carbon (AC_rem) as

$$\begin{array}{}\text{(A3)}& {\mathrm{AC}}_{\mathrm{rem}}={\mathrm{DIC}}_{\mathrm{rem}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{ALK}}_{\mathrm{rem}}.\end{array}$$

Appendix B: δ¹³C in cGENIE

cGENIE represents ¹³C as an explicit tracer (separate from and in addition to bulk carbon) in the model, tracking its concentration in all the same gaseous, dissolved, and solid forms that carbon exists in, reporting δ¹³C in per mille relative to the standard Vienna Pee Dee Belemnite (VPDB). The current scheme is based on that described in Ridgwell (2001) and updated as described in Ridgwell et al. (2007) and is evaluated for the modern ocean (alongside simulated Δ¹⁴C) in cGENIE, in Turner and Ridgwell (2016).

In the aqueous phase, the isotopic partitioning of carbon between CO₂(aq), ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, and ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ is resolved and follows Zeebe and Wolf-Gladrow (2001) (their Sect. 3.2). The empirical fractionation factors used are from Zhang et al. (1995). The air–sea fractionation scheme follows that of Marchal et al. (1998) with the individual fractionation factors again taken from Zhang et al. (1995).

For the isotopic composition of organic carbon (δ¹³C_POC), the model of Rau et al. (1996) is adapted, assuming that the isotopic signature of exported POC reflects that of phytoplankton biomass. Following Ridgwell (2001), the full equation of Rau et al. (1996) is simplified to

$$\begin{array}{}\text{(B1)}& \mathit{\delta }{}^{\mathrm{13}}{\mathrm{C}}^{\mathrm{POC}}=\mathit{\delta }{}^{\mathrm{13}}{\mathrm{C}}^{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}}-\mathit{ϵ}{}_{\mathrm{f}}+\left(\mathit{ϵ}{}_{\mathrm{f}}-\mathit{ϵ}{}_{\mathrm{d}}\right)\cdot {\displaystyle \frac{K_Q}{\left[{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}\right]}},\end{array}$$

where [CO₂(aq)] is the ambient concentration of aqueous CO₂, and δ¹³C(aq) is its isotopic composition. K_Q is a temperature-only-dependent approximation of the full cell-dependent size and growth rate parameterization in the Rau et al. (1996) model (see Ridgwell, 2001). We take an intermediate value for the enzymatic isotope fractionation factor associated with intracellular C fixation (ϵ_f) of −25 ‰ following Rau et al. (1996, 1997), and we assume a temperature-invariant value for ϵ_d of 0.7 ‰.

The result of applying this scheme in cGENIE is a zonal mean profile characterized by δ¹³C_POC of −22 ‰ to −21 ‰ in the tropics, declining with increasing latitude to reach −28 ‰ to −30 ‰ in the Southern Ocean. This latitudinal pattern is comparable to measurements made on suspended particulate organic matter as discussed in Ridgwell (2001).

For ¹³C fractionation into biogenic carbonates at the ocean surface (e.g. foraminiferal tests and coccolithophorid coccoliths), cGENIE follows Mook (1986) and employs a simple temperature-dependent fractionation between the δ¹³C of aqueous ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and calcite.