Leaf-scale quantification of the effect of photosynthetic gas exchange on Δ¹⁷O of atmospheric CO₂

Understanding the processes that affect the triple oxygen isotope composition of atmospheric CO₂ during gas exchange can help constrain the interaction and fluxes between the atmosphere and the biosphere. We conducted leaf cuvette experiments under controlled conditions using three plant species. The experiments were conducted at two different light intensities and using CO₂ with different Δ¹⁷O. We directly quantify the effect of photosynthesis on Δ¹⁷O of atmospheric CO₂ for the first time. Our results demonstrate the established theory for δ¹⁸O is applicable to Δ¹⁷O(CO₂) at leaf level, and we confirm that the following two key factors determine the effect of photosynthetic gas exchange on the Δ¹⁷O of atmospheric CO₂. The relative difference between Δ¹⁷O of the CO₂ entering the leaf and the CO₂ in equilibrium with leaf water and the back-diffusion flux of CO₂ from the leaf to the atmosphere, which can be quantified by the c_m∕c_a ratio, where c_a is the CO₂ mole fraction in the surrounding air and c_m is the one at the site of oxygen isotope exchange between CO₂ and H₂O. At low c_m∕c_a ratios the discrimination is governed mainly by diffusion into the leaf, and at high c_m∕c_a ratios it is governed by back-diffusion of CO₂ that has equilibrated with the leaf water. Plants with a higher c_m∕c_a ratio modify the Δ¹⁷O of atmospheric CO₂ more strongly than plants with a lower c_m∕c_a ratio. Based on the leaf cuvette experiments, the global value for discrimination against Δ¹⁷O of atmospheric CO₂ during photosynthetic gas exchange is estimated to be $-\mathrm{0.57}\pm \mathrm{0.14}$ ‰ using c_m∕c_a values of 0.3 and 0.7 for C₄ and C₃ plants, respectively. The main uncertainties in this global estimate arise from variation in c_m∕c_a ratios among plants and growth conditions.

1 Introduction

Stable isotope measurements of CO₂ provide important information about the magnitude of the CO₂ fluxes between atmosphere and biosphere, which are the largest components of the global carbon cycle (Farquhar et al., 1989, 1993; Ciais et al., 1997a, b; Flanagan and Ehleringer, 1998; Yakir and Sternberg, 2000; Gillon and Yakir, 2001; Cuntz et al., 2003a, b). A better understanding of the terrestrial carbon cycle is essential for predicting future climate and atmospheric CO₂ mole fractions (Booth et al., 2012). Gross primary productivity (GPP), the total carbon dioxide uptake by vegetation during photosynthesis, can only be determined indirectly and remains poorly constrained (Cuntz, 2011; Welp et al., 2011). For example, Beer et al. (2010) estimated global GPP to be 102–135 PgC yr⁻¹ (85 % confidence interval, CI) using machine learning techniques by extrapolating from a database of eddy covariance measurements of CO₂. This estimate has since then been widely used as target for terrestrial vegetation models (Sitch et al., 2015) and replicated based on cross-consistency checks with atmospheric inversions, sun-induced fluorescence (SIF), and global vegetation models (Jung et al., 2020). As an alternative, Welp et al. (2011) estimated global GPP to be 150–175 PgC yr⁻¹ using variations in δ¹⁸O of atmospheric CO₂ after the 1997/98 El Niño event; see Eq. (1) for definition of the δ value.

The concept behind the latter study was that atmospheric CO₂ exchanges oxygen isotopes with leaf and soil water, and this isotope exchange mostly determines the observed variations in δ¹⁸O of CO₂ (Francey and Tans, 1987; Yakir, 1998). Following the 97/98 El Niño–Southern Oscillation (ENSO) event, the anomalous δ¹⁸O signature imposed on tropical leaf and soil waters was transferred to atmospheric CO₂, before slowly disappearing as a function of the lifetime of atmospheric CO₂. This in turn is governed by the land vegetation uptake of CO₂ during photosynthesis, as well as soil invasion of CO₂ (Miller et al., 1999; Wingate et al., 2009). For the photosynthesis term, the equilibration of CO₂ with water is an uncertain parameter in this calculation, partly because the δ¹⁸O of water at the site of isotope exchange in the leaf is not well defined. Importantly, a significant δ¹⁸O variation can occur in leaves due to the preferential evaporation of ${\mathrm{H}}_{\mathrm{2}}^{\mathrm{16}}\mathrm{O}$ relative to ${\mathrm{H}}_{\mathrm{2}}^{\mathrm{18}}\mathrm{O}$ (Gan et al., 2002, 2003; Farquhar and Gan, 2003; Cernusak et al., 2016), which induces a considerable uncertainty in estimating δ¹⁸O of CO₂. Similar considerations for the transfer of the δ¹⁸O signature of precipitation into the soils, and then up through the roots, stems, and leaves makes ¹⁸O of CO₂ a challenging measurement to interpret (Peylin et al., 1999; Cuntz et al., 2003a, b).

Classical isotope theory posits that oxygen isotope distributions are modified in a mass-dependent way. This means that the ¹⁷O∕¹⁶O ratio changes by approximately half of the corresponding change in ¹⁸O∕¹⁶O (Eq. 2), and it applies to the processes involved in gas exchange between atmosphere and plants. However, in 1983 Thiemens and co-workers (Heidenreich and Thiemens, 1983, 1986; Thiemens and Heidenreich, 1983) reported a deviation from mass-dependent isotope fractionation in ozone (O₃) formation called mass-independent isotope fractionation (Δ¹⁷O, Eq. 3). In the stratosphere, the Δ¹⁷O of O₃ is transferred to CO₂ via isotope exchange of CO₂ with O(¹D) produced from O₃ photolysis (Yung et al., 1991, 1997; Shaheen et al., 2007), which results in a large amount of Δ¹⁷O in stratospheric CO₂ (Thiemens et al., 1991, 1995; Lyons, 2001; Lämmerzahl et al., 2002; Thiemens, 2006; Kawagucci et al., 2008; Wiegel et al., 2013).

Once Δ¹⁷O has been created in stratospheric CO₂, the only process that modify its signal is isotope exchange with leaf water, soil water and ocean water at the Earth's surface, after CO₂ has reentered the troposphere (Boering, 2004; Thiemens et al., 2014; Liang and Mahata, 2015; Hofmann et al., 2017). Isotope exchange with leaf water is more efficient relative to ocean water due to the presence of the enzyme carbonic anhydrase (CA), which effectively catalyzes the conversion of CO₂ and H₂O to ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and H⁺ and vice versa (Francey and Tans, 1987; Friedli et al., 1987; Badger and Price, 1994; Gillon and Yakir, 2001). The isotope exchange in the atmosphere is negligible due to lower liquid water content, lower residence time, and the absence of carbonic anhydrase (Mills and Urey, 1940; Miller et al., 1971; Johnson, 1982; Silverman, 1982; Francey and Tans, 1987).

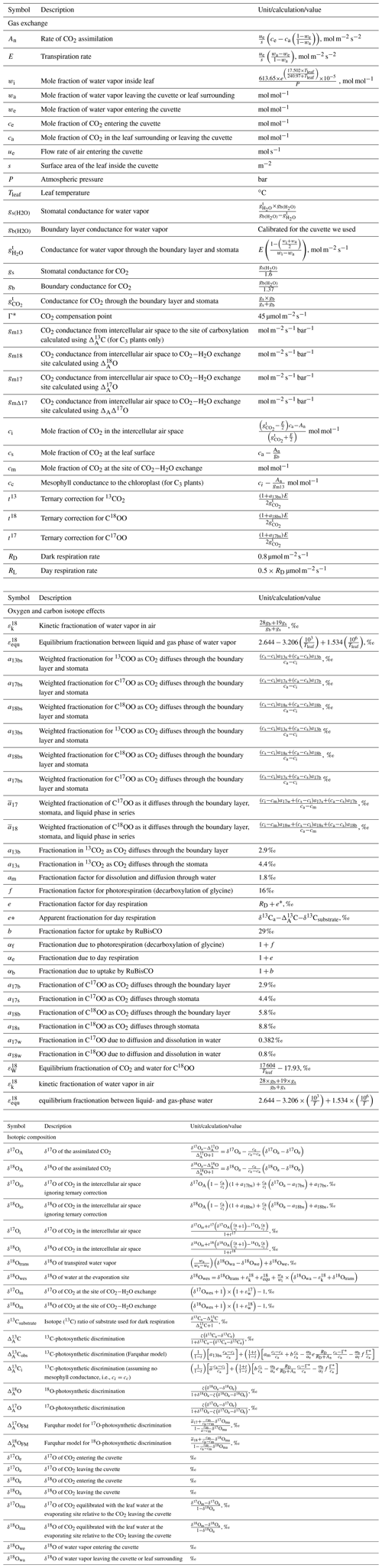
Δ¹⁷O of CO₂ has been suggested as an additional independent tracer for constraining global GPP (Hoag et al., 2005; Thiemens et al., 2013; Hofmann et al., 2017; Liang et al., 2017b; Koren et al., 2019) because the processes involved in plant–atmosphere gas exchange are all mass dependent. Therefore, Δ¹⁷O at the CO₂−H₂O exchange site in the leaf will vary much less than δ¹⁸O. Nevertheless, mass-dependent isotope fractionation processes with slightly different three-isotope fractionation slopes are involved, which have been precisely established in the past years. Figure 1 shows how the different processes affect Δ¹⁷O of the H₂O and CO₂ reservoirs involved. The triple isotope slope of oxygen in meteoric waters is taken as reference slope, λ_Ref=0.528 (Meijer and Li, 1998; Barkan and Luz, 2007; Landais et al., 2008; Luz and Barkan, 2010; Uemura et al., 2010), and we assume that soil water is similar to meteoric water. Due to transpiration and diffusion in the leaf, Δ¹⁷O of leaf water gets modified following a humidity-dependent three-isotope slope ${\mathit{\theta }}_{\mathrm{trans}}=\mathrm{0.522}-\mathrm{0.008}\times h$ (Landais et al., 2006). Exchange of oxygen isotopes between leaf water and CO₂ follows ${\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.5229}$ (Barkan and Luz, 2012), which determines the Δ¹⁷O of CO₂ inside the leaf at the CO₂−H₂O exchange site. Finally, the Δ¹⁷O of the CO₂ is modified when CO₂ diffuses into and out of the leaf with λ_diff=0.509 (Young et al., 2002).

Figure 1 Schematic for mass-dependent isotope fractionation process that affects the Δ¹⁷O of the CO₂ and H₂O during the photosynthetic gas exchange (not to scale). The triple oxygen isotope relationships for the individual isotope fractionation processes (both kinetic and equilibrium fractionation) are assigned with θ. ${\mathit{\theta }}_{\mathrm{trans}}=\mathrm{0.522}-\mathrm{0.008}\times h$, where h is relative humidity (Landais et al., 2006). In this study the humidity is 75 %, θ_trans=0.516, ${\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ (Barkan and Luz, 2012), ${\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{diff}}$ (Young et al., 2002), ${\mathit{\theta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{v}\right)-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{l}\right)}$ (Barkan and Luz, 2005), and ${\mathit{\theta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{v}\right)-\mathrm{diff}}$ (Barkan and Luz, 2007), where v and l are vapor and liquid water, respectively. ε¹⁸O is enrichment or depletion in ¹⁸O isotope composition due to the corresponding isotope fractionation process, and diff and trans stand for diffusion and transpiration, respectively.

In the first box model study of Hoag et al. (2005), the small deviations in Δ¹⁷O of CO₂ due to differences in three-isotope slopes were neglected and exchange with water was assumed to reset Δ¹⁷O to 0. Hofmann et al. (2017) included the different isotope effects shown in Fig. 1 in their box model. Koren et al. (2019) incorporated all the physicochemical processes affecting Δ¹⁷O of CO₂ in a 3D atmospheric model and investigated the spatiotemporal variability of Δ¹⁷O and its use as tracer for GPP. Using these and other similar models, numerous measurements of Δ¹⁷O in atmospheric CO₂ from different locations have been performed and used to estimate GPP (Liang et al., 2006; Barkan and Luz, 2012; Thiemens et al., 2014; Liang and Mahata, 2015; Laskar et al., 2016; Hofmann et al., 2017). The three-isotope slopes of the processes involved in the gas exchange (Fig. 1) have been precisely determined in idealized experiments. In the advanced models mentioned above it is assumed that when all the pieces are put together they result in a realistic overall modification of Δ¹⁷O of CO₂ in the atmosphere surrounding the leaf. However, this has not been confirmed by measurements previously.

In this study we report the effect of photosynthesis on Δ¹⁷O of CO₂ in the surrounding air at the leaf scale. We measured Δ¹⁷O of CO₂ entering and leaving a leaf cuvette to calculate the isotopic fractionation associated with photosynthesis for three species that are representative for three different biomes. The fast-growing annual herbaceous C₃ species Helianthus annuus (sunflower) has a high photosynthetic capacity (A_n) and high stomatal conductance (g_s) and is representative for temperate and tropical crops (Fredeen et al., 1991). The slower-growing perennial evergreen C₃ species Hedera hibernica (ivy) is representative of forests and other woody vegetation and stress-subjected habitats (Pons et al., 2009). The fast-growing, agronomically important crop Zea mays (maize) is an herbaceous annual C₄ species with a high A_n and a low g_s, typical for savanna type vegetation (van der Weijde et al., 2013). The mole fraction of CO₂ at the CO₂−H₂O exchange site (c_m) is an important parameter to determine the effect of photosynthesis on Δ¹⁷O of CO₂. In C₃ plants, the CO₂−H₂O exchange can occur anywhere between the plasma membrane and the chloroplast since the catalyzing enzyme CA has been found in the chloroplast, cytosol, mitochondria, and plasma membrane (Fabre et al., 2007; DiMario et al., 2016). For C₄ plants, CA is mainly found in the cytosol, and the CO₂−H₂O exchange occurs there (Badger and Price, 1994). In our experiments, sunflower and ivy are used to cover the wide c_m∕c_a ratio range among C₃ plants and maize represents the c_m∕c_a ratio for the C₄ plants. Using our results from the leaf-scale experiments, we estimated the effect of terrestrial vegetation on Δ¹⁷O of CO₂ in the global atmosphere.

2 Theory

2.1 Notation and definition of δ values

Isotopic composition is expressed as the deviation of the heavy-to-light isotope ratio in a sample relative to a reference ratio and is denoted as δ, expressed in per mill (‰). In the case of oxygen isotopes, the isotope ratios are ${}^{\mathrm{18}}\mathrm{R}={[}^{\mathrm{18}}\mathrm{O}]/{[}^{\mathrm{16}}\mathrm{O}]$ and ${}^{\mathrm{17}}\mathrm{R}={[}^{\mathrm{17}}\mathrm{O}]/{[}^{\mathrm{16}}\mathrm{O}]$ and the reference material is Vienna Standard Mean Ocean Water (VSMOW):

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^n\mathrm{O}={\displaystyle \frac{{}^n{\mathrm{R}}_{\mathrm{sample}}}{{}^n{\mathrm{R}}_{\mathrm{VSMOW}}}}-\mathrm{1},n\text{refers to}\mathrm{17}\text{or}\mathrm{18}.\end{array}$$

For most processes, isotope fractionation depends on mass, and therefore the fractionation against ¹⁷O is approximately half of the fractionation against ¹⁸O (Eq. 3).

$$\begin{array}{}\text{(2)}& \ln \left({\mathit{\delta }}^{\mathrm{17}}\mathrm{O}+\mathrm{1}\right)=\mathit{\lambda }\times \ln \left({\mathit{\delta }}^{\mathrm{18}}\mathrm{O}+\mathrm{1}\right)\end{array}$$

The mass-dependent isotope fractionation factor λ ranges from 0.5 to 0.5305 for different molecules and processes (Matsuhisa et al., 1978; Thiemens, 1999; Young et al., 2002; Cao and Liu, 2011). Δ¹⁷O is used to quantify the degree of deviation from Eq. (2) (see Eq. 3). Note that Δ¹⁷O changes not only by mass-independent isotope fractionation processes but also by mass-dependent isotope fractionation processes with a different λ value from the one used in the definition of Δ¹⁷O (Barkan and Luz, 2005, 2011; Landais et al., 2006, 2008; Luz and Barkan, 2010; Pack and Herwartz, 2014).

$$\begin{array}{}\text{(3)}& {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}=\ln \left({\mathit{\delta }}^{\mathrm{17}}\mathrm{O}+\mathrm{1}\right)-\mathit{\lambda }\times \ln \left({\mathit{\delta }}^{\mathrm{18}}\mathrm{O}+\mathrm{1}\right)\end{array}$$

The choice of λ is in principle arbitrary, and in this study we use λ=0.528, which was established for meteoric waters (Meijer and Li, 1998; Landais et al., 2008; Brand et al., 2010; Luz and Barkan, 2010; Barkan and Luz, 2012; Sharp et al., 2018). Equation (3) can be linearized to ${\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}={\mathit{\delta }}^{\mathrm{17}}\mathrm{O}-\mathit{\lambda }\times {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}$ (Miller, 2002), but this approximation causes an error that increases with δ¹⁸O (Miller, 2002; Bao et al., 2016).

2.2 Discrimination against Δ¹⁷O of CO₂

The overall isotope fractionation associated with the photosynthesis of CO₂ is commonly quantified using the term discrimination, as described in Farquhar and Richards (1984), Farquhar et al. (1989), and Farquhar and Lloyd (1993). We use the symbol Δ_A for discrimination due to assimilation in this paper since the commonly used Δ is already used for the definition of Δ¹⁷O (see Eq.  3). Δ_A quantifies the enrichment or depletion of carbon and oxygen isotopes of CO₂ in the surrounding atmosphere relative to the CO₂ that is assimilated (Farquhar and Richards, 1984). It can be calculated from the isotopic composition of the CO₂ entering and leaving the leaf cuvette (Evans et al., 1986; Gillon and Yakir, 2000a; Barbour et al., 2016) as follows:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{obs}}& ={\displaystyle \frac{{}^{\mathrm{n}}{\mathrm{R}}_{\mathrm{a}}}{{}^{\mathrm{n}}{\mathrm{R}}_{\mathrm{A}}}}-\mathrm{1}={\displaystyle \frac{{}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{a}}-{\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{A}}}{\mathrm{1}+{\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{A}}}}\\ & ={\displaystyle \frac{\mathit{\zeta }\times \left({\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{a}}-{\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{e}}\right)}{\mathrm{1}+{\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{a}}-\mathit{\zeta }\times \left({\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{a}}-{\mathit{\delta }}^{\mathrm{n}}{\mathrm{O}}_{\mathrm{e}}\right)}},\end{array}\end{array}$$

where the indices e, a and A refer to CO₂ entering and leaving the cuvette and being assimilated, respectively. $\mathit{\zeta }=\frac{c_{\mathrm{e}}}{c_{\mathrm{e}}-c_{\mathrm{a}}}$, where c_e and c_a are the mole fractions of CO₂ entering and leaving the cuvette. For quantifying the effect of photosynthesis on Δ¹⁷O in our experiments, the Δ_AΔ¹⁷O is calculated from ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}\mathrm{O}$ and ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ using the three-isotope slope λ_RL=0.528, similar to Eq. (3). In previous studies slightly different formulations have been used to define the effect of photosynthesis on Δ¹⁷O, and a comparison of the different definitions is provided in the Supplement (Eqs. S37–S40).

It is important to note that when the logarithmic definition of Δ¹⁷O or Δ_AΔ¹⁷O is used, values are not additive (Kaiser et al., 2004). In linear calculations, the error gets larger when the relative difference in δ¹⁸O between the two CO₂ gases increases regardless of the Δ¹⁷O of the individual CO₂ gases (Fig. S1 in the Supplement). Therefore, Δ_AΔ¹⁷O values have to be calculated from the individual ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}\mathrm{O}$ and ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ values and not by linear combinations of the Δ¹⁷O of air entering and leaving a plant chamber.

3 Materials and methods

3.1 Plant material and growth conditions

Sunflower (Helianthus annuus L. cv “sunny”) was grown from seeds in 0.6 L pots with potting soil (Primasta, the Netherlands) for about 4 weeks. All leaves appearing above the first leaf pair were removed to avoid shading. Established juvenile ivy (Hedera hibernica L.) plants were pruned and planted in 6 L pots for 6 weeks. Ivy leaves that had developed and matured were used for the experiments. Maize (Z. mays L. cv “saccharate”) was grown from seed in 1.6 L pots for at least 7 weeks. For maize, the fourth or higher leaf number was used for the experiments when it was mature. A section of the leaf at about one-third from the tip was inserted into the leaf cuvette. They were placed on a sub-irrigation system that provided water during the growth period in a controlled-environment growth chamber, with an air temperature of 20 ^∘C, relative humidity of 70 %, and CO₂ mole fraction of about 400 ppm. The photosynthetic photon flux density (PPFD) was about 300 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ during a daily photoperiod of 16 h measured with a PPFD meter (Li-Cor LI-250A, Li-Cor Inc, NE, USA).

3.2 Gas exchange experiments

Gas exchange experiments were performed in an open system where a controlled flow of air enters and leaves the leaf cuvette, similar to the setup used by Pons and Welschen (2002). A schematic for the gas exchange experimental setup is shown in Fig. 2. The leaf cuvette had dimensions of $\mathrm{7}\times \mathrm{7}\times \mathrm{7}$ cm³ ($l\times w\times h$) and the top part of the cuvette was transparent. The temperature of the leaf was measured with a K type thermocouple. The leaf chamber temperature was controlled by a temperature-controlled water bath kept at 20 ^∘C (Tamson TLC 3, The Netherlands). A halogen lamp (Pradovit 253, Ernst Leitz Wetzlar GmbH, Germany) in a slide projector was used as a light source. Infrared was excluded by reflection from a cold mirror. The light intensity was varied with spectrally neutral filters (Pradovit 253, Ernst Leitz Wetzlar GmbH, Germany).

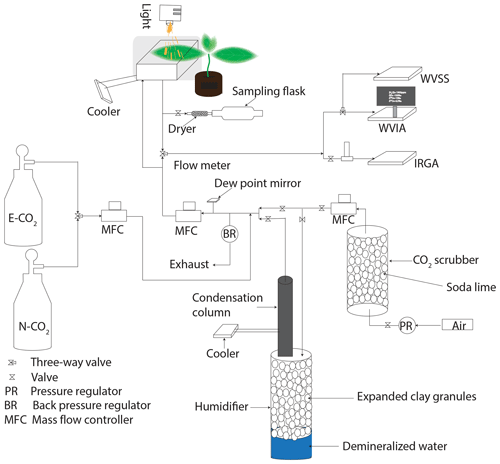
Figure 2 Schematic diagram of the leaf cuvette experimental setup. IRGA stands for the infrared gas analyzer, WVSS is the water vapor standard source, WVIA is the water vapor isotope analyzer, N-CO₂ is normal CO₂, and E-CO₂ is ¹⁷O-enriched CO₂.

The CO₂ mole fraction of the incoming and outgoing air was measured with an infrared gas analyzer (IRGA, model LI-6262, Li-Cor Inc., NE, USA). The isotopic composition and mole fraction of the incoming and outgoing water vapor were measured with a triple water vapor isotope analyzer (WVIA, model 911-0034, Los Gatos Research, USA). Compressed air (ambient outside air without drying) was passed through soda lime to scrub the CO₂. The CO₂-free air could be humidified depending on the experiment conditions (see Fig. 2). The humidity of the inlet air was monitored continuously with a dew point meter (HYGRO-M1, General Eastern, Watertown, MA, USA). Pure CO₂ (either normal CO₂ or isotopically enriched CO₂) was mixed with the incoming air to produce a CO₂ mole fraction of 500 ppm. The isotopically enriched CO₂ was prepared by photochemical isotope exchange between CO₂ and O₂ under UV irradiation (Adnew et al., 2019).

An attached leaf or part of it was inserted into the cuvette, the composition of the inlet air was measured, and both IRGA and WVIA were switched to measure the outlet air. Based on the CO₂ mole fraction of the outgoing air the flow rate of the incoming air to the cuvette was adjusted to establish a drawdown of 100 ppm CO₂ due to photosynthesis in the plant chamber. The water vapor content entering the cuvette was adjusted depending on the transpiration rate relative to CO₂ uptake to avoid condensation (Fig. 2). The outgoing air was measured continuously until a steady state was reached for CO₂ and H₂O mole fractions and δD and δ¹⁸O of the water vapor. After a steady state was established, the air was directed to the sampling flask while the IRGA and WVIA were switched back to measure the inlet air. The air passed through a Mg(ClO₄)₂ dryer before entering the sampling flask.

After sampling, the leaf area inside the cuvette was measured with a LI-3100C area meter (Li-Cor Inc., USA). Immediately afterward, the leaf was placed in a leak-tight 9 mL glass vial and kept in a freezer at −20 ^∘C until leaf water extraction.

3.3 Calibration of the water vapor isotope analyzer (WVIA) and leaf water analysis

The WVIA was calibrated using five water standards provided by IAEA (Wassenaar et al., 2018) for both δ¹⁸O and δD (Fig. S2). We did not calibrate the WVIA for δ¹⁷O, so the δ¹⁷O data are not used in the quantitative evaluation. The isotopic composition of the water standards ranged from −50.93 ‰ to 3.64 ‰ and −396.98 ‰ to 25.44 ‰ for δ¹⁸O and δD, respectively. The detailed characterization and calibration of the WVIA is provided in the Supplement (Figs. S2 to S4).

Leaf water was extracted by cryogenic vacuum distillation for 4 h at 60 ^∘C following a well-established procedure as shown in Fig. S5 (Wang and Yakir, 2000; Landais et al., 2006; West et al., 2006). Details are provided in the Supplement. The δ¹⁷O and δ¹⁸O of leaf water were determined at the Laboratoire des Sciences du Climat et de l'Environnement laboratory using a fluorination technique as described in Barkan and Luz (2005) and Landais et al. (2006, 2008).

3.4 Carbon dioxide extraction and isotope analysis

CO₂ was extracted from the air samples in a system made from electropolished stainless steel (Fig. S6). Our system used four commercial traps (MassTech, Bremen, Germany). The first two traps were operated at dry ice temperature (−78 ^∘C) to remove moisture and some organics. The other two traps were operated at liquid nitrogen temperature (−196 ^∘C) to trap CO₂. The flow rate during extraction was 55 mL min⁻¹ controlled by a mass flow controller (Brooks Instruments, the Netherlands). The reproducibility of the extraction system was 0.030 ‰ for δ¹⁸O and 0.007 ‰ for δ¹³C determined on 14 extractions (1σ standard deviation, Table S1 in the Supplement).

The Δ¹⁷O of CO₂ was determined using the CO₂−O₂ exchange method (Mahata et al., 2013; Barkan et al., 2015; Adnew et al., 2019). The CO₂−O₂ exchange system used at Utrecht University is described in Adnew et al. (2019). In short, equal amounts of CO₂ and O₂ were mixed in a quartz reactor containing a platinum sponge catalyst and heated at 750 ^∘C for 2 h. After isotope equilibration, the CO₂ was trapped at liquid nitrogen temperature, while the O₂ was collected with 1 pellet of a 5Å molecular sieve (1.6 mm, Sigma Aldrich, USA) at liquid nitrogen temperature. The isotopic composition of the isotopically equilibrated O₂ was measured with a Delta^PlusXL isotope ratio mass spectrometer in dual-inlet mode with reference to a pure O₂ calibration gas that has been assigned values of δ¹⁷O=9.254 ‰ and δ¹⁸O=18.542 ‰ by Eugeni Barkan at the Hebrew University of Jerusalem. The reproducibility of the Δ¹⁷O measurement was better than 0.01 ‰ (Table S1).

3.5 Leaf cuvette model

We used a simple leaf cuvette model to evaluate the dependence of Δ_AΔ¹⁷O on key parameters. In this model, the leaf is partitioned into three different compartments: the intercellular air space, the mesophyll cell, and the chloroplast. In the leaf cuvette model, we used a 100 ppm down-draw of CO₂, similar to the leaf exchange experiments, i.e., the CO₂ mole fraction decreases from 500 ppm in the entering air (c_e) to 400 ppm in the outgoing air (c_o), which is identical to the air surrounding the leaf (c_a) as a result of thorough mixing in the cuvette. The assimilation rate is set to 20.0 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$. The leaf area and flow rate of air are set to 30 cm² and 0.7 L min⁻¹, respectively. The isotope composition of leaf water at the site where the H₂O−CO₂ exchange occurs is δ¹⁷O=5.39 ‰ and δ¹⁸O=10.648 ‰, which is the mean of the measured δ¹⁷O and δ¹⁸O values of bulk leaf water in our experiments. The leaf water temperature is set to 22 ^∘C (similar to the experiment). In the model, the δ¹⁸O of the CO₂ entering the cuvette is set to 30.47 ‰ for all the simulations, as in the normal CO₂ experiments, but the assigned Δ¹⁷O values range from −0.5 ‰ to 0.5 ‰, which encompasses both the stratospheric intrusion and combustion components. The corresponding δ¹⁷O of the CO₂ entering the cuvette is calculated from the assigned δ¹⁸O value (30.47 ‰) and Δ¹⁷O values (−0.5 ‰ to 0.5 ‰). For the calculations with this model, we assumed an infinite boundary layer conductance. The leaf cuvette model is illustrated in the Supplement (Fig. S7), and the detailed code and description is available at https://git.wur.nl/leaf_model (last access: 23 March 2020, Koren et al., 2020).

4 Results

4.1 Gas exchange parameters

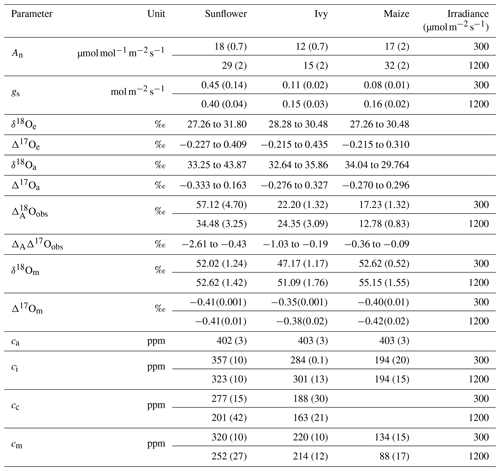
Table 1 summarizes the isotopic composition and mole fraction of the CO₂ used in this study for sunflower, ivy and maize. The Δ¹⁷O of CO₂ used in this study varies from −0.215 ‰ to 0.44 ‰, while the δ¹⁸O value is close to 30 ‰ for all the experiments. For all the experiments, the mole fraction of CO₂ entering the leaf (c_a) is 400 ppm, whereas the mole fraction of the CO₂ in the intercellular air space (c_i), at the CO₂−H₂O exchange site (c_m), and in the chloroplast (c_c) varies depending on the assimilation rate and metabolism type of the plants. Estimating the mesophyll conductance is described in the companion paper. A detailed description for estimating c_m and c_c is provided in the Supplement. A list of variables and parameters used in this study are summarized in Table 2.

Table 1 Summary of gas exchange parameters and isotopic compositions of maize, sunflower, and ivy. Mole fraction at the site of exchange (c_m) is calculated assuming complete isotopic equilibrium with the water at the CO₂−H₂O exchange site. The water at the CO₂−H₂O exchange site is assumed to be the same as the isotopic composition at the site of evaporation. Numbers in parentheses are the standard deviations of the mean (1σ).

Table 2 List of symbols and variables.

4.2 Discrimination against ¹⁸O of CO₂

Figure 3a shows discrimination against ¹⁸O associated with photosynthesis (${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$) for sunflower, ivy, and maize as a function of the c_m∕c_a ratio. ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ varies with c_m∕c_a, as found in previous studies (Gillon and Yakir, 2000a; Barbour et al., 2016) . For sunflower, we observe ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ values between 29 ‰ and 64 ‰ for c_m∕c_a between 0.54 and 0.86. Ivy shows relatively little variation in ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ around a mean of 22 ‰ for c_m∕c_a between 0.48 and 0.58. For maize, ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ is lower than for the C₃ plants measured in this study, with values between 10 ‰ and 20 ‰ for c_m∕c_a between 0.15 and 0.37.

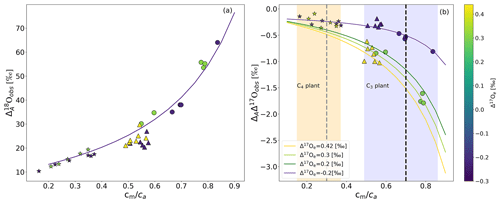
Figure 3 (a) ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ during photosynthesis for two C₃ plants, sunflower (circles) and ivy (triangles), and C₄ plant maize (stars), as a function of c_m∕c_a. The solid lines show results from the leaf cuvette model, where δ¹⁸O of the CO₂ entering the cuvette is 30.47 ‰. (b) Δ_AΔ¹⁷O of CO₂ as a function of c_m∕c_a for isotopically different CO₂ gases entering the cuvette (color bar shows Δ¹⁷O_e) for sunflower (circles), ivy (triangles), and maize (stars). Δ_AΔ¹⁷O values calculated using the leaf cuvette model are shown as solid lines in corresponding colors (Δ¹⁷O_e values are given in the legend). The shaded areas indicate the c_m∕c_a ranges for C₄ and C₃ plants, and the vertical dashed lines indicate the mean c_m∕c_a ratio used for extrapolating from the leaf scale to the global scale. The solid line is the leaf cuvette model results for the corresponding c_m∕c_a ratio.

For sunflower, changing the irradiance from 300 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ (low light, hereafter LL) to 1200 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ (high light, hereafter HL) leads to a clear decrease in ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ (average 22 ‰). For maize, the ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ change is only 4.4 ‰ on average. For ivy, changing the light intensity does not significantly change the observed ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$. The solid lines in Fig. 3a show the results of leaf cuvette model calculations, where the dependence of ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ on c_m∕c_a is explored for a set of calculations with otherwise fixed parameters. The model agrees well with the experimental results, except for ivy, where the model overestimates the discrimination.

4.3 Discrimination against Δ¹⁷O of CO₂

The discrimination of photosynthesis against Δ¹⁷O of CO₂ (Δ_AΔ¹⁷O) is shown in Fig. 3b. Δ_AΔ¹⁷O is negative for all experiments, it depends strongly on the c_m∕c_a ratio, and |Δ_AΔ¹⁷O| increases with c_m∕c_a ratio. For instance, for Δ¹⁷O of CO₂ entering the cuvette of −0.215 ‰, Δ_AΔ¹⁷O is −0.25 ‰ for maize with c_m∕c_a ratio of 0.3, −0.3 ‰ for ivy with c_m∕c_a ratio of 0.5 ‰, and −0.5 ‰ for sunflower with c_m∕c_a ratio of 0.7 (Fig. 3b). For sunflower and ivy, Δ_AΔ¹⁷O is also strongly dependent on the Δ¹⁷O of CO₂ supplied to the cuvette, whereas no significant dependence is found for maize. For an increase in Δ¹⁷O of CO₂ entering the cuvette from −0.215 ‰ to 0.435 ‰, Δ_AΔ¹⁷O increases from −0.3 ‰ to −0.9 ‰ at c_m∕c_a ratio of 0.5 for ivy. For sunflower, an increases Δ¹⁷O of CO₂ entering the cuvette from −0.215 ‰ to 0.31 ‰ increases Δ_AΔ¹⁷O from −0.8 ‰ to −1.7 ‰ at c_m∕c_a ratio of 0.8. The leaf cuvette model results illustrate the shape of the dependence on the c_m∕c_a ratio and agree well with the experiments. For the leaf cuvette model, the Δ¹⁷O value of the water is assigned a constant value of −0.122 ‰ (average Δ¹⁷O value for the bulk leaf water).

Figure 4b shows the same values of Δ_AΔ¹⁷O as a function of the difference between Δ¹⁷O of CO₂ entering the leaf and the calculated Δ¹⁷O of leaf water at the evaporation site where CO₂−H₂O exchange takes place (Δ¹⁷O_a−Δ¹⁷O_wes) for different c_m∕c_a ratios. The leaf cuvette model results (solid lines in Fig. 4b) suggest a linear dependence between Δ_AΔ¹⁷O and (Δ¹⁷O_a−Δ¹⁷O_wes). The experimental results agree with the hypothesis that Δ_AΔ¹⁷O is linearly dependent on Δ¹⁷O_a−Δ¹⁷O_wes at a certain c_m∕c_a ratio. Figure 4a shows the corresponding relation where Δ_AΔ¹⁷O is divided by Δ¹⁷O_a−Δ¹⁷O_m. All the values follow the same relationship as a function of the c_m∕c_a ratio, which can be approximated quite well by an exponential function (Eq. 5). This function quantifies the dependence of Δ_AΔ¹⁷O on c_m∕c_a and thus the effect of the diffusion of isotopically exchanged CO₂ back to the atmosphere, which increases with increasing c_m∕c_a ratio.

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{{\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}}{{\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{a}}-{\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{m}}}}=-\mathrm{0.150}\times \exp \left(\mathrm{3.707}\times c_{\mathrm{m}}/c_{\mathrm{a}}\right)+\mathrm{0.028}\end{array}$$

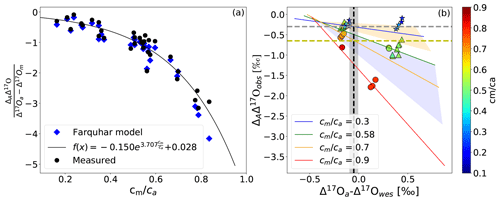
Figure 4 (a) Dependency of Δ_AΔ¹⁷O on the relative difference of the Δ¹⁷O(CO₂) entering the leaf and the Δ¹⁷O of CO₂ in equilibrium with leaf water against the c_m∕c_a ratio. (b) Dependency of Δ_AΔ¹⁷O on the difference between the Δ¹⁷O of CO₂ entering the cuvette and the Δ¹⁷O of leaf water at the evaporation site color coded for different c_m∕c_a ratios. The solid lines are the results of the leaf cuvette model for different c_m∕c_a ratios as stated in the legend. The vertical dashed black line indicates the difference between the global average Δ¹⁷O value for CO₂ (−0.168 ‰) and leaf water (−0.067 ‰) (Koren et al., 2019). The gray and yellow horizontal dashed lines indicate global Δ_AΔ¹⁷O of C₄ and C₃ plants for a c_m∕c_a ratio of 0.3 and 0.7, respectively.

Figure 5a and c show results from the leaf cuvette model that illustrates in more detail how Δ¹⁷O_e and Δ¹⁷O_wes affect Δ¹⁷O_a and Δ_AΔ¹⁷O and their dependence on c_m∕c_a. At lower c_m∕c_a, only a very small fraction of CO₂ that has undergone isotopic equilibration in the mesophyll diffuses back to the atmosphere, and therefore Δ¹⁷O_a stays close to the incoming Δ¹⁷O_e, modified by the fractionation during CO₂ diffusion through the stomata (Fig. 5a). Figure 5c confirms that at low c_m∕c_a, Δ_AΔ¹⁷O approaches the fractionation constant expected for diffusion, −0.170 ‰. This diffusional fractionation is independent of the isotopic composition of the CO₂ entering the leaf, and therefore at low c_m∕c_a, the Δ_AΔ¹⁷O curves for the different values of the anomaly of the CO₂ entering the leaf converge. For a high c_m∕c_a ratio, the back-diffusion flux of CO₂ that has equilibrated with water becomes the dominant factor, and, in this case, the isotopic composition of the outgoing CO₂ converges towards this isotope value, independent of the isotopic composition of the incoming CO₂ (Fig. 5a). This can lead to a very wide range of values for the discrimination against Δ¹⁷O because now the effect on Δ¹⁷O of the ambient CO₂ depends strongly on the difference in isotopic composition between incoming CO₂ and CO₂ in isotopic equilibrium with the leaf water.

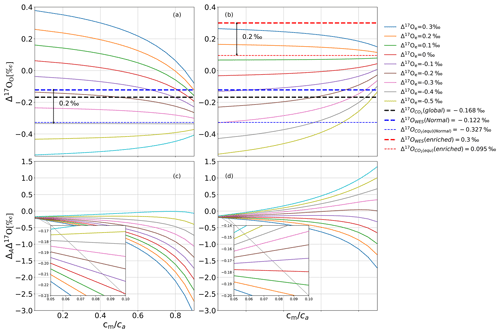
Figure 5 (a, b) Δ¹⁷O_a as a function of c_m∕c_a for various values of Δ¹⁷O_e (see legend) for ${\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{wes}}=-\mathrm{0.122}$ ‰ in (a) and Δ¹⁷O_wes=0.300 ‰ in (b). Panels (c, d) show the corresponding values for Δ_AΔ¹⁷O. Δ¹⁷O_global is the global average Δ¹⁷O value for atmospheric CO₂ (Koren et al., 2019). When Δ¹⁷O of CO₂ entering the cuvette is approximately 0.2 ‰ lower than the Δ¹⁷O of leaf water at the CO₂−H₂O exchange site, Δ¹⁷O of the CO₂ leaving the cuvette does not change when the c_m∕c_a ratio varies.

In the model calculations shown in Fig. 5b and d, the isotopic composition of the water was changed from ${\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{wes}}=-\mathrm{0.122}$ ‰ to 0.300 ‰, whereas all other parameters were kept the same. The value of Δ¹⁷O_e for which Δ¹⁷O_a does not depend on c_m∕c_a is shifted accordingly, again being similar to Δ¹⁷O_m. At low $c_{\mathrm{m}}/c_{\mathrm{a}},{\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}$ converges to the same value as in Fig. 5c, confirming the role of diffusion into the stomata as discussed above.

Figure 6 shows how δ¹⁸O and Δ¹⁷O vary in key compartments of the leaf cuvette system that determine the oxygen isotope effects associated with photosynthesis, based on the previously established three-isotope slopes of the various processes (Fig. 1). The irrigation water has a Δ¹⁷O value of 0.017 ‰. The measured bulk leaf water is 6 ‰ to 16 ‰ enriched in ¹⁸O and its Δ¹⁷O value is lower by −0.075 ‰ to −0.200 ‰ (mean value −0.121 ‰) than the irrigation water, calculated using a three-isotope slope of θ_trans=0.516 % at 80 % humidity (Landais et al., 2006). Δ¹⁷O of leaf water at the evaporation site, calculated from the transpired water, has slightly lower Δ¹⁷O, with values between −0.119 ‰ and −0.237 (average −0.184 ‰). Note that the bulk leaf water was not measured for all the experiments. For the experiments where the bulk leaf water is measured, Δ¹⁷O of leaf water at the evaporation site ranges from −0.160 ‰ to −0.231 ‰ with an average value of $-\mathrm{0.190}\pm \mathrm{0.020}$ ‰. The calculated isotopic composition of water at the exchange site was thus similar but slightly lower in Δ¹⁷O than the values measured for bulk leaf water. CO₂ exchanges with the water in the leaf with a well-established fractionation constant (see Eq. S17) and a three-isotope slope of ${\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.5229}$ (Barkan and Luz, 2012), leading to the lower Δ¹⁷O values of the equilibrated CO₂. In our experiments, the Δ¹⁷O value of CO₂ in equilibrium with leaf water is lower than the Δ¹⁷O value of CO₂ entering the leaf. The Δ¹⁷O of the CO₂ in the intercellular air space is a mixture between two end-members, the Δ¹⁷O of the CO₂ entering the leaf and Δ¹⁷O of the CO₂ in equilibrium with leaf water. This explains why the observed values of Δ_AΔ¹⁷O are negative for the experiments performed in this study.

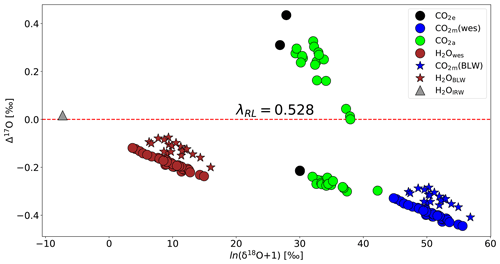
Figure 6 Isotopic composition of various relevant oxygen reservoirs that affect the Δ¹⁷O of atmospheric CO₂ during photosynthesis: irrigation water (gray triangle), calculated leaf water at the evaporation site (brown circles), measured bulk leaf water (brown star), CO₂ entering the cuvette (black circles), CO₂ leaving the leaf cuvette (green circles), CO₂ equilibrated with leaf water at the evaporation site (blue circles), and CO₂ equilibrated with bulk leaf water (blue stars). Δ¹⁷O is calculated with λ=0.528.

5 Discussion

5.1 Discrimination against δ¹⁸O of CO₂

The higher ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ values for sunflower compared to maize and ivy (Fig. 3a) are mainly due to a higher back-diffusion flux ($c_{\mathrm{m}}/(c_{\mathrm{a}}-c_{\mathrm{m}})$). The back-diffusion flux is higher for the C₃ plants sunflower and ivy than for the C₄ plant maize, a consequence of the lower stomatal conductance and higher assimilation rate of C₄ plants (Gillon and Yakir, 2000a; Barbour et al., 2016). In C₄ plants most of the CO₂ entering the stomata is carboxylated by phosphoenolpyruvate carboxylase (PEPC), resulting in a lower CO₂ mixing ratio in the mesophyll, which results in a lower back-diffusion flux. The increase in assimilation rate with higher light intensity decreases the c_m∕c_a ratio and thus leads to a lower back-diffusion flux, which explains the decreases in ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ for maize and most clearly for sunflower. A similar trend of increase in ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ with an increase in c_m∕c_a ratio has been reported in previous studies (Gillon and Yakir, 2000b, a; Osborn et al., 2017). For ivy, ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ and ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{obs}}$ do not decrease with an increase in irradiance because the change in assimilation rate with irradiance is small. Thus, c_m will not decrease strongly and the effect on the back diffusion is smaller than the variability in ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ of different leaves of the same plant.

In our experiments, photosynthesis causes an enrichment in the δ¹⁸O of atmospheric CO₂ for both C₃ and C₄ plants, i.e., positive value of ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$. In principle, ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ can also be negative if the δ¹⁸O_m is depleted relative to the ambient CO₂. This is in contrast to ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{13}}\mathrm{C}$, which will always be positive since it is determined by the fractionation due to the PEPC and RuBisCO enzyme activity (Figs. S8 and S9). In general, in our experiments the ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ values are about 5 times larger than δ¹⁸O_a−δ¹⁸O_e, the δ¹⁸O difference between CO₂ entering and leaving the cuvette (Figs. S10 to S12). This is easy to understand from the definition of Δ_A. Taking ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}\mathrm{O}$ as an example, ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}=\frac{\mathit{\zeta }\left({\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{a}}-{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{e}}\right)}{\mathrm{1}+{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{a}}-\mathit{\zeta }\left({\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{a}}-{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{e}}\right)}\approx \left({\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{a}}-{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{e}}\right)$, and in our experiments $\mathit{\zeta }=c_{\mathrm{e}}/\left(c_{\mathrm{e}}-c_{\mathrm{a}}\right)\approx \mathrm{500}/(\mathrm{500}-\mathrm{400})=\mathrm{5}$.

5.2 Discrimination against the Δ¹⁷O of CO₂

The leaf cuvette model includes the isotope fractionations of all the individual processes that have been quantified in dedicated experiments previously (Fig. 1). The good agreement of the model results with the measurements (Fig. 3a) demonstrates that when all these processes are combined in the quantitative description of a gas exchange experiment, they actually result in a correct quantification of the isotope effects associated with photosynthesis. This has already been demonstrated before for ${\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{obs}}$ but has now been confirmed for Δ_AΔ¹⁷O.

Unlike ivy and sunflower, maize does not show a significant change in Δ_AΔ¹⁷O when CO₂ gases with different Δ¹⁷O are supplied to the plant. The C₄ plant maize has a small back-diffusion flux due to its high assimilation rate and low stomatal conductance, leading to a low c_m∕c_a ratio. At low c_m∕c_a ratios, Δ_AΔ¹⁷O is expected to be close to the weighted fractionation due to diffusion through boundary layer and stomata. In general, the effect of diffusion on Δ¹⁷O of atmospheric CO₂ can be expressed as follows:

$$\begin{array}{}\text{(6)}& {\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{Modified}}={\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{a}}+\left({\mathit{\lambda }}_{\mathrm{RL}}-{\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{diff}}\right)\times \ln {\mathit{\alpha }}_{\mathrm{diffusion}},\end{array}$$

where Δ¹⁷O_a is the Δ¹⁷O of the CO₂ surrounding the leaf; Δ¹⁷O_modified is the Δ¹⁷O of the CO₂ modified due to diffusional fractionation; and ${\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{diff}}$, λ_RL, and α_diffusion are the oxygen three-isotope relationships during diffusion from the CO₂−H₂O exchange site to the atmosphere, the reference slope used, and the fractionation against ¹⁸O for CO₂ during diffusion through the stomata. Using the values λ_RL=0.528, ${\mathit{\theta }}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{diff}}=\mathrm{0.509}$ (Young et al., 2002), and α_diffusion=0.9912 (Farquhar and Lloyd, 1993), the effect of diffusional fractionation on the Δ¹⁷O of atmospheric CO₂ is −0.168 ‰ regardless of the anomaly of the CO₂ entering the leaf, and the model results confirm this at low c_m∕c_a ratios (Fig. 5c and d, inset).

At a high c_m∕c_a ratio, Δ¹⁷O_a is dominated by the back-diffusion flux of CO₂ that has equilibrated with water. As a consequence, Δ¹⁷O_a converges to a common value that is independent of the anomaly of the CO₂ entering the cuvette and is determined by the isotopic composition of leaf water. Figure 5 confirms that the end-member is equal to the Δ¹⁷O of CO₂ in equilibrium with leaf water, Δ¹⁷O_m. In fact, when Δ¹⁷O_a=Δ¹⁷O_m, Δ¹⁷O_a does not change with c_m∕c_a, indicating that in this case the Δ¹⁷O of the CO₂ diffusing back from the leaf is the same as the Δ¹⁷O(CO₂) entering the leaf.

${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ is the overall discrimination occurring during the diffusion of ¹²C¹⁸O¹⁶O from the ambient air surrounding the leaf to the CO₂−H₂O exchange site (see Table 2 for the list of variables). In our study ${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ ranges from 5 ‰ to 7.2 ‰, lower than the literature estimate of 7.4 ‰ (Farquhar et al., 1993). ${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ depends on the ratio of stomatal conductance, which is associated with a strong fractionation of 8.8 ‰, to mesophyll conductance with an associated fractionation of only 0.8 ‰. Therefore, the higher the ratio (g_s∕g_m18) the lower the ${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ (Table S2). The difference in ${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ of 2.4 ‰ between the literature value of 7.4 ‰ and the lowest ${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ estimate in this study will introduce an error of only 0.046  ‰ in the Δ¹⁷O value (see Eq. 6). The uncertainty ${\stackrel{\mathrm{‾}}{a}}_{\mathrm{18}}$ has lower influence on the Δ_AΔ¹⁷O of C₃ plants compared to C₄ plants since the diffusional fractionation is less important at the higher c_m∕c_a ratio where C₃ plants operate.

5.3 Global average value of Δ_AΔ¹⁷O and Δ¹⁷O isoflux

We can use the established relationship between Δ_AΔ¹⁷O and Δ¹⁷O_a−Δ¹⁷O_wes for a certain c_m∕c_a ratio to provide a bottom-up estimate for the global effect of photosynthesis on Δ¹⁷O in atmospheric CO₂, based on data obtained in real gas exchange experiments. For this, we use results from a recent modeling study, which provides global average values for CO₂ and leaf water (${\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{CO}}_{\mathrm{2}}\right)=-\mathrm{0.168}$ ‰, ${\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{-\mathrm{leaf}}\right)=-\mathrm{0.067}$ ‰; Koren et al., 2019; Figs. S13 and 14). The Δ¹⁷O(CO₂) values agree well with the limited amount of available measurements (Table 3).

Table 3 Summary of the parameters used for the extrapolation of leaf-scale experiments to the global scale and the results obtained, as well as an overview of available Δ¹⁷O measurements.

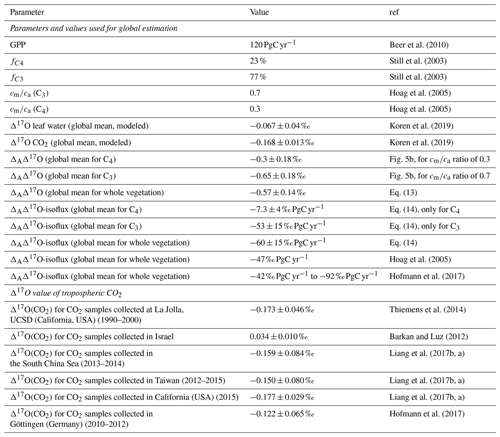
To extrapolate Δ_AΔ¹⁷O determined in the leaf-scale experiments to the global scale, global average c_m∕c_a ratios of 0.7 and 0.3 are used for C₃ and C₄ plants, respectively, similar to previous studies (Hoag et al., 2005; Liang et al., 2017b). From the SIBCASA model results we obtained an annual variability of c_i∕c_a values with a standard deviation of 0.12 and 0.17 for C₄ and C₃ plants, respectively (Fig. S15) (Schaefer et al., 2008; Koren et al., 2019). We use this variability as the upper limit of the error estimate for c_m∕c_a, as shown in the light orange and light pink shaded areas in Fig. 4b. This error is converted to an error in Δ_AΔ¹⁷O using the relation with c_m∕c_a. Based on the linear dependency of Δ_AΔ¹⁷O and Δ¹⁷O_a−Δ¹⁷O_wes, we estimate the Δ_AΔ¹⁷O for tropospheric CO₂ based on the Δ¹⁷O of leaf water and c_m∕c_a ratio. In Fig. 4b, the vertical dashed black line indicates Δ¹⁷O_a−Δ¹⁷O_wes obtained from the 3D global model (Koren et al., 2019). The results of the global estimate and parameters used for the extrapolation of a leaf-scale study to the global scale are summarized in Table 3.

The δ¹⁷O value of atmospheric CO₂ (21.53 ‰) is calculated from the global δ¹⁸O and Δ¹⁷O values (41.5 ‰ and −0.168 ‰, respectively) (Koren et al., 2019). The δ¹⁷O and δ¹⁸O values of global mean leaf water are calculated from the soil water. A global mean δ¹⁸O value of soil water is −8.4 ‰ assuming soil water to be similar to precipitation (Bowen and Revenaugh, 2003; Koren et al., 2019). The δ¹⁷O value of soil water is −4.4 ‰, calculated using Eq. (7) (Luz and Barkan, 2010).

$$\begin{array}{}\text{(7)}& \ln \left({\mathit{\delta }}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{soil}}+\mathrm{1}\right)=\mathrm{0.528}\times \ln \left({\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{soil}}+\mathrm{1}\right)+\mathrm{0.033}\end{array}$$

δ¹⁷O and δ¹⁸O of leaf water are calculated from δ¹⁷O and δ¹⁸O of soil water with fractionation factors of 1.0043 and 1.0084, respectively (Hofmann et al., 2017; Koren et al., 2019). The fractionation factor for δ¹⁷O is calculated using ${\mathit{\alpha }}^{\mathrm{17}}={\left({\mathit{\alpha }}^{\mathrm{18}}\right)}^{\mathrm{trans}}$ with λ_trans=0.516, assuming relative humidity to be 75 % (Landais et al., 2006). The δ¹⁷O and δ¹⁸O values of global mean leaf water are then −0.136 ‰ and −0.131 ‰, respectively. Thus, the difference between global atmospheric CO₂ and leaf water is ${\mathit{\delta }}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{water}}=\mathrm{21.666}$ ‰ and ${\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{water}}=\mathrm{41.631}$ ‰. This yields ${\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{CO}}_{\mathrm{2}}-\mathrm{water}}=-\mathrm{0.101}$ ‰, and this value is indicated as a dashed black line in Fig. 4. The gray shaded area indicates the propagated error using the standard deviation of the relevant parameters in 180×360 grid boxes for 12 months of leaf water and 45×60 grid boxes for 24 months for CO₂ (Koren et al., 2019). In Fig. 4b, the intersection between the vertical dashed black line and the discrimination lines for the representative c_m∕c_a ratios of C₃ and C₄ plants corresponds to the Δ_AΔ¹⁷O value of C₃ and C₄ plants. For C₄ plants ($c_{\mathrm{m}}/c_{\mathrm{a}}=\mathrm{0.3}$) this yields ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}=-\mathrm{0.3}$ ‰ (dashed gray line in Fig. 4b), and for C₃ plants it yields ($c_{\mathrm{m}}/c_{\mathrm{a}}=\mathrm{0.7}$) ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}=-\mathrm{0.65}$ ‰ (dashed black line in Fig. 4b).

Three main factors contribute to the uncertainty of the extrapolated Δ_AΔ¹⁷O value. The first is the measurement error, which contributes 0.25 ‰ (standard error for individual experiments). The second factor is the uncertainty in the difference between Δ¹⁷O of atmospheric CO₂ and leaf water, and we use results from the global model to estimate an error. For Δ¹⁷O of atmospheric CO₂, statistics for all 45×60 grid boxes for 24 months (2012–2013) show a range of −0.218 ‰ to −0.151 ‰, with a mean of −0.168 ‰ and a standard deviation of 0.013 ‰ (Fig. S13). For Δ¹⁷O of the leaf water statistics for all 180×360 grid boxes for 12 months show a range of −0.236 ‰ and −0.027 ‰ (Fig. S14). The mean is −0.067 ‰ with a standard deviation of 0.041 ‰. From the combined errors we estimate the error in (Δ¹⁷O_a−Δ¹⁷O_wes) to be 0.043 ‰. The third uncertainty in the extrapolation of Δ¹⁷O comes from the uncertainty in the c_m∕c_a ratio. For C₃ and C₄ plants, these errors are indicated by the light orange and light blue shadings in Fig. 4b.

Taking these uncertainties into account leads to a mean value of ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}=-\mathrm{0.3}\pm \mathrm{0.18}$ ‰ for C₄ plants and ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}=-\mathrm{0.65}\pm \mathrm{0.18}$ ‰ for C₃ plants. The leaf-scale discrimination against Δ¹⁷O is then extrapolated to global vegetation using these representative values of Δ_AΔ¹⁷O and the relative fractions of photosynthesis by C₄ and C₃ plants, respectively, as follows:

$$\begin{array}{}\text{(8)}& {\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}{\mathrm{O}}_{\mathrm{global}}=f_{{\mathrm{C}}_{\mathrm{4}}}\times {\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{C}}_{\mathrm{4}}}+f_{{\mathrm{C}}_{\mathrm{3}}}\times {\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{C}}_{\mathrm{3}}},\end{array}$$

where $f_{{\mathrm{C}}_{\mathrm{4}}}$ and $f_{{\mathrm{C}}_{\mathrm{3}}}$ are the photosynthesis-weighted global coverage of C₄ and C₃ vegetation. ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{C}}_{\mathrm{4}}}$ and ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{C}}_{\mathrm{3}}}$ quantify the discrimination against Δ¹⁷O by C₄ and C₃ plants, which are calculated using estimated values of c_m∕c_a from a model. Using assimilation-weighted fractions of 23 % for C₄ and 77 % for C₃ vegetation (Still et al., 2003), the global mean value of Δ_AΔ¹⁷O obtained from Eq. (8) is $-\mathrm{0.57}\pm \mathrm{0.14}$ ‰.

Isoflux is the product of isotope composition and gross mass flux of the molecule. In the case of assimilation, the net flux $F_{\mathrm{A}}=F_{\mathrm{AL}}-F_{\mathrm{LA}}$ is multiplied with the discrimination associated with assimilation (Ciais et al., 1997a). F_LA and F_AL are total CO₂ fluxes from leaf to the atmosphere and from atmosphere to leaf, respectively. The global-scale Δ¹⁷O_A isoflux is calculated by multiplying the discrimination with the assimilation flux as follows:

$$\begin{array}{}\text{(9)}& F_{\mathrm{A}}\times {\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}\mathrm{O}=A\times \left(f_{{\mathrm{C}}_{\mathrm{4}}}\times {\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{C}}_{\mathrm{4}}}+f_{{\mathrm{C}}_{\mathrm{3}}}\times {\mathrm{\Delta }}_{\mathrm{A}}^{\mathrm{17}}{\mathrm{O}}_{{\mathrm{C}}_{\mathrm{3}}}\right),\end{array}$$

where $A=\mathrm{0.88}\times \text{GPP}$ is the terrestrial assimilation rate. The factor 0.88 accounts for the fraction of CO₂ released due to autotrophic respiration (Ciais et al., 1997a). The Δ_AΔ¹⁷O isoflux due to photosynthesis is calculated using a GPP value of 120 PgC yr⁻¹ (Beer et al.,  2010) and $A=\mathrm{0.88}\times \text{GPP}$, resulting in an isoflux of $-\mathrm{60}\pm \mathrm{15}$ ‰ PgC yr⁻¹ globally. This is the first global estimate of Δ_AΔ¹⁷O based on direct measurements of the discrimination during assimilation. Our value is in good agreement with previous model estimates. Hofmann et al. (2017) estimated an isoflux ranging from −42 ‰ PgC yr⁻¹ to −92 ‰ PgC yr⁻¹ (converted to a reference line with λ=0.528) using an average c_m∕c_a ratio of 0.7 for both C₄ and C₃ plants and Δ¹⁷O of −0.147 ‰ for atmospheric CO₂. A model-estimated value from Hoag et al. (2005) is −47 ‰ PgC yr⁻¹ (converted to our reference slope of λ=0.528), derived with a more simple model and using Δ¹⁷O of −0.146 ‰ with c_m∕c_a ratio of 0.33 and 0.66 for C₄ and C₃ plants, respectively.

The main uncertainty in the extrapolation of Δ_AΔ¹⁷O from the leaf experiments to the global scale is the uncertainty in the c_m∕c_a ratio. The error from the uncertainty in c_m∕c_a ratio increases when the relative difference in Δ¹⁷O between CO₂ and leaf water increases (Fig. 5b). It is difficult to determine a single representative c_m value for different plants because this value would need to be properly weighted with temperature, irradiance, CO₂ mole fraction, and other environmental factors (Flexas et al., 2008, 2012; Shrestha et al., 2019). Recent developments in laser spectroscopy techniques (McManus et al., 2005; Nelson et al., 2008; Tuzson et al., 2008; Kammer et al., 2011) might enable more and easier measurements of c_m∕c_a both in the laboratory and under field conditions. This could lead to a better understanding of variations in the c_m∕c_a ratio among plant species temporally, spatially, and environmentally.

6 Conclusions

In order to directly quantify the effect of photosynthetic gas exchange on the Δ¹⁷O of atmospheric CO₂, gas exchange experiments were carried out in leaf cuvettes using two C₃ plants (sunflower and ivy) and one C₄ plant (maize) with isotopically normal and slightly anomalous (¹⁷O-enriched) CO₂. Results for ¹⁸O agree with results reported in the literature previously. Our results for Δ¹⁷O confirm that the formalism developed by Farquhar and others for δ¹⁸O is also applicable to the evaluation of Δ¹⁷O. In particular, our experiments confirm that two parameters determine the effect of photosynthesis on CO₂: (1) the Δ¹⁷O difference between the incoming CO₂ and CO₂ in equilibrium with leaf water and (2) the c_m∕c_a ratio, which determines the degree of back-flux of isotopically exchanged CO₂ from the mesophyll to the atmosphere. At low c_m∕c_a ratios, Δ_AΔ¹⁷O is mainly influenced by the diffusional fractionation. Under our experimental conditions, the isotopic effect increased with c_m∕c_a, e.g., Δ_AΔ¹⁷O was −0.3 ‰ and −0.65 ‰ for maize and sunflower with c_m∕c_a ratios of 0.3 and 0.7, respectively. However, experiments with mass independently fractionated CO₂ demonstrate that the results depend strongly on the Δ¹⁷O difference between the incoming CO₂ and CO₂ in equilibrium with leaf water. This is supported by calculations with a leaf cuvette model.

δ¹⁸O is largely affected by kinetic and equilibrium processes between CO₂ and leaf water, and also leaf water isotopic inhomogeneity and dynamics. The Δ¹⁷O variation is much smaller compared to δ¹⁸O and is better defined since conventional biogeochemical processes that modify δ¹⁷O and δ¹⁸O follow a well-defined three-isotope fractionation slope. Results from the leaf exchange experiments were upscaled to the global atmosphere using modeled values for Δ¹⁷O of leaf water and CO₂, which results in ${\mathrm{\Delta }}_{\mathrm{A}}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}=-\mathrm{0.57}\pm \mathrm{0.14}$ ‰ and a value for the Δ¹⁷O isoflux of $-\mathrm{60}\pm \mathrm{15}$ ‰ PgC yr⁻¹. This is the first study that provides such an estimate based on direct leaf chamber measurements, and the results agree with previous Δ¹⁷O calculations. The largest contribution to the uncertainty originates from uncertainty in the c_m∕c_a ratio and the largest contributions to the isoflux come from C₃ plants, which have both a higher share of the total assimilation and higher discrimination. Δ_AΔ¹⁷O is less sensitive to c_m∕c_a ratios at lower values of c_m∕c_a, for instance for C₄ plants such as maize.

Δ¹⁷O of tropospheric CO₂ is controlled by photosynthetic gas exchange, respiration, soil invasion, and stratospheric influx. The stratospheric flux is well established and the effect of photosynthetic gas exchange can now be quantified more precisely. To untangle the contribution of each component to the Δ¹⁷O atmospheric CO₂, we recommend measuring the effects of foliage respiration and soil invasion both in the laboratory and at the ecosystem scale.